| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015437 | |
| Published online | 23 November 2010 | |
Structural and core parameters of the hot B subdwarf KPD 0629-0016 from CoRoT g-mode asteroseismology⋆
1
Laboratoire d’Astrophysique de Toulouse-Tarbes, Université de Toulouse,
CNRS,
14 av. E. Belin,
31400
Toulouse,
France
e-mail: valerie.vangrootel@ast.obs-mip.fr
2
Département de Physique, Université de Montréal,
CP 6128, Succursale Centre-Ville,
Montréal, QC
H3C 3J7,
Canada
3
Steward Observatory, University of Arizona,
933 North Cherry
Avenue, Tucson,
AZ
85721,
USA
Received:
20
July
2010
Accepted:
6
September
2010
Context. The asteroseismic exploitation of long period, g-mode hot B subdwarf pulsators (sdBVs), undermined so far by limitations associated with ground-based observations, has now become possible, thanks to high quality data obtained from space such as those recently gathered with the CoRoT (COnvection, ROtation, and planetary Transits) satellite.
Aims. We propose a detailed seismic analysis of the sdBVs star KPD 0629-0016, the first compact pulsator monitored with CoRoT, using the g-mode pulsations recently uncovered by that space-borne observatory during short run SRa03.
Methods. We use a forward modeling approach on the basis of our latest sdB models, which are now suitable for the accurate computation of the g-mode pulsation properties. The simultaneous match of the independent periods observed in KPD 0629-0016 with those of the models leads objectively to the identification of the pulsation modes and, more importantly, to the determination of the structural and core parameters of the star.
Results. The optimal model we found closely reproduces the 18 observed periods retained in our analysis at a 0.23% level on average. These are identified as low-degree (ℓ = 1 and 2), intermediate-order (k = −9 through −74) g-modes. The structural and core parameters for KPD 0629-0016 are the following (formal fitting errors only): Teff = 26290 ± 530 K, log g = 5.450 ± 0.034, M∗ = 0.471 ± 0.002 M⊙, log (Menv / M∗) = −2.42 ± 0.07, log (1 − Mcore / M∗) = −0.27 ± 0.01, and Xcore(C+O) = 0.41 ± 0.01. We additionally derive an age of 42.6 ± 1.0 Myr after the zero-age extreme horizontal branch, the radius R = 0.214 ± 0.009 R⊙, the luminosity L = 19.7 ± 3.2 L⊙, the absolute magnitude MV = 4.23 ± 0.13, the reddening index E(B − V) = 0.128 ± 0.023, and the distance d = 1190 ± 115 pc.
Conclusions. The advent of high-precision time-series photometry from space with instruments like CoRoT now allows as demonstrated with KPD 0629-0016 the full exploitation of g-modes as deep probes of the internal structure of these stars, in particular for determining the mass of the convective core and its chemical composition.
Key words: stars: oscillations / stars: interiors / subdwarfs / stars: individual: KPD 0629-0016
© ESO, 2010
1. Introduction
The asteroseismic exploitation of long period, g-mode hot B subdwarf pulsators (sdBVs) has been a long sought objective that was undermined, thus far, by the difficulty of obtaining sufficiently precise and continuous time-series data from the ground (see, e.g., Randall et al. 2006). Time-series photometry from space appears to be the only means for gathering well-constrained asteroseismic data for this type of star. The sdBVs stars are found in the cooler (Teff ≲ 30 000 K) and less compact (log g ≲ 5.6) region in the effective temperature-surface gravity plane occupied by hot B subdwarfs. The latter cover the ranges of Teff = 20000−40000 K and log g = 5.0−6.2, and are core-helium burning objects occupying the Extreme Horizontal Branch (EHB). Because the g-modes in hot B subdwarfs propagate mostly in the deep core (Charpinet et al. 2000), it has been hoped ever since their discovery (Green et al. 2003) that the long-period pulsating B subdwarfs would reveal the internal structure of the deepest regions in stars of this type, including the thermonuclear furnace.
 |
Fig. 1 Left panel: model fit (heavy curve) to all the hydrogen and strong helium lines (thin curve) available in our high S / N, low-resolution optical spectrum of KPD 0629-0016. The fit was done using a 3D grid of NLTE synthetic spectra (Teff, log g, log N(He)/N(H)), in which the abundances of C, N, O, S, Si, and Fe were held fixed at amounts consistent with Blanchette et al. (2008). Right panel: similar, but for our intermediate-resolution MMT spectrum. |
KPD 0629-0016 is one of the rare sdB stars identified in the CoRoT field with a confirmed pulsational nature (Koen & Green 2007). It was consequently selected as the primary target for the third short run in the Galactic anticenter direction (SRa03) scheduled in March 2010. The results of the ~24 day long outstanding CoRoT photometric observations are presented in Charpinet et al. (2010). A total of 17 gravity-type pulsations are clearly identified in the Fourier spectrum, with periods ranging from 2600 to 10 500 s and amplitudes between 0.25% and 0.024% of the mean star brightness (43.2 to 4.2 times the local noise level). In addition, seven possible peaks emerge with amplitudes in the range 0.020% and 0.024% (3.6−4.0 times the local noise). This CoRoT observation provides more modes than are typically detected for sdB stars from the ground and, more importantly, the frequencies of all uncovered g-modes are reliably measured. This paves the way for a detailed seismic analysis of KPD 0629-0016. In this article, we report on the results of such an analysis, only the second one exploiting g-modes in hot B subdwarfs after the very recent study of Van Grootel et al. (2010) on a similar object.
2. Atmospheric parameters from spectroscopy
Independent spectroscopic estimates for Teff and log g are essential constraints for lifting degeneracies encountered in seismic analyses of sdB pulsators (Charpinet et al. 2005). As part of a long-term program to characterize hot B subdwarfs in general, we had gathered a first spectrum of KPD 0629-0016 on 2002 September 26 using the Multiple Mirror Telescope on Mount Hopkins, Arizona. This spectrum, obtained with a total exposure time of 1000 s covers the wavelength range from ~4000 to ~5000 Å with a mean resolution of 1.05 Å and S / N ~ 75. A mean spectrum was also built from eight low resolution (9.1 Å) spectra obtained with the Steward Observatory 2.3 m Bok Telescope from 2002 October 7 to 2003 November 30. This mean spectrum shows a high sensitivity (S / N ~ 310) and covers the spectral range from ~3600 to ~6900 Å. While the Bok mean spectrum is a true time-averaged measurement, this is not the case for the MMT data. Nevertheless, the amplitudes of the oscillations are so small (0.25% for the largest amplitude mode; Charpinet et al. 2010) that the MMT spectrum can still be considered as a useful indicator of the mean effective temperature and surface gravity.
We analyzed these two spectra with the help of new grids of NLTE model atmospheres and synthetic spectra developed for studying hot subdwarfs of the B and O types. These models were constructed with the public codes TLUSTY and SYNSPEC. In this application, we chose a representative heavy-element composition inspired from Blanchette et al. (2008). These authors used FUSE spectroscopy and suitable NLTE model spectra to determine the abundances of several astrophysically important elements in the atmospheres of five typical long-period pulsating sdB stars very similar to KPD 0629-0016. On the basis of their results, we assumed atmospheres containing C (1/10 solar), N (solar), O (1/10 solar), Si (1/10 solar), S (solar), and Fe (solar).
Figure 1 shows the best fits we have obtained. Weighted means of the two sets of atmospheric parameters according to their formal errors lead to the following estimates for KPD 0629-0016: Teff = 26484 ± 196 K, log g = 5.473 ± 0.027, and log N(He)/N(H) = −2.789 ± 0.041. The quoted uncertainties are only formal errors of the fits and do not include systematic effects, which remain difficult to evaluate. These values of the atmospheric parameters have been used to guide the search for a seismic solution within a region of parameter space consistent with a 3σ uncertainty range in effective temperature and surface gravity. To provide a measure of the effects of metals, we have refitted our two spectra using equivalent models with no metals. The weighted means now come out as Teff = 26 973 ± 251 K, log g = 5.494 ± 0.030, and log N(He)/N(H) = −2.758 ± 0.044, indicating that the presence of metals (at least in the amounts assumed) is not a critical issue in the determination of the atmospheric parameters of KPD 0629-0016.
3. Asteroseismic analysis
 |
Fig. 2 Left panel: slice of the S2 function (in logarithmic units) along the M∗ − log q(H) plane with the parameters log q(core) and Xcore(C+O) set to the optimal values obtained for the best-fit seismic model. Right panel: slice of the S2 function (in log) along the log q(core) – Xcore(C+O) plane with the parameters M∗ and log q(H) set to their optimal values. White contours show regions where the period fits have S2 values within the 1σ, 2σ, and 3σ confidence level relative to the best-fit solution. |
3.1. Models and method
The forward modeling approach developed to perform objective asteroseismic studies of sdB pulsators has been described in detail in Charpinet et al. (2005, 2008). The basic principle is to fit simultaneously all observed pulsation periods with theoretical ones calculated from sdB models, in order to minimize in parameter space a merit function defined by 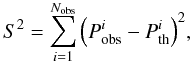 (1)where Nobs is the number of observed periods and
(1)where Nobs is the number of observed periods and 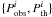 are the associated pairs of observed/computed periods. Efficient optimization codes have been developed to explore the vast model parameter space and find the minima of the merit function S2, which constitute the potential asteroseismic solutions. The results of this procedure are the mode identification and, more importantly, the structural parameters of the star.
are the associated pairs of observed/computed periods. Efficient optimization codes have been developed to explore the vast model parameter space and find the minima of the merit function S2, which constitute the potential asteroseismic solutions. The results of this procedure are the mode identification and, more importantly, the structural parameters of the star.
In order to carry out quantitative seismology of g-mode pulsators, we developed “third-generation” (3G) models, suitable for the accurate evaluation of the g-mode pulsation periods. These are complete stellar structures in thermal equilibrium that include a detailed description of the central regions. Details about our 3G models are given in Brassard & Fontaine (2008, 2009). The input parameters needed to characterize a 3G model are (1) the total stellar mass M∗, (2) the fractional mass of the outer hydrogen-rich envelope log (Menv / M∗), (3) the fractional mass of the mixed convective core log (1 − Mcore / M∗), and (4) the chemical composition of the core (under the constraint X(He) + X(C) + X(O) = 1). These static parameterized structures offer much needed flexibility over evolutionary models for thoroughly exploring parameter space.
The effective temperature Teff and surface gravity log g are computed a posteriori for a given 3G model. We then incorporate the atmospheric parameters determined by spectroscopy as external constraints in the optimization procedure for the search of a best-fit model. Only those models that have atmospheric parameter values within 3σ of the spectroscopic estimates are considered acceptable, thus ensuring consistency with spectroscopy. In the specific case of KPD 0629-0016, acceptable solutions have to fall in the ranges of parameters defined by Teff = 26484 ± 588 K and log g = 5.473 ± 0.123. Note that there is no guarantee, a priori, that a good period match exists within these constraints.
Mode identification and details of the period fit obtained from the optimal model.
3.2. Search for the optimal model
The present seismic analysis is based on the frequencies uncovered by Charpinet et al. (2010) and presented in their Table 1. We selected the frequencies with amplitudes above or equal to 4 times the local noise level. Two out of these 20 pulsations, namely f10 and u1, are very close to the higher amplitude peaks f1 and f16 and were consequently left aside. It is not clear at this stage if these close frequencies are associated with components of multiplets split by slow rotation (which is the usual case for single sdB stars) or with residual structure from the prewhitening of a dominant frequency whose amplitude and/or phase experienced significant changes during the run. This is not critical for the present analysis and we decided to ignore them, leaving 18 pulsation modes that can be safely assumed to be independent, while still providing enough modes to tightly constrain the asteroseismic solution. Finally, the additional pulsation modes u3 to u6 (with amplitudes between 3.6 and 3.8 times the local noise) are neglected in the asteroseismic analysis that follows. We will discuss below how these additional frequencies may be interpreted and compared to the theoretical periods of the optimal model solution uncovered.
The search for best-fit solutions was carried out in a domain defined by 0.30 ≤ M∗ / M⊙ ≤ 0.70, −5.0 ≤ log q(H) ≡ log (Menv / M∗) ≤ −1.8, −0.45 ≤ log q(core) ≡ log (1 − Mcore / M∗) ≤ −0.10 and 0 ≤ Xcore(C+O) ≤ 0.99, where Xcore(C+O) is the fractional part (in mass) of carbon and oxygen in the convective core1. The ranges considered for log q(H) and M∗ rely on predictions from various hot subdwarf formation scenarios (see Han et al. 2002, 2003), whereas the limits on the size of the core are loosely inspired by horizontal branch stellar evolutionary calculations (Dorman et al. 1993). We considered all modes of degrees ℓ = 1 and 2 in the 2500−10 650 s period range in order to match the 18 pulsation periods retained for our analysis. These limits on the degree ℓ correspond to the minimum value that can fully explain the observed mode density. No other assumption on the mode identification has been imposed.
The optimization code spotted one clear family of solutions with a minimum value of S2 corresponding to the following model: M∗ = 0.4711 M⊙, log q(H) = −2.424, log q(core) = −0.269 and Xcore(C+O) = 0.407. The computed atmospheric parameters for this model are Teff = 26290 K and log g = 5.450, in excellent agreement with the spectroscopic estimates, i.e, within the 1σ averaged uncertainties (see Sect. 2). The maps shown in Fig. 2 illustrate the behavior of the S2 function in the vicinity of the best-fit seismic solution. In both panels, the merit function S2 incorporates the spectroscopic constraints on atmospheric parameters, namely, an exponential correction factor multiplies the merit function if the model effective temperature and surface gravity are outside the averaged 3σ spectroscopic uncertainties. This degrades in effect the S2 value of the model, and corresponds to regions in red in Fig. 2.
3.3. Period fit and mode identification
 |
Fig. 3 Distribution of the 18 observed periods of KPD 0629-0016 compared to the ℓ = 1 and ℓ = 2 g-mode theoretical pulsation spectrum of the optimal model. The radial order k of the computed modes is indicated for each series of degree ℓ. |
The details on the fit of the observed periods Pobs to the theoretical values Pth are given in Table 1. The table also lists along with the mode identification (degree ℓ and radial order k) the logarithm of the kinetic energy log E and the dimensionless Ledoux coefficient Ckl. The optimal model isolated for KPD 0629-0016 can account for the 18 observed pulsations to within 0.23%, which corresponds to an averaged absolute dispersion of 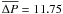 s and
s and 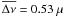 Hz. The standard deviations on these quantities are 7.67 s and 0.41 μHz respectively. This excellent agreement, graphically represented in Fig. 3, is comparable to the best results obtained on p-mode sdB pulsators, and is equivalent to the fit quality achieved for the g-mode pulsator KPD 1943+4058 (Van Grootel et al. 2010). The 18 observed periods retained in our analysis are identified as low-degree (ℓ = 1 and 2), intermediate-order (k = −9 through −74) g-modes.
Hz. The standard deviations on these quantities are 7.67 s and 0.41 μHz respectively. This excellent agreement, graphically represented in Fig. 3, is comparable to the best results obtained on p-mode sdB pulsators, and is equivalent to the fit quality achieved for the g-mode pulsator KPD 1943+4058 (Van Grootel et al. 2010). The 18 observed periods retained in our analysis are identified as low-degree (ℓ = 1 and 2), intermediate-order (k = −9 through −74) g-modes.
The presence of excited pulsation modes in sdB stars is understood by the action of a κ-effect associated with an opacity bump caused by partial ionization of heavy metals – especially iron – that are locally enhanced by radiative levitation at work in the envelope (Charpinet et al. 2001; Fontaine et al. 2003). Although our current models fairly well match the instability strip observed for the short-period p-mode pulsators, there is a well known discrepancy for the g-mode pulsators that remains to be solved (Charpinet et al. 2007). Beyond iron, the importance of nickel for the opacity profiles, as well as the opacity sources themselves (OPAL vs. OP), have been underlined by Jeffery & Saio (2006, 2007; see also Hu et al. 2009). It is likely that the radiative levitation of at least nickel, in addition to iron, has to be included in our next generation of sdB models (which we currently work on) in order to evaluate more accurately the stability of the modes and reconcile the theoretical and observed g-mode instability domain.
It is interesting to see how the additional frequencies may be compared to the theoretical periods of the seismic model. The pulsation modes u3, u4 and u6 (with amplitudes between 3.6 and 3.8 times the local noise) can find a corresponding mode in the ℓ = 1 and ℓ = 2 series without significantly degrading the fit (see details in Table 1). The left-aside f10, u1 and u5 frequencies could possibly be associated with the (ℓ,k) = (2, −34), (2, −60) and (4, −45) modes respectively, but their origins are uncertain given their proximity to higher amplitude peaks. Better resolution data would definitely provide more information about them.
3.4. Structural and core parameters
Table 2 summarizes the properties of KPD 0629-0016 inferred from the spectroscopic and seismic analyses. The quoted 1σ uncertainties are the formal errors of the fit and do not include external and systematic errors. In particular, they assume perfect input physics for the models. These uncertainties are represented in Fig. 2 by white dashed contours (1σ, 2σ and 3σ limits, assuming that the S2 has a chi-squared distribution) around the solution indicated by a yellow mark. The uncertainties on the derived atmospheric parameters Teff and log g are obtained from the uncertainties of the primary quantities. A set of secondary parameters (stellar radius R, luminosity L, absolute magnitude MV, reddening index E(B − V), and distance from Earth d) is also derived on the basis of primary parameters.
The structural parameters inferred for KPD 0629-0016 indicate a “typical” sdB star, whose stellar mass and envelope thickness are close to the expected values for hot B subdwarfs (Dorman et al. 1993a; Han et al. 2002, 2003). The most interesting feature is the determination of the helium-burning core properties, including size and composition, thanks to the sensitivity of g-modes to the deep regions of the star. The mixed convective core (whose boundary is defined by the chemical transition He/C/O − He) includes 46% of the total mass of the star, after it has burned a little over 40% of its helium nuclear fuel. This size is slightly above the expectations based on evolutionary tracks with pure convective core defined by the Schwarzschild criterion (Dorman et al. 1993a). Van Grootel et al. (2010) also found the same in a different star. This may be an indication of the presence of overshooting and/or semi-convection, or any process that is able to carry out the (C+O) material beyond the convection zone itself. One of our long-term goals is to test the convection-related theories in hot B subdwarfs (Dorman et al. 1993b; Straniero et al. 2003). Finally, a comparison with an evolutionary sequence built on the same input physics for a star with similar structural and core parameters (including a moderate mechanical overshooting) indicates an age of 42.6 ± 1.0 Myr after the zero-age extreme horizontal branch.
Structural and core parameters inferred for KPD 0629-0016.
4. Conclusion
This article reported on the detailed asteroseismic analysis of the long-period, g-mode hot B subdwarf pulsator KPD 0629-0016. This has been made possible thanks to the outstanding light curve obtained by CoRoT in March 2010. For only the second time (see Van Grootel et al. 2010), a successful seismic analysis of a sdBVs star has been carried out. In both cases, space observations have proven essential for the exploitation of g-mode seismology for this type of star. This new era in hot B subdwarfs seismology permits us the investigation of helium-burning cores – including their size and composition – along with the determination of structural parameters of the star. Our results suggest that overshooting and semiconvection are important processes that shape the helium-burning cores. Since all helium-burning cores share very similar characteristics, pulsating B subdwarfs are excellent probes of the interior properties of horizontal branch stars in general, an intermediate and underrated stage of stellar evolution.
Acknowledgments
V.V.G. acknowledges grant support from the Centre National d’Études Spatiales (CNES, France). V.V.G. and S.C. thank the Programme National de Physique Stellaire (PNPS, CNRS/INSU, France) for financial support. Numerical experiments presented in this paper were carried out using the Grid’5000 experimental testbed, an initiative from the French Ministry of Research through the ACI GRID incentive action, INRIA, CNRS and RENATER, and other contributing partners (see http://www.grid5000.fr). G.F. acknowledges the support of the NSERC of Canada and the contribution of the Canada Research Chair Program.
References
- Blanchette, J.-P., Chayer, P., Wesemael, F. et al. 2008, ApJ, 678, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., & Fontaine, G. 2008, ASPC, 392, 261 [Google Scholar]
- Brassard, P., & Fontaine, G. 2009, JPhCS, 172, 2016 [NASA ADS] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 2000, ApJS, 131, 223 [Google Scholar]
- Charpinet, S., Fontaine, G., & Brassard, P. 2001, PASP, 113, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., & Brassard, P., et al. 2005, A&A, 437, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Fontaine, G., & Brassard, P., et al. 2007, CoAst, 150, 241 [Google Scholar]
- Charpinet, S., van Grootel, V., Reese, D., et al. 2008, A&A, 489, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Green, E. M., Baglin, A., et al. 2010, A&A, 516, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorman B., & Rood, R. T. 1993b, ApJ, 409, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, B., Rood, R. T. & O’Connell, R. W. 1993a, ApJ, 419, 596 [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2003, ApJ, 597, 518 [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P., et al. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P., et al. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, H., Nelemans, G., Aerts, C., & Dupret, M. A. 2009, A&A, 508, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffery, C. S., & Saio, H. 2006, MNRAS, 372, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, C. S., & Saio, H. 2007, MNRAS, 378, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., & Green, E. M. 2007, MNRAS, 377, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, S. K., Green, E. M., Fontaine, G. et al. 2006, ApJ, 645, 1484 [NASA ADS] [Google Scholar]
- Straniero, O., Dominguez, I., Imbriani, G., & Piersanti, L. 2003, ApJ, 583, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Van Grootel, V., Charpinet, S., Fontaine, G., et al. 2010, ApJ, 718, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Mode identification and details of the period fit obtained from the optimal model.
All Figures
 |
Fig. 1 Left panel: model fit (heavy curve) to all the hydrogen and strong helium lines (thin curve) available in our high S / N, low-resolution optical spectrum of KPD 0629-0016. The fit was done using a 3D grid of NLTE synthetic spectra (Teff, log g, log N(He)/N(H)), in which the abundances of C, N, O, S, Si, and Fe were held fixed at amounts consistent with Blanchette et al. (2008). Right panel: similar, but for our intermediate-resolution MMT spectrum. |
| In the text | |
 |
Fig. 2 Left panel: slice of the S2 function (in logarithmic units) along the M∗ − log q(H) plane with the parameters log q(core) and Xcore(C+O) set to the optimal values obtained for the best-fit seismic model. Right panel: slice of the S2 function (in log) along the log q(core) – Xcore(C+O) plane with the parameters M∗ and log q(H) set to their optimal values. White contours show regions where the period fits have S2 values within the 1σ, 2σ, and 3σ confidence level relative to the best-fit solution. |
| In the text | |
 |
Fig. 3 Distribution of the 18 observed periods of KPD 0629-0016 compared to the ℓ = 1 and ℓ = 2 g-mode theoretical pulsation spectrum of the optimal model. The radial order k of the computed modes is indicated for each series of degree ℓ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


