EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 524 (December 2010) A&A, 524 (2010) A54 Full HTML
Free Access
Issue
A&A
Volume 524, December 2010
Article Number A54
Number of page(s) 5
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201015426
Published online 23 November 2010

© ESO, 2010

1. Introduction

Eta Carinae is a particularly rich source of forbidden [Fe II] emission lines, but they are also observed in the spectra of many other stellar objects. A detailed study of these spectra requires accurate atomic data, and particularly transition rates. The transitions discussed in this Note have been observed in η Car (Gull et al. 1999), though they were first identified by Merrill (1928).

Using a laser probing technique (LPT) Gurell et al. (2009) recently measured the lifetimes of two metastable states of Fe II, namely those of a 4G5.5 and b 4D0.5 belonging to 3d6(3G)4s and 3d6(3D)4s configurations respectively. They also concluded that lifetime of b 2H5.5 measured previously by Hartman et al. (2003) was found to be only five times greater than that of its neighbour a 4G5.5 whereas in earlier theoretical results this factor ranged from 7.4 (Quinet et al. 1996) through 11.9 (Garstang 1962). In the present research note we explain this discrepancy in terms of the level mixing of the two neighbouring levels separated by 741 cm-1. We also show, through our large scale CI calculation, that the apparent agreement of lifetimes of a 4G5.5 between the new measurement (Gurell et al. 2009) and previous calculations may be better than the accuracy of either result.

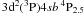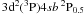Regarding the experimental method, it was demonstrated by Palmeri et al. (2008) that at least some LPT measurements contained errors as large as 50% or more, even without the experimental uncertainties. This was shown (Palmeri et al. 2008) for the lifetimes measurements of $3{\rm d}^2(^3{\rm P})4s b\,^4{\rm P}_{2.5}$ and $3{\rm d}^2(^3{\rm P})4s b\,^2{\rm P}_{0.5}$ levels of Ti II. For both these levels the calculated lifetimes are shown to be closer to the corrected measurement of Palmeri et al. (2008) based on an innovative idea of Royen et al. (2007) which avoids the repopulation effects. Additionally, it is also well known that within the storage ring, particle collisions sometimes impact negatively on the measured lifetimes: collisional de-excitation leads to quenching, yielding lifetimes that appeared shorter than pure radiative lifetimes.

2. Theoretical method

In the present work we have used the CIV3 code (Hibbert 1975; Hibbert et al. 1991) to compute M 1 and E 2 [Fe II] transitions between all levels of 3d7, 3d64s and 3d54s2 configurations. Here we report on a few of them which have attracted observational and laboratory interest. We have used almost the same set of optimised orbitals generated in recent calculations from our group (Corrégé & Hibbert 2005, 2006). However, we have made one change: in order to get better ab initio energy differences for the 3d7 levels we used the Hartree-Fock (HF) 3d function given by Clementi and Roetti (1974) for 3d74F instead of their 3d of the 3d64s ground configuration chosen in previous calculations (Corrégé & Hibbert 2005, 2006).

The choice of configuration state functions (CSFs) is made in two steps: (a) initially the 3s and 3p subshells are kept closed and up to two promotions are allowed from the valence subshells to 4s, 4p, 4d, 4f, 5s, 5p, 5d, 6s, 6p, 6d, 7s and 7p orbitals, with all possible angular momentum couplings. LS energies of all the states of interest belonging to all possible symmetries are calculated. It is found that many of these CSFs produce negligibly small components (with an absolute value smaller than 0.001) in all the relevant eigenvectors of a given LS symmetry. We therefore deleted them for subsequent calculations; (b) we then allowed selective one and two promotions from 3s and 3p subshells, just to 3d and 4l subshells. This introduces 15 core replacement configurations: 3s3p63d8, 3p63d9, 3s3p63d74s, 3s3p63d74d, 3p63d74s2, 3p63d84s, 3s23p43d9, 3s23p43d74s2, 3s23p43d84s, 3s23p43d74p2, 3s23p53d74f, 3s23p43d64s4p2, 3s23p53d64s4f, 3s23p43d54s24p2 and 3s23p53d54s24f. The CSFs generated from these configurations were added to the list of reduced CSFs in step (a) for each of the symmetries. The relativistic effects are included via the Breit-Pauli approximation: the operators used are the mass correction and Darwin terms, plus a modified spin-orbit interaction which reproduces almost exactly the values of the matrix elements of the full spin-orbit plus spin-other-orbit operators. We then used these sets of CSFs and the above listed Breit-Pauli operators to create the LSJ Hamiltonian matrix, with all possible LS symmetries combined for each of the even J values (0.5–6.5). The total number of CSFs used for each of the J values are follows:

J 0.5 1.5 2.5 3.5 4.5 5.5 6.5
CSFs 8339 12915 16145 15313 11589 6024 2167

The Hamiltonian matrix for each of the J values was then diagonalised to obtain the ab initio energies and eigenvectors for the required levels. The excitation energies of these levels relative to the ground state, 3d6(5D)4s 6D4.5, are in general higher than the corresponding experimental energies (Ralchenko et al. 2008) by between a few tens even up to a few thousand cm-1. Using our fine-tuning technique whereby we make adjustments to the diagonal elements of the Hamiltonian matrix, we were able to bring our calculated energies very close to those of experimental energies. These adjustments to the Hamiltonian matrix give rise to the corresponding changes to the eigenvector compositions.

In the present calculation we have carefully studied the level mixing of the two neighbouring levels of a 4G5.5 and b 2H5.5 separated by 741.397 cm-1 and arranged them in the format M(N) where M is the percentage composition of the leading level and N is the next leading percentage composition as shown in Table 1.

It may be seen that the ab initio value of the crucial energy separation of the strongly interacting levels is in error by only 47 cm-1 and the fine-tuned separation is almost exact. The calculations “A” and “B” are produced by changing only the fine-tuning correction of the b 2H5.5 level, keeping the a 4G5.5 level energy unchanged. Our aim in undertaking these calculations is simply to show that a relatively small change in the calculated energy separation of the two levels leads to substantial changes in the mixing of the two levels. It is clear that as the energy gap between the two levels increases, both the levels become purer and mixing between them becomes weaker.

Table 1

Mixing coefficients of two neighbouring levels a 4G5.5 and b 2H5.5 in four different calculations.

Table 2

Dominant A-values (in s-1) contributing to the lifetime calculation of 3d6(3H)4s b 2H5.5.

Table 3

Dominant A-values (in s-1) contributing to the lifetime calculation of 3d6(3G)4s a 4G5.5.

3. Results

In the present research note our primary aim is to consider the ratio of the lifetimes of these two levels. The SUPERSTRUCTURE (SST) and Cowan (HFR) calculations of Quinet et al. (1996) predicted a lifetime ratio of between 8.5 and 7.4 respectively, with Garstang (1962) giving almost 12, whereas the experimental ratio is only 5. We present in Table 2 all the transition probabilities contributing to the lifetimes of b 2H5.5, with corresponding results for a 4G5.5 displayed in Table 3, for the three cited calculations as well as our own fine-tuned results. We also show some results of the “A” and “B” calculations, but only for the most significant transitions. It is interesting to note from Table 2 that the HFR results of Quinet et al. (1996) agree quite closely with our ab initio calculations. For the strongest of the transitions, those involving a 4F, the SST results are lower than the HFR results, although Quinet et al. recommend the SST results. We note though that the fine-tuning process substantially changes the A-values, because of the increased component of the 4G in the 2H wave function even though, as shown in Table 1, the corrections are quite small. We note that our calculation A (12% mixing) still gives values similar to the ab initio results, while calculation B (10% mixing) leads to values approaching the SST result of Quinet et al. (1996). A similar pattern emerges for the a 4F3.5 → b 2H5.5 transition. 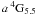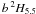This indicates that the level mixings between $a\,^4{\rm G}_{5.5}$ and $b\,^2H_{5.5}$ in the SST and HFR calculations of Quinet et al. (1996) were possibly somewhat similar to those of our ab initio, or even to the “A” and “B”, calculations. Two other significant transitions in this Table involve a 2G4.5 and a 4H4.5, and also show a similar equivalence of our ab initio results and HFR results of Quinet et al. (1996). However, our fine tuned results for the former are about 27% lower and for the latter about 50% higher than corresponding HFR results.

The corresponding results for the transitions with a 4G5.5 as the upper level are shown in Table 3. This time, our A-values are much lower than those of previous authors. Again these are affected by variation in the mixing between the two upper levels, though proportionally not as much as for the transitions in Table 2, essentially because the 4G component is already at 76% in our calculation. Clearly, as that component increases, with corresponding decrease in the mixing, as in calculations “A” or “B”, the A-value also slowly increases.

In Table 4 we compare our calculated lifetimes of a number of levels with values obtained by others. We have selected levels for which experimental measurements have been obtained by the same group, based at Lund, but at various times. We note firstly that our value of 3.7 s for the lifetime of b 2H5.5 is very close to the experimental value of 3.8 s and is the only calculated result which lies inside the experimental error bars. By contrast, our result for a 4G5.5 lies outside the rather wider experimental error bars. We discuss this further in Sect. 4.3.

Table 4

Lifetimes τ(s) of six metastable levels.

4. Discussion

In view of the disparity amongst the calculations, and between them and experiment, it is desirable that some critical discussion of accuracy is undertaken. Let us begin with our own work.

4.1. The present calculations

For the M1 transitions shown in Tables 2 and 3, there is quite close agreement amongst the calculations. However, the main contributions to the J = 5.5 lifetimes are E2 transitions, principally those with a 4FJ as the lower level. For this discussion we will focus on the case of J = 4.5. There are several potential sources of error.

Firstly, we remark that while the principal mixing is between the upper levels – 3d64s 4   G5.5 and 3d64s 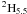$^2{\rm H}_{5.5}$ – some other non-negligible mixing does arise, in the sense of contributing significantly to the A-values of the two transitions under discussion. Specifically, 3d74F4.5 mixes with 3d64s 2G4.5 and the two upper states mix also with 3d7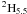$^2{\rm H}_{5.5}$ and 3d64s 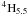$^4{\rm H}_{5.5}$. We find that the optimal 4s function is almost independent of the LS term, but the 3d function changes significantly depending on the occupancy of the 3d subshell. That is, the 3d function of 3d7 states, while being similar from one to another, is quite different from that of the 3d64s states, and different again from that of the 3d54s2 states. In addition to the core orbitals of 1s, 2s, 2p, 3s and 3p, our calculations have included four d-functions to allow for this variation, and four s-functions to describe any variation in the 4s function from state to state. However, a more accurate set of results might be obtained if we had used ‘non-orthogonal’ orbitals, in which particularly the different 3d functions were included explicitly in the calculations.

Secondly, our calculations have involved rather extensive CI using these orbitals as well as four additional p-functions plus 4f, and allowing all single and double replacements from the 3d and 4s subshells in each of 3d7, 3d64s and 3d54s2 to any of these orbitals. Furthermore, as noted in Sect. 2, we include the main correlation effects in the 3s and 3p subshells. In this way, we account for the term-dependency of the valence electrons and a substantial amount of electron correlation in all the states under investigation. This represents by far the most extensive ab initio treatment of electron correlation undertaken to date. We believe that the source of error noted in the previous paragraph will be largely overcome by the extensive nature of this calculation. In addition, final refinements using our “fine-tuning” process ensures good agreement between our calculated energies and the corresponding experimental values. But this again is a potential source of error. While experience in the past has led us to believe that this process is capable of replicating closely the effect of the addition of (many) more CSFs, it is nonetheless not quite as accurate as actually adding in those CSFs. To check this, we have undertaken some very simple calculations, involving only a few CSFs, followed by fine-tuning, and we found that the level of CI mixing between the important terms was quite close to the large-scale calculations. So we think that this potential source of error is also small.

Thirdly, we have represented relativistic effects by using the Breit-Pauli operators. This is in itself a further approximation and therefore source of error, but for Fe II, this approximation should again have only a very small influence on the results. Much more significant is, we believe, our omission of the spin-spin term and particularly the replacement of the spin-other-orbit term by a modified spin-orbit term. The parameters were chosen so that this modified operator gave almost identical matrix elements between key CSFs to those of the full spin-orbit and spin-other-orbit operators combined. And in a calculation actually including all the operators instead, but with rather fewer CSFs, we found that the calculated energies differed by less than 15 cm-1 for the J = 4.5 levels and 25 cm-1 for the J = 5.5 levels. This must be seen in the context of correlation energies obtained in our calculation of the order of 40 000 cm-1. But the problem we found is that the off-diagonal Hamiltonian matrix element between 3d64s 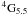$^4{\rm G}_{5.5}$ and 3d64s 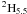$^2{\rm H}_{5.5}$ reduced by about 15 cm-1, which is about 6% of its value, and so the mixing coefficient is reduced by this amount too. This suggests that the A-value of the transition between a 4F4.5 and 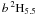$b\,^2{\rm H}_{5.5}$ may be a little too high, even by up to 15% (because of the contributions from other LSJ symmetries), and the A-value of the other transition may be too low by 4–5%.

Fourthly, the overall magnitude of the A-values is governed by the square of the radial quadrupole integrals 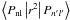$\left \langle P_{\rm nl} \left | r^2 \right | P_{n^{\prime}l^{\prime}} \right \rangle $. The integral involved in the dominant contributions to the A-values has nl=3d and n′l′ = 4s. It is therefore natural that the 3d should be that of the 3d74F4.5 and that happens to be the choice we made for the 3d function. It is also the choice made by Garstang (1962) and our radial integrals agree very closely with his. Smaller contributions to the A-values involve n′l′ = 3d, and for these, our choice of 3d is not the most appropriate. But we believe that our additional d-functions make adequate allowance for this, and in any case those contributions are fairly small.

4.2. Other calculations

In the early work by Garstang (1962), Hamiltonian matrix elements were expressed in terms of a number of electrostatic and spin-orbit parameters, separately for each of 3d7, 3d64s and 3d54s2, together with other correction factors, and CI between these configurations was incorporated. In calculating the A-values, the radial integrals chosen depended on which 3d function was the most relevant to each transition. Thus, for the two transitions discussed here, he used the 3d function of the 3d7 states, as we also have done. The main difference between the outcomes of our calculation and his is the calculated energy separations of the two upper states. Garstang obtained a difference of 1128 cm-1. This is considerably larger than the experimental value or even our ab initio value, shown in Table 1. Therefore the mixing of the two upper levels in Garstang’s calculation will be much weaker than in ours and leads to the much smaller A-value shown in the first line of Table 2. The first transition in Table 3 is consequentially larger than our value, but the sum of the two A-values (just less than 1.0 s-1) is similar in the two calculations, as might be expected given the use of the same 3d function in the quadrupole radial integral.

The sum of the two A-values for the HFR calculation of Quinet et al. (1996) is rather larger, at 1.2 s-1, with a substantially larger value for the A-value of the a 4F–a 4G transition, when compared with our result, and a lower value for a 4F–b 2H. In this calculation, the electrostatic radial integrals are used as parameters fitted to experimental energies, with (as in Garstang’s work) different values for each of 3d7, 3d64s and 3d54s2. These fitted values are 15–20% lower than ab initio HF values, as is common in such calculations, but it is not clear if a similar scaling is applied to the quadrupole radial integral. Certainly, their value is consistent with a rather larger value for the quadrupole radial integral than we have obtained.

The SST method is closer in concept to our own, with substantial CI and the use of term energy corrections (TEC) which is akin to our fine-tuning process. The SST results of Quinet et al. (1996) lie below their HFR values for both transitions, but the low A-value of a 4F–b 2H suggests a much weaker mixing of the upper levels than we obtain. We note that the TECs for the two upper states are rather different, suggesting that their ab initio energies for these two levels are much further apart (1148 cm-1, close to Garstang’s value) than our ab initio values or the experimental difference (see Table 1). The much more extensive CI in our calculation is a factor in our reaching such an improvement in the energy separation of the two upper states. Quinet et al. do include three d-functions in their calculation, though the scaling parameters of the model potentials used to obtain these functions are optimised so as to minimise the sum of 24 term energies, so inevitably some compromise is introduced, perhaps also in the size of the quadrupole radial integral. We remark that in our calculation, a very simple but fined-tuned CI did give an A-value of around 0.1 s-1 for the a 4F4.5–b 2H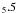${_5.5}$ transition but the additional CSFs introduced to account for the bulk of electron correlation omitted in the simple calculation each contributed small amounts so that the A-value was raised to 0.16 s-1.

4.3. Comparison with experimental results

The experimental values of the lifetimes of the upper levels (Gurell et al. 2009; Hartman et al. 2003), shown in Table 4, suggest A-values of around 1.0 s-1 for a 4F – a 4G and around 0.15 s-1 for a 4F – b 2H. The latter is in keeping with our result, but the former is around 25% larger. However, we note that the error bars for the lifetime of a 4G are quite broad and the upper edge of the bar would correspond to an A-value of around 0.9 s-1.

We have included in Table 4 a comparison of our results with other work for several levels not discussed above. There is general agreement between the relatively recent determinations of the lifetime of the a 6S2.5 level and some consensus for the b 4D3.5 level. However, for the other two levels included in Table 4 – a 4G4.5 and b 4D0.5 – the HFR calculations of Quinet et al. (1996) are clearly the closest to the experimental determinations. We would remark that the SST results of Quinet et al. (1996) might be expected to be closer to ours than are the HFR values, since the SST method involves modelling only at the stage of determining the orbital radial functions (the radial integrals are not then scaled further). We are therefore surprised that it is the HFR results which give the best agreement with experiment, for these levels. Indeed, Quinet et al. (1996) state a preference for their SST results, a view supported by their “Note added in proof” which suggests that the HFR results may not be sufficiently converged with respect to the addition of further configurations.

Another point of discrepancy in Table 4 concerns the J-dependence of the lifetimes of levels within a term. The a 4G5.5 and a 4G4.5 lifetimes differ in our calculations by 0.088 s, close to the experimental difference of 0.10, whereas in the other calculations no substantial difference is noted. By contrast, for the b 4D levels, all the calculations predict a difference of 0.05–0.06 s between J = 0.5 and J = 3.5, whereas the experimental difference is much smaller.

5. Conclusion

The present work is by far the most extensive calculation of these transitions so far undertaken. Ab initio energy differences are in much better agreement than had previously been achievable so that that fine-tuning process, particularly for the transitions discussed here, made only a small difference to the ab initio A-values. Still, the degree of mixing between a 4G5.5 and b 2H5.5 remains very sensitive to quite small potential errors, such as in

the Hamiltonian matrix elements between them. Our calculated lifetime for b 2H5.5 agrees well with experiment, while the lifetime comparison for a 4G5.5 is made more difficult because of experimental uncertainties, though we do not expect that our calculated A-values for the strongest transitions are more than a few percent below their true values. That said, it is clear from the discussion of Sect. 4.3 that some unresolved issues remain. It would be useful to undertake a calculation as extensive as the present one, but using “non-orthogonal” orbitals, thus allowing for the 3d functions to be optimal for each of the states under investigation.

Acknowledgments

The authors would like to thank PPARC/STFC, UK for support under Rolling Grant PP/D00103X/1.

References

  1. Clementi, E., & Roetti, C. 1974, At. Data Nucl. Data Tables, 14, 177 [NASA ADS] [CrossRef] [Google Scholar]
  2. Corrégé, G., & Hibbert, A. 2005, ApJ, 627, L157 [NASA ADS] [CrossRef] [Google Scholar]
  3. Corrégé, G., & Hibbert, A. 2006, ApJ, 636, 1166 [NASA ADS] [CrossRef] [Google Scholar]
  4. Garstang, R. H. 1962, MNRAS, 124, 321 [NASA ADS] [Google Scholar]
  5. Gull, T. R., Ishibashi, K, Davidson, K., & the Cycle 7 STIS Go Team 1999, in Eta Carinae at The Millennium, ASP Conf. Ser., 179, 144 [Google Scholar]
  6. Gurell, J., Hartman, H., Blackwell-Whitehead, R., et al. 2009, A&A, 508, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Hartman, H., Derkatch, A., Donnelly, M.P., et al. 2003, A&A, 397, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Hibbert, A. 1975, Comput. Phys. Commun., 9, 141 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hibbert, A., Glass, R., & Fischer, C. F. 1991, Comput. Phys. Commun., 64, 455 [NASA ADS] [CrossRef] [Google Scholar]
  10. Merrill, P. W. 1928, ApJ, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
  11. Palmeri, P., Quinet, P., Biémont, E., et al. 2008, J. Phys. B, 41, 125703 [Google Scholar]
  12. Quinet, P., Le Dourneuf, M., & Zeippen, C. J. 1996, A&AS, 120 361 [Google Scholar]
  13. Ralchenko, Yu., Kramida, A. E., Reader, J., et al. 2008, NIST Atomic Spectra Database, version 3.1.5, http://physics.nist.gov/asd3, National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
  14. Rostohar, D., Derkatch, A., Hartman, H., et al. 2001, Phys. Rev. Lett., 86, 1446 [Google Scholar]
  15. Royen, P., Gurell, J., Lundin, P., et al. 2007, Phys. Rev. A, 76, 030502(R) [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Mixing coefficients of two neighbouring levels a 4G5.5 and b 2H5.5 in four different calculations.

In the text
Table 2

Dominant A-values (in s-1) contributing to the lifetime calculation of 3d6(3H)4s b 2H5.5.

In the text
Table 3

Dominant A-values (in s-1) contributing to the lifetime calculation of 3d6(3G)4s a 4G5.5.

In the text
Table 4

Lifetimes τ(s) of six metastable levels.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.