| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015274 | |
| Published online | 19 November 2010 | |
Phase connecting multi-epoch radio data for the ultracool dwarf TVLM 513-46546
1
Armagh Observatory, College Hill, Armagh
BT61 9DG, N.
Ireland
e-mail: jgd@star.arm.ac.uk
2
Department of Astronomy, Faculty of Physics, St Kliment Ohridski,
University of Sofia, 1164
Sofia,
Bulgaria
3
Jeremiah Horrocks Institute for Astrophysics &
Supercomputing, University of Central Lancashire, Preston, PR1 2HE, UK
4
Computational Astrophysics Laboratory, I.T. Building, National
University of Ireland, Galway, Ireland
5
Department of Astronomy, University of California,
Berkeley, CA
94720-3411,
USA
Received: 24 June 2010
Accepted: 14 August 2010
Context. Radio data obtained for the ultracool dwarf TVLM 513-46546 has indicated a rotation period of ≈1.96 h via regular radio pulses, but how stable is this period. This has major implications regarding the stability of the magnetic field structures responsible for the radio emission from the ultracool dwarf.
Aims. The aim of the present work is to investigate the stability of this rotation period using two datasets taken ≈40 days apart, some 12 months after the first report of periodical pulses in the radio data.
Methods. Here we use a Bayesian analysis method which is a statistical procedure that endeavours to estimate the parameters of an underlying model probability distribution based on the observed data.
Results. Periodical pulses are detected in datasets taken in April and June 2007, with the pulses being confined to a narrow range in the rotation period. This is in contradiction to a previous report of only aperiodic activity in the April 2007 dataset, while in fact both datasets have a periodic signal with a false alarm probability ≪ 10-12. These two datasets are then used to derive a more accurate period (previously determined to be 1.96 h) of 1.96733 ± 0.00002 h.
Conclusions. The similarly in the burst structure in datasets taken several weeks apart point towards the stability of an electric field structure which is somehow generated and sustained within the magnetosphere of the ultracool dwarf. The derived period of 1.96733 h is consistent with the period derived via radio and optical data taken some 12 months prior to the present observations and implies the near phase constancy of the pulsed emission. This suggest the presence of stable large-scale magnetic fields on timescales of more than 1 year. The characteristics of the pulses suggest that they are produced by the electron cyclotron maser (ECM) instability.
Key words: methods: statistical / stars: magnetic field / stars: activity / stars: low-mass / radio continuum: stars / polarization
© ESO, 2010
1. Introduction
The detection of radio emission from the coronae of a wide range of main sequence stars was a major breakthrough with the advent of large radio interferometers such as the VLA. The quiescent emission suggested the presence of a non-thermal corona with large populations of electrons at high energies. This quiescent emission has generally been attributed to non-thermal gyrosynchrotron radiation. One possible explanation for its persistent nature and low degree of variability in M dwarfs is that it is due to continuous unresolved low-level flaring (Stewart 1992) together with efficient trapping of accelerated electrons in coronal loops. Given the above considerations, it was expected that radio emission from ultracool dwarfs (UCDs – spectral type M8 and later) should be weak or absent, in accordance with the empirical correlation of Güdel & Benz (1993).
Less than a decade ago it was considered that the cool neutral atmospheres in UCDs, coupled with high electrical resistivities (Mohanty et al. 2002), lead to a decoupling of magnetic lines from the upper atmosphere, and hence reduced or zero activity in the outer atmosphere. There are now a number of confirmed radio detections at and below the substellar boundary in recent years (Berger et al. 2001; Berger 2002; Burgasser & Putman 2005; Berger et al. 2005; Hallinan et al. 2006; Phan-Bao et al. 2007; Antonova et al. 2007) violating the Güdel & Benz relation by up to four orders of magnitude.
A summary of the radio observations for TVLM 513.
Recently, we have detected periodic pulses of 100% circularly polarized radio emission from four ultracool dwarfs (Hallinan et al. 2007, 2008; Antonova et al. 2008), with the periodicity for three of these dwarfs confirmed to correspond to the rotation period of the dwarf (Lane et al. 2007; Hallinan et al. 2008). Due to the high degree of polarization, the emission process for these pulses must be coherent. The data collected to date, suggest that the pulses are produced at the poles by the electron cyclotron maser (hereafter ECM) instability, the same mechanism known to be responsible for the radio emission from the magnetized planets in our solar system (Zarka 1998). This mechanism is also the source of certain classes of solar and stellar bursts (Melrose & Dulk 1982; Bingham et al. 2001; Osten & Bastian 2006). It was also suggested to be operational in the magnetic chemically peculiar star CU Vir where 100% circularly polarized, bright and highly directive radio bursts were detected (Kellett et al. 2007; Trigilio et al. 2007), and for the compact binary RX J080 6.3+1527 (Ramsay et al. 2007).
The emission process for the unpolarizied “quiescent” emission is less clear. Many publications suggest gyrosynchrotron (e.g. Berger et al. 2001) as the main source, in-fact, Berger et al. (2008) argue towards the gyrosynchrotron interpretation as the radio emission mechanism in UCDs for both the pulses and “quiescent” emission. A two emission model involving both incoherent gyrosynchrotron and the coherent electron cyclotron maser emission was suggested as a possibility by Hallinan et al. (2006) for TVLM 513-46546 and by Berger et al. (2009) for the observations of an L dwarf binary. An alternative view, suggested first by Hallinan et al. (2006) was that the unpolarized component of the emission was due to depolarization of the coherent electron cyclotron process.
Hallinan et al. (2008) reported on radio observations of the M8.5 dwarf LSR J1835+3259 and the L3.5 dwarf 2MASS J00361617+1821104, which provided strong evidence that the electron cyclotron maser instability is the dominant mechanism producing the radio emission (including the unpolarized emission from 2MASS J00361617+1821104, see the above paper for further details). In this model, some of the emission is depolarized on traversing the ultracool dwarf magnetosphere, possibly due to propagation effects such as scattering. Further evidence for this idea comes from radio observations of an M 4 star, V374 Peg (Hallinan et al. 2009).
 |
Fig. 1 8.4 GHz light curves of TVLM 513 in Stokes I (upper panel) and Stokes V (lower panel) on June 1, 2007 and April 20, 2007. The upper light-curve shows the data smoothed over 60 s while the lower light-curve shows smoothing over 10 s. The 60 s data has been shifted in flux to best show the variability. |
Here, we address only the issue of the pulses. Radio monitoring for a number of ultracool dwarfs has confirmed that the pulses can vary in brightness, disappear and reappear (Hallinan et al. 2006, 2007; Antonova et al. 2007). If the magnetic field is stable, such pulses should always be confined to a particular range of phase of rotation of the dwarf governed by the topology of the magnetic field. This can be investigated through correlating the phase of the radio pulses from datasets obtained at different epochs. Here, we report on observations of TVLM 513-46546 (hereafter TVLM 513) taken in June 2007, these being followup observations to the earlier detection of pulses in data acquired in 2006. In addition, we re-analyze archival data, in particular, data taken in late April 2007 (Berger et al. 2008), i.e. ≈40 days earlier than our data.
2. TVLM 513-46546: a potted history
Berger (2002) reported variable emission from TVLM 513 at an average flux of 308 μJy during ≈2 h observation in September 2001. A brightening towards the end of the observation was interpreted as a flare. Osten et al. (2006) re-observed TVLM 513 in January 2004 during a 12 h observation period, sampling three frequencies, 8.4 GHz, 4.8 Hz and 1.4 GHz. The 8.4 GHz observation had an average flux of 228 μJy; however due to sequential sampling of three different frequencies, the time resolution was not sufficient to allow a variability study. In January 2005, Hallinan et al. (2006) observed the same target simultaneously at 8.4 GHz and 4.9 GHz for a total of 5 h. These authors reported a periodicity at both frequencies of ≈2 h (later confirmed as the rotation period of the dwarf, Lane et al. 2007), with a ≈400 μJy flux at 8.4 GHz. The first report of pulsed emission from TVLM 513 was by Hallinan et al. (2007) who observed the target in May 2006 for ≈10 h on consecutive days at 8.4 GHz and 4.9 GHz. The derived period was 1.96 h, in agreement with the period derived by Lane et al. (2007) from I-band data. Approximately 9 h of data obtained in April 2007 by Berger et al. (2008) report a non-periodicity in the pulses/flaring activity (see later). A summary of the radio observations of TVLM 513 is given in Table 1.
3. Observations
On 1 June 2007, follow-up observations of TVLM 513 at 8.6 GHz were conducted for ≈8 h using the VLA in full array mode with the A configuration. The flux density was determined using the extragalactic source 1331+305 (3C 286) which was observed both at the start and the end of the observation. Phase was monitored using the source 1513+236 observed for 110 s every 10 min. Data reduction was carried out with the Astronomical Image Processing System (AIPS) software package. The visibility data were inspected for quality both before and after the standard calibration procedures, and noisy points removed. For imaging the data, we used the task IMAGR. There were three background sources in the field, one of which was stronger than TVLM 513. The other two were of comparable intensity. We CLEANed the region around each source and used the UVSUB routine to subtract the resulting source model of the background sources from the visibility data. The tangent point coordinates of TVLM 513 were shifted to coincide with the phase center and the light curves were generated by plotting the real part of the visibilities as a function of time.
4. Results and discussion
TVLM 513 was detected with a mean flux level of 318 ± 9 μJy. This flux is ≈100 μJy lower than the one found in January 2005 and May 2006, yet it is similar to that reported by Berger (2002). The Stokes V map of the source did not produce a source at the position of the dwarf, thus the net polarization for the total time of the observation could only be constrained by an upper limit on the polarized flux (SV < 30 μJy) to be fc < 10%. However, inspection of the light curve (see Fig. 1) of TVLM 513 revealed a number of bright, highly polarized bursts of short duration, similar to the May 2006 observations of the same dwarf. As in the earlier TVLM 513 data, this points towards a coherent process, such as the electron cyclotron maser. The Stokes V map of a single 10 min scan containing one such burst gives a detection with a mean flux level SV = 348 ± 43 μJy. In the left-hand side of Fig. 1 we plot the Stokes I and V data for 1 June 2007 at two time resolutions; 10 and 60 s smoothing. For this we used a Gaussian filter (FWHM = 2.354 × σ), where σ equals 10 and 60 respectively.
 |
Fig. 2 Lomb-Scargle periodogram for the April and June 2007 datasets, plus for comparison the May 2006 data. For each dataset, the false alarm probability of 10-12 is indicated. |
This is a second epoch observation of pulsed radio emission from TVLM 513, thus suggesting that the emission mechanism is stable on long times scales. From previous observations we know that the rotation period is ≈1.96 h (Hallinan et al. 2006; Lane et al. 2007). The main difference between the present data and the 2006 data reported by Hallinan et al. (2007) is that the intervals of activity are longer, typically spread over 0.25 phase, comprising of several pulses. For the June 2007 data shown in Fig. 1, the period of activity are best seen in Stokes V, e.g. we can visually identify intervals of activity at ≈2.8 h, ≈4.8 h, ≈6.7 h and ≈8.6 h, again implying a ≈2 h periodicity.
The periodicity is more clearly seen in the Lomb-Scargle periodogram (Fig. 2), which has two peaks at frequencies ~0.5 h-1 and ~1 h-1, corresponding to a period of ≈1.96 h, as is the case for the January 2005 and May 2006 data. In addition, we have an inter-pulse at ≈3.8 h (best seen in Stokes I but also visible in Stokes V), i.e. 0.5 phase later than the pulse at ≈2.8 h. As shown by Hallinan et al. (2007), due to the beaming of the ECM emission, additional activity can be observed ≈0.5 phase later. However, depending on the local density condition, this secondary activity 0.5 phase later is not always observed. At ≈8 h, we observe an event/flare, confirming that the detected periodical emission does not exclude the presence of random flare events. Flares have been reported in the optical, UV and X-ray bands as well as in spectral lines such as Hα (Rutledge et al. 2000; Liebert et al. 2003; Schmitt & Liefke 2002; Fuhrmeister & Schmitt 2004) on several UCDs.
As noted in Sect. 2, data was also obtained in April 2007 for TVLM 513 (see Berger et al. 2008). However, these authors did not report a periodicity, thus this data was obtained from the archive and reduced in a similar manner as the June 2007 data. The resulting Stokes I and V light-curves are also shown in Fig. 1. Looking at the Stokes I data, we can identify by eye four intervals of activity separated by ≈2 h; e.g. at ≈5.5 h, ≈7.4 h, ≈9.4 h and ≈11.3 h. These events were reported by Berger et al. (2008) as random flaring events. We show in Fig. 2 the Lomb-Scargle periodogram for the April 2007 data and for comparison, the Lomb-Scargle periodogram for the May 2006 data. The periodicity in all three datasets is unquestionable, with a Lomb-Scargle false alarm probability ≪ 10-12.
In the April 2007 data, we detect two other pulses of activity at ≈4.5 h and ≈6.8 h. The activity at ≈4.5 h can be explained by the ECM beaming model (Hallinan et al. 2008), while the event at ≈6.8 h is another random flare event. In order to distinguish between periodic and random flares, it is essential to do a proper period analysis.
To determine a precise measure of the periodicity within the April and June 2007 Stokes I data, the Bayesian oscillation parameter estimation code of Marsh et al. (2008) is applied. The advantage of this method is that it determines precise estimates of the oscillation parameters and their 1σ errors based on probability theory. It is also suited to low signal to noise and unevenly sampled data. As described by Bretthorst (1988), the resolution with which the frequency of an oscillatory signal may be determined is dependent upon the signal to noise ratio within the data. Using periodogram-type methods, an arbitrary estimate of the uncertainty of an oscillation frequency, such as the half width at half maximum of the periodogram peak, has no relation to the limit with which a frequency may be resolved. Marsh et al. (2008) demonstrate the increased frequency resolution obtained using the Bayesian method compared to that estimated using a Fourier and wavelet transform. For their single frequency time series, with a signal to noise ratio of one, the Bayesian method had an order of magnitude greater frequency resolution than that estimated using the Fourier transform. The basic principal of the Bayesian method is based on the probability of obtaining the oscillatory model given the observed data. The fitting of the oscillation model to the data is similar to least squares fitting, but with the advantage of a self-consistent statistical derivation of the parameter errors, and a reduction in the dimensions of the fitted parameter space. A full description of the method is given in Marsh et al. (2008), and references within, to which the reader is referred for further details.
 |
Fig. 3 Phase-folded plot for the April (dotted line) and June 2007 (solid black line) data with the 1.96733 h period. The red and blue lines indicate the 1σ errors, i.e. 0.00002 h. |
To determine a precise measure of the ≈1.96 h period within the Stokes I data, the code of Marsh et al. (2008) is applied to the April and June datasets as a whole, taking advantage of the ability to analyse unevenly sampled data. The precise frequency measurement that is obtained also allows the phase constancy to be confirmed by applying a phase-folding analysis (see Fig. 3). To evaluate the most significant sources of power within the data, at frequencies around 0.5, 1.0, and 3.5 h-1, the data is fitted with an oscillation model comprised of three distinct frequencies of the form: 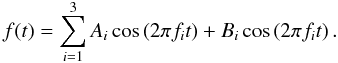 (1)This results in a three-dimensional probability density function for this model, and determines the most probable oscillation model frequency, amplitude and phase expressed in polar form (see Table 2). Considering the ≈1.96 h period of TVLM 513, this determines the period and 1σ error to be 1.96733 ± 0.00002 h. We find excellent agreement (see the phase-folding Fig. 3) between the two datasets suggesting (i) that the pulse locations are stable remaining confined to a narrow range of rotational phase (although they may vary in intensity and duration) and (ii) that a more accurate period may be derived based on these two datasets. The stability of the field structure has major implications with the pulsed emission giving vital information on the characteristic size and topology of magnetic fields in ultracool dwarfs.
(1)This results in a three-dimensional probability density function for this model, and determines the most probable oscillation model frequency, amplitude and phase expressed in polar form (see Table 2). Considering the ≈1.96 h period of TVLM 513, this determines the period and 1σ error to be 1.96733 ± 0.00002 h. We find excellent agreement (see the phase-folding Fig. 3) between the two datasets suggesting (i) that the pulse locations are stable remaining confined to a narrow range of rotational phase (although they may vary in intensity and duration) and (ii) that a more accurate period may be derived based on these two datasets. The stability of the field structure has major implications with the pulsed emission giving vital information on the characteristic size and topology of magnetic fields in ultracool dwarfs.
Most probable oscillation frequency, phase and amplitude.
The similarity between the two datasets and near phase constancy of the pulsed emission suggests that the magnetic field structures are stable on timescales of at least 6 weeks for this UCD and considering that a similar period was obtained for the May 2006 data, these magnetic structure are stable for at least 1 yr. In fact, Zeeman Doppler Imaging by Morin et al. (2008) has shown that the magnetic topology for an M 4 dwarf is stable on a time-scale of 1 yr. Such information on the magnetic field is crucial to understanding the means by which persistent levels of ECM emission are sustained in the magnetospheres of UCDs. This persistent generation of ECM emission in turn, implies the presence of stable electric fields, which are somehow generated and sustained within the magnetosphere of the ultracool dwarf. Such electric fields may be a fundamental source of electron acceleration, and hence radio emission, for plasma trapped in a large-scale magnetic field.
The above may have implications for the non-pulsed emission, which, as noted in the introduction, has been largely interpreted as gyrosynchrotron. In fact, many authors, e.g. Berger et al. (2008), initially interpreted both the non-pulsed emission and the pluses as gyrosynchrotron; however, if the ECM emission can become depolarized as it propagates through the ultracool dwarf magnetosphere, then a two-source model may not be required (Hallinan et al. 2008, 2009). Further work is however needed to investigate this aspect.
5. Conclusions
Using data taken ≈40 days apart, we have established to a high degree of accuracy the lack of evolution in the morphology of the periodic light curves, although changes in the structure of the pulses are observable from one rotation to the next. Nevertheless, the overall pulse interval does still occur (within a few minutes) at the same orbital phase. However, further monitoring, particularly at a higher cadence and frequency resolution is required in order to investigate the location, extent, and morphology of the sub-pluses which are clearly observable in each burst interval. Phase connecting both datasets, gives a more accurate period
of 1.96733 ± 0.00002 h. Aperiodic flaring events are possible, thus in order to distinguish between periodic and random flares, it is essential to do a proper period analysis.
Acknowledgments
Armagh Observatory is grant-aided by the N. Ireland Dept. of Culture, Arts & Leisure. G.H. and A.G. gratefully acknowledge the support of Science Foundation Ireland (grant No. 07/RFP/PHYF553). J.G.D. & S.Y. thank the Leverhulme Trust for support. A.A. gratefully acknowledges the support of the Scientific Research Fund of “St. Kl. Ohridski” University of Sofia (grant Nos. 80/2009 and 138/2010). M.S.M. is supported by the Science and Technology Facilities Council (STFC) under grant number ST/F002769/1.
References
- Antonova, A., Doyle, J. G., Hallinan, G., Golden, A., & Koen, C. 2007, A&A, 472, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonova, A., Doyle, J. G., Hallinan, G., Bourke, S., & Golden, A. 2008, A&A, 487, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, E. 2002, ApJ, 2005, 572, 503 [Google Scholar]
- Berger, E., Ball, S., Becker, K. M., et al. 2001, Nature, 410, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Berger, E., Rutledge, R. E., Reid, I. N., et al. 2005, ApJ, 627, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Gizis, J. E., Giampapa, M. S., et al. 2008, ApJ, 673, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Rutledge, R. E., Phan-Bao, N., et al. 2009, ApJ, 695, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Bingham, R., Cairns, R. A., & Kellett, B. J. 2001, A&A, 370, 1000 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bretthorst, G. L. 1988, Bayesian Spectral Analysis and Parameter Estimation (New York: Springer) [Google Scholar]
- Burgasser, A. J., & Putman, M. E. 2005, ApJ, 626, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., & Schmitt, J. H. M. M. 2004, A&A, 420, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., & Benz, A. O. 1993, ApJ, 405, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Antonova, A., Doyle, J. G., et al. 2006, ApJ, 653, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Lane, C., Bourke, S., et al. 2007, ApJ, 663, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Antonova, A., Doyle, J. G., et al. 2008, ApJ, 684, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Doyle, J. G., Antonova, A., et al. 2009, Proceedings of the 15th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, AIP Conf. Proc., 1094, 146 [Google Scholar]
- Kellett, B. J., Graffagnino, V., Bingham, R., Muxlow, T. W. B., & Gunn, A. G. 2007, [arXiv:astro-ph/0701214] [Google Scholar]
- Lane, C., Hallinan, G., Zavala, R. T., et al. 2007, ApJ, 668, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Liebert, J., Kirkpatrick, J. D., Cruz, K. L., et al. 2003, AJ, 125, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, M. S., Ireland, & Kucera, T. 2008, ApJ, 681, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B., & Dulk, G. A. 1982, ApJ, 259, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Basri, G., Shu, F., Allard, F., & Chabrier, G. 2002, ApJ, 571, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J.-F., Forveille, T., et al. 2008, MNRAS, 384, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Osten, R. A., & Bastian, T. S. 2006, ApJ, 637, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Osten, R. A., Hawley, S. L., Bastian, T. S., & Reid, I. N. 2006, ApJ, 637, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Phan-Bao, N., Osten, R. A., Lim, J., Martín, E. L., & Ho, P., T. P. 2007, ApJ. 658, 553 [Google Scholar]
- Ramsay, G., Brocksopp, C., Wu, K., Slee, B., & Saxton, C. J. 2007, MNRAS, 382, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Rutledge, R. E., Basri, G., Martin, E. L., & Bildsten, L. 2000, ApJ, 538, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Trigilio, C., Leto, P., Umana, G., Buemi, C. S., & Leone, F. 2008, MNRAS, 384, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., & Liefke, C. 2002, A&A, 382, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stewart, R. T. 1992, Lect. Notes Phys. (Springer), 399, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Zarka, P. 1998, JGR, 103, 20159 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 8.4 GHz light curves of TVLM 513 in Stokes I (upper panel) and Stokes V (lower panel) on June 1, 2007 and April 20, 2007. The upper light-curve shows the data smoothed over 60 s while the lower light-curve shows smoothing over 10 s. The 60 s data has been shifted in flux to best show the variability. |
| In the text | |
 |
Fig. 2 Lomb-Scargle periodogram for the April and June 2007 datasets, plus for comparison the May 2006 data. For each dataset, the false alarm probability of 10-12 is indicated. |
| In the text | |
 |
Fig. 3 Phase-folded plot for the April (dotted line) and June 2007 (solid black line) data with the 1.96733 h period. The red and blue lines indicate the 1σ errors, i.e. 0.00002 h. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


