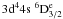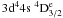| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201015200 | |
| Published online | 22 November 2010 | |
Electron-impact excitation of Cr ii
A theoretical calculation of collision and effective collision strengths for forbidden transitions⋆
Department of Applied Mathematics & Theoretical PhysicsThe
Queen’s University of Belfast,
Belfast BT7 1NN,
Northern Ireland,
UK
e-mail: iwasson01@qub.ac.uk
Received: 11 June 2010
Accepted: 14 August 2010
Context. Absorption or emission lines of Cr ii are observed in a wide variety of astrophysical spectra and accurate atomic data are urgently needed to interpret these lines. Many of these data are impossible to measure experimentally and a full theoretical treatment is the only means by which these data can be obtained.
Aims. In this paper, we present collision strengths and effective collision strengths for electron-impact excitation of Cr ii for forbidden transitions among the lowest-lying 74 fine-structure levels. Effective collision strengths have been computed for 18 individual electron temperatures of astrophysical importance, ranging from 2000–100 000 K.
Methods. The parallel suite of R-matrix packages, RMATRX II, which has recently been extended to allow for the inclusion of relativistic effects, has been used in the present work to compute the collision strengths and effective collision strengths for electron-impact excitation of Cr ii. We concentrate in this publication on low-lying forbidden lines among the lowest 74 jj fine-structure levels with configurations 3d5 and 3d44s, although atomic data has been evaluated for all 39 060 transitions among the 280 jj levels of configurations 3d5, 3d44s and 3d44p. This work constitutes the largest evaluation ever performed for this ion involving 1932 coupled channels.
Results. Collision and effective collision strengths are presented for all transitions among the lowest 74 Jπ states of Cr ii and comparisons made with the work of Bautista et al. (2009). While the effective collision strengths agree well for some transitions, significant discrepancies exist for others. We believe that the present atomic data represents the most accurate, most sophisticated and most complete data set for electron-impact excitation of Cr ii and we would recommend them to astrophysicists and plasma physicists in their application work. We would expect that the effective collision strengths presented for the important low-lying forbidden lines are accurate to within 15%.
Key words: atomic data / atomic processes / methods: numerical / scattering / plasmas
Table 4 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/524/A35
© ESO, 2010
1. Introduction
Singly-ionized chromium is a member of the astrophysically significant, yet computationally difficult to treat, group of iron-peak elements running from Sc to Cu in the periodic table. Atomic data for Cr ii are well known to be of critical importance in the analysis of a broad range of stellar and nebular spectra. Numerous publications regularly appear in the literature pertaining to Cr ii emission lines. For example Monier et al. (2009) have recently reported the first discovery of a damped Lyα System (DLA) using the GALEX Satellite which indicated the presence of unusually strong absorption due to metal lines of Cr ii, Zn ii, Mn ii and Fe ii. Significantly, several facets of galaxy formation and evolution can be considered through follow-up studies of the properties of these DLA’s. For example, their metal abundances provide an insight into the chemical evolution of the neutral hydrogen gas over cosmic timescales. In addition Klochkova et al. (2008) have obtained high-resolution optical spectroscopy of the variable F-type star V2324 Cyg where more than 200 absorption features (mostly Cr ii, Fe ii and Ti ii) were identified within the 4549–7880 Å wavelength region. This particular object was identified as a candidate young planetary nebula (pPN) which presents an opportunity to observe the result of stellar nucleosynthesis mixing and dredge-up of the products of nuclear reactions during the previous evolution of the star. Castelli & Hubrig (2007) publish a refined analysis of the very young ( ~ 107 years), remarkable chemically peculiar star HR6000 using UVES spectra in the near-UV and visual spectral regions. Their spectral analysis revealed the presence of emission lines for Cr ii, Fe ii and Mn ii. Finally stellar abundance studies by Babel & Lanz (1992), Rice & Wehlau (1994), López-García et al. (2001) and Dimitrijević et al. (2007) have all highlighted the need for accurate atomic data for the Fe-peak element Cr ii.
Modeling the Cr ii ion, as with all the Fe-peak elements, is made particularly difficult by the presence of an open 3d-shell which leads to hundreds of fine structure states and thousands of coupled channels. Hence the theoretical calculation of the much needed atomic data requires large configuration interaction expansions to properly represent the target wavefunctions and energy levels. Despite these difficulties a number of theoretical works have emerged in the literature over the last number of years which investigate the electron-impact excitation of these lowly-ionized Fe-peak elements and evaluate the associated collisional and radiative data. Ramsbottom et al. (2007, 2009) provided the largest atomic dataset of collision strengths and effective collision strengths for forbidden and allowed fine-structure transitions in Fe ii, while Cassidy et al. (2010) computed a similar dataset for Ni ii. In addition a substantial Fe iii calculation has recently been completed and submitted for publication (Scott et al. 2010). These works represent the first applications of the new RMATRX II R-matrix package (Burke et al. 1994) in the internal region. Relativistic fine-structure effects have been incorporated in the Cassidy et al. (2010) calculation via the recently completed FINE package (Burke, priv. comm.). The PSTGF parallel program (Ballance & Griffin 2004) was used in the external region to complete the suite of computer codes. These new and powerful parallel codes allow us to take full advantage of MPP supercomputing facilities and carry out the sophisticated investigation of these difficult Fe-peak ions.
In the present work we intend to use these parallel codes to investigate the electron-impact excitation of singly ionized chromium. To date the largest calculation performed for this ion was reported by Bautista et al. (2009) primarily as part of an ongoing study into the chemical abundances of the strontium filament found in the ejecta of η Carinae. In this calculation electron-impact collision strengths for transitions among the lowest 162 levels of Cr ii were evaluated. The computed fine-structure collision strengths and corresponding effective collision strengths were not published, but have been obtained from the authors by private communication for comparative purposes in this study.
In the present model we extend the calculation of Bautista et al. (2009) by computing the fine-structure collisional data for Cr ii for all transitions among the lowest 280 levels arising from the basis configurations 3d5, 3d44s and 3d44p. This corresponds to a substantial 1932 coupled channel problem.
In Sect. 2 we describe in detail the atomic models developed for the collisional calculation, while in Sect. 3 we discuss the collisional calculation itself. Section 4 details the results obtained with a graphical and detailed comparison made with the previous data of Bautista et al. (2009) for a selection of important low-lying transitions. This qualitative comparison involves both the collision strengths and the astrophysically desirable Maxwellian averaged effective collision strengths for a range of temperature values. Table 4 contains the computed effective collision strengths for all of the low lying forbidden transitions among the lowest 28 fine structure levels for a total of 18 individual temperatures ranging from 2000–100 000 K. Finally, in Sect. 5 conclusions are drawn.
2. The model
To determine accurate representations for both the Cr ii target and the collision wavefunctions a careful balance between size and accuracy is required. When performing a structure calculation it is usual to include many target terms and pseudo orbitals to improve the accuracy of the target model. Very large configuration-interaction (CI) expansions are thus often utilized. In a collision calculation, however, these large CI expansions can lead to an unmanageable and computationally impossible approximation due to the large numbers of (N + 1)-electron configurations and coupled channels involved. A careful balance is thus necessary between the two to create the optimum model.
In the present work all spectroscopic target levels arising from the 3 basis configurations 3d5, 3d44s and 3d44p, including all doublet, quartet and sextet spin states, were included in the expansion of the target wavefunction. This leads to a substantial 108 LS, 280 jj-level model with a maximum of 1932 coupled channels and 39 060 individual transitions. These spectroscopic states are optimally represented by CI type expansions in terms of orthogonal basis orbitals. The radial part of each orbital is expanded as a a linear combination of Slater-type orbitals 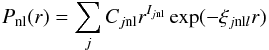 (1)The orbital parameters (Ijnl, Cjnl, ξjnl) for the ground state Hartree-Fock orbitals (1s, 2s, 2p, 3s, 3p and 3d) were obtained from the tables of Clementi & Roetti (1974). any further orbitals were obtained variationally using the CIV3 code of Hibbert (1975). The parameters for the 4s and 4p spectroscopic orbitals were obtained by optimising on the lowest energies of the 3d44s and 3d44p states respectively. A further
(1)The orbital parameters (Ijnl, Cjnl, ξjnl) for the ground state Hartree-Fock orbitals (1s, 2s, 2p, 3s, 3p and 3d) were obtained from the tables of Clementi & Roetti (1974). any further orbitals were obtained variationally using the CIV3 code of Hibbert (1975). The parameters for the 4s and 4p spectroscopic orbitals were obtained by optimising on the lowest energies of the 3d44s and 3d44p states respectively. A further  correction orbital was also obtained by optimising on the
correction orbital was also obtained by optimising on the 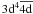 state, again using CIV3. The parameters utilized for the non Hartree-Fock orbitals are presented in Table 1.
state, again using CIV3. The parameters utilized for the non Hartree-Fock orbitals are presented in Table 1.
Roothaan-Hartree-Fock parameters for Slater-type orbitals 4s, 4p and 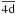 , as used in the Cr ii calculation.
, as used in the Cr ii calculation.
A key to the different models considered when building the target.
 |
Fig. 1 Graphic representation of the percentage difference of the LS energy levels compared to NIST per model. |
Energy differences from the Ground State for the lowest 28 3d5 and 3d44s target states, and 9 other 3d44p target states, per model.
In Table 2 we present a build up of the Cr ii models which were investigated in the current calculation. Model M3 contains only the basis spectroscopic configurations 3d4, 3d44s and 3d44p. Model M6 then incorporates an additional 3 correlation functions 3d34s2, 3d34p2 and 3d34s4p. In model M10 we add an additional orbital, the 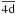 pseudo-orbital, which acts as a correction to the 3d orbital and consequently four further configurations
pseudo-orbital, which acts as a correction to the 3d orbital and consequently four further configurations 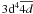 ,
, 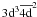 ,
, 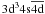 ,
, 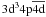 , were incorporated. In model M14 we open up the 3p core and allow one electron excitation from the 3p shell to the 3d shell. Earlier investigations by Ramsbottom et al. (2009) and Cassidy et al. (2010) have found the addition of these correlation functions improves the accuracy of the target model. Finally in model M18 we allow two electron promotions from the 3p shell to the 3d shell, thereby adding a further four correction terms.
, were incorporated. In model M14 we open up the 3p core and allow one electron excitation from the 3p shell to the 3d shell. Earlier investigations by Ramsbottom et al. (2009) and Cassidy et al. (2010) have found the addition of these correlation functions improves the accuracy of the target model. Finally in model M18 we allow two electron promotions from the 3p shell to the 3d shell, thereby adding a further four correction terms.
In Table 3 we display the calculated target states energies in Rydbergs relative to the 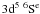 ground state, for all of the models listed in Table 2. For conciseness only the lowest 28 LS states with configurations 3d5 and 3d44s were included together with 9 of the 3d44p levels to indicate the accuracy of the odd parity states. The present theoretical energies are compared with experimental values found in the NIST database. To complement Table 3 and provide a visual aid to the differences between theory and experiment, we present in Fig. 1 the percentage differences from experiment for each of the 5 models adopted, for the even parity states and odd parity states individually, as well as the collective percentage differences for all states. We clearly see that the basic M3 model provides poor energy levels particularly for the even states with percentage differences of on average 25%. For some of the low-lying levels the differences are considerably worse. On the other hand the odd parity states are quite well represented, even in this most basic model, with an average error of 19%. Incorporating the additional CI terms in model M6 has only a very small impact on these energy levels. the overall average error has now improved to 24% with some of the odd parity states now agreeing to within 6% of the experimental values. Adding the
ground state, for all of the models listed in Table 2. For conciseness only the lowest 28 LS states with configurations 3d5 and 3d44s were included together with 9 of the 3d44p levels to indicate the accuracy of the odd parity states. The present theoretical energies are compared with experimental values found in the NIST database. To complement Table 3 and provide a visual aid to the differences between theory and experiment, we present in Fig. 1 the percentage differences from experiment for each of the 5 models adopted, for the even parity states and odd parity states individually, as well as the collective percentage differences for all states. We clearly see that the basic M3 model provides poor energy levels particularly for the even states with percentage differences of on average 25%. For some of the low-lying levels the differences are considerably worse. On the other hand the odd parity states are quite well represented, even in this most basic model, with an average error of 19%. Incorporating the additional CI terms in model M6 has only a very small impact on these energy levels. the overall average error has now improved to 24% with some of the odd parity states now agreeing to within 6% of the experimental values. Adding the 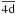 corrector orbital provides, however, a marked improvement on many of the low-lying levels. The average error now drops to 17% which can clearly be seen in Fig. 1. Opening up the 3p core in model M14 indicates a further marked improvement particularly for the low-lying even parity states which are the most difficult to locate. The average error is now 15% and all errors greater than 20% lie in the low-lying energy region. The odd parity states have been further refined and all now lie within 10% at worst and 1% at best to the experimental values. Interestingly, allowing 2e − excitations from the 3p shell to the 3d shell in model M18 indicates very little improvement on model M14. The average energy level has improved by only 0.4%. Although satisfied with the current target state representations in models M14 and M18, the present collision calculation has been performed with the energies of the spectroscopic target levels shifted so as to agree with the experimental values listed in NIST. Such adjustments are made to ensure that the target state thresholds lie in their exact positions.
corrector orbital provides, however, a marked improvement on many of the low-lying levels. The average error now drops to 17% which can clearly be seen in Fig. 1. Opening up the 3p core in model M14 indicates a further marked improvement particularly for the low-lying even parity states which are the most difficult to locate. The average error is now 15% and all errors greater than 20% lie in the low-lying energy region. The odd parity states have been further refined and all now lie within 10% at worst and 1% at best to the experimental values. Interestingly, allowing 2e − excitations from the 3p shell to the 3d shell in model M18 indicates very little improvement on model M14. The average energy level has improved by only 0.4%. Although satisfied with the current target state representations in models M14 and M18, the present collision calculation has been performed with the energies of the spectroscopic target levels shifted so as to agree with the experimental values listed in NIST. Such adjustments are made to ensure that the target state thresholds lie in their exact positions.
3. Collision calculation
We have completed a full scattering calculation for the 10 and 14 configuration models (M10 and M14) using powerful parallel codes on state of the art national parallel computing facilities. The small improvements in energy found by model M18 were not sufficient to merit a full collisional treatment on this model. Model M10 represents a complete set of configurations between the N-electron target and the (N + 1)-electron collisional complex. Model M14, however, does not represent a complete set due to the opening of the 3p core. The RMATRX II R-Matrix suite of packages (Burke et al. 1994) were used to compute the diagonalised hamiltonian matrices from the internal region in LS coupling. RMATRX II is made up of three main modules, RAD which calculates the radial integrals, ANG which computes the angular integrals and finally HAM which forms and diagonalises the Hamiltonian matrix elements. The module FINE (Burke, priv. comm.) transforms the R-Matrix in LS-coupling at energy E into an R-matrix in pair coupling. However, instead of carrying out this transformation at each energy, the energy independent surface amplitudes are transformed at the R-matrix boundary. FINE also takes account of the term splitting in the target by employing the term coupling coefficients which are the mixing coefficients for the individual LiSiπi states form a Jiπi state. One of the main advantages of this method, over other transformation procedures, is that it allows us to include some fine-structure channels in the external region as the transformation occurs earlier on the R-matrix boundary as opposed to the asymptotic boundary. This method also allows for the inclusion of complex configuration-interaction wavefunctions to represent the target model in the internal region where LS coupling is used. Finally the PSTGF code of Ballance & Griffin (2004) was used to compute the collision cross sections over a very fine mesh of incident electron energies.
The present 280 jj-level calculation was computed for all incident partial waves up to L = 10 (2J = 14) for all singlet, triplet, quintet and septet multiplicities and for both even and odd parities, giving rise to a total of 88 (N + 1)-electron symmetries. This was found to be sufficient to ensure convergence of the collision strengths for the forbidden lines which we are primarily concerned with in this publication. Twenty continuum orbitals were included for each orbital angular momentum and the R-Matrix boundary was set at 10 au. A very fine mesh (10-4 Ryds) was adopted to ensure proper resolution of the infinite number of rydberg resonances which converge onto the target state thresholds. Approximately 11 000 individual energy points were considered in the resonance region. A coarser mesh (10-2) was adopted at higher energies.
4. Results
The collision strength Ωif between an initial state “i” and final state “f” has been computed in the present work adopting models M10 and M14 previously discussed. The corresponding effective collision strengths, Υif, of importance in astrophysical and plasma applications, are obtained by averaging over a Maxwellian distribution of electron velocities so that 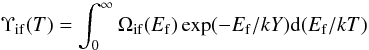 (2)where Ef is the final kinetic energy of the electron, T is the electron temperature in Kelvin and k is Boltzmann’s constant.
(2)where Ef is the final kinetic energy of the electron, T is the electron temperature in Kelvin and k is Boltzmann’s constant.
 |
Fig. 2 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
In Fig. 2 we present the effective collision strength as a function of log electron temperature in Kelvin, for the three lowest lying fine structure transitions from the ground state to the first metastable level, the 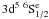 →
→ 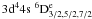 (transitions 1–2, 1–3 and 1–4). Comparisons are made between the results obtained from the models M10, M14 and the results of Bautista et al. (2009). Clearly the effective collision strengths obtained from M10 and M14 are in near perfect agreement for all three transitions considered, and at all temperatures considered. This would suggest that although opening up the 3p core and allowing single electron excitations from 3p to 3d shells improved the energy separations for the target levels, the inclusion of these additional CI in the wavefunction representation of the collisional model made little difference to the atomic data produced. The data produced by the 162 level model of Bautista et al. (2009) lie consistently higher than the present M10 and M14 results by approximately 20% for all three transitions and for all temperatures considered. We also note that the present work extends the temperature range to log (T) = 5.0 K.
(transitions 1–2, 1–3 and 1–4). Comparisons are made between the results obtained from the models M10, M14 and the results of Bautista et al. (2009). Clearly the effective collision strengths obtained from M10 and M14 are in near perfect agreement for all three transitions considered, and at all temperatures considered. This would suggest that although opening up the 3p core and allowing single electron excitations from 3p to 3d shells improved the energy separations for the target levels, the inclusion of these additional CI in the wavefunction representation of the collisional model made little difference to the atomic data produced. The data produced by the 162 level model of Bautista et al. (2009) lie consistently higher than the present M10 and M14 results by approximately 20% for all three transitions and for all temperatures considered. We also note that the present work extends the temperature range to log (T) = 5.0 K.
In an attempt to investigate the origin of these differences we plot in Fig. 3 the original collisional strength data from which these Maxwellian averaged rates were obtained. In Fig. 3 we plot the collision strength as a function of incident electron energy in Rydbergs for the 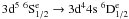 line (transition 1–2) and compare the present 14 configuration M14 model with the data produced by Bautista et al. (2009). Although many of the large rydberg resonance structures agree well both in regard to position and magnitude, it is clear that the background cross section is consistently higher in the work of Bautista et al. (2009). The collision strengths of the other two transitions
line (transition 1–2) and compare the present 14 configuration M14 model with the data produced by Bautista et al. (2009). Although many of the large rydberg resonance structures agree well both in regard to position and magnitude, it is clear that the background cross section is consistently higher in the work of Bautista et al. (2009). The collision strengths of the other two transitions 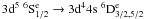 (1–3 and 1–4) depict a similar behavior which accounts for the 20% differences found when the Maxwellian averaging has been performed.
(1–3 and 1–4) depict a similar behavior which accounts for the 20% differences found when the Maxwellian averaging has been performed.
 |
Fig. 3 Collision strengths as a function of incident electron energy in Rydbergs for the fine structure transition |
 |
Fig. 4 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
 |
Fig. 5 Collision strengths as a function of incident electron energy in Rydbergs for the fine structure transition |
In Fig. 4 a very different picture emerges when we plot effective collision strengths for fine structure transitions from the 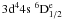 level to the higher lying
level to the higher lying 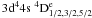 levels (transitions 2–7, 2–8 and 2–9).
levels (transitions 2–7, 2–8 and 2–9).
Again excellent agreement between models M10 and M14 is evident for all three transitions and across all temperature values. Differences of on average 6% are found. Unlike the previous set of transitions, however, the data of Bautista et al. (2009) now lie consistently lower than either of the present models. Differences of up to 40% are seen for many of the temperatures considered. Again to investigate these differences we plot in Fig. 5 the collision strength for the 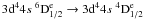 transition (2–7). Again the overall structure and magnitude of the collision strength is similar in both calculations but the background predicted by Bautista et al. (2009) is somewhat lower.
transition (2–7). Again the overall structure and magnitude of the collision strength is similar in both calculations but the background predicted by Bautista et al. (2009) is somewhat lower.
 |
Fig. 6 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
Finally in Fig. 6 we present effective collision strengths for the spin changing transitions 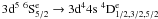 (transitions 1–7, 1–8 and 1–9). Again models M10 and M14 agree well at all temperatures and also with the predictions of Bautista et al. (2009) for the majority of temperatures where a comparison is possible. The largest discrepancies appear for very low temperatures (log (T) = 3.1−3.7 K) but for the higher temperatures (log (T) = 3.7−4.5K) agreement is really quite acceptable.
(transitions 1–7, 1–8 and 1–9). Again models M10 and M14 agree well at all temperatures and also with the predictions of Bautista et al. (2009) for the majority of temperatures where a comparison is possible. The largest discrepancies appear for very low temperatures (log (T) = 3.1−3.7 K) but for the higher temperatures (log (T) = 3.7−4.5K) agreement is really quite acceptable.
To conclude the graphical comparison with previous works we see that for some transitions agreement is excellent, for some the present models predict higher effective collision strengths while for others the converse is true. Any differences predicted will however have a marked effect on the diagnostic applications and modeling where this data is used.
Finally in Table 4 we present the effective collision strengths computed in the present 10 configuration model M10. This data was chosen as it was computed from a model where a complete set of configurations was adopted for both the N-electron target and the (N + 1)-electron collisional system. We consider in this table all forbidden lines from the lowest 28 LS even states listed in Table 3, corresponding to 74 jj levels. A total of 2701 individual forbidden lines are considered in the table and Maxwellian averaged effective collision strengths are listed for 18 electron temperature values of particular astrophysical interest.
The effective collision strengths for the remaining forbidden lines are available from the authors. Due to the large number of incident electron energies included in the collision strengths (~11 200), these data are also available from the authors.
5. Conclusions
We report in this paper the evaluation of accurate collision strengths and effective collision strengths for the electron-impact excitation of Cr ii. The parallel RMATRX II R-Matrix packages, which have recently been extended to allow for the inclusion of relativistic effects, have been utilized in the computations. Target states corresponding to the 3d5, 3d44s and 3d44p configurations were included in the collision calculation, giving rise to a 280 jj level, 1932 coupled channel problem with a total of 39 060 individual transitions. This constitutes the largest evaluation ever performed for this ion. In this publication we concentrate on the astrophysically important low-lying forbidden transitions among the lowest 74 fine-structure levels corresponding to the 3d5 and 3d44s states. However, atomic data for all 39 060 forbidden and allowed lines have been computed and are available from the authors on request. To assess the accuracy of these effective collision strengths we compare with the earlier work of Bautista et al. (2009). This comparison, however, yielded a mixed bag of results. For some transitions the agreement is excellent across all temperatures considered, while for others disparities of up to 40% were found. These differences will have a marked effect on any diagnostic application work which utilizes these data. Exactly the same conclusions were made by Cassidy et al. (2010) when investigating the electron impact excitation of Ni ii and comparing with the evaluations of Bautista (2004). It seems these lowly ionized iron-peak ions are very sensitive to CI effects, resonance resolution and target model. Convergence between the differing theoretical approaches is difficult to achieve for many transitions.
It is difficult to assess the accuracy of the effective collision strengths conclusively. The major test of the quality of the atomic data will come from astrophysical or diagnostic applications. We can, however, gauge accuracy by considering a number of points.
-
Firstly, this work represents the largest scattering calculation todate ever performed for the Cr ii ion. Thetheoretical approximation is fully consistent in that allconfiguration interaction configurations which couple into thetarget list during the collision are included in the model. In otherwords the N-electron target and (N + 1)-electron complex form a complete set. This consistency ensures that important CI terms in the expansions of the wavefunctions are not omitted. The 162 level model of Bautista et al. (2009) is not complete since there are 280 levels of Cr ii with configurations 3d5, 3d44s, 3d44p. Hence all the Rydberg resonances converging to these additional thresholds will be absent from their collision strengths and hence will not be included in the Maxwellian averaging to evaluate the effective collision strengths.
-
In addition, resonance structures in the low-energy region of the collision cross sections have been properly delineated in the present work by including many thousands of incident electron energies with a very small mesh. This mesh size has been carefully investigated to ensure convergence. This ensures that the Maxwellian averaging to compute the astrophysically desirable effective collision strengths is accurate. There is no evidence of such an investigation of mesh size in the work of Bautista et al. (2009).
-
Finally, the present calculation extends the temperature range out to 100 000 K and provides data for a wider range of temperature values than the Bautista et al. (2009) work. Their focus was, however, on the particular application of the strontium filament in the Homunculus of η Carinae.
We believe that the present atomic data represents the most accurate, most sophisticated and most complete data set for electron-impact excitation of Cr ii and we would recommend them to astrophysicists and plasma physicists in their application work. We would expect that the effective collision strengths presented for the important low-lying forbidden lines are accurate to within 15%. For some of the higher lying lines, larger discrepancies may be found due to the omission of higher lying 4s4p states in the target list. As stated previously the conclusive test of this atomic data will come from diagnostic and application work.
Acknowledgments
The authors wish to acknowledge the years of dedicated work of P. G. Burke, V. M. Burke and C. J. Noble at Daresbury Laboratory (UK) who have been responsible for the development of the internal region codes. Special acknowledgement is extended to M. Bautista for supplying unpublished data for comparison purposes. The work presented in this paper is supported by STFC and I. R. Wasson is supported by a DEL Studentship. The computations were carried out on the IBM HPCx facility at the CLRC Daresbury Laboratory.
References
- Babel, J., & Lanz, T. 1992, A&A, 263, 232 [NASA ADS] [Google Scholar]
- Ballance, C. P., & Griffin, D. C. 2004, J. Phys. B, 37, 2943 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A. 2004, A&A, 420, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, M. A., Ballance, C., Gull, T. R., et al. 2009, MNRAS, 393, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, P. G., Burke, V. M., & Dunseath, K. M. 1994, J. Phys. B: At. Mol. Opt. Phys., 27, 5341 [Google Scholar]
- Cassidy, C. M., Ramsbottom, C. A., Scott, M. P., & Burke, P. G. 2010, A&A, 513, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Hubrig, S. 2007, A&A, 475, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clementi, E., & Roetti, C. 1974, At. Data Nucl. Data Tables, 14, Nos 3-4 [Google Scholar]
- Dimitrijević, M. S., Ryabchikova, T., Simić, Z., Popović, L. *error*˘C., & Dac˘ić, M. 2007 A&A, 469, 681 [Google Scholar]
- Hibbert, A. 1975, Comput. Phys. Comm., 9, 141 [Google Scholar]
- Klochkova, V. G., Chentsov, E. L., & Panchuk, V. E. 2008, Astrophys. Bull., 63, 112 [NASA ADS] [CrossRef] [Google Scholar]
- López-García, Z., Adelman, S. J., & Pintado, O. I. 2001, A&A, 367, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monier, E. M., Turnshek, D. A., Rao, S. M., & Weyant, A. 2009, AJ, 138, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- NIST Atomic Spectra Database, http://physics.nist.gov/PhysRefData [Google Scholar]
- Ramsbottom, C. A. 2009, At. Data Nucl. Data Tables, 95, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsbottom, C. A., Hudson, C. E., Norrington, P. H., & Scott, M. P. 2007, A&A, 475, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, J. B., & Wehlau, W. H. 1994, A&A, 291, 825 [NASA ADS] [Google Scholar]
- Scott, M. P. 2010, submitted [Google Scholar]
All Tables
Roothaan-Hartree-Fock parameters for Slater-type orbitals 4s, 4p and 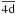 , as used in the Cr ii calculation.
, as used in the Cr ii calculation.
Energy differences from the Ground State for the lowest 28 3d5 and 3d44s target states, and 9 other 3d44p target states, per model.
All Figures
 |
Fig. 1 Graphic representation of the percentage difference of the LS energy levels compared to NIST per model. |
| In the text | |
 |
Fig. 2 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
| In the text | |
 |
Fig. 3 Collision strengths as a function of incident electron energy in Rydbergs for the fine structure transition |
| In the text | |
 |
Fig. 4 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
| In the text | |
 |
Fig. 5 Collision strengths as a function of incident electron energy in Rydbergs for the fine structure transition |
| In the text | |
 |
Fig. 6 Effective collision strengths as a function of log electron temperature in Kelvin for the fine structure transitions |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.