| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201015013 | |
| Published online | 23 November 2010 | |
The MeqTrees software system and its use for third-generation calibration of radio interferometers
Netherlands Institute for Radio Astronomy (ASTRON),
PO Box 2,
7990AA
Dwingeloo,
The Netherlands
e-mail: noordam@astron.nl; smirnov@astron.nl
Received:
18
May
2010
Accepted:
16
August
2010
Context. The formulation of the radio interferometer measurement equation (RIME) for a generic radio telescope by Hamaker et al. has provided us with an elegant mathematical apparatus for better understanding, simulation and calibration of existing and future instruments. The calibration of the new radio telescopes (LOFAR, SKA) would be unthinkable without the RIME formalism, and new software to exploit it.
Aims. The MeqTrees software system is designed to implement numerical models, and to solve for arbitrary subsets of their parameters. It may be applied to many problems, but was originally geared towards implementing Measurement Equations in radio astronomy for the purposes of simulation and calibration. The technical goal of MeqTrees is to provide a tool for rapid implementation of such models, while offering performance comparable to hand-written code. We are also pursuing the wider goal of increasing the rate of evolution of radio astronomical software, by offering a tool that facilitates rapid experimentation, and exchange of ideas (and scripts).
Methods. MeqTrees is implemented as a Python-based front-end called the meqbrowser, and an efficient (C++-based) computational back-end called the meqserver. Numerical models are defined on the front-end via a Python-based Tree Definition Language (TDL), then rapidly executed on the back-end. The use of TDL facilitates an extremely short turn-around time (hours rather than weeks or months) for experimentation with new ideas. This is also helped by unprecedented visualization capabilities for all final and intermediate results. A flexible data model and a number of important optimizations in the back-end ensures that the numerical performance is comparable to that of hand-written code.
Results. MeqTrees is already widely used as the simulation tool for new instruments (LOFAR, SKA) and technologies (focal plane arrays). It has demonstrated that it can achieve a noise-limited dynamic range in excess of a million, on WSRT data. It is the only package that is specifically designed to handle what we propose to call third-generation calibration (3GC), which is needed for the new generation of giant radio telescopes, but can also improve the calibration of existing instruments.
Key words: methods: numerical / methods: data analysis / techniques: interferometric / techniques: polarimetric
© ESO, 2010
1. Introduction
The MeqTrees software system has been designed to implement an arbitrary measurement equation (i.e. a numerical model of an instrument and/or process), and to solve for arbitrary subsets of its parameters. In this paper we will concentrate on the simulation and calibration of data taken with radio telescopes. After all, that is the subject for which MeqTrees was developed originally, and for which it is most urgent. It is also an excellent subject for demonstrating the special capabilities of MeqTrees.
Until recently, radio interferometers like WSRT, VLA, ATCA, GMRT were designed so that they could be approximated by a relatively simple instrumental model. Their stations1 were carefully designed so that the shape of their spatial response beams could be assumed to be “identical” at all times. In addition, the instrumental error associated with a station can be represented in this model by only two complex gain factors (one for each polarization), which may vary in time and frequency. Because their stations are parabolic dishes that are pointed towards the observed field, instrumental polarization effects can be treated (or not) as small “leakage” terms.
Before 1980, first-generation calibration (1GC) was based on “open-loop” methods, making separate calibrator observations before and after, and relying on instrumental stability in between. The result was a dynamic range2 of about 100:1. However modest, this was enough for a plethora of important discoveries.
Around 1980, the invention of self-calibration (Cornwell & Wilkinson 1981; see also summary by Ekers 1983) ushered in the era of second-generation calibration (2GC). Selfcal is a “closed-loop” method which continuously estimates the complex station gain factors with the help of one or more bright sources in the field of view. In this process, the utilized Sky Model is improved also. Selfcal has been spectacularly successful, and has led to a blossoming of techniques, software packages, and beautiful results. It allows astronomers to achieve dynamic ranges in excess of 104 − 105 as a matter of routine, depending on how well the instrument approximates its simplified model. Record dynamic ranges of well over 106 have been achieved at the WSRT by de Bruyn (2006), de Bruyn et al. (2010, in prep.; see also Sect. 8).
Radio astronomy is currently going through a remarkable worldwide burst of building new telescopes and upgrading existing ones3. These instruments present a new, two-pronged calibration challenge. On the one hand, they are much more sensitive, so more subtle instrumental effects will have to be taken into account to reach the thermal noise. On the other hand, the use of new technology like phased arrays complicates the instrumental model. Therefore, what we propose to call third-generation calibration (3GC) will require a more complex, able, and a general form of selfcal.
In 1996, Hamaker et al. developed a formulation of an explicit radio interferometer measurement equation (RIME) for a generic radio telescope. Further work by Hamaker (2000) led to a fully 2 × 2 matrix formulation of the RIME, which provides the mathematical underpinnings for 3GC. Without this full-polarization formalism, calibration of the new telescopes would be difficult. However, although the RIME is widely recognized as being correct, complete and universal, its actual adoption has been slow. This is caused to a large extent by the sustained success of the existing 2GC data reduction packages (AIPS, NEWSTAR, MIRIAD, DIFMAP). The ensuing low rate of evolution of calibration techniques could be a risk factor for the new telescopes.
One of the most important challenges of 3GC is dealing with Direction-Dependent Effects (DDEs), i.e. instrumental effects that can no longer be assumed to be constant over the field of view. The most important DDEs are typically caused by the ionosphere (mostly phase and Faraday rotation), and by station beamshapes that differ substantially from each other, and/or vary individually in frequency and time. Tackling DDEs implies that one has to solve for a much larger number of RIME parameters than before. Besides the practical problem of extra processing (which may well turn out to be a major bottleneck, but will not be discussed here), this raises some more fundamental issues about whether there is enough information available for 3GC. And, last but not least, methods are needed to correct for DDEs once they are known, which is non-trivial.
At this moment, it is not yet clear how some of the new generation of telescopes will be calibrated to the necessary precision. The MeqTrees software system is a tool that can play a role in building that understanding on several levels. First of all, it is firmly based on the explicit RIME. Secondly, it has many built-in features for generalized selfcal, such as allowing for arbitrary RIMEs with arbitrary parameterizations, and solving for arbitrary subsets of RIME parameters, including source parameters. These parameterizations may be experimented with rather rapidly, since the art of modelling (in Python) is separated from the complex and efficient numerical machinery (in C++) “under the hood”. Rapid progress is also greately helped by the many possibilities for visualization of intermediate results, enabling one to easily see what is actually going on.
The heart of this paper, Sects. 2−6, is a detailed description of how MeqTrees works. Section 7 gives a brief description of the RIME, explains why it is such a powerful formalism, and shows how it pertains to MeqTrees. In Sect. 8, we present some recent results that give a taste of what MeqTrees can do.
2. Nodes, trees, forests
This section gives a broad overview of MeqTrees design (Sect. 2.1) and implementation (Sect. 2.2). Subsequent sections will then elaborate on some of the important concepts and features.
2.1. Design: expression trees
According to Donald Knuth, “trees have been in existence since the third day of creation, and perhaps earlier”. The use of trees as information structures is ubiquitous throughout computing science; Knuth (1973) provides a good introduction. MeqTrees uses trees to represent mathematical expressions. This particular idea dates back to very early work on compilers (Hopper 1952), and in fact was the first application of trees to computer science.
A tree is a type of graph whose nodes are connected in a parent-child hierarchy. A tree node can be parent to zero or more child nodes, and can itself be a child of zero or more other nodes4. Cycles are not allowed. A node having no children is traditionally called a leaf, a node with no parents is called a root. A forest contains multiple trees, which may be interlinked.
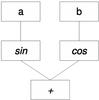 |
Fig. 1 An expression tree. |
A traditional expression tree corresponding to the expression sina + cosb is shown in Fig. 1. This illustrates the main concepts of a tree: a and b are leaf nodes (having no children), representing atomic components of the expression such as constants or variables; “sin” and “cos” are unary function nodes (performing some mathematical operation on their children), and “+” is a binary function node. To compute the value of the expression, we start at the leaves and propagate the values through their parents, performing the appropriate mathematical operations along the way, until we get to the root node (the “+” node, in this case), the result of which is the value of the expression.
In this traditional view, the result of the computation at any one node is a single value, the value of some expression. MeqTrees goes a step further by making the results functions. A typical MeqTree implements a real- or complex-valued function of N real variables, f(x(1),...,x(n)). The most common variables – at least in radioastronomy – are time t and frequency ν. For simplicity, we’ll just use t and ν in all further examples, with the understanding that everything we describe can be generalized to N-dimensional variable space. MeqTrees calls time and frequency axes of variability, or simply axes5. In the example above, if we imagine that a is a function of time, a = a(t), and b is a function of frequency, b = b(ν), then the result of the tree becomes a function of time and frequency, f(t,ν) = sina(t) + cosb(ν).
MeqTrees represents functions as samples on a grid. To do this, we pick a domain in t,ν, and define a gridding over that domain – essentially, two vectors (t1,...,tn) and (ν1,...,νm). The function f can then be represented by a two-dimensional array of samples, {fij = f(ti,νj) } . The result of the root node above – the function f(t,ν) – is then the array { fij } .
 |
Fig. 2 A node computes the value of some function on a grid (which we call the cells) within some domain. The domain on the left is two-dimensional (t,ν) and has identical and contiguous cells on a regular grid. It is also possible to have irregular grids of non-contiguous cells with different sizes, as illustrated on the right (cell size is only relevant for some rather obscure operations). Higher-dimensioned domains are also possible. |
This then, in a nutshell, is the way MeqTrees work. A a request object is created that contains (among other things) the two vectors, (t1,...,tn) and (ν1,...,νm). These are called cells in MeqTree parlance, since they represent the rectangular cells of a two-dimensional grid. Note that the grid stepping does not need to be regular – see Fig. 2 for an example. The request object is a request to compute a function (whatever function happens to be defined by this tree) on a certain grid. This request is passed to a node of the tree (usually the root node). To compute the function, a typical node will pass the request on to its children, and then perform some mathematical operation on the returned results.
This also describes the interface to a node – a node is given a request (representing a gridding), and returns a result (representing a function sampled on that grid). Indeed, since the interface to any tree is via its root node, operationally a tree is indistinguishable from the root node. When parent nodes deal with child nodes, they have no knowledge (nor do they need any) of whether those child nodes are individual leaf nodes, or have whole subtrees hiding behind them.
The result of a parent node is (usually) determined by performing some mathematical operation on the results of its children. The exact operation is determined by a node’s class. Let’s say a parent of class H implements the binary operation (or function) H(a,b). If the results of its two child nodes (or, equivalently, the subtrees rooted at their nodes) correspond to the functions f(t,ν) and g(t,ν), then the result of the parent corresponds to h(t,ν) = H(f(t,ν),g(t,ν)).
A leaf node has no children, and can compute its result (i.e. the function f that it implements) in a self-contained way. This is also determined by its class, for example:
-
MeqConstant
nodes return a constant value,f(t,ν) ≡ c;
-
MeqFreq
nodes return the frequency, f(t,ν) = ν;
-
MeqParm
nodes compute, e.g., a polynomial f(t,ν) = c00 + c10ν + c01t, where cij are read from an external parameter table (these are typically solvable parameters, as will be described below);
-
MeqFITSImage
nodes return, e.g., an image of the sky read from a FITS file. In mathematical terms, an image is a sampled brightness distribution, I(ν,l,m). The sky coordinates l,m are another example of axes of variability;
-
MeqSpigot
nodes interface to a Measurement Set (MS) used to store observational data in radioastronomy, and return visibilities sampled by a particular interferometer, V(t,ν).
To sumarize, a typical tree computes a function defined on a grid in N-dimensional variable space. A forest of trees computes a collection of functions, which together constitute a numerical model. The model may contain solvable parameters which may be optimized in various interesting ways (Sect. 5).
2.2. Implementation
The implementation of MeqTrees consists of three main components:
-
1.
the Tree Definition Language (TDL) is a Python-basedlanguage for building expression trees. It allowsone to succinctly specify nodes and their connections by means ofclass, name, children, and other options;
-
2.
the meqserver is the computational back-end of MeqTrees. It is mostly implemented in C++. A meqserver process takes care of constructing and evaluating trees, and interfacing them to datasets;
-
3.
the meqbrowser is a separate GUI (implemented in Python, and running in a separate process) for controlling meqservers. It parses TDL scripts, instructs servers to build the corresponding trees, and takes care of visualizing the results. (Note that it is also possible to run meqservers in non-interactive mode, without a browser.)
2.2.1. Specifying trees in TDL
Figure 3 gives a (very simple) example of how to specify a tree using TDL. Part of a TDL script is displayed in the middle section of the meqbrowser (see Sect. 2.2.3). TDL (Smirnov 2008) is basically regular Python, plus some operator overloading that allows one to succinctly specify nodes and their connections. The TDL code shown in Fig. 3 demonstrates the basic syntax for specifying nodes.
Rather than always building trees from individual nodes, it is often far more efficient to manipulate higher-level Python objects and frameworks which, while presenting a simplified interface, cause trees to be constructed behind the scene. This can hide a lot of unnecessary detail from the non-expert user, and accelerate development of complicated trees. Python as a languauge is very well-suited for developing hierarchical object-oriented frameworks. We have developed a number of such frameworks in the context of radioastronomy: a lower-level framework called “Meow” (Measurement Equation Object frameWork), and two higher-level frameworks for simulation (“Siamese”) and calibration (“Calico”). More will surely follow.
2.2.2. Meqbrowser and meqserver
Being a semi-interpreted language, Python offers wonderful flexibility and ease of programming, but computing efficiency is not one of its stronger points. The actual computations in MeqTrees are performed by a fast, optimized back-end called the meqserver, which is written mostly in C++. A GUI front-end called the meqbrowser (written in Python) provides a rich interface to the computational back-end. In a typical session, operations are divided as follows:
-
the user loads a TDL script into the front-end (meqbrowser).This script – along with any associated optionsettings – specifies the exact structure of a tree(essentially, the structure of a computation);
-
the meqbrowser executes the TDL code, which results in a string of instructions on how to assemble the tree to be sent to the back-end (meqserver);
-
the meqserver constructs its internal tree representation based on the supplied instructions;
-
the user operates the GUI to specify external data (e.g. a Measurement Set to be calibrated, etc.); references to this data (pathnames, etc.) are also passed to the meqserver;
-
the user operates the GUI to instruct the meqserver to start processing data;
-
the meqbrowser monitors progress and (optionally, upon the user’s instruction) fetches and visualizes intermediate results (see Sect. 2.2.4);
-
it is also possible to bypass the GUI front-end, and operate the meqserver noninteractively (i.e. in batch mode).
Such an architecture allows for great flexibility in specifying how computations are to be carried out (since all the specification is done in TDL/Python), yet avoids the computational inefficiency associated with scripting languages. A lot of thought has been put into making the computational engine as efficient as possible (see Sect. 6). And while in principle a MeqTrees-based computation cannot match the theoretical performance of hand-optimized compiled code, in real-life testing its performance has proven to be either equivalent, or (in the worst case) within a factor of 2 − 3 of hand-optimized implementations.
2.2.3. The meqbrowser GUI
The meqbrowser GUI is composed of three main sections, and a choice of menus and other buttons (Fig. 3). In this example, the contents of the TDL script myFirstTree.py has been loaded by means of the TDL menu at the top, and is displayed in the middle section. The TDL code in the _define_forest() function defines the nodes that make up this very simple tree. The Python code may be edited directly in the browser, or with an external editor. After compilation (i.e. generation of nodes on the meqserver side), the tree is displayed in the left section, where it may be browsed by opening and closing branches. Clicking on a node displays its contents in various ways in a panel in the right section, which may then be inspected interactively. The tree is executed by issuing a request to a named node (here called “rootnode”). The execution is done by means of a _tdl_job() function in myFirstTree.py, which may be called via the TDL Exec button. Upon execution, the various display panels on the right will come alive, showing the node results.
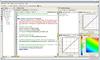 |
Fig. 3 The meqbrowser GUI. |
A TDL script may have compile-time options, whose values may be set interactively in a popup window under the TDL Options button. The script may also have run-time options, which may be set in a popup window under the TDL Exec button. It also offers a choice of available “TDL jobs” to be executed. Clicking on one of them executes the forest, or performs some other function like invoking the CASA imager. Currently selected values of TDL options are retained in a configuration file, which greatly increases the ease of using MeqTrees in practice. The configuration file also comes in handly when a TDL script needs to be executed in batch mode, without the meqbrowser.
Obviously, we have described only the basic functionality of the meqbrowser, which has many powerful features to make it easy (and fun!) for the user to execute trees and to inspect node results. For instance, it has a bookmark button that offers shortcuts to the display of predefined groups of nodes. The Purr button (“Purr is Useful for Remembering Reductions”) activates a rather useful scheme to save and describe all intermediate steps of a data reduction project. Debugging functionality (stop, step, resume etc.) is available along the left edge. It also has a profiler, which measures the processing of all nodes, either individually or by class. Execution progress messages are displayed along the botton, and any errors may be inspected in detail.
2.2.4. Visualization
One of the cornerstones of MeqTrees is its emphasis on visualization at all levels. This is based on the conviction that the quickest way to develop and debug an algorithm is to be able to see what is going on. It cannot be stressed enough that all this visualization is optional, and does not affect computational efficiency when it is not used. We expect that this capability will be very popular, and will soon become the norm. Therefore we envisage a steady increase in sophistication of both standard and application-specific visualization.
In addition to making visualization possible, the meqbrowser also makes it easy. Clicking on any node in the meqbrowser will display either the node status record (very instructive!), or a specific field, or a plot of the latest result in its cache. Various different types of plots or representations may be selected by right-clicking on a node. When displaying images, middle-clicking on the plot itself will produce a vertical and horizontal cross-section through that point. Optionally, flags may be indicated in the plots. As illustrated in Fig. 3, the plotter will adapt automatically to the dimensions of the displayed result: frequency, time, both, etc. If the result has more than 2 dimensions, different cross-sections may be selected. There is also a multidimensional plotter.
Some nodes display their results in specific ways. The MeqSolver node produces plots that indicate the quality of the solution, and its evolution over successive iterations. The ultimate goal is some kind of visualization of the χ2 surface. The MeqComposer node produces a so-called inspector plot, i.e. averaged time-tracks of its multiple results, side-by-side in the same panel. The inspector is a cumulative plot in the sense that the time-tracks just grow in length with succesive results. The MeqDataCollect node also displays the results of multiple nodes in the same plot, but is refreshed each time. It offers two modes, spectra or real vs. imaginary, and is hierarchical: the results of various MeqDataCollect nodes may be combined in the same plot, e.g. with different colors or symbols.
Ease of use is greatly increased by a menu of meqbrowser bookmarks. Clicking on a bookmark conjures up the visualization of a specific node, or a bookpage of associated nodes. Bookmarks are defined by the tree designer, to highlight particular aspects of what the tree is doing. Selected bookpages remain close at hand by means of tabs (see Fig. 3). Nodes make their information available for display by publishing it, i.e. sending it off into the void, to be picked up by another program. A node may be induced to publish every time it gets a new result, which is the default for bookmarked nodes. This makes it easy to watch intermediate results while the tree is executing a sequence of requests.
Although the standard visualization of MeqTrees offers substantial functionality, we expect that many users will develop specialised visualisation nodes for their specific application areas. This will be encouraged and supported, for instance by offering nodes and other tools (like a result object) to make this easier. For the moment, the user-definable nodes PyNode and PrivateFunction should do.
2.2.5. On the choice of languages
While for a lot of scientific software, programming language is chosen on the basis of nothing more than the author(s) personal preference and/or proficiency, and needs no further justification, MeqTrees development has taken the unusual route of combining two languages (C++ and Python). The reasons for this perhaps require further elaboration.
Python is sometimes thought of as “only” a scripting language, but in fact it is a powerful high-level language for structured and object-oriented programming. A number of very capable Python libraries and frameworks for scientific programming have emerged in recent years (most prominently numpy/scipy6), and it also offers bindings to C++ GUI and visualization toolkits such as Qt and Qwt. This makes it feasible to write large and feature-rich applications completely in Python (the meqbrowser being a case in point). Casual programmers find it easier to pick up than a compiled and strongly-typed language such as C++, which is why many astronomers dabble in Python scripts, but very few dare to write C++ programs. On the other hand, programmers equally proficient in both can usually (in the authors’ personal experience, at least) implement a given algorithm in Python much more rapidly than in C++. These are the reasons behind Python’s recent success and adoption as the high-level language component of many projects, including CASA and MeqTrees (specifically, TDL).
The question then remains, why use C++ at all. Being semi-interpreted and late-binding, Python has two drawbacks. The first of these is that errors (with the exception of syntax) are only detected when the offending piece of code is actually executed, whereas a compiled language will catch many errors at the compilation stage. This can lead to some unusual bugs, and makes proper test coverage all the more important, especially for large applications. In the authors’ experience, however, this consideration is far outweighed by the considerably increased development speed. It is probably true that a poorly-tested Python application will tend to have more bugs than a poorly-tested C++ application (though the two will probably be equally useless!). On the other hand, the Python application will have been developed much faster, leaving much more time to find and fix the bugs. This drawback, therefore, only really applies to poorly-tested code.
The second – and far more fundamental – drawback of Python is that a semi-interpreted language is inherently slower to execute than compiled code. Any computation requiring a large number of iterations over multiple lines of code (such as e.g. the nested loops so often appearing in numerical programming) becomes grossly inefficient when implemented in Python. In addition, the relatively high abstraction level of the language makes it practically impossible to optimize for memory access and CPU cache usage, which makes it a poor choice for High-Performance Computing (HPC) applications. These remain the domain of low-level languages such as FORTRAN, C and C++.
A common way to get the best of both worlds (easy and rapid development, plus computational efficiency) is to implement the core computations in a low-level language, while using Python as a high-level binding. Different projects take a different approach to where they put the language boundary. For example, CASA can be thought of as coarse-grained, since it consists of rather large tasks written in C++, with Python used for high-level task control and “glue”. At the other end of the spectrum, the numpy/scipy library is very fine-grained, implementing array operations (including some rather advanced operations such as FFT, filtering, statistics and morphology) in C, while leaving the rest of the algorithm to be implemented in Python. MeqTrees occupies a position somewhat between the two (while in fact adopting some components of both).
Note that the Python component of MeqTrees is implemented as a layer on top of the core C++ libraries. The tree-building and evaluation layer has no awareness of nor dependence on Python. In priciple, this means that the core libraries can be directly called as a C++-only toolkit. The success of TDL, however, has meant that we have not (to date) explored this possibility.
3. Data model
We have described how MeqTrees uses trees to represent mathematical expressions that comprise a numerical model. This is only half of the story; the other half is the actual computation, i.e. what kind of data can be fed into these expressions, and how efficiently can it be processed. The capabilities of MeqTrees are in large part determined (and limited) by this underlying data model. This section describes the data model in more details.
3.1. Grids and functions
As stated previously, the atomic unit of computation in MeqTrees is a function represented by a set of samples over an N-dimensional grid, e.g., a function of frequency and time f(t,ν). Internally, this is represented by a cells object specifying the grid – containing vectors of, e.g., times (ti) and frequencies (νj) – and an N-dimensional array of samples, e.g. (fij = f(ti,νj)). For historical reasons the latter object is called a vells. A vells object is placed into a container called a vellset (the rationale for this will be explained in Sect. 5). A cells and a vellset together then constitute a result object (Fig. 4). A result object is the unit of data that is passed between nodes.
 |
Fig. 4 The layout of a basic result object. |
If a function does not vary over a given axis, then the dimension of its vells along that axis can be equal to 1, i.e. it can be represented by fewer actual data points. For example, given a cells of M times and N frequencies (and assuming time is the first axis and frequency is the second axis in our grid – the ordering of axes is fixed prior to computation), a function can be represented by vells with dimensions of:
-
M × N,
for a function variable both in time and frequency;
-
M × 1,
(or, equivalently, just an M-vector) for a function variable only in time;
-
1 × N,
(this is not equivalent to an N-vector, since frequency is the second axis); for a function variable only in frequency;
-
1,
for a constant value.
All mathematical operations transparently handle vells of different dimensions. For example, if the “+” node in Fig. 1 receives an M × 1 array from one child and a M × 1 array from the other child, it will perform M additions and return a M × 1 array (i.e. a function of time only). If, on the other hand, it receives an M × 1 array (function of time) and a 1 × N array (function of frequency), then it will perform M × N operations and the result will be an M × N array (function of time and frequency). These decisions are made directly in the tree at runtime, so the exact same tree can be used to compute an expression involving only constants, or an expression involving functions of time, frequency, etc. In the latter case the computation is automatically optimized in the sense that the tree keeps track of what values depend on what axes, and only executes the mimimum number of calculations.
This is actually one of the most powerful features of MeqTrees. It is often the case in numerical modeling that one starts with a simple model (i.e. constant parameters), and adds complexity (e.g. parameters with time dependence) later. With traditional code, adding a time dependency to a particular branch of a calculation requires that arrays be resized, for-loops added to iterate over time, bugs introduced and squashed again, etc. Depending on the complexity of a piece of code, this can become quite a daunting task, if not an insurmountable barrier to experimentation. With MeqTrees, you only need to change the property of a parameter up in the tree, and time dependence is then automatically propagated throughout all calculations.
3.2. Scalars and tensors
Scalar functions have a single real or complex value at each grid point. A tensor function of type (dimensionality) n1,n2,...,nk has n1 × ... × nk values for every grid point. For example, the 2 × 2 coherency and Jones matrices used in the RIME are type-2, 2 tensor functions. An efficient representation of tensor functions is therefore important for efficient implementations of the RIME.
MeqTrees represents tensors by a result object containing a list of n1 × ... × nk vellsets, and a vector of integers (n1,...,nk) describing the dimensionality. Figure 5 shows a tensor result corresponding to a 2 × 2 matrix. Each matrix element is represented by a separate vellset (though all share a common cells object, thus a common grid definition). This means, among other things, that each element of a matrix can have independent axes of variability. Operationally, it is quite common to see diagonal matrices where the diagonal elements are functions of frequency and/or time, while the off-diagonal elements are zero (and thus constant). Such tensors can be most efficiently represented with this scheme.
 |
Fig. 5 The layout of a tensor result object. |
Most node classes can transparently accept tensor arguments. The normal convention is to perform the corresponding mathematical operation element-by-element. All arguments must then have the same tensor dimensions (or, as a special case, be scalar, in which case the scalar value is reused for all elements), and an error is reported otherwise.
MeqTrees also provides a few specialized tensor nodes. The MatrixMultiply node is used to multiply matrices (as well as vectors). The MatrixInvert22 node inverts 2 × 2 matrices7. The Composer can combine the results of multiple nodes into a single tensor, and the Selector extracts individual tensor elements.
4. Data flags
Radio astronomy has to operate in an environment in which there are many external and internal sources of Radio Frequency Interference (RFI). It is therefore important to be able to flag bad data values, and propagate these flags throughout all calculations, so that results derived from bad data are also properly flagged and ignored as necessary.
MeqTrees can associate a flag vells with each vellset of a result. A flag vells is an array of integer flagwords that follows the same dimensionality rules as for normal vells arrays (see Sect. 3.1), i.e. given a cells of N time and M frequency points, a flag vells may have dimensions of 1, N, 1 × M, or N × M. The latter case associates a separate flagword with every time/frequency point – a raised bit in the flagword wij indicates bad data at ti,νj. The intermediate cases correspond to entire times or frequencies being flagged at once, while the first (and admittedly not very useful) case has a single flagword for the entire domain. The different vellsets of a tensor result may have different flag vells, or may share flags by reference (see Fig. 6).
 |
Fig. 6 The layout of a result object with flags. Note that vellsets 1, 1 and 2, 2 share the same flags, while vellsets 1, 2 and 2, 1 have no flags at all. |
Flag vells are automatically propagated through tree nodes in a mathematically sensible manner. For example, when an Add node receives flagged results from its children, the flag vells associated with its result is a bitwise-OR of all the child flags. This means that at the root of the tree, the final result will have flags for every t,ν point where the resulting value is derived from something that was flagged. Statistical and reduction operations (such as taking the mean over a certain set of axes) will also ignore flagged values when computing the statistics.
The flagword contains 32 individual bits, which allows for some very versatile flag management. Since flags can be built up via different procedures (automatic flagging algorithms, heuristics based on metadata describing system status during measurement, manually raised flags), it is exteremely useful to associate these different flagsets with different bit positions in the flagword. The user then has the option of activating or ignoring specific flagsets via a bitmask of currently active flags.
Flags can be preserved under storage, if the data format supports them. For radio astronomical data, a standard storage type is the Measurement Set (Kemball & Wieringa 1996), which defines standard columns for boolean flags. MeqTrees extends this by specifying an additional column of bitwise flags.
4.1. Flagging
Flags can also be generated directly inside a tree. MeqTrees offers a very simple but versatile scheme for this. The MeqZeroFlagger node sets flags in its child result based on a comparison to zero. The user then has to supply some subtree that produces a result that can be used as a discriminator, e.g. in which “bad” data corresponds to values greater than zero. The MeqMergeFlags node is then used to merge the new flags with those of the original data.
Since the discriminator expression is supplied by an arbitrary subtree, any type of flagging can be implemented, from simple data clipping, to flagging based on the value of some completely unrelated expression defined over the same domain (such as the value of a solution, see Sect. 5).
5. Parameters and model fitting
Consider a mathematical model, i.e. some function M(ν,t) that depends on a number of parameters (p1,...,pk) = p. We denote this as M(ν,t;p). Model fitting is the process of finding a value of p that minimizes the difference (according to some predefined metric) between measured data Dij = D(νi,tj) and Mij(p) = M(νi,tj;p). We also call this solving for p. In radio astronomy, the model M is given by some parameterization of the RIME, and the process of model fitting is called calibration. This is explained in more detail in Sect. 7, here we first want to describe the general approach to model fitting employed in MeqTrees.
5.1. Solving in MeqTrees
The MeqTrees approach to solving is as follows (Fig. 7). A set of subtrees of arbitrary complexity implements the model M. The model is not necessarily a single function, but can be a whole set of functions, e.g. {M(pq)} , giving the visibilities per baseline p − q (see Sect. 7). These model trees can be quite similar to the simulation trees discussed in that section. At certain parts of the model are the unknown parameters – these are represented by MeqParm nodes. MeqParms are initialized with best guesses (or previous solutions read from disk, if available).
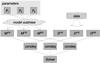 |
Fig. 7 A schematic layout of a solver tree. |
A parallel set of subtrees provides the data D(pq). These subtrees can be (and usually are) as simple as a single MeqSpigot node (which interfaces to a Measurement Set containing visibility data), but can also contain preprocessing steps as needed. The two sets of subtrees are linked up via MeqCondeq nodes, which are in turn all children of a MeqSolver.
At the beginning of a solution, the MeqSolver issues a special request that designates a subset of the MeqParms as solvable. Subsequently, trees that contain solvable MeqParms, when asked to compute a result, automatically augument it with partial derivatives with respect to the solvable parameters ∂M(pq)/∂pk. Note that this is completely transparent to the user – any tree that can compute a function can also compute the derivatives of that function (see below).
MeqCondeq nodes then form up the difference Δ(pq) = M(pq) − D(pq), and also the partial derivatives w.r.t. each solvable parameter, ∂Δ(pq)/∂pk, and return these to the solver. The solver uses some algorithm to determine a set of incremental parameter updates Δp, and sends these updates back up the tree to the MeqParms, at which point the procedure is repeated until convergence has been achieved, or a maximum number of iterations has been reached.
5.2. Estimating the derivatives
MeqTrees currently estimates first derivatives via finite differencing. If a subtree implementing the function f(ν,t) depends on the solvable parameters p1 and p2, then the vellset in its result (Fig. 8) will actually contain three vells: the “main” value f(ν,t;p1,p2), plus two “perturbed” values f(ν,t;p1 + δ1,p2), f(ν,t;p1,p2 + δ2).
 |
Fig. 8 The layout of a result object with perturbed values. |
If another subtree for g(ν,t) depends on solvable parameters p2 and p3, then its result will likewise contain three values: g(ν,t;p2,p3), g(ν,t;p2 + δ2,p3), g(ν,t;p2,p3 + δ3). Note that each vellset also contains a vector of spids (solvable parameter identifiers), which indicate what solvable a particular perturbed value is associated with.
Now consider how this information propagates down the tree. If f
and g are the child nodes of a MeqAdd node returning
h(ν,t) = f(ν,t) + g(ν,t),
then the addition must be executed four times: 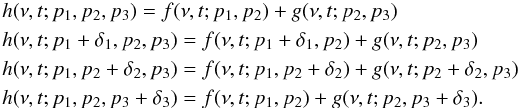 Note that the left-hand side contains the “main” value of h plus three
perturbed values of h with respect
to p1,p2,p3,
while the right-hand side contains a mix of main and perturbed values
of f and g, combined according to a simple looping
algorithm. This kind of loop over perturbed values is automatically executed inside every
MeqTrees node, thus ensuring that the root of the tree computes perturbed values for every
solvable parameter in the tree.
Note that the left-hand side contains the “main” value of h plus three
perturbed values of h with respect
to p1,p2,p3,
while the right-hand side contains a mix of main and perturbed values
of f and g, combined according to a simple looping
algorithm. This kind of loop over perturbed values is automatically executed inside every
MeqTrees node, thus ensuring that the root of the tree computes perturbed values for every
solvable parameter in the tree.
Given a main and a perturbed value, the actual derivative is estimated as:
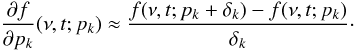 Note
that we keep writing ν,t here to emphasize the fact that
both f and its derivatives are potentially functions of many variables
such as frequency and time. That is, a separate value and a separate derivative are
computed at every time-frequency point.
Note
that we keep writing ν,t here to emphasize the fact that
both f and its derivatives are potentially functions of many variables
such as frequency and time. That is, a separate value and a separate derivative are
computed at every time-frequency point.
5.3. Least-squares solver
A (weighted) least-squares solver minimizes the
difference D − M in a least-squares sense, i.e. finds
a p that minimizes the chi-squared sum: 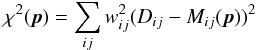 (1)where
wij are (optional) weights. Different
methods of minimizing χ2 are known; the suitability of a
particular method depends on properties of M such as degree of linearity
with respect to p, etc. Since MeqTrees can implement models
of arbitrary complexity, our initial designs have tended towards a “policy-free” solving
scheme that works adequately in most cases but is not necessarily the optimal one for each
particular case. We have therefore decided to use the AIPS++/CASA solver (Brouw 1996), which implements the Levenberg-Marquard
algorithm (Madsen et al. 2004). The LM algorithm is
a type of gradient descent method which is particularly well-suited to nonlinear problems.
(1)where
wij are (optional) weights. Different
methods of minimizing χ2 are known; the suitability of a
particular method depends on properties of M such as degree of linearity
with respect to p, etc. Since MeqTrees can implement models
of arbitrary complexity, our initial designs have tended towards a “policy-free” solving
scheme that works adequately in most cases but is not necessarily the optimal one for each
particular case. We have therefore decided to use the AIPS++/CASA solver (Brouw 1996), which implements the Levenberg-Marquard
algorithm (Madsen et al. 2004). The LM algorithm is
a type of gradient descent method which is particularly well-suited to nonlinear problems.
An important problem with any solver is the handling of ill-conditioned problems (i.e. when there’s not enough information to solve for all unknowns). The AIPS++/CASA solver works by accumulating normal equations (received from the MeqCondeqs), then inverting the solution matrix. The inversion is done by SVD, which detects ill-conditioning and handles it by effectively reducing the number of unknowns (this is called reducing the rank of the solution). A number of solver diagnostics, including rank and condition numbers, is automatically generated by the MeqSolver node, and may be visualized by the user to get an indication of the quality of the fit.
5.4. Alternative approaches
Other kinds of solvers are being actively considered for inclusion in MeqTrees. These may require different ways of calculating the derivatives:
-
analytic derivatives are known to produce more stablesolutions. MeqTree nodes can be adapted to compute andpropagate analytic derivatives via the chain rule (and fall back tofinite differencing should a node be encountered that cannotcompute analytic derivatives);
-
second derivatives may allow for better solvers. Second derivatives may be computed via double-differencing, or analytically;
-
Bayesian solvers, rather than using derivatives, sample the function over a “cloud” in parameter space. That is, they generate a random set of vector offsets δ1,...,δn, and compute the perturbed model at each offset M(p + δk). Note that our current scheme of computing perturbed values with respect to each solvable parameter can be considered a special case of this, each vector offset δk being a simple shift along axis k in parameter space, orthogonal to all the other offsets.
In principle the MeqTree code and internal data structures can be easily adapted to any of the approaches listed here.
5.5. MeqParms
A MeqParm node represents solvable parameters of the model. One of the most powerful features of MeqTrees is that each parameter can be a function of ν,t (and, naturally, any other dimensions). The current implementation provides a polynomial, so the actual solvables are coefficients of the polynomial. The degree of the polynomial may be specified separately for each MeqParm, and for each solution. Other smooth functions of ν,t may of course be obtained by combining polynomial MeqParms into subtrees.
MeqParms can store their solutions to MEP tables. The solutions are identified by domain (e.g. in ν,t). A typical calibration procedure involves solving for one subset of parameters, storing these solutions, then going on to solve for another subset, while using the stored solutions of the first set when evaluating the model. MEP tables have a Python interface, so the stored solutions can be analyzed, plotted and/or reprocessed with external tools.
5.6. Continuity and solve domains
In many problems, radio astronomy not excepted, data volumes preclude processing an entire observation at once. Instead, data has to be broken up into chunks along the e.g. time and/or frequency axes, and processed sequentially. MeqTrees calls such chunks tiles. When solving for parameters, solutions are by necessity generated on a tile-by-tile basis. On the other hand, physical considerations can often provide continuity constraints between tiles, and it is important to take advantage of these constraints.
In the simplest case, a MeqParm will generate one solution per tile, and use that solution as the starting value for the next tile. No explicit continuity constraint is imposed. In this case one makes the tile size small, in accordance to how quickly a parameter is expected to vary. It is possible that the expected variation in a parameter is slower than the largest practical tile size. An extreme case of this is when trying to solve for a single value across the entire measurement. If the data for the entire measurement does not fit in memory, obtaining a global solution requires multiple runs through the data, which may impose unacceptable I/O penalties. In general this is a very thorny problem. One (rather inelegant) way around this is doing tile-by-tile solutions with the largest possible tile, and smoothing the solutions afterwards. Other options are averaging the data, or extracting a strided subset of the data.
A more complicated case relates to scenarios where we want to simultaneously solve for parameters that have different degrees of variability. A typical example from radio astronomy would be receiver phases (which are almost constant in frequency, but vary rapidly in time) and bandpasses (which vary very slowly in time, but have very complex behaviour in frequency). MeqParms address this via a technique called subtiling. Each MeqParm may be setup with its own subtile size, and an independent solution is then done within each subtile of the larger overall tile. In the example here, phases would have a subtile of size 1 in time, and bandpasses would have a subtile of size 1 in frequency. A separate phase solution per timeslot (constant across all frequencies) and a separate bandpass per frequency (constant across all times in the tile) would then be obtained.
The combination of tile size, subtiling and polynomial degrees makes for a very flexible way to specify parameter behaviour. It is in fact a challenge to present all these options to the user in a non-bewildering fashion.
6. Performance considerations
Given the large data volumes produced by radio astronomical instruments (and the even bigger volumes required to simulate instruments of the future such as the SKA), computational performance is always going to be an important issue, both in terms of processing speed and memory use.
With any software, there is generally a tradeoff between flexibility and efficiency. Highly optimized code is by its nature difficult to revise and extend, and vice versa. MeqTrees tries to get around this problem by providing highly optimized building blocks (i.e. nodes), while offering maximum flexibility in putting them together.
There is always some overhead associated with navigating a tree and passing results around, but this overhead is independent of domain size, whereas actual computational cost increases linearly with the number of, e.g., time and frequency points. This implies that MeqTrees is at its least efficient when using single-cell domains, where housekeeping overhead dominates, and at its most efficient when using large domains, where computational cost dominates. In practice, when using domains of 500 − 1000 cells, the performance of MeqTrees becomes comparable with that of hand-optimized code. This is achieved through a number of generic optimization techniques, which will be described below.
6.1. Optimal use of axes
Recall from Sect. 3.1 that a vells represents the value of a function using the minimum required number of axes of variability. Values with only a time or only a frequency dependence are passed around as vectors, and are expanded to arrays only when both a time and frequency dependence arises. This avoids redundant computation. It is also possible to explicitly structure trees to take advantage of this, i.e. to introduce extra axes as “late” in the computation as possible.
6.2. Result caching
Each node maintains an optional result cache, which allows computations to be reused. A straightforward but very powerful scheme of dependency tracking allows a node to figure out exactly when a result may be usefully cached. For example:
-
a node with multiple parents should cache its result until allparents have retrieved it;
-
when solving, a result with no dependence on solvable parameters can be cached until the next iteration. Results that do depend on solvable parameters are never cached, since they’re updated with each iteration;
-
a result with no dependence on time can be cached until the next tile (assuming we’re iterating over time);
-
if all parents have cached their results, a child may discard cache.
In practice, this means that only the minimum necessary part of the tree is reevaluated when going from one solver iteration to the next, or from one tile to the next. It is also possible to fine-tune the caching policies to trade off computing time vs. memory footprint, etc.
6.3. Parallelism
In these days of cheap computing, parallel processing is the obvious approach to large computational problems. MeqTrees has been designed and implemented with this in mind. The tree paradigm provides ample opportunities for parallelisation, since different branches of the tree (and different trees of the forest) may be executed concurrently. On the other hand, the fact that trees may (and usually do) share branches towards the top makes for interesting scheduling problems – it’s not much use to execute branches in parallel if they are going to spend most of their time waiting for the result of a single shared sub-branch.
Meqserver has supported multithreading for a long time, so multiple-core machines may execute different branches of a tree concurrently. It employs a worker thread pool scheme, which avoids shared-branch bottlenecks. If a thread becomes stuck waiting for the result of a shared branch, another worker thread is woken up and assigned to a different part of the tree. In practice, this means that on a modern four-core machine, MeqTrees will happily keep all four cores fully occupied (as long as there’s sufficient paralellism in the tree itself).
Parallelism across a cluster is a far trickier proposition – one has to consider not only scheduling problems, but also cost of data transport between cluster nodes. In 2008, the first MPI version of MeqTrees was tested on a cluster in Oxford, with an eye on large-scale simulations for the SKA radio telescope8. This version allows parts of the tree to be distributed across a cluster, and uses MPI to pass results between children and parents that reside on different nodes. This version was tested across 8 cluster nodes and scaled reasonably well, albeit on a rather simple simulation problem. It is clear that the biggest amount of thinking needs to be put into the problem of how to distribute a given tree across a cluster efficiently.
7. The measurement equation of a generic radio interferometer (RIME)
The pressing need for 3GC is uncontroversial, but its specific development may follow various routes. Important issues are the dynamic range limitations caused by bright sources, the application of DDEs, and the imaging and deconvolution of residuals. We propose to expose our approach to the DDE problem in a follow-up paper, and avoid discussing specific calibration schemes here. Some examples, however, will be necessary, in order to show how MeqTrees can support such flexible schemes (and, indeed, why it was designed the way it was).
What is clear is that the Measurement Equation (RIME) has a vital role to play. In this section, we will therefore discuss the general structure of the RIME, and some of its properties. We hope to make clear how elegant it is, and thereby to smooth the path to its wider adoption by the radio astronomical community. We will also indicate how the universality and modularity of the RIME opens the way for MeqTrees to offer a set of generic TDL processing scripts, which may be quickly adapted to a wide range of experiments with any radio telescope. The latter is done by means of the simple expedient of plugging in different Jones matrices, or a different sky model. Note that the description of the RIME given here is by necessity qualitative and brief, since we will concentrate on how the RIME pertains to MeqTrees rather than give a full formal exposition.
The RIME was formulated by Hamaker et al. (1996) following preparatory work by Morris et al. (1964). Hamaker (2000) then rewrote it in 2 × 2 matrix form, which is the one we follow here9. Note that, since all the existing 2GC packages were written before the RIME was formulated, they implicitly implement a limited and approximate form of the RIME, usually optimized for a specific telescope.
The RIME is a formalism rather than one specific equation, and so it may
be written down in many forms. A particularly elegant and simple form describes a “mostly
empty” sky of discrete sources. In this form of the RIME, the predicted value of the
visibility sample Vpq is given by:
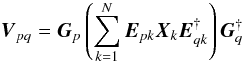 (2)where
Vpq is the 2 × 2 visibility
(also called coherency, or uv-data) matrix measured by the
interferometer formed by stations p and q. The sum is
taken over the contributions Xk
from N discrete sources in the field, at
positions lk,mk.
They are corrupted by instrumental effects that are represented by so-called Jones matrices
(Jones 1941). All the terms of Eq. (2) are 2 × 2 matrices, and “†” represents the
Hermitian (or conjugate) transpose operator. The
Epk term is itself product of
a number of Jones matrices corresponding to direction-dependent effects (DDEs)
associated with station p and
direction lk,mk,
while Gp is a product of Jones
matrices for the direction-independent effects (DIEs) associated with
station p.
(2)where
Vpq is the 2 × 2 visibility
(also called coherency, or uv-data) matrix measured by the
interferometer formed by stations p and q. The sum is
taken over the contributions Xk
from N discrete sources in the field, at
positions lk,mk.
They are corrupted by instrumental effects that are represented by so-called Jones matrices
(Jones 1941). All the terms of Eq. (2) are 2 × 2 matrices, and “†” represents the
Hermitian (or conjugate) transpose operator. The
Epk term is itself product of
a number of Jones matrices corresponding to direction-dependent effects (DDEs)
associated with station p and
direction lk,mk,
while Gp is a product of Jones
matrices for the direction-independent effects (DIEs) associated with
station p.
Note that Eq. (2) assumes that all instrumental effects are station-based, i.e. can be fully described by Jones matrices, each associated with a particular station p. This is called the selfcal assumption. It is crucial because it increases the ratio between the number of equations (given by measured uv-data) and independent unknowns to the level where selfcal generates non-trivial solutions. In principle the observed data is also corrupted by interferometer-based errors (also called closure errors), which are conventionally modelled via extra multiplicative and additive terms on the elements of Vpq. These can then be solved for (with some care), assuming the errors are sufficiently smooth in time.
The 4 elements of Vpq represent the 4 possible
correlations between the two pairs of output signals from the two stations of an
interferometer. These signals are usually labelled X and Y
for linearly polarized receptors, or L and R for
circularly polarized receptors10:
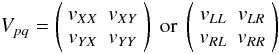 in
which element vYX predicts the value of the
correlation between the Y signal of station p with the
X signal of station q etc.
in
which element vYX predicts the value of the
correlation between the Y signal of station p with the
X signal of station q etc.
7.1. Implementing the RIME in MeqTrees
Implementing an equation like (2) in MeqTrees is very straightforward. On the top level, Eq. (2) is just a small subtree composed of MeqAdd, MeqMatrixMultiply and MeqConjTranspose nodes (see Fig. 9). Such a subtree is constructed for every p,q pair. Note that the children of the subtree – nodes returning the constituent matrices of Eq. (2), shown in lighter colour in the figure – can themselves be represented by arbitrary subtrees.
Figure 9 captures the essense of the modularity and flexibility of MeqTrees. The ability to plug in arbitrary subtrees (including arbitrary solvable parameters) to represent the source contributions Xk and the Jones matrices Epk and Gp effectively allows for arbitrary parameterizations of the sky and instrumental models.
7.2. The local sky model
The RIME predicts the visibilities observed by a particular radio telescope, given a
particular source distribution. In Eq. (2),
Xk is the intrinsic
coherency that represents source k. The exact form of this matrix, and
the corresponding subtree of Fig. 9, depends on the
source model. In principle, X is a function of
u,v coordinates X(u,v)
(which, per each baseline pq, are themselves a function of time and
frequency) that is a Fourier Transform (FT) of the brightness
distribution ℬ(l,m), relative to source
center. In the case of a point source (i.e. a delta function), this is trivial:
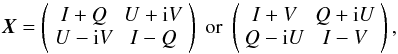 (3)depending on whether a
linear (i.e. orthonormal) or circular polarization basis is used11. For extended sources, more complicated forms
of X(u,v) may be provided via their own
subtrees. The following forms have been implemented in MeqTrees at time of writing:
(3)depending on whether a
linear (i.e. orthonormal) or circular polarization basis is used11. For extended sources, more complicated forms
of X(u,v) may be provided via their own
subtrees. The following forms have been implemented in MeqTrees at time of writing:
-
Gaussian components.
Slightly extended sources may beapproximated by a two-dimensional Gaussian distribution in thelm-plane, as is done in the NEWSTAR package. The FT of this is a Gaussian in the uv-plane, which is provided by a simple subtree with flux, extent and orientation parameters.
-
Images.
Most 2GC packages use images (i.e. a gridded ℬ(l,m) representation) as their standard sky model. For images, an FFT followed by degridding provides a computationaly effective way of estimating X(u,v). MeqTrees implements this approach via a combination of MeqFFTBrick and MeqUVInterpol nodes (Abdalla 2009).
-
Shapelets
are another way to efficiently model extended source structure. ℬ(l,m) is decomposed into shapelets in the lm-plane; this can be efficiently evaluated in the uv-plane. The use of this in MeqTrees has been pioneered by Yatawatta et al. (2010, in prep.).
The above source representations may be freely mixed, simply by plugging in different kinds of subtrees for the different Xk terms in Fig. 9. Note how this differs from the traditional 2GC view of a single “sky image”. An image has the advantage of modelling arbitrary source structure, but it is limited by gridding errors (and distortions introduced by DDEs). To maximize dynamic range, a mixed sky model may be required. Such a mixed model may consist of, e.g. point sources and shapelets for the brightest sources, and one or more images for the faint background. This is in principle straightforward to implement via different subtrees.
 |
Fig. 10 The user interface to the MeqTrees Local Sky Model. |
The definitions of the various sources that are relevant for a particular observation are stored in a Local Sky Model (LSM). MeqTrees provides an end-user tool for managing this information (see Fig. 10). Once the user has supplied an LSM, the relevant subtrees are constructed programmatically.
Last but not least, we should note that the parameters of the different source parameterizations are automatically functions of, e.g., frequency and time, and may in principle be solved for just like any other parameter in a tree (always provided the observational data is sufficient to constrain the problem, of course). MeqTrees makes no distinction between instrumental and source parameters: it is possible to solve for any subset of RIME parameters.
7.3. Jones matrices
In Eq. (2), the intrinsic LSM source coherency matrices Xk are “corrupted” by means of 2 × 2 Jones matrices. These are the real heart of the RIME. They represent the DDEs (Epk) associated with station p and direction lk,mk, and DIEs (Gp) associated with station p.
Epk and Gp are in principle themselves matrix products of a series of Jones matrices corresponding to individual physical effects12. Matrix multiplication does not commute, so the individual Jones terms must be placed into the equation in the correct order, corresponding to their physical order in the signal propagation path (but see below).
It is very useful to have a common letter-based nomenclature for the standard Jones
matrices. Below we will give a by no means exhaustive list, with nomenclature mostly
following Noordam (1996). Where appropriate, we
will mention what form the Jones matrix usually takes. Three important forms are the
diagonal matrix, the rotation matrix, and the
scalar matrix: 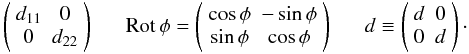 Note
that diagonal or rotational form is subject to choice of basis. For example, a rotation in
an orthonormal basis becomes a special kind of diagonal matrix in the circular
polarization basis. (Below, we will assume an orthonormal basis unless otherwise noted.)
Scalar matrices, on the other hand, are scalar regardless of basis. Within formulae, we
shall use normal-weight capitals (e.g. A as opposed
to A) to distinguish scalar matrices.
Note
that diagonal or rotational form is subject to choice of basis. For example, a rotation in
an orthonormal basis becomes a special kind of diagonal matrix in the circular
polarization basis. (Below, we will assume an orthonormal basis unless otherwise noted.)
Scalar matrices, on the other hand, are scalar regardless of basis. Within formulae, we
shall use normal-weight capitals (e.g. A as opposed
to A) to distinguish scalar matrices.
These three forms are important due to matrix commutation. Scalar matrices commute with everything, while diagonal matrices commute among themselves, as do rotations. This allows us to commute certain Jones terms around the RIME in order to derive new forms of the equation and/or for purposes of computational efficiency.
Common DDEs, in order of appearance in the signal path, are:
-
K-Jones:
the phase term, accounting for the geometric delay andfringe stopping associated with station p and direction l,m. This is a scalar matrix of the form Kp = expi(upl + vpm + wpn), so it may be commuted to any part of the RIME (in fact, phase itself is a sum of contributions from different parts of the signal path, which are commuted together into the overall K-Jones). Commuting Kp and
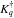 next to
each other, then multiplying them gives the Fourier Transform kernel – it could be
said that K-Jones is at the heart of all interferometery!
next to
each other, then multiplying them gives the Fourier Transform kernel – it could be
said that K-Jones is at the heart of all interferometery! -
Z-Jones:
ionospheric phase and amplitude effects. The latter are usually small enough to be ignored. The phase delay ζ has a known frequency dependence ( ∝ ν-1). Z is a scalar matrix, and so may be commuted anywhere13. For narrow fields, Z can be treated as a DIE (and, for calibration purposes, is absorbed in G-Jones, see below).
-
F-Jones:
ionospheric Faraday rotation. This is a rotation matrix; the angle has a frequency ( ∝ ν-2) dependence.
-
T-Jones:
tropospheric phase delay and extinction, another scalar matrix. For narrow fields, T can be treated as a DIE, and also absorbed in G-Jones during calibration. Alternatively, its values may be provided externally by water-vapour radiometers, as with mm-wave telescopes like ALMA.
-
E-Jones:
the station beamshape (i.e. primary beam gain/phase in direction l,m). This is the most telescope-specific Jones matrix of them all, and the least well understood. For 2GC, it is usually assumed that E-Jones is time-independent and identical across stations, which means that it can be incorporated into the local sky model (in the form of apparent rather than intrinsic fluxes). That this is not the case can severly limit imaging fidelity at instruments such as the VLA (Bhatnagar et al. 2008). Indeed, it can be argued that every radio telescope has or will have an E-Jones problem.
-
P-Jones:
projection matrix, corresponding to the projected position angle of the two receptors of a station on the sky. For dishes with narrow FoVs, this is a DIE, and is a simple rotation (constant for equatorial mounts, and offset by the time-variable parallactic angle for alt-az mounts). For a horizontal dipole array like a LOFAR station, P becomes a more complicated expression (which can also be incorporated into an E-Jones model).
Commonly used DIEs are:
-
D-Jones:
“on-axis” polarization leakage14 between the two receptors.This may be parameterized in terms of dipole orientation error(for linear receptors) and ellipticity. Note that theconcept of “leakage” itself is a carry-over from2GC packages, and is only a first-orderapproximation to the rather complicated polarization behaviourthat can be more generally described by using proper E-Jonesmodels. D-Jones is usually an almost-unity matrix, with smallnon-zero off-diagonal terms.
-
G-Jones:
complex gain, the staple of 2GC. Nominally, this corresponds to the electronic gain of the receivers, but for calibration purposes it cannot always be distinguished from the Z- and T-Jones terms, and so ends up subsuming all three effects. It is a diagonal matrix (unless electronic cross-talk is also incorporated, in which case the off-diagonal terms take on small non-zero values) with rapid variation in time, but little to none in frequency.
-
B-Jones:
electronic bandpass. This is a diagonal matrix like G-Jones, but it has considerable structure in frequency, and only slow (if any) variation in time. Since D-Jones varies on similar timescales, it may be useful to combine the two into a full 2 × 2 matrix.
7.4. Simulation vs. calibration
Real-life applications of the RIME in MeqTrees have, to date, fallen into two broad categories, simulation and calibration.
Simulation has become an increasingly important field in the past decade, due to the large number of new radio telescopes being designed and built. For simulation, the RIME (plus an optional noise term) predicts the output of a [real or theoretical] telescope observing a model sky. Given a sky model, and a set of Jones matrices for the DDE and DIE components (see e.g. Fig. 12), MeqTrees constructs a set of per-baseline trees corresponding to a RIME such as that in Eq. (2), and evaluates them for a series of times and frequencies specified by a Measurement Set (MS). The resulting simulated visibility data is then written out to the MS.
Calibration is, essentialy, model fitting, as described in Sect. 5. The RIME is used to predict model visibilities (similar to the simulation case), but the outputs of the subtrees are then treated as the model functions M(pq) of Sect. 5, and fitted (by solving for their parameters) to the observed data D(pq), which is read from an MS. The resulting residuals are also written out to the MS. If the parameters being solved for are the complex station gains (the G-Jones term), this procedure is the equivalent of traditional 2GC selfcal. However, since MeqTrees in principle allows for arbitrary parameterizations, the same approach can be used to solve for, e.g., coefficients of beam models, ionospheric models, etc.
These two applications of the RIME are superficially similar, in that in both cases the RIME is used to predict model visibilities. However, the kinds of Jones matrices employed can be significantly different. For simulations, we are usually interested in a realistic representation of the underlying physics, so we use some of the Jones terms listed above, as relevant to a particular simulation. For example, a simulation may usefully incorporate separate Z-Jones, T-Jones and G-Jones terms, employing different numerical models for their matrix elements. During calibration, on the other hand, we may be unable to solve for these effects separately, since they all add up into one rapidly varying per-station phase term (assuming a narrow frequency band and FoV, where the different frequency behaviour of Z-, T- and G-Jones cannot be distinguished, and Z- and T-Jones become direction-independent). Nor do we need to, since it is only the overall phase term that we need to calibrate in order to image the data properly. Therefore, for calibration purposes, all three effects can be captured by a single G-Jones term with solvable (complex) diagonal elements.
We call such forms of the RIME phenomenological, since they are meant to
provide sufficient degrees of freedom (i.e. solvable parameters) to capture the
effect of the instrument on observed data, with little regard to the
underlying physics. Here’s an example of a real-life phenomenological RIME for
polarization calibration of the WSRT: 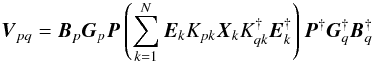 (4)here,
Bp is a solvable full 2 ×
2 matrix to capture bandpass and leakage (highly variable in frequency, but only slowly
variable in time), Gp is a
solvable diagonal matrix to capture rapidly variable amplitude and phase effects
(no variation in frequency, rapid variation in time), P is a
dipole orientation matrix (known, constant, and same for all stations),
Ek = E(lk,mk)
is an apriori primary beam model (same for all stations),
and Kp is the usual phase term.
(4)here,
Bp is a solvable full 2 ×
2 matrix to capture bandpass and leakage (highly variable in frequency, but only slowly
variable in time), Gp is a
solvable diagonal matrix to capture rapidly variable amplitude and phase effects
(no variation in frequency, rapid variation in time), P is a
dipole orientation matrix (known, constant, and same for all stations),
Ek = E(lk,mk)
is an apriori primary beam model (same for all stations),
and Kp is the usual phase term.
At very high (>105) dynamic ranges, short-term low-level instability
of the WSRT bandpass makes it impossible to separate the B
and G solutions, so a simpler form of the RIME may be used
instead. This form is roughly equivalent to per-channel selfcal in 2GC terminology:
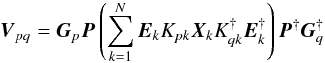 (5)here,
Gp is solvable, with rapid
variation in frequency and time on the diagonal, and slow variation in time on the
off-diagonal. Another version of this equation was used by Smirnov (2010, in prep.) to
produce the result in Fig. 13 (see Sect. 8):
(5)here,
Gp is solvable, with rapid
variation in frequency and time on the diagonal, and slow variation in time on the
off-diagonal. Another version of this equation was used by Smirnov (2010, in prep.) to
produce the result in Fig. 13 (see Sect. 8): 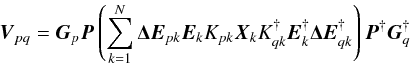 (6)here,
differential gain
ΔEpk
is a phenomenological Jones term capturing the source-dependent complex gain variations
(which can be due to any combination of physical effects). It is diagonal, and solvable on
large time and frequency scales.
(6)here,
differential gain
ΔEpk
is a phenomenological Jones term capturing the source-dependent complex gain variations
(which can be due to any combination of physical effects). It is diagonal, and solvable on
large time and frequency scales.
7.5. RIME and software modularity
Early thinking about implementations of the RIME in software (Noordam 1996) tended towards a “one equation to rule them all” doctrine. A particular sequence of Jones terms was chosen and carefully elaborated on, with the implicit expectation that it would be appropriate to all telescopes and scenarios, if only all the required Jones matrices were properly implemented. This thinking also had a strong influence on the AIPS++/CASA calibration modules.
Our subsequent work on the subject has convinced us that a more flexible approach is vital. The discussion in the previous section suggests that no specific set of Jones terms can be appropriate to all cases – not even if we restrict ourselves to one relatively simple instrument such as the WSRT, as is clear from Eqs. (4 − 6). The need to build arbitrary measurement equations drove the design of MeqTrees from the beginning.
Fortunately, the structure of the RIME itself encourages just such a flexible and modular approach. Any specific knowledge about an instrument can be encoded in the form of Jones matrices, and all Jones matrices work the same way. This has the very considerable advantage that each instrumental effect can be modelled in isolation, while it will still be taken into account correctly within the RIME. This is a far cry from the intractable and approximate mathematical expressions in older data reduction packages, which are often not implemented explicitly, but scattered in poorly documented bits and pieces throughout the code.
 |
Fig. 11 Schematic structure of a typical TDL processing script. Thanks to the RIME, with its Jones matrices and Local Source Model, such scripts are highly modular, and may quickly be adapted to different telescopes and experiments. This greatly facilitates collaboration and rapid experimentation. See also the text. |
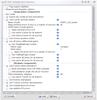 |
Fig. 12 The Options GUI of a typical processing script. A number of Jones modules may be selected for inclusion in the tree. Each Jones module can implement its own custom option set, which is displayed in submenus. |
Figure 11 shows schematically how the modularity of the RIME can be exploited to generate a set of generic processing scripts that can be adapted for use with any radio telescope. Rather than being written in basic TDL from scratch, these scripts are based on a set of generic Python frameworks called the Cattery, which ships with MeqTrees 1.1. The user selects a Cattery script for a particular operation (e.g. simulation, or visualization, or some sort of calibration), and perhaps customizes it by changing a few lines of Python code. The user then selects a suitable sequence of Jones modules from a “Jones repository”15. Finally, the user selects a Local Sky Model, for which a number of model formats are supported. All these modules are free to define their own custom processing options (solvable parameters, etc.) MeqTrees automatically extracts the relevant option set from the selected modules, and presents it to the user via a GUI (Fig. 12). When used in batch mode, it can load these options from configuration files.
8. Some results
 |
Fig. 13 This WSRT 21 cm image of the field around the bright radio source 3C 147 is virtually noise-limited, and has a dynamic range of 1.6 million. This dynamic range, achieved by de Bruyn et al. (2010, in prep.) using regular selfcal with the NEWSTAR package, is high enough to clearly show ring-like artifacts around moderately bright off-axis sources (see left inset) which are caused by DDEs. We used MeqTrees to apply differential gain solutions to the original data (with a sky model built up by de Bruyn et al. during their NEWSTAR reduction), which completely eliminated the artifacts (right inset). |
 |
Fig. 14 Differential phase solutions in the direction of 6 different sources (per 5 antennas), as a function of time. The integration time is 30 min. Note that the S/N is large enough to show slow variations. |
Smirnov (2009, has used MeqTrees to address DDEs in high-dynamic range WSRT observations of the 3C 147 field. WSRT has been the “world champion” in dynamic range for the last few decades due to its extremely favourable design characteristics, and in particular comparatively benign DDEs, but at extreme dynamic ranges (and even not so extreme, in some observational modes) DDEs do become a problem. The result in Fig. 13 shows how a modified form of the RIME may be used to address it. This image has a virtually noise-limited dynamic range of 1.6 million. It is an improvement over the image obtained with NEWSTAR by de Bruyn (2006); de Bruyn (2010, in prep.) with the same data, primarily because it corrects for DDEs in the map by solving for differential gains (Eq. (6)). With WSRT, time-variable DDEs manifest themselves as faint ring-like structures around off-axis sources (see left inset of Fig. 13), which cannot be deconvolved. Differential gains eliminate these structures (see right inset). Figure 14 shows the differential phase solutions for 5 of the 14 WSRT telescopes as a function of time in the direction of six moderately bright sources in the field. The values are relative to the phase solution in the direction of the dominating source (3C 147, 22 Jy). With an integration time of 30 min, the S/N of the differential phases is clearly large enough to detect slowly varying real effects. Interpreting these is another matter, and will be discussed further in a separate paper (Smirnov 2010, in prep.).
Yatawatta et al. (2010) has been using MeqTrees to make the first all-sky images with initial LOFAR stations. LOFAR observations are subject to complex DDEs caused by the ionosphere and time-variable primary beam patterns, so its calibration is a challenge, with many alternative approaches being (and waiting to be) explored. MeqTrees, with its rapid experimentation capability, has proven to be a perfect vehicle for this.
On the simulations side, the ability to implement arbitrary RIMEs has allowed MeqTrees to be used for simulation of new and unusual telescope designs. Willis (2008a,b) has been using MeqTrees to simulate interferometers composed of dishes with Focal Plane Arrays (FPA), with a particular emphasis on studying the effects caused by rotating beam patterns (as in an alt-az mount without a derotator) and polarimetric fidelity. Mevius and Van Bemmel have been using MeqTrees to develop an ionospheric simulations framework called LIONS (Anderson 2008).
9. Conclusions
MeqTrees raises the art of instrumental modelling to the level where user-developers can concentrate on the physics of the problem, while the complex numerical machinery, e.g. for solving for arbitrary subsets of parameters, is hidden “under the hood”. In the special case of radio astronomy, the correct treatment of various instrumental effects is greatly facilitated by the elegant matrix formalism of the Measurement Equation of a generic radio telescope (RIME). The latter is well on its way to becoming the new Common Language of radio astronomy.
The present collection of node classes offers basic functionality, with bias towards radio astronomy (see Appendix A). There are various TDL (Python) frameworks to help the user in building complex trees; these in fact evolve much more rapidly than the binary release cycle. We also intend to offer a MeqWizard tool to help both novices and experts to find their way in the multiverse of possibilities. The MeqTrees kernel is robust and efficient, and has been tested thoroughly on real data (see Sect. 8).
MeqTrees is (slowly) beginning to find its place, propelled by the increasingly urgent need for 3GC simulation and calibration software for radio astronomy. It plays its designated role as pathfinder for LOFAR calibration, as illustrated by impressive all-sky LOFAR images (Yatawatta et al. 2010). It has been used as the main education tool in several international workshops, to train the new generation of radio astronomers in the use of the RIME and 3GC.
MeqTrees is freely distributed under the terms of the GNU General Public License. A stable binary release (version 1.1.1 at time of writing) is available. This is shipped as binary packages for the major Linux distros, so installation is relatively painless (while users of unsupported platforms always have the option of building from source). A Mac OSX version has been tested, but is not (yet) part of the binary release. MeqTrees is natively multi-threaded to take full advantage of multi-core machines common today. An experimental MPI-based cluster version was developed jointly with Oxford Astrophysics and OeRC, and is currently being tested by Tony Willis at DRAO (Canada).
For further information on downloading and installing the software, please refer to the MeqTrees Wiki: http://www.astron.nl/meqwiki. You can also join the MeqTrees forum hosted at UCL: https://great08.projects.phys.ucl.ac.uk/meqtrees/.
Some formulations include a factor of 1/2 in the definition of X. See Smirnov (2010, in prep.) for a discussion of these issues. Note also that it is common to use B instead of X, calling it the source brightness (and indeed, the brightness of a source at the phase centre is equivalent to its coherency). In this paper we’ll use X, reserving B for the bandpass Jones, below.
At time of writing, a number of standard Jones modules were included in the MeqTrees 1.1.1 binary release. More modules can be checked out manually from a designated area on our Subversion server. We intend to set up a more formally structured repository as more diverse Jones modules are implemented.
Acknowledgments
Up to now, the following people have made direct contributions to MeqTrees, either by implementing and testing nodes, or by writing and exercising TDL scripts: Sarod Yatawatta, Tony Willis, Maaijke Mevius, Ger van Diepen, Ronald Nijboer, Filipe Abdalla, Rob Assendorp, Ilse van Bemmel, Ian Heywood, Hans-Rainer Kloeckner, Rense Boomsma, Michiel Brentjens, Joris van Zwieten, Alessio Magro. Many more should follow, and will be acknowledged, as our collaborative network grows. Others have contributed to the distribution of MeqTrees and its operation on different platforms: Chris Williams, Stef Salvini, Mike Sipior, James Anderson and George Heald. Ger de Bruyn has provided data, models, advise, and a wealth of inspirational ideas. Helpful comments were extracted from Wim Brouw. MeqTrees uses various modules from AIPS++/CASA, particularly those written by Ger van Diepen, Wim Brouw and Tim Cornwell. Ger van Diepen and Malte Maquarding have also been instrumental in making the CASA installation more robust. For the application of DDEs we have been influenced by the work of Sanjay Bhatnagar and Steve Gull. The MeqTrees binary package repository is kindly hosted by the Oxford e-Research Centre, and operated by Chris Williams. The MeqTrees Forum website is kindly hosted by University College London, and operated by Julien Girard of the Observatoire de Paris. The authors are particularly grateful for the faith and patience of a succession of ASTRON managers over the years: Marco de Vos, Mike Garrett, Ronald Nijboer, Arnold van Ardenne, Kjeld van der Schaaf, Harvey Butcher. And finally, the very substantial support of Steve Rawlings (Oxford Astrophysics), Peter Dewdney and Sean Dougherty (NRC DRAO) and Anne Trefethen (Oxford e-Research Centre) has made all the difference.
References
- Abdalla, F. B. 2009, in MCCT SKADS Mixed Workshop: Towards third-generation calibration in radio astronomy [Google Scholar]
- Anderson, J. M. 2008, in Deep Surveys of the Radio Universe with SKA Pathfinders, Perth [Google Scholar]
- Bhatnagar, S., Cornwell, T. J., Golap, K., & Uson, J. M. 2008, A&A, 487, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brouw, W. N. 1996, AIPS++ Note 224: AIPS++ Least Squares background, Tech. Rep. [Google Scholar]
- Cornwell, T. J., & Wilkinson, P. N. 1981, MNRAS, 196, 1067 [NASA ADS] [Google Scholar]
- de Bruyn, A. G. 2006, in SKA Calibration and Imaging Workshop 2006 [Google Scholar]
- Ekers, R. D. 1983, in Serendipitous Discoveries in Radio Astronomy, ed. K. I. Kellermann, & B. Sheets, 154 [Google Scholar]
- Hamaker, J. P. 2000, A&AS, 143, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopper, G. M. 1952, in ACM ’52: Proceedings of the 1952 ACM national meeting, Pittsburgh (New York, NY, USA: ACM), 243 [Google Scholar]
- Jones, R. C. 1941, J. Opt. Soc. America, 31, 488 [Google Scholar]
- Kemball, A. J., & Wieringa, M. H. 1996, AIPS++ Note 229: MeasurementSet definition version 2.0, Tech. Rep. [Google Scholar]
- Knuth, D. E. 1973, The Art of Computer Programming, Vol. 1, Fundamental Algorithms, 2nd ed. (Reading, Massachusetts: Addison-Wesley) [Google Scholar]
- Madsen, K., Nielsen, H. B., & Tingleff, O. 2004, Methods for Non-Linear Least Squares Problems, 2nd ed. [Google Scholar]
- Morris, D., Radhakrishnan, V., & Seielstad, G. A. 1964, ApJ, 139, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Noordam, J. E. 1996, AIPS++ Note 185: The Measurement Equation of a Generic Radio Telescope, Tech. Rep. [Google Scholar]
- Smirnov, O. M. 2008, The TDL Bedside Companion [Google Scholar]
- Smirnov, O. M. 2009, in SKA Calibration and Imaging Workshop 2009 [Google Scholar]
- Willis, A. G. 2008a, in Frontiers of Astrophysics: A Celebration of NRAO’s 50th Anniversary, ed. A. H. Bridle, J. J. Condon, & G. C. Hunt, ASP Conf. Ser., 395, 382 [Google Scholar]
- Willis, A. G. 2008b, in Astronomical Data Analysis Software and Systems XVII, ed. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 717 [Google Scholar]
- Yatawatta, S., Brentjens, M. A., de Bruyn, A. G., et al. 2010, Experimental Astronomy, Special LOFAR issue, in press [Google Scholar]
Appendix A: Available node classes
Perhaps the most concise description of the capabilities of MeqTrees for the discerning user is an overview of the node classes that are available already, and the ones that are desirable in the near future:
-
Leaf nodes:
Constant, Parm, Freq, Time, Grid, GaussNoise,RandomNoise, Spigot, FITSImage (and several other FITSinterface nodes).
-
Unary operations:
Exp, Log, Abs, Invert, Negate, Sqrt, Pow2(8), Sin, Cos, Tan, Acos, Asin, Atan, Cosh, Sinh, Tanh, Norm, Arg, Real, Imag, Conj, Ceil, Floor, Identity. See also Sect. 3.2.
-
Binary operations:
(two children): Subtract, Divide, Pow, Mod, ToComplex(real, imag), Polar(ampl, phase). See also Sect. 3.2.
-
Accumulation:
(one or more children): Add, Multiply, WSum, WMean. The last two need a vector of weights. See also Sect. 3.2.
-
Reduction nodes:
Sum, Mean, Product, StdDev, Rms, Min, Max, NElements. These reduce a result along selected axes. The default is all axes, in which case the result is a scalar. See also Sect. 3.2.
-
Tensor operations:
Composer, Selector, Paster. Tensor nodes are nodes with multiple vellsets in their Result (see Sect. 3.2).
-
Matrix operations:
Transpose, ConjTranspose, MatrixMultiply, MatrixInvert22. The latter operates on 2x2 matrices only, which is sufficient for the RIME (see Sect. 7).
-
Flow control:
ReqSeq, ReqMux, Sink, VisDataMux. They regulate the order in which their children get Requests, and which Result to pass on. They also synchronize the flow of Requests and Results in parallel trees.
-
Domain Control:
ModRes, Resampler, CoordTransform. ModRes modifies the Request before it is passed on, Resampler modifies the Result itself. CoordTransform modifies the Request passed to its second child.
-
Flagging:
ZeroFlagger, MergeFlags (see Sect. 4).
-
Solving:
Condeq, Solver, Parm (see Sect. 5). For the moment, MeqTrees offers only a Levenberg-Marquard non-linear solver.
-
Visualization
: all nodes, DataCollect, Inspector(=Composer) (see Sect. 2.2.4).
-
Coordinates:
(mostly radio astronomy): UVW, LMN(radec, radeq0), AzEl(radec, xyz), RaDec(azel, xyz), LMRaDec(lm), ObjectRaDec(name), LST(domain, xyz), ParAngle(radec, xyz), LongLat(xyz). The vector xyz is an Earth position in IRTF coordinates.
-
Transforms:
FFTBrick, UVInterpol (collectively known as UVBrick) (see Sect. 7).
-
User-definable nodes:
PyNode, Functional, PrivateFunction. These allow the user to insert his own function, written in Python or C++, to read the Results from one or more child nodes, and to generate a customized Result.
A full description of these nodes is outside the scope of this paper. The present collection has an obvious bias towards radio astronomy. This may change as MeqTrees is used in other application areas. We envisage a core collection of nodes that offer basic functionality, surrounded by collections of more specialised nodes (and Python frameworks) for use in specific areas. The latter should be mostly contributed by users – we strive towards an Open Source developement model where everybody contributes, while a small core team keeps the mainline development on track. Some of the contributed nodes will eventually find their way into the core collection, while some of the present nodes will be moved out. In the meantime, the various types of user-definable nodes (such as the PyNode) allow experimentation with new node classes before they are implemented as a regular C++ node class. Obviously, we will have to solve the technical problem of linking such contributed nodes into MeqTrees with a minimum of fuss.
All Figures
 |
Fig. 1 An expression tree. |
| In the text | |
 |
Fig. 2 A node computes the value of some function on a grid (which we call the cells) within some domain. The domain on the left is two-dimensional (t,ν) and has identical and contiguous cells on a regular grid. It is also possible to have irregular grids of non-contiguous cells with different sizes, as illustrated on the right (cell size is only relevant for some rather obscure operations). Higher-dimensioned domains are also possible. |
| In the text | |
 |
Fig. 3 The meqbrowser GUI. |
| In the text | |
 |
Fig. 4 The layout of a basic result object. |
| In the text | |
 |
Fig. 5 The layout of a tensor result object. |
| In the text | |
 |
Fig. 6 The layout of a result object with flags. Note that vellsets 1, 1 and 2, 2 share the same flags, while vellsets 1, 2 and 2, 1 have no flags at all. |
| In the text | |
 |
Fig. 7 A schematic layout of a solver tree. |
| In the text | |
 |
Fig. 8 The layout of a result object with perturbed values. |
| In the text | |
 |
Fig. 9 A subtree implementing the RIME given by Eq. (2). |
| In the text | |
 |
Fig. 10 The user interface to the MeqTrees Local Sky Model. |
| In the text | |
 |
Fig. 11 Schematic structure of a typical TDL processing script. Thanks to the RIME, with its Jones matrices and Local Source Model, such scripts are highly modular, and may quickly be adapted to different telescopes and experiments. This greatly facilitates collaboration and rapid experimentation. See also the text. |
| In the text | |
 |
Fig. 12 The Options GUI of a typical processing script. A number of Jones modules may be selected for inclusion in the tree. Each Jones module can implement its own custom option set, which is displayed in submenus. |
| In the text | |
 |
Fig. 13 This WSRT 21 cm image of the field around the bright radio source 3C 147 is virtually noise-limited, and has a dynamic range of 1.6 million. This dynamic range, achieved by de Bruyn et al. (2010, in prep.) using regular selfcal with the NEWSTAR package, is high enough to clearly show ring-like artifacts around moderately bright off-axis sources (see left inset) which are caused by DDEs. We used MeqTrees to apply differential gain solutions to the original data (with a sky model built up by de Bruyn et al. during their NEWSTAR reduction), which completely eliminated the artifacts (right inset). |
| In the text | |
 |
Fig. 14 Differential phase solutions in the direction of 6 different sources (per 5 antennas), as a function of time. The integration time is 30 min. Note that the S/N is large enough to show slow variations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


