| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015254 | |
| Published online | 10 November 2010 | |
White-dwarf kicks and implications for barium stars
1
Institut d’Astronomie et d’Astrophysique, Université Libre de
Bruxelles, Boulevard du
Triomphe, 1050
Brussels, Belgium
e-mail: izzard@astro.uni-bonn.de
2
Argelander-Institut für Astronomie, University of
Bonn, Auf dem Hügel
71, 53121
Bonn,
Germany
3
Lund Observatory, Box 43221 00
Lund,
Sweden
4 Centre for Stellar and Planetary
Astrophysics, School of Mathematical Sciences, Monash University,
VIC 3800,
Australia
Received:
22
June
2010
Accepted:
13
August
2010
The formation mechanism of the barium stars is thought to be well understood. Barium-rich material, lost in a stellar wind from a thermally-pulsing asymptotic-giant branch star in a binary system, is accreted by its companion main-sequence star. Now, many millions of years later, the primary is an unseen white dwarf and the secondary has itself evolved into a giant which displays absorption lines of barium in its spectrum and is what we call a barium star. A similar wind-accretion mechanism is also thought to form the low-metallicity CH and carbon-enhanced metal-poor stars. Qualitatively the picture seems clear but quantitatively it is decidedly murky: several key outstanding problems remain which challenge our basic understanding of binary-star physics. Barium stars with orbital periods less than about 4000days should – according to theory – be in circular orbits because of tidal dissipation, yet they are often observed to be eccentric. Only one barium-star period longer than 104days has been published although such stars are predicted to exist in large numbers. In this paper we attempt to shed light on these problems. First, we consider the impact of kicking the white dwarf at its birth, a notion which is supported by independent evidence from studies of globular clusters. Second, we increase the amount of orbital angular momentum loss during wind mass transfer, which shrinks barium-star binaries to the required period range. We conclude with a discussion of possible physical mechanisms and implications of a kick, such as the break up of wide barium-star binaries and the limits imposed on our models by observations.
Key words: stars: chemically peculiar / binaries: close / stars: AGB and post-AGB / Galaxy: stellar content / nuclear reactions, nucleosynthesis, abundances
© ESO, 2010
1. Introduction
The barium stars are population I red giants which show strong absorption lines of barium in their spectra. They make up about 1% of all G/K giants. They are not evolved enough to have produced the barium themselves, rather it was made in a companion star which has long since ceased nuclear burning. This is borne out by the observation that all barium stars are in binary stellar systems (McClure & Woodsworth 1990).
Barium is an s-process element made during the thermally-pulsing asymptotic giant branch (TPAGB) stellar evolutionary phase. In sufficiently close binaries containing a TPAGB star, the primary becomes large enough that Roche-lobe overflow (RLOF) terminates the TPAGB and lessens the production of barium, preventing barium-star formation. At large separations the strong stellar wind of the TPAGB star leads to mass accretion on the secondary and this is the favoured channel for barium star formation. An intermediate regime may exist in which some wind mass-transfer occurs before RLOF begins (e.g. Han et al. 1995).
While the wind-accretion scenario is generally accepted, it does not explain the distribution of eccentricities and periods of barium stars. Most barium stars with P ≲ 500 days are in (near-)circular orbits as predicted by tidal circularisation theory (e.g. Zahn 1977, 1989). Most of the rest of the barium stars have periods between 500 and 104 days and eccentricities 0 ≤ e ≲ 0.4 (Jorissen et al. 1998).
Population synthesis studies remain the best way to study the orbital characteristics of barium stars in a statistical manner. Models such as those of Pols et al. (2003) show that our understanding of barium-star formation is incomplete. While the models confirm that short-period systems are indeed (almost) circular, they predict circularisation for all systems with periods shorter than about 4000days which is not seen in the observations. They also predict a long-period tail of eccentric barium stars extending to 105 days, also not seen in the observations. Binaries with periods greater than 104 days are difficult to detect but the fraction of barium stars with measured periods is large (35/37 for strong barium stars) so a population with undetected, longer-period orbits can be ruled out as an explanation of the discrepancy between models and observations. The combination of large eccentricities and relatively short periods of the barium stars remains an unresolved problem.
If tides are as efficient as predicted a mechanism must exist which generates eccentricity in barium-star systems at the end of the TPAGB phase of the primary. This is evident from the observed eccentricities of binary post-AGB stars which show a distribution strikingly similar to the barium stars. Many sources of eccentricity have been investigated such as enhanced mass-transfer at periastron (Soker 2000), interaction with a circumbinary disc (Frankowski & Jorissen 2007) and eccentricity pumping induced by a wind-RLOF hybrid mass transfer (Bonačić Marinović et al. 2008).
Recently and independently of the study of barium stars several authors have suggested that white dwarfs are kicked when they are born, i.e. at the end of the TPAGB phase. This result is based on a comparison of the velocity dispersion of young white dwarfs with old white dwarfs and main-sequence stars in globular clusters (Davis et al. 2008). The young white dwarfs have a higher velocity dispersion than expected by a few km s-1 and are cited as a possible mechanism for preventing globular cluster collapse (Heyl 2008; Fregeau et al. 2009). If white-dwarf kicks occur they must affect the orbital parameters of the barium stars as well as their low-metallicity equivalents, the carbon-enhanced metal-poor (CEMP) and CH stars.
The cause of the white-dwarf kicks is unknown. Candidate mechanisms include asymmetric mass loss during the AGB (e.g. Fellhauer et al. 2003), magnetic fields (Spruit 1998) and perhaps non-radial stellar pulsations. Dynamical interactions inside the globular cluster may also play a role but it is not clear why these should affect only young white dwarfs. Studies of planetary nebulae may be able to constrain any connection between asymmetric mass loss (e.g. Sahai & Trauger 1998), magnetic fields (Lee et al. 2007) and a kick to the central, proto-white dwarf, star. However, it is often difficult to determine the velocity of the central star compared to the expanding planetary nebula because of interaction of the nebula with a non-uniform interstellar medium.
In this paper we investigate the possibility that a kick to the newly-born white dwarf is the cause of the eccentricity in the barium stars. In Sect. 2 we describe our population synthesis models, in Sect. 3 we present our results and compare them to observed barium star periods and eccentricities, Sect. 4 discusses successes and potential problems of our model before we conclude with Sect. 5.
2. Modelling Ba stars with white-dwarf kicks
Our binary population synthesis model is based on that of Hurley et al. (2002) with nucleosynthesis as described by Izzard et al. (2004, 2006, 2009). Binary systems have initial primary masses M1 distributed according to the Kroupa et al. (1993) initial mass function between 1.2 and 3 M⊙, a flat distribution in the mass ratio q = M1/M2 (where M1 ≥ M2) and a flat distribution in log a between 400 and 105 R⊙. Initial eccentricities are chosen from a distribution f(e) ∝ e between 0 and 1. We assume that all stars form in binaries and our models have a grid resolution NM1 × NM2 × Na × Ne = 30 × 30 × 60 × 30.
We model tides following Hurley et al. (2002) who base their model on the formalisms of Zahn (1977) and Hut (1981). The tidal circularisation timescale during the TPAGB τcirc ~ 104(a/3R)8 years (e.g. Soker 2000). This implies that tides rapidly circularise any binary containing an AGB star with a separation less than a few stellar radii.
Systems which are close enough to enter Roche-lobe overflow during the AGB undergo common envelope evolution with rapid circularisation, ejection of the stellar envelope and little barium production and accretion onto the secondary. These systems perhaps lead to short-period barium stars. Some authors have speculated about stable case-C mass transfer which may lead to the formation of the shortest-period barium stars (e.g. Han et al. 1995) and the intriguing possibility of a radiation-distorted Roche geometry (Dermine et al. 2009). We do not explore this channel in detail here because we focus on the wind mass-transfer scenario.
Our nucleosynthesis model includes third dredge up with an efficiency given by Karakas et al. (2002) and s-process abundances based on the models of Busso et al. (2001). Our initial metallicity is Z = 0.008 with an abundance mixture according to Anders & Grevesse (1989). The 13C pocket efficiency, 13ξ, is a multiplicative factor used to change the amount of of 13C relative to the 2.8 × 10-6 M⊙ in the standard pocket of Gallino et al. (1998). We set it to 1 in order to make sufficient barium stars at Z = 0.008 (about 1% of GK giants). At Z = 0.02 even with 13ξ = 2 we cannot make enough Ba stars, however the amount of third dredge up is also rather uncertain and can be increased artificially to obtain the desired 1% ratio (as noted by Han et al. 1995). We do not try to constrain either 13ξ or the amount of third dredge up, this has been attempted by others (e.g. Bonačić Marinović et al. 2006, see also the discussion in Sect. 4.4).
Mass loss during the TPAGB is parameterised by the formula of Vassiliadis & Wood (1993) and mass accretion onto the secondary is at the rate given by Bondi & Hoyle (1944) as described in Hurley et al. (2002, Eq. (6)) with an efficiency parameter αW = 1.5 and an accretion rate limited by |Ṁ2| < 0.8|Ṁ1| (where star 1 is the donor, star 2 the accretor). At the end of the TPAGB phase of the primary star a kick is applied to the nascent white dwarf with a fixed speed σWD and random direction according to the method described in Hurley et al. (2002, Appendix A1, but without the Maxwellian velocity distribution). We apply the kick whether the TPAGB is terminated by a stellar wind or common-envelope ejection.
We count stars as giants after they leave the main sequence (as defined by Hurley et al. 2002) and before they become white dwarfs.We select stars with only G and K spectral types corresponding to 3620 ≤ Teff/K ≤ 5150 (Jaschek & Jaschek 1995). Of these, strong barium stars have [Ba/Fe] ≥ 0.5 and mild barium stars have 0.2 ≤ [Ba/Fe] < 0.5.
3. Simulated Ba-star populations
In this section we present the results of our population syntheses with the systematic inclusion of progressively more speculative physics as required to reproduce the observed e − log P distribution of the barium stars.
We compare our models with the observations of Jorissen et al. (1998) but without the triple system BD +38° 118. For the strong barium stars the sample is almost complete (35 out of 37 have measured periods and eccentricities). Our weak barium star sample is augmented with observations of 56 Uma (Griffin 2008) and the latest results of the HERMES survey (Dermine & Jorissen, in prep.). Very few barium stars do not have a measured period and eccentricity and the missing stars do not affect any of the general conclusions we present in this paper.
3.1. Our canonical model
 |
Fig. 1 Our canonical barium-star e − log P distribution. Darker greyscale/colour indicates a greater number density of systems. The plus symbols + are the observations of Jorissen et al. (1998) without the triple system BD +38°118, the diagonal crosses × are the latest HERMES observations (Dermine & Jorissen, in prep.) and the square □ is 56 Uma (Griffin 2008). Where points are joined by lines there are multiple possible orbital solutions. |
Our canonical model result, i.e. without white-dwarf kicks or otherwise modified physics, is shown in Fig. 1 and well reproduces previous studies such as Pols et al. (2003) and Bonačić Marinović et al. (2008). Our simulated barium-star systems with periods of less than about 4000 days are circular. At longer periods our modelled barium stars are eccentric and some have periods as large as 105days. The observed barium stars do not match either property of our simulated systems, most being eccentric and having periods typically less than 104days.
An obvious solution to the long-period tail is to decrease the wind accretion efficiency through the αW parameter. However, this has the effect of reducing the number ratio of barium to G/K giants to significantly below 1% so is not justified by the observations. It may be that a more complicated dependence of αW on the orbital separation allows the formation of barium stars only at periods less than 104 days. However, without a suitable formalism it is difficult to test anything but an even more ad-hoc solution to this problem than simply altering the constant αW. As such, we keep αW = 1.5 in the remainder of this paper (except where stated otherwise).
The gap in our simulated population at ~1000 days is because of our chosen common envelope evolution prescription. The AGB core and companion star spiral together inside the common envelope so the period shortens, in some cases to less than 100days. Some observed barium stars indeed have such short periods, but are not necessarily circular. We discuss our common envelope prescription in more detail in Sect. 3.3 below.
3.2. White-dwarf kicks
In Fig. 2 we show our simulated barium-star population with the inclusion of a 4 km s-1 kick at the moment of birth of the white dwarf. Our simulation and the observations are in much better agreement than in the model of the previous section (c.f. Fig. 1). Even the short-period systems acquire a small eccentricity. However, the problematic long-period tail extends to even longer periods than in our canonical model. These systems are weakly bound and a kick forces the binary into a wider orbit. However, too strong a kick leads to many disrupted binaries which are not observed, see Sect. 4.2.
3.3. Common envelope evolution
Our common-envelope prescription is based on the energy-balance formalism of Hurley et al. (2002) with α = 1 and λ fitted to detailed stellar models (Dewi & Tauris 2000). It leads to the spiral in of systems with periods around 1000days and hence the period gap observed in Fig. 1 (as noted by e.g. Han et al. 1995). The period gap is not seen in the observed barium-star period distribution and so one is forced to ask how it can be removed.
The most obvious solution is to increase the efficiency of common-envelope ejection and hence reduce the amount of spiral-in before the envelope is lost. We do this by adding a fraction λion of the recombination energy of the envelope to the energy used to eject the envelope. In the simulations described in Sects. 3.1 and 3.2, λion = 0. However, because TPAGB envelopes are cool and weakly bound, even a small value of λion, just a few per cent, is sufficient to close the period gap, as shown in Fig. 3 for λion = 0.1. For the shortest-period barium stars a smaller value of λion is required which suggests it may not be realistic to take a constant value as we have assumed. We note that use of the common-envelope prescription of Nelemans & Tout (2005) gives a similar result.
3.4. Orbital angular momentum
 |
Fig. 4 As Fig. 3 but for a population very efficient orbital angular momentum loss according to the Hurley et al. (2002) formalism (Eq. (1) and an accretion parameter αW = 100, see text for details). |
Wind accretion is not likely to be 100% efficient, that is, some material is always lost
from the system. The material that is lost carries away orbital angular momentum so the
orbital separation changes. It is not clear how much angular momentum is lost per unit
mass ejected. Our standard model, as presented in the sections above, uses the
prescription of Hurley et al. (2002) which provides
the following formula, 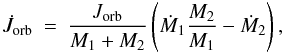 (1)which is always negative
because Ṁ1 < 0 and
Ṁ2 > 0 (where star 1 is the donor TPAGB star and star 2 is
the accretor). When wind accretion is very efficient, the term
− Ṁ2 is significant, the orbit shrinks and we obtain the
results shown in Fig. 4. In the Hurley et al. (2002) model efficient wind accretion can be simulated
with a large value of αW. The accretion rate is then limited
to |Ṁ2|< 0.8|Ṁ1|. Figure 4 shows the case with
αW = 100 which is effectively 80% efficient accretion because
of the imposed limit
|Ṁ2| ≤ 0.8|Ṁ1|. Most of the
long-period barium stars in our model shrink their orbits to periods less than
104days so agree much better with the observations.
(1)which is always negative
because Ṁ1 < 0 and
Ṁ2 > 0 (where star 1 is the donor TPAGB star and star 2 is
the accretor). When wind accretion is very efficient, the term
− Ṁ2 is significant, the orbit shrinks and we obtain the
results shown in Fig. 4. In the Hurley et al. (2002) model efficient wind accretion can be simulated
with a large value of αW. The accretion rate is then limited
to |Ṁ2|< 0.8|Ṁ1|. Figure 4 shows the case with
αW = 100 which is effectively 80% efficient accretion because
of the imposed limit
|Ṁ2| ≤ 0.8|Ṁ1|. Most of the
long-period barium stars in our model shrink their orbits to periods less than
104days so agree much better with the observations.
One may ask whether the Hurley et al. (2002)
formalism should be believed. If
Ṁ1 = −Ṁ2, i.e. mass transfer is
conservative, one would expect 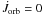 which is clearly not the case. This has lead us to consider
a simpler prescription in which material lost from the binary system carries away some
multiple of the specific orbital angular momentum,
which is clearly not the case. This has lead us to consider
a simpler prescription in which material lost from the binary system carries away some
multiple of the specific orbital angular momentum, 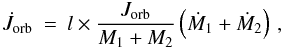 (2)where l is a free parameter.
This formula has the advantage that
(2)where l is a free parameter.
This formula has the advantage that 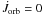 in the case of conservative mass transfer. It is difficult
to constrain l but Fig. 5 shows the
case l = 2 which looks very similar to Fig. 4 but without the requirement of a very large αW.
The long-period tail is always present, but the number of stars we predict there is small.
in the case of conservative mass transfer. It is difficult
to constrain l but Fig. 5 shows the
case l = 2 which looks very similar to Fig. 4 but without the requirement of a very large αW.
The long-period tail is always present, but the number of stars we predict there is small.
4. Discussion
The physical mechanism for the white dwarf kick is unknown but candidates include magnetic fields (Spruit 1998), asymmetric mass loss (Fellhauer et al. 2003) and mass transfer at periastron (Soker 2000). According to the evidence from globular clusters the mechanism must be at work in both single and binary stars (Davis et al. 2008).
We are working on an alternative mechanism which may be of relevance to barium stars, that of eccentricity pumping due to a circumbinary disk (Dermine et al. in prep.), but again this cannot be active in single stars. It would seem that asymmetric AGB wind loss and/or interaction with a magnetic field is the leading candidate if white-dwarf kicks are to occur in both single and binary stars. Still, a number of open questions remain and we briefly address a few of them here.
 |
Fig. 5 As Fig. 4 but with our alternative orbital angular momentum loss formula (Eq. (2) with l = 2 and an accretion parameter αW = 1.5). |
4.1. Fast and slow kicks – and in which direction?
In all our models presented above we have assumed an instantaneous kick is given to the white dwarf at the end of the primary AGB phase. However, any kick which is imparted by an asymmetric wind is likely to be effective during the superwind phase of the primary AGB star, i.e. on a timescale of ~104 years. This is of the same order as the tidal circularisation timescale and much longer than the orbital period. A coupling of the orbital dynamics with a “slow” kick is beyond the scope of this paper but there may still be an effect on the eccentricity particularly if the kick is coupled to the orbital phase.
The direction of the kick is also an issue crucial to the further evolution of the binary system. Close barium stars, with P ≲ 4000 days, are circular by the end of the AGB so any kick increases the eccentricity of the orbit. In wide systems which remain eccentric throughout the AGB phase the eccentricity may increase or decrease depending on the kick direction. For simplicity, we choose a fixed kick speed and a random direction: this may not be realistic in a binary system in which there is a well defined axis of symmetry. The presence or otherwise of a preferred direction would depend on the kick mechanism, which is still unclear.
4.2. Disrupted systems
 |
Fig. 6 The fraction of binary systems which are disrupted as a result of a white-dwarf kick as a function of the kick speed. The models are as those of Sect. 3.2 (λion = 0, αW = 1.5 and orbital angular momentum loss according to Eq. (1)). |
A consequence of kicking a component of a binary star which is well known in the study of massive stars is disruption of the binary system. The fraction of binaries which are disrupted as a result of kicks in our otherwise canonical model (c.f. Sect. 2) is shown in Fig. 6. For small velocities, ≲3 km s-1, the number of disrupted systems is less than a few per cent. This is a useful constraint on the kick mechanism because Jorissen et al. (1998) present 65 binary barium stars and possibly one single star in a complete strong barium star sample, hence the disruption fraction is less than one in 65, or about 1.5%, corresponding to a maximum σWD = 2−3 km s-1. To the authors′ knowledge no conclusively-single giant barium stars have yet been found, but their number may be few and they may have been missed. Some may be present among subgiant CH stars.
Wide binaries are most easily disrupted for a given σWD. We find a smaller breakup fraction when we consider our models with efficient orbital angular momentum loss because these barium stars have shorter periods and so are more tightly bound. For example, using Eq. (2) with l = 4 we obtain a breakup fraction of only 0.7% with σWD = 4 km s-1 compared to 10% in our canonical model with the same kick speed.
4.3. Mass loss, the angular momentum budget and Mira
We have hitherto ignored the uncertainty introduced by our choice of mass loss rate. Our chosen rate, that of Vassiliadis & Wood (1993), tends to be small during most the TPAGB but strong during the final superwind phase. This is advantageous for barium star formation as it allows for many thermal pulses and associated barium production. A smaller but more steady mass-loss rate may lead to fewer and weaker third dredge up episodes because the envelope is more quickly reduced in mass, but conversely any barium dredged up is less diluted so the amount of barium in transferred material may be similar. In any case, the efficiency of accretion is so poorly understood that the abundance of barium in the primary is unlikely to be the largest uncertainty in our analysis (although see Stancliffe & Jeffery 2007; Cristallo et al. 2009, for suitable analyses).
It is not unreasonable to assume efficient loss of orbital angular momentum, e.g. Eq. (2) with l > 1, if there is significant locking of the stellar wind with a magnetic field or mass is lost from a circumstellar or circumbinary disc. An alternative explanation is that the Hurley et al. (2002) angular momentum formula, our Eq. (1), is correct in the case of efficient accretion on the companion. Efficient accretion may already have been seen in systems such as Mira in which the stellar wind is channelled onto the companion star (Karovska et al. 2005). Recent simulations of wind-RLOF hybrid mass transfer suggest accretion is indeed efficient (Mohamed & Podsiadlowski 2007). An alternative into which we are looking is the implementation of the work of Sepinsky et al. (2009) which would allow us to follow non-conservative mass transfer in detail, but this is beyond the scope of this paper.
4.4. Mild vs strong barium stars
The differences between the distribution of strong and mild barium stars in the e − log P diagram may help us constrain uncertain physics. Our models predict that strong barium stars are more likely to be made in the intermediate period range 103−104days because at short periods RLOF truncates the primary AGB evolution while at long periods wind accretion is not efficient. In contrast, mild barium stars are made over the whole period range of 102−105days. The Jorissen et al. (1998) data may support this view. For the 30 mild barium stars with known periods, the mean period is 2900days with a standard deviation of 1900days, while for the 35 strong barium stars with known periods the mean period is 2000days with a standard deviation of 1700days. The new HERMES data further lengthens the mean period of the mild barium stars.
There are five strong (binary) barium stars with periods less than 500days which prompt questions about their origin. It is possible that the presence of a companion star enhances third dredge up through the effects of tidal locking and rotational mixing (the stellar core will not spin at the same rate as the envelope, we are working on detailed models of AGB binaries to test this hypothesis). Also, mass accretion may occur during the common envelope phase and lead to strong barium star formation (Ricker & Taam 2008).
In principle we could use the properties and number of barium stars to constrain AGB physics, such as the amount of third dredge up, the efficiency of the 13C pocket and the amount of s-process element production. In practice this is difficult because we can increase the amount of third dredge up but decrease the 13C pocket efficiency in our models yet obtain the same barium/GK giant fraction. Similarly, if we artificially increase the amount of dredge up in the primary AGB star we can reduce the efficiency of accretion on the secondary and obtain the same result. For these reasons we have chosen the standard 13C pocket of Busso et al. (2001) with the efficiency of third dredge up as predicted by Karakas et al. (2002). At a metallicity Z = 0.008 we find that the Ba/GK-giant number ratio is ~1%, as observed.
Similarly, we could perhaps use the masses of barium stars (e.g. Allen & Barbuy 2006) to constrain the amount of accreted material, but without prior knowledge of the abundance of the accreted material, the amount of (or lack of) thermohaline mixing or the initial mass of the (now) barium star, this is difficult if not impossible, for example see Husti et al. (2009) and the CEMP star equivalent Bisterzo et al. (2009).
4.5. Implications for planetary nebulae
Stars leaving the AGB pass through a planetary nebula phase before they go on to become white dwarfs. Any asymmetry in the AGB superwind might manifest itself as an asymmetric planetary nebula and indeed most planetary nebulae have an axisymmetric rather than spherical structure. A large number present large-scale deviations from axisymmetry which can be explained by the presence of a binary companion.
Soker et al. (1998) investigated how an eccentric binary can explain deviations from axisymmetry and Soker (2000) proposed that the origin of the eccentricity is enhanced mass loss at periastron passages. However, this process requires a seed eccentricity which is not present in short-period barium-star progenitor systems which are circularised by tides.
As white-dwarf kicks apparently occur in both single and binary stars, we should see the effect of the kick in single-star planetary nebulae. However, it is difficult to infer a kick from the structure of a planetary nebula, e.g. a shift in the position of the central star relative to the nebula, because its distortion can arise from the interaction between the nebula and the interstellar medium or the proper motion of the central star.
5. Conclusions
The combination of a white-dwarf kick with a speed of a few km s-1, efficient common-envelope ejection and orbital angular momentum loss enables us to much better match the distribution of eccentricities and periods of observed barium stars with our models. A small kick speed is compatible with observations of both globular clusters and barium stars. Efficient common-envelope ejection is required to prevent barium-star systems from spiralling to short periods during the common envelope phase.
Our orbital angular momentum loss mechanism is less certain. With the existing formalism in our binary model, based on Hurley et al. (2002), we can shrink barium-star orbits into the observed period range with an accretion efficiency of 80%. However, we are probably extrapolating their wind accretion model beyond its validity. If, instead, we assume that material lost from the system carries away twice the specific orbital angular momentum we achieve a similar result.
In any case, a white-dwarf kick is a plausible mechanism for generating the eccentricity observed in the barium stars. It is supported by independent evidence from globular clusters and is apparently not a uniquely binary-star phenomenon. If it acts in barium stars it should also be of consequence to the formation of CH and CEMP stars. Hopefully, future studies of asymmetric planetary nebulae, circumbinary disks in (post-)AGB stars, and globular-cluster and field white dwarfs may pin down both the origin of the white-dwarf kicks and barium-star eccentricity. While white-dwarf kicks may explain the barium star mystery, the evidence as it stands is circumstantial and concrete proof will only come from a combination of observations and improved modelling.
Acknowledgments
We would like to thank the referee, Oscar Straniero, for his very helpful comments. R.G.I. would like to thank Sophie Van Eck, Lionel Siess, Melvyn Davies and Chris Tout for many useful discussions and in particular Alain Jorissen and Thomas Masseron for both useful discussions and proofreading, John Fregeau for his inspirational talk on white-dwarf kicks at the Lorentz Centre workshop Stellar Mergers and Lund Observatory for lending him the visitors’ office. R.G.I. is the recipient of a Marie Curie-Intra European Fellowship at ULB. The research leading to these results has received funding from the Seventh Framework Programme of the European Community under
grant agreement 220440. T.D. is Boursier F.R.I.A. R.P.C. would like to thank the Wenner-Gren foundation for a stipend.
References
- Allen, D. M., & Barbuy, B. 2006, A&A, 454, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geoch. Cosmoch. Acta, 53, 197 [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., & Aoki, W. 2009, Publ. Astron. Soc. Austr., 26, 314 [Google Scholar]
- Bonačić Marinović, A., Izzard, R. G., Lugaro, M., & Pols, O. R. 2006, Mem. Soc. Astron. Ital., 77, 879 [NASA ADS] [Google Scholar]
- Bonačić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. S., Richer, H. B., King, I. R., et al. 2008, MNRAS, 383, L20 [NASA ADS] [Google Scholar]
- Dermine, T., Jorissen, A., Siess, L., & Frankowski, A. 2009, A&A, 507, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Fellhauer, M., Lin, D. N. C., Bolte, M., Aarseth, S. J., & Williams, K. A. 2003, ApJ, 595, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Frankowski, A., & Jorissen, A. 2007, Baltic Astron., 16, 104 [Google Scholar]
- Fregeau, J. M., Richer, H. B., Rasio, F. A., & Hurley, J. R. 2009, ApJ, 695, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Griffin, R. F. 2008, The Observatory, 128, 176 [NASA ADS] [Google Scholar]
- Han, Z., Eggleton, P. P., Podsiadlowski, P., & Tout, C. A. 1995, MNRAS, 277, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Heyl, J. S. 2008, MNRAS, 385, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Husti, L., Gallino, R., Bisterzo, S., Straniero, O., & Cristallo, S. 2009, Publ. Astron. Soc. Austr., 26, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaschek, C., & Jaschek, M. 1995, The behavior of chemical elements in stars (Cambridge; New York: Cambridge University Press) [Google Scholar]
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Karakas, A. I., Lattanzio, J. C., & Pols, O. R. 2002, PASA, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Karovska, M., Schlegel, E., Hack, W., Raymond, J. C., & Wood, B. E. 2005, ApJ, 623, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, T., Stanghellini, L., Ferrario, L., & Wickramasinghe, D. 2007, AJ, 133, 987 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2007, in 15th European Workshop on White Dwarfs, ed. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [Google Scholar]
- Nelemans, G., & Tout, C. A. 2005, MNRAS, 356, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Karakas, A. I., Lattanzio, J. C., & Tout, C. A. 2003, in ed. R. L. M. Corradi, J. Mikolajewska, & T. J. Mahoney, ASP Conf. Ser., 303, 290 [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Sahai, R., & Trauger, J. T. 1998, AJ, 116, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Sepinsky, J. F., Willems, B., Kalogera, V., & Rasio, F. A. 2009, ApJ, 702, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2000, A&A, 357, 557 [NASA ADS] [Google Scholar]
- Soker, N., Rappaport, S., & Harpaz, A. 1998, ApJ, 496, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1998, A&A, 333, 603 [NASA ADS] [Google Scholar]
- Stancliffe, R. J., & Jeffery, C. S. 2007, MNRAS, 375, 1280 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Our canonical barium-star e − log P distribution. Darker greyscale/colour indicates a greater number density of systems. The plus symbols + are the observations of Jorissen et al. (1998) without the triple system BD +38°118, the diagonal crosses × are the latest HERMES observations (Dermine & Jorissen, in prep.) and the square □ is 56 Uma (Griffin 2008). Where points are joined by lines there are multiple possible orbital solutions. |
| In the text | |
 |
Fig. 2 As Fig. 1 but for a population including 4 km s-1 natal white-dwarf kicks. |
| In the text | |
 |
Fig. 3 As Fig. 2 but for a population with efficient common-envelope ejection (λion = 0.1). |
| In the text | |
 |
Fig. 4 As Fig. 3 but for a population very efficient orbital angular momentum loss according to the Hurley et al. (2002) formalism (Eq. (1) and an accretion parameter αW = 100, see text for details). |
| In the text | |
 |
Fig. 5 As Fig. 4 but with our alternative orbital angular momentum loss formula (Eq. (2) with l = 2 and an accretion parameter αW = 1.5). |
| In the text | |
 |
Fig. 6 The fraction of binary systems which are disrupted as a result of a white-dwarf kick as a function of the kick speed. The models are as those of Sect. 3.2 (λion = 0, αW = 1.5 and orbital angular momentum loss according to Eq. (1)). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


