| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014180 | |
| Published online | 10 November 2010 | |
Helium-star evolutionary channel to super-Chandrasekhar mass type Ia supernovae
1
Department of PhysicsShangqiu Normal University,
Shangqiu
476000,
PR China
e-mail: chenwc@nju.edu.cn
2
School of Physics and State Key Laboratory of Nuclear Physics and
Technology, Peking University, Beijing
100871, PR
China
3
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing
University), Ministry of
Education, Nanjing
210093, PR
China
4
National Astronomical Observatories/Yunnan Observatory, the
Chinese Academy of Sciences, Kunming
650011, PR
China
5
Key Laboratory for the Structure and Evolution of Celestial
Objects, the Chinese Academy of Sciences, Kunming
650011, PR
China
Received: 2 February 2010
Accepted: 27 July 2010
The recent discovery of several overluminous type Ia supernovae (SNe Ia) indicates that the explosive masses of white dwarfs may significantly exceed the canonical Chandrasekhar-mass limit. Rapid differential rotation may support these massive white dwarfs (WDs). Based on the single-degenerate scenario and assuming that the WDs would differentially rotate when the accretion rate Ṁ > 3 × 10-7 M⊙ yr-1, we performed the numerical calculations for ~ 1000 binary systems consisting of a He star and a CO WD with Eggleton’s stellar evolution code. We present the initial parameters in the orbital period − helium star-mass plane (for WD masses of 1.0 M⊙ and 1.2 M⊙, respectively), which lead to super-Chandrasekhar mass SNe Ia. Our results indicate that for an initially massive WD of 1.2 M⊙, a large number of SNe Ia may result from super-Chandrasekhar mass WDs. The highest mass of the WD at the moment of the SNe Ia explosion is 1.81 M⊙, but very massive ( > 1.85 M⊙) WDs cannot be formed. However, when the initial mass of WDs is 1.0 M⊙, the explosive masses of SNe Ia are nearly uniform, which is consistent with the rareness of super-Chandrasekhar mass SNe Ia in observations.
Key words: binaries: general / stars: rotation / stars: evolution / supernovae: general / white dwarfs
© ESO, 2010
1. Introduction
Type Ia supernovae (SNe Ia) are generally believed to be the thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs) in binaries (for a review see Nomoto et al. 1997). Because of a uniform luminosity, SNe Ia are used as the standard candlelight to determine the cosmological distances and estimate the cosmological parameters Ω and Λ (e.g. Riess et al. 1998; Perlmutter et al. 1999). However, some key issues including the properties of their progenitors and the physical mechanisms of the explosion are still poorly known by astrophysicists (Hillebrandt & Niemeyer 2000; Röpke & Hillebrandt 2005; Wang et al. 2008; Podsiadlowski et al. 2008).
At present, there exist two progenitor models of SNe Ia, i.e. single-degenerate model (Whelan & Iban 1973; Nomoto 1982) and a double-degenerate model (Iben & Tutukov 1984; Webbink 1984). Over the past decade, many groups have widely investigated the single-degenerate model, in which the CO WD accretes H/He-rich material from a non-degenerate companion star. In this scenario, the donor star of WD may be a main-sequence star, a subgiant star or a red-giant star (see Hachisu et al. 1996; Li & van den Heuvel 1997; Hachisu et al. 1999a,b; Langer et al. 2000; Han & Podsiadlowski 2004, 2006; Chen & Li 2007; Han 2008; Chen & Li 2009; Meng et al. 2009; Lü et al. 2009; Wang et al. 2010; Meng & Yang 2010a,b).
Limongi & Tornambe (1991) were the first to study the evolution of the binary consisting of a CO WD and a He star, in which the CO WD accretes He matter from the He star and gains mass up to the canonical Chandrasekhar limit of 1.4 M⊙. Yoon & Langer (2003) also found that CO WD + He star systems can form a reliable channel that produces SNe Ia. Recently, Wang et al. (2009a) systematically explored the evolution of 2600 close WD binaries that include a He MS star or He subgiant, and obtained the parameter spaces for the progenitor of SNe Ia. With a detailed binary population synthesis approach, Wang et al. (2009b) suggested that this channel can contribute a SN Ia birthrate of 3 × 10-4 yr-1 in the Galaxy, and can result in the short delay times ( ≲ 100 Myr) between the formation of the progenitor systems and the explosions.
Recently, the overluminous SN Ia 2003fg has been detected (Astier et al. 2006), and its explosive mass was estimated to be ~ 2.1 M⊙ (Howell et al. 2006)1. Later, several possible overluminous SNe Ia 2006gz, 2007if, and 2009dc were also discovered (Hicken et al. 2007; Yuan et al. 2007; Tanaka et al. 2010; Scalzo et al. 2010; Silverman et al. 2010). The differential rotation may support these massive WDs (Yoon et al. 2004; Yoon & Langer 2004; Yoon & Langer 2005), which may also result from the merger of two massive WDs (Tutukov & Yungelson 1994; Howell 2001; Piersanti et al. 2003). Based on the single degenerate model and the assumption that the WD rotates differentially, Chen & Li (2009) have explored the evolution of close binaries consisting of a WD and a H main sequence star. Their results indicate that for an initial massive WD with 1.2 M⊙, the maximum explosive mass of the WDs is 1.76 M⊙.
It is an interesting issue to explore the progenitors of overluminous SNe Ia based on the single-degenerate model. In this paper, we attempt to explore whether the WD + He star systems can produce overluminous SNe Ia. To obtain the distribution of the initial He star mass and the initial orbital period of the progenitor binaries, we have calculated the evolution of 1000 WD binaries that include a He star and a rotating CO WD. In Sect. 2 we give a detailed description of the input physics including the formation of WD + He star systems and the binary evolution code. In Sect. 3 we present the calculated results. Finally, a brief discussion and summary are presented.
2. Input physics
2.1. Formation of WD + He star systems
In young stellar populations with relatively late star-formation exist intermediate-mass binary systems, which can evolve into CO WD + He star systems. For a large range of initial parameters, close binaries can evolve into a system consisting of a more massive WD and a less massive He star (Tornambè & Matteucci 1986; Iben & Tutukov 1987; Iben et al. 1987). The mass-transfer rate in these systems is only ~ 3 × 10-8 M⊙ yr-1, which may result in an explosion of SN magnitude after the WD accumulates ~ 0.15 M⊙ of helium (Iben & Tutukov 1991). However, Iben & Tutukov (1994) proposed that WD + massive He star systems can be formed via binary evolution, and the He shell burning on the surface of the CO WD could be in a quasi-stationary after the massive He star fills its Roche lobe.
Using the rapid binary star evolution (BSE) code (Hurley et al. 2000, 2002), we calculated the formation process of a massive CO WD + He star system. We consider a primordial binary consisting of a primary (star 1) of M1 = 7.5 M⊙ and a star 2 of M2 = 4.0 M⊙ (Z = 0.02) and with an orbital separation of a = 50.93 R⊙. Owing to the nuclear evolution, when t = 42.42 Myr the primary firstly fills its Roche lobe, and transfers its material to the star 2. Because of a relatively high initial mass ratio, the mass transfer occurs on a short thermal timescale. When t = 42.52 Myr, M1 = 1.482 M⊙, M2 = 10.001 M⊙, and the first Roche-lobe overflow ceases. When t = 52.20 Myr, the primary that evolves into a He star fills its Roche lobe again, and then evolves into a CO WD of M1 = 1.103 M⊙ after the second Roche-lobe overflow ceases. At the same time, the star 2 is in a Hertzsprung gap, and M2 = 10.194 M⊙. When t = 64.33 Myr, the star 2 continues to evolve and fills its Roche lobe. Due to the ultra-high mass ratio, a common envelope is possibly quickly formed because of the dynamically unstable mass transfer. After the common envelope is ejected, a close binary system consisting of a CO WD (M1 = 1.103 M⊙) and a He star (M2 = 2.247 M⊙) is formed. This formation channel is known as the He star channel (for details see Wang et al. 2009b), which allows stable Roche-lobe overflow to produce massive WD + He star systems (rather than lead to dynamical mass transfer and a common envelope phase).
In addition, another two channels such as the early asymptotic giant branch channel and the thermal-pulsing asymptotic-giant branch channel can also produce CO WD + He star systems (Wang et al. 2009b). Employing Hurley’s rapid BSE code, Wang et al. (2009b) investigated the initial parameter distribution of WD + He star systems. Their simulated results show that the initial mass of the CO WDs is in the range of 0.85–1.2 M⊙2, and the initial mass of the He stars is in the range of 1.0–2.8 M⊙, which depends on the common-envelope parameters αCEλ. Figure 1 presents the distribution of the initial WD + He star systems in MHe − MWD diagram, in which we have followed the evolution of 4 × 107 sample binaries from the star formation to the formation of the WD + He star systems and adopt αCEλ = 0.5. Based on this work, for input parameters we take the initial mass of the WDs MWD,i = 1.0,1.2 M⊙, the initial mass of the He stars MHe,i = 1.0–2.8 M⊙, and the initial orbital period log (Porb,i / d) = − 1.4 − 0 (see Fig. 3 in Wang et al. 2009b).
 |
Fig. 1 Distribution of initial WD + He star systems in MHe − MWD diagram. Basic input parameters for Monte Carlo simulations correspond to the standard model of Wang et al. (2009b). |
2.2. Binary evolution code
Employing the stellar evolution code developed by Eggleton (see Eggleton 1971, 1972, 1973), which has been updated with the latest input physics (Han et al. 1994; Pols et al. 1995, 1998), we study the evolution of close binaries consisting of a rotating CO WD (of mass MWD) and a He star (of mass MHe). The stellar OPAL opacities come from Rogers & Iglesias (1992) and Alexander & Ferguson (1994) for a low temperature. In our calculations, we set the ratio of mixing length to local pressure scale height to be 2.0, and the overshooting parameter of the He stars (with chemical abundance Y = 0.98, Z = 0.02) is taken to be 0 (Dewi et al. 2002).
In a WD + He star system, due to the nuclear evolution or the loss of orbital angular momentum the He star fills its Roche lobe at He main sequence or He subgiant stage, and then begins the mass transfer. The He-rich material from the He star is accreted by the WD, and is converted into CO heavier elements via thermonuclear burning onto the surface of the WD. In input physics, we adopt an optically thick wind scenario (Kato & Hachisu 1994; Hachisu et al. 1996) and the description for He mass accumulation efficiency onto the surface of the WD given by Kato & Hachisu (2004). Firstly, if the mass transfer rate |ṀHe| is above a critical rate (Nomoto 1982) 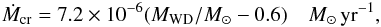 (1)we take that He burning is steady, and the He-rich material on the surface of the WD is converted into CO elements at a rate Ṁcr. Secondly, if | ṀHe | is lower than Ṁcr but higher than Ṁst (Kato & Hachisu 2004), which is the minimum accretion rate that the He-shell steadily burns, the He burning is thought to be steady, and all accreting material is converted into CO elements. Thirdly, if | ṀHe | is lower than Ṁst but higher than Ṁlow = 4.0 × 10-8 M⊙yr-1, in which the weak He-shell flashes occur3, a part of the envelope material of the WD is assumed to be blown off the surface of the WD (Woosley et al. 1986). Finally, if |ṀHe| is lower than Ṁlow, the strong He-shell flashes occur, and no material can be accumulated onto the WD. Summarizing the above prescriptions, the accumulation efficiency of the accreting He can be written as (Wang et al. 2009a)
(1)we take that He burning is steady, and the He-rich material on the surface of the WD is converted into CO elements at a rate Ṁcr. Secondly, if | ṀHe | is lower than Ṁcr but higher than Ṁst (Kato & Hachisu 2004), which is the minimum accretion rate that the He-shell steadily burns, the He burning is thought to be steady, and all accreting material is converted into CO elements. Thirdly, if | ṀHe | is lower than Ṁst but higher than Ṁlow = 4.0 × 10-8 M⊙yr-1, in which the weak He-shell flashes occur3, a part of the envelope material of the WD is assumed to be blown off the surface of the WD (Woosley et al. 1986). Finally, if |ṀHe| is lower than Ṁlow, the strong He-shell flashes occur, and no material can be accumulated onto the WD. Summarizing the above prescriptions, the accumulation efficiency of the accreting He can be written as (Wang et al. 2009a) 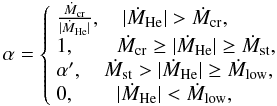 (2)where α′ is determined by a linearly interpolated way from a grid computed by Kato & Hachisu (2004).
(2)where α′ is determined by a linearly interpolated way from a grid computed by Kato & Hachisu (2004).
Actually, the accumulation efficiency mentioned above is limited to non-rotating WDs and is inadequate to calculate the mass increase of rotating WD. Considering the spin-up of the WDs via accretion, Yoon & Langer (2004) found that the rotation can stabilize He-shell burning, and help He-accreting CO WD gain mass. Assuming that the CO WDs rotate rigidly, the simulated results by Domínguez et al. (2006) proposed that massive progenitors result in higher 56Ni mass and explosive luminosity, and more massive WDs at the moment of explosion.
 |
Fig. 2 Evolution tracks of WD binary with MHe,i = 1.8 M⊙, MWD,i = 1.2 M⊙, and log(Porb,i / day) = − 1.2. The solid, dashed, and dotted curves represent the evolution of ṀHe, ṀWD, and MWD, respectively. The solid vertical line indicates the position where the WD is expected to explode as a SN Ia. |
To consider the influence of rotation on the mass accumulation of WDs, we adopt the following input physics (e.g. Chen & Li 2009). (1) With the mass transfer from the He star, the WDs obtain a large amount of angular momentum from the accreting material, and are spun up to a high rotation velocity (Durisen 1977; Ritter 1985; Narayan & Pophm 1989; Langer et al. 2000). (2) Considering the lifting effect in the hydrostatic equilibrium (Domínguez et al. 1996), we introduce an effective mass Meff of the WD by taking account of the centrifugal force. (3) According to different ranges of the polar angle, we divide the surface of the WD into three zones as follows: the equatorial zone (EZ, θ = 60°–120°), the middle zone (MZ, θ = 30°–60° and 120°–150°), and the polar zone (PZ, θ = 0°–30° and 150° − 180°). (4) Assuming that each zone accretes the transferred material at a rate proportional to its area, we can obtain an accretion fraction fi = 0.5, 0.366, and 0.134 for EZ, MZ, and PZ, respectively. Therefore, the mass growth rate of the rotating WD is given by4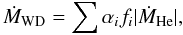 (3)where αi is the mass accumulation efficiency for different zones on the surface of the WD. The mass-loss rate of the binary system is Ṁ = (1 − ∑ αifi)ṀHe, which is assumed to be ejected in the vicinity of the WD in the form of isotropic winds or outflows, and taking away the specific orbital angular momentum of the WD.
(3)where αi is the mass accumulation efficiency for different zones on the surface of the WD. The mass-loss rate of the binary system is Ṁ = (1 − ∑ αifi)ṀHe, which is assumed to be ejected in the vicinity of the WD in the form of isotropic winds or outflows, and taking away the specific orbital angular momentum of the WD.
In our calculations, we set the initial surface velocity at the WD’s equator to be 10 kms-1, and the radius of the WD changes with 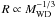 . The criterion that the WD rotates differentially is a key input physics in this work. We adopt the conclusion derived by Yoon & Langer (2004), in which the WD should rotate differentially when its accretion rate ≳ 3 × 10-7M⊙ yr-1. As a result of differential rotation, the central carbon ignition of the WD cannot occur even if its mass exceeds the canonical Chandrasekhar limit of 1.4 M⊙. Once MWD ≥ 1.4 M⊙ and Ṁ < 3 × 10-7 M⊙, we stop the calculation and assume the WD to explode as a SN Ia (we use MSN to denote the explosive mass of the WD) because there is no more differential rotation to support the massive WD. Considering the prescriptions above for the mass accumulation on the surface of the WD in Eggleton’s stellar evolution code, we have calculated the evolution of WD + He star systems, and obtained the initial parameters of the WD binaries that lead to SNe Ia.
. The criterion that the WD rotates differentially is a key input physics in this work. We adopt the conclusion derived by Yoon & Langer (2004), in which the WD should rotate differentially when its accretion rate ≳ 3 × 10-7M⊙ yr-1. As a result of differential rotation, the central carbon ignition of the WD cannot occur even if its mass exceeds the canonical Chandrasekhar limit of 1.4 M⊙. Once MWD ≥ 1.4 M⊙ and Ṁ < 3 × 10-7 M⊙, we stop the calculation and assume the WD to explode as a SN Ia (we use MSN to denote the explosive mass of the WD) because there is no more differential rotation to support the massive WD. Considering the prescriptions above for the mass accumulation on the surface of the WD in Eggleton’s stellar evolution code, we have calculated the evolution of WD + He star systems, and obtained the initial parameters of the WD binaries that lead to SNe Ia.
3. Binary evolution results
An example of the evolutionary sequences of a WD binary (with MHe,i = 1.8 M⊙, MWD,i = 1.2 M⊙, and log(Porb,i / day) = − 1.20) are shown in Figs. 2 and 3. We plot the evolution of ṀHe, ṀWD and MWD varying with time in Fig. 2. When the age of the He star is 1.76 × 106 yr, the Roche-lobe overflow occurs, and the WD accretes the material from the He star. In the earlier phase of the mass transfer, the orbital period decreases until log(Porb,i / day ≈ − 1.24, because the material is transferred from the more massive He star to the less massive WD, and then increases when the WD mass grows and exceeds the He star mass. After the mass exchange of 2.75 × 105 yr, the mass transfer rate decline to be 3 × 10-7 M⊙ yr-1, and the WD cannot differentially rotate and SN Ia explosion is triggered. At the moment of the SN explosion, the WD grows to 1.81 M⊙, the mass of the He star is 0.96 M⊙, and log(Porb / day) = − 1.06. During the stable He shell burning, the mass-accretion rate of the WD is 10-7 − 10-5 M⊙yr-1. By LX ~ ϵHe | ṀHe | (ϵHe = 6.0 × 1017 ergg-1 is the released energy rate by He burning), we can estimate the X-ray luminosity of the WD + He star system to be ~ 1036 − 1038 ergs-1. This estimate is consistent with the observed X-ray luminosity for supersoft X-ray sources (SSSs, Kahabka & van den Heuvel 1997), and confirms the conclusion that WD + He star systems may appear as SSSs before SN Ia explosions (Iben & Tutukov 1994; Yoon & Langer 2003).
 |
Fig. 3 Evolutionary track of the He star is shown as a solid curve, and the evolution of orbital period is shown as a dashed curve. The vertical dotted line and open stars indicate the place where the WD explodes as a SN Ia. |
To obtain the distribution of the initial He star mass and the initial orbital period for the progenitors of super-Chandrasekhar mass SNe Ia, we have calculated the evolutions of about 1000 WD binaries with different input parameters, which include the initial mass of the donor star MHe,i, the initial orbital period Porb,i, and the initial mass of the WD MWD,i (which we take to be 1.2 M⊙ and 1.0 M⊙). Figure 4 shows our calculation results in MHe,i − log Porb,i diagram when MWD,i = 1.2 M⊙, and the regions enclosed by the solid, dashed, and dotted curves represent the distribution areas of initial WD binaries with MSN ≥ 1.7 M⊙, MSN ≥ 1.6 M⊙, and MSN ≥ 1.4 M⊙, respectively. Beyond the boundary enclosed by the dotted curve, the mass of the WD cannot reach the Chandrasekhar limit due to either a low mass-accumulation efficiency on the surface of the WD or unstable mass-transfer. In particular, there exist eight WD binaries with an explosive mass of MSN ≥ 1.8 M⊙ (see the star signs in Fig. 4), while the maximum explosive mass is 1.76 M⊙ for WD binaries with a main sequence or sub-giant companion (Chen & Li 2009). When MWD,i = 1.0 M⊙, the progenitors distribution of SNe Ia in the MHe,i − log Porb,i diagram is plotted in Fig. 5, in which the solid and dashed curves represent the region boundaries with 1.5 M⊙ ≥ MSN ≥ 1.45 M⊙, and MSN ≥ 1.4 M⊙, respectively. In this case, the mass of the WD cannot grow to ≥ 1.5 M⊙. It is obvious that for a WD with MWD,i = 1.2 M⊙, its maximum accumulated mass is greater than those of the WD with MWD,i = 1.0 M⊙ by more than ~ 0.1 M⊙. This difference mainly originates from the different mass-accumulation efficiency on the surface of the WD. One can see that the higher the WD mass, the higher the critical mass transfer rate, and hence the higher mass-accumulation efficiency under an approximate equal mass transfer rate (see Eqs. (1) and (2)).
Figures 6 and 7 present the distribution of the donor stars at the moment of SNe Ia in the H-R diagram when MWD,i = 1.2 M⊙, and MWD,i = 1.0 M⊙, respectively. They have luminosities in the range of log (L / L⊙) ~ 3.2 − 4.4 and effective temperatures in the range of 10000 − 150000 K. These properties may be compared with and testified by future optical observations of SN Ia remnants.
 |
Fig. 4 Distribution of the initial orbital periods Porb,i and the initial He star masses MHe,i of the progenitors of super-Chandrasekhar mass SNe Ia when MWD,i = 1.20 M⊙. |
4. Discussion and summary
Overluminous SNe Ia may originate from the thermonuclear explosion of super-Chandrasekhar mass WDs, which may be supported by rapid differential rotation. Inspired by the works of Wang et al. (2009a,b), Wang & Han (2010a) and Chen & Li (2009), in this paper we investigated the evolutionary channel of He star + WD with differential rotation, which may be the progenitor of super-Chandrasekhar mass SNe Ia like SN Ia 2003fg. Assuming that the WD rotates differentially when Ṁ > 3 × 10-7 M⊙yr-1, we performed the numerical calculations for ~ 1000 WD binaries that consist of a WD and a He star.
 |
Fig. 6 Distribution of the donor stars at the moment of SN Ia explosions in the H-R diagram when MWD,i = 1.2 M⊙. The open circles, open stars, open triangles, and solid stars denote systems with 1.4 M⊙ ≤ MSN < 1.6 M⊙, 1.6 M⊙ ≤ MSN < 1.7 M⊙, 1.7 M⊙ ≤ MSN < 1.8 M⊙, and MSN ≥ 1.8 M⊙, respectively. |
 |
Fig. 7 Similar to Fig. 6, but for MWD,i = 1.0 M⊙. The open circles and solid triangles denote systems with 1.40 M⊙ ≤ MSN < 1.45 M⊙, and MSN ≥ 1.45 M⊙, respectively. |
Our main results can be summarized as follows:
-
1.
When the initial mass of the WDsMWD,i = 1.2 M⊙, the explosive masses of the WDs are in the range of 1.40 − 1.81 M⊙. This implies that a large number of SNe Ia may result from super-Chandrasekhar mass WDs, while very massive (MSN > 1.85 M⊙) WDs cannot be formed. As Chen & Li (2009), our He-star evolutionary channel cannot produce super-Chandrasekhar mass SN Ia with MSN ~ 2.1 M⊙ like 2003fg (Howell et al. 2006). It seems that the merger of two massive WDs may be responsible for this peculiar SN Ia (Tutukov & Yungelson 1994; Howell 2001).
-
2.
When MWD,i = 1.0 M⊙, all the explosive masses of the WDs are less than 1.5 M⊙, i.e. the explosive luminosity of SNe Ia are nearly uniform. These results are consistent with the rareness of overluminous SNe Ia in observations.
-
3.
Compared with the main sequence star, subgiant star, and red-giant channel, the He-star channel has higher explosive masses, less orbital separation, and a shorter mass-transfer timescale.
The WD + He star systems may be the candidate of SSSs. Di Stefano & Kong (2003) found that some SSSs in spiral galaxies are associated with spiral arms, which shows that they are young systems with an age of ≲ 0.1 Gyr. The WD + He stars channel can explain SNe Ia with short delay times ( ≲ 108 yr) (Wang et al. 2009a,b; Meng & Yang 2010b), therefore this channel may be related to the young SSSs. In addition, the WD + He star channel may be responsible for the origin of the hypervelocity stars (Wang & Han 2009).
The system HD 49798/RXJ 0648.0-418 is confirmation of the existence of a rapidly rotating massive WD + He star system. Based on data from the XMM − Newton satellite, the masses of the hot subdwarf HD 49798 and the WD are constrained to be 1.50 ± 0.05 M⊙ and 1.28 ± 0.05 M⊙, respectively (Mereghetti et al. 2009). Wang & Han (2010c) suggested that the hot subdwarf HD 49798 and its X-ray pulsating companion could evolve into an SN Ia in the future. The system V445 Pup is another candidate of a massive WD + He star system, in which the mass of the WD is ≳ 1.35 M⊙, and the mass of the He star is ≳ 0.85 M⊙ (Kato et al. 2008; Woudt et al. 2009).
The formation mechanism of the overluminous SNe Ia is still an open question. Both the merger of two massive WDs and the differentially rotating WDs in a close binary may be the progenitors of overluminous SNe Ia. For the latter, the mass-accumulation efficiency onto the surface of the WD with differential rotation needs more detailed numerical simulations. In this paper, we adopted a simple procedure, whereas the actual process of the thermonuclear burning on the surface of the WDs is likely very complicated. However, the He-star evolutionary channel may play an important role in the formation of brighter SNe Ia, which are more frequent in the young stellar population (Hamuy et al. 1995; Hamuy et al. 1996; Aubourg et al. 2008). We expect more detailed multi-waveband observations for the companions of SNe Ia to confirm the He-star evolutionary channel in the future, though it is predicted that SNe Ia from this channel may be rare (Kato et al. 2008).
Hillebrandt et al. (2007) suggested that a lopsided explosion due to the off-center ignition of nuclear burning in a WD with Chandrasekhar mass may be responsible for the high brightness of 2003fg.
The rapid-binary evolution code presents a rough statistical result, while the standard stellar evolutionary theory suggested that 1.1 M⊙ is the maximum mass of the CO core. Assuming that the envelope of AGB star is lost when the binding energy of the envelope is equal to zero, Han et al. (1994) and Meng et al. (2008) found that the maximum mass of CO WD is 1.1 M⊙ and 1.05 M⊙ (Z = 0.02), respectively. If a CO core with 1.2 M⊙ is produced by stellar evolution, a C burning should occur and result in the formation of ONeMg WD. Therefore, it is very difficult to form a 1.2 M⊙ CO WD from a stellar evolutionary channel. Certainly, the maximum mass of the CO WD is related to the definition of the core, and the necessary condition ejecting the envelope of an AGB star. In addition, the lifting effect caused by rotation may help in producing larger CO core masses. We expect additional detailed studies to confirm if the most massive CO WD can exceed ~ 1.1 M⊙ as a result of binary interaction. Similar to Hachisu et al. (1996) and Li & van den Heuvel (1997), in this work we still take a maximum initial mass of 1.2 M⊙ for WDs.
When weak He-shell flashes occur, the mass accumulation efficiency strongly depend on the chemical composition or the radius of the WD (Kato & Hachisu 2004).
Acknowledgments
We are grateful to the anonymous referee for his/her constructive suggestions that improved this manuscript. This work was supported by the Natural Science Foundation of China (NSFC) under grant number 10873011, China Postdoctoral Science Foundation funded project, and Program for Science & Technology Innovation Talents in Universities of Henan Province, China. Z.H. thanks the support of NSFC (Grant No. 10821061), the Chinese Academy of Sciences (Grant No. KJCX2-YW-T24) and the 973 project (Grant No. 2007CB815406).
References
- Aldering, G., Goldhaber, G., Perlmutter, S., et al., 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Aldering, G., Antilogus, P., Scalzo, R. A., et al. 2010, ApJ, 713, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Aubourg, E., Tojeiro, R., Jimenez, R., et al. 2008, A&A, 492, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W.-C., & Li, X.-D. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., Pols O. R.,Savonije, G. J., & van den Heuvel, E. P. J. 2002, MNRAS, 331, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kong, A. K. H. 2003, ApJ, 592, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Straniero, O., Tornambè, A., & Isern, J. 1996, ApJ, 472, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Piersanti, L., Bravo, E., et al. 2006, ApJ, 644, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Durisen, R. H. 1977, ApJ, 213, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Challis, P., Riess, A. G., et al., 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Garnavich, P. M., Prieto, J. L., & Han, Z. 2008, ApJ, 677, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Regnault, N., Astier, P., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999a, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1999b, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Maza, J., et al. 1995, AJ, 109, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, P. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2006, MNRAS, 368, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Garnavich, P. M., Prieto, J. L., et al. 2007, ApJ, 669, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J, C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., Sim, S. A., & Röpke, F. K. 2007, A&A, 465, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howell, D. A. 2001, ApJ, 554, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Tutukov, A. V. 1987, ApJ, 313, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Tutukov, A. V. 1991, ApJ, 370, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Tutukov, A. V. 1994, ApJ, 431, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., Nomoto, K., Tornambè, A., & Tutukov, A. V. 1987, ApJ, 317, 717 [Google Scholar]
- Kahabka, P., & van den Heuvel, E. P. J., 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 1994, ApJ, 437, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., Hachisu I., Kiyota S., & Saio H. 2008, ApJ, 684, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Yamanaka, M., Tanaka, M., et al. 2010, ApJ, 714, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Limongi, M., & Tornambe, A. 1991, ApJ, 371, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010a, MNRAS, 401, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010b, ApJ, 710, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2008, A&A, 487, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Science, 325, 1222 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Narayan, R., & Popham, R. 1989, ApJ, 346, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Iwamoto, K., & Kishimoto, N. 1997, Science, 276, 1378 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Piersanti, L., Gagliardi, S., Iben, I. Jr., & Tornambe, A. 2003, ApJ, 598, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Mazzali, P., Lesaffre, P., Han, Z., & Forster, F. 2008, NewAR, 52, 381 [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Schroder, K. P., Hurly, J. R., & Tout, C. A. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 1985, A&A, 148, 207 [NASA ADS] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., & Hillebrandt, W. 2005, A&A, 431, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silverman, J. M., et al. 2010, MNRAS, in press [arXiv:1003.2417] [Google Scholar]
- Sullivan, M., Nugent, P. E., Howell, D. A., et al., 2006, Nature, 443, 308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tornambè, A., & Matteucci, F. 1986, MNRAS, 223, 69 [NASA ADS] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1994, MNRAS, 268, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2009, A&A, 508, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., & Han, Z. 2010a, A&A, 515, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., & Han, Z. 2010b, RAA, 10, 681 [Google Scholar]
- Wang, B., Meng, X., Wang, X., & Han, Z. 2008, ChJAA, 8, 71 [NASA ADS] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, X.-D., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iban, I. Jr. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Steeghs, D., Karovska, M., et al. 2009, ApJ, 706, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S. -C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S. -C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S. -C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S. -C.,Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, R. F., Akerlof, C., Miller, J., et al. 2007, Astron. Telegr., 1212, 1 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Distribution of initial WD + He star systems in MHe − MWD diagram. Basic input parameters for Monte Carlo simulations correspond to the standard model of Wang et al. (2009b). |
| In the text | |
 |
Fig. 2 Evolution tracks of WD binary with MHe,i = 1.8 M⊙, MWD,i = 1.2 M⊙, and log(Porb,i / day) = − 1.2. The solid, dashed, and dotted curves represent the evolution of ṀHe, ṀWD, and MWD, respectively. The solid vertical line indicates the position where the WD is expected to explode as a SN Ia. |
| In the text | |
 |
Fig. 3 Evolutionary track of the He star is shown as a solid curve, and the evolution of orbital period is shown as a dashed curve. The vertical dotted line and open stars indicate the place where the WD explodes as a SN Ia. |
| In the text | |
 |
Fig. 4 Distribution of the initial orbital periods Porb,i and the initial He star masses MHe,i of the progenitors of super-Chandrasekhar mass SNe Ia when MWD,i = 1.20 M⊙. |
| In the text | |
 |
Fig. 5 Similar to Fig. 4, but for an initial WD mass of 1.0 M⊙. |
| In the text | |
 |
Fig. 6 Distribution of the donor stars at the moment of SN Ia explosions in the H-R diagram when MWD,i = 1.2 M⊙. The open circles, open stars, open triangles, and solid stars denote systems with 1.4 M⊙ ≤ MSN < 1.6 M⊙, 1.6 M⊙ ≤ MSN < 1.7 M⊙, 1.7 M⊙ ≤ MSN < 1.8 M⊙, and MSN ≥ 1.8 M⊙, respectively. |
| In the text | |
 |
Fig. 7 Similar to Fig. 6, but for MWD,i = 1.0 M⊙. The open circles and solid triangles denote systems with 1.40 M⊙ ≤ MSN < 1.45 M⊙, and MSN ≥ 1.45 M⊙, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


