| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201014923 | |
| Published online | 09 November 2010 | |
K-shell energy levels and radiative rates for transitions in Si xi⋆
1
School of Physics, Shandong University,
Jinan,
Shandong
250100,
PR China
e-mail: sjr@bao.ac.cn
2
National Astronomical Observatories, Chinese Academy of Sciences,
Beijing
100012, PR
China
Received: 4 May 2010
Accepted: 3 June 2010
Context. Atomic data for K-shell transitions are essential for modeling the K absorption lines, which have been observed in the spectra of active galaxies by high-resolution X-ray observatories, e.g. XMM, Chandra, and Suzaku. These accurate atomic data are also needed for line identifications and spectroscopic diagnostic of plasmas in laboratory generated by laser or beam-foil method.
Aims. We calculate atomic data using the atomic code flexible atomic code (FAC) taking relativistic effects and configuration interactions into account.
Methods. We calculate the K-shell transitions among the configurations of 1s22s2, 1s22s2p, 1s22p2, 1s22sn′l′, 1s22pn′l′, 1s2s22p, 1s2s2p2, 1s2p3, 1s2s2pn′l′, and 1s2p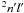 , n′ ≤ 4, l′ ≤ n′ for beryllium-like Si xi. We present the K-shell energy levels, wavelengths, radiative rates, and oscillator strengths for Si xi. To assess the accuracy of current data, we compare our results with both former experiments and other theoretical works.
, n′ ≤ 4, l′ ≤ n′ for beryllium-like Si xi. We present the K-shell energy levels, wavelengths, radiative rates, and oscillator strengths for Si xi. To assess the accuracy of current data, we compare our results with both former experiments and other theoretical works.
Results. The present K-shell level energies and wavelengths are accurate to within 2 eV and 10 mÅ, respectively. The radiative rates have an accuracy of around 20% for the majority of our transitions.
Key words: atomic data / atomic processes
Complete Tables 1, 3, and 4 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/viz-bin/qcat?J/A+A/522/A103
© ESO, 2010
1. Introduction
K-shell absorption features in active galaxy nuclei (AGNs) and quasars have been detected by X-ray observatories, such as XMM-Newton, Chandra, and Suzaku (Kaspi et al. 2000; Sako et al. 2001; Krongold et al. 2003; Holczer et al. 2007). Silicon absorption features are among those often observed (Kaspi et al. 2001; 2002; Kallman et al. 2009). The He-like Si absorption lines have been used to determine the outflow velocities (Young et al. 2005), and the He-like triplet component ratios are most often used as temperature and density diagnostics (Gabriel & Jordan 1969; Porquet et al. 2000). The column density, ionization state and velocity of the absorbing gas surrounding the central engine have been measured by modeling these high resolution spectra. Furthermore, the mechanisms of driving disk wind onto black holes have been able to be determined (Miller et al. 2006). In addition to absorption lines originating in He-like ions, K-shell absorption lines from low ionizing ions are also often detected, such as the Li-like oxygen and carbon ions (Lee et al. 2001; Sako et al. 2003), and Be-like oxygen ions (Holczer et al. 2010). The Be-like Si xi lines are also commonly detected for AGNs (Mercedes et al. 2010), disk winds around compact objects (Miller et al. 2006), and the interstellar medium (ISM) (Lee et al. 2001). However, a lack of reliable atomic data has impeded progress in modeling and analyzing these high resolution spectra; particularly, it is difficult to identify plenty of weak lines (Kallman et al. 2009).
Various experiments and calculations have been carried out to derive these data. Using the beam-foil method, Trabert et al. (1979; 1982) reported the X-ray spectra of foil-excited fast H-like to Be-like silicon ions. These emission lines originate mainly from 2p–1s transitions. Mosnier et al. (1986) derived similar results for a smaller energy range but at higher resolution. Unlike the inner-shell excitation populating the excited levels in the beam-foil experiment, dielectronic recombination is more important in laser plasma experiments. Faenov et al. (1994) reported the wavelengths of an He-like ion resonance-line satellites from Be-like silicon ion in a CO2 laser plasma, and used MZ code (Vainshtein & Safronova 1978; 1980) to compute the wavelengths, A-values, and Auger rates. Chen (1985) calculated the K-vacancy level energies, wavelengths, A-values, and Auger and radiative widths of Be-like ions using the multiconfiguration Dirac-Fock (MCDF) method. The wavelengths, transitions probabilities, and autoionization rates of Be-like isoelectronic sequences were computed by Nilsen et al. (1995) with the MZ code, while the wavelengths and oscillator strengths for the 1s–np (n ≤ 3) transitions in ions of Ne, Mg, Al, Si, S, Ar, and Ca were calculated by Behar & Netzer (2002) using the HULLAC (Hebrew University Lawrence Livermore Atomic Code). Palmeri et al. (2008) computed the level energies, wavelengths, A-values, and radiative and Auger widths for K-vacancy state of Ne, Mg, Si, S, Ar, and Ca with the codes HFR (Cowan 1981) and AUTOSTRUCTURE (Badnell 1986; 1997).
Previous work has mainly concentrated on the 1s–2p transitions between the configurations 1s22s2, 1s22s2p, 1s22p2, 1s2s22p, 1s2s2p2, and 1s2p3, namely between ground states/low excited states and K-vacancy states. Few works related to K-shell transitions from high excited states have been reported yet these transitions are important and necessary to model and analyze the absorption spectra of radiatively heated plasmas (Jin et al. 2008; Wei et al. 2008). The K-shell absorptions lines originating from these high excited states of Be-like O v have been observed (Holczer et al. 2010). Similar transitions from Si xi are expected to account for the unidentified lines in warm absorbers around compact objects (Kallman et al. 2009).
In this work, we report the results of K-shell transitions between 1s22s2, 1s22s2p, 1s22p2, 1s22sn′l′, 1s22pn′l′, 1s2s22p, 1s2s2p2, 1s2p3, 1s2s2pn′l′, and 1s2p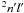 , n′ ≤ 4, l′ ≤ n′.The calculated energy levels and wavelengths are compared with available experimental and theoretical results in Sect. 2, while radiative rates and oscillator strengths are discussed in Sect. 3. Two supplementary tables are described in Sect. 4, and the summary and conclusions are drawn in Sect. 5.
, n′ ≤ 4, l′ ≤ n′.The calculated energy levels and wavelengths are compared with available experimental and theoretical results in Sect. 2, while radiative rates and oscillator strengths are discussed in Sect. 3. Two supplementary tables are described in Sect. 4, and the summary and conclusions are drawn in Sect. 5.
2. Energy levels and wavelengths
We employed flexible atomic codes (FAC) developed by Gu (2003) to calculate the atomic data. These are fully relativistic codes based on the Dirac equation that account for configuration interactions. The basis state functions are constructed by radial orbitals generated from a modified Dirac-Fock-Slater central-field potential in the self-consistent iteration procedure. This potential is optimized for a fictitious mean configuration with fractional occupation numbers to represent the electronic screening effect. Level energies of a specific configuration are then corrected by applying the difference between the configuration’s average energy calculated by this potential and that calculated by the potential optimized to this configuration. To assess the effects of different configurations in our calculated results, a small model involving 40 levels among the configurations of 1s22s2, 1s22s2p, 1s22p2, 1s2s22p, 1s2s2p2, and 1s2p3 was developed (hereafter, FAC1). And a larger model involving 680 energy levels of Si xi belonging to configurations of 1s22s2, 1s22s2p, 1s22p2, 1s22sn′l′, 1s22pn′l′, 1s2s22p, 1s2s2p2, 1s2p3, 1s2s2pn′l′ and 1s2p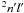 , n′ ≤ 4, l′ ≤ n′ was also developed (hereafter, FAC2). To facilitate comparison with other results, only 40 calculated energy levels belonging to the configurations 1s22s2, 1s22s2p, 1s22p2, 1s2s22p, 1s2s2p2, and 1s2p3 are listed in Table 1. There is a lack of both theoretical and experimental data related to K-shell transitions from high excited levels, namely levels belonging to configurations of 1s22sn′l′ and 1s22pn′l′. These two sets of model calculations could be used to assess the accuracy of our energy levels. The energy differences between these two sets of values are mostly smaller than 1 eV. The largest energy difference is no greater than 1.5 eV, which suggests that the effects of different configurations in our calculations are generally small ( < 2%).
, n′ ≤ 4, l′ ≤ n′ was also developed (hereafter, FAC2). To facilitate comparison with other results, only 40 calculated energy levels belonging to the configurations 1s22s2, 1s22s2p, 1s22p2, 1s2s22p, 1s2s2p2, and 1s2p3 are listed in Table 1. There is a lack of both theoretical and experimental data related to K-shell transitions from high excited levels, namely levels belonging to configurations of 1s22sn′l′ and 1s22pn′l′. These two sets of model calculations could be used to assess the accuracy of our energy levels. The energy differences between these two sets of values are mostly smaller than 1 eV. The largest energy difference is no greater than 1.5 eV, which suggests that the effects of different configurations in our calculations are generally small ( < 2%).
Target levels of Si xi and their threshold energies (in eV). The complete table is available at the CDS.
Although we could only concentrate on judging the accuracy of K-shell transition results from ground/low excited states of FAC2, these comparison results could give us some measure of the accuracy of our results. Compiled energy levels of Si xi can be found in NIST database version 3.1.5 1 and are listed in Table 1 (hereafter, NIST). For all the available energy levels considered here, the differences in energy level between experiments and FAC2 are smaller than 2 eV. Palmeri et al. (2008) calculated energy levels and radiative rates for K-shell transitions in the Si isonuclear sequences and other elements. Their calculations are based on the code HFR (Cowan 1981), which calculates the atomic structures with nonorthogonal orbital bases optimized for each configurations. The relativistic corrections, such as the spin-orbit interactions, the non-fine-structure mass variations, and the one-body Darwin correction, are applied to the Hamiltonian to calculate the wave function. The two-body Breit interaction is neglected. Forty levels of Si xi from their results are also listed in Table 1 (hereafter, HFR1). As stated above, their transitions includes configurations between K-vacancy states and ground/low excited states, which are the same as our FAC1 model. The energy differences between their results and NIST are smaller than 2 eV, which is comparable to our results. Detailed level by level comparison shows that the differences are smaller than 1.5 eV between FAC2 and HFR1. The agreement is even closer between FAC1 and HFR1 because the same configurations are used in the calculations. In conclusion, the energy levels listed in Table 1 from our FAC2 or the results of Palmeri et al. (2008) are accurate to 2 eV. However, there is minor differences in level ordering in K-vacancy states, e.g., levels 18, 19, 20, and 21 in Table 1. As mentioned above, the reason for this is that, Palmeri et al. (2008) neglected the Breit effects. Apart from this, configuration interactions have also some effects on this ordering, e.g. the level order 19 and 20 are exchanged in our FAC1 and FAC2 results. Similar results were found by Aggarwal et al. (2005). We note that the level ordering of FAC2 is consistent with those listed in the NIST database.
The measurement of wavelength for these K-shell transitions is difficult. In the laboratory, when restricted by the spectral resolution, lines cannot be separated from each other, and form a line band (Mosnier et al. 1986). These high excited K-vacancy states may also decay by means of autoionization process instead of fluorescence yielding. Thus, the intensities of these emission lines from Si xi are very weak. Furthermore, the observed spectra in laser plasma experiments are usually time integrated, which increases the complexity of spectra analysis and line identification. The available measurements of the wavelengths of Si xi are listed in Table 2.
Wavelengths of K-shell transitions in Si xi.
Compared to the measured wavelengths listed by Faenov et al. (1994), the average wavelength differences are 0.4 mÅ ± 2 mÅ. Similarly good agreements (2.5 mÅ) are also found when comparing our theoretical wavelengths with the experimental results reported by Trabert et al. (1979). When compared with the experimental wavelengths from Mosnier et al. (1986), however, relatively large discrepancies are found. The average difference increases from 0.4 mÅ to 14 mÅ (see Table 2). In their work, we note that, wavelengths for the same transitions differ from those of Faenov et al. (1994). Agreement cannot be achieved even if the experimental errors are taken into account. One possible explanation is that these Si xi lines have been misidentified due to very weak intensities in this beam foil experiment.
Theoretical calculations of the wavelengths of He-like resonance-line satellites of Be-like ions (12 ≤ Z ≤ 30) are reported by Boiko et al. (1979) using relativistic Z-expansion method (Safronova & Urnov 1979). As shown in Fig. 1, the largest wavelength difference is smaller than 6 mÅ. The average wavelength difference between our results and theirs is 1 mÅ ± 2.4 mÅ. Boiko et al. (1979) also reported the experimental measurements, which were reanalyzed by Faenov et al. (1994). Comparison with those wavelengths presented by Palmeri et al. (2008) are also shown in Fig. 1. The agreement with HFR1 is generally closer than 5 mÅ and improves as the wavelengths decrease. The average wavelength difference is 1 mÅ ± 1.8 mÅ. This is unsurprising if we note that their results have been empirically shifted to the experimental wavelengths listed by Faenov et al. (1994). No wavelength shifts were performed in our FAC2 calculations. The wavelength of the strongest K-transition from the ground state for Si xi listed by Behar & Netzer (2002) is 6 mÅ longer than the FAC2 results. This is also in agreement with other theoretical calculations. Combining these comparisons, we conclude that the wavelengths computed with FAC2 are accurate to about 10 mÅ.
 |
Fig. 1 The wavelength differences between present FAC2 calculations and HFR1 results, as well as results from relativistic Z-expansion method. The two sets of differences are plotted versus FAC2 wavelengths in Å for Si xi. Squares: HFR1 (Palmeri et al. 2008). Cross: relativistic Z-expansion method (Boiko et al. 1979). |
3. Radiative rates
The radiative rate, namely the A-coefficient value in the calculation of Behar & Netzer (2002), for the strongest 1s–2p absorption lines of Si xi, is 3.17E + 13s-1. This value is in excellent agreement with our results (3.33E + 13s-1). A test of the accuracy of our results is made by performing a detailed comparison with those from Palmeri et al. (2008). However, as stated above, only the radiative rates for transitions from ground and low excited states can be assessed because of a lack of data for transitions from high excited states. All the high radiative rates in our calculations ( > 1E + 13s-1) show good agreement with theirs (within 10%), while around 78% of our transitions show agreement to within 20% (see Fig. 2). We note that discrepancies of several magnitudes are found for a few weak transitions. Aggarwal et al. (2005) suggested that this differences can be attributed to the different configurations involved in different calculations. Apart from this, strong level mixing and the different methods adopted in the calculations may also cause large differences (Liang et al. 2009). The effects of configuration interactions on radiative rates are tentatively tested by comparing between our results obtained from 40 and 680 level models, respectively. Although large differences are found between the results of FAC1 and FAC2 for weak transitions, agreements are generally achieved within 20% for strong transitions (see Fig. 2). In fact, totally 76% of the transitions are within 20% when compared FAC2 with FAC1.
 |
Fig. 2 Comparison of radiative rates between FAC2 and the results from HFR1 and FAC1. Squares: HFR1 (Palmeri et al. 2008). Circles: FAC1 (with radiative rates greater than 1E+13(s-1)). The agreement is generally to within 20% for the majority of the transitions in both comparisons. |
4. Supplementary electronic tables
Two electronic tables are supplied as a supplement to this paper. The energy levels of all the configurations mentioned in Sect. 2 are listed in Table 3. The total angular quantum number, parity, and state configurations are also included. It should be noted that, because of including the configurations from high excited states (e.g. 1s22sn′l′, 1s22pn′l′), the order of the energy levels differs from those listed in Table 1. From level 11, all the level indices listed in Table 1 need to be added 88 when they are listed in Table 3. The computed wavelengths, A-values, and absorption oscillator strengths are tabulated in Table 4 with their level index (listed in Table 3) for upper and low levels.
The level energies of K-shell transitions for Si xi.
The K-shell transitions of Si xi.
5. Summary and conclusions
We have presented the energy levels, wavelengths, radiative rates, and oscillator strengths for the K-shell transitions of Si xi calculated with the fully relativistic atomic code FAC (Gu 2003). The transitions between high excited states and K-vacancy states are presented for the first time. Detailed comparison with experimental and theoretical results has been carried out for the transitions between ground/low excited states and K-vacancy states.
The energy levels reported here agree with the results compiled in the NIST database and the theoretical results of Palmeri et al. (2008) to within 2 eV. Average wavelength differences are smaller than 3 mÅ when compared with the experimental results from Faenov et al. (1994) and Trabert et al. (1979), while large wavelength differences (up to 14 mÅ) are found compared to the experimental wavelengths measured by Mosnier et al. (1986). Comparison of present FAC2 wavelengths with theoretical results from Palmeri et al. (2008) and Boiko et al. (1979) confirms that the average wavelength differences are smaller than 3 mÅ. No wavelength shifts need to be applied to our results. The radiative rates have an accuracy of around 20% for the majority of our transitions.
As mentioned in the introduction, absorption transitions from high excited states to K-vacancy states may account for the unidentified lines in compact objects (Kallman et al. 2009). However, the detailed modeling and spectral analysis to study this idea are out of scope of this paper. Future work will extend similar calculations to other silicon isonuclear ions.
Acknowledgments
We would like to thank discussion with Dr. G. Y. Liang, Mr. L. Di and Dr. J. Y. Zhong. We thank the anonymous referee for helpful suggestions. This work was supported by the National Natural Science Foundation of China under grants 10821061 and 10876040, by the Chinese Academy of Sciences under grant KJCX2-YW-T01, and by the National Basic Research Program of China under grant 2007CB815103.
References
- Aggarwal, K. M., Keenan, F. P., & Nakazaki, S. 2005, A&A, 436, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R. 1986, J. Phys. B, 19, 3827 [Google Scholar]
- Badnell, N. R. 1997, J. Phys. B, 30, 1 [Google Scholar]
- Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2003, A&A, 403, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boiko, V. A., Chugunov, A. Yu., Ivanova, T. G., et al. 1979, MNRAS, 185, 305 [Google Scholar]
- Behar, E., & Netzer, H. 2002, ApJ, 570, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M. H. 1985, Phys. Rev. A, 31, 1449 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra Berkeley (Univ. California Press) [Google Scholar]
- Faenov, A. Ya., Pikuz, S. A., & Shlyaptseva, A. S. 1994, Phys. Scr., 49, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., & Jordan, C. 1969, MNRAS, 145, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Holczer, T., Behar, E., & Kaspi, S. 2007, ApJ, 663, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Holczer, T., Behar, E., & Kaspi, S. 2010, ApJ, 708, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Jin F. T.,Zeng, J. L., & Yuan, J. M. 2008, J. Quant. Spect. Rad. Trans., 109, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Brandt, W. N., Netzer, H., et al. 2000, ApJ, 535, L17 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kaspi, S., Brandt, W. N., Netzer, H., et al. 2001, ApJ, 554, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Brandt, W. N., George, I. M., et al. 2002, ApJ, 574, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Brickhouse, N. S., et al. 2003, ApJ, 597, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T. R., Bautista, M. A., Goriely, S., et al. 2009, ApJ, 701, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Ogle, P. M., Canizares, C. R., et al. ApJ, 554, L13 [Google Scholar]
- Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2009, J. Phys. B: At. Mol. Opt. Phys., 42, 225002 [Google Scholar]
- Andrade-Velzquez, M., Krongold, Y., Elvis, M., et al. 2010, ApJ, 711, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Raymond, J., Fabian, A., et al. 2006, Nature, 441, 953 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mosnier, J. P., Barchewitz, R., Senemaud, C., et al. 1986 J. Phys. B: At. Mol. Opt. Phys., 19, 2531 [Google Scholar]
- Nilsen, J., Safronova, U. I., & Safronova, M. S. 1995, Phys. Scr., 51, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2008, ApJS, 177, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Porquet D., & Dubau J. 2000, A&AS, 143, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team 2008, NIST Atomic Spectra Database version 3.1.5, http://physics.nist.gov/asd3 [2010, March 3], National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Sako, M., Kahn, S. M., Behar, E., et al. 2001, A&A, 365, L168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sako, M., Kahn, S. M., Branduardi-Raymont, G., et al. 2003, ApJ, 596, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Safronova, U. I., & Urnov, A. M. 1979, J. Phys. B: At. Mol. Opt. Phys., 12, 3171 [NASA ADS] [CrossRef] [Google Scholar]
- Trabert, E., Armour, I. A., Bashkin, S., et al. 1979, J. Phys. B: At. Mol. Opt. Phys., 12, 1665 [NASA ADS] [CrossRef] [Google Scholar]
- Trabert, E., Fawcett, B. C., & Silver, J. D. 1982 J. Phys. B: At. Mol. Opt. Phys., 15, 3587 [Google Scholar]
- Vainshtein, L. A., & Safronova, U. I. 1978, At. Data Nucl. Data Tables, 21, 49 [Google Scholar]
- Vainshtein, L. A., & Safronova, U. I. 1980, At. Data Nucl. Data Tables, 25, 311 [Google Scholar]
- Wei, H. G., Shi, J. R., Zhao, G., et al. 2008, ApJ, 683, 577 [Google Scholar]
- Young, A. J., Lee, J. C., Fabian, A. C., et al. 2005, ApJ, 631, 733 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Target levels of Si xi and their threshold energies (in eV). The complete table is available at the CDS.
All Figures
 |
Fig. 1 The wavelength differences between present FAC2 calculations and HFR1 results, as well as results from relativistic Z-expansion method. The two sets of differences are plotted versus FAC2 wavelengths in Å for Si xi. Squares: HFR1 (Palmeri et al. 2008). Cross: relativistic Z-expansion method (Boiko et al. 1979). |
| In the text | |
 |
Fig. 2 Comparison of radiative rates between FAC2 and the results from HFR1 and FAC1. Squares: HFR1 (Palmeri et al. 2008). Circles: FAC1 (with radiative rates greater than 1E+13(s-1)). The agreement is generally to within 20% for the majority of the transitions in both comparisons. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


