EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 522 (November 2010) A&A, 522 (2010) A98 Full HTML
Highlight
Free Access
Issue
A&A
Volume 522, November 2010
Article Number A98
Number of page(s) 15
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201014741
Published online 08 November 2010

© ESO, 2010

1. Introduction

Photometry in the uvby–β system (Strömgren 1963; Crawford 1966) is well suited to the determination of basic stellar atmospheric parameters for F-, G-, and K-type stars through the color indices (b–y), m1 = (v–b) − (b–y) and c1 = (u–v) − (v − b). Several empirical calibrations exist in the literature to transform (b–y) or β to Teff (e.g. Alonso et al. 1996, 1999; Clem et al. 2004; Ramírez & Meléndez 2005b, hereafter RM05b; Holmberg et al. 2007; Casagrande et al. 2010), while the m1 index can be used to determine [Fe/H] in dwarfs (e.g. Strömgren 1964; Gustafsson & Nissen 1972; Olsen 1984; Schuster & Nissen 1989; Malyuto 1994; Haywood 2002; Martell & Laughlin 2002; Martell & Smith 2004; Ramírez & Meléndez 2005a, hereafter RM05a; Twarog et al. 2007; Holmberg et al. 2007) and giants (e.g. Bond 1980; Arellano Ferro & Mantegazza 1996; Hilker 2000; Ramírez & Meléndez 2004; Calamida et al. 2007, 2009), as reviewed by Árnadóttir et al. (2010). The evolutionary stage of stars can be determined using the c1 index together with other uvby color indices (e.g. Crawford 1975; Olsen 1984; Nissen & Schuster 1991; Schuster et al. 2004; Twarog et al. 2007).

Since there are many difficulties in observing the Sun with the same instrumentation as we observe other stars (e.g. Stebbins & Kron 1957; Gallouëtte 1964; Clements & Neff 1979; Tueg 1982; Lockwood et al. 1992), the Sun cannot be used to set the zero-points of transformations between color indices and fundamental stellar parameters. Accurate transformations are important in many areas of astrophysics. For example, in the study of the primordial lithium abundance, an accurate Teff scale is needed to compare the Li abundance of metal-poor stars with that obtained from Big Bang Nucleosynthesis (e.g. Meléndez et al. 2010a; Sbordone et al. 2010). The terrestrial planet signatures found in the chemical composition of the Sun (Meléndez et al. 2009, hereafter M09; Ramírez et al. 2009, hereafter R09; Ramírez et al. 2010) shows that for accurate comparisons between the Sun and stars an accurate temperature scale must be used in the determination of chemical abundances. Although there is inconclusive evidence about whether the Sun is too metal-rich with respect to stars of similar age and Galactic orbit (Haywood 2008; Holmberg et al. 2009) implying that the Sun could have been born in the inner part of the Galaxy (Wielen et al. 1996), this apparent offset between the Sun and stars could be partly due to zero-point errors in the photometric metallicity scale (see e.g. Table 3 of Árnadóttir et al. 2010, for systematic differences between spectroscopic and photometric metallicities). Furthermore, we note that zero-point errors in the Teff scale, as well as errors in the metallicity scale, would introduce systematic errors in the ages of stars determined from isochrones.

According to their similarity to the Sun, stars can be classified as “solar-type stars” (late F to early K stars), “solar analogs” (G0 − G5 dwarfs with solar metallicity within  ~ a factor of 2 − 3), and “solar twins” (stars almost identical to the Sun) (e.g. Secchi 1868; Cayrel de Strobel 1996; Soderblom & King 1998; M09). Many works have used either solar-type stars or solar analogs to infer solar colors to improve or check the effective temperature scale, the performance of model atmospheres, and the absolute flux calibration of the Sun (e.g. Pettit & Nicholson 1928; Kuiper 1938; Stebbins & Whitford 1945; Stebbins & Kron 1957; Johnson 1962; Kron 1963; van den Bergh 1965; Croft et al. 1972; Olsen 1976; Schuster 1976; Barry et al. 1978; Hardorp 1978, 1980a,b; Clements & Neff 1979; Cayrel de Strobel et al. 1981; Neckel & Labs 1981; Chmielewski 1981; Tueg & Schmidt-Kaler 1982; Magain 1983; Taylor 1984; Mitchell & Schuster 1985; Neckel 1986; Vandenberg & Poll 1989; Gray 1992, 1995; Straizys & Valiauga 1994; Taylor 1994; Cayrel de Strobel 1996; Colina et al. 1996, hereafter C96; Hauck & Kunzli 1996; Bessell et al. 1998; Mironov et al. 1998; Sekiguchi & Fukugita 2000; Meléndez & Ramírez 2003; RM05b; Holmberg et al. 2006; Pasquini et al. 2008; Rieke et al. 2008; Casagrande et al. 2010).

Solar twins have spectra almost identical to the Sun (Cayrel de Strobel 1996), hence are better suited to setting the zero-points of fundamental calibrations, especially since they are found without assuming a priori a temperature scale, but their identification is based purely on a model-independent analysis of their spectra with respect to a solar spectrum obtained with the same instrumentation. However, until a few years ago only one solar twin was known (18 Sco; Porto de Mello & da Silva 1997; Soubiran & Triaud 2004). The situation has changed dramatically with the identification of many stars similar to the Sun (Meléndez et al. 2006, hereafter M06; Meléndez & Ramírez 2007, hereafter MR07; Takeda et al. 2007, hereafter T07; Takeda & Tajitsu 2009, hereafter T09; M09; R09; Baumann et al. 2010, hereafter B10). It is now feasible to use solar twins with accurately determined stellar parameters to test the predictions of model atmospheres and the accuracy of empirical photometric calibrations. In the present work, we perform this study for the widely used uvby–β system.

2. Photometric observations

2.1. Selection of the sample

Before starting our systematic survey of stars similar to the Sun in the Hipparcos catalogue, we performed pilot observations of solar-twin candidates to test our selection criteria. Our pilot study (M06) found zero-point offsets in our Teff scale (RM05b). We therefore applied small corrections to the solar colors predicted by RM05b to increase our chances of finding stars resembling the Sun. In particular, we searched for solar twins around the Tycho color (B − V)T = 0.7225 instead of (B − V)T = 0.689 predicted by our earlier color-Teff relations (RM05b). Our improved Teff scale (Casagrande et al. 2010) indeed corrected the zero-point problem, and now predicts a solar (B − V)T = 0.730, in good agreement with our tentative correction.

The main parameters used to select solar-twin candidates from the Hipparcos catalogue were parallaxes and (B − V)T colors. Additional criteria used (when available) were other optical-infrared colors (e.g. VT − K, b − y), photometric variability, information on multiplicity, previous literature values for [Fe/H] (obtained from an updated version of the Cayrel de Strobel et al. 2001, catalogue), rotation, and chromospheric activity. We found initially about one hundred stars satisfying our selection criteria within 75 pc. We later expanded our search to cover the whole Hipparcos catalogue, increasing our sample by about 1/3.

2.2. Observations and data reduction

The uvby–β data presented here in Table 1 for the solar twins were taken using the H. L. Johnson 1.5 m telescope at the San Pedro Mártir Observatory, Baja California, México (hereafter SPM), and the same six-channel uvby–β photoelectric photometer as for the northern observations of Schuster & Nissen (1988, hereafter SN), for all the uvby–β observations of Schuster et al. (1993, hereafter SPC), the northern data of very-metal-poor stars by Schuster et al. (1996), the uvby–β data for very-metal-poor stars in Table 1 of Schuster et al. (2004), and the uvby–β data for high-velocity and metal-poor stars in Table 1 of Schuster et al. (2006). The new uvby–β values for solar twins included here in Table 1 were taken during three observing runs in November 2007 (8 nights), April 2008 (7 nights), and September 2008 (4 nights).

The uvby–β solar-twin data were taken and reduced using techniques very nearly the same as for SN and SPC (see these previous papers for more details). The four-channel uvby section of the SPM photometer is really a spectrograph-photometer that employs exit slots and optical interference filters to define the bandpasses. The grating angle of this spectrograph-photometer was calibrated using a cadmium lamp at the beginning of each observing run to position the spectra on the exit slots to within about  ± 1   Å. Whenever possible, extinction-star observations were made nightly over an air-mass range of at least 0.8 (see Schuster & Parrao 2001; also Schuster et al. 2002), and spaced throughout each night several “drift” stars were observed symmetrically with respect to the local meridian (two hours east and then two hours west). Using these observations, the atmospheric extinction coefficients and time dependences of the night corrections could be obtained for each of the nights of observation (see Grønbech et al. 1976). Finding charts were employed at SPM to confirm identifications of the program stars and to select regions for the “sky” measurements. As for previous studies, such as SN and SPC, the program stars were observed at SPM to at least 50 000 counts in all four channels of uvby and to at least 30 000 counts for the two channels centered at Hβ. For all program stars, the sky background was measured until its contributing error was equal to or smaller than the error in the stellar count. At SPM, an attempt was made to obtain three or more independent uvby observations for each of the program stars, i.e. photometric observations during at least three independent nights; this aim was achieved, or exceeded, for all solar twins except HIP 75923 and HIP 77883 for which we obtained two observations each.

As for the SN and SPC catalogues, all data reduction was carried out following the precepts of Grønbech et al. (1976) using computer programs kindly loaned by T. Andersen (see Parrao et al. 1988). At SPM, the uvby–β standard stars observed were taken from the same lists as for the previous catalogues, and are mostly secondary standards from the catalogues of Olsen (1983, 1984). The reduction programs create a single instrumental photometric system for each observing run, including nightly atmospheric extinctions and night corrections with linear time dependences. Then transformation equations from the instrumental to the standard systems of V, (b–y), m1, c1, and β are obtained using all standard stars observed during that observing period. The equations for the transformation to the standard uvby–β system are the linear ones of Crawford & Barnes (1970) and Crawford & Mander (1966). Small linear terms in (b–y) are included in the standard transformation equations for m1 and c1 to correct for bandwidth effects in the v filter. Our y measurements were transformed onto the V system of Johnson et al. (1966).

Thirty-six uvby–β standard stars were employed during the observing run of November 2007 providing instrumental photometric errors ranging from 0.002 mag in (b–y) to 0.009 mag in c1, and errors in the transformations to the standard photometric system from 0.004 to 0.011 mag, respectively. For April 2008, these values were for 33 standard stars, 0.002 − 0.010 mag, and 0.005 − 0.013 mag, respectively, and for September 2008, for 35 standard stars, 0.002 − 0.008 mag, and 0.006 − 0.009 mag, respectively. Instrumental and transformation errors in the magnitude V and in the indices m1 and β were always intermediate in value between those given above.

2.3. The catalogue

Table 1 presents the uvby–β catalogue for the 73 solar-twin candidates observed at SPM. Column 1 lists the Hipparcos number; Col. 2 gives the HD (or BD) number, Col. 3 the V magnitude on the standard Johnson UBV system; and Cols. 4 − 6 and 9, the indices (b–y), m1, c1 and β on the standard systems of Olsen (1983, 1984), which are essentially the systems of Crawford & Barnes (1970) and Crawford & Mander (1966) with north-south systematic differences corrected. Columns 7, 8, and 10 give NV, Nuvby, and Nβ, the total numbers of independent V, uvby, and β observations.

A very small subset of our photometric observations was made through light cirrus clouds in the absence of moonlight. It has been well documented (e.g. SN; Olsen 1983) that observations in the indices b–y, m1, c1, and β made with simultaneous multichannel photometers are not affected in any significant way by light (or even moderate) cirrus, while the V magnitude, obtained from only the y band, is affected. For this reason, a few of the solar twins, such as HIP 60314, HIP 74389, and HIP 118159, have fewer independent observations of the V magnitude than the indices.

2.4. Comparisons with other photometric data

We searched for uvby–β photometry in the General Catalogue of Photometric Data (Mermilliod et al. 1997; Hauck & Mermilliod 1998) and found data for 23 solar-twin candidates and 12 solar analogs (observed by ourselves spectroscopically for other projects). The photometry of these 35 stars is given in Table 2.

The accuracy of uvby–β photometry obtained at SPM has been extensively tested (e.g. SN; Arellano Ferro et al. 1990; Schuster et al. 1993, 1996), and we illustrate below that our solar-twin photometry is also in excellent agreement with the literature, in all cases with mean differences well below 0.01 mag. There are 12 stars in common between our sample and previous work. The average difference (ours – literature) in (b–y) is only  − 0.001 (σ = 0.004). Our V Johnson photometry is also in good agreement, with a mean difference (ours – literature) of only +0.001 (σ = 0.006). The colors m1 and c1 also compare well, with a difference (ours – literature) of only +0.002 (σ = 0.006) and +0.006 (σ = 0.015).

Considering the excellent agreement between the photometry available in the literature and in our own data sets, and considering the previously shown accuracy and precision of the SPM uvby–β photometry, we conclude that both data sets, of Tables 1 and 2, provide solar-color indices very close to the standard uvby–β system.

Table 4

Global fits for color = A + B (Teff – 5777) + C (log g – 4.44) + D [Fe/H].

3. The solar-color indices

Our observations comprise the largest photometric data set yet taken of stars very similar to the Sun in the uvby–β system. Adding other photometry available in the literature and using our own accurate stellar parameters (M09; R09; Meléndez et al. 2010b, hereafter M10b), and taking into account the variations in colors with Teff, log g and [Fe/H], we can infer the “solar” colors by interpolating them to the stellar parameters of the Sun: Teff = 5777 K, log g = 4.44, and [Fe/H] = 0.00 (e.g. Cox 2000; Gray 2005; RM05b).

The quality of our stellar parameters (M06; MR07; M09; R09; M10b) is very high because both the Sun (reflected light of asteroids) and the solar twins were observed with the same instrumentation during the same observing runs, and all data reduction and analysis were performed in an identical way. Our spectra have typically a resolution of 60 000 and S / N  ~  200 for stars observed with the 2.7 m telescope at McDonald and S / N  ~  450 for stars observed with 6.5 m Magellan Clay telescope at Las Campanas. Errors as low as  ~ 25 K in Teff, 0.04 dex in log g, and 0.025 dex in [Fe/H] can be obtained in the best cases, and abundance ratios with errors as low as 0.01 − 0.02 dex have been obtained with the above data, showing that the Sun is a star with a peculiar chemical composition (M09; R09). Additional spectra available in the literature for solar-twin candidates were analyzed by B10 using similar techniques. The spectra are from HARPS observations available at the ESO archive and from the S4N database (Allende Prieto et al. 2004)1. In both cases, a solar spectrum taken with the same instrumentation was employed in the differential analysis.

The stellar parameters were determined homogeneously by our own group (M06; MR07; M09; R09; M10b; B10) using Kurucz model atmospheres and a line-by-line differential analysis with respect to the Sun. The Teff, log g, [Fe/H], and microturbulence were determined iteratively until both the differential excitation equilibrium of FeI lines and the differential ionization balance of FeI and FeII, were achieved. The microturbulence was also determined simultaneously, by requiring no dependence of the iron abundance (from FeI lines) on the reduced equivalent width.

Since our solar-twin sample spans a relatively narrow range in atmospheric parameters relative to the Sun, in principle simple linear fits of color versus (vs.) each parameter (Teff, log g, and [Fe/H]) would provide sufficiently good estimates of the solar colors. As suggested by the referee, a global fit (e.g. Mitchell & Schuster 1985) to all stellar parameters (color = f(Teff, log g, [Fe/H])) would be preferable due to the mutual interdependence of the stellar parameters. Fortunately our sample includes also solar analogs covering a broader range in colors and stellar parameters than the solar twins, so that the dependence on the different stellar parameters can be well determined by a global fit. The following formula was employed: color=A+B(Teff−5777)+C(logg−4.44)+D[Fe/H].\begin{equation} {\rm color} = A + B \, (T_{\rm eff} - 5777) \, + \, C \, (\log\,g - 4.44) + D \, {\rm [Fe/H]}. \end{equation}(1)The advantage of this equation is that A will give us directly the solar color, while its uncertainty could be determined from the error in A or from the scatter of the fit.

From our sample of stars, we selected a group of solar twins with Teff, log g, and [Fe/H] within 100 K, 0.1 dex, and 0.1 dex of the solar parameters2 given above. To perform a more robust global fit, we extended our solar twin sample with solar analogs covering a range in Teff, log g, and [Fe/H]. Thus, to explore the metallicity dependence of the colors, we selected a sample of solar analogs with the same constraints in Teff and log g, but covering a broader range in metallicity (−0.4  <  [Fe/H]  <   − 0.1 dex, +0.1  <  [Fe/H]  <  +0.4 dex). In a similar way, to improve the fit to Teff, we selected a group of solar analogs with the same constraints on log g and [Fe/H] as the solar twins, but with Teff in the range (5617  <  Teff  <  5677 K, 5877  <  Teff  <  5937 K). Finally, to fit the trend with log g, we used a sample of solar analogs with the same constraints on Teff and [Fe/H] as the solar twins, but covering a broader range in log g (4.29  ≤  log g  <  4.34 dex, 4.54  ≤  log g  <  4.59 dex).

The stellar parameters were taken from our work on solar twins (M06; MR07; M09; R09; M10b; B10) and complemented in some cases with other accurate values available in the literature (Valenti & Fischer 2005, hereafter VF05; Luck & Heiter 2006, hereafter LH06, T07; Sousa et al. 2008, hereafter S08, T09). The adopted stellar parameters for the solar twins and solar analogs are given in Table 3.

The global fits to (b–y) had only three outliers, HIP 7245, HIP 81512, and HIP 88427, which seem too red in (b–y) for their Teff and [Fe/H]. Using the Karataş & Schuster (2010) intrinsic-color calibration, we find that these three stars may be slightly reddened (E(b − y)  ~  0.015 − 0.023), although we have to bear in mind that the accuracy of the reddening calibration is of the same order3. These stars were removed from the global fits. The results from the fits are presented in Table 4 and in Figs. 1 − 4, where filled circles represent the solar twins and open circles the solar analogs across a broader range of stellar parameters.

3.1. The (b–y) solar color

thumbnail Fig. 1

(b–y) vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel, with a dot-dashed line at (b − y)⊙). The results of the global fit vs. the observed (b − y) color is presented in the lower right panel, with the dotted line indicating equality. Solar twins and solar analogs are represented by filled and open circles, respectively. The dependences of the fit on Teff and [Fe/H] are shown by dashed lines, while the relative predictions of MARCS models (normalized to our inferred solar colors) are shown by solid lines.

The global fit of (b–y) (Fig. 1 and Table 4) shows strong dependences on Teff (at the 14-σ level) and [Fe/H] (10-σ). There is no dependence (within the errors) on log g, therefore this parameter was excluded from the global fit. The star-to-star scatter from the fit is only 0.005 mag, which is what is expected from the observational uncertainties (0.004 − 0.006 mag).

The standard error (s.e.) in the solar color was obtained from the observed star-to-star scatter and the number of data-points (s.e. = 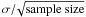$\sigma/\!\sqrt{\rm sample~size}$). The error in (b–y)⊙ (and the other solar colors) was conservatively adopted as three times the standard error. Thus, we propose 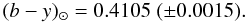(b−y)⊙=0.4105(±0.0015).\begin{equation} (b-y)_{\odot} = 0.4105 \; (\pm 0.0015). \end{equation}(2)A plot of (b–y) vs. V magnitude can help us to reveal whether fainter (i.e., more distant) stars bias the above derived solar color, due to possible interstellar reddening. This plot is shown in the lower left panel of Fig. 1. As can be seen, there is no trend with V magnitude. A linear fit of (b–y) vs. V, indeed shows a zero slope within the errors (slope = 0.0003  ±  0.0008). We note that most stars of the sample used in the global fit are brighter than V = 9, i.e. closer than  ~ 68 pc. Even the faintest stars (V  ~  9.3) extend only to  ~ 78 pc. According to NaI interstelar absorption maps, very little NaI absorption is detected for distances up to  ~ 80 pc from the Sun (Lallement et al. 2003; Welsh et al. 2010). Thus, most of our sample is not expected to be significantly affected by interstellar absorption. As already mentioned above, the few stars that show some small sign of interstellar reddening were not included in the global fits.

3.2. The β solar color

The global fit of β shows a dependence on Teff, log g, and [Fe/H] (Table 4). Interestingly, the strongest dependence is with [Fe/H] (slope significant at the 5-σ level), while the dependence with both Teff (2.9σ) and log g (2.7σ) is only at the 3-σ level. In Fig. 2, we show the dependence of the β color index with respect to Teff and [Fe/H]. The scatter from the fit is 0.006 mag, which is compatible with the observational errors in β.

The adopted β solar color is 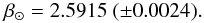β⊙=2.5915(±0.0024).\begin{equation} \beta_{\odot} = 2.5915 \; (\pm 0.0024). \end{equation}(3)

thumbnail Fig. 2

β vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel). The results of the global fit vs. the observed β color is presented in the lower right panel. Symbols are as in Fig. 1, except that two curves are presented for MARCS models: the shallower curve is the one computed by us while the other one is from O09. Neither curve is able to explain the low β colors observed for [Fe/H]  <   − 0.2.

Although there is a clear trend of β vs. V magnitude (Fig. 2), it is not related to reddening because the β index is not affected by interstellar absorption. The bright stars (V  <  6) that are causing the trend are within  ~ 17 pc, hence they are not reddened. The bright (V  <  6) solar twins and analogs falling systematically above the derived β⊙, are stars hotter than the Sun, or more metal-rich than the Sun (or both), and therefore with a β color systematically higher than solar because β increases with both increasing metallicity and Teff. We note that the trend seen in nearby stars for β is not present in (b–y) because this color has opposite trends with Teff and [Fe/H]. Thus, by performing a deeper solar-twin survey than previous works, we avoided systematic biases (such as selecting mainly hotter and more metal-rich stars) that might have been present if only brighter stars were studied.

3.3. The m1 solar color

It is well known that the m1 color correlates very well with metallicity (see references in the introduction), and this is clearly shown in Table 4, where according to the global fit the dependence on [Fe/H] is significant at the 21-σ level. The second most important parameter is Teff (10σ), but log g also produces an important dependence (slope significant at the 5-σ level).

The tight correlation between m1 and [Fe/H] is shown in Fig. 3. The star-to-star scatter from the global fit is only 0.006 mag, which is compatible with the observational uncertainties. The m1 solar color recommended for the Sun is 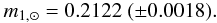m1,⊙=0.2122(±0.0018).\begin{equation} m_{1, \odot} = 0.2122 \; (\pm 0.0018). \end{equation}(4)

thumbnail Fig. 3

m1 vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel). The results of the global fit vs. the observed m1 color is presented in the lower right panel. Symbols are as in Fig. 1.

3.4. The c1 solar color

In Fig. 4, we show the relation between c1 and log g, which is significant at the 4-σ level. As already noticed in the literature (e.g. Twarog et al. 2002; Önehag et al. 2009, hereafter O09), the c1 index in late G dwarfs has a sensitivity to metallicity. Our global fit (Table 4) confirms the dependence on [Fe/H], which is actually more significant (8-σ) than the dependence on log g (Fig. 4).

The predicted c1 solar color from the global fit is 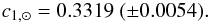c1,⊙=0.3319(±0.0054).\begin{equation} c_{1, \odot} = 0.3319 \; (\pm 0.0054). \end{equation}(5)The star-to-star scatter in the global fit is 0.0165, which is considerably larger than the observational errors (0.009 − 0.013) for the c1 index. Following the suggestions of the referee, we explored whether this index is particularly sensitive to either anomalies in the chemical composition or the microturbulence velocities.

thumbnail Fig. 4

c1 vs. log g (upper left panel), [Fe/H] (upper right panel) and V magnitude (lower left panel). The results of the global fit vs. the observed c1 color is presented in the lower right panel. Symbols are as in Fig. 1.

Previous works show the effects of C and N upon the Strömgren 4-color uvby filter-measurements, via the NH and CN bands. For example, it seems that the NH band at 3360A affects the u measurements while CN affects the v measurements. Thus, the c1 color that depends on both u and v should be affected by abundance anomalies (Bond & Neff 1969; Bond 1974; Zacs et al. 1998; Grundahl et al. 2000, 2002; Schuster et al. 2004; Yong et al. 2008). In this context, it would be important to assess whether the small abundance anomalies in the solar chemical composition (M09; R09), in particular the difference between the highly volatile elements (C, N, O) and Fe, may affect the uvby colors. As discussed by Stromgren et al. (1982), variations in the He abundance may also affect the c1 index. Although the Hyades c1 anomaly for stars with (b − y) close to solar was found initially to be Δc1  ~  0.03 − 0.04 (Hyades – field stars, or Hyades – Coma), it seems that the anomaly may only amount to Δc1 = 0.024 − 0.025 after instrumental effects are corrected (Joner & Taylor 1995). Another important parameter affecting the colors may be microturbulence (Conti & Deutsch 1966; Nissen 1981).

To test the above effects, synthetic spectra were computed for solar twins with variations in Δ[C, N, O/Fe] =  − 0.05 dex (M09), Δvmicro = +0.1 km s-1 (most solar twins and close solar analogs have vmicro within  ± 0.1 km s-1 of the solar value), and an increase of 10% in the He abundance (by number). Fluxes were computed with the code SYNTHE (Kurucz & Avrett 1981; Sbordone et al. 2004; Kurucz 2005) using ATLAS12 model atmospheres (Kurucz 1996, 2005; Castelli 2005) computed for the different aforementioned assumptions. The atomic line list adopted in the spectral computations is based on the compilations by Coelho et al. (2005) and Castelli & Hubrig (2004), and the molecules C2, CH, CN, CO, H2, MgH, NH, OH, SiH, and SiO from Kurucz (1993) were included. The change in He does not significantly affect the c1 index ( < 0.001 mag), but the change in microturbulence increases c1 by +0.0035 mag, while the change in C, N, O increases c1 by +0.003 mag4. Thus, small changes in chemical composition and microturbulence may help to explain the extra scatter seen in the global fit. Casagrande et al. (in prep.) demonstrate that the Strömgren system is not only sensitive to [Fe/H], but that it is possible to obtain information about the [α/Fe] ratio using uvby photometry. The Δc1 anomaly in the Hyades could be due to the effect of metallicity on c1. According to Friel & Boesgaard (1992), Hyades has an iron abundance 0.18 dex higher than Coma, which according to Table 4 corresponds to Δc1  =  +0.022 mag, which is very close to the Hyades anomaly relative to Coma (0.024 − 0.025 mag) (Joner & Taylor 1995).

4. Comparison with previous empirical determinations

As can be seen in Table 5 (lower part), our inferred (b − y),m1,c1, and β solar colors agree well (within 1-σ) with most earlier empirical results. However, previous determinations of solar colors have much lower control and homogeneity in Teff, log g, and [Fe/H], thus in some cases the agreement (within the error bars) could be due to fortuitous compensations of Teff, log g, and [Fe/H] effects on colors, or due to large errors in other studies.

Several previous works (Saxner & Hammarback 1985; Gray 1992; Edvardsson et al. 1993; Casagrande et al. 2010) give (b − y)⊙ values that agree with ours within 0.005 mag, but other determinations are either too blue (Cayrel de Strobel 1996; Clem et al. 2004; RM05b; Holmberg et al. 2006) or too red (Gehren 1981). A previous empirical result for β⊙ (Saxner & Hammarback 1985, β⊙ = 2.591  ±  0.005) is in excellent agreement with our value (2.5915  ±  0.0024). Previous determinations of m1, ⊙  and c1, ⊙  (Clem et al. 2004; Holmberg et al. 2006) also agree with ours within the errors, but note that the errors given by Holmberg et al. (2006) are very large (0.03 and 0.07 for m1 and c1, respectively), so their solar colors cannot be used to perform stringent tests of model atmospheres and the temperature and metallicity scales.

Although our inferred solar colors agree with previous determinations based on solar-type stars, our values based on solar twins should be preferred because of their more accurate and precise stellar parameters, resulting in correspondingly accurate and precise inferred solar colors. We use our “solar” colors below to test absolutely calibrated solar spectra, model atmospheres and the Teff and metallicity uvby–β scales.

5. Comparison with measurements on reflected (asteroid) solar spectra

Olsen (1976) measured the β⊙ color of reflected solar light from asteroids, which seems justifiable because the β index should be largely independent of the wavelength dependence of the albedo. His measurement (β⊙ = 2.5955  ±  0.0024) is in good agreement (within 1-σ) with our inferred value (β⊙ = 2.5915  ±  0.0024). Olsen (1976) did not measure the solar (b–y), but indirectly estimated (b − y)⊙ from a color transformation using β⊙. His (b − y)⊙ = 0.390  ±  0.004 disagrees with ours (0.4105  ±  0.0015), but this is probably due to the errors introduced by his adopted transformation from β to (b–y). Using the (b − y)0–β intrinsic color calibration of Karataş & Schuster (2010), the β⊙ = 2.5955 from Olsen (1976) indeed implies that (b–y)⊙ = 0.4062, in good agreement with our (b–y)⊙. Using the same transformation, our β⊙ = 2.5915 gives (b–y)⊙ = 0.4089.

Unfortunately, direct measurements of the (b–y), m1 and c1 color indices for reflected solar spectra are not very useful because of the color of the asteroid albedos5. A comparison with solar colors inferred from absolute spectrophotometry of the Sun is presented below.

6. Comparison with synthetic colors

Our accurate and precise colors inferred for the Sun can be used to test the performance of theoretical solar flux models and the quality of absolute solar flux measurements. However, additional ingredients enter the computation of synthetic colors, namely the adopted set of filters and the flux/magnitude zero-points adopted. We discuss them in the following.

Since intermediate-band Strömgren filters are centered on specific spectral features, a correct characterization of the total throughout becomes crucial for generating synthetic colors (e.g. Lester et al. 1986, O09). To test the influence of the filter transmission curves on our results, we computed uvby indices using two different sets of pass-bands, the original ones of Crawford & Barnes (1970) and a set that should be more representative of the SPM observations (Bessell 2005).

The β index is defined as the ratio of the flux measured through narrow (half-width of about 30 Å) and wide (about 150 Å) profiles both centered on the Hβ line. In this case, the (212, 214) filter transmission curves (Crawford & Mander 1966), the photomultiplier sensitivity, the atmospheric transmission, and the reflectivity of aluminum given in Castelli & Kurucz (2006) were used to generate the total Tβ throughout, according to the prescriptions of the beta.forcd program at the Kurucz website6. Indices calculated using Tβ define the natural system β′, which should be transformed using a set of equations to agree to the standard system β defined by the observations of Crawford & Mander (1966). For the filter set (212, 214), the transformation equation is β = 0.248 + 1.368β′ (Crawford & Mander 1966).

In principle, to mimic the uvby–β observations presented here, synthetic photometry should reproduce the SPM instrumental system, and the same transformation equations should then be applied to generate the standard system. In practice, this can hardly be done, since the SPM instrument is a six-channel spectrophotometer, and we follow the approach normally adopted in the literature, i.e. of reproducing the standard system directly, by fixing the zeropoints using Vega. In Sect. 2.4, we have shown the excellent agreement between our observations and other photometric measurements, meaning that the transformation from the instrumental to the standard system is indeed accurate, we therefore expect our approach to return meaningful synthetic colors.

The spectral energy distribution adopted for Vega and its observed indices also affect the outcome of synthetic photometry in the process of establishing the zeropoints of a photometric system (e.g. Casagrande et al. 2006). We used a spectrum obtained with the STIS spectrograph onboard the HST (Bohlin 2007) of resolution ℛ = 500, which enables the highest accuracy ( ~ 1%) measurements achievable to date, and adopted the following averaged values for Vega: (b − y) = 0.003, m1 = 0.157, c1 = 1.088 and β = 2.904 from Hauck & Mermilliod (1998). If we had adopted the colors of Vega given in Crawford et al. (1972), the differences would have amounted to 0.001 mag at most.

Despite the complications posed by the pole-on and rapidly rotating nature of Vega, the effects on the blue part of the spectrum are expected to be small or negligible (e.g. Casagrande et al. 2006; Bohlin 2007, and references therein). It is more relevant that we use the observed HST spectrophotometry of Vega; additional comments on this issue are made in the following subsections.

6.1. Colors from Kurucz and MARCS models

Although synthetic uvby–β colors computed using earlier MARCS and Kurucz models are found in the literature (see Table 5), we feel it appropriate to make our comparisons using the most recent releases available (Castelli & Kurucz 2004; Gustafsson et al. 2008). In addition, as we have already mentioned, different ingredients enter the computation of synthetic colors, and we differ from most of the previous works in that we use an observed spectrum of Vega to define the zeropoints. In principle, this should be the best approach for replicating observations and for a correct comparison of solar flux models and absolute measurements with the colors determined from our solar twins. This choice mimics the observational approach, and the successes or failures of synthetic colors depend mostly on the quality of the solar input spectra. In practice, the situation is less clear, as we discuss further below and in Sect. 6.2.

When computing synthetic colors from theoretical models, the use of a model atmosphere to describe also Vega may have the advantage of (partly) compensating for model inaccuracies by including these in the zero-points.

thumbnail Fig. 5

Comparison between solar and synthetic colors obtained from different spectra. Left panel: using Vega STIS observations to set the zero-points. Right panel: using ATLAS9 Vega model for the same purpose. Δmag = our derived solar colors minus the synthetic ones.

We performed this exercise by taking from the Kurucz website the latest ATLAS9 model fluxes for Vega and the Sun; because of the internal consistency of this approach, it should also determine which set of filters should be used. For the colors of the Sun we obtain (b − y) = 0.413, m1 = 0.236 and c1 = 0.297 using the filters of Crawford & Barnes (1970), and (b − y) = 0.406, m1 = 0.214, c1 = 0.303 for the Bessell (2005) filters. While (b–y)⊙ is reproduced with the two set of filters, the latter set of filters provides results that are more comparable to our measured m1, ⊙  and c1, ⊙ , and therefore in the following we consider only the Bessell (2005) passbands. The effect of instead using those of Crawford & Barnes (1970) can be easily estimated from the above differences.

The resolution of the spectra used to generate synthetic colors may also in principle affect the results. We tested ATLAS9 model fluxes for Vega and the Sun at various resolutions ranging from ℛ = 500000 to 200 and verified that for various combinations of these, differences in (b–y), m1 and c1 always lie below 0.001 mag7.

However, for ℛ ≲ 2000 the synthetic β index scales differently for Vega and the Sun, i.e. even if synthetic spectra of the same resolution are used for the two stars, the value obtained for β depends on ℛ to an extent that may vary from a few milli-magnitudes up to several hundredths of a magnitude. For example, using high resolution ATLAS9 spectra for both Vega and the Sun, we obtain β = 2.587, which is in good agreement with our solar value. Using instead synthetic spectra of Vega and the Sun at ℛ = 500 sampled at the same wavelength points, we obtain β = 2.601 from which we estimate a (model-dependent) correction of 0.014 mag when working at this low ℛ.

Because of this limitation on the STIS resolution of the Balmer line, the β indices computed for Table 5 have been obtained as follows: the solar spectra were downgraded to ℛ = 500, sampled at the same wavelength points as the STIS spectrum, and the aforementioned correction was then applied. Using instead a high resolution ATLAS9 spectrum of Vega to define the zero-points does not require a downgrade to the resolution of the solar spectra, and the β indices are changed by  − 0.030 mag (i.e. are bluer). We verified that for the other Strömgren indices the STIS resolution is high enough. The effect of using an ATLAS9 model flux of Vega to set the zero-points amounts to  − 0.004, 0.006, and 0.027 mag for the (b–y), m1, and c1 indices, respectively. In Fig. 5, synthetic colors obtained with these two choices for Vega, i.e. STIS vs. ATLAS9, are compared.

If the STIS spectrum of Vega is used, the Kurucz solar flux returns a value of (b–y) in excellent agreement with our observed value, whereas a considerably bluer color is obtained with MARCS. The greater accuracy of the Kurucz with respect to the MARCS solar flux in b and y bands can be noticed also from the spectrophotometric comparison presented in Edvardsson (2008). For m1, the Kurucz model is still in better agreement than the MARCS, one being slightly bluer and the other redder with respect to our m1, ⊙ . The same bluer and redder performance is also obtained for c1, although both models provide a rather poor match. The β index is similar for both models and considerably redder than our β⊙.

In general, the ATLAS9 solar flux model performs better than the MARCS model, but they both have problems in reproducing c1, ⊙  (in opposite directions) and β⊙ (both systematically redder). Changing to the ATLAS9 flux of Vega to set the zero-points has a negligible impact on (b–y) and m1, but brings the theoretical β index in almost perfect agreement in both cases. For the c1 index, only the ATLAS9 result is helped by this choice, and this could partly stem from compensating errors in the ATLAS9 models of Vega and the Sun.

In Table 5, we also show the color indices computed by O09 using MARCS models (also for the flux of Vega) and the passbands of Crawford & Barnes (1970). Their (b–y) agrees with our synthetic one, but their m1 and c1 colors are somewhat redder and bluer, respectively, in a way that is consistent with the different passbands they adopted. The c1 solar color computed by O09 is in excellent agreement (within 1-σ) with our c1, ⊙ .

6.2. Colors from solar spectra

We computed (b–y), m1, c1, and β indices using the absolute measurements of solar spectra by C96, Neckel (1999, hereafter N99), and Thuillier et al. (2004). The spectrum of Rieke et al. (2008) was not employed because of its very low resolution (R ~ 100). The STIS Vega observations and the ATLAS9 Vega model were again used to define the zero points.

The C96 composite spectrum represents both satellite (Woods et al. 1996) and ground (Neckel & Labs 1984) observations below and above 4100 Å. While its (b–y) is redder, m1 is considerably bluer, and c1 is in good agreement with our solar values. Not unexpectedly, the same conclusions about (b–y) and m1 hold for the N99 atlas, which is an update of the Neckel & Labs (1984) measurements included in C96. However, Neckel (2003, hereafter N03) noticed a possible systematic error in those absolute measurements and provides a simple analytical formula for correction, after which (b–y) and m1 are in closer agreement with our solar values. Thuillier et al. (2004) published two composite solar reference spectra assembled using space measurements during distinct solar activity levels; differences concern only the m1 and c1 indices in a negligible manner (a few millimagnitudes only), and therefore in Table 5 the averaged values of the two are given. Thuillier et al. (2004) provide closer agreement than previous spectra in (b–y) and m1, but their c1 is considerably bluer.

Thus, while on average (b–y) and m1 are in agreement with our solar values, there is the tendency for c1 to be considerably bluer. The β indices were computed following the same prescriptions as in the previous section and are systematically redder. Switching to the model flux of Vega solves most of the discrepancies for these two indices, with the synthetic values being now distributed at the red and blue sides of our solar colors (see the right panel of Fig. 5). It is not obvious why a model flux for Vega also brings absolute solar flux measurements into closer agreement with our empirical solar colors. While the measured spectra of Vega should be superior to any model of it, we can speculate about possible reasons for this not being true over the full wavelength range. The difference STIS vs. ATLAS9 amounts to few millimagnitudes in (b–y) and m1, but is considerable in c1 and β, and those differences could reflect measurement problems in the u band and the issue already mentioned about the spectral resolution around the Balmer line.

In the wavelength range of interest to us, the accuracy of the solar absolute fluxes is on the order of 5 − 3% from data acquired in space (C96, Thuillier et al. 2004) and probably lower for ground-based data measurements. The culprit could thus be inaccuracy in solar flux measurements rather than in Vega! For the sake of computing indices, we are not interested in the absolute flux scale, but rather in the relative accuracy of measuring the shape of the solar spectral energy distribution. This accuracy is rather difficult to assess, but the above differences provide an idea of the complexity associated with this kind of measurement, and the corresponding rather large uncertainties. In addition, the choice for Vega and the set of filters used also affect the analysis, introducing systematic errors.

In this section, we have presented various issues concerning synthetic solar colors, which are often taken for granted when comparing observed vs. synthetic colors. While the comparison with a specific solar-flux measurement has limited significance, with appropriate choices for Vega, it is comforting that there are no large systematic trends between our solar colors and these observations taken together. Thus, our solar colors can help considerably in establishing the necessary reliability of synthetic colors.

6.3. Testing the effects of changes in Teff, log g, and [Fe/H] on synthetic MARCS colors

As discussed in the previous sections, our uvby–β solar colors are useful for testing absolute solar spectra and the performance of model atmospheres, as well as checking the subtleties in the transformation from fluxes to synthetic colors. Since our solar twins and analogs span a range in Teff, log g, and [Fe/H], we can also use them to test how well model atmospheres predict the relative change of colors due to variations in atmospheric parameters.

For this test, we used relative fluxes predicted by the MARCS models, normalizing the results to our “observed” solar colors. As shown in Figs. 1 − 4, where the relative variation in the MARCS (b–y), β, m1, and c1 colors are shown by solid lines, there is a satisfactory overall relative agreement between MARCS models and both the solar twins and solar analogs. The only clear discrepancy is in the predicted metallicity variation in β (Fig. 2), which is much shallower than observed. We also checked whether the MARCS β colors computed by O09 solve this problem (Fig. 2), but although they do help to slightly alleviate the discrepancy (the Önehag et al. β colors are slightly steeper than ours), they also do not match the low β indices observed below [Fe/H]  ~   − 0.2. It would be important to observe more metal-poor solar analogs to confirm whether we have detected a potential problem in the line formation of Hβ.

The strong variation in c1 with metallicity for G-type stars (Twarog et al. 2002, Fig. 4, see also O09) is reproduced well by the MARCS models (as already demonstrated by O09 for somewhat cooler dwarfs), so it can potentially be used to estimate [Fe/H] in solar metallicity and metal-rich solar analogs.

Our tests provide confidence in the relative variation in stellar fluxes with atmospheric parameters as predicted by the MARCS models, at least in the atmospheric parameter space studied here.

7. The zero-point of the Teff scale

Our solar (b–y) color can also be used to estimate how well different Teff scales reproduce the solar value of Teff (5777 K). Different color-Teff relations in the literature have been employed to obtain the Teff for our (b − y)⊙, and these values have then been subtracted from the solar effective temperature. These differences, shown in Table 6, are the zero-point corrections needed to place different Teff calibrations on the same Teff scale as the Sun. As can be seen, the Teff scale by Casagrande et al. (2010) seems the most accurate, with a negligible offset of only 10(±10) K with respect to the Sun, which is much smaller than the offset (109 K) of our earlier Teff calibration (RM05b).

Table 6

Δ Teff needed to correct the zeropoint of the most recent Teff scales.

The widely used Teff (b–y) scale of Alonso et al. (1996) is too cool by 137 K. Thus, the elemental chemical abundances determined using this scale (e.g. Israelian et al. 1998; Chen et al. 2000; Reddy et al. 2003; Allende Prieto et al. 2004; Jonsell et al. 2005) may be systematically incorrect by as much as 0.14 dex (e.g. for V from VI lines and for N from NH lines), albeit the impact on abundance ratios [X/Fe] should be smaller (and in a few cases mostly cancel) for lines of low to moderate excitation potential because of the compensating impact of the iron abundance obtained from FeI lines; however, for abundances obtained from lines of high excitation potential (e.g. CI, NI, OI, PI, SI) the impact could be as high as 0.2 dex. Thus, inaccurate temperature scales may be one of the reasons why the small peculiarities in the solar chemical composition (M09; R09) have not been discovered in the past (Ramírez et al. 2010).

Zero-point errors in Teff also affect stellar ages inferred from isochrones. For example, for an offset of 130 K and using Y2 isochrones (Demarque et al. 2004), a systematic offset as high as 1.5 − 2 Gyr may result for a solar analog.

8. The zero-point of the metallicity scale

Árnadóttir et al. (2010) made a critical evaluation of different metallicity calibrations for dwarf stars in the uvby system, finding zero-point offsets in many of these metallicity scales, ranging from  − 0.17 dex (Nordström et al. 2004) to +0.33 (O09), although the latter is a purely theoretical calibration intended to test model atmospheres and not for application to real stars. After extensive testing for potential problems in different metallicity calibrations, such as trends in the Δ[Fe/H] residuals (spectroscopic-photometric) with [Fe/H], (b − y),c0, and m0, Árnadóttir et al. (2010) find that the calibrations by RM05a has the best overall performance, albeit with a small (0.04 dex) zero-point offset.

The zero-point offset cannot be overstated, especially when comparing the Sun to the stars (Gustafsson 2008), because offsets in the zero-point of the metallicity scale could make the Sun appear abnormal (see Haywood 2008; Gustafsson et al. 2010, and references therein for a discussion about apparent anomalies in the solar metallicity).

Table 7

Δ [Fe/H] needed to correct the zero-point of different uvby metallicity scales.

Our solar colors can be used to check the zero-point of different metallicity calibrations, by computing [Fe/H] for our inferred solar colors and subtracting these metallicities from the solar metallicity ([Fe/H] = 0). Those differences, which are the zero-point corrections needed to place different metallicity calibrations on the same metallicity scale as the Sun, are shown in Table 7, along with the offsets found by Árnadóttir et al. (2010) for a broad range of colors and metallicities.

Most metallicity calibrations do require a correction to place them on the same metallicity scale as the Sun. In particular, the RM05a metallicity calibration recommended by Árnadóttir et al. (2010) to derive [Fe/H] from Strömgren photometry, needs a zero-point correction of +0.04 dex. This offset is identical to the offset found by Árnadóttir et al. (2010) using a sample spanning a much broader range in Teff. We are currently revising the metallicity calibration employed in the GCS survey (Nordström et al. 2004; Holmberg et al. 2007) and plan to assess the apparent anomalously high metallicity of the Sun with a new accurate metallicity scale (Casagrande et al., in prep.).

9. Conclusions

New uvby–β photometry has been presented for solar-twin candidates observed at the SPM observatory. Comparisons with existing Strömgren photometry shows that our data are in excellent agreement (to better than 0.01 mag) with previous observations.

Using accurate spectroscopically derived stellar parameters, the uvby–β photometry for the solar twins, and also for solar analogs covering a wider range in metallicities, the solar colors (b − y)⊙ = 0.4105  ±  0.0015, m1, ⊙  = 0.2122  ±  0.0018, c1, ⊙  = 0.3319  ±  0.0054, and β⊙ = 2.5915  ±  0.0024 have been inferred.

As discussed in the manuscript, our solar-twin data have provided stringent constraints on absolute fluxes, the performance of model atmospheres, and the zero-points of temperature and metallicity scales. In particular, we show that the widely used Alonso et al. (1996) (b–y) calibration is too cool by  ~ 140 K, while our new Teff calibration (Casagrande et al. 2010) has a negligible zero-point offset (10  ±  10 K). Regarding model atmospheres, the Kurucz ATLAS9 solar model provides a closer fit of our solar colors than the MARCS 2008 solar model. The relative variation in colors with stellar parameters seem to be reproduced well by MARCS models, except for the metallicity variation in the β index, which is flatter than observed in solar twins and solar analogs, thus suggesting that there are existing limitations on the modeling of Balmer lines.

We are pursuing photometric observations of our solar-twin sample in other photometric systems, to perform similar evaluations of absolute fluxes, model atmospheres, and fundamental calibrations in astrophysics.

Online material

Table 1

Photometry (V Johnson and uvby–β) of 73 solar-twin candidates from San Pedro Mártir Observatory.

Table 1

continued.

Table 2

Literature photometry (V Johnson and uvby–β) of solar-twin candidates and solar analogs (Mermilliod et al. 1997; Hauck & Mermilliod 1998).

Table 3

Stellar parameters.

Table 3

continued.

Table 5

Solar colors and predictions from models atmospheres. Our synthetic colors (this work) were computed using the Bessell (2005) filters, with zero points based on both the STIS observed and ATLAS9 synthetic spectrum of Vega.

1

S4N: Spectroscopic Survey of Stars in the Solar Neighborhood; available online at http://hebe.as.utexas.edu/s4n/

2

Strictly speaking, a solar-twin star must be identical to the Sun within the observational uncertainties. Our definition based on derived stellar parameters is simply more practical because it is less dependent on the quality of the stellar and solar spectra available.

3

The star HIP 79186 also seems reddened according to the Karataş & Schuster (2010) calibration, but the stellar parameters of this star (Teff, log g, and [Fe/H]) = (5709 K, 4.27 dex,  −0.12 dex) (R09) do not fall either in our solar-twin or our solar-analog samples, so it was not considered in the global fits.

4

The changes in (b − y) and m1 due to changes in He, CNO, and microturbulence are even smaller than for c1.

5

Although the colors of the Sun measured using asteroids may be affected, our spectroscopic analysis based on high-resolution spectra should not because we measure the flux relative to the adjacent continuum for narrow spectral lines

7

The Castelli & Kurucz (2004) grid of fluxes has a resolution varying from 150 to 250 in the wavelength region of interest, and for this reason we took instead model fluxes at higher resolution from the Kurucz website.

Acknowledgments

We thank A. Önehag and B. Gustafsson for computing the solar color indices (in the O09 system) given in Table 5, and also by comments on our results. W.J.S. is very grateful to the DGAPA-PAPIIT (UNAM) (projects Nos. IN101495, and IN111500) and to CONACyT (México) (projects Nos. 1219–E9203, 27884E, and 49434F) for funding which permitted travel and also the maintenance and upgrading of the uvby–β photometer. J.M. would like to acknowledge support from Fundação para a Ciência e a Tecnologia (FCT, Portugal) in the form of a grant (PTDC/CTE-AST/098528/2008) and a Ciência 2007 fellowship. P.C. is grateful to F. Castelli, P. Bonifacio and L. Sbordone for their long term help with the SYNTHE and ATLAS12 codes. This publication has made use of the SIMBAD database, operated at CDS, Strasbourg, France.

References

  1. Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
  3. Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Arellano Ferro, A., & Mantegazza, L. 1996, A&A, 315, 542 [NASA ADS] [Google Scholar]
  5. Arellano Ferro, A., Parrao, L., Schuster, W., et al. 1990, A&AS, 83, 225 [Google Scholar]
  6. Árnadóttir, A. S., Feltzing, S., & Lundström, I. 2010, A&A, 521, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Barry, D. C., Cromwell, R. H., & Schoolman, S. A. 1978, ApJ, 222, 1032 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baumann, P., Ramírez, I., Meléndez, J., & Asplund, M. 2010, A&A, 519, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bessell, M. S. 2005, ARA&A, 43, 293 (B2005) [NASA ADS] [CrossRef] [Google Scholar]
  10. Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
  11. Blackwell, D. E., & Lynas-Gray, A. E. 1998, A&AS, 129, 505 [Google Scholar]
  12. Bohlin, R. C. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken (San Francisco: ASP), ASP Conf. Ser., 364, 315 [Google Scholar]
  13. Bond, H. E. 1974, ApJ, 194, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bond, H. E. 1980, ApJS, 44, 517 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bond, H. E., & Neff, J. S. 1969, ApJ, 158, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  16. Calamida, A., Bono, G., Stetson, P. B., et al. 2007, ApJ, 670, 400 [NASA ADS] [CrossRef] [Google Scholar]
  17. Calamida, A., Bono, G., Stetson, P. B., et al. 2009, ApJ, 706, 1277 [NASA ADS] [CrossRef] [Google Scholar]
  18. Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
  19. Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Castelli, F. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 25 [Google Scholar]
  21. Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
  22. Castelli, F., & Hubrig, S. 2004, A&A, 425, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Castelli, F., & Kurucz, R. L. 2006, A&A, 454, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
  25. Cayrel de Strobel, G. 1996, A&A Rev., 7, 243 [CrossRef] [Google Scholar]
  26. Cayrel de Strobel, G., Knowles, N., Hernandez, G., & Bentolila, C. 1981, A&A, 94, 1 [NASA ADS] [Google Scholar]
  27. Cayrel de Strobel, G., Soubiran, C., & Ralite, N. 2001, A&A, 373, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Chmielewski, Y. 1981, A&A, 93, 334 [NASA ADS] [Google Scholar]
  30. Clem, J. L., VandenBerg, D. A., Grundahl, F., & Bell, R. A. 2004, AJ, 127, 1227 [NASA ADS] [CrossRef] [Google Scholar]
  31. Clements, G. L., & Neff, J. S. 1979, A&A, 75, 193 [NASA ADS] [Google Scholar]
  32. Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Colina, L., Bohlin, R. C., & Castelli, F. 1996, AJ, 112, 307 (C96) [NASA ADS] [CrossRef] [Google Scholar]
  34. Conti, P. S., & Deutsch, A. J. 1966, ApJ, 145, 742 [NASA ADS] [CrossRef] [Google Scholar]
  35. Cox, A. N. 2000, Allen’s Astrophysical Quantities, 4th ed. (New York: AIP Press/Springer) [Google Scholar]
  36. Crawford, D. L. 1966, Spectral Classification and Multicolour Photometry, 24, 170 [Google Scholar]
  37. Crawford, D. L. 1975, AJ, 80, 955 [NASA ADS] [CrossRef] [Google Scholar]
  38. Crawford, D. L., & Mander, J. 1966, AJ, 71, 114 [NASA ADS] [CrossRef] [Google Scholar]
  39. Crawford, D. L., & Barnes, J. V. 1970, AJ, 75, 978 [NASA ADS] [CrossRef] [Google Scholar]
  40. Crawford, D. L., Barnes, J. V., Gibson, J., et al. 1972, A&AS, 5, 109 [Google Scholar]
  41. Croft, S. K., McNamara, D. H., & Feltz, K. A., Jr. 1972, PASP, 84, 515 [NASA ADS] [CrossRef] [Google Scholar]
  42. Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
  43. Edvardsson, B. 2008, Phys. Scr., T133, 014011 [NASA ADS] [CrossRef] [Google Scholar]
  44. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
  45. Friel, E. D., & Boesgaard, A. M. 1992, ApJ, 387, 170 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gallouëtte, L. 1964, Ann. Astrophys., 27, 423 [NASA ADS] [Google Scholar]
  47. Gehren, T. 1981, A&A, 100, 97 [NASA ADS] [Google Scholar]
  48. Gratton, R. G., Carretta, E., & Castelli, F. 1996, A&A, 314, 191 [NASA ADS] [Google Scholar]
  49. Gray, D. F. 1992, PASP, 104, 1035 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gray, D. F. 1995, PASP, 107, 120 [NASA ADS] [CrossRef] [Google Scholar]
  51. Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, 3rd ed. (Cambridge, UK: Cambridge University Press) [Google Scholar]
  52. Grønbech, B., Olsen, E. H., & Strömgren, B. 1976, A&AS, 26, 155 [Google Scholar]
  53. Grundahl, F., Vandenberg, D. A., Stetson, P. B., Andersen, M. I., & Briley, M. 2000, Liege Internat. Astrophys. Colloquia, 35, 503 [NASA ADS] [Google Scholar]
  54. Grundahl, F., Briley, M., Nissen, P. E., & Feltzing, S. 2002, A&A, 385, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Gustafsson, B. 2008, Phys. Scr., T130, 014036 [NASA ADS] [CrossRef] [Google Scholar]
  56. Gustafsson, B., & Nissen, P. E. 1972, A&A, 19, 261 [Google Scholar]
  57. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Gustafsson, B., Meléndez, J., Asplund, M. & Yong, D. 2010, ApSS, 328, 185 [Google Scholar]
  59. Hauck, B., & Kunzli, M. 1996, Baltic Astron., 5, 303 [NASA ADS] [Google Scholar]
  60. Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Hardorp, J. 1978, A&A, 63, 383 [NASA ADS] [Google Scholar]
  62. Hardorp, J. 1980a, A&A, 88, 334 [NASA ADS] [Google Scholar]
  63. Hardorp, J. 1980b, A&A, 91, 221 [NASA ADS] [Google Scholar]
  64. Haywood, M. 2002, MNRAS, 337, 151 [NASA ADS] [CrossRef] [Google Scholar]
  65. Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
  66. Hilker, M. 2000, A&A, 355, 994 [NASA ADS] [Google Scholar]
  67. Holmberg, J., Flynn, C., & Portinari, L. 2006, MNRAS, 367, 449 [NASA ADS] [CrossRef] [Google Scholar]
  68. Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  69. Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Israelian, G., García López, R. J., & Rebolo, R. 1998, ApJ, 507, 805 [NASA ADS] [CrossRef] [Google Scholar]
  71. Johnson, H. L. 1962, ApJ, 135, 69 [NASA ADS] [CrossRef] [Google Scholar]
  72. Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewski, W. Z. 1966, Comm. Lunar and Planetary Lab. (Tucson: Univ. of Arizona), 4, 99 [Google Scholar]
  73. Joner, M. D., & Taylor, B. J. 1995, PASP, 107, 124 [NASA ADS] [CrossRef] [Google Scholar]
  74. Jonsell, K., Edvardsson, B., Gustafsson, B., et al. 2005, A&A, 440, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Karataş, Y., & Schuster, W. J. 2010, New Astron., 15, 444 [NASA ADS] [CrossRef] [Google Scholar]
  76. Kron, G. E. 1963, PASP, 75, 288 [NASA ADS] [CrossRef] [Google Scholar]
  77. Kuiper, G. P. 1938, ApJ, 88, 429 [NASA ADS] [CrossRef] [Google Scholar]
  78. Kurucz, R. L. 1991, in Precision Photometry: Astrophysics of the Galaxy, ed. A. G. D. Philip, A. R. Upgren, & K. A. Janes (Schenectady, NY: Davis Press), 27 [Google Scholar]
  79. Kurucz, R. 1993, Diatomic Molecular Data for Opacity Calculations. Kurucz CD-ROM, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 15 [Google Scholar]
  80. Kurucz, R. L. 1996, IAU Symp., 176, 523 [NASA ADS] [Google Scholar]
  81. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 14 [Google Scholar]
  82. Kurucz, R. L., & Avrett, E. H. 1981, SAO Sp. Rep., 391 [Google Scholar]
  83. Lallement, R., Welsh, B. Y., Vergely, J. L., Crifo, F., & Sfeir, D. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
  84. Lester, J. B., Gray, R. O., & Kurucz, R. L. 1986, ApJS, 61, 509 [NASA ADS] [CrossRef] [Google Scholar]
  85. Lockwood, G. W., Tueg, H., & White, N. M. 1992, ApJ, 390, 668 [NASA ADS] [CrossRef] [Google Scholar]
  86. Luck, R. E., & Heiter, U. 2006, AJ, 131, 3069 (LH06) [NASA ADS] [CrossRef] [Google Scholar]
  87. Magain, P. 1983, A&A, 122, 225 [NASA ADS] [Google Scholar]
  88. Malyuto, V. 1994, A&AS, 108, 441 [Google Scholar]
  89. Martell, S., & Laughlin, G. 2002, ApJ, 577, L45 [NASA ADS] [CrossRef] [Google Scholar]
  90. Martell, S. L., & Smith, G. H. 2004, PASP, 116, 920 [NASA ADS] [CrossRef] [Google Scholar]
  91. Meléndez, J., & Ramírez, I. 2003, A&A, 398, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Meléndez, J., & Ramírez, I. 2007, ApJ, 669, L89 (MR07) [NASA ADS] [CrossRef] [Google Scholar]
  93. Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006, ApJ, 641, L133 (M06) [NASA ADS] [CrossRef] [Google Scholar]
  94. Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 (M09) [NASA ADS] [CrossRef] [Google Scholar]
  95. Meléndez, J., Casagrande, L., Ramírez, I., Asplund, M., & Schuster, W. J. 2010a, A&A, 515, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Meléndez, J., Ramírez, I., Casagrande, L., et al. 2010b, ApSS, 328, 193 (M10b) [Google Scholar]
  97. Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Mironov, A. V., Moshkalev, V. G., & Kharitonov, A. V. 1998, Astron. Rep., 42, 799 [NASA ADS] [Google Scholar]
  99. Mitchell, R. I., & Schuster, W. J. 1985, AJ, 90, 2116 [NASA ADS] [CrossRef] [Google Scholar]
  100. Neckel, H. 1986, A&A, 169, 194 [NASA ADS] [Google Scholar]
  101. Neckel, H. 1999, Sol. Phys., 184, 421 (N99) [NASA ADS] [CrossRef] [Google Scholar]
  102. Neckel, H. 2003, Sol. Phys., 212, 239 (N03) [NASA ADS] [CrossRef] [Google Scholar]
  103. Neckel, H., & Labs, D. 1981, Sol. Phys., 74, 231 [NASA ADS] [CrossRef] [Google Scholar]
  104. Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
  105. Nissen, P. E. 1981, A&A, 97, 145 [NASA ADS] [Google Scholar]
  106. Nissen, P. E., & Schuster, W. J. 1991, A&A, 251, 457 [NASA ADS] [Google Scholar]
  107. Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Olsen, E. H. 1976, A&A, 50, 117 [NASA ADS] [Google Scholar]
  109. Olsen, E. H. 1983, A&AS, 54, 55 [Google Scholar]
  110. Olsen, E. H. 1984, A&AS, 57, 443 [Google Scholar]
  111. Önehag, A., Gustafsson, B., Eriksson, K., & Edvardsson, B. 2009, A&A, 498, 527 (O09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Parrao, L., Schuster, W. J., & Arellano Ferro, A. 1988, Reporte Técnico, 52, Instituto de Astronomía, Universidad Nacional Autónoma de México [Google Scholar]
  113. Pasquini, L., Biazzo, K., Bonifacio, P., Randich, S., & Bedin, L. R. 2008, A&A, 489, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Pettit, E., & Nicholson, S. B. 1928, ApJ, 68, 279 [NASA ADS] [CrossRef] [Google Scholar]
  115. Porto de Mello, G. F., & da Silva, L. 1997, ApJ, 482, L89 [NASA ADS] [CrossRef] [Google Scholar]
  116. Ramírez, I., & Meléndez, J. 2004, A&A, 417, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 (RM05a) [Google Scholar]
  118. Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 (RM05b) [Google Scholar]
  119. Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 (R09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Ramírez, I., Asplund, M., Baumann, P., Meléndez, J., & Bensby, T. 2010, A&A, 521, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Reddy, B. E., Tomkin, J., Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
  122. Relyea, L. J., & Kurucz, R. L. 1978, ApJS, 37, 45 [NASA ADS] [CrossRef] [Google Scholar]
  123. Rieke, G. H., Blaylock, M., Decin, L., et al. 2008, AJ, 135, 2245 [NASA ADS] [CrossRef] [Google Scholar]
  124. Saxner, M., & Hammarback, G. 1985, A&A, 151, 372 [NASA ADS] [Google Scholar]
  125. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. Ital. Suppl., 5, 93 [Google Scholar]
  126. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Schuster, W. J. 1976, Rev. Mex. Astron. Astrofis., 1, 327 [NASA ADS] [Google Scholar]
  128. Schuster, W. J., & Nissen, P. E. 1988, A&AS, 73, 225 (SN) [Google Scholar]
  129. Schuster, W. J., & Nissen, P. E. 1989, A&A, 221, 65 [NASA ADS] [Google Scholar]
  130. Schuster, W. J., & Parrao, L. 2001, Rev. Mex. Astron. Astrofis., 37, 187 [NASA ADS] [Google Scholar]
  131. Schuster, W. J., Parrao, L., & Contreras Martínez, M. E. 1993, A&AS, 97, 951 (SPC) [Google Scholar]
  132. Schuster, W. J., Nissen, P. E., Parrao, L., Beers, T. C., & Overgaard, L. P. 1996, A&AS, 117, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Schuster, W. J., Parrao, L., & Guichard, J. 2002, J. Astron. Data, 8, 2 [Google Scholar]
  134. Schuster, W. J., Beers, T. C., Michel, R., Nissen, P. E., & García, G. 2004, A&A, 422, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  135. Schuster, W. J., Moitinho, A., Márquez, A., Parrao, L., & Covarrubias, E. 2006, A&A, 445, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Secchi, A. 1868, Tip. Belle Arti, Roma, 68, tav. f. t.; OCCC 4 368 III [Google Scholar]
  137. Sekiguchi, M., & Fukugita, M. 2000, AJ, 120, 1072 [NASA ADS] [CrossRef] [Google Scholar]
  138. Smalley, B., & Dworetsky, M. M. 1995, A&A, 293, 446 [NASA ADS] [Google Scholar]
  139. Smalley, B., & Kupka, F. 1997, A&A, 328, 349 [NASA ADS] [Google Scholar]
  140. Soderblom, D. R., & King, J. R. 1998, in Solar Analogs: Characteristics and Optimum Candidates, ed. J. C. Hall (Flagstaff, Arizona: Lowell Observatory), 41 [Google Scholar]
  141. Soubiran, C., & Triaud, A. 2004, A&A, 418, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 (S08) [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  143. Stebbins, J., & Kron, G. E. 1957, ApJ, 126, 266 [NASA ADS] [CrossRef] [Google Scholar]
  144. Stebbins, J., & Whitford, A. E. 1945, ApJ, 102, 318 [NASA ADS] [CrossRef] [Google Scholar]
  145. Straizys, V., & Valiauga, G. 1994, Baltic Astron., 3, 282 [Google Scholar]
  146. Strömgren, B. 1963, QJRAS, 4, 8 [NASA ADS] [Google Scholar]
  147. Strömgren, B. 1964, Astrophys. Norveg., 9, 333 [Google Scholar]
  148. Stromgren, B., Gustafsson, B., & Olsen, E. H. 1982, PASP, 94, 5 [NASA ADS] [CrossRef] [Google Scholar]
  149. Takeda, Y., & Tajitsu, A. 2009, PASJ, 61, 471 (T09) [NASA ADS] [Google Scholar]
  150. Takeda, Y., Kawanomoto, S., Honda, S., Ando, H., & Sakurai, T. 2007, A&A, 468, 663 (T07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Taylor, B. J. 1984, ApJS, 54, 167 [NASA ADS] [CrossRef] [Google Scholar]
  152. Taylor, B. J. 1994, PASP, 106, 444 [NASA ADS] [CrossRef] [Google Scholar]
  153. Thuillier, G., Floyd, L., Woods, T. N., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
  154. Tueg, H. 1982, A&A, 105, 395 [NASA ADS] [Google Scholar]
  155. Tueg, H., & Schmidt-Kaler, T. 1982, A&A, 105, 400 [NASA ADS] [Google Scholar]
  156. Twarog, B. A., Anthony-Twarog, B. J., & Tanner, D. 2002, AJ, 123, 2715 [NASA ADS] [CrossRef] [Google Scholar]
  157. Twarog, B. A., Vargas, L. C., & Anthony-Twarog, B. J. 2007, AJ, 134, 1777 [NASA ADS] [CrossRef] [Google Scholar]
  158. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 (VF05) [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  159. van den Bergh, S. 1965, JRASC, 59, 253 [NASA ADS] [Google Scholar]
  160. Vandenberg, D. A., & Bell, R. A. 1985, ApJS, 58, 561 [NASA ADS] [CrossRef] [Google Scholar]
  161. Vandenberg, D. A., & Poll, H. E. 1989, AJ, 98, 1451 [NASA ADS] [CrossRef] [Google Scholar]
  162. Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  163. Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314, 438 [NASA ADS] [Google Scholar]
  164. Woods, T. N., Prinz, D. K., Rottman, G. J., et al. 1996, J. Geophys. Res., 101, 9541 [Google Scholar]
  165. Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008, ApJ, 684, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  166. Zacs, L., Nissen, P. E., & Schuster, W. J. 1998, A&A, 337, 216 [NASA ADS] [Google Scholar]

All Tables

Table 4

Global fits for color = A + B (Teff – 5777) + C (log g – 4.44) + D [Fe/H].

In the text
Table 6

Δ Teff needed to correct the zeropoint of the most recent Teff scales.

In the text
Table 7

Δ [Fe/H] needed to correct the zero-point of different uvby metallicity scales.

In the text
Table 1

Photometry (V Johnson and uvby–β) of 73 solar-twin candidates from San Pedro Mártir Observatory.

In the text
Table 1

continued.

In the text
Table 2

Literature photometry (V Johnson and uvby–β) of solar-twin candidates and solar analogs (Mermilliod et al. 1997; Hauck & Mermilliod 1998).

In the text
Table 3

Stellar parameters.

In the text
Table 3

continued.

In the text
Table 5

Solar colors and predictions from models atmospheres. Our synthetic colors (this work) were computed using the Bessell (2005) filters, with zero points based on both the STIS observed and ATLAS9 synthetic spectrum of Vega.

In the text

All Figures

thumbnail Fig. 1

(b–y) vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel, with a dot-dashed line at (b − y)⊙). The results of the global fit vs. the observed (b − y) color is presented in the lower right panel, with the dotted line indicating equality. Solar twins and solar analogs are represented by filled and open circles, respectively. The dependences of the fit on Teff and [Fe/H] are shown by dashed lines, while the relative predictions of MARCS models (normalized to our inferred solar colors) are shown by solid lines.
In the text
thumbnail Fig. 2

β vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel). The results of the global fit vs. the observed β color is presented in the lower right panel. Symbols are as in Fig. 1, except that two curves are presented for MARCS models: the shallower curve is the one computed by us while the other one is from O09. Neither curve is able to explain the low β colors observed for [Fe/H]  <   − 0.2.
In the text
thumbnail Fig. 3

m1 vs. Teff (upper left panel), [Fe/H] (upper right panel), and V magnitude (lower left panel). The results of the global fit vs. the observed m1 color is presented in the lower right panel. Symbols are as in Fig. 1.
In the text
thumbnail Fig. 4

c1 vs. log g (upper left panel), [Fe/H] (upper right panel) and V magnitude (lower left panel). The results of the global fit vs. the observed c1 color is presented in the lower right panel. Symbols are as in Fig. 1.
In the text
thumbnail Fig. 5

Comparison between solar and synthetic colors obtained from different spectra. Left panel: using Vega STIS observations to set the zero-points. Right panel: using ATLAS9 Vega model for the same purpose. Δmag = our derived solar colors minus the synthetic ones.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.