| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014026 | |
| Published online | 04 November 2010 | |
Water formation on bare grains: When the chemistry on dust impacts interstellar gas
1
Kapteyn Astronomical Institute,
PO box 800,
9700AV
Groningen,
The Netherlands
e-mail: cazaux@astro.rug.nl
2
LERMA, UMR 8112 du CNRS, Observatoire de Paris et Université de
Cergy Pontoise, 5 Mail
Gay-Lussac, 95031
Cergy-Pontoise Cedex,
France
3
SRON, National Institute for Space Research,
PO Box 800,
9700 AV
Groningen, The
Netherlands
4
School of Physics and Astronomy, University of Leeds,
LS2 9JT,
Leeds,
UK
Received:
8
January
2010
Accepted:
2
July
2010
Context. Water and O2 are important gas phase ingredients for cooling dense gas when forming stars. On dust grains, H2O is an important constituent of the icy mantle in which a complex chemistry is taking place, as revealed by hot core observations. The formation of water can occur on dust grain surfaces, and can impact gas phase composition.
Aims. The formation of molecules such as OH, H2O, HO2 and H2O2, as well as their deuterated forms and O2 and O3 is studied to assess how the chemistry varies in different astrophysical environments, and how the gas phase is affected by grain surface chemistry.
Methods. We use Monte Carlo simulations to follow the formation of molecules on bare grains as well as the fraction of molecules released into the gas phase. We consider a surface reaction network, based on gas phase reactions, as well as UV photo-dissociation of the chemical species.
Results. We show that grain surface chemistry has a strong impact on gas phase chemistry, and that this chemistry is very different for different dust grain temperatures. Low temperatures favor hydrogenation, while higher temperatures favor oxygenation. Also, UV photons dissociate the molecules on the surface, which can subsequently reform. The formation-destruction cycle increases the amount of species released into the gas phase. We also determine the timescales to form ices in diffuse and dense clouds, and show that ices are formed only in shielded environments, as supported by observations.
Key words: dust, extinction / ISM: abundances / ISM: molecules / stars: formation
© ESO, 2010
1. Introduction
There is water everywhere in the cosmos. In cold and dense regions of the interstellar medium, dust grains become covered by icy mantles consisting mainly of water (Williams et al. 1992; Gibb et al. 2004). In the star formation process, the ices that were retained onto dust grains evaporate and drive a very rich chemistry (Caselli et al. 1993; Cazaux et al. 2003). When planets are formed, at a later stage, the water still trapped in solid form is carried by asteroids and comets, and can be brought to the different planets, giving birth, as on our own planet, to oceans.
Gas-phase chemical theory predicts that H2O and O2, along with O and CO, constitute the gas-phase reservoirs of elemental oxygen in molecular gas that is well shielded from ultraviolet radiation (e.g., Millar 1990). As a consequence, water and O2 can be important coolants for dense gas (Goldsmith & Langer 1978; Hollenbach 1988; Neufeld et al. 1995).
The formation and constitution of icy mantles has been studied by several authors (Tielens & Hagen 1982; Cuppen & Herbst 2007). Observations have revealed that icy mantles are sensitive to hard radiation, and therefore could only exist in shielded environments (Whittet et al. 2001; Papoular 2005). Ices are assumed to be produced when gas phase species freeze out onto dust grains, these gas phase species having previously formed on the grain or in the gas phase. Because the binding energy of water on bare carbonaceous grains is lower than for water on ice, it is essential to form the first layer in order to form the icy mantle (Papoular 2005). This could have an important impact on the snow line position (Marseille & Cazaux submitted). We note that for water sticking on bare silicate grains this may be different (Goumans et al. 2009; Schiff 1973)
Because of the inefficiency of the gas phase routes, the use of grain surface chemistry is required to explain the observed abundances of water in molecular clouds (D’Hendecourt et al. 1985; Hasegawa et al. 1992). H2O abundances can range from <10-8 in the coldest clouds, which can be explained by the freeze-out of water onto dust, to >10-4 in warm gas and shocks, due to ice evaporation or sputtering and exothermic gas phase reactions (Bergin et al. 1998, 2000; Hollenbach et al. 2009).
In this work, we investigate the formation of molecules such as OH, H2O, H2O2, and their deuterated forms in different astrophysical environments. In particular, we concentrate on grain surface chemistry, and the amounts of species that this process releases into the gas phase. The interactions between species and carbon surfaces (graphite or amorphous carbon) has received much attention (Ghio et al. 1980; Pirronello et al. 1997; Jeloaica & Sidis 1999; Sha & Jackson 2002; Bergeron et al. 2008). Theoretical and experimental studies of the interactions between chemical species and these types of surfaces provide a considerable number of constraints for our model. On the other hand, silicates, are more complex surfaces that are more difficult to treat theoretically, resulting in fewer constraints on the interactions between species and surface. However, Goumans et al. (2009) discovered that the formation of water differs strongly as it is formed on olivine or on carbon grains. On olivine surfaces, the formation of water occurs via species strongly bound to the surface that can dissipate the excess energy in an efficient way via phonons. This allows most of the newly formed species to remain on the surface. Therefore, the formation of species on olivine surfaces appears not to affect the gas phase significantly. In this study, because we wish to assess how the chemistry on dust grains can influence the interstellar gas, we exclusively follow the chemistry that occurs on carbon grains. To do so, we use Monte Carlo simulations to describe the formation of chemical species on these surfaces. We also consider several environments with different physical conditions, and establish how chemical species form on dust as well as how they are subsequently released in the gas phase. Finally, we discuss the formation of icy mantles in atomic and molecular clouds, and show that our model reproduces the finding that grains are covered by ices only in shielded environments.
2. Grain surface chemistry
2.1. Formation of water and its deuterated forms using Monte Carlo simulations
Cazaux et al. (2008) discussed the formation of H2, HD, and D2 on surfaces that are typical of the interstellar medium. We found that the formation of molecules depends on the binding energy of atoms with the surface and on the barrier that gas phase atoms have to cross to become strongly bound to the surface. There are indeed two types of interactions between the atoms and the surface: a weak one, called physisorption (van der Waals interaction), and a strong one, called chemisorption (covalent bound). Atoms from the gas phase can easily access the physisorbed sites and become physisorbed atoms. These weakly bound atoms can travel on the surface at very low dust temperatures, meeting each other to form molecules. At higher dust temperatures, the physisorbed atoms evaporate and the formation of molecules is assured by the contribution of chemisorbed atoms. The atoms from the gas phase can also enter into a chemisorbed site (and have to cross a barrier to do so), and can meet an already chemisorbed atom. This process will allow molecules to form for a wide range of dust grain temperatures (up to few hundreds of kelvins).
We use a step-by-step Monte Carlo simulations to follow the chemistry occurring on dust
grains. The dust grains are divided into square lattices of 100 × 100 adsorption sites.
Each site on the grid corresponds to a physisorbed site and a chemisorbed site, so that
the grain can be seen as two superimposed grids. Species originating from the gas phase
arrive at a random time and location on the dust surface. This arrival time depends on the
rate at which gas species collide with the grain. This rate of accretion can be written as
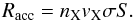 (1)where
nX and vX are the densities and
velocities, respectively, of the species X, σ is the cross-section of the
dust particule, and S is the sticking coefficient of the species with the
dust. We consider S = 1, meaning that when a species arrives at a point
of the grid, it can become physisorbed, or, if its chemisorption states exists and its
energy is high enough to cross the barrier against chemisorption, it becomes chemisorbed.
Jones & Williams (1985) show that the
sticking coefficient depends on the proportion of physisorbed/chemisorbed sites on the
surface, and that for a gas at 100 K, most of the hydrogen atoms populate the chemisorbed
sites. In our model, however, because of the high barrier to access chemisorbed sites, H
atoms mostly arrive from the gas phase in physisorbed sites. In this sense, we
overestimate the sticking coefficient since we consider that all atoms that arrive on the
grain stick.
(1)where
nX and vX are the densities and
velocities, respectively, of the species X, σ is the cross-section of the
dust particule, and S is the sticking coefficient of the species with the
dust. We consider S = 1, meaning that when a species arrives at a point
of the grid, it can become physisorbed, or, if its chemisorption states exists and its
energy is high enough to cross the barrier against chemisorption, it becomes chemisorbed.
Jones & Williams (1985) show that the
sticking coefficient depends on the proportion of physisorbed/chemisorbed sites on the
surface, and that for a gas at 100 K, most of the hydrogen atoms populate the chemisorbed
sites. In our model, however, because of the high barrier to access chemisorbed sites, H
atoms mostly arrive from the gas phase in physisorbed sites. In this sense, we
overestimate the sticking coefficient since we consider that all atoms that arrive on the
grain stick.
The species present on the surface may go return to the gas phase if they evaporate. This
evaporation rate of the speciescan be written as
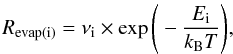 (2)where
Ei is the binding energy of the considered species i, as
reported in Table 1.
(2)where
Ei is the binding energy of the considered species i, as
reported in Table 1.
The species that arrive at a location on the surface can move randomly across the surface
by means of tunneling effects and thermal hopping. The diffusion rates
Rij for an atom to go from a site i (physisorbed or
chemisorbed) to a site j (physisorbed or chemisorbed) can be written as
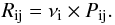 (3)where
νi is the oscillation factor of the atom
in the site i (which is of 1012 s-1 for physisorbed atoms), and
Pij is the probability for the atom to go from a site i to j
by tunneling effects or thermal hopping, as described in Cazaux & Tielens (2004). When thermal hopping predominates, which is
usually the case for species going from a physisorbed sites to another physisorbed site,
or for high temperatures, this probability can be written as
(3)where
νi is the oscillation factor of the atom
in the site i (which is of 1012 s-1 for physisorbed atoms), and
Pij is the probability for the atom to go from a site i to j
by tunneling effects or thermal hopping, as described in Cazaux & Tielens (2004). When thermal hopping predominates, which is
usually the case for species going from a physisorbed sites to another physisorbed site,
or for high temperatures, this probability can be written as 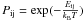 , where Eij is
the energy of the barrier between the site i and j, and T the temperature of the surface.
The hopping barriers to go from a physisorbed site to another physisorbed site are assumed
to be 2/3 of the binding energy (Ei, listed in Table 1) of the species on the surface, with a width of 3 Å,
which is the value we derived for the case of H2 formation of carbonaceous and
silicate surfaces (Cazaux & Tielens 2004).
The barrier for a physisorbed atom to become chemisorbed is discussed in Sect. 2.2.2.
, where Eij is
the energy of the barrier between the site i and j, and T the temperature of the surface.
The hopping barriers to go from a physisorbed site to another physisorbed site are assumed
to be 2/3 of the binding energy (Ei, listed in Table 1) of the species on the surface, with a width of 3 Å,
which is the value we derived for the case of H2 formation of carbonaceous and
silicate surfaces (Cazaux & Tielens 2004).
The barrier for a physisorbed atom to become chemisorbed is discussed in Sect. 2.2.2.
Reactions adopted in our chemical model.
Species present on the surface can also receive a UV photon and become dissociated at the rates reported in Sect. 2.4. Once two species meet in the same site, they can form a new species if the activation barrier for the formation can be overcome. The different reactions that can occur on the dust grains as well as their activation barriers Ea are listed in Table 1. When the barrier for a reaction has not been studied on the surface, we assume that the reactions are similar to gas phase reactions and use the NIST database (Manion et al. 2008). However, studies have shown that reactions that have a barrier in the gas phase can be barrierless on the dust surface (Ioppolo et al. 2008). Each time a reaction with a barrier occurs, we calculate the rate for crossing the barrier, which is REa = ν × PEa, where ν is the oscillation factor of the considered species, and PEa is the probability that a chemical species thermalized on the grain at a temperature Tdust crosses the activation barrier Ea. We assume here that these barriers have a width of 1 Å. We compare the rate of crossing the barrier REa to the rate for the chemical species to move out of the site Rij. If the rate of leaving the site is lower, then the reaction will occur, if not, the species will leave the site and go to a neighboring site. In this study, we assume that the species remaining on the grains are thermalized, and therefore that there is no preferential direction for the dissociated products that remain on the surface. We therefore consider the probabilities of visiting the neighboring sites to be equal.
Once a chemical species present on the dust moves, or adsorbs a photon, or meets another species, the next event that occurs to this species is determined as well as its time of occurrence. Therefore, the events that concern every species on the dust are ordered by time of occurrence, and for each event that occurs, a next event for the concerned species is determined. The chemical species considered in our model are the following: H, D, O, OH, OD, O2, H2O, HDO, D2O, O3, HO2, H2O2, DO2, HDO2, and D2O2. Apart from H and D, which may also become chemisorbed as discussed in the next section, all the other species only fill the physisorbed sites.
With the inclusion of deuterium, different products can be formed for the same reaction.
We report the branching ratios of these reactions in Table 1. For example, if we consider the reaction HD + O, the HD molecule has to be
dissociated, and the oxygen reacts either with H or D. For this reaction, the branching
ratio is strongly dependent on the temperature. At low temperatures, tunneling dominates
the reaction and HD + O produces mostly OH + D (with a rate
kHD) and very few OD + H (kDH).
At 300 K, the ratio 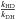 is of
the order of 15 (Robie et al. 1987), and strongly
increases as temperature decreases. Therefore, we assume that at low temperatures, the
branching ratio kDH is negligible compared to
kHD. For the case of H2O2 + D, the
reaction of one of the H atoms with a D atom, which gives HD + HO2, then breaks
the O=O bound, and finally adds the free oxygen to HD. The final products are therefore OH
+ HDO (Albers et al. 1971). For the other reactions,
when no branching ratios have been reported (in the NIST database) we assume equal
branching ratios.
is of
the order of 15 (Robie et al. 1987), and strongly
increases as temperature decreases. Therefore, we assume that at low temperatures, the
branching ratio kDH is negligible compared to
kHD. For the case of H2O2 + D, the
reaction of one of the H atoms with a D atom, which gives HD + HO2, then breaks
the O=O bound, and finally adds the free oxygen to HD. The final products are therefore OH
+ HDO (Albers et al. 1971). For the other reactions,
when no branching ratios have been reported (in the NIST database) we assume equal
branching ratios.
2.2. Binding energies
2.2.1. Physisorption
The binding energies of the different species in physisorbed sites on carbon surfaces were discussed by Cuppen & Herbst (2007) and references therein. As discussed by these authors, the binding energies of species on the surface are poorly known. On amorphous carbon grains, it seems that only H and H2 physisorption energies have been determined (Pirronello et al. 1997; Katz et al. 1999). For most of the other binding energies, we refer to graphitic surfaces. On these surfaces, H atoms have a binding energy of 550 K (Bergeron et al. 2008 and references therein; Ghio et al. 1980), which is similar to their binding energy on amorphous carbon. The physisorption energy of molecular hydrogen on carbon nanoparticles (graphitic platelets) and polycyclic aromatic hydrocarbons (PAHs) has been found to be attractive between 420 and 860 K, depending on both the orientation of H2 and the particle size. These energies are also dependent on the temperature of the surface (Heine et al. 2004). We therefore use a binding energy of 600 K, determined for graphene surfaces (Akai & Saito 2003). Bergeron et al. (2008) found that oxygen can be physisorbed on graphitic surfaces with energies of 1400 K, if the atom is placed on a top site (above a C atom) or on a bridge site (between two C atoms). This value is quite high compared to the value of 800 K used in Cuppen & Herbst (2007), initially taken from Tielens & Hagen (1982). Lee et al. (2009) calculated the binding energy of ozone on graphene. Ozone molecules adsorb on the graphene basal plane with binding energy of 2900 K, and the physisorbed molecule can chemically react with graphene to form an epoxide group and an oxygen molecule. The activation energy barrier from physisorption to chemisorption is very high (8000 K), and we therefore neglect the possibility of ozone molecules overcoming this barrier and being dissociated. For the other species, we consider similar energies as in Cuppen & Herbst (2007). The energies of physisorption of the different species are reported in Table 2.
2.2.2. Chemisorption
Physisorption and chemisorption energies of the considered species.
Hydrogen atoms can chemisorb on graphite surfaces, but this process has an associated activation energy of 0.2 eV (Hornekær et al. 2006; Sha & Jackson 2002; Jeloaica & Sidis 1999). It has been shown that once a first H atom is chemisorbed on a graphite surface, a second atom can chemisorb on the same benzene, in the site opposing this first atom (para site), without a barrier (Hornekær et al. 2006; Rougeau et al. 2006) and a third atom can form a molecule with one of these two adsorbed atoms without a barrier (Bachellerie et al. 2007). This process is important to form H2 efficiently at high dust temperatures. This process incorporated into our simulations in a coming paper (Cazaux & Morisset, in prep.). For now, we only consider that H atoms can become chemisorbed (with an energy of 0.7 eV) by crossing a barrier of 0.2 eV by tunneling effects (low temperatures) or thermal hopping (high temperatures), and approximate the barriers as being squared. Nevertheless, DFT calculations show that these barriers are far from being square leading to higher rates for H atoms to become chemisorbed. This will be discussed in a future work (Cazaux & Morisset, in prep.) If the process discussed by Bachellerie et al. (2007) were to be taken into account, once a first atom is present in a chemisorbed site, there would be a barrier-less way to form and desorb a H2 molecule. In this study, we thus underestimate the rate of H2 formation. This can have a small effect on the formation of molecules in diffuse clouds, which are mostly atomic environments, but has no effect for molecular environments, since the reactions that form molecules involve H2.
Theoretical and experimental studies show that oxygen atoms chemisorb preferably above the middle of the C–C bond, creating a stable epoxide-like structure. Oxygen has adsorption energies of ~2.3–2.4 eV, with a barrier against chemisorption on the order of 0.15–0.2 eV, depending on whether the O chemisorbs above a C or in the middle of the C–C bond (Fromherz et al. 1993). In the singlet state, oxygen atoms can be chemisorbed with an energy of 2.5 eV (Jelea et al. 2004), and can react with H atoms to form OH radicals by means of an Eley-Rideal mechanism with an activation barrier that varies from 0.17 eV to 0.29 eV. However, oxygen is found mostly in its triplet form in the ISM. Bergeron et al. (2008) show that the chemisorption of oxygen in a triplet state has an associated barrier of 0.2 eV, with a “meta-stable” chemisorbed state, meaning that the well lies above the energy level for 3O + graphite at infinite separation. Therefore, only for high temperature gas (2000 K) can the chemisorbed state of oxygen (triplet) be populated. In this work, because oxygen is found mostly in the triplet form in the ISM, we assume that oxygen atoms cannot be chemisorbed.
2.3. Desorption upon formation
Once a reaction occurs on the surface, there is a certain probability that the product of
the reaction desorbs into the gas phase. This process depends on the energy released upon
formation (enthalpy of reaction) and on the binding energy of the final product. The
desorption upon formation concerns only physisorbed species that react with each other to
form a product that is also physisorbed. Because of the excess energy contained in the
molecule, when reactions have high enthalpies, this physisorbed product can be ejected
into the gas phase.This process was discussed by Garrod
et al. (2007). These authors quantify the probability of desorption using
Rice-Ramsperger-Kessel (RRK) theory. However, this theory is designed for large molecules,
and we expect a different behavior for diatomic molecules. With this method, they derive a
probability P that for a certain reaction, a certain energy
E, higher than the binding energy of the product
(E ≥ EB), is found in the bond. This
probability can be written as ![\begin{equation} P=\left[ 1- \frac{E_{\rm B}}{E_{\rm{reac}}} \right]^{s-1}, \end{equation}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq41.png) (4)where the energy
released during the reaction is Ereac, and s
is the number of atoms in the molecule that is produced. Once this probability is known,
these authors use a method that depends on the energy loss on the surface, and that
calculates the fraction of newly formed molecules that would desorb from the surface upon
formation. This fraction is written as
(4)where the energy
released during the reaction is Ereac, and s
is the number of atoms in the molecule that is produced. Once this probability is known,
these authors use a method that depends on the energy loss on the surface, and that
calculates the fraction of newly formed molecules that would desorb from the surface upon
formation. This fraction is written as
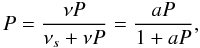 (5)where
νs is the rate at which the total energy is
lost to the surface, ν is the oscillation factor of the molecule in the
potential well, and
(5)where
νs is the rate at which the total energy is
lost to the surface, ν is the oscillation factor of the molecule in the
potential well, and 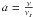 . We speculate
that the energy loss will depend on the porosity of the surface, meaning that a newly
formed species lose its energy more efficiently on a porous surface because it will then
encounter and bump into more obstacles. Since water ices are supposed to be more porous
than bare surfaces, molecules produced on bare grains should have higher probabilities of
desorbing directly into the gas phase upon formation. Garrod et al. (2007) use the data of Kroes
& Andersson (2005) to determine the rate
νs, and derive a factor
a = 0.012. In the case of bare grains, on the other hand, Katz et al. (1999), Cazaux & Tielens (2004), and Cuppen
& Herbst (2005), infer from the experiments of Pirronello et al. (1997) that the fraction of H2 that
directly desorbs into the gas phase upon formation is about 70% for silicates and 60% for
amorphous carbon grains. With the theory developed in Garrod et al. (2007), we obtain 1%,
which is far from what has been derived for H2. If we assume the energy loss to
be much less efficient in the case of bare grains, such that the factor a
is a few orders of magnitude higher than the 0.012 determined by Garrod et al. (2007), we
obtain a very similar fraction of desorption upon formation for H2 and
H2O (if a = 0.7, we obtain 40% and 39% for the desorption
upon formation of H2 and H2O, respectively). In the discussion of
Cuppen & Herbst (2007), it seems that the
fraction of water that desorbs upon formation is quite small (Kroes & Andersson 2005). This study deals with water ice, but
for non-porous surfaces such as bare grains this fraction is different.
. We speculate
that the energy loss will depend on the porosity of the surface, meaning that a newly
formed species lose its energy more efficiently on a porous surface because it will then
encounter and bump into more obstacles. Since water ices are supposed to be more porous
than bare surfaces, molecules produced on bare grains should have higher probabilities of
desorbing directly into the gas phase upon formation. Garrod et al. (2007) use the data of Kroes
& Andersson (2005) to determine the rate
νs, and derive a factor
a = 0.012. In the case of bare grains, on the other hand, Katz et al. (1999), Cazaux & Tielens (2004), and Cuppen
& Herbst (2005), infer from the experiments of Pirronello et al. (1997) that the fraction of H2 that
directly desorbs into the gas phase upon formation is about 70% for silicates and 60% for
amorphous carbon grains. With the theory developed in Garrod et al. (2007), we obtain 1%,
which is far from what has been derived for H2. If we assume the energy loss to
be much less efficient in the case of bare grains, such that the factor a
is a few orders of magnitude higher than the 0.012 determined by Garrod et al. (2007), we
obtain a very similar fraction of desorption upon formation for H2 and
H2O (if a = 0.7, we obtain 40% and 39% for the desorption
upon formation of H2 and H2O, respectively). In the discussion of
Cuppen & Herbst (2007), it seems that the
fraction of water that desorbs upon formation is quite small (Kroes & Andersson 2005). This study deals with water ice, but
for non-porous surfaces such as bare grains this fraction is different.
Bergeron et al. (2008) show that once physisorbed H and O atoms recombine on graphite surface, the nascent molecules can either directly desorb, if the translational energy is large enough, or the molecule is trapped in a quasi-stationary state where it oscillates in the physisorption well with a signicant amount of vibrational and rotational energy. As the H atoms repeatedly collide with O atoms, OH escapes from the surface (the so-called complex mechanism). Bachellerie et al. (2007) show that H2 molecules mostly desorb from the surface upon formation. They also demonstrate that on a graphene surface at low temperatures, only 3% of the newly formed H2 molecules remain on the surface (they consider that species remaining for more than 12 ps are trapped). Therefore, we assume that a significant fraction of newly formed species can desorb directly into the gas phase upon formation.
We therefore use an approximation derived by Vasta et al. (2005, unpublished), where the
desorption of H2 is high, and that of H2O is low, depending on the
binding energy of the final product and the enthalpy of reaction. This approximation,
which reproduces the fraction of H2 that desorbs upon formation on silicates
and amorphous carbon, also keeps this fraction small for water, and is more adequate for
our purposes in modeling the formation of chemical species on bare grains. The empirical
formula 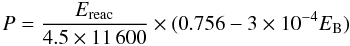 (6)infers that 70% (60%)
of H2 molecules desorb upon formation on silicate (amorphous carbon) surfaces,
where H2 molecules have a binding energy of 300 K (500 K). The fraction of
molecules that desorbs upon formation linearly scales with the enthalpy of reaction. In
our model, 60% of the newly formed H2 molecules desorb upon formation, whereas
this fraction is 36% for the reaction H + O → OH and 15% for OH + H → H2O.
This fraction depends on the route to form the chemical species, since it becomes only 4%
when OH is formed from O + H2 and 0.8% when H2O is formed from OH +
H2. Therefore, the fraction of species released into the gas phase will
depend strongly on whether the species are formed in atomic or molecular environments.
(6)infers that 70% (60%)
of H2 molecules desorb upon formation on silicate (amorphous carbon) surfaces,
where H2 molecules have a binding energy of 300 K (500 K). The fraction of
molecules that desorbs upon formation linearly scales with the enthalpy of reaction. In
our model, 60% of the newly formed H2 molecules desorb upon formation, whereas
this fraction is 36% for the reaction H + O → OH and 15% for OH + H → H2O.
This fraction depends on the route to form the chemical species, since it becomes only 4%
when OH is formed from O + H2 and 0.8% when H2O is formed from OH +
H2. Therefore, the fraction of species released into the gas phase will
depend strongly on whether the species are formed in atomic or molecular environments.
2.4. Photo-dissociation and photo-desorption
Photodissociation reactions.
Interstellar dust grains are present in environments that are subject to radiation. Stars
in the neighborhood can emit FUV photons that impinge on the interstellar dust grains. The
flux of FUV photons can be written to be (Hollenbach
et al. 2009) 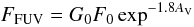 (7)where
F0 ~108 photons cm-2
s-1 is the approximate local interstellar flux between 6 and 13.6 eV,
G0 is a scaling factor for which the value 1 corresponds to
the Milky Way interstellar radiation field in the FUV band, and
AV is the visual extinction.
(7)where
F0 ~108 photons cm-2
s-1 is the approximate local interstellar flux between 6 and 13.6 eV,
G0 is a scaling factor for which the value 1 corresponds to
the Milky Way interstellar radiation field in the FUV band, and
AV is the visual extinction.
Once a UV photon arrives on a species, this species can be photo-dissociated. The products of the dissociation can be released directly into the gas phase, or one or both fragments can be trapped on the surface. Andersson & van Dishoeck (2008) calculated the outcomes of the photodissociation of water molecules in water ices. Once a water molecule is broken into OH and H in the first monolayer of ice, several processes can occur with different probabilities depending on whether the ices are crystalline or amorphous (Andersson et al. 2006): a) H atoms are released into the gas phase and OH molecules are trapped (amorphous: 92%, crystalline: 70%); b) H and OH are trapped (amorphous: 5%, crystalline: 14%); c) OH and H desorb (amorphous: 2% and crystalline: 6%); d) OH and H recombine and form H2O, which can be trapped (amorphous: 1%, crystalline: 0.05%) or desorb (amorphous: 0.7%, crystalline: 1%). These results differ from those of crystalline and amorphous ices. In particular, H atoms produced by dissociations are trapped less in crystalline ice than amorphous ice. According to these authors, the yield of desorption of water molecules is rather small (0.2%) for both types of ices, as confirmed by experiments from Oberg et al. (2008).
In our simulations, we assume that an UV photon absorbed by a water molecule can lead to desorption of OH and H with a probability of 2%. We otherwise assume that the products remain on the grain surface as OH and H. Because we consider bare surfaces, OH and H have different mobilities and therefore the probability of the reaction and reformation of the water molecule should differ from that on ices. We also consider that H atoms remain on the grain upon dissociation. Because of our lack of knowledge about the direct photo-desorption of species other than water, we only consider the desorption of water as OH and H into the gas phase. For the other species, we assume that there is no photo-desorption, but that photo-dissociation is possible, as discussed in the next paragraph. This seems to be a correct approximation, since, as discussed by Andersson & van Dishoeck (2008), photo-dissociation (processes a and b discussed above) is more important than direct photo-desorption (process c).
In this study, we assume that only photons that arrive directly on the species can photo-dissociate them, meaning that the cross-section of reaction is similar to that in the gas phase. Table 3 presents the different photodissociation reactions and their associated photo-dissociation rates. We also assume that 2% of the products from a photo-dissociation reaction directly desorb into the gas phase, while 98% of the same products remain on the grain surface. We do not consider here the possibility of one product staying and the other one desorbing. We also take into account cosmic-ray-induced photons. These photons can interact with species present on the grain surface, and dissociate them with rates similar to the gas phase ones. These rates are also reported in Table 3. In our simulations, we assume that the products of the photodissociation are directly thermalized on the surface, meaning that they lose their excess energy on very short timescales. The two products of the dissociation are placed in neighboring sites.
2.5. Water clusters
If a water molecule is located in a site next to another water molecule, a dimer can be created, making the total binding energy larger. Bolina et al. (2005) and Brown & Bolina (2007) performed temperature programmed desorption (TPD) experiments for the desorption of pure H2O ice on a graphite surface (highly ordered pyrolytic graphite). The experimental data showed that with increasing coverage, water molecules desorb at higher temperature. Water molecules are arranged in clusters, for which the binding energy increases with increasing size. Therefore, as the coverage increases, the cluster becomes more important, and a higher surface temperature is needed to desorb the molecules. Ab initio calculations from Lin et al. (2005) and González et al. (2007), determined the adsorption energies of a single water molecule, and to water molecules arrange as dimers, trimers, up to hexamers. These binding energies increase with the number of water molecules present in the cluster, but only if the cluster has two dimensions. Lin et al. (2005) show that the binding energy of a 3D cluster mainly depends on the number of water molecules close to the graphite surface. In this study, because we consider grain surfaces at low temperatures (≤30 K), we do not take into account the formation of water clusters, since any newly formed water molecule that is not ejected upon formation remains on the surface. Water clusters and their impact on the freeze-out of water mantles and the snow line in proto-stellar environments is treated in another work (Marseille & Cazaux, submitted).
3. Results
3.1. Test case: the effect of the dust temperature and UV photons
We calculate the number of molecules formed on the dust grain and released into the gas phase as a function of time for different dust grain temperatures. Only grain surface chemistry is considered here, and the gas phase reactions and abundances are not treated in this paper. We start our analysis with a high O/H and D/H ratio of 0.1, and nH = 103 cm-3, to understand how grain temperature influences the chemistry occurring on interstellar grains. We also add a UV radiation field to assess the changes in grain surface chemistry in the presence of photons. In this section, we consider parameters that are not representative of any astrophysical environment to understand how these parameters influence the chemistry on dust and its impact on gas phase.
The population of the chemical species present on the dust grain and released into the gas phase, in the absence of UV radiation, are presented in Fig. 1. When looking at the fraction of the species covering the grain (with monolayer equal to 1 corresponding to a surface that is completely covered), it appears that the chemistry occurring on the dust grain is very different if the grain has a temperature of 10 K or 30 K. At 10 K, the atoms and molecules do not eVaporate into the gas phase, and the H atoms (and D atoms) are the only species mobile on the surface. Therefore, the dominating process is hydrogenation and most of the oxygen is found in the form of H2O and HDO. On the grain surface, as shown in Fig. 1, top left panel, H2O and HDO are the dominant species. Each time an OH species is formed and stays on the dust grain, a H (D) atom already present on the surface finds this OH (OD) radical and associates itself with it to form H2O (HDO). Therefore, the successive hydrogenations are very efficient, and O rapidly converts to OH and H2O. The species released into the gas phase, represented in Fig. 1, top right panel, are identical to those formed on the grain: ~30% of the oxygen arriving on the grain is released in the gas phase as OH, and ~5% as H2O. On 30 K grains, on the other hand, the H and D atoms evaporate, while oxygen atoms, more strongly physisorbed to the surface, stay and can encounter each other. Therefore, plenty of oxygen-bearing species are formed that contain more than one oxygen atom. The grain surface composition is rich in H2O and HDO (Fig. 1, bottom left panel). Plenty of chemical species are only transitory, such as OH, OD and HO2. and turn very rapidly into H2O, explaining their absence from the grain surface. The species released into the gas phase are more complex than grain surface species, as shown in Fig. 1, bottom right panel. Oxygen atoms arriving onto the grain are released into the gas phase in the form of OH (20%), O2 (10%), H2O (5%), OD (2%), and H2O2 (1%). These species are released into the gas upon formation. At these temperature ranges, this process is the most important for populating the gas phase with species formed on dust because evaporation is negligible.
 |
Fig. 1 Chemical species present on a grain surface of 10 K in monolayer (1 monolayer is a total coverage of the surface) as function of time (left panels). Fraction of newly formed oxygen-bearing molecules f(O) that are released into the gas phase in the form of other species (right panels). Top: temperature of the grain surface is set to 10 K. Bottom: temperature of the grain surface is set to 30 K. |
Parameters used in our simulations.
When dust grains are subject to strong UV radiation fields, the species present on their surface can be photo-dissociated. If we consider 10 K and 30 K dust grains in an environment subject to a UV radiation field of G0 = 103, and at an extinction of AV = 1 mag, the molecules on the grain surface are photo-dissociated very rapidly (Fig. 2, left panels). Each time a molecule forms and remains on the surface, it can be destroyed by an incident UV photon. Because of the high fraction of atoms on the surface, OH radicals are transitory species that rapidly convert into H2O. The fraction of H2O that covers the surface reaches an equilibrium between photo-dissociation into OH and H and reformation. The amount of water that is released in the gas phase upon formation is enhanced by the presence of the UV radiation field (Fig. 2, right panels). Without a UV field, this amount is on the order of 5%. This fraction becomes much higher ~12–15% in the presence of a strong radiation field. This is because each water molecule that forms has a probability of being released into the gas, but if this molecule stays, it can be dissociated and reform with the same probability of being desorbed. In this sense, the water molecules follow a cycle of formation-destruction that enhances their probability of being released in the gas phase. We find analytically that the amount of water that directly desorbs into the gas upon formation should be ~5.4% (0.64 × 0.15 = 0.054, fraction of OH that stays on the surface upon formation times the fraction of H2O that desorbs upon formation). When a strong UV radiation field is present, the molecules can then dissociated into products that can meet, and reform the same molecules. The probability that the H atom coming from the dissociation meets the other product OH to reform H2O is determined in the Appendix A. We found that this process, commonly called backdiffusion, has a probability of 45% of occurring, and therefore enhances the fraction of water released into the gas phase by a factor 2 (~10% see Appendix A). This value is slightly lower than the one we found with our simulations, meaning that backdiffusion is enhanced by grain size limitations that we have not considered. Our calculations for the backdiffusion in Appendix A differ from those of Chang et al. (2005) who studied the H + H system and of Krug (2004) who concentrated on stepped surfaces. In our study, only H atoms can move on the surface of bare grains, and we concentrated on the probability of H atoms resulting from the dissociation of water molecules to visit the location of the other product of the dissociation.
It seems obvious that low dust temperatures favor hydrogenation and deuteration of the species on the surface. For higher dust temperatures, hydrogen and deuterium can evaporate into the gas phase because of their low binding energies, while oxygen atoms, which have a higher binding energy, become mobile on the surface without evaporating. The resulting chemistry is oxygenation which leads to a chemistry rich in oxygen-bearing molecules. UV photons can dissociate most of the species on the surface. The products of the dissociation can meet again and reform the original species. Because each new species formed has a probability of being ejected into the gas phase upon formation, the cycle formation-destruction-formation increases the total fraction of species released into the gas phase.
 |
Fig. 2 Same as Fig. 1 with a UV radiation field of G0 = 103. UV photons dissociate the chemical species present on the surface, which explains the small coverage of the grain surface (left panels). On the other hand, the amount of species released into the gas phase can be enhanced. |
 |
Fig. 3 Chemical species present on dust grains and released into the gas phase in diffuse clouds. Left panel: chemical species present on a grain surface in monolayer (1 monolayer is a total coverage of the surface) as function of time. Right panel: fraction of newly formed oxygen-bearing molecules f(O) that are released into the gas phase in the form of other species. The error bars have been derived using 7 simulations and represent 95% confidence levels. |
4. From diffuse to dense clouds and PDRs
We now discuss the formation of molecules onto grains in different environments. The parameters used in our simulations are based on Snow & McCall (2006) and reported in Table 4. For each environment, we performed at least 4 different simulations with different seeds, and we report the errors bars that represent the 95% confidence level.
We first compute the chemistry occurring on dust grains in diffuse clouds, where the gas phase composition is mostly atomic. We assume a density of 100 atoms cm-3, a visual extinction of 0.5 mag and an impinging UV radiation field of G0 = 1. The species present on dust grains and released into the gas phase are reported in Fig. 3. In this environment, the process of forming water involves the association of H and O atoms. The water formed on the grains can either desorb or remain. The fraction of the incoming oxygen atoms that come and leave the grain as OH is ~35%, while it is ~10% as H2O. An oxygen atom that arrives on a grain and meets a H atom, will form OH. Because of the energy released during this reaction, OH desorbs in 35% of the cases. The fraction that remains on the surface (65%) can meet another H atom to form H2O. This reaction is again exothermic and in 15% of the cases, the product H2O is ejected into the gas phase. In total, 10% of the O arriving onto grains transforms into gas phase H2O (0.65 × 0.15 = 0.1). The water that remains on the surface accumulates very slowly until it reaches 0.2% after ~100 years. This shows that almost no water ice covers dust grains in diffuse clouds, as reported by observations (Whittet et al. 2001).
In translucent clouds, on the other hand, the medium is mostly molecular. We assume a density of 500 atoms cm-3, a visual extinction of 1 mag and an impinging UV radiation field of G0 = 1. In this cloud, the deuterium and oxygen species remain in atomic form. Because in these clouds the hydrogen is in molecular form, the most efficient route to form H2O is H2 + O → OH + H. At Tdust = 14 K, the hydrogen atoms evaporate, and water forms through the association of OH with H2. Because the enthalpies of reactions are much lower for the formation of H2O when the reaction involves H2 than when it involves H atoms, the desorption upon formation becomes 3.2% for H2 +O and 0.88% for H2+OH. Therefore, the newly formed species mostly remain on the grain surface, and we find that no species are released into the gas phase ( see Fig. 4). The first layer of ice grows until it reaches a coverage of a few percent, confirming the absence of ice on the surface of dust grains in translucent clouds.
In dense clouds, the medium is also molecular, but denser. We consider a cloud with a density of 5000 cm-3, at a visual extinction of 5 mag, and an impinging UV field of G0 = 1. At this extinction, oxygen and deuterium remain in atomic form and the dust grains are colder, Tdust = 12 K. The formation of H2O involves the reaction H2 + O → OH + H. As discussed before, this reaction releases less energy than the reaction involving atomic H, and therefore only a small percentage of OH (~3%) is released into the gas phase. Because the dust grains are at a lower temperature than in the translucent cloud case, H atoms do not evaporate. The products of this reaction, OH and H, that stay on the surface can react and form H2O. If these two products meet, 15% of the formed H2O is released into the gas phase. Our results, presented in Fig. 5, indicate that more than 10% of the oxygen is released as H2O into the gas phase. This means that the products H and OH have a probability of 60% of meeting each other. The OH that does not meet the H atoms will encounter an H2 molecule and form H2O + H. The part released into the gas phase through this process is negligible.
We also calculate the formation of molecules on dust grains in photo-dissociation regions. For this, we use the results of Meijerink & Spaans (2005) for a PDR with a density of 103 atoms cm-3, with a UV radiation field of G0 = 103 and a visual extinction of 5 mag. Hydrogen is converted into H2 but oxygen and deuterium are still in atomic form. The grain and gas temperatures are as high as 30 K. For these grain temperatures, the chemistry is very different than from above, as shown in Fig. 6. Because of their low binding energy, H atoms and H2 molecules evaporate efficiently, while oxygen atoms remain on the grain to form O2 and O3 molecules. The formation of water occurs through the successive hydrogenation of O2 (Miyauchi et al. 2008; Ioppolo et al. 2008), i.e., H +O2 → HO2 and HO2 + H → H2O2 and H2O2 + H → H2O. Another important formation route is the hydrogenation of O3, as shown by Mokrane et al. (2009), i.e., O3+H → OH + O2 and OH + H → H2O.
 |
Fig. 4 Same as Fig. 3 for translucent clouds. Note that no oxygen-bearing species are released into the gas phase. The error bars have been derived using 4 simulations and represent the 95% confidence level. |
5. Discussion and conclusions
We used Monte Carlo methods to follow the chemistry involving H, D, and O species on interstellar dust grain surfaces. The formation of surface species as well as species released into the gas phase is computed and allows us to estimate the efficiency for the formation of O bearing species. Our model shows a strong chemical differentiation with grain temperature. At Tdust = 10 K, processes involving hydrogenation are favored, while Tdust = 30 K favors oxygenation. UV photons can dissociate the species present on the surface, and the product of this dissociation can meet again and reform the initial species. Because plenty of chemical reactions used in this work are exothermic, a fraction of the newly formed species desorbs directly into the gas phase. Therefore, the cycle formation-dissociation-formation increases the fraction of the species released into the gas phase significantly.
We applied our model to different astrophysical environments. In diffuse clouds, water is formed through the successive hydrogenation of oxygen. These reactions are exothermic and allow an important fraction of newly formed OH and H2O to desorb into the gas phase (~35% and ~15% respectively). In translucent clouds, on the other hand, the medium is molecular and the formation of water involves molecular hydrogen and atomic oxygen. These reactions produce a very small amount of energy, and therefore no species are released into the gas phase (~3% for OH and ~1% for H2O). In diffuse clouds, the temperature of the dust grains is slightly lower, and H atoms do not evaporate. Therefore, as in the case of translucent clouds, oxygen meets H2 to give OH and H, but in this case the H atoms produced remain on the grain. Water can form through the association of OH and this H (with a probability of 45%), and again, an important fraction of H2O is released into the gas phase (~7%). In environments with warmer dust grains, such as PDRs, the chemistry occurring on the grain and the products released into the gas phase are very different. The formation of water involves O2 (Ioppolo et al. 2008) and O3 (Mokrane et al. 2009), and many oxygenated species are released into the gas phase.
The formation of ices requires very long timescales in diffuse and translucent clouds, as already discussed by Cuppen & Herbst (2007). In their work, these authors showed that a time of 105 years is required to form the first monolayer of ice in dense clouds, while water coverage would reach a maximum of 50% of the surface in translucent clouds and 10% of the surface in diffuse clouds. In our model, the water ice coverage reaches 0.3% in diffuse clouds and 1% in translucent clouds after 30 years. We obtain a water ice coverage much lower than Cuppen & Herbst (2007) since we consider that for each reaction that occurs on the surface, a certain fraction directly desorbs into the gas phase upon formation. In diffuse clouds, this fraction is 36% and 15% for the formation of OH and H2O, respectively. Our model also differs from Cuppen & Herbst (2007) since it does not allow species to accrete on top of each other and therefore does not consider the formation of ices.
 |
Fig. 5 Same as Fig. 3 for dense clouds. The error bars have been derived using 5 simulations and represent the 95% confidence level. |
 |
Fig. 6 Same as Fig. 3 for PDRs. The error bars have been derived using 7 simulations and represent the 95% confidence level. |
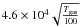 cm s-1)
, σ the cross-section of the grain, and ϵ the formation
efficiency of the water that stays on the grain. This efficiency depends directly on the
formation route of water in different environments. In the case of diffuse clouds, water
forms through the reactions O + H → OH, for which 64% stays on the dust grain (see Sect.
2.3), and OH + H → H2O for which 85% stays on the dust, yielding an efficiency
on the order of 50%. In translucent clouds, water forms through O + H2 → OH + H
(96% stays on dust) and OH + H2 → H2O + H (99.2% stays on the dust),
which brings the efficiency of water formation to ~95%. In dense clouds, this
efficiency depends on the reactions O + H2 → OH + H and OH + H →
H2O, and therefore is on the order of ~81%. Note that in the PDR case,
water formation follows another route involving O2 that brings the efficiency to
5%. The destruction by UV can be written as:
Rdes = 8 × 10-10G0nH2O
exp(−2.2AV). In steady state, the fraction of the water
molecules that covers the surface of a dust grain can be written as:
cm s-1)
, σ the cross-section of the grain, and ϵ the formation
efficiency of the water that stays on the grain. This efficiency depends directly on the
formation route of water in different environments. In the case of diffuse clouds, water
forms through the reactions O + H → OH, for which 64% stays on the dust grain (see Sect.
2.3), and OH + H → H2O for which 85% stays on the dust, yielding an efficiency
on the order of 50%. In translucent clouds, water forms through O + H2 → OH + H
(96% stays on dust) and OH + H2 → H2O + H (99.2% stays on the dust),
which brings the efficiency of water formation to ~95%. In dense clouds, this
efficiency depends on the reactions O + H2 → OH + H and OH + H →
H2O, and therefore is on the order of ~81%. Note that in the PDR case,
water formation follows another route involving O2 that brings the efficiency to
5%. The destruction by UV can be written as:
Rdes = 8 × 10-10G0nH2O
exp(−2.2AV). In steady state, the fraction of the water
molecules that covers the surface of a dust grain can be written as:
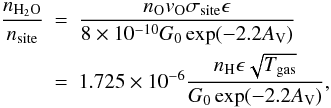 (8)where
σsite is the cross-section of one site
(~10-15 cm2) and nH the total
density of hydrogen. This fraction is ~0.3% in diffuse clouds, which is
consistent with our calculations that show that this coverage is reached after 100 years
(time to reach the steady state; see Fig. 3). In
translucent clouds, the density is higher, and the coverage at steady state is on the order
of 5%. For dense clouds, the medium is shielded, with an extinction of 5 mag and the
coverage becomes larger than 1, meaning that dust grains are covered by icy mantles with
several layers. In PDR environments, with high impinging UV radiation field
(103), and for an extinction of 5 mag, the coverage of ice is of 0.25%. These
estimates, confirmed by our Monte Carlo simulations, show that ices that cover dust grains
can only exist in shielded environments, if the UV radiation field is not too important.
This is supported by observations of ices in diffuse and dense environments (Whittet et al. 2001). Jones & Williams (1984) estimate that the efficiency with which water is
formed on dust grains through repetitive hydrogenation of oxygen should be higher than 25%
to reproduce the observations of the ice band in the Taurus molecular cloud. In this work,
we find that the efficiency for the formation of water is at least of 50%, which agrees with
their findings. However, we established that the successive hydrogenation of oxygen to form
water was not important in molecular clouds, but that the reaction of oxygen with
H2 is the dominant route. Indeed, even if an important barrier exists for
oxygen to react with H2, these reactions are possible on surfaces since the
species can repetitively meet each other, increasing the cumulative probability of
overcoming the barrier. In this sense, dust grain surfaces can provide natural place for
reactions with high barriers to occur, while these reactions would be highly unlikely in the
gas phase.
(8)where
σsite is the cross-section of one site
(~10-15 cm2) and nH the total
density of hydrogen. This fraction is ~0.3% in diffuse clouds, which is
consistent with our calculations that show that this coverage is reached after 100 years
(time to reach the steady state; see Fig. 3). In
translucent clouds, the density is higher, and the coverage at steady state is on the order
of 5%. For dense clouds, the medium is shielded, with an extinction of 5 mag and the
coverage becomes larger than 1, meaning that dust grains are covered by icy mantles with
several layers. In PDR environments, with high impinging UV radiation field
(103), and for an extinction of 5 mag, the coverage of ice is of 0.25%. These
estimates, confirmed by our Monte Carlo simulations, show that ices that cover dust grains
can only exist in shielded environments, if the UV radiation field is not too important.
This is supported by observations of ices in diffuse and dense environments (Whittet et al. 2001). Jones & Williams (1984) estimate that the efficiency with which water is
formed on dust grains through repetitive hydrogenation of oxygen should be higher than 25%
to reproduce the observations of the ice band in the Taurus molecular cloud. In this work,
we find that the efficiency for the formation of water is at least of 50%, which agrees with
their findings. However, we established that the successive hydrogenation of oxygen to form
water was not important in molecular clouds, but that the reaction of oxygen with
H2 is the dominant route. Indeed, even if an important barrier exists for
oxygen to react with H2, these reactions are possible on surfaces since the
species can repetitively meet each other, increasing the cumulative probability of
overcoming the barrier. In this sense, dust grain surfaces can provide natural place for
reactions with high barriers to occur, while these reactions would be highly unlikely in the
gas phase.
A major result of this paper is that the chemistry on bare grains has an important impact on gas phase chemistry because of the exothermicity of certain reactions on the surface. Once the grains become covered by icy mantles, the binding energies are much higher and the newly formed species remain trapped on the surface. Therefore, it would be very interesting to follow the chemistry that occurs in a diffuse cloud as it evolves into a dense cloud under the influence of hydrodynamics and gravity, and measure the impact of the grain surface chemistry on the gas phase composition while the grains are still bare grains.
We should mention that the probability of chemical species desorbing from grain surfaces upon formation has been seen experimentally (Pirronello et al. 1997) and has demonstrated theoretically (Bachellerie et al. 2007; Bergeron et al. 2008). However, the dependence of this probability on the exothermicity of the reaction is unknown and has only been estimated empirically. The impact of grain surface chemistry on gas phase has been estimated in this work with the assumption that species forming on dust surfaces have higher probabilities of being released in the gas as the reaction is exothermic. Further studies are requires to assess this point and more clearly understand the effect of grain surface chemistry on the gas phase composition.
Acknowledgments
S.C. is supported by the Netherlands Organization for Scientific Research (NWO).
Appendix A: Photo-desorption enhanced by photo-dissociation: recombination probability
First, we assume that photo-dissociation occurs, leading to one product on the
(x = 0,y = 0) site and the other next to it. The
probability Px,y(i), at a
given position (x,y) on the grid, of finding the product of the
photo-dissociation after i steps can be inferred from the previous probabilities at the
step i−1: ![\appendix \setcounter{section}{1} \begin{eqnarray} P_{x,y} &=& \frac{1}{4}\Big[P_{x-1,y}(i-1)\\\nonumber &&\,+\,P_{x+1,y}(i-1)+P_{x,y-1}(i-1)+P_{x,y+1}(i-1)\Big]. \end{eqnarray}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq99.png) (A.1)After
further investigation, one can show that for the special position
(x = 1,y = 0), just next to the initial location, the
probability can be written by separating even and odd cases as
(A.1)After
further investigation, one can show that for the special position
(x = 1,y = 0), just next to the initial location, the
probability can be written by separating even and odd cases as
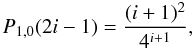 (A.2)
(A.2)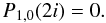 (A.3)More
generally, the probablity
(A.3)More
generally, the probablity 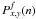 that the product arrives after exactly
n steps on a specified site situated at (x,y) is given
by
that the product arrives after exactly
n steps on a specified site situated at (x,y) is given
by ![\appendix \setcounter{section}{1} \begin{equation} P^f_{x,y}(n) = \left[\displaystyle\prod_{i=1}^{n-1}\left(1-P_{x,y}(i)\right)\right]P_{x,y}(n). \end{equation}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq105.png) (A.4)If
n = 2k,k ∈ N*, then one can conclude that
(A.4)If
n = 2k,k ∈ N*, then one can conclude that
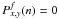 , whereas if
n = 2k−1,k ∈ N*,
, whereas if
n = 2k−1,k ∈ N*,
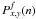 exists and can be simplified to
exists and can be simplified to
![\appendix \setcounter{section}{1} \begin{equation} P^f_{x,y}(2k-1) = \left[\displaystyle\prod_{j=1}^{k-1}\left(1-P_{x,y}(2j-1)\right)\right]P_{x,y}(2k-1). \end{equation}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq109.png) (A.5)Hence for the case
where x = 1 and y = 0
(A.5)Hence for the case
where x = 1 and y = 0
![\appendix \setcounter{section}{1} \begin{equation} P^f_{1,0}(2k-1) = \left[\displaystyle\prod_{i=2}^k\left(1-4^{-i}i^2\right)\right]\frac{(k+1)^2}{4^{k+1}}\cdot \end{equation}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq112.png) (A.6)In this last equation,
the product term can be seen as a function of integers
ϕ(k) with the first terms
(A.6)In this last equation,
the product term can be seen as a function of integers
ϕ(k) with the first terms
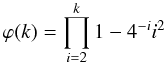 (A.7)
(A.7)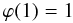 (A.8)
(A.8)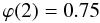 (A.9)
(A.9) (A.10)
(A.10)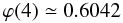 (A.11)
(A.11)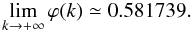 (A.12)Here
we see how fast this function converges to unique value. At the end, the probability
P1,0 that the initial product comes back to its site of
production is
(A.12)Here
we see how fast this function converges to unique value. At the end, the probability
P1,0 that the initial product comes back to its site of
production is 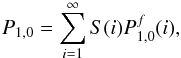 (A.13)where
S(i) is the cumulative distribution of the number of
steps that the product will do. According to the previous results that we obtained, this
probability can be re-written as
(A.13)where
S(i) is the cumulative distribution of the number of
steps that the product will do. According to the previous results that we obtained, this
probability can be re-written as
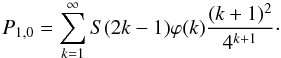 (A.14)First, if we assume that
the product can make as many steps as it wishes
(∀k,S(2k−1) = 1), P1,0 can
be approximated as
(A.14)First, if we assume that
the product can make as many steps as it wishes
(∀k,S(2k−1) = 1), P1,0 can
be approximated as 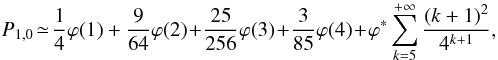 (A.15)where
ϕ* is the limit value when k → + ∞. To
obtain a clearer idea of how fast this series converges, we note that the sum in the last
term of the previous equation has an algebraically defined value, which is very small
compared to the other terms. Indeed
(A.15)where
ϕ* is the limit value when k → + ∞. To
obtain a clearer idea of how fast this series converges, we note that the sum in the last
term of the previous equation has an algebraically defined value, which is very small
compared to the other terms. Indeed
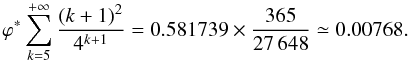 (A.16)Here we see that
the direct recombination effect is enhanced mainly by the first term of the sum, i.e.,
when k < 5, hence a number of steps smaller than 9. This shows
that one can assume that a product has left its initial position after 10 steps if it has
not come back at least one time to its initial position (or neighbourhood here). Finally,
we can estimate P1,0 to be
(A.16)Here we see that
the direct recombination effect is enhanced mainly by the first term of the sum, i.e.,
when k < 5, hence a number of steps smaller than 9. This shows
that one can assume that a product has left its initial position after 10 steps if it has
not come back at least one time to its initial position (or neighbourhood here). Finally,
we can estimate P1,0 to be
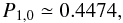 (A.17)giving a new intrinsic
probability of photo-desorption Pspd enhanced compared to the
initial value. Indeed, if we take into account that a new molecule that is not
photo-desorbed can be split by photo-dissociation, then the product can encounter for a
second time the reactant, giving it a second chance to photo-desorb, and so on. Thus, an
enhanced value of the spontaneous photo-desorption
(A.17)giving a new intrinsic
probability of photo-desorption Pspd enhanced compared to the
initial value. Indeed, if we take into account that a new molecule that is not
photo-desorbed can be split by photo-dissociation, then the product can encounter for a
second time the reactant, giving it a second chance to photo-desorb, and so on. Thus, an
enhanced value of the spontaneous photo-desorption 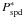 can be expressed as
can be expressed as
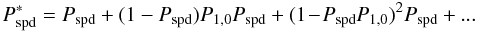 (A.18)
(A.18)![\appendix \setcounter{section}{1} \begin{eqnarray} = P_\mathrm{spd}\displaystyle\sum_{i=0}^{+\infty}\left[(1\!-\!P_\mathrm{spd})P_{1,0}\right]^i. \end{eqnarray}](/articles/aa/full_html/2010/14/aa14026-10/aa14026-10-eq135.png) (A.19)Since
last term is a geometric series that converges because
|(1−Pspd)P1,0| < 1, one
can simplify to
(A.19)Since
last term is a geometric series that converges because
|(1−Pspd)P1,0| < 1, one
can simplify to 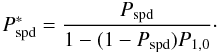 (A.20)In the case of water
formation with the reaction O+ H → OH and OH + H → H2O, the fraction of
water that desorbs upon formation is 5%. In the presence of a UV field, this value becomes
9.4%.
(A.20)In the case of water
formation with the reaction O+ H → OH and OH + H → H2O, the fraction of
water that desorbs upon formation is 5%. In the presence of a UV field, this value becomes
9.4%.
References
- Akai, Y., & Saito, S. 2003, Jpn. J. Appl. Phys., 42, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Albers, E., Hoyermann, K., Wagner, H., & Wolfrum, J. 1971, 13th Symp. Combust., The Combustion Institute, Pittsburgh [Google Scholar]
- Andersson, S., & van Dishoeck, E. F. 2008, A&A, 491, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersson, S., Al-Halabi, A., Kroes, G., & van Dishoeck, E. F. 2006, J. Chem. Phys., 124, 064715 [NASA ADS] [CrossRef] [Google Scholar]
- Bachellerie, D., Sizun, M., Teillet-Billy, D., Rougeau, N., & Sidis, V. 2007, Chem. Phys. Lett., 448, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, H., Rougeau, N., Sidis, V., et al. 2008, J. Phys. Chem. A, 112, 11921 [CrossRef] [PubMed] [Google Scholar]
- Bergin, E. A., Neufeld, D. A., & Melnick, G. J. 1998, ApJ, 499, 777 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bolina, A. S., Wolff, A., & Brown, W. A. 2005, J. Phys. Chem. B, 109, 16836 [CrossRef] [PubMed] [Google Scholar]
- Brown, W. A., & Bolina, A. S. 2007, MNRAS, 374, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Hasegawa, T. I., & Herbst, E. 1993, ApJ, 408, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., Caselli, P., Cobut, V., & Le Bourlot, J. 2008, A&A, 483, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, Q., Cuppen, H. M., & Herbst, E. 2005, A&A, 434, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2005, MNRAS, 361, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2007, ApJ, 668, 294 [Google Scholar]
- D’Hendecourt, L. B., Allamandola, L. J., & Greenberg, J. M. 1985, A&A, 152, 130 [NASA ADS] [Google Scholar]
- Fromherz, T., Mendoza, C., & Ruette, F. 1993, MNRAS, 263, 851 [NASA ADS] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghio, E., Mattera, L., Salvo, C., Tommasini, F., & Valbusa, U. 1980, J. Chem. Phys., 73, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1978, ApJ, 222, 881 [NASA ADS] [CrossRef] [Google Scholar]
- González, B. S., Hernández-Rojas, J., Bretón, J., & Gomez Llorente, J. M. 2007, J. Phys. Chem. C, 111, 14862 [CrossRef] [Google Scholar]
- Goumans, T. P. M., Richard, C., Catlow, A., et al. 2009, Phys. Chem. Chem. Phys., 11 [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Heine, T., Zhechkov, L., & Seifert, G. 2004, Phys. Chem. Chem. Phys., 6, 980 [CrossRef] [Google Scholar]
- Hollenbach, D. 1988, Astrophys. Lett. Commun. 26, 191 [Google Scholar]
- Hollenbach, D., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
- Hornekær, L., Rauls, E., Xu, W., et al. 2006, Phys. Rev. Lett. 97, 186102 [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
- Jelea, A., Marinelli, F., Ferro, Y., Allouche, A., & Brosset, C. 2004, Carbon, 42, 3189 [CrossRef] [Google Scholar]
- Jeloaica, L., & Sidis, V. 1999, Chem. Phys. Lett. 300, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., & Williams, D. A. 1984, MNRAS, 209, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., & Williams, D. A. 1985, MNRAS, 217, 413 [NASA ADS] [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kroes, G. J., & Andersson, S. 2005, in Astrochemistry: Recent Successes and Current Challenges, ed. D. C. Lis, G. A. Blake, & E. Herbst, IAU Symposium, 231, 427 [Google Scholar]
- Krug, J. 2004, [arXiv:cond-mat/0405066] [Google Scholar]
- Lee, G., Lee, B., Kim, J., & CHO, K. 2009, J. Phys. Chem. C, 113, 14225 [CrossRef] [Google Scholar]
- Lee, J. H., Michael, J. V., Payne, W. A., & Stief, L. J. 1978, J. Chem. Phys., 69, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. S., Zhang, R. Q., Lee, S. T., et al. 2005, J. Chem. Phys. B, 109, 14183 [Google Scholar]
- Manion, J. A., Huie, R. E., Levin, R. D., et al. 2008, NIST Chemical Kinetics Database, NIST Standard Reference Database 17, Version 7.0 (Web Version), Release 1.4.3, Data version 2008.12, National Institute of Standards and Technology, Gaithersburg, Maryland, 20899 8320. Web address: http://kinetics.nist.gov/ [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyauchi, N., Hidaka, H., Chigai, T., et al. 2008, Chem. Phys. Lett. 456, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Mokrane, H., Chaabouni, H., Accolla, M., et al. 2009, ApJ, 705, L195 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Lepp, S., & Melnick, G. J. 1995, ApJS, 100, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Oberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009, ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Papoular, R. 2005, MNRAS, 362, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Pirronello, V., Liu, C., Shen, L., & Vidali, G. 1997, ApJ, 475, L69+ [NASA ADS] [CrossRef] [Google Scholar]
- Robie, D. C., Arepalli, S., Presser, N., Kitsopoulos, T., & Gordon, R. 1987, J. Chem. Phys. Lett., 134 [Google Scholar]
- Rougeau, N., Teillet-Billy, D., & Sidis, V. 2006, Chem. Phys. Lett., 431, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Schiff, H. I. 1973, in Astrophysics and Space Science Library, Physics and Chemistry of Upper Atmospheres, ed. B. M. McCormac, 35, 85 [Google Scholar]
- Sha, X., & Jackson, B. 2002, Surface Science, 496, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [NASA ADS] [Google Scholar]
- Walch, S. P. and Rolfing, C. M., Melius, C. F., & Bauschlicher, C. W. 1988, J. Chem. Phys., 88, 6273 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Hough, J. H., & Shenoy, S. S. 2001, ApJ, 547, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. A., Hartquist, T. W., & Whittet, D. C. B. 1992, MNRAS, 258, 599 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Chemical species present on a grain surface of 10 K in monolayer (1 monolayer is a total coverage of the surface) as function of time (left panels). Fraction of newly formed oxygen-bearing molecules f(O) that are released into the gas phase in the form of other species (right panels). Top: temperature of the grain surface is set to 10 K. Bottom: temperature of the grain surface is set to 30 K. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 with a UV radiation field of G0 = 103. UV photons dissociate the chemical species present on the surface, which explains the small coverage of the grain surface (left panels). On the other hand, the amount of species released into the gas phase can be enhanced. |
| In the text | |
 |
Fig. 3 Chemical species present on dust grains and released into the gas phase in diffuse clouds. Left panel: chemical species present on a grain surface in monolayer (1 monolayer is a total coverage of the surface) as function of time. Right panel: fraction of newly formed oxygen-bearing molecules f(O) that are released into the gas phase in the form of other species. The error bars have been derived using 7 simulations and represent 95% confidence levels. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for translucent clouds. Note that no oxygen-bearing species are released into the gas phase. The error bars have been derived using 4 simulations and represent the 95% confidence level. |
| In the text | |
 |
Fig. 5 Same as Fig. 3 for dense clouds. The error bars have been derived using 5 simulations and represent the 95% confidence level. |
| In the text | |
 |
Fig. 6 Same as Fig. 3 for PDRs. The error bars have been derived using 7 simulations and represent the 95% confidence level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


