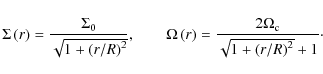| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | L56 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201015700 | |
| Published online | 19 October 2010 | |
LETTER TO THE EDITOR
Averting the magnetic braking catastrophe on small scales: disk formation due to Ohmic dissipation
W. B. Dapp and S. Basu
Department of Physics & Astronomy, The University of Western Ontario, 1151 Richmond St., London, ON, N6A 3K7, Canada
Received 6 September 2010 / Accepted 1 October 2010
Abstract
We perform axisymmetric resistive MHD calculations that demonstrate
that centrifugal disks can indeed form around Class 0 objects
despite magnetic braking. We follow the evolution of a prestellar core
all the way to near-stellar densities and stellar radii. Under
flux-freezing, the core is braked and disk formation is inhibited,
while Ohmic dissipation renders magnetic braking ineffective within the
first core. In agreement with observations that do not show evidence
for large disks around Class 0 objects, the resultant disk forms in
close proximity to the second core and has a radius of only ![]()
![]() early on. Disk formation does not require enhanced resistivity. We
speculate that the disks can grow to the sizes observed around Class II
stars over time under the influence of both Ohmic dissipation and
ambipolar diffusion, as well as internal angular momentum
redistribution.
early on. Disk formation does not require enhanced resistivity. We
speculate that the disks can grow to the sizes observed around Class II
stars over time under the influence of both Ohmic dissipation and
ambipolar diffusion, as well as internal angular momentum
redistribution.
Key words: magnetohydrodynamics (MHD) - protoplanetary disks - stars: formation - stars: magnetic field
1 Introduction
Understanding how protostellar and protoplanetary disks form is of
fundamental importance to theories of star- and planet formation.
Observations show their ubiquity around Class II objects (e.g., Andrews & Williams 2005). In recent years, doubt was cast on their accepted formation mechanism, when it was shown that for flux freezing magnetic braking is so effective in removing angular momentum from the parent core that large-scale (![]()
![]() )
disks are suppressed entirely (Hennebelle & Fromang 2008; Mellon & Li 2008; Allen et al. 2003). This scenario held true even when a simplified version of ambipolar diffusion (Mellon & Li 2009) was included in the model, and has been referred to as the magnetic braking catastrophe. Recently, Hennebelle & Ciardi (2009)
demonstrated that inclination effects can modify the efficiency of
magnetic braking, but a supercritical mass-to-flux ratio by a factor
>3-5 (i.e., a weak magnetic field) was still required to form a
large-scale disk. Duffin & Pudritz (2009)
performed three-dimensional simulations with ambipolar diffusion, but
only resolved the first core, and did not find Keplerian motion.
)
disks are suppressed entirely (Hennebelle & Fromang 2008; Mellon & Li 2008; Allen et al. 2003). This scenario held true even when a simplified version of ambipolar diffusion (Mellon & Li 2009) was included in the model, and has been referred to as the magnetic braking catastrophe. Recently, Hennebelle & Ciardi (2009)
demonstrated that inclination effects can modify the efficiency of
magnetic braking, but a supercritical mass-to-flux ratio by a factor
>3-5 (i.e., a weak magnetic field) was still required to form a
large-scale disk. Duffin & Pudritz (2009)
performed three-dimensional simulations with ambipolar diffusion, but
only resolved the first core, and did not find Keplerian motion.
Runaway collapse of a prestellar core can effectively trap the magnetic flux in the prestellar phase (e.g., Basu & Mouschovias 1994).
If the evolution continued to proceed under flux-freezing, a big
magnetic flux problem would remain, since the emerging star would hold
10 3-105 times more magnetic flux than observed in T Tauri stars. At densities ![]()
![]() ,
ambipolar diffusion causes flux leakage, while at even higher densities, matter decouples entirely from the magnetic field, and Ohmic dissipation becomes dominant (e.g., Nakano et al. 2002). Both effects are revitalized after the formation of a central star (Li & McKee 1996; Contopoulos et al. 1998). Recently, Krasnopolsky et al. (2010)
have shown that for an isothermal core without self-gravity, only an
``anomalous'' resistivity - a factor of 100 larger than the canonical
level - allows disks of size
,
ambipolar diffusion causes flux leakage, while at even higher densities, matter decouples entirely from the magnetic field, and Ohmic dissipation becomes dominant (e.g., Nakano et al. 2002). Both effects are revitalized after the formation of a central star (Li & McKee 1996; Contopoulos et al. 1998). Recently, Krasnopolsky et al. (2010)
have shown that for an isothermal core without self-gravity, only an
``anomalous'' resistivity - a factor of 100 larger than the canonical
level - allows disks of size
![]() to form during the Class 0 phase. However, their simulations are
dominated by numerical reconnection events that make precise statements
about the efficacy of magnetic braking difficult.
to form during the Class 0 phase. However, their simulations are
dominated by numerical reconnection events that make precise statements
about the efficacy of magnetic braking difficult.
Currently, there is no evidence for the presence of centrifugal disks larger than ![]()
![]() around Class 0 or Class I objects (e.g., Maury et al. 2010).
However, there are outflows observed even at these early ages. It is
therefore reasonable to assume that disks form at a small scale and
only subsequently grow to the larger sizes observed in the Class II
phase. We demonstrate the first part explicitly by using a canonical
level of Ohmic dissipation alone, and speculate that the combined
effects of ambipolar diffusion and Ohmic dissipation will allow for the
second part. Additionally, an initially small disk could expand
significantly if angular momentum transport is regulated by internal
processes (e.g., Vorobyov & Basu 2007; Basu 1998).
around Class 0 or Class I objects (e.g., Maury et al. 2010).
However, there are outflows observed even at these early ages. It is
therefore reasonable to assume that disks form at a small scale and
only subsequently grow to the larger sizes observed in the Class II
phase. We demonstrate the first part explicitly by using a canonical
level of Ohmic dissipation alone, and speculate that the combined
effects of ambipolar diffusion and Ohmic dissipation will allow for the
second part. Additionally, an initially small disk could expand
significantly if angular momentum transport is regulated by internal
processes (e.g., Vorobyov & Basu 2007; Basu 1998).
Machida et al. (2007) performed three-dimensional simulations of resistive MHD on a nested grid, following the evolution to stellar densities, but were only able to integrate until a few days after stellar core formation. We extend their calculations in a dimensionally-simplified model in order to simultaneously address the magnetic flux problem, integrate further in time, and study the formation of a centrifugal disk. We show that catastrophic magnetic braking can be avoided, and that a small disk forms in a very early phase of evolution.
2 Method
We solve the normalized MHD equations in axisymmetric thin-disk geometry (see Basu & Mouschovias 1994; Ciolek & Mouschovias 1993), assuming vertical hydrostatic equilibrium in a vertical one-zone approximation. An integral method for calculating the self-gravity of an infinitesimally-thin disk is used (detailed in Ciolek & Mouschovias 1993), with modifications for the finite extent and finite thickness of the flattened core.
In our model, the magnetic field points solely in the vertical
direction inside the disk, but also possesses radial and azimuthal
components (Br and ![]() )
at the disk surfaces and above. Br is determined from a potential field assuming force-free and current-free conditions in the external medium. We calculate
)
at the disk surfaces and above. Br is determined from a potential field assuming force-free and current-free conditions in the external medium. We calculate ![]() and implement magnetic braking using a steady-state approximation to
the transport of Alfvén waves in the external medium, as in Basu & Mouschovias (1994).
Owing to numerical complexity, a calibration of this method with
results of three-dimensional MHD wave propagation through a stratified
compressible medium has not been done to date. We modify the ideal-MHD
induction equation to include Ohmic dissipation:
and implement magnetic braking using a steady-state approximation to
the transport of Alfvén waves in the external medium, as in Basu & Mouschovias (1994).
Owing to numerical complexity, a calibration of this method with
results of three-dimensional MHD wave propagation through a stratified
compressible medium has not been done to date. We modify the ideal-MHD
induction equation to include Ohmic dissipation:
Here,
We use the parametrization of Machida et al. (2007) for the resistivity calculated by Nakano et al. (2002), with a dimensionless scaling parameter
![]() whose standard value is unity. The resistivity is then
whose standard value is unity. The resistivity is then
where n is the volume number density, and the term in square brackets is a cutoff representing the restoration of flux freezing at high densities. The uncertainties in
For simplicity, we replace the detailed energy equation by a barotropic relation. The temperature-density relation of Masunaga & Inutsuka (2000) is transformed into a pressure-density relation using the ideal gas law
![]() ,
where P is the pressure,
,
where P is the pressure,
![]() is Boltzmann's constant, and T
is the temperature. We calculate the midplane pressure
self-consistently, including the effects of the weight of the gas
column, constant external pressure (
is Boltzmann's constant, and T
is the temperature. We calculate the midplane pressure
self-consistently, including the effects of the weight of the gas
column, constant external pressure (
![]() ), magnetic pressure, and the extra squeezing added by a central star (once present).
), magnetic pressure, and the extra squeezing added by a central star (once present).
The MHD equations are solved with the method of lines (e.g., Schiesser 1991)
using a finite volume approach on an adaptive grid with up to 1024
radial cells in logarithmic spacing. The smallest cell is initially
![]() and as small as
and as small as
![]() at the highest refinement. We use the second-order van-Leer TVD advection scheme (van Leer 1977),
and calculate all derivatives to second-order accuracy on the
nonuniform grid. The code will be described in detail in a forthcoming
paper.
at the highest refinement. We use the second-order van-Leer TVD advection scheme (van Leer 1977),
and calculate all derivatives to second-order accuracy on the
nonuniform grid. The code will be described in detail in a forthcoming
paper.
3 Initial conditions and normalization
We assume that our initial state was reached by core contraction preferentially along magnetic field lines (e.g., Fiedler & Mouschovias 1993) and rotational flattening, and start with initial profiles for the column density and angular velocity given by
Here,
We assume an initial profile for
![]() in a way that the normalized mass-to-flux ratio
in a way that the normalized mass-to-flux ratio
![]() everywhere, which is the approximate starting point of runaway collapse (e.g., Basu & Mouschovias 1994).
The radial velocity is initially zero. The initial state is not far
from equilibrium, because the pressure gradient and magnetic and
centrifugal forces add up to
everywhere, which is the approximate starting point of runaway collapse (e.g., Basu & Mouschovias 1994).
The radial velocity is initially zero. The initial state is not far
from equilibrium, because the pressure gradient and magnetic and
centrifugal forces add up to ![]()
![]() of the gravitational force. Our results do not depend strongly on the
choice of initial state as long as gravity remains dominant.
of the gravitational force. Our results do not depend strongly on the
choice of initial state as long as gravity remains dominant.
The initial central column density and number density are
![]() and
and
![]() ,
respectively. The total mass and radius of the core are
,
respectively. The total mass and radius of the core are
![]() and
and
![]() ,
respectively. The initial central magnetic field strength is
,
respectively. The initial central magnetic field strength is
![]() .
We choose the external density in a way that
.
We choose the external density in a way that
![]() ,
(i.e.,
,
(i.e.,
![]() ), and the central angular velocity
), and the central angular velocity
![]() so that the cloud's edge rotates at a rate of
so that the cloud's edge rotates at a rate of
![]() ,
consistent with observations of molecular cloud cores (Caselli et al. 2002; Goodman et al. 1993).
,
consistent with observations of molecular cloud cores (Caselli et al. 2002; Goodman et al. 1993).
4 Results
4.1 Prestellar phase and formation of the second core
During the prestellar phase (for number densities
![]() )
the collapse proceeds in a nearly self-similar fashion. We find that -
insensitive to initial conditions - the column density is approximately
)
the collapse proceeds in a nearly self-similar fashion. We find that -
insensitive to initial conditions - the column density is approximately
![]() for three orders of magnitude of central enhancement, which corresponds to the volume density being
for three orders of magnitude of central enhancement, which corresponds to the volume density being
![]() for a central enhancement of
for a central enhancement of ![]() 106. This profile is characteristic of a collapsing prestellar core (e.g., Larson 1969).
The collapse proceeds dynamically, and to a good approximation under
isothermality, flux-freezing, and without significant magnetic braking (Basu & Mouschovias 1994).
106. This profile is characteristic of a collapsing prestellar core (e.g., Larson 1969).
The collapse proceeds dynamically, and to a good approximation under
isothermality, flux-freezing, and without significant magnetic braking (Basu & Mouschovias 1994).
Once the density reaches ![]()
![]() ,
the central region becomes opaque and traps the energy released by the
collapse, which previously could escape freely as radiation. This
region heats up (Masunaga & Inutsuka 2000; Larson 1969) and its thermal pressure gradient temporarily stabilizes it against further collapse. This is the first core. Its density and temperature increase with continued accretion, while its size stays almost constant at
,
the central region becomes opaque and traps the energy released by the
collapse, which previously could escape freely as radiation. This
region heats up (Masunaga & Inutsuka 2000; Larson 1969) and its thermal pressure gradient temporarily stabilizes it against further collapse. This is the first core. Its density and temperature increase with continued accretion, while its size stays almost constant at ![]() a few AU, bounded by an accretion shock. The external gravitational
potential of this object closely resembles that of a point mass, and an
expansion wave develops and moves outward at nearly the sound speed (Shu 1977). Material within this region moves at near free-fall speed.
a few AU, bounded by an accretion shock. The external gravitational
potential of this object closely resembles that of a point mass, and an
expansion wave develops and moves outward at nearly the sound speed (Shu 1977). Material within this region moves at near free-fall speed.
When the temperature in the first core reaches ![]()
![]() ,
for
,
for
![]() ,
hydrogen molecules are collisionally dissociated. This process provides
an energy sink, so that the temperature rise stagnates, and the
collapse reinitiates. As the temperature rises yet further, hydrogen is
ionized sufficiently that flux freezing is re-established. Collapse is
then finally halted, and sufficiently high densities are reached that
electron degeneracy becomes important (Masunaga & Inutsuka 2000). A protostellar core (the second core) forms with a radius
,
hydrogen molecules are collisionally dissociated. This process provides
an energy sink, so that the temperature rise stagnates, and the
collapse reinitiates. As the temperature rises yet further, hydrogen is
ionized sufficiently that flux freezing is re-established. Collapse is
then finally halted, and sufficiently high densities are reached that
electron degeneracy becomes important (Masunaga & Inutsuka 2000). A protostellar core (the second core) forms with a radius ![]() a few
a few ![]() (e.g., Larson 1969). This Class 0 object initially only has a mass of a few
(e.g., Larson 1969). This Class 0 object initially only has a mass of a few
![]() .
The gravitational potential resembles that of a point mass outside the
second core, and an expansion wave once again moves outward from the
accretion shock, eventually consuming the entire region of the previous
first core.
.
The gravitational potential resembles that of a point mass outside the
second core, and an expansion wave once again moves outward from the
accretion shock, eventually consuming the entire region of the previous
first core.
Figure 1 shows the profiles of column density, mass-to-flux ratio and angular velocity shortly after the second core forms (![]()
![]() into the simulation). For
into the simulation). For
![]() ,
Ohmic dissipation becomes dynamically important (Nakano et al. 2002),
because all charge carriers decouple from the magnetic field, and flux
is dissipated. While the density in the first core increases, we find
the magnetic field strength remains stagnant. A magnetic wall (Li & McKee 1996; Contopoulos et al. 1998) forms at
,
Ohmic dissipation becomes dynamically important (Nakano et al. 2002),
because all charge carriers decouple from the magnetic field, and flux
is dissipated. While the density in the first core increases, we find
the magnetic field strength remains stagnant. A magnetic wall (Li & McKee 1996; Contopoulos et al. 1998) forms at ![]()
![]() ,
visible as a sharp transition in column density in the resistive model (
,
visible as a sharp transition in column density in the resistive model (
![]() ,
top panel). Here, infalling neutrals within the expansion wave are
temporarily slowed down by the relatively well-coupled magnetic field
that is expelled from the first core with a radius
,
top panel). Here, infalling neutrals within the expansion wave are
temporarily slowed down by the relatively well-coupled magnetic field
that is expelled from the first core with a radius ![]()
![]() .
Further inward, the neutrals resume near-free-fall motion, but with
enhanced magnetic support and at a greater column density than for
flux-freezing (
.
Further inward, the neutrals resume near-free-fall motion, but with
enhanced magnetic support and at a greater column density than for
flux-freezing (
![]() ,
dotted line). Under angular momentum conservation (no magnetic
braking), the additional rotational support stabilizes the first core
against further collapse (top panel, dash-dotted line), consistent with
previous findings (e.g., Saigo & Tomisaka 2006).
,
dotted line). Under angular momentum conservation (no magnetic
braking), the additional rotational support stabilizes the first core
against further collapse (top panel, dash-dotted line), consistent with
previous findings (e.g., Saigo & Tomisaka 2006).
Because of magnetic flux dissipation, the mass-to-flux ratio increases
by almost three orders of magnitude in the first core region for
![]() ,
but by almost two orders of magnitude even for
,
but by almost two orders of magnitude even for
![]() as low as 0.01 (Fig. 1, middle panel). The torque on the cloud caused by magnetic braking scales linearly with the amount of enclosed flux (Basu & Mouschovias 1994).
Ohmic dissipation therefore allows spin-up to proceed, even though the
rotation rate is still reduced by a factor of a few outside the first
core, compared with the case without magnetic braking (Fig. 1,
bottom panel, dash-dotted line). In the flux-freezing case, the
comparatively slow evolution of the first core allows enough time for
magnetic braking to spin down the first core region, and
``catastrophically'' brake it (Fig. 1, bottom panel, dotted line).
as low as 0.01 (Fig. 1, middle panel). The torque on the cloud caused by magnetic braking scales linearly with the amount of enclosed flux (Basu & Mouschovias 1994).
Ohmic dissipation therefore allows spin-up to proceed, even though the
rotation rate is still reduced by a factor of a few outside the first
core, compared with the case without magnetic braking (Fig. 1,
bottom panel, dash-dotted line). In the flux-freezing case, the
comparatively slow evolution of the first core allows enough time for
magnetic braking to spin down the first core region, and
``catastrophically'' brake it (Fig. 1, bottom panel, dotted line).
4.2 Evolution after second core formation
When the second core forms, the thin-disk formulation breaks down,
because the object is now truly hydrostatic and spherical. Presumably,
dynamo processes within the fully convective protostar will also take
over, and the magnetic field will mostly decouple from that of its
parent core (Mestel & Landstreet 2005). Therefore, we switch off magnetic braking in the second core, and introduce a sink cell with a size of
![]() ,
slightly larger than the second core. The processes within it are
beyond the scope of our model, but are not expected to significantly
influence the surroundings. This is not necessarily the case with a
sink cell of size
,
slightly larger than the second core. The processes within it are
beyond the scope of our model, but are not expected to significantly
influence the surroundings. This is not necessarily the case with a
sink cell of size ![]()
![]() ,
as is the more common approach (e.g., Vorobyov & Basu 2007; Mellon & Li 2008,2009).
,
as is the more common approach (e.g., Vorobyov & Basu 2007; Mellon & Li 2008,2009).
Figure 2
shows the profiles of column density, infall velocity, and the ratio of
centrifugal to gravitational acceleration about a year after the
introduction of the sink cell. Centrifugal balance is achieved in a
small region (![]()
![]() )
close to the center (bottom panel) in the resistive model. This is a
necessary and sufficient condition for the formation of a
centrifugally-supported disk. At the same time all infall is halted
there and the radial velocity plummets (middle panel). After a few
years of evolution, a Toomre instability develops, and the
rotationally-supported structure breaks up into a ring (top panel). At
this point, we stop the simulation, because more physics would be
required to follow the further evolution of the disk. Our model allows
a clear distinction between a magnetic pseudo-disk, a flattened
(disk-like) prestellar core, and a centrifugal (nearly Keplerian) disk.
This distinction is not clear in profiles from three-dimensional
simulations (Machida et al. 2007; Duffin & Pudritz 2009).
)
close to the center (bottom panel) in the resistive model. This is a
necessary and sufficient condition for the formation of a
centrifugally-supported disk. At the same time all infall is halted
there and the radial velocity plummets (middle panel). After a few
years of evolution, a Toomre instability develops, and the
rotationally-supported structure breaks up into a ring (top panel). At
this point, we stop the simulation, because more physics would be
required to follow the further evolution of the disk. Our model allows
a clear distinction between a magnetic pseudo-disk, a flattened
(disk-like) prestellar core, and a centrifugal (nearly Keplerian) disk.
This distinction is not clear in profiles from three-dimensional
simulations (Machida et al. 2007; Duffin & Pudritz 2009).
![\begin{figure}
\par\includegraphics[width=9cm]{15700fig1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15700-10/Timg63.png)
|
Figure 1:
Spatial profiles of various quantities after the second collapse (after |
| Open with DEXTER | |
Figure 3 shows the magnetic field line topology above and below the disk on two scales (
![]() and
and
![]() ),
for both flux-freezing and resistive models. They are calculated
immediately after the formation of the second core, assuming force-free
and current-free conditions above a thin disk (Mestel & Ray 1985). The split monopole of the
),
for both flux-freezing and resistive models. They are calculated
immediately after the formation of the second core, assuming force-free
and current-free conditions above a thin disk (Mestel & Ray 1985). The split monopole of the
![]() model (dashed lines) is created as field lines are dragged in by the freely falling material within the expansion wave front at
model (dashed lines) is created as field lines are dragged in by the freely falling material within the expansion wave front at ![]()
![]() .
This is replaced by a much more relaxed field line structure in the
resistive case (solid lines). The extreme flaring of field lines in the
.
This is replaced by a much more relaxed field line structure in the
resistive case (solid lines). The extreme flaring of field lines in the
![]() model is a fundamental cause of the magnetic braking catastrophe. Galli et al. (2009) presented similar field configurations resulting from a simplified model for resistive collapse.
model is a fundamental cause of the magnetic braking catastrophe. Galli et al. (2009) presented similar field configurations resulting from a simplified model for resistive collapse.
![\begin{figure}
\par\includegraphics[width=8.5cm]{15700fig2.eps} \vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/13/aa15700-10/Timg67.png)
|
Figure 2:
Spatial profiles of various quantities |
| Open with DEXTER | |
| Figure 3:
Magnetic field lines. The box on the left has dimensions
|
|
| Open with DEXTER | |
5 Discussion and conclusions
We demonstrate the formation of a centrifugally-supported disk despite
the presence of magnetic braking. The magnetic braking catastrophe is
averted by including the canonical level of Ohmic dissipation, which
removes large amounts of magnetic flux from the high-density region of
the first core. In the absence of Ohmic dissipation, this region would
be spun down tremendously prior to the second collapse. We emphasize
that disk formation happens very shortly after the second collapse in a
region very close to the central object, while it is still very small
(<
![]() ). This is consistent with the observational evidence of outflows at a very young age.
). This is consistent with the observational evidence of outflows at a very young age.
Our simulations yield ![]()
![]() magnetic fields, comparable to those observed in T Tauri stars (e.g., Johns-Krull 2007), ina central object of mass
magnetic fields, comparable to those observed in T Tauri stars (e.g., Johns-Krull 2007), ina central object of mass ![]()
![]() .
This is achieved by non-ideal MHD effects reducing the field strength by
.
This is achieved by non-ideal MHD effects reducing the field strength by ![]() 103
compared to a flux-freezing model. Our model does not have the
capability of including outflows or jets, even though those are
launched very close to the stellar surface.
103
compared to a flux-freezing model. Our model does not have the
capability of including outflows or jets, even though those are
launched very close to the stellar surface.
There is presently no evidence for centrifugal disks ![]()
![]() around Class 0 objects (e.g., Maury et al. 2010; André et al. 2002). ALMA will allow observers to improve on this, and to probe for disks down to
around Class 0 objects (e.g., Maury et al. 2010; André et al. 2002). ALMA will allow observers to improve on this, and to probe for disks down to ![]()
![]() .
We anticipate that the centrifugal disk that forms in our simulations can grow over time into disks of size
.
We anticipate that the centrifugal disk that forms in our simulations can grow over time into disks of size ![]()
![]() observed around Class II objects. Recent work (Machida et al. 2010)
shows that magnetic braking can be cut off at late times as the
envelope is accreted, and the existing disk can also grow by internal
angular momentum redistribution processes (e.g., Vorobyov & Basu 2007). Furthermore, we speculate that ambipolar diffusion (e.g., Kunz & Mouschovias 2010)
has the potential to dissipate enough flux outside the first core (an
area not significantly affected by Ohmic dissipation) to reduce braking
and to allow the disk to form there as well. We will present results of
a study including both non-ideal MHD effects and grain physics in an
upcoming paper.
observed around Class II objects. Recent work (Machida et al. 2010)
shows that magnetic braking can be cut off at late times as the
envelope is accreted, and the existing disk can also grow by internal
angular momentum redistribution processes (e.g., Vorobyov & Basu 2007). Furthermore, we speculate that ambipolar diffusion (e.g., Kunz & Mouschovias 2010)
has the potential to dissipate enough flux outside the first core (an
area not significantly affected by Ohmic dissipation) to reduce braking
and to allow the disk to form there as well. We will present results of
a study including both non-ideal MHD effects and grain physics in an
upcoming paper.
The authors thank the participants of the CC2YSO conference for engaging and illuminating discussions. W.B.D. was supported by an NSERC Alexander Graham Bell Canada Graduate Scholarship, and S.B. by an NSERC Discovery Grant.
References
- André, P., Bouwman, J., Belloche, A., & Hennebelle, P. 2002, Ap&SS, 292, 325 [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, A., Li, Z.-Y., & Shu, F. H. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S. 1997, ApJ, 485, 240 [CrossRef] [Google Scholar]
- Basu, S. 1998, ApJ, 509, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Mouschovias, T. Ch. 1994, ApJ, 432, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., & Mouschovias, T. Ch. 1993, ApJ, 418, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., Ciolek, G. E., & Königl, A. 1998, ApJ, 504, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Dapp, W. B., & Basu, S. 2009, MNRAS, 395, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Duffin, D. F., & Pudritz, R. E. 2009, ApJ, 706, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Fiedler, R. A., & Mouschovias, T. Ch. 1993, ApJ, 415, 640 [NASA ADS] [Google Scholar]
- Galli, D., Cai, M., Lizano, S., & Shu, F. H. 2009, RevMexAA, 36, 143 [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Ciardi, A. 2009, A&A, 506, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johns-Krull, C. M. 2007, ApJ, 664, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, R., Li, Z.-Y., & Shang, H. 2010, ApJ, 716, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Mouschovias, T. Ch. 2010, MNRAS, 408, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1977, JCP, 23, 276 [NASA ADS] [Google Scholar]
- Li, Z.-Y., & McKee, C. F. 1996, ApJ, 464, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-i., & Matsumoto, T. 2007, ApJ, 670, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-I., & Matsumoto, T. 2010, PASJ, submitted [arXiv:1009.2140v1] [Google Scholar]
- Masunaga, H., & Inutsuka, S.-i. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Hennebelle, P., et al. 2010, A&A, 512, 40 [Google Scholar]
- Mellon, R. R., & Li, Z.-Y. 2008, ApJ, 681, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Mellon, R. R., & Li, Z.-Y. 2009, ApJ, 698, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L., & Ray, T. P. 1985, MNRAS, 212, 275 [NASA ADS] [Google Scholar]
- Mestel, L., & Landstreet, J. D. 2005, in Lecture Notes in Physics, Cosmic Magnetic Fields, ed. R. Wielebinski, & R. Beck, 664, 183 [Google Scholar]
- Nakano, T., Nishi, R., & Umebayashi, T. 2002, ApJ, 573, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Saigo, K., & Tomisaka, K. 2006, ApJ, 645, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Schiesser, W. E. 1991, The Numerical Method of Lines: Method of Integration of Partial Differential Equations (San Diego: Academic) [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2007, MNRAS, 381, 1009 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{15700fig1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15700-10/Timg63.png)
|
Figure 1:
Spatial profiles of various quantities after the second collapse (after |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{15700fig2.eps} \vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/13/aa15700-10/Timg67.png)
|
Figure 2:
Spatial profiles of various quantities |
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
Magnetic field lines. The box on the left has dimensions
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



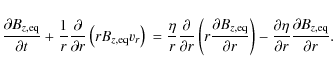
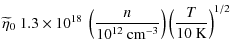
![$\displaystyle \hspace*{2.5cm}\times~\left[1-\tanh \left( \frac{n}{10^{15}~{\rm cm}^{-3}}\right)\right] ~{\rm cm}^{2}~{\rm s}^{-1},$](/articles/aa/full_html/2010/13/aa15700-10/img26.png)