EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) L60 Full HTML
Highlight
Free Access
Issue
A&A
Volume 521, October 2010
Article Number L60
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201015472
Published online 21 October 2010
A&A 521, L60 (2010)

LETTER TO THE EDITOR

Two planets orbiting the recently formed post-common envelope binary NN Serpentis[*]

K. Beuermann1 - F. V. Hessman1 - S. Dreizler1 - T. R. Marsh2 - S. G. Parsons2 - D. E. Winget3 - G. F. Miller3 - M. R. Schreiber4 - W. Kley5 - V. S. Dhillon6 - S. P. Littlefair 6 - C. M. Copperwheat2 - J. J. Hermes3

1 - Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
2 - Department of Physics, University of Warwick, Coventry, CV4 7AL, UK
3 - Dept. of Astronomy, University of Texas at Austin, RLM 16.236, Austin, TX 78712, USA
4 - Departamento de Fisica y Astronomia, Universidad de Valparaiso, Av. Gran Bretana 1111, Valparaiso, Chile
5 - Institut für Astronomie & Astrophysik, Universität Tübingen, Morgenstelle 10, 72076 Tübingen, Germany
6 - Department of Physics & Astronomy, University of Sheffield, S3 7RH, UK

Received 26 July 2010 / Accepted 6 October 2010

Abstract
Planets orbiting post-common envelope binaries provide fundamental information on planet formation and evolution. We searched for such planets in NN Ser ab, an eclipsing short-period binary that shows long-term eclipse time variations. Using published, reanalysed, and new mid-eclipse times of NN Ser ab obtained between 1988 and 2010, we find excellent agreement with the light-travel-time effect produced by two additional bodies superposed on the linear ephemeris of the binary. Our multi-parameter fits accompanied by N-body simulations yield a best fit for the objects NN Ser (ab)c and d locked in the 2:1 mean motion resonance, with orbital periods $P_{\rm c} \simeq 15.5$ yrs and $P_{\rm d} \simeq 7.7$ yrs, masses $M_{\rm c}~ {\rm sin}~ i_{\rm c} \simeq 6.9$  $M_{\rm Jup}$ and $M_{\rm d}~ {\rm sin}~ i_{\rm d} \simeq 2.2$  $M_{\rm Jup}$, and eccentricities $e_{\rm c} \simeq 0$ and $e_{\rm d} \simeq 0.20$. A secondary $\chi^2$ minimum corresponds to an alternative solution with a period ratio of 5:2. We estimate that the progenitor binary consisted of an A star with $\sim$$2~M_\odot$ and the present M dwarf secondary at an orbital separation of $\sim$1.5 AU. The survival of two planets through the common-envelope phase that created the present white dwarf requires fine tuning between the gravitational force and the drag force experienced by them in the expanding envelope. The alternative is a second-generation origin in a circumbinary disk created at the end of this phase. In that case, the planets would be extremely young with ages not exceeding the cooling age of the white dwarf of 106 yrs.

Key words: binaries: eclipsing - planetary systems - stars: individual: NN Ser - novae - cataclysmic variables -
planets and satellites: formation - stars: evolution

1 Introduction

NN Ser ab[*] is a short-period ( $P_{\rm orb} = 3.12$ h) eclipsing binary at a distance of 500 pc. The detached system contains a hot hydrogen-rich white dwarf NN Ser a of spectral type DAO1 and an M4 dwarf star NN Ser b with masses of 0.535 $M_\odot$ and 0.111 $M_\odot$, respectively (Parsons et al. 2010a). With an effective temperature of 57 000 K (Haefner et al. 2004), the white dwarf has a cooling age of only 106 yrs (Wood 1995). The present system resulted from a normal binary with a period of $\sim$1 year when the more massive component evolved to a giant and engulfed the orbit of its companion. The subsequent common envelope (CE) phase led to the expulsion of the envelope, laying bare the newly born white dwarf and substantially shortening the orbital period.

Some eclipsing post-CE binaries display long-term eclipse time variations, among them V471 Tau (Kaminski et al. 2007), QS Vir and NN Ser (Parsons et al. 2010b, and references therein). The latter possesses deep and well-defined eclipses, which allow measurements of the mid-eclipse times to an accuracy of 100 ms and better (Brinkworth et al. 2006; Parsons et al. 2010b). The processes advanced to explain them include the long-term angular momentum loss by gravitational radiation and magnetic braking, possible quasi-periodicities caused, e.g., by Applegate's (1992) mechanism, and the strict periodicities produced by apsidal motion or the presence of a third body in the system. Finding the correct interpretation requires measurements of high precision and a coordinated effort over a wide range of time scales. The existence of a third body orbiting NN Ser ab was previously considered by Qian et al. (2009), but the orbital parameters suggested by them are incompatible with more recent data (Parsons et al. 2010b). In this Letter, we present an analysis of the eclipse time variations of NN Ser ab, based on published data, the reanalysis of published data, and new measurements obtained over the first half of 2010.

2 The data

After their 1988 discovery of deep eclipses in NN Ser, Haefner et al. (2004) acquired a series of accurate mid-eclipse times in 1989. After a hiatus of ten years, they added a potentially very accurate trailed CCD imaging observation using the ESO VLT. From 2002 on, the Warwick group systematically secured a total of 22 mid-eclipse times of high precision (Brinkworth et al. 2006; Parsons et al. 2010b, this work). Parsons et al. (2010b) list all published mid-eclipse times by other authors until the end of 2009. These are included in our analysis that weights them by their statistical errors. Since the individual Warwick mid-eclipse times between 2002 and 2009 were separated by about one year, information on eclipse time variations on a shorter time scale is lacking. We, therefore, organized a collaborative effort of the Göttingen, McDonald, and Warwick groups to monitor NN Ser over the first half of 2010. We used the remotely controlled MONET/North 1.2-m telescope at McDonald Observatory via the MONET internet remote-observing interface, the McDonald 2.1-m telescope, and the ESO 3.5-m NTT. The MONET data were taken in white light, the McDonald data with a BG40 filter, and the NTT observations were acquired with the ULTRACAM high-speed CCD camera equipped with Sloan filters. The mid-eclipse times measured in Sloan u', g', and i' are consistent, and we used the g' data as the most accurate set for the present purpose. Table 1 lists the new mid-eclipse times shifted to the solar system barycenter and corrected for leap seconds. The table also gives the 1-$\sigma$ statistical errors and the residuals relative to our final fit shown in Fig. 2 and discussed in Sect. 4, below.

Table 1:   Revised and new eclipse times of NN Ser ab with residuals for the light-travel-time effect produced by the two planets of Model 2a1.

The mid-eclipse time derived by Haefner et al. (2004) from the trailed VLT image of 11 June 1999[*] is the most variant of the published eclipse time measurements and was assigned a large error of 17 s, although this should be a very precise measurement, given the very simple form of the eclipses in NN Ser and the use of an 8.2 m telescope. We reanalysed the image of 11 June 1999, which started 04:53:05.537 UT with an exposure of 1125.7462 s and was taken in good atmospheric conditions. The key issue is the conversion of the track from pixel space to time. Using two independent methods, we found that the original analysis by Haefner et al. (2004) was in error and that the mid-eclipse time can be determined with an accuracy of 0.20 s (Table 1, cycle E = 30721). We also reanalysed the less accurate data of Pigulski & Michalska (2002) (cycle E =33233) by including the effects of the finite integration times.

3 The light-travel-time effect in NN Ser

\begin{figure} \par\includegraphics[bb=165 59 540 699,height=88mm,angle=-90,clip... ...55 540 699,height=88mm,angle=-90,clip]{15472f1c.ps} \vspace{-2.9mm} \end{figure} Figure 1:

Top: observed - calculated mid eclipse time differences relative to the best-fit linear ephemeris for Model 1 of a single planet orbiting NN Ser ab. Center and bottom: residuals relative to the eccentric-orbit fit for two selected time intervals.

Open with DEXTER

\begin{figure} \par\includegraphics[bb=165 59 540 699,height=88mm,angle=-90,clip... ...55 540 699,height=88mm,angle=-90,clip]{15472f2c.ps} \vspace{-2.9mm} \end{figure} Figure 2:

Same as Fig. 1 for Model 2a of two planets orbiting NN Ser ab. The contributions of components b and c are indicated by the dashed and dot-dashed curves, respectively, the solid curve shows the combined effect.

Open with DEXTER

All measurements of mid-eclipse times of NN Ser ab are displayed in Figs. 1 and 2 as O-C values relative to the model-dependent linear ephemerides of the respective fits. Data points with errors <1 s and >1 s are shown as green and yellow dots, respectively. The eclipse time measurements dominating the fit are the 1989 data points of Haefner et al. (2004) near the abscissa value JD' = JD-2 450 000 = -2295, the reevaluated VLT point on JD' = 1340, the 2002-2009 series of Warwick eclipse times since JD' = 2411 (Parsons et al. 2010b), and the data of this work since JD' = 5212. In particular, the revised VLT mid-eclipse time implies a twofold change in the time derivative of O-C and excludes the simple quadratic ephemerides used by Brinkworth et al. (2006) and Parsons et al. (2010b). The available data do not exclude abrupt period changes or an ultimate aperiodicity, but there is no physical process that predicts such behavior. We consider a periodic behavior the most promising assumption and proceed to explore this possibility.

Strictly periodic O-C variations may result from apsidal motion of the binary orbit or an additional body orbiting the binary. Given the parameters of NN Ser ab, classical apsidal motion for small eccentricities $e_{\rm bin}$ produces a sinusoidally varying time shift with an amplitude $P_{\rm bin}e_{\rm bin}/\pi = 3577 e_{\rm bin}$ s (Todoran 1972). As a result, $e_{\rm bin} \sim 0.01$ would suffice to produce the observed amplitude. However, the likewise predicted variation of the FWHM of the eclipse and the time shift of the secondary eclipse are not observed (Parsons et al. 2010b, this work). Furthermore, the observed variation is not sinusoidal and, given an apsidal motion constant for the secondary star NN Ser b of $k_{22}\simeq0.11$, the period of the apsidal motion would be as short as $\sim$0.4 years. Such periodicity is not detected (see Fig. 2, bottom panel).

This leaves us with the third-body hypothesis, at least for the major fraction of the observed eclipse time variations. In general, it would be possible that different physical processes combine to produce the observed signal. We find, however, that a perfect fit within the very small statistical errors can be obtained for a signal that consists of the periodicities produced by two objects orbiting NN Ser ab. Guided by Ockham's razor and the history of discoveries in the Solar system, we consider that a fourth body in the presence of a third one is a natural assumption.

4 One-planet and two-planet fits to the data

Including the light-travel-time effect of the objects NN Ser (ab)c and NN Ser (ab)d, the times of mid-eclipse become

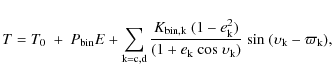
\begin{displaymath}T=T_0~+~P_{\rm bin}E + \sum_{\rm k=c,d} \frac{K_{\rm bin,k}~(... ...upsilon_{\rm k})}~{\rm sin}~(\upsilon_{\rm k}-\varpi_{\rm k}), \end{displaymath} (1)

where time is measured from a fiducial mid-eclipse time T0. A linear binary ephemeris is assumed with $P_{\rm bin}$ the orbital period and E the cycle number. The five free parameters for planet k are the orbital period $P_{\rm k}$, the eccentricity $e_{\rm k}$, the longitude of periastron $\varpi_{\rm bin,k}$measured from the ascending node in the plane of the sky, the time $T_{\rm k}$ of periastron passage, and the amplitude of the eclipse time variation $K_{\rm k} = a_{\rm bin,k}$ sin $i_{\rm k}$/c, with $a_{\rm bin,k}$ the semi-major axis of the orbit of the center of mass of the binary about the common center of mass of the system, $i_{\rm k}$ the inclination, and c the speed of light. In the denominator, $\upsilon_{\rm k}$ is the true anomaly, which progresses through 2$\pi$ over the orbital period $P_{\rm k}$.

We explored the multi-dimensional $\chi^2$ space of the two-planet model, using the Levenberg-Marquardt routine implemented in IDL and an independent code. The search showed that compensation effects render some parameters ill defined. This uncertainty results, in particular, from the long hiatus between the accurate measurements of 1989 (Haefner et al. 2004) and 1999 (VLT, this work). We selected the best model, therefore, by imposing the additional requirement that the derived orbits be secularly stable. We investigated all solutions permitted by the data with numerical N-body simulations with a variable time step Runge-Kutta integrator, following the orbits over 105 yrs, and find that only a narrow range in parameter space corresponds to stable solutions. In what follows, we consider the one-planet and the two-planet models in turn.

Model 1 with seven free parameters describes a single planet with eccentricity e. The fit requires $e \ga 0.60$ and is bad for any value of e, with a reduced $\chi^2_\nu \ge 23.3$(  $\chi^2 = 1052$ for 45 degrees of freedom). The top panel of Fig. 1 shows the case e = 0.65. The residuals based on the statistical errors of the data points (center panel) reach 23 standard deviations and indicate that there is an additional modulation at about half the orbital period. The residuals of the 2010 data (bottom panel) demonstrate the lack of O-C fluctuations on a short time scale.

Model 2 for two planets requires some restriction in parameters, because the grid search yields good fits for a range of eccentricities of the outer planet $e_{\rm c}$, including zero, and for a period ratio $r_{\rm p} = P_{\rm c}/P_{\rm d} = 1.90\pm0.30$ or $r_{\rm p} = 2.50\pm0.15$ (1-$\sigma$ errors), with the former slightly preferred. The dichotomy in $r_{\rm p}$ arises from the uncertain phasing of the singular 1989 point relative to the train of the 1999-2010 data. Further minima at still larger $r_{\rm p}$ do not exist. Only a small fraction of the parameter space allowed by the fits corresponds to secularly stable orbits, however. Near $r_{\rm p} \simeq 2$, orbits with $e_{\rm c} > 0.1$ tend to be unstable, while the stability region is broad in the remaining parameters for $e_{\rm c} \approx 0.02$. Furthermore, all solutions with $r_{\rm p} \la 1.9$ are unstable, with only some solutions stable at $r_{\rm p} = 1.9$. The solutions near $r_{\rm p} = 2.5$ are more generally stable. We consider Models 2a and 2b, representing the cases of $r_{\rm p} \simeq 2.0$ and 2.5, respectively, both with $e_{\rm c} \equiv 0$. Model 2a provides the slightly better fit and is shown in Fig. 2. It yields $K_{\rm c} = 27.4$ s, $K_{\rm d} = 5.7$ s, $P_{\rm c} = 15.5$ yrs, $P_{\rm d} = 7.75$ yrs, and $e_{\rm d} = 0.20$ with $\chi^2_\nu=0.78~(~\chi^2 = 32.9$ for 42 d.o.f.). Periastron passage of NN Ser (ab)d occurred last on JD $' \simeq 4515$. At that time NN Ser (ab)c was at longitude $213^\circ$. For the low value of $e_{\rm c} = 0.03$, a shallow minimum of $\chi^2$ is attained for aligned apses. From the present data, we cannot infer the true value of $r_{\rm p}$ with certainty, but it is intriguing that objects c and d may be locked in either the 2:1 resonance, found also in other planetary systems, or the 5:2 resonance. The parameters for Models 2a and 2b are listed in Table 2, together with their 1-$\sigma$ errors. A simpler model with two circular orbits reaches only $\chi^2_\nu=1.96~( \chi^2 = 86.2$ for 44 d.o.f.) at $r_{\rm p} = 2.46$ and can be excluded.

Table 2:   Parameters of the models fitted to the measured mid-eclipse time variations of NN Ser, where $\equiv $ indicates a fixed parameter.

Using Model 2a as input to our N-body simulations, we find that $e_{\rm c}$ and $e_{\rm d}$ oscillate around 0.02 and 0.22 with amplitudes of 0.02 and 0.05, respectively. The difference $\Delta \varpi$ of the periastron longitudes circulates on a time scale of 400 yrs. The periods perform small-amplitude anti-phased oscillations, which cause $r_{\rm p}$ to oscillate between 1.9 and 2.2. Even if the two planets are secularly locked in the 2:1 mean motion resonance, therefore, the observed period ratio at any given time may deviate slightly from its nominal value.

For Model 2a, the best-fit binary ephemeris is T = BJED 2 447 344.524425(40) + 0.1300801419(10) E, where the errors refer to the last digits. Adding a quadratic term BE2 to the ephemeris does not improve the two-planet fit and yields a 1-$\sigma$ limit of $\mid B \mid < 1.5 \times 10^{-13}$ days, leaving room for a period change by gravitational radiation or a long-term activity-related effect (Brinkworth et al. 2006; Parsons et al. 2010b).

5 Discussion

The large amplitude of the O-C eclipse time variations in NN Ser can only be explained by a third body in the system, while the still substantial residuals from a single-planet fit could, in principle, have a different origin from that of a fourth body. The two-planet model, however, possesses the beauty of simplicity, and the fact that the residuals for the entire data set vanish simultaneously imposes tight restrictions on any other mechanism. In particular, the lack of short-term variability of the residuals in the first half of 2010 argues against any process that acts on a short time scale or leads to erratic eclipse time variations. Hence, there is strong evidence for two planets orbiting NN Ser ab.

With masses $M_{\rm c}~{\rm sin}~i_{\rm c} \simeq 6$  $M_{\rm Jup}$ and $M_{\rm d}~{\rm sin}~i_{\rm d} \simeq 2$  $M_{\rm Jup}$, NN Ser (ab)c and NN Ser (ab)d both qualify as giant planets for all inclinations $i_{\rm ~c}>$ 28$^\circ$ and $i_{\rm ~d}> 9^\circ$, respectively. The probable detection of resonant motion with a period ratio of either 2:1 or 5:2 is a major bonus, which adds to the credence of the two-planet model. It is the second planetary system found by eclipse timing, after HW Vir (Lee et al. 2009).

Given a pair of planets orbiting a post-CE binary, two formation scenarios are possible. They could either be old first-generation planets that formed in a circumbinary protoplanetary disk or they could be young second-generation planets formed $\la$106 yrs ago in a disk that resulted from the CE (Perets 2010). To evaluate both scenarios, we have reconstructed the CE evolution of NN Ser ab using the improved algorithm by Zorotovic et al. (2010), who constrain the CE efficiency to a range $\alpha \simeq 0.2{-}0.3$. Possible solutions for the progenitor binary of NN Ser ab are not very sensitive to $\alpha$: for $\alpha=0.25$, the progenitor was a giant of 2.08 $M_\odot$ and radius 194 $R_\odot$ with the present secondary star at a separation of 1.44 AU. When the CE engulfed the secondary star, dynamic friction caused the latter to spiral in rapidly, thereby dramatically decreasing the binary separation to the current 0.0043 AU. Stability arguments imply that any planet from the pre-CE phase must have formed with semi-major axes exceeding 3.5 AU (Holman & Wiegert 1999). With three quarters of the central mass expelled in the CE event, pre-existing planets would move outward or may even be lost from the system. However, given a sufficiently dense and slowly expanding CE, the dynamical force experienced by them may have ultimately moved them inward (Alexander et al. 1976). Since the dragprimarily affects the more massive and more slowly moving outer planet, such a scenario could lead to resonant orbits, so a first-generation origin appears possible.

The alternative post-CE origin in a second-generation of planet formation is also possible, since the formation of circumbinary disks is a common phenomenon among post-AGB binary stars and the concentration of a slow, dusty wind to the orbital plane of the binary is thought to favor the formation of planets (e.g. Perets 2010; van Winckel et al. 2009). In particular the tiny separation of the present binary poses no problem for stable orbits of second-generation planets even at significantly shorter distances than the inner planet that we have detected (Holman & Wiegert 1999). A particularly intriguing aspect of a second-generation origin of the planets in NN Ser would be their extreme youth, equal to or less than the 106 yrs cooling age of the white dwarf (Wood 1995). This feature would distinguish them from all known exoplanets and may ultimately lead to their direct detection. While we cannot presently prove a second-generation origin for these planets, modeling the CE event may allow us to distinguish between the two scenarios.

Acknowledgements
We would like to thank Dr. Reinhold Haefner for information concerning the original VLT observations and analyses and Dr. Andrzej Pigulski for sending us his original photometry. This work is based on data obtained with the MONET telescopes funded by the ``Astronomie & Internet'' program of the Alfried Krupp von Bohlen und Halbach Foundation, Essen, on observations with the ESO NTT under ESO programme 085.D-0541, and on data obtained from the ESO/ST-ECF Science Archive Facility. T.R.M., V.S.D., C.M.C., and S.P.L. acknowledge grant support from the UK's STFC. M.R.S. acknowledges support from FONDECYT under grant number 1061199 (MRS) and the Centre of Astrophysics Valparaíso. D.E.W. acknowledges the support of the Norman Hackerman Advanced Research Program under grant 003658-0255-2007.


References

  1. Alexander, M. E., Chau, W. Y., & Henriksen, R. N. 1976, ApJ, 204, 879 [NASA ADS] [CrossRef] [Google Scholar]
  2. Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brinkworth, C. S., Marsh, T., Dhillon, V. S., & Knigge, C. 2006, MNRAS, 365,287 [NASA ADS] [CrossRef] [Google Scholar]
  4. Haefner, R., Fiedler, A., Butler, K., & Barwig, H. 2004, A&A, 428, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] [Google Scholar]
  6. Kaminski, K. Z., Rucinski, S. M., Matthews, J. M., et al. 2007, AJ, 134, 1206 [NASA ADS] [CrossRef] [Google Scholar]
  7. Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
  8. Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010a, MNRAS, 402, 2591 [NASA ADS] [CrossRef] [Google Scholar]
  9. Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010b, MNRAS, 407, 2362 [NASA ADS] [CrossRef] [Google Scholar]
  10. Perets, H. B. 2010, ApJ, submitted [arXiv:1001.0581] [Google Scholar]
  11. Pigulski, A., & Michalska, G. 2002, IBVS, 5218, 1 [NASA ADS] [Google Scholar]
  12. Qian, S.-B., Dai, Z.-B., Liao, W.-P., et al. 2009, ApJ, 706, L96 [NASA ADS] [CrossRef] [Google Scholar]
  13. Todoran, I. 1972, Ap&SS, 15, 229 [NASA ADS] [CrossRef] [Google Scholar]
  14. van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Wood, J. H., & Marsh, T. R. 1991, ApJ, 381, 561 [Google Scholar]
  16. Wood, M. A. 1995, in White Dwarfs, ed. D. Koester, & K. Werner (Heidelberg: Springer), LNP No. 443, 41 [Google Scholar]
  17. Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, 86 [Google Scholar]

Online Material

Table 3:   Previously published, reanalysed, and new mid-eclipse times of the white dwarf in NN Ser with residuals for the light-travel-time effect produced by the two planets of Model 2a.

Footnotes

... Serpentis[*]
Table 3 is only available in electronic form at http://www.aanda.org
...NN Ser ab[*]
On recommendation by the Editor of A&A, we refer to the system as NN Ser, to the binary explicitly as NN Ser ab, and to the objects orbiting the binary as NN Ser (ab)c and NN Ser (ab)d.
... 1999[*]
http://www.eso.org/public/images/eso9936b/

All Tables

Table 1:   Revised and new eclipse times of NN Ser ab with residuals for the light-travel-time effect produced by the two planets of Model 2a1.

Table 2:   Parameters of the models fitted to the measured mid-eclipse time variations of NN Ser, where $\equiv $ indicates a fixed parameter.

Table 3:   Previously published, reanalysed, and new mid-eclipse times of the white dwarf in NN Ser with residuals for the light-travel-time effect produced by the two planets of Model 2a.

All Figures

  \begin{figure} \par\includegraphics[bb=165 59 540 699,height=88mm,angle=-90,clip... ...55 540 699,height=88mm,angle=-90,clip]{15472f1c.ps} \vspace{-2.9mm} \end{figure} Figure 1:

Top: observed - calculated mid eclipse time differences relative to the best-fit linear ephemeris for Model 1 of a single planet orbiting NN Ser ab. Center and bottom: residuals relative to the eccentric-orbit fit for two selected time intervals.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=165 59 540 699,height=88mm,angle=-90,clip... ...55 540 699,height=88mm,angle=-90,clip]{15472f2c.ps} \vspace{-2.9mm} \end{figure} Figure 2:

Same as Fig. 1 for Model 2a of two planets orbiting NN Ser ab. The contributions of components b and c are indicated by the dashed and dot-dashed curves, respectively, the solid curve shows the combined effect.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.