| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015293 | |
| Published online | 22 October 2010 | |
The nature of long-GRB host galaxies from chemical abundances
X. L. Fan1,2 - J. Yin3,1 - F. Matteucci1,2
1 - Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
2 - INAF Osservatorio Astronomico di
Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
3 - Key Laboratory for Research in Galaxies and Cosmology,
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
Received 29 June 2010 / Accepted 23 July 2010
Abstract
Context. Gamma-ray bursts (GRBs) were the most energetic
events after the Big Bang and they have been observed up to very high
redshift. Measurements of the chemical abundances are now available for
the galaxies hosting such events, which are assumed to originate from
the explosion of very powerful supernovae (Type Ib/c), and provide the
opportunity to study the nature of these host galaxies.
Aims. We identify the hosts of long GRBs (LGRBs) observed at
both low and high redshift to determine whether the hosts are galaxies
of the same type at different cosmic epochs.
Methods. We adopt detailed chemical evolution models for
galaxies of different morphological type (ellipticals, spirals,
irregulars) that follow the time evolution of the abundances of several
chemical elements (H, He, ![]() -elements, Fe), and compare the results with the observed abundances and abundance ratios in galaxies hosting LGRBs.
-elements, Fe), and compare the results with the observed abundances and abundance ratios in galaxies hosting LGRBs.
Results. We find that the abundances and abundance ratios
predicted by models devised for typical irregular galaxies can
reproduce the abundances of the hosts at both high and low redshift. We
also find that the predicted Type Ib/c supernova rate for irregulars is
in good agreement with observations. Models for spirals and
particularly ellipticals fit neither the high-redshift hosts of LGRBs
(DLA systems) nor the low redshift hosts: in particular, ellipticals
cannot possibly be the hosts of gamma-ray bursts at low redshift since
they exhibit little star formation, hence no supernovae Ib/c.
Conclusions. We conclude that the observed abundance and
abundance ratios in LGRBs hosts suggest that these hosts are irregular
galaxies at both high and low redshift, thus demonstrating that the
host galaxies are the same type of galaxies observed at different ages.
Key words: galaxies: high-redshift - Galaxy: abundances - galaxies: ISM - gamma rays: galaxies - gamma rays: ISM
1 Introduction
Gamma-ray bursts (GRBs) were the most energetic events after the Big Bang. They can be detected back to the onset of reionization (e.g., Tanvir et al. 2009; Salvaterra et al. 2009; Greiner et al. 2009) due to their brightness in the first few hours after the explosion (Lamb & Reichart 2000). Long GRBs (LGRBs) (Different systems are selected by different methods from high to low redshift. Two kinds of LGRB associated systems are selected: LGRB host galaxies at low redshift and LGRB-associated damped Lyman-alpha systems (LGRB-DLAs) at high redshift. LGRB host galaxies have been studied by several authors using observational data (e.g. Castro Cerón et al. 2010; Levesque et al. 2010a; Michaowski et al. 2008; Chary et al. 2007; Savaglio et al. 2009; Wolf & Podsiadlowski 2007, among others) and simulations (e.g. Lapi et al. 2008; Chisari et al. 2010; Calura et al. 2009; Mao 2010; Nuza et al. 2007; Campisi et al. 2009, among others). All these results find that at low redshift (z<2), the typical hosts of LGRB are small, star-forming, low-metallicity irregular galaxies.
At high redshift (z >2), as for QSO-DLA systems (
![]() cm-2), the LGRB-DLAs are observed (e.g. Prochaska et al. 2007a; Fynbo et al. 2009; Jakobsson et al. 2006).
The nature of DLAs remains a matter of debate. The DLAs in QSO spectra
are assumed to form in the ISM of galaxies located in front of the QSO.
The high luminosity of the QSOs usually makes it difficult detect the
DLA galaxies directly. The hypothesis that these DLAs are the
progenitors of present disk galaxies (Naab & Ostriker 2006; Wolfe et al. 1986) is challenged by the low metallicity (
cm-2), the LGRB-DLAs are observed (e.g. Prochaska et al. 2007a; Fynbo et al. 2009; Jakobsson et al. 2006).
The nature of DLAs remains a matter of debate. The DLAs in QSO spectra
are assumed to form in the ISM of galaxies located in front of the QSO.
The high luminosity of the QSOs usually makes it difficult detect the
DLA galaxies directly. The hypothesis that these DLAs are the
progenitors of present disk galaxies (Naab & Ostriker 2006; Wolfe et al. 1986) is challenged by the low metallicity (![]()
![]() )
of DLAs
and the flat age-metallicity relation of disk stars (the disk is rapidly enriched to
)
of DLAs
and the flat age-metallicity relation of disk stars (the disk is rapidly enriched to ![]()
![]() )
(Pettini 2006; Akerman et al. 2004). Using detailed chemical evolution models, Calura et al. (2009,2003)
investigated the nature of DLAs and suggested that the majority of
them, including the LGRB-DLAs, may be either spiral disks observed at
large galactocentric distances, irregular galaxies such as the LMC, or
starburst dwarf irregulars observed at different times after the last
burst of star formation. On the other hand, massive elliptical galaxies
are unlikely to be DLA systems even at very high redshift owing to
their intensive quick enrichment, which produces high [
)
(Pettini 2006; Akerman et al. 2004). Using detailed chemical evolution models, Calura et al. (2009,2003)
investigated the nature of DLAs and suggested that the majority of
them, including the LGRB-DLAs, may be either spiral disks observed at
large galactocentric distances, irregular galaxies such as the LMC, or
starburst dwarf irregulars observed at different times after the last
burst of star formation. On the other hand, massive elliptical galaxies
are unlikely to be DLA systems even at very high redshift owing to
their intensive quick enrichment, which produces high [![]() /Fe]
ratios, that is inconsistent with the data observed for DLAs. However,
among the identified high redshift DLA host galaxies, one DLA host
galaxy is a luminous Lyman-break galaxy (DLA 2206-19A, Møller et al. 2002). By comparing the luminosity functions of DLAs and LBGs, Wolfe (2005) concluded that there is a significant overlap between the DLA and LBG populations. Fynbo et al. (2008)
compared the metallicity distributions of LGRB-DLAs and LBGs. Their
results support the hypothesis that LGRB-DLAs could arise from a
population of LBGs that are not heavily obscured. LBGs are understood
to be small young star-forming ellipticals (Matteucci & Pipino 2002; Pipino et al. 2010). Additionally, Zwaan et al. (2005) showed that in the local universe the luminosity distribution of galaxies producing DLAs is nearly flat from
/Fe]
ratios, that is inconsistent with the data observed for DLAs. However,
among the identified high redshift DLA host galaxies, one DLA host
galaxy is a luminous Lyman-break galaxy (DLA 2206-19A, Møller et al. 2002). By comparing the luminosity functions of DLAs and LBGs, Wolfe (2005) concluded that there is a significant overlap between the DLA and LBG populations. Fynbo et al. (2008)
compared the metallicity distributions of LGRB-DLAs and LBGs. Their
results support the hypothesis that LGRB-DLAs could arise from a
population of LBGs that are not heavily obscured. LBGs are understood
to be small young star-forming ellipticals (Matteucci & Pipino 2002; Pipino et al. 2010). Additionally, Zwaan et al. (2005) showed that in the local universe the luminosity distribution of galaxies producing DLAs is nearly flat from
![]() to
to
![]() ,
which implies that the DLA host galaxies should belong to a complex
population (a single type population could not span such a wide
luminosity range).
it is normally unknown in which region of the galaxy the line of sight
from the QSO and LGRBs intersect the ISM of the galaxy. Prochaska et al. (2007b)
argued that LGRB-DLAs preferentially probes denser, more depleted,
higher metallicity gas located in the inner few kpc of the ISM compared
to QSO-DLAs. This idea is supported by the distribution of H I column densities for GRB absorbers produced using a high resolution simulation of galaxy formation (Pontzen et al. 2010). In principle, it should be possible for high-redshift LGRB-DLAs to be
a phase of low-mass star-forming ellipticals, which is what we test in this paper.
,
which implies that the DLA host galaxies should belong to a complex
population (a single type population could not span such a wide
luminosity range).
it is normally unknown in which region of the galaxy the line of sight
from the QSO and LGRBs intersect the ISM of the galaxy. Prochaska et al. (2007b)
argued that LGRB-DLAs preferentially probes denser, more depleted,
higher metallicity gas located in the inner few kpc of the ISM compared
to QSO-DLAs. This idea is supported by the distribution of H I column densities for GRB absorbers produced using a high resolution simulation of galaxy formation (Pontzen et al. 2010). In principle, it should be possible for high-redshift LGRB-DLAs to be
a phase of low-mass star-forming ellipticals, which is what we test in this paper.
In this article, we use the most recently observed abundances of the LGRB-associated systems, LGRB-DLAs at high redshift and LGRB host galaxies at low redshift, to try to determine: i) which galaxies are the hosts of LGRBs? ii) whether the LGRB-associated systems represent an evolutionary sequence, i.e., whether the same objects at low and high redshift are just seen at different phases of their evolution? To do this, we adopt updated chemical evolution models for galaxies of different morphological type that reproduce the properties of galaxies (Pipino et al. (2010) for ellipticals, Yin et al. (2010b) for irregulars and spirals), and compare our predicted chemical abundances with the observed ones.
The paper is organized as follows: in Sect. 2, we describe our galaxy formation scenario; in Sect. 3 we summarize the observational constraints; our results and discussions are presented in Sect. 4; and our summary and conclusions are drawn in Sect. 5. Throughout the paper, we adopt a (0.7, 0.3, 0.7) cosmology.
2 Galaxy formation scenario
We now summarize our adopted galaxy formation models for galaxies of different morphological type. We direct the reader to Pipino et al. (2010) (ellipticals) and Yin et al. (2010b) (irregular and spirals) for equations and related details. Galaxies of different morphological type have different star formation histories (Matteucci 2001). Different star formation histories produce different abundance ratios, particularly in terms of [2.1 Ellipticals
The elliptical galaxies are assumed to evolve following an instantaneous mixing of gas but not according to the instantaneous recycling approximation, i.e., we take into account stellar lifetimes. The model we adopt is similar to that described in Pipino et al. (2010) except that we do not consider the dust production and evolution since here we compare our results only with extinction-corrected data (Levesque et al. 2010a; Savaglio 2006; Savaglio et al. 2009), assuming that their dereddenings are reliable (but see Li et al. 2008). The initial conditions for ellipticals allow formation by either collapse of a gas cloud into the potential well of a dark matter halo or, more realistically, the merging of several gas clouds. In any case, the timescale for both processes,2.2 Spirals and irregulars
Spirals and irregulars are galaxies harboring either recent or active star formation activity. At variance with elliptical galaxies, a slow and continuous star formation regime is assumed in spirals and irregulars. In the irregular galaxies, the efficiency of star formation is assumed to be lower than in spirals, an assumption that has been proven to be correct.Following the work of Yin et al. (2010b,a),
we build a one-zone model for irregulars,
and assume that the galaxy is built up by continuous infall of
primordial
gas until a given mass is accumulated. For the spiral disks, we develop
the same model as for irregulars but with higher star formation
efficiency (SFE) and higher luminous mass. As
suggested by Calura & Matteucci (2006), the
main properties of local galaxies of different morphological type
could be reproduced mainly by decreasing the star formation efficiency from early to late
types. Therefore, we assume for spirals and irregulars a continuous SFR with SFE lower than the one used for ellipticals (![]() 3-22 Gyr-1), e.g.
3-22 Gyr-1), e.g.
![]() 1 Gyr-1 for spirals and
1 Gyr-1 for spirals and ![]() 0.1-0.05 Gyr-1 for irregulars.
The irregulars are assumed to assemble by infall of gas on a relatively short timescale (
0.1-0.05 Gyr-1 for irregulars.
The irregulars are assumed to assemble by infall of gas on a relatively short timescale (
![]() Gyr) and the infall mass is assumed to be
Gyr) and the infall mass is assumed to be
![]() for all models, whereas the spiral disks are proposed to form by means of a slower accreting process (
for all models, whereas the spiral disks are proposed to form by means of a slower accreting process (
![]() Gyr) and the total infall mass is
Gyr) and the total infall mass is
![]() .
Galactic winds triggered by SNe are also considered in the same way as
for ellipticals. According to the different SFE in each model, and
consequently different SN feedback, the galactic wind develops at
different times in different models, which then end up with different
final stellar masses.
.
Galactic winds triggered by SNe are also considered in the same way as
for ellipticals. According to the different SFE in each model, and
consequently different SN feedback, the galactic wind develops at
different times in different models, which then end up with different
final stellar masses.
Therefore, the main difference between models for galaxies of different morphological type in is the efficiency star formation, which is higher in more massive, early-type objects, and consequently whether a galactic wind occurs and when.
3 LGRB data
The high-redshift LGRB-DLA data are inferred from the rest-frame ultraviolet (UV) absorption lines. On the other hand, low-redshift LGRB host-galaxy data are measured using the rest-frame optical emission lines of H II regions. The absorption lines in the UV and emission lines in the optical band have little overlap in terms of wavelength, making the detection of LGRB-DLAs and LGRB host galaxies for the same target particularly hard. In this section, we briefly summarize the observations used in this paper.3.1 Low redshift case: LGRB host galaxies
The properties of GRB host galaxies were studied by Savaglio et al. (2009) using the largest sample studied to date (40 LGRBs in total 46 GRBs). Owing to the limitation of measurements, 893.1.1 Morphology
The typical morphology of LGRB host galaxies remains unclear. The
typical observed hosts of LGRB are small, star-forming, low-metallicity
galaxies. But since there is no reason for LGRBs to assume any
particular galactic morphology, they should be, in principle, observed
in galaxies of all morphological types.
However, by comparing the most faint observed star-forming LGRB host
galaxies
and the rapid evolution of elliptical galaxies, we can deduce that any
elliptical hosting a low-redshift (![]() )
LGRBs should be small (
)
LGRBs should be small (![]()
![]() )
and in its very early phase of formation.
This formation scenario is consistent with the model of Pipino et al. (2010), where we suggested that the QSO hosts
(
)
and in its very early phase of formation.
This formation scenario is consistent with the model of Pipino et al. (2010), where we suggested that the QSO hosts
(![]()
![]() )
formed at
)
formed at ![]() and the LBGs (
and the LBGs (![]()
![]() )
formed at
)
formed at ![]() implying that at higher redshift (z>1) one could observe more
massive LGRB host elliptical galaxies. If this scenario were correct, we would observe
a mass-redshift relation for LGRB hosts.
implying that at higher redshift (z>1) one could observe more
massive LGRB host elliptical galaxies. If this scenario were correct, we would observe
a mass-redshift relation for LGRB hosts.
3.1.2 Star formation rates
The SFRs are inferred from either the rest-frame UV (3.1.3 Stellar mass
The stellar mass can be estimated from observed multi-band optical- near-infrared (NIR) photometry by performing spectral energy distribution (SED) fittingTable 1: Model predictions at 13 Gyr.
3.1.4 Metallicity
The metallicity (expressed as log(O/H)+12) was inferred from extinction-corrected emission-line fluxes using R23, O3N2-metallicity relation, and auroral [O III] ![]() 4363 diagnostics by Savaglio et al. (2009) and Levesque et al. (2010a). The majority of the measured oxygen abundances are subsolar.
However, two super-solar host galaxies are reported (Graham et al. 2009; Levesque et al. 2010b).
Those super-solar metallicities challenge the assumption of a low
metallicity threshold for LGRB progenitors. As we later show, their
hosts may be described by our spiral/irregular model with
4363 diagnostics by Savaglio et al. (2009) and Levesque et al. (2010a). The majority of the measured oxygen abundances are subsolar.
However, two super-solar host galaxies are reported (Graham et al. 2009; Levesque et al. 2010b).
Those super-solar metallicities challenge the assumption of a low
metallicity threshold for LGRB progenitors. As we later show, their
hosts may be described by our spiral/irregular model with
![]() (see Fig. 2). In this case, the hosts may be the disks of spirals.
(see Fig. 2). In this case, the hosts may be the disks of spirals.
3.2 High redshift case: LGRB-DLAs
The high-redshift GRB-DLA data are measured by the rest-frame UV absorption lines detected in the optical afterglow spectra. Using the rest-frame UV absorption-line column densities, one measures the cold gas-phase (In the literature (e.g. Savaglio 2006),
by adopting one reliable element abundance tracer and available
dust-depletion corrections, the metallicity is generally given by that
particular element abundance.
Since the elements are produced by different stars with different
lifetimes, the metallicity estimated by those elements cannot represent
the true metallicity (which is normally estimated by [O/H]). Measuring
LGRB-DLA metallicity is a challenge at z<1.6, since the Ly![]() absorption line is in the UV. Rau et al. (2010) presented an extremely metal-poor LGRB-DLA system (
absorption line is in the UV. Rau et al. (2010) presented an extremely metal-poor LGRB-DLA system (
![]() ).
They measured several chemical abundances and suggested that the
apparent conflict between the high [Si/Fe] and low [O/Fe] ratios found
in this object is caused by the underestimate of the O column density.
).
They measured several chemical abundances and suggested that the
apparent conflict between the high [Si/Fe] and low [O/Fe] ratios found
in this object is caused by the underestimate of the O column density.
4 Results and discussion
The nature of DLAs remains unclear, but many authors have suggested
that their chemical properties and star-formation histories can be
reproduced by models of irregular galaxies that slowly evolve due to a
mild SFR (Bradamante et al. 1998; Yin et al. 2010b; Romano et al. 2006).
Typical elliptical galaxies are instead very unlikely to host the DLAs
observed at high redshift primarily because ellipticals form rapidly
(in less than 1.5 Gyr, see Pipino et al. 2010; Pipino & Matteucci 2004)
consuming and then losing any residual gas so quickly that additional
star formation is inhibited. Therefore, to observe an elliptical when
it is still forming stars, one should observe it at very high redshift,
higher than the typical redshift of DLAs. Moreover, if the DLAs
represent an early phase of galaxy formation, regardless of their
morphological type, we should observe DLAs with different properties
(e.g. different [![]() /Fe] versus [Fe/H] relations), which reflect the different morphological galaxy evolution history, and this is not the case.
/Fe] versus [Fe/H] relations), which reflect the different morphological galaxy evolution history, and this is not the case.
To verify what has been stated above, we computed chemical evolution models for galaxies of different morphological type.
In Table 1,
we summarize some model results: in the first column we present the
model identification, in the second column the total infall mass, in
the third column the assumed SFE, in the fourth column the predicted
present-time gas mass, in the fifth column the predicted present-time
stellar mass, and in the sixth column the predicted present-time
(13.7 Gyr) SFR expressed in ![]() yr-1. Models from 1 to 4 refer to dwarf irregulars and all assume an infall mass of
yr-1. Models from 1 to 4 refer to dwarf irregulars and all assume an infall mass of
![]() ,
whereas model 5 refers to an infall mass of
,
whereas model 5 refers to an infall mass of
![]() and the disk of a spiral. Model 6 represents a small elliptical with infall mass
and the disk of a spiral. Model 6 represents a small elliptical with infall mass ![]()
![]() and model 7 a massive elliptical with infall mass of
and model 7 a massive elliptical with infall mass of
![]() .
We note that the predicted SFRs for dwarf irregulars agree with the lowest values
estimated by Savaglio et al. (2009),
while the SFR for the spiral disk agrees with the highest observed
values, and the gas masses agree with the values measured for dwarf
irregulars. No star formation occurs in the elliptical model after the
galactic wind (occurring before 1.5 Gyr since the beginning of
star formation), which implies that ellipticals cannot be the observed
nearby (z<1) host galaxies of LGRBs, unless they just formed.
On the other hand, the outermost regions of galactic disks could be
associated with DLAs simply because their chemical and gaseous
properties resemble those of irregular galaxies, as shown in previous
works.
.
We note that the predicted SFRs for dwarf irregulars agree with the lowest values
estimated by Savaglio et al. (2009),
while the SFR for the spiral disk agrees with the highest observed
values, and the gas masses agree with the values measured for dwarf
irregulars. No star formation occurs in the elliptical model after the
galactic wind (occurring before 1.5 Gyr since the beginning of
star formation), which implies that ellipticals cannot be the observed
nearby (z<1) host galaxies of LGRBs, unless they just formed.
On the other hand, the outermost regions of galactic disks could be
associated with DLAs simply because their chemical and gaseous
properties resemble those of irregular galaxies, as shown in previous
works.
4.1 Metallicity-redshift relation for LGRB-associated systems
![\begin{figure}
\par\includegraphics[width=3in]{15293fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg43.png)
|
Figure 1:
12+log(X/H) as a function of redshift. Predicted lines are from the irregular galaxy model with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg44.png)
|
Figure 2:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg45.png)
|
Figure 3:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg46.png)
|
Figure 4:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg47.png)
|
Figure 5:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for the spiral galaxy model with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg48.png)
|
Figure 6:
[Si/Fe] as function of [Fe/H] of LGRB-DLA systems. The predictions are
our from chemical evolution models of elliptical galaxies with
|
| Open with DEXTER | |
In Fig. 5, we show again the log(X/H)+12 versus redshift plot predicted by a model with
![]() but an infall mass of
but an infall mass of
![]() that should represent the disk of a spiral galaxy such as the Milky Way
(model 5). In this model, we also assumed that the gas accreted
more slowly than dwarf irregulars. Detailed chemical evolution models
for the Milky Way (e.g. Chiappini et al. 1997; Hou et al. 2000; Yin et al. 2009; Boissier & Prantzos 1999; Chiappini et al. 2001)
predict that the Milky Way disk formed in several Gyrs and inside-out.
Here, we present a simplified one-zone model for a galactic disk that
predicts average abundances, which helps to verify the behavior of the
age-metallicity relation of a more massive galaxy with a higher SFE
than typical irregulars. Figure 5 shows that this model, as happens for the model with infall mass
that should represent the disk of a spiral galaxy such as the Milky Way
(model 5). In this model, we also assumed that the gas accreted
more slowly than dwarf irregulars. Detailed chemical evolution models
for the Milky Way (e.g. Chiappini et al. 1997; Hou et al. 2000; Yin et al. 2009; Boissier & Prantzos 1999; Chiappini et al. 2001)
predict that the Milky Way disk formed in several Gyrs and inside-out.
Here, we present a simplified one-zone model for a galactic disk that
predicts average abundances, which helps to verify the behavior of the
age-metallicity relation of a more massive galaxy with a higher SFE
than typical irregulars. Figure 5 shows that this model, as happens for the model with infall mass
![]() and SFE typical of a spiral disk (model 1), cannot fit any of the
LGRB hosts and therefore should be rejected. We note that we assumed a
common redshift of galaxy formation for all the models (
and SFE typical of a spiral disk (model 1), cannot fit any of the
LGRB hosts and therefore should be rejected. We note that we assumed a
common redshift of galaxy formation for all the models (
![]() )
irrespective of the galaxy morphological type because old stars are in
general found in every galaxy. If galaxies formed later, clearly they
can not be the hosts of high-redshift LGRBs. However, irregulars may be
the hosts of low-redshift LGRBs if they formed at redshift z=1, although in this case a slightly lower SFE would be required.
)
irrespective of the galaxy morphological type because old stars are in
general found in every galaxy. If galaxies formed later, clearly they
can not be the hosts of high-redshift LGRBs. However, irregulars may be
the hosts of low-redshift LGRBs if they formed at redshift z=1, although in this case a slightly lower SFE would be required.
![\begin{figure}
\par\includegraphics[width=3in]{15293fg7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg54.png)
|
Figure 7:
[S/Fe] as function of [Fe/H] of LGRB-DLA systems. The predictions are
from chemical evolution models for the elliptical galaxies with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg55.png)
|
Figure 8: Predicted [Fe/H] versus galactic age for two irregular and two elliptical models, as indicated in the figure. The horizontal lines mark [Fe/H]=-1.0 and [Fe/H]=-3.0. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg56.png)
|
Figure 9:
Predicted SNIb/c rate evolution as a function of galactic age for
irregulars and ellipticals. The predictions are from our chemical
evolution model of a elliptical galaxy assuming the star formation
efficiency
|
| Open with DEXTER | |
4.2 Abundance ratios
The abundance ratios of chemical elements, which have different timescales of production (such as ![]() -elements and Fe), can be used as useful criterion to study the star formation history in galaxies (see Matteucci 2001).
In Figs. 6 and 7, we compare the [Si/Fe] and [S/Fe] ratios predicted by irregular and elliptical models with the available data for LGRB-DLAs.
The data are derived from Savaglio (2006) and Rau et al. (2010).
Although the error bars in the data are very large, the results imply
that most of the data
cannot be well fitted by the predictions of elliptical models. They are
instead reproduced by the predictions of irregular models with a
-elements and Fe), can be used as useful criterion to study the star formation history in galaxies (see Matteucci 2001).
In Figs. 6 and 7, we compare the [Si/Fe] and [S/Fe] ratios predicted by irregular and elliptical models with the available data for LGRB-DLAs.
The data are derived from Savaglio (2006) and Rau et al. (2010).
Although the error bars in the data are very large, the results imply
that most of the data
cannot be well fitted by the predictions of elliptical models. They are
instead reproduced by the predictions of irregular models with a
![]() Gyr-1, thus confirming the results shown in Figs 1-4.
However, more accurate data are necessary in the future to confirm this result.
Gyr-1, thus confirming the results shown in Figs 1-4.
However, more accurate data are necessary in the future to confirm this result.
In the case both of Si and S, because of the large error bars in the
observational data, the predictions
of the elliptical models are marginally acceptable.
In general, our predictions indicate that ellipticals, when forming
stars (a passive evolutionary phase is of no interest because is
without star formation and SNe Ib/c are connected to star formation
since they originate in massive stars), have higher [![]() /Fe] ratios than spirals and irregulars and that their evolution is much shorter. Hence, if one measure were to the [
/Fe] ratios than spirals and irregulars and that their evolution is much shorter. Hence, if one measure were to the [![]() /Fe]
ratios of the gas in star-forming ellipticals at high redshift, one
should find super-solar values. However, ellipticals are predicted to
remain in a phase where their gas has a metallicity [Fe/H] in common
with those of DLAs (between -2.0 and -3.0) for a very short
time interval (<0.1 Gyr), as shown in Fig. 8.
Therefore, it is very difficult to observe these galaxies in this short
time interval, another reason for excluding even small ellipticals from
being DLA systems.
If the DLAs did represent a particular evolutionary phase of a galaxy,
regardless of morphological type,
we should then observe DLAs with a wide range of properties (e.g. [
/Fe]
ratios of the gas in star-forming ellipticals at high redshift, one
should find super-solar values. However, ellipticals are predicted to
remain in a phase where their gas has a metallicity [Fe/H] in common
with those of DLAs (between -2.0 and -3.0) for a very short
time interval (<0.1 Gyr), as shown in Fig. 8.
Therefore, it is very difficult to observe these galaxies in this short
time interval, another reason for excluding even small ellipticals from
being DLA systems.
If the DLAs did represent a particular evolutionary phase of a galaxy,
regardless of morphological type,
we should then observe DLAs with a wide range of properties (e.g. [![]() /Fe]), which reflecting the different
star formation histories of galaxies of morphological type.
/Fe]), which reflecting the different
star formation histories of galaxies of morphological type.
Since LGRBs are associated with SNe Ib/c, we also computed these rates
for different galaxies, and compared the predicted present-time
SN Ib/c rate with the observed one, as shown in Fig. 9. To compute this rate, we assumed that the progenitors of these SNe are either Wolf-Rayet stars with
![]() or massive binary systems in the mass range
or massive binary systems in the mass range
![]() ,
as described in detail in Bissaldi et al. (2007). For the observational SN Ib/c rate,
we assumed the value of the SN Ib/c rate per unit mass provided by Mannucci et al. (2005) for irregular galaxies, which is
0.54 +0.66-0.38 SNe (100 yr)
,
as described in detail in Bissaldi et al. (2007). For the observational SN Ib/c rate,
we assumed the value of the SN Ib/c rate per unit mass provided by Mannucci et al. (2005) for irregular galaxies, which is
0.54 +0.66-0.38 SNe (100 yr)
![]() .
We then multiplied
this value by the predicted present-time stellar mass in each model (Table 1).
The results show that our irregular models predict SN Ib/c rates in reasonable agreement with observations.
In addition, the observed GRB redshift distribution peaks around z=1 (Fig. 1 in Savaglio et al. 2009) in reasonable agreement with our predicted peak of SN Ib/c rate (at z=1 corresponding to a galactic age
.
We then multiplied
this value by the predicted present-time stellar mass in each model (Table 1).
The results show that our irregular models predict SN Ib/c rates in reasonable agreement with observations.
In addition, the observed GRB redshift distribution peaks around z=1 (Fig. 1 in Savaglio et al. 2009) in reasonable agreement with our predicted peak of SN Ib/c rate (at z=1 corresponding to a galactic age ![]() 5 Gyr, see Fig. 9). The sharp break in the SN Ib/c rate for ellipticals and irregulars with
5 Gyr, see Fig. 9). The sharp break in the SN Ib/c rate for ellipticals and irregulars with
![]() occurs because at that time the galactic wind develops (
occurs because at that time the galactic wind develops (
![]() is too low to develop a wind). Gas is lost through the wind and the gas surface density decreases sharply (see Sect. 2 for details). As a consequence, the SFR drops and the SN Ib/c rate then also drops.
is too low to develop a wind). Gas is lost through the wind and the gas surface density decreases sharply (see Sect. 2 for details). As a consequence, the SFR drops and the SN Ib/c rate then also drops.
5 Summary
We have compared the data of LGRB-associated systems, LGRB-DLAs at high redshift, and LGRB host galaxies at low redshift, with chemical evolution models for galaxies of different morphological type. We have attempted to answer the following questions: i) which galaxies are the hosts of LGRBs? ii) are the LGRB systems part of an evolutionary sequence, in other words are they the same objects at low and high redshift as seen in different phases of their evolution?
Our conclusions can be summarized as follows:
- 1.
- If the observed high-redshift LGRB-DLAs and local LGRB host
galaxies belonged to an evolutionary sequence, they should be
irregulars with a common galaxy-formation redshift as high as
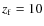 ,
observed at different phases of their evolution. We can fit the
majority of these systems using slowly evolving irregular models with a
star formation efficiency,
,
observed at different phases of their evolution. We can fit the
majority of these systems using slowly evolving irregular models with a
star formation efficiency,
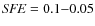 .
The adopted models were previously tested on local dwarf irregulars (see Yin et al. 2010b,a) and they may reproduce their properties.
.
The adopted models were previously tested on local dwarf irregulars (see Yin et al. 2010b,a) and they may reproduce their properties.
- 2.
- We tested models with
 ,
which resemble the evolution of the disk of the Milky Way (Chiappini et al. 1997; François et al. 2004; Cescutti et al. 2007).
We considered the average properties of such a disk, and concluded that
they fit neither high nor low redshift data since they predict too high
absolute abundances. We cannot exclude, however, that they correspond
to the outermost regions of spiral disks, since their properties are
similar to those of irregulars (see Matteucci et al. 1997).
,
which resemble the evolution of the disk of the Milky Way (Chiappini et al. 1997; François et al. 2004; Cescutti et al. 2007).
We considered the average properties of such a disk, and concluded that
they fit neither high nor low redshift data since they predict too high
absolute abundances. We cannot exclude, however, that they correspond
to the outermost regions of spiral disks, since their properties are
similar to those of irregulars (see Matteucci et al. 1997).
- 3.
- The rapid chemical enrichment at high redshift and subsequent
passive evolution, following the occurrence of a galactic wind several
Gyrs ago, of elliptical galaxies, suggests that they cannot be LGRB
host galaxies at low redshift and that they are very unlikely hosts of
LGRB-DLAs even at high redshift. The high observed [
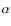 /Fe] ratios in ellipticals
indicate in particular that most LGRB-DLAs can be neither a phase nor a part of ellipticals.
/Fe] ratios in ellipticals
indicate in particular that most LGRB-DLAs can be neither a phase nor a part of ellipticals.
- 4.
- We have confirmed that the star formation history is the main driver of galaxy evolution. In particular, the properties of galaxies of different morphological type can be reproduced by simply changing the efficiency of star formation. By comparing the observed and predicted chemical properties of LGRB hosts, we have shown that they are most closely fitted by galaxy models with a lower SFE than either spirals or ellipticals, which is typical instead of irregular galaxies.
- 5.
- The elliptical models to which we compared the data refer to a very massive elliptical of infall mass
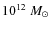 ,
which is reproduced well by assuming a
,
which is reproduced well by assuming a
 Gyr-1, and to a small elliptical of infall mass
Gyr-1, and to a small elliptical of infall mass
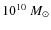 ,
which is reproduced well by assuming a lower
,
which is reproduced well by assuming a lower
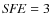 Gyr-1.
These assumptions reflect the downsizing in star formation that is
necessary to reproduce the majority of the chemical and photometric
properties of ellipticals. (e.g. downsizing in chemical enrichment, see
Pipino & Matteucci 2006,2008,2004).
According to our anti-hierarchical galaxy formation scenario, we should
with future data observe a mass-redshift relation for LGRB hosts.
Gyr-1.
These assumptions reflect the downsizing in star formation that is
necessary to reproduce the majority of the chemical and photometric
properties of ellipticals. (e.g. downsizing in chemical enrichment, see
Pipino & Matteucci 2006,2008,2004).
According to our anti-hierarchical galaxy formation scenario, we should
with future data observe a mass-redshift relation for LGRB hosts.
Our thanks go to the anonymous referee for valuable comments and useful suggestions. J.Y. and F.M. acknowledge the financial support from PRIN2007 from Italian Ministry of Research, Prot. No. 2007JJC53X-001. J.Y. thanks the hospitality of the Department of Physics of the University of Trieste where this work was accomplished. J.Y. also thanks the financial support from the National Science Foundation of China No. 10573028, the Key Project No. 10833005, the Group Innovation Project No. 10821302, and 973 program No. 2007CB815402.
References
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., Naab, T., McIntosh, D. H., et al. 2006, ApJ, 640, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Bissaldi, E., Calura, F., Matteucci, F., Longo, F., & Barbiellini, G. 2007, A&A, 471, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Bradamante, F., Matteucci, F., & D'Ercole, A. 1998, A&A, 337, 338 [NASA ADS] [Google Scholar]
- Calura, F., & Matteucci, F. 2006, ApJ, 652, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Matteucci, F., & Vladilo, G. 2003, MNRAS, 340, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Dessauges-Zavadski, M., Prochaska, J. X., & Matteucci, F. 2009, ApJ, 693, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Campisi, M. A., De Lucia, G., Li, L., Mao, S., & Kang, X. 2009, MNRAS, 400, 1613 [NASA ADS] [CrossRef] [Google Scholar]
- Castro Cerón, J. M., Micha▯owski, M. J., Hjorth, J., et al. 2010, ApJ, 721, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chary, R., Berger, E., & Cowie, L. 2007, ApJ, 671, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X. Y., Liang, Y. C., Hammer, F., et al. 2010, A&A, 515, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Chisari, N. E., Tissera, P. B., & Pellizza, L. J. 2010, MNRAS, 408, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Jakobsson, P., Prochaska, J. X., et al. 2009, ApJS, 185, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, J. F., Fruchter, A. S., Kewley, L. J., et al. 2009, AIPCS, 1133, 269 [Google Scholar]
- Greiner, J., Krühler, T., Fynbo, J. P. U., et al. 2009, ApJ, 693, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hou, J. L., Prantzos, N., & Boissier, S. 2000, A&A, 362, 921 [NASA ADS] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jakobsson, P., Fynbo, J. P. U., Ledoux, C., et al. 2006, A&A, 460, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kistler, M. D., Yüksel, H., Beacom, J. F., Hopkins, A. M., & Wyithe, J. S. B. 2009, ApJ, 705, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, D. Q., & Reichart, D. E. 2000, ApJ, 536, 1 [Google Scholar]
- Lanfranchi, G. A., & Matteucci, F. 2003, MNRAS, 345, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Kawakatu, N., Bosnjak, Z., et al. 2008, MNRAS, 386, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Berger, E., Kewley, L. J., & Bagley, M. M. 2010a, AJ, 139, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Kewley, L. J., Graham, J. F., & Fruchter, A. S. 2010b, ApJ, 712, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Liang, S. L., Kann, D. A., et al. 2008, ApJ, 685, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, S. L., & Li, A. 2009, ApJ, 690, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mao, J. 2010, ApJ, 717, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2001, The chemical evolution of the Galaxy, Ap&SS Library, 253 [Google Scholar]
- Matteucci, F., & Padovani, P. 1993, ApJ, 419, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Pipino, A. 2002, ApJ, 569, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., Molaro, P., & Vladilo, G. 1997, A&A, 321, 45 [NASA ADS] [Google Scholar]
- Matteucci, F., Ponzone, R., & Gibson, B. K. 1998, A&A, 335, 855 [NASA ADS] [Google Scholar]
- Micha▯owski, M. J., Hjorth, J., Castro Cerón, J. M., & Watson, D. 2008, ApJ, 672, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P., Warren, S. J., Fall, S. M., Fynbo, J. U., & Jakobsen, P. 2002, ApJ, 574, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2006, MNRAS, 366, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Nuza, S. E., Tissera, P. B., Pellizza, L. J., et al. 2007, MNRAS, 375, 665 [CrossRef] [Google Scholar]
- Padovani, P., & Matteucci, F. 1993, ApJ, 416, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M. 2006, in The Fabulous Destiny of Galaxies: Bridging Past and Present, ed. V. Le Brun, A. Mazure, S. Arnouts, & D. Burgarella, 319 [Google Scholar]
- Pian, E., Mazzali, P. A., Masetti, N., et al. 2006, Nature, 442, 1011 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pipino, A., & Matteucci, F. 2004, MNRAS, 347, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., & Matteucci, F. 2006, MNRAS, 365, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., & Matteucci, F. 2008, A&A, 486, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pipino, A., Fan, X., Matteucci, F., et al. 2010, A&A, accepted [arXiv:1008.3875] [Google Scholar]
- Pontzen, A., Deason, A., Governato, F., et al. 2010, MNRAS, 402, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Chen, H., Bloom, J. S., et al. 2007a, ApJS, 168, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Chen, H., Dessauges-Zavadsky, M., & Bloom, J. S. 2007b, ApJ, 666, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Savaglio, S., Krühler, T., et al. 2010, ApJ, 720, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Salucci, P., & Chiappini, C. 2000, ApJ, 539, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Tosi, M., & Matteucci, F. 2006, MNRAS, 365, 759 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Salvaterra, R., Della Valle, M., Campana, S., et al. 2009, Nature, 461, 1258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Savaglio, S. 2006, New J. Phys., 8, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Savaglio, S., Glazebrook, K., & Le Borgne, D. 2009, ApJ, 691, 182 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Erb, D. K., et al. 2005, ApJ, 626, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, K. M., Levan, A. J., Tanvir, N. R., Fruchter, A. S., & Strolger, L. 2010, MNRAS, 405, 57 [NASA ADS] [Google Scholar]
- Tanvir, N. R., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, C., & Podsiadlowski, P. 2007, MNRAS, 375, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M. 2005, in Probing Galaxies through Quasar Absorption Lines, ed. P. Williams, C.-G. Shu, & B. Menard, IAU Colloq., 199, 148 [Google Scholar]
- Wolfe, A. M., Turnshek, D. A., Smith, H. E., & Cohen, R. D. 1986, ApJS, 61, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006a, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006b, AIPCS, 836, 398 [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yin, J., Magrini, L., Matteucci, F., et al. 2010a, A&A, 520, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yin, J., Matteucci, F., & Vladilo, G. 2010b, A&A, submitted [Google Scholar]
- Yoon, S., Langer, N., Cantiello, M., Woosley, S. E., & Glatzmaier, G. A. 2008, IAUS, 250, 231 [NASA ADS] [Google Scholar]
- Zwaan, M. A., van der Hulst, J. M., Briggs, F. H., Verheijen, M. A. W., & Ryan-Weber, E. V. 2005, MNRAS, 364, 1467 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... fitting
![[*]](/icons/foot_motif.png)
- The mass fitting is robust (Shapley et al. 2005), despite the metallicity, dust extinction, and age being degenerate (see Chen et al. 2010, who compared six evolutionary population synthesis (EPS) models and concluded that different EPS models are necessary to reproduce different stellar populations).
All Tables
Table 1: Model predictions at 13 Gyr.
All Figures
![\begin{figure}
\par\includegraphics[width=3in]{15293fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg43.png)
|
Figure 1:
12+log(X/H) as a function of redshift. Predicted lines are from the irregular galaxy model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg44.png)
|
Figure 2:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg45.png)
|
Figure 3:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg46.png)
|
Figure 4:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg47.png)
|
Figure 5:
12+log(X/H) as a function of redshift. The same as Fig. 1 but for the spiral galaxy model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg48.png)
|
Figure 6:
[Si/Fe] as function of [Fe/H] of LGRB-DLA systems. The predictions are
our from chemical evolution models of elliptical galaxies with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg54.png)
|
Figure 7:
[S/Fe] as function of [Fe/H] of LGRB-DLA systems. The predictions are
from chemical evolution models for the elliptical galaxies with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg55.png)
|
Figure 8: Predicted [Fe/H] versus galactic age for two irregular and two elliptical models, as indicated in the figure. The horizontal lines mark [Fe/H]=-1.0 and [Fe/H]=-3.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3in]{15293fg9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa15293-10/Timg56.png)
|
Figure 9:
Predicted SNIb/c rate evolution as a function of galactic age for
irregulars and ellipticals. The predictions are from our chemical
evolution model of a elliptical galaxy assuming the star formation
efficiency
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


