The wide variety of evolutionary stages among 34 unstudied Teutsch open clusters

C. Bonatto; E. Bica

doi:10.1051/0004-6361/201015222

Home

All issues

Volume 521 (October 2010)

A&A, 521 (2010) A74

Full HTML

Free Access

Issue		A&A Volume 521, October 2010


Article Number		A74
Number of page(s)		18
Section		Galactic structure, stellar clusters, and populations
DOI		https://doi.org/10.1051/0004-6361/201015222
Published online		22 October 2010

A&A 521, A74 (2010)

The wide variety of evolutionary stages among 34 unstudied Teutsch open clusters

C. Bonatto - E. Bica

Universidade Federal do Rio Grande do Sul, Departamento de Astronomia CP 15051, RS, Porto Alegre 91501-970, Brazil

Received 16 June 2010 / Accepted 15 July 2010

Abstract
Context. Close investigations of unstudied open-cluster candidates may improve the statistics of objects undergoing the dissolution phase.
Aims. We plan to settle the nature and derive astrophysical (fundamental, structural, and stellar mass content) parameters for 34 unstudied open cluster candidates from the near-infrared Teutsch list.
Methods. The analysis employs 2MASS photometry, field-star decontamination (to enhance the intrinsic colour-magnitude diagram morphology), and colour-magnitude filters (for high contrast in stellar radial density profiles).
Results. We find 8 clusters younger than $\sim$ 30 Myr, 21 with ages within 100-900 Myr, 3 older than 1 Gyr, and possibly 1 as old as $\sim$ 7 Gyr. Part of the sample is affected by reddening as high as $\mbox{$A_V$ }\sim9$ , and about half is located more than $\mbox{$d_\odot$ }\sim3$ kpc away from the Sun, with a few reaching $\mbox{$d_\odot$ }=6{-}9$ kpc. The sample contains essentially low-luminosity clusters in the optical, with $\langle M_V\rangle\approx-3\pm3$ . These properties are consistent with their near-infrared origin. Cluster size increases both with Galactocentric distance and height over the plane, which is consistent with the low level of tidal stress (and field contamination) associated with these regions. The average mass density falls off with cluster radius as $\rho\sim R^{-3}$ , which in clusters younger than $\sim$ 20 Myr and more massive than $\sim$ $10^3~\mbox{$M_\odot$ }$ has been interpreted as diffusion-related cluster expansion.
Conclusions. Besides the derivation of astrophysical parameters for a sample of unstudied open clusters, in this paper we identify a set of clusters older than several 10² Myr, with 4 of them having survived a few Gyr. Surveys of open cluster candidates should be further explored to fill in the gap between the detected and predicted number of clusters. An improved statistic, especially on the population of clusters in highly evolved phases, can be used to investigate cluster formation rates and constrain the dissolution-time scale in the Galaxy.

Key words: open clusters and associations: general - Galaxy: structure

1 Introduction

Star formation is a mass and size scale-free process that yields a power-law mass distribution ${\rm d}N/{\rm d}M\propto M^{-2}$ (e.g. Elmegreen 2008). Thus, open cluster (OC) formation is biased towards low masses, and large numbers of low-mass OCs are expected to form. Indeed, estimates based on different approaches (e.g. Piskunov et al. 2006; Bonatto et al. 2006) consistently indicate that the Galaxy may harbour a population of $\sim$ 10⁵ OCs. However, widely-used databases, such as WEBDA and the Catalog of Optically Visible Open Clusters and Candidates (Dias et al. 2002), contain less than the 2000 OC candidates detected so far. Only about half of these have unambiguously determined OC nature, and most are located relatively close to the Sun and projected towards the Galactic anti-centre. Given the high levels of field-star contamination associated with large distances (particularly towards the bulge), part of the detection problem is related to completeness, especially for the low-mass OCs (Bonatto et al. 2006). The OC fading associated with the stellar evolution is also important.

Most OCs dwell in or close to the Galactic disk and, because of such orbits, they continually suffer tidal stress from Galactic substructures, which produces different degrees of mass loss that might lead to dissolution into the field. Over time, stellar evolution-related mass loss, mass segregation and evaporation, tidal interactions with the disk and/or bulge, and encounters with giant molecular clouds, affect the critical balance between velocity dispersion and escape velocity. These processes tend to accelerate the dynamical evolution and change the internal cluster structure to varying degrees, so that the vast majority of the OCs still dissolve in the embedded phase (e.g. Lada & Lada 2003). Theoretical and observational evidence (e.g. Spitzer 1958; Oort 1958; Baumgardt & Makino 2003; Goodwin & Bastian 2006; Lamers & Gieles 2006; Khalisi et al. 2007; Piskunov et al. 2007) point to a disruption time scale of a few 10² Myr near the solar circle. As a consequence, most OCs dissolve in the Galactic stellar field (e.g. Lamers et al. 2005) or leave poorly-populated remnants (e.g. Pavani & Bica 2007), long before $\sim$ 1 Gyr (e.g. Goodwin & Bastian 2006).

Probably because of the age/dissolution effect, only $\approx$ $13\%$ of the WEBDA OCs with known age are older than 1 Gyr, while $\approx$ $42\%$ are younger than 100 Myr. Besides the obvious importance of deriving astrophysical parameters of unstudied clusters of any age, the identification of OCs older than several 10² Myr will thus increase the statistics of objects undergoing the dissolution phase. This, in turn, can be used for constraining the dissolution-time scale in the Galaxy.

In the present paper we investigate the nature of 34 unstudied Teutsch (hereafter Teu) OC candidates and derive their astrophysical parameters. In short, the analysis involves the following steps for each cluster: (i) extraction of 2MASS photometry (Skrutskie et al. 1997) in a wide circular region; (ii) field-star decontamination to enhance the intrinsic colour-magnitude diagram (CMD) morphology (essential for a proper derivation of reddening, age, and distance from the Sun); and (iii) construction of colour-magnitude filters, for more contrasted stellar radial density profiles (RDPs). In previous works (e.g. Bica et al. 2008), we have shown that steps (ii) and (iii) are essential for a robust determination of fundamental parameters, especially for low-latitude and/or bulge-projected OCs.

Table 1: Fundamental parameters.

This paper is organised as follows. In Sect. 2 we discuss formation of the unstudied Teutsch sample. In Sect. 3 we present the 2MASS photometry and the field-star decontaminated CMDs. In Sect. 4 we discuss the derivation of fundamental cluster parameters. In Sect. 5 we investigate cluster structure. In Sect. 6 we present stellar mass estimates. In Sect. 7 we investigate relations among parameters and with respect to their location in the Galaxy. Concluding remarks are given in Sect. 8.

2 The sample of unstudied Teutsch clusters

After inspecting the Digitized Sky Survey (DSS) and 2MASS images of selected Milky Way regions, Kronberger et al. (2006) reported the discovery of several stellar groupings with morphology, CMD, and stellar RDP, which suggest uncatalogued, possible OCs. SIMBAD lists 146 objects under the designation of Teutsch OC candidates.

Our first step was to search in the ``Catalog of Optically Visible Open Clusters and Candidates'' (Dias et al. 2002) and WEBDA for Teutsch objects that are still considered as candidates, i.e., with no determination of their fundamental parameters. This survey came up with 34 targets, for which a further object search in SAO/NASA ADS confirmed that, besides the discovery work (Kronberger et al. 2006), have not been subject to further investigation.

Images of the Teutsch clusters that came up from this search are shown in Appendix A. The images are centred on slightly different coordinates (Table 1) than those given in Dias et al. (2002). By default, we always assume the original coordinates to centre the 2MASS photometry extraction. However, in most cases the RDPs built after field decontamination - to maximise membership probability (Sect. 3), presented a dip in the innermost radial bin, so the central coordinates were computed again according to the following strategy. After field decontamination, we divided the central (usually $\rm 1\hbox{$^\prime$ }$ in radius) region in cells of $0.0125\hbox{$^\prime$ }$ width both in right ascension and declination. Then, for each cell we built an RDP using its coordinates as the centre. After repeating the last step for all cells, we searched through the full RDP set for the most cluster-like one, i.e., the one that maximises the stellar density in the innermost bin, followed by a rather smooth decrease towards large radii (Sect. 5). Finally, we adopted these cell coordinates as the cluster's central position. Incidentally, differences in the central coordinates are relatively small for the present sample (Table 1).

3 Photometric analysis

2MASS provides the spatial and photometric uniformity that are essential for wide angular extractions. This in turn provides the high star-count statistics required for the determination of the background level (Sect. 5) and the colour/magnitude characterisation of the field stars (see below). In all cases we extracted the 2MASS photometry from VizieR, in a circular field of radius $\mbox{$R_{\rm ext}$ }=60\hbox{$^\prime$ }$ . To preserve the photometric quality and, at the same time, keep a statistically significant number of stars, we use only photometric errors in J, H, and $K_{\rm s}$ that are lower than 0.15 mag. Reddening corrections are based on the absorption relations A_J/A_V=0.276, A_H/A_V=0.176, $A_{K_{\rm S}}/A_V=0.118$ , and $A_J=2.76\times\mbox{$E(J-H)$ }$ given by Dutra et al. (2002), with R_V=3.1, considering the extinction curve of Cardelli et al. (1989).

The clusters are distributed over all Galactic quadrants (Table 1), so that field-stars are expected to contaminate the CMDs at different degrees, usually high in the 1st and 2nd quadrants and low in the 3rd and 4th (e.g. Bonatto et al. 2006). Also, since most of the clusters are relatively poorly populated (Figs. 1-7), the field-star contamination should be taken into account so that the derived parameters are more constrained. In particular, we expect to obtain CMDs in which clusters' evolutionary sequences and field stars are reasonably disentangled.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig1.eps}} \end{figure}$	Figure 1: CMDs of Teu 54, 40, 49, 64, and 144 for a representative cluster region (top panels) and the equal-area comparison field (middle). The decontaminated CMDs (bottom) are shown with the isochrone solution (solid line) and the colour-magnitude filter (shaded polygon).
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig2.eps}} \end{figure}$	Figure 2: Same as Fig. 1 for Teu 11, 27, 79, 48, and 52.
Open with DEXTER

$\begin{figure} \resizebox{9cm}{!}{\includegraphics{Fig3.eps}} \end{figure}$	Figure 3: Same as Fig. 1 for Teu 126, 7, 12, 66, and 14a.
Open with DEXTER

$\begin{figure} \resizebox{9cm}{!}{\includegraphics{Fig4.eps}} \end{figure}$	Figure 4: Same as Fig. 1 for Teu 13 ( left panel). The remaining clusters (Teu 23, 7, 76, 55, and 132) are shown in $\mbox{$J$ }\times\mbox{$(J-K_{\rm s})$ }$ CMDs. Also shown is the reddening vector for $\mbox{$A_V$ }=0$ to $\mbox{$A_V$ }=5$ .
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig5.eps}} \end{figure}$	Figure 5: Same as Fig. 1 for Teu 124, 50, 77, 43, and 2. Isochrones younger than the adopted ones are also shown for an estimate of a lower limit to the age.
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig6.eps}} \end{figure}$	Figure 6: Same as Fig. 1 for Teu 28, 44, 31, 85, and 106.
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig7.eps}} \end{figure}$	Figure 7: Same as Fig. 1 but with $\mbox{$J$ }\times\mbox{$(J-K_{\rm s})$ }$ CMDs of Teu 45, 39, 162, and 53.
Open with DEXTER

For this purpose we work with the statistical decontamination algorithm that has been developed by our group for the proper identification and characterisation of star clusters, especially near the Galactic equator and/or with many faint stars. We start by defining the cluster and comparison field regions, taken within the wide circular extractions. CMDs extracted within the cluster region for our objects are shown in Figs. 1-7 (top panels), which should be contrasted with the representative (i.e. equal-area) comparison-field CMDs (middle panels). The equal-area field extractions are only used for qualitative comparisons, since the algorithm uses the whole surrounding area (as defined above) for high statistical representativeness. For most stars the error bars are smaller than the symbol. Our approach assumes that the field colour-magnitude distribution is (i) statistically representative of the cluster contamination; and (ii) presents some degree of spatial uniformity. These assumptions are usually matched in the 3rd and 4th Galactic quadrants. More details on the decontamination algorithm are in Bonatto & Bica (2007b) and Bonatto & Bica (2010a). For clarity, we sketch how it works.

A cluster CMD is divided into a 3D grid of cells with axes along the J magnitude and the (J-H) and $(J-K_{\rm s})$ colours, with initial dimensions $\Delta\mbox{$J$ }=1$ and $\Delta\mbox{$(J-H)$ }=\Delta\mbox{$(J-K_{\rm s})$ }=0.2$ . Then, we compute the probability that a given star is found in a particular cell. For a star with measured magnitude and colour uncertainties $J\pm\sigma_J$ , $\mbox{$(J-H)$ }\pm\sigma_{(J-H)}$ , and $\mbox{$(J-K_{\rm s})$ }\pm\sigma_{(J-K_{\rm S})}$ , the probability is proportional to the difference between the error function computed at the borders of the cell. This step is taken for all stars and cells, resulting in a number density of $\rm member+field$ stars for each cell ( $\eta^{\rm cell}_{\rm tot}$ ). The same steps are applied to the comparison field CMD, from which we estimate the field number density ( $\eta^{\rm cell}_{\rm fs}$ ) for each cell. Next, we subtract the corresponding field number density for each cluster cell to obtain a decontaminated number density ( $\eta^{\rm cell}_{\rm mem}=\eta^{\rm cell}_{\rm tot}-\eta^{\rm cell}_{\rm fs}$ ). Finally, $\eta^{\rm cell}_{\rm fs}$ is converted back into number of stars and subtracted from each cell, and the $N^{\rm cell}_{\rm clean}$ stars that remain in the cell are identified. We also compute the subtraction efficiency ( $f_{\rm sub}$ ), which is the sum over all cells of the difference between the expected number of field stars (usually fractional) and the number of stars effectively subtracted (integer). In all cases we obtained $f_{\rm sub}>90\%$ .

The above procedure is repeated for 729 different setups (taking independent variations of cell size and grid positioning into account). Each setup produces a total number of member stars $N_{\rm mem}=\sum_{\rm cell}N^{\rm cell}_{\rm clean}$ , from which we compute the expected total number of member stars $\left<N_{\rm mem}\right>$ by averaging out $N_{\rm mem}$ over all setups. Stars (identified above) are ranked according to the number of times they survive all runs, and only the $\left<N_{\rm mem}\right>$ highest ranked stars are considered cluster members and transposed to the respective decontaminated CMD. The decontaminated CMDs of the present sample are shown in Figs. 1-7 (bottom panels).

Finally, we classify each case as Quality 1, 2, or 3 according to a subjective analysis based on how cluster-like the image (Appendix A), decontaminated CMD (Figs. 1-7), and RDP (Sect. 5) are.

4 Derivation of fundamental parameters

The decontaminated CMD morphology, coupled to Padova isochrones (Girardi et al. 2002) computed with the 2MASS filters, are used to derive the fundamental parameters (reddening, age, and distance from the Sun). These isochrones are very similar to the Johnson-Kron-Cousins ones (e.g. Bessel & Brett 1988), with differences of at most 0.01 mag in colour (Bonatto et al. 2004). With respect to metallicity, the difference between, e.g. solar and subsolar metallicity isochrones for a given age is small, to within the 2MASS photometric uncertainties (Appendix 8). Thus, we adopt the solar metallicity for simplicity.

A first look at the decontaminated CMDs suggests OCs in a wide variety of evolutionary stages (bottom panels of Figs. 1-7). In particular, the presence of somewhat distant and evolved (in different degrees) OCs is suggested by the giant clumps and red giant branches that show up in a significant fraction of the sample clusters (Figs. 1-3, 5, 6). On the other hand, young clusters are also seen that still contain PMS stars (Figs. 4 and 7).

With respect to the derivation of fundamental parameters, several sophisticated approaches for analytical CMD fitting are available (a summary is in Naylor & Jeffries 2006). However, for simplicity we adopt a more direct approach that compares isochrones and the decontaminated CMD morphology. Specifically, the solutions are searched by eye, using the combined main sequence (MS) and evolved stellar distributions (or the PMS for the young clusters) as constraint. Variations due to photometric uncertainties (which are usually small, because of the restrictions imposed in Sect. 3) and the presence of binaries (which tend to produce a redwards bias in the MS) are also taken into account. Starting with the isochrones set for zero distance modulus and reddening, we shift them in magnitude and colour until a satisfactory match with the CMD is obtained. The best fits, according to this approach, are shown in Figs. 1-7 (bottom panels), and the respective parameters are given in Table 1.

Open clusters younger than $\sim$ 30 Myr are expected to be affected by differential reddening. Indeed, as shown by, e.g. Yadav & Sagar (2001), the differential reddening tends to increase towards younger ages, in some cases reaching $\Delta\mbox{$E(B-V)$ }\approx1$ mag, or $\Delta\mbox{$A_V$ }\approx3$ mag. Since we cannot derive the extinction for individual stars with 2MASS photometry, we examine the effect of differential reddening simply by means of a reddening vector (Figs. 4 and 7) for $\Delta\mbox{$A_V$ }\approx5$ mag, which surpasses the upper limit of Yadav & Sagar (2001). Thus, most of the scatter, especially in the PMS, can be accounted for by differential reddening. Consequently, it is impossible to assign a precise mass value for each PMS star (Sect. 6).

We find that 7 clusters are younger than $\sim$ 50 Myr, 6 of which still harbour a varying fraction of PMS stars. Among the remaining, 21 have ages within 100-900 Myr, while 4 appear to be older than 1 Gyr (see below). With respect to the distance from the Sun, they are distributed as near as $\mbox{$d_\odot$ }\sim1$ kpc, with a few more distant than $\mbox{$d_\odot$ }=5$ kpc, and reaching distances as far as $\mbox{$d_\odot$ }\sim9$ kpc. We'll return to this point in Sect. 7.

From a comparison with CMDs of known OCs, Kronberger et al. (2006) provide estimates for the distance from the Sun and reddening for Teu 43 ( $\mbox{$d_\odot$ }=8.1$ kpc, $\mbox{$E(B-V)$ }=0.54$ ), Teu 48 ( $\mbox{$d_\odot$ }=7.0$ kpc, $\mbox{$E(B-V)$ }=0.96$ ), and Teu 79 ( $\mbox{$d_\odot$ }=6.7\pm0.4$ kpc, $\mbox{$E(B-V)$ }=0.95\pm0.12$ ). While our values for Teu 48 are comparable, they are very different for the other clusters. Given the decontaminated CMDs of Teu 43 (Fig. 5), Teu 48, and Teu 79 (Fig. 2), the age (and consequently, the reddening and distance) is rather constrained to within the quoted errors in Table 1. A probable source for such differences is the lack of field star decontamination in the analysis of Kronberger et al. (2006).

Finally, it should be noted that in some cases in which the observed CMDs present similarities, the age estimates contrast, as for Teu 126 ( $\sim$ 400 Myr; Fig. 3) and Teu 55 ( $\sim$ 5 Myr; Fig. 4). Although the similarity between the observed CMDs (top panels), the decontaminated ones (bottom) are significantly different, with Teu 126 displaying a rather well-populated and long MS, together with the typical ``redwards bending'' of clusters a few 10⁸ yr old. In contrast, Teu 55 presents a nearly vertical and short MS with a distribution of PMS-like stars. In addition, both objects show different aspects in their optical images (Sect. A), with evidence of dust in Teu 55, which is consistent with our age estimates for both objects.

4.1 Interesting cases

The majority of the present Teutsch clusters are quite normal in terms of age; i.e., they are younger than 1 Gyr. However, we find 4 cases for which the CMDs indicate ages of a few Gyr. They are Teu 43, 50, 77, and 124 (Fig. 5). Along with their images (Appendix A), the decontaminated CMDs are typical of old clusters, especially Teu 124. Indeed, the isochrones that best represent the CMDs of Teu 43, 50, and 77 indicate ages of 2 and 3 Gyr. Clearly, these clusters are older than 1 Gyr, as shown by the rather inconsistent - when compared to the adopted fits - and tentative solutions with younger isochrones. The CMD of Teu 124 indicates a significantly older cluster, for which we estimate the age 7^-3₊₂ Gyr. Again, the CMD morphology indicates that Teu 124 cannot be younger than $\sim$ 3 Gyr.

The only object for which we could not find a satisfactory CMD solution is Teu 53 (Fig. 7). As suggested by its image (Appendix A), it probably is a very distant, poorly-populated cluster, with about 20 faint stars distributed in a region of $\approx$ $1\hbox{$^\prime$ }$ in radius. Both the observed and decontaminated CMDs do not allow any inference on age. The RDP (Fig. 9) shows a density excess for $R\la1\hbox{$^\prime$ }$ , but it does not follow any analytical cluster profile (Sect. 5). Clearly, Teu 53 requires deeper photometry for a proper analysis.

Finally, the decontaminated CMDs of Teu 52, 54, and 85 appear to display a second, reddened MS or giant clump. To a lesser degree, the same applies to Teu 126. Since Teu 85 is projected not far from the Galactic centre ( $\ell\approx347\hbox{$^\circ$ }$ , $b\approx-0.5\hbox{$^\circ$ }$ ), this feature may be an artifact of the decontamination algorithm associated with the high stellar background and spatial variation of the extinction towards the bulge. The other OCs, on the other hand, are located in the $2{\rm nd}$ quadrant, which minimises the possibility of a decontamination artifact. Alternatively, that feature might suggest a more distant cluster (not seen in the respective images shown in Appendix A) caught in the line of sight. Deeper photometry would be required to settle this point.

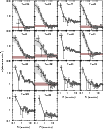
5 Cluster structure

Structural parameters are derived by means of the RDPs. We start by using the decontaminated CMD morphologies and corresponding isochrone solutions (Figs. 1-7) to build a colour-magnitude filter for each cluster. Noise in the RDPs is minimised when stars with colours (and magnitude) that are clearly discordant of those assumed to represent the cluster are excluded. Also, the contrast with the background is enhanced (e.g. Bonatto & Bica 2007b).

Table 2: Structural parameters derived from the RDPs.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig8.eps}} \end{figure}$	Figure 8: Stellar RDPs (empty circles), the best-fit King-like profile (solid line), the $1\sigma$ uncertainty (light-shaded region), and the residual background level (shaded polygon).
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig9.eps}} \end{figure}$	Figure 9: Same as Fig. 8 for the remaining clusters. It was not possible to fit the King-like profile for some cases.
Open with DEXTER

Table 3: Stellar mass estimate.

When the RDPs are built in rings of increasing width with distance from the cluster centre, the spatial resolution is preserved along the full radial range with moderate error bars. Specifically, we use $\Delta~R=0.25,\ 0.5,\ 1.0,\ 2.5,\ {\rm and}\ 5\hbox{$^\prime$ }$ , respectively for $0\hbox{$^\prime$ }\le R<0.5\hbox{$^\prime$ }$ , $0.5\hbox{$^\prime$ }\le R<2\hbox{$^\prime$ }$ , $2\hbox{$^\prime$ }\le R<5\hbox{$^\prime$ }$ , $5\hbox{$^\prime$ }\le R<20\hbox{$^\prime$ }$ , and $R\ge20\hbox{$^\prime$ }$ . Obviously, for any magnitude bin, field stars with the same colour as the cluster's are not excluded by the filtering process. This residual background level is evaluated as the average number density of stars in the comparison field. We take the R coordinate (and uncertainty) of each ring as the average position (and standard deviation) of the stars inside the ring. The resulting RDPs (and residual background) are shown in Figs. 8, 9. By measuring the distance from the cluster centre where the RDP and residual background are statistically indistinguishable, we get an estimate of the cluster radius ( $R_{\rm RDP}$ ). Thus, $R_{\rm RDP}$ can be considered as an observational truncation radius, whose value depends both on the radial distribution of member stars and the field density.

The RDPs are fitted with the function $\sigma(R)=\sigma_{\rm bg}+\sigma_0/(1+(R/R_{\rm c})^2)$ , where $\sigma_0$ and $\sigma_{\rm bg}$ are the central and residual background stellar densities, and $R_{\rm c}$ is the core radius. Applied to star counts, this function is similar to the one used by King (1962) to describe surface-brightness profiles in the central parts of globular clusters. Degrees of freedom are minimised by allowing only $\sigma_0$ and $R_{\rm c}$ to vary in the fits, while $\sigma_{\rm bg}$ is previously measured in the surrounding field and kept fixed. The best-fit solutions are shown in Figs. 8-9, and the structural parameters are given in Table 2.

Within uncertainties, the adopted King-like function provides a reasonable description along the full radial range of the RDPs for most ( $\approx$ $80\%$ ) of the sample. The exceptions are Teu 39, 44, 45, 53, 77, 85, and 162, which present irregular RDPs that cannot be fitted by the adopted profile. Also, Teu 54 ( $\rm age\sim900$ Myr) and Teu 144 ( $\sim$ 800 Myr) present a pronounced density enhancement in the innermost RDP bin. This feature has been attributed to a post-core collapse structure in some globular clusters (e.g. Trager et al. 1995). Such a dynamical evolution-related feature has also been detected in the RDP of some Gyr-old OCs, e.g. NGC 3960 (Bonatto & Bica 2006) and LK 10 (Bonatto & Bica 2009a).

Compared to the distribution of core radii derived for a sample of relatively nearby OCs by Piskunov et al. (2007, their Fig. 3), the present clusters occupy the small- $R_{\rm c}$ tail. Finally, given the 2MASS photometric limit and the range of distances spanned by the present cluster sample (Table 1), it is clear that our analysis does not include considerable (and varying) fractions of the low-mass MS. The effect of depth-limited photometry on the derivation of structural parameters has been fully discussed by, e.g., Bonatto & Bica (2008a). One conclusion is that, when the 2MASS photometry reaches a few magnitudes below the MS, the depth-limited 2MASS photometry may underestimate $R_{\rm RDP}$ by less than $\approx$ $10\%$ . The core radius (derived by means of the King-like fit), on the other hand, may be underestimated by $\approx$ $30\%$ (OCs younger than $\sim$ 10 Myr) and $\approx$ $20\%$ (OCs older than $\sim$ 1 Gyr). Thus, our conclusions with respect to the structural radii are not significantly affected by the 2MASS depth limit.

6 Cluster mass estimate

As a consequence of combining the somewhat limited 2MASS photometric depth with the relatively large distance of several of our OCs (Table 1), the CMDs in Figs. 1-7 do not contain the whole mass range expected especially for OCs older than a few 10⁷ Myr. Thus, we estimate the stellar mass by means of the mass function (MF), built for the observed MS mass range according to Bonatto & Bica (2006). The MS MF is then fitted with the function $\phi(m)\propto{m}^{-(1+\chi)}$ . Results of this approach are given in Table 3, where we also show the number and mass of the evolved stars. In most cases the detected MS mass range is restricted to $\ga$ $1~\mbox{$M_\odot$ }$ , with a few cases reaching $\approx$ $0.6~\mbox{$M_\odot$ }$ . Thus, assuming that the low-mass content is still present, we combine our MF with Kroupa's (2001) MF to estimate the total stellar mass, down to the H-burning mass limit ( $0.08~\mbox{$M_\odot$ }$ ). When the MS is determined well over a relatively large mass interval, we use our MF over that mass range and Kroupa's (2001) MF for lower masses. However, in some cases - usually the oldest and/or distant OCs - the MS MF is excessively noisy. In these cases we straightforwardly adopted Kroupa's (2001) MF, under the condition that the MF, integrated over the detected MS mass range, gives the observed number of stars. The (extrapolated) cluster mass is given in Col. 8 of Table 3. Finally, having estimated the cluster radius and mass, we also computed the average cluster mass density $\rho(\mbox{$M_\odot$ }~{\rm pc}^{-3})=\frac{3}{4\pi}M_{\rm clus}~R^{-3}_{\rm RDP}$ (Col. 9).

For the OCs with conspicuous PMS, we simply count the number of MS stars and, for each star, we take the corresponding mass value from the adopted isochrone. Differential reddening makes it impossible to attribute a precise mass value to each PMS star. Thus, we again count the number of PMS stars and adopt an average mass value for the PMS stars to estimate $n_{\rm PMS}$ and $m_{\rm PMS}$ . Assuming that the mass distribution of the PMS stars also follows Kroupa's (2001) MF, the average PMS mass - for masses within the range $0.08\la m(\mbox{$M_\odot$ })\la7$ - is $\langle m_{\rm PMS}\rangle \approx0.6\mbox{$M_\odot$ }$ . Thus, we simply multiply the number of PMS stars (Table 4) by this value to estimate the PMS mass. Finally, we add the latter value to the MS mass to obtain an estimate of the total stellar mass. Obviously, similar to the MS stars, 2MASS cannot detect the very low-mass PMS stars. Consequently, these values should be taken as lower limits.

Table 4: Stellar mass estimate for the clusters with PMS.

7 Discussion

The fundamental and structural parameters derived in the previous sections can be used to compare the present Teutsch sample among the wide variety of OCs found in the literature. In particular, we wish to examine the representativeness of the present sample with respect to the Galactic OCs.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig10.eps}} \end{figure}$	Figure 10: General properties of the present OCs (filled circles) compared to Galactic clusters (empty circles) taken from Dias et al. (2002) and WEBDA (panels a), b), and c)), and Piskunov et al. (2008) d). All cases are investigated with distribution functions.
Open with DEXTER

7.1 General properties

We start by considering the distance from the Sun, reddening, age, and cluster mass distribution functions (Fig. 10). For the first three parameters we take values from Dias et al. (2002) and WEBDA, corresponding to about 1100 OCs. However, since neither database deals with cluster mass, we use the uniform, semi-empirical mass determination for 650 OCs of Piskunov et al. (2008). Qualitatively, the Teutsch sample presents similar distributions to the Galactic OCs, especially with respect to the age. The same applies to cluster mass (especially for masses higher than $\sim$ $100~\mbox{$M_\odot$ }$ ), although Piskunov et al. (2008) includes OC masses as high as $\sim$ $10^5~\mbox{$M_\odot$ }$ .

7.2 Location in the Galaxy

The present Teutsch clusters are shown projected onto the Galactic plane in Fig. 11, which depicts Milky Way's spiral arms according to Momany et al. (2006) and Drimmel & Spergel (2001). This structure was derived from HII regions and molecular clouds (e.g. Russeil 2003); the Galactic bar is shown with an orientation of 14 $^\circ$ and 6 kpc of total length (Freudenreich 1998; Vallée 2005). We also show, for comparison, the WEBDA OCs with known age and distance from the Sun separated in two age groups of clusters younger or older than 1 Gyr.

Figure 11 shows that all directions present a decreasing number of detected OCs for distances farther than $\sim$ 2 kpc from the Sun. This can be explained by completeness (due to crowding and high background levels) and enhanced disruption rates, which begin to critically affect OCs in regions more distant than $\sim$ 2 kpc from the Sun, especially towards the bulge (e.g. Bonatto et al. 2006). The inner Galaxy presents high dissolution rates, related to dynamical interactions with the disk, the tidal pull of the bulge, and collisions with giant molecular clouds (e.g. Friel 1995; Bergond et al. 2001; Bonatto & Bica 2007a). Consequently, old OCs are mainly found outside the solar circle, a region with relatively low tidal stress. In contrast, the presence of bright stars allows young OCs to be detected farther than the old ones, even towards the central Galaxy.

The spatial distribution of the present Teutsch sample roughly matches that of the WEBDA OCs, with the distant ones restricted essentially to the $2{\rm nd}$ and $3\rm {rd}$ quadrants. Most of them are located between (or close to) the Perseus and Sagittarius-Carina arms, with seven others that are beyond the Perseus arm.

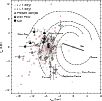
$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig11.eps}} \end{figure}$	Figure 11: Schematic projection of the Galaxy, as seen from the North Pole, with 7.2 kpc as the Sun's distance to the Galactic centre, in which the projected distribution of the present Teutsch star clusters (triangles) is compared to the WEBDA OCs younger (circles) and older than 1 Gyr (squares). Clusters with PMS stars are shown as filled triangles. Main Galactic structures are identified.
Open with DEXTER

7.3 Relations with cluster size

Despite some scatter, a first-order dependence of cluster size on Galactocentric distance shows up in Fig. 12 (panel a), similar to what has already been observed by, e.g. Lyngå (1982), Tadross et al. (2002), and van den Bergh et al. (1991). Although with more scatter, a similar relation occurs for cluster size and height over the Galactic plane $\vert\mbox{$Z_{\rm GC}$ }\vert$ (panel b). Both relations are consistent with a lower frequency of encounters with giant molecular clouds and the disk for OCs at large Galactocentric distances and high $\vert\mbox{$Z_{\rm GC}$ }\vert$ , with respect to those orbiting in the inner Galaxy and/or closer to the plane. However, part of the $\mbox{$R_{\rm RDP}$ }\times \vert\mbox{$Z_{\rm GC}$ }\vert$ relation may arise from differential completeness. Given that the average background+foreground contamination decreases with increasing $\vert\mbox{$Z_{\rm GC}$ }\vert$ , the external parts of an OC (where the surface brightness is intrinsically low) can be detected at larger distances (from the cluster centre) for high- $\vert\mbox{$Z_{\rm GC}$ }\vert$ objects than for those near the plane (Bonatto et al. 2006). Thus, on average, high- $\vert\mbox{$Z_{\rm GC}$ }\vert$ clusters tend to seem bigger than those near the plane.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig12.eps}} \end{figure}$

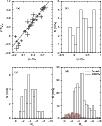
Figure 12:

Top: relation of the cluster radius with Galactocentric distance ( left) and distance from the plane ( right). Middle left: cluster and core radii are related as $R_{\rm RDP}\sim R_{\rm core}$ . Right: dependence of $R_{\rm RDP}$ on cluster age. Bottom left: relation between cluster mass and core radius. Grey circles show the reference OCs. Right: the average mass density falls with cluster radius as $\rho \sim R^{-3}_{\rm RDP}$ . Filled symbols indicate the clusters with conspicuous PMS. Arrows indicate the lower limit for the cluster mass and density. Shaded region in (c): $1\sigma$ fit uncertainty.

Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig13.eps}} \end{figure}$

Figure 13:

The integrated and reddening-corrected colours correlate (panel a)) as $\mbox{$(J-K_{\rm s})_{\rm O}$ }=(-0.05\pm0.02)+(1.39\pm0.05)\times\mbox{$(J-H)_{\rm O}$ }$ . Panels b) and c): histograms with the number of OCs within bins of $(J-H)_{\rm O}$ and M_J. Panel d): the extrapolated M_V values of the Teutsch sample (shaded histogram) is compared to the Galactic OCs (empty histogram) of Lata et al. (2002) and Battinelli et al. (1994).

Open with DEXTER

Panel (c) suggests that the present Teutsch OCs follow the relatively tight correlation between core and cluster radius that has been derived for a sample of bright and nearby OCs (e.g. Bonatto & Bica 2009c, and references therein). Such a relation is described by $R_{\rm RDP}=(8.9\pm0.3)\times R_{\rm core}^{(1.0\pm0.1)}$ , which suggests that both radii undergo a similar scaling, in the sense that, on average, large clusters tend to have large cores.

The relation between cluster radius and age, which is intimately related to cluster survival/dissociation rates, is examined in panel (d). While some of the clusters appear to expand as they age, others seem to shrink, with a bifurcation occurring at $\sim$ 1 Gyr. The same applies to the core radius, given the correlation between $R_{\rm RDP}$ and $R_{\rm c}$ (c). A similar relation of core radius with age has been observed by Mackey & Gilmore (2003) in LMC and SMC star clusters. Mackey & Gilmore (2008) attributed the slow $R_{\rm core}$ contraction to dynamical relaxation and/or core collapse. The expansion may come from stellar evolution-related mass loss in a mass-segregated or centrally concentrated cluster, and from heating due to a significant population of black holes that are scattered into the cluster halo or ejected from the cluster (e.g. Mackey et al. 2007; Merritt et al. 2004).

Table 5: Integrated magnitude and colours.

As discussed in Bonatto & Bica (2009b), when the projected mass density of a star cluster follows a King-like profile (e.g. Bonatto & Bica 2008a), the cluster mass ( $M_{\rm clus}$ ) can be expressed as a function of the core radius and the central surface mass density ( $\sigma_{\rm M0}$ ) according to $M_{\rm clus}\approx13.8\sigma_{\rm M0}~R^2_{\rm C}$ . The distribution of the present Teutsch OCs in the plane $\mbox{$R_{\rm c}$ }\times M_{\rm clus}$ is shown in panel (e), where we also include the sample of bright and nearby OCs (Bonatto & Bica 2009c, and references therein) for comparison. Similar to the reference sample, most of the Teutsch clusters are constrained within $\rm 30\la\sigma_{M0}~(\mbox{$M_\odot$ }~pc^{-2})\la1000$ . The exceptions are Teu 31, 79, and 124, which present the smallest core radii (Table 2) of the sample and indeed have RDPs (Figs. 8, 9) that suggest a high central concentration of stars (and mass).

Finally, we investigated the distribution of the Teutsch clusters on the plane cluster radius and average mass density, $R_{\rm RDP}$ vs. $\rho$ (panel f). The density decreases smoothly with cluster radius - over the full radius ( $\rm0.4\la\mbox{$R_{\rm RDP}$ }(pc)\la9$ ) and density ( $0.1\la\rho(\mbox{$M_\odot$ }~{\rm pc}^{-3})\la600$ ) scales - as $\rho\propto R^{-(3.0\pm0.3)}_{\rm RDP}$ , as for the sample of starburst clusters studied by Pfalzner (2009). Both radius and density scales overlap those of the starburst and leaky clusters of Pfalzner (2009), which has clusters more massive than $10^3~\mbox{$M_\odot$ }$ and density within the very wide range $10^{-2}\la\rho(\mbox{$M_\odot$ }~{\rm pc}^{-3})\la10^{6}$ . The boundary between starburst and leaky clusters occurs at $R_{\rm RDP}\sim4$ pc and $\rho\sim100~\mbox{$M_\odot$ }~\rm pc^{-3}$ . The $\rho \sim R^{-3}_{\rm RDP}$ dependence (in clusters younger than $\sim$ 20 Myr and more massive than $\sim$ $10^3~\mbox{$M_\odot$ }$ - Pfalzner 2009) is taken as consequence of simple diffusion, in the sense that the clusters expand without further mass loss (which would lead to a steeper dependence, such as $\rho\sim R^{-4}_{\rm RDP}$ ).

7.4 Integrated colours and magnitudes

The decontaminated photometry (Sect. 3) and structural parameters (Sect. 5) are used to compute the integrated (apparent and absolute) magnitudes and reddening-corrected colours for the 2MASS bands. Since the decontamination efficiency is lower than 100% (Sect. 3), we start by applying the colour-magnitude filter to the decontaminated photometry. Then we sum the flux (for a given band) of all stars within $R\le\mbox{$R_{\rm RDP}$ }$ (Table 2) to compute the cluster+residual field stars flux ( $F_J^{\rm cl+fs}=\sum 10^{-0.4J}$ ). The same is done for all the comparison field stars, to estimate the residual contamination flux ( $F_{\rm fs}$ ). Thus, the integrated magnitude is given by $m_J=-2.5\log\left(F_J^{\rm cl+fs}- \Omega\times F_J^{\rm fs}\right)$ , where $\Omega$ is the ratio between the projected areas of the cluster and the comparison field. This procedure is applied to the J, H, and $K_{\rm s}$ bands, and should minimise decontamination efficiency effects.

Since most of the evolved clusters contain giant and MSTO stars (Figs. 1-6), which by far dominate the luminosity, the integrated magnitudes should not be significantly affected by not detecting the low-MS stars associated with the depth-limited 2MASS photometry. Reddening and distance from the Sun (for the absolute magnitude and reddening-corrected colours) are those computed in Sect. 4, and the results are given in Table 5. Figure 13 (panel a) shows that the $(J-K_{\rm s})_{\rm O}$ and $(J-H)_{\rm O}$ colours are tightly correlated according to $\mbox{$(J-K_{\rm s})_{\rm O}$ }=(-0.05\pm0.02)+(1.39\pm0.05)\times\mbox{$(J-H)_{\rm O}$ }$ , so we can restrict the remaining analysis to $(J-H)_{\rm O}$ . The reddening-corrected $(J-H)_{\rm O}$ colours are roughly distributed (b) around the average value $\mbox{$(J-H)_{\rm O}$ }\approx0.3$ , with a $\pm0.5$ mag spread. The absolute J magnitude distributes nearly as a Gaussian around the average value $\langle M_J\rangle \approx-4$ , with a $\pm$ 1.7 mag standard deviation.

Finally, we use the relation between M_V and M_J, $M_V = (1.41\pm0.27)+ (0.96\pm0.03)\times M_J$ , derived for Galactic globular clusters by Bonatto & Bica (2010b) to estimate the absolute V magnitude of the Teutsch OCs. This relation was derived for the relatively wide magnitude range $-12\la M_J\la-6.5$ . Extrapolating it to the M_J values derived for our Teutsch clusters, we find M_V values in the range $-6\la M_V\la0$ (panel d of Fig. 13 and Table 5). We now compare the Teutsch M_V values with those measured for 140 Galactic OCs (MWOCs) by Lata et al. (2002) together with 106 OCs of Battinelli et al. (1994). Most ( $\approx$ $72\%$ ) of the MWOCs have M_V within $-5.5\la M_V\la-2.5$ , but the remaining ones can be as luminous as $M_V\approx-10$ . Clearly, our Teutsch clusters, in general, appear to be intrinsically faint in the optical, with an M_V distribution somewhat biased to the low-luminosity tail of the MWOCs distribution.

8 Summary and conclusions

In the present paper we have investigated the nature of 34 unstudied Teutsch clusters, and derived their astrophysical parameters. Distributed over all Galactic quadrants, we analysed them with field-star decontaminated 2MASS photometry that, by enhancing CMD evolutionary sequences and producing stellar RDPs that strongly contrast with the background, yields constrained astrophysical parameters. We could derive fundamental parameters for 33 objects, with the exception of (the apparently too distant) Teu 53.

Since the Teutsch clusters have been discovered in the near-infrared, we derived relatively high reddening values for some clusters, $0.1\la\mbox{$E(B-V)$ }\la3.0$ (or equivalently, $0.3\la\mbox{$A_V$ }\la9$ ). Also, about half of the sample is located more distant than $\mbox{$d_\odot$ }=3$ kpc from the Sun. The absolute J magnitudes distribute around $\langle M_J\rangle \approx-4\pm1.7$ , while the M_V distribution is shifted about 2 mag towards fainter values. This suggests that our sample is essentially composed of low-luminosity clusters in the optical. In general, the stellar RDPs are highly contrasted with respect to the background and follow the King-like profile for most of the radial range. Cluster size correlates with Galactocentric distance and, to a lesser degree, with distance to the plane. Both relations are consistent with a low frequency of tidal stress (as well as low degree of field contamination), associated with large Galactocentric distances and high- $\vert\mbox{$Z_{\rm GC}$ }\vert$ regions. We also found that the average mass density scales with cluster radius as $\rho\sim R^{-3}$ . In clusters younger than $\sim$ 20 Myr and more massive than $\sim$ $10^3~\mbox{$M_\odot$ }$ , this relation is typical of expansion by simple diffusion (Pfalzner 2009).

With respect to the age, 8 clusters are younger than $\sim$ 30 Myr (7 still hosting PMS stars), and 21 have ages within 100 Myr-900 Myr. Of particular interest is the possibility of Teu 43, 50, and 77 having ages around 2-3 Gyr, while Teu 124 may be a significantly older cluster, probably reaching $\sim$ 7 Gyr.

Given the several dissolution mechanisms originating in its substructures, our Galaxy is a harsh environment for star clusters, especially the low-mass ones, to the point that most do not survive beyond a few 10² Myr. In this context, besides deriving astrophysical parameters for a significant sample of unstudied clusters, the main relevance of the present work lies in identifying open clusters older than several 10² Myr. In turn, an improved statistics on the population of clusters undergoing such evolved phases can be used to constrain the dissolution-time scale in the Galaxy.

Acknowledgements

We thank an anonymous referee for interesting comments and suggestions. We acknowledge support from the Brazilian Institution CNPq. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research made use of the WEBDA database, operated at the Institute for Astronomy of the University of Vienna. This research made use of NASA's Astrophysics Data System Service. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France.

Appendix B: Metallicity estimate with Padovaisochrones

Our CMD analysis - and subsequent derivation of fundamental parameters - is based on the updated set of Padova isochrones, whose distinctive features are centred mostly on the greatly-improved treatment of the thermally-pulsating asymptotic giant branch (TP-AGB) phase. The updated isochrones preserve several peculiarities associated with the TP-AGB tracks, i.e. the cool tails of C-type stars (by using proper molecular opacities as convective dredge-up occurs along the TP-AGB), the bell-shaped sequences in CMDs for stars with hot-bottom burning, the pulsation mode changes between fundamental and first overtone, the sudden changes in mean mass-loss rates as the surface chemistry changes from M- to C-type, etc. (Marigo et al. 2008). Isochrones are available for any age within 0-17 Gyr, metallicities within $0.0001\le Z\le0.03$ ( $-2.28\le \rm [Fe/H]\le+0.2$ ), and masses in the range $0.15\le m(\mbox{$M_\odot$ })\le100$ . We now discuss the possibility of using Padova isochrones and 2MASS photometry to estimate metallicity.

As discussed by, e.g. Friel (2002, 1995), the location of a given OC in the Galaxy seems to be more important for determining its overall metallicity than the age. Indeed, both works show a nice trend towards decreasing OC metallicity with increasing Galactocentric distance. On the other hand, they also point to a lack of correlation with cluster age. These works show that the observed OC metallicities, in general, range from solar ( $\rm [Fe/H]=0$ , or Z=0.019) to sub solar ( $\rm [Fe/H]=-0.5$ , $Z=0.006\approx0.3~Z_\odot$ ) values. A similar metallicity range is obtained when we consider the observed metallicity gradient (Fig. 2 in Friel 2002) coupled to the derived Galactocentric distances of the present cluster sample (Sect. 4).

$\begin{figure}\resizebox{9cm}{!}{\includegraphics{Fig14.eps}} \end{figure}$	Figure B.1: Comparison among Padova isochrones of different ages (10 Myr, 100 Myr, 500 Myr, and 1 Gyr) and metallicities ( $\rm [Fe/H]=-0.5,~0.0,~{\rm and} +0.2$ ).
Open with DEXTER

Considering the above, we compare in Fig. B.1 isochrones of ages that characterise the values found for the present OCs (Sect. 4) and different metallicities. As the lower limit to the metallicity, we use $\rm [Fe/H]=-0.5$ (Friel 2002), while for the upper limit we take the highest available Padova metallicity, $\rm [Fe/H]=+0.2$ .

The metal-rich isochrones are essentially indistinguishable in the near infrared, while differences with respect to lower metallicities are restricted to stars brighter than the MSTO and ages younger than $\sim$ 500 Myr. Basically, metal-poor isochrones present somewhat brighter ( $\Delta\mbox{$J$ }\approx0.5$ mag) and bluer ( $\Delta\mbox{$(J-H)$ }\approx0.15$ mag) giant clumps and red-giant branches. Thus, it is difficult to assign a precise metallicity for poorly-populated clusters (especially with respect to evolved stars), such as those dealt with in this paper (Figs. 1-7).

References

Allison, R. J., Goodwin, S. P., Parker, R. J., et al. 2009, ApJ, 700, L99
Battinelli, P., Brandimarti, A., & Capuzzo-Dolcetta, R. 1994, A&AS, 104, 379
Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227
van den Bergh, S., Morbey, C., & Pazder, J. 1991, ApJ, 375, 594
Bergond, G., Leon, S., & Guilbert, J. 2001, A&A, 377, 462
Bessel, M. S., & Brett, J. M. 1988, PASP, 100, 1134
Bica, E., Bonatto, C., & Camargo, D. 2008, MNRAS, 385, 349
Bonatto, C., Bica, E., & Girardi, L. 2004, A&A, 415, 571
Bonatto, C., Kerber, L. O., Bica, E., & Santiago, B. X. 2006, A&A, 446, 121
Bonatto, C., & Bica, E. 2006, A&A, 455, 931
Bonatto, C., & Bica, E. 2007a, A&A, 473, 445
Bonatto, C., & Bica, E. 2007b, MNRAS, 377, 1301
Bonatto, C., & Bica, E. 2008a, A&A, 477, 829
Bonatto, C., & Bica, E. 2009a, MNRAS, 392, 483
Bonatto, C., & Bica, E. 2009b, MNRAS, 394, 2127
Bonatto, C., & Bica, E. 2009c, MNRAS, 397, 1915
Bonatto, C., & Bica, E. 2010a, A&A, 516, A81
Bonatto, C., & Bica, E. 2010b, MNRAS, 407, 1728
Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245
Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871
Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181
Dutra, C. M., Santiago, B. X., & Bica, E. 2002, A&A, 383, 219
Elmegreen, B. G. 2008, in Globular Clusters - Guides to Galaxies, ESO Astrophysics Symposia (Berlin Heidelberg: Springer), 2009, 87
Freudenreich, H. T. 1998, ApJ, 492, 495
Friel, E. D. 1995, ARA&A, 33, 381
Friel, E. D., Janes, K. A., Tavarez, M., et al. 2002, AJ, 124, 2693
Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195
Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752
Khalisi, E., Amaro-Seoane, P., & Spurzem, R. 2007, MNRAS, 374, 703
King, I. 1962, AJ, 67, 471
Kronberger, M., Teutsch, P., Alessi, B., et al. 2006, A&A, 447, 921
Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57
Lamers, H. J. G. L. M., & Gieles, M. 2006, A&AL, 455, 17
Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117
Lata, S., Pandey, A. K., Sagar, R., & Mohan, V. 2002, A&A, 388, 158
Lyngå, G. 1982, A&A, 109, 213
Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 338, 120
Mackey, A. D., Wilkinson, M. I., Davies, M. B., & Gilmore, G. F. 2007, MNRAS, 379, 40
Mackey, A. D., Gilmore, G. F., Davies, M. B., & Gilmore, G. F. 2008, MNRAS, 386, 65
Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883
Merritt, D., Piatek, S., Portegies Zwart, S., & Hemsendorf, M. 2004, ApJ, 608, 25
Momany, Y., Zaggia, S., Gilmore, G., et al. 2006, A&A, 451, 515
Naylor, T., & Jeffries, R. D. 2006, MNRAS, 373, 1251
Oort, J. H. 1958, in Ricerche Astronomiche, 5, 415, Specola Vaticana, Proc. of a Conference at Vatican Observatory, Castel Gandolfo, May 20-28, 1957, ed. D. J. K. O'Connell
Pavani, D. N., & Bica, E. 2007, MNRAS, 468, 139
Pfalzner, S. 2009 A&A, 498, 37
Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R.-D. 2006, A&A, 445, 545
Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Röser, S., & Scholz, R.-D. 2007, A&A, 468, 151
Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Röser, S., & Scholz, R.-D. 2008, A&A, 477, 165
Russeil, D. 2003, A&A, 397, 133
Skrutskie, M., Schneider, S. E., Stiening, R., et al. 1997, in The Impact of Large Scale Near-IR Sky Surveys, ed. F. Garzon, B. Burton, N. Epchtein, A. Omont, & P. Persi (Netherlands: Kluwer), 210, 187
Spitzer, L. 1958, ApJ, 127, 17
Tadross, A. L., Werner, P., Osman, A., & Marie, M. 2002, NewAst, 7, 553
Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218
Vallée, J. P. 2005, AJ, 130, 56
Yadav, R. K. S., & Sagar, R. 2001, MNRAS, 328, 370

Online Material

Appendix A: LEDAS images

The images have been taken from LEDAS, with a field of view adequate to the angular dimension of each cluster. The same applies to the image band. Information on field of view and image band can be read directly on each image.

$\begin{figure}\par\mbox{\includegraphics[width=4.5cm]{Teu54.eps}\includegraphics... ...width=4.5cm]{Teu14a.eps}\includegraphics[width=4.5cm]{Teu13.eps} }\end{figure}$	Figure A.1: LEDAS images of the target clusters. From top to bottom and left to right: Teu 54, 40, 49, and 64; Teu 144, 11, 27, and 79; Teu 48, 52, 126, and 7; Teu 12, 66, 14a, and 13.
Open with DEXTER

$\begin{figure}\par\includegraphics[width=4.5cm]{Teu23.eps}\includegraphics[width... ...ics[width=4.5cm]{Teu45.eps}\includegraphics[width=4.5cm]{Teu39.eps} \end{figure}$	Figure A.2: Same as Fig. A.1 for Teu 23, 76, 55, and 132; Teu 124, 60, 77, and 43; Teu 2, 28, 44, and 31; Teu 85, 106, 45, and 39.
Open with DEXTER

$\begin{figure}\par\mbox{\includegraphics[width=4.5cm]{Teu162.eps}\hspace*{9cm} \includegraphics[width=4.5cm]{Teu53.eps} } \par \end{figure}$	Figure A.3: Same as Fig. A.1 for Teu 162 and 53.
Open with DEXTER

Footnotes

... clusters: Appendix A is only available in electronic form at http://www.aanda.org
... WEBDA: http://www.univie.ac.at/webda
... Candidates: http://www.astro.iag.usp.br/wilton/
... photometry: http://www.ipac.caltech.edu/2mass/releases/allsky/
... SIMBAD: simbad.u-strasbg.fr/simbad/
... Candidates'': http://www.astro.iag.usp.br/ wilton/
... VizieR: vizier.u-strasbg.fr/viz-bin/VizieR?-source=II/246
... regions: This step is iterative, since we first build the RDP (Sect. 5) to estimate the cluster size and the location of the comparison field. After decontamination, we build the colour-magnitude filter, rebuild the RDP, recompute the cluster size, and repeat the decontamination.
... filters: stev.oapd.inaf.it/cgi-bin/cmd
... match: In the sense that any isochrone solution that occurs within the photometric error bars is taken as acceptable.
... cluster: They are wide enough to take photometric uncertainties and binaries into account (or other multiple systems).
... feature: Alternatively, clusters that form dynamically cool and with significant substructure will probably develop an irregular central region, unless such a region collapses and smooths out the initial substructure (Allison et al. 2009).
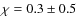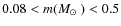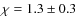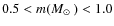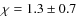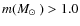... MF: $\chi=0.3\pm0.5$ for $0.08<m(\mbox{$M_\odot$ })<0.5$ , $\chi=1.3\pm0.3$ for $0.5<m(\mbox{$M_\odot$ })<1.0$ , and $\chi=1.3\pm0.7$ for $m(\mbox{$M_\odot$ })>1.0$ .
...Battinelli et al. (1994): Both samples have similar M_V distributions. For the OCs in common we used the more recent values of Lata et al. (2002).
... LEDAS: Leicester Database and Archive Service (LEDAS) DSS/DSS-II service on ALBION; ledas-www.star.le.ac.uk/DSSimage.

All Tables

Table 1: Fundamental parameters.

Table 2: Structural parameters derived from the RDPs.

Table 3: Stellar mass estimate.

Table 4: Stellar mass estimate for the clusters with PMS.

Table 5: Integrated magnitude and colours.

All Figures

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig1.eps}} \end{figure}$	Figure 1: CMDs of Teu 54, 40, 49, 64, and 144 for a representative cluster region (top panels) and the equal-area comparison field (middle). The decontaminated CMDs (bottom) are shown with the isochrone solution (solid line) and the colour-magnitude filter (shaded polygon).
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig2.eps}} \end{figure}$	Figure 2: Same as Fig. 1 for Teu 11, 27, 79, 48, and 52.
Open with DEXTER
In the text

$\begin{figure} \resizebox{9cm}{!}{\includegraphics{Fig3.eps}} \end{figure}$	Figure 3: Same as Fig. 1 for Teu 126, 7, 12, 66, and 14a.
Open with DEXTER
In the text

$\begin{figure} \resizebox{9cm}{!}{\includegraphics{Fig4.eps}} \end{figure}$	Figure 4: Same as Fig. 1 for Teu 13 ( left panel). The remaining clusters (Teu 23, 7, 76, 55, and 132) are shown in $\mbox{$J$ }\times\mbox{$(J-K_{\rm s})$ }$ CMDs. Also shown is the reddening vector for $\mbox{$A_V$ }=0$ to $\mbox{$A_V$ }=5$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig5.eps}} \end{figure}$	Figure 5: Same as Fig. 1 for Teu 124, 50, 77, 43, and 2. Isochrones younger than the adopted ones are also shown for an estimate of a lower limit to the age.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig6.eps}} \end{figure}$	Figure 6: Same as Fig. 1 for Teu 28, 44, 31, 85, and 106.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig7.eps}} \end{figure}$	Figure 7: Same as Fig. 1 but with $\mbox{$J$ }\times\mbox{$(J-K_{\rm s})$ }$ CMDs of Teu 45, 39, 162, and 53.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig8.eps}} \end{figure}$	Figure 8: Stellar RDPs (empty circles), the best-fit King-like profile (solid line), the $1\sigma$ uncertainty (light-shaded region), and the residual background level (shaded polygon).
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig9.eps}} \end{figure}$	Figure 9: Same as Fig. 8 for the remaining clusters. It was not possible to fit the King-like profile for some cases.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig10.eps}} \end{figure}$	Figure 10: General properties of the present OCs (filled circles) compared to Galactic clusters (empty circles) taken from Dias et al. (2002) and WEBDA (panels a), b), and c)), and Piskunov et al. (2008) d). All cases are investigated with distribution functions.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig11.eps}} \end{figure}$	Figure 11: Schematic projection of the Galaxy, as seen from the North Pole, with 7.2 kpc as the Sun's distance to the Galactic centre, in which the projected distribution of the present Teutsch star clusters (triangles) is compared to the WEBDA OCs younger (circles) and older than 1 Gyr (squares). Clusters with PMS stars are shown as filled triangles. Main Galactic structures are identified.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig12.eps}} \end{figure}$	Figure 12: Top: relation of the cluster radius with Galactocentric distance ( left) and distance from the plane ( right). Middle left: cluster and core radii are related as $R_{\rm RDP}\sim R_{\rm core}$ . Right: dependence of $R_{\rm RDP}$ on cluster age. Bottom left: relation between cluster mass and core radius. Grey circles show the reference OCs. Right: the average mass density falls with cluster radius as $\rho \sim R^{-3}_{\rm RDP}$ . Filled symbols indicate the clusters with conspicuous PMS. Arrows indicate the lower limit for the cluster mass and density. Shaded region in (c): $1\sigma$ fit uncertainty.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{Fig13.eps}} \end{figure}$	Figure 13: The integrated and reddening-corrected colours correlate (panel a)) as $\mbox{$(J-K_{\rm s})_{\rm O}$ }=(-0.05\pm0.02)+(1.39\pm0.05)\times\mbox{$(J-H)_{\rm O}$ }$ . Panels b) and c): histograms with the number of OCs within bins of $(J-H)_{\rm O}$ and M_J. Panel d): the extrapolated M_V values of the Teutsch sample (shaded histogram) is compared to the Galactic OCs (empty histogram) of Lata et al. (2002) and Battinelli et al. (1994).
Open with DEXTER
In the text

$\begin{figure}\resizebox{9cm}{!}{\includegraphics{Fig14.eps}} \end{figure}$	Figure B.1: Comparison among Padova isochrones of different ages (10 Myr, 100 Myr, 500 Myr, and 1 Gyr) and metallicities ( $\rm [Fe/H]=-0.5,~0.0,~{\rm and} +0.2$ ).
Open with DEXTER
In the text

$\begin{figure}\par\mbox{\includegraphics[width=4.5cm]{Teu54.eps}\includegraphics... ...width=4.5cm]{Teu14a.eps}\includegraphics[width=4.5cm]{Teu13.eps} }\end{figure}$	Figure A.1: LEDAS images of the target clusters. From top to bottom and left to right: Teu 54, 40, 49, and 64; Teu 144, 11, 27, and 79; Teu 48, 52, 126, and 7; Teu 12, 66, 14a, and 13.
Open with DEXTER
In the text

$\begin{figure}\par\includegraphics[width=4.5cm]{Teu23.eps}\includegraphics[width... ...ics[width=4.5cm]{Teu45.eps}\includegraphics[width=4.5cm]{Teu39.eps} \end{figure}$	Figure A.2: Same as Fig. A.1 for Teu 23, 76, 55, and 132; Teu 124, 60, 77, and 43; Teu 2, 28, 44, and 31; Teu 85, 106, 45, and 39.
Open with DEXTER
In the text

$\begin{figure}\par\mbox{\includegraphics[width=4.5cm]{Teu162.eps}\hspace*{9cm} \includegraphics[width=4.5cm]{Teu53.eps} } \par \end{figure}$	Figure A.3: Same as Fig. A.1 for Teu 162 and 53.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.