| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 5 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201014997 | |
| Published online | 20 October 2010 | |
Diluting the material forming the second generation stars in globular clusters: the contribution by unevolved stars
(Research Note)
R. G. Gratton1 - E. Carretta2
1 -
INAF-Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122
Padova, Italy
2 -
INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127
Bologna, Italy
Received 17 May 2010 / Accepted 14 July 2010
Abstract
In this short communication we consider the possibility that stars
less evolved than the polluters
are the source of the dilution needed to explain the observed composition of
second-generation globular cluster (GC) stars and the Na-O and Mg-Al anticorrelations. If these
stars can lose 0.5-1% of their mass during the relevant epochs, there is enough diluting
material to produce the observed anticorrelations. In this case, the original mass
of proto-GCs was several tens times higher than the current
mass of GCs. While not strictly impossible, this is a stringent hypothesis that needs
more support. Should this
scenario be found true, then the link between the primordial (first-generation)
population in GC and the field population would be very strong.
Key words: stars: abundances - stars: atmospheres - stars: population II - globular clusters: general
1 Introduction
For the past few years, it has been known that at least two stellar generations are
present in all globular clusters (GCs) (Gratton et al. 2001; Ramirez & Cohen 2002;
see Gratton et al. 2004, for a review). Extensive studies have shown that
the second generation, characterized by overabundance of Na and sometimes
Al, and by a deficiency in O (that has been transformed into N) is dominant,
since it is responsible for about 2/3 of the stars (Carretta et al. 2009a); the
remaining ![]() 1/3 of the stars have a composition that is virtually indistinguishable
from that of field stars. The stars overabundant in Na and deficient in O
are generally distributed over a range of values in [Na/Fe] and [O/Fe], describing an
Na-O anticorrelation and a similar (but not identical) Al-Mg one (Kraft 1994;
see Carretta et al. 2009a,b, for several examples). Prantzos &
Charbonnel (2006) show that these anticorrelations can be reproduced by
assuming a typical polluter composition, which is then diluted by different
amounts of pristine material. Such a dilution
would also help explain the constraints from observed Li abundances, because significant
amounts of this easily destroyed element appear to be present in most
GC stars (Bonifacio et al. 2002; Pasquini et al. 2005;
Lind et al. 2009; D'Orazi et al. 2010).
1/3 of the stars have a composition that is virtually indistinguishable
from that of field stars. The stars overabundant in Na and deficient in O
are generally distributed over a range of values in [Na/Fe] and [O/Fe], describing an
Na-O anticorrelation and a similar (but not identical) Al-Mg one (Kraft 1994;
see Carretta et al. 2009a,b, for several examples). Prantzos &
Charbonnel (2006) show that these anticorrelations can be reproduced by
assuming a typical polluter composition, which is then diluted by different
amounts of pristine material. Such a dilution
would also help explain the constraints from observed Li abundances, because significant
amounts of this easily destroyed element appear to be present in most
GC stars (Bonifacio et al. 2002; Pasquini et al. 2005;
Lind et al. 2009; D'Orazi et al. 2010).
The observed homogeneity in heavy elements (Fe, ![]() - and Fe-group
species) in GCs and the very peculiar chemical composition of the polluters
strongly suggest that
they only belong to a limited range of masses, which marginally
contributes to the overall galactic chemical enrichment. When combined with
the large fraction of GC stars belonging to the second generation,
this suggests that only a small fraction of the primordial population remains
bound to the cluster and that the original episode of star formation
was much larger (Prantzos & Charbonnel 2006; Carretta et al. 2010).
- and Fe-group
species) in GCs and the very peculiar chemical composition of the polluters
strongly suggest that
they only belong to a limited range of masses, which marginally
contributes to the overall galactic chemical enrichment. When combined with
the large fraction of GC stars belonging to the second generation,
this suggests that only a small fraction of the primordial population remains
bound to the cluster and that the original episode of star formation
was much larger (Prantzos & Charbonnel 2006; Carretta et al. 2010).
While these facts have been assessed well, a number of important issues still remain open, precluding full understanding of the early phases of these massive clusters. They include (i) the nature of the polluters, which may be either massive asymptotic giant branch (AGB) stars undergoing hot bottom burning (Ventura et al. 2001) or fast-rotating massive stars (FRMS; Decressin et al. 2007), and other hypotheses also proposed (e.g. massive binaries, de Mink et al. 2009); (ii) the distribution of stars along the anticorrelation, which might be either continuous or clumped at some specific value (see e.g. the case of NGC 2808: D'Antona & Caloi 2004; Carretta et al. 2006, etc.); and (iii) the origin of the diluting material. In this short paper, we focus our attention on this last issue.
D'Ercole et al. (2008) and Decressin et al. (2007) have considered scenarios for justifying this diluting material. According to Decressin et al. (2007), second-generation stars form in circumstellar disks around FRMS. Depending on the epoch when mass loss occurs, the polluted material is mixed with various amounts of unprocessed material previously expelled by the outer regions of the same massive stars, so that stars form with progressively higher fraction of polluting material. This scenario has serious difficulties in explaining clumpy distribution of stars along the Na-O anticorrelation, such as those observed in NGC 2808. Furthermore, it is not clear how this scenario can generate a bound cluster.
On the other hand, D'Ercole et al. (2008) proposes that the slow winds from the massive AGB stars generate a cooling flow, creating a very dense cloud from which second-generation stars form. In their scenario, dilution is obtained by assuming that part of the original gas is left in a torus, which for some not entirely clear reasons is not polluted by the ejecta of the core collapse supernovae of the primordial population, and then after some time falls back onto the dense cloud that is forming the second-generation stars, hence stars with a progressively larger fraction of diluting material form. Both a clumpy distribution (see also D'Ercole et al. 2010) and a strongly bound cluster can be easily obtained. However, the hypothesis that a reservoir of pristine gas exists appears ad hoc, and somewhat unacceptable.
In this paper we explore an alternative origin for the reservoir of pristine gas, which combines concepts from both the Decressin et al. and D'Ercole et al. scenarios. We consider the possibility that the reservoir of pristine gas is produced by mass lost from less evolved stars (typically - but not only - main sequence stars) than those producing the polluting material. This hypothesis has several interesting features: (i) the mechanism is not ad hoc, since stars of lower mass than the polluters are surely losing some mass simultaneously to the more massive ones, which are in later evolutionary phases (actually, this mass should be incorporated into the hydrodynamical and chemical models); (ii) the material lost by these stars will still be unprocessed, but see discussion at the end of Sect. 4; (iii) we should not worry about the exact timing of the fallback of an unprocessed cloud; (iv) we do not expect this material to be significantly enriched by the core collapse supernovae of the primordial population. However, this hypothesis may work only if enough mass is lost by the lower mass stars at the relevant epoch, as discussed in the rest of this paper.
2 The basic idea
We need some material with original composition to dilute the polluted one, in
order to (i) reproduce the observed run of O and Na; and (ii) to have some Li saved.
Evidence for this last point comes from NGC 6397, where Bonifacio et al. (2002) find
![]() (Li)
(Li) ![]() 2.3 in most stars, and from NGC 6752 where Pasquini et al.
(2005) find in Na-rich/O-depleted stars
2.3 in most stars, and from NGC 6752 where Pasquini et al.
(2005) find in Na-rich/O-depleted stars ![]() (Li)
(Li) ![]() 1.93 for
1.93 for
![]() dex. In this hypothesis, Li should be depleted as O.
dex. In this hypothesis, Li should be depleted as O.
We note that the dilution factor in GCs is in the range 0-0.7![]() :
this is the amount required to place on the Na-O anticorrelation the
intermediate I stars, that represent the bulk of the cluster population
(see Gratton et al. 2010; Carretta et al. 2009a).
This means that the amount of primordial, diluting
material is roughly equal to half the amount of processed material.
However, to be conservative, we assumed that the diluting mass is
similar to the polluting one throughout this paper.
:
this is the amount required to place on the Na-O anticorrelation the
intermediate I stars, that represent the bulk of the cluster population
(see Gratton et al. 2010; Carretta et al. 2009a).
This means that the amount of primordial, diluting
material is roughly equal to half the amount of processed material.
However, to be conservative, we assumed that the diluting mass is
similar to the polluting one throughout this paper.
How it is possible to achieve this? The explanation proposed by D'Ercole et al. (2008) is some primordial gas saved from pollution by core-collapse SNe. An alternative solution, explored in this note, is to consider the mass lost from the stars less evolved than the polluters.
Our working hypotheses are:
- 1.
- the stars distribute by number as
n(M)=Mx. We assume a lower mass
limit of
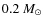 ,
and an upper limit of
,
and an upper limit of
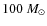 .
As an alternative,
we use the Kroupa (2001) mass function (between 0.01 and 100
.
As an alternative,
we use the Kroupa (2001) mass function (between 0.01 and 100 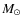 );
);
- 2.
- the polluted material comes from stars with masses in the mass range
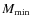 to
to
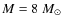 ,
and they lose all the mass except for
that is left in compact remnants. This is assumed to be a linear function of
the original mass of the star, which is
,
and they lose all the mass except for
that is left in compact remnants. This is assumed to be a linear function of
the original mass of the star, which is
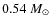 for a star of
for a star of
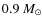 ,
and
,
and
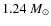 for a star of
for a star of 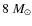 (see Ferrario et al. 2005);
(see Ferrario et al. 2005);
- 3.
- The diluting primordial material comes from mass lost by all stars with masses
less than
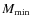 (including low-mass stars).
(including low-mass stars).
3 The toy model
In our toy model we consider that all stars with masses
less than
![]() lose a
fraction
lose a
fraction ![]() of their mass during the relevant phase.
For this case, the exponent of the mass function x, the fraction of mass
enclosed in stars in the different mass ranges, the values of
of their mass during the relevant phase.
For this case, the exponent of the mass function x, the fraction of mass
enclosed in stars in the different mass ranges, the values of ![]() required to produce as much diluting as polluting mass, and the ratio
between the mass in the primordial generation and in the GC
required to produce as much diluting as polluting mass, and the ratio
between the mass in the primordial generation and in the GC![]() , are listed in
Table 1.
, are listed in
Table 1.
Table 1:
Fraction of mass (![]() )
lost by less evolved stars assuming a maximum
polluter mass of
)
lost by less evolved stars assuming a maximum
polluter mass of ![]() .
.
The minimum mass required to produce the right amount of unpolluted material
from stars is given roughly by the relation:
if
An exam of the values listed in Table 1 shows that the ratio between the
original mass of the primordial population and that of the GC is roughly
given by ![]()
![]() .
Furthermore,
to have the right amount of diluting material,
.
Furthermore,
to have the right amount of diluting material, ![]() should be
about proportional to the range of masses of the polluters: a wider range
of masses requires a higher value of
should be
about proportional to the range of masses of the polluters: a wider range
of masses requires a higher value of ![]() .
.
As an alternative case we may consider a given value of e.g. x=-2.3 (or the Kroupa mass function) and assume that
the range of mass of the polluters is
always equal to ![]() .
In this way we get the values of Table 2.
On the other hand,
.
In this way we get the values of Table 2.
On the other hand, ![]() represents the total mass lost during the
relevant period. The length of this period depends on the range of mass under
consideration. The mass loss rates required to produce the same value
of
represents the total mass lost during the
relevant period. The length of this period depends on the range of mass under
consideration. The mass loss rates required to produce the same value
of ![]() should then scale inversely proportional to this length.
should then scale inversely proportional to this length.
Table 2:
Fraction of mass (![]() )
lost by less evolved stars assuming various
ranges of polluter masses and either x=-2.3 or the Kroupa (2001) mass function).
)
lost by less evolved stars assuming various
ranges of polluter masses and either x=-2.3 or the Kroupa (2001) mass function).
Table 3:
Age, turn-off mass,
![]() ,
and mass of AGB stars,
,
and mass of AGB stars,
![]() .
.
We quantified the relevant data in Table 3, using the isochrones
by Bertelli et al. (2008). The time required for the
evolution of 5-8 ![]() stars is from
stars is from
![]() to
to
![]() yr after the
start of the formation of primordial
generation stars, that is, the mass lost by less evolved stars over an interval of about
70 Myr may be used to dilute the polluting material. On the other hand,
if the polluters were limited to the range of masses from 7.3 to 8
yr after the
start of the formation of primordial
generation stars, that is, the mass lost by less evolved stars over an interval of about
70 Myr may be used to dilute the polluting material. On the other hand,
if the polluters were limited to the range of masses from 7.3 to 8 ![]() ,
the interval of time would be only 8 Myr. The same value of
,
the interval of time would be only 8 Myr. The same value of ![]() would
then require almost ten times higher mass loss rates. Since the length of the
useful interval of time scales with
would
then require almost ten times higher mass loss rates. Since the length of the
useful interval of time scales with
![]() more rapidly than
more rapidly than ![]() ,
a higher mass loss rate is required to produce the required dilution if
the range of mass is narrower. Alternatively, if the mass loss rate (for stars
of the same mass) is the same for all GCs, we should expect less dilution
(hence a more clumpy distribution of abundances along the anticorrelation)
for those GCs with a more restricted mass range for polluters.
,
a higher mass loss rate is required to produce the required dilution if
the range of mass is narrower. Alternatively, if the mass loss rate (for stars
of the same mass) is the same for all GCs, we should expect less dilution
(hence a more clumpy distribution of abundances along the anticorrelation)
for those GCs with a more restricted mass range for polluters.
4 Limits on 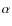
There are upper limits to ![]() from other observations and considerations;
for example,
from other observations and considerations;
for example, ![]() for solar type stars is limited because too much mass loss would not be
compatible with both Li depletion in the pre-main sequence phase and
observation of the Spite plateau, as well as with the dilution observed in
normal Population II stars at the base of the subgiant branch.
for solar type stars is limited because too much mass loss would not be
compatible with both Li depletion in the pre-main sequence phase and
observation of the Spite plateau, as well as with the dilution observed in
normal Population II stars at the base of the subgiant branch.
Unfortunately, the mass loss rates are largely uncertain. For solar type stars, Wood et al. (2002)
suggest
![]() ,
but also a saturation at young ages
(at
,
but also a saturation at young ages
(at
![]() /yr), with an uncertainty of a factor 5. The best estimate of the mass
lost during the epoch 40-110 Myr is
/yr), with an uncertainty of a factor 5. The best estimate of the mass
lost during the epoch 40-110 Myr is
![]() ,
but the upper
limit is
,
but the upper
limit is
![]() .
According to Holzwarth & Jardine (2007), a value 100 times solar
(
.
According to Holzwarth & Jardine (2007), a value 100 times solar
(
![]() /yr) is reasonable for solar type stars in this age range.
This makes the total mass lost of
/yr) is reasonable for solar type stars in this age range.
This makes the total mass lost of
![]() two orders of magnitudes too low over the relevant period.
On the other hand, empirical evidence (Lednicka & Stepien 2008) suggests an upper
limit of 0.05
two orders of magnitudes too low over the relevant period.
On the other hand, empirical evidence (Lednicka & Stepien 2008) suggests an upper
limit of 0.05 ![]() for Praesepe (0.7 Gyr). If this is lost at a constant
rate, it would give
for Praesepe (0.7 Gyr). If this is lost at a constant
rate, it would give
![]() ,
which is
,
which is
![]() /yr.
Integrated over
/yr.
Integrated over
![]() yr, this gives
yr, this gives
![]() .
.
In turn, the Li-dip may be explained if 0.05 ![]() is lost from 1.3
is lost from 1.3 ![]() (solar metallicity) stars (Schramm et al. 1990; see also Russell 1995). The
proposed mechanism is related to the main instability strip, with a mass loss rate of
(solar metallicity) stars (Schramm et al. 1990; see also Russell 1995). The
proposed mechanism is related to the main instability strip, with a mass loss rate of
![]() /yr. Integrated over 70 Myr, this yields
/yr. Integrated over 70 Myr, this yields
![]() .
.
Summarizing, an upper limit to mass lost during the 40-110 Myr epoch for a solar
type star is 0.01 ![]() .
This implies a maximum mass loss rate of
.
This implies a maximum mass loss rate of
![]()
![]() /yr. On the other hand, in our approach,
/yr. On the other hand, in our approach, ![]() is
a suitable average value for the fraction of mass lost during this phase
by all stars that are less evolved than those causing the pollution.
This average also includes (i) low-mass stars that are still in the
pre-main sequence phase at the relevent epoch (
is
a suitable average value for the fraction of mass lost during this phase
by all stars that are less evolved than those causing the pollution.
This average also includes (i) low-mass stars that are still in the
pre-main sequence phase at the relevent epoch (
![]() :
Di Criscienzo et al. 2009)
:
Di Criscienzo et al. 2009)![]() ; (ii) the same stars later providing the
polluting material, but in earlier evolutionary phases (e.g. while they are
in the Cepheids instability strip, see e.g. Neilson & Lester 2009); and
(iii) interacting binaries (see e.g. Mennickent et al. 2010). All these classes
of objects may have mass-loss rates (in units of the stellar mass) that are significantly
more than solar type stars of similar ages. The assumption of a value
; (ii) the same stars later providing the
polluting material, but in earlier evolutionary phases (e.g. while they are
in the Cepheids instability strip, see e.g. Neilson & Lester 2009); and
(iii) interacting binaries (see e.g. Mennickent et al. 2010). All these classes
of objects may have mass-loss rates (in units of the stellar mass) that are significantly
more than solar type stars of similar ages. The assumption of a value
![]() % therefore does not appear completely implausible.
% therefore does not appear completely implausible.
It should, however, be noticed that the chemical composition of the winds from these
other classes of stars might not precisely reflect the original composition.
Low-mass stars should have burnt Li during the pre-main sequence phase,
when they were still fully convective. If they contributed significantly
to the dilution required to explain the O-Na anticorrelation, then the Li
observed in second-generation stars with a high degree of dilution should have been
produced by the same polluters, and there should not be a simple Na-Li
anticorrelation. As a matter of fact, this is not at all excluded by
current observations (see e.g. D'Orazi & Marino 2010). For
the other classes of objects, Luck & Lambert (1992) made a chemical abundance
analysis of Cepheids in the LMC and SMC. The [O/Fe], [Na/Fe], [Mg/Fe], and
[Al/Fe] ratios are roughly solar, so that a putative wind from these stars
may contribute to the dilution needed to explain the Na-O and Mg-Al
anticorrelations. However, these stars are depleted in C and Li, with
evidence of dredge-up of N-rich material. For interacting
binaries, depletion of C and excesses of N have been found in most Algols
(Parthasarathy et al. 1983; Tomkin et al. 1993), and
even O is depleted in the more massive ![]() Lyr (Balachandran et al. 1986;
indeed, massive binaries have been proposed as a source of the polluting
material, rather than as diluters: de Mink et al. 2009). If these two classes
of objects were indeed the source of the diluters, we should then expect
that the Na-O and the C-N anticorrelations should appear quite different.
This prediction might be compared with the actual data (see e.g.
Briley et al. 2004).
Lyr (Balachandran et al. 1986;
indeed, massive binaries have been proposed as a source of the polluting
material, rather than as diluters: de Mink et al. 2009). If these two classes
of objects were indeed the source of the diluters, we should then expect
that the Na-O and the C-N anticorrelations should appear quite different.
This prediction might be compared with the actual data (see e.g.
Briley et al. 2004).
5 Limits on the ratio primordial population/GC
The ratio of primordial population/GC cannot be greater than the ratio between
the mass of the halo and the mass in GCs, which is ![]() 100. In the current
framework, this provides a lower
limit for
100. In the current
framework, this provides a lower
limit for ![]() ,
that is,
,
that is,
![]() .
.
If we assume
![]() and x=-2.3, we should expect a mass ratio
of primordial population to the GC of
and x=-2.3, we should expect a mass ratio
of primordial population to the GC of ![]() 40. In this framework,
to produce a cluster with a current mass of
40. In this framework,
to produce a cluster with a current mass of
![]() (like NGC 2808 or 47 Tuc
(like NGC 2808 or 47 Tuc![]() ), one
should start with
), one
should start with ![]()
![]() of gas with a very homogeneous
composition (
of gas with a very homogeneous
composition (![]() [Fe/H]
[Fe/H] ![]() 0.04 dex); possibly a value of
0.04 dex); possibly a value of ![]()
![]() for the cloud mass would be more reasonable, considering a
reasonable
for the cloud mass would be more reasonable, considering a
reasonable ![]() 0.5 star formation efficiency for the primordial (original)
generation. Star formation for the primordial generation cannot have lasted very long, or else SNe
would have either (i) stopped it or (ii) contributed to the nucleosynthesis. A
reasonable upper limit is 107 yr. Such a massive (
0.5 star formation efficiency for the primordial (original)
generation. Star formation for the primordial generation cannot have lasted very long, or else SNe
would have either (i) stopped it or (ii) contributed to the nucleosynthesis. A
reasonable upper limit is 107 yr. Such a massive (
![]() ,
stellar mass)
star-forming region should be very luminous (
,
stellar mass)
star-forming region should be very luminous (
![]() ).
).
Almost all (98.7%) of the original cluster population would have been lost from
the expansion of the cluster after SNe explosion and mass loss. The second
burst of star formation (the one producing the second generation) would then
be a much smaller episode. With a mass of
![]() of stars
produced, it should have a luminosity of MV=-14 at peak. At this
epoch, the fading original population should still have a luminosity of MV=-
16, dominating the compact central cluster of second-generation stars.
of stars
produced, it should have a luminosity of MV=-14 at peak. At this
epoch, the fading original population should still have a luminosity of MV=-
16, dominating the compact central cluster of second-generation stars.
Assuming a ratio M/L=2, all galactic GCs summed up have a mass of
![]() .
The primordial population should then be
.
The primordial population should then be ![]()
![]() .
This
requires that roughly half of the halo/thick disk mass comes from GCs
(see Gratton et al. 2010, in preparation, where we will discuss
the metallicity distribution and the element-to-element abundance ratios of the
primordial population, which are very similar to that of the halo-thick disk).
.
This
requires that roughly half of the halo/thick disk mass comes from GCs
(see Gratton et al. 2010, in preparation, where we will discuss
the metallicity distribution and the element-to-element abundance ratios of the
primordial population, which are very similar to that of the halo-thick disk).
6 Can the wind from main sequence stars contribute to the second generation?
Winds from main sequence stars are quite fast, with typical velocities of
a few hundred km s-1 (Neugebauer 1994; Dupree 2005). This is much higher than
the escape velocity from a proto-GC. Could this wind be contributing to the
second generation?
To address this issue, we follow the same arguments considered by Smith
(1999), who considered the case for dissipation of intracluster gas (lost at
low speed by red giants) from the energy injection by the high-velocity
wind from the main sequence. We should replace the wind by red giants with the
much stronger winds of AGB stars. The specific mass-loss rate for massive
AGB stars is about two orders of magnitude more than that for current red
giants:
![]() s-1. On the other hand,
the specific mass loss rate for the diluters should be comparable to that of
the AGB stars, or else dilution would be negligible.
s-1. On the other hand,
the specific mass loss rate for the diluters should be comparable to that of
the AGB stars, or else dilution would be negligible.
Neglecting cooling for the moment, the winds from the diluters are kept within
the cluster if Eq. (8) of Smith (1999) holds. Assuming
![]() ,
this equation requires that the
wind velocity from the polluter
,
this equation requires that the
wind velocity from the polluter
![]() satisfies the relation
satisfies the relation
![]() ,
where
,
where
![]() is the
line of sight velocity spread of the proto-GCs. Current values of
is the
line of sight velocity spread of the proto-GCs. Current values of
![]() are
are ![]() 20 km s-1 for almost all GCs. It is likely
that
20 km s-1 for almost all GCs. It is likely
that
![]() could have been slightly higher for proto-GCs.
We conclude that winds with velocities <100 km s-1 were almost certainly kept
within the clusters. These include potential polluters like red giants in those
phases preceding the AGB, close binaries, and perhaps surviving disks around
low-mass stars.
could have been slightly higher for proto-GCs.
We conclude that winds with velocities <100 km s-1 were almost certainly kept
within the clusters. These include potential polluters like red giants in those
phases preceding the AGB, close binaries, and perhaps surviving disks around
low-mass stars.
On the other hand, even faster winds could contribute to dilution if
the input kinetic energy is dissipated by radiative cooling. This may
happen if radiative cooling losses are greater than the heating due
to thermalization of the diluters' winds. To estimate when this may occur,
we use inequality (21) of Smith (1999), which must be solved
simultaneously with his Eq. (10). In this inequality, we should consider the
radiative cooling coefficient appropriate to the central temperature
of the intracluster wind, which can be taken from Faulkner & Freeman (1977),
as done by Smith (1999). Assuming a protocluster (core) radius of 1 pc and
central density of 105 ![]() pc-3 (which are typical values
for present GCs), we find that cooling was efficient at the relevant epoch
insofar
pc-3 (which are typical values
for present GCs), we find that cooling was efficient at the relevant epoch
insofar
![]() .
This value should
be taken only as an order of magnitude estimate, owing to the approximations
made and because several quantities are not well known. For instance, it
assumes a wind velocity from MS stars of 600 km s-1, and is valid for the
radius and densities considered above. It is possible that
proto-GCs were more compact (
.
This value should
be taken only as an order of magnitude estimate, owing to the approximations
made and because several quantities are not well known. For instance, it
assumes a wind velocity from MS stars of 600 km s-1, and is valid for the
radius and densities considered above. It is possible that
proto-GCs were more compact (![]() 0.5 pc) and much denser (>106
0.5 pc) and much denser (>106 ![]() pc-3)
(Marks & Kroupa 2010). If we use the values for the original radius and
central density from these authors, we get typical upper limits of
pc-3)
(Marks & Kroupa 2010). If we use the values for the original radius and
central density from these authors, we get typical upper limits of
![]() ,
which is compatible
with a significant dilution by winds from main sequence stars.
,
which is compatible
with a significant dilution by winds from main sequence stars.
We conclude that the wind from stars that are less evolved than the polluters might have contributed to the diluting material. This is very likely if a substantial fraction of this wind is at velocity <100 km s-1, but it is still possible even for faster winds, at velocities of a few hundred km s-1.
7 Conclusions
Assuming that the fraction of mass lost is roughly independent of stellar mass, then
mass loss during MS (or more in general during the relevant period by stars
less evolved than the polluters) may provide the diluting mass only if ![]() 1% (within a
factor of 2) of the mass is lost in the relevant phase and the ratio of masses
between the primordial generation and the GC is greater than 40 (still within a factor
of 2).
This requires that a
considerable fraction of the halo (at least half) originated in proto-GCs,
and also that these proto-GCs lost about >95% of their primordial
generation stars.
Although we do not have direct access to events that occurred a Hubble time
ago, chemical abundances allow us to put strong constraints even on those
early phases of GC evolution. It is currently well known that second-generation
stars are formed from the ejecta of massive stars of the primordial
generation (e.g. Gratton et al. 2001). From our ongoing FLAMES survey we also
know the current proportions of primordial and second-generation stars in GCs. The
latter represent the bulk of stars in GCs (about 2/3) whereas the primordial
component is still present, but at a level of only a third of the current
stellar population. Taken together, these two observations mean that a large
fraction of stars of the primordial generation must necessarily be lost from GCs.
1% (within a
factor of 2) of the mass is lost in the relevant phase and the ratio of masses
between the primordial generation and the GC is greater than 40 (still within a factor
of 2).
This requires that a
considerable fraction of the halo (at least half) originated in proto-GCs,
and also that these proto-GCs lost about >95% of their primordial
generation stars.
Although we do not have direct access to events that occurred a Hubble time
ago, chemical abundances allow us to put strong constraints even on those
early phases of GC evolution. It is currently well known that second-generation
stars are formed from the ejecta of massive stars of the primordial
generation (e.g. Gratton et al. 2001). From our ongoing FLAMES survey we also
know the current proportions of primordial and second-generation stars in GCs. The
latter represent the bulk of stars in GCs (about 2/3) whereas the primordial
component is still present, but at a level of only a third of the current
stellar population. Taken together, these two observations mean that a large
fraction of stars of the primordial generation must necessarily be lost from GCs.
Theoretical considerations about star formation efficiency (e.g. Parmentier et al. 2008), violent relaxation (Lynden-Bell 1967) and gas expulsion (e.g. Baumgardt et al. 2008) predict that a huge mass loss occurs in early phases of the GC lifetimes.
In Carretta et al. (2010) we explored the estimates of the initial mass of the
primordial generation in GCs required to satisfy these two
observational features. With suitable (and realistic) assumptions on the initial
mass function of primordial and second-generation stars, mass ranges of the
preferred polluters (either AGBs or FRMS), and initial-final mass relation we
were able to show that a proto-GC should have lost ![]()
![]() of its primordial
stellar population. This is a value that is not very distant from the >95% we derive in
the present paper.
of its primordial
stellar population. This is a value that is not very distant from the >95% we derive in
the present paper.
As mentioned in Sect. 2, we assumed that the diluting mass is equal to the polluting one. Actually, it might be half of this value, so relaxing these constraints a bit. We conclude that, on the whole, this scenario is then quite constraining and not entirely implausible. Of course, a better determination of the mass loss from young stars would be highly welcomed.
AcknowledgementsWe thank the referee for her/his very interesting comments, as well as for reminding us of the very interesting paper by Smith (1999). We thank Franca D'Antona and Annibale D'Ercole for useful discussions and Valentina D'Orazi for a critical reading of the paper. This research has been funded by PRIN MIUR 20075TP5K9.
References
- Apai, D., Luhman, K., & Liu, M. C. 2007, ASP Conf. Ser., 384, 383 [NASA ADS] [Google Scholar]
- Balachandran, S., Lambert, D. L., Tomkin, J., & Parthasarathy, M. 1986, MNRAS, 219, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Kroupa, P., & Parmentier, G. 2008, MNRAS, 384, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briley, M. M., Harbeck, D., Smith, G. H., & Grebel, E. K. 2004, AJ, 127, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Mamajek, E. E., Hillenbrand, L. A., & Meyer, M. R. 2006, ApJ, 651, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Antona, F., & Caloi, V. 2004, ApJ, 611, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekstrom, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Ercole, A., Vesperini, E., D'Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- D'Ercole, A., D'Antona, F., Ventura, P., Vesperini, E., & McMillan, S. L. W. 2010, MNRAS, 407, 854 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- di Criscienzo, M., Ventura, P., & D'Antona, F. 2009, A&A, 496, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Orazi, V., & Marino, A. F. 2010, ApJ, 716, L166 [NASA ADS] [CrossRef] [Google Scholar]
- D'Orazi, V., Lucatello, S., Gratton, R. G., et al. 2010, ApJ, 713, l1 [Google Scholar]
- Dupree, A. K., & Brickhouse, N. S. 2005, Protostars and Planets V, LPI Contribution, 1286, 8458 [Google Scholar]
- Faulkner, D. J., & Freeman, K. C. 1977, ApJ, 211, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrario, L., Wickramasinghe, D., Liebert, J., & Williams, K. A. 2005, MNRAS, 361, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D'Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., et al. 1998, AJ, 116, 181 [Google Scholar]
- Holzwarth, V., & Jardine, M. 2007, A&A, 463, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lednika, A., & Stepien, K. 2008, AN, 3299, 359 [Google Scholar]
- Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Luck, R. E., & Lambert, D. L. 1992, ApJS, 79, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, M., & Kroupa, P. 2010, MNRAS, 406, 2000 [NASA ADS] [Google Scholar]
- Mennickent, R. E., Kolaczkowski, Z., Graczyk, D., & Ojeda, J. 2010, MNRAS, 405, 1947 [NASA ADS] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2009, ApJ, 690, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, M. 1994, in Mass Supply and Flows in the Solar Corona, ed. B. Fleck, G. Noci, & G. Poletto (Dordrecht: Kluwer), 319 [Google Scholar]
- Parmentier, G., Goodwin, S. P., Kroupa, P., & Baumgardt, H. 2008, ApJ, 678, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Parthasarathy, M., Lambert, D. L., & Tomkin, J. 1983, MNRAS, 203, 1063 [NASA ADS] [Google Scholar]
- Pasquini, L., Bonifacio, P., Molaro, P., et al. 2005, A&A, 441, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramirez, S., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Russell, S. C. 1995, ApJ, 451, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Schramm, D. N., Steigman, G., & Dearborn, D. S. P. 1990, ApJ, 359, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. 1999, PASP, 111, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Tomkin, J., Lambert, D. L., & Lemke, M. 1993, MNRAS, 265, 581 [NASA ADS] [Google Scholar]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Muller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... 0-0.7
![[*]](/icons/foot_motif.png)
- Stars with a dilution
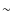 1 can essentially be identified
with the primordial population.
1 can essentially be identified
with the primordial population.
- ... the GC
![[*]](/icons/foot_motif.png)
- This is the mass of the GC after formation of the second generation. Current mass should be lower.
- ...2009)
![[*]](/icons/foot_motif.png)
- We notice that T Tau stars
have disks with masses of
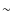 0.01
0.01 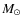 ,
which however are probably
dissipated on a timescale of
,
which however are probably
dissipated on a timescale of 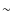 6 Myr (Hillenbrand et al. 1998;
Haisch et al. 2001). The dissipation time might be longer for stars of
lower mass and brown dwarfs (Carpenter et al. 2006; Apai et al.
2007).
6 Myr (Hillenbrand et al. 1998;
Haisch et al. 2001). The dissipation time might be longer for stars of
lower mass and brown dwarfs (Carpenter et al. 2006; Apai et al.
2007).
- ... 47 Tuc
![[*]](/icons/foot_motif.png)
- We neglect here the mass lost by the GC after its formation.
All Tables
Table 1:
Fraction of mass (![]() )
lost by less evolved stars assuming a maximum
polluter mass of
)
lost by less evolved stars assuming a maximum
polluter mass of ![]() .
.
Table 2:
Fraction of mass (![]() )
lost by less evolved stars assuming various
ranges of polluter masses and either x=-2.3 or the Kroupa (2001) mass function).
)
lost by less evolved stars assuming various
ranges of polluter masses and either x=-2.3 or the Kroupa (2001) mass function).
Table 3:
Age, turn-off mass,
![]() ,
and mass of AGB stars,
,
and mass of AGB stars,
![]() .
.
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


