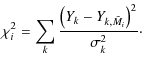| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201014084 | |
| Published online | 15 October 2010 | |
Accounting for stochastic fluctuations when analysing the integrated light of star clusters
I. First systematics
M. Fouesneau - A. Lançon
Observatoire Astronomique de Strasbourg, Université de Strasbourg & CNRS (UMR 7550), 67100 Strasbourg, France
Received 18 January 2010 / Accepted 19 April 2010
Abstract
Context. Star clusters are studied widely both as benchmarks
for stellar evolution models and in their own right. Cluster age
distributions and mass distributions within galaxies are probes of star
formation histories and of cluster formation and disruption processes.
The vast majority of clusters in the Universe are small, and it is well
known that the integrated fluxes and colours of all but the most
massive ones have broad probability distributions, owing to small
numbers of bright stars.
Aims. This paper goes beyond describing predicted probability
distributions to present results of the analysis of cluster energy
distributions in an explicitly stochastic context.
Methods. The method developed is Bayesian. It provides posterior
probability distributions in the age-mass-extinction space, using
multi-wavelength photometric observations and a large collection of
Monte-Carlo simulations of clusters of finite stellar masses. The main
priors are the assumed intrinsic distributions of current mass and
current age for clusters in a galaxy. Both UBVI and UBVIK data sets are considered, and the study conducted in this paper is restricted to the solar metallicity.
Results. We first use the collection of simulations to reassess
and explain errors arising from the use of standard analysis methods,
which are based on continuous population synthesis models: systematic
errors on ages and random errors on masses are large, while systematic
errors on masses tend to be smaller. The age-mass distributions
obtained after analysis of a synthetic sample are very similar to those
found for real galaxies in the literature. The Bayesian approach, on
the other hand, is very successful in recovering the input ages
and masses over ages ranging between 20 Myr and 1.5 Gyr, with
only limited systematics that we explain.
Conclusions. Considering stochasticity is important, more
important for instance than the choice of adding or removing near-IR
data in many cases. We found no immediately obvious reason to reject
priors inspired by previous (standard) analyses of cluster populations
in galaxies, i.e., cluster distributions that scale with mass as M-2 and are uniform on a logarithmic age scale.
Key words: methods: data analysis - techniques: photometric - open clusters and associations: general - Galaxy: stellar content - galaxies: photometry
1 Introduction
In the early decades of astrophysics, star clusters have been our main key to understanding stellar evolution. While clusters continue to provide precious constraints on stellar physics, they are studied in their own right today and as tracers of the histories of galaxies. It has become clear that a significant fraction of star formation occurs in clusters and that events such as interacting galaxies can trigger their formation (Meurer et al. 1995; Barton et al. 2000; Harris 1991; Di Matteo et al. 2007). Questions have been raised regarding the IMF in clusters in various environments, about the systematic trends in their colour distributions, about their lifetimes as gravitationally bound objects, and about the initial and current cluster mass functions.
Resolved observations of individual stars remain the most precise way of investigating the nature of clusters and will be possible out to distances of 10 Mpc with future extremely large telescopes. However, measurements of the integrated light of unresolved star clusters already reach far beyond this scale today, and will remain the path of choice for the studies of large samples.
All our studies of individual clusters and of cluster populations in galaxies rest on our ability to estimate their current ages, masses, and metallicities, while accounting for extinction. The standard method of analysing integrated cluster light is based on direct comparison of the observed colours with predictions from continuous population synthesis models. These models predict fluxes with the assumption that each mass bin along the stellar mass function (SMF) is populated according to the average value given by this SMF. Studies based on continuous population synthesis models have led to results that have a broad impact on today's description of cluster ``demographics''. For instance, it is now usually admitted that the current cluster mass function decreases with mass as a power law with an index close to -2 (Bik et al. 2003; Zhang & Fall 1999; Boutloukos & Lamers 2003) and the debate on the cluster survival rate also rests on distributions obtained using continuous models (Lada & Lada 2003; Fall & Zhang 2001; Rafelski & Zaritsky 2005; Vesperini 1998). The continuous approach has been coupled with statistical data analysis, for instance to provide the impression that including near-IR photometry (K band) solves the age-metallicity degeneracy for clusters (Puzia et al. 2002; Goudfrooij et al. 2001; Anders et al. 2004; Bridzius et al. 2008). Still in the context of continuous population synthesis, Cid Fernandes & González Delgado (2010) followed by González Delgado & Cid Fernandes (2010) have developed a Bayesian analysis of the integrated spectra of star clusters.
The continuous population synthesis models are strictly valid only in
the limit of a stellar population containing an infinite number of
stars. Real clusters, however, count a finite number of stars.
Furthermore most of the light is provided by very few bright stars,
in particular in the near-IR. The so-called stochastic fluctuations
in the integrated photometric properties are the result of the random
presence of these luminous stars. Some of these can be quantified using
selected information provided by continuous population synthesis models
(e.g. Cerviño & Luridiana 2006; Cerviño et al. 2002; Lançon & Mouhcine 2000; Cerviño & Luridiana 2004), but others require using discrete population synthesis
models (Girardi & Bica 1993; Barbaro & Bertelli 1977; Piskunov et al. 2009; Bruzual 2002; Popescu & Hanson 2010; Deveikis et al. 2008).
The predicted luminosity and colour distributions depend strongly on
the total mass (or star number) in the cluster, and can be far
from Gaussian even when the total mass exceeds
![]() .
The most probable colours are offset from those predicted by continuous population synthesis when masses
are below
.
The most probable colours are offset from those predicted by continuous population synthesis when masses
are below
![]() ,
because the single most luminous star in such clusters will be on the
main sequence more often than in the red giant phases of evolution.
Attempts to describe the colour distributions analytically have made
progress (e.g. Cerviño & Luridiana 2006), but are not yet easy to apply.
,
because the single most luminous star in such clusters will be on the
main sequence more often than in the red giant phases of evolution.
Attempts to describe the colour distributions analytically have made
progress (e.g. Cerviño & Luridiana 2006), but are not yet easy to apply.
The present piece of work is based on discrete population synthesis. For the first time, we use the discrete models not only to predict colour distributions but also to analyse the energy distributions of clusters. We present a Bayesian approach to the probabilistic determination of age, mass, and extinction, based on a large library of Monte-Carlo simulations of clusters. This method is a close analogue to the one introduced by Kauffmann et al. (2003) for the study of star formation histories in the Sloan Digital Sky Survey. However the variety of observable properties has completely different origins in both contexts: stochasticity at a given age, mass, and metallicity all play predominant roles here, while different star formation histories provide all the diversity in the model collections used in galaxy studies. We compare determinations based on the Bayesian approach with traditional estimates, thus providing new insight into systematic effects and their consequences. In this first paper, we focus on data sets consisting of either UBVI or UBVIK photometry. Future work will extend to other pass-bands and the addition of the metallicity dimension.
2 Synthetic populations
The analysis of cluster colours must be based on synthetic spectra that
explicitly account for the random fluctuations due to small numbers of
bright stars. We have constructed large catalogues of synthetic
clusters using Monte-Carlo (MC) methods to populate the stellar mass
function (SMF) with a finite number of stars. For the purposes of
this paper, all synthetic clusters host simple stellar populations
(SSP); i.e., their stars are coeval and have a common initial
composition. The synthetic clusters are generated with a discrete
population synthesis code we derived from P ´EGASE (Fioc & Rocca-Volmerange 1997). Stellar evolution at solar metallicity is modeled with the evolutionary tracks of Bressan et al. (1993). The input stellar spectra are based on the library of Lejeune et al. (1998), as we are mostly interested in broad band photometry. The SMF is taken from Kroupa (1993), and extends from 0.1 to
![]() .
Nebular emission (lines and continuum) is included in the calculated
spectra of young objects under the assumption that no ionizing photon
escapes. When extinction corrections are considered, they are based on
the standard law of Cardelli et al. (1989).
.
Nebular emission (lines and continuum) is included in the calculated
spectra of young objects under the assumption that no ionizing photon
escapes. When extinction corrections are considered, they are based on
the standard law of Cardelli et al. (1989).
Our current collection of MC-clusters contains two types of catalogues.
The first set of catalogues contains collections of clusters with equal
numbers of stars. In these (earlier) catalogues, the cluster
ages take 69 values that are distributed on an approximate
logarithmic scale between 1 Myr and 20 Gyr. Metallicity is
solar (Z=0.02). They are available for clusters of 103,
![]() ,
,
![]() ,
104,
,
104,
![]() ,
,
![]() ,
and 105 stars. They contain a total of 69 000 clusters (1000 for each of the 69 time steps).
,
and 105 stars. They contain a total of 69 000 clusters (1000 for each of the 69 time steps).
Most of the results in this paper are based on a second catalogue, which consists of 1.5 ![]() 106 clusters with 309 ages distributed between 1 Myr and 20 Gyr, with masses above about
106 clusters with 309 ages distributed between 1 Myr and 20 Gyr, with masses above about
![]() .
Available metallicities are Z=0.004, Z=0.008, Z=0.02 and Z=0.05,
but we only discuss solar metallicity here. The distribution of ages is
flat on a logarithmic scale above
20 Myr (younger ages are currently under-represented). The number
of stars in a given cluster is drawn randomly from a power law
distribution with index -2. As a result, the mass
distribution of the clusters in the sample falls off approximately
as M-2. (Note that M is the current stellar mass of the cluster, not its initial mass.) These age and mass distributions were chosen as
a possible representation of real distributions in galaxies (Fall et al. 2009),
although we caution that empirical determinations in the current
literature are based on non-stochastic studies. At this point,
the N-2 distribution simply has the
convenient feature that it includes many small clusters, those for
which the distributions of predicted properties are most complex.
It would
be a significantly larger computational challenge to produce a
collection with a flatter distribution and a similar number of small
clusters. On the other hand, the current collection includes only
a small number of very massive clusters. Although the properties of the
latter are better-behaved, we consider the catalogue incomplete above
.
Available metallicities are Z=0.004, Z=0.008, Z=0.02 and Z=0.05,
but we only discuss solar metallicity here. The distribution of ages is
flat on a logarithmic scale above
20 Myr (younger ages are currently under-represented). The number
of stars in a given cluster is drawn randomly from a power law
distribution with index -2. As a result, the mass
distribution of the clusters in the sample falls off approximately
as M-2. (Note that M is the current stellar mass of the cluster, not its initial mass.) These age and mass distributions were chosen as
a possible representation of real distributions in galaxies (Fall et al. 2009),
although we caution that empirical determinations in the current
literature are based on non-stochastic studies. At this point,
the N-2 distribution simply has the
convenient feature that it includes many small clusters, those for
which the distributions of predicted properties are most complex.
It would
be a significantly larger computational challenge to produce a
collection with a flatter distribution and a similar number of small
clusters. On the other hand, the current collection includes only
a small number of very massive clusters. Although the properties of the
latter are better-behaved, we consider the catalogue incomplete above
![]() and focus on smaller clusters for the time being.
and focus on smaller clusters for the time being.
The differences between the properties of discrete populations and the
standard predictions from continuous population synthesis are generally
greater than standard observational errors. This becomes particularly
true in the near-infrared bands and for young and intermediate ages.
It requires clusters with several
![]() to narrow down the stochastic fluctuations to 5% in the K-band (Lançon et al. 2008). Figure 1
illustrates the scatter of observable properties associated with some
of our synthetic cluster catalogues, and allows direct comparison with
standard predictions from continuous synthesis. In the left hand panel,
the lower luminosity clusters all contain 103 stars (with the assumed SMF, their mass distribution peaks around
to narrow down the stochastic fluctuations to 5% in the K-band (Lançon et al. 2008). Figure 1
illustrates the scatter of observable properties associated with some
of our synthetic cluster catalogues, and allows direct comparison with
standard predictions from continuous synthesis. In the left hand panel,
the lower luminosity clusters all contain 103 stars (with the assumed SMF, their mass distribution peaks around
![]() ), while the higher luminosity clusters contain 105 stars.
It is clear that the distributions are highly mass-dependent. Most
low-mass clusters have no post-main sequence star, because the average
number of such stars (given by continuous population synthesis) is
lower than one. The model density map in the right hand panel
represents our main catalogue. Owing to the N-2 distribution
of star numbers and to stellar lifetimes in various evolutionary
phases, islands of high model density are present. Distributions in
other colour-colour and colour-magnitude diagrams can be found in later
sections. Note that the general aspect of this and subsequent model
density maps will not change if the total number of clusters is
increased to include a larger absolute number of high-mass objects.
), while the higher luminosity clusters contain 105 stars.
It is clear that the distributions are highly mass-dependent. Most
low-mass clusters have no post-main sequence star, because the average
number of such stars (given by continuous population synthesis) is
lower than one. The model density map in the right hand panel
represents our main catalogue. Owing to the N-2 distribution
of star numbers and to stellar lifetimes in various evolutionary
phases, islands of high model density are present. Distributions in
other colour-colour and colour-magnitude diagrams can be found in later
sections. Note that the general aspect of this and subsequent model
density maps will not change if the total number of clusters is
increased to include a larger absolute number of high-mass objects.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{14084fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg18.png)
|
Figure 1: Stochastic properties of star clusters at solar metallicity. In the left hand panel, the dots represent photometric properties of individual clusters containing 103 and 105 stars each. The solid lines show the corresponding age sequences from ``standard'' predictions (figure inspired by Bruzual 2002). In the right hand panel, we show the corresponding density distribution of models in our main catalogue, constructed by assuming a power law with a index -2 for the cluster mass function. |
| Open with DEXTER | |
3 Analysis methods
The above synthetic populations can be used to analyse photometric observations of clusters. The properties we seek to estimate in this paper are the cluster ages and masses. We wish to account for the possibility that observed colours can be affected by unknown amounts of extinction. Accounting for uncertainties in the metallicity is postponed to a future paper.
In this section, we describe the Bayesian method developed for
the analysis. Two other analysis methods are briefly described for
comparison. One is a simple best-![]() fit to all the data in the synthetic cluster catalogue, the other
is the usual estimate based on continuous population synthesis
predictions. The comparison between results obtained with the three
methods provides important insights into systematic effects.
fit to all the data in the synthetic cluster catalogue, the other
is the usual estimate based on continuous population synthesis
predictions. The comparison between results obtained with the three
methods provides important insights into systematic effects.
3.1 Standard estimates: the ``infinite limit''
The standard procedure implicitly considers that the mass
distribution of the stars in a cluster is continuous. It has been
applied widely, but as already mentioned, it is strictly only
valid for populations of infinite mass. It becomes a reasonable
approximation for clusters with masses above an age-dependent limit of
about
![]() .
We include this method mainly to quantify the errors produced when it
is applied for analysing the light of clusters of lower masses.
.
We include this method mainly to quantify the errors produced when it
is applied for analysing the light of clusters of lower masses.
In families of spectra predicted with continuous models, mass
is a simple scaling factor that applies to all fluxes. Therefore model
spectra are frequently published scaled to a total population mass of
![]() .
Spectra are described only by age and extinction (and metallicity).
.
Spectra are described only by age and extinction (and metallicity).
Assuming observational errors are Gaussian and independent, the most
likely continuous model for a given set of broad-band fluxes is a
minimum of the following function:
where
We allow for extinction by looping through positive values of AV and repeating the optimization procedure.
3.2 Bayesian estimates
As opposed to its continuous analogue, this approach explicitly accounts for the discrete and stochastic nature of the stellar populations. The cost in computation time is rather high, as the collections of synthetic clusters explored must be large (see Sect. 6.2.1).
As in all Bayesian approaches, the results are stated in probabilistic terms, and they depend on a priori probability distributions of some model parameters. In our case, the most probable ages and masses for a cluster, given a set of photometric observations, will depend on the age distribution and mass distribution of the synthetic clusters in the model catalogue. (The statement can be extended to include extinction and metallicity.)
We assume observational errors are Gaussian with known standard deviations. (A preliminary study of Lançon & Fouesneau 2010, used boxcar functions for the error distributions.) An intrinsic model property X, for given photometric values Y, has the probability
Since errors are assumed to be Gaussian, the probability
Then, the probability distribution of an intrinsic property, such as the age or mass of an individual cluster, is given by the following relation. The probability that property X is located in an interval [x1,x2], given photometric measurements
In the above,
An analogue of Eq. (4) can be written for joint probability distributions, for instance for age, mass, and extinction. The most probable ages and masses given in this paper are the age and mass coordinates of the maximum of the joint distribution. Error bars can be given by examining all models above a given probability threshold.
In our main catalogue, as we mentioned before, the prior mass function is a power law with an index -2, and log(age) is distributed uniformly (above 50 Myr). Clearly, it will be necessary to investigate the effects of these assumptions quantitatively, by varying them within reasonable limits. We are in the process of producing the extended MC-catalogue that will allow us to vary the priors in Eq. (4) without the restrictions currently due to the lack of massive clusters.
3.3 Single best-fit
As a simple first step towards accounting for stochastic fluctuations,
one may look at the one model in the catalogue that minimizes the
standard ![]() function
function
4 Analysis of UBVIK photometry
As a first study, we compare the results from the three methods above in the joint analysis of U, B, V, I, and K band fluxes. The analysis is applied to the synthetic absolute magnitudes of a subsample of clusters from our main catalogue. The presentation is twofold: the synthetic magnitudes are used unchanged in Sects. 4.2 and 4.3, while in Sect. 4.4 noise is added before the analysis is performed.
4.1 Input sample description
The comparison of mass and age estimates is presented for clusters with relatively low-masses, where our catalogue is most complete and where the effects of stochasticity are most important. Figure 2 shows the mass-age distribution of our input sample. It contains 1000 models randomly selected from our main MC catalogue. It covers a relatively narrow mass range, but a broad range of ages (though mostly above 10 Myr). The model colours are not reddened (unless otherwise stated), and the model cluster distances are set to 10 pc - the observable properties associated with the models are absolute magnitudes or fluxes. The selected sample reflects the intrinsic prior mass and age distributions of the catalogue.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14084fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg34.png)
|
Figure 2: Model sample of 1000 models from our main MC catalogue, randomly extracted from the catalogue to identify systematics. Selected clusters are low-mass populations and cover a broad range of ages. Fluxes are not reddened and calibrated as absolute fluxes, corresponding to a 10 pc distance. |
| Open with DEXTER | |
4.2 Estimates from photometry without noise
The estimates of age and mass obtained from the synthetic data with the standard method and with the stochastic Bayesian method are shown in Fig. 3. Estimates from the single best-fit method are not shown, as this method returns the input model itself when no noise is added to the synthetic data. The standard deviations in the above Eqs. (1), (4) and (5) are set arbitrarily to 0.05 mag. In this first experiment, the absence of extinction is considered to be known to the ``observer''. This could be constrained for instance with emission line measurements or with estimations of the total gas content of the host galaxy. The alternative experiment, where the extinction is a free parameter of the analysis, is described in Sect. 4.3.
4.2.1 Biases in the estimates from the standard method
The bottom panels of Fig. 3
reveal the inadequacy of continuous population synthesis models for
analysing the colours of realistic clusters with low-masses. The fits
to the UBVIK data are poor with 93% of the ![]() values more than 3
values more than 3![]() above the value expected for a good fit if one assumes observational errors of 0.05 mag (
above the value expected for a good fit if one assumes observational errors of 0.05 mag (![]() refers to the standard deviation of a
refers to the standard deviation of a ![]() -law with 4 degrees of freedom). In other words, no statistically acceptable match is found in most cases.
-law with 4 degrees of freedom). In other words, no statistically acceptable match is found in most cases.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg31.eps}\hspace*{5mm...
...eps}\hspace*{5mm}
\includegraphics[width=8.5cm,clip]{14084fg34.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg35.png)
|
Figure 3:
Estimations based on U, B, V, I and K band fluxes without noise, when assuming no extinction (AV=0, ``true'' value). Estimations from the
Bayesian approach are given in the two upper panels, and standard estimation considering an infinite number of stars are given in the two lower panels. The x-axes represent, respectively, the original age and mass of the sampled populations whereas the y-axes
represent the estimated values from the two methods. Dashed lines
highlight the identity function. Labels are features refered within the
text. Open circles highlight poor fits where the |
| Open with DEXTER | |
Cluster ages are typically underestimated, with a few exceptions. Errors of 1 or 1.5 dex are not rare. As a consequence, mass estimates are highly dispersed. And if one fails to reject clusters with poor fits, the masses are on average underestimated by 0.3 to 0.5 dex.
![\begin{figure}
\par\includegraphics[width=8.3cm]{14084fg41.eps}\hspace*{1cm}
\in...
...1cm}
\includegraphics[width=8.5cm]{14084fg44.eps}
\vspace*{0.45cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg36.png)
|
Figure 4: Photometric properties of stochastic populations compared to average predictions at solar metallicity. In the left hand panels, the dots represent colours of individual clusters contained in our MC catalogue. Large regions overlap between age bins, and older models hide younger models in certain areas of the figure. The extinction vector is given by the arrows assuming a Cardelli extinction law (Cardelli et al. 1989). In the right hand panels, the corresponding density distributions of the models are shown, assuming cluster masses follow a power law with an index -2. The solid lines represent the corresponding age sequences from ``standard'' predictions. Numeric labels in the bottom left panel correspond to the age sequence from 1 Myr to 20 Gyr. Dotted lines emphasize high-density regions mentioned in Sect. 4.2. |
| Open with DEXTER | |
Figure 4 helps us
understand why derived ages tend to concentrate around 5-9 Myr and
80-100 Myr, in features that we labelled 3![]() and 3
and 3![]() in Fig. 3,
leaving gaps at other ages. This remarkable effect is seen in many
cluster mass distributions presented in the literature (e.g. Gieles 2009) and has received partial explanations (e.g. Fall et al. 2005). Since there is no extinction, the optimization simply searches for the
nearest continuous model in the UBVIK-space.
For intermediate age clusters, hooks in the locus of continuous
models make individual ages more or less attractive. For instance,
the supergiant evolution phase, which occurs around 9 Myr in
our models, is very attractive and translates into the feature 3
in Fig. 3,
leaving gaps at other ages. This remarkable effect is seen in many
cluster mass distributions presented in the literature (e.g. Gieles 2009) and has received partial explanations (e.g. Fall et al. 2005). Since there is no extinction, the optimization simply searches for the
nearest continuous model in the UBVIK-space.
For intermediate age clusters, hooks in the locus of continuous
models make individual ages more or less attractive. For instance,
the supergiant evolution phase, which occurs around 9 Myr in
our models, is very attractive and translates into the feature 3![]() in Fig. 3. The
accumulation around 100 Myr (feature 3
in Fig. 3. The
accumulation around 100 Myr (feature 3![]() )
results from the redward excursion of V-K
when the upper asymptotic giant branch (AGB) first becomes populated.
The attractive effect of these particular points is enforced by spread
of the models being significantly wider in V-I than in U-B (Fig. 4): moving across wide parts of the distribution in U-B has a lower cost in terms of
)
results from the redward excursion of V-K
when the upper asymptotic giant branch (AGB) first becomes populated.
The attractive effect of these particular points is enforced by spread
of the models being significantly wider in V-I than in U-B (Fig. 4): moving across wide parts of the distribution in U-B has a lower cost in terms of ![]() variations than moving along V-I or V-K. Although in most cases the best
variations than moving along V-I or V-K. Although in most cases the best ![]() values
are not statistically acceptable, the match nevertheless provides
a decent age for relatively old populations. Finally, objects that
happen to contain a larger number of luminous stars than the average
predicted by continuous models tend to be very red. With no extinction,
this particular situation leads to overestimates of the
population ages, which produces feature 3
values
are not statistically acceptable, the match nevertheless provides
a decent age for relatively old populations. Finally, objects that
happen to contain a larger number of luminous stars than the average
predicted by continuous models tend to be very red. With no extinction,
this particular situation leads to overestimates of the
population ages, which produces feature 3![]() in Fig. 3.
in Fig. 3.
Typically, young continuous models are more luminous, per unit mass, than older ones. Hence any trend in the age estimates will translate into the equivalent effect on the derived masses. Therefore, this method tends to also underestimate masses of small clusters.
4.2.2 Bayesian estimates
Unlike the standard method, the Bayesian analysis based on stochastic cluster catalogues returns ages and masses in excellent agreement with the input values as shown by the top panels of Fig. 3. As already mentioned, the single best-fit model is exactly the model used to synthesize the photometry for the analysis. Shown here are the most probable model properties, after a Bayesian analysis that assumes observational errors of 0.05 mag (although no noise was actually added to the input photometry).
The masses assigned from the Bayesian method are distributed symmetrically around the input values, except for a cut-off at
![]() due
to the low-mass limit of our cluster catalogue. About 20% of the
analysed clusters are potentially affected by this limit. The standard
deviation of the residuals are of 0.1 dex in age above 20 Myr
and 0.08 dex in mass above
due
to the low-mass limit of our cluster catalogue. About 20% of the
analysed clusters are potentially affected by this limit. The standard
deviation of the residuals are of 0.1 dex in age above 20 Myr
and 0.08 dex in mass above
![]() (the age and mass lower limits are set to avoid statistical biases
resulting from the current limitations of our MC-catalogue).
(the age and mass lower limits are set to avoid statistical biases
resulting from the current limitations of our MC-catalogue).
4.3 When extinction is a free parameter
In the previous section, reddening-free cluster colours were analysed by comparing them with models with no extinction. We showed that, in most of cases, the standard analysis method leads to under-estimated ages and masses, even with high-quality photometric data across the spectrum from U to K. The fraction of clusters with underestimated ages was significantly reduced when adopting stochastic models rather than the classical continuous ones.
We now assume that no independent information on extinction is available to the ``observer''. For the analysis we allow the extinction, AV, to vary between 0 and 3 with steps of 0.2. Figure 5 shows the results obtained when repeating the analysis of the reddening-free sample of Sect. 4.1. The colours of a reddened sample are analysed in Sect. 4.3.3.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg51.eps}\hspace*{1cm...
...m}
\includegraphics[width=8.5cm,clip]{14084fg54.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg41.png)
|
Figure 5: Estimates based on U, B, V, I, and K band fluxes without noise, allowing an extinction AV from 0 to 3. The conventions and axis significations are the same as in Fig. 3. On the left-hand side, the age estimations. On the right-hand side, the mass estimations. |
| Open with DEXTER | |
4.3.1 Estimates from the standard method
The bottom panels of Fig. 5 confirm the inadequacy of continuous population models for the analysis of realistic clusters of low-masses. By authorizing the extinction to vary, we do increase the fraction of clusters whose colours can be fitted satisfactorily with continuous models, but only to 22%. Again assigned ages are highly clustered, and most of them are underestimated. As a consequence, mass estimates are highly dispersed.
In the standard method, dereddening is the only cost-free way, in terms of ![]() ,
to move an observed cluster to the line representing the continuous models. If we look at the UBVI or UBVK colour-colour planes shown in Fig. 4
(left panels), the reddening vector is almost orthogonal to the loci of
stochastic clusters of constant age. Recall that the
input sample is drawn from the stochastic collection even if it is
analysed with the continuous models. Dereddening therefore leads to
underestimated ages.
,
to move an observed cluster to the line representing the continuous models. If we look at the UBVI or UBVK colour-colour planes shown in Fig. 4
(left panels), the reddening vector is almost orthogonal to the loci of
stochastic clusters of constant age. Recall that the
input sample is drawn from the stochastic collection even if it is
analysed with the continuous models. Dereddening therefore leads to
underestimated ages.
The derived ages tend to concentrate around around
5-9 Myr, 80-100 Myr, and also 1 Gyr, figures that are
labelled 5![]() ,
5
,
5![]() ,
and 5
,
and 5![]() in Fig. 5. Using the direction of the extinction vector in Fig. 4
and starting from the bending points of the line of
continuous models, one can define large areas of the colour-colour
planes in which all clusters are assigned the same ages (with fits of
medium or poor quality). For instance, all clusters with -0.5 <
U-B < 0.3 and V-K < 1.5 (or V-I < 0.2)
(clusters in the yellow or blue age bins and below the continuous model
line) are be assigned ages of 5-7 Myr, which causes
feature 5
in Fig. 5. Using the direction of the extinction vector in Fig. 4
and starting from the bending points of the line of
continuous models, one can define large areas of the colour-colour
planes in which all clusters are assigned the same ages (with fits of
medium or poor quality). For instance, all clusters with -0.5 <
U-B < 0.3 and V-K < 1.5 (or V-I < 0.2)
(clusters in the yellow or blue age bins and below the continuous model
line) are be assigned ages of 5-7 Myr, which causes
feature 5![]() ,
very similar to the previously described 3
,
very similar to the previously described 3![]() .
Old clusters are primarily located on two branches of high model
density in our (prior-dependent) MC-model collection. Those two
regions, emphasized by the dotted lines in the right panels of
Fig. 4, cross each other around U-B = 0. Clusters in the lower branch, with the higher model density (at V-K
.
Old clusters are primarily located on two branches of high model
density in our (prior-dependent) MC-model collection. Those two
regions, emphasized by the dotted lines in the right panels of
Fig. 4, cross each other around U-B = 0. Clusters in the lower branch, with the higher model density (at V-K ![]() 2), are assigned an age of 1 Gyr and produce feature 5
2), are assigned an age of 1 Gyr and produce feature 5![]() .
The older of these are assigned higher extinction values. Clusters near the second and more diagonal branch (V-K > 2.5)
are assigned ages between 100 Myr and 1 Gyr, with a
systematic trend towards younger ages for redder, older clusters
(feature 5
.
The older of these are assigned higher extinction values. Clusters near the second and more diagonal branch (V-K > 2.5)
are assigned ages between 100 Myr and 1 Gyr, with a
systematic trend towards younger ages for redder, older clusters
(feature 5![]() ). The accumulation 3
). The accumulation 3![]() ,
described previously, is still present but weaker. Feature 3
,
described previously, is still present but weaker. Feature 3![]() has disappeared.
has disappeared.
Again, young continuous models are typically more luminous per unit mass than older ones. In most cases, this age effect is stronger than the luminosity variation associated with the dereddening procedure. Therefore, obtained masses are usually lower than the actual masses. There are exceptions however, for clusters associated with large estimated (i.e. overestimated) amounts of extinction.
4.3.2 Bayesian estimates
Despite the additional degree of freedom associated with extinction,
the Bayesian analysis based on stochastic cluster catalogues
generally returns ages and masses in good agreement with the input
values (top panels of Fig. 5).
Above 20 Myr, 90% of the most probable ages lie within
0.3 dex of the actual age (rms dispersion of 0.1 dex).
For the remaining 10% of the clusters in the sample, the age
estimates present attraction points again, and this leads to
underestimates of up to 1.5 dex. The favoured ages are
located just below 1 Gyr and around 100 Myr. The
corresponding features are labelled 3.a and 3.b in Fig. 5. While their locations are not far from those of ![]() and
and ![]() ,
their origins are different.
,
their origins are different.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14084fg61.eps}\hspace*{1cm}
\includegraphics[width=8cm,clip]{14084fg62.eps}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg47.png)
|
Figure 6: Derived age (left) and mass (right) distributions using the Bayesian method analysing UBVIK data when 1 mag extinction (assuming Cardelli extinction law) is applied to the input population properties. This figure compares directly with Fig. 5. |
| Open with DEXTER | |
The Bayesian ``attractors'' are regions of high concentration in the model density plots of the right panels of Fig. 4. They do not lie along the locus of continuous population synthesis models. Since all models with magnitudes within about 0.05 of the observations are given strong weights in the computation of the posterior probability distribution, areas of high model density along the dereddening line are favoured. An illustration is provided in Fig. A.2 and discussed further in Sect. 6.2. The clusters affected by this issue are usually located in regions of low model density of the colour-colour and colour-magnitude planes, and are assigned positive extinction values.
4.3.3 Reddened input clusters
As the extinction plays in the analyses, we repeat the experiment
above after applying one magnitude of optical extinction to the fluxes
of the input sample. Figure 6
presents the derived age and mass distributions when using the Bayesian
method. For 97% of the clusters, the derived extinction is
correct. The standard deviations of the residuals are 0.2 dex in
age above 20 Myr and 0.1 dex in mass above
![]() .
Trend features presented in Fig. 6
are very similar to the previously mentioned ones. A few clusters
now have overestimated ages, because reddening has moved them from the
blue to the red side of a region of high model density and typically
older ages. Such a region of high model density becomes a Bayesian
attractor for these reddened clusters, while it was out of bounds in
the reddening-free case (reaching this region of high model density
would have required negative extinction corrections).
.
Trend features presented in Fig. 6
are very similar to the previously mentioned ones. A few clusters
now have overestimated ages, because reddening has moved them from the
blue to the red side of a region of high model density and typically
older ages. Such a region of high model density becomes a Bayesian
attractor for these reddened clusters, while it was out of bounds in
the reddening-free case (reaching this region of high model density
would have required negative extinction corrections).
4.4 Estimates from noisy fluxes
We now reproduce the analysis of Sect. 4.3 for the same inputs, but after adding Gaussian noise to the input fluxes (5%). Figure 7 presents the results. At the top of this figure are also plotted estimates derived from the single best-Although the inputs are now noisy, the trends obtained remain similar. In particular, there is no important difference with the noise-free case when the analysis is based on standard, continuous population synthesis models (bottom panels): most fits are poor, ages tend to be underestimated, and masses are highly dispersed around the correct values.
Bayesian estimates remain close to the expected values even though the dispersion has increased. The standard deviation of the residuals are of 0.15 dex in age and 0.13 dex in mass except for models in features 6.a and 6.b. Only 13% of the model clusters are assigned underestimated ages.
A pleasant fact is that the single best-![]() fit provides results that are similar to the Bayesian ones (see discussion in Sect. 6.2.1).
Although individual clusters are assigned
different ages, the estimated properties of the sample as a whole are
described similarly with both methods. For 84% of the clusters,
the single best-fit age and the Bayesian ages are both within
0.3 dex of the actual ages. Of the 16% that deviate,
3% deviate only with the single best-fit method, 3% only with
the full Bayesian method, and 10% deviate in similar ways with
both methods.
fit provides results that are similar to the Bayesian ones (see discussion in Sect. 6.2.1).
Although individual clusters are assigned
different ages, the estimated properties of the sample as a whole are
described similarly with both methods. For 84% of the clusters,
the single best-fit age and the Bayesian ages are both within
0.3 dex of the actual ages. Of the 16% that deviate,
3% deviate only with the single best-fit method, 3% only with
the full Bayesian method, and 10% deviate in similar ways with
both methods.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg71.eps}\hspace*{1cm...
...
\includegraphics[width=8.5cm,clip]{14084fg76.eps}
\vspace*{0.37cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg48.png)
|
Figure 7: Estimations based on U, B, V, I, and K band fluxes with 5% noise added to the photometry inputs, allowing an extinction AV from 0 to 3. From top to bottom, the direct fit of the noised populations by our catalogue, the Bayesian estimations and the standard estimations. The conventions and axis significations are the same as in Fig. 5. |
| Open with DEXTER | |
5 When there is no K band data
It is common understanding that near-IR light is a better tracer of
mass in galaxies than optical light and that including near-IR
photometry helps break degeneracies and estimate ages. Particularly
illustrative figures on the latter point can be found in Bridzius et al. (2008). However, all these statements rest on models that are valid only within the limit of large numbers of stars, i.e. not
for most of the real star clusters in the Universe. This section re-assesses the role of photometry beyond wavelengths of Figure 8 shows the results obtained for the sample of Sect. 4.1 when using noise-free UBVI input fluxes. Extinction is a free parameter although, as above, the clusters analysed are not reddened. Figure 8 compares directly to Fig. 5. With fewer observational constraints, it is much easier to obtain statistically acceptable ![]() values.
Eighty percent of the clusters in the sample now find an acceptable
match among the standard, continuous population synthesis models (with
extinction when convenient).
values.
Eighty percent of the clusters in the sample now find an acceptable
match among the standard, continuous population synthesis models (with
extinction when convenient).
A very unusual result is that, between about 108 and 109 yr, the standard method (based on continuous models) produces better ages when the K data
is absent than when it is present. This is due to the relative
locations of the line of continuous models and the regions of high
model densities in colour space (Fig. 4). At intermediate ages, the offset is of one
full magnitude in (V-K),
whereas it remains small in other colours. For a cluster that is
typically located in the high-density region, the nearest
continuous model will produce a decent ![]() without need for much reddening in UBVI but high
without need for much reddening in UBVI but high ![]() values in UBVIK.
The rare but luminous AGB stars strongly increase the impact of
stochasticity on the derived properties so that one should consider
throwing K band data away when the UBVI-estimated age is between 100 and 500 Myr.
values in UBVIK.
The rare but luminous AGB stars strongly increase the impact of
stochasticity on the derived properties so that one should consider
throwing K band data away when the UBVI-estimated age is between 100 and 500 Myr.
At other ages, the standard method applied to UBVI fluxes shows artefacts: a very strong accumulation is found at estimated ages around 1 Gyr, and hardly any cluster is assigned ages between 2 and 7 Gyr. But these artefacts are not much worse than those seen in the analysis of UBVIK data with continuous models.
In terms of estimated masses, the distributions around the correct values are similar regardless of whether one uses UBVI or UBVIK
data as input to the standard method (continuous population synthesis).
On average, the masses of the clusters for which the UBVI fit is satisfactory are underestimated slightly (0.2 dex at
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg81.eps}\hspace*{1cm...
...cm}
\includegraphics[width=8.5cm,clip]{14084fg84.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg50.png)
|
Figure 8: Same figure as Fig. 5 but excluding information on the K band: estimations are based on U, B, V, I bands without noise, allowing an extinction AV from 0 to 3. |
| Open with DEXTER | |
When using the Bayesian analysis based on stochastic models, the loss of the K band
information translates into stronger artefacts in the derived age
distributions. The model-density distribution in colour space plays a
more important role in Eq. (4) when there is less contrast in the ![]() distribution, i.e. when K fluxes
are absent. Ages in high-density regions along the de-reddening lines
become more attractive. These artefacts disappear if the amount of
reddening is known rather than being a free parameter.
distribution, i.e. when K fluxes
are absent. Ages in high-density regions along the de-reddening lines
become more attractive. These artefacts disappear if the amount of
reddening is known rather than being a free parameter.
The artefacts in the age distributions of the standard and the stochastic method, without the K band, appear oddly similar (left panels of Fig. 8). In fact, the clusters in features 7.b and ![]() are mostly identical, while the clusters in features 7.a and
are mostly identical, while the clusters in features 7.a and ![]() form two subsets with very little overlap.
form two subsets with very little overlap.
One must distinguish three main behaviours for clusters that have ages between 1 and 10 Gyr. Feature ![]() comes
from the clusters located in the main high-density region of model
colour space, i.e. the region that runs parallel to the line of
old continuous models in the lower right panel of Fig. 4
but is not superimposed on that line. These clusters
will be assigned correct ages with the Bayesian method, but an age
around 1 Gyr (and a positive extinction) with the standard method.
Feature 7.a
is comes from clusters located in the secondary high-density region of
colour-space, which happens to be superimposed on the line of old
continuous models (when there is no K band data). These
clusters will be assigned correct ages with the
standard method, but will be attracted to younger ages with the
Bayesian method (with a positive extinction) because of the contrast in
the model-density maps. Finally, the rarer clusters with higher values
than typical V-I colours
will be attracted to ages around 100 Myr (with a positive
extinction), both with the standard and the Bayesian methods
(features 7.b and
comes
from the clusters located in the main high-density region of model
colour space, i.e. the region that runs parallel to the line of
old continuous models in the lower right panel of Fig. 4
but is not superimposed on that line. These clusters
will be assigned correct ages with the Bayesian method, but an age
around 1 Gyr (and a positive extinction) with the standard method.
Feature 7.a
is comes from clusters located in the secondary high-density region of
colour-space, which happens to be superimposed on the line of old
continuous models (when there is no K band data). These
clusters will be assigned correct ages with the
standard method, but will be attracted to younger ages with the
Bayesian method (with a positive extinction) because of the contrast in
the model-density maps. Finally, the rarer clusters with higher values
than typical V-I colours
will be attracted to ages around 100 Myr (with a positive
extinction), both with the standard and the Bayesian methods
(features 7.b and ![]() ).
).
As noted earlier, underestimated ages lead to underestimated masses
because stellar populations fade with time and extinction corrections
do not quite compensate for this. In our sample, many of the old
clusters affected by the age artefacts get assigned masses near the
lower limit (
![]() )
of our catalogue (see Sect. 6.2).
)
of our catalogue (see Sect. 6.2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg91.eps}\hspace*{1cm}
\includegraphics[width=8.3cm,clip]{14084fg92.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg53.png)
|
Figure 9:
Age-mass and age-luminosity distributions obtained for our test
sample, when analysing UBVI
data with standard, continuous, population synthesis models. Grey dots
represent the test sample and black ones the recovered properties. In the right panel, masses have been converted to luminosities using the (continuous) mass-to-light ratio given by Pégase (solid line:
|
| Open with DEXTER | |
Outside the main age artefacts seen for old clusters (when extinction
is a free parameter), the Bayesian method recovers ages and masses
just as well whether the K band fluxes are included in the input data or not. If we exclude objects lying in the features 7.a and 7.b, as well as objects affected by the low-mass limit of our MC catalogue, masses recovered with UBVI data sets are not significantly more dispersed (
![]() )
than those obtained with UBVIK data sets (
)
than those obtained with UBVIK data sets (
![]() ). Further aspects of photometric band-pass selection are discussed in Sect. 6.3.
). Further aspects of photometric band-pass selection are discussed in Sect. 6.3.
6 Discussion
Several decades have passed since the stochasticity of stellar populations was first mentioned as a serious issue (Barbaro & Bertelli 1977). With powerful computers, stochasticity can now be taken into account explicitly when analysing the properties of unresolved populations.
Considering stellar populations as stochastic requires some changes in habits. For instance, mass is not a simple scaling factor anymore. Errors on absolute fluxes (e.g. due to uncertainties on distances) can affect estimated ages, and observations of only colours can provide some information on the mass. Clearly, more work is needed to explore the consequences of stochasticity more exhaustively.
6.1 Non-stochastic studies: mass and age distributions
The analysis of the integrated light of small clusters with
continuous population synthesis models produces strong age-dependent
artefacts in the derived ages, and a broad distribution of random
errors in the derived masses. The good news is that there is no large
systematic offset between estimated and real masses if the photometric data are of good quality and if
observations that cannot find a statistically acceptable match among
the continuous models are rejected. When the data have larger errors,
fewer model fits are rejected. Then, a systematic trend appears in
addition to the random errors: masses are underestimated on average.
The value of the offset depends on the photometric pass-bands available
and on the existence (or not) of independent information on
extinction. The average error is of 0.3 dex for a sample of
clusters of masses around
![]() observed in UBVIK, when extinction is treated as a free parameter.
observed in UBVIK, when extinction is treated as a free parameter.
This means that mass distributions of large samples of clusters based
on an analysis with continuous population synthesis models are probably
not too strongly biased. Several empirical determinations in the
literature (see Rafelski & Zaritsky 2005, and references therein) favour M-2 mass
distributions, and we used such a law as a prior in our Bayesian
analysis. We find no immediate reason to apply a correction to this
result, although a detailed investigation of each individual dataset in
the literature would be worthwhile. If, for instance, low masses
are systematically underestimated by 0.3 dex while high masses are
not, the power-law index of the mass distribution would require a small
correction![]() .
.
Figure 9 shows the age-mass distribution obtained when UBVI data
for our test sample of clusters is analysed with non-stochastic
population synthesis models and no fit is rejected. While the
properties of the test sample are smoothly distributed,
the estimated properties are highly clustered. The figure looks
similar with UBVIK data, but we chose UBVI for comparison with the (UBVI+H![]() )-based age-luminosity distribution of (more massive) Antennae clusters (Fall et al. 2005). The right panel of Fig. 9
shows the derived distribution in the age-luminosity plane, after
conversion of the estimated masses into luminosities
with the age-dependent mass-to-light ratio given by Pégase. In an
observational context, such a figure would be truncated at low
luminosity by some instrumental sensitivity limit.
)-based age-luminosity distribution of (more massive) Antennae clusters (Fall et al. 2005). The right panel of Fig. 9
shows the derived distribution in the age-luminosity plane, after
conversion of the estimated masses into luminosities
with the age-dependent mass-to-light ratio given by Pégase. In an
observational context, such a figure would be truncated at low
luminosity by some instrumental sensitivity limit.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg101.eps}\hspace*{1cm}
\includegraphics[width=8.3cm,clip]{14084fg102.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg56.png)
|
Figure 10: Resulting age-mass distributions from the Bayesian ( left panel) and standard ( right panel) analysis methods on the test-sample clusters. Grey dots are estimates from UBVIK bands, whereas black dots are only from UBVI bands. UBVIK distribution in the right panel is presented in the left panel of Fig. 9. Binning effects are visible on the Bayesian distribution as mentioned in the Sect. 6.2. The original age-mass distribution is presented in Fig. 2. |
| Open with DEXTER | |
The similarity between the distribution in Figs. 9 and in 1 of Fall et al. (2005) is striking, even more so when one mentally corrects for the sharp low-mass limit of our sample and our relative lack of young clusters. Accumulations and gaps occur at essentially the same ages (differences can be traced back to the different sets of evolutionary tracks used by the authors). We have discussed the origins of the artefacts in our test sample age distribution in Sect. 4: they arise because real, stochastic clusters of low masses are distributed over a wide range of colours and can therefore fall quite far off on the line of continuous models when only extinction is available to alter their colours. The clusters in the Antennae sample, however, are typically 50 times more luminous than the ones in our study. More massive clusters should lie closer to the lines of continuous models. Why then are these artefacts so strongly seen in the Antennae cluster distribution? Our interpretation is that the combined effects of observational errors and real extinction disperse the clusters enough in colour-space to produce a global derived age distribution that is similar to the distribution produced at lower masses by stochasticity.
The input age distribution of the clusters in our test sample (and in our main MC catalogue of clusters) is constant in logarithmic age bins, and this produces derived age-luminosity distributions that are very similar to the ones in the literature. Our tentative conclusion is that the adopted age-distribution is, for the time being, an adequate prior for the Bayesian, stochastic studies. Clearly, it would be desirable to explore quantitatively how sensitive the derived distributions are to the actual age and mass distributions, especially in the presence of observational errors. Any firm conclusion about the Antennae clusters, for instance, would require such a study.
6.2 Prospects of the stochastic analysis
The analysis of cluster colours based on a library of stochastic models provides ages and masses with small random errors and with systematics that will be negligible in many situations. Figure 10 shows the derived age-mass distributions for our test sample, based on either UBVI or UBVIK data sets. Similar results are obtained if the input sample is reddened (Fig. 11). The situation can be improved even more if there are independent constraints on extinction. The figures show the grid pattern due to the finite sizes of our bins in estimated ages and masses. This is because we compute the posterior probabilities of Eq. (4) for finite intervals.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg11.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg57.png)
|
Figure 11: Resulting age-mass distributions from the Bayesian analysis methods in the 1-mag reddened test-sample clusters. Grey dots are estimates from UBVIK bands, whereas black dots are from only UBVI bands. Corresponding marginal distribution histograms follow the same colour conventions. The dotted line in the histograms represents the test-sample distribution. |
| Open with DEXTER | |
The binning procedure has a caveat and an advantage. The caveat is that results are sometimes sensitive to the choice of the bin sizes or boundaries. We looked at many probability maps in 2D projections of age-mass-extinction space to check where this occurs. Examples are given in Appendix A (all cannot be developed here). As expected, the results are robust with respect to the binning (i.e. errors are less than or equal to one bin size) when the maps are simple and single-peaked (Fig. A.1), while they can strongly depend on binning when the maps are complex (i.e. in cases in which uncertainty estimates based on contours of equal probability would give large error bars). The second type of situation occurs especially when there is no a priori information on extinction. Figure A.2 illustrates this event: the dereddening vector of an object crosses several regions of high model density. The model properties within each of these regions end up with similar probabilities. Which one dominates, depends on the binning as shown in Fig. A.3 (and on the density pattern itself).
The advantage of binning is that we can, to first order, assign the
same a priori probabilities to the ages, metallicities, and
extinction of a given bin. This allows us to rescale the derived
probability maps for a cluster after calculation, if we wish to
change the adopted priors (a worthwhile gain in computation time).
In our current catalogue, the total number of clusters with
masses above about
![]() is too small to allow us to study flatter mass distributions of
clusters immediately, and we also lack clusters with ages below 107 yr. We have therefore chosen to postpone the description of consequences of changes in the priors to a future article.
is too small to allow us to study flatter mass distributions of
clusters immediately, and we also lack clusters with ages below 107 yr. We have therefore chosen to postpone the description of consequences of changes in the priors to a future article.
6.2.1 Other practical aspects
Although conceptually simple, the implementation of the Bayesian,
stochastic analysis is not immediate. Constructing the stochastic
library requires CPU time and data storage. For each cluster, the
spectra of at least the brightest 1000 stars need to be summed
individually. The remaining low-mass stars could be represented with a
continuous sequence to save computation time. Synthetic
broad band colours can then be measured on the resulting total
spectrum. We decided to save all the spectra and to compute a set of
60 standard broad band fluxes (standard UBVRIJHK,
but also most HST filters and some from other telescopes). For
three metallicities and several millions of models in total,
the computation took a couple of month on six
3 GHz CPUs, and half a terabyte of data was accumulated. Browsing through the collection to compute probabilities also takes
time, even with the restriction to a few photometric bands.
A few CPU-hours are required to construct probability
distributions of age, mass, and extinction for 1000 clusters with
our main MC catalogue, allowing for extinction to vary in the range
described above. It is somewhat faster to use a simple best-![]() .
This may be
good enough for statistical studies of large samples, but it must be
kept in mind that the single best-fit can be far from the most probable
Bayesian model in individual cases. Very small changes in the observed
colours (due to small observational errors) can modify single
best-fit parameters, while they leave Bayesian estimates unchanged.
To provide error bars on the single best-fit parameters, one has
to explore the vicinity of the minimum
.
This may be
good enough for statistical studies of large samples, but it must be
kept in mind that the single best-fit can be far from the most probable
Bayesian model in individual cases. Very small changes in the observed
colours (due to small observational errors) can modify single
best-fit parameters, while they leave Bayesian estimates unchanged.
To provide error bars on the single best-fit parameters, one has
to explore the vicinity of the minimum ![]() .
For instance, one could compare the properties of all the models with a
.
For instance, one could compare the properties of all the models with a ![]() below a predefined threshold, as done for large clusters in Bridzius et al. (2008) or Anders et al. (2004). Doing this exhaustively would be conceptually similar, and essentially as long to run as our Bayesian approach.
below a predefined threshold, as done for large clusters in Bridzius et al. (2008) or Anders et al. (2004). Doing this exhaustively would be conceptually similar, and essentially as long to run as our Bayesian approach.
All the results in this paper are based on one single set of population synthesis models. Some caveats of these models are that they do not include the formation of carbon stars or Mira-type variability and that they do not account for binaries or for stellar rotation. We have not yet compared the amplitude of the errors arising from stochasticity (studied here) with those from uncertainties in the physical assumptions of the models. However, we expect qualitatively similar systematics with any set of stellar evolution tracks. It will unfortunately be necessary to recompute a completely new library if one wishes to explore different sets of stellar evolution tracks, to assume a different stellar mass function, or to use a different library of stellar spectra. This will clearly limit the pace at which the comparisons can be made.
6.3 Impact of the photometric band selections
In the present paper, the estimation of ages and masses has been shown to be affected by stochasticity and also by the photometric datasets used during the analysis. We chose to focus on explaining behaviours rather than multiplying experiments with different passbands, so we have restricted our quantitative comparisons to two combinations. In a large fraction of stellar population studies, the UBVI combination is used as the standard selection, because it provides a reasonable compromise between depth and spectral coverage for most of the available instruments. Moreover, it corresponds to a wavelength range where spectral libraries are most accurate. Adding the K band improves mass estimates in the non-stochastic regime of high total masses, but it has an observational cost as by requiring the use of a different instrument. Testing the UBVIK combination in the stochastic regime provides useful information for designing future surveys.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg121.eps}\hspace*{1c...
...
\includegraphics[width=8.6cm,clip]{14084fg124.eps}
\vspace*{0.3cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg58.png)
|
Figure 12:
Age-luminosity distributions recovered for our test-sample. Grey dots
are the original distributions and black dots are respectively the
recovered distributions from the standard (left panels) and Bayesian (right panels) methods when analysing UBVI (top panels) and UBVIK (bottom panels) data sets. Recovered masses are
converted to luminosities using Pégase (continuous) factor of which the solid lines represent the evolution of a
|
| Open with DEXTER | |
In Sect. 5, we presented some effects of the presence of K band data in addition to UBVI photometry. The K band does not significantly improve the situation when continuous models are being used (right panel of Fig. 10). In particular, we mentioned that including the K band in the analysis of populations with AGB stars (100-500 Myr) may lead to even worse estimates (again with continuous models). This effect is also visible in the left-hand side panels of Fig. 12. On the other hand, we find only mild improvements when including K band data in the Bayesian analysis: the presence of K band information translates into weaker artefacts in the derived age distributions (artefacts which disappear when reddening is not a free parameter). The left panel of Fig. 10 presents recovered age-mass distributions for UBVI and UBVIK datasets using the Bayesian approach with free extinction. Age-mass estimates of old populations (>1 Gyr) reflect the original distribution better when K band constraints are included. This is also visible in the right panels of Fig. 12, where the resulting distributions are significantly improved.
Most small and young clusters have HR diagrams that resemble a
truncated main sequence. Even if the stellar mass function from which
their stars are drawn randomly extends to
![]() ,
a small zero age cluster will in general contain no ionizing
stars, and a small cluster aged 10 Myr will contain no red
supergiants. Two such objects are basically indistinguishable,
be it with or without K band
data. This problem shows up clearly when we run the Bayesian analysis
at young ages, but quantifying this effect requires that we add more
young clusters to our reference catalogue.
,
a small zero age cluster will in general contain no ionizing
stars, and a small cluster aged 10 Myr will contain no red
supergiants. Two such objects are basically indistinguishable,
be it with or without K band
data. This problem shows up clearly when we run the Bayesian analysis
at young ages, but quantifying this effect requires that we add more
young clusters to our reference catalogue.
The UV spectral range raises questions similar to the near-infrared. We repeated some of the above experiments with the UBVI and the F218W filter, centred on 220 nm (WFPC2 instrument on-board the Hubble Space Telescope). A brief summary is that the effects of adding this UV band have amplitudes similar to those obtained when adding K. The dispersions in the results are comparable to those without UV, both for Bayesian or standard estimates. Artefacts are also qualitatively similar. Age estimates below 20 Myr are improved only slightly. If one does, however, want to include UV bands, the choice of an extinction law becomes more of an issue. Extinction laws indeed express a range of behaviours in the UV bands (e.g. Calzetti et al. 2000; Cardelli et al. 1989; Fitzpatrick & Massa 1986; Allen 1976).
The decision of which filters to use rests on considerations of the astrophysical problem to tackle. Using either UV or K photometry does not deeply affect the resulting estimates ages and masses of small clusters. One may first want to consider using discrete population models instead of continuous ones.
7 Conclusions
Studies of star cluster populations in galaxies have until now relied on continuous population synthesis models, which provide a very poor approximation of the integrated light of clusters of low and intermediate masses because this light is determined by so few luminous stars.
Using large collections of Monte-Carlo simulations of star clusters that each contain a finite number of stars, this paper explores systematic errors that occur when the integrated fluxes of realistic clusters of low mass we analysed in terms of mass and age. Our main collection is built with the cluster age and mass distributions of Fall et al. (2009), extrapolated to masses lower than those observed in the Antennae galaxies.
With the standard methods (continuous models), large systematic errors affect estimated ages and large random errors affect masses. If observational uncertainties on cluster fluxes are large and, as a consequence, quality-of-fit criteria fail to reject the numerous poor fits, systematic errors (of a few tenths of a dex) are also present in the estimated masses. Derived age-mass or age-luminosity distributions for samples in which actual ages and masses are distributed as in our main collection display clustered patterns that very closely resemble those found in empirical samples in the current literature. We find no immediately obvious reason to reject the age and mass distributions of our main collection, but clearly this essential point requires detailed study with real observations.
A Bayesian method as described and implemented, in order to explicitly account for the finite nature of clusters in the analysis. It is shown that their age and mass can be recovered with error bars that will be small enough for many purposes. Young low-mass clusters will remain difficult to age-date because the HR-diagrams of many of them look like truncated main sequences with no ionizing or post-main sequence stars. At intermediate ages, the variability of luminous AGB stars is expected to cause difficulties that we have not yet solved.
The comparison between the results obtained with UBVI and UBVIK data sets shows that, in the stochastic context, the benefits of adding the K band to optical observations are rather few, except for determining the mass of clusters older than 1 Gyr. Clearly, adding near-IR or UV information is secondary, compared to the need to move from continuous to stochastic cluster models.
The Bayesian analysis method can now be applied to existing data on cluster samples in nearby galaxies with the aim of constraining the actual age and mass distributions of these clusters. We will also extend the study of systematic errors to the case where metallicity is an unknown parameter.
AcknowledgementsWe are grateful to Michel Fioc for kindly providing his Fortran 90 version of P EGASE, and to M. Fioc and B. Rocca-Volmerange for their support in implementing discrete population synthesis.
Appendix A: Examples of probability maps
The method we developed to take the stochasticity into account when estimating intrinsic parameters (age, total number of stars or total mass, metallicity, extinction) of unresolved population follows a Bayesian approach. Given a set of photometric measurements and uncertainties, we establish the joint probability distributions of these parameters based on a large catalogue of Monte-Carlo simulations. In this Appendix, we present examples of probability distributions.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{14084fgA11.eps}\hspace*{1...
...s}\hspace*{1cm}
\includegraphics[width=7.35cm,clip]{14084fgA14.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg60.png)
|
Figure A.1:
Example of probability map for a population of 33 Myr and
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=7.35cm,clip]{14084fgA21.eps}\hspace*{1cm}
...
...s}\hspace*{1cm}
\includegraphics[width=7.35cm,clip]{14084fgA24.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg62.png)
|
Figure A.2:
Example of probability maps for a population of
2.3 Gyr and
|
| Open with DEXTER | |
First an example is given in Fig. A.1,
for which we obtain single-peaked probability distributions
leading to an unambiguous probabilistic determination of age, mass, and
extinction estimates. In this example, we recover that the most
likely have no extinction and the most probable age and mass are
35 Myr and
![]() ,
very close to the expected values.
,
very close to the expected values.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fgA23.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{14084fgA3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg64.png)
|
Figure A.3: Illustration of the effect of binning using the cluster of Fig. A.2. In left-hand side panel the correct age is recovered with 40 bins; however, as the right panel illustrates, a different binning (50 bins) favours a much younger age with (erroneously) high extinction. The cluster is now moved to feature 5.b in Fig. 5. |
| Open with DEXTER | |
As discussed in Sect. 6.2, it also happens that the probability distributions are not single peaked. Complex maps occur when there is no independently known information on the amount of extinction. Figure A.2 illustrates how the extinction factor increases the complexity of the probability maps. The top-left panel contours show how the colour distributions are affected along the dereddening vector. In this example, the object crosses three regions of high model density. The resulting age-mass probability distribution is multi-modal (trimodal).
Complex distributions are subject to binning issues. The example probability distributions given in Fig. A.2 yields three modes with similar probabilities. If one changes the number of bins on which the probabilities are computed, peak values might vary to eventually change the dominant mode of the distributions. Figure A.3 shows that the variations in the resulting age estimates can be significant: from 2.3 Gyr to 50 Myr. A determination of the optimal binning remains an open question.
References
- Allen, D. A. 1976, MNRAS, 174, 29P [NASA ADS] [Google Scholar]
- Anders, P., Bissantz, N., Fritze-v. Alvensleben, U., & de Grijs, R. 2004, MNRAS, 347, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Barbaro, C., & Bertelli, C. 1977, A&A, 54, 243 [NASA ADS] [Google Scholar]
- Barton, E. J., Geller, M. J., & Kenyon, S. J. 2000, ApJ, 530, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Gieles, M., Lamers, H. J. G. L. M., Scheepmaker, R. A., & de Grijs, R. 2005, A&A, 431, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bik, A., Lamers, H. J. G. L. M., Bastian, N., Panagia, N., & Romaniello, M. 2003, A&A, 397, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS] [Google Scholar]
- Bridzius, A., Narbutis, D., Stonkute, R., Deveikis, V., & Vansevicius, V. 2008, Baltic Astron., 17, 337 [Google Scholar]
- Boutloukos, S. G., & Lamers, H. J. G. L. M. 2003, MNRAS, 338, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual A., G. 2002, Extragalactic Star Clusters, 207, 616 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., & González Delgado, R. M. 2010, MNRAS, 403, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2004, A&A, 413, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerviño, M., Valls-Gabaud, D., Luridiana, V., & Mas-Hesse, J. M. 2002, A&A, 381, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deveikis, V., Narbutis, D., Stonkute, R., Bridzius, A., & Vansevicius, V. 2008, Baltic Astron., 17, 351 [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., Chandar, R., & Whitmore, B. C. 2005, ApJ, 631, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., Chandar, R., & Whitmore, B. C. 2009, ApJ, 704, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [Google Scholar]
- Gieles, M. 2009, MNRAS, 394, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., & Bica, E. 1993, A&A, 274, 279 [NASA ADS] [Google Scholar]
- González Delgado, R. M., & Cid Fernandes, R. 2010, MNRAS, 403, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Alonso, M. V., Maraston, C., & Minniti, D. 2001, MNRAS, 328, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lançon, A., & Mouhcine, M. 2000, Massive Stellar Clusters, 211, 34 [NASA ADS] [Google Scholar]
- Lançon, A., & Fouesneau, M. 2010, Proc. Workshop held at the CIT, Pasadena, California, 10-12 November 2008, ed. C. Lietherer, P. Bennett, P. Morris, & J. van Loon (San Francisco, ASP), ASP Conf. Ser., 425, 55 [Google Scholar]
- Lançon, A., Gallagher, J. S., III, Mouhcine, M., et al. 2008, A&A, 486, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [Google Scholar]
- Mengel, S., Lehnert, M. D., Thatte, N., & Genzel, R. 2005, A&A, 443, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meurer, G. R., Heckman, T. M., Leitherer, C., et al. 1995, AJ, 110, 2665 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Schilbach, E., et al. 2009, A&A, 507, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, B., & Hanson, M. M. 2010, ApJ, 713, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Puzia, T. H., Zepf, S. E., Kissler-Patig, M., et al. 2002, A&A, 391, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafelski, M., & Zaritsky, D. 2005, AJ, 129, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E. 1998, MNRAS, 299, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., & Fall, S. M. 1999, ApJ, 527, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Footnotes
- ... correction
![[*]](/icons/foot_motif.png)
- We have not investigated any systematics for massive clusters. See Anders et al. (2004) for that regime.
All Figures
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{14084fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg18.png)
|
Figure 1: Stochastic properties of star clusters at solar metallicity. In the left hand panel, the dots represent photometric properties of individual clusters containing 103 and 105 stars each. The solid lines show the corresponding age sequences from ``standard'' predictions (figure inspired by Bruzual 2002). In the right hand panel, we show the corresponding density distribution of models in our main catalogue, constructed by assuming a power law with a index -2 for the cluster mass function. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14084fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg34.png)
|
Figure 2: Model sample of 1000 models from our main MC catalogue, randomly extracted from the catalogue to identify systematics. Selected clusters are low-mass populations and cover a broad range of ages. Fluxes are not reddened and calibrated as absolute fluxes, corresponding to a 10 pc distance. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg31.eps}\hspace*{5mm...
...eps}\hspace*{5mm}
\includegraphics[width=8.5cm,clip]{14084fg34.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg35.png)
|
Figure 3:
Estimations based on U, B, V, I and K band fluxes without noise, when assuming no extinction (AV=0, ``true'' value). Estimations from the
Bayesian approach are given in the two upper panels, and standard estimation considering an infinite number of stars are given in the two lower panels. The x-axes represent, respectively, the original age and mass of the sampled populations whereas the y-axes
represent the estimated values from the two methods. Dashed lines
highlight the identity function. Labels are features refered within the
text. Open circles highlight poor fits where the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm]{14084fg41.eps}\hspace*{1cm}
\in...
...1cm}
\includegraphics[width=8.5cm]{14084fg44.eps}
\vspace*{0.45cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg36.png)
|
Figure 4: Photometric properties of stochastic populations compared to average predictions at solar metallicity. In the left hand panels, the dots represent colours of individual clusters contained in our MC catalogue. Large regions overlap between age bins, and older models hide younger models in certain areas of the figure. The extinction vector is given by the arrows assuming a Cardelli extinction law (Cardelli et al. 1989). In the right hand panels, the corresponding density distributions of the models are shown, assuming cluster masses follow a power law with an index -2. The solid lines represent the corresponding age sequences from ``standard'' predictions. Numeric labels in the bottom left panel correspond to the age sequence from 1 Myr to 20 Gyr. Dotted lines emphasize high-density regions mentioned in Sect. 4.2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg51.eps}\hspace*{1cm...
...m}
\includegraphics[width=8.5cm,clip]{14084fg54.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg41.png)
|
Figure 5: Estimates based on U, B, V, I, and K band fluxes without noise, allowing an extinction AV from 0 to 3. The conventions and axis significations are the same as in Fig. 3. On the left-hand side, the age estimations. On the right-hand side, the mass estimations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14084fg61.eps}\hspace*{1cm}
\includegraphics[width=8cm,clip]{14084fg62.eps}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg47.png)
|
Figure 6: Derived age (left) and mass (right) distributions using the Bayesian method analysing UBVIK data when 1 mag extinction (assuming Cardelli extinction law) is applied to the input population properties. This figure compares directly with Fig. 5. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg71.eps}\hspace*{1cm...
...
\includegraphics[width=8.5cm,clip]{14084fg76.eps}
\vspace*{0.37cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg48.png)
|
Figure 7: Estimations based on U, B, V, I, and K band fluxes with 5% noise added to the photometry inputs, allowing an extinction AV from 0 to 3. From top to bottom, the direct fit of the noised populations by our catalogue, the Bayesian estimations and the standard estimations. The conventions and axis significations are the same as in Fig. 5. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg81.eps}\hspace*{1cm...
...cm}
\includegraphics[width=8.5cm,clip]{14084fg84.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg50.png)
|
Figure 8: Same figure as Fig. 5 but excluding information on the K band: estimations are based on U, B, V, I bands without noise, allowing an extinction AV from 0 to 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg91.eps}\hspace*{1cm}
\includegraphics[width=8.3cm,clip]{14084fg92.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg53.png)
|
Figure 9:
Age-mass and age-luminosity distributions obtained for our test
sample, when analysing UBVI
data with standard, continuous, population synthesis models. Grey dots
represent the test sample and black ones the recovered properties. In the right panel, masses have been converted to luminosities using the (continuous) mass-to-light ratio given by Pégase (solid line:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg101.eps}\hspace*{1cm}
\includegraphics[width=8.3cm,clip]{14084fg102.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg56.png)
|
Figure 10: Resulting age-mass distributions from the Bayesian ( left panel) and standard ( right panel) analysis methods on the test-sample clusters. Grey dots are estimates from UBVIK bands, whereas black dots are only from UBVI bands. UBVIK distribution in the right panel is presented in the left panel of Fig. 9. Binning effects are visible on the Bayesian distribution as mentioned in the Sect. 6.2. The original age-mass distribution is presented in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg11.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg57.png)
|
Figure 11: Resulting age-mass distributions from the Bayesian analysis methods in the 1-mag reddened test-sample clusters. Grey dots are estimates from UBVIK bands, whereas black dots are from only UBVI bands. Corresponding marginal distribution histograms follow the same colour conventions. The dotted line in the histograms represents the test-sample distribution. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fg121.eps}\hspace*{1c...
...
\includegraphics[width=8.6cm,clip]{14084fg124.eps}
\vspace*{0.3cm}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg58.png)
|
Figure 12:
Age-luminosity distributions recovered for our test-sample. Grey dots
are the original distributions and black dots are respectively the
recovered distributions from the standard (left panels) and Bayesian (right panels) methods when analysing UBVI (top panels) and UBVIK (bottom panels) data sets. Recovered masses are
converted to luminosities using Pégase (continuous) factor of which the solid lines represent the evolution of a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{14084fgA11.eps}\hspace*{1...
...s}\hspace*{1cm}
\includegraphics[width=7.35cm,clip]{14084fgA14.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg60.png)
|
Figure A.1:
Example of probability map for a population of 33 Myr and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=7.35cm,clip]{14084fgA21.eps}\hspace*{1cm}
...
...s}\hspace*{1cm}
\includegraphics[width=7.35cm,clip]{14084fgA24.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg62.png)
|
Figure A.2:
Example of probability maps for a population of
2.3 Gyr and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14084fgA23.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{14084fgA3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14084-10/Timg64.png)
|
Figure A.3: Illustration of the effect of binning using the cluster of Fig. A.2. In left-hand side panel the correct age is recovered with 40 bins; however, as the right panel illustrates, a different binning (50 bins) favours a much younger age with (erroneously) high extinction. The cluster is now moved to feature 5.b in Fig. 5. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



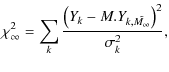
![$\displaystyle \qquad\times \sum_{\tilde{M}_i~/~ X(\tilde{M_i})\in[x_1,x_2]}
\ma...
...~ {\rm e}^{ -\frac{\left( Y_k - Y_{k,\tilde{M}_i}
\right)^2}{2\sigma_k^2}}\cdot$](/articles/aa/full_html/2010/13/aa14084-10/img30.png)