| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913377 | |
| Published online | 15 October 2010 | |
Are C-rich ultra iron-poor stars also He-rich?
G. Meynet1 - R. Hirschi2,3 - S. Ekstrom1 - A. Maeder1 - C. Georgy1 - P. Eggenberger1 - C. Chiappini1
1 - Geneva Observatory, Geneva University, 1290 Sauverny, Switzerland
2 -
Astrophysics Group, EPSAM Institute, University of Keele, Keele, ST5 5BG, UK
3 -
Institute for the Physics and Mathematics of the Universe, University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8583, Japan
Received 30 September 2009 / Accepted 28 April 2010
Abstract
Context. The three most iron-poor stars presently known
([Fe/H] equal to -5.96, -5.4 and -4.75) are carbon-rich, so they are
called C-Rich Ultra-Metal Poor Stars (CRUMPS). The origin of their
peculiar surface abundances is not understood.
Aims. We propose a synthetic view of the different models
proposed so far to explain the peculiar abundances observed on the
surface of the CRUMP stars. We deduce some expected trends based on
nucleosynthetic arguments and look for signatures that allow models to
be distinguished. We discuss the conditions for having CRUMP stars
which are He-rich, i.e. with a mass fraction of helium greater
than 0.30 and up to 0.60.
Methods. We discuss the chemical composition of stars made of
interstellar medium mixed with wind material of very metal-poor massive
stars, with wind plus supernova ejecta and with material extracted from
the envelope of early asymptotic giant branch (AGB) stars. Rotating and
non-rotating models are considered.
Results. The high nitrogen abundances observed in CRUMP stars
imply that the material that is responsible for their peculiar
abundance pattern must be heavily enriched in primary nitrogen. We show
that rotating stars (both massive and intermediate-mass stars) can
produce the required amount of primary nitrogen, and can also account
for the observed enhancements in C, O, Na, Mg, and Al. CRUMP stars
formed from wind material of massive stars mixed with small amounts of
pristine interstellar medium are He-rich (helium mass fraction
between 0.30 and 0.60), Li-depleted, and present low 12C/13C
ratios (inferior to 10 in number). Such He-rich stars, if
discovered, would confirm that the most metal-poor CRUMPs formed from
essentially pure wind/envelope material. They would provide the most
direct way of probing the nucleosynthetic outputs of the first
generations of stars.
Conclusions. We show that rotation is a key ingredient in
explaining the abundance patterns of CRUMPS stars and probably also of
at least some carbon-enhanced metal poor (CEMP) stars, in particuliar
the CEMP-no stars. Similar non-rotating models, without any
extra-mixing, do not succeed in explaining the enhancements in the
three CNO elements.
Key words: stars: abundances - stars: rotation - stars: chemically peculiar - stars: AGB and post-AGB - stars: early-type - nuclear reactions - nucleosynthesis, abundances
1 Introduction
The most iron-poor objects found to date in the Universe are halo field stars with [Fe/H] as low as
-5.96 (Frebel et al. 2008). Surprisingly, the three most iron-poor stars present strong overabundances of C with respect to Fe.
More generally, Lucatello et al. (2006) find a lower limit of 21 ![]() 2% for the number of stars with [Fe/H]
2% for the number of stars with [Fe/H] ![]() -2.0 and [C/Fe]
-2.0 and [C/Fe] ![]() +1.0.
These stars are collectively named C-Enhanced Metal-Poor (CEMP) stars. The
C-Rich Ultra Metal Poor Stars (CRUMPS) are a subset of CEMP stars, those with
+1.0.
These stars are collectively named C-Enhanced Metal-Poor (CEMP) stars. The
C-Rich Ultra Metal Poor Stars (CRUMPS) are a subset of CEMP stars, those with
![]() .
A more correct name would be C-rich ultra iron-poor
stars. The overall metallicity, where the metals would contain not only
iron but all the elements heavier than He, would amount to an [M/H]
above -1, which is, by far,
not ultra-metal poor!
.
A more correct name would be C-rich ultra iron-poor
stars. The overall metallicity, where the metals would contain not only
iron but all the elements heavier than He, would amount to an [M/H]
above -1, which is, by far,
not ultra-metal poor!
For some of these stars, strong overabundances of N, O, Na, Mg, and Al with respect to Fe have been found. Compared to solar values, the abundance ratios may be one to four orders of magnitudes greater depending on the element and/or star considered.
The CEMP stars can be classified into different categories according to the presence or absence of s- and/or r-process elements (see the discussion in Masseron et al. 2010). In the present work, when comparisons are made with observations, we focus on the ``CEMP-no'' category, i.e., on those stars that present no evidence of enhancements in the s- and r-process elements. The absence of s-process elements makes it less likely possible that the peculiar surface abundances of these stars result from accretion of material from an AGB companion, which is in general rich in s-process elements. As can be seen in Fig. 21 of Masseron et al. (2010), the ``CEMP-no'' category contains the most iron-poor objects and are thus the best candidates for studying the enrichment processes due to short-lived massive stars. Despite concentrating here on ``CEMP-no'' stars, the model studied in this work may also be relevant for at least some CEMP stars of other categories.
The main purpose is to discuss in detail the consequences of the ``spinstar'' model proposed by Meynet et al. (2006) and Hirschi (2007) where CRUMPS are formed from material ejected by metal-poor rotating stars (hereafter called the source material) mixed with some amount of interstellar material. We present the various outputs that can be obtained from such models and distinguish the following three possibilities for the origin of the source material:
- 1.
- the wind material ejected by one massive spinstar (spinstar wind model);
- 2.
- material ejected in the form of wind material during the whole massive spinstar lifetime, together with some amount of matter ejected at the time of the supernova event (spinstar wind and supernova model);
- 3.
- the envelope of an intermediate-mass spinstar at the early AGB phase (spinstar E-AGB model).
The fact that some CEMP or CRUMP stars may be He-rich have important consequences for determining their physical characteristics:
- the mass determinations of the C-rich stars will be different depending on the abundance of helium considered. Typically, at any given position in the HR diagram, a star has a lower mass if it is He-rich;
- adopting an He-rich model atmosphere modifies the temperature and density structure of the outer layers where the absorption lines are formed. This may have an impact on the abundances deduced from spectral synthesis.
Helium-rich stars are already indirectly found in some globular clusters (see e.g. Piotto et al. 2007). They may also be present in elliptical galaxies. All ellipticals show the UV upturn phenomenon, i.e. an UV excess, observed in their spectra. These excesses are caused by a population of stars on the blue end of the horizontal branch, i.e. by an old population of hot He-burning stars (see the review by O'Connell 1999). Different models have been proposed to explain the origin of this population (see e.g. Bressan et al. 1994; Han et al. 2007). A possibility, still to be explored, would be that these stars are the descendants of He-rich stars (Meynet et al. 2008a). Helium-rich low mass stars are indeed expected to populate the blue end of the horizontal branch (Decressin et al. 2009).
The paper is organized as follows. In Sect. 2, we recall the main characteristics of the ``spinstar'' model. Sections 3 to 5 discuss the chemical abundance of CRUMPS expected in the frame of the three possibilities listed above. In each case, we compare the theoretical expectations with the observed abundances in the most iron-poor stars known today and in CEMP-no stars. In Sect. 6 we briefly discuss consequences of alternative scenarios found in the literature. The isotopic ratio 12C/13C can be used to distinguish between different models. This is presented in Sect. 7. Conclusions and perspectives are given in Sect. 8.
Table 1: Masses ejected by stellar winds from different rotating models and 12C/13C number ratios in the ejecta.
2 The ``spinstar'' model
![\begin{figure}
\par\includegraphics[height=12cm, angle=-90, width=17cm,clip]{13377fig1.eps}\vspace{-5mm}
\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg21.png)
|
Figure 1: Schematic representation of the ``spinstar'' model for explaining the origin of the peculiar abundance patterns of CRUMP/CEMP-no stars: A) A metal poor massive rotating star evolves during the core H-burning phase. B) During the core He-burning phase, strong winds, triggered by self enhancement of the surface metallicity appear. C) Wind material mixed with some amount of interstellar medium form clumps. The end of the evolution of the spinstars can either be a Black Hole with no supernova explosion (D1) or it can explode as a supernova (D2) which can further enrich the clumps. The fast rotation of the core may produce a non isotropic explosion. Some clumps form small mass stars, which are the CRUMP/CEMP stars that we can observe today. |
| Open with DEXTER | |
The term ``spinstar'' refers to those very metal-poor stars that rotate fast enough for their evolution to be strongly affected by rotation (Meynet et al. 2008b). Spinstars can be either massive or intermediate-mass stars.
Rotation is needed for two purposes. First, it allows mixing between the He- and the H-burning regions and thus the synthesis of important amounts of primary 13C, 14N, and 22Ne. Rotation also deeply affects the s-process element nucleosynthesis (Pignatari et al. 2008). Second, rotation is important for triggering strong mass-loss episodes occurring during the evolution of these very metal poor stars. This is again due to rotational mixing, which transports primary elements to the surface. This increases the opacity of the outer layers and thus stimulates mass loss by line driven winds.
A very metal poor environment (Z below 0.001) is needed because rotational mixing is more efficient at low metallicity (Maeder & Meynet 2001). In addition, stars seem to rotate faster on average at low metallicities (see e.g. the review by Meynet et al. 2008c, and references therein).
The effects discussed above are consequences of the same physics as, when applied to more familiar metallicities, are able to reproduce successfully many observed features, such as the changes in the surface abundances (Maeder et al. 2009), the correct number ratio of blue- to red-supergiants at low metallicity (Maeder & Meynet 2001), the variation with metallicity in the number ratio of Wolf-Rayet (WR) to O-type stars, the existence of WR with surface abundances rich in both H- and He-burning products, the correct WN/WC number ratio at low metallicity (Meynet & Maeder 2005), and the variation with metallicity in the ratio of type Ib and Ic to type II supernovae (Georgy et al. 2009).
With respect to the models reproducing the above observed trends,
only two ingredients have been taken
differently: obviously, the metallicity, which was chosen very low (
Z = 10-8 and 10-5), and the initial ZAMS
rotational velocity on the equator. At such low metallicities, there is
no guideline for choosing the initial rotational velocity, except that
it should be inferior
to the critical velocity (i.e., the velocity at which the centrifugal
acceleration at the equator
compensates for the local gravity).
We chose ratios of
![]() between 50 and 70% on the ZAMS depending
on the initial mass and metallicity considered (see Table 1). These values are well below 1 but above the usual ratio adopted for
solar metallicity models, which is 40%.
between 50 and 70% on the ZAMS depending
on the initial mass and metallicity considered (see Table 1). These values are well below 1 but above the usual ratio adopted for
solar metallicity models, which is 40%.
The general qualitative outline of the spinstar scenario is shown in Fig. 1. In A) a metal-poor rotating star evolves during the core H-burning phase. It may happen that the surface velocity reaches the critical velocity during this phase, forming an equatorial disk enriched in H-burning products. At the very low metallicity considered here, however, the amount of mass lost in that way is quite modest. B) During the core He-burning phase, as a result of rotational and convective mixing, which brings to the surface primary CNO elements, the opacity of the outer layers is increased. The star evolves to the red part of the HR diagram. A deep outer convective zone appears, dredging up large quantities of CNO elements to the surface. This triggers strong mass loss. The wind is made of both H- and He-burning products. C) Part of the wind material forms clumps. Some amount of interstellar medium may enter into their composition. If stars form later in these clumps, their initial composition will bear the mark of the composition of the spinstar's ejected material (source material). Sufficienly long-lived low-mass stars formed in that way produce the CRUMP stars that we observe today.
The end of the evolution of the spinstars, if massive, can be a black hole with no supernova explosion (D1). In that case there is no risk that the clumps be destroyed or further enriched by the supernova ejecta. The massive spinstar might also explode as a supernova (D2). In this case, the fast rotation of the core may produce a non-isotropic explosion (Tominaga et al. 2007a), which may allow some clumps to survive the explosion. More probably, an intermediate situation will arise where a faint supernova explosion occurs with a lot of material falling back on the nascent black hole as proposed by Umeda & Nomoto (2003).
Enrichment of some clumps by supernova ejecta may occur. Therefore, in this general frame, various enrichment scenarios are possible depending on the nature of the spinstar, on the degree of mixing with interstellar material, and on the importance of the wind's contribution with respect to the supernova one.
![\begin{figure}
\par\hspace*{4mm} \includegraphics[height=11cm, width=9cm,clip]{13377fig2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg22.png)
|
Figure 2:
Evolution of the surface abundances for a 60 |
| Open with DEXTER | |
3 The spinstar wind model
In Fig. 2, we show how the surface abundances evolve as a function of the actual mass of the star (which
decreases as a function of time) for a 60 ![]() model at Z=0.00001 and with
model at Z=0.00001 and with
![]() .
During the main sequence (MS) phase, the star
loses only a little more than 6
.
During the main sequence (MS) phase, the star
loses only a little more than 6 ![]() .
The material ejected during the MS phase bears the usual signature
of the CNO cycle, i.e. increase in 14N and decrease in 12C, 16O, and of the 12C/13C
ratio. We note also the consequences at the surface of the action
of the Ne-Na and Mg-Al chains, which are active in the H-burning core (decrease in Ne and Mg isotopes and increase
in 23Na and 27Al).
At any given point (in Fig. 2 when the actual mass is around 50
.
The material ejected during the MS phase bears the usual signature
of the CNO cycle, i.e. increase in 14N and decrease in 12C, 16O, and of the 12C/13C
ratio. We note also the consequences at the surface of the action
of the Ne-Na and Mg-Al chains, which are active in the H-burning core (decrease in Ne and Mg isotopes and increase
in 23Na and 27Al).
At any given point (in Fig. 2 when the actual mass is around 50 ![]() ), He-burning products, such as 12C and
16O appear on the surface,
while those due to H burning, such as nitrogen, are also
increased. Rotational diffusion transports He-burning products in the
H-burning shell
where part of them are transformed by the CNO processing (explaining
the strong 13C and 14N enhancements). Part of
the He-burning products succeed in diffusing through the H-burning
shell up to the surface without being
destroyed by the CNO cycle (explaining the strong 12C and 16O abundances).
), He-burning products, such as 12C and
16O appear on the surface,
while those due to H burning, such as nitrogen, are also
increased. Rotational diffusion transports He-burning products in the
H-burning shell
where part of them are transformed by the CNO processing (explaining
the strong 13C and 14N enhancements). Part of
the He-burning products succeed in diffusing through the H-burning
shell up to the surface without being
destroyed by the CNO cycle (explaining the strong 12C and 16O abundances).
During the MS phase, the sum of the CNO element remains constant (see the upper curve in Fig. 2). When the
actual mass of about 50 ![]() is reached, the sum of CNO elements increases strongly as a result of rotational
mixing in previous phases and the deepening of the outer convective zone. At that stage the star has an effective
temperature of the order of 3.85.
is reached, the sum of CNO elements increases strongly as a result of rotational
mixing in previous phases and the deepening of the outer convective zone. At that stage the star has an effective
temperature of the order of 3.85.
In Table 1, we indicate
the following quantities for the various rotating models computed at
very low metallicity: Cols. 2 to 5 give
the initial mass, metallicity, the initial rotation velocity on the
ZAMS,
![]() ,
and the ratio
,
and the ratio
![]() respectively.
The total mass ejected by the winds is given in Col. 6. The total masses ejected in
the form of H, He, 12C, 13C, 14N, and 16O are given in Cols. 7 to 12, respectively. The number ratio 12C/13C is indicated in Col. 13. The models for
Z =10-8 ([Fe/H] = -6.6)
are from Hirschi (2007) except for one, model C, taken from Meynet et al. (2006).
Models at 10-5 ([Fe/H] = -3.6) are from Meynet et al. (2006).
Some differences in the input physics explain the different outputs for
otherwise similar models (see the above references for more details).
respectively.
The total mass ejected by the winds is given in Col. 6. The total masses ejected in
the form of H, He, 12C, 13C, 14N, and 16O are given in Cols. 7 to 12, respectively. The number ratio 12C/13C is indicated in Col. 13. The models for
Z =10-8 ([Fe/H] = -6.6)
are from Hirschi (2007) except for one, model C, taken from Meynet et al. (2006).
Models at 10-5 ([Fe/H] = -3.6) are from Meynet et al. (2006).
Some differences in the input physics explain the different outputs for
otherwise similar models (see the above references for more details).
From Table 1, it is easy to compute the initial chemical abundance that a star would have if formed
from a mixture of wind material and of some amount of pristine interstellar matter. If
![]() is the mass ejected in the form of wind and
is the mass ejected in the form of wind and
![]() the mass of interstellar material with which
the wind material is mixed, then let us define D, the dilution factor, as the ratio
the mass of interstellar material with which
the wind material is mixed, then let us define D, the dilution factor, as the ratio
![]() .
Then the mass fraction of element i, Xi, in the star formed from wind ejecta and interstellar matter is given by
.
Then the mass fraction of element i, Xi, in the star formed from wind ejecta and interstellar matter is given by
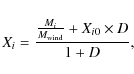
where Mi is the mass of element i ejected by the winds, and Xi0 the mass fraction of element i present in the interstellar material. The quantity
![\begin{displaymath}[X_{i}/{\rm H}]=\log
\left(
{
{M_i \over M_{\rm wind}}
+X_{i0...
...right)
-\log
\left(
{X_{i\odot} \over X_{\rm H\odot}}
\right)
,\end{displaymath}](/articles/aa/full_html/2010/13/aa13377-09/img29.png)
where
To compute the expected chemical composition of CRUMP stars made of such wind material, a first step consists in obtaining information on the dilution factor. This is the topic of the next section.
3.1 Constraint on the dilution factor
An interesting element to be used for constraining the dilution factor is Li. It was used by Decressin et al. (2007b) for estimating the dilution factor in another context, namely that of the chemical anomalies observed in globular clusters. We follow here the same line of reasoning in the context of the CRUMP stars found in the field of the halo.
Lithium has a reasonably well known value in the pristine interstellar medium equal to the value given by standard Big Bang nucleosynthesis. It is completely destroyed in massive stars and also in AGB stars. Thus any mixing of such stellar ejecta with pristine interstellar material will increase the abundance of Li with respect to the abundance in the source material. The dilution to be adopted is the one that will allow the observed Li abundance to be reproduced. Of course, this is correct as long as the abundance of Li is not affected by internal mixing processes having occurred in the CRUMP star itself.
For the star HE 1327-2326 (
![]() ), Frebel et al. (2008) obtained an upper value
of
), Frebel et al. (2008) obtained an upper value
of ![]() (Li) of 0.62, with
(Li) of 0.62, with ![]() (Li) defined as
(Li) defined as
![]() ,
where N(Li) and N(H) are the density number
of Li and H. This is a very low value, compared both to the abundance
of Li expected from standard Big Bang nucleosynthesis
(2.72 according to Cyburt et al. 2008), and to the value of Li observed in the bulk of normal metal-poor halo stars on the Spite plateau
(2.10 according to Bonifacio et al. 2007).
,
where N(Li) and N(H) are the density number
of Li and H. This is a very low value, compared both to the abundance
of Li expected from standard Big Bang nucleosynthesis
(2.72 according to Cyburt et al. 2008), and to the value of Li observed in the bulk of normal metal-poor halo stars on the Spite plateau
(2.10 according to Bonifacio et al. 2007).
As indicated above, HE 1327-2326 is either an evolved MS or an early subgiant star with an effective temperature of about 6200 K. Although there are no ``normal stars'' (i.e. not C-enhanced) observed with such a low Fe content, hence no possibility of knowing the level of the Spite plateau in this range of Fe content, HE 1327-2326 presents all the characteristics (evolutionary stage and effective temperature) for belonging to the Spite plateau. Thus one would have expected a value around 2.10 instead of an upper limit of 0.62.
Recently, Korn et al. (2009) have computed the effects of atomic diffusion
including gravitational settling, thermal diffusion and radiative accelerations in models with masses around 0.78 ![]() and an
Fe content similar or lower than that of HE 1327-2326.
In one model, an additional ad hoc diffusion coefficient is added with
no attempt to connect it to a physical process like rotation.
This diffusion coefficient was chosen to reproduce the observed
abundance trends between stars from the turn off point to the red giant
branch in NGC 6397 (Lind et al. 2008; Korn et al. 2007).
For what concerns Li, the model with no additional diffusion shows
a depletion of
1.2 dex, and the one with additional diffusion shows a depletion
by 0.3 dex. Thus we see that, according to this study, depletion
mechanisms
would not succeed in decreasing the Li abundance from the cosmological
value below the observed upper limit. Indeed to obtain such a result,
a depletion of at least 2.1 dex is required! Moreover, the case
with no additional mixing, which produces the greatest depletion
factor, is probably not the favored one since it
cannot explain the observed trends in NGC 6397. From this we
conclude that at the present time there is no strong reason to suppose
that the very low Li abundance observed today in HE 1327-2326
results mainly from internal depletion processes.
Thus we are left with the second possibility that the low Li-abundance
observed today mainly results
from the fact that this star was formed from very Li-poor material.
and an
Fe content similar or lower than that of HE 1327-2326.
In one model, an additional ad hoc diffusion coefficient is added with
no attempt to connect it to a physical process like rotation.
This diffusion coefficient was chosen to reproduce the observed
abundance trends between stars from the turn off point to the red giant
branch in NGC 6397 (Lind et al. 2008; Korn et al. 2007).
For what concerns Li, the model with no additional diffusion shows
a depletion of
1.2 dex, and the one with additional diffusion shows a depletion
by 0.3 dex. Thus we see that, according to this study, depletion
mechanisms
would not succeed in decreasing the Li abundance from the cosmological
value below the observed upper limit. Indeed to obtain such a result,
a depletion of at least 2.1 dex is required! Moreover, the case
with no additional mixing, which produces the greatest depletion
factor, is probably not the favored one since it
cannot explain the observed trends in NGC 6397. From this we
conclude that at the present time there is no strong reason to suppose
that the very low Li abundance observed today in HE 1327-2326
results mainly from internal depletion processes.
Thus we are left with the second possibility that the low Li-abundance
observed today mainly results
from the fact that this star was formed from very Li-poor material.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[height=12cm, width=9cm,clip]{13377fig3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg33.png)
|
Figure 3:
Predicted abundances in stars made of a mixture of wind ejecta of massive rotating stars
and of pristine interstellar medium plotted as a function of the dilution factor D, the ratio between the mass
of interstellar medium and the mass
ejected in the wind involved in the mixture. The rotating models
are for 40 and 85 |
| Open with DEXTER | |
In the bottom panel of Fig. 3, the continuous lines show how the abundance of Li varies in a body formed from
spinstar winds (completely Li-free) and of pristine interstellar material having WMAP Li abundance
when the dilution factor is increased. The two lines corresponding to our 40 and
85 ![]() models do not
superpose because the wind ejecta of these two models do not have the same mean hydrogen abundance and
models do not
superpose because the wind ejecta of these two models do not have the same mean hydrogen abundance and ![]() (Li)
show the variation in the abundance of Li with respect to H (see the definition just above).
(Li)
show the variation in the abundance of Li with respect to H (see the definition just above).
Let us consider the case of the 40 ![]() model. If no Li-depletion at all occurred in the CRUMP star,
then the present day observed value is equal to the initial value. In that case,
Fig. 3 tells us that the star
should be made from pure ejecta. Any dilution would rapidly bring the Li abundance above the observed upper limit.
model. If no Li-depletion at all occurred in the CRUMP star,
then the present day observed value is equal to the initial value. In that case,
Fig. 3 tells us that the star
should be made from pure ejecta. Any dilution would rapidly bring the Li abundance above the observed upper limit.
If the depletion factor is 1.2 dex (maximum and probably unrealistic value inferred from the models of Korn et al. 2009), then the observed upper limit would be compatible with
a dilution factor inferior to about 0.13 (cf. the abscissa of the point on the 40 ![]() model with an ordinate equal to 0.62+1.2 = 1.82).
Although not zero, the dilution factor remains extremely small.
model with an ordinate equal to 0.62+1.2 = 1.82).
Although not zero, the dilution factor remains extremely small.
We have also indicated in the bottom panel of Fig. 3 the upper limit abundance measured in 6 CEMP MS stars as obtained from the SAGA database of Suda et al. (2008). There are only 7 stars in total with measured Li abundance and low [Fe/H]. Except for one star, which is on the Spite plateau, the 6 other stars in this sample all have values of Li inferior to 1.75, and the two stars in this sample with [Fe/H] < -4 have an upper limit for the Li abundance of 1.5 and 1.1, respectively. The upper limit of 1.75 is compatible with a dilution factor of 0.11 and 0.25 if there has been no Li-depletion or a 0.3 dex depletion in these CEMP stars. In case depletion of 0.6 dex is allowed (difference between the WMAP and Spite Plateau), then the dilution factor can be at most 0.65.
From the discussion above we conclude that for a reasonable value of Li-depletion having occurred in the CRUMP star itself, then the low values of Li observed in some of the CEMP stars can only be explained if two conditions are fulfilled: 1) low Li-CEMP stars are made of Li-free (or nearly free) material, and 2) a small amount of pristine interstellar medium can be added, at most 65%.
Interestingly, this means that the appropriate abundances for the low Li-CEMP stars must be obtained mainly from the source. The dilution factor cannot be used as a free parameter allowing adjustment of the level of the abundances. This also implies that all the potential sources able to produce Li are discarded as candidates for providing low Li-CEMP stars material.
![\begin{figure}
\par\hspace*{2mm}\includegraphics[height=9cm, width=9cm,clip]{13377fig4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg34.png)
|
Figure 4: The [C/H], [N/H], and [O/H] ratios in the wind ejecta of various rotating models mixed with at most 15% of pristine interstellar medium are shown (dilution factor D=0.15). The models are those presented in Table 1. The models obtained for the same initial mass, metallicity, and rotation, but computed with different prescriptions, cover the shaded areas. The vertical hatched columns show the range in observed values for CEMP-no stars with log g superior to 3.8 (left) and with log g inferior to 3.8 (right). The values were taken from Tables 1 and 2 of Masseron et al. (2010). Only upper limits are given for [O/H], which is why the columns extend down to the bottom. The star symbols show the observed values for the most iron-poor star known today (Frebel et al. 2008). The left part of the figure indicates for each model the total mass ejected in solar masses, the mass fraction of He (case with D=0), the upper mass limit for Li abundance (obtained with D=0.15), and the isotopic ratio 12C/13C in number. |
| Open with DEXTER | |
3.2 Consequence of the small dilution factor: some CEMP stars are He-rich
In the upper panel of Fig. 3, we show how the abundance of He (in mass fraction) varies in a body formed from spinstar winds and of interstellar material with a mass fraction of He equal to 0.24 when the dilution factor is increased.
As can be seen from Table 1, the masses ejected by both the 40 and 85 ![]() models are sufficient for forming at least
one 0.8
models are sufficient for forming at least
one 0.8 ![]() stars. Such a star, made of a pure rotating 85 (40)
stars. Such a star, made of a pure rotating 85 (40) ![]() star wind ejecta would have an initial
star wind ejecta would have an initial
![]() (0.32).
For any dilution factors inferior to about 4.1 (0.3), a CEMP star made of wind ejecta of
a 85 (40)
(0.32).
For any dilution factors inferior to about 4.1 (0.3), a CEMP star made of wind ejecta of
a 85 (40) ![]() model, would have a He mass fraction superior to 0.30.
model, would have a He mass fraction superior to 0.30.
This conclusion can be formulated in a more general way: any stars formed mainly from the envelope of an evolved massive or intermediate mass star, rotating or not, would be He-rich (see Table 2 in Meynet et al. 2010a). Thus He-richness would not be a hint per se that the spinstar model we propose here is correct but that the CRUMP stars are mainly formed from the envelope of evolved stars.
Would He-rich stars necessarily be Li-poor? The answer is no.
The example above shows that even with a dilution factor of 4
(see the case of the 85 ![]() model), we still have a He-rich star, while the initial
Li abundance, obtained with such
a dilution factor, would be nearly equal to the
cosmological value!
Are Li-poor stars necessarily He-rich? No, because the CRUMP star may be formed
from a high fraction of interstellar medium and Li may have then been depleted
by internal mixing processes in the CRUMP star itself, although this is unlikely to happen in current stellar evolution models.
model), we still have a He-rich star, while the initial
Li abundance, obtained with such
a dilution factor, would be nearly equal to the
cosmological value!
Are Li-poor stars necessarily He-rich? No, because the CRUMP star may be formed
from a high fraction of interstellar medium and Li may have then been depleted
by internal mixing processes in the CRUMP star itself, although this is unlikely to happen in current stellar evolution models.
3.3 Predictions for CNO abundances in CRUMP/CEMP-no stars
In Fig. 4, we show the values of the [C/H], [N/H], and [O/H] ratios obtained in the wind ejecta of our rotating models
for dilution factors between 0 and 0.15.
Except for the 85 ![]() (see error bars for the values of the 85
(see error bars for the values of the 85 ![]() model), the values obtained with D=0 and 0.15 are identical.
The He mass fractions are indicated for a dilution factor equal to 0.
The upper value of the abundance of Li is given using D=0.15. The ratio 12C/13C is insensitive to such small variations
in the dilution factor (see Sect. 7).
model), the values obtained with D=0 and 0.15 are identical.
The He mass fractions are indicated for a dilution factor equal to 0.
The upper value of the abundance of Li is given using D=0.15. The ratio 12C/13C is insensitive to such small variations
in the dilution factor (see Sect. 7).
In Fig. 4, the vertical hatched zones show the range of observed values for CEMP-no stars with log g superior to 3.8 (left dark grey column, 5 stars in the sample) and with log g inferior to 3.8 (right light grey column, 20 stars in the sample, red in the online version). The observed data were taken from Table 2 of Masseron et al. (2010). The star symbols show the observed values for the most iron-poor star known today (HE 1327-2326, Frebel et al. 2008). The second (HE 0107-5240, Christlieb et al. 2004) and third (HE 0557-4840, Norris et al. 2007) most metal-poor star known today belong to the group of the CEMP-no stars with log g inferior to 3.8. These last two stars are giants, therefore their surface abundances may have been affected by the first dredge-up.
Before discussing the comparisons with the observed abundances in HE 1327-2326 and CEMP-no stars, we note a few general trends of the theoretical ratios:
- in the solar mixture, the CNO elements represent a number of atoms equivalent to about 80 times the number of Fe atoms,
and the number of N atoms corresponds to about 3 times the number of Fe atoms. Let us suppose that these
proportions are approximately the same at all metallicities. (This is the hypothesis we made for determining the initial
distribution of the heavy elements in our model stars.) In that case, the maximum [N/H] value
one might expect if all the carbon and oxygen initially present in the star were transformed into nitrogen would be equal to
[N/H]
 (80/3) + [Fe/H] = 1.4 + [Fe/H].
Any [N/H] value shifted upwards by more than about 1.4 dex with
respect
to [Fe/H] is an indication that nitrogen has to be produced in a
primary process. This happens in all the computed models
shown in Fig. 4;
(80/3) + [Fe/H] = 1.4 + [Fe/H].
Any [N/H] value shifted upwards by more than about 1.4 dex with
respect
to [Fe/H] is an indication that nitrogen has to be produced in a
primary process. This happens in all the computed models
shown in Fig. 4;
- primary nitrogen can only be produced in a star that simultaneously has an H- and an He-burning region. In addition, some mixing process must occur between these two nuclear active regions. Rotational mixing is the mechanism we propose here to trigger this mixing. As recalled above, the mechanism that allows the ejection of that material is the self enrichment of the surface, also triggered by rotation. Thus rotational mixing, which produces the peculiar abundance pattern, also allows the chemically peculiar matter to be ejected by the star.
We see that the present models provide trends toward qualitative
agreement with the observations of HE 1327-2326: low Li abundances and high [X/H] ratios simultaneously for C, N, and O,
low 12C/13C (although only an upper limit is given for HE 1327-2326). All the models also
predict He-rich (
![]() )
stars.
None of the present models, however, fits all the observed data perfectly.
But here three facts need to be recalled.
1) The models are not at all adjusted to fit the observed abundances. We have simply plotted
our predictions for the wind ejecta composition. As explained above, the dilution factor does not offer any
degree of freedom. 2) Changes in the initial rotational velocities, in the initial masses, and probably,
although to a lesser extent, in the initial metallicity would widen the range of values predicted by the models.
3) Depending on the evolutionary stage at which
the mass is ejected by stellar winds, its chemical composition can vary a lot.
This is the point we discuss in the next section.
)
stars.
None of the present models, however, fits all the observed data perfectly.
But here three facts need to be recalled.
1) The models are not at all adjusted to fit the observed abundances. We have simply plotted
our predictions for the wind ejecta composition. As explained above, the dilution factor does not offer any
degree of freedom. 2) Changes in the initial rotational velocities, in the initial masses, and probably,
although to a lesser extent, in the initial metallicity would widen the range of values predicted by the models.
3) Depending on the evolutionary stage at which
the mass is ejected by stellar winds, its chemical composition can vary a lot.
This is the point we discuss in the next section.
Comparing the predictions of our spinstar wind models with the observations of CEMP-no stars (see hatched columns in Fig. 4), we see that the situation is generally rather encouraging. We see that many models cover the hatched regions.
3.4 The spinstar shell model
In this section we explore a slightly different version of the spinstar wind model explained in the previous section. In this model the CRUMP stars are still formed from spinstar ejecta but now, instead of considering the well-mixed material ejected by winds during the whole stellar lifetime, we consider shells of material ejected at different evolutionary stages. We still suppose that stellar winds are continuous but we consider that only wind material emitted during an interval of time is used to form the CRUMP star.
We begin by examining at which stage the wind ejected material presents the greatest similarities with the abundances
observed on the surface of HE 1327-2326.
In Fig. 5 the evolution of the [X/H] ratios and of the number ratio 12C/13C are shown on the surface of the 60 ![]() model
with Z=10-5 (model E in Table 1).
The 12C/13C
is very low most of the time (below 10), while the initial ratio
used for computing the models is above 75. However its evolution
is
not monotonic. It first decreases, as a result of the CNO cycle; then
when He-burning products appear, a rapid increase in the ratio occurs
(around 50
model
with Z=10-5 (model E in Table 1).
The 12C/13C
is very low most of the time (below 10), while the initial ratio
used for computing the models is above 75. However its evolution
is
not monotonic. It first decreases, as a result of the CNO cycle; then
when He-burning products appear, a rapid increase in the ratio occurs
(around 50 ![]() in Fig. 5). Then owing to the continuous action
of the H-burning shell it decreases again.
in Fig. 5). Then owing to the continuous action
of the H-burning shell it decreases again.
In Fig. 5 we have overplotted the level of the observed ratios in HE 1327-2326 as given by Frebel et al. (2008). The chemical composition of the wind has the greatest similarity with the abundances observed in the Frebel star when He-burning products begin to appear at the surface. Before that time, the matter would be depleted in C and O, and after it, the enhancements of the CNO elements would be too high. Of course, the evolution shown in Fig. 5 changes when the initial mass of the star changes or when the initial velocity is varied.
In contrast to Fig. 5, where instantaneous values of the surface
composition are plotted, the composition in shells of material is shown
in Fig. 6. For instance,
for our 85 ![]() star,
we consider 20 events of mass loss, each 3.25
star,
we consider 20 events of mass loss, each 3.25 ![]() (summing a total of 65
(summing a total of 65 ![]() lost during the life of this star).
Only the compositions of four or five shells are shown in each panel of Fig. 6.
The lower curve corresponds to the first shell ejection and the upper one to the last one.
When evolution proceeds, the [X/H]'s shift upwards.
lost during the life of this star).
Only the compositions of four or five shells are shown in each panel of Fig. 6.
The lower curve corresponds to the first shell ejection and the upper one to the last one.
When evolution proceeds, the [X/H]'s shift upwards.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[height=9cm, width=9cm,clip]{13377fig5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg38.png)
|
Figure 5: Same as Fig. 2 for the [X/H] ratios. The curve labelled 12C/13C shows the evolution in the number ratio of the two carbon isotopes. The horizontal dotted lines show the values obtained for HE 1327-2326 (Frebel et al. 2008). In the case of the carbon isotopic ratio, only a lower limit is given. The shaded area represents the portion of the mass ejected in the form of stellar winds which shows, once well mixed, the chemical composition plotted as the third curve from the bottom in left panel of Fig. 7. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm,clip]{13377fig6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg39.png)
|
Figure 6: The [C/H], [N/H], and [O/H] ratios in wind-shells ejecta of various rotating models are shown (see text). The models plotted are the models A, C, and D of Table 1. The masses of the shells are indicated along with the age of the star when half of the mass of the shell is ejected. The mass fraction of He and the 12C/13C in number in the shells are indicated (case with D=0). The stars show the observed values for the most iron-poor star known today (Frebel et al. 2008). The vertical hatched zones have the same meaning as in Fig. 4. |
| Open with DEXTER | |
From Fig. 6 the following remarks can be made:
- already when the first shells are ejected, the 12C/13C ratio is quite low. It takes values near the one expected from CNO equilibrium. This occurs because this ratio is one of the first to change on the stellar surface. This is true for all the models discussed here;
- when evolution proceeds, some 12C produced in the He-burning region does appear on the surface and increases the 12C/13C ratio to values above the equilibrium value. In further evolutionary stages, the continuous action of the H-burning shell again produces a decrease in this ratio. Thus, in the framework of the spinstar model, we see that a value of the 12C/13C ratio slightly above the equilibrium CNO value, as observed in the Frebel star, favors material ejected at the transition between the phase when only H-burning products are ejected, and that when both H- and He-burning products are ejected. This confirms what was deduced for Fig. 5;
- as time goes on, matter processed by H- and He-burning are ejected and the CNO abundance ratios are enhanced by many orders of magnitude, as is the mass fraction of He;
- in all three cases, there are shells that would fit
the observed CNO abundances for the Frebel star (see e.g. the shell
ejected at a mean age of 5.28 My by the 40
 stellar model). Similar cases might be found for the other models, changing
the mass of the shells and/or the time interval during which it is ejected.
stellar model). Similar cases might be found for the other models, changing
the mass of the shells and/or the time interval during which it is ejected.
![\begin{figure}
\par\includegraphics[width=6.5cm, angle=-90,clip]{13377fig7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg40.png)
|
Figure 7: Left panels: the [C/H], [N/H], [O/H], [F/H] and [Ne/H] ratios in different shells wind-ejected by models E of Table 1. In the left part of the left panel are indicated for each shell the mean age at the time of shell ejection, the mean mass fraction of He, and the isotopic ratio 12C/13C in number (case with D=0) in the shell. Right panels: the [X/Fe] ratios are shown for 19F, 20,22Ne, 23Na, 24,25,26Mg, and 27Al. The stars show the observed values for the most iron poor star known today (Frebel et al. 2008). The hatched areas correspond to the range of values covered by observed values in CEMP-no stars. The left column corresponds to unevolved stars (sample of 6 stars), the right column to evolved stars (sample of 17 stars). The observations were taken from the SAGA database (Suda et al. 2008). |
| Open with DEXTER | |
3.5 Predictions for Na, Mg and Al abundances in CRUMP stars
Since the Z=10-5 models were computed accounting for the Ne-Na and Mg-Al chains, we show in the right panel of Fig. 7 the theoretical ratios expected for 19F, 20,22Ne, 23Na, 24,25,26Mg, and 27Al. The Ne-Na and Mg-Al chains are active in H-burning regions. Their main effect is to transform Ne into Na and Mg into Al. In the beginning, the shells have near solar [X/Fe] ratios. (The curve corresponding to the first shell is the nearly horizontal line just above the [X/Fe] = 0 line, see right panel of Fig. 7.) The composition is not exactly solar because some surface enrichments have already occurred (see Fig. 2), and the initial composition adopted to compute the present models are slightly different from the Asplund et al. (2005) solar composition, which is used to normalise the plotted values.
Then when evolution proceeds, the general trend is the following: [Ne/Fe] decreases and [Na/Fe] increases, [Mg/Fe] decreases and [Al/Fe] increases, as is expected from the activity of the Ne-Na and Mg-Al cycle. The sawtooth shape of the abundance distribution pattern is more pronounced in shells ejected at the end of the evolution than at the beginning.
Some effects might blur this simple picture, such as the arrival on the surface of some primary elements.
During the core H-burning phase, there is no possibility of producing primary Na and Al, since
there is no way for the star at this stage to produce Ne and Mg. Thus Na and Al are built up from
the initial Ne and Mg present in the star. During the core He-burning phase, some Ne, through
![]() Ne in the most massive stars, and Mg, through
Ne in the most massive stars, and Mg, through ![]() captures on 22Ne,
can be produced at the end of the core He-burning phase. Note that 22Ne
has a strong primary component in rotating models
since this isotope is produced by the transformation of primary
nitrogen, which has diffused from the
H-burning shell into the He-burning core. Since the Ne and Mg are
produced at the very end of the core He-burning phase, there is little
time left for these
elements to diffuse in the H-burning shell, to be transformed into Na
and Mg, and to be ejected into the stellar winds. In the present
models,
no primary components of Ne, Mg, Na, and Al are present in the wind
material.
captures on 22Ne,
can be produced at the end of the core He-burning phase. Note that 22Ne
has a strong primary component in rotating models
since this isotope is produced by the transformation of primary
nitrogen, which has diffused from the
H-burning shell into the He-burning core. Since the Ne and Mg are
produced at the very end of the core He-burning phase, there is little
time left for these
elements to diffuse in the H-burning shell, to be transformed into Na
and Mg, and to be ejected into the stellar winds. In the present
models,
no primary components of Ne, Mg, Na, and Al are present in the wind
material.
Fluorine is built up in regions partially burnt by He-burning (periphery of the convective core during the core He-burning phase or of the He-burning shell). It results from transformation of part of the 14N. Its abundance can be boosted by the production of primary nitrogen in rotating models. Since it is only produced in a relatively small part of the star, its apparition at the surface is very sensitive to many parameters of the models. In the model shown in Fig. 7, F is slightly depleted (with respect to Fe) in the wind ejecta.
When we compare the global shape of the distribution pattern predicted in the shells with the observations, the first striking feature is the fact that the observations do not show the expected sawtooth pattern between Mg and Al. Magnesium remains more abundant than Al in HE 1327-2326 and in all the CEMP-no stars for which the abundances of these two elements have been measured. Thus this seems to be a general feature and not just a peculiar circumstance.
In the frame of the sole activity of the Mg-Al chain, such a pattern might be explained if the material had just been very partially processed by this chain. In that case Mg can be depleted very little while Al can be significantly increased. (Since initially Mg/Al is about a factor 10, the transformation of 10% of Mg into Al would already increase the Al abundance by a factor 2.) This may explain the relative abundance of Mg with respect of Al. But one difficulty in that case would be to explain the absolute values. Since Mg would be depleted little, the high observed [Mg/Fe] would correspond to nearly the initial [Mg/Fe] ratio and this would indicate that at [Fe/H] equal to -5.96, the relative number of Mg atoms with respect to iron is about 100 times greater than the similar ratio in the Sun. Looking at the observations of Cayrel et al. (2004), this does not appear to be the case. In normal halo stars, values of [Mg/Fe] around 0.2 are found down to an [Fe/H] equal to -4.2.
Another possibility would be that some Mg and Al produced in He-burning
regions are ejected either in the winds or by the supernova.
This is quite a reasonable solution, especially since a very tiny
amount of core material would be sufficient. This can be seen
in Fig. 10 where the chemical composition of material composed of the stellar winds plus supernova ejecta
is shown for different values of the mass cut (see Sect. 4 for more details). We see that ejecting at the time
of the supernova only the outermost 7 ![]() stellar layers would allow for the correct Mg/Al ratio
(see curve with a mass cut = 30
stellar layers would allow for the correct Mg/Al ratio
(see curve with a mass cut = 30 ![]() in Fig. 10). In that case, some dilution is needed to obtain
the correct enrichment level. This is discussed in Sect. 4.
in Fig. 10). In that case, some dilution is needed to obtain
the correct enrichment level. This is discussed in Sect. 4.
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg43.png)
|
Figure 8:
Abundance profiles for various elements (in mass fraction) as a function of the Lagrangian mass in the outer layers
of a 60 |
| Open with DEXTER | |
There is still one striking point to underline when looking at the right panels of Fig. 7: in most CEMP-no stars, Al is depleted with respect to Fe. This contrasts with the peculiar case of HE 1327-2326 and does appear difficult to reconcile with what we know about the nucleosynthesis of Al: no matter chain of reactions intervenes, Al is produced not destroyed! At that moment we only mention that Al abundances are determined from resonance lines that are very sensitive to NLTE effects (Cayrel et al. 2004). The abundances obtained from NLTE models might be 0.8 dex above the LTE abundances (Andrievsky et al. 2008)! In view of this, it might be premature to discuss solutions to that problem in too much details . We briefly come back to it in the next section.
4 The spinstar wind and supernova model
In Fig. 8, the chemical structure of our model E in Table 1 is shown. We make the hypothesis that the outer layers of this model already have, at the stage represented on this figure (end of core He-burning), the chemical composition they would have at the presupernova stage. This is only approximatively correct, but for the elements we are interested in here, it is a reasonable hypothesis.
For deciding what fraction of the mass is ejected at the time of the supernova explosion, one needs to know the mass cut between the ejected shells and the layers that will finally be incorporated into the compact stellar remnant. Here we consider the value of this mass cut as a free parameter. If this mass cut is chosen equal to the presupernova mass, then the supernova does not contribute to the enrichment of the ISM and the star will only contribute through its winds. When the mass cut is less than the presupernova mass, the mass ejected by the supernova is added to the mass ejected by the winds during the whole previous lifetime, and this constitutes the material composed of wind material and of supernova ejecta.
The composition of the wind+supernova material is shown in Fig. 10 for various values of the mass cut.
Down to a mass cut of about 31 ![]() ,
the supernova ejecta would not change the composition a lot with
respect to the composition of the wind material alone. As explained above, one sees the clear signature
of the activity of the Ne-Na and Mg-Al chains. When He-burning regions are ejected, typically when the mass cut
is decreased from 31 to 30
,
the supernova ejecta would not change the composition a lot with
respect to the composition of the wind material alone. As explained above, one sees the clear signature
of the activity of the Ne-Na and Mg-Al chains. When He-burning regions are ejected, typically when the mass cut
is decreased from 31 to 30 ![]() ,
a big change occurs. We see that C and O increase a lot,
while
the sawtooth pattern typical of the Ne-Na and Mg-Al chains is reversed.
One notes also that the 12C/13C number ratio increases by orders of magnitude.
A mass cut as low as 28
,
a big change occurs. We see that C and O increase a lot,
while
the sawtooth pattern typical of the Ne-Na and Mg-Al chains is reversed.
One notes also that the 12C/13C number ratio increases by orders of magnitude.
A mass cut as low as 28 ![]() and beyond would produce O-rich stars.
and beyond would produce O-rich stars.
From Fig. 10, we can therefore deduce that to explain N abundances
superior to those of C and O as
observed
in HE 1327-2326 for instance, the mass cut should be high, superior or equal to 30 ![]() in the case of the model plotted in Fig. 10, and therefore the
supernova contribution should be small. We see that
adding deeper layers (lowering the mass cut below 30
in the case of the model plotted in Fig. 10, and therefore the
supernova contribution should be small. We see that
adding deeper layers (lowering the mass cut below 30 ![]() )
would rapidly lower the N/C and N/O ratios
and thus prevent ratios higher than 1 as observed in HE 1327-2326.
This means that most of the supernova ejecta fall back in the black hole and a little amount of the mass of the He-core
is ejected (so not much C and O are finally ejected). This would be in line with the model proposed
by Umeda & Nomoto (2003).
In that model, in addition to strong fall back,
mixing is supposed to occur in a fraction of the He-core at the time of
the explosion. This
mixing process, which was found to take place in SN1987A and various
explosion models (see the above reference), allows
some iron, present in the deep layers, to be dredged-up in the ejected
material. The mixing and fallback model also mimics the effect of
asymmetric explosions in which matter from deep layers is ejected along
the poles, while most of the matter falls back on the remnant at other
lattitudes.
Such models might be invoked for explaining possibly negative [Al/Fe]
ratios, while still maintaining CNO overabundances compatible with
those observed in CRUMPS.
)
would rapidly lower the N/C and N/O ratios
and thus prevent ratios higher than 1 as observed in HE 1327-2326.
This means that most of the supernova ejecta fall back in the black hole and a little amount of the mass of the He-core
is ejected (so not much C and O are finally ejected). This would be in line with the model proposed
by Umeda & Nomoto (2003).
In that model, in addition to strong fall back,
mixing is supposed to occur in a fraction of the He-core at the time of
the explosion. This
mixing process, which was found to take place in SN1987A and various
explosion models (see the above reference), allows
some iron, present in the deep layers, to be dredged-up in the ejected
material. The mixing and fallback model also mimics the effect of
asymmetric explosions in which matter from deep layers is ejected along
the poles, while most of the matter falls back on the remnant at other
lattitudes.
Such models might be invoked for explaining possibly negative [Al/Fe]
ratios, while still maintaining CNO overabundances compatible with
those observed in CRUMPS.
It is interesting to compare these results with those that would be obtained from a non-rotating model.
The chemical structure of such a model is shown in Fig. 9![]() . The differences
are striking. The most important ones are the following. The rotating model has lost more than 23
. The differences
are striking. The most important ones are the following. The rotating model has lost more than 23 ![]() by stellar winds, while the non-rotating model has lost nearly no mass.
The envelope of the rotating model is enriched in primary 12C, 13C, 14N and 16O.
The envelope of the non-rotating model presents the usual marks of CNO processing, without primary production
of any of the CNO isotopes.
The He-burning shell of the rotating model is significantly enriched in
primary 19F and 22Ne, and the CO core has a mass of 30
by stellar winds, while the non-rotating model has lost nearly no mass.
The envelope of the rotating model is enriched in primary 12C, 13C, 14N and 16O.
The envelope of the non-rotating model presents the usual marks of CNO processing, without primary production
of any of the CNO isotopes.
The He-burning shell of the rotating model is significantly enriched in
primary 19F and 22Ne, and the CO core has a mass of 30 ![]() .
In the non-rotating
model, there is no significant primary 19F and 22Ne, and the CO core has a mass of 18.2
.
In the non-rotating
model, there is no significant primary 19F and 22Ne, and the CO core has a mass of 18.2 ![]() .
.
The chemical composition of the material composed (mainly) of supernova ejecta from the non-rotating model
is shown in Fig. 10
for two values of the mass cut. (The curves for the non-rotating models
have been shifted downwards by 2.7 for clarity, see caption.) When
the mass cut is chosen so that only CNO processed material is ejected
(mass cut = 23 ![]() ),
then we obtain N enhanced with respect to C and O. The absolute values
of C and O are very low, of the order of -4 for [C/H]
and of -3.5 for [O/H], much lower than the values observed in
CRUMP stars.
The abundance of N is also low, even accounting for the value plotted
in Fig. 10
being shifted by 2.7 dex. The model plotted here has an initial metallicity equal to
[Fe/H]
),
then we obtain N enhanced with respect to C and O. The absolute values
of C and O are very low, of the order of -4 for [C/H]
and of -3.5 for [O/H], much lower than the values observed in
CRUMP stars.
The abundance of N is also low, even accounting for the value plotted
in Fig. 10
being shifted by 2.7 dex. The model plotted here has an initial metallicity equal to
[Fe/H] ![]() -3.3.
Had we taken an [Fe/H]
-3.3.
Had we taken an [Fe/H] ![]() -6, the abundance of nitrogen would be 2.7 dex lower (i.e. would
be at the position plotted in Fig. 10).
When the mass cut is 23
-6, the abundance of nitrogen would be 2.7 dex lower (i.e. would
be at the position plotted in Fig. 10).
When the mass cut is 23 ![]() ,
the 12C/13C number ratio is quite low in the non-rotating model ejecta. It is typical of the CNO cycle
,
the 12C/13C number ratio is quite low in the non-rotating model ejecta. It is typical of the CNO cycle![]() .
.
When the mass cut is chosen to be equal to 18.2 ![]() ,
N is not significantly changed, while C and O are increased by many orders of magnitudes.
The 12C/13C number ratio also reaches much higher ratios than in the material ejected
by the rotating model.
,
N is not significantly changed, while C and O are increased by many orders of magnitudes.
The 12C/13C number ratio also reaches much higher ratios than in the material ejected
by the rotating model.
![\begin{figure}
\par\hspace*{2mm} \includegraphics[width=9cm, height=9cm,clip]{13377fig9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg45.png)
|
Figure 9:
Same as Fig. 8 for a non-rotating 60 |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig10.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg46.png)
|
Figure 10:
Composition of the mixture composed of wind material of 60 |
| Open with DEXTER | |
The non-rotating model would predict C-rich stars, but without strong enhancement of nitrogen (only secondary nitrogen). Such a model would also predict an extremely high value for the 12C/13C ratio. With dilution, D=100, the ratio would be about 1550.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig11.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg47.png)
|
Figure 11:
Comparisons between abundances in various stellar model ejecta and the
abundances observed in CEMP-no stars. The continuous curve with filled
circles shows the composition of the mixture composed of material
ejected by the rotating 60 |
| Open with DEXTER | |
5 The spinstar AGB model
As explained in Sect. 6.3, AGB stellar models are invoked as a possible cause for the
CEMP stars. In the models published until now (see e.g. Suda et al. 2004),
the CEMP star has acquired its characteristic surface composition
because it accreted some AGB wind material at its surface. The
model we present here is different
in at least two respects. First we suppose that the AGB star that
provides the peculiar chemical composition
material originates in a star that was a fast rotator during the
MS phase. Second, we suppose that
the whole CEMP star, or at least a large part of it, is made from a
mixture of AGB envelope and of pristine interstellar medium, not just
its 0.01 ![]() exterior layers as assumed by Suda et al. (2004). The situation
in the present model is similar to the one sketched in Fig. 1,
except that, in panels A to C, instead of having a massive
star, we consider here the case of an intermediate mass star
(panels D1 and D2 of course do not apply in that case.)
exterior layers as assumed by Suda et al. (2004). The situation
in the present model is similar to the one sketched in Fig. 1,
except that, in panels A to C, instead of having a massive
star, we consider here the case of an intermediate mass star
(panels D1 and D2 of course do not apply in that case.)
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig12.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg48.png)
|
Figure 12:
Variation in the abundances of various elements (in mass fraction) as a function of the Lagrangian mass in the outer layers
of a 7 |
| Open with DEXTER | |
Before making the comparisons with observed abundances at the surface of CEMP-no stars, we want to make two remarks.
First, our 7 ![]() stellar
mass model is in the early-AGB phase. During the subsequent phase,
the thermal-pulse AGB phase, the
chemical structure of the envelope will change and strong mass loss
will occur.
Thus the present models should be pursued in the TP-AGB phase
before any more
quantitative conclusions can be reached. At the moment, the results
presented here may,
however, be relevant in the frame of the close binary scenario.
If our intermediate-mass star belongs to a close binary system, some
mass transfer may occur when the primary inflates to join the early
AGB.
In that case some mass can be accreted by the secondary and/or lost by
the system as a whole
stellar
mass model is in the early-AGB phase. During the subsequent phase,
the thermal-pulse AGB phase, the
chemical structure of the envelope will change and strong mass loss
will occur.
Thus the present models should be pursued in the TP-AGB phase
before any more
quantitative conclusions can be reached. At the moment, the results
presented here may,
however, be relevant in the frame of the close binary scenario.
If our intermediate-mass star belongs to a close binary system, some
mass transfer may occur when the primary inflates to join the early
AGB.
In that case some mass can be accreted by the secondary and/or lost by
the system as a whole![]() .
.
The second remark is that, according to the
Z = 10-5 models of Meynet & Maeder (2002), computed for initial velocities of 300 km s-1, similar
behaviours are obtained at least down to 2 ![]() .
Thus, rotational mixing will have an impact not only on the chemical
structure
of the most massive AGB stars, or those rotating fast, but also on
the whole range of initial masses and rotational velocities.
.
Thus, rotational mixing will have an impact not only on the chemical
structure
of the most massive AGB stars, or those rotating fast, but also on
the whole range of initial masses and rotational velocities.
In Figs. 12 and 13 the chemical structure of our rotating and non-rotating 7 ![]() models at Z=10-5
are shown.
As for the most massive stars, the differences
are striking and are qualitatively the same. The only point that is
very different than the massive star case, is that, up to this point,
even the rotating intermediate mass star model has lost very little
from stellar winds, because the surface enrichments in the rotating
model occurred just before
the evolutionary stage shown in Fig. 12 and thus the enhanced mass loss had no time to peel off the star.
models at Z=10-5
are shown.
As for the most massive stars, the differences
are striking and are qualitatively the same. The only point that is
very different than the massive star case, is that, up to this point,
even the rotating intermediate mass star model has lost very little
from stellar winds, because the surface enrichments in the rotating
model occurred just before
the evolutionary stage shown in Fig. 12 and thus the enhanced mass loss had no time to peel off the star.
In the rotating model, in the zone between the He-burning shell (at about 1.3 ![]() )
and the H-burning one
(at 1.6
)
and the H-burning one
(at 1.6 ![]() ), the levels of primary 13C, 14N, and 22Ne are higher than in the rotating 60
), the levels of primary 13C, 14N, and 22Ne are higher than in the rotating 60 ![]() model, because the 7
model, because the 7 ![]() evolves rapidly to the red part of the HR diagram at the end
of the MS phase, as a result of the rapid core contraction and envelope expansion. Thus a strong
evolves rapidly to the red part of the HR diagram at the end
of the MS phase, as a result of the rapid core contraction and envelope expansion. Thus a strong ![]() -gradient is present at the border of the He-burning core during most of the
He-burning phase, making an efficient diffusion of He-burning products into the H-burning shell and of
H-burning products into the He-burning core possible.
-gradient is present at the border of the He-burning core during most of the
He-burning phase, making an efficient diffusion of He-burning products into the H-burning shell and of
H-burning products into the He-burning core possible.
In Fig. 11 we show the composition of a star made of the envelopes of such AGB stars mixed with interstellar material (dilution factor equal to 100). We see that we obtain a reasonable fit if we consider our rotating model. Such a star would not be He-rich, and would present a 12C/13C ratio equal to 104. Our non-rotating model cannot account for the high nitrogen abundance. Moreover, the 12C/13C ratio would be close to 8000 (after dilution).
The spinstar AGB model would, however, have some difficulty explaining the lower-than-solar [Al/Fe] ratios (if real!). Such stars do not eject any Fe, while they inject some Al, thus they would predict positive [Al/Fe] values as is observed in HE 1327-2326!
6 Alternative models
In this section we briefly discuss alternative models for explaining CRUMPS. They invoke either AGB stars in binary systems or supernovae. Venn & Lambert (2008), on the other hand, suggest that the abundance pattern observed today on the surface of CRUMPS does not reflect the initial abundances of the cloud from which the star was born, but results from processes occurring in or around the star. Let us begin by examining this hypothesis.
![\begin{figure}
\par\hspace*{2mm} \includegraphics[width=9cm, height=9cm,clip]{13377fig13.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg50.png)
|
Figure 13:
Same as Fig. 12 for a non-rotating 7 |
| Open with DEXTER | |
6.1 Are CRUMPS produced by in situ processes?
Venn & Lambert (2008) suggest that CRUMPS are not actually all that metal poor, but may have their photosphere deprived in heavy elements owing to a separation of gas and dust beyond the stellar surface, followed by the accretion of dust-depleted gas. Such a process is invoked to explain Lambda Bootis stars, which are MS stars with a spectral type from A to mid-F, found all along the MS phase. They are expected to have a solar-like composition but show significant metal deficiencies. The authors propose some tests of their hypothesis, for instance looking at the abundances of sulphur and zinc. Dust formation does not deplete these two elements much so that in the framework of this scenario, they should not show the same depletion as the rest of metals. Unfortunately, no such observations are available yet.
While this explanation is indeed quite interesting, it can probably not be invoked to explain all the observed cases. Our main argument is the following: if the dust-gas separation process may produce different elemental ratios, it should not change isotopic ratios! Such a scenario has difficulty explaining why, for instance in G77-6 (Plez & Cohen 2005), which is an unevolved star, values as low as 5 of the 12C/13C ratio have been measured. This value is well below the 12C/13C ratios measured on the surface of stars belonging to the ``unmixed'' sample of red-giants metal-poor stars observed by Spite et al. (2006), so results from a nuclear process that occurred in stars of previous generations and not from an in-situ fractionation process.
6.2 Non-rotating supernovae models
CRUMPS might form from material made of a mixture of supernova ejecta (originating in non-rotating progenitors) and of interstellar material. One question that immediately arises when suggesting this origin for CRUMPS is why they are produced at very low metallicity. From physical considerations, one expects that supernovae developing from zero metallicity or very metal poor progenitors present different characteristics from supernovae coming from solar metallicity progenitors. At zero or very low metallicity, progenitors are more compact. This favors a higher amount of fallback (Chevalier 1989). The more compact structure of the presupernova at very low metallicity reduces the extent of the region where Rayleigh-Taylor instabilities grow and where the mixing of the ejecta can occur. A consequence of this is that the yields of such a supernova explosion are very sensitive to the amount of fallback. Thus it may be that the ejecta at very low metallicity present very different characteristics from those expected at standard metallicities.
Many models invoking supernovae have been proposed to explain the peculiar abundance pattern of CEMP stars (Limongi et al. 2003; Umeda & Nomoto 2003; Tominaga et al. 2007b; Joggerst et al. 2009). For instance, the zero-metallicity models of Joggerst et al. (2009) show overproductions of C and O compared to Fe, a trend corresponding to what is observed in CRUMPS. However, such models have difficulty reproducing the strong N overabundances, quite in line with what we obtained with our non-rotating models (see above). As indicated by these authors, accounting for the effects of rotation might help in resolving this difficulty.
Another difficulty that may emerge from these models is that
they need a very high dilution factor with a pristine interstellar
medium to reproduce
the observed levels of the overabundances. As we have seen this is
contrary to
the observed very low Li abundances unless depletion mechanisms that
are much stronger than those usually accounted for in current models
are supposed![]() .
Even in the case of a very strong Li depletion mechanism, such a model cannot account for those CEMPS stars with low 12C/13C number ratios (see also Sect. 7).
.
Even in the case of a very strong Li depletion mechanism, such a model cannot account for those CEMPS stars with low 12C/13C number ratios (see also Sect. 7).
Supernovae imply large dilution factors, therefore such models cannot predict He-rich CRUMPS! Detection of He enhancement in CRUMPS would imply small dilution factors and thus eliminate a strong contribution by supernova ejecta (at least in He-rich CRUMP stars).
6.3 AGB stars in binary systems
Many authors argue that the peculiar surface abundances of CEMP stars have been acquired in a mass transfer episode. The most commonly accepted scenario follows the general line that, when the primary has evolved into the AGB phase, part of its wind material is accreted by the secondary (today the CEMP star), giving it the peculiar surface abundances that we can observe today.
The following observed features have been invoked as supporting the AGB binary scenario:
- the presence of s-process elements in CEMP-s stars is interpreted as a mark of the AGB nuclesosynthesis;
- the very low iron abundances imply a nucleosynthetic source that does lead to very weak or no iron enrichment. AGB stars do not produce iron;
- binarity indeed seems to be observed (through radial velocity variations) for most of the CEMP-s (Lucatello et al. 2005);
- there seems to be a continuity of properties between the C-enhanced stars and the CH-stars (Masseron et al. 2010);
- a similar argument also seems to hold between the CEMP-no and the CEMP-s with a weak overabundance in s-process elements (Masseron et al. 2010).
This scenario presents a reasonable way to explain the CEMP-s
stars. Besides
explaining the peculiar surface abundances of CEMP stars, it may
provide an explanation of why the C-rich stars are more frequent at low
metallicity. Let us recall that about 20% of stars with
![]() exhibit enhancement of the surface carbon abundance (Lucatello et al. 2006), while only 1% of the Pop II stars are characterized by enhanced
CH bands in the spectra (Luck 1991).
The higher frequency of C-rich stars at very low metallicity might be
because
the helium-flash-driven, deep-mixing phenomenon does appear as a
distinct feature of the evolution of extremely metal-poor stars of low
and intermediate mass. Also a companion has been detected
around 68% of the CEMP-s stars (Lucatello et al. 2005).
exhibit enhancement of the surface carbon abundance (Lucatello et al. 2006), while only 1% of the Pop II stars are characterized by enhanced
CH bands in the spectra (Luck 1991).
The higher frequency of C-rich stars at very low metallicity might be
because
the helium-flash-driven, deep-mixing phenomenon does appear as a
distinct feature of the evolution of extremely metal-poor stars of low
and intermediate mass. Also a companion has been detected
around 68% of the CEMP-s stars (Lucatello et al. 2005).
In that scenario the peculiar abundance results from the accretion of a very small amount of material,
0.01 ![]() for matching HE 0107-5240, which is a red giant (Suda et al. 2004)
for matching HE 0107-5240, which is a red giant (Suda et al. 2004)![]() ! Even smaller amounts of material
would be needed to reproduce the abundances observed at the surface of unevolved stars presenting similar surface enrichments.
This means that such a scenario would obviously not predict He-rich stars.
! Even smaller amounts of material
would be needed to reproduce the abundances observed at the surface of unevolved stars presenting similar surface enrichments.
This means that such a scenario would obviously not predict He-rich stars.
While this scenario is quite successful in many respects, it also has some drawbacks. For instance, according to Stancliffe & Glebbeek (2008), (non-rotating) AGB models do not predict substantial enhancements of both carbon and nitrogen at the same time (except in a very narrow mass range). The spinstar AGB model presented previously would provide a way to overcome that difficulty.
7 Possible origin of CRUMP stars with 12C/13C below 30
In this section we want to specifically address the origin of CRUMP stars showing a low 12C/13C isotopic ratio, typically below 30. In the SAGA databasis, except for two stars, all the other CEMP-no stars (7 stars) present 12C/13C below 25. The two exceptions have upper limits in the range of 40-50.
The 12C/13C isotopic ratio has four properties that make it an excellent probe of various nucleosynthetic environments:
- 1.
- in a low-mass main-sequence or subgiant star like HE 1327-2326, there is no known process for modifying this number ratio on the surface. Thus this quantity has the advantage over Li that its present-day value on the surface of unevolved stars is equal to the initial value of this ratio;
- 2.
- the 12C/13C number ratio presents strong variations depending on the source material being considered;
- 3.
- isotopic ratios depend on the nuclear paths, because they are not sensitive to fractionation effects;
- 4.
- finally from a nucleosynthetic point of view, low 12C/13C can only be obtained when a small amount of pure He-burning material is ejected.
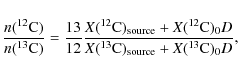
where n is the number fraction of the element considered and X its mass fraction in the source material (subscript
Of course there is no guarantee that these values are the same at much lower values of [Fe/H]. With the chemical evolution model of Chiappini et al. (2008), we obtain values at [Fe/H] = -5 that differ a lot if considering yields from slow- or fast-rotating models. Slow-rotating models, i.e. with angular momentum lower than for massive stars at solar metallicity, would yield very high values around 31 000! Fast-rotating models, i.e. with angular momentum content of similar magnitude to that of massive solar metallicity stars, predict ratios equal to 30. These models are to be preferred since they also reproduce the observed [N/O] and [C/O] trends with [Fe/H] and [O/H] in the halo (Chiappini et al. 2006). Regardless of the correct answer, we can at least say that the initial 12C/13C ratio at very low metallicity is probably greater than 30.
The effect of dilution is very different depending on the primary or secondary nature of the nucleosynthetic
path leading to the synthesis of the two carbon isotopes in the source material. In case both isotopes have a strong primary
component, as is the case in spinstar models![]() ,
then the 12C/13C ratio will not be affected by dilution much. Typically at Z=10-8 the initial abundances of 12C and 13C, which we
used to compute the models, are
,
then the 12C/13C ratio will not be affected by dilution much. Typically at Z=10-8 the initial abundances of 12C and 13C, which we
used to compute the models, are
![]() and
and
![]() ,
respectively, while the abundances in the winds of the 85
,
respectively, while the abundances in the winds of the 85 ![]() model at Z=10-8
are 0.097 (12C) and 0.009 (13C)
(see Table 1). Thus, for any dilution factors below about 108, the number ratio, equal to 11, is given
by
model at Z=10-8
are 0.097 (12C) and 0.009 (13C)
(see Table 1). Thus, for any dilution factors below about 108, the number ratio, equal to 11, is given
by
![]() and is independent of the dilution factor.
and is independent of the dilution factor.
In the spinstar models, the only way to obtain values for the 12C/13C ratio below 30 is to consider only wind material of massive stars with no or only a small amount of pure products from He-burning. Models that would lose this envelope, not by winds but at the end of the evolution when they explode as supernova, would eject material with nearly identical compositions to the wind models presented here.
Would rotating AGB models be able to produce low 12C/13C number ratios?
If we consider the mass fractions of the two carbon isotopes in the envelope of our
7 ![]() model, we have
model, we have
![]() for 12C and
for 12C and
![]() for 13C. The initial abundances at Z=10-5 are
for 13C. The initial abundances at Z=10-5 are
![]() (12C) and
(12C) and
![]() (13C)
respectively so at least three orders of magnitude lower than the
abundances in the envelope at the early AGB phase. If the dilution
factor is well below 10 000, then one would obtain a 12C/13C number ratio equal to 79, and if the dilution factor
is greater than 10 000, one would obtain a 12C/13C number ratio equal to that of the interstellar medium, between 30 and 31 000 (see the discussion above)!
Therefore, it does appear
that our early-AGB (E-AGB) model would not predict very low 12C/13C number ratio, but this is only one model at a peculiar stage. At the moment,
we cannot exclude the possibility that AGB material also yields very low 12C/13C material.
(13C)
respectively so at least three orders of magnitude lower than the
abundances in the envelope at the early AGB phase. If the dilution
factor is well below 10 000, then one would obtain a 12C/13C number ratio equal to 79, and if the dilution factor
is greater than 10 000, one would obtain a 12C/13C number ratio equal to that of the interstellar medium, between 30 and 31 000 (see the discussion above)!
Therefore, it does appear
that our early-AGB (E-AGB) model would not predict very low 12C/13C number ratio, but this is only one model at a peculiar stage. At the moment,
we cannot exclude the possibility that AGB material also yields very low 12C/13C material.
For non-spinstar models, we discuss here only the case of the supernova models, for which the published
data allow easy calculation of the expected 12C/13C ratio in the CRUMP star.
Using the yields of the 40 ![]() Pop. III supernovae
computed by Tominaga et al. (2007b), we consider their model 40B in their Table 2. With their mass cut of 10.7
Pop. III supernovae
computed by Tominaga et al. (2007b), we consider their model 40B in their Table 2. With their mass cut of 10.7 ![]() ,
we obtain mass fractions
of 12C and 13C in the supernova ejecta equal to 0.012 and
,
we obtain mass fractions
of 12C and 13C in the supernova ejecta equal to 0.012 and
![]() .
Mixed with primordial material, we obtain a 12C/13C number ratio equal to
.
Mixed with primordial material, we obtain a 12C/13C number ratio equal to
![]() independent of the dilution factor. Similar values would be obtained from other models by Tominaga et al. (2007b). This is
not a conclusion linked to the peculiar supernova model cited above. The supernova ejecta will be richer than the winds in 12C and, at least, if they
are computed from non-rotating models, would be poor in 13C. This means that the 12C/13C number ratio will be very high!
independent of the dilution factor. Similar values would be obtained from other models by Tominaga et al. (2007b). This is
not a conclusion linked to the peculiar supernova model cited above. The supernova ejecta will be richer than the winds in 12C and, at least, if they
are computed from non-rotating models, would be poor in 13C. This means that the 12C/13C number ratio will be very high!
From the above considerations, it appears that an unevolved CEMP star with a 12C/13C number ratio inferior to about 30 cannot be made from (non-spinstar) Pop III supernova ejecta regardless of the dilution factor. It can be made from the winds of spinstars, even those highly diluted with interstellar material.
8 Discussion and perspectives
8.1 Some general considerations
Table 2: Theoretical interpretations of observed features and consequences for helium in CRUMP stars.
In this section, we want to collect some general conclusions that do not depend on a peculiar model for the source of the material responsible for the abundances observed in CEMP stars.
In Table 2, we enumerate 12 observed features (see Col. 2). Each of these is given a number N (for further reference). It is
indicated in Col. 1. Column 4 indicates what can be concluded from the observed
feature and the hypothesis given in Col. 3.
The CEMP stars are supposed to be composed
of some amount of source material,
![]() (Li-free) and of interstellar medium material (with WMAP Li).
In Col. 3, depletion refers to
Li and the symbol ``ISM[X/Fe]'' indicates the value of the ratio in the interstellar medium at the time of
CRUMP/CEMP star formation.
In Col. 4, D is the dilution factor, ``H and He burn'' means that the source material from which
the CRUMP/CEMP star is made is
rich in both H- and He-burning products, ``no He-only'' means that this material does not contain
(or has very small amounts of) matter only processed by He burning, while ``+ He-only'' means that
the source material contains a significant amount of pure He-burning products.
Column 5 indicates whether the CRUMP/CEMP
star is He-rich (YES) or not (NO), while question mark indicates that both cases are possible.
The following general comments are worth making:
(Li-free) and of interstellar medium material (with WMAP Li).
In Col. 3, depletion refers to
Li and the symbol ``ISM[X/Fe]'' indicates the value of the ratio in the interstellar medium at the time of
CRUMP/CEMP star formation.
In Col. 4, D is the dilution factor, ``H and He burn'' means that the source material from which
the CRUMP/CEMP star is made is
rich in both H- and He-burning products, ``no He-only'' means that this material does not contain
(or has very small amounts of) matter only processed by He burning, while ``+ He-only'' means that
the source material contains a significant amount of pure He-burning products.
Column 5 indicates whether the CRUMP/CEMP
star is He-rich (YES) or not (NO), while question mark indicates that both cases are possible.
The following general comments are worth making:
- 1.
- if Li is not depleted by the CEMP star itself, then any low observed Li abundance implies a very small dilution factor (feature 1);
- 2.
- if Li is observed to be low and Li is depleted in the CEMP star, the dilution factor cannot be constrained from the current Li surface abundance (feature 2);
- 3.
- if Li is observed to have a value along the Spite plateau, then the dilution factor cannot be constrained from the current Li surface abundance and the depletion, if any, would be similar to those in normal halo field stars (feature 3);
- 4.
- low 12C/13C ratios (below 30) indicate that the source material has been strongly processed by the CNO cycle. The high abundance of carbon (in the form of 12C) implies a strong primary 13C production. This can occur only if some mixing has occurred in the source between the He- and the H-burning regions (feature 4);
- 5.
- high 12C/13C ratios (above 30) indicate either a high dilution factor and/or domination of the source material by He-burning products (feature 5);
- 6.
- the source material is rich in primary nitrogen for CRUMP/CEMP stars showing feature 6. A secondary process inside the star can produce at most an [N/H] value about 1.4 dex above [Fe/H]. This is true, of course, as long as the initial abundances of carbon and oxygen are not orders of magnitudes more abundant with respect to Fe than in the Sun. At the moment, looking at the data by Cayrel et al. (2004), [C/Fe] is solar and [O/Fe] is about 3 times solar in metal-poor normal halo stars;
- 7.
- the [N/C] and [N/O] ratios are a measure of the importance of the CNO-processed material in the source material. If these ratios are large, this indicates a high proportion of CNO processed material (feature 7). As indicated many times above, He-burning products are not absent since they allow the overabundances with respect to iron of carbon and oxygen;
- 8.
- if the [N/C] and [N/O] ratios are small, this favors He-burning processed material (feature 8). This is independent of the dilution factors because all these elements are primary, hence in much greater abundance in the source material than in the interstellar medium. Probably, only an unrealistic large dilution factor can change the ratios obtained in the mixture. One can have [N/C] < 0 and [N/O] > 0 or the inverse in material ejected with both H- and He-burning material and some pure He-burning material;
- 9.
- in a similar way, large [Na/Ne] and [Al/Mg] ratios point towards material having been processed mainly by the Ne-Na and Mg-Al chains active in hot H-burning regions (feature 9). A word of caution, however, has to be given here. Since the pattern of the Ne-Na, Mg-Al chains manly results from a secondary process, dilution can modify somewhat the final shape of the abundance pattern. Indeed the elements between Ne and Al probably have initial abundances within the same order of magnitude, so that the transformations of, for instance, 90% of Mg into Al will produce a contrast between the source material and the interstellar material of at most one order of magnitude. Such a low contrast can thus be erased by a small dilution factor;
- 10.
- small [Na/Ne] and [Al/Mg] ratios are indicative of material processed in He-burning zones (feature 10);
- 11.
- feature 11 is compatible with source material processed by the Mg-Al chain;
- 12.
- feature 12 implies that some iron is ejected by the source;
- 13.
- If He-rich CRUMP/CEMP stars exist, they should be found among the stars presenting the features 4, 6, 7, 9, 11 indicated in Table 2. Stars showing these features are however not necessarily He-rich.
Table 3: Spinstar models compatible with sets of observed features given in Table 2.
8.2 The main results from our spinstar models
One of the points from that study is that rotation does play a key role in explaining the abundance pattern observed in CEMP stars. This is true even when the source material comes from massive star winds, from intermediate mass star winds or from a supernova.
The spinstar scenario that we have presented has consequences for other topical questions related to the chemical evolution of the galactic halo. First, this scenario is indirectly supported by fast-rotating stars seeming needed to reproduce the high N/O plateau observed in the halo of our Galaxy and also the C/O upturn towards low metallicities (Chiappini et al. 2006). An advantage of our scenario is therefore that the same kinds of objects can be responsible for the properties of both normal halo stars and the CRUMPS. The normal ones are made up of a well-mixed reservoir that has been enriched by massive rotating stars of different masses and metallicities as proposed by Hirschi (2007). The CRUMP stars are formed in the vicinity of one massive (or intermediate) rotating star and are made up of material taken from the external layers of such stars.
Second, spinstars may also be invoked to explain the chemically peculiar stars
observed in globular clusters![]() .
At the metallicity of the globular clusters, fast-rotating stars may lose large amounts
of mass when the star reaches the critical limit. This only occurs during the MS phase. The material in the disk
is thus only enriched in H-burning products. This material is released very slowly in the cluster's interstellar medium
and can thus be retained by its shallow gravitational potential. It can then be used to form stars bearing the signature
of H-burning processes as explained in Decressin et al. (2007b,a). When the star evolves further, fast winds develop
and escape from the cluster. The same is true for the supernova ejecta.
.
At the metallicity of the globular clusters, fast-rotating stars may lose large amounts
of mass when the star reaches the critical limit. This only occurs during the MS phase. The material in the disk
is thus only enriched in H-burning products. This material is released very slowly in the cluster's interstellar medium
and can thus be retained by its shallow gravitational potential. It can then be used to form stars bearing the signature
of H-burning processes as explained in Decressin et al. (2007b,a). When the star evolves further, fast winds develop
and escape from the cluster. The same is true for the supernova ejecta.
As sketched in our Fig. 1 we see that some of the CRUMPS stars may receive some SN ejecta (see panel D2). This may explain some r-process enrichment. For the s-process, we think that rotation may strongly affect the nucleosynthesis of these elements and that massive stars might be the source of a much broader range of s-process elements than presently believed (Pignatari et al. 2008). Also the impact of rotation in the s-process element synthesis in intermediate mass star at very low metallicity also needs to be investigated Siess et al. (2004).
In Table 3, we indicate which spinstar model does the best job of reproducing the various sets of compatible observed features listed in Table 2. Below we draw some conclusions:
- 1.
- CRUMP stars originating in the winds of spinstars present strong signs of material processed by H-burning, i.e., high [N/C] and [N/O] ratios and low 12C/13C ratios. This is independent of the dilution factor. If the dilution factor is small, these stars are He-rich and Li-poor;
- 2.
- the spinstar wind model does appear in the present study as the only model to explain CEMP stars with a low 12C/13C ratio. It might be that new rotating AGB star models could also be potential interesting candidates, but this has to be confirmed by further computations;
- 3.
- some CRUMPS can also be formed of a mixture of both wind and SN ejecta from massive fast-rotating stars. Supernovae from non-rotating models cannot reproduce the abundance pattern observed in CRUMPS;
- 4.
- stars made of the envelope of E-AGB stars resulting from rotating models also present an abundance pattern in qualitative agreement with CEMP-no stars. Similar non-rotating models do not fit the observed abundances;
- 5.
- both the wind+supernova model and the spinstar AGB model require some dilution with a pristine interstellar medium to obtain a reasonable fit. This means that these stars would not be He-rich and would present high 12C/13C ratios.
8.3 Why are there no analogs of CRUMPS at higher metallicities?
One may wonder why the scenario leading to the formation of CRUMPS no longer works in the present universe. Two reasons can be invoked. 1) At high metallicity, rotation cannot produce primary nitrogen, hence the peculiar simultaneous overabundance of CNO elements. 2) At high metallicity, the chemically enriched winds of massive stars propagate in a medium that has already been pushed away by the strong and fast O-type star stellar winds. This may prevent the formation of stars made almost completely of pure chemically enriched ejecta. At very low metallicity, the situation can be very different, the line-driven stellar winds are first very weak, preventing the star from pushing out the circumstellar material. Only when the stellar surface is enriched in heavy elements does the star lose a large amount of material by stellar winds. Therefore, these enriched, slow winds (slow because ejected when the star is a supergiant) will have to pass through a dense circumstellar medium. This may favor the formation of clumps. Further detailed hydrodynamical modelings are needed to confirm or reject these scenarios.
8.4 How to show that some CRUMPS are He-rich?
Let us end by saying a few words about the possibility of testing the hypothesis that CRUMPS (or maybe also some CEMP) stars are He-rich. Although detection of He will remain problematic in cool stars, it is not hopeless. Among all the possibilities, let us cite the following ones.
- Helium lines may be observable in cool stars,
whose strength might be related to the He abundance.
The line He I 10 830 Å was used by Moehler et al. (2000) mainly for velocity diagnostics.
It is not a
straightforward line to interpret because it arises from a very excited
metastable level in He I. However, according to Dupree (private communication) if stars of
similar
 are observed, a relative measure could be done. It might also be possible
to get abundances, but that would probably need non-LTE modeling
are observed, a relative measure could be done. It might also be possible
to get abundances, but that would probably need non-LTE modeling![[*]](/icons/foot_motif.png) .
An additional difficulty with this approach comes from the fact that atomic diffusion would
deplete the surface in He (see the models by Korn et al. 2009).
.
An additional difficulty with this approach comes from the fact that atomic diffusion would
deplete the surface in He (see the models by Korn et al. 2009).
- Asteroseismology may help in revealing the He-abundance of these stars.
- We could observe an eclipsing binary system whose components are CRUMPS or CEMP stars and determine the positions of the two components in the HR diagram as well as their masses. The comparison with the stellar models may bring out the need to enhance the He-abundance in order to simultaneously reproduce all the observed features.
- The presence of a significant population of extremely blue horizontal branch stars in the halo field may be an indirect hint of He-rich stars, since such stars can be the descendants of He-rich stars.
8.5 What to conclude if He-enhancement is detected? What to conclude if He abundance is normal?
If He-enhancement is detected and found to be a feature that concerns the whole star and not just its surface, then this would definitely imply that the material from which the CRUMPS are made do contain a relatively small amount of interstellar medium. This would discard models explaining CRUMPS as formed by the accretion of a small amount of mass at the top of the secondary in a binary system. It would also discard the normal supernovae as a possible source for the material from which the CRUMPS are made, because the dilution factors used to bring the composition of normal supernova ejecta to the level of the observed abundances in CRUMPS are much too high to make the star He-rich. Faint supernovae with large fallback would remain interesting, as would the effects of rotation for explaining the high nitrogen enhancements. As discussed in the present work, the wind of spinstars would also be a favored candidate in that case. Let us stress here that this model is compatible with the faint supernova model, and both may be linked in a same evolutionary history, rotation allowing enrichment of the envelope in H- and He-burning products and its ejection as a wind before the faint supernova event. As indicated in the introduction, finding He-enhancement in the CRUMPS will also modify the estimates of the mass of these objects. It may be that the most massive of these He-rich stars now populate the blue end of the horizontal branch.
If He-abundance is found to be normal, i.e. with values near the primordial helium abundance, then it favors either models invoking a small amount of accreted mass (as in the AGB model described above) or models with high dilution factors. In the latter case, the very low abundance of Li observed in some CEMP stars should be due to depletion mechanism in the star itself. Many of the spinstar models discussed here are compatible with normal He-stars (see Table 3). In particular, the wind of spinstars model would remain an interesting model for normal He-stars showing small 12C/13C number ratios, since combinations of dilution factor and of the initial mass of the spinstar may yield very modest helium enrichments, while still allowing very low 12C/13C number ratios.
AcknowledgementsThe authors thank the referee for constructive and helpful comments and the language editor, J. Adams, for the very careful reading. The authors are very grateful to Dr. Takuma Suda for giving access to the very useful SAGA database (http://www.astro.keele.ac.uk/saga/), to Dr. Thomas Masseron for providing the electronic tables of the paper by Masseron et al. (2010) before publication and to Dr. Andrea Dupree for interesting discussions of He lines in cool stars. R. Hirschi acknowledges support from the Marie Curie grant IIF 221145 and an STFC rolling grant.
References
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Chiosi, C., & Fagotto, F. 1994, ApJS, 94, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W., & Fowler, W. A. 1971, ApJ, 164, 111 [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chevalier, R. A. 1989, ApJ, 346, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christlieb, N., Gustafsson, B., Korn, A. J., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2008, J. Cosmol. Astro-Part. Phys., 11, 12 [Google Scholar]
- Decressin, T., Charbonnel, C., & Meynet, G. 2007a, A&A, 475, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007b, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Baumgardt, H., Kroupa, P., Meynet, G., & Charbonnel, C. 2009, IAU Symp. 258, ed. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 265 [NASA ADS] [Google Scholar]
- Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Iben, I. J., & Hollowell, D. 1990, ApJ, 349, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Georgy, C., Meynet, G., Walder, R., Folini, D., & Maeder, A. 2009, A&A, 502, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Lynas-Gray, A. E. 2007, MNRAS, 380, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joggerst, C. C., Woosley, S. E., & Heger, A. 2009, ApJ, 693, 1780 [NASA ADS] [CrossRef] [Google Scholar]
- Komiya, Y., Suda, T., Minaguchi, H., et al. 2007, ApJ, 658, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A. J., Richard, O., Mashonkina, L., et al. 2009, ApJ, 698, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., Chieffi, A., & Bonifacio, P. 2003, ApJ, 594, L123 [CrossRef] [Google Scholar]
- Lind, K., Korn, A. J., Barklem, P. S., & Grundahl, F. 2008, A&A, 490, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 1991, ApJS, 75, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Meynet, G., Ekström, S., & Georgy, C. 2009, Commun. Asteroseismol., 158, 72 [NASA ADS] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneguzzi, M., Audouze, J., & Reeves, H. 1971, A&A, 15, 337 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581, Paper XI [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Decressin, T., & Charbonnel, C. 2008a, Mem. Soc. Astron. Ital., 79, 584 [NASA ADS] [Google Scholar]
- Meynet, G., Ekström, S., Maeder, A., et al. 2008b, in First Stars III, ed. B. W. O'Shea, & A. Heger, AIP Conf. Ser., 990, 212 [Google Scholar]
- Meynet, G., Ekström, S., Maeder, A., et al. 2008c, ed. F. Bresolin, P. A. Crowther, & J. Puls, IAU Symp., 250, 147 [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010a, ed. K. Cunha, M. Spite, & B. Barbuy, IAU Symp., 265, 98 [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010b, [arXiv:1001.1864] [Google Scholar]
- Moehler, S., Sweigart, A. V., Landsman, W. B., & Heber, U. 2000, A&A, 360, 120 [NASA ADS] [Google Scholar]
- Norris, J. E., Christlieb, N., Korn, A. J., et al. 2007, ApJ, 670, 774 [NASA ADS] [CrossRef] [Google Scholar]
- O'Connell, R. W. 1999, ARA&A, 37, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatari, M., Gallino, R., Meynet, G., et al. 2008, ApJ, 687, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B., & Cohen, J. G. 2005, A&A, 434, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Goriely, S., & Langer, N. 2004, A&A, 415, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Suda, T., Aikawa, M., Machida, M. N., Fujimoto, M. Y., & Iben, I. J. 2004, ApJ, 611, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
- Tominaga, N., Maeda, K., Umeda, H., et al. 2007a, ApJ, 657, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Umeda, H., & Nomoto, K. 2007b, ApJ, 660, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [Google Scholar]
- Venn, K. A., & Lambert, D. L. 2008, ApJ, 677, 572 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Sun
![[*]](/icons/foot_motif.png)
- For the quantities of the type [A/B], the result is the same using mass fraction or number fraction, provided of course the same type of quantities is used to compute the elemental abundances in the star and in the Sun.
- ...
![[*]](/icons/foot_motif.png)
- Since that model was computed without accounting for the Ne-Na and Mg-Al chains, these elements are not shown in the figure.
- ... CNO cycle
![[*]](/icons/foot_motif.png)
- However, since here C and O abundances depend on the initial abundances, any mixing with interstellar material would rapidly increase the 12C/13C number ratio up to its value in the interstellar medium.
- ... whole
![[*]](/icons/foot_motif.png)
- Such a scenario can occur in a binary wide enough for the star to evolve into the E-AGB phase, and tight enough so that mass transfer occurs during the E-AGB phase.
- ... supposed
![[*]](/icons/foot_motif.png)
- Looking at Fig. 3 of Tominaga et al. (2007b), it might seem that a star produced from supernova ejecta with high dilution by the ISM would produce Li-depleted stars. This is an artefact because what has been plotted are the ratios of the abundances of these elements with respect to Fe in the ejecta alone. For heavy elements this is equal to the ratio of the elements after dilution since the primordial matter contains no heavy elements. However, this is not the case for H, He, D and Li. We checked that this interpretation is correct (Tominaga, private communication).
- ...(Suda et al. 2004)
![[*]](/icons/foot_motif.png)
- HE 0107-5240 is not a CEMP-s star. Despite that, this star is discussed in detail in the paper by Suda et al. (2004) in the framework of the AGB binary scenario.
- ... models
![[*]](/icons/foot_motif.png)
- Regardless of the spinstar model considered: AGB envelope, wind material, or supernova ejecta.
- ... clusters
![[*]](/icons/foot_motif.png)
- It is striking that chemically peculiar stars found in the field and in the globular clusters are quite different (rich in both H- and He-burning products in the field and rich in H-burning products in the clusters). A possible explanation for this fact is proposed in Meynet et al. (2010b).
- ... modeling
![[*]](/icons/foot_motif.png)
- In the hotter HB stars (
 > 10 000)
other He lines become
visible, and those have been used to determine abundances (see Moehler et al. 2000).
> 10 000)
other He lines become
visible, and those have been used to determine abundances (see Moehler et al. 2000).
All Tables
Table 1: Masses ejected by stellar winds from different rotating models and 12C/13C number ratios in the ejecta.
Table 2: Theoretical interpretations of observed features and consequences for helium in CRUMP stars.
Table 3: Spinstar models compatible with sets of observed features given in Table 2.
All Figures
![\begin{figure}
\par\includegraphics[height=12cm, angle=-90, width=17cm,clip]{13377fig1.eps}\vspace{-5mm}
\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg21.png)
|
Figure 1: Schematic representation of the ``spinstar'' model for explaining the origin of the peculiar abundance patterns of CRUMP/CEMP-no stars: A) A metal poor massive rotating star evolves during the core H-burning phase. B) During the core He-burning phase, strong winds, triggered by self enhancement of the surface metallicity appear. C) Wind material mixed with some amount of interstellar medium form clumps. The end of the evolution of the spinstars can either be a Black Hole with no supernova explosion (D1) or it can explode as a supernova (D2) which can further enrich the clumps. The fast rotation of the core may produce a non isotropic explosion. Some clumps form small mass stars, which are the CRUMP/CEMP stars that we can observe today. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{4mm} \includegraphics[height=11cm, width=9cm,clip]{13377fig2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg22.png)
|
Figure 2:
Evolution of the surface abundances for a 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[height=12cm, width=9cm,clip]{13377fig3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg33.png)
|
Figure 3:
Predicted abundances in stars made of a mixture of wind ejecta of massive rotating stars
and of pristine interstellar medium plotted as a function of the dilution factor D, the ratio between the mass
of interstellar medium and the mass
ejected in the wind involved in the mixture. The rotating models
are for 40 and 85 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[height=9cm, width=9cm,clip]{13377fig4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg34.png)
|
Figure 4: The [C/H], [N/H], and [O/H] ratios in the wind ejecta of various rotating models mixed with at most 15% of pristine interstellar medium are shown (dilution factor D=0.15). The models are those presented in Table 1. The models obtained for the same initial mass, metallicity, and rotation, but computed with different prescriptions, cover the shaded areas. The vertical hatched columns show the range in observed values for CEMP-no stars with log g superior to 3.8 (left) and with log g inferior to 3.8 (right). The values were taken from Tables 1 and 2 of Masseron et al. (2010). Only upper limits are given for [O/H], which is why the columns extend down to the bottom. The star symbols show the observed values for the most iron-poor star known today (Frebel et al. 2008). The left part of the figure indicates for each model the total mass ejected in solar masses, the mass fraction of He (case with D=0), the upper mass limit for Li abundance (obtained with D=0.15), and the isotopic ratio 12C/13C in number. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[height=9cm, width=9cm,clip]{13377fig5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg38.png)
|
Figure 5: Same as Fig. 2 for the [X/H] ratios. The curve labelled 12C/13C shows the evolution in the number ratio of the two carbon isotopes. The horizontal dotted lines show the values obtained for HE 1327-2326 (Frebel et al. 2008). In the case of the carbon isotopic ratio, only a lower limit is given. The shaded area represents the portion of the mass ejected in the form of stellar winds which shows, once well mixed, the chemical composition plotted as the third curve from the bottom in left panel of Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm,clip]{13377fig6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg39.png)
|
Figure 6: The [C/H], [N/H], and [O/H] ratios in wind-shells ejecta of various rotating models are shown (see text). The models plotted are the models A, C, and D of Table 1. The masses of the shells are indicated along with the age of the star when half of the mass of the shell is ejected. The mass fraction of He and the 12C/13C in number in the shells are indicated (case with D=0). The stars show the observed values for the most iron-poor star known today (Frebel et al. 2008). The vertical hatched zones have the same meaning as in Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm, angle=-90,clip]{13377fig7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg40.png)
|
Figure 7: Left panels: the [C/H], [N/H], [O/H], [F/H] and [Ne/H] ratios in different shells wind-ejected by models E of Table 1. In the left part of the left panel are indicated for each shell the mean age at the time of shell ejection, the mean mass fraction of He, and the isotopic ratio 12C/13C in number (case with D=0) in the shell. Right panels: the [X/Fe] ratios are shown for 19F, 20,22Ne, 23Na, 24,25,26Mg, and 27Al. The stars show the observed values for the most iron poor star known today (Frebel et al. 2008). The hatched areas correspond to the range of values covered by observed values in CEMP-no stars. The left column corresponds to unevolved stars (sample of 6 stars), the right column to evolved stars (sample of 17 stars). The observations were taken from the SAGA database (Suda et al. 2008). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg43.png)
|
Figure 8:
Abundance profiles for various elements (in mass fraction) as a function of the Lagrangian mass in the outer layers
of a 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm} \includegraphics[width=9cm, height=9cm,clip]{13377fig9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg45.png)
|
Figure 9:
Same as Fig. 8 for a non-rotating 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig10.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg46.png)
|
Figure 10:
Composition of the mixture composed of wind material of 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig11.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg47.png)
|
Figure 11:
Comparisons between abundances in various stellar model ejecta and the
abundances observed in CEMP-no stars. The continuous curve with filled
circles shows the composition of the mixture composed of material
ejected by the rotating 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=9cm, height=9cm,clip]{13377fig12.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg48.png)
|
Figure 12:
Variation in the abundances of various elements (in mass fraction) as a function of the Lagrangian mass in the outer layers
of a 7 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm} \includegraphics[width=9cm, height=9cm,clip]{13377fig13.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13377-09/Timg50.png)
|
Figure 13:
Same as Fig. 12 for a non-rotating 7 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


