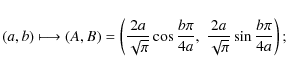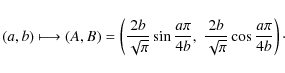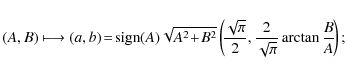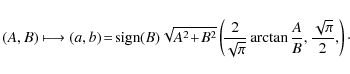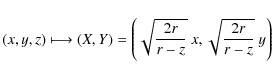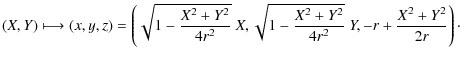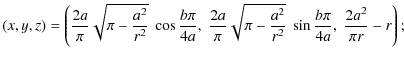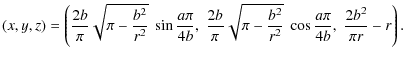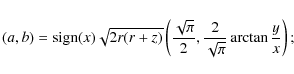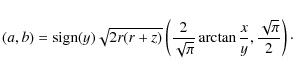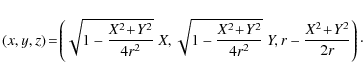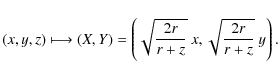New uniform grids on the sphere

D. Roşca

doi:10.1051/0004-6361/201015278

Home

All issues

Volume 520 (September-October 2010)

A&A, 520 (2010) A63

Full HTML

Free Access

Issue		A&A Volume 520, September-October 2010


Article Number		A63
Number of page(s)		4
Section		Numerical methods and codes
DOI		https://doi.org/10.1051/0004-6361/201015278
Published online		04 October 2010

A&A 520, A63 (2010)

New uniform grids on the sphere

D. Rosca

Technical University of Cluj-Napoca, Department of mathematics, str. Memorandumului 28, 400114 Cluj-Napoca, Romania

Received 24 June 2010 / Accepted 17 July 2010

Abstract
Aims. A method for constructing new uniform grids on the sphere is given.
Methods. We define a bijection in $\mathbb R^{2}$ , which maps squares onto discs and preserves areas. Then we use this bijection, combined with Lambert azimuthal projection, for lifting uniform grids from the square to the sphere.
Results. We can obtain uniform spherical grids that allow a hierarchical data manipulation and have an isolatitudinal distribution of cells. Compared with HEALPix grids, nowadays the most used in astronomy and astrophysics, our grids have the advantage of allowing easier implementation, and in addition one can move approximating functions from the square to the sphere by a simple technique.

Key words: miscellaneous - methods: data analysis - methods: numerical - methods: statistical

1 Introduction

The analysis of functions defined on spherical domains plays a central role in geosciences. In many applications, one needs uniform grids on the sphere. The standard manipulation of spherical data includes convolutions with local and global kernels, Fourier analysis with spherical harmonics, wavelet analysis, nearest neighbour search, etc. Some of these manipulations become very slow if the sampling of functions on the sphere and the related discrete data set are not designed well. Thus, the discrete data should have the following properties: (a) hierarchical tree structure (allowing construction of a multiresolution analysis); (b) equal area for the discrete elements of the partition of the sphere; (c) isolatitudinal distribution for the discrete area elements (essential for fast computations involving spherical harmonics).

There are plenty of spherical grids and sampling points, many of them mentioned in Gorsky et al. (2005). A complete description of all known spherical projections used in cartography is realized in (Grafarend & Krumm 2006; Snyder 1993). Until the construction of the HEALPix grid, no grid satisfied simultaneous the requirements (a)-(c). In this paper we give a method for constructing uniform grids and sampling points on the 2-sphere, satisfying these requirements simultaneously. We start with a bijection on $\mathbb R^{2}$ , which preserves areas and maps a square in a disc. Thus, any uniform grid of the square can be mapped bijectively onto a uniform grid on the disc, and then onto a uniform grid on the sphere, via Lambert's equal area azimuthal projection. Compared to the projections used for HEALPix grids and to the planar domains mapped there, our method has the nice property that, besides the uniform grids and sampling points on the sphere, one can transport any function from the square to the sphere by the technique used in Rosca & Antoine (2009). In addition, if we have a set of real functions defined on the square, the corresponding spherical functions preserve the following properties: orthonormal basis, Riesz basis, frame, and local support.

Consider the square of edge 2L and the circle with the same area, both centred on the origin O (Fig. 1). The radius of the circle will be $R=2L/\sqrt{\pi}.$ We want to construct a bijection T from the domain

$\begin{eqnarray*}S_L=\{ (x,y)\in \mathbb R^2, \ \vert x\vert\leq L,~ \vert y\vert\leq L \}\nonumber \end{eqnarray*}$

to the disc of radius R,

$\begin{eqnarray*}C_L=\left \{ (x,y)\in \mathbb R^2,\ x^2+y^2 \leq \frac{4L^2}{\pi} \right \},\nonumber \end{eqnarray*}$

such that

$\begin{displaymath}% \mathcal A (D)=\mathcal A (T(D)) \mbox{ for every domain }D\subseteq S_L. \end{displaymath}$

(1)

Here $\mathcal A (D)$ denotes the area of D.

The first idea is to construct a map by keeping the direction of the position vector, that is, for $M\in S_L$ to take T(M) on the half-line OM. If we define such an application which maps the square

$\begin{eqnarray*}\partial S_l=\{ (x,y)\in \mathbb R^2, \ \vert x\vert=l,~ \vert y\vert=l \}, \nonumber \end{eqnarray*}$

into the circle

$\begin{eqnarray*}\partial C_l=\left \{ (x,y)\in \mathbb R^2,\ x^2+y^2 = \frac{4l^2}{\pi} \right \}, \nonumber \end{eqnarray*}$

for every $l\in (0,L],$ we see that such an application does not satisfy (1).

Therefore, an alternative would be to take a rotation around O, followed by an appropriate move along the radius. This construction is described bellow. We focus for the moment on the first octant I of the plane, intersected with the square S_L,

$\begin{eqnarray*}{I}=\{(a,b)\in \mathbb R^2, \ 0\leq b \leq a \}.\nonumber \end{eqnarray*}$

The map T will be defined in such a way that each half-line $d_m \subset {I}$ of equation y=mx $(0\leq m\leq 1)$ is mapped into the half-line d_k(m) of equation y=k(m) x, with

$\begin{eqnarray*}k(m)=\tan \frac {m\pi} 4\cdot \nonumber \end{eqnarray*}$

In this way, the half lines y=0 and y=x, situated on the boundary of I are invariant under T and $d_{k(m)}\subset {I}$ for all $m\in [0,1]$ . We want the other boundary edge x=L situated in I to be mapped on the arc of the circle C_L situated in I, so let $M(a,b)\in {I}\cap S_{L}$ and $Q(L,mL)\in \partial S_L$ the intersection of OM with the square $\partial S_L$ (see Fig. 1), where

$\begin{eqnarray*}m=\frac ba\cdot \nonumber \end{eqnarray*}$

The point Q will be mapped on the point P(X,Y), the intersection of the half-line d_k(m) with the circle $\partial C_L$ . Thus, we have X²+k(m)²X²=R², whence

$\begin{eqnarray*}X=\frac{R}{\sqrt{1+k(m)^2}}=\frac{R}{\sqrt{1+\tan^2\frac{m\pi}4}}=R \cos \frac{m\pi}4\cdot \nonumber \end{eqnarray*}$

Therefore, the point P has the coordinates

$\begin{eqnarray*}P\left( R \cos \frac {m\pi}4,R \sin \frac{m\pi}4 \right)\cdot \nonumber \end{eqnarray*}$

We define N=T(M) such that $N\in OP$ and $\frac{ON}{OP}=\frac{OM}{OQ}$ . A simple calculation gives $\frac{OM}{OQ}=\frac aL,$ and therefore we find

$\begin{eqnarray*}N\left( \frac {2a}{\sqrt \pi}\cos \frac{b \pi}{4a},\; \frac {2a}{\sqrt \pi}\sin \frac{b \pi}{4a}\right)\cdot \nonumber \end{eqnarray*}$

Straightforward calculations show that the Jacobian of the map T, restricted to I, is indeed 1, and therefore T preserves the areas of the domains situated in the first octant I.

By similar arguments for the seven other octants, we find that the map $T:S_L \to C_L$ preserving areas is defined as follows:

1.

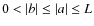For $0<\vert b\vert\leq \vert a\vert \leq L$ ,

$\begin{displaymath}% (a,b) \longmapsto (A,B)=\left( \frac {2a}{\sqrt \pi}\cos \f... ...\pi}{4a},\; \frac {2a}{\sqrt \pi}\sin \frac{b \pi}{4a}\right); \end{displaymath}$

(2)

2.

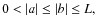
For $0<\vert a\vert \leq \vert b\vert \leq L,$

$\begin{displaymath}% (a,b) \longmapsto (A,B)= \left( \frac {2b}{\sqrt \pi}\sin \... ...{4b},\; \frac {2b}{\sqrt \pi}\cos \frac{a \pi}{4b}\right)\cdot \end{displaymath}$

(3)

For the origin we take T(0,0)=(0,0). One can prove that T is continuous and that the Jacobian of T is 1. Figure 2 shows the images of the horizontal lines. Figure 3 show images of two uniform grids of S_L, each obtained from uniform grids on the square consisting of lines parallel to the edges.

The inverse of T is given by the following formulas:

1.

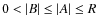For $0<\vert B\vert\leq \vert A\vert \leq R$ ,

$\begin{displaymath}% (A,B) \longmapsto (a,b) \!= \! \mbox{sign}(A)\sqrt{A^{2}\!... ...ac{\sqrt \pi}2,\frac 2{\sqrt \pi}\arctan \frac BA \!\right); \end{displaymath}$

(4)

2.

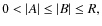
For $0<\vert A\vert \leq \vert B\vert \leq R,$

$\begin{displaymath}% (A,B) \longmapsto (a,b) \!=\! \mbox{sign}(B)\sqrt{A^{2}\!... ...{\sqrt \pi}\arctan \frac AB,\frac{\sqrt \pi}2, \!\right)\cdot \end{displaymath}$

(5)

$\begin{figure} \par\includegraphics[width=6cm,clip]{15278fig1.eps} \end{figure}$	Figure 1: The action of the transform T. Points N and P are the images of M and Q, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig2.eps} \end{figure}$	Figure 2: A horizontal grid and its image grid on the disc. The image of the bold line on the left is the bold curve on the right.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig3.eps} \end{figure}$	Figure 3: Two uniform grids of the disc, where the right one is the refinement of the left one.
Open with DEXTER

2 Spherical grids

We intend to use our transform to construct uniform grids on the sphere. In a uniform grid, all the cells have the same area. The idea is to start from a uniform grid on a square, first to map it onto a disc using the map T and then use an equal area projection from the disc to the sphere. An example of such a projection is Lambert's azimuthal projection.

2.1 Lambert's azimuthal equal area projection

This projection was constructed in 1772 by J. H. Lambert, and it is the most used projection in cartography for mapping one hemisphere of the Earth onto a disc. This projection establishes a bijection between a sphere of radius r, without a point, and the interior of a disc of radius 2r and it preserves areas. To define the Lambert azimuthal projection (see Fig. 4), we need the plane tangent to the sphere at some point S on the sphere. Let P be an arbitrary point on the sphere other than the antipode of S. Let d be the Euclidean distance between S and P (not the distance along the sphere surface). The projection of P will be the point P' on the plane, such that SP'=d. Geometrically, it can be constructed as follows. We consider the unique circle centred on S, passing through P and perpendicular to the plane. This circle intersects the plane at two points and we take P' those point that is closer to P. This is the projected point (Fig. 4). The antipode of S is excluded from the projection because the required circle is not unique. The projection of S is taken as S.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{15278fig4.eps} \end{figure}$	Figure 4: Lambert azimuthal projection.
Open with DEXTER

If we take the sphere $\mathbb S^2_r$ of equation x²+y²+z²=r² and S(0,0,-r) the south pole, then Lambert's projection and its inverse can be described, in Cartesian coordinates, by the following formulas:

$\begin{displaymath}% (x,y,z) \longmapsto (X,Y)=\left( \sqrt{ \frac{2r}{r-z}}~x,\sqrt{ \frac{2r}{r-z}}~y \right) \end{displaymath}$

(6)

and

$\displaystyle (X,Y) \longmapsto (x,y,z)= \left( \sqrt{1-\frac{X^2+Y^2}{4r^2}}~X,\sqrt{1-\frac{X^2+Y^2}{4r^2}}~Y,-r+\frac{X^2+Y^2}{2r} \right)\cdot$

(7)

2.2 Spherical uniform grids using Lambert's azimuthal projection for the whole sphere

We want to construct a uniform grid on the sphere $\mathbb S^2_r$ starting from a uniform grid of the square $S_{r\sqrt \pi}$ of edge $2r \sqrt \pi$ . By combining the formulas (7) and (2), (3), we obtain that a point $(a,b)\in S_{r\sqrt \pi}$ is mapped into the point $(x,y,z)\in \mathbb S^2_r$ with the following coordinates:

1.

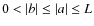For $0<\vert b\vert\leq \vert a\vert \leq L$ ,

$\displaystyle (x,y,z)= \left( \frac {2a}{\pi}\sqrt{\pi-\frac {a^2}{r^2}}~ \cos ... ...qrt{\pi-\frac {a^2}{r^2}}~\sin \frac{b \pi}{4a},\; \frac{2a^2}{\pi r}-r\right);$

(8)

2.

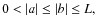
For $0<\vert a\vert \leq \vert b\vert \leq L,$

$\displaystyle (x,y,z)= \left( \frac {2b}{\pi}\sqrt{\pi-\frac {b^2}{r^2}}~ \sin ... ...qrt{\pi-\frac {b^2}{r^2}}~\cos \frac{a \pi}{4b},\; \frac{2b^2}{\pi r}-r\right).$

(9)

For the inverse, combining formulas (6) and (4), (5), we obtain that a point $(x,y,z)\in \mathbb S^2_r$ is mapped onto the point $(a,b)\in S_{r\sqrt \pi}$ with the following coordinates:

1.

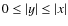For $0\leq \vert y\vert\leq \vert x\vert$ ,

$\begin{displaymath}% (a,b)=\mbox{sign}(x)\sqrt{2r(r+z)}\left( \frac{\sqrt \pi}{2},\frac 2{\sqrt \pi}\arctan \frac yx \right); \end{displaymath}$

(10)

2.

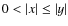
For $0<\vert x\vert \leq \vert y\vert$

$\begin{displaymath}% (a,b)=\mbox{sign}(y)\sqrt{2r(r+z)}\left( \frac 2{\sqrt \pi}\arctan \frac xy,\frac{\sqrt \pi}{2} \right)\cdot \end{displaymath}$

(11)

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig5.eps} \end{figure}$	Figure 5: The grids in Fig. 3, projected on the sphere by Lambert's projection.
Open with DEXTER

Two examples of such spherical uniform grids are given in Fig. 5. One can see that, because of the Lambert projection, the distortion of shape increases towards the north pole. For this reason, one can construct another type of spherical grids, by applying the Lambert projection separately for the two hemispheres.

2.3 Spherical grid using Lambert's azimuthal projection for each of the hemispheres

When we use Lambert's projection, we can choose to map only the southern hemisphere with respect to the south pole, and separately, the northern hemisphere with respect to the north pole. If the sphere has the radius r, then the projected discs of each hemisphere have the radius $\sqrt 2 r$ and therefore the corresponding square will be $S_{r\sqrt{\pi/2}}$ of edge $r\sqrt{2\pi}$ . The formula for the spherical image (x,y,z) of a point (X,Y) of the disc $C_{r\sqrt 2}$ are the one given in (7) for (x,y,z) in the southern hemisphere, while for the northern hemisphere it is given by

$\begin{displaymath}% (x,y,z) \!=\!\left( \sqrt{1-\frac{X^2\!+\!Y^2}{4r^2}}~X,\sq... ...ac{X^2\!+\!Y^2}{4r^2}}~Y,r-\frac{X^2\!+\!Y^2}{2r} \right)\cdot \end{displaymath}$

(12)

For the inverse projection, a point (x,y,z) on the southern hemisphere projects according to formula (6), while for a point (x,y,z) on the northern hemisphere, the projection onto the disc $C_{r\sqrt 2}$ is given by

$\begin{displaymath}% (x,y,z) \longmapsto (X,Y)=\left( \sqrt{ \frac{2r}{r+z}}~x,\sqrt{ \frac{2r}{r+z}}~y \right). \end{displaymath}$

(13)

Similarly, formulas (8), (9) are the ones used for the points (x,y,z) on the southern hemisphere, while for the northern hemisphere, only the sign of z changes in both of these formulas. As for the images in the square $S_{r \sqrt 2}$ of a point (x,y,y) on the northern hemisphere, the formulas are similar to (10), (11), with (r+z) replaced with (r-z). Such uniform spherical grids are depicted in Fig. 6.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig6.eps} \end{figure}$	Figure 6: The grids in Fig. 3, projected on the sphere by Lambert's projection, separately for the northern and southern hemispheres.
Open with DEXTER

The number of cells at each latitude for the square grid

We focus on the spherical grid with 8n² cells, for which the grid on each hemisphere is the image of a uniform grid of the square [-L,L], with $L=r\sqrt{\pi/2 }$ . On this square we consider the grid containing (2n)² small squares of the same area, formed by lines parallel to the edges. The centres of the cells of the spherical grid are equally distributed on 2n latitudinal circles, symmetric with respect to the equator. The latitudinal circles are, in fact, images of squares centred on O. The number of cells in the northern hemisphere (and of course, symmetric on the southern hemisphere) will be 4(2i-1) on the ith latitudinal circle.

3 Conclusions

The equal area projection that maps squares onto circles (to the best of our knowledge this projection has not been constructed before) allowed us to construct uniform grids on a disc and on a sphere. We presented here only the pictures for the spherical grid generated by a square grid with square cells, but of course there are many other uniform grids on the square, which can be mapped to nice uniform grids on the sphere.

There are still many open questions. Do the centers of some spherical grid cells constitute fundamental systems of points? How do cubature formulas with such points behave? Which wavelets on the interval can be efficiently mapped on the sphere? How efficient are the new grids for geo-statistical applications? In which applications are our grids preferable to other grids? These will be the subjects of future work.

Acknowledgements

This work is supported by the grant POSDRU/89/ 1.5/S/62557, funded by the European Social Fund.

References

Gorski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
Grafarend, E. W., & Krumm, F. W. 2006, Map Projections (Berlin-Heidelberg: Springer Verlag) [Google Scholar]
Rosca, D., & Antoine, J. P. 2009, Math. Probl. Eng [Google Scholar]
Snyder, J. P. 1993, Flattening the Earth (Chicago and London: University of Chicago Press) [Google Scholar]

All Figures

$\begin{figure} \par\includegraphics[width=6cm,clip]{15278fig1.eps} \end{figure}$	Figure 1: The action of the transform T. Points N and P are the images of M and Q, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig2.eps} \end{figure}$	Figure 2: A horizontal grid and its image grid on the disc. The image of the bold line on the left is the bold curve on the right.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig3.eps} \end{figure}$	Figure 3: Two uniform grids of the disc, where the right one is the refinement of the left one.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{15278fig4.eps} \end{figure}$	Figure 4: Lambert azimuthal projection.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig5.eps} \end{figure}$	Figure 5: The grids in Fig. 3, projected on the sphere by Lambert's projection.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{15278fig6.eps} \end{figure}$	Figure 6: The grids in Fig. 3, projected on the sphere by Lambert's projection, separately for the northern and southern hemispheres.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Gorski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]

[2] Grafarend, E. W., & Krumm, F. W. 2006, Map Projections (Berlin-Heidelberg: Springer Verlag) [Google Scholar]

[3] Rosca, D., & Antoine, J. P. 2009, Math. Probl. Eng [Google Scholar]

[4] Snyder, J. P. 1993, Flattening the Earth (Chicago and London: University of Chicago Press) [Google Scholar]