EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A104 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A104
Number of page(s) 7
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201014912
Published online 11 October 2010
A&A 520, A104 (2010)

Dark energy domination in the Virgocentric flow

A. D. Chernin1,2 - I. D. Karachentsev3 - O. G. Nasonova3 - P. Teerikorpi1 - M. J. Valtonen1 - V. P. Dolgachev2 - L. M. Domozhilova2 - G. G. Byrd4

1 - Tuorla Observatory, Department of Physics and Astronomy, University of Turku, 21500 Piikkiö, Finland
2 - Sternberg Astronomical Institute, Moscow University, Moscow 119899, Russia
3 - Special Astrophysical Observatory, Nizhnii Arkhys 369167, Russia
4 - University of Alabama, Tuscaloosa, AL 35487-0324, USA

Received 3 May 2010 / Accepted 1 June 2010

Abstract
Context. The standard $\Lambda$CDM cosmological model implies that all celestial bodies are embedded in a perfectly uniform dark energy background, represented by Einstein's cosmological constant, and experience its repulsive antigravity action.
Aims. Can dark energy have strong dynamical effects on small cosmic scales as well as globally? Continuing our efforts to clarify this question, we now focus on the Virgo Cluster and the flow of expansion around it.
Methods. We interpret the Hubble diagram from a new database of velocities and distances of galaxies in the cluster and its environment, using a nonlinear analytical model, which incorporates the antigravity force in terms of Newtonian mechanics. The key parameter is the zero-gravity radius, the distance at which gravity and antigravity are in balance.
Results. 1. The interplay between the gravity of the cluster and the antigravity of the dark energy background determines the kinematical structure of the system and controls its evolution. 2. The gravity dominates the quasi-stationary bound cluster, while the antigravity controls the Virgocentric flow, bringing order and regularity to the flow, which reaches linearity and the global Hubble rate at distances ${\ga}15$ Mpc. 3. The cluster and the flow form a system similar to the Local Group and its outflow. In the velocity-distance diagram, the cluster-flow structure reproduces the group-flow structure with a scaling factor of about 10; the zero-gravity radius for the cluster system is also 10 times larger.
Conclusions. The phase and dynamical similarity of the systems on the scales of 1-30 Mpc suggests that a two-component pattern may be universal for groups and clusters: a quasi-stationary bound central component and an expanding outflow around it, caused by the nonlinear gravity-antigravity interplay with the dark energy dominating in the flow component.

Key words: Local Group - galaxies: clusters: individual: Virgo cluster - dark matter - dark energy

1 Introduction

Early studies of the motion of our Galaxy (reviewed by Huchra 1988) led to the discovery of the peculiar velocity of the Local Group towards the Virgo cluster. To illustrate this, imagine the distance to Virgo to be 17 Mpc and the Hubble constant H0 = 72 km s-1 Mpc-1, then the expected cosmological velocity of the cluster is 1224 km s-1. The observed velocity is about 1000 km s-1. The difference reflects our peculiar velocity of about 220 km s-1 towards Virgo.

This estimate of the retarded expansion (the so-called ``Virgo infall'') views the universal expansion as existing not only on ``truly cosmological'' scales ${\sim}1000$ Mpc, but also on local scales of ${\sim}10$ Mpc only weakly disturbed. Observational and theoretical aspects of the Virgo infall were studied e.g. by Silk (1974, 1977), Peebles (1976), Hoffman & Salpeter (1982), Sandage (1986), Teerikorpi et al. (1992), and Ekholm et al. (1999, 2000).

1.1 The Virgocentric flow

The Virgo infall is a particular feature of what is known as the Virgocentric flow: hundreds of galaxies (our Galaxy among them) are receeding away from the Virgo cluster. Recent data (Karachentsev & Nasonova 2010) show that the flow velocities range from nearly zero around 5-8 Mpc from the cluster center to about 2000 km s-1 at the distances of about 30 Mpc. For  R > 10-15 Mpc, a roughly linear velocity-distance relation may be seen in the flow, making it resemble the global Hubble expansion. But strong deviations from the linear relation exist at smaller distances, not surprisingly: 1) the linear expansion flow, V = H R, is the property of the universe beyond the cosmic ``cell of uniformity'' (${\ge}300$ Mpc); 2) the Virgo cluster is a strong local overdensity; 3) the matter distribution around the cluster is highly nonuniform up to the distance of about 30 Mpc.

Besides the natural deviations, we have here an example of a paradox realized by Sandage (1986, 1999). He saw a mystery in the fact that the local expansion proceeds in a quite regular way. Moreover, the rate of expansion is similar, if not identical, to the global Hubble constant (Ekholm et al. 2001; Thim et al. 2003; Karachentsev 2005; Karachentsev et al. 2002a, 2003b; Whiting 2003). Originally, the Friedmann theory described the expansion of a smooth, uniform self-gravitating medium. But the linear cosmological expansion was discovered by Hubble where it should not be: in the lumpy environment at distances <20 Mpc.

1.2 The local relevance of dark energy

Soon after the discovery of dark energy (Riess et al. 1998; Perlmutter et al. 1999) on global scales, we suggested (Chernin et al. 2000; Chernin 2001; Baryshev et al. 2001; Karachentsev et al. 2003a; Chernin et al. 2004; Teerikorpi et al. 2006) that dark energy with its omnipresent and uniform density (represented by Einstein's cosmological constant) may provide the dynamical background for a regular quiescent expansion on local scales, resolving the Hubble-Sandage paradox. Our key argument came from the fact that the antigravity produced by dark energy is stronger than the gravity of the Local Group at distances larger than about 1.5 Mpc from the group center[*].

The present paper extends our work from groups to the scale of clusters, focusing on the Virgo cluster.

2 The phase space structure

Recent observations of the Virgo cluster and its vicinity permit a better understanding of the physics behind the visible structure and kinematics of the system.

2.1 The dataset

The most complete list of data on the Virgo Cluster and the Virgocentric flow has been collected by Karachentsev & Nasonova (2010). These include distance moduli of galaxies from the Catalogue of the Neighbouring Galaxies (=CNG, Karachentsev et al. 2005) and also from the literature with the best measurements prefered. Distances from the tip of the red giant branch (TRGB) and the Cepheids are used from the CNG together with new TRGB distances (Karachentsev et al. 2006; Makarov et al. 2006; Mei et al. 2007). For galaxy images in two or more photometric bands obtained with WFPC2 or ACS cameras at the Hubble Space Telescope, the TRGB method yields distances with an accuracy of about 7% (Rizzi et al. 2007). The database includes also data on 300 E and S0 galaxies from the surface brightness fluctuation (SBF) method by Tonry et al. (2000) with a typical distance error of 12%. The total sample contains the velocities and distances of 1371 galaxies within 30 Mpc from the Virgo cluster center. Especially interesting is the sample of 761 galaxies selected to avoid the effect of unknown tangential (to the line of sight) velocity components. The velocity-distance diagram for this sample taken from Karachentsev & Nasonova (2010) is given in Fig. 1.

\begin{figure} \par\includegraphics[width=9cm,clip]{14912fig1} \end{figure} Figure 1:

Hubble diagram with Virgocentric velocities and distances for 761 galaxies of the Virgo Cluster and the outflow (Karachentsev & Nasonova 2010). The two-component pattern is outlined by bold dashed lines. The zero-gravity radius $R_{\rm ZG} \sim 10$ Mpc is located in the zone between the components. The broken line is the running median used by K & N to find the zero-velocity radius R0 = 6-7 Mpc. Two lines from the origin indicate the Hubble ratios H = 72 km s-1 Mpc-1 and HV = 65 km s-1 Mpc-1. Two curves show special trajectories, corresponding to the parabolic motion (E = 0; the upper one) and to the minimal escape velocity from the cluster potential well (the lower one). The flow galaxies with the most accurate distances and velocities (big dots) occupy the area between these curves.

Open with DEXTER

2.2 The zero-velocity radius and the cluster mass

The zero-velocity radius within the retarded expansion field around a point-like mass concentration means the distance where the radial velocity relative to the concentration is zero. In the ideal case of the mass concentration at rest within the expanding Friedmann universe this is the distance where the radial peculiar velocity towards the concentration is equal to the Hubble velocity for the same distance. Using Tully-Fisher distances in the Hubble diagram, Teerikorpi et al. (1992) could for the first time see the location of the zero-velocity radius R0 for the Virgo system, so that $R_0/R_{\rm Virgo} \approx 0.45$ or $R_0 \approx 7.4$ Mpc. The work by Karachentsev & Nasonova (2010) puts the zero-velocity radius at R0 = 5.0-7.5 Mpc. For R < R0, positive and negative velocities appear in practically equal numbers; for R > R0, the velocities are positive with a few exceptions likely due to errors in distances. The zero-velocity radius gives the upper limit of the size of the gravitationally bound cluster, and the diagram shows that the Virgocentric flow starts at $R \ge R_0$ and extends at least up to 30 Mpc.

The zero-velocity radius has been often used for estimating the total mass M0 of a gravitationally bound system. According to Lynden-Bell (1981) and Sandage (1986), the spherical model with $\Lambda =0$ leads to the estimator

\begin{displaymath}% M_0 = (\pi^2/8G) t_{\rm U}^{-2} R_0^3. \end{displaymath} (1)

With the age of the universe $t_{\rm U} = 13.7$ Gyr (Spergel et al. 2007), Karachentsev & Nasonova (2010) find the Virgo cluster mass $M_0 = (6.3 \pm 2.0)$ $\times$ $10^{14}~M_{\odot}$. This result agrees with the virial mass $M_{\rm vir} = 6$ $\times$ $10^{14}~M_{\odot}$ estimated by Hoffman & Salpeter (1982) and ${\sim}4$ $\times$ $10^{14}~M_{\odot}$ of Valtonen et al. (1985) and Saarinen & Valtonen (1985). Teerikorpi et al. (1992) and Ekholm et al. (1999, 2000) found that the real cluster mass might be from 1 to 2 the virial mass, or  (0.6-1.2) $\times$ $10^{15}~M_{\odot}$. Tully & Mohayaee (2004) derived the mass 1.2 $\times$ $10^{15}~M_{\odot}$ with the ``numerical action'' method.

2.3 The Virgo infall

Figure 1 clearly shows the Virgo infall: at distances R > R0, the galaxies are located mostly below the Hubble line $V_{\rm H} = H R$ with H = 72 km s-1 Mpc-1 (Spergel et al. 2007). The deviation of the median velocity of the flow $V_{\rm m}$ from the Hubble velocity is well seen in the distance range 7-13 Mpc. At larger distances the retardation effect gets weaker and gradually sinks below the measurement error level.

For the distance and peculiar velocity of the Milky Way, we take the figures from Karachentsev & Nasonova (2010): the distance to the Virgo cluster 17 Mpc, the recession velocity 1004 $\pm$ 70 km s-1; with the Hubble constant H = 72 km s-1 Mpc-1 the regular expansion velocity is 1224 km s-1. Then the peculiar velocity directed to the cluster center $\delta V = 220$ $\pm$ 70 km s-1 (this agrees with the result based on TF distances and a different ana-lysis by Theureau et al. 1997; a complete velocity field on the scale of 10-20 Mpc is given by Tully et al. 2008). The effect is not very strong. It is much more instructive, however, that there are big nonlinear deviations from the linear velocity-distance law near the cluster: the infall effect is strongest there.

2.4 Two-component phase structure

The Virgo system reveals an obvious two-component structure in Fig. 1: the cluster and the flow, outlined roughly with bold dashed lines. As we noted, the positive and negative velocities (from -2000 to +1700 km s-1) are seen in the cluster area in equal numbers, so the component is rather symmetrical to the horizontal line V = 0. The border zone between the components, in the range 6 < R < 12 Mpc, is poorly populated, and the velocities are considerably less scattered here, from -400 to +600 km s-1. This zone contains the zero-velocity radius. The flow component with positive velocities is at distances >12 Mpc. It is rather symmetrical to the line V = H R. The velocities are scattered within $\pm 1000$ km s-1 around the symmetry line.

A much lower velocity dispersion is seen in the more accurate data on 75 galaxies with TRGB and Cepheid distances (mostly from CNG) located from 10 to 25 Mpc from the cluster center. In the diagram of Fig. 1, the subsample (dots) occupies a strip less than 500 km s-1 wide. They are scattered with the mean dispersion of about 250 km s-1 around the line V = HV R, where $H_V \simeq 65$ km s-1 Mpc-1. This line is the median line for the subsample.

2.5 Similarity with the Local system

The two-component phase structure of the Virgo system looks very similar to that of the Local system (the Local Group and the outflow). The diagram of Fig. 2 (Karachentsev et al. 2009) is based on the most complete and accurate data obtained with the TRGB method using the HST. The velocities within the Local Group range from -150 to +160 km s-1, about 10 times less than the velocity spread in the Virgo cluster. The zone between the two components of the Local system is in the range 0.7-1.2 Mpc, also 10 times less than in Fig. 1. The local flow has a dispersion of about 30 km s-1 around the line V = HL R, where $H_L = H_V \simeq 60$ km s-1 Mpc-1. This line defines the median for the local flow. The dispersion is about 10 times less than in the Vigocentric flow for the subsample of the accurate distances. The local phase diagram of Fig. 2, if zoomed by a factor of 10, would roughly reproduce the phase structure of the Virgo system. We will see that the phase similarity is also supported by the dynamical similarity.

\begin{figure} \par\includegraphics[width=9cm,clip]{14912fig2} \end{figure} Figure 2:

Hubble diagram for 57 galaxies of the Local Group and the local flow (Karachentsev et al. 2009). The thin line indicates the zero-velocity radius R0 = 0.7-0.9 Mpc. The two-component phase structure is outlined by the bold dashed line. Zoomed in about 10 times, the group-scale structure well reproduces the cluster-scale structure (Fig. 1). The zero-gravity radius  $R_{\rm ZG}$ is about 10 times smaller for the group than the same key quantity of the cluster system. The similarity supports a universal cosmic two-component grand-design for groups and clusters.

Open with DEXTER

3 Gravity-antigravity interplay

Dark energy is a form of cosmic energy that produces antigravity and causes the global cosmological acceleration discovered by Riess et al. (1998) and Perlmutter et al. (1999) in observations of SNe type Ia at horizon-size distances of about 1000 Mpc. These and other observations, especially the cosmic microwave background (CMB) anisotropies (Spergel et al. 2007), indicate that the global dark energy density, $\rho_V = (0.73 \pm 0.03)$ $\times$ 10-29 g cm-3, makes up nearly 3/4 of the total energy of the universe.

3.1 Antigravity in Newtonian description

According to the simplest, most straightforward and quite likely view adopted in the $\Lambda$CDM cosmology, dark energy is represented by Einstein's cosmological constant $\Lambda$, so that $\rho_V = (c^2/8 \pi G) \Lambda$. If so, then dark energy is the energy of the cosmic vacuum (Gliner 1965) and is described macroscopically as a perfectly uniform fluid with the equation of state $p_V = - \rho_V$ (here pV is the dark energy pressure; c = 1). This interpretation implies that dark energy exists everywhere in space with the same density and pressure.

Local dynamical effects of dark energy have been studied by Chernin et al. (2000, 2009), Chernin (2001), Baryshev et al. (2001), Karachentsev et al. (2003a), Byrd et al. (2007), and Teerikorpi et al. (2008). For the Local Group and the outflow close to it, we showed that the antigravity produced by the dark energy background exceeds the gravity of the group at distances beyond ${\simeq}1.5$ Mpc from the group barycenter. Similar results were obtained for the nearby M 81 and Cen A groups (Chernin et al. 2007a,b).

Extending now our approach to the cluster scale, we consider the Virgo system (the cluster and the flow) embedded in the uniform dark energy background. We describe the system - in the first approximation - in a framework of a spherical model (Silk 1974, 1977; Peebles 1976) where the cluster is considered as a spherical gravitationally bound quasi-stationary system. The galaxy distribution in the flow is represented by a continuous dust-like (pressureless) matter. The flow is expanding, and it is assumed that the concentric shells of matter do not intersect each other in their motion (the mass within each shell keeps constant).

Because the velocities in the cluster and the flow are much less than the speed of light, we may analyze the dynamics of the cluster-flow system in terms of Newtonian forces. A spherical shell with a Lagrangian coordinate r and a Eulerian distance R(r,t) from the cluster center is affected by the gravitation of the cluster and the flow galaxies within the sphere of the radius R(r,t). According to the Newtonian gravity law, the shell experiences an acceleration

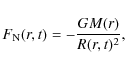
\begin{displaymath}% F_{\rm N} (r,t) = - \frac{GM(r)}{R(r,t)^2}, \end{displaymath} (2)

in the reference frame related to the cluster center. Here M(r) is the total mass within the radius R(r,t).

The flow is also affected by the repulsion produced by the local dark energy. The resulting acceleration in Newtonian terms is given by the ``Einstein antigravity law'':

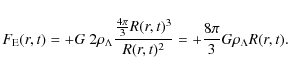
\begin{displaymath}% F_{\rm E}(r,t) = + G~ 2 \rho_{\Lambda} \frac{\frac{4 \pi}{3}R(r,t)^3}{R(r,t)^2} = + \frac{8 \pi}{3} G\rho_{\Lambda} R(r,t). \end{displaymath} (3)

Here $-2 \rho_{\Lambda} = \rho_{\Lambda} + 3 p_{\Lambda}$ is the effective (General Relativity) gravitating density of dark energy (for details see, e.g., Chernin 2001). It is negative, and therefore the acceleration is positive, speeding up the shell away from the center.

3.2 Zero-gravity radius in the point-mass approximation

The equation of motion of an individual shell has the form

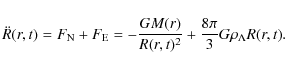
\begin{displaymath}% \ddot R(r,t) = F_{\rm N} + F_{\rm E} = - \frac{GM(r)}{R(r,t)^2} + \frac{8 \pi}{3} G\rho_{\Lambda} R(r,t). \end{displaymath} (4)

Its integration leads to the mechanical energy conservation law for each matter shell:

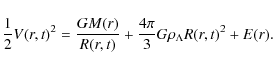
\begin{displaymath}% \frac{1}{2} V(r,t)^2 = \frac{G M(r)}{R(r,t)} + \frac{4 \pi}{3} G\rho_{\Lambda} R(r,t)^2 + E(r). \end{displaymath} (5)

Here $V(r,t) = \dot R(r,t)$ is the Eulerian radial velocity of the shell, and E(r) is its total mechanical energy (per unit mass). This is the basic equation which describes the outflow in our model. It is the Newtonian analogue of the LTB spacetime of General Relativity (e.g., Gromov et al. 2001).

A simpler model results if we can assume that the cluster mass M0 makes up the majority of the mass M(r), and the flow galaxies can be treated as test particles. Curiously enough, this assumption makes the model more general in the sense that no spherical symmetry is required now for the galaxy distribution in the flow (not necessarily concentric shells around the cluster). However, the gravity force produced by the cluster at the distances of the flow is still isotropic. The model remains also nonlinear: no restriction on the strength of the dynamical effects is assumed.

The mass-point model may seem overly simple, because it is known that the Virgo cluster contributes only 20% of the bright galaxies within the volume up to the distance of the Local Group (Tully 1982). However, Tully & Mohayaee (2004) conclude from their numerical action method that the mass-to-luminosity ratio of the E-galaxy rich Virgo cluster must be several times higher (they give $M/L \sim 900$) than in the surrounding region (${\sim}125$) in order to produce the infall velocities observed close to Virgo (a qualitatively similar result was found by Teerikorpi et al. 1992). Therefore, the model with most of the mass in and close to the Virgo cluster could be a sufficient first approximation.

In this simplified/generalized version, the mass M(r) = M is constant in Eq. (4), which shows that antigravity and gravity balance each other at the distance $R = R_{\rm ZG}$, where

\begin{displaymath}% R_{\rm ZG} = \left[\frac{3 M}{8\pi \rho_{\Lambda}}\right]^{1/3} \end{displaymath} (6)

is the zero-gravity radius (Chernin et al. 2000; Chernin 2001; Dolgachev et al. 2003, 2004). Gravity dominates at $R < R_{\rm ZG}$, and antigravity is stronger than gravity at $R > R_{\rm ZG}$. The zero-gravity radius is the major quantitative factor in the gravity-antigravity interplay in the system.

According to various estimates (Sect. 2), the total mass of the Virgo cluster is 1-2 times the virial mass: M = (0.6-1.2) $\times$ $10^{15}~M_{\odot}$. Then the known global  $\rho_{\Lambda}$ gives

\begin{displaymath}% R_{\rm ZG} = (9{-}11)~{\rm Mpc}. \end{displaymath} (7)

Karachentsev & Nasonova (2010) argue in favor of one virial mass for the cluster mass; if that is the case, the lower limit for $R_{\rm ZG}$ in Eq. (7) may be more realistic.

Equations (6) and (7) indicate that the zero-gravity radius  $R_{\rm ZG}$ of the Virgo system is not far from the zero-velocity radius R0 = 5.0-7.5 Mpc. Indeed, one expects that $R_{\rm ZG}$ is slightly larger than R0 (Teerikorpi et al. 2008) in the standard cosmology. The zero-velocity radius constrains the size of the cluster (Sect. 2), and there gravity also dominates ( $R < R_0 \la R_{\rm ZG}$), the necessary condition for a gravitationally bound cluster. On the other hand, the Virgocentric flow is located beyond the distance $R_{\rm ZG} \simeq R_0$, hence the flow is dominated dynamically by the dark energy antigravity.

The zero-gravity radius of the Virgo system is about 10 times larger than that of the Local system for which $R_{\rm ZG} = 1{-}1.3$ Mpc (Chernin 2001; Chernin et al. 2000, 2009). We see here the same factor 10 as for the phase structures of the Virgo and Local systems (Sect. 2). Thus the phase similarity is complemented by the dynamical similarity.

3.3 Antigravity push

Now we return to the Milky Way and estimate the net gravity-antigravity effect at its distance $R_{\rm MW} = 17$ Mpc from the cluster center. With $R_{\rm ZG} = 9{-}11$ Mpc, we find that here the antigravity force is stronger than the gravity:

\begin{displaymath}% F_{\rm E}/\vert F_{\rm N}\vert \simeq 4-7, \;\;\; R = R_{\rm MW}. \end{displaymath} (8)

As we see, the extra gravity produced by the Virgo cluster mass is actually overbalanced by the antigravity of the dark energy located within the sphere of the radius  $R_{\rm MW}$around the cluster. Thus the Milky Way experiences not a weak extra pull (cf. Sects. 1 and 2), but rather a strong push (in the Virgocentric reference frame) from the Virgo direction.

The dark energy domination in the flow changes the current dynamical situation drastically in comparison with the earlier models by Silk (1974, 1977) and Peebles (1976). At the peri-phery of the Virgocentric flow (at about 30 Mpc) the force ratio is impressively high: $F_E/\vert F_N\vert \simeq 20{-}37$.

3.4 Antigravity domination

The basic trend of the flow evolution is seen from Eq. (5). With $M(r) = M = {\rm const.}$, it takes at prolonged times the form

\begin{displaymath}% V(r,t = \infty) = \left[\frac{8 \pi}{3} G\rho_{\Lambda}\right]^{1/2} R. \end{displaymath} (9)

In this limit, $F_{\rm E}/\vert F_{\rm N}\vert \rightarrow \infty$, and the gravity of the cluster is practically negligible compared to the dark energy antigravity. As a result, the flow asymptotically acquires the linear velocity-distance relation with the constant Hubble factor expressed via the dark energy density only:

\begin{displaymath}% H_{\Lambda} = \left[\frac{8 \pi G}{3}\rho_{\Lambda}\right]^{1/2} = 63{-}65~{\rm km~s^{-1}~Mpc^{-1}}. \end{displaymath} (10)

At a given moment of time (that of observation) t = t0 Eq. (5) presents the spatial structure of the flow. At large distances

\begin{displaymath}% V(r = \infty,t_0) \rightarrow H_{\Lambda}R(r,t_0). \end{displaymath} (11)

The flow trajectories converge to the asymptotic of Eq. (11) in general independently of the ``boundary/initial conditions'' near the cluster (see Fig. 2 in Teerikorpi & Chernin 2010). In particular, strong perturbations at small distances in the flow are compatible with its regularity at larger distances. No tuning of the model parameters is required for this - the only significant quantity is the zero-gravity radius  $R_{\rm ZG}$ determined by the cluster mass and the DE density.

Thus, dark energy dominates the dynamics of the Virgocentric flow on its entire observed extension from 12 to at least 30 Mpc. Because of the strong antigravity, the flow proves to be rather regular, acquiring the linear Hubble relation at distances ${\ga}15$ Mpc from the cluster center. This major conclusion from the model also resolves the Hubble-Sandage paradox on the scale of ${\sim}10$ Mpc, in harmony with our general approach to the old puzzle (Sect. 1).

4 Discussion

We discuss here some specific features and implications of the dark energy domination in the Virgocentric flow.

4.1 The Einstein-Straus radius

The mass of dark matter and baryons in the Virgo Cluster, M = (0.6-1.2) $\times$ $10^{15}~M_{\odot}$, was initially collected from the volume which at the present epoch has the radius $R_{\rm ES} = [\frac{3M}{4\pi \rho_{\rm M}(t_0)}]^{1/3} = 15{-}19$ Mpc, where  $\rho_{\rm M}(t_0)$ is the mean matter density in the Universe. The quantity  $R_{\rm ES}$ is known as the Einstein-Straus radius in the vacuole model. In the presence of dark energy (Chernin et al. 2006; Teerikorpi et al. 2008), $R_{\rm ES} = [\frac{2 \rho_{\Lambda}}{\rho_{\rm M}(t_0)}]^{1/3} R_{\rm ZG} = 1.7~R_{\rm ZG}$. Within the E-S vacuole, the spherical layer between the radii R0 and  $R_{\rm ES}$ does not contain any mass. Therefore the approximation of test particles adopted in the model of Sect. 3 works well in this layer. Beyond the distance $R_{\rm ES}\simeq R_{\rm MW}$ the model needs modification, but remains qualitatively correct up to the distances of 25-30 Mpc. However, because $2\rho_{\Lambda} > \rho_{\rm M}(t_0)$, the antigravity of dark energy dominates in the entire area of the Virgocentric flow in Fig. 1.

4.2 Two special trajectories

Equation (5) shows that the flow has zero velocity at $R = R_{\rm ZG} \simeq R_0$, if the total energy of the shell or an individual galaxy

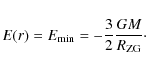
\begin{displaymath}% E(r) = E_{\rm min} = -\frac{3}{2} \frac{GM}{R_{\rm ZG}}\cdot \end{displaymath} (12)

It is easy to see that $E_{\rm min}$ is the minimal energy needed for a particle to escape from the potential well of the cluster. Equation (5) with $E(r) = E_{\rm min}$ gives the corresponding velocity  $V_{\rm min}(R)$ of the flow at different distances in the flow:

\begin{displaymath}% V_{\rm min} = H_{\Lambda} R \left[1 + 2 \left(\frac{R_{\rm ... ...right)^3 - 3 \left(\frac{R_{\rm ZG}}{R}\right)^2\right]^{1/2}. \end{displaymath} (13)

At large distances ( $R \gg R_{\rm ZG}$), the trajectories with $E(r) = E_{\rm min}$ approach the asymptotic given by Eq. (11).

Another special value of the mechanical energy is E(r) = 0, corresponding to parabolic motion. In this case,

\begin{displaymath}% V_{\rm par} = H_{\Lambda} R \left[1 + 2 \left(\frac{R_{\rm ZG}}{R}\right)^3\right] ^{1/2}. \end{displaymath} (14)

The two special trajectories with $E(r) = E_{\rm min}$ and E(r) = 0 (see Fig. 1) converge to the asymptotic of Eq. (11) at large distances - in agreement with the results of Sect. 3.

It is quite interesting that the most accurate data on the flow (from the TRGB and Cepheids; dots in Fig. 1) show a low dispersion around the line $V = H_{\rm V} R$, and the corresponding trajectories occupy the area just between the curves  $V_{\rm min}(R)$ and  $V_{\rm par}(R)$. The rather wide spread of the other data in Fig. 1 is mostly due to observational errors (Karachentsev & Nasonova 2010 - especially their Fig. 7b). Still, the restriction $E_{\rm min} \le E \le 0$ puts an upper limit on the value |E| in Eq. (5), and because of this, the asymptotic of Eq. (11) may be reached more easily in the flow.

It is also significant that the Local Group outflow has the same feature: the galaxies prefer the area between $V_{\rm min}$ and $V_{\rm par}$ in the Hubble diagram of Fig. 2 (cf. Teerikorpi et al. 2008). This is another similarity aspect between the Virgo system and the Local system (Sect. 2). Mathematically, the similarity reflects that Eqs. (13) and (14) have exactly the same view for both systems in the dimensionless form y(x) = 0 with $y = V/(H_{\Lambda}R_{\rm ZG}), x = R/R_{\rm ZG}$; the scale factor is again about 10.

This similarity suggests that the condition $E_{\rm min} \le E \le 0$ has more general significance; it may reflect the kinematical state of the flow at the early formation epoch. For example, $V > V_{\rm min}$ follows, if the galaxies of the flow initially escaped from the cluster (Chernin et al. 2004, 2007c).

4.3 Comparison with cosmology

The zero-gravity radius $R_{\rm ZG}$ is a local spatial counterpart of the redshift $z_{\Lambda} \simeq 0.7$ at which the gravity and the antigravity balance each other in the Universe as a whole. Globally, the balance takes place only at one moment  $t(z_{\Lambda})$ in the entire co-moving space, while the local gravity-antigravity balance exists during the whole life-time of the system since its formation, but only on the sphere of the radius  $R_{\rm ZG}$.

The Virgocentric flow should not be identified with the global cosmological expansion. The Virgo system lies deeply inside the cosmic cell of uniformity and does not ``know'' about the universe of the horizon scales. In the early epoch of weak protogalactic perturbations, the dark matter and baryons of the system participated in the cosmological expansion. But later, at the epoch of nonlinear perturbations, the matter separated from the expansion and underwent violent evolution. Contrary to that, the unperturbed flow at horizon-scale distances was not similarly affected, and up to now the initial isotropy of its expansive motion and the uniformity of its matter distribution are conserved. Therefore, it is mysterious that the global Hubble constant 72 km s-1 Mpc-1 is so close to the local expansion rate 65 km s-1 Mpc-1 in the Virgocentric flow (two beams in Fig. 1). This is one aspect of the Hubble-Sandage paradox (Sect. 1).

Trying to find an explanation, we note that the Friedmann equation for the scale factor a(t) has much the same form as the local energy conservation Eq. (5):

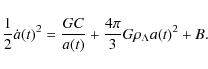
\begin{displaymath}% \frac{1}{2} \dot a(t)^2 = \frac{G C}{a(t)} + \frac{4 \pi}{3}G\rho_{\Lambda} a(t)^2 + B. \end{displaymath} (15)

The constant $C = \frac{4 \pi}{3}\rho_{\rm M}(t) a(t)^3$ has the dimension of mass, and $\rho_{\rm M}(t)$ is the density of matter (dark and baryonic); the energy constant B = 0 in the standard flat cosmology. The cosmological Hubble factor comes from this equation:

\begin{displaymath}% H(t) = \frac{\dot a(t)}{a} = \left[\frac{8 \pi G}{3}\left(\... ...} \left[1 + \frac{\rho_m}{2 \rho_{\Lambda}}\right]^{1/2}\cdot \end{displaymath} (16)

When time goes to infinity, the matter density drops to zero, the dark energy becomes dominant, and the cosmological Hubble factor becomes time-independent:

\begin{displaymath}% H(t) \rightarrow H_{\Lambda} = \left[\frac{8 \pi G}{3}\rho_{\Lambda}\right]^{1/2} = 63{-}65~{\rm km~s^{-1}~Mpc^{-1}}. \end{displaymath} (17)

At the present epoch, $t_{\rm U} = 13.7$ Gyr, the Hubble rate

\begin{displaymath}% H = H_{\Lambda} \left[1 + \frac{\Omega_{\rm M}}{ \Omega_{\Lambda}}\right]^{1/2} \simeq 72~{\rm km~s^{-1}~Mpc^{-1}}, \end{displaymath} (18)

which is equal to the empirical (WMAP) value.

As we see, the Virgocentric flow and the global cosmological expansion have a common asymptotic in the limit of dark energy domination: for the local flow, this is the asymptotic in space (large distances from the cluster center), and for the global flow, this is the asymptotic in time (a future of the Universe). If the asymptotic is approached now both globally and locally, we would have $H \simeq H_{\Lambda}$ on the largest scales and $H_V \simeq H_{\Lambda}$ in the Virgocentric flow.

In their present states, both flows are near the asymptotic, though they do not quite reach it. That is why H, HV, and  $H_{\Lambda}$ have similar values. The flows are not directly related to each other; but, they ``feel'' the same uniform dark energy background, and in this way both are controlled by the antigravity force, which is equally effective near the cosmic horizon and at the periphery of the Virgocentric flow. As a result, the local flow at its large distances looks much like a ``part'' of the global horizon-distance flow.

The near coincidence of the values H, $H_{\rm V}$, and $H_{\Lambda}$ explained by our model clarifies the Hubble-Sandage paradox (Sect. 1) for the Virgocentric flow: asymptotically, the flow reaches not only the linear Hubble law (Sect. 3), but also acquires the expansion rate $H_{\rm V}$, which approaches the global rate when the measuring accuracy is improved.

4.4 Probing local dark energy

The global density of dark energy can be derived if the redshift  $z_{\Lambda}$is found at which the gravity of matter is exactly balanced by the dark energy antigravity, and also the present matter density is known. The same logic works in local studies: just find the zero-gravity radius  $R_{\rm ZG}$ from the outflow observations and the mass of the local system.

We may now restrict the value of $R_{\rm ZG}$ using the diagram of Fig. 1. Because the zero-gravity surface lies outside the cluster volume, it should be $R_{\rm ZG} > R_0 \simeq 6{-}7$ Mpc. On the other hand, the linear velocity-distance relation, with the Hubble ratio close to H, is clearly seen from a distance of about 15 Mpc. This suggests that $R_{\rm ZG} < 15$ Mpc. The argument that the zero-gravity surface is located below the point where the local flow reaches the global expansion rate gained support from the calculations by Teerikorpi & Chernin (2010). As for the cluster mass, we adopt the range M = (0.6-1.2) $\times$ $10^{15}~M_{\odot}$ (Sect. 2). Then Eq. (6) in the form $\rho_{x} = M/(\frac{8\pi}{3} R_{\rm ZG}^3)$ directly leads to robust upper and lower limits to the unknown local dark energy density $\rho_x$:

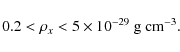
\begin{displaymath}% 0.2 < \rho_{x} < 5 \times 10^{-29}~{\rm g~cm^{-3}}. \end{displaymath} (19)

Indeed, the upper limit obtained from the cluster size ( $R_{\rm ZG}$) is conservative. We note that the theoretical minimum velocity curve in Fig. 1 would be shifted up to the velocity-distance relation defined by the TRGB and Cepheid distances, if one takes $\rho_{x} = 1.4$ $\times$ $10^{-29}~{\rm g~cm^{-3}}$. This would be a more realistic upper limit, and near the limit similarly obtained in Teerikorpi et al. (2008) using the Local Group and the M 81 group. Thus the local dark energy density is near the global value or may be the same; $\rho_{\Lambda} = 0.73$ $\times$ $10^{-29}~{\rm g~cm^{-3}}$ lies comfortably in the range of Eq. (19). Similar estimates for the dark energy come from studies of the Local Group, M 81 group and Cen A group (Chernin et al. 2007a,b, 2009).

We may now argue reversely: let us assume that the density of dark energy is known from cosmological observations and the zero-gravity radius  $R_{\rm ZG}$ is between 6 and 15 Mpc. Then we may independently estimate the mass of the Virgo Cluster: M = (0.3-4) $\times$ $10^{15}~M_{\odot}$. The value of the cluster mass adopted earlier is within this interval.

4.5 The origin of the local flows

The model of Sect. 3 describes the present structure of the Virgocentric flow and also predicts its future evolution. However, it says almost nothing about the initial state of the flow. Our discussion suggests that the Virgo cluster and the outflow form a system with a common origin and evolutionary history. Its formation was most probably caused by complex linear and nonlinear processes (collisions and merging of galaxies and protogalactic units, violent relaxation of the system in its self-gravity field, etc.). Similar processes are expected in the early history of the Local Group and other systems with the two-component structure. Their basic features might be recognized from big N-body simulations, like the Millennium Simulation (Li & White 2008). We leave it for a later study to clarify the way in which the galaxies of local flows gain their initial expansion velocities.

5 Conclusions

The recently published systematic and most accurate data on the velocities and distances of galaxies in the Virgo cluster and its environment (Karachentsev & Nasonova 2010) shed light on the physics behind the observed properties of the cluster and the flow. We find that

1.
The cluster and the flow can be treated together as a physical system embedded in the uniform dark energy background; this is adopted in our analytical nonlinear model.

2.
The nonlinear interplay between the gravity produced by the cluster mass (dark matter + baryons) and the antigravity of the dark energy is the major dynamical factor determining the kinematic structure of the system and controlling its evolution; our model enables one to describe this in a simple (exact or approximate) quantitative way.

3.
The key physical parameter of the system is its zero-gravity radius, 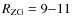$R_{\rm ZG} = 9{-}11$ Mpc, below which the gravity dominates the quasi-stationary bound cluster, while the antigravity dominates the expanding Virgocentric flow.

4.
The dark energy antigravity brings order and regularity to the Virgocentric flow and the flow acquires the linear velocity-distance relation at the Virgocentric distances R > 15 Mpc. Thus, the Hubble-Sandage paradox is understood on the cluster scale.

5.
In the velocity-distance diagram, the zero-gravity radius is near to or somewhat larger than the zero-velocity radius R0 = 5.0-7.5 Mpc, as determined by Karachentsev & Nasonova (2010).

6.
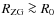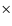
With the value of $R_{\rm ZG} \ga R_0$ found from the diagram, one may estimate the mass of the Virgo cluster, using the known global density of dark energy: M = (0.3-4) $\times$ $10^{15}~M_{\odot}$.

7.
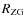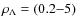
With the same value of $R_{\rm ZG}$, one may estimate the local density of the dark energy in the Virgo system, if the mass of the cluster is considered known (from the virial or the zero-velocity method): $\rho_{\Lambda} = (0.2{-}5)$ $\times$ $10^{-29}~{\rm g~cm^{-3}}.$

8.
The two-component Virgo system is similar to the Local system formed by the Local Group together with the local outflow around it. In the velocity-distance diagram, the Virgo system reproduces the Local system with the scale factor of about 10. A dynamical similarity is seen in that the zero-gravity radius for the Virgo system is about 10 times larger than for the Local system.

9.
The similarity suggests that a universal two-component grand design may exist with a quasi-stationary bound central component and an expanding outflow around it on the spatial scales of 1-30 Mpc. The phase and dynamical structure of the real two-component systems reflects the nonlinear gravity-antigravity interplay with dark energy domination in the flow component.

Acknowledgements
A.C., V.D., and L.D. thank the RFBR for partial support via the grant 10-02-00178. We also thank the anonymous referee for useful comments.

References

  1. Balaguera-Antolinez, A., Mota, D. F., & Nowakowski, M. 2007, MNRAS, 382, 621 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bambi, C. 2007, PhRvD, 75h3003 [Google Scholar]
  3. Baryshev, Yu. V., Chernin, A. D., & Teerikorpi, P. 2001, A&A, 378, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Byrd, G. G., Chernin, A. D., & Valtonen, M. J. 2007, Cosmology: Foundations and Frontiers, URSS, Moscow [Google Scholar]
  5. Chernin, A. D. 2001, Physics-Uspekhi, 44, 1099 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chernin, A. D. 2008, Physics-Uspekhi, 51, 267 [Google Scholar]
  7. Chernin, A. D., Teerikorpi, P., & Baryshev, Yu. V. 2000, Adv. Space Res., 31, 459 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chernin, A. D., Karachentsev, I. D., Valtonen, M. J., et al. 2004, A&A, 415, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Chernin, A. D., Teerikorpi, P., & Baryshev, Yu. V. 2006, A&A, 456, 13 [Google Scholar]
  10. Chernin, A. D., Karachentsev, I. D., Nasonova, O. G., et al. 2007a, Astrophys., 50, 405 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chernin, A. D., Karachentsev, I. D., Makarov, D. I., et al. 2007b, A&AT, 26, 275 [NASA ADS] [Google Scholar]
  12. Chernin, A. D., Karachentsev, I. D., Valtonen, M. J., et al. 2007c, A&A, 467, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2009, A&A, 507, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dolgachev, V. P., Domozhilova, L. M., & Chernin, A. D. 2003, Astr. Rep., 47, 728 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dolgachev, V. P., Domozhilova, L. M., & Chernin, A. D. 2004, Astr. Rep., 48, 787 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ekholm, T., Lanoix, P., Paturel, G., Teerikorpi, P., & Fouqué, P. 1999, A&A, 351, 827 [NASA ADS] [Google Scholar]
  17. Ekholm, T., Lanoix, P., Teerikorpi, P., Fouqué, P., & Paturel, G. 2000, A&A, 355, 835 [NASA ADS] [Google Scholar]
  18. Ekholm, T., Baryshev, Yu. V., Teerikorpi, P., Hanski, M., & Paturel, G. 2001, A&A, 368, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gliner, E. B. 1965, JETP, 49, 542 (1966, Sov. Phys. JETP, 22, 376) [Google Scholar]
  20. Gromov, A., Baryshev, Yu., Suson, D., & Teerikorpi, P. 2001, Gravitation & Cosmology, 7, 140 [NASA ADS] [Google Scholar]
  21. Guo, Q., & Shan, H.-Y. 2009, RAA, 9, 151 [NASA ADS] [Google Scholar]
  22. Hoffman, G. L., & Salpeter, E. E. 1982, ApJ, 263, 485 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hoffman, Y., Martinez-Vaquero, L. A., Yepes, G., & Gottlöber, S. 2008, MNRAS, 386, 390 [NASA ADS] [CrossRef] [Google Scholar]
  24. Huchra, J. P. 1988, in The Extragalactic Distance Scale, ASP, 257 [Google Scholar]
  25. Karachentsev, I. D. 2005, AJ, 129, 178 [NASA ADS] [CrossRef] [Google Scholar]
  26. Karachentsev, I. D., & Nasonova, O. G. 2010, MNRAS, 405, 1075 [NASA ADS] [Google Scholar]
  27. Karachentsev, I. D., Sharina, M. E., Dolphin, A. E., et al. 2002a, A&A, 385, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Karachentsev, I. D., Sharina, M. E., Makarov, D. I., et al. 2002b, A&A, 389, 812 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Karachentsev, I. D., Chernin, A. D., & Teerikorpi, P. 2003a, Astrophys., 46, 491 [Google Scholar]
  30. Karachentsev, I. D., Makarov, D. I., Sharina, M. E., et al. 2003b, A&A, 398, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Karachentsev, I. D., Dolphin, A. E., Tully, R. B., et al. 2006, AJ, 131, 1361 [NASA ADS] [CrossRef] [Google Scholar]
  32. Karachentsev, I. D., Kashibadze, O. G., Makarov, D. I., et al. 2009, MNRAS, 393, 1265 [NASA ADS] [CrossRef] [Google Scholar]
  33. Li, Y.-S., & White, S. M. D. 2008, MNRAS, 384, 1459 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lynden-Bell, D. 1981, The Observatory, 101, 111 [NASA ADS] [Google Scholar]
  35. Macciò, A. V., Governato, F., & Horellou, C. 2005, MNRAS, 359, 941 [NASA ADS] [CrossRef] [Google Scholar]
  36. Makarov, D., Makarova, L., Rizzi, L., et al. 2006, AJ, 132, 2729 [NASA ADS] [CrossRef] [Google Scholar]
  37. Martinez-Vaquero, L., Yepes, G., Hoffman, Y., Gottlöber, S., & Sivan, M. 2009, MNRAS, 397, 2070 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mei, S., Blakeslee, J. P., Côte, P., et al. 2007, ApJ, 655, 144 [NASA ADS] [CrossRef] [Google Scholar]
  39. Niemi, S.-M., & Valtonen, M. J. 2009, A&A, 494, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Peebles, P. J. E. 1976, ApJ, 205, 318 [NASA ADS] [CrossRef] [Google Scholar]
  41. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  42. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  43. Rizzi, L., Tully, R. B., Makarov, D., et al. 2007, ApJ, 661, 815 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  44. Saarinen, S., & Valtonen, M. J. 1985, A&A, 153, 130 [NASA ADS] [Google Scholar]
  45. Sandage, A. 1986, ApJ, 307, 1 [NASA ADS] [CrossRef] [Google Scholar]
  46. Sandage, A. 1999, ApJ, 527, 479 [NASA ADS] [CrossRef] [Google Scholar]
  47. Sandage, A., Tammann, G., & Saha, A. 2006, ApJ, 653, 843 [NASA ADS] [CrossRef] [Google Scholar]
  48. Silk, J. 1974, ApJ, 193, 525 [NASA ADS] [CrossRef] [Google Scholar]
  49. Silk, J. 1977, A&A, 59, 53 [NASA ADS] [Google Scholar]
  50. Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
  51. Teerikorpi, P., & Chernin, A. D. 2010, A&A, 516, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Teerikorpi, P., Bottinelli, L., Gouguenheim, L., & Paturel, G. 1992, A&A, 260, 17 [NASA ADS] [Google Scholar]
  53. Teerikorpi, P., Chernin, A. D., & Baryshev, Yu. V. 2006, A&A, 483, 383 [Google Scholar]
  54. Teerikorpi, P., Chernin, A. D., Karachentsev, I. D., et al. 2008, A&A, 483, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Theureau, G., Hanski, M., Ekholm, T., et al. 1997, A&A, 322, 730 [NASA ADS] [Google Scholar]
  56. Thim, F., Tammann, G., Saha, A., et al. 2003, ApJ, 590, 256 [NASA ADS] [CrossRef] [Google Scholar]
  57. Tonry, J. L., Blakeslee, J. P., Ajhar, E. A., & Dressler, A. 2000, ApJ, 530, 625 [NASA ADS] [CrossRef] [Google Scholar]
  58. Tully, R. B. 1982, ApJ, 257, 389 [NASA ADS] [CrossRef] [Google Scholar]
  59. Tully, R. B., & Mohayaee, R. 2004 in Outskirts of Galaxy Clusters, ed. A. Diaferio, IAU Coll., 195, 205 [Google Scholar]
  60. Tully, R. B., Shaya, E. T., Karachentsev, I. D., et al. 2008, ApJ, 676, 184 [NASA ADS] [CrossRef] [Google Scholar]
  61. Valtonen, M. J., Innanen, K. A., Huang, T. Y., & Saarinen, S. 1985, A&A, 143, 182 [NASA ADS] [Google Scholar]
  62. Valtonen, M. J., Niemi, S., Teerikorpi, P., et al. 2008, DDA, 39.0103 [Google Scholar]
  63. Whiting, A. B. 2003, ApJ, 587, 186 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... center[*]
The increasing observational evidence and theoretical considerations favoring this view have been discussed by Macciò et al. (2005), Sandage (2006), Teerikorpi et al. (2006, 2008), Chernin et al. (2006, 2007a-c), Byrd et al. (2007), Valtonen et al. (2008), Balaguera-Antolinez et al. (2007), Bambi (2007), Chernin (2008), Niemi & Valtonen (2009), Guo & Shan (2009). For some counter-arguments to this new approach see Hoffman et al. (2008) and Martinez-Valquero et al. (2009).

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{14912fig1} \end{figure} Figure 1:

Hubble diagram with Virgocentric velocities and distances for 761 galaxies of the Virgo Cluster and the outflow (Karachentsev & Nasonova 2010). The two-component pattern is outlined by bold dashed lines. The zero-gravity radius $R_{\rm ZG} \sim 10$ Mpc is located in the zone between the components. The broken line is the running median used by K & N to find the zero-velocity radius R0 = 6-7 Mpc. Two lines from the origin indicate the Hubble ratios H = 72 km s-1 Mpc-1 and HV = 65 km s-1 Mpc-1. Two curves show special trajectories, corresponding to the parabolic motion (E = 0; the upper one) and to the minimal escape velocity from the cluster potential well (the lower one). The flow galaxies with the most accurate distances and velocities (big dots) occupy the area between these curves.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{14912fig2} \end{figure} Figure 2:

Hubble diagram for 57 galaxies of the Local Group and the local flow (Karachentsev et al. 2009). The thin line indicates the zero-velocity radius R0 = 0.7-0.9 Mpc. The two-component phase structure is outlined by the bold dashed line. Zoomed in about 10 times, the group-scale structure well reproduces the cluster-scale structure (Fig. 1). The zero-gravity radius  $R_{\rm ZG}$ is about 10 times smaller for the group than the same key quantity of the cluster system. The similarity supports a universal cosmic two-component grand-design for groups and clusters.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.