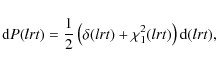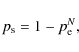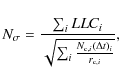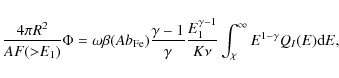| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014706 | |
| Published online | 27 September 2010 | |
Puzzling fluorescent emission from Orion
S. Czesla - J. H. M. M. Schmitt
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 1 April 2010 / Accepted 24 June 2010
Abstract
Fluorescent X-ray emission offers a rare possibility for studying
cool material surrounding active, young stars in the X-ray regime. In
this work, we develop a new method to search for fluorescent emission
and analyze its temporal behavior, which we apply to a sample of
106 young, active stars in Orion. Our analysis yields a sample of
23 X-ray sources with fluorescent emission, including
6 objects already reported on in an earlier study. The fluorescent
sources show a wide variety of temporal behavior. While the fluorescent
emission is associated with soft X-ray flares in some cases,
it sometimes appears as a (quasi) persistent feature, or is
seen during truly quiescent periods. We conclude that fluorescent X-ray
emission can be observed in a much higher fraction of young, active
stars than previously believed. Whether photoionization alone is the
excitation mechanism of fluorescent X-ray emission or if electronic
collisional excitation also contributes remains debatable. The temporal
variability is often hard to reconcile with the photoionization model,
which remains plausible if we allow for suitable geometries.
Photoionization is preferred to electronic, collisional excitation
mainly because the energetics of the latter challenge our current
physical understanding.
Key words: stars: activity - stars: flare - X-rays: stars
1 Introduction
Fluorescent emission pushes the horizon of X-ray astronomy beyond the observation of high-energy material, carrying the imprint of cold matter into the X-ray regime. The origin of fluorescent photons is cool, neutral matter pervaded by ionizing photon or particle radiation coming from a nearby high-energy source. Following an inner shell ionization in the cold matter, excited ions potentially release their energy in the form of fluorescent photons, which convey information on the existence, structure, and composition of their creation site. Geometries appropriate for producing a detectable amount of fluorescent emission are common in a variety of celestial X-ray sources, and fluorescent X-ray emission has been reported in many targets including active galactic nuclei and young stellar objects.
The interaction of an ion with high-energy radiation can end up
removing one of the ion's inner shell electrons. In the context of
fluorescent emission, two conceivable mechanisms of K-shell electron
removal are at issue: photoionization by soft X-rays and collisional
excitation by electrons with kinetic energy in excess of the K-shell
ionization edge. Independent of the interacting particle,
an excited ion returns to a lower energy state through
rearrangement of its electron configuration, as a consequence of
which the excess energy of the excited state is released by one of two
competing processes. Either it is deposited in an ``Auger electron'',
which is expelled from the ion, or it is released in the form of a
fluorescent photon. The probability of photon emission rises strongly
with increasing atomic number (Bambynek et al. 1972) and is termed the ``fluorescence yield''. Consulting typical solar system or cosmic abundance patterns (e.g., Anders & Grevesse 1989)
shows that iron becomes the most promising candidate when searching for
fluorescent emission. The K-shell ionization energy of neutral iron is
7.112 keV, and the energy of its K![]() line lies in the X-ray regime at about 6.4 keV; both numbers change slowly with increasing ionization (e.g., Kaastra & Mewe 1993). Spin-orbit interaction and the effects of photon scattering create a characteristic line profile (e.g., Sunyaev & Churazov 1996), which can, however, hardly be resolved with today's instrumentation in astronomy.
line lies in the X-ray regime at about 6.4 keV; both numbers change slowly with increasing ionization (e.g., Kaastra & Mewe 1993). Spin-orbit interaction and the effects of photon scattering create a characteristic line profile (e.g., Sunyaev & Churazov 1996), which can, however, hardly be resolved with today's instrumentation in astronomy.
Astronomical detections of the fluorescent K![]() line of neutral or weakly ionized iron (in the following ``Fe K
line of neutral or weakly ionized iron (in the following ``Fe K![]() I line'') were first obtained from solar observations (e.g., Neupert et al. 1967; Doschek et al. 1971),
in particular, during solar flares. The question of how much
photoionization and collisional excitation by electrons contribute to
the observed solar fluorescent emission was addressed by several
authors. Parmar et al. (1984) analyzed
a sample of solar flares and conclude that ``most, if not all'',
of the fluorescent X-rays are due to photoionization and that their
results agree well with associated simulations provided by Bai (1979). Even though Zarro et al. (1992) and Emslie et al. (1986)
do find evidence for fluorescent photons from electron collisional
excitation during the impulsive phase of individual flares, they also
agree that the bulk of the fluorescent emission must be attributed to
photoionization. The argument for photoionization as the dominant
process is based on the strength or equivalent width of the fluorescent
line, as well as on its temporal relation to the observed hard and
soft X-ray flux.
I line'') were first obtained from solar observations (e.g., Neupert et al. 1967; Doschek et al. 1971),
in particular, during solar flares. The question of how much
photoionization and collisional excitation by electrons contribute to
the observed solar fluorescent emission was addressed by several
authors. Parmar et al. (1984) analyzed
a sample of solar flares and conclude that ``most, if not all'',
of the fluorescent X-rays are due to photoionization and that their
results agree well with associated simulations provided by Bai (1979). Even though Zarro et al. (1992) and Emslie et al. (1986)
do find evidence for fluorescent photons from electron collisional
excitation during the impulsive phase of individual flares, they also
agree that the bulk of the fluorescent emission must be attributed to
photoionization. The argument for photoionization as the dominant
process is based on the strength or equivalent width of the fluorescent
line, as well as on its temporal relation to the observed hard and
soft X-ray flux.
About thirty years after the reports of fluorescent emission in solar X-ray spectra, Tanaka et al. (1995) published their discovery of the Fe K![]() I line
in the spectrum of the active galactic nucleus (AGN) MGC-6-30-15.
In excess of an imprint of cold material, this line also carries
information on the relativistic space-time structure at its origin,
providing deep insight into the inner parts of an AGN. Ballantyne & Fabian (2003)
argue that in AGN sources photoionization is more important than
electron or proton collisional excitation, too. The discovery of Tanaka et al. intensified the search for the Fe K
I line
in the spectrum of the active galactic nucleus (AGN) MGC-6-30-15.
In excess of an imprint of cold material, this line also carries
information on the relativistic space-time structure at its origin,
providing deep insight into the inner parts of an AGN. Ballantyne & Fabian (2003)
argue that in AGN sources photoionization is more important than
electron or proton collisional excitation, too. The discovery of Tanaka et al. intensified the search for the Fe K![]() I line
in X-ray sources, in the wake of which fluorescent emission was also
discovered in several stellar sources other than the Sun.
I line
in X-ray sources, in the wake of which fluorescent emission was also
discovered in several stellar sources other than the Sun.
The stellar sources with reported fluorescent emission include YLWA 16 (Imanishi et al. 2001) with Fe K![]() I line emission detected during a flare, HR 9024, for which Testa et al. (2008) present evidence of the Fe K
I line emission detected during a flare, HR 9024, for which Testa et al. (2008) present evidence of the Fe K![]() I line in a Chandra High Energy Transmission Grating spectrum, and Elias 29, which shows a fluorescent line of variable strength (Giardino et al. 2007).
With the exception of HR 9024, the above stars are young stellar
objects (YSOs). While photoionization remains the most common
explanation for the origin of the fluorescent photons, Giardino et al. (2007)
argue that the characteristics of the fluorescent emission observed
from Elias 29 are hard to reconcile with the predictions of the
photoionization scenario, so they suggest a nonthermal electron
population invisible in soft X-rays as a possible explanation for their
findings.
I line in a Chandra High Energy Transmission Grating spectrum, and Elias 29, which shows a fluorescent line of variable strength (Giardino et al. 2007).
With the exception of HR 9024, the above stars are young stellar
objects (YSOs). While photoionization remains the most common
explanation for the origin of the fluorescent photons, Giardino et al. (2007)
argue that the characteristics of the fluorescent emission observed
from Elias 29 are hard to reconcile with the predictions of the
photoionization scenario, so they suggest a nonthermal electron
population invisible in soft X-rays as a possible explanation for their
findings.
As YSOs are known to possess large amounts of cold
circumstellar material in the form of disks or envelopes, it seems
reasonable to search for the Fe K![]() I line
in star-forming regions. The Orion Nebula is a center of recent and
ongoing star formation, harboring a wealth of YSOs in various
evolutionary states. Orion was also the target of a long Chandra observation known as the ``Chandra Orion Ultradeep Project'' (COUP) (e.g., Getman et al. 2005). Tsujimoto et al. (2005) carried out a search for the Fe K
I line
in star-forming regions. The Orion Nebula is a center of recent and
ongoing star formation, harboring a wealth of YSOs in various
evolutionary states. Orion was also the target of a long Chandra observation known as the ``Chandra Orion Ultradeep Project'' (COUP) (e.g., Getman et al. 2005). Tsujimoto et al. (2005) carried out a search for the Fe K![]() I line in the COUP data and presented a sample of seven COUP sources with a fluorescent Fe K
I line in the COUP data and presented a sample of seven COUP sources with a fluorescent Fe K![]() I line detection. One of their sources was further analyzed by Czesla & Schmitt (2007), who reported the temporal concentration of the observed Fe K
I line detection. One of their sources was further analyzed by Czesla & Schmitt (2007), who reported the temporal concentration of the observed Fe K![]() I line flux in the rise phase of one of two flares.
I line flux in the rise phase of one of two flares.
In this study we analyze the X-ray data of 106 COUP sources, including the sample presented by Tsujimoto et al. (2005). We systematically search for fluorescent Fe K![]() I line
emission and present an analysis emphasizing its temporal evolution.
Therefore, we first introduce a method for obtaining the light curve of
the Fe K
I line
emission and present an analysis emphasizing its temporal evolution.
Therefore, we first introduce a method for obtaining the light curve of
the Fe K![]() I line
feature and discuss its significance as obtained from spectral fitting.
We then proceed with an analysis of the Fe K
I line
feature and discuss its significance as obtained from spectral fitting.
We then proceed with an analysis of the Fe K![]() I line behavior in the Tsujimoto et al. (2005)
sources and some additional sources with fluorescent emission. Finally,
we discuss the impact of our findings on the commonly accepted
photoionization model of fluorescent emission and its alternatives.
I line behavior in the Tsujimoto et al. (2005)
sources and some additional sources with fluorescent emission. Finally,
we discuss the impact of our findings on the commonly accepted
photoionization model of fluorescent emission and its alternatives.
2 Detection and analysis of transient spectral features
Longer integration times lead to the accumulation of signal,
allowing for better constrained results unless transient features are
under consideration, which are flattened out during longer
integrations. Inspired by the problem of analyzing the behavior of the
fluorescent Fe K![]() I line (Czesla & Schmitt 2007),
we present a systematic method to detect transient spectral features
and analyze their temporal variability, often with a higher resolution
than allowed for by pure spectral analysis. In the following we
apply the relations between several narrow-band light curves to derive
the ``light curve'' of a particular spectral feature.
I line (Czesla & Schmitt 2007),
we present a systematic method to detect transient spectral features
and analyze their temporal variability, often with a higher resolution
than allowed for by pure spectral analysis. In the following we
apply the relations between several narrow-band light curves to derive
the ``light curve'' of a particular spectral feature.
2.1 The ``line light curve (LLC)'' method
Assume we are given a spectrum with an overall shape described well by some model, M,
and further, that the overall spectral shape (but not necessarily its
normalization) only varies slowly with respect to the temporal
resolution of the feature under scrutiny. Our model is supposed to
describe the observed spectrum; i.e., it already accounts for our
instrument. Below, we assume a thermal model,
![]() ,
with an additional emission line, which is, however, not a necessary precondition.
,
with an additional emission line, which is, however, not a necessary precondition.
We are interested in the temporal behavior of the emission line, which is supposed to have a central energy of
![]() ,
and is completely covered by the ``emission band''
,
and is completely covered by the ``emission band''
![]() .
The number,
.
The number, ![]() ,
of photons expected within this band is given by the sum of the thermal contribution,
,
of photons expected within this band is given by the sum of the thermal contribution,
![]() ,
given by
,
given by
![]() and the line contribution,
and the line contribution,
![]() ,
such that
,
such that
Now we choose a ``comparison band'',
we obtain the number of expected line photons by
For a given energy interval and model, the continuum ratio,
Accordingly, we define the ``line light curve (LLC)'' as a sequence of pairs,
![]() ,
where llci denotes the quantity
,
where llci denotes the quantity
which is basically the number of excess photons in the
An integration of the LLC over a time span yields a measure of excess
emission observed within this span. Formally, we define the
``cumulative LLC'' (CLLC) as
With no excess emission, the expectation value of cllcn is zero by definition, but what is its distribution? Because the values of the summands are statistically determined, the problem of finding the distribution of cllcn compares to finding the endpoint distribution of a random walk. By definition the quantity
which is a shifted Poisson distribution with a variance of
Equation (6) indicates that the cumulated LLC, cllcn,
is a sum of Poisson-distributed quantities, hence
Poisson-distributed (but shifted) itself. Consequently,
the standard deviation of cllcn becomes
This quantity yields an approximation to the expected width of the endpoint distribution of the random walk defined by the numbers obtained from Eq. (5) increasing the upper summation boundary, n, step by step.
Combining the estimate of the line strength with that of the underlying continuum, we can also derive an estimate of the EW, which is given by
2.2 The choice of the energy intervals
For any application of the above method, appropriate emission and
comparison energy bands must be found. In the specific case of the
fluorescent Fe K![]() I line centered at 6.4 keV, we argue in favor of the following intervals.
I line centered at 6.4 keV, we argue in favor of the following intervals.
For the emission interval it is convenient to apply
![]() ,
which, at the spectral resolution provided by the Chandra ACIS and XMM-Newton EPIC instruments, contains
,
which, at the spectral resolution provided by the Chandra ACIS and XMM-Newton EPIC instruments, contains
![]() % of all Fe K
% of all Fe K![]() I line
photons. Unfortunately, the ``iron line complex'', a number
of lines pertaining to Fe XXV and other high ionization stages of
iron, is located close to the high-energy boundary of the emission
band at about 6.7 keV. To avoid contamination, an asymmetric
band with respect to the Fe K
I line
photons. Unfortunately, the ``iron line complex'', a number
of lines pertaining to Fe XXV and other high ionization stages of
iron, is located close to the high-energy boundary of the emission
band at about 6.7 keV. To avoid contamination, an asymmetric
band with respect to the Fe K![]() I line center was chosen.
I line center was chosen.
For the comparison interval, ![]() ,
we use an energy band extending from 6.2 keV to lower energy.
Compared to an interval beyond 6.5 keV, typical stellar X-ray
spectra provide more photons at lower energies, the detectors onboard Chandra and XMM-Newton
are more sensitive here, and, finally, no prominent lines are
located there. In practice, we use 5.2 keV as a lower
boundary for the comparison interval.
,
we use an energy band extending from 6.2 keV to lower energy.
Compared to an interval beyond 6.5 keV, typical stellar X-ray
spectra provide more photons at lower energies, the detectors onboard Chandra and XMM-Newton
are more sensitive here, and, finally, no prominent lines are
located there. In practice, we use 5.2 keV as a lower
boundary for the comparison interval.
2.3 The dependences of the continuum ratio on spectral parameters
At the heart of the LLC approach is the subtraction of the continuum
contribution underlying a spectral feature. The continuum has to be
extrapolated (or maybe interpolated) from another part of the
spectrum, and the ``predictor'' of its contribution is the continuum
ratio, ![]() .
As we are concerned with thermal spectra, a major issue to be addressed is the temperature dependence of
.
As we are concerned with thermal spectra, a major issue to be addressed is the temperature dependence of ![]() .
Source temperatures do not remain perfectly constant, and we are not
able to determine them with arbitrary accuracy. Therefore, it is
essential to show that small variations in temperature do not have a
serious impact on the continuum ratio.
.
Source temperatures do not remain perfectly constant, and we are not
able to determine them with arbitrary accuracy. Therefore, it is
essential to show that small variations in temperature do not have a
serious impact on the continuum ratio.
| Figure 1:
The continuum ratio, |
|
| Open with DEXTER | |
In Fig. 1 we show
the continuum ratio for a wide range of temperatures. The solid and
dashed lines indicate the ratio as obtained with and without
considering the effect of a varying effective area. In the example
we use 6.2-6.5 keV and 5.2-6.2 keV as the boundaries of the
emission and comparison bands, and the effective area is modeled with a
linear dependence on energy.
We use
![]() ,
which in the energy range under consideration is quite representative of numbers obtained for Chandra and XMM-Newton.
,
which in the energy range under consideration is quite representative of numbers obtained for Chandra and XMM-Newton.
Clearly, ![]() varies quickly for temperatures below
varies quickly for temperatures below
![]() keV
and then approaches an almost constant value. When the effective area
effect is taken into account, the ratio increases
as more photons are detected where the effective area is larger, but
the overall behavior remains unaffected. We conclude that
keV
and then approaches an almost constant value. When the effective area
effect is taken into account, the ratio increases
as more photons are detected where the effective area is larger, but
the overall behavior remains unaffected. We conclude that ![]() is robust against small (and even large) temperature variations for temperatures beyond 2 keV.
is robust against small (and even large) temperature variations for temperatures beyond 2 keV.
3 Spectral binning and the fit statistics
We are concerned with an individual feature at a well known energy.
Therefore, we can adapt our binning approach to meet our purpose best.
In particular, we are interested in the narrow Fe K![]() I emission line at 6.4 keV. In view of that, we use a fixed bin-size of
I emission line at 6.4 keV. In view of that, we use a fixed bin-size of
![]() eV (actually 7 Chandra channels, which is a little more than 100 eV) chosen so that one bin is centered on the Fe K
eV (actually 7 Chandra channels, which is a little more than 100 eV) chosen so that one bin is centered on the Fe K![]() I line energy. For spectral fitting we use the C-statistics (Cash 1979), which can handle low photon numbers per bin, but provides no goodness-of-fit indicator such as
I line energy. For spectral fitting we use the C-statistics (Cash 1979), which can handle low photon numbers per bin, but provides no goodness-of-fit indicator such as ![]() does.
does.
3.1 The significance of a spectral emission line
The test for the existence of a spectral line belongs to a category of
statistical problems frequently encountered in X-ray astronomy:
hypothesis testing in the case of nested models. For a given data
set, D, we define two alternative models,
![]() and
and
![]() ,
specified by their parameter vectors
,
specified by their parameter vectors
![]() and
and
![]() with n1 and n2 free parameters. Let n2>n1 and m1 be a subset of m2, so that m1 is nested within m2. The problem consists in deciding which of the models is to be preferred.
with n1 and n2 free parameters. Let n2>n1 and m1 be a subset of m2, so that m1 is nested within m2. The problem consists in deciding which of the models is to be preferred.
In our particular case, m1 is a thermal model and m2
is the same thermal model extended by a narrow Gaussian line at a fixed
energy of 6.4 keV. As a measure of the ``quality'' with which
a given parameter vector,
![]() ,
reproduces the data, we use the likelihood statistics.
,
reproduces the data, we use the likelihood statistics.
The maximum likelihood achieved with m1 is
![]() ,
and the fit with the additional narrow spectral line at 6.4 keV provides another likelihood
,
and the fit with the additional narrow spectral line at 6.4 keV provides another likelihood
![]() .
As m1 is nested within m2,
the introduction of the additional component cannot worsen the fit
result. A popular tool for finding the preferred model is the
likelihood-ratio-test (LRT). Protassov et al. (2002),
however, pointed out that this test, while being applicable in a
variety of other cases, fails in this particular situation, basically
because the topology of the underlying parameter space does not fulfill
the requirements demanded by the test.
.
As m1 is nested within m2,
the introduction of the additional component cannot worsen the fit
result. A popular tool for finding the preferred model is the
likelihood-ratio-test (LRT). Protassov et al. (2002),
however, pointed out that this test, while being applicable in a
variety of other cases, fails in this particular situation, basically
because the topology of the underlying parameter space does not fulfill
the requirements demanded by the test.
In the case of a narrow emission line, the difference in the dimensions of the parameter spaces (n2-n1)
before and after the introduction of the line is one, and with an
appropriate (valid) parameter space, the LRT test statistics,
![]() ,
follows a
,
follows a ![]() distribution with a single degree of freedom. This is not
the case here, a deficit that cannot be cured by more signal or
better instruments, but is inherent in the mathematical structure of
the test. Protassov et al. (2002)
carried out Monte-Carlo calculations (cf. their Sect. 3.2)
and found that in the case of a narrow emission line the false-positive
rate is considerably overestimated by the
distribution with a single degree of freedom. This is not
the case here, a deficit that cannot be cured by more signal or
better instruments, but is inherent in the mathematical structure of
the test. Protassov et al. (2002)
carried out Monte-Carlo calculations (cf. their Sect. 3.2)
and found that in the case of a narrow emission line the false-positive
rate is considerably overestimated by the ![]() distribution. At the nominal 5% cut-off of the
distribution. At the nominal 5% cut-off of the ![]() distribution the ``true'' (simulated) value is only 2.6%.
distribution the ``true'' (simulated) value is only 2.6%.
To ``calibrate'' (cf., Protassov et al. 2002)
the LRT statistics for this particular case, we consider the following
argument. Assume we are given a continuum model and a narrow line at
fixed
energy, which may appear as either an emission or an absorption line.
In this case, the quantity
![]() should, indeed, follow the
should, indeed, follow the ![]() distribution.
If we now only allow for one of two possibilities, either emission
or absorption, the introduction of the line will not result in any
enhancement in the fit statistics where the other possibility is
needed. In those cases we obtain
distribution.
If we now only allow for one of two possibilities, either emission
or absorption, the introduction of the line will not result in any
enhancement in the fit statistics where the other possibility is
needed. In those cases we obtain
![]() .
How often this occurs depends on the form of the distribution
underlying the data, which, in our case, is the Poisson
distribution. As this distribution is approximately symmetrical
around its expectation value,
.
How often this occurs depends on the form of the distribution
underlying the data, which, in our case, is the Poisson
distribution. As this distribution is approximately symmetrical
around its expectation value, ![]() ,
at least for
,
at least for ![]() ,
about half of the line fits should result in
,
about half of the line fits should result in
![]() .
In spite of this, the distribution of the likelihood ratio for the emission components remains unaffected if it is present.
.
In spite of this, the distribution of the likelihood ratio for the emission components remains unaffected if it is present.
Following this argument, the probability of obtaining a value of the LRT statistics,
![]() ,
in the interval
,
in the interval
![]() is given by
is given by
where
To corroborate the validity of our reasoning, we carried out Monte Carlo simulations similar to those of Protassov et al. (2002).
We simulate a number of observations using a constant continuum model
and Poisson statistics. First, we fit the normalization yielding a
likelihood of
![]() ,
and, second, we fit both the continuum normalization and the line
normalization simultaneously to the same observation. For every
simulated observation, we record the value of the LRT statistics,
,
and, second, we fit both the continuum normalization and the line
normalization simultaneously to the same observation. For every
simulated observation, we record the value of the LRT statistics,
![]() .
.
The results of the Monte Carlo simulations with a continuum expectation value of 2 photons per bin
are shown in Fig. 2. Clearly, the nominal ![]() distribution
with a single degree of freedom fails to reproduce the simulated
findings, whereas the distribution given in Eq. (9) provides a considerably better approximation.
distribution
with a single degree of freedom fails to reproduce the simulated
findings, whereas the distribution given in Eq. (9) provides a considerably better approximation.
Therefore, when testing for the presence of a narrow emission line, we can interpret the numbers obtained for the LRT statistics using Eq. (9) as a reference distribution. In practice, this means that our sensitivity is approximately twice as high as a blind application of the LRT implies.
| Figure 2:
Distribution of the LRT statistics obtained from Monte Carlo simulations (solid line), the nominal |
|
| Open with DEXTER | |
3.2 Significance estimates in time-resolved spectroscopy
Let us assume an observation of length T to be at our disposal, and in the data we detect a source, which is only slightly variable on the time scale T. Likewise, we choose an arbitrary time interval of length t so that ![]() and
carry out a spectral analysis, using only the data pertaining to that
sub-interval. Our analysis leaves us with an emission line to which we
can assign a high probability,
and
carry out a spectral analysis, using only the data pertaining to that
sub-interval. Our analysis leaves us with an emission line to which we
can assign a high probability, ![]() ,
for being set apart from the noise along the lines of the LRT presented
in the previous section. Now we ask for the probability of finding an
emission line with the same significance in any of the time intervals
of length t - let there be an integer number
,
for being set apart from the noise along the lines of the LRT presented
in the previous section. Now we ask for the probability of finding an
emission line with the same significance in any of the time intervals
of length t - let there be an integer number
![]() - contained in our observation under the assumption that no emission line is present.
- contained in our observation under the assumption that no emission line is present.
This set-up can be interpreted as a ``Bernoulli experiment'' with its
probability of success given by the probability for a spurious
detection,
![]() .
Therefore, the chance,
.
Therefore, the chance, ![]() ,
to obtain one (or more) such emission line(s) from the analysis of any of the N subintervals by pure chance amounts to
,
to obtain one (or more) such emission line(s) from the analysis of any of the N subintervals by pure chance amounts to
which must be interpreted as the ``true'' significance of our detection.
The main restriction above is that the source may only be slightly
variable. While this assumption is essential for interpretation as a
Bernoulli experiment, it is known to be invalid for many X-ray
sources. For example a strong flare may provide the majority of
the source photons and also Fe K![]() I line photons, while still being short. In such a case, Eq. (10)
no longer provides a meaningful estimate of the significance.
To obtain a meaningful number in these cases, we propose to use
I line photons, while still being short. In such a case, Eq. (10)
no longer provides a meaningful estimate of the significance.
To obtain a meaningful number in these cases, we propose to use
![]() in Eq. (10), where
in Eq. (10), where
![]() is the total number of observed source photons in an appropriate band and
is the total number of observed source photons in an appropriate band and
![]() is the number of photons in the interval under consideration.
is the number of photons in the interval under consideration.
If the source is constant both approaches are equivalent and mathematically correct. In the case of a variable source, none of the above approaches is strictly correct. Nonetheless, we use Eq. (10) to obtain significance estimators, accounting for the choice of a particular fraction of the data.
4 Data analysis
The Orion Nebular Cloud is among the best-studied star-forming
regions. In particular, it was the target of a large Chandra program aimed at uncovering the X-ray properties of young stars - the Chandra Orion Ultra Deep Project
(COUP). The COUP campaign consists of six consecutive observations of
Orion providing a total observation time of
![]() ks distributed over nearly 13 days, which corresponds to a time coverage fraction of
ks distributed over nearly 13 days, which corresponds to a time coverage fraction of
![]() %.
%.
Table 1: The COUP observations.
In Table 1 we summarize the basic information on the COUP observations and refer the reader to Getman et al. (2005) for a more detailed discussion. The last column in Table 1 gives the identifier we use throughout this work to refer to the individual observations.
4.1 Defining the search sample
The entire COUP source sample comprises 1616 X-ray sources (Getman et al. 2005). From these sources, we extracted the subsample used in our search for the fluorescent Fe K![]() I line.
Since the line has a fixed energy of 6.4 keV, it is advisable
to only include those sources that show a sufficient number of counts
in an appropriate energy interval around 6.4 keV. In our
analysis we used only sources with more than 30 counts in the
``emission-band'' (6.2-6.5 keV). In particular, we iterated
through the sources presented by Getman et al. (2005),
extracted the source counts in the emission band, corrected them for
the PSF coverage of our extraction region, and included the source
when our search criterion was matched. For the weakest source
included in the sample of Tsujimoto et al. (2005) (COUP 649), we find 31 emission band photons, making our sample include the Tsujimoto et al. sources as a subsample.
I line.
Since the line has a fixed energy of 6.4 keV, it is advisable
to only include those sources that show a sufficient number of counts
in an appropriate energy interval around 6.4 keV. In our
analysis we used only sources with more than 30 counts in the
``emission-band'' (6.2-6.5 keV). In particular, we iterated
through the sources presented by Getman et al. (2005),
extracted the source counts in the emission band, corrected them for
the PSF coverage of our extraction region, and included the source
when our search criterion was matched. For the weakest source
included in the sample of Tsujimoto et al. (2005) (COUP 649), we find 31 emission band photons, making our sample include the Tsujimoto et al. sources as a subsample.
Our final sample comprises a total of 108 COUP sources, which
provide the the most promising candidates for our search for
fluorescent emission. For our purpose, COUP 123 and COUP 124
can be treated as a single source, because they are too close to be
resolved (1.4 arcsec,
![]() arcmin
off-axis). Their spectrum is appropriately described by a single
temperature thermal model, which indicates that both may, indeed, refer
to the same X-ray source. Additionally, we had to exclude COUP 90
and COUP 828 from our sample, because they are located on chip
edges, which prevented us from obtaining appropriate spectra
(CIAO 4.1), so that the sample size reduces to 106 COUP
sources.
arcmin
off-axis). Their spectrum is appropriately described by a single
temperature thermal model, which indicates that both may, indeed, refer
to the same X-ray source. Additionally, we had to exclude COUP 90
and COUP 828 from our sample, because they are located on chip
edges, which prevented us from obtaining appropriate spectra
(CIAO 4.1), so that the sample size reduces to 106 COUP
sources.
4.2 Extraction regions and pile-up
For most of our sources we used circular extraction regions covering the entire source. Our search sample necessarily contained the most X-ray luminous sources in the COUP field, which may suffer from severe pile-up. To avoid a strong pile-up effect, we used annulus shaped extraction regions in 29 cases. Whether pile-up becomes severe depends not only on the source count rate, but also on its temporal behavior and positioning on the detector. We chose the annulus parameters in accordance with these considerations and note whenever an annulus shaped region was used for extraction.
4.3 A standard analysis
Our search sample consists of 106 sources. To achieve a homogeneous scan for the fluorescent Fe K![]() I line,
they should be treated with standard criteria, eliminating biases
arising from individual, subjective choices during the analysis.
I line,
they should be treated with standard criteria, eliminating biases
arising from individual, subjective choices during the analysis.
4.3.1 Bayesian block analysis of the broad-band light curves
A key ingredient in the LLC method is determining of the correct continuum ratio. The observed count rate for individual X-ray sources can vary by orders of magnitude during the COUP campaign. Although the continuum ratio is relatively robust against temperature variations (see Sect. 2.3), it is advisable to distinguish between periods of different count rate regimes, possibly indicating different source spectra and continuum ratios. Of course a transition between different spectra may not always be accompanied by a count rate change, but we neglect this possibility here.
Our count rate analysis is based on the broad-band (2-9 keV) light curve. To separate the entire campaign data of individual sources into intervals with comparable count rate, we applied the concept of ``Bayesian blocks'' elaborated by Scargle (1998). The method of Bayesian blocks ``converts raw photon counts into the most probable piecewise constant representation of brightness as a function of time'' (Scargle 1998).
We applied an iterative algorithm to find individual change points in the light curves. According to Scargle (1998), this does not represent the exact mathematical treatment of the problem, but, nonetheless, yields comparable results. As pointed out by Scargle, an appropriate condition must be found to stop the iteration before segmenting the data set excessively. Instead of applying the Bayes factor (Eq. (48) in Scargle 1998) and a prior, we used the likelihood ratio, which can be easily calculated, to decide whether to introduce a change point or not.
As the continuum ratio only weakly depends on the spectral temperature, we aimed at a coarse segmentation of the light curves in order to separate periods between which the spectrum of the associated source may significantly differ and with it the continuum ratio. To introduce a change point, we demanded no less than 100 counts per block, a minimum block length of 20 ks, and a value of the LRT statistics over 100.
With this method we separated the 106 source light curves into 419 intervals with comparable count rates, and proceeded by generating spectra for every individual source and block, which can be used to determine the corresponding continuum ratio.
4.3.2 Automated model fits
For our analysis we used both thermal and power-law models,
for which we set up automated fit procedures using XSPEC. The fits
of the thermal model are based on the 0.3-9 keV energy band.
As a basis for our fits, we used an absorbed two-temperature APEC
(e.g. Smith et al. 2001) model extended by an emission line representing the fluorescent Fe K![]() I line
at 6.4 keV. Additionally, we allowed for emission lines at various
other energies, which are later used to substantiate our results. The
nominal intrinsic width of all lines is 0 eV. All element
abundances but that of iron were treated as a single fit-parameter,
which was also shared among the two thermal components.
In contrast, the iron abundance represents an independent
fit-parameter in both thermal components.
I line
at 6.4 keV. Additionally, we allowed for emission lines at various
other energies, which are later used to substantiate our results. The
nominal intrinsic width of all lines is 0 eV. All element
abundances but that of iron were treated as a single fit-parameter,
which was also shared among the two thermal components.
In contrast, the iron abundance represents an independent
fit-parameter in both thermal components.
Starting a fit process with unfavorable initial conditions can easily lead to unphysical results, even if the fit converges appropriately. Therefore, the process must be set up carefully to avoid converging to unrealistic solutions. Our approach is the following. We start using only one of the two available thermal components and then add in the second. If the enhancement in C-statistics exceeds 6.4 by introducing the later component, this solution is kept, otherwise the one temperature solution is used. The value of 6.4 corresponds to the 90% cut-off in a likelihood ratio test comparing models that differ by 3 degrees of freedom, which are temperature, iron abundance, and normalization here. The numerical equality with the fluorescent line energy is purely accidental.
Furthermore, we apply a number of restrictions to the temperatures and abundances to avoid unphysical solutions. If the temperature of any thermal component exceeds 8 keV, we fix it at 8 keV and reiterate the fit, because temperatures beyond this limit can hardly be resolved in Chandra ACIS I spectra. If one of the iron abundances exceeds 10 times the solar value, it is fixed to the value of the global abundance pattern, because it is usually not constrained well in this case. Similarly, the global abundances are fixed at solar values, if the fit result exceeds 10 times the solar value.
After an acceptable solution was found, we obtained fluxes and equivalent widths for the fluorescent line and the comparison line on the basis of these fits. Finally, the fits were used to derive the continuum ratio for the Bayesian block under consideration. In the same vein, effective area and absorption were automatically accounted for in its derivation.
To complement the results of the thermal model, we also adapted
an absorbed power-law model using only the high energy tail
(3-9 keV band) of the spectra. This model was extended by narrow
emission lines accounting for the Fe K![]() I line
at 6.4 keV and the hot iron line complex at 6.7 keV. The
results of these fits are particularly interesting as they yield the EW of the hot iron line complex, and they provide means to check whether the adaption of the thermal model failed.
I line
at 6.4 keV and the hot iron line complex at 6.7 keV. The
results of these fits are particularly interesting as they yield the EW of the hot iron line complex, and they provide means to check whether the adaption of the thermal model failed.
4.3.3 Line light curve analysis
As soon as the continuum ratios are determined, the LLC and the CLLC can be calculated. According to our reasoning, periods of bona fide fluorescent emission are characterized by an increase in the CLLC. Taking an impartial position, the morphology of the increase is unknown. We can neither say on what time scales the CLLC typically evolves, nor say whether the rise is continuous or not, nor even whether it is correlated with the soft X-ray continuum.
In our search for candidate intervals, we first exclude those
sources that do not show a larger CLLC excess than the expected one
(cf. Eq. (7)).
For each remaining source, we search all conceivable connected
intervals longer than 20 ks for the largest relative excess in
fluorescent photons. About 4000 of such intervals can be
constructed considering that we have 89 bins of
![]() ks length each. For each of these conceivable intervals, we calculate the quantity
ks length each. For each of these conceivable intervals, we calculate the quantity
![]() defined by
defined by
where i is an index running over all light curve bins in the interval,
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8.5cm,clip]{14706fg3.p...
...degraphics[angle=-90,width=8.5cm,clip]{14706fg9.ps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg72.png)
|
Figure 3: Panel A) to G): light curves for the objects reported on by Tsujimoto et al. (2005). The time axis refers to the begin of the COUP campaign (MJD 52 647.87). Upper panel: broad-band (2-9 keV) light curve (BBLC). Lower panel: the cumulated LLC (CLLC) and an estimate of its width (gray shaded, see Eq. (7)). Vertical separators mark change points associated with a shift of the activity level (determined by the Bayesian block analysis of the BBLC). |
| Open with DEXTER | |
The most promising candidate interval is the one with the highest
![]() value. Nevertheless, as every source will contain one such interval, we have to choose a reasonable limit for
value. Nevertheless, as every source will contain one such interval, we have to choose a reasonable limit for
![]() ;
only beyond this limit intervals shall valid candidate intervals be
considered. Replacing the Poisson distributions by normal
distributions, it may be shown that
;
only beyond this limit intervals shall valid candidate intervals be
considered. Replacing the Poisson distributions by normal
distributions, it may be shown that
![]() approximately follows a standard normal distribution. Therefore, the probability that
approximately follows a standard normal distribution. Therefore, the probability that
![]() exceeds a limit, L, becomes
exceeds a limit, L, becomes

|
(12) |
where n is the number of intervals for which
Following this approach, we found candidate intervals in 25 of
our sample sources, and we proceeded by extracting the associated
spectra. We then applied the same automated thermal fits as above to
find a spectral model. On the basis of this model, we calculated the
significance of the fluorescent Fe K![]() I line in the interval using Eq. (9) and applied Eq. (10) to account for our interval choice. We evaluated Eq. (10)
using both definitions of the number of repetitions in the Bernoulli
experiment, i.e., interval length and the number of enclosed
photons. The maximum of both results was than used as a significance
estimator. We prefer the maximum to the more conservative minimum here,
because the latter would necessarily underestimate the significance
during a flare, which is typically short but intense. We also note that
the application of Eq. (10)
is no longer fully justified here, because the ``experiments'' are not
fully independent when a distinguished interval is chosen in advance.
Nonetheless, the number is used as an estimate.
I line in the interval using Eq. (9) and applied Eq. (10) to account for our interval choice. We evaluated Eq. (10)
using both definitions of the number of repetitions in the Bernoulli
experiment, i.e., interval length and the number of enclosed
photons. The maximum of both results was than used as a significance
estimator. We prefer the maximum to the more conservative minimum here,
because the latter would necessarily underestimate the significance
during a flare, which is typically short but intense. We also note that
the application of Eq. (10)
is no longer fully justified here, because the ``experiments'' are not
fully independent when a distinguished interval is chosen in advance.
Nonetheless, the number is used as an estimate.
In Table 2 we list those sources with a line detection at a significance level of ![]() %. Our sample comprises 23 sources including 6 sources already reported on by Tsujimoto et al. (2005).
We excluded COUP 554 from the list, because a correct analysis of
this source was impeded by pile-up. When consulting the 95% limit,
we estimate that 1-2 detection given in Table 2 must be attributed to noise. Considering the difficulties in defining the true significance of the Fe K
%. Our sample comprises 23 sources including 6 sources already reported on by Tsujimoto et al. (2005).
We excluded COUP 554 from the list, because a correct analysis of
this source was impeded by pile-up. When consulting the 95% limit,
we estimate that 1-2 detection given in Table 2 must be attributed to noise. Considering the difficulties in defining the true significance of the Fe K![]() I line
in this temporally resolved analysis, we note that also accepting
3-4 spurious detections, does not seriously alter the outcome of
the analysis.
I line
in this temporally resolved analysis, we note that also accepting
3-4 spurious detections, does not seriously alter the outcome of
the analysis.
Table 2: Most promising intervals for fluorescent emission and basic fit results.
5 Discussion
This section starts with a presentation of individual sources,
proceeds with an analysis of several sample properties, and finally
closes with a discussion of the physical scenario of Fe K![]() I line creation in light of our results.
I line creation in light of our results.
5.1 Previously known COUP sources with fluorescent emission
Tsujimoto et al. (2005) present a sample of 7 COUP sources (COUP sequence numbers 331, 561, 621, 647, 649, 1030, and 1040) with a detection of fluorescent emission. The authors, however, did not carry out time-resolved spectroscopy, but used time-averaged spectra. Below we present the outcomes obtained for the Tsujimoto et al. sources to demonstrate the techniques developed so far. In the following, values given in parentheses refer to the 90% confidence range for the given parameter.
5.1.1 COUP 331 - V 1486 Ori
This source was already discussed in detail in a previous publication by Czesla & Schmitt (2007).
V 1486 Ori shows two major flare events during the COUP
campaign. The first, rather short one, takes place towards the end
of O1 (``Flare I'' in Czesla & Schmitt 2007), and no significant fluorescent Fe K![]() I line emission was detected here. In Fig. 3
(panel A) we show the broad-band light curve, the change points
returned by the Bayesian analysis, and the resulting CLLC. The first
flare is not accompanied by a considerable excess in the CLLC. The
spectrum is well-fitted by an absorbed thermal model with a strong
(hot) iron line complex at
I line emission was detected here. In Fig. 3
(panel A) we show the broad-band light curve, the change points
returned by the Bayesian analysis, and the resulting CLLC. The first
flare is not accompanied by a considerable excess in the CLLC. The
spectrum is well-fitted by an absorbed thermal model with a strong
(hot) iron line complex at
![]() keV.
keV.
The CLLC clearly indicates that the fluorescent Fe K![]() I line
emission is present during the rise phase of a second, more violent
flare ignited during O6, which is in line with previous findings (Czesla & Schmitt 2007). The automated search for intervals with fluorescent Fe K
I line
emission is present during the rise phase of a second, more violent
flare ignited during O6, which is in line with previous findings (Czesla & Schmitt 2007). The automated search for intervals with fluorescent Fe K![]() I emission returned the
1080-1110 ks period (cf. Table 2) as the most promising candidate interval. In Fig. 4
we present the LLC and the spectrum for the corresponding part of the
observation. The LLC clearly shows the concentration of Fe K
I emission returned the
1080-1110 ks period (cf. Table 2) as the most promising candidate interval. In Fig. 4
we present the LLC and the spectrum for the corresponding part of the
observation. The LLC clearly shows the concentration of Fe K![]() I line emission in the rise phase of the flare, and the spectral analysis yields an EW of
1440(960-1930) eV for the line.
I line emission in the rise phase of the flare, and the spectral analysis yields an EW of
1440(960-1930) eV for the line.
| Figure 4: Left: LLC and (scaled) broad-band light curve (2.5 ks binning) for COUP 331 (O6). Right: excerpt of the spectrum (corresponding to the gray-shaded time span in the left panel). Both a model with and one without extra line emission are indicated. |
|
| Open with DEXTER | |
The measured EW of this Fe K![]() I line exceeds typical model predictions (see Sect. 6)
by an order of magnitude, so it is particularly interesting.
A more detailed discussion about the origin of this Fe K
I line exceeds typical model predictions (see Sect. 6)
by an order of magnitude, so it is particularly interesting.
A more detailed discussion about the origin of this Fe K![]() I line is given later in Sect. 6.3.
I line is given later in Sect. 6.3.
5.1.2 COUP 561
Figure 3B shows the results of our light curve analysis for COUP 561. The CLLC shows two phases of increase. During the second COUP observation, as in the longest part of the COUP campaign, COUP 561 is encountered in a quiescent state to judge from the BBLC. Nonetheless, the CLLC indicates about 10 excess photons in the emission band.
| Figure 5:
Left panel: the LLC and the broad-band light curve (both
10 ks binning) of COUP 561. The latter is scaled to show the
same maximal count rate as the LLC. The gray-shaded area denotes the
time span for which an excerpt of the spectrum is shown in the right panel.
There we show the X-ray spectrum around 6.4 keV and indicate both
a thermal model with and one without excess emission at the energy of
the fluorescent Fe K |
|
| Open with DEXTER | |
In Fig. 5 (left panel) we show the LLC pertaining the first half of the COUP campaign and the most promising candidate interval (100-414 ks) for fluorescent emission. In the right panel we plot the spectrum obtained for this interval, which shows a fluorescent line with an EW of 570(280-910) eV. The hot iron-line complex is virtually absent.
During the flare in the following observation, the CLLC indicates
another increase of about 10 photons. This number is confirmed by
a spectral analysis of the associated span (504-544 ks), where we
find an Fe K![]() I line with an EW of
132(12-270) eV. Because of the larger flare continuum, the line is
much less prominent here, and with 96% it is also much less
significant.
I line with an EW of
132(12-270) eV. Because of the larger flare continuum, the line is
much less prominent here, and with 96% it is also much less
significant.
5.1.3 COUP 621
The outcome of the light curve analysis for COUP 621 is shown in Fig. 3C.
COUP 621 shows two flares with the first one fully covered by the
observation (except for a probably small fraction of the rise-phase)
and the second one remaining unobserved for
![]() ks
of its central phase. None of these flares is accompanied by a CLLC
excess. The CLLC shows an increase that is not associated with one of
the flares, but instead emerges during a period of quiescence to judge
from the BBLC.
ks
of its central phase. None of these flares is accompanied by a CLLC
excess. The CLLC shows an increase that is not associated with one of
the flares, but instead emerges during a period of quiescence to judge
from the BBLC.
| Figure 6: COUP 621, as in Fig. 5. |
|
| Open with DEXTER | |
In Fig. 6 we show the LLC corresponding to O2 and O3 in the left panel where we also indicate the most promising interval (cf. Table 2). In the right panel we show the associated spectrum. Excess emission at the location of the fluorescent line is prominent with a line EW of 600(310-970) eV, and the hot iron line complex is weak compared to it.
This case is special because two flares detected in soft X-rays are not accompanied by fluorescent Fe K![]() I line
emission, while there is a line detection during a period preceding the
first flare. The line emission may be attributed to a hidden flare
located at a geometrically quite favorable position. At least it
must be attributed to an event that does not show up in soft X-rays.
I line
emission, while there is a line detection during a period preceding the
first flare. The line emission may be attributed to a hidden flare
located at a geometrically quite favorable position. At least it
must be attributed to an event that does not show up in soft X-rays.
5.1.4 COUP 647
Among the sources analyzed by Tsujimoto et al., COUP 647 is by far the most deeply embedded one with a hydrogen column density of
![]()
![]() 1022 cm-2.
The CLLC shows two phases of increase. One associated with a flare
towards the end of the COUP campaign and another one earlier in a
presumably quiescent phase of the source (see Fig. 3D).
Our automated CLLC analysis returns the first phase, in particular the
50-626 ks interval, as the most promising candidate interval,
for which we show the spectrum in the left hand panel of Fig. 7. The EW of the line in this phase is
440(194-767) eV. Additionally, we show the spectrum of the flare during which the line shows up with an EW of
150(10-300) eV.
1022 cm-2.
The CLLC shows two phases of increase. One associated with a flare
towards the end of the COUP campaign and another one earlier in a
presumably quiescent phase of the source (see Fig. 3D).
Our automated CLLC analysis returns the first phase, in particular the
50-626 ks interval, as the most promising candidate interval,
for which we show the spectrum in the left hand panel of Fig. 7. The EW of the line in this phase is
440(194-767) eV. Additionally, we show the spectrum of the flare during which the line shows up with an EW of
150(10-300) eV.
| Figure 7: Left panel: excerpt of the spectrum during the bona fide quiescent phase of COUP 647. Right panel: the same part of the spectrum during the flare. |
|
| Open with DEXTER | |
5.1.5 COUP 649
Among the sources of fluorescent emission reported on by Tsujimoto et al. (2005), COUP 649 is the one with the weakest Fe K![]() I line. Figure 3E
shows the BBLC and the associated CLLC. The source signal is dominated
by a single flare, beyond which the source is virtually invisible. This
source was rejected by our automated analysis, because the determined
excess is not sufficient
to fulfill our criteria. The light curve of COUP 649 shows rapid
variability where the source is visible, and we speculate that this
impedes an appropriate light curve analysis.
I line. Figure 3E
shows the BBLC and the associated CLLC. The source signal is dominated
by a single flare, beyond which the source is virtually invisible. This
source was rejected by our automated analysis, because the determined
excess is not sufficient
to fulfill our criteria. The light curve of COUP 649 shows rapid
variability where the source is visible, and we speculate that this
impedes an appropriate light curve analysis.
In a spectral analysis of the flare, however, we find a fluorescent emission with an EW of
![]() eV, compatible with the results given by Tsujimoto et al. (2005). In this case, the EW is not affected by time averaging, because only the flare contributes signal.
eV, compatible with the results given by Tsujimoto et al. (2005). In this case, the EW is not affected by time averaging, because only the flare contributes signal.
5.1.6 COUP 1030
Figure 3F shows the light curves pertaining to COUP 1030. A flare occurs in O4, and we find that the source is piled-up in this state. In the following analysis we, therefore, revert to an annulus-shaped source region neglecting the innermost 0.6 arcsec.
| Figure 8: COUP 1030, as in Fig. 5. |
|
| Open with DEXTER | |
The automated CLLC analysis yields the 206-716 ks interval as the most promising for detecting fluorescent Fe K![]() I emission.
This interval covers the flare, which, according to the CLLC, provides
the largest contribution of fluorescent photons. In the right hand
panel of Fig. 8, we show
the spectrum of COUP 1030 during the most promising interval, and
our spectral analysis shows a fluorescent line with an EW of
143(56-231) eV. The result is compatible with the values given by Tsujimoto et al. (2005), and time averaging has no effect on the EW
if the signal is strongly concentrated in a single flare. This source
appears much like a ``text book'' example of fluorescent emission
originating from photoionization both with respect to temporal behavior
and EW.
I emission.
This interval covers the flare, which, according to the CLLC, provides
the largest contribution of fluorescent photons. In the right hand
panel of Fig. 8, we show
the spectrum of COUP 1030 during the most promising interval, and
our spectral analysis shows a fluorescent line with an EW of
143(56-231) eV. The result is compatible with the values given by Tsujimoto et al. (2005), and time averaging has no effect on the EW
if the signal is strongly concentrated in a single flare. This source
appears much like a ``text book'' example of fluorescent emission
originating from photoionization both with respect to temporal behavior
and EW.
5.1.7 COUP 1040
COUP 1040 remains virtually invisible in the >6.2 keV band, except for a flare period during O2. Figure 3G shows the light curves. The LLC indicates fluorescent emission accompanying a flare. There is a steep rise in a short (
![]() ks)
interval in the central flare, and the CLLC continues to rise during
the decay phase. Our automated analysis determines an interval
containing the decay phase (266-544 ks) of the flare to be the
most promising candidate interval to be searched for fluorescent
Fe K
ks)
interval in the central flare, and the CLLC continues to rise during
the decay phase. Our automated analysis determines an interval
containing the decay phase (266-544 ks) of the flare to be the
most promising candidate interval to be searched for fluorescent
Fe K![]() I emission. In Fig. 9
(left panel) we show the spectrum pertaining to this interval. Indeed,
there may be excess emission at 6.4 keV; however,
the continuum in the 5.2-6.2 keV range is not well fitted by
the model, so that the CLLC may be misleading in this case.
I emission. In Fig. 9
(left panel) we show the spectrum pertaining to this interval. Indeed,
there may be excess emission at 6.4 keV; however,
the continuum in the 5.2-6.2 keV range is not well fitted by
the model, so that the CLLC may be misleading in this case.
| Figure 9: Left panel: the spectrum during the automatically determined, most promising fluorescent interval of COUP 1040. Right panel: the spectrum during the second COUP observation (O2). |
|
| Open with DEXTER | |
The right hand panel of Fig. 9
shows the spectrum during the O2, which covers the flare and its
decay phase. The signal is much stronger here, and the fluorescent line
is detectable. While the line flux of
11(6-20) ![]() 10-7 ph (cm2 s)-1 is considerably higher than the value reported by Tsujimoto et al. (2005), our EW of
178(90-310) eV is compatible with their result, as it remains
unchanged by time averaging if no further signal is accumulated.
10-7 ph (cm2 s)-1 is considerably higher than the value reported by Tsujimoto et al. (2005), our EW of
178(90-310) eV is compatible with their result, as it remains
unchanged by time averaging if no further signal is accumulated.
5.2 Three individual sources with distinct behavior
In the following section we present three additional individual
sources with a detection of fluorescent emission. The sources show
three different types of temporal behavior of the Fe K![]() I line, and further demonstrate the variety of Fe K
I line, and further demonstrate the variety of Fe K![]() I line emitters.
I line emitters.
5.2.1 COUP 267
The X-ray spectrum of COUP 267 shows the characteristics of a ``two-absorber X-ray source'' (TAX source, e.g., Güdel et al. 2007), with a mildly absorbed soft component dominating below about 1 keV and a hard component hidden behind a significantly higher column of material. During the leading 100 ks of COUP campaign data, COUP 267 shows a flare (see Fig. 10, upper panel). A comparison of the soft (0.3-1.2 keV) light curve and its hard counterpart (1.2-9.0 keV) uncovers that the flare exclusively affects the hard band.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg22.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg23.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg93.png)
|
Figure 10:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 267. Lower panel: the spectrum during the 30-196 ks interval with a close-up of the Fe K |
| Open with DEXTER | |
In Fig. 10 we show the light curves and the spectrum of COUP 267 during the 30-196 ks time span selected by our automatic search for fluorescence, which basically covers the decay phase of the flare. The EW of the fluorescent line amounts to 400(180-670) eV here. The two differently absorbed thermal components can be clearly distinguished in the spectral model, and excess emission at the energy of the fluorescent line is visible. The upper right hand box in Fig. 10 shows a close-up of this region, where the best-fit line is also indicated.
The TAX nature of this source implies a considerable amount of circumstellar material surrounding the central star, where fluorescent emission may well have its origin. Although the measured EW appears higher than the model predictions (see Sect. 6), the fluorescent emission is associated with the flare, and we conclude that photoionization provides a reasonable explanation for the observation.
5.2.2 COUP 599
The strength of the X-ray source COUP 599 remains constant through the entire COUP campaign as demonstrated by the light curve shown in Fig. 11. The CLLC rises almost without interruption. Accordingly, the most promising fluorescent interval found in our automated search comprises almost all data.
In the lower panel of Fig. 11, we show the spectrum of the source in the 10-1080 ks interval. There is excess emission at 6.4 keV, which we attribute to the fluorescent line, and we determine an EW of 450(220-660) eV for it. The position of COUP 599 is about 1 arcsec northwest of the Becklin-Neugebauer object (Becklin & Neugebauer 1967), and as already noted by Garmire et al. (2000) in a pre-COUP study, the X-ray source may be related to it, although an independent origin cannot be excluded.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg24.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg25.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg94.png)
|
Figure 11:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 599. Lower panel: the spectrum in the 10-1080 ks interval and a close-up of the Fe K |
| Open with DEXTER | |
The X-ray luminosity of this source is constant and so is its Fe K![]() I line flux. Again, the EW is higher than typical values derived by Drake et al. (2008), but the strong absorption with a column density of
I line flux. Again, the EW is higher than typical values derived by Drake et al. (2008), but the strong absorption with a column density of
![]()
![]() 1022 H cm-2, points towards the presence of circumstellar material, which could yield quite favorable geometry.
1022 H cm-2, points towards the presence of circumstellar material, which could yield quite favorable geometry.
5.2.3 COUP 1499, V NX Ori
While V NX Ori is found in quiescence for the longest part of
the COUP campaign, it also shows a period of remarkable activity.
This begins with a very short flare taking place towards the end of the
second observation. Here, the count rate skyrockets to about
40 c ks-1 (2-9 keV band) within 2 ks and then decays quickly, so that the entire event does not last for more than
![]() ks.
ks.
The next observation starts with another short flare that shades into a long-lasting, possibly related flare event. In Fig. 12 we show the spectrum during the 384-524 ks time span found by our automated analysis (see Table 2), which approximately covers the second, long-lasting flare.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg26.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg27.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg97.png)
|
Figure 12:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 1499. Lower panel: the spectrum in the 384-524 ks interval and a close-up of the Fe K |
| Open with DEXTER | |
While the CLLC does not indicate fluorescent emission during the first, short, and more violent event, it does during the longer flare. The associated spectrum demonstrates line emission for which we measure an EW of 370(145-630) eV.
5.3 Consequences of temporal resolution on the Fe K I line equivalent widths
I line equivalent widths
In the preceding passages we demonstrated the temporal behavior of the Fe K![]() I line for a number of sources including those presented by Tsujimoto et al. (2005). The EW of the Fe K
I line for a number of sources including those presented by Tsujimoto et al. (2005). The EW of the Fe K![]() I line
is often used to check whether the observations can be reconciled with
predictions from theory. Therefore, it is worth briefly discussing
the effects of the time resolution on this quantity.
I line
is often used to check whether the observations can be reconciled with
predictions from theory. Therefore, it is worth briefly discussing
the effects of the time resolution on this quantity.
In sources where one major flare provides the majority of all source photons, including Fe K![]() I line
photons, such as COUP 649 and COUP 1030, time averaging over
a wider span has no effect on the calculated EW, because line
and continuum emission are both scaled by the same factor.
It does, however, have an effect on the measured fluxes, which are
then too low.
I line
photons, such as COUP 649 and COUP 1030, time averaging over
a wider span has no effect on the calculated EW, because line
and continuum emission are both scaled by the same factor.
It does, however, have an effect on the measured fluxes, which are
then too low.
The measured EW will be too low if the quiescent
phases, which are usually much longer than active periods, or several
flares contribute a significant amount of flux, as for instance in
COUP 331 and COUP 621. In these cases, continuum signal
is accumulated, which, afterwards, is compared to the Fe K![]() I line signal being collected during a shorter period. Here, both the measured average Fe K
I line signal being collected during a shorter period. Here, both the measured average Fe K![]() I line flux and the associated EW will be lower than values determined for appropriate time spans.
I line flux and the associated EW will be lower than values determined for appropriate time spans.
As it is impossible to accumulate negative signal in the Fe K![]() I line
or the underlying continuum, maybe with the exception of background and
statistical fluctuations, the time-averaged values can be regarded as a
lower limit on both the Fe K
I line
or the underlying continuum, maybe with the exception of background and
statistical fluctuations, the time-averaged values can be regarded as a
lower limit on both the Fe K![]() I line flux and EW.
I line flux and EW.
5.4 Combined excess emission
In the previous sections, we have presented a sample of sources with
excess emission at 6.4 keV, which we attribute to the fluorescent
Fe K![]() I line. In this section we combine a larger amount of data to further corroborate this statement.
I line. In this section we combine a larger amount of data to further corroborate this statement.
In Fig. 13 we show the summed residuals corresponding to all intervals listed in Table 2 in the upper panel and, in the lower one, the summed residuals for all sources showing no fluorescent emission according to our analysis. For each spectrum we determined the residuals by subtracting the best-fit model from the observed data and added up the individual results. We prefer this approach to adding up the individual spectra themselves, because these differ significantly from each other both in flux level and spectral shape. The residuals already account for the differences in spectral shape, and the contribution of spectra with more photons grows with the square root of the photon number, and not linearly as would be the case otherwise.
An emission line feature, which is not accounted for in the models but present in some or all of the spectra, should lead to an accumulation of residual photons at the respective energy. In Fig. 13 we show the result using the residuals with respect to the thermal model (cf. Sect. 4.3) and a power-law model extended by a Gaussian line of variable width (but <0.1 keV) and normalization at a fixed energy of 6.7 keV to account for the hot iron lines.
In both cases, an excess at 6.4 keV can be clearly
identified. We find that this excess is represented well by a Gaussian
centered at 6.4 keV. The best-fit width of the Gaussian is
100 eV, which is consistent with an intrinsically narrow,
instrumentally broadened line
at the location of the fluorescent Fe K![]() I line.
Leaving the central energy as a free fit-parameter does not alter this
result. Depending on the considered energy range for adapting the
Gaussian and on whether we allow an offset for the Gaussian line, we
find amplitudes of 300-400 photons. Therefore, we argue for the
presence of
I line.
Leaving the central energy as a free fit-parameter does not alter this
result. Depending on the considered energy range for adapting the
Gaussian and on whether we allow an offset for the Gaussian line, we
find amplitudes of 300-400 photons. Therefore, we argue for the
presence of
![]() excess photons, which can be attributed to the fluorescent Fe K
excess photons, which can be attributed to the fluorescent Fe K![]() I line in these spectra. This number can be converted into an average line EW of roughly 250 eV, which we find in good agreement with previous results.
I line in these spectra. This number can be converted into an average line EW of roughly 250 eV, which we find in good agreement with previous results.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{14706fg28.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg99.png)
|
Figure 13: The summed residuals from all bona-fide fluorescent intervals (panel a)) and the same for all sources not showing intervals with fluorescent emission (panel b)). Solid (black) line: the residuals with respect to thermal models, dashed (red) line: the residuals with respect to a power-law model with an additional hot iron line at 6.7 keV. |
| Open with DEXTER | |
Instead of collecting the residuals only from the periods of bona-fide
fluorescent emission, the collection can also be inverted to comprise
only data of those sources in which no Fe K![]() I line
emission was detected. Neither of the resulting curves, whether
calculated with respect to either the thermal or the power law-models,
shows a distinct feature at 6.4 keV (Fig. 13,
lower panel). The residuals collected from the thermal models show a
substructure indicating that the average spectral slope is too steep.
Such an effect is not present in the power-law models, which, however,
cover much less of the spectrum. After consulting the power-law fit
residuals, a small excess of
I line
emission was detected. Neither of the resulting curves, whether
calculated with respect to either the thermal or the power law-models,
shows a distinct feature at 6.4 keV (Fig. 13,
lower panel). The residuals collected from the thermal models show a
substructure indicating that the average spectral slope is too steep.
Such an effect is not present in the power-law models, which, however,
cover much less of the spectrum. After consulting the power-law fit
residuals, a small excess of
![]() photons
at 6.4 keV may still be present, but it is not clearly set apart
from the noise. We also find no surplus of negative residuals here as
would be expected, if we had only removed sources showing a
positive noise excess from the sample.
photons
at 6.4 keV may still be present, but it is not clearly set apart
from the noise. We also find no surplus of negative residuals here as
would be expected, if we had only removed sources showing a
positive noise excess from the sample.
5.5 Comparison features at different energies
For the following analysis, we revert to the Bayesian block data,
i.e., a subdivision made without paying special attention to
the presence or absence of the Fe K![]() I line,
even though this might be the case due to physical reasons. Starting
from the best-fit thermal model, we add a narrow emission line at
various energies between 5.5 keV and 6.7 keV. For each
Bayesian block, we record the best-fit line fluxes and EWs.
I line,
even though this might be the case due to physical reasons. Starting
from the best-fit thermal model, we add a narrow emission line at
various energies between 5.5 keV and 6.7 keV. For each
Bayesian block, we record the best-fit line fluxes and EWs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14706fg29.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg100.png)
|
Figure 14: Mean (solid line) and median (dashed line) flux for narrow emission line at various energies. |
| Open with DEXTER | |
In Fig. 14 we show
the mean and median line flux determined for the emission line,
shifting it from 5.5 keV to 6.7 keV in steps of 100 eV.
This set-up includes the actual Fe K![]() I line
at 6.4 keV as a special case. Both mean and median line flux are
>0 everywhere, since we demand an emission line. We do not expect
any strong features between 5.5 keV and 6.3 keV,
so that the results can be attributed to the photon noise.
I line
at 6.4 keV as a special case. Both mean and median line flux are
>0 everywhere, since we demand an emission line. We do not expect
any strong features between 5.5 keV and 6.3 keV,
so that the results can be attributed to the photon noise.
The mean line flux shown in Fig. 14 remains constant until the line energy exceeds 6.1 keV, after which the mean flux rises, reaches a maximum at 6.4 keV, and falls again. The decrease towards 6.7 keV happens because the thermal models include the hot iron lines. To assure that only a few high values do not dominate the plot, which is conceivable if the mean line flux is considered, we also give the median line flux, which is more stable against outliers. At a lower level, the median flux shows the same basic pattern with a maximum at 6.4 keV. The level shows that many values are close to zero, reflecting the cases in which an absorption line would formally yield a better fit.
At each line energy the statistic for the comparison line is
different, because it is affected by the spectral shape and the
effective area. Under the hypothesis that there is nothing special
about the Fe K![]() I line
energy, so that the majority of our detections should actually be
attributed to noise, the derived result is implausible. If this
hypothesis was to be accepted, there should be a gradual evolution of
the mean and median line fluxes over the entire range, which is indeed
the case until the line energy exceeds 6.1 keV, but not beyond.
I line
energy, so that the majority of our detections should actually be
attributed to noise, the derived result is implausible. If this
hypothesis was to be accepted, there should be a gradual evolution of
the mean and median line fluxes over the entire range, which is indeed
the case until the line energy exceeds 6.1 keV, but not beyond.
The findings summarized in Fig. 14
are compatible with an instrumentally broadened emission line at
6.4 keV, and we adduce that this is a corroboration of our
interpretation of the observed excess emission as fluorescent Fe K![]() I line emission, which is distinct from photon noise.
I line emission, which is distinct from photon noise.
5.6 Duty cycle of Fe K I line emission
I line emission
In Table 2 we list the sources and time spans that show significant Fe K![]() I line
emission according to our analysis. The table comprises
23 sources, with a total observation time of 23
I line
emission according to our analysis. The table comprises
23 sources, with a total observation time of 23 ![]() 838 ks
838 ks ![]() 19 000 ks. Summing up the interval lengths, we find that fluorescent emission is detected during
19 000 ks. Summing up the interval lengths, we find that fluorescent emission is detected during
![]() % of this time.
% of this time.
Using the entire sample of 106 sources as a reference, fluorescent emission is detectable during about 10% of the observation time, and it is distributed among 20% of the sample sources. This consideration only takes into account those sources in which fluorescent emission can be claimed with reasonable certainty. Based on the creation scenario for fluorescent emission, it seems likely that there are more fluorescent sources, yet a detection cannot be claimed where the signal remains insufficient. The duty cycle derived here should, therefore, be regarded as a minimum, limited by the sensitivity of the instrument and, of course, by our method.
6 Origin of the Fe K
 I line emission
I line emission
The reality of the fluorescent Fe K![]() I line
has so far been established in several stellar sources. While all
authors agree that neutral or weakly ionized iron gives rise to the
photons making up this spectral component, there is still some debate
whether nonthermal electrons contribute to the excitation of the iron
ions. In the following, we briefly juxtapose photoionization and
electron collisional excitation regarding the expected EWs and temporal behavior.
I line
has so far been established in several stellar sources. While all
authors agree that neutral or weakly ionized iron gives rise to the
photons making up this spectral component, there is still some debate
whether nonthermal electrons contribute to the excitation of the iron
ions. In the following, we briefly juxtapose photoionization and
electron collisional excitation regarding the expected EWs and temporal behavior.
6.1 Implications of photoionization
The fluorescent emission caused by photoionized neutral or weakly
ionized iron was investigated theoretically by a number of authors. Bai (1979) and Drake et al. (2008) carried out Monte Carlo calculations, simulating solar and stellar flares. George & Fabian (1991) simulated an accretion disk illuminated with a power-law spectrum approaching the situation in AGN sources. George & Fabian (1991) obtained typical EWs between 100-200 eV for a centrally illuminated disk using power-law photon-indices between
![]() .
The EWs obtained by Bai (1979) and Drake et al. (2008) for thermal input spectra tend be smaller, rarely exceeding 100 eV.
.
The EWs obtained by Bai (1979) and Drake et al. (2008) for thermal input spectra tend be smaller, rarely exceeding 100 eV.
While the above results refer to solar iron abundances of
![]()
![]() 10-5 Fe/H, the Fe K
10-5 Fe/H, the Fe K![]() I line EW caused by photoionized iron can be increased, when larger iron abundances are assumed (Drake et al. 2008). In an analysis of the correlation between iron abundance and Fe K
I line EW caused by photoionized iron can be increased, when larger iron abundances are assumed (Drake et al. 2008). In an analysis of the correlation between iron abundance and Fe K![]() I line EW, however, Ballantyne et al. (2002) found that the EW cannot be increased beyond any limit. As already indicated by Bai (1979) (Fig. 4) or Matt et al. (1997), the EW rises linearly for iron abundances close to or lower than the solar value, beyond which the relation flattens. According to Ballantyne et al. (2002), the maximal obtainable Fe K
I line EW, however, Ballantyne et al. (2002) found that the EW cannot be increased beyond any limit. As already indicated by Bai (1979) (Fig. 4) or Matt et al. (1997), the EW rises linearly for iron abundances close to or lower than the solar value, beyond which the relation flattens. According to Ballantyne et al. (2002), the maximal obtainable Fe K![]() I line EW is around 800 eV.
I line EW is around 800 eV.
The Fe K![]() I line EWs expected from photoionized iron is, thus,
I line EWs expected from photoionized iron is, thus,
![]() eV and may reach
eV and may reach
![]() eV under very favorable conditions. The light curve of the Fe K
eV under very favorable conditions. The light curve of the Fe K![]() I line
should be correlated with the light curve of the incident soft X-ray
continuum, but reverberation effects may be present. Assuming a typical
scale of 20 AU for the extent of a stellar source, delays,
if present, would be
I line
should be correlated with the light curve of the incident soft X-ray
continuum, but reverberation effects may be present. Assuming a typical
scale of 20 AU for the extent of a stellar source, delays,
if present, would be
![]() ks.
ks.
High Fe K![]() I line EWs
and a virtually unpredictable temporal behavior may be obtained,
if totally or partially hidden X-ray sources are considered,
as proposed by Drake et al. (2008).
The continuum emission by those sources can contribute to the
reprocessed photon field, but their direct continuum radiation remains
invisible, so that the measured Fe K
I line EWs
and a virtually unpredictable temporal behavior may be obtained,
if totally or partially hidden X-ray sources are considered,
as proposed by Drake et al. (2008).
The continuum emission by those sources can contribute to the
reprocessed photon field, but their direct continuum radiation remains
invisible, so that the measured Fe K![]() I line flux may be significant, providing a large EW, which appears to be uncorrelated with the measured continuum.
I line flux may be significant, providing a large EW, which appears to be uncorrelated with the measured continuum.
6.2 Electron collisional excitation
The subject of electron collisional excitation of the fluorescent Fe K![]() I line was, for example, investigated by Emslie et al. (1986). These authors calculated the Fe K
I line was, for example, investigated by Emslie et al. (1986). These authors calculated the Fe K![]() I line photon flux,
I line photon flux, ![]() ,
due to electron excitation, and the result is given in their
Eq. (12). In combination with their Eq. (7), the
relation can be recast and written as
,
due to electron excitation, and the result is given in their
Eq. (12). In combination with their Eq. (7), the
relation can be recast and written as
where
Assuming
![]() ,
,
![]()
![]() 10-5, E1 = 20 keV, and a distance of 450 pc, Eq. (13) can be partially evaluated as
10-5, E1 = 20 keV, and a distance of 450 pc, Eq. (13) can be partially evaluated as
where AF(>E1) is the incident energy flux in the form of electrons in erg s-1. Using Eq. (14) we derive that, for the typical Fe K
This number is enormous compared to solar values, where the total energy deposited in nonthermal electrons during a flare is of the order of 1032 erg. Even though flares in Orion YSOs may be ``several orders of magnitude more powerful than any solar flare'' (Getman et al. 2008), the energetics remain problematic. Using Eq. (17) from Saint-Hilaire & Benz (2005), we estimate the amount of thermal energy,
![]() ,
contained in the plasma of a large flare to be
,
contained in the plasma of a large flare to be
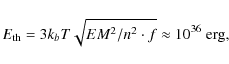
|
(15) |
assuming an emission measure of 1055 cm-3, a density of n=1012 cm-3, a temperature of kbT=10 keV, and a filling factor, f, of unity. In their analysis of RHESSI data of medium sized solar flares, Saint-Hilaire & Benz (2005) conclude that
As pointed out by Emslie et al. (1986), a contribution of electron induced fluorescent emission may be observed during the impulsive phase of a flare. The Fe K![]() I line
flux due to electron collisional excitation should be temporally
correlated with the hard X-ray flux, which was, indeed observed by Emslie et al. (1986). Such data are, however, not available for Orion, so that we cannot revert to this line of argumentation.
I line
flux due to electron collisional excitation should be temporally
correlated with the hard X-ray flux, which was, indeed observed by Emslie et al. (1986). Such data are, however, not available for Orion, so that we cannot revert to this line of argumentation.
Recently, Peterson et al. (2010)
presented high-resolution radio images of the Algol binary system
resolving a large coronal loop reaching from one to the other pole of
the K giant secondary, being orientated towards the primary
B star. The authors modeled the radio emission observed from this
loop by assuming synchrotron emission from an electron population with
a homogeneous density of
![]() electrons/cm-3 and a power-law spectrum so that
electrons/cm-3 and a power-law spectrum so that
![]() where
where
![]() keV. Assuming that the electrons are moving at the speed of light, we estimate an electron flux of roughly 3
keV. Assuming that the electrons are moving at the speed of light, we estimate an electron flux of roughly 3 ![]()
![]() = 3
= 3 ![]() 1013 electrons/cm-2. When also assuming a loop length of 1012 cm and a radius-to-loop length ratio of 0.1 (Favata et al. 2005), the electron flux over the entire loop cross section becomes
1013 electrons/cm-2. When also assuming a loop length of 1012 cm and a radius-to-loop length ratio of 0.1 (Favata et al. 2005), the electron flux over the entire loop cross section becomes
![]() electrons/cm2.
If we attribute an energy of 100 keV to all of these
electrons, the resulting energy flux in the form of energetic electrons
becomes 1028 erg s-1. Although this number is still far below the needed value, we note that Favata et al. (2005) find evidence of large magnetic loops with half lengths of
electrons/cm2.
If we attribute an energy of 100 keV to all of these
electrons, the resulting energy flux in the form of energetic electrons
becomes 1028 erg s-1. Although this number is still far below the needed value, we note that Favata et al. (2005) find evidence of large magnetic loops with half lengths of
![]() cm
in their analysis of large COUP flares, which may connect the stellar
photosphere with a disk. Although unable to give a detailed physical
modeling, we do not exclude that under certain conditions sufficient
fluxes of energetic electrons may be sustained in large magnetic
structures.
cm
in their analysis of large COUP flares, which may connect the stellar
photosphere with a disk. Although unable to give a detailed physical
modeling, we do not exclude that under certain conditions sufficient
fluxes of energetic electrons may be sustained in large magnetic
structures.
When a population of high-energy electrons hits a thick target
such as a stellar photosphere, the electrons thermalize in the plasma
and heat it. This gives rise to the evaporation of soft X-ray emitting
loops observed during solar and stellar flares. Inspired by their
findings, Giardino et al. (2007)
elaborate on a mechanism that can prevent a population of accelerated
electrons from causing a soft X-ray flare. Basically, the authors
suggest that, if the plasma density in the flux tube into which
the electrons are injected is high enough, the electrons do not
thermalize in the photosphere, but are decelerated in situ. During this
process, energy is deposited in nonthermal hard X-rays and collisional
excitation of heavier ions such as iron, potentially resulting in
Fe K![]() I line
photons. Appropriate conditions for this mechanism to work may, indeed,
be found in young stars with ongoing accretion.
I line
photons. Appropriate conditions for this mechanism to work may, indeed,
be found in young stars with ongoing accretion.
6.3 Putting our analysis into context
As outlined in Sect. 6, model calculations of the Fe K![]() I line strength based on photoionization rarely predict line EWs > 100 eV. Yet, the EWs listed in Table 2
tend to be significantly more than 100 eV, even though some may be
smaller considering the errors. The values reported in Table 2 are qualitatively compatible with the numbers published for Elias 29, for which Giardino et al. (2007) derive EWs of up to
I line strength based on photoionization rarely predict line EWs > 100 eV. Yet, the EWs listed in Table 2
tend to be significantly more than 100 eV, even though some may be
smaller considering the errors. The values reported in Table 2 are qualitatively compatible with the numbers published for Elias 29, for which Giardino et al. (2007) derive EWs of up to
![]() eV during their second time segment.
eV during their second time segment.
If photoionization is to be held responsible for the line emission, it must explain all of these observations: both the observed EW and the temporal behavior. Since the observed EWs tend to be higher than typical predictions, this issue should be addressed first. Drake et al. (2008) discuss four ways in which the Fe K![]() I line EW
may be raised. These are supersolar Fe abundances, disk flaring, a
contribution of electron collisional excitation, and line-of-sight
obscuration of the central flaring source. According to Drake et al. disk flaring, which increases the solid angle coverage of the reflector, can increase the expected EW by factors <2, and increasing the iron abundance leads to a roughly linear response of the line EW. EWs
on the order of 400 eV as in the majority of our detections, are,
therefore, within reach without reverting to extreme physical
conditions. Additionally, we note that obscuration of the X-ray source
does not only increase the Fe K
I line EW
may be raised. These are supersolar Fe abundances, disk flaring, a
contribution of electron collisional excitation, and line-of-sight
obscuration of the central flaring source. According to Drake et al. disk flaring, which increases the solid angle coverage of the reflector, can increase the expected EW by factors <2, and increasing the iron abundance leads to a roughly linear response of the line EW. EWs
on the order of 400 eV as in the majority of our detections, are,
therefore, within reach without reverting to extreme physical
conditions. Additionally, we note that obscuration of the X-ray source
does not only increase the Fe K![]() I line EW
when the absorber is impenetrable, but also if it only has small
optical thickness. The reason is that fluorescent photons at
6.4 keV can be created as the X-rays are passing the absorber,
while continuum photons can only be destroyed. Yaqoob et al. (2010)
show, in a different context, that the optically thin approximation for
the fluorescence problem breaks down for column densities as low as
I line EW
when the absorber is impenetrable, but also if it only has small
optical thickness. The reason is that fluorescent photons at
6.4 keV can be created as the X-rays are passing the absorber,
while continuum photons can only be destroyed. Yaqoob et al. (2010)
show, in a different context, that the optically thin approximation for
the fluorescence problem breaks down for column densities as low as
![]()
![]() 1022 H cm-2,
which should also be the scale on which this effect may become
noticeable. The effect may well be responsible for a fraction of the
observed EW in sources with large enough absorbing columns, i.e., in about half of our sources (see Table 2).
1022 H cm-2,
which should also be the scale on which this effect may become
noticeable. The effect may well be responsible for a fraction of the
observed EW in sources with large enough absorbing columns, i.e., in about half of our sources (see Table 2).
The most extreme Fe K![]() I line is observed during the rise phase of a flare in V 1486 Ori, where we determine a line EW of
I line is observed during the rise phase of a flare in V 1486 Ori, where we determine a line EW of
![]() eV (see Sect. 5.1.1)
exceeding typical model predictions by an order of magnitude.
To explain this measurement in the frame of photoionization, Drake et al. (2008) suggest that the Fe K
eV (see Sect. 5.1.1)
exceeding typical model predictions by an order of magnitude.
To explain this measurement in the frame of photoionization, Drake et al. (2008) suggest that the Fe K![]() I line
stems from photoionization by a partially hidden X-ray source. While
this is an appealing idea, the LLC shown in Fig. 4 also suggests an impulsive peak, as presented by Emslie et al. (1986) (Fig. 3) for the case of the Sun. According to Emslie et al. (1986), this peak, which, however, lasted for no longer than
I line
stems from photoionization by a partially hidden X-ray source. While
this is an appealing idea, the LLC shown in Fig. 4 also suggests an impulsive peak, as presented by Emslie et al. (1986) (Fig. 3) for the case of the Sun. According to Emslie et al. (1986), this peak, which, however, lasted for no longer than
![]() s there, is associated with Fe K
s there, is associated with Fe K![]() I line
emission due to electron collisional excitation. Assuming that this is
also true for V 1486 Ori, we can calculate the electron flux
needed to excite the observed line. Applying Eq. (14) and substituting the line flux of
I line
emission due to electron collisional excitation. Assuming that this is
also true for V 1486 Ori, we can calculate the electron flux
needed to excite the observed line. Applying Eq. (14) and substituting the line flux of
![]()
![]() 10-6 ph (cm2 s)-1 during the time span given in Table 2 yields an energy input of about 3
10-6 ph (cm2 s)-1 during the time span given in Table 2 yields an energy input of about 3 ![]() 1036 ergs s-1, which would be required to sustain this line by electron collisional excitation. Whether the observed Fe K
1036 ergs s-1, which would be required to sustain this line by electron collisional excitation. Whether the observed Fe K![]() I line
emission of V 1486 Ori contains a contribution coming from
electron collisional excitation cannot ultimately be decided from the
data at hand, but if is does, the energy released into electrons must
be enormous.
I line
emission of V 1486 Ori contains a contribution coming from
electron collisional excitation cannot ultimately be decided from the
data at hand, but if is does, the energy released into electrons must
be enormous.
Even though EWs of
![]() eV
may be explained by photoionization, some sources still show puzzling
temporal behavior. For example COUP 621, one of the Tsujimoto et al. (2005) sources, shows two flares, which do not seem to be accompanied by fluorescent emission, whereas Fe K
eV
may be explained by photoionization, some sources still show puzzling
temporal behavior. For example COUP 621, one of the Tsujimoto et al. (2005) sources, shows two flares, which do not seem to be accompanied by fluorescent emission, whereas Fe K![]() I line
emission is observed during a bona-fide quiescent period preceding the
first flare. This observation may be attributed to a ``hidden flare''
somewhere behind the star or the disk, which is only visible in its
reprocessed light. It may also be associated with an event
preceding and maybe preparing the first flare, such as magnetic
reconnection releasing high-energy electrons. Feigelson et al. (1998)
show that there are large-scale magnetic structures in an X-ray
protostar in Corona Australis and that the observed polarized radio
emission arises from a nonthermal electron population spiraling along
the field lines. Giardino et al. (2007)
argue that magnetic reconnection can be sustained for several days, but
they do not give a physical model for it. As the energetics
of collisional electron excitation is very challenging
(see Eq. (14)),
however, this explanation seems physically problematic, and,
in light of current knowledge, photoionization by a hidden flare
appears a more straightforward answer. Similar to COUP 621, other
sources like V 1486 Ori
and V NX Ori show flares both with and without detectable
fluorescent emission. We interpret this as a relic of a manifold
geometry. Depending on the location of flare eruption, the conditions
for photoionizing iron and creating fluorescent photons, at least
towards our line of sight, can be quite different. Perhaps some flares
are associated with large magnetic structures connecting photosphere
and disk, as proposed by Giardino et al. (2007) or Favata et al. (2005), but also different locations above the photosphere itself have considerable consequences for the observed Fe K
I line
emission is observed during a bona-fide quiescent period preceding the
first flare. This observation may be attributed to a ``hidden flare''
somewhere behind the star or the disk, which is only visible in its
reprocessed light. It may also be associated with an event
preceding and maybe preparing the first flare, such as magnetic
reconnection releasing high-energy electrons. Feigelson et al. (1998)
show that there are large-scale magnetic structures in an X-ray
protostar in Corona Australis and that the observed polarized radio
emission arises from a nonthermal electron population spiraling along
the field lines. Giardino et al. (2007)
argue that magnetic reconnection can be sustained for several days, but
they do not give a physical model for it. As the energetics
of collisional electron excitation is very challenging
(see Eq. (14)),
however, this explanation seems physically problematic, and,
in light of current knowledge, photoionization by a hidden flare
appears a more straightforward answer. Similar to COUP 621, other
sources like V 1486 Ori
and V NX Ori show flares both with and without detectable
fluorescent emission. We interpret this as a relic of a manifold
geometry. Depending on the location of flare eruption, the conditions
for photoionizing iron and creating fluorescent photons, at least
towards our line of sight, can be quite different. Perhaps some flares
are associated with large magnetic structures connecting photosphere
and disk, as proposed by Giardino et al. (2007) or Favata et al. (2005), but also different locations above the photosphere itself have considerable consequences for the observed Fe K![]() I line
EW (e.g., Bai 1979; Drake et al. 2008).
I line
EW (e.g., Bai 1979; Drake et al. 2008).
7 Conclusion
As a first result of this work, we state that there are far more X-ray sources with detectable fluorescent Fe K![]() I line emission in the COUP field than previously reported. While it extends the sample of known stellar Fe K
I line emission in the COUP field than previously reported. While it extends the sample of known stellar Fe K![]() I line sources, the major part of this study is dedicated to analyzing of the temporal behavior of the Fe K
I line sources, the major part of this study is dedicated to analyzing of the temporal behavior of the Fe K![]() I line emission, which yields another result: strong diversity in the relation between Fe K
I line emission, which yields another result: strong diversity in the relation between Fe K![]() I line emission and soft X-ray continuum.
I line emission and soft X-ray continuum.
Fluorescent emission is found to accompany a flare in some cases,
sometimes it is a persistent feature, and in other cases it appears
``out of nothing'' with no obvious response by the soft X-ray
continuum. The diverse temporal behavior of fluorescent Fe K![]() I line
emission cannot always be easily reconciled with the picture of
photoionization as the dominant excitation mechanism of this emission.
Even in sources that show flares during the COUP campaign,
the majority of fluorescent photons may still be observed in
bona-fide quiescent phases. In those cases, but also in others, the
observed EWs are often appreciably higher than predicted by
photoionization-based model calculations that apply conventional
assumptions on geometry and elemental abundances.
I line
emission cannot always be easily reconciled with the picture of
photoionization as the dominant excitation mechanism of this emission.
Even in sources that show flares during the COUP campaign,
the majority of fluorescent photons may still be observed in
bona-fide quiescent phases. In those cases, but also in others, the
observed EWs are often appreciably higher than predicted by
photoionization-based model calculations that apply conventional
assumptions on geometry and elemental abundances.
Nonetheless, we argue that photoionization remains the most
promising explanation for the observations. The alternative mechanism
of electron collisional excitation is appealing in some cases, because
it provides an explanation for Fe K![]() I line
emission not accompanied by a change in the level of soft X-ray
emission, but the energetics are challenging. To explain the
observed Fe K
I line
emission not accompanied by a change in the level of soft X-ray
emission, but the energetics are challenging. To explain the
observed Fe K![]() I line
fluxes, enormous fluxes of energetic electrons, which otherwise remain
invisible, must sometimes be sustained for days. Electron collisional
excitation may certainly provide a fraction of the fluorescent line
photons, but it can hardly explain the majority.
I line
fluxes, enormous fluxes of energetic electrons, which otherwise remain
invisible, must sometimes be sustained for days. Electron collisional
excitation may certainly provide a fraction of the fluorescent line
photons, but it can hardly explain the majority.
The observations can be reconciled with predictions based on photoionization, if we assume more complicated environments. This includes partially or completely hidden X-ray sources as well as modification of the iron abundance. Also, fluorescence occurring in the circumstellar absorbing material, currently not accounted for in the models, possibly accounts for (a fraction of) the observed EWs.
Our current understanding of the fluorescent Fe K![]() I line
is certainly unsatisfactory, and the great diagnostic power of the line
for a variety of celestial sources makes further observations clearly
desirable.
I line
is certainly unsatisfactory, and the great diagnostic power of the line
for a variety of celestial sources makes further observations clearly
desirable.
This work made use of data obtained from the Chandra data archive. S.C. acknowledges support from the DLR under grant 50OR0105. We thank Eric D. Feigelson for providing us with the outcomes of their analysis of the COUP data.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Bai, T. 1979, Sol. Phys., 62, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., & Fabian, A. C. 2003, ApJ, 592, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Fabian, A. C., & Ross, R. R. 2002, MNRAS, 329, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Bambynek, W., Crasemann, B., Fink, R. W., et al. 1972, Rev. Mod. Phys., 44, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Becklin, E. E., & Neugebauer, G. 1967, ApJ, 147, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., & Schmitt, J. H. H. M. 2007, A&A, 470, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doschek, G. A., Meekins, J. F., Kreplin, R. W., Chubb, T. A., & Friedman, H. 1971, ApJ, 170, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Ercolano, B., & Swartz, D. A. 2008, ApJ, 678, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., Phillips, K. J. H., & Dennis, B. R. 1986, Sol. Phys., 103, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Favata, F., Flaccomio, E., Reale, F., et al. 2005, ApJS, 160, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., Carkner, L., & Wilking, B. A. 1998, ApJ, 494, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Garmire, G., Feigelson, E. D., Broos, P., et al. 2000, AJ, 120, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Getman, K. V., Flaccomio, E., Broos, P. S., et al. 2005, ApJS, 160, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Getman, K. V., Feigelson, E. D., Broos, P. S., Micela, G., & Garmire, G. P. 2008, ApJ, 688, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Giardino, G., Favata, F., Pillitteri, I., et al. 2007, A&A, 475, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Telleschi, A., Audard, M., et al. 2007, A&A, 468, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hombourger, C. 1998, J. Phys. B Atom. Mol. Phys., 31, 3693 [Google Scholar]
- Imanishi, K., Koyama, K., & Tsuboi, Y. 2001, ApJ, 557, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., & Mewe, R. 1993, A&AS, 97, 443 [NASA ADS] [Google Scholar]
- Matt, G., Fabian, A. C., & Reynolds, C. S. 1997, MNRAS, 289, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Neupert, W. M., Gates, W., Swartz, M., & Young, R. 1967, ApJ, 149, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Parmar, A. N., Culhane, J. L., Rapley, C. G., et al. 1984, ApJ, 279, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, W. M., Mutel, R. L., Güdel, M., & Goss, W. M. 2010, Nature, 463, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Saint-Hilaire, P., & Benz, A. O. 2005, A&A, 435, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1998, ApJ, 504, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Churazov, E. M. 1996, Astron. Lett., 22, 648 [NASA ADS] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., Drake, J. J., Ercolano, B., et al. 2008, ApJ, 675, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, M., Feigelson, E. D., Grosso, N., et al. 2005, ApJS, 160, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Yaqoob, T., Murphy, K. D., Miller, L., & Turner, T. J. 2010, MNRAS, 401, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Zarro, D. M., Dennis, B. R., & Slater, G. L. 1992, ApJ, 391, 865 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
All Tables
Table 1: The COUP observations.
Table 2: Most promising intervals for fluorescent emission and basic fit results.
All Figures
| |
Figure 1:
The continuum ratio, |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Distribution of the LRT statistics obtained from Monte Carlo simulations (solid line), the nominal |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8.5cm,clip]{14706fg3.p...
...degraphics[angle=-90,width=8.5cm,clip]{14706fg9.ps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg72.png)
|
Figure 3: Panel A) to G): light curves for the objects reported on by Tsujimoto et al. (2005). The time axis refers to the begin of the COUP campaign (MJD 52 647.87). Upper panel: broad-band (2-9 keV) light curve (BBLC). Lower panel: the cumulated LLC (CLLC) and an estimate of its width (gray shaded, see Eq. (7)). Vertical separators mark change points associated with a shift of the activity level (determined by the Bayesian block analysis of the BBLC). |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Left: LLC and (scaled) broad-band light curve (2.5 ks binning) for COUP 331 (O6). Right: excerpt of the spectrum (corresponding to the gray-shaded time span in the left panel). Both a model with and one without extra line emission are indicated. |
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
Left panel: the LLC and the broad-band light curve (both
10 ks binning) of COUP 561. The latter is scaled to show the
same maximal count rate as the LLC. The gray-shaded area denotes the
time span for which an excerpt of the spectrum is shown in the right panel.
There we show the X-ray spectrum around 6.4 keV and indicate both
a thermal model with and one without excess emission at the energy of
the fluorescent Fe K |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: COUP 621, as in Fig. 5. |
| Open with DEXTER | |
| In the text | |
| |
Figure 7: Left panel: excerpt of the spectrum during the bona fide quiescent phase of COUP 647. Right panel: the same part of the spectrum during the flare. |
| Open with DEXTER | |
| In the text | |
| |
Figure 8: COUP 1030, as in Fig. 5. |
| Open with DEXTER | |
| In the text | |
| |
Figure 9: Left panel: the spectrum during the automatically determined, most promising fluorescent interval of COUP 1040. Right panel: the spectrum during the second COUP observation (O2). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg22.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg23.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg93.png)
|
Figure 10:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 267. Lower panel: the spectrum during the 30-196 ks interval with a close-up of the Fe K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg24.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg25.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg94.png)
|
Figure 11:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 599. Lower panel: the spectrum in the 10-1080 ks interval and a close-up of the Fe K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14706fg26.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14706fg27.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg97.png)
|
Figure 12:
Upper panel: the 2-9 keV band light curve and the CLLC of COUP 1499. Lower panel: the spectrum in the 384-524 ks interval and a close-up of the Fe K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{14706fg28.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg99.png)
|
Figure 13: The summed residuals from all bona-fide fluorescent intervals (panel a)) and the same for all sources not showing intervals with fluorescent emission (panel b)). Solid (black) line: the residuals with respect to thermal models, dashed (red) line: the residuals with respect to a power-law model with an additional hot iron line at 6.7 keV. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14706fg29.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14706-10/Timg100.png)
|
Figure 14: Mean (solid line) and median (dashed line) flux for narrow emission line at various energies. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




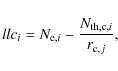
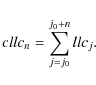
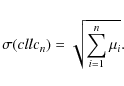
![\begin{displaymath}%
EW\; \mbox{[emission band width]}=\frac{N_{\rm e}-N_{\rm th...
...N_{\rm th}/r_{\rm c}}=r_{\rm c}\frac{N_{\rm e}}{N_{\rm th}}-1.
\end{displaymath}](/articles/aa/full_html/2010/12/aa14706-10/img30.png)