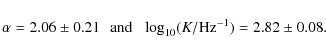| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014484 | |
| Published online | 07 October 2010 | |
VHE  -ray emission of
PKS 2155-304: spectral and temporal variability
-ray emission of
PKS 2155-304: spectral and temporal variability
HESS Collaboration -
A. Abramowski4 - F. Acero15
- F. Aharonian1,13 - A. G. Akhperjanian2
- G. Anton16 - U. Barres de
Almeida8,![]() - A. R. Bazer-Bachi3 -
Y. Becherini12 - B. Behera14
- W. Benbow1 - K. Bernlöhr1,5
- A. Bochow1 - C. Boisson6
- J. Bolmont19 - V. Borrel3
- J. Brucker16 - F. Brun19
- P. Brun7 - R. Bühler1
- T. Bulik29 - I. Büsching9
- T. Boutelier17 -
P. M. Chadwick8 -
A. Charbonnier19 - R. C.
G. Chaves1 - A. Cheesebrough8
- L.-M. Chounet10 -
A. C. Clapson1 -
G. Coignet11 - J. Conrad31
- L. Costamante1,34 - M. Dalton5
- M. K. Daniel8 -
I. D. Davids22,9 -
B. Degrange10 - C. Deil1
- H. J. Dickinson8 -
A. Djannati-Ataï12 -
W. Domainko1 - L. O'C. Drury13
- F. Dubois11 - G. Dubus17
- J. Dyks24 - M. Dyrda28
- K. Egberts1,30 - P. Eger16
- P. Espigat12 - L. Fallon13
- C. Farnier15 - S. Fegan10
- F. Feinstein15 - M.
V. Fernandes4 - A. Fiasson11
- A. Förster1 - G. Fontaine10
- M. Füßling5 - S. Gabici13
- Y. A. Gallant15 -
L. Gérard12 - D. Gerbig21
- B. Giebels10 -
J. F. Glicenstein7 -
B. Glück16 - P. Goret7
- D. Göring16 - D. Hampf4
- M. Hauser14 - S. Heinz16
- G. Heinzelmann4 - G. Henri17
- G. Hermann1 -
J. A. Hinton33 -
A. Hoffmann18 - W. Hofmann1
- P. Hofverberg1 - M. Holleran9
- S. Hoppe1 - D. Horns4
- A. Jacholkowska19 -
O. C. de Jager9 -
C. Jahn16 - I. Jung16
- K. Katarzynski27 - U. Katz16
- S. Kaufmann14 -
M. Kerschhaggl5 - D. Khangulyan1
- B. Khélifi10 - D. Keogh8
- D. Klochkov18 - W. Kluzniak24
- T. Kneiske4 - Nu. Komin7
- K. Kosack7 - R. Kossakowski11
- G. Lamanna11 - J.-P. Lenain6
- T. Lohse5 - C.-C. Lu1
- V. Marandon12 - A. Marcowith15
- J. Masbou11 - D. Maurin19
- T. J. L. McComb8 -
M. C. Medina6 -
J. Méhault15 - R. Moderski24
- E. Moulin7 - M. Naumann-Godo10
- M. de Naurois19 -
D. Nedbal20 - D. Nekrassov1
- N. Nguyen4 - B. Nicholas26
- J. Niemiec28 -
S. J. Nolan8 - S. Ohm1
- J.-F. Olive3 - E. de Oña
Wilhelmi1 - B. Opitz 4
- K. J. Orford8 -
M. Ostrowski23 - M. Panter1
- M. PazArribas5 - G. Pedaletti14
- G. Pelletier17 -
P.-O. Petrucci17 - S. Pita12
- G. Pühlhofer18 - M. Punch12
- A. Quirrenbach14 -
B. C. Raubenheimer9 -
M. Raue1,34 -
S. M. Rayner8 -
O. Reimer30 - M. Renaud12
- R. de los Reyes1 -
F. Rieger1,34 - J. Ripken31
- L. Rob20 - S. Rosier-Lees11
- G. Rowell26 - B. Rudak24
- C. B. Rulten8 -
J. Ruppel21 - F. Ryde32
- V. Sahakian2 - A. Santangelo18
- R. Schlickeiser21 -
F. M. Schöck16 -
A. Schönwald5 - U. Schwanke5
- S. Schwarzburg18 -
S. Schwemmer14 - A. Shalchi 21
- I. Sushch5 - M. Sikora24
- J. L. Skilton25 -
H. Sol6 -
- A. R. Bazer-Bachi3 -
Y. Becherini12 - B. Behera14
- W. Benbow1 - K. Bernlöhr1,5
- A. Bochow1 - C. Boisson6
- J. Bolmont19 - V. Borrel3
- J. Brucker16 - F. Brun19
- P. Brun7 - R. Bühler1
- T. Bulik29 - I. Büsching9
- T. Boutelier17 -
P. M. Chadwick8 -
A. Charbonnier19 - R. C.
G. Chaves1 - A. Cheesebrough8
- L.-M. Chounet10 -
A. C. Clapson1 -
G. Coignet11 - J. Conrad31
- L. Costamante1,34 - M. Dalton5
- M. K. Daniel8 -
I. D. Davids22,9 -
B. Degrange10 - C. Deil1
- H. J. Dickinson8 -
A. Djannati-Ataï12 -
W. Domainko1 - L. O'C. Drury13
- F. Dubois11 - G. Dubus17
- J. Dyks24 - M. Dyrda28
- K. Egberts1,30 - P. Eger16
- P. Espigat12 - L. Fallon13
- C. Farnier15 - S. Fegan10
- F. Feinstein15 - M.
V. Fernandes4 - A. Fiasson11
- A. Förster1 - G. Fontaine10
- M. Füßling5 - S. Gabici13
- Y. A. Gallant15 -
L. Gérard12 - D. Gerbig21
- B. Giebels10 -
J. F. Glicenstein7 -
B. Glück16 - P. Goret7
- D. Göring16 - D. Hampf4
- M. Hauser14 - S. Heinz16
- G. Heinzelmann4 - G. Henri17
- G. Hermann1 -
J. A. Hinton33 -
A. Hoffmann18 - W. Hofmann1
- P. Hofverberg1 - M. Holleran9
- S. Hoppe1 - D. Horns4
- A. Jacholkowska19 -
O. C. de Jager9 -
C. Jahn16 - I. Jung16
- K. Katarzynski27 - U. Katz16
- S. Kaufmann14 -
M. Kerschhaggl5 - D. Khangulyan1
- B. Khélifi10 - D. Keogh8
- D. Klochkov18 - W. Kluzniak24
- T. Kneiske4 - Nu. Komin7
- K. Kosack7 - R. Kossakowski11
- G. Lamanna11 - J.-P. Lenain6
- T. Lohse5 - C.-C. Lu1
- V. Marandon12 - A. Marcowith15
- J. Masbou11 - D. Maurin19
- T. J. L. McComb8 -
M. C. Medina6 -
J. Méhault15 - R. Moderski24
- E. Moulin7 - M. Naumann-Godo10
- M. de Naurois19 -
D. Nedbal20 - D. Nekrassov1
- N. Nguyen4 - B. Nicholas26
- J. Niemiec28 -
S. J. Nolan8 - S. Ohm1
- J.-F. Olive3 - E. de Oña
Wilhelmi1 - B. Opitz 4
- K. J. Orford8 -
M. Ostrowski23 - M. Panter1
- M. PazArribas5 - G. Pedaletti14
- G. Pelletier17 -
P.-O. Petrucci17 - S. Pita12
- G. Pühlhofer18 - M. Punch12
- A. Quirrenbach14 -
B. C. Raubenheimer9 -
M. Raue1,34 -
S. M. Rayner8 -
O. Reimer30 - M. Renaud12
- R. de los Reyes1 -
F. Rieger1,34 - J. Ripken31
- L. Rob20 - S. Rosier-Lees11
- G. Rowell26 - B. Rudak24
- C. B. Rulten8 -
J. Ruppel21 - F. Ryde32
- V. Sahakian2 - A. Santangelo18
- R. Schlickeiser21 -
F. M. Schöck16 -
A. Schönwald5 - U. Schwanke5
- S. Schwarzburg18 -
S. Schwemmer14 - A. Shalchi 21
- I. Sushch5 - M. Sikora24
- J. L. Skilton25 -
H. Sol6 - ![]() . Stawarz23 -
R. Steenkamp22 - C. Stegmann16
- F. Stinzing16 - G. Superina10
- A. Szostek23,17 -
P. H. Tam14 -
J.-P. Tavernet19 - R. Terrier12
- O. Tibolla1 - M. Tluczykont4
- K. Valerius16 -
C. van Eldik1 -
G. Vasileiadis15 - C. Venter9
- L. Venter6 -
J. P. Vialle11 -
A. Viana7 - P. Vincent19
- M. Vivier7 -
H. J. Völk1 - F. Volpe1,10
- S. Vorobiov15 -
S. J. Wagner14 -
M. Ward8 -
A. A. Zdziarski24 -
A. Zech6 - H.-S. Zechlin4
. Stawarz23 -
R. Steenkamp22 - C. Stegmann16
- F. Stinzing16 - G. Superina10
- A. Szostek23,17 -
P. H. Tam14 -
J.-P. Tavernet19 - R. Terrier12
- O. Tibolla1 - M. Tluczykont4
- K. Valerius16 -
C. van Eldik1 -
G. Vasileiadis15 - C. Venter9
- L. Venter6 -
J. P. Vialle11 -
A. Viana7 - P. Vincent19
- M. Vivier7 -
H. J. Völk1 - F. Volpe1,10
- S. Vorobiov15 -
S. J. Wagner14 -
M. Ward8 -
A. A. Zdziarski24 -
A. Zech6 - H.-S. Zechlin4
1 - Max-Planck-Institut für Kernphysik, PO Box 103980, 69029
Heidelberg, Germany
2 - Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036
Yerevan, Armenia
3 - Centre d'Étude Spatiale des Rayonnements, CNRS/UPS, 9 Av. du
Colonel Roche, BP 4346, 31029 Toulouse Cedex 4, France
4 - Universität Hamburg, Institut für Experimentalphysik, Luruper
Chaussee 149, 22761 Hamburg, Germany
5 - Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15,
12489 Berlin, Germany
6 - LUTH, Observatoire de Paris, CNRS, Université Paris Diderot,
5 place Jules Janssen, 92190 Meudon, France
7 - CEA Saclay, DSM/IRFU, 91191 Gif-Sur-Yvette Cedex, France
8 - University of Durham, Department of Physics, South Road, Durham DH1
3LE, UK
9 - Unit for Space Physics, North-West University, Potchefstroom 2520,
South Africa
10 - Laboratoire Leprince-Ringuet, École Polytechnique, CNRS/IN2P3,
91128 Palaiseau, France
11 - Laboratoire d'Annecy-le-Vieux de Physique des Particules,
Université de Savoie, CNRS/IN2P3, 74941 Annecy-le-Vieux, France
12 - Astroparticule et Cosmologie (APC), CNRS, Université Paris 7 Denis
Diderot, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13,
France
![]()
13 - Dublin Institute for Advanced Studies, 5 Merrion Square, Dublin 2,
Ireland
14 - Landessternwarte, Universität Heidelberg, Königstuhl, 69117
Heidelberg, Germany
15 - Laboratoire de Physique Théorique et Astroparticules, Université
Montpellier 2, CNRS/IN2P3, CC 70, Place Eugène Bataillon, 34095
Montpellier Cedex 5, France
16 - Universität Erlangen-Nürnberg, Physikalisches Institut,
Erwin-Rommel-Str. 1, 91058 Erlangen, Germany
17 - Laboratoire d'Astrophysique de Grenoble, INSU/CNRS, Université
Joseph Fourier, BP 53, 38041 Grenoble Cedex 9, France
18 - Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1, 72076 Tübingen, Germany
19 - LPNHE, Université Pierre et Marie Curie Paris 6, Université Denis
Diderot Paris 7, CNRS/IN2P3, 4 place Jussieu, 75252 Paris
Cedex 5, France
20 - Charles University, Faculty of Mathematics and Physics, Institute
of Particle and Nuclear Physics, V Holesovickách 2, 180 00 Prague 8,
Czech Republic
21 - Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und
Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
22 - University of Namibia, Department of Physics, Private Bag 13301,
Windhoek, Namibia
23 - Obserwatorium Astronomiczne, Uniwersytet Jagiellonski, ul. Orla
171, 30-244 Kraków, Poland
24 - Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716
Warsaw, Poland
25 - School of Physics & Astronomy, University of Leeds, Leeds
LS2 9JT, UK
26 - School of Chemistry & Physics, University of Adelaide,
Adelaide 5005, Australia
27 - Torun Centre for Astronomy, Nicolaus Copernicus University,
ul. Gagarina 11, 87-100 Torun, Poland
28 - Instytut Fizyki Jadrowej PAN, ul. Radzikowskiego 152, 31-342
Kraków, Poland
29 - Astronomical Observatory, The University of Warsaw,
Al. Ujazdowskie 4, 00-478 Warsaw, Poland
30 - Institut für Astro- und Teilchenphysik,
Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck, Austria
31 - Oskar Klein Centre, Department of Physics, Stockholm University,
Albanova University Center, 10691 Stockholm, Sweden
32 - Oskar Klein Centre, Department of Physics, Royal Institute of
Technology (KTH), Albanova, 10691 Stockholm, Sweden
33 - Department of Physics and Astronomy, The University of Leicester,
University Road, Leicester, LE1 7RH, UK
34 - European Associated Laboratory for Gamma-Ray Astronomy, jointly
supported by CNRS and MPG
Received 22 March 2010 / Accepted 14 May 2010
Abstract
Context. Observations of very high-energy ![]() -rays from
blazars provide information about acceleration mechanisms occurring in
their innermost regions. Studies of variability in these objects lead
to a better understanding of the mechanisms in play.
-rays from
blazars provide information about acceleration mechanisms occurring in
their innermost regions. Studies of variability in these objects lead
to a better understanding of the mechanisms in play.
Aims. To investigate the spectral and temporal
variability of VHE (
![]() )
)
![]() -rays of the
well-known high-frequency-peaked BL Lac object
PKS 2155-304 with the HESS imaging atmospheric Cherenkov
telescopes over a wide range of flux states.
-rays of the
well-known high-frequency-peaked BL Lac object
PKS 2155-304 with the HESS imaging atmospheric Cherenkov
telescopes over a wide range of flux states.
Methods. Data collected from 2005 to 2007 were
analyzed. Spectra were derived on time scales ranging from
3 years to 4 min. Light curve variability was studied
through doubling timescales and structure functions and compared with
red noise process simulations.
Results. The source was found to be in a low state
from 2005 to 2007, except for a set of exceptional flares that occurred
in July 2006. The quiescent state of the source is
characterized by an associated mean flux level of ![]()
![]()
![]() above
above
![]() ,
or approximately
,
or approximately ![]() of the Crab Nebula, and a power-law photon index of
of the Crab Nebula, and a power-law photon index of ![]() .
During the flares of July 2006, doubling timescales of
.
During the flares of July 2006, doubling timescales of ![]() are found. The spectral index variation is examined over two orders of
magnitude in flux, yielding different behavior at low and high fluxes,
which is a new phenomenon in VHE
are found. The spectral index variation is examined over two orders of
magnitude in flux, yielding different behavior at low and high fluxes,
which is a new phenomenon in VHE ![]() -ray emitting blazars. The
variability amplitude characterized by the fractional rms
-ray emitting blazars. The
variability amplitude characterized by the fractional rms ![]() is strongly energy-dependent and is
is strongly energy-dependent and is ![]() .
The light curve rms correlates with the flux. This is the signature of
a multiplicative process that can be accounted for as a red noise with
a Fourier index of
.
The light curve rms correlates with the flux. This is the signature of
a multiplicative process that can be accounted for as a red noise with
a Fourier index of ![]() .
.
Conclusions. This unique data set shows evidence of
a low-level ![]() -ray
emission state from PKS 2155-304 that possibly has a different
origin than the outbursts. The discovery of the light curve lognormal
behavior might be an indicator of the origin of aperiodic variability
in blazars.
-ray
emission state from PKS 2155-304 that possibly has a different
origin than the outbursts. The discovery of the light curve lognormal
behavior might be an indicator of the origin of aperiodic variability
in blazars.
Key words: gamma rays: general - galaxies: active - galaxies: jets - BL Lacertae objects: individual: PKS 2155-304
1 Introduction
The BL Lacertae (BL Lac) category of active galactic nuclei (AGN) represents the vast majority of the population of energetic and extremely variable extragalactic very high-energyIt has been difficult, however, to ascertain whether ![]() -ray
emission is present only during high flux states or also when the
source is in a more stable or quiescent state but with a flux that is
below the instrumental limits. The advent of the current generation of
atmospheric Cherenkov telescopes with unprecedented sensitivity in the
VHE regime gives
new insight into these questions.
-ray
emission is present only during high flux states or also when the
source is in a more stable or quiescent state but with a flux that is
below the instrumental limits. The advent of the current generation of
atmospheric Cherenkov telescopes with unprecedented sensitivity in the
VHE regime gives
new insight into these questions.
The high-frequency-peaked BL Lac object (HBL)
PKS 2155-304, located at redshift z=0.117,
initially discovered as a VHE ![]() -ray emitter by the Mark 6
telescope (Chadwick et al. 1999),
has been detected by the first HESS telescope in 2002-2003 (Aharonian
et al. 2005b).
It has been frequently observed by the full array of four telescopes
since 2004, either sparsely during the HESS monitoring program or
intensely during dedicated campaigns, such as described in Aharonian
et al. (2005c),
showing mean flux levels of
-ray emitter by the Mark 6
telescope (Chadwick et al. 1999),
has been detected by the first HESS telescope in 2002-2003 (Aharonian
et al. 2005b).
It has been frequently observed by the full array of four telescopes
since 2004, either sparsely during the HESS monitoring program or
intensely during dedicated campaigns, such as described in Aharonian
et al. (2005c),
showing mean flux levels of ![]() of the Crab Nebula flux for energies above
of the Crab Nebula flux for energies above ![]() .
During the summer of 2006, PKS 2155-304 exhibited
unprecedented
flux levels accompanied by strong variability (Aharonian
et al. 2007a),
making temporal and spectral variability studies possible on timescales
on the order of a few minutes. The VHE
.
During the summer of 2006, PKS 2155-304 exhibited
unprecedented
flux levels accompanied by strong variability (Aharonian
et al. 2007a),
making temporal and spectral variability studies possible on timescales
on the order of a few minutes. The VHE ![]() -ray emission is usually
thought to originate from a relativistic jet, emanating from
the vicinity of a supermassive black hole (SMBH). The physical
processes in play are still poorly understood, but the analysis of the
-ray emission is usually
thought to originate from a relativistic jet, emanating from
the vicinity of a supermassive black hole (SMBH). The physical
processes in play are still poorly understood, but the analysis of the ![]() -ray flux
spectral and temporal characteristics is well-suited to providing
deeper insight.
-ray flux
spectral and temporal characteristics is well-suited to providing
deeper insight.
For this goal, the data set of HESS observations of PKS 2155-304 between 2005 and 2007 is used. After describing the observations and the analysis chain in Sect. 2, the emission from the ``quiescent'', i.e. nonflaring, state of the source is characterized in Sect. 3. Section 4 explains the spectral variability related to the source intensity. Section 5 describes the temporal variability during the highly active state of the source and its possible energy dependence. Section 6 illustrates the observed variability phenomenon by a random stationary process, characterized by a simple power density spectrum. Section 7 shows how limits on the characteristic time of the source can be derived. The multi-wavelength aspects from the high flux state will be presented in a second paper.
2 Observations and analysis
HESS is an array of four imaging atmospheric Cherenkov telescopes
situated in the Khomas Highland of Namibia (
![]() South,
South,
![]() East),
at an elevation of 1800 m above sea level (see Aharonian
et al. 2006).
PKS 2155-304 was observed by HESS each year after 2002;
results of observations in 2002, 2003, and 2004 can be found in
Aharonian et al. (2005b),
Aharonian et al. (2005c)
and Giebels et al. (2005).
The data reported here were collected between 2005 and 2007. In 2005,
12.2 h of observations were taken. A similar observation time
was scheduled in 2006, but following the strong flare of
July 26 (Aharonian et al. 2007a),
it was decided to increase this observation time significantly.
Ultimately, from June to October 2006, this source was
observed for 75.9 h, with a further 20.9 h in 2007.
East),
at an elevation of 1800 m above sea level (see Aharonian
et al. 2006).
PKS 2155-304 was observed by HESS each year after 2002;
results of observations in 2002, 2003, and 2004 can be found in
Aharonian et al. (2005b),
Aharonian et al. (2005c)
and Giebels et al. (2005).
The data reported here were collected between 2005 and 2007. In 2005,
12.2 h of observations were taken. A similar observation time
was scheduled in 2006, but following the strong flare of
July 26 (Aharonian et al. 2007a),
it was decided to increase this observation time significantly.
Ultimately, from June to October 2006, this source was
observed for 75.9 h, with a further 20.9 h in 2007.
| Figure 1: Zenith angle distribution for the 202 4-telescopes observation runs from 2005 to 2007. The inset shows, for each zenith angle, the energy threshold associated with the analysis presented in Sect. 2. |
|
| Open with DEXTER | |
Table 1: Summary of observations for each year.
The data were recorded during runs of 28 min nominal
duration, with the telescopes pointing at ![]() from the source position in the sky to enable a simultaneous estimate
of the background. This offset was taken alternatively in both right
ascension and declination (with both signs), in order to
minimize systematics. Only the runs passing the HESS data-quality
selection criteria were used for the analyses presented below. These
criteria imply good atmospheric conditions and checks that the hardware
state of the cameras is satisfactory. The number of runs thus selected
is 22 for 2005, 153 for 2006, and 35 for 2007, corresponding to
live-times of 9.4, 66.1, and 13.8 h respectively. During these
observations, zenith angles were between 7 and 60 degrees,
resulting in large variations in the instrument energy
threshold (
from the source position in the sky to enable a simultaneous estimate
of the background. This offset was taken alternatively in both right
ascension and declination (with both signs), in order to
minimize systematics. Only the runs passing the HESS data-quality
selection criteria were used for the analyses presented below. These
criteria imply good atmospheric conditions and checks that the hardware
state of the cameras is satisfactory. The number of runs thus selected
is 22 for 2005, 153 for 2006, and 35 for 2007, corresponding to
live-times of 9.4, 66.1, and 13.8 h respectively. During these
observations, zenith angles were between 7 and 60 degrees,
resulting in large variations in the instrument energy
threshold (
![]() ,
see Fig. 1)
and sensitivity. This variation has been accounted for in the spectral
and temporal variability studies presented below.
,
see Fig. 1)
and sensitivity. This variation has been accounted for in the spectral
and temporal variability studies presented below.
Table 2: The various data sets used in the paper, referred to in the text by the labels presented in this table.
The data have been analyzed following the prescription
presented in Aharonian et al. (2006), using the loose
set of cuts that are well adapted for bright sources with moderately
soft spectra, and the Reflected-Region method for
the definition of the on-source and off-source data regions.
A year-wise summary of the observations and the resulting
detections are shown in Table 1.
A similar summary is given in Appendix A for the
67 nights of data taken, showing that the emission of
PKS 2155-304 is easily detected by HESS almost every night.
For 66 nights out of 67, the significance per square
root of the live-time (
![]() ,
where T is the observation live-time) is at
least equal to
,
where T is the observation live-time) is at
least equal to ![]() ,
the only night with a lower value -
MJD 53705 - corresponding to a very short exposure.
In addition, for 61 nights out of 67 the
source emission is high enough to enable a detection of the source with
5
,
the only night with a lower value -
MJD 53705 - corresponding to a very short exposure.
In addition, for 61 nights out of 67 the
source emission is high enough to enable a detection of the source with
5![]() significance
in one hour or less, a level usually required in this domain to firmly
claim a new source detection. In 2006 the source exhibits very
strong activity (38 nights, between MJD 53916-53999)
with a nightly
significance
in one hour or less, a level usually required in this domain to firmly
claim a new source detection. In 2006 the source exhibits very
strong activity (38 nights, between MJD 53916-53999)
with a nightly
![]() varying from 3.6 to 150, and being higher than
varying from 3.6 to 150, and being higher than ![]() for 19 nights. The activity of the source climaxes on
MJD 53944 and 53946 with statistical significances
that are unprecedented at these energies, the rate of detected
for 19 nights. The activity of the source climaxes on
MJD 53944 and 53946 with statistical significances
that are unprecedented at these energies, the rate of detected ![]() -rays
corresponding to 2.5 and
-rays
corresponding to 2.5 and ![]() ,
with 150 and
,
with 150 and
![]() respectively.
respectively.
For subsequent spectral analysis, an improved energy
reconstruction method with respect to the one described in Aharonian
et al. (2006)
was applied. This method is based on a look-up table determined from
Monte-Carlo simulations, which contains the relation between an image's
amplitude and its reconstructed impact parameter as a function of the
true energy, the observation zenith angle, the position of the source
in the camera, the optical efficiency of the telescopes (which tend to
decrease due to the aging of the optical surfaces), the number of
triggered telescopes and the reconstructed altitude of the shower
maximum. Thus, for a given event, the reconstructed energy is
determined by requiring the minimal ![]() between the image amplitudes and those expected from the look-up table
corresponding to the same observation conditions. This method yields a
slightly lower energy threshold (shown in Fig. 1 as a function of
zenith angle), an energy resolution that varies from 15% to
20% over all the energy range, and biases in the energy reconstruction
that are smaller than 5%, even close to the threshold. The
systematic uncertainty in the normalization of the HESS energy scale is
estimated to be as large as 15%, corresponding for such soft
spectrum source to 40% in the overall flux normalization as
quoted in Aharonian et al. (2009).
between the image amplitudes and those expected from the look-up table
corresponding to the same observation conditions. This method yields a
slightly lower energy threshold (shown in Fig. 1 as a function of
zenith angle), an energy resolution that varies from 15% to
20% over all the energy range, and biases in the energy reconstruction
that are smaller than 5%, even close to the threshold. The
systematic uncertainty in the normalization of the HESS energy scale is
estimated to be as large as 15%, corresponding for such soft
spectrum source to 40% in the overall flux normalization as
quoted in Aharonian et al. (2009).
All the spectra presented in this paper have been obtained
using a forward-folding maximum likelihood method based on the measured
energy-dependent on-source and off-source distributions. This method,
fully described in Piron et al. (2001), performs
a global deconvolution of the instrument functions (energy resolution,
collection area) and the parametrization of the spectral shape. Two
different sets of parameters, corresponding to a power law and
to a power law with an exponential cut-off, are used for the
spectral shape, with the following equations:
Finally, various data sets have been used for subsequent analyses. These are summarized in Table 2.
3 Characterization of the quiescent state
| Figure 2:
Monthly averaged integral flux of PKS 2155-304 above |
|
| Open with DEXTER | |
As can be seen in Fig. 2,
with the exception of the high state of July 2006
PKS 2155-304 was in a low state during the observations from
2005 to 2007. This section explores the variability of the
source during these periods of low-level activity, based on the
determination of the run-wise integral fluxes for the data
set
![]() ,
which excludes the flaring period of July 2006 and also those
runs whose energy threshold is higher than
,
which excludes the flaring period of July 2006 and also those
runs whose energy threshold is higher than ![]() (see 3.1
for justification). As for Sects. 5
and 6,
the control of systematics in such a study is particularly
important, especially because of the strong variations of the energy
threshold throughout the observations.
(see 3.1
for justification). As for Sects. 5
and 6,
the control of systematics in such a study is particularly
important, especially because of the strong variations of the energy
threshold throughout the observations.
3.1 Method and systematics
The integral flux for a given period of observations is determined in a
standard way. For subsequent discussion purposes, the formula
applied is given here:
where T represents the corresponding live-time, A(E) and R(E,E') are, respectively, the collection area at the true energy E and the energy resolution function between E and the measured energy E', and S(E) the shape of the differential energy spectrum as defined in Eqs. (1) and (2). Finally,
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{14484fg3nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg74.png)
|
Figure 3:
Distributions of the logarithms of integral fluxes above |
| Open with DEXTER | |
In the case that S(E) is a power
law, an important source of systematic error in the determination
of the integral flux variation with time comes from the value chosen
for the index ![]() .
The average 2005-2007 energy spectrum yields a very well determined
power-law index
.
The average 2005-2007 energy spectrum yields a very well determined
power-law index![]() .
However, in Sect. 4
it will be shown that this index varies depending on the flux level of
the source. Moreover, in some cases the energy spectrum of the source
shows some curvature in the TeV region, giving slight
variations in the fitted power-law index depending on the energy range
used.
.
However, in Sect. 4
it will be shown that this index varies depending on the flux level of
the source. Moreover, in some cases the energy spectrum of the source
shows some curvature in the TeV region, giving slight
variations in the fitted power-law index depending on the energy range
used.
For runs whose energy threshold is lower than ![]() ,
a simulation performed under the observation conditions corresponding
to the data shows that an index variation of
,
a simulation performed under the observation conditions corresponding
to the data shows that an index variation of ![]() implies a flux error at the level of
implies a flux error at the level of ![]() ,
this relation being quite linear up to
,
this relation being quite linear up to ![]() .
However, this relation no longer holds when the energy threshold is
above
.
However, this relation no longer holds when the energy threshold is
above
![]() ,
as the determination of
,
as the determination of ![]() becomes much more dependent on the choice of
becomes much more dependent on the choice of ![]() .
For this reason, only runs whose energy threshold is lower than
.
For this reason, only runs whose energy threshold is lower than ![]() will be kept for the subsequent light curves. The value of
will be kept for the subsequent light curves. The value of
![]() is chosen as
is chosen as ![]() ,
which is a compromise between a low value which maximizes the excess
numbers used for the flux determinations and a high value which
maximizes the number of runs whose energy threshold is lower
than
,
which is a compromise between a low value which maximizes the excess
numbers used for the flux determinations and a high value which
maximizes the number of runs whose energy threshold is lower
than
![]() .
.
3.2 Run-wise distribution of the integral flux
From 2005 to 2007, PKS 2155-304 is almost always detected when
observed (except for two nights for which the exposure was very low),
indicating the existence, at least during these observations, of a
minimal level of activity of the source. Focussing on data
set
![]() (which excludes the July 2006 data where the source is in a
high state), the distribution of the integral fluxes of the individual
runs above
(which excludes the July 2006 data where the source is in a
high state), the distribution of the integral fluxes of the individual
runs above ![]() has been determined for the 115 runs, using a spectral index
has been determined for the 115 runs, using a spectral index ![]() (the best value for this data set, as shown
in 3.4).
This distribution has an asymmetric shape, with mean value
(the best value for this data set, as shown
in 3.4).
This distribution has an asymmetric shape, with mean value ![]()
![]()
![]() and root mean square (rms)
and root mean square (rms) ![]()
![]()
![]() ,
and is very well described with a lognormal function. Such a behavior
implies that the logarithm of fluxes follows a normal distribution,
centered on the logarithm of
,
and is very well described with a lognormal function. Such a behavior
implies that the logarithm of fluxes follows a normal distribution,
centered on the logarithm of ![]()
![]()
![]() .
This is shown in the left panel of Fig. 3, where
the solid line represents the best fit obtained with a
maximum-likelihood method, yielding results independent of the choice
of the intervals in the histogram. It is interesting to note
that this result can be compared to the fluxes measured by HESS from
PKS 2155-304 during its construction phase, in 2002 and 2003
(see Aharonian et al. 2005b,c).
As shown in Table 3, these flux
levels extrapolated down to
.
This is shown in the left panel of Fig. 3, where
the solid line represents the best fit obtained with a
maximum-likelihood method, yielding results independent of the choice
of the intervals in the histogram. It is interesting to note
that this result can be compared to the fluxes measured by HESS from
PKS 2155-304 during its construction phase, in 2002 and 2003
(see Aharonian et al. 2005b,c).
As shown in Table 3, these flux
levels extrapolated down to ![]() were close to the value corresponding to the peak shown in the left
panel of Fig. 3.
were close to the value corresponding to the peak shown in the left
panel of Fig. 3.
Table 3: Integral fluxes and their statistical errors from 2002 and 2003 observations of PKS 2155-304 during the HESS construction phase.
The right panel of Fig. 3 shows how the flux distribution is modified when the July 2006 data are taken into account (data set D in Table 2): the histogram can be accounted for by the superposition of two Gaussian distributions (solid curve). The results, summarized in Table 4, are also independent of the choice of the intervals in the histogram. Remarkably enough, the characteristics of the first Gaussian obtained in the first step (left panel) remain quite stable in the double Gaussian fit.
Table 4: The distribution of the flux logarithm.
This leads to two conclusions. First, the flux distribution of PKS 2155-304 is well described considering a low state and a high state, for each of which the distribution of the logarithms of the fluxes follows a Gaussian distribution. The characteristics of the lognormal flux distribution for the high state are given in Sects. 5-7. Secondly, PKS 2155-304 has a level of minimal activity that seems to be stable on a several-year time-scale. This state will henceforth be referred to as the ``quiescent state'' of the source.
3.3 Width of the run-wise flux distribution
In order to determine if the measured width of the flux distribution
(left panel of Fig. 3) can
be explained as statistical fluctuations from the measurement process a
simulation has been carried out considering a source that emits an
integral flux above ![]() of 4.32
of 4.32 ![]()
![]() with a power-law spectral index
with a power-law spectral index ![]() (as determined in the next section). For each run of the data
set
(as determined in the next section). For each run of the data
set
![]() the number
the number
![]() expected by convolving the assumed differential energy spectrum with
the instrument response corresponding to the observation conditions is
determined. A random smearing around this value allows
statistical fluctuations to be taken into account. The number of events
in the off-source region and also the number of background events in
the source region are derived from the measured values
expected by convolving the assumed differential energy spectrum with
the instrument response corresponding to the observation conditions is
determined. A random smearing around this value allows
statistical fluctuations to be taken into account. The number of events
in the off-source region and also the number of background events in
the source region are derived from the measured values
![]() in the data set. These are also smeared in order to take into account
the expected statistical fluctuations.
in the data set. These are also smeared in order to take into account
the expected statistical fluctuations.
10 000 such flux distributions have been simulated,
and for each one its mean value and rms (which will be called below
RMSD) are determined. The distribution of RMSD thus obtained, shown in
Fig. 4,
is well described by a Gaussian centred on 0.98 ![]()
![]() (which represents a relative flux dispersion of 23%) and with
a
(which represents a relative flux dispersion of 23%) and with
a ![]() of 0.07
of 0.07 ![]()
![]() .
.
It should be noted that here the effect of atmospheric
fluctuations in the determination of the flux is only taken into
account at the level of the off-source events, as these
numbers are taken from the measured data. But the effect of the
corresponding level of fluctuations on the source signal is very
difficult to determine. If a conservative value of
20% is considered![]() that is added in the simulations as a supplementary fluctuation factor
for the number of events expected from the source, a RMSD distribution
centred on 1.30
that is added in the simulations as a supplementary fluctuation factor
for the number of events expected from the source, a RMSD distribution
centred on 1.30 ![]()
![]() with a
with a
![]() of 0.09
of 0.09 ![]()
![]() is obtained. Even in this conservative case, the measured value for the
flux distribution rms (
is obtained. Even in this conservative case, the measured value for the
flux distribution rms (
![]()
![]()
![]() )
is very far (more than 8 standard deviations) from the
simulated value. All these elements strongly suggest the existence of
an intrinsic variability associated with the quiescent state
of PKS 2155-304.
)
is very far (more than 8 standard deviations) from the
simulated value. All these elements strongly suggest the existence of
an intrinsic variability associated with the quiescent state
of PKS 2155-304.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg100.png)
|
Figure 4:
Distribution of RMSD obtained when the instrument response to a fixed
emission (
|
| Open with DEXTER | |
3.4 Quiescent-state energy spectrum
The energy spectrum associated with the data set ![]() ,
shown in Fig. 5,
is well described by a power law with a differential flux at
1 TeV of
,
shown in Fig. 5,
is well described by a power law with a differential flux at
1 TeV of ![]()
![]()
![]() and an index of
and an index of ![]()
![]()
![]() .
The stability of these values for spectra measured separately for 2005,
2006 (excluding July), and 2007 is presented in Table 5. The
corresponding average integral flux is
.
The stability of these values for spectra measured separately for 2005,
2006 (excluding July), and 2007 is presented in Table 5. The
corresponding average integral flux is ![]()
![]()
![]() ,
which is as expected in very good agreement with the mean value of the
distribution shown in the left panel of Fig. 3.
,
which is as expected in very good agreement with the mean value of the
distribution shown in the left panel of Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg105.png)
|
Figure 5: Energy spectrum of the quiescent state for the period 2005-2007. The green band correponds to the 68% confidence-level provided by the maximum likelihood method. Points are derived from the residuals in each energy bin, only for illustration purposes. See Sect. 3.4 for further details. |
| Open with DEXTER | |
Table 5: Parametrization of the differential energy spectrum of the quiescent state of PKS 2155-304, determined in the energy range 0.2-10 TeV, first for the 2005-2007 period and also separately for the 2005, 2006 (excluding July) and 2007 periods.
Bins above 2 TeV correspond to ![]() ray excesses
lower than 20
ray excesses
lower than 20![]() and significances lower than
and significances lower than ![]() .
Above 5 TeV excesses are even less significant (
.
Above 5 TeV excesses are even less significant (
![]() or less) and 99% upper-limits are used. There is no
improvement of the fit when a curvature is taken into account.
or less) and 99% upper-limits are used. There is no
improvement of the fit when a curvature is taken into account.
4 Spectral variability
4.1 Variation of the spectral index for the whole data set 2005-2007
The spectral state of PKS 2155-304 has been monitored since
2002. The first set of observations (Aharonian et al. 2005b), from
July 2002 to September 2003, shows an average energy
spectrum well described by a power law with an index of ![]()
![]()
![]() ,
for an integral flux (extrapolated down to
,
for an integral flux (extrapolated down to ![]() )
of
)
of ![]()
![]()
![]() .
No clear indication of spectral variability was seen.
Consecutive observations in October and November 2003
(Aharonian et al. 2005c)
gave a similar value for the index,
.
No clear indication of spectral variability was seen.
Consecutive observations in October and November 2003
(Aharonian et al. 2005c)
gave a similar value for the index, ![]()
![]()
![]() ,
for a slightly higher flux of
,
for a slightly higher flux of
![]()
![]()
![]() .
Later, during HESS observations of the first (MJD 53944,
Aharonian et al. 2007a)
and second (MJD 53946, Aharonian et al. 2009)
exceptional flares of July 2006, the source reached much
higher average fluxes, corresponding to
.
Later, during HESS observations of the first (MJD 53944,
Aharonian et al. 2007a)
and second (MJD 53946, Aharonian et al. 2009)
exceptional flares of July 2006, the source reached much
higher average fluxes, corresponding to ![]()
![]()
![]() and
and ![]()
![]()
![]()
![]() respectively. In the first
case, no strong indications for spectral variability were found and the
average index
respectively. In the first
case, no strong indications for spectral variability were found and the
average index ![]()
![]()
![]() was close to those associated with the 2002 and 2003 observations. In
the second case, clear evidence of spectral hardening with increasing
flux was found.
was close to those associated with the 2002 and 2003 observations. In
the second case, clear evidence of spectral hardening with increasing
flux was found.
The observations of PKS 2155-304 presented in this
paper also include the subsequent flares of 2006 and the data of 2005
and 2007. Therefore, the evolution of the spectral index is studied for
the first time for a flux level varying over two orders of magnitude.
This spectral study has been carried out over the fixed energy range
0.2-1 TeV in order to minimize both systematic effects due to
the energy threshold variation and the effect of the curvature observed
at high energy in the flaring states. The maximal energy has been
chosen to be at the limit where the spectral curvature seen in high
flux states begins to render the power law or exponential
curvature hypotheses distinguishable.
As flux levels observed in July 2006 are
significantly higher than in the rest of the data set (see
Fig. 6),
the flux-index behavior is determined separately first for the
July 2006 data set itself (
![]() )
and secondly for the 2005-2007 data excluding this data set (
)
and secondly for the 2005-2007 data excluding this data set (
![]() ).
).
| Figure 6:
Integral flux above |
|
| Open with DEXTER | |
On both data sets, the following method was applied. The integral flux
was determined for each run assuming a power law shape with an
index of ![]() (average spectral index for the whole data set), and runs were sorted
by increasing flux. The set of ordered runs was then divided into
subsets containing at least an excess of 1500
(average spectral index for the whole data set), and runs were sorted
by increasing flux. The set of ordered runs was then divided into
subsets containing at least an excess of 1500 ![]() above
above ![]() and the energy spectrum of each subset was determined
and the energy spectrum of each subset was determined![]() .
.
The left panel of Fig. 7 shows
the photon index versus integral flux for
data sets
![]() (grey crosses) and
(grey crosses) and
![]() (black points). Corresponding numbers are summarized in
Appendix B.
While a clear hardening is observed for integral fluxes above
a few
(black points). Corresponding numbers are summarized in
Appendix B.
While a clear hardening is observed for integral fluxes above
a few ![]() ,
a break in this behavior is observed for lower fluxes. Indeed,
for the data set
,
a break in this behavior is observed for lower fluxes. Indeed,
for the data set
![]() (black points) a linear fit yields a slope
(black points) a linear fit yields a slope ![]() /
/
![]()
![]()
![]() ,
whereas the same fit for data set
,
whereas the same fit for data set
![]() (grey crosses) yields a slope
(grey crosses) yields a slope ![]() /
/
![]()
![]()
![]() .
The latter corresponds to a
.
The latter corresponds to a ![]() probability
probability ![]() ;
a fit to a constant yields
;
a fit to a constant yields ![]() but with a constant fitted index incompatible with a linear
extrapolation from higher flux states at a 3
but with a constant fitted index incompatible with a linear
extrapolation from higher flux states at a 3![]() level.
This is compatible with conclusions obtained either with an independent
analysis or when these spectra are processed following a different
prescription. In this prescription the runs were sorted as a function
of time in contiguous subsets with similar photon statistics, rather
than as a function of increasing flux.
level.
This is compatible with conclusions obtained either with an independent
analysis or when these spectra are processed following a different
prescription. In this prescription the runs were sorted as a function
of time in contiguous subsets with similar photon statistics, rather
than as a function of increasing flux.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14484fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg139.png)
|
Figure 7:
Evolution of the photon index |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{14484f8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg145.png)
|
Figure 8:
Integrated flux versus time for PKS 2155-304 on
MJD 53944-53947 for four
energy bands and with a 4-min binning. From top to
bottom: |
| Open with DEXTER | |
The form of the relation between the index versus integral flux is
unprecedented in the TeV regime. Prior to the results
presented here, spectral variability has been detected only in two
other blazars, Mrk 421 and Mrk 501. For
Mrk 421, a clear hardening with increasing flux
appeared during the 1999/2000 and 2000/2001 observations performed with
HEGRA (Aharonian et al. 2002) and also
during the 2004 observations performed with HESS (Aharonian
et al. 2005a).
In addition, the Mrk 501 observations carried out
with CAT during the strong flares of 1997 (Djannati-Ataï
et al. 1999)
and also the recent observation performed by MAGIC in 2005 (Albert
et al. 2007)
have shown a similar hardening. In both studies, the VHE peak has been
observed in the ![]() distributions
of the flaring states of Mrk 501.
distributions
of the flaring states of Mrk 501.
4.2 Variation of the spectral index for the four flaring nights of July 2006
In this section, the spectral variability during the flares of
July 2006 is described in more detail. A zoom on the
variation of the integral flux (4-min binning) for the four nights
containing the flares (nights MJD 53944, 53945, 53946, and
53947, called the ``flaring period'') is presented in the top panel of
Fig. 8.
This figure shows two exceptional peaks on MJD 53944 and
MJD 53946 that climax respectively at fluxes higher than
2.5 ![]()
![]() and 3.5
and 3.5 ![]()
![]() (
(![]() and
and ![]() times
the Crab Nebula level above the same energy), both about two orders of
magnitude above the quiescent state level.
times
the Crab Nebula level above the same energy), both about two orders of
magnitude above the quiescent state level.
The variation with time of the photon index is shown in the
bottom panel of Fig. 8.
To obtain these values, the ![]() excess above
excess above ![]() has been determined for each 4-min bin. Then, successive bins
have been grouped in order to reach a global excess higher than
600
has been determined for each 4-min bin. Then, successive bins
have been grouped in order to reach a global excess higher than
600 ![]() .
Finally, the energy spectrum of each data set has been determined in
the 0.2-1 TeV energy range, as before (corresponding
numbers are summarized in Appendix Table B.4).
There is no clear indication of spectral variability within each night,
except for MJD 53946 as shown in Aharonian et al. (2009).
However, a variability can be seen from night to night, and
the spectral hardening with increasing flux level already shown in
Fig. 7
is also seen very clearly in this manner.
.
Finally, the energy spectrum of each data set has been determined in
the 0.2-1 TeV energy range, as before (corresponding
numbers are summarized in Appendix Table B.4).
There is no clear indication of spectral variability within each night,
except for MJD 53946 as shown in Aharonian et al. (2009).
However, a variability can be seen from night to night, and
the spectral hardening with increasing flux level already shown in
Fig. 7
is also seen very clearly in this manner.
It is certainly interesting to directly compare the spectral
behavior seen during the flaring period with the hardness of the energy
spectrum associated with the quiescent state. This is shown in the
right panel of Fig. 7,
where black points correspond to the four flaring nights; these were
determined in the same manner as for the left panel (see 4.1 for
details). A linear fit here yields a slope ![]() /
/
![]()
![]()
![]() .
The grey cross corresponds to the integral flux and the photon index
associated with the quiescent state (derived in a consistent way in the
energy range from 0.2-1 TeV), showing a clear rupture with the
tendancy at higher fluxes (typically above
.
The grey cross corresponds to the integral flux and the photon index
associated with the quiescent state (derived in a consistent way in the
energy range from 0.2-1 TeV), showing a clear rupture with the
tendancy at higher fluxes (typically above
![]() ).
).
These four nights were further examined to search for
differences in the spectral behavior between periods in which the
source flux was clearly increasing and periods in which it was
decreasing.
For this, the first 16 min of the first flare
(MJD 53944) are of special interest because they present a
very symmetric situation: the flux increases during the first half, and
then decreases to its initial level. The averaged fluxes are similar in
both parts (![]()
![]()
![]() ),
and the observation conditions (and thus the instrument response) are
almost constant - the mean zenith angle of each part being
respectively 7.2 and 7.8 degrees. Again, the spectra have been
determined in the 0.2-1 TeV energy range, giving indices of
),
and the observation conditions (and thus the instrument response) are
almost constant - the mean zenith angle of each part being
respectively 7.2 and 7.8 degrees. Again, the spectra have been
determined in the 0.2-1 TeV energy range, giving indices of ![]()
![]()
![]() and
and ![]()
![]()
![]() respectively. To further investigate this question and avoid
potential systematic errors from the spectral method determination, the
hardness ratios were derived (defined as the ratio of the excesses in
different energy bands), using for this the energy (TeV) bands
[0.2-0.35], [0.35-0.6] and [0.6-5.0]. For any combination,
no differences were found beyond the
respectively. To further investigate this question and avoid
potential systematic errors from the spectral method determination, the
hardness ratios were derived (defined as the ratio of the excesses in
different energy bands), using for this the energy (TeV) bands
[0.2-0.35], [0.35-0.6] and [0.6-5.0]. For any combination,
no differences were found beyond the ![]() level between the
increasing and decreasing parts. A similar approach has been
applied - when possible - for the rest of the flaring
period. No clear dependence has been found within the
statistical error limit of the determined indices, which is distributed
between 0.09 and 0.20.
level between the
increasing and decreasing parts. A similar approach has been
applied - when possible - for the rest of the flaring
period. No clear dependence has been found within the
statistical error limit of the determined indices, which is distributed
between 0.09 and 0.20.
Finally, the persistence of the energy cut-off in the
differential energy spectrum along the flaring period has been
examined. For this purpose, runs were sorted again by
increasing flux and grouped into subsets containing at least an excess
of 3000 ![]() above
above ![]()
![]() . For the seven subsets
found, the energy spectrum has been determined in the
0.2-10 TeV energy range both for a simple power law
and a power law with an exponential cut-off. This last hypothesis was
found to be favoured systematically at a level varying from 1.8 to 4.6
. For the seven subsets
found, the energy spectrum has been determined in the
0.2-10 TeV energy range both for a simple power law
and a power law with an exponential cut-off. This last hypothesis was
found to be favoured systematically at a level varying from 1.8 to 4.6![]() compared to the simple power law and is always compatible with
a cut-off in the 1-2 TeV range.
compared to the simple power law and is always compatible with
a cut-off in the 1-2 TeV range.
5 Light curve variability and correlation studies
This section is devoted to the characterization of the temporal
variability of PKS 2155-304, focusing
on the flaring period observations. The high number of ![]() -rays
available not only enabled
minute-level time scale studies, such as those presented for
MJD 53944 in Aharonian et al. (2007a),
but also to derive detailed light curves for three energy bands
(Fig. 8):
0.2-0.35 TeV, 0.35-0.6 TeV and 0.6-5 TeV.
-rays
available not only enabled
minute-level time scale studies, such as those presented for
MJD 53944 in Aharonian et al. (2007a),
but also to derive detailed light curves for three energy bands
(Fig. 8):
0.2-0.35 TeV, 0.35-0.6 TeV and 0.6-5 TeV.
The variability of the energy-dependent light curves of
PKS 2155-304 is in the following quantified through
their fractional rms
![]() defined in Eq. (4)
(Nandra et al. 1997;
Edelson et al. 2002).
In addition, possible time lags between light curves in two
energy bands are investigated.
defined in Eq. (4)
(Nandra et al. 1997;
Edelson et al. 2002).
In addition, possible time lags between light curves in two
energy bands are investigated.
5.1 Fractional rms Fvar
All fluxes in the energy bands of Fig. 8 show a
strong variability that is quantified through their fractional
rms
![]() (which depends on observation durations and their sampling).
Measurement errors
(which depends on observation durations and their sampling).
Measurement errors
![]() on each of the N fluxes
on each of the N fluxes ![]() of the light curve are taken into account in the definition
of
of the light curve are taken into account in the definition
of
![]() :
:
where S2 is the variance
and where
The energy-dependent variability ![]() has been calculated for the flaring period according to Eq. (4) in all three
energy bands. The uncertainties on
has been calculated for the flaring period according to Eq. (4) in all three
energy bands. The uncertainties on
![]() have been estimated according to the parametrization derived by Vaughan
et al. (2003b),
using a Monte Carlo approach which accounts for the
measurement errors on the simulated light curves.
have been estimated according to the parametrization derived by Vaughan
et al. (2003b),
using a Monte Carlo approach which accounts for the
measurement errors on the simulated light curves.
Figure 9
shows the energy dependence of ![]() over the four nights for a sampling of 4 min where only fluxes
with a significance of at least 2 standard deviations were
considered. There is a clear energy-dependence of the variability
(a null probability of
over the four nights for a sampling of 4 min where only fluxes
with a significance of at least 2 standard deviations were
considered. There is a clear energy-dependence of the variability
(a null probability of
![]() ). The points in Fig. 9 are fitted
according to a power law showing that the variability follows
). The points in Fig. 9 are fitted
according to a power law showing that the variability follows ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg9nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg163.png)
|
Figure 9:
Fractional rms |
| Open with DEXTER | |
This energy dependence of ![]() is also perceptible within each individual night. In Table 6 the
values of
is also perceptible within each individual night. In Table 6 the
values of
![]() ,
the relative mean flux and the observation duration, are reported night
by night for the flaring period. Because of the steeply falling
spectra, the low-energy events dominate in the light curves. This lack
of statistics for high energy prevents to have a high fraction of
points with a significance more than 2 standard deviation in
light curves night by night for the three energy bands previously
considered. On the other hand, the error contribution dominates,
preventing the estimation of the
,
the relative mean flux and the observation duration, are reported night
by night for the flaring period. Because of the steeply falling
spectra, the low-energy events dominate in the light curves. This lack
of statistics for high energy prevents to have a high fraction of
points with a significance more than 2 standard deviation in
light curves night by night for the three energy bands previously
considered. On the other hand, the error contribution dominates,
preventing the estimation of the
![]() in all these three energy bands. Therefore, only two energy bands were
considered: low (0.2-0.5 TeV) and high (0.5-5 TeV).
As can be seen in Table 6 also
night by night the high-energy fluxes seem to be more variable than
those at lower energies.
in all these three energy bands. Therefore, only two energy bands were
considered: low (0.2-0.5 TeV) and high (0.5-5 TeV).
As can be seen in Table 6 also
night by night the high-energy fluxes seem to be more variable than
those at lower energies.
Table 6:
Mean Flux and the fractional rms ![]() night by night for MJD 53944-53947.
night by night for MJD 53944-53947.
5.2 Doubling/halving timescale
While ![]() characterizes the mean variability of a source, the shortest
doubling/halving time (Zhang et al. 1999) is an
important parameter in view of finding an upper limit on a possible
physical shortest time scale of the blazar.
characterizes the mean variability of a source, the shortest
doubling/halving time (Zhang et al. 1999) is an
important parameter in view of finding an upper limit on a possible
physical shortest time scale of the blazar.
If ![]() represents the light curve flux at a time Ti,
for each pair of
represents the light curve flux at a time Ti,
for each pair of ![]() one may calculate
one may calculate ![]() ,
where
,
where ![]() = Tj-Ti,
= Tj-Ti,
![]() =
= ![]() and
and ![]() .
Two possible definitions of the doubling/halving are proposed by Zhang
et al. (1999):
the smallest doubling time of all data pairs in a light
curve (T2), or the
mean of the 5 smallest T2i,j
(in the following indicated as
.
Two possible definitions of the doubling/halving are proposed by Zhang
et al. (1999):
the smallest doubling time of all data pairs in a light
curve (T2), or the
mean of the 5 smallest T2i,j
(in the following indicated as
![]() ). One should keep in mind
that, according to Zhang et al. (1999), these
quantities are ill defined and strongly depend on the length of the
sampling intervals and on the signal-to-noise ratio in the observation.
). One should keep in mind
that, according to Zhang et al. (1999), these
quantities are ill defined and strongly depend on the length of the
sampling intervals and on the signal-to-noise ratio in the observation.
This quantity was calculated for the two nights with the
highest fluxes, MJD 53944 and MJD 53946, considering
light curves with two different binnings (1 and
2 min). Bins with flux significances more than ![]() and flux ratios with an uncertainty smaller than 30% were
required to estimate the doubling time scale. The uncertainty
on T2 was estimated
by propagating the errors on the
and flux ratios with an uncertainty smaller than 30% were
required to estimate the doubling time scale. The uncertainty
on T2 was estimated
by propagating the errors on the ![]() ,
and a dispersion of the 5 smallest values was included in
the error for
,
and a dispersion of the 5 smallest values was included in
the error for
![]() .
.
In Table 7,
the values of T2 and ![]() for the two nights are shown. The dependence with respect to the
binning is clearly visible for both observables. In this table, the
last column shows that the fraction of pairs in the light curves that
are kept in order to estimate the doubling times is on average
for the two nights are shown. The dependence with respect to the
binning is clearly visible for both observables. In this table, the
last column shows that the fraction of pairs in the light curves that
are kept in order to estimate the doubling times is on average ![]() 45%.
Moreover, doubling times T2
and
45%.
Moreover, doubling times T2
and
![]() have been estimated for two sets of pairs in the light curves where
have been estimated for two sets of pairs in the light curves where ![]() =
= ![]() is increasing or decreasing respectively. The values of the doubling
time for the two cases are compatible within
is increasing or decreasing respectively. The values of the doubling
time for the two cases are compatible within ![]() ,
therefore no significant asymmetry has been found.
,
therefore no significant asymmetry has been found.
Table 7: Doubling/Halving times for the high intensity nights MJD 53944 and MJD 53946 estimated with two different samplings, using the two definitions explained in the text.
It should be noted that these values are strongly dependent on
the time binning and on the experiment's sensitivity, so that
the typical fastest doubling timescale should be conservatively
estimated as being less than ![]() ,
which is compatible with the values reported in
Aharonian et al. (2007a)
and in Albert et al. (2007),
the latter concerning the blazar Mrk 501.
,
which is compatible with the values reported in
Aharonian et al. (2007a)
and in Albert et al. (2007),
the latter concerning the blazar Mrk 501.
5.3 Cross-correlation analysis as a function of energy
Time lags between light curves at different energies can provide insight into acceleration, cooling and propagation effects of the radiative particles.
The discrete correlation function (DCF) as a function of the delay (White & Peterson 1984; Edelson & Krolik 1988) is used here to search for possible time lags between the energy-resolved light curves. The uncertainty on the DCF has been estimated using simulations. For each delay, 105 light curves (in both energy bands) have been generated within their errors, assuming a Gaussian probability distribution. A probability distribution function (PDF) of the correlation coefficients between the two energy bands has been estimated for each set of simulated light curves. The rms of these PDF are the errors related to the DCF at each delay. Figure 10 shows the DCF between the high and low-energy bands for the four-night flaring period (with 4 min bins) and for the second flaring night (with 2 min bins). The gaps between each 28 min run have been taken into account in the DCF estimation.
The position of the maximum of the DCF has been estimated by a
Gaussian fit that shows no time lag between low and high energies for
either the 4 or 2 min binned light curves. This sets
a limit of 14 ![]()
![]() from the observation of MJD 53946. A detailed study
on the limit on the energy scale on which quantum gravity effects could
become important, using the same data set, are reported in Aharonian
et al. (2008a).
from the observation of MJD 53946. A detailed study
on the limit on the energy scale on which quantum gravity effects could
become important, using the same data set, are reported in Aharonian
et al. (2008a).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14484fg10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg177.png)
|
Figure 10:
DCF between the light curves in the energy ranges 0.2-0.5 TeV
and 0.5-5 TeV and Gaussian fits around the peak. Full circles
represent the DCF for MJD 53944-53947 4-min light curve and
the solid line is the Gaussian fit around the peak with mean value of
43 |
| Open with DEXTER | |
5.4 Excess rms-flux correlation
Having defined the shortest variability time scales, the nature of the
process that generates the fluctuations is investigated, using another
estimator: the excess rms. It is defined as the variance of a
light curve (Eq. (5))
after subtracting the measurement error:
Figure 11
shows the correlation between the excess rms of the light curve and the
flux, where the flux here considered are selected with an energy
threshold of
![]() .
The excess variance is estimated for 1- and 4-min binned light curves,
using 20 consecutive flux points
.
The excess variance is estimated for 1- and 4-min binned light curves,
using 20 consecutive flux points ![]() that are at least at the
that are at least at the ![]() significance level
(81% of the 1 min binned sample). The correlation
factors are r1=0.60+0.21-0.25
and r4=0.87+0.10-0.24for
the 1 and 4 min binning, excluding an absence of
correlation at the
significance level
(81% of the 1 min binned sample). The correlation
factors are r1=0.60+0.21-0.25
and r4=0.87+0.10-0.24for
the 1 and 4 min binning, excluding an absence of
correlation at the ![]() and
and ![]() levels
respectively, implying that fluctuations in the flux are probably
proportional
to the flux itself, which is a characteristic of lognormal
distributions (Aitchinson & Brown 1963). This
correlation has also been investigated extending the analysis to a
statistically more significant data set including observations with a
higher energy threshold in which the determination of the flux above
levels
respectively, implying that fluctuations in the flux are probably
proportional
to the flux itself, which is a characteristic of lognormal
distributions (Aitchinson & Brown 1963). This
correlation has also been investigated extending the analysis to a
statistically more significant data set including observations with a
higher energy threshold in which the determination of the flux above ![]() requires an extrapolation (grey points in the top panel in
Fig. 8).
In this case the correlations found are compatible (
requires an extrapolation (grey points in the top panel in
Fig. 8).
In this case the correlations found are compatible (
![]() and
and ![]() for the 1 and 4 min binning, respectively) and also
exclude an absence of correlation with a higher significance (
for the 1 and 4 min binning, respectively) and also
exclude an absence of correlation with a higher significance (![]() and
and ![]() ,
respectively).
,
respectively).
Such a correlation has already been observed for X-rays in the
Seyfert class AGN (Edelson et al. 2002; Vaughan
et al. 2003a,b;
M![]() Hardy
et al. 2004)
and in X-ray binaries (Uttley & M
Hardy
et al. 2004)
and in X-ray binaries (Uttley & M![]() Hardy 2001; Uttley 2004; Gleissner
et al. 2004),
where it is considered as evidence for an underlying stochastic
multiplicative
process (Uttley et al. 2005),
as opposed to an additive process. In additive processes,
light curves are considered as the sum of individual flares ``shots''
contributing from several zones (multi-zone models) and the relevant
variable that has a Gaussian distribution (namely Gaussian variable) is
the flux. For multiplicative (or cascade) models the Gaussian variable
is the logarithm of the flux. Therefore, this first observation of a
strong rms-flux correlation in the VHE domain fully confirms the
log-normality of the flux distribution presented
in Sect. 3.2.
Hardy 2001; Uttley 2004; Gleissner
et al. 2004),
where it is considered as evidence for an underlying stochastic
multiplicative
process (Uttley et al. 2005),
as opposed to an additive process. In additive processes,
light curves are considered as the sum of individual flares ``shots''
contributing from several zones (multi-zone models) and the relevant
variable that has a Gaussian distribution (namely Gaussian variable) is
the flux. For multiplicative (or cascade) models the Gaussian variable
is the logarithm of the flux. Therefore, this first observation of a
strong rms-flux correlation in the VHE domain fully confirms the
log-normality of the flux distribution presented
in Sect. 3.2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14484fg11_nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg185.png)
|
Figure 11:
The excess rms |
| Open with DEXTER | |
6 Characterization of the lognormal process during the flaring period
This section investigates whether the variability of
PKS 2155-304 in the flaring period can be described by a
random stationary process, where, as shown in Sect. 5.4, the Gaussian
variable is the logarithm of the flux. In this case the variability can
be characterized through its Power Spectral
Density (PSD) (van der Klis 1997),
which indicates the density of variance as function of the
frequency ![]() .
The PSD is an intrinsic indicator of the variability, usually
represented in large frequency intervals by power laws (
.
The PSD is an intrinsic indicator of the variability, usually
represented in large frequency intervals by power laws (
![]() )
and is often used to define different ``states'' of variable objects
(see e.g., Paltani et al. 1997;
and
Zhang et al. 1999,
for the PSD of PKS 2155-304 in the optical and X-rays). The
PSD of the light curve of one single night (MJD 53944) was
given in Aharonian et al. (2007a)
between 10-4 and
)
and is often used to define different ``states'' of variable objects
(see e.g., Paltani et al. 1997;
and
Zhang et al. 1999,
for the PSD of PKS 2155-304 in the optical and X-rays). The
PSD of the light curve of one single night (MJD 53944) was
given in Aharonian et al. (2007a)
between 10-4 and ![]() ,
and was found to be compatible with a red noise process
(
,
and was found to be compatible with a red noise process
(
![]() )
with
)
with ![]() times
more power as in archival X-ray data (Zhang et al. 1999), but with a
similar index. This study implicitely assumed the
times
more power as in archival X-ray data (Zhang et al. 1999), but with a
similar index. This study implicitely assumed the ![]() -ray flux to
be the Gaussian variable. In the present paper, the PSD is
determined using data from 4 consecutive nights
(MJD 53944-53947) and assuming a lognormal process. Since
direct Fourier analysis is not well adapted to light curves extending
over multiple days and affected by uneven sampling and uneven flux
errors, the PSD will be further determined on the basis of parametric
estimation and simulations.
-ray flux to
be the Gaussian variable. In the present paper, the PSD is
determined using data from 4 consecutive nights
(MJD 53944-53947) and assuming a lognormal process. Since
direct Fourier analysis is not well adapted to light curves extending
over multiple days and affected by uneven sampling and uneven flux
errors, the PSD will be further determined on the basis of parametric
estimation and simulations.
In the hypothesis where the process is stationary, i.e., the
PSD is time-independent, a power-law shape of the PSD was assumed, as
for X-ray emitting blazars. The PSD was defined as depending on two
parameters and as follows: ![]() ,
where
,
where ![]() is the variability spectral index and K
denotes the ``power'' (i.e., the variance density) at a
reference
frequency
is the variability spectral index and K
denotes the ``power'' (i.e., the variance density) at a
reference
frequency
![]() .
This latter was conventionally chosen to be
.
This latter was conventionally chosen to be ![]() ,
where the two parameters
,
where the two parameters ![]() and K are found to be decorrelated. Since a
lognormal process is considered,
and K are found to be decorrelated. Since a
lognormal process is considered, ![]() is the density of
variance of the Gaussian variable
is the density of
variance of the Gaussian variable ![]() .
The natural logarithm of the flux is conveniently
used here, since its variance over a given frequency interval
.
The natural logarithm of the flux is conveniently
used here, since its variance over a given frequency interval![]() is close to the
corresponding value of
is close to the
corresponding value of
![]() ,
at least for small fluctuations. For a given set of
,
at least for small fluctuations. For a given set of ![]() and K, it is possible to simulate
many long time series and to modify them according to experimental
effects, namely those of background events and of flux measurement
errors. Light curve segments are further extracted from this
simulation, with exactly the same time structure (observation and
non-observation intervals) and the same sampling rates as those of real
data. The distributions of several observables obtained from
simulations for different values of
and K, it is possible to simulate
many long time series and to modify them according to experimental
effects, namely those of background events and of flux measurement
errors. Light curve segments are further extracted from this
simulation, with exactly the same time structure (observation and
non-observation intervals) and the same sampling rates as those of real
data. The distributions of several observables obtained from
simulations for different values of ![]() and K will be compared to those determined
from observations, thus allowing these parameters to be determined from
a maximum-likelihood fit.
and K will be compared to those determined
from observations, thus allowing these parameters to be determined from
a maximum-likelihood fit.
The simulation characteristics will be described in
Sect. 6.1.
Sections 6.2-6.4 will be devoted to
the determination of ![]() and K by three methods, each of them based
on an experimental result: the excess rms-flux correlation,
the Kolmogorov first-order structure function (Rutman 1978; Simonetti
et al. 1985)
and doubling-time measurements.
and K by three methods, each of them based
on an experimental result: the excess rms-flux correlation,
the Kolmogorov first-order structure function (Rutman 1978; Simonetti
et al. 1985)
and doubling-time measurements.
6.1 Simulation of realistic time-series
For practical reasons, simulated values of ![]() were calculated from Fourier series, thus with a discrete PSD. The
fundamental frequency
were calculated from Fourier series, thus with a discrete PSD. The
fundamental frequency ![]() that corresponds to an elementary bin
that corresponds to an elementary bin ![]() in frequency, must be much lower than 1/T
if T is the duration of the observation.
The ratio T0/T
was chosen to be of the order of 100, in such a way that the
influence of a finite value of T0
on the average variance of a light curve of duration T
would be less than about 2%. Taking T0
= 9
in frequency, must be much lower than 1/T
if T is the duration of the observation.
The ratio T0/T
was chosen to be of the order of 100, in such a way that the
influence of a finite value of T0
on the average variance of a light curve of duration T
would be less than about 2%. Taking T0
= 9 ![]()
![]() ,
this condition is fulfilled for the following studies. With this
approximation, the simulated flux logarithms are given by:
,
this condition is fulfilled for the following studies. With this
approximation, the simulated flux logarithms are given by:
|
(7) |
where
From the long simulated time-series, light curve segments were extracted with the same durations as the periods of continuous data taking and with the same gaps between them. The simulated fluxes were further smeared according to measurement errors, according to the observing conditions (essentially zenith angle and background rate effects) in the corresponding data set.
6.2 Characterization of the lognormal process by the excess rms-flux relation
For a fixed PSD, characterized by a set of parameters ![]() ,
500 light curves were simulated, reproducing the observing
conditions of the flaring period (MJD 53944-53947), according
to the procedure explained in Sect. 6.1.
,
500 light curves were simulated, reproducing the observing
conditions of the flaring period (MJD 53944-53947), according
to the procedure explained in Sect. 6.1.
For each set of simulated light curves, segments of
20 min duration sampled every minute (and alternatively
segments of 80 min duration sampled every 4 min) were
extracted and, for each of them, the excess rms
![]() and the mean flux
and the mean flux
![]() were calculated as explained in Sect. 5.4. For a wide
range of values of
were calculated as explained in Sect. 5.4. For a wide
range of values of ![]() and K, simulated light curves reproduce
well the high level of correlation found in the measured light curves.
On the other hand, the fractional variability
and K, simulated light curves reproduce
well the high level of correlation found in the measured light curves.
On the other hand, the fractional variability
![]() and
and
![]() are essentially uncorrelated and will be used in the following.
A likelihood function of
are essentially uncorrelated and will be used in the following.
A likelihood function of ![]() and K was obtained by comparing the
simulated distributions of
and K was obtained by comparing the
simulated distributions of
![]() and
and
![]() to the experimental ones. An additional
observable that is sensitive to
to the experimental ones. An additional
observable that is sensitive to ![]() and K is the fraction of those light curve
segments for which
and K is the fraction of those light curve
segments for which ![]() cannot be calculated because large measurement errors lead to a
negative value for the excess variance. The comparison between the
measured value of this fraction and those obtained from simulations is
also taken into account in the likelihood function. The
cannot be calculated because large measurement errors lead to a
negative value for the excess variance. The comparison between the
measured value of this fraction and those obtained from simulations is
also taken into account in the likelihood function. The ![]() confidence
contours for the two parameters
confidence
contours for the two parameters ![]() and K obtained from the maximum likelihood
method are shown in Fig. 12 for both
kinds of light curve segments. The two selected domains in the
and K obtained from the maximum likelihood
method are shown in Fig. 12 for both
kinds of light curve segments. The two selected domains in the ![]() plane have a large overlap which restricts the values of
plane have a large overlap which restricts the values of ![]() to the interval (1.9, 2.4).
to the interval (1.9, 2.4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg213.png)
|
Figure 12:
95% confidence domains for |
| Open with DEXTER | |
6.3 Characterization of the lognormal process by the structure function analysis
Another method for determining ![]() and K is based on Kolmogorov structure
functions (SF). For a signal X(t),
measured at N pairs of times separated by a
delay
and K is based on Kolmogorov structure
functions (SF). For a signal X(t),
measured at N pairs of times separated by a
delay ![]() ,
,
![]() (i=1,...,N), the first-order
structure function is defined as (Simonetti et al. 1985):
(i=1,...,N), the first-order
structure function is defined as (Simonetti et al. 1985):
In the present analysis, X(t)
represents the variable whose PSD is being estimated, namely ![]() .
The structure function is a powerful tool for studying aperiodic
signals (Rutman 1978;
Simonetti et al. 1985),
such as the luminosity of blazars at various wavelengths.
Compared to the direct Fourier analysis, the SF has the advantage of
being less affected by ``windowing effects'' caused by large gaps
between short observation periods in VHE
observations. The first-order structure function is adapted to those
PSDs whose variability spectral index is less than 3 (Rutman 1978), which is the
case here, according to the results of
the preceding section.
.
The structure function is a powerful tool for studying aperiodic
signals (Rutman 1978;
Simonetti et al. 1985),
such as the luminosity of blazars at various wavelengths.
Compared to the direct Fourier analysis, the SF has the advantage of
being less affected by ``windowing effects'' caused by large gaps
between short observation periods in VHE
observations. The first-order structure function is adapted to those
PSDs whose variability spectral index is less than 3 (Rutman 1978), which is the
case here, according to the results of
the preceding section.
Figure 13
shows the first-order SF estimated for the flaring period (circles) for
![]() h.
At fixed
h.
At fixed ![]() ,
the distribution of
,
the distribution of ![]() expected for a given set of
parameters
expected for a given set of
parameters ![]() is obtained from 500 simulated light curves. As an example,
taking
is obtained from 500 simulated light curves. As an example,
taking ![]() and
and ![]() ,
values of
,
values of ![]() are found to
lie at 68% confidence level within the shaded region
in Fig. 13.
are found to
lie at 68% confidence level within the shaded region
in Fig. 13.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg13_v2_nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg222.png)
|
Figure 13:
First order structure function SF for the observations carried out in
the period MJD 53944-53947 (circles). The shaded area
corresponds to the 68% confidence limits obtained from
simulations for the lognormal stationary process characterized by |
| Open with DEXTER | |
In the case of a power law PSD with index ![]() ,
the SF averaged over an ensemble of light curves is expected show a
variation as
,
the SF averaged over an ensemble of light curves is expected show a
variation as
![]() (Kataoka et al. 2001).
However, this property does not take into account the effect of
measurement errors, nor of the limited sensitivity of Cherenkov
telescopes at lower fluxes. For the present study, it was
preferable to use the distributions of
(Kataoka et al. 2001).
However, this property does not take into account the effect of
measurement errors, nor of the limited sensitivity of Cherenkov
telescopes at lower fluxes. For the present study, it was
preferable to use the distributions of
![]() obtained from realistic simulations including all experimental
effects. Using such distributions expected for a given set of
parameters
obtained from realistic simulations including all experimental
effects. Using such distributions expected for a given set of
parameters
![]() ,
a likelihood function can be obtained from the experimental SF
and further maximized with respect to these two parameters.
Furthermore, the likelihood fit was restricted to values of
,
a likelihood function can be obtained from the experimental SF
and further maximized with respect to these two parameters.
Furthermore, the likelihood fit was restricted to values of ![]() lower than
lower than ![]() ,
for which the expected fluctuations are not too large and are
well-controlled. The 95% confidence region in the
,
for which the expected fluctuations are not too large and are
well-controlled. The 95% confidence region in the ![]() plane
thus obtained is indicated by the dotted line in Fig. 12.
It is in very good agreement with those based on the excess
rms-flux correlation and give the best values for
plane
thus obtained is indicated by the dotted line in Fig. 12.
It is in very good agreement with those based on the excess
rms-flux correlation and give the best values for ![]() and K:
and K:
The variability index
6.4 Characterization of the lognormal process by doubling times
Simulations were also used to investigate if the estimator T2
can be used to constrain the values of ![]() and K. However, for
and K. However, for ![]() less than 2, no significant constraints on those
parameters are obtained from the values of T2.
For higher values of
less than 2, no significant constraints on those
parameters are obtained from the values of T2.
For higher values of ![]() ,
doubling times only provide loose confidence intervals on K
that are compatible with the values reported above. This can be seen in
Table 8,
showing the 68% confidence intervals predicted for T2
and
,
doubling times only provide loose confidence intervals on K
that are compatible with the values reported above. This can be seen in
Table 8,
showing the 68% confidence intervals predicted for T2
and
![]() for a lognormal process with
for a lognormal process with ![]() and
and ![]() ,
as obtained from simulation. Therefore, the variability of
PKS 2155-304 during the flaring period can be consistently
described by the lognormal random process whose PSD is characterized by
the
parameters given by Eq. (9).
,
as obtained from simulation. Therefore, the variability of
PKS 2155-304 during the flaring period can be consistently
described by the lognormal random process whose PSD is characterized by
the
parameters given by Eq. (9).
Table 8:
Confidence interval at 68% c.l. for T2
and ![]() predicted by simulations for
predicted by simulations for ![]() = 2 and
= 2 and ![]() for the two high-intensity nights MJD 53944 and
MJD 53946, with two different sampling intervals
(1 and 2 min).
for the two high-intensity nights MJD 53944 and
MJD 53946, with two different sampling intervals
(1 and 2 min).
7 Limits on characteristic time of PKS 2155-304
In Sect. 5.2
the shortest variability time scale of PKS 2155-304 using
estimators like doubling times have been estimated. This corresponds to
exploring the high-frequency behavior of the PSD. In this section the
lower (
![]() )
frequency part of the PSD will be considered, aiming to set a limit on
the timescale above which the PSD, characterized in Sect. 6,
starts to steepen to
)
frequency part of the PSD will be considered, aiming to set a limit on
the timescale above which the PSD, characterized in Sect. 6,
starts to steepen to ![]() > 2.
A break in the PSD is expected to avoid infrared divergences
and the time at which this break occurs can be considered as a
characteristic time, from which physical mechanisms occurring in AGN
could be inferred.
> 2.
A break in the PSD is expected to avoid infrared divergences
and the time at which this break occurs can be considered as a
characteristic time, from which physical mechanisms occurring in AGN
could be inferred.
Clearly the description of the source variability during the
flaring period by a stationary lognormal random process is in good
agreement with the flux distributions shown in Fig. 3.
Considering the second Gaussian fit in the right panel of Fig. 3, the
excess variance in the flaring regime reported in Table 9, although
affected by a large error, is an estimator of the intrinsic
variance of the stationary process. It has been demonstrated
that
![]() represents the asymptotic value of the first-order structure function
for large values of the delay
represents the asymptotic value of the first-order structure function
for large values of the delay ![]() (Simonetti et al. 1985).
On the other hand, as already mentioned, a PSD
proportional to
(Simonetti et al. 1985).
On the other hand, as already mentioned, a PSD
proportional to
![]() with
with ![]() cannot be extrapolated to arbitrary low frequencies; equivalently, the
average structure function cannot rise as
cannot be extrapolated to arbitrary low frequencies; equivalently, the
average structure function cannot rise as
![]() for arbitrarily long times. Therefore, by setting
a 95% confidence interval on
for arbitrarily long times. Therefore, by setting
a 95% confidence interval on ![]() of
of
![]() from Table 9,
it is possible to evaluate a confidence interval on a
timescale above which the average value of the
structure function cannot be described by a power law. Taking
account of the uncertainties on
from Table 9,
it is possible to evaluate a confidence interval on a
timescale above which the average value of the
structure function cannot be described by a power law. Taking
account of the uncertainties on ![]() and K given by Eq. (9), leads to the
95% confidence interval for this
characteristic time
and K given by Eq. (9), leads to the
95% confidence interval for this
characteristic time
![]() of the blazar in the flaring regime:
of the blazar in the flaring regime:

This is compatible with the behavior of the experimental structure function at times
8 Discussion and conclusions
This data set, which exhibits unique features and results,
is the outcome of a long-term monitoring program and
dedicated, dense, observations. One of the main results here is the
evidence for a VHE ![]() -ray
quiescent-state emission, where the variations in the flux are found to
have a lognormal distribution. The existence of such a state was
postulated by Stecker & Salamon (1996) in order to
explain the extragalactic
-ray
quiescent-state emission, where the variations in the flux are found to
have a lognormal distribution. The existence of such a state was
postulated by Stecker & Salamon (1996) in order to
explain the extragalactic ![]() -ray background at 0.03-
-ray background at 0.03-
![]() detected by EGRET (Fichtel 1996;
Sreekumar et al. 1998)
as coming from quiescent-state unresolved blazars. Such a background
has not yet been detected in the VHE range, as it is
technically difficult with the atmospheric Cherenkov technique to find
an isotropic extragalactic emission and even more to distinguish it
from the cosmic-ray electron flux (Aharonian et al. 2008b).
In addition, the EBL attenuation limits the distance from
which
detected by EGRET (Fichtel 1996;
Sreekumar et al. 1998)
as coming from quiescent-state unresolved blazars. Such a background
has not yet been detected in the VHE range, as it is
technically difficult with the atmospheric Cherenkov technique to find
an isotropic extragalactic emission and even more to distinguish it
from the cosmic-ray electron flux (Aharonian et al. 2008b).
In addition, the EBL attenuation limits the distance from
which ![]() TeV
TeV ![]() -rays can
propagate to
-rays can
propagate to ![]() (Aharonian et al. 2007b).
As pointed out by Cheng et al. (2000), emission
mechanisms might be simpler to understand during quiescent states in
blazars, and they are also the most likely state to be found
observationally. In the X-ray band, the existence of a steady
underlying emission has also been invoked for two other VHE emitting
blazars (Mrk 421, Fossati et al. 2000; and
1ES 1959+650, Giebels et al. 2002). Being able to
separate, and detect, flaring and nonflaring states in VHE
(Aharonian et al. 2007b).
As pointed out by Cheng et al. (2000), emission
mechanisms might be simpler to understand during quiescent states in
blazars, and they are also the most likely state to be found
observationally. In the X-ray band, the existence of a steady
underlying emission has also been invoked for two other VHE emitting
blazars (Mrk 421, Fossati et al. 2000; and
1ES 1959+650, Giebels et al. 2002). Being able to
separate, and detect, flaring and nonflaring states in VHE ![]() -rays is
thus important for such studies.
-rays is
thus important for such studies.
Table 9:
Variability estimators (definitions in Sect. 5.1) relative to ![]() both for the ``quiescent'' and flaring regime, as defined in
Sect. 3.2.
both for the ``quiescent'' and flaring regime, as defined in
Sect. 3.2.
The observation of the spectacular outbursts of
PKS 2155-304 in July 2006 represents one of the most
extreme examples of AGN variability in the TeV domain, and
allows spectral and timing properties to be probed over two orders of
magnitude in flux. For the flaring states a clear hardening of
the spectrum with increasing flux above a few ![]() is observed, as was seen for the blazars Mrk 421 and
Mrk 501. In contrast, for the quiescent
state of PKS 2155-304 an indication of a softening is noted.
If confirmed, this is a new and intruiging observation in the
VHE regime of blazars. The blazar PKS 0208-512
(of the FSRQ class) also shows such initial softening and
subsequent hardening with flux in the MeV range, but no general trend
could be found for
is observed, as was seen for the blazars Mrk 421 and
Mrk 501. In contrast, for the quiescent
state of PKS 2155-304 an indication of a softening is noted.
If confirmed, this is a new and intruiging observation in the
VHE regime of blazars. The blazar PKS 0208-512
(of the FSRQ class) also shows such initial softening and
subsequent hardening with flux in the MeV range, but no general trend
could be found for ![]() -ray
blazars (Nandikotkur et al. 2007).
In the framework of synchrotron self-Compton scenarios, VHE
spectral softening with increasing flux can be associated with, for
example, an increase in magnetic field intensity, emission region size,
or the power law index of the underlying electron distribution, keeping
all other parameters constant. A spectral hardening can
equally be
obtained by increasing the maximal Lorentz factor of the electron
distribution or the Doppler
factor (see e.g. Fig. 11.7 in Kataoka 1999).
A better understanding of the mechanisms in play would require
multi-wavelength observations to be taken over a similar time span and
with similar sampling density as the data set presented here.
-ray
blazars (Nandikotkur et al. 2007).
In the framework of synchrotron self-Compton scenarios, VHE
spectral softening with increasing flux can be associated with, for
example, an increase in magnetic field intensity, emission region size,
or the power law index of the underlying electron distribution, keeping
all other parameters constant. A spectral hardening can
equally be
obtained by increasing the maximal Lorentz factor of the electron
distribution or the Doppler
factor (see e.g. Fig. 11.7 in Kataoka 1999).
A better understanding of the mechanisms in play would require
multi-wavelength observations to be taken over a similar time span and
with similar sampling density as the data set presented here.
It is shown that the variability time scale ![]() of a few minutes are only upper limits for the intrinsic lowest
characteristic time scale. Doppler factors of
of a few minutes are only upper limits for the intrinsic lowest
characteristic time scale. Doppler factors of ![]() of the emission region are derived by Aharonian et al. (2007a)
using the
of the emission region are derived by Aharonian et al. (2007a)
using the ![]()
![]() black hole (BH) Schwarzschild radius light crossing time as a limit,
while Begelman et al. (2008)
argue that such fast time scales cannot be linked to the size of the BH
and must occur in regions of smaller scales, such as
``needles'' of matter moving faster than average within a larger jet
(Ghisellini & Tavecchio 2008),
small components in the jet dominating at TeV energies
(Katarzynski et al. 2008),
or jet ``stratification'' (Boutelier et al. 2008). Levinson (2007) attributes
the variability to dissipation in the jet coming from radiative
deceleration of shells with high Lorentz factors.
black hole (BH) Schwarzschild radius light crossing time as a limit,
while Begelman et al. (2008)
argue that such fast time scales cannot be linked to the size of the BH
and must occur in regions of smaller scales, such as
``needles'' of matter moving faster than average within a larger jet
(Ghisellini & Tavecchio 2008),
small components in the jet dominating at TeV energies
(Katarzynski et al. 2008),
or jet ``stratification'' (Boutelier et al. 2008). Levinson (2007) attributes
the variability to dissipation in the jet coming from radiative
deceleration of shells with high Lorentz factors.
The flaring period allowed the study of light curves in
separated energy bands and the derivation of a power law
dependence of
![]() with the energy (
with the energy (
![]() ).
This dependence is comparable to that reported in Giebels
et al. (2007),
Lichti et al. (2008),
Maraschi et al. (2002),
where
).
This dependence is comparable to that reported in Giebels
et al. (2007),
Lichti et al. (2008),
Maraschi et al. (2002),
where ![]() between the optical and X-ray energy bands was found for
Mrk 421 and PKS 2155-304, respectively.
An increase with the energy of the flux variability has been
found for Mrk 501 (Albert et al. 2007) in VHE
between the optical and X-ray energy bands was found for
Mrk 421 and PKS 2155-304, respectively.
An increase with the energy of the flux variability has been
found for Mrk 501 (Albert et al. 2007) in VHE ![]() -rays on
timescales comparable to those observed here.
-rays on
timescales comparable to those observed here.
The flaring period showed for the first time that the
intrinsic variability of PKS 2155-304 increases
with the flux, which can itself be described by a lognormal process,
indicating that the aperiodic variability of PKS 2155-304
could be produced by a multiplicative process. The flux in the
``quiescent regime'', which is on average 50 times lower than
in the flaring period and has a 3 times
lower
![]() ,
also follows a lognormal distribution, suggesting similarities between
these two regimes.
,
also follows a lognormal distribution, suggesting similarities between
these two regimes.
It has been possible to characterize a power spectral density
of the flaring period in the frequency range 10-4-
![]() ,
resulting in a power law of index
,
resulting in a power law of index ![]()
![]() 0.21 valid for frequencies down to
0.21 valid for frequencies down to ![]() .
The description of the rapid variability of
a TeV blazar as a random stationary process must be
taken into account by time-dependent blazar models. For
PKS 2155-304 the evidence of this log-normality has been found
very recently in X-rays (Giebels & Degrange 2009) and as
previously mentioned, X-ray binaries and Seyfert galaxies also show
lognormal variability, which is thought to originate from the accretion
disk
(M
.
The description of the rapid variability of
a TeV blazar as a random stationary process must be
taken into account by time-dependent blazar models. For
PKS 2155-304 the evidence of this log-normality has been found
very recently in X-rays (Giebels & Degrange 2009) and as
previously mentioned, X-ray binaries and Seyfert galaxies also show
lognormal variability, which is thought to originate from the accretion
disk
(M![]() Hardy
et al. 2004;
Lyubarskii et al. 1997;
Arévalo & Uttley 2006),
suggesting a connection between the disk and the jet. This
variability behavior should therefore be searched for in existing
blazar light curves, independently of the observed wavelength.
Hardy
et al. 2004;
Lyubarskii et al. 1997;
Arévalo & Uttley 2006),
suggesting a connection between the disk and the jet. This
variability behavior should therefore be searched for in existing
blazar light curves, independently of the observed wavelength.
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of HESS is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment.
Appendix A: Observations summary
The journal of observations for the 2005-2007 is presented in Table A.1.Table A.1: Summary of the 2005 to 2007 observations.
Appendix B: Spectral variability
The numerical information associated with Fig. 7 is given in Tables B.1 (left panel, grey points), B.2 (left panel, black points) and B.3 (right panel). In addition, numerical information associated with Fig. 8 is given in Table B.4.Table B.1:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to grey points in the left panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to grey points in the left panel of Fig. 7.
Table B.2:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to black points in the left panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to black points in the left panel of Fig. 7.
Table B.3:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to the right panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to the right panel of Fig. 7.
Table B.4:
MJD, integral flux (
![]() )
in the 0.2-1 TeV energy range, and photon index corresponding
to the entries of Fig. 8.
)
in the 0.2-1 TeV energy range, and photon index corresponding
to the entries of Fig. 8.
References
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. (HEGRA. Collaboration) 2002, A&A, 393, 89 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2005a, A&A, 437, 95 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2005b, A&A, 430, 865 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2005c, A&A, 442, 895 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2006, A&A, 457, 899 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2007a, ApJ, 664, L71 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (HESS Collaboration) 2007b, A&A, 475, L9 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (HESS Collaboration) 2008a, Phys. Rev. Lett., 101, 170402 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (HESS Collaboration) 2008b, Phys. Rev. Lett, 101, 261104 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. (HESS Collaboration) 2009, A&A, 502, 749 [Google Scholar]
- Aitchinson, J., & Brown, J. A. C. 1963, The Lognormal Distribution (Cambridge: Cambridge University Press) [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. (MAGIC Collaboration) 2007, ApJ, 669, 862 [Google Scholar]
- Arévalo, P., & Uttley, P. 2006, MNRAS, 367, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Fabian, A. C., & Rees, M. J. 2008, MNRAS, 384, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Boutelier, T., Henri, G., & Petrucci, P. O. 2008, MNRAS, 390, 73 [Google Scholar]
- Chadwick, P. M., Lyons, K., McComb, T. J. L., et al. 1999, ApJ, 513, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Zhang, X., & Zhang, L. 2000, ApJ, 537, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Djannati-Ataï, A., Piron, F., Barrau, A., et al. 1999, A&A, 350, 17 [NASA ADS] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Fichtel, C. 1996, A&AS, 120, 23 [Google Scholar]
- Fossati, G., Celotti, A., Chiaberge, M., et al. 2000, ApJ, 541, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2008, MNRAS, 386, 28 [Google Scholar]
- Giebels, B., & Degrange, B. 2009, A&A, 503, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giebels, B., Bloom, E. D., Focke, W., et al. 2002, ApJ, 571, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Giebels, B., et al. (HESS Collaboration) 2005, Proc. Annual meeting of the French Society of Astronomy and Astrophysics (Strasbourg), 527 [Google Scholar]
- Giebels, B., Dubus, G., & Khelifi, B. 2007, A&A, 462, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gleissner, T., Wilms, J., Pottschmidt, K., et al. 2004, A&A, 414, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzynski, K., Lenain, J.-P., Zech, A., Boisson, C., & Sol, H. 2008, MNRAS, 390, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, J. 1999, X-ray Study of Rapid Variability in TeV Blazars and the Implications on Particle Acceleration in Jets, ISAS RN 710 [Google Scholar]
- Kataoka, J., Takahashi, T., Wagner, S. J., et al. 2001, ApJ, 560, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine-Goumard, M., Degrange, B., & Tluczykont, M. 2006, Astropart. Phys., 25, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Levinson, A. 2007, ApJ, 671, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Lichti, G. G., Bottacini, E., Ajello, M., et al. 2008, A&A, 486, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubarskii, Y. E. 1997, MNRAS, 292, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., et al. 2002, Proc. Symposium ``New Visions of the X-ray Universe in the XMM-Newton and Chandra Era'', ESTEC 2001 [arXiv:0202418v1] [Google Scholar]
- M Hardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Nandikotkur, G., Jahoda, K. M., Hartman, R. C., et al. 2007, ApJ, 657, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., Courvoisier, T. J.-L., Blecha, A., & Bratschi, P. 1997, A&A, 327, 539 [NASA ADS] [Google Scholar]
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., & Stern, B. E. 2008, Int. J. Mod. Phys., 17, 1619 [NASA ADS] [Google Scholar]
- Rutman, J. 1978, Proc. IEEE, 66, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Simonetti, J. H., Cordes, J. M., & Heeschen, D. S. 1985, ApJ, 296, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1998, ApJ, 494, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., & Salamon, M. H. 1996, ApJ, 464, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, B. E. 2003, MNRAS, 345, 590 [Google Scholar]
- Stern, B. E., & Poutanen, J. 2006, MNRAS, 372, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, M., Ghisellini, G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Kataoka, J., Madejski, G., et al. 2000, ApJ, 542, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P. 2004, MNRAS, 347, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., & M Hardy, I. M. 2001, MNRAS, 323, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., M Hardy, I. M., & Vaughan, S. 2005, MNRAS, 359, 345 [Google Scholar]
- van der Klis, M. 1997, Proc. Conf. Statistical Challenges in Modern Astronomy II, Pennsylvania State University (Berlin: Springer-Verlag), 321 [Google Scholar]
- Vaughan, S., Fabian, A. C., & Nandra, K. 2003a, MNRAS, 339, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003b, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. J., & Peterson, B. M. 1994, PASP, 106, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H., Celotti, A., Treves, A., et al. 1999, ApJ, 527, 719 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Supported by CAPES Foundation, Ministry of Education of Brazil.
- ... France
![[*]](/icons/foot_motif.png)
- UMR 7164 (CNRS, Université Paris VII, CEA, Observatoire de Paris)
- ... index
![[*]](/icons/foot_motif.png)
- The resulting spectral index is
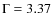
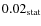 .
The alternative hypothesis with a curvature in the spectrum (Eq. (2)) is favored at
.
The alternative hypothesis with a curvature in the spectrum (Eq. (2)) is favored at 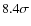 ,
yelding a harder index (
,
yelding a harder index (
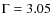
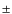
 )
with an exponential cut-off at
)
with an exponential cut-off at
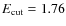
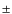
 .
As the integral flux is dominated by the low-energy part of the
spectrum, the choice of the model has a little effect on the integral
flux values above
.
As the integral flux is dominated by the low-energy part of the
spectrum, the choice of the model has a little effect on the integral
flux values above
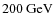 .
.
- ... considered
![[*]](/icons/foot_motif.png)
- A similar procedure has been
carried out on the Crab Nebula observations. Assuming this source is
perfectly stable, it allows the derivation of an upper limit to
the fluctuations of the Crab signal due to the atmosphere. Nonetheless,
this value,
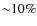 ,
is linked to the observations' epoch and zenith angles, and to the source spectral shape.
,
is linked to the observations' epoch and zenith angles, and to the source spectral shape.
- ...
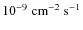
![[*]](/icons/foot_motif.png)
- Corresponding to data set T200 in Aharonian et al. (2009).
- ... determined
![[*]](/icons/foot_motif.png)
- Even for lower fluxes, the significance associated with each subset is always higher than 20 standard deviations.
- ...
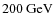
![[*]](/icons/foot_motif.png)
- To be significant, the determination of an energy cut-off needs a higher number of
 than for a power-law fit.
than for a power-law fit.
- ... interval
![[*]](/icons/foot_motif.png)
- If
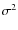 is the variance of
is the variance of 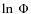 ,
,
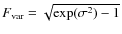 .
.
All Tables
Table 1: Summary of observations for each year.
Table 2: The various data sets used in the paper, referred to in the text by the labels presented in this table.
Table 3: Integral fluxes and their statistical errors from 2002 and 2003 observations of PKS 2155-304 during the HESS construction phase.
Table 4: The distribution of the flux logarithm.
Table 5: Parametrization of the differential energy spectrum of the quiescent state of PKS 2155-304, determined in the energy range 0.2-10 TeV, first for the 2005-2007 period and also separately for the 2005, 2006 (excluding July) and 2007 periods.
Table 6:
Mean Flux and the fractional rms ![]() night by night for MJD 53944-53947.
night by night for MJD 53944-53947.
Table 7: Doubling/Halving times for the high intensity nights MJD 53944 and MJD 53946 estimated with two different samplings, using the two definitions explained in the text.
Table 8:
Confidence interval at 68% c.l. for T2
and ![]() predicted by simulations for
predicted by simulations for ![]() = 2 and
= 2 and ![]() for the two high-intensity nights MJD 53944 and
MJD 53946, with two different sampling intervals
(1 and 2 min).
for the two high-intensity nights MJD 53944 and
MJD 53946, with two different sampling intervals
(1 and 2 min).
Table 9:
Variability estimators (definitions in Sect. 5.1) relative to ![]() both for the ``quiescent'' and flaring regime, as defined in
Sect. 3.2.
both for the ``quiescent'' and flaring regime, as defined in
Sect. 3.2.
Table A.1: Summary of the 2005 to 2007 observations.
Table B.1:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to grey points in the left panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to grey points in the left panel of Fig. 7.
Table B.2:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to black points in the left panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to black points in the left panel of Fig. 7.
Table B.3:
Integral flux (
![]() )
in the 0.2-1 TeV energy range versus photon index
corresponding to the right panel of Fig. 7.
)
in the 0.2-1 TeV energy range versus photon index
corresponding to the right panel of Fig. 7.
Table B.4:
MJD, integral flux (
![]() )
in the 0.2-1 TeV energy range, and photon index corresponding
to the entries of Fig. 8.
)
in the 0.2-1 TeV energy range, and photon index corresponding
to the entries of Fig. 8.
All Figures
| |
Figure 1: Zenith angle distribution for the 202 4-telescopes observation runs from 2005 to 2007. The inset shows, for each zenith angle, the energy threshold associated with the analysis presented in Sect. 2. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Monthly averaged integral flux of PKS 2155-304 above |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{14484fg3nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg74.png)
|
Figure 3:
Distributions of the logarithms of integral fluxes above |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg100.png)
|
Figure 4:
Distribution of RMSD obtained when the instrument response to a fixed
emission (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg105.png)
|
Figure 5: Energy spectrum of the quiescent state for the period 2005-2007. The green band correponds to the 68% confidence-level provided by the maximum likelihood method. Points are derived from the residuals in each energy bin, only for illustration purposes. See Sect. 3.4 for further details. |
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Integral flux above |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14484fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg139.png)
|
Figure 7:
Evolution of the photon index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{14484f8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg145.png)
|
Figure 8:
Integrated flux versus time for PKS 2155-304 on
MJD 53944-53947 for four
energy bands and with a 4-min binning. From top to
bottom: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg9nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg163.png)
|
Figure 9:
Fractional rms |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14484fg10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg177.png)
|
Figure 10:
DCF between the light curves in the energy ranges 0.2-0.5 TeV
and 0.5-5 TeV and Gaussian fits around the peak. Full circles
represent the DCF for MJD 53944-53947 4-min light curve and
the solid line is the Gaussian fit around the peak with mean value of
43 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14484fg11_nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg185.png)
|
Figure 11:
The excess rms |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg213.png)
|
Figure 12:
95% confidence domains for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14484fg13_v2_nv.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14484-10/Timg222.png)
|
Figure 13:
First order structure function SF for the observations carried out in
the period MJD 53944-53947 (circles). The shaded area
corresponds to the 68% confidence limits obtained from
simulations for the lognormal stationary process characterized by |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



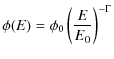
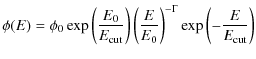
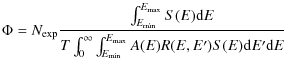
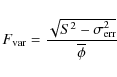
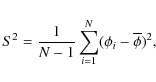
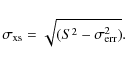
![$\displaystyle \frac{1}{N}\sum_{i=1}^{N}[X(t_i)-X(t_i+\tau)]^2$](/articles/aa/full_html/2010/12/aa14484-10/img217.png)
![$\displaystyle \frac{1}{N}\sum_{i=1}^{N}[\ln \Phi(t_i)-\ln \Phi(t_i+\tau)]^2.$](/articles/aa/full_html/2010/12/aa14484-10/img218.png)