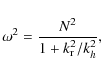| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014461 | |
| Published online | 13 October 2010 | |
The core helium flash revisited
III. From Population I to Population III stars
M. Mocák1 - S. W. Campbell2,3 - E. Müller4 - K. Kifonidis4
1 - Institut d'Astronomie et d'Astrophysique, Université Libre de
Bruxelles, CP 226, 1050 Brussels, Belgium
2 - Departament de Física i Enginyeria Nuclear, EUETIB, Universitat
Politécnica de Catalunya, C./Comte d'Urgell 187, 08036 Barcelona, Spain
3 - Centre for Stellar and Planetary Astrophysics, School of
Mathematical Sciences, Monash University, Melbourne 3800, Australia
4 - Max-Planck-Institut für Astrophysik, Postfach 1312, 85741 Garching,
Germany
Received 18 March 2010 / Accepted 13 June 2010
Abstract
Context. Degenerate ignition of helium in low-mass
stars at the end of the red giant branch phase leads to dynamic
convection in their helium cores. One-dimensional (1D) stellar
modeling of this intrinsically multi-dimensional dynamic event is
likely to be inadequate. Previous hydrodynamic simulations imply that
the single convection zone in the helium core of metal-rich
Pop I stars grows during the flash on a dynamic timescale.
This may lead to hydrogen injection into the core and to a double
convection zone structure as known from one-dimensional core helium
flash simulations of low-mass Pop III stars.
Aims. We perform hydrodynamic simulations of the
core helium flash in two and three dimensions to better constrain the
nature of these events. To this end we study the hydrodynamics of
convection within the helium cores of a 1.25 ![]() metal-rich Pop I star (Z=0.02), and, for
the first time, a 0.85
metal-rich Pop I star (Z=0.02), and, for
the first time, a 0.85 ![]() metal-free Pop III star (Z=0) near the peak
of the flash. These models possess single and double convection zones,
respectively.
metal-free Pop III star (Z=0) near the peak
of the flash. These models possess single and double convection zones,
respectively.
Methods. We use 1D stellar models of the core helium
flash computed with state-of-the-art stellar evolution codes as initial
models for our multidimensional hydrodynamic study, and simulate the
evolution of these models with the Riemann solver based hydrodynamics
code Herakles, which integrates the Euler equations coupled with source
terms corresponding to gravity and nuclear burning.
Results. The hydrodynamic simulation of the
Pop I model involving a single convection zone covers
27 h of stellar evolution, while the hydrodynamic simulations
of a double convection zone, in the Pop III model, span
1.8 h of stellar life. We find differences between the
predictions of mixing length theory and our hydrodynamic simulations.
The simulation of the single convection zone in the Pop I
model shows a strong growth of the size of the convection zone due to
turbulent entrainment. We therefore predict that for the Pop I
model a hydrogen injection phase (i.e., hydrogen injection
into the helium core) will commence after about 23 days, which
should eventually lead to a double convection zone structure known from
1D stellar modeling of low-mass Pop III stars. Our two and
three-dimensional hydrodynamic simulations of the double
(Pop III) convection zone model show that the velocity field
in the convection zones is different from that given by stellar
evolutionary calculations. The simulations suggest that the double
convection zone decays quickly, the flow eventually being dominated by
internal gravity waves. The decay could be an artefact caused by the
mapping of the initial stellar model to the numerical grid of our
hydrodynamics code.
Key words: stars: evolution - hydrodynamics - convection
1 Introduction
Runaway nuclear burning of helium in the core of low-mass red giant stars leads to convective mixing and burning on dynamic timescales. One-dimensional evolutionary simulations (which assume much longer timescales than the dynamical ones) may miss key features of this rapid phase that could have significant effects on the further evolution of the stars. Furthermore, 1D hydrodynamical simulations of this intrinsically multi-dimensional event is likely to be inadequate.
Our previous hydrodynamic simulations (Mocák et al. 2008,2009)
imply that a 1.25 ![]() solar-like star can experience injection of
hydrogen into its helium core during the canonical core helium
flash near its peak. The hydrogen injection results from the growth of
the convection zone (which is sustained by helium burning) owing
turbulent
entrainment on a dynamic timescale (Meakin
& Arnett 2007), and
probably occurs for all low-mass Pop I stars, as the
properties of
their cores are similar at the peak of the core helium flash
(Sweigart & Gross 1978).
An obvious consequence of this scenario is
that the convection zones are enlarged in these stars. Whether they
fail to dredge up nuclear ash to the atmosphere shortly after the
flash is still unclear. However, such a dredge up could explain the
Al-Mg anticorrelation found in red giants at the tip of the red giant
branch (RGB)
(Shetrone
1996a; Yong
et al. 2006; Shetrone 1996b). In 1D
simulations one has to
manipulate the properties of the core helium flash to achieve such a
dredge up, e.g., by changing the ignition position of the
helium in the
core (Paczynski &
Tremaine 1977) or by forcing inward mixing
of hydrogen (Fujimoto
et al. 1999).
solar-like star can experience injection of
hydrogen into its helium core during the canonical core helium
flash near its peak. The hydrogen injection results from the growth of
the convection zone (which is sustained by helium burning) owing
turbulent
entrainment on a dynamic timescale (Meakin
& Arnett 2007), and
probably occurs for all low-mass Pop I stars, as the
properties of
their cores are similar at the peak of the core helium flash
(Sweigart & Gross 1978).
An obvious consequence of this scenario is
that the convection zones are enlarged in these stars. Whether they
fail to dredge up nuclear ash to the atmosphere shortly after the
flash is still unclear. However, such a dredge up could explain the
Al-Mg anticorrelation found in red giants at the tip of the red giant
branch (RGB)
(Shetrone
1996a; Yong
et al. 2006; Shetrone 1996b). In 1D
simulations one has to
manipulate the properties of the core helium flash to achieve such a
dredge up, e.g., by changing the ignition position of the
helium in the
core (Paczynski &
Tremaine 1977) or by forcing inward mixing
of hydrogen (Fujimoto
et al. 1999).
Canonical one-dimensional stellar evolution calculations
predict hydrogen
injection during the core helium flash and subsequent dredge-up of
nuclear ashes to the atmosphere only for Pop III![]() and extremely metal-poor (EMP; with intrinsic metallicities [Fe/H]
and extremely metal-poor (EMP; with intrinsic metallicities [Fe/H]
![]() -4) stars.
This is a promising scenario for explaining the
peculiar abundances of carbon and nitrogen observed in Galactic EMP
halo stars (Campbell &
Lattanzio 2008). If these stars are assumed to be polluted by
accretion of
CNO-rich interstellar matter, they will possibly experience hydrogen
injection but no subsequent dredge-up, because a high CNO
metallicity (as compared to the intrinsic [Fe/H] metallicity) in the
stellar envelope influences the ignition site of the first major core
helium flash, hence the occurrence of the dredge-up
(Hollowell et al. 1990).
The helium abundance adopted in the stellar
models also seems to influence the process of hydrogen injection
itself as shown by Schlattl
et al. (2001), while the same
authors find that the injection process seems to be independent of the
assumed convection model.
-4) stars.
This is a promising scenario for explaining the
peculiar abundances of carbon and nitrogen observed in Galactic EMP
halo stars (Campbell &
Lattanzio 2008). If these stars are assumed to be polluted by
accretion of
CNO-rich interstellar matter, they will possibly experience hydrogen
injection but no subsequent dredge-up, because a high CNO
metallicity (as compared to the intrinsic [Fe/H] metallicity) in the
stellar envelope influences the ignition site of the first major core
helium flash, hence the occurrence of the dredge-up
(Hollowell et al. 1990).
The helium abundance adopted in the stellar
models also seems to influence the process of hydrogen injection
itself as shown by Schlattl
et al. (2001), while the same
authors find that the injection process seems to be independent of the
assumed convection model.
Stellar models with a higher intrinsic metallicity,
i.e., [Fe/H] > - 4,
do not inject hydrogen into the helium core, and consequently there is
also no dredge-up of CNO-rich nuclear ashes to the atmosphere
(Campbell
& Lattanzio 2008; Fujimoto et al. 1990;
Hollowell
et al. 1990). Whether this
is the final answer remains unclear, however, as Fujimoto et al. (1999)
with his semi-analytic study and a postulated hydrogen injection
followed by a dredge-up could show that such a scenario can explain
some peculiarities observed in the spectra of red-giant stars (related
to CNO elements and 24Mg) with metallicities as
large as [Fe/H]
![]() .
.
There are two main reasons for hydrogen injection episodes
occurring
only in Pop III and EMP stars: (i) these stars
possess a flatter
entropy gradient in the hydrogen burning shell; and (ii) they
ignite
helium far off center, relatively close to the hydrogen-rich envelope
(Fujimoto et al. 1990).
However, Pop II and Pop I stars could also
mix hydrogen into the helium core during the core helium flash![]() :
:
- if the flash was more violent, and thus the helium convection zone wider (Despain & Scalo 1976; Despain 1981). This scenario is disfavored by the facts that the flash is less violent in stars with higher metallicity as less energy is needed to lift the degeneracy of the less massive cores (Sweigart & Gross 1978), and that helium ignition occurs at lower densities (Fujimoto et al. 1990);
- or if the entropy gradient between the hydrogen and helium
burning shell was sufficiently shallow (Fujimoto 1977; Iben 1976).
A small entropy gradient would allow the convective shell in the helium
core to reach the hydrogen layers even though the flash itself would
not be very violent. This scenario is also disfavored as solutions to
the stellar structure equations seem to be robust with many different
groups getting very similar results i.e., no hydrogen
injection (Campbell
& Lattanzio 2008; Fujimoto et al. 1990;
Hollowell
et al. 1990)
![[*]](/icons/foot_motif.png) ;
;
- or if a growth of the helium convection zone through turbulent entrainment at the convective boundaries (Mocák et al. 2008,2009) could be sustained for a sufficiently long period of time.
Hydrogen injection is found to occur in more massive stars (
![]()
![]() )
with low metallicity during the TPAGB (Siess et al. 2002; Chieffi
et al. 2001; Iwamoto et al. 2004),
in ``Late Hot Flasher'' stars experiencing
strong mass loss on the RGB (Cassisi et al. 2003;
Brown
et al. 2001),
and in H-deficient post AGB (PAGB) stars. These events are referred to
with various names in the literature. Here we use the nomenclature
``dual flashes'' (Campbell
& Lattanzio 2008), since they all have in common
simultaneous hydrogen and helium flashes.
)
with low metallicity during the TPAGB (Siess et al. 2002; Chieffi
et al. 2001; Iwamoto et al. 2004),
in ``Late Hot Flasher'' stars experiencing
strong mass loss on the RGB (Cassisi et al. 2003;
Brown
et al. 2001),
and in H-deficient post AGB (PAGB) stars. These events are referred to
with various names in the literature. Here we use the nomenclature
``dual flashes'' (Campbell
& Lattanzio 2008), since they all have in common
simultaneous hydrogen and helium flashes.
Dual flash events often lead to a splitting of the single
helium
convection zone (HeCZ) into two parts (double convection zone): one
sustained by helium burning and a second one by hydrogen burning via
CNO cycles (Fig. 1).
Double convection zones are
structures that are commonly encountered in stellar models, but their
hydrodynamic properties have so far only been studied for the oxygen
and carbon burning shell of a 23 ![]() star by Meakin & Arnett
(2006).
star by Meakin & Arnett
(2006).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14461figkipd.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg52.png)
|
Figure 1:
Upper panel: Kippenhahn diagram of a stellar
evolutionary calculation during the core helium flash of a
0.85 |
| Open with DEXTER | |
In the following we describe two-dimensional (2D) and three-dimensional (3D) hydrodynamic simulations of a helium core during the core helium flash with a single convection zone (Pop I; in 3D only) and a double convection zone (Pop III, in 2D and 3D), respectively. Previous studies have indicated that there is a strong interaction between the adjacent shells of a double convection zone by internal gravity waves (Meakin & Arnett 2006).
We introduce the stellar models used as input for our hydrodynamic simulations in Sect. 2, briefly discuss the physics included in our simulations in Sect. 3, and give a short description of our hydrodynamics code and the computational setup in Sect. 4. Subsequently, we present and compare the results of our 2D and 3D hydrodynamic simulations in Sect. 5. In particular, we discuss turbulent entrainment at the convective boundaries for our single convection zone model, the temporal evolution of its kinetic energy density, and how our results compare with the predictions of mixing-length theory (MLT). We proceed similarly for our hydrodynamic double convection zone models, except for turbulent entrainment as these models were not convective for a sufficiently long time (see Sect. 5.3). Finally, a summary of our findings is given in Sect. 6.
2 Physical conditions and initial data
Our initial helium core models (Table 1) with single and
double convection zones (models M and SC, respectively) are
obtained
from 1D stellar evolutionary calculations of a Pop I star (Z
= 0.02) with a mass of 1.25 ![]() ,
and a Pop III star (Z = 0) with a mass of
0.85
,
and a Pop III star (Z = 0) with a mass of
0.85 ![]()
![]() , respectively. Both models
are characterized by an off-center helium
ignition which results in convection zones characterized by a
temperature gradient close to the adiabatic
, respectively. Both models
are characterized by an off-center helium
ignition which results in convection zones characterized by a
temperature gradient close to the adiabatic![]() one above the helium burning source.
one above the helium burning source.
The helium cores of both models are composed of a gas which is
almost
completely ionized, as the ionization potentials of both He and He+(
![]() eV
and
eV
and ![]() eV,
respectively) are very small compared to the thermal energy,
i.e.,
eV,
respectively) are very small compared to the thermal energy,
i.e.,
| (1) |
where
In the central part of the models (beneath the convection zones) the
electron density is so high that the gas is highly degenerate. On the
other hand, the density of electrons in the single and double
convection zone is much lower due to a strong expansion that occurred a
little earlier in the evolution![]() .
Thus, the degeneracy has been lifted in the convection zones,
i.e., the ratio of the Fermi energy
.
Thus, the degeneracy has been lifted in the convection zones,
i.e., the ratio of the Fermi energy
![]() of the electrons (Weiss
et al. 2004) and their typical thermal energy is
small,
of the electrons (Weiss
et al. 2004) and their typical thermal energy is
small,
| (2) |
where
The ions can be described as an ideal, non-relativistic Boltzmann gas,
because the ratio of their Fermi energy
![]() and their typical
thermal energy is small,
and their typical
thermal energy is small,
| (3) |
where
Table 1: Initial models M & SC.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figinimt1.eps}\includegraphics[width=7.5cm,clip]{14461figinimt2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg94.png)
|
Figure 2: Left: temperature distribution in the helium core in model M (long-dashed), and in model SC (solid) with its stabilized counterpart (dash-dotted red), respectively. The two parts of the double convection zone present in model SC are denoted by CVZ-1 and CVZ-2, respectively. Right: entropy distribution of model M (solid) and model SC (long-dashed), respectively. |
| Open with DEXTER | |
Convection may become turbulent showing random spatial and temporal
fluctuations. This can be characterized by the dimensionless Reynolds
number ![]() (Landau & Lifshitz
1966) which is basically the ratio
of inertial to viscous forces. The turbulent regime is entered once
(Landau & Lifshitz
1966) which is basically the ratio
of inertial to viscous forces. The turbulent regime is entered once
![]() exceeds a
certain critical value
exceeds a
certain critical value
![]() ,
typically being of the order of 103, at which
small fluctuations in the flow are no
longer damped. We estimate that the Reynolds numbers in the central
convection zones of our models are
,
typically being of the order of 103, at which
small fluctuations in the flow are no
longer damped. We estimate that the Reynolds numbers in the central
convection zones of our models are
| (4) |
where
![]() (
(
![]() ),
),
![]() (
(
![]() ),
),
![]() (
(
![]() ),
and
),
and
![]() (
(
![]() )
are the typical
densities, lengths, velocities, and viscosities
)
are the typical
densities, lengths, velocities, and viscosities![]() of the convective flow in model M (SC) as predicted by stellar
evolutionary calculations. These values imply that the flow is highly
turbulent, which leads to complications when trying to simulate such
flows, as turbulence is an intrinsically three-dimensional phenomenon
involving a large range of spatial and temporal scales. We recall
that, in three-dimensional turbulent flow, large structures are
unstable and cascade into smaller vortices according to Kolmogorov's
theory down to molecular scales where the kinetic
energy of the flow is eventually dissipated into heat.
of the convective flow in model M (SC) as predicted by stellar
evolutionary calculations. These values imply that the flow is highly
turbulent, which leads to complications when trying to simulate such
flows, as turbulence is an intrinsically three-dimensional phenomenon
involving a large range of spatial and temporal scales. We recall
that, in three-dimensional turbulent flow, large structures are
unstable and cascade into smaller vortices according to Kolmogorov's
theory down to molecular scales where the kinetic
energy of the flow is eventually dissipated into heat.
If L is the largest (integral) scale
characterizing a flow, and lthe scale where viscous
dissipation dominates, one has the well known
relation:
In the convection zone, where the Reynolds number
To account for turbulence on the numerically unresolved scales, one usually adopts sub-grid scale models e.g., the quite popular one by Smagorinsky (1963), which describe the energy transfer from the smallest numerically resolved turbulent elements to those at the dissipation length scale using various (phenomenological and/or physical) model and flow dependent parameters. We did not employ a sub-grid scale model, as it seems not to lead to qualitative differences in the hydrodynamic behavior of the core helium flash (Achatz 1995). Moreover Sitine et al. (2000) showed that the PPM method used in our hydrodynamics code gives results consistent with the decay of turbulent eddies according to Kolmogorov's cascade.
2.1 Initial stellar model M
The initial model M (Table 1, Fig. 2) was
obtained with the stellar evolution code GARSTEC
(Weiss
& Schlattl 2000,2007) by Achim Weiss,
and
represents a 1.25 ![]() star at the peak of the core helium flash
characterized by an off-center temperature maximum at the base of a
single convection zone sustained by helium burning. Additional
information about the model can be found in Mocák et al. (2008,2009).
star at the peak of the core helium flash
characterized by an off-center temperature maximum at the base of a
single convection zone sustained by helium burning. Additional
information about the model can be found in Mocák et al. (2008,2009).
As we are interested here only in the hydrodynamic evolution
of the
helium core![]() , we consider of model M
only the shell between
, we consider of model M
only the shell between ![]() cm
to
cm
to ![]() cm,
which contains the single convection zone
powered by triple-
cm,
which contains the single convection zone
powered by triple-![]() burning. Originally, the convection zone
reaches from
burning. Originally, the convection zone
reaches from ![]() cm
(local pressure scale height
cm
(local pressure scale height
![]() cm)
to
cm)
to ![]() cm
(local pressure scale
height
cm
(local pressure scale
height ![]() cm).
From the bottom to the top of the
convection zone the pressure changes by
cm).
From the bottom to the top of the
convection zone the pressure changes by ![]() 1 order of magnitude,
from
1 order of magnitude,
from
![]() to
to
![]() .
We
note that both the base and the top of the convection zone are located
sufficiently far away from the (radial) grid boundaries.
.
We
note that both the base and the top of the convection zone are located
sufficiently far away from the (radial) grid boundaries.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figinicomp1.eps}\includegraphics[width=7.5cm,clip]{14461figinicomp2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg120.png)
|
Figure 3:
Left: chemical composition of the helium core
in model heflpopIII.2d.2 (SC). Right: nuclear
energy production rate as a function of radius r.
Initial rates (at t=0) are indicated by
dotted-black curves. Rates in model heflpopI.3d (SC) at t
= 6400 s (solid-red), and in model M at
|
| Open with DEXTER | |
Model M contains the chemical species 1H,
3He, 4He,
12C, 13C, 14N,
15N, 16O ,17O,24Mg,
and 28Si. However, since we are not interested
in details of its
chemical evolution, we considered only the abundances of 4He,
12C, and 16O in our
hydrodynamic simulations. This is
justified as the triple ![]() reaction dominates the nuclear energy
production rate during the core helium flash. For the remaining
composition we assume that it can be represented by a gas with a mean
molecular weight equal to that of 20Ne, as its
nucleon number agrees
well with the average nucleon number of the neglected nuclear species.
reaction dominates the nuclear energy
production rate during the core helium flash. For the remaining
composition we assume that it can be represented by a gas with a mean
molecular weight equal to that of 20Ne, as its
nucleon number agrees
well with the average nucleon number of the neglected nuclear species.
The stellar model had to be relaxed into hydrostatic equilibrium after it was mapped to the numerical grid of our hydrodynamics code. This was achieved with an iterative procedure, which keeps the density distribution of the model almost constant, but modifies its pressure distribution to achieve hydrostatic equilibrium (Mocák 2009). This mapping process has usually a negligible effect on the stellar structure.
2.2 Initial stellar model SC
The initial model SC (Table 1, Figs. 1 to 3) was computed
by Simon W. Campbell using the
Monash/Mount Stromlo stellar evolution code (MONSTAR)
(Campbell
& Lattanzio 2008; Wood & Zarro 1981). It
corresponds to a metal-free Pop III
star with a mass of 0.85 ![]() near the peak of the core helium
flash. Metal-free stars with masses
near the peak of the core helium
flash. Metal-free stars with masses ![]() 1
1 ![]() do not undergo
the core helium flash (as opposed to
do not undergo
the core helium flash (as opposed to
![]()
![]() at solar
metallicity). The helium core flash commences with a very off-center
ignition of helium in a relatively dense environment under degenerate
conditions, and results in a fast growing convection zone powered by
helium burning that relatively quickly reaches the surrounding
hydrogen shell (Fujimoto
et al. 1990). This causes sudden mixing of
protons down into the hot helium core (Fig. 3), and
leads to rapid nuclear burning via the CNO cycle i.e., a
hydrogen flash.
Since the core helium flash is still ongoing we refer to this as a
``Dual Core Flash'' (DCF). We note that this event has also been
referred to as ``helium flash induced mixing''
(Cassisi
et al. 2003; Weiss et al. 2004;
Schlattl
et al. 2001), and ``helium flash-driven deep
mixing''
(Suda et al. 2004).
The CNO burning leads to an increase of the
temperature inside the helium-burning driven convection zone, and
causes it to split into two. The result is a lower convection zone
still powered by helium burning and a second one powered by the CNO
cycle (Fig. 3,
right panel). In the following we will refer to the split convection
zone as a double convection zone.
at solar
metallicity). The helium core flash commences with a very off-center
ignition of helium in a relatively dense environment under degenerate
conditions, and results in a fast growing convection zone powered by
helium burning that relatively quickly reaches the surrounding
hydrogen shell (Fujimoto
et al. 1990). This causes sudden mixing of
protons down into the hot helium core (Fig. 3), and
leads to rapid nuclear burning via the CNO cycle i.e., a
hydrogen flash.
Since the core helium flash is still ongoing we refer to this as a
``Dual Core Flash'' (DCF). We note that this event has also been
referred to as ``helium flash induced mixing''
(Cassisi
et al. 2003; Weiss et al. 2004;
Schlattl
et al. 2001), and ``helium flash-driven deep
mixing''
(Suda et al. 2004).
The CNO burning leads to an increase of the
temperature inside the helium-burning driven convection zone, and
causes it to split into two. The result is a lower convection zone
still powered by helium burning and a second one powered by the CNO
cycle (Fig. 3,
right panel). In the following we will refer to the split convection
zone as a double convection zone.
The electron degeneracy in the double convection zone has
already been
significantly lifted to ![]() .
It can be
shown that for a degeneracy parameter
.
It can be
shown that for a degeneracy parameter ![]() ,
the gas pressure is
essentially that of a nondegenerate gas (Clayton
1968). This
confirms our previous conclusion based on the ratio of the Fermi and
thermal energy of the electrons (Sect. 2).
,
the gas pressure is
essentially that of a nondegenerate gas (Clayton
1968). This
confirms our previous conclusion based on the ratio of the Fermi and
thermal energy of the electrons (Sect. 2).
In our hydrodynamic simulations we considered a shell from
model SC
which extends from ![]() cm to
cm to
![]() cm
containing the double convection zone. Initially, the inner convection
zone (powered by triple-
cm
containing the double convection zone. Initially, the inner convection
zone (powered by triple-![]() burning) covers a region from
burning) covers a region from
![]() cm
(local pressure scale height
cm
(local pressure scale height
![]() cm)
to
cm)
to ![]() cm
(local pressure scale
height
cm
(local pressure scale
height ![]() cm),
while the outer convection zone stretches
from there up to
cm),
while the outer convection zone stretches
from there up to ![]() cm
(local pressure scale height
cm
(local pressure scale height
![]() cm).
From the bottom to the top of the double convection zone
the pressure changes by
cm).
From the bottom to the top of the double convection zone
the pressure changes by ![]() 3
orders of magnitude from
3
orders of magnitude from
![]() erg to
erg to
![]() .
Again, we have
ensured that the region of interest was located sufficiently far away
from the radial grid boundaries.
.
Again, we have
ensured that the region of interest was located sufficiently far away
from the radial grid boundaries.
Our hydrodynamic simulations were performed adopting the mass fractions of all the species used in the corresponding stellar evolutionary calculations, namely 1H, 3He, 4He, 12C, 14N, and 16O. Since the evolutionary model did not include 13C and 13N, we determined their mass fractions assuming that the CNO cycle had been operating in equilibrium. The remaining composition is represented by a gas with the molecular weight of 20Ne.
The model was relaxed to hydrostatic equilibrium in the same manner as in case of model M. This process resulted in small fluctuations in the temperature profile (Fig. 2), which were smeared out after the onset of convection.
3 Input physics
The input physics of our hydrodynamic simulations is identical
to that
one described in Mocák
et al. (2008), except for the number of nuclear
species employed in the simulations based on the initial model SC. We
use an equation of state that includes contributions from radiation,
ideal Boltzmann gases, and an electron-positron component
(Timmes & Swesty 2000).
Thermal transport was neglected as the
maximum amount of energy transported by radiation and heat conduction
is smaller than the convective flux by at least seven (three) orders
of magnitude in model M (SC). Neutrinos act as a nuclear
energy sink,
but carry away less than <
![]() .
This is a negligible amount
(especially for the timescales covered by our simulations) when
compared to the maximum nuclear energy production
.
This is a negligible amount
(especially for the timescales covered by our simulations) when
compared to the maximum nuclear energy production
![]() ,
which is
,
which is ![]()
![]() for
model M, and
for
model M, and ![]()
![]() in
model SC, respectively (Fig. 3).
in
model SC, respectively (Fig. 3).
3.1 Nuclear reactions
We employed two different nuclear networks for our simulations, as the nuclear species considered in models M and SC differ. The nuclear reaction network used in the hydrodynamic simulation based on the initial model M (Table 1) consists of four nuclei (Sect. 2.1) coupled by seven reactions. The network is identical to that one described by Mocák et al. (2008) i.e.,
| He 4 | + | C12 |
|
O16 | + | ||||
| He 4 | + | O16 |
|
Ne20 | + | ||||
| O16 | + |
|
He 4 | + | C12 | ||||
| Ne20 | + |
|
He 4 | + | O16 | ||||
| C12 | + | C12 |
|
Ne20 | + | He 4 | |||
| He 4 | + | He4 | + | He4 |
|
C12 | + | ||
| C12 | + |
|
He4 | + | He 4 | + | He4 |
The nuclear reactions considered in the hydrodynamic simulations based on the initial model SC (Table 1) are described by a reaction network consisting of nine nuclei (Sect. 2.2) coupled by the following 16 reactions:
| H1 | + | He3 |
|
He4 | + | ||||||
| He4 | + | C12 |
|
O16 | + | ||||||
| He4 | + | N13 |
|
H1 | + | O16 | |||||
| H1 | + | C13 |
|
N14 | + | ||||||
| H1 | + | C12 |
|
N13 | + | ||||||
| H1 | + | O16 |
|
He4 | + | N13 | |||||
| He4 | + | O16 |
|
Ne20 | + | ||||||
| C12 | + | C12 |
|
He4 | + | Ne20 | + | ||||
| N13 | + |
|
|
H 1 | + | C12 | |||||
| N14 | + |
|
|
H 1 | + | C13 | |||||
| O16 | + |
|
|
He4 | + | C12 | |||||
| Ne20 | + |
|
|
He4 | + | O16 | |||||
| C12 | + |
|
|
He4 | + | He4 | + | He4 | |||
| He4 | + | He4 | + | He4 |
|
C12 | + | ||||
| He3 | + | He3 |
|
H1 | + | H1 | + | He4 | + | ||
| H1 | + | H1 | + | He4 |
|
He3 | + | He3 | + |
This network reproduces the nuclear energy generation rate of the original stellar model very well (Fig. 3).
Note, that although the value of the temperature maximum, ![]() ,
is higher in model SC than in model M, the energy generation
rate is
lower at
,
is higher in model SC than in model M, the energy generation
rate is
lower at ![]() in model SC, because the helium mass fraction
X(4He) is smaller in that
model (0.956 as compared to 0.970 for
model M).
in model SC, because the helium mass fraction
X(4He) is smaller in that
model (0.956 as compared to 0.970 for
model M).
Table 2: Some properties of the 3D simulation based on model M.
4 Hydrodynamic code and computational setup
We use the hydrodynamics code Herakles (Kifonidis et al. 2003; Mocák et al. 2008,2009; Kifonidis et al. 2006) which solves the Euler equations coupled with source terms corresponding to gravity and nuclear burning. The hydrodynamic equations are integrated with the piecewise parabolic method of Colella & Woodward (1984) and a Riemann solver for real gases according to Colella & Glaz (1984). The evolution of the nuclear species is described by a set of additional continuity equations (Plewa & Müller 1999). Self-gravity is implemented according to Müller & Steimnetz (1995) and nuclear burning is treated by the semi-implicit Bader-Deuflhard scheme (Press et al. 1992).
We performed one 3D simulation based on the initial model M,
which
covered roughly 27 h of stellar evolution
(Table 2).
This model (henceforth heflpopI.3d) was
evolved on a computational grid consisting of a
![]() -wide
wedge in both
-wide
wedge in both ![]() and
and ![]() -direction
centered at the equator. The small
angular size of the grid allowed us to achieve a relatively high
angular resolution (
-direction
centered at the equator. The small
angular size of the grid allowed us to achieve a relatively high
angular resolution (
![]() )
with a modest number of angular zones
(
)
with a modest number of angular zones
(
![]() ).
).
In addition, we performed two 2D (henceforth models
heflpopIII.2d.1
and heflpopIII.2d.2) and one 3D simulation (henceforth model
heflpopIII.3d) based on the initial model SC covering about
1.8 h
and 0.39 h of stellar evolution, respectively
(Table 4).
We used a computational grid consisting of a
![]() -wide angular wedge centered
at the equator in case of models
heflpopIII.2d.1 and heflpopIII.3d, and of a
-wide angular wedge centered
at the equator in case of models
heflpopIII.2d.1 and heflpopIII.3d, and of a
![]() wedge in case of
model heflpopIII.2d.2.
wedge in case of
model heflpopIII.2d.2.
We imposed reflective boundary conditions in the radial direction and periodic ones in the angular directions in all our multi-dimensional simulations.
5 Results
In this section, we first present the characteristics of the hydrodynamic simulation based on the initial model M, i.e., model heflpopI.3d, which shows a fast growth of the convection zone (Sect. 5.1). A growth rate of this magnitude likely leads to a hydrogen injection phase (Sect. 5.2), which may resemble the one seen in the initial model SC, whose hydrodynamic properties are discussed in Sect. 5.3.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figveloc.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg159.png)
|
Figure 4:
Radial velocity distributions for the 3D model heflpopI.3d. The dotted
and green dashed lines show the time (from 10 000 s
to 30 000 s) and angle-averaged radial velocity, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figflx.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg160.png)
|
Figure 5: Convective and kinetic energy fluxes (FC and FK, respectively) as a function of radius averaged (from 33 000 s to 53 000 s) over about 20 convective turnover timescales for the 3D model heflpopI.3d. The dotted vertical lines mark the edges of the single convection zone in the initial model M according to the Schwarzschild criterion. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figtmpgradpop1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg161.png)
|
Figure 6:
Radial distribution of the adiabatic temperature gradient
|
| Open with DEXTER | |
5.1 Single flash
Table 2
provides some characteristic parameters of our
3D simulation heflpopI.3d based on the initial model M. After
convection reaches a quasi steady-state in this model, the maximum
temperature rises at the rate of 80 K s-1,
i.e., only 20% slower than
predicted by canonical stellar evolution theory. This corresponds to
an increase of the nuclear energy production rate from
![]() at
at ![]() s to
s to
![]() at
at
![]() s. Consequently, the
maximum convective velocities
rise by 26% from about
s. Consequently, the
maximum convective velocities
rise by 26% from about
![]() to
to
![]()
![]() . As illustrated in
Fig. 4
these velocities match those
given by the mixing length theory quite well. During the first
third of the simulation (up to about 30 000 s) the
angle and time
averaged radial velocity in the convective layer exceeds the velocity
given for inital model M by the mixing-length theory,
. As illustrated in
Fig. 4
these velocities match those
given by the mixing length theory quite well. During the first
third of the simulation (up to about 30 000 s) the
angle and time
averaged radial velocity in the convective layer exceeds the velocity
given for inital model M by the mixing-length theory,
![]() ,
by about 20%, while the velocity modulus,
,
by about 20%, while the velocity modulus,
![]() ,
is about 30%
larger than
,
is about 30%
larger than ![]()
![]() . Towards the end of our
simulation the angle and time averaged modulus of the velocity is about
twice as large as
. Towards the end of our
simulation the angle and time averaged modulus of the velocity is about
twice as large as ![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figexppop1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg171.png)
|
Figure 7:
Radial distribution of the expansion velocity, |
| Open with DEXTER | |
Contrary to our previous study (Mocák
et al. 2009), we do not find a
sub-adiabatic gradient in the outer part of the convection zone![]() . The reason for this
difference is probably the increased grid
resolution of our present 3D simulation, which results in less heat
diffusion due to numerical dissipation, and hence a super-adiabatic
temperature gradient similar to the initial one
(Fig. 6)
. The reason for this
difference is probably the increased grid
resolution of our present 3D simulation, which results in less heat
diffusion due to numerical dissipation, and hence a super-adiabatic
temperature gradient similar to the initial one
(Fig. 6)
At a radius
![]() cm
convection transports almost
90% of the liberated nuclear energy, i.e.,
cm
convection transports almost
90% of the liberated nuclear energy, i.e.,
![]() (Fig. 5). The energy flux
due to thermal transport is
negligible (Sect. 3).
(Fig. 5). The energy flux
due to thermal transport is
negligible (Sect. 3).
We observe internal gravity waves![]() or g-modes in the convectively stable layers. These g-modes are
strongly instigated only during certain evolutionary phases (g-mode
events) because of the intermittent nature of the convective flow. The
g-mode events are correlated with outbursts in kinetic energy of the
convection zone (Meakin
& Arnett 2007).
or g-modes in the convectively stable layers. These g-modes are
strongly instigated only during certain evolutionary phases (g-mode
events) because of the intermittent nature of the convective flow. The
g-mode events are correlated with outbursts in kinetic energy of the
convection zone (Meakin
& Arnett 2007).
![\begin{figure}
\par\includegraphics[height=5.2cm]{14461figsvelbndry1.eps}\includ...
...elbndry2.eps}\includegraphics[height=5.2cm]{14461figsvelbndry3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg176.png)
|
Figure 8:
Color maps of the modulus of the velocity (in units of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=7.4cm]{14461figkened.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg177.png)
|
Figure 9:
Temporal evolution of radial distribution of the (color coded)
logarithm of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
We observe a growth of the size of the single convection zone due to
turbulent entrainment at the convective boundary on a dynamic
timescale (Figs. 8
to 10),
and
estimate the corresponding entrainment speeds by adopting the
prescription of Meakin
& Arnett (2007). Turbulent entrainment
involves mass entrainment (Fig. 8) rather
than a
diffusion process, which acts to reduce the buoyancy jump at the
convective boundary allowing matter to be mixed further. The
entrainment velocity or the interface migration velocity, ![]() ,
is
given by (see Eq. (32) of Meakin & Arnett 2007)
,
is
given by (see Eq. (32) of Meakin & Arnett 2007)
where
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461figcargrow1.eps}\includegraphics[width=8.5cm,clip]{14461figcargrow2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg185.png)
|
Figure 10:
Angular averaged 12C mass fraction as a
function of radius near the inner ( left) and outer
edge ( right) of the convection zone in the 3D model
heflpopI.3d at t
= 100 000 s. The thick line gives the corresponding
temperature stratification, and the vertical dotted lines mark the
edges of the convection zone at t = 0 s.
The observed entrainment velocities |
| Open with DEXTER | |
The entrainment velocity derived for our models, ![]() ,
are calculated
by measuring the radial position of the convective boundaries defined
by the condition X(12C)
,
are calculated
by measuring the radial position of the convective boundaries defined
by the condition X(12C)
![]() ,
as 12C is much
less abundant outside the convection zone (Fig. 10).
The expansion velocity (zero in hydrostatic equilibrium) is given by
,
as 12C is much
less abundant outside the convection zone (Fig. 10).
The expansion velocity (zero in hydrostatic equilibrium) is given by
![]() ,
where
,
where ![]() is the partial time derivative of the mass
is the partial time derivative of the mass ![]() of a shell of density
of a shell of density ![]() at a radius r.
at a radius r.
We find in our models that ![]() ,
which includes the expansion velocity
,
which includes the expansion velocity ![]() ,
agrees very well with the velocity
,
agrees very well with the velocity ![]() predicted
by theoretical considerations of the entrainment process (see
Eq. (6)),
despite the crude estimate of the divergence of
the buoyancy flux
predicted
by theoretical considerations of the entrainment process (see
Eq. (6)),
despite the crude estimate of the divergence of
the buoyancy flux![]() through
through ![]() .
The velocity given by the difference
.
The velocity given by the difference
![]() ,
which is the actual entrainment speed in our models, differs
from the theoretically estimate
,
which is the actual entrainment speed in our models, differs
from the theoretically estimate ![]() by 0.8
by 0.8
![]() and
2.1
and
2.1
![]() at
the inner and outer convection boundary, respectively.
at
the inner and outer convection boundary, respectively.
Table 3: Some quantities characterizing the convective boundaries of the 3D model heflpopI.3d.
It seems that turbulent entrainment is a robust process which has been seen to operate under various conditions in different stars (Mocák et al. 2009; Meakin & Arnett 2007). This process may be behind the observed Al/Mg anti-correlation (Shetrone 1996a; Yong et al. 2006; Shetrone 1996b), which could result from an injection of hydrogen into the helium core and a subsequent dredge-up (Fujimoto et al. 1999; Langer et al. 1997; Langer & Hoffman 1995; Langer et al. 1993).
5.2 From the single to the dual flash
If the radial position of the innermost edge of the hydrogen-rich
layers was fixed at its initial value in model M at
![]() cm
(no expansion), the outer convection boundary would reach
the hydrogen-rich layer due to the turbulent entrainment within only
17 days, and the helium core would experience a dual core flash (DCF)
known from low-mass Pop III stars.
cm
(no expansion), the outer convection boundary would reach
the hydrogen-rich layer due to the turbulent entrainment within only
17 days, and the helium core would experience a dual core flash (DCF)
known from low-mass Pop III stars.
However, the hydrogen layer will initially expand outwards at a faster rate than the outer convective boundary (Fig. 7). This delays the expected onset of the hydrogen injection a little, as the outer convection boundary has to catch up with the hydrogen layer expanding away from the HeCZ. As the expansion velocities of our hydrodynamic models are biased by the imposed reflective boundaries in radial direction, we did not use these values here. To get an estimate for the onset of the hydrogen injection we instead used the expansion speed of the helium core as predicted by stellar evolutionary calculations (Table 3), and find that the injection of hydrogen into the helium core should take place within 23 days.
Table 4: Some properties of the 2D and 3D hydrodynamic models based on initial model SC.
![\begin{figure}
\par\includegraphics[width=5.4cm,height=7.95cm,clip]{14461figsnap...
...
\includegraphics[width=5cm,height=7.5cm,clip]{14461figsnap2d3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg213.png)
|
Figure 11:
Snapshots of the spatial distribution of the velocity modulus
|
| Open with DEXTER | |
This is still a very short time, and even if our estimate for the time
until the onset of the hydrogen injection was wrong by 5 orders of
magnitude, the injection will occur before the first subsequent mini
helium flash![]() takes place, which is
supposed to occur in roughly 105 years.
takes place, which is
supposed to occur in roughly 105 years.
Figure 11 shows snapshots from 2D hydrodynamic simulations (Mocák et al. 2009) of a (single) core helium flash based on initial model M (left panel), and of a dual core (helium + hydrogen) flash based on initial model SC (middle and right panels). The figure suggests that even if the core helium flash starts out with a single convection zone in a low-mass Pop I star, this convection zone may evolve due to its growth by turbulent entrainment (indicated by the arrow in the left panel of the figure) into a double convection zone like that found in models of Pop III stars. Although the upper boundary of the single convection zone is still far away from the hydrogen-rich layers at the end of the simulation, it should get there eventually. We find no reason in any of our 2D or 3D simulations including the new model heflpopI.3d why turbulent entrainment should cease before the outer convective boundary reaches the edge of the helium core. Actually, as the maximum temperature of the helium core grows and the convective flow becomes faster, entrainment will eventually speed up (Mocák et al. 2009).
On the other hand, subsequent mini helium flashes are unlikely
to occur,
because we estimate that at the observed entrainment velocity the inner
convective boundary will reach the center of the star in ![]() 90 days.
Note in this respect that the fast entrainment speed of the
inner convective boundary derived from our previous 2D models
(Mocák et al. 2008)
is not confirmed by the new 3D model. The
entrainment rate is actually slower in the new 3D model, which
was
expected (Mocák et al. 2009).
90 days.
Note in this respect that the fast entrainment speed of the
inner convective boundary derived from our previous 2D models
(Mocák et al. 2008)
is not confirmed by the new 3D model. The
entrainment rate is actually slower in the new 3D model, which
was
expected (Mocák et al. 2009).
The turbulent entrainment at the inner convection boundary
heats the
layers beneath at a rate
![]() K s-1, i.e., it is
quite efficient in lifting the electron degenaracy in the matter below
the convection zone.
K s-1, i.e., it is
quite efficient in lifting the electron degenaracy in the matter below
the convection zone.
According to the above discussion we propose a somewhat
speculative
scenario for the core helium flash in low-mass Pop I stars.
These
stars ignite helium burning under degenerate conditions and develop a
single convection zone, which at some point extends due to turbulent
enrainment up to their hydrogen-rich surface layers. The convection
zone eventually penetrates these layers, and dredges down hydrogen
into the helium core. This ignites a secondary flash driven by CNO
burning, which together with triple-![]() burning and inwards
turbulent entrainment leads eventually to the lifting of the core's
degeneracy, i.e., the star will settle down on the horizontal
branch.
burning and inwards
turbulent entrainment leads eventually to the lifting of the core's
degeneracy, i.e., the star will settle down on the horizontal
branch.
5.3 Dual flash
We have performed three simulations of the core helium flash based on the Pop III initial model SC which possesses two convection zones sustained by helium and CNO burning, respectively. Some characteristic properties of these dual flash simulations are summarized in Table 4.
5.3.1 Model heflpopIII.2d.2
Despite a nuclear energy production rate due to CNO burning in the
outer convection zone (
![]() ,
which is roughly eight times higher than that due to
triple-
,
which is roughly eight times higher than that due to
triple-![]() burning in the inner zone
burning in the inner zone
![]() ),
convective motions first appear within the
inner convection zone after about 200 s. The onset of
convection in
the outer zone is delayed until about 500 s
(Figs. 12, 15). After some
time the model relaxes into a quasi steady-state, where the r.m.s
values of the angular velocity are comparable or even larger than
those of the radial component (Fig. 12). This
property of the velocity field implies the presence of g-modes or
internal gravity waves (Asida
& Arnett 2000), which is a surprising fact.
G-modes should not exist in the convection zone according to the
canonical theory, as any density perturbation in a convectively
unstable zone will depart its place of origin exponentially fast
(Kippenhahn & Weigert
1990) until the flow becomes convectively stable.
),
convective motions first appear within the
inner convection zone after about 200 s. The onset of
convection in
the outer zone is delayed until about 500 s
(Figs. 12, 15). After some
time the model relaxes into a quasi steady-state, where the r.m.s
values of the angular velocity are comparable or even larger than
those of the radial component (Fig. 12). This
property of the velocity field implies the presence of g-modes or
internal gravity waves (Asida
& Arnett 2000), which is a surprising fact.
G-modes should not exist in the convection zone according to the
canonical theory, as any density perturbation in a convectively
unstable zone will depart its place of origin exponentially fast
(Kippenhahn & Weigert
1990) until the flow becomes convectively stable.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figkindnstdec1.eps}\par\includegraphics[width=8cm,clip]{14461figkindnstdec2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg221.png)
|
Figure 12:
Temporal evolution of the radial distribution of the (color coded)
logarithm of the angular averaged radial (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figtmpgradpop3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg222.png)
|
Figure 13:
Adiabatic temperature gradient
|
| Open with DEXTER | |
When convection begins to operate in both zones, the total
energy
production rate temporarily drops by ![]() 20%, but continues to
rise at a rate of
20%, but continues to
rise at a rate of ![]()
![]() after
after
![]() s.
Nevertheless, the convective flow decays fast in both
convection zones - at a rate of
s.
Nevertheless, the convective flow decays fast in both
convection zones - at a rate of
![]()
![]() (Fig. 15),
probably because the initial conditions
represented by the stabilized remapped initial model are too
different from those of the original stellar model. They disfavor
convection since the stabilized remapped model has a slightly
smaller temperature gradient than the original one
(Fig. 13).
Stabilization of the remapped initial model was essential, to prevent
it from strongly deviating from hydrostatic equilibrium. However,
keeping the density fixed while adjusting the pressure in the remapped
model does not guarantee that entropy gradients are preserved. Since
convection depends sensitively on these gradients, it can affect the
results.
(Fig. 15),
probably because the initial conditions
represented by the stabilized remapped initial model are too
different from those of the original stellar model. They disfavor
convection since the stabilized remapped model has a slightly
smaller temperature gradient than the original one
(Fig. 13).
Stabilization of the remapped initial model was essential, to prevent
it from strongly deviating from hydrostatic equilibrium. However,
keeping the density fixed while adjusting the pressure in the remapped
model does not guarantee that entropy gradients are preserved. Since
convection depends sensitively on these gradients, it can affect the
results.
Shortly after convection is triggered in both the outer and the inner zone this double convection structure vanishes, and after about 2000 s there is no evidence left for two separate convection zones (Fig. 12).
Due to the relatively short temporal coverage of the evolution and due to the decaying convective flow, we did not analyze the energy fluxes and turbulent entrainment of this model. Penetrating plumes do not exist in the convection zone (initially determined by the Schwarzschild criterion), as it is dominated rather by g-modes. Hence, firm conclusions are difficult to derive, but we plan to address this issue elsewhere. We are now going to introduce some basic characteristic of internal gravity waves or g-modes that are required to draw further conclusions.
G-modes:
In a convectively stable region, any displaced mass element or blob
(density perturbation) is pushed back by the buoyancy force. On its
way back to its original position, the blob gains momentum and
therefore starts to oscillate around its original position. Assuming,
the element is displaced by a distance ![]() ,
has an excess
density
,
has an excess
density ![]() ,
and is in pressure equilibrium with the
surrounding gas (
,
and is in pressure equilibrium with the
surrounding gas (
![]() ), one can derive an equation
for the
acceleration of the element:
), one can derive an equation
for the
acceleration of the element:
where g is the gravitational acceleration,
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14461figbrunt1.eps}\par\includegraphics[width=6.5cm,clip]{14461figbrunt2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg234.png)
|
Figure 14:
Radial distributions of the (square of the) Brunt-Väisälä buoyancy
frequency N2 in the
2D model heflpopIII.2d.2 averaged between 1480 s and
6000 s (top), and in the 3D model
heflpopI.3d averaged between 6600 s and
100 000 (bottom), respectively.
The angular and temporal variation of N2
at a given radius are indicated by the gray shaded region. The inserts
show a zoom of the region around N2
= 0 to enlarge the variations of N2
in the convection zone which are |
| Open with DEXTER | |
Let us assume now that the element, after an initial displacement
![]() ,
moves adiabatically (
,
moves adiabatically (
![]() )
through a convectively stable layer. The element
is accelerated back towards its equilibrium position and starts to
oscillate around this position according to the solution of
Eq. (7):
)
through a convectively stable layer. The element
is accelerated back towards its equilibrium position and starts to
oscillate around this position according to the solution of
Eq. (7):
| (8) |
where the (square of the) Brunt-Väisälä frequency is given by
In a convectively unstable region (assuming
G-modes appear in layers of gas stratified under gravity and
are
spatial oscillatory displacements of density perturbations. The
dispersion relation of such density displacements, assumed to vary as
![]() ,
reads
(Dalsgaard 2003)
,
reads
(Dalsgaard 2003)
where
We find such horizontal structures in our models visible mainly in the
radiative layer of the splitted convection zone (Fig. 11). By
decomposition of the specific kinetic energy density of the model into
the radial (
![]() /2) and horizontal (
/2) and horizontal (
![]() /2) component, we also find
that the horizontal displacements are characterized by higher values
of the kinetic energy density compared to the corresponding values of
the vertical displacements already 2000 s after the start of
the
simulation (Fig. 12).
Additionally, N2 is
mostly positive in these models (Fig. 14), indicating
convective stability throughout the double convection zone. This
proves the existence of internal gravity waves in the decaying double
convection zone. The situation is different in our 3D model
heflpopI.3d, where N2 is (on
average) small and negative
everywhere in the single convection zone (Fig. 14).
/2) component, we also find
that the horizontal displacements are characterized by higher values
of the kinetic energy density compared to the corresponding values of
the vertical displacements already 2000 s after the start of
the
simulation (Fig. 12).
Additionally, N2 is
mostly positive in these models (Fig. 14), indicating
convective stability throughout the double convection zone. This
proves the existence of internal gravity waves in the decaying double
convection zone. The situation is different in our 3D model
heflpopI.3d, where N2 is (on
average) small and negative
everywhere in the single convection zone (Fig. 14).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figtmpevol1.eps}\includegraphics[width=7.5cm,clip]{14461figtmpevol2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg249.png)
|
Figure 15:
Left panel: temporal evolution of the nuclear
energy production rate E (left)
in units of the solar luminosity |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,height=7.8cm,clip]{14461figsnap3d1...
...}\includegraphics[width=5cm,height=7.8cm,clip]{14461figsnap3d3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg250.png)
|
Figure 16:
Snapshots of the spatial distribution of the velocity modulus |v|
(in units of
|
| Open with DEXTER | |
Within the double convection zone originally determined by the Schwarzschild criterion the temperature gradient drops everywhere below the adiabatic one (Fig. 13). It does not imply that convection must cease. Even if the temperature gradient is not everywhere super-adiabatic nuclear burning may create hot blobs, which although cooling faster than the environment can still be hotter than the latter, and thus can rise upwards.
This supports our conclusions based on the distribution of the Brunt-Väisälä frequency, which might be, however, a result of insufficient resolution, as the gradient increases with increasing resolution.
Consequently, we do not find the typical 2D convective pattern characterized by vortices in the double convection zone at later times t > 2000 s.
Radiative barrier:
Stellar evolutionary calculations of low-mass Pop III stars
predict
that the helium flash-driven convection zone splits into two, when the
hydrogen-burning luminosity (driven by the entrainment of H) exceeds
the helium-burning luminosity. At this point, a radiative barrier is
created between both convective zones, as energy flows inwards from
the layers where hydrogen-burning takes place. The radiative barrier
is thought to prevent the flow of isotopes into the helium burning
layers and vice versa, hence preventing the reaction 13C
(![]() ,
n) 16O to become a source of
neutrons.
,
n) 16O to become a source of
neutrons.
Also an eventual mixing of isotopes from the helium-burning layer into the stellar atmosphere should be inhibited. However, this scenario is difficult to prove due to numerical problems arising when modelling this event in 1D (Hollowell et al. 1990).
Our hydrodynamic model heflpopIII.2d.2 with the double
convective zone
shows that the radiative barrier allows for some interaction between
both zones via g-modes (Figs. 11, 12). In
addition, there is some mixing of hydrogen into the radiative layer,
which
was initially completely devoid of hydrogen (i.e., X(1H) = 10-30).
Hydrogen must have been mixed there either by convective
motion from the hydrogen-rich layers or dredged down by penetrating
convective plumes from the lower convection zone. The downward mixing
of hydrogen extends to an approximate radius of
![]() cm
(X(1H)
cm
(X(1H) ![]() 10-10) by the end of our
simulation
heflpopIII.2d.2 (Fig. 18).
It is likely that deeper
mixing of hydrogen into the helium burning layers is not possible,
since protons are captured via the reaction 12C
(p,
10-10) by the end of our
simulation
heflpopIII.2d.2 (Fig. 18).
It is likely that deeper
mixing of hydrogen into the helium burning layers is not possible,
since protons are captured via the reaction 12C
(p, ![]() )
13N on timescales shorter than that on which
protons are mixed
inwards (Hollowell
et al. 1990). At a temperature
)
13N on timescales shorter than that on which
protons are mixed
inwards (Hollowell
et al. 1990). At a temperature
![]() K
(
K
(
![]() cm)
the proton lifetime against capture by
12C is as short as
cm)
the proton lifetime against capture by
12C is as short as ![]() 102 s (Caughlan & Fowler 1988).
This is
an order of magnitude smaller than the observed initial convective
turnover
timescales (Table 4).
102 s (Caughlan & Fowler 1988).
This is
an order of magnitude smaller than the observed initial convective
turnover
timescales (Table 4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461figkindnst1.eps}\includegraphics[width=8.5cm,clip]{14461figkindnst2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg254.png)
|
Figure 17:
Temporal evolution of the radial distribution of the (color coded)
logarithm of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461hyddist.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg255.png)
|
Figure 18:
Hydrogen mass fraction as a function of radius for the 2D model
heflpopIII.2d.2 at t = 6400 s. The
vertical lines mark the initial border between hydrogen and helium rich
layers (dashed-red), and the layer (dotted) where the timescale for
proton capture on 12C equals 102 s
(
|
| Open with DEXTER | |
5.3.2 Simulation heflpopIII.2d.1 and heflpopIII.3d
We now discuss the qualitative behavior of 2D and 3D Pop III models which were simulated using the same number of radial and angular zones, but which have a lower radial and angular resolution than the 2D model heflpopIII.2d.2 discussed in the previous subsection. The quantitative properties of the convection zone of these models will obviously be different as an increased grid resolution implies less numerical viscosity and larger Reynolds numbers. We again stress here that the characteristic Reynolds numbers in our 2D and 3D simulations (Table 4) are still many orders of magnitude smaller than the values predicted by theory (see Sect. 2).
The comparison between the 2D and 3D simulations, heflpopIII.2d.1 and heflpopIII.3d, provides important information on the impact of the symmetry restriction imposed in the 2D models. Contrary to the 2D models, our 3D hydrodynamic simulations of turbulent flow performed with the PPM scheme (Sect. 4) are geometrically unconstrained, i.e., in the inertial regime turbulent eddies can decay along the Kolmogorov cascade down to the finest resolved scales (Sitine et al. 2000).
Due to the large computational cost we evolved the 3D model heflpopIII.3d and the corresponding 2D model heflpopIII.2d.1 for 0.39 h of stellar life, only. We find the following qualitative differences between the 3D and 2D model (Fig. 15): (i) in 3D convection starts earlier in the outer part of the double convection zone; (ii) convective velocities are smaller there; and (iii) the convective structures have a plume-like shape in 3D (Fig. 16) and are vortex-like in 2D (Fig. 11). On the other hand, the models also exhibit the following common qualitative evolutionary properties (Fig. 15): (i) a decrease of the total nuclear energy production rate; (ii) a decrease of the maximum temperature; (iii) a decay of the velocity field in the convection zones (Fig. 17), and (iv) the presence of internal gravity waves in the radiative barrier.
The differences observed between the 2D and 3D simulation do not come as a surprise, as it is well known that 2D simulations lead to an overestimate of the flow velocities (Meakin & Arnett 2006; Muthsam et al. 1995). On the other hand, the common properties of the 2D and 3D model are also shared by the high resolution simulation heflpopIII.2d.2, except for the nuclear energy production rate, which does not decrease after convection is fully established. This implies that both our 2D model heflpopIII.2d.1 and 3D model heflpopIII.3d are not resolved well enough, although they show the most important characteristics of the high resolution model heflpopIII.2d.2 described in Sect. 5.3.1, i.e., the presence of a decaying convective flow in both convection zones which are later dominated by internal gravity waves. This also holds for the intermediate radiative layer.
Contrary to the low resolution 2D model heflpopIII.2d.1, the
convective velocities found for the 3D model heflpopIII.3d![]() in the inner convection
zone sustained by helium burning match those
given by stellar evolutionary calculations relatively well, although
the modulus of the velocity is about a factor of two larger
in the inner convection
zone sustained by helium burning match those
given by stellar evolutionary calculations relatively well, although
the modulus of the velocity is about a factor of two larger![]() . In the outer part of the
convection zone, sustained by the CNO cycle, the modulus of the
velocity and the individual velocity components are smaller by more
than a factor of two. In both of these models, as well as the other 2D
Pop III model heflpopIII.2d.2, the convective velocities in
the inner
convection zone CVZ-1 are higher than the velocities in the outer
convection zone CVZ-2 (see Table 4). This is the
opposite situation to that found in the 1D stellar calculations, in
which CVZ-1 has lower velocities than CVZ-2.
. In the outer part of the
convection zone, sustained by the CNO cycle, the modulus of the
velocity and the individual velocity components are smaller by more
than a factor of two. In both of these models, as well as the other 2D
Pop III model heflpopIII.2d.2, the convective velocities in
the inner
convection zone CVZ-1 are higher than the velocities in the outer
convection zone CVZ-2 (see Table 4). This is the
opposite situation to that found in the 1D stellar calculations, in
which CVZ-1 has lower velocities than CVZ-2.
Interestingly, we find convection to be triggered spontaneously in these simulations - even without nuclear burning. This is highlighted by the fact that the temporal evolution of the kinetic energy of the 3D model heflpopIII.3d with no nuclear nuclear energy production is almost identical to that of the corresponding model with burning switched in (Fig. 15). Thus, we conclude that the hydrodynamic convective flow observed in our models is mainly driven by the adopted temperature gradient which is inherited from the 1D stellar model, and is only partially sustained by nuclear burning within the hydrodynamic simulation.
6 Summary
We have performed and analyzed a 3D hydrodynamic simulation of a core helium flash near its peak in a Pop I star possessing a single convection zone (single flash) sustained by helium burning. The simulation covers 27 h of stellar life, or roughly 100 convective turnover timescales. In addition, we have performed and studied 2D and 3D simulations of the core helium flash near its peak in a Pop III star which has a double convection zone (dual flash) sustained by helium and CNO burning, respectively. These simulations cover only 1.8 h and 0.39 h of stellar life, respectively, as convection dies out shortly after it appears.
The convective velocities in our hydrodynamic simulation of the single flash model and those given by stellar evolutionary calculations agree approximately. Contrary to our previous findings, the temperature gradient in the convection zone remains superadiabatic, probably because of the increased spatial resolution of these simulations as compared to our old models. As expected, the simulation shows that the convection zone grows on a dynamic timescale due to turbulent entrainment. This growth can lead to hydrogen injection into the helium core as predicted by stellar evolutionary calculation of extremely metal-poor or metal-free Pop III stars. Hydrogen injection leads to a split of the single convection zone into two parts separated by a supposedly impenetrable radiative zone. Our hydrodynamic simulations of the double convection zone show that the two zones vanish as their convective motion decays very fast. However, this result may be caused by an insufficient spatial grid resolution or probably because the conditions represented by the stabilized initial model are a bit different from those of the original stellar model. While the convective velocities in our 2D hydrodynamic models do not match those given by stellar evolutionary calculations for the double convection zone at all, a rough agreement is found in our 3D model for the velocities in the inner convection zone sustained by helium burning.
AcknowledgementsThe simulations were performed at the Leibniz-Rechenzentrum of the Bavarian Academy of Sciences & Humanities on the SGI Altix 4700 system. The authors want to thank Frank Timmes for some of his publicly available Fortran subroutines which we used in the Herakles code. Miroslav Mocák acknowledges financial support from the Communauté francaise de Belgique - Actions de Recherche Concertes. S.W.C. acknowledges the support of the Consejo Superior de Investigaciones Científicas (CSIC, Spain) JAE-DOC postdoctoral grant and the MICINN grant AYA2007-66256. Part of this study utilized the Australian National Facility supercomputers, under Project Code g61. The authors are grateful to the referee Dave Arnett for his comments which helped to improve this manuscript.
References
- Achatz, K. 1995, in Master's thesis, Technical University München [Google Scholar]
- Arnett, D., Meakin, C., & Young, P. A. 2009, ApJ, 690, 1715 [CrossRef] [Google Scholar]
- Asida, S. M., & Arnett, D. 2000, ApJ, 545, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, S. W., & Lattanzio, J. C. 2008, A&A, 490, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Schlattl, H., Salaris, M., & Weiss, A. 2003, ApJ, 582, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
- Chieffi, A., Domínguez, I., Limongi, M., & Straniero, O. 2001, ApJ, 554, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D. 1968, Principles of stellar evolution and nucleosynthesis (New York: McGraw-Hill) [Google Scholar]
- Colella, P., & Glaz, H. H. 1984a, J. Comput. Phys., 59, 264 [Google Scholar]
- Colella, P., & Woodward, P. R. 1984b, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dalsgaard, J. C. 2003, Stellar Oscillations (Institut for Fysik og Astronomi, Aarhus Universitet) [Google Scholar]
- Despain, K. H., & Scalo, J. M. 1976, ApJ, 208, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Despain, K. H. 1981, ApJ, 251, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fujimoto, M. Y. 1977, PASJ, 29, 331 [NASA ADS] [Google Scholar]
- Fujimoto, M. Y., Iben, I. J., & Hollowell, D. 1990, ApJ, 349, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Aikawa, M., & Kato, K. 1999, ApJ, 519, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Ikeda, Y., & Iben, I. J. 2000, ApJ, 529, L25 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hollowell, D., Iben, I. J., & Fujimoto, M. Y. 1990, ApJ, 351, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I. 1976, ApJ, 208, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Kohyama, Y., & Takeuchi, H. 1987, ApJ, 317, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, N., Kajino, T., Mathews, G. J., Fujimoto, M. Y., & Aoki, W. 2004, ApJ, 602, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2003, A&A, 408, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kifonidis, K., Plewa, T., Scheck, L., Janka, H.-T., & Müller, E. 2006, A&A, 453, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution, Stellar Structure and Evolution, XVI, 468, 192 figs. (Berlin, Heidelberg, New York: Springer-Verlag), Also A&A Library [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1966, Hydrodynamik (Lehrbuch der theoretischen Physik) (Berlin: Akademie-Verlag) [Google Scholar]
- Langer, G. E., & Hoffman, R. D. 1995, PASP, 107, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, G. E., Hoffman, R. E., & Zaidins, C. S. 1997, PASP, 109, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Mocák, M. 2009, Ph.D. Thesis, Max-Planck-Institut für Astrophysik, Garching bei München [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2008, A&A, 490, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2009, A&A, 501, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, E., & Steimnetz, M. 1995, Comp. Phys. Comm., 89, 45 [Google Scholar]
- Muthsam, H. J., Goeb, W., Kupka, F., Liebich, W., & Zoechling, J. 1995, A&A, 293, 127 [NASA ADS] [Google Scholar]
- Paczynski, B., & Tremaine, S. D. 1977, ApJ, 216, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Plewa, T., & Müller, E. 1999, A&A, 342, 179 [NASA ADS] [Google Scholar]
- Porter, D. H., & Woodward, P. R. 1994, ApJS, 93, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Tukolsky, S. A., Vetterling, W. T., & P., F. B. 1992, in Numerical Recipes in FORTRAN, The Art of Scientific Computing, Second Edition (Cambridge: Cambridge University Press), 1 [Google Scholar]
- Schlattl, H., Cassisi, S., Salaris, M., & Weiss, A. 2001, ApJ, 559, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M. D. 1996a, AJ, 112, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M. D. 1996b, AJ, 112, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Livio, M., & Lattanzio, J. 2002, ApJ, 570, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Sitine, I. V., Porter, D. H., Woodward, P. R., Hodson, S. W., & Winkler, K.-H. 2000, J. Comput. Phys., 158, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Smagorinsky, J. S. 1963, Mon. Weather Rev., 91, 99 [Google Scholar]
- Suda, T., Aikawa, M., Machida, M. N., Fujimoto, M. Y., & Iben, I. J. 2004, ApJ, 611, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Hillebrandt, W., Thomas, H.-C., & Ritter. 2004, Cox and Giuli's Principles of Stellar Structure (Gardners Books) [Google Scholar]
- Weiss, A., & Schlattl, H. 2000, A&AS, 144, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Schlattl, H. 2007, Ap&SS, 341 [Google Scholar]
- Weiss, A., Schlattl, H., Salaris, M., & Cassisi, S. 2004, A&A, 422, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, P. R., & Zarro, D. M. 1981, ApJ, 247, 247 [Google Scholar]
- Yong, D., Aoki, W., & Lambert, D. L. 2006, ApJ, 638, 1018 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Pop III
![[*]](/icons/foot_motif.png)
- Population III stars are supposed to be the first stars in
the Universe and seem to be extremely rare, as the most metal-poor
star discovered up to now has a metallicity of [Fe/H]
 -5.5 (Frebel et al. 2005).
-5.5 (Frebel et al. 2005).
- ... flash
![[*]](/icons/foot_motif.png)
- According to Schlattl et al. (2001) the occurrence of a hydrogen flash is favored by a higher electron degeneracy in the helium core, which leads to helium ignition closer to the hydrogen shell.
- ...
) ![[*]](/icons/foot_motif.png)
- The agreement may however only reflect the similar physics included in the 1D codes, such as the similar implementations of the mixing-length theory (MLT).
- ... (TPAGB)
![[*]](/icons/foot_motif.png)
- If hydrogen injection occurs at the tip of the RGB, it does not occur on the AGB; instead, the star evolves like a normal thermally pulsating Pop I or II star (Schlattl et al. 2001).
- ...
![[*]](/icons/foot_motif.png)
- Metal-free stars with masses
 1
1 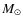 ignite helium at the center before electrons become degenerate (Fujimoto et al. 2000).
ignite helium at the center before electrons become degenerate (Fujimoto et al. 2000).
- ... adiabatic
![[*]](/icons/foot_motif.png)
- The entropy S (Fig. 2) and the
degeneracy parameter
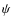 remain almost constant in the convection zones, which is a result of
the almost adiabatic temperature gradient, i.e., the
temperature relation
remain almost constant in the convection zones, which is a result of
the almost adiabatic temperature gradient, i.e., the
temperature relation 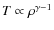 with the adiabatic exponent
with the adiabatic exponent 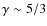 holds. Since
holds. Since 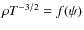 ,
the degeneracy parameter
,
the degeneracy parameter 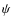 is constant.
is constant.
- ... evolution
![[*]](/icons/foot_motif.png)
- 1D stellar evolutionary codes force hydrostatic equilibrium, so the actual expansion would have most likely been even stronger.
- ... viscosities
![[*]](/icons/foot_motif.png)
- The estimate of
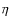 for a strongly degenerate and completely ionized helium gas is based on
the formula of Itoh et al.
(1987).
for a strongly degenerate and completely ionized helium gas is based on
the formula of Itoh et al.
(1987).
- ... core
![[*]](/icons/foot_motif.png)
- The helium core is basically a white dwarf sitting inside a red giant star. It has a relatively small radius - comparable to that of the Earth - but contains almost half of the total mass of the star (Table 1).
- ...
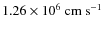
![[*]](/icons/foot_motif.png)
- The depth of the convection zone CVZ in our single flash model is approximately 2.3 pressure scale heights.
- ...
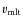
![[*]](/icons/foot_motif.png)
- The difference between convection velocities typical for
our hydrodynamic simulation and convection velocities of our 1D initial
stellar model given by MLT could be significant as some processes in
stellar interior depend on the velocity of convection v
to a large power. For instance, the entrainment rates of convection
boundaries
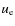 depend on v at the boundaries as vn,
where
depend on v at the boundaries as vn,
where 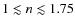 (Meakin & Arnett 2007)
and the energy transported by acoustic waves in stable layers next to
convection zones goes even as v6
(Arnett et al.
2009).
(Meakin & Arnett 2007)
and the energy transported by acoustic waves in stable layers next to
convection zones goes even as v6
(Arnett et al.
2009).
- ... zone
![[*]](/icons/foot_motif.png)
- A sub-adiabatic gradient does not imply that convective blobs are cooler than their environment and that consequently convection ceases (the latter is only true when assuming adiabatically rising blobs). It only means that blobs cool faster than their environment.
- ... waves
![[*]](/icons/foot_motif.png)
- In a convectively stable region, any displaced mass element is pushed back by the buoyancy force. On its way back to its original position, the blob gains momentum and therefore starts to oscillate. These oscillations are called internal gravity waves (Dalsgaard 2003).
- ... flux
![[*]](/icons/foot_motif.png)
-
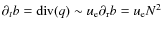 is
a rather crude approximation which provides an order of magnitude
estimate only (Meakin
& Arnett 2007).
is
a rather crude approximation which provides an order of magnitude
estimate only (Meakin
& Arnett 2007).
- ... flash
![[*]](/icons/foot_motif.png)
- When the helium burning shell of the first major helium
flash becomes too narrow, it is not able to lift the overlying mass
layers. It expands slowly, i.e.,
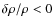 ,
but remains almost in hydrostatic equilibrium
,
but remains almost in hydrostatic equilibrium 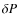 /
/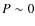 ,
which in turn leads to a rise of its temperature
,
which in turn leads to a rise of its temperature  /T
> 0 (Kippenhahn &
Weigert 1990). Hence, helium is re-ignited, but less
violently than in the first main helium flash. In general, one refers
to this event as a thermal pulse, but we prefer to call it a mini
helium flash. This process repeats itself several times until the star
settles on the horizontal branch.
/T
> 0 (Kippenhahn &
Weigert 1990). Hence, helium is re-ignited, but less
violently than in the first main helium flash. In general, one refers
to this event as a thermal pulse, but we prefer to call it a mini
helium flash. This process repeats itself several times until the star
settles on the horizontal branch.
- ... heflpopIII.3d
![[*]](/icons/foot_motif.png)
- The convective velocities are measured just after convection appears for the first time during the simulation, as the convective flow decays very fast later.
- ... larger
![[*]](/icons/foot_motif.png)
- The depth of the inner convection zone sustained by helium burning CVZ-1 is approximately 4 pressure scale heights (Hp), whereas the depth of CVZ-2, sustained by the CNO cycle, is roughly 3 Hp
All Tables
Table 1: Initial models M & SC.
Table 2: Some properties of the 3D simulation based on model M.
Table 3: Some quantities characterizing the convective boundaries of the 3D model heflpopI.3d.
Table 4: Some properties of the 2D and 3D hydrodynamic models based on initial model SC.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14461figkipd.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg52.png)
|
Figure 1:
Upper panel: Kippenhahn diagram of a stellar
evolutionary calculation during the core helium flash of a
0.85 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figinimt1.eps}\includegraphics[width=7.5cm,clip]{14461figinimt2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg94.png)
|
Figure 2: Left: temperature distribution in the helium core in model M (long-dashed), and in model SC (solid) with its stabilized counterpart (dash-dotted red), respectively. The two parts of the double convection zone present in model SC are denoted by CVZ-1 and CVZ-2, respectively. Right: entropy distribution of model M (solid) and model SC (long-dashed), respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figinicomp1.eps}\includegraphics[width=7.5cm,clip]{14461figinicomp2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg120.png)
|
Figure 3:
Left: chemical composition of the helium core
in model heflpopIII.2d.2 (SC). Right: nuclear
energy production rate as a function of radius r.
Initial rates (at t=0) are indicated by
dotted-black curves. Rates in model heflpopI.3d (SC) at t
= 6400 s (solid-red), and in model M at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figveloc.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg159.png)
|
Figure 4:
Radial velocity distributions for the 3D model heflpopI.3d. The dotted
and green dashed lines show the time (from 10 000 s
to 30 000 s) and angle-averaged radial velocity, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figflx.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg160.png)
|
Figure 5: Convective and kinetic energy fluxes (FC and FK, respectively) as a function of radius averaged (from 33 000 s to 53 000 s) over about 20 convective turnover timescales for the 3D model heflpopI.3d. The dotted vertical lines mark the edges of the single convection zone in the initial model M according to the Schwarzschild criterion. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figtmpgradpop1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg161.png)
|
Figure 6:
Radial distribution of the adiabatic temperature gradient
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figexppop1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg171.png)
|
Figure 7:
Radial distribution of the expansion velocity, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=5.2cm]{14461figsvelbndry1.eps}\includ...
...elbndry2.eps}\includegraphics[height=5.2cm]{14461figsvelbndry3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg176.png)
|
Figure 8:
Color maps of the modulus of the velocity (in units of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=7.4cm]{14461figkened.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg177.png)
|
Figure 9:
Temporal evolution of radial distribution of the (color coded)
logarithm of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461figcargrow1.eps}\includegraphics[width=8.5cm,clip]{14461figcargrow2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg185.png)
|
Figure 10:
Angular averaged 12C mass fraction as a
function of radius near the inner ( left) and outer
edge ( right) of the convection zone in the 3D model
heflpopI.3d at t
= 100 000 s. The thick line gives the corresponding
temperature stratification, and the vertical dotted lines mark the
edges of the convection zone at t = 0 s.
The observed entrainment velocities |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.4cm,height=7.95cm,clip]{14461figsnap...
...
\includegraphics[width=5cm,height=7.5cm,clip]{14461figsnap2d3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg213.png)
|
Figure 11:
Snapshots of the spatial distribution of the velocity modulus
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14461figkindnstdec1.eps}\par\includegraphics[width=8cm,clip]{14461figkindnstdec2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg221.png)
|
Figure 12:
Temporal evolution of the radial distribution of the (color coded)
logarithm of the angular averaged radial (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figtmpgradpop3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg222.png)
|
Figure 13:
Adiabatic temperature gradient
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14461figbrunt1.eps}\par\includegraphics[width=6.5cm,clip]{14461figbrunt2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg234.png)
|
Figure 14:
Radial distributions of the (square of the) Brunt-Väisälä buoyancy
frequency N2 in the
2D model heflpopIII.2d.2 averaged between 1480 s and
6000 s (top), and in the 3D model
heflpopI.3d averaged between 6600 s and
100 000 (bottom), respectively.
The angular and temporal variation of N2
at a given radius are indicated by the gray shaded region. The inserts
show a zoom of the region around N2
= 0 to enlarge the variations of N2
in the convection zone which are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14461figtmpevol1.eps}\includegraphics[width=7.5cm,clip]{14461figtmpevol2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg249.png)
|
Figure 15:
Left panel: temporal evolution of the nuclear
energy production rate E (left)
in units of the solar luminosity |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,height=7.8cm,clip]{14461figsnap3d1...
...}\includegraphics[width=5cm,height=7.8cm,clip]{14461figsnap3d3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg250.png)
|
Figure 16:
Snapshots of the spatial distribution of the velocity modulus |v|
(in units of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461figkindnst1.eps}\includegraphics[width=8.5cm,clip]{14461figkindnst2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg254.png)
|
Figure 17:
Temporal evolution of the radial distribution of the (color coded)
logarithm of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14461hyddist.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14461-10/Timg255.png)
|
Figure 18:
Hydrogen mass fraction as a function of radius for the 2D model
heflpopIII.2d.2 at t = 6400 s. The
vertical lines mark the initial border between hydrogen and helium rich
layers (dashed-red), and the layer (dotted) where the timescale for
proton capture on 12C equals 102 s
(
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



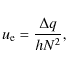
![$\displaystyle \frac{\partial^2 (\Delta r)}{\partial t^2} = \frac{g \delta}{H_{\...
...}} - \nabla_{\rm {surr}} + \frac{\varphi}{\delta} \nabla_{\mu} \right] \Delta r$](/articles/aa/full_html/2010/12/aa14461-10/img228.png)