| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014298 | |
| Published online | 05 October 2010 | |
XMM-Newton and SUZAKU detection of an X-ray emitting shell around the pulsar wind nebula G54.1+0.3
F. Bocchino1 - R. Bandiera2 - J. Gelfand3,![]()
1 - INAF - Osservatorio Astronomico di Palermo, Piazza del Parlamento 1,
90134 Palermo, Italy
2 -
INAF - Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 1
Firenze, Italy
3 -
Center for Cosmology and Particle Physics, New York University,
4 Washington Place, New York, NY 10003, USA
Received 22 February 2010 / Accepted 15 April 2010
Abstract
Context. X-ray observations have proven to be very effective
in detecting previously unknown supernova remnant shells around pulsar
wind nebulae (PWNe), and in these cases the characteristics of the
shell provide information about the evolutionary stage of the embedded
PWN. However, it is not clear why some PWNe are ``naked''.
Aims. We perform an X-ray observational campaign targeting the
PWN G54.1+0.3, the ``close cousin'' of the Crab Nebula, to try to
detect the associated SNR shell.
Methods. We analyze XMM-Newton and Suzaku observations of G54.1+0.3 to model the contribution of a dust scattering halo.
Results. We detecte an intrinsic faint diffuse X-ray emission surrounding the PWN out to ![]()
![]() (
(![]() 10 pc) from the pulsar, characterized by a hard spectrum, which can be modeled with either a power law (
10 pc) from the pulsar, characterized by a hard spectrum, which can be modeled with either a power law (
![]() )
or a thermal plasma model (kT = 2.0 keV.)
)
or a thermal plasma model (kT = 2.0 keV.)
Conclusions. Assuming the shell to be thermal, we derive an explosion energy
![]() erg, a pre-shock ISM density of 0.2 cm-3, and an age of
erg, a pre-shock ISM density of 0.2 cm-3, and an age of ![]() 2000 yr.
Using these results in the MHD model of PWN-SNR evolution, we obtain
excellent agreement between the predicted and observed location of the
shell and PWN shock.
2000 yr.
Using these results in the MHD model of PWN-SNR evolution, we obtain
excellent agreement between the predicted and observed location of the
shell and PWN shock.
Key words: ISM: supernova remnants - dust, extinction - ISM: individuals objects: G54.1+0.3
1 Introduction
One of the most intriguing problem in the study of the pulsar wind
nebulae (PWNe) study has been the lack of a shell around some of these
objects. This is somewhat disconcerting for the consolidated picture of a
remnant of a core-collapse supernova, which indicates that the PWN is
expanding inside the host supernova remnant, producing
a variety of complex phenomena, such as reverberation, Rayleigh-Taylor
instability at the interface between the PWN and ejecta, and rejuvenation
of the shell (e.g., van der Swaluw et al. 2001; Blondin et al. 2001; Chevalier 2005;
Gelfand et al. 2009, and references therein). One reason may be
the lack of deep observations targeting the PWN surroundings.
A shell-like component has been observed in many objects, such as
G21.5-0.9 (Bandiera & Bocchino 2004; Bocchino et al. 2005), G0.9+0.1 (Porquet et al. 2003),
and 3C58 (Bocchino et al. 2001; Gotthelf et al. 2007). Therefore,
X-ray observations are very effective discovering
associated shell components, even for high absorption
column densities (G21.5-0.9 has
![]() ;
G0.9+0.1
has
;
G0.9+0.1
has ![]()
![]() ).
).
The objects in which a pulsar, plerion, and shell are all detected (collectively known as composite SNRs) are extremely important when defining the physical conditions in their modeling. The properties and the evolution of a PWN are determined by the interaction of the pulsar wind with the ambient medium. The effectiveness with which the surrounding matter confines the PWN is very important for determining the level of the synchrotron emission from the nebula. Therefore, measuring density and pressure in the shell component is needed to more tightly constrain the models of the PWN. Moreover, the pulsar, the PWN, and the shell would allow us to estimate in independent ways some quantities, such as the true age of the object, or the internal pressure of the nebula. This redundancy would also allow us to verify our assumptions, such as that about the level of equipartition in the PWN and how reliable the age estimated from the pulsar spin-down properties.
G54.1+0.3 is the Galactic PWN that most closely resembles
the Crab Nebula: this is why Lu et al. (2002) dubbed it
``a close cousin of the Crab Nebula''. Using Chandra data, Lu et al. (2002)
clearly detected a torus of ![]() 10'' in diameter,
and a feature elongated in the E and W directions, which could be
ascribed to X-ray jets. From these data, the size of the X-ray nebula
appears
10'' in diameter,
and a feature elongated in the E and W directions, which could be
ascribed to X-ray jets. From these data, the size of the X-ray nebula
appears ![]() 1', but the outer part of the nebula is very faint, its
edge being poorly defined. At radio wavelengths, instead, the nebular size
is
1', but the outer part of the nebula is very faint, its
edge being poorly defined. At radio wavelengths, instead, the nebular size
is ![]() 1.5' (Velusamy & Becker 1988), corresponding to
1.5' (Velusamy & Becker 1988), corresponding to ![]() 2.7 d6.2 pc
where d6.2 is the distance of G54.1+0.3 in units of that estimated by
Leahy et al. (2008), namely
d6.2=d/6.2+1.0-0.6 kpc. It is important
to understand the extent to which this difference in size is real (i.e., due to
synchrotron losses of the emitting electrons), or is an artifact of
the limited X-ray sensitivity.
2.7 d6.2 pc
where d6.2 is the distance of G54.1+0.3 in units of that estimated by
Leahy et al. (2008), namely
d6.2=d/6.2+1.0-0.6 kpc. It is important
to understand the extent to which this difference in size is real (i.e., due to
synchrotron losses of the emitting electrons), or is an artifact of
the limited X-ray sensitivity.
Radio maps exhibit a rather amorphous structure, but the radio emission from
G54.1+0.3 is highly polarized, up to 20-30% (Velusamy & Becker 1988), and this
indicates (as in the case of the Crab nebula) that the nebular
field is highly ordered. The X-ray spectrum is a power law with a photon
index -1.9, an absorption column density
![]() ,
and an X-ray luminosity
,
and an X-ray luminosity
![]() .
Camilo et al. (2002) detected the pulsar PSR J1930+1852 at the center of
the nebula, which has a period of 136 ms, a characteristic age of 2900 yr and a spin-down luminosity of
.
Camilo et al. (2002) detected the pulsar PSR J1930+1852 at the center of
the nebula, which has a period of 136 ms, a characteristic age of 2900 yr and a spin-down luminosity of
![]() erg s-1.
erg s-1.
The source G54.1+0.3 has attracted new interest since Koo et al. (2008)
identified an IR shell surrounding the PWN at a distance of ![]() 1.5'from the pulsar. The shell contains a dozen of IR compact sources.
Koo et al. (2008) suggests that the sources are young stellar objects,
whose formation has been triggered by the wind of the progenitor of the SN.
This intriguing possibility has been questioned by Temim et al. (2010),
who pointed out that the IR shell may be ejecta dust, rather than a
pre-existing ISM dense cloud. Leahy et al. (2008) detected
a molecular cloud partially interacting with the PWN, on the basis
of the CO emission around the nebula. Therefore, even if there is no
hint of a radio shell around this PWN, there is some evidence
of interaction between the PWN and the surroundings, so it is worth
searching for an X-ray shell.
1.5'from the pulsar. The shell contains a dozen of IR compact sources.
Koo et al. (2008) suggests that the sources are young stellar objects,
whose formation has been triggered by the wind of the progenitor of the SN.
This intriguing possibility has been questioned by Temim et al. (2010),
who pointed out that the IR shell may be ejecta dust, rather than a
pre-existing ISM dense cloud. Leahy et al. (2008) detected
a molecular cloud partially interacting with the PWN, on the basis
of the CO emission around the nebula. Therefore, even if there is no
hint of a radio shell around this PWN, there is some evidence
of interaction between the PWN and the surroundings, so it is worth
searching for an X-ray shell.
In Sect. 2, we present our deep X-ray campaign targeting this PWN, which led to the detection of such a shell. In Sect. 3, we estimate the contribution of the dust scattering halo, showing that it is negligible at the shell location, and in Sect. 4 we discuss our findings, and compare them to a PWN-SNR evolution model.
2 Deep XMM-Newton and SUZAKU observations
Table 1: X-ray observations used in this work.
We observed the PWN G54.1+0.3 with XMM-Newton (Jansen et al. 2001) and SUZAKU (Mitsuda et al. 2007) in 2006 and 2007,
respectively. Table 1 summarizes the observations used in this
work. The data were analyzed with the latest software available,
namely SAS v8.0 for XMM-Newton and the pipeline v.2.1.6 with HEASOFT v6.6
for SUZAKU. The XMM-Newton data were screened for proton flares using the
sigma clipping algorithm described in Snowden & Kuntz (2007), while for SUZAKU we
used the standard screening. The image of G54.1+0.3 obtained with the
EPIC PN and MOS CCD cameras of XMM-Newton (Turner et al. 2001; Strüder et al. 2001,
with a resolution of
![]() HPD) and the XIS CCD camera of
SUZAKU (Koyama et al. 2007,
HPD) and the XIS CCD camera of
SUZAKU (Koyama et al. 2007,
![]() FWHM) are shown in
Fig. 1, in the upper and lower panels respectively.
FWHM) are shown in
Fig. 1, in the upper and lower panels respectively.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{h14298f1a.eps} \includegraphics[width=9cm,clip]{h14298f1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14298-10/Timg26.png)
|
Figure 1:
Top panel: XMM-Newton EPIC image in the 1-7 keV energy
band. The image is a mosaic of background-subtracted and
vignetting-corrected images obtained with the PN, MOS1, and MOS2
cameras. The color scale has been chosen to maximize the visibility
of the faint diffuse emission around the bright PWN. The inner (black)
circle has a radius of
|
| Open with DEXTER | |
There is a diffuse extended emission surrounding the bright plerion in
both images. This diffuse emission seems to have spatial structures
as small as
![]() .
The contrast in the surface brightness
of the diffuse emission and the core of the PWN is
about 1000.
.
The contrast in the surface brightness
of the diffuse emission and the core of the PWN is
about 1000.
Table 2: SUZAKU spectral fitting results.
We investigated the X-ray faint diffuse emission by
studying its spectrum with both XMM-Newton and SUZAKU. For spectral
analysis purposes, we defined a core region and a shell region. Centered on the pulsar, the
core region is a circle of radius
![]() .
This includes all the regions occupied by the radio nebula
and its X-ray emission is dominated by the synchrotron emission
originating in the PWN. The shell region is an annulus with a inner radius equal
to the radius of the core region and an outer radius of
.
This includes all the regions occupied by the radio nebula
and its X-ray emission is dominated by the synchrotron emission
originating in the PWN. The shell region is an annulus with a inner radius equal
to the radius of the core region and an outer radius of
![]() .
We
estimated that the contribution of the core emission in the shell region
is 25% for SUZAKU and 1% for XMM-Newton, purely because of the instrumental
PSF wings and excluding the additional contribution of dust scattered
X-rays. In the case of XMM-Newton, the shell region was reduced further to
a pie sector between polar angles
.
We
estimated that the contribution of the core emission in the shell region
is 25% for SUZAKU and 1% for XMM-Newton, purely because of the instrumental
PSF wings and excluding the additional contribution of dust scattered
X-rays. In the case of XMM-Newton, the shell region was reduced further to
a pie sector between polar angles ![]() and
and ![]() (from N,
anti-clockwise, where most of the knots are located. The background
was taken from the same chip for SUZAKU, while in the case of XMM-Newton we used both blank fields and the same observation to collect
background (in the latter case, an annular region with
(from N,
anti-clockwise, where most of the knots are located. The background
was taken from the same chip for SUZAKU, while in the case of XMM-Newton we used both blank fields and the same observation to collect
background (in the latter case, an annular region with
![]() and
and
![]() was used), verifying that the results did not change
with the particular choice of the background. We fitted the core region,
finding that a power-law model describes the data very well. Therefore,
we fitted the shell region using a combination of the power-law model
used in the core (with parameters fixed to their best-fit core values,
including interstellar absorption) and an additional component, chosen
among a thermal and a non-thermal model. The core model was used (and
rescaled) in the shell region to take into account possible contamination
from dust-scattering and from instrumental point spread function. The
SUZAKU results are summarized in Table 2, and seem to indicate
that the shell emission can be modeled with either a thermal
component or a non-thermal power law in the shell spectrum. XMM-Newton gives similar results. The SUZAKU spectrum of the core and the shell are
reported in Fig. 2 along with their best-fit models. The
core is also detected between 15 and 25 keV using the non-imaging SUZAKU Hard X-ray Detector (HXD) silicon PIN diodes (spectrum also reported in
Fig. 2, upper panel), with a flux of
was used), verifying that the results did not change
with the particular choice of the background. We fitted the core region,
finding that a power-law model describes the data very well. Therefore,
we fitted the shell region using a combination of the power-law model
used in the core (with parameters fixed to their best-fit core values,
including interstellar absorption) and an additional component, chosen
among a thermal and a non-thermal model. The core model was used (and
rescaled) in the shell region to take into account possible contamination
from dust-scattering and from instrumental point spread function. The
SUZAKU results are summarized in Table 2, and seem to indicate
that the shell emission can be modeled with either a thermal
component or a non-thermal power law in the shell spectrum. XMM-Newton gives similar results. The SUZAKU spectrum of the core and the shell are
reported in Fig. 2 along with their best-fit models. The
core is also detected between 15 and 25 keV using the non-imaging SUZAKU Hard X-ray Detector (HXD) silicon PIN diodes (spectrum also reported in
Fig. 2, upper panel), with a flux of ![]()
![]() erg cm-2 s-1 in this band. The normalization constant between
the PIN and the XIS CCD spectra is
1.3(1.0-1.6), a range that includes
the expected value of 1.15 (Kokubun et al. 2007).
erg cm-2 s-1 in this band. The normalization constant between
the PIN and the XIS CCD spectra is
1.3(1.0-1.6), a range that includes
the expected value of 1.15 (Kokubun et al. 2007).
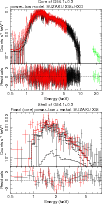
|
Figure 2: Top: SUZAKU spectrum of the core region and the best-fit model. XIS0+3, XIS2, and HXD spectra are shown. Bottom: SUZAKU XIS0+3 and XIS2 spectra of the shell region. The total best-fit thermal + residual non-thermal component from the core is overplotted, as long as the individual components (dashed). |
| Open with DEXTER | |
3 Removal of dust-scattering halo
A foreground medium may affect in many ways the observed
emission from an X-ray source. The most accurately modeled effect is photoelectric
absorption, but dust scattering of the X-ray photons may also be important.
This produces an apparent halo around the intrinsic source, that is more
prominent at lower energies and may considerably hamper both spectral mapping
analysis of diffuse sources and searches for faint surrounding features.
Scattering halos may be relevant whenever the column density of the intervening
material (![]() )
is high.
We can derive
)
is high.
We can derive ![]() by fitting the photoelectric absorption of the X-ray
spectrum, and the scattering optical depth (
by fitting the photoelectric absorption of the X-ray
spectrum, and the scattering optical depth (
![]() ,
estimated at a
reference photon energy of 1 keV) by fitting the halo. Predehl & Schmitt (1995) show
that the linear regression
,
estimated at a
reference photon energy of 1 keV) by fitting the halo. Predehl & Schmitt (1995) show
that the linear regression
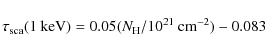
|
(1) |
can be drawn between these two quantities. For the measured value of
Halos of strong, point-like X-ray sources are targeted to investigate properties of the dust grains, but in our case we have to deal with a fainter, diffuse intrinsic source and therefore the modeling of the halo is less accurate. On the other hand, our goal here is simply to develop a modeling approach that can efficiently subtract the halo component, without pretending to infer reliable physical properties of the dust distribution.
In the case of a point-like source, we can describe the halo with the
function:
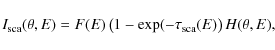
|
(2) |
where F(E) is the source intrinsic flux and
In our case, however, the intrinsic source is spatially resolved, and
we should convolve the halo for a point-like source with the surface
brightness distribution of the true intrinsic source to obtain the
observed map. This is in general a very complex and numerically heavy
task. If just one energy band were considered, the number of possible
solutions would even be infinite. To solve the problem of distinguishing
intrinsic source and halo, one must then perform a combined fit to radial
profiles at different energies, by taking advantage of the known energy
dependence of the halo properties. To model the energy dependence of the
scattering halo, for each instrument we produced 4 images, corresponding
to the spectral bands 1.0-1.75 keV, 1.75-2.5 keV, 2.5-3.9 keV, and
3.9-7.25 keV. The spectral boundaries were chosen to ensure similar
numbers of photons in the various bands, with the additional constraint
that photons softer than 1 keV were excluded, photons for which the
simple Rayleigh-Gans scalings with the photon energy (namely optical
depth
![]() and halo size
and halo size
![]() )
are no longer
valid. The reference energies of the four bands are 1.4, 2.05, 3.07,
and 4.94 keV, respectively, and are obtained by averaging the energies
of all photons collected in each band.
)
are no longer
valid. The reference energies of the four bands are 1.4, 2.05, 3.07,
and 4.94 keV, respectively, and are obtained by averaging the energies
of all photons collected in each band.
Since the intrinsic source is centrally peaked and more concentrated than
the halo, and the wings of XMM-Newton PSF are narrower than the observed
radial profile, we applied a simplified approach, by approximating
the halo with that for a point-like source. For our final fits, we
only used 2 free parameters to model the halo, namely
![]() and
and
![]() .
Before then, we also attempted fits using
a larger number of parameters, but with the moderate statistics of our
data we found that: i. a partial degeneracy between power-law index of
the grain size distribution (q) and the spatial scale (
.
Before then, we also attempted fits using
a larger number of parameters, but with the moderate statistics of our
data we found that: i. a partial degeneracy between power-law index of
the grain size distribution (q) and the spatial scale (
![]() ),
and therefore we chose a rather usual value for q (3.5, see
e.g., Predehl & Schmitt 1995); ii. our fits were typically consistent with
a wide spread of z (i.e., the position along the line of sight,
normalized to the source distance), and therefore we decided
to assume a homogeneous distribution of dust along the line of sight
(
),
and therefore we chose a rather usual value for q (3.5, see
e.g., Predehl & Schmitt 1995); ii. our fits were typically consistent with
a wide spread of z (i.e., the position along the line of sight,
normalized to the source distance), and therefore we decided
to assume a homogeneous distribution of dust along the line of sight
(
![]() and
and
![]() ). All quantities cited here are described in
Appendix A.
). All quantities cited here are described in
Appendix A.
For the intrinsic source, we chose the modeling
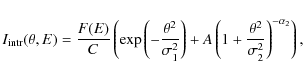
|
(3) |
where
From each image, we extracted a logarithmically spaced radial profile.
To minimize the statistical noise, the flux values are
averaged over several points. In the case of MOS1, because of the absence
of the damaged CCD#6, data are missing for a region that is relevant
to our purposes, so we use MOS2 only. By analyzing the emission
at distances larger than
![]() from the source center, we estimated
the MOS2 background levels for the 4 bands, to be about 10-4 times
the surface brightness in the brightest areas. Therefore, we did not
apply any correction to the background. With this, we are confident
that our profiles are usable over a dynamical range close to 104.
from the source center, we estimated
the MOS2 background levels for the 4 bands, to be about 10-4 times
the surface brightness in the brightest areas. Therefore, we did not
apply any correction to the background. With this, we are confident
that our profiles are usable over a dynamical range close to 104.
Table 3: X-ray dust scattering halo best-fit parameters for G54.1+0.3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h14298f3.eps} \vspace*{0.4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14298-10/Timg66.png)
|
Figure 3:
X-ray normalized profiles in the bands 1.0-1.75, 1.75-2.5,
2.5-3.9, and 3.9-7.25 keV of G54.1+0.3 as seen by MOS2 camera of
XMM-Newton EPIC. Along the x-axis, we report the logarithmic distance from
the center in arcsec. We have overplotted the best-fit halo model,
with individual components (intrinsic source, long-dashed line, and
halo, short-dashed line). The radial range of the fit extends only to
|
| Open with DEXTER | |
|
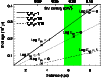
Figure 4:
Sedov solutions for the SNR age and distance computed using
the X-ray derived parameters of G54.1+0.3 (kT=2 keV, SNR radius
|
| Open with DEXTER | |
For the fits, we used at first only the inner
![]() of the radial
profiles, to allow an unbiased analysis of structures that may
appear at larger radii. However, we also present the results
obtained in the inner
of the radial
profiles, to allow an unbiased analysis of structures that may
appear at larger radii. However, we also present the results
obtained in the inner
![]() of the radial profiles. The results of the
fits are presented in Table 3. The results are in general
rather similar between different choices of maximum fitting radius.
of the radial profiles. The results of the
fits are presented in Table 3. The results are in general
rather similar between different choices of maximum fitting radius.
Figure 3 shows the combined MOS2 fits to the 4 bands
(for a maximum fitting radius of
![]() marked by the vertical
dashed line) and the extrapolation of the best-fit profiles to larger
radial distances, compared to the observed profiles. The observed
radial profile exhibits an emission excess at distances from the center >
marked by the vertical
dashed line) and the extrapolation of the best-fit profiles to larger
radial distances, compared to the observed profiles. The observed
radial profile exhibits an emission excess at distances from the center >
![]() that cannot be explained by the dust-scattering halo.
If we normalize to the fluxes produced by both the source and the halo in the
that cannot be explained by the dust-scattering halo.
If we normalize to the fluxes produced by both the source and the halo in the
![]() region, the model predicts that the
flux due to the halo in the outer
region, the model predicts that the
flux due to the halo in the outer
![]() annulus are 0.20, 0.10, 0.04, and 0.01 in the 1.0-1.75, 1.75-2.5, 2.5-3.9,
and 3.9-7.25 keV, respectively (the flux of the source is 0.01 in the same
region), while the observed values are
annulus are 0.20, 0.10, 0.04, and 0.01 in the 1.0-1.75, 1.75-2.5, 2.5-3.9,
and 3.9-7.25 keV, respectively (the flux of the source is 0.01 in the same
region), while the observed values are
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ,
significantly higher than the predicted
halo model. We therefore conclude that the excess is caused by intrinsic
emission from the G54.1+0.3 shell.
,
significantly higher than the predicted
halo model. We therefore conclude that the excess is caused by intrinsic
emission from the G54.1+0.3 shell.
4 Discussion
We have reported for the first time the detection of an extensive area of faint diffuse
X-ray emission around the PWN G54.1+0.3. We have seen that this excess cannot
be due to the X-ray dust scattering halo, because an accurate modeling
of the halo presented in Sect. 3 section and in the Appendix A shows
that the halo model underpredicts the observed emission between
![]() and
and
![]() from the center, where the shell is
observed. This shell emission has an irregular morphology, but can be
enclosed at most inside a circle of 5.7 arcmin radius centered on the
pulsar position, corresponding to
from the center, where the shell is
observed. This shell emission has an irregular morphology, but can be
enclosed at most inside a circle of 5.7 arcmin radius centered on the
pulsar position, corresponding to ![]() 10.3 d6.2 pc.
10.3 d6.2 pc.
We have seen that the halo spectrum can be interpreted either as thermal
or non-thermal emission. By assuming that it is the long sought thermal
emission of the G54.1+0.3 shell, we have derived some interesting quantities
related to the remnant evolution by assuming an expansion governed by the
Sedov (1959) solution. The best-fit model emission measure is
![]() cm-5, and the best-fit temperature is 2 keV. According to
the model of Ghavamian et al. (2007), electrons cannot be heated directly at this
temperature by the shock, so the Coulomb heating by the shocked ions must
be at work. Using Eqs. (6)-(10) of Bocchino & Bandiera (2003), and the
best-fit model emission measure and temperature, we have computed the plot
of Fig. 4, which plots all the possible solutions versus the
remnant distance. We have specifically taken into account the case in
which electrons are not thermalized with ions, by reporting 3 different
cases of electron-ion temperatures in Fig. 4, namely
cm-5, and the best-fit temperature is 2 keV. According to
the model of Ghavamian et al. (2007), electrons cannot be heated directly at this
temperature by the shock, so the Coulomb heating by the shocked ions must
be at work. Using Eqs. (6)-(10) of Bocchino & Bandiera (2003), and the
best-fit model emission measure and temperature, we have computed the plot
of Fig. 4, which plots all the possible solutions versus the
remnant distance. We have specifically taken into account the case in
which electrons are not thermalized with ions, by reporting 3 different
cases of electron-ion temperatures in Fig. 4, namely
![]() (electron-ion full equilibration),
(electron-ion full equilibration),
![]() (moderate
electron-ion disequilibrium), and
(moderate
electron-ion disequilibrium), and
![]() (strong disequilibrium, as
in other young SNRs, Ghavamian et al. 2007, and references therein). When we use
a distance of 6.2 kpc, we find a range of remnant ages between 2500
and 3300 yr for the equipartition case (solid line in Fig. 4),
which is in agreement with the more uncertain estimate of the remnant age
(1500-6000 yr) given by Camilo et al. (2002). The inferred ISM pre-shock
density is
(strong disequilibrium, as
in other young SNRs, Ghavamian et al. 2007, and references therein). When we use
a distance of 6.2 kpc, we find a range of remnant ages between 2500
and 3300 yr for the equipartition case (solid line in Fig. 4),
which is in agreement with the more uncertain estimate of the remnant age
(1500-6000 yr) given by Camilo et al. (2002). The inferred ISM pre-shock
density is ![]() 0.2 cm-3 and the swept-up mass is between 23
and 32
0.2 cm-3 and the swept-up mass is between 23
and 32 ![]() ,
while the X-ray emitting mass is 15-20
,
while the X-ray emitting mass is 15-20 ![]() .
The explosion energy range is
.
The explosion energy range is
![]() erg. However,
when we no longer assume equipartition between electron and ions,
we find that
erg. However,
when we no longer assume equipartition between electron and ions,
we find that
![]() erg for a distance of 6.2 kpc
when
erg for a distance of 6.2 kpc
when
![]() .
In this case, the derived age is between 1800
and 2400 yr (dotted line in Fig. 4). Lower values of
.
In this case, the derived age is between 1800
and 2400 yr (dotted line in Fig. 4). Lower values of
![]() (i.e.
(i.e. ![]() 1/10) are disfavored by relative high explosion energies
(dashed line in Fig. 4). We have seen that the XMM spectral
fittings suggest a similar temperature to the SUZAKU values, but a
normalization 10 times lower. In this case, the estimate of the ISM
density, explosion energy, and swept-up mass must decrease by a factor
of 3. A cross-check with the non-radiative SNR model of Truelove & McKee (1999)
gives a transition from ejecta-dominated to Sedov phase at 2500 yr, so
the remnant is entering in the adiabatic phase. Given the faintness
of the diffuse emission, only a deeper X-ray observation would allow us
to derive more reliable values of the shell parameters.
1/10) are disfavored by relative high explosion energies
(dashed line in Fig. 4). We have seen that the XMM spectral
fittings suggest a similar temperature to the SUZAKU values, but a
normalization 10 times lower. In this case, the estimate of the ISM
density, explosion energy, and swept-up mass must decrease by a factor
of 3. A cross-check with the non-radiative SNR model of Truelove & McKee (1999)
gives a transition from ejecta-dominated to Sedov phase at 2500 yr, so
the remnant is entering in the adiabatic phase. Given the faintness
of the diffuse emission, only a deeper X-ray observation would allow us
to derive more reliable values of the shell parameters.
The derived values of density and swept-up mass are indicative of an expansion in
rarefied medium for most of the remnant lifetime. This seems to be in
agreement with the findings of Leahy et al. (2008) about the environment of
G54.1+0.3. The remnant projected location inside a large IR shell opens up the
possibility that G54.1+0.3 originated in a SN belonging to the same
star cluster whose winds have created the large IR shell. Although the
IR shell distance seems to be a little bit larger than the PWN distance
(7.2 kpc versus 6.2 kpc), according to Leahy et al. (2008) the uncertainties
in the distance do not rule out the association, and the values of
the density that we derived with the X-ray spectral analysis go in the
same direction. The X-ray shell seems to be larger than the CO cloud
reported by Leahy et al. (2008), as shown by the CO contours overplotted in
Fig. 1. Koo et al. (2008) showed that G54.1+0.3 interacted
with a star-forming loop located very close to the nebula center (at
![]()
![]() from the pulsar). The loop contains at least 11 young
stellar objects (YSOs) which are very bright in the AKARI 15
from the pulsar). The loop contains at least 11 young
stellar objects (YSOs) which are very bright in the AKARI 15 ![]() m
image of the core of the PWN. Koo et al. (2008) argue that there is no direct
evidence of the interaction of the SNR shock with this dense material,
so they conclude that the IR loop is a partial shell in a low-density
medium and that the SNR shock has propagated well beyond it. This is in
agreement with the position of the X-ray shell we have discovered, since
we can now compute (using the Truelove & McKee 1999 model) that the shock was
at the IR loop position at just 1/10 of the present age. Temim et al. (2010)
proposed an explanation in terms of ejecta dust for the IR loop, which
is not inconsistent with the presence of the X-ray shell.
m
image of the core of the PWN. Koo et al. (2008) argue that there is no direct
evidence of the interaction of the SNR shock with this dense material,
so they conclude that the IR loop is a partial shell in a low-density
medium and that the SNR shock has propagated well beyond it. This is in
agreement with the position of the X-ray shell we have discovered, since
we can now compute (using the Truelove & McKee 1999 model) that the shock was
at the IR loop position at just 1/10 of the present age. Temim et al. (2010)
proposed an explanation in terms of ejecta dust for the IR loop, which
is not inconsistent with the presence of the X-ray shell.
If the faint diffuse emission that we have discovered around the PWN
G54.1+0.3 is really the associated SNR shell, then we can compare its
properties
with the PWN-SNR evolutionary model of Gelfand et al. (2009). This model couples
the dynamical and radiative evolution of the PWN with the dynamical
properties of the surrounding non-radiative SNR, and predicts several
distinctive evolutionary stages, namely the initial expansion, the reverse
shock collision, the re-expansion, and the second compression. We run
the model using as input parameters
![]() and
and
![]() cm-3, derived from the best-fit thermal model of the X-ray shell
(Fig. 4,
cm-3, derived from the best-fit thermal model of the X-ray shell
(Fig. 4,
![]() case of a moderate deviation
from electron-ion equipartition). We assumed an ejecta mass of 8
case of a moderate deviation
from electron-ion equipartition). We assumed an ejecta mass of 8
![]() ,
and a spin-down timescale of 500 years (close to the value
of the Crab; this corresponds to an initial period P0=56 ms of
the pulsar). The pulsar wind properties are the same as in Table
2 of Gelfand et al. (2009). The resulting dynamical evolution of the
shock of the shell and the PWN nebula is shown in Fig. 5,
where we plot the ratio of the shell radius to the PWN radius
(
,
and a spin-down timescale of 500 years (close to the value
of the Crab; this corresponds to an initial period P0=56 ms of
the pulsar). The pulsar wind properties are the same as in Table
2 of Gelfand et al. (2009). The resulting dynamical evolution of the
shock of the shell and the PWN nebula is shown in Fig. 5,
where we plot the ratio of the shell radius to the PWN radius
(
![]() )
versus time, and a vertical line marks the
time when the pulsar has the same characteristic age as measured
by Camilo et al. (2002), and its period and period-derivative match the
observed values (
)
versus time, and a vertical line marks the
time when the pulsar has the same characteristic age as measured
by Camilo et al. (2002), and its period and period-derivative match the
observed values (
![]() yr and a true age of 2400 yr). The predicted
yr and a true age of 2400 yr). The predicted
![]() is remarkably similar to the observed value, and the
SNR and PWN sizes (8.7 and 2.8 pc) are in relatively good agreement with
observations
is remarkably similar to the observed value, and the
SNR and PWN sizes (8.7 and 2.8 pc) are in relatively good agreement with
observations![]() . According to this model, the
PWN has not yet been crushed by the reverse shock (Fig. 5 shows
that it will happen at an age of
. According to this model, the
PWN has not yet been crushed by the reverse shock (Fig. 5 shows
that it will happen at an age of ![]() 7000 yr, when
7000 yr, when
![]() reaches a minimum), in agreement with the lack of signs of crushing,
as noted by Temim et al. (2010). We conclude that the thermal parameters that we
have measured in the faint diffuse emission around the PWN and the emission's dimensions
are in good agreement with what we expect for a putative shell of the
SNR G54.1+0.3, on the basis of a complete modeling of the SNR-PWN system.
We interpret this as an additional indication that what we observe is indeed
the long sought shell of the remnant.
reaches a minimum), in agreement with the lack of signs of crushing,
as noted by Temim et al. (2010). We conclude that the thermal parameters that we
have measured in the faint diffuse emission around the PWN and the emission's dimensions
are in good agreement with what we expect for a putative shell of the
SNR G54.1+0.3, on the basis of a complete modeling of the SNR-PWN system.
We interpret this as an additional indication that what we observe is indeed
the long sought shell of the remnant.
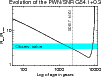
|
Figure 5:
Ratio of the shell radius to PWN radius according to
the model of Gelfand et al. (2009), with input parameters tailored to
the G54.1+0.3 system (see text for details). The observed value is also
reported as a cyan stripe, whose spread is caused by the uncertainties
in defining the real PWN radius (we have used a minimum of
|
| Open with DEXTER | |
5 Summary and conclusions
We have analyzed an XMM-Newton and a SUZAKU observation of the PWN
G54.1+0.3, in the framework of a program designed to survey the
region around this isolated nebula in search for the X-ray shell of the
associated supernova remnant. We detected very faint X-ray emission
around the PWN, extending from the outskirts of the PWN (at ![]()
![]() from the central pulsar) to a radius
from the central pulsar) to a radius ![]() 3.8 times
the PWN radius (i.e.,
3.8 times
the PWN radius (i.e., ![]()
![]() ,
around 10.3 pc at the distance
of the nebula). This extended diffuse emission is more evident toward
the south and has an irregular morphology on a angular scale of
,
around 10.3 pc at the distance
of the nebula). This extended diffuse emission is more evident toward
the south and has an irregular morphology on a angular scale of ![]()
![]() .
We modeled the X-ray dust scattering halo around G54.1+0.3, and
found that the detected faint diffuse emission cannot be caused by
this effect, but must be intrinsic to the source. We modeled the X-ray
spectrum of the diffuse emission with a thermal model, finding a best-fit
temperature of
.
We modeled the X-ray dust scattering halo around G54.1+0.3, and
found that the detected faint diffuse emission cannot be caused by
this effect, but must be intrinsic to the source. We modeled the X-ray
spectrum of the diffuse emission with a thermal model, finding a best-fit
temperature of ![]() 2 keV, which may be indicative of electron heating
by the shocked ions. This value, and the apparent size
and the emission measure of the X-ray emitting plasma, is consistent
with a SNR shell expanding into a
2 keV, which may be indicative of electron heating
by the shocked ions. This value, and the apparent size
and the emission measure of the X-ray emitting plasma, is consistent
with a SNR shell expanding into a ![]() 0.2 cm-3 ISM, whose
explosion energy is
0.2 cm-3 ISM, whose
explosion energy is ![]() 1051 erg, and whose most probable age
is 1800-2400 yr, a bit less than the characteristic age of the pulsar
PSR J1930+1852, located at the center of the PWN. However, due to
limited counting statistics, the X-ray spectrum of the diffuse emission
can alternatively be fitted well with a non-thermal power-law
model, whose photon index (
1051 erg, and whose most probable age
is 1800-2400 yr, a bit less than the characteristic age of the pulsar
PSR J1930+1852, located at the center of the PWN. However, due to
limited counting statistics, the X-ray spectrum of the diffuse emission
can alternatively be fitted well with a non-thermal power-law
model, whose photon index (
![]() )
is roughly consistent with
an interpretation in terms of synchrotron emission from accelerated
particles. The morphology of the large diffuse emission seems to be
directly linked to neither the IR shell observed around the PWN by Koo et al. (2008),
nor to the molecular cloud detected by Leahy et al. (2008) and reported
as contours in Fig. 1, but the fact that the X-ray shell is
incomplete is probably related to the interaction between the PWN and
these inhomogeneities of the ISM.
)
is roughly consistent with
an interpretation in terms of synchrotron emission from accelerated
particles. The morphology of the large diffuse emission seems to be
directly linked to neither the IR shell observed around the PWN by Koo et al. (2008),
nor to the molecular cloud detected by Leahy et al. (2008) and reported
as contours in Fig. 1, but the fact that the X-ray shell is
incomplete is probably related to the interaction between the PWN and
these inhomogeneities of the ISM.
We have compared the PWN and SNR sizes with the prediction of the evolutionary model of Gelfand et al. (2009) for composite SNRs, and we found excellent agreement. We conclude that the faint diffuse emission around the PWN G54.1+0.3 may indeed be the shell of the associated remnant. However, deeper X-ray and radio observations are required to definitely distinguish between a thermal and non-thermal interpretation. Given the detections of X-ray shells around other PWNe, our results suggest that the lack of shell around remaining isolated PWNe may be caused by high absorption and/or lack of long observations, and that the X-ray band may be very effective in discovering them.
AcknowledgementsWe thank Prof. D. Leahy and Dr. Wenwu Tian for providing us with the electronic version of Fig. 3 of their work Leahy et al. (2008). J.D.G. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-0702957. This work is partially supported by the ASI-INAF contract I/088/06/0.
Appendix A: An approximated treatment of dust-scattering X-ray halos
We assume that the scatterings are in the Rayleigh-Gans regime (this is
typically valid above
![]() ;
see, e.g., Smith & Dwek (1998) for more
details on the different scattering regimes). In addition, we assume that scattering angles are small,
and we do not consider multiple scatterings (e.g.,
Predehl & Klose 1996). In this way, one can take advantage of two simple
scaling laws: the scattering optical depth scales with the photon energy
as E-2, while the angular scale of the halo scales as E-1.
;
see, e.g., Smith & Dwek (1998) for more
details on the different scattering regimes). In addition, we assume that scattering angles are small,
and we do not consider multiple scatterings (e.g.,
Predehl & Klose 1996). In this way, one can take advantage of two simple
scaling laws: the scattering optical depth scales with the photon energy
as E-2, while the angular scale of the halo scales as E-1.
The radial profile of the halo of a point-like source, at a given photon
energy, is derived by calculating the following integral
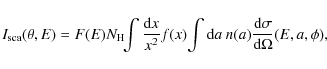
|
(A.1) |
where
The differential cross-section for single scattering can be expressed as
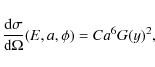
|
(A.2) |
where C contains information about the grain composition, y is defined to be
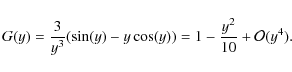
|
(A.3) |
Therefore, assuming a constant f(x) between
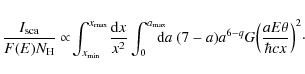
|
(A.4) |
In the limit
| (A.5) |
while, in the opposite limit, it is equal to

|
(A.6) |
where we have defined
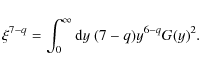
|
(A.7) |
The quantity
We introduce a ``step-like'' approximation for the function G(y)2, where is
equal to unity for ![]() and vanishing elsewhere.
This approximation is equivalent to approximating the integral in a by
matching its two limits.
In this way, it is possible to integrate analytically the integral in Eq. (A.7).
The result is proportional to function
and vanishing elsewhere.
This approximation is equivalent to approximating the integral in a by
matching its two limits.
In this way, it is possible to integrate analytically the integral in Eq. (A.7).
The result is proportional to function
![]() whose shape defined to be
whose shape defined to be
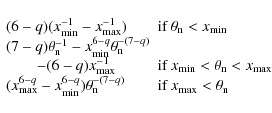
|
(A.8) |
where
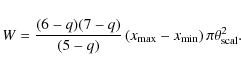
|
(A.9) |
It is then convenient to redefine
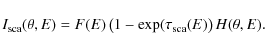
|
(A.10) |
With respect to the profile derived here, an exact solution would produce a slightly smoother profile. However, this effect is minor compared to the uncertainties related to how sharp the upper cutoff in the distribution with size is and how sharp the boundaries of the spatial distribution of grains are.
We note a few properties of
![]() .
As expected,
.
As expected,
![]() ,
and
,
and
![]() .
In addition, if
.
In addition, if
![]() and
and
![]() are both changed by a factor
are both changed by a factor ![]() ,
the shape of H does not change, provided that
,
the shape of H does not change, provided that
![]() changes as
changes as ![]() .
This, for instance, implies that the effect of dust extending from the source
to a minimum normalized distance (
.
This, for instance, implies that the effect of dust extending from the source
to a minimum normalized distance (
![]() )
to the observer is equivalent
to the case of a uniform spatial distribution of the dust, but with a size
distribution extending to
)
to the observer is equivalent
to the case of a uniform spatial distribution of the dust, but with a size
distribution extending to
![]() instead of to
instead of to
![]() :
this effect
would lead to an overestimate of the value of
:
this effect
would lead to an overestimate of the value of
![]() .
.
Since here we do not wish to study the actual properties of the foreground
dust but simply model the shape of the scattering halo, without loss of
generality, in the following we assume
![]() (i.e.,
(i.e.,
![]() ).
).
References
- Bandiera, R., & Bocchino, F. 2004, Adv. Space Res., 33, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Chevalier, R. A., & Frierson, D. M. 2001, ApJ, 563, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchino, F., & Bandiera, R. 2003, A&A, 398, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchino, F., Warwick, R. S., Marty, P., et al. 2001, A&A, 369, 1078 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchino, F., van der Swaluw, E., Chevalier, R., & Bandiera, R. 2005, A&A, 442, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchino, F., Warwick, R. S., Marty, P., et al. 2001, A&A, 369, 1078 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camilo, F., Lorimer, D. R., Bhat, N. D. R., et al. 2002, ApJ, 574, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 2005, ApJ, 619, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Gelfand, J. D., Slane, P. O., & Zhang, W. 2009, ApJ, 703, 2051 [NASA ADS] [CrossRef] [Google Scholar]
- Ghavamian, P., Laming, J. M., & Rakowski, C. E. 2007, ApJ, 654, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., Helfand, D. J., & Newburgh, L. 2007, ApJ, 654, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokubun, M., Makishima, K., Takahashi, T., et al. 2007, PASJ, 59, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, B., McKee, C. F., Lee, J., et al. 2008, ApJ, 673, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
- Leahy, D. A., Tian, W., & Wang, Q. D. 2008, AJ, 136, 1477 [Google Scholar]
- Lu, F. J., Wang, Q. D., Aschenbach, B., Durouchoux, P., & Song, L. M. 2002, ApJ, 568, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Porquet, D., Decourchelle, A., & Warwick, R. S. 2003, A&A, 401, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., & Klose, S. 1996, A&A, 306, 283 [NASA ADS] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Smith, R. K., & Dwek, E. 1998, ApJ, 503, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S., & Kuntz, K. 2007, XMM-Newton ESAS manual, ftp://xmm.esac.esa.int/pub/xmm-esas/xmm-esas.pdf, 2 [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Temim, T., Slane, P., Reynolds, S. P., Raymond, J. C., & Borkowski, K. J. 2010, ApJ, 710, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Swaluw, E., Achterberg, A., Gallant, Y. A., & Tóth, G. 2001, A&A, 380, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Velusamy, T., & Becker, R. H. 1988, AJ, 95, 1162 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- NSF Astronomy and Astrophysics Postdoctoral Fellow.
- ... them
![[*]](/icons/foot_motif.png)
- Equation (3) corresponds to the PSF analytical description discussed in the EPIC Calibration status document available in the ESA XMM-Newton Calibration Portal (http://xmm2.esac.esa.int). However, our best-fit model parameters are in general larger since the PWN is extended. For the purpose of our halo modeling, we just need an empirical relation to take into account the PSF+source effect.
- ...
observations
![[*]](/icons/foot_motif.png)
- We have verified that, by running the PWN-SNR
model using the results of the equipartition case (
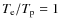 in
Fig. 4) we would not reproduce the observed size of the remnant,
unless a far too low ejecta mass is used.
in
Fig. 4) we would not reproduce the observed size of the remnant,
unless a far too low ejecta mass is used.
All Tables
Table 1: X-ray observations used in this work.
Table 2: SUZAKU spectral fitting results.
Table 3: X-ray dust scattering halo best-fit parameters for G54.1+0.3.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{h14298f1a.eps} \includegraphics[width=9cm,clip]{h14298f1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14298-10/Timg26.png)
|
Figure 1:
Top panel: XMM-Newton EPIC image in the 1-7 keV energy
band. The image is a mosaic of background-subtracted and
vignetting-corrected images obtained with the PN, MOS1, and MOS2
cameras. The color scale has been chosen to maximize the visibility
of the faint diffuse emission around the bright PWN. The inner (black)
circle has a radius of
|
| Open with DEXTER | |
| In the text | |

|
Figure 2: Top: SUZAKU spectrum of the core region and the best-fit model. XIS0+3, XIS2, and HXD spectra are shown. Bottom: SUZAKU XIS0+3 and XIS2 spectra of the shell region. The total best-fit thermal + residual non-thermal component from the core is overplotted, as long as the individual components (dashed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h14298f3.eps} \vspace*{0.4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14298-10/Timg66.png)
|
Figure 3:
X-ray normalized profiles in the bands 1.0-1.75, 1.75-2.5,
2.5-3.9, and 3.9-7.25 keV of G54.1+0.3 as seen by MOS2 camera of
XMM-Newton EPIC. Along the x-axis, we report the logarithmic distance from
the center in arcsec. We have overplotted the best-fit halo model,
with individual components (intrinsic source, long-dashed line, and
halo, short-dashed line). The radial range of the fit extends only to
|
| Open with DEXTER | |
| In the text | |

|
Figure 4:
Sedov solutions for the SNR age and distance computed using
the X-ray derived parameters of G54.1+0.3 (kT=2 keV, SNR radius
|
| Open with DEXTER | |
| In the text | |

|
Figure 5:
Ratio of the shell radius to PWN radius according to
the model of Gelfand et al. (2009), with input parameters tailored to
the G54.1+0.3 system (see text for details). The observed value is also
reported as a cyan stripe, whose spread is caused by the uncertainties
in defining the real PWN radius (we have used a minimum of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


