| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201014030 | |
| Published online | 30 September 2010 | |
Hysteresis of atmospheric parameters of
12 RR Lyrae stars based on multichannel simultaneous Strömgren
photometry![[*]](/icons/foot_motif.png)
K. S. de Boer - G. Maintz
Argelander Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 8 January 2010 / Accepted 17 May 2010
Abstract
Aims. RR Lyrae stars have been observed to improve
the insight into processes at work in their atmospheres.
Methods. Simultaneous Strömgren-photometry allows to
obtain a rapid sequence of measurements in which photometric indices
are unaffected by non-optimum observing conditions. The indices y,
b-y, and c1
are used with an established calibration to derive
![]() and to determine the gravity,
and to determine the gravity,
![]() from the Balmer jump, throughout the pulsation cycle. By employing the
equations for stellar structure, additional parameters can be derived.
from the Balmer jump, throughout the pulsation cycle. By employing the
equations for stellar structure, additional parameters can be derived.
Results. Strömgren photometry and its calibration in
terms of ![]() and
and ![]() can be used to determine the run of R and the
atmosphere pulsation velocity. We find that the Balmer-line strengths
are correlated with
can be used to determine the run of R and the
atmosphere pulsation velocity. We find that the Balmer-line strengths
are correlated with ![]() and that the strength of the Ca II K
line correlates well with the radius of the star and thus the
pulsation-dependent density of the atmosphere. The density in the
stellar atmosphere fluctuates as indicated by the changes in the
gravity
and that the strength of the Ca II K
line correlates well with the radius of the star and thus the
pulsation-dependent density of the atmosphere. The density in the
stellar atmosphere fluctuates as indicated by the changes in the
gravity ![]() ,
derived from c1, between 2.3
and 4.5 dex. Also the Strömgren metal index, m1,
fluctuates. We find a disagreement between
,
derived from c1, between 2.3
and 4.5 dex. Also the Strömgren metal index, m1,
fluctuates. We find a disagreement between
![]() ,
the gravity calculated from
,
the gravity calculated from ![]() ,
L, and the mass M, and the
gravity
,
L, and the mass M, and the
gravity ![]() .
This can be used to reassess the mass and the absolute magnitude of an
individual star. The curves derived for the pulsational velocity
.
This can be used to reassess the mass and the absolute magnitude of an
individual star. The curves derived for the pulsational velocity
![]() differ from curves obtained from spectra needed to apply the
Baade-Wesselink method; we think these differences are due to phase
dependent differences in the optical depth levels sampled in continuum
photometry and in spectroscopy. We find an atmospheric oscillation in
these fundamental mode RR Lyrae stars of periodicity P/7.
differ from curves obtained from spectra needed to apply the
Baade-Wesselink method; we think these differences are due to phase
dependent differences in the optical depth levels sampled in continuum
photometry and in spectroscopy. We find an atmospheric oscillation in
these fundamental mode RR Lyrae stars of periodicity P/7.
Conclusions. Carefully conducted
Strömgren-photometry allows to derive a large number of parameters for
RR Lyrae stars. It provides a means of deriving masses and
absolute magnitudes. When comparing photometry results with
spectroscopic analyses it appears that optical depth effects affect all
interpretations.
Key words: stars: variables: RR Lyrae - stars: horizontal-branch - stars: oscillations - Galaxy: halo - techniques: photometric - stars: fundamental parameters
1 Introduction
When lower mass stars evolve and come to core He burning, their properties can become those of the ``instability strip'' in the HRD. The atmospheric structure then reaches, as it were, a certain ``undecidedness'', causing rhythmic attempts to reach a stable state. The atmosphere cannot find its ``thermal equilibrium'' in the sense explored at a general level by Renzini et al. (1992) in the gedankenexperiment the ``gravothermal hysteresis cycle''.
The rhythmic expansion and contraction of the atmosphere of
pulsating RR Lyrae stars is caused by the ![]() -effect. The
optical depth
-effect. The
optical depth ![]() in the layer in which He is ionized has a rhythmic variation: a higher
level of ionization causes lower opacity, leading to a higher photon
throughput, causing local cooling, which leads to recombination and
thus to higher opacity, reduced radial energy transport so to
increasing inner temperatures, coming full circle to increase
ionization (see, e.g., Cox 1980;
Gautschy & Saio 1995).
This cyclic behaviour produces hysteresis effects in the colour indices
of the emergent stellar radiation as well as in various other
observables (such as spectral line strengths). These all are based on,
of course, hysteresis in surface gravity and effective temperature.
in the layer in which He is ionized has a rhythmic variation: a higher
level of ionization causes lower opacity, leading to a higher photon
throughput, causing local cooling, which leads to recombination and
thus to higher opacity, reduced radial energy transport so to
increasing inner temperatures, coming full circle to increase
ionization (see, e.g., Cox 1980;
Gautschy & Saio 1995).
This cyclic behaviour produces hysteresis effects in the colour indices
of the emergent stellar radiation as well as in various other
observables (such as spectral line strengths). These all are based on,
of course, hysteresis in surface gravity and effective temperature.
Using photometry of RR Lyr stars, one can derive the variation
in the parameters of the stellar surface. The first investigations of
this kind were carried out by Oke & Bonsack (1960), Oke
et al. (1962),
Oke (1966),
and Danziger & Oke (1967),
who used spectral scanner data in comparison with model atmospheres to
obtain ![]() and
and ![]() to calculate the change in radius. They noted that the changes in the
atmosphere imply that one observes light from different atmospheric
layers so that the radii thus derived might not be reliable.
to calculate the change in radius. They noted that the changes in the
atmosphere imply that one observes light from different atmospheric
layers so that the radii thus derived might not be reliable.
The information can also be obtained from Strömgren
photometry. After the establishment of the Strömgren-photometric system
and its early calibration (see, e.g., Breger 1974) this
photometry was used by van Albada & de Boer (1975) to derive the
parameters ![]() ,
,
![]() ,
and R for all phases of the pulsation. McNamara
& Feltz (1977)
and Siegel (1982)
also used the Strömgren-system. Similar studies were performed by Lub (1977a,b, 1979) with the
Walraven photometric system.
,
and R for all phases of the pulsation. McNamara
& Feltz (1977)
and Siegel (1982)
also used the Strömgren-system. Similar studies were performed by Lub (1977a,b, 1979) with the
Walraven photometric system.
Only for a few RR Lyrae stars has the cycle of variation been followed in photometric detail in the Strömgren system. Thus only for a few of these stars is the variation in parameter values over the cycle accurately known. Photometry is normally performed sequentially in whichever wavelength bands selected. Sequentiality mandates good photometric conditions to obtain accurate colour indices for the derivation of reliable stellar parameters. Moreover, sequential measurements in the chosen bands are asynchronous among the bands. Performing measurements simultaneously in well selected photometric bands allows to obtain precise colour indices even in poor photometric conditions. For the research presented here, we used the Bonn University Simultaneous CAmera, BUSCA (Reif et al. 1999). To transform the colour indices to astrophysical parameters, the calibration of the Strömgren system by Clem et al. (2004) has been used. BUSCA also allows a rapid succession of measurements leading to a better coverage of fine structure in light curves.
The Baade-Wesselink method (Baade 1926; Wesselink 1946)
requires the measurement of the radial velocity variation to produce a
full characterization of a pulsating star. Following
van Albada & de Boer (1975) we will again
show that, with accurate photometry, R can be
derived (rather, the apparent angular extent, which indicates the
radius when the distance to the star is known) and the changes in R
can be used to calculate the run of atmospheric velocities
![]() through the pulsational cycle. Strömgren photometry allows, in
principle, to derive astrophysical parameters more accurately than
possible from the widely used Johnson photometry.
through the pulsational cycle. Strömgren photometry allows, in
principle, to derive astrophysical parameters more accurately than
possible from the widely used Johnson photometry.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14030f1.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg27.png)
|
Figure 1: Lightcurves of the RR Lyrae stars in y. Data from subsequent cycles have been combined (see Table 1 for observing dates). The curves have been shifted arbitrarily in y to fit them into one panel. For the stars lower in the figure, the lightcurve coverage is incomplete. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg28.png)
|
Figure 2: Lightcurves of RR Gem and SY Ari observed with BUSCA in the Strömgren-system. Note the different brightness amplitude of the two stars. At the bottom, the instrumental brightness of the mean of two comparison stars (selected in the field of each variable) is shown. |
| Open with DEXTER | |
2 Observations and data reduction
The observations were carried out in three sessions at the Calar Alto Observatory of the Deutsch-Spanisches Astronomie Zentrum (DSAZ) in southern Spain in three successive winter seasons, between 4 and 9 Jan. 2005, between 16 and 19 Dec. 2005, and between 26 and 28 Nov. 2006.
The times of maximum brightness within the observing sessions
were calculated for each star from the period P and
a reference epoch as
![]() with appropriate n. This allowed optimal
phase-coverage planning of the photometry. In the various figures to
follow, the data are plotted against phase
with appropriate n. This allowed optimal
phase-coverage planning of the photometry. In the various figures to
follow, the data are plotted against phase ![]() based on the observed maximum. For a few stars, the maximum could not
be measured so the phase was determined from early epoch maxima.
based on the observed maximum. For a few stars, the maximum could not
be measured so the phase was determined from early epoch maxima.
Our programme consisted of observing 18 relatively bright RR Lyrae (for accurate positions and additional data, see Maintz 2005). Of 12 of these, (almost) complete lightcurves were obtained (coverage >70%) as given in Table 1 and Fig. 1 (and Fig. 2). However, for X CMi we missed the maximum. Of 6 stars (GM And, OV And, GI Gem, TY Cam, TT Lyn, CZ Lac), only smaller portions (15 to 57%) of the light curve could be obtained; these stars are not discussed further.
The stars selected are fundamental mode pulsators (see Fig. 3). They generally have lightcurve bumps.
Table 1: The stars with basic information, the J.D. of the observations, and the phase ranges covered.
BUSCA (Reif et al. 1999) is operated at the 2.2 m telescope of the Calar Alto Observatory. BUSCA splits the telescope beam above the Cassegrain focus via dichroic beam splitters in 4 wavelength channels between 3200 and 9000 Å, with edges at 4300, 5400 and 7300 Å. Each channel is equipped with a (4k)2 CCD. In each channel, a filter wheel allows the placement of appropriate filters.
For the measurements we used the Strömgren u, v, b,
y-system, extended by the Cousins I
band![]() . The y band
is close to the cut-off of a BUSCA-dichroic
filter; however, the transformation of y into the
standard system could be performed without problems. Because of the
proximity of the wavelengths of u and v,
their filters are in the same BUSCA channel.
Since the u and v bands
could not be measured simultaneously, the photometry alternated between
the simultaneous exposures in y,b,v,(I)
and y,b,u,(I).
For two stars, light curves in the four Strömgren-bands are shown in
Fig. 2.
More data are shown in Maintz (2008a).
. The y band
is close to the cut-off of a BUSCA-dichroic
filter; however, the transformation of y into the
standard system could be performed without problems. Because of the
proximity of the wavelengths of u and v,
their filters are in the same BUSCA channel.
Since the u and v bands
could not be measured simultaneously, the photometry alternated between
the simultaneous exposures in y,b,v,(I)
and y,b,u,(I).
For two stars, light curves in the four Strömgren-bands are shown in
Fig. 2.
More data are shown in Maintz (2008a).
| Figure 3: Plot of the amplitude in y versus period of our stars showing that they are fundamental mode RRa-type pulsators. The band between the dotted lines marks the zone of RRa and RRb pulsators (see Ledoux & Walraven 1958). |
|
| Open with DEXTER | |
To calibrate the data, the instrumental brightness of each variable was
obtained by comparison with two non-variable stars in the field. Where
possible, one star with a brightness near the
![]() of the RR Lyrae star was used and another of brightness close
to
of the RR Lyrae star was used and another of brightness close
to ![]() of the variable. (In the data a known suspected variable was
quantified; see Maintz 2008b.)
The airmass correction was obtained from these comparison stars.
of the variable. (In the data a known suspected variable was
quantified; see Maintz 2008b.)
The airmass correction was obtained from these comparison stars.
To secure the absolute calibration, we observed appropriate
stars from the list of Perry et al. (1987) at moments
in the light cycle of the variable where the changes in brightness were
small or monotonous. The instrumental magnitudes of the
(airmass-corrected) photometry were related to the true magnitudes of
the calibration stars. This permitted the calibration of the
RR Lyrae star photometry. First, the RR Lyrae y
measurements were calibrated. Since the instrumental
![]() from BUSCA is more accurate than
from BUSCA is more accurate than
![]() -
-
![]() (the same is true for the
other indices), the calibrated b-y
and v-b were obtained from the
instrumental index and that of the calibration stars. The sequentially
obtained colour indices u-y and v-y
were then used to interpolate in time to obtain u-v,
which was calibrated. Using these indices,
c1=
(u-v)-(v-b)
and m1
= (v-b) - (b-y)
were calculated.
(the same is true for the
other indices), the calibrated b-y
and v-b were obtained from the
instrumental index and that of the calibration stars. The sequentially
obtained colour indices u-y and v-y
were then used to interpolate in time to obtain u-v,
which was calibrated. Using these indices,
c1=
(u-v)-(v-b)
and m1
= (v-b) - (b-y)
were calculated.
The RR Lyrae star CCD photometry was performed with
equal exposure times throughout the cycle, of 20 s for the
brightest and 70 s for the faintest stars. Exposure times are
given in Table 1.
For three stars the exposure times in the u,b,y
measurements were ![]() those of the v,b,y
measurements (see Table 1).
The (simultaneous) reading-out of the CCDs took about 2 min.
Thus the CCD exposures followed each other quickly, within
2.5 min for the brighter stars and 3.5 min for the
fainter ones. The short exposure times did not lead to large time
smearing, not even when the star changed quickly in brightness. In most
cases, two stars were observed alternatingly in rapid succession to
achieve good light curve coverage for as many stars as possible. This
alternation explains why most light curves presented have data
intervals longer than 3.5 min.
those of the v,b,y
measurements (see Table 1).
The (simultaneous) reading-out of the CCDs took about 2 min.
Thus the CCD exposures followed each other quickly, within
2.5 min for the brighter stars and 3.5 min for the
fainter ones. The short exposure times did not lead to large time
smearing, not even when the star changed quickly in brightness. In most
cases, two stars were observed alternatingly in rapid succession to
achieve good light curve coverage for as many stars as possible. This
alternation explains why most light curves presented have data
intervals longer than 3.5 min.
Basic data (d, E(B-V), [M/H]) were taken from Beers et al. (2000), Fernley et al. (1998), and Layden (1994), in part taking averages. Some of the stars are known to be behind gas with extinction and we corrected for that using expressions given by Clem et al. (2004). For four stars we calculated d from MV based on [Fe/H] using the formula of Fernley et al. (1998). The adopted distances are given in Table 1.
3 Colour-index loops
For three stars the run through the cycle of the derived absolutely calibrated colour indices is shown in Fig. 4. The b-y versus c1 diagram for two typical stars from our sample, RR Gem and TZ Aur (Fig. 5, left panel), shows clear colour index loops. The index m1 varies in line with c1 (Fig. 4). Figure 5 (right panel) shows the very moderate m1 loops in a colour-colour plot.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14030f4.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg39.png)
|
Figure 4: Lightcurves in the calibrated Strömgren-indices of the stars RR Gem, SY Ari, and BR Tau. The phase coverage of the photometry can be reconstructed from the information given in Table 1 (for BR Tau the coverage is only 70%) and can be recognised in Fig. 1. |
| Open with DEXTER | |
The (c1,b-y)
curves show the interplay of the surface parameters ![]() and
and ![]() during the cycle. The loop is essentially due to c1,
which represents (above
during the cycle. The loop is essentially due to c1,
which represents (above
![]() K)
the strength of the Balmer jump. At low
K)
the strength of the Balmer jump. At low
![]() ,
the Balmer level is hardly populated. When the temperature increases
(bluer b-y),
,
the Balmer level is hardly populated. When the temperature increases
(bluer b-y),
![]() and
and ![]() (and thus
(and thus ![]() )
of the atmosphere gas increase and (collisional) excitation of hydrogen
becomes noticeable. When the temperature decreases the population of
the Balmer level decreases as well. In RR Lyrae star
atmospheres, the ionisation of hydrogen hardly plays a role (except for
an increase in
)
of the atmosphere gas increase and (collisional) excitation of hydrogen
becomes noticeable. When the temperature decreases the population of
the Balmer level decreases as well. In RR Lyrae star
atmospheres, the ionisation of hydrogen hardly plays a role (except for
an increase in ![]() )
because the highest temperatures in the pulsational cycle are
)
because the highest temperatures in the pulsational cycle are
![]() K.
K.
It is evident from the data that the highest temperatures
appear when the star is close to maximum light. During most of the
period, the measured colour indices indicate low temperatures (large b-y,
small c1), as visible in the
clump of data points in the lower-right corner of the left-side panels
of Fig. 5.
The brightening leg and the dimming leg of the colour curves do not
overlap. During brightening, b-y
changes faster than c1,
which is indicative of a faster rise in
![]() than in the excitation to the Balmer level. In the dimming branch the
converse is found (see Fig. 5, left). Thus the
colour curve exhibits hysteresis.
than in the excitation to the Balmer level. In the dimming branch the
converse is found (see Fig. 5, left). Thus the
colour curve exhibits hysteresis.
As for the loops in m1
(Fig. 5
right), these are quite moderate and do not show much in the sense of
hysteresis. The change in m1
over the cycle is on average 0.1 mag (m1
is largest at maximum light). For our stars, m1
is larger for stars known to have larger [M/H] (see also the
calibration for red giant stars by Hilker 2000), while for
stars with [M/H] <-1 dex m1
is only marginally metal dependent. At the
![]() of RR Lyrae stars, cycle variations in m1
related to the [M/H] are small. Nevertheless, using these trends, we
estimated [M/H] for the two stars for which these values were
unavailable from other sources (see Table 1). The variation in
m1 over the cycle must be
caused by changes in temperature and electron density, which both
influence the level of ionisation and excitation of ions.
of RR Lyrae stars, cycle variations in m1
related to the [M/H] are small. Nevertheless, using these trends, we
estimated [M/H] for the two stars for which these values were
unavailable from other sources (see Table 1). The variation in
m1 over the cycle must be
caused by changes in temperature and electron density, which both
influence the level of ionisation and excitation of ions.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f5-1.ps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14030f5-2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg42.png)
|
Figure 5:
Colour loops in b-y,c1
(at left) and in b-y,m1
(at right) of several stars. The data points of
the brightening phase are marked with |
| Open with DEXTER | |
4 Behaviour of atmospheric parameters
4.1 Deriving parameters in the stationary case
The parameters ![]() and
and ![]() were determined from our photometry using the conversion grids given by
Clem et al. (2004).
These grids are based on modelled spectral energy distributions and are
provided in steps of 0.5 dex of metal content [M/H]. Clem
et al. made extensive calibrations of the Strömgren system
against the parameters of non-variable stars.
They show that individual Population II star colours can be
matched with models to within
were determined from our photometry using the conversion grids given by
Clem et al. (2004).
These grids are based on modelled spectral energy distributions and are
provided in steps of 0.5 dex of metal content [M/H]. Clem
et al. made extensive calibrations of the Strömgren system
against the parameters of non-variable stars.
They show that individual Population II star colours can be
matched with models to within ![]() 200 K and
200 K and ![]() 0.1 dex,
showing what is the ultimate uncertainty of a match. For
Population I stars, the effect of small variations in metal
content (0.3 dex) on the colours, and thus on the derived
0.1 dex,
showing what is the ultimate uncertainty of a match. For
Population I stars, the effect of small variations in metal
content (0.3 dex) on the colours, and thus on the derived
![]() and
and ![]() ,
is small. The dependence of colours on metal content is significant
only for
,
is small. The dependence of colours on metal content is significant
only for ![]() K.
For each star we used the grid for which [M/H] was closest to the metal
content of each star.
K.
For each star we used the grid for which [M/H] was closest to the metal
content of each star.
The parameters ![]() and
and ![]() can be used to derive additional parameters describing the behaviour of
the stellar atmosphere. The conditions in a regularly pulsating stars
are in ``quasi-hydrostatic equilibrium'' (Cox 1980;
Ch. 8.3), meaning that the use of a calibration based on
stable stars is justified.
can be used to derive additional parameters describing the behaviour of
the stellar atmosphere. The conditions in a regularly pulsating stars
are in ``quasi-hydrostatic equilibrium'' (Cox 1980;
Ch. 8.3), meaning that the use of a calibration based on
stable stars is justified.
However, when a RR Lyrae star brightens from
![]() to
to ![]() within approximately one hour, the atmosphere is probably not in
quasi-hydrostatic equilibrium. Doubling of Ca and H lines has been seen
(e.g., Struve 1947;
Sanford 1949) and H lines have been seen in emission (e.g., Preston
& Paczynski 1964)
in that part of the RR Lyrae cycle, which according to Abt (1959) originate
from dynamic effects. Since no models exist that take these effects for
photometry into account there is no other option than to use static
models. Furthermore, the light we detect comes from the photosphere,
i.e., the layer in which, at the particular wavelength observed, the
optical depth is
within approximately one hour, the atmosphere is probably not in
quasi-hydrostatic equilibrium. Doubling of Ca and H lines has been seen
(e.g., Struve 1947;
Sanford 1949) and H lines have been seen in emission (e.g., Preston
& Paczynski 1964)
in that part of the RR Lyrae cycle, which according to Abt (1959) originate
from dynamic effects. Since no models exist that take these effects for
photometry into account there is no other option than to use static
models. Furthermore, the light we detect comes from the photosphere,
i.e., the layer in which, at the particular wavelength observed, the
optical depth is ![]() .
This means that in the course of the pulsational cycle it is not
necessarily the same gas from which the light detected emanates. We
return to these aspects later (Sect. 8.2).
.
This means that in the course of the pulsational cycle it is not
necessarily the same gas from which the light detected emanates. We
return to these aspects later (Sect. 8.2).
The luminosity of a star is related to the surface parameters R
and ![]() through the familiar equation
through the familiar equation
![]() ,
which can be rewritten in the relative logarithmic form
,
which can be rewritten in the relative logarithmic form
The surface gravity of a star is defined as
Using Eqs. (1) and (2), one can then eliminate the radius so that the combined equation has the stellar mass, temperature, gravity, and luminosity as variables,
where
4.2 Deriving parameters in the pulsating case
In a pulsating atmosphere the parameters
![]() ,
,
![]() ,
and R vary continuously (note that no time
subscripts are used in this paper).
,
and R vary continuously (note that no time
subscripts are used in this paper).

-
 ,
L. The time-dependent values L
and
,
L. The time-dependent values L
and  can be derived from the photometry if one knows the stars distance.
can be derived from the photometry if one knows the stars distance.
 is simply inferred from a calibrated b-y
(using the grid of Clem et al. 2004). L
has to be determined from y, the integral over the
spectral energy distribution and the distance d of
the star.
is simply inferred from a calibrated b-y
(using the grid of Clem et al. 2004). L
has to be determined from y, the integral over the
spectral energy distribution and the distance d of
the star.
As for L, an RR Lyrae star has the convenient property that the maximum of its spectral energy distribution (in
 )
lies close to the middle of the visual wavelength band, near
Johnson V or Strömgren y.
This is true during the entire cycle:
)
lies close to the middle of the visual wavelength band, near
Johnson V or Strömgren y.
This is true during the entire cycle:
 actually varies only between roughly 5000 and 9000 K.
This means that the bolometric correction is neither large nor varies a
lot. We have performed the bolometric correction using the classic
values of Schmidt-Kaler (1982).
We fitted a quadratic equation in the temperature range relevant for
RR Lyrae stars.
actually varies only between roughly 5000 and 9000 K.
This means that the bolometric correction is neither large nor varies a
lot. We have performed the bolometric correction using the classic
values of Schmidt-Kaler (1982).
We fitted a quadratic equation in the temperature range relevant for
RR Lyrae stars. Distances were adopted as described in Sect. 2. If the distance d of a star were off by 20%, this would result in an error of 0.08 in
 .
.
Results for L and
 are shown in Fig. 6.
are shown in Fig. 6.

- R. The radius can be calculated from Eq. (1). For examples of radius change see Fig. 7.

 ,
,
 ,
,
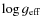 .
The surface gravity g can be calculated from
Eq. (3)
if one knows the luminosity of the star (discussed above) and its mass
(see below). This gravity is like an overall equilibrium gravity and is
henceforth called g(T,L,M).
.
The surface gravity g can be calculated from
Eq. (3)
if one knows the luminosity of the star (discussed above) and its mass
(see below). This gravity is like an overall equilibrium gravity and is
henceforth called g(T,L,M).
There is a further aspect affecting the gravity. In a pulsating atmosphere, the actual surface gravity (g(T,L,M) at the level
 )
is modified due to acceleration of the atmosphere during the pulsation
cycle with respect to the ``normal'' gravity. Thus, g
is modified by an acceleration term,
)
is modified due to acceleration of the atmosphere during the pulsation
cycle with respect to the ``normal'' gravity. Thus, g
is modified by an acceleration term,
 .
The total gravity is called the ``effective'' gravity
.
The total gravity is called the ``effective'' gravity
indicating the vertical gravitational force in the atmosphere.![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg59.png)
Figure 6: For four RR Lyrae (TW Lyn, RR Gem, AS Cnc, and SY Ari), the run of
 and L is shown in an HRD. The originally derived
values are plotted as 3-pointed stars, the resampled curve (in steps of
0.02 in phase, Sect. 4.3)
is shown as a full line. The mean values over the cycle (from
Table 2)
are given as
and L is shown in an HRD. The originally derived
values are plotted as 3-pointed stars, the resampled curve (in steps of
0.02 in phase, Sect. 4.3)
is shown as a full line. The mean values over the cycle (from
Table 2)
are given as  .
The background data (ZAMS, metal-poor ZAHB, the evolution tracks of a
0.55 and a 0.6
.
The background data (ZAMS, metal-poor ZAHB, the evolution tracks of a
0.55 and a 0.6  HB star) are taken from de Boer & Seggewiss (2008;
Fig. 10.9). Two lines of constant R
are indicated. The almost vertical dashed lines mark the approximate
location of the pulsational instability strip from Gautschi &
Saio (1995). The stellar surface parameters of the RR Lyrae
show hysteresis.
HB star) are taken from de Boer & Seggewiss (2008;
Fig. 10.9). Two lines of constant R
are indicated. The almost vertical dashed lines mark the approximate
location of the pulsational instability strip from Gautschi &
Saio (1995). The stellar surface parameters of the RR Lyrae
show hysteresis.
Open with DEXTER Table 2: Cycle averages of several RR Lyr star parameters.
The time-dependent Strömgren photometry measures the actual condition of a stellar atmosphere. The gravity derived from b-y,c1 is a function of gas density, visible in the excitation of the Balmer level and in c1 representing the Balmer jump. We will call this gravity the ``Balmer-jump'' gravity,
 .
This gravity is independent of
.
This gravity is independent of
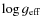 and instead represents the pressure of the gas sampled, i.e.,
and instead represents the pressure of the gas sampled, i.e.,
 .
.
We will return to the values derived for
 and
and  in Sect. 9.
in Sect. 9.

- MV,
M. RR Lyrae star distances have thus
far been derived using a reference value for MV.
This value of MV
does not apply to all RR Lyrae stars since horizontal-branch
(HB) stars evolve over more than
 on the HB. If, e.g., MV
of a star were to differ by 0.25 mag from the reference value
adopted, L would be off by 0.10.
on the HB. If, e.g., MV
of a star were to differ by 0.25 mag from the reference value
adopted, L would be off by 0.10.
The mass of RR Lyrae stars is in the range from 0.6 to
 .
We adopted a mass of
.
We adopted a mass of  ,
thereby considering that our RR Lyrae stars can deviate 15%
from that value. This deviation propagates to a maximum deviation of
0.06 dex in a calculated
,
thereby considering that our RR Lyrae stars can deviate 15%
from that value. This deviation propagates to a maximum deviation of
0.06 dex in a calculated
 .
.
A few observational determinations of the absolute magnitude MV and mass M of horizontal-branch and RR Lyrae stars exist, such as those of de Boer et al. (1995), Moehler et al. (1995), de Boer et al. (1997), Moehler et al. (1997), Tsujimoto et al. (1998), and Gratton (1998).
We return to the effect of incorrect values of these reference parameters in Sect. 4.5.
4.3 Phase resampling in steps of 0.02
To facilitate the calculation of averages over the phase and additional
analyses, we resampled the curves of L,
![]() ,
R, and
,
R, and ![]() as derived from the observational data using steps of
as derived from the observational data using steps of
![]() (starting with i=0 near maximum light). These
resampled values (given henceforth with subscript 0.02) can be easily
integrated (fixed time step). The result of these resamplings can be
seen as curves in Figs. 6
and 7
(and in further figures).
(starting with i=0 near maximum light). These
resampled values (given henceforth with subscript 0.02) can be easily
integrated (fixed time step). The result of these resamplings can be
seen as curves in Figs. 6
and 7
(and in further figures).
Time averages over the cycle of our stars have been calculated based on the 0.02 phase stepped lightcurves. For a few stars, the lightcurve coverage was not complete and we made reasonable interpolations in the gaps to obtain the time averages.
4.4 Time-averaged quantities
The structure of a ``non-pulsating RR Lyr star'' is given by the
time-averaged parameters
![]() ,
,
![]() and
and
![]() .
The time-averaged gravity,
.
The time-averaged gravity,
![]() ,
has in a purely periodic system zero contribution from
,
has in a purely periodic system zero contribution from
![]() .
.
Oke and collaborators and van Albada & de Boer felt
that since g varies strongly, the ``average'' value
is best derived from the quiet part of the cycle, i.e., from
![]() .
However, Fig. 9
makes clear that this has shortcomings. In that phase interval,
.
However, Fig. 9
makes clear that this has shortcomings. In that phase interval,
![]() is (for most stars) lower than average by between 0.1
and 0.2 dex, because the atmosphere is then slowly
but continuously contracting (but see Sect. 9).
is (for most stars) lower than average by between 0.1
and 0.2 dex, because the atmosphere is then slowly
but continuously contracting (but see Sect. 9).
The time-averaged quantities of essential parameters were
calculated from the resampled curves in steps of
![]() (see above), the integral was derived as the sum
of 50 values. Thus
(see above), the integral was derived as the sum
of 50 values. Thus

|
(4) |
and

|
(5) |
individual values of L0.02 being calculated as described in Sect. 4.2. The averages of the two gravity versions are

|
(6) |
and

|
(7) |
Time-averaged values for 11 stars are given in Table 2 and are for four stars included in Fig. 6. It can immediately be seen that the values of
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f7.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg77.png)
|
Figure 7:
Run of the parameters |
| Open with DEXTER | |
4.5 Error budget
In our analyses, the following uncertainties had to be taken into account.
Photometric errors are, given the instrumental characteristics of BUSCA, small. We estimated the uncertainties in y to be 0.03 mag. The bolometric corrections are small and introduce errors of up to 2%. This leads to a total typical photometric uncertainty in L of 3%. In the colour indices b-y, m1, and c1, the uncertainties are 0.02 mag (smaller than the error in y because of the simultaneity of the measurements).
We used distances from the literature. The effect of their uncertainties on L is given below.
To obtain ![]() and
and ![]() ,
the indices b-y and c1
were used with the grid of Clem et al. (2004). The grid is
not perfect and reading
,
the indices b-y and c1
were used with the grid of Clem et al. (2004). The grid is
not perfect and reading ![]() and
and ![]() from that grid by eye, we assessed that (based on readings performed
three times for the entire cycle for one star) the uncertainty in
from that grid by eye, we assessed that (based on readings performed
three times for the entire cycle for one star) the uncertainty in
![]() is about 1%,
and in
is about 1%,
and in ![]() about 0.05 dex. Since the effects of metallicity, [M/H], are only
significant for
about 0.05 dex. Since the effects of metallicity, [M/H], are only
significant for ![]() K,
which occurs for only 3 of our less well-observed stars near minimum
light, we are confident that our error estimates are only at those
temperatures affected by a possibly small mismatch in [M/H].
K,
which occurs for only 3 of our less well-observed stars near minimum
light, we are confident that our error estimates are only at those
temperatures affected by a possibly small mismatch in [M/H].
Given the measurement uncertainties in L
(3%) and ![]() (1%), it follows that the uncertainty in the calculated R
values is 4%. If, in addition, a distance were incorrect by +10% that
would give an additional offset for a given star in R
of +5%.
(1%), it follows that the uncertainty in the calculated R
values is 4%. If, in addition, a distance were incorrect by +10% that
would give an additional offset for a given star in R
of +5%.
As mentioned in Sect. 4.2, we
assumed a fixed mass for all stars of 0.7 ![]() ,
and indicated a margin of error of 15%. This error would lead for a
given star to an offset of 0.06 dex in a calculated
,
and indicated a margin of error of 15%. This error would lead for a
given star to an offset of 0.06 dex in a calculated
![]() .
.
The values of ![]() calculated from Eq. (3)
have a measurement error of about 8% or 0.03 dex. A distance
error of +10% leads to an offset in
calculated from Eq. (3)
have a measurement error of about 8% or 0.03 dex. A distance
error of +10% leads to an offset in
![]() of -0.04, an error in the mass M of +10% to an
offset in
of -0.04, an error in the mass M of +10% to an
offset in ![]() of +0.04.
of +0.04.
Finally we note that the distances of RR Lyrae have
essentially all been derived from a reference MV
(distance from distance modulus), in some cases adjusted for metal
content, [Fe/H]. For a review of the latest calibrations we refer to
Sandage & Tamman (2006).
However, in spite of all calibration efforts, MV
has a spread in MV
of between 0.2 and 0.4 mag for a given [Fe/H] or an
uncertainty of even up to 1.0 mag if [Fe/H] is unknown.
Moreover, given the evolution of RR Lyrae stars on the HB, a
single and universal value of MV
does not exist anyway; the evolution of an HB star may lead to an
increase in ![]() of 0.5 dex when reaching the terminal-age HB (see, e.g.,
de Boer & Seggewiss 2008; their Fig. 10.9).
Therefore, if a considered star were brighter than the chosen reference
value, its derived distance modulus and thus distance would be too
small. If the true MV
of the star is unbeknown to be 0.25 mag brighter than the
reference value, the distance (as given in Table 1) will turn out to
be too small by 12%. This affects the derived L,
then being too small by 0.10 dex.
of 0.5 dex when reaching the terminal-age HB (see, e.g.,
de Boer & Seggewiss 2008; their Fig. 10.9).
Therefore, if a considered star were brighter than the chosen reference
value, its derived distance modulus and thus distance would be too
small. If the true MV
of the star is unbeknown to be 0.25 mag brighter than the
reference value, the distance (as given in Table 1) will turn out to
be too small by 12%. This affects the derived L,
then being too small by 0.10 dex.
The mean values of Table 2 were derived
from a large number of individual measurements, so the observational
scatter is basically cancelled. What remains is the error related to
the calibration grid and also the error in the assumed distance and/or MV
(affecting ![]() and L as just indicated, as well as R).
and L as just indicated, as well as R).
5
Hysteresis of the parameters T
 ,
R, and log g
,
R, and log g
The values of the atmospheric parameters for all points in the cycle
were derived from the photometry as described above. In Fig. 6 we show the run
of ![]() and L of four of our stars in an HRD. These
parameters exhibit loops through the diagram extending over and beyond
the instability strip. The loopings are reminiscent of hysteresis. In
the older literature, the lagging behind in the change of some
parameter compared to another parameter is called ``phase-lag'' (see,
e.g., Cox 1980).
and L of four of our stars in an HRD. These
parameters exhibit loops through the diagram extending over and beyond
the instability strip. The loopings are reminiscent of hysteresis. In
the older literature, the lagging behind in the change of some
parameter compared to another parameter is called ``phase-lag'' (see,
e.g., Cox 1980).
The behaviour of ![]() and
and ![]() against phase (Fig. 7)
shows remarkable features. For all stars,
against phase (Fig. 7)
shows remarkable features. For all stars,
![]() begins to increase about
begins to increase about ![]() before
before ![]() starts to increase.
Furthermore,
starts to increase.
Furthermore, ![]() reaches its highest value when
reaches its highest value when
![]() has increased about halfway to its maximum value. And when
has increased about halfway to its maximum value. And when
![]() reaches its maximum,
reaches its maximum, ![]() is already decreasing (at phase
is already decreasing (at phase ![]() 0). The resulting value of R
(that of Fig. 7
is derived from Eq. (1))
indicates that R is smallest when
0). The resulting value of R
(that of Fig. 7
is derived from Eq. (1))
indicates that R is smallest when
![]() is largest.
is largest.
The run of R shows that RR Lyrae
are relatively extended stars for about half of the cycle (
![]() ), while large changes in
radius take place between
), while large changes in
radius take place between
![]() ,
with the most rapid change occurring between
,
with the most rapid change occurring between
![]() .
At
.
At ![]() ,
a drastic reduction in the derived R takes place
(the atmosphere apparently starts to collapse), reaching the smallest R
near
,
a drastic reduction in the derived R takes place
(the atmosphere apparently starts to collapse), reaching the smallest R
near ![]() .
At smallest R the atmosphere must have a high
density. Up to the highest density,
.
At smallest R the atmosphere must have a high
density. Up to the highest density,
![]() is at the same level as in the quiet phase leading up to the collapse.
Soon after
is at the same level as in the quiet phase leading up to the collapse.
Soon after ![]() ,
R increases again.
,
R increases again.
In general, when y is brightest
![]() is at its highest and R is very small; but
immediately after minimum light, at the high peak in
is at its highest and R is very small; but
immediately after minimum light, at the high peak in
![]() ,
R is at its smallest.
,
R is at its smallest.
6 Spectral line strengths
For three of our stars (TZ Aur, RR Gem, RS
Boo), spectra were obtained (in January 2006, independently of the
Strömgren-photometry) with the focal reducer spectrograph at the
1 m telescope of the Observatory ``Hoher List'' of the AIfA.
Radial velocities could not be obtained with this instrument. The
spectra have a resolution of ![]() 3 Å. Because of telescope size and
focal-reducer set-up, exposure times had to be rather long, of the
order of 3% of the period, leading to phase smearing. We determined the
equivalent withs of the lines of H
3 Å. Because of telescope size and
focal-reducer set-up, exposure times had to be rather long, of the
order of 3% of the period, leading to phase smearing. We determined the
equivalent withs of the lines of H![]() ,
H
,
H![]() ,
H
,
H![]() ,
Na I D, and Ca
II K.
,
Na I D, and Ca
II K.
For RR Gem and TZ Aur, we show
(Fig. 8)
how the strengths of the H![]() and Ca K lines vary during the cycle. Results for
RS Boo are not shown because the lightcurve coverage was poor.
and Ca K lines vary during the cycle. Results for
RS Boo are not shown because the lightcurve coverage was poor.
H![]() .
The strength of Balmer lines is governed by
.
The strength of Balmer lines is governed by
![]() as expected since the Balmer level can be populated only during the
higher
as expected since the Balmer level can be populated only during the
higher ![]() part of the RR Lyrae cycle. The temporal behaviour of W(H
part of the RR Lyrae cycle. The temporal behaviour of W(H![]() )
and
)
and ![]() (Fig. 8)
is indeed very similar.
(Fig. 8)
is indeed very similar.
Ca II K. The strength of Ca K is predominantly set by the gas density, i.e., the ionization balance forces Ca II to be reduced at higher density (when R is smallest). The curves of W(CaK) and R are very similar in terms of their temporal behaviour (clearly for RR Gem).
The Na I D
absorption is very weak and provides little information, except that
Na I D is strong when
![]() is at its lowest; the increased strength is caused by the shift of the
ionization balance towards the neutral state at lower
is at its lowest; the increased strength is caused by the shift of the
ionization balance towards the neutral state at lower
![]() .
.
7 The
variation in the pulsation velocity V

7.1 The coarse variation in 
Figure 7
shows for three stars the change in radius, R, as
derived from Eq. (1).
One can thus calculate the velocity of the stellar atmosphere (the
``pulsation velocity'', ![]() ). We used
). We used
where R is at intervals of fixed value
| Figure 8:
For RR Gem and TZ Aur, the run of the equivalent
widths W of the spectral lines Ca II K
and H |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{fig9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg88.png)
|
Figure 9:
The change in |
| Open with DEXTER | |
The calculated variation in ![]() over the cycle (see Fig. 7)
has a general pattern. There is a pronounced minimum close to
over the cycle (see Fig. 7)
has a general pattern. There is a pronounced minimum close to
![]() where
where ![]() to -400 km s-1, followed by a
steep rise to a level of
to -400 km s-1, followed by a
steep rise to a level of
![]() to 100 km s-1. In the course
of the cycle,
to 100 km s-1. In the course
of the cycle, ![]() then slowly decreases and slowly becomes negative reaching a level of
then slowly decreases and slowly becomes negative reaching a level of
![]() km s-1.
A sudden additional decrease sets then in to reach the most negative
value of
km s-1.
A sudden additional decrease sets then in to reach the most negative
value of ![]() ,
the value this description started with. It shows that the atmosphere
really collapses between
,
the value this description started with. It shows that the atmosphere
really collapses between ![]() and 1.0. Thereafter, the expansion is drastic but beyond
and 1.0. Thereafter, the expansion is drastic but beyond
![]() it is far more gradual (at
it is far more gradual (at
![]() km s-1)
as it decelerates.
km s-1)
as it decelerates.
The behaviour of ![]() is similar to that of a model atmosphere as presented in the
gedankenexperiment by Renzini et al. (1992). That
gedankenexperiment had a star with a core and an envelope, in which the
luminosity offered to the base of the envelope,
is similar to that of a model atmosphere as presented in the
gedankenexperiment by Renzini et al. (1992). That
gedankenexperiment had a star with a core and an envelope, in which the
luminosity offered to the base of the envelope, ![]() ,
was manipulated. A gentle decrease in this
,
was manipulated. A gentle decrease in this ![]() from a high
from a high ![]() state could be accommodated by the envelope until some critical value
of
state could be accommodated by the envelope until some critical value
of ![]() at which the envelope collapsed. Then, in the gedankenexperiment,
at which the envelope collapsed. Then, in the gedankenexperiment, ![]() was raised again and the now compact atmosphere slowly expanded until
some other critical value of
was raised again and the now compact atmosphere slowly expanded until
some other critical value of ![]() was reached, now leading to a run-away expansion.
was reached, now leading to a run-away expansion.
In the case of RR Lyrae, the run of L is controlled by the opacity in the He+-He++ ionization boundary layer. With increasing transmission of energy through the envelope, L increases and the star expands until at some limit the envelope has become so tenuous that (since L can no longer increase) it must collapse.
Having determined the run of
![]() one can derive
one can derive
![]() .
These acceleration values change considerably during the pulsational
cycle. However, because of the uncertainty in all
.
These acceleration values change considerably during the pulsational
cycle. However, because of the uncertainty in all
![]() values due to opacity effects to be discussed in Sect. 8, we refrain
from commenting on these acceleration values.
values due to opacity effects to be discussed in Sect. 8, we refrain
from commenting on these acceleration values.
7.2 The detailed variation in
 and a correlation with
and a correlation with 
The small-scale variations in the curves of
![]() (Fig. 9)
might be regarded as due to photometric noise. However, on closer
inspection there is significant structure.
(Fig. 9)
might be regarded as due to photometric noise. However, on closer
inspection there is significant structure.
We selected the well-behaved
![]() -curves
to
determine an average
-curves
to
determine an average ![]() -curve for
an RR Lyr star. For that, we chose the stars RR Gem,
TW Lyn, AS Cnc, and SY Ari (the top row
panels in Fig. 9).
Before the curves can be added for averaging, small phase shifts were
applied because the chosen
-curve for
an RR Lyr star. For that, we chose the stars RR Gem,
TW Lyn, AS Cnc, and SY Ari (the top row
panels in Fig. 9).
Before the curves can be added for averaging, small phase shifts were
applied because the chosen ![]() was not perfectly aligned with the epoch relation and the resampling at
0.02 intervals in phase may also have introduced small phase
shifts.
Figure 9
shows the results for these stars. It is evident that the wiggles in
the
was not perfectly aligned with the epoch relation and the resampling at
0.02 intervals in phase may also have introduced small phase
shifts.
Figure 9
shows the results for these stars. It is evident that the wiggles in
the ![]() -curves are very similar for
these four stars. For the four less well-observed stars not included in
the averaging, a comparison with the average
-curves are very similar for
these four stars. For the four less well-observed stars not included in
the averaging, a comparison with the average
![]() -curve
shows
that these stars have also the same behaviour in
-curve
shows
that these stars have also the same behaviour in
![]() .
.
For all stars, the wiggles in the average
![]() indicate that after the collapse the envelope oscillates (continues to
oscillate) with a rhythm of about 1/7 of the period P.
This rhythm at P/7 is the same for all our stars,
independent of their actual period. It is as if the envelope has a
residual oscillation triggered by the collapse. The collapse itself
occurs from
indicate that after the collapse the envelope oscillates (continues to
oscillate) with a rhythm of about 1/7 of the period P.
This rhythm at P/7 is the same for all our stars,
independent of their actual period. It is as if the envelope has a
residual oscillation triggered by the collapse. The collapse itself
occurs from ![]() through the highest collapse velocity back to
through the highest collapse velocity back to
![]() km s-1,
which is a time equal to about P/7.
km s-1,
which is a time equal to about P/7.
One might suspect that P/7 is due to our resampling at 0.02 phase intervals, the period being (almost) exactly 7 of our data points. However, we note that Paparó et al. (2009) reported a specific role of the 7th harmonic in one well-studied C OR OT RR Lyr star. The C OR OT data do not have the 0.02 phase resampling rhythm. Barcza (2003) found in the RR Lyr star SU Dra from photometry an ``undulation''' of P/5. It is unclear what the cause of these periodicities is.
8 Comparison with literature data and optical depth effects
We derived the time-dependent radius of each star from our photometry and from its change the velocity of the atmosphere. The analysis above was performed without considering analyses of other RR Lyrae data presented in the literature.
A well-known method for deriving the radius of RR Lyrae stars is the Baade-Wesselink method, where the radial velocities observed over the cycle are integrated to infer the variation in radius (see, e.g., Liu & Janes 1990). This method has been applied to several RR Lyrae stars.
8.1 Comparison with other results
For two of our stars (RR Gem and AR Per), cycle velocities were presented by Liu & Janes (1989). Their velocities were obtained by cross-correlating their RR Lyrae star spectra with spectra of two standard stars, one of spectral type F6 IV and one of A2 IV. The values they derived from the two standard stars are very similar so, that their final velocity curves are based on just the standard of type A2 IV.
Our velocity curve for RR Gem has a shape quite
different from the one of Liu & Janes (1989). Note that in
their Fig. 5 they give the observed radial
velocity, whereas in our Fig. 9 the velocity as
seen from the stellar centre is given. Their velocity curve shows a
large speed away from the stellar centre at
![]() followed by a gradual slowing down to approach the minimum in velocity
at
followed by a gradual slowing down to approach the minimum in velocity
at ![]() .
The velocity curves of other RR Lyrae stars of Liu &
Janes show the same behaviour. The amplitude in their velocity curves
is
.
The velocity curves of other RR Lyrae stars of Liu &
Janes show the same behaviour. The amplitude in their velocity curves
is ![]() 60 km s-1.
Adopting the usual geometry factor p=1.32 (see Liu
& Janes 1990;
but see Fernley 1994)
to convert from observed radial velocity to pulsational velocity, their
velocities translate into an amplitude in
60 km s-1.
Adopting the usual geometry factor p=1.32 (see Liu
& Janes 1990;
but see Fernley 1994)
to convert from observed radial velocity to pulsational velocity, their
velocities translate into an amplitude in
![]() of
of ![]() 80 km s-1.
80 km s-1.
On the other hand, our stars have amongst themselves similar
behaviour. Their outer layers experience during the cycle only a modest
change in velocity except for a rapid fall toward the stellar centre as
of ![]() to a fastest centre approach at
to a fastest centre approach at
![]() ,
followed by a rapid decline in velocity to reach a modest expansion
velocity near
,
followed by a rapid decline in velocity to reach a modest expansion
velocity near ![]() .
In our data, the full amplitude of the velocity
.
In our data, the full amplitude of the velocity
![]() is
is ![]() 300 km s-1.
300 km s-1.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg102.png)
|
Figure 10:
Run of the two aspects of |
| Open with DEXTER | |
The difference between our velocity curves and those of Liu &
Janes is mostly caused by the drastic reduction of R
we find at ![]() .
Eliminating this behaviour from our R curves
(eliminating the R data for
.
Eliminating this behaviour from our R curves
(eliminating the R data for
![]() )
results in a velocity amplitude of
)
results in a velocity amplitude of
![]() of up to
of up to ![]() 90 km s-1,
quite similar to the one of Liu & Janes mentioned above. In
short, the radius change of an RR Lyrae star based on the
Baade-Wesselink radial velocity curves does not
chime with the pronounced change in R we derived
(using Eq. (1))
from the photometry. This difference is almost certainly caused by
effects of optical depth.
90 km s-1,
quite similar to the one of Liu & Janes mentioned above. In
short, the radius change of an RR Lyrae star based on the
Baade-Wesselink radial velocity curves does not
chime with the pronounced change in R we derived
(using Eq. (1))
from the photometry. This difference is almost certainly caused by
effects of optical depth.
8.2 Effects of optical depth 
When analysing our data we tacitly assumed that the detected light
originates, throughout the cycle, in the same gas and thus from the
same atmospheric layer. Such assumptions have been made in almost all
analyses of variable star data (also with the Baade-Wesselink method),
but they need not be correct. Furthermore, Abt (1959) noted that
the continuum light originates in layers with
![]() while the spectral lines rather are formed in layers with
while the spectral lines rather are formed in layers with
![]() .
.
During the cycle, compaction of the atmosphere and/or changes
in level of ionization may lead to changes in ![]() in that gas, thus to different layers being sampled in the photometry.
This is also the case for spectral lines: changes in the density and
temperature of a layer due to vertical motion will lead to changes in
the local ionization balance and the excitation state of ions, thus to
a varying strength of the relevant absorption lines. During the cycle a
spectral line may therefore form in different gas layers. Furthermore,
the strength of a line formed at greater depths is also influenced by
the level of photon scattering filling in the spectral line.
in that gas, thus to different layers being sampled in the photometry.
This is also the case for spectral lines: changes in the density and
temperature of a layer due to vertical motion will lead to changes in
the local ionization balance and the excitation state of ions, thus to
a varying strength of the relevant absorption lines. During the cycle a
spectral line may therefore form in different gas layers. Furthermore,
the strength of a line formed at greater depths is also influenced by
the level of photon scattering filling in the spectral line.
The phase lag between lines from metals and hydrogen
discovered by van Hoof & Struve (1953) in a ![]() Cepheid
star has been attributed to similar optical depth effects. For
RR Lyrae stars, this ``van Hoof effect'' was studied by, e.g.,
Mathias et al. (1995)
and Chadid & Gillet (1998).
Our sketchy spectral data (Fig. 8, Ca II
and H
Cepheid
star has been attributed to similar optical depth effects. For
RR Lyrae stars, this ``van Hoof effect'' was studied by, e.g.,
Mathias et al. (1995)
and Chadid & Gillet (1998).
Our sketchy spectral data (Fig. 8, Ca II
and H![]() )
exhibit a phase lag too, which can easily be attributed to changes in
the gas conditions that also cause the hysteresis in
)
exhibit a phase lag too, which can easily be attributed to changes in
the gas conditions that also cause the hysteresis in
![]() and
and ![]() .
.
In spectra of several RR Lyrae stars, line doubling
has been reported near ![]() (see, e.g., Sanford 1949). Considerable increases in line width may
also occur near that phase (e.g., Fe II lines;
see, e.g., Chadid 2000).
Spectral line doubling implies that there are gas layers in the same
line of sight with the same ions but which are at different (radial)
velocities. This doubling is seen mostly in the lower level Balmer
series lines but also in other intrinsically strong lines such as Ca
H&K. Thus, the spectral absorption in those lines comes from
different geometric depths in the atmosphere. Note that when for the
determination of radial velocities template spectra are used, any
velocity differences between ionic species are averaged out.
(see, e.g., Sanford 1949). Considerable increases in line width may
also occur near that phase (e.g., Fe II lines;
see, e.g., Chadid 2000).
Spectral line doubling implies that there are gas layers in the same
line of sight with the same ions but which are at different (radial)
velocities. This doubling is seen mostly in the lower level Balmer
series lines but also in other intrinsically strong lines such as Ca
H&K. Thus, the spectral absorption in those lines comes from
different geometric depths in the atmosphere. Note that when for the
determination of radial velocities template spectra are used, any
velocity differences between ionic species are averaged out.
8.3 Photometry and spectroscopy sample different layers
Consider an outward moving dense layer of the stellar atmosphere. Upon
its expansion and cooling, its continuum optical depth becomes smaller.
Thus, the level of ![]() from which the continuum light emerges moves physically downward
through the gas, leading to smaller photometrically derived R
values. If this intrinsic
from which the continuum light emerges moves physically downward
through the gas, leading to smaller photometrically derived R
values. If this intrinsic ![]() -level
moves rapidly, the concomittant rapid decrease in derived R
is naturally interpreted as an extremely rapid downward velocity, even
when the gas itself hardly has a vertical motion. The level from which
the (metal) spectral lines emerge (near
-level
moves rapidly, the concomittant rapid decrease in derived R
is naturally interpreted as an extremely rapid downward velocity, even
when the gas itself hardly has a vertical motion. The level from which
the (metal) spectral lines emerge (near
![]() )
will exhibit this effect later, i.e., only after the gas has been
lifted further to larger radii (cooled and rarefied further to
lower
)
will exhibit this effect later, i.e., only after the gas has been
lifted further to larger radii (cooled and rarefied further to
lower ![]() ).
This happens later than the change in the gas levels releasing the
continuum light. In this case, geometrically deeper levels may then be
(spectroscopically) sampled suggesting a decrease in R
even if the gas itself still moves outward. We note one can see a
difference in that sense between lines of Fe II
and Fe I (Chadid & Gillet
1998).
Finally, the intrinsically strong lines, such as the lower Balmer
series lines and a few other lines with large intrinsic absorption
capability, will exhibit this effect yet later. However, in deeper
layers (at different radial velocity) the local Balmer absorption may
already show up with its own radial velocity (
).
This happens later than the change in the gas levels releasing the
continuum light. In this case, geometrically deeper levels may then be
(spectroscopically) sampled suggesting a decrease in R
even if the gas itself still moves outward. We note one can see a
difference in that sense between lines of Fe II
and Fe I (Chadid & Gillet
1998).
Finally, the intrinsically strong lines, such as the lower Balmer
series lines and a few other lines with large intrinsic absorption
capability, will exhibit this effect yet later. However, in deeper
layers (at different radial velocity) the local Balmer absorption may
already show up with its own radial velocity (![]() -shifted with respect to the
Balmer line in higher layers), thus leading to line-doubling from lower
levels of the Balmer series.
-shifted with respect to the
Balmer line in higher layers), thus leading to line-doubling from lower
levels of the Balmer series.
The presented data do not allow us to asses the details of
these optical depth effects. We emphasize that the parameters derived
from the photometry always refer to the conditions in the layer with
![]() ,
the layer from which the measured continuum light emanates. It may be
that some of our interpretations need to be revised once more detailed
measurements of the particular gas layers would be available.
,
the layer from which the measured continuum light emanates. It may be
that some of our interpretations need to be revised once more detailed
measurements of the particular gas layers would be available.
The differences between our run of R (and
of ![]() derived from it) and the Baade-Wesselink run of
derived from it) and the Baade-Wesselink run of
![]() (and of R derived from it) can be understood as
being caused by the sampling of layers with different
(and of R derived from it) can be understood as
being caused by the sampling of layers with different ![]() .
The Baade-Wesselink method samples layers with
.
The Baade-Wesselink method samples layers with ![]() smaller than
smaller than ![]() of the layers sampled with continuum photometry. It thus is
unsurprising that the run of R as derived from
these methods differs in important ways, all due to the physical
condition (
of the layers sampled with continuum photometry. It thus is
unsurprising that the run of R as derived from
these methods differs in important ways, all due to the physical
condition (![]() )
of the gas layer from which the measured radiation (be it spectral
lines or the continuum) emerges.
)
of the gas layer from which the measured radiation (be it spectral
lines or the continuum) emerges.
At the end of Sect. 7.2 it was noted
that oscillations are visible in
![]() with P/7. Perhaps these variations are also caused
by temporal small optical depth effects (
with P/7. Perhaps these variations are also caused
by temporal small optical depth effects (
![]() and
and
![]() )
and do not represent fluctuations in gas velocity.
)
and do not represent fluctuations in gas velocity.
9 The variations in log g(T, L, M)
and log g ,
and verifications of distance and mass
,
and verifications of distance and mass
The run of ![]() was derived from Eq. (3).
The actual surface gravities,
was derived from Eq. (3).
The actual surface gravities,
![]() ,
were derived from b-y,c1.
In Fig. 10
we plot three parameters:
,
were derived from b-y,c1.
In Fig. 10
we plot three parameters: ![]() ,
,
![]() and the logarithmic ratio
and the logarithmic ratio
![]() .
When
.
When ![]() (or
(or ![]() )
the atmosphere is clearly compressed (collapsed).
)
the atmosphere is clearly compressed (collapsed).
The data in Fig. 10
indicate that in the quiet part of the cycle (
![]() )
the gravity
)
the gravity ![]() is, for several stars, not equal to
is, for several stars, not equal to
![]() .
However, in those quiet parts of the cycle, all parameters are
apparently stable (there are most likely no optical depth effects at
this point) and so we would expect
.
However, in those quiet parts of the cycle, all parameters are
apparently stable (there are most likely no optical depth effects at
this point) and so we would expect
![]() and
and ![]() to be equal there. We can explore how one might adjust d
and M to make
to be equal there. We can explore how one might adjust d
and M to make
![]() from Eq. (3)
equal to
from Eq. (3)
equal to ![]() in that phase interval.
For RR Lyrae stars, that phase (
in that phase interval.
For RR Lyrae stars, that phase (
![]() )
has
)
has ![]() K,
only a little higher than
K,
only a little higher than
![]() .
.
The distances of our stars were defined as described in Sect. 2. They are taken from the literature and they are primarily determined from an adopted reference value of MV. For some stars we calculated d from MV (including effects of [Fe/H]).
We recall from Sect. 4.5 (on the
error budget) that the sum of the measurement errors in
![]() and
and ![]() may be as large as 0.08 dex. If these two gravities were to be
equal
and if we assumed the full margin of error of 0.08, then, e.g.,
may be as large as 0.08 dex. If these two gravities were to be
equal
and if we assumed the full margin of error of 0.08, then, e.g.,
![]() for RR Gem should be reduced by
for RR Gem should be reduced by ![]() 0.22 dex, that of AS
Cnc by
0.22 dex, that of AS
Cnc by ![]() 0.12,
while that of TW Lyn should be larger by
0.12,
while that of TW Lyn should be larger by ![]() 0.07 dex.
0.07 dex.
If the adopted MV (or d) and M of our stars were wrong and had to be changed, this would produce (when using Eq. (3)) the tabulated effects:
| Assumed change | Effects | ||||
| MV | (d) | M |
|
L | R |
| -0.20 | +10% | -0.04 | +20% | +10% | |
| +10% | +0.04 | - | - | ||
We note again that changing the distance is for the stars observed only implicit; distances of RR Lyrae stars have (except for those in the papers referred to in Sect. 4.2) not been determined by other means than through MV. Thus only MV or the mass M can be changed.
For our stars a change in either MV
or M (or perhaps a combination thereof) is needed
to make ![]() and
and ![]() match. The changes in MV
indicated below are within the range permissible by the non-uniqueness
of MV, as
mentioned in Sect. 4.5.
For the stars shown in Fig. 10
the changes are:
match. The changes in MV
indicated below are within the range permissible by the non-uniqueness
of MV, as
mentioned in Sect. 4.5.
For the stars shown in Fig. 10
the changes are:
- -
- RR Gem: MV
1.0 mag brighter, M 50% smaller. The
optimum would be to change MV
leading to L larger by a factor 2.5
(0.4 dex in
 ).
Reducing the mass by 50% is no option, it then would be too low. A
combination of changes might also fit.
).
Reducing the mass by 50% is no option, it then would be too low. A
combination of changes might also fit. - -
- TW Lyn: MV
0.4 mag fainter, M 20% larger. Changing MV
is not the right option because its L value would,
in Fig. 6,
be even further below the ZAHB. Hence M should be
20% higher at 0.85
 . Note that (in Fig. 6) the mean value
of L can be made larger when adopting a yet larger
mass.
. Note that (in Fig. 6) the mean value
of L can be made larger when adopting a yet larger
mass. - -
- AS Cnc: MV 0.6 mag brighter, M 30% lower. Changes similar to but smaller than those for RR Gem would be needed.
- -
- SY Ari: no changes are needed within the errors.
- -
- SZ Gem: M smaller by
0.1 dex, to give
 .
.
- -
- BH Aur: no changes are needed within the errors.
- -
- TZ Aur: to make the two gravities match,
 should be
should be  0.3 dex
lower. This would be achieved if M were
considerably lower. Alternatively, MV
should (with
0.3 dex
lower. This would be achieved if M were
considerably lower. Alternatively, MV
should (with  )
be so much brighter, that L is doubled. In both
cases, TZ Aur would then be a well-evolved HB star.
)
be so much brighter, that L is doubled. In both
cases, TZ Aur would then be a well-evolved HB star.
10 The lightcurve bump
The stars in our programme were primarily selected from the class said to have lightcurve ``bumps''. These bumps in the run of brightness need not be very pronounced (for y-magnitudes see Fig. 1). One goal of the observations was to investigate whether these bumps in brightness affect the colours of the stars. Examples of the bump region for a few stars are given in Fig. 11.
First, we note that most of our stars with good light-curve coverage hardly show the light-curve bump in the Strömgren colour indices. Among these are TW Lyn, BH Aur, X CMi, TZ Aur, BR Tau, and RR Gem, which have either a prolonged low level bump or no clear colour-index bump at all. While SY Ari has a bump in y that has no effect in its colour indices, AS Cnc does show an effect. For the other stars, light-curve coverage was either poor or missing in this range of phases.
In AS Cnc the brightening and dimming is clearly
recognisable and takes place in a short timespan. We note that the
colour indices u-b and u-v
change before y brightens. Both indices become
bluer meaning that the Balmer continuum radiation brightens without an
increase in ![]() .
In this part of the cycle, the atmosphere is cool and the Balmer
continuum brightening could mean that the gas cools even further
leading to an additional reduction in opacity based on the lower Balmer
level excitation. Since T has not yet changed, the
changes should be due to a reduction in gas density. Does extra light
escape because of the lower
.
In this part of the cycle, the atmosphere is cool and the Balmer
continuum brightening could mean that the gas cools even further
leading to an additional reduction in opacity based on the lower Balmer
level excitation. Since T has not yet changed, the
changes should be due to a reduction in gas density. Does extra light
escape because of the lower ![]() ? At this point in the cycle,
the atmosphere is quite extended and about to shrink. This happens at
? At this point in the cycle,
the atmosphere is quite extended and about to shrink. This happens at
![]() (see Fig. 11
and earlier ones).
(see Fig. 11
and earlier ones).
Bono & Stellingwerf (1994) attribute the bump feature to shockfronts.
| Figure 11: Three examples of Strömgren-photometry light curves of RR Lyrae stars near the possible ``bump'' in brightness. TW Lyn either does not show a bump or its bump is rather extended in phase; there is no or little effect on the colour indices. SY Ari does exhibit a bump in y but there are no effects in its colour indices. For AS Cnc, the colour indices u-b and u-v clearly change before y changes, indicating a change in the Balmer jump before a brightness change. The index b-y (representing temperature) changes somewhat later. |
|
| Open with DEXTER | |
11 Further remarks
11.1 Comparison with models
Numerous models have been constructed for the pulsation and
for various other detailed aspects of RR Lyrae (see, e.g.,
Fokin et al. 1999).
A comparison with models is of limited value since most models are
one-dimensional. More importantly, it is not always clear how theory
has been transformed to observables. Do the theoretical predictions for
V, R, spectral line strengths,
and velocities all refer to information from the layer with the
relevant ![]() (thus to what one really would observe) or to a matter-defined gas
layer?
(thus to what one really would observe) or to a matter-defined gas
layer?
Parameters of RR Lyrae stars have been determined using different kinds of data and with different modelling. We refer to the analysis of Sódor et al. (2009) for results based on the Baade-Wesselink method and its refinements as well as to additional literature.
11.2 Blazhko effect
A good portion of RR Lyrae stars shows cycle-to-cycle variations in their light curves, the so-called Blazhko effect (for references see, e.g., Jurcsik et al. 2009). Some of the stars of our sample are also known to be Blazhko stars but they exhibit these variations only at a moderate level. However, these variations may affect the stellar parameters derived. The data we acquired cover to short a time span to address and assess possible cycle-to-cycle variations in the stellar parameters.
11.3 Relation between stellar mass and kinematics
Six of our stars were part of the study of kinematics of RR Lyrae stars (Maintz & de Boer 2005). Of these, five (CI And, AR Per, TZ Aur, RR Gem, and TW Lyn) are stars of the disk population (according to their kinematics), while SZ Gem is a star with halo kinematics. Halo RR Lyrae are understood to be older than disk RR Lyrae, so should (on average) have a lower mass.
For TW Lyn, we found that its mass should be higher
than the adopted reference value and instead be ![]() 0.85
0.85 ![]() ,
which chimes with it being a star of the disc. We note that Sódor
et al. (2009)
found a mass of
,
which chimes with it being a star of the disc. We note that Sódor
et al. (2009)
found a mass of ![]() 0.82
0.82 ![]() for RR Gem, our analysis indicated
for RR Gem, our analysis indicated ![]() 0.7
0.7 ![]() .
For SZ Gem, we found a mass of
.
For SZ Gem, we found a mass of ![]() 0.56
0.56 ![]() ,
this low mass being in line with the expected (larger age and) lower
mass of halo stars.
,
this low mass being in line with the expected (larger age and) lower
mass of halo stars.
BH Aur and SY Ari are found to correspond
to the reference value of M=0.7 ![]() ,
which is in line with their being disk stars.
,
which is in line with their being disk stars.
12 Conclusions
Based on simultaneous Strömgren photometry and a comparison of the
photometric indices with a calibrated
![]() ,
,
![]() grid,
accurate atmospheric parameters of RR Lyrae stars have been
determined. Curves of phase related runs of
grid,
accurate atmospheric parameters of RR Lyrae stars have been
determined. Curves of phase related runs of
![]() (the gravity from the Balmer jump) and
(the gravity from the Balmer jump) and
![]() were derived. One can then calculate the change in radius of the stars
over the cycle. By including additionally obtained spectra, one arrives
at the following description of the behaviour of RR Lyrae
stars.
were derived. One can then calculate the change in radius of the stars
over the cycle. By including additionally obtained spectra, one arrives
at the following description of the behaviour of RR Lyrae
stars.
The straightforward interpretation of the data derived for R
is that at phase ![]() the atmosphere begins to collapse soon reaching a high gas density
(when the star has its greatest brightness). This manifests itself in a
large Balmer jump (large
the atmosphere begins to collapse soon reaching a high gas density
(when the star has its greatest brightness). This manifests itself in a
large Balmer jump (large ![]() ). Within an
interval
). Within an
interval ![]() the atmosphere then expands again.
the atmosphere then expands again.
An alternative interpretation is that at phase
![]() the optical depth of the extended outer layers has become so small that
the level of
the optical depth of the extended outer layers has become so small that
the level of ![]() sampled in the photometry rushes through the gas inward mimicking a
drastic reduction in radius. The contraction taking place anyway then
elevates the density in that level having
sampled in the photometry rushes through the gas inward mimicking a
drastic reduction in radius. The contraction taking place anyway then
elevates the density in that level having
![]() ,
raising the optical depth there so that photometry subsequently samples
layers again higher up in the atmosphere, suggesting a rapid expansion.
The sudden increase in density manifests itself in lage values of
,
raising the optical depth there so that photometry subsequently samples
layers again higher up in the atmosphere, suggesting a rapid expansion.
The sudden increase in density manifests itself in lage values of
![]() .
.
During all these changes the atmosphere exhibits oscillation ripples with a rhythm of P/7.
A possible mismatch of the observed
![]() and the calculated
and the calculated ![]() in the quiet, descending part of the light curve can be used to assess
the applicability of the mean parameters adopted for the stars, i.e.,
the absolute brightness MV
(no geometric distances are known) and the mass M.
One can then determine the individual values of MV
and M for a star.
in the quiet, descending part of the light curve can be used to assess
the applicability of the mean parameters adopted for the stars, i.e.,
the absolute brightness MV
(no geometric distances are known) and the mass M.
One can then determine the individual values of MV
and M for a star.
Extending this kind of simultaneous Strömgren-photometry while avoiding multiplexing two stars would provide a much denser coverage of the light curves and thus a more accurate determination of the cycle variation in R. If spectra were then taken simultaneously, in which a range of spectral lines is included (lower and higher ionisation stages, strong and weak lines of the Balmer series) and of a nature to allow velocity determinations, one may hope to distinghuish the effects caused by the sampling of light from layers at different optical depth.
AcknowledgementsWe thank Oliver Cordes, Klaus Reif and the AIfA electronics group for their dedication to BUSCA, and the staff at the Calar Alto Observatory and at the Observatorium Hoher List for their technical support. We thank K. Kolenberg, M. Paparó and K. Werner for advice. We are grateful that the referee, Dr. Á. Sódor, graciously gave many suggestions for improvement and asked pertinent questions. These stimulated us to carry the interpretation a step further. We thank C. Halliday for linguistic advice.
References
- Abt, H. 1959, ApJ, 130, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W. 1926, AN, 228, 359 [NASA ADS] [Google Scholar]
- Barcza, S. 2003, A&A, 403, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., Chiba, M., Joshii, Y., et al. 2000, AJ, 119, 2688 [Google Scholar]
- Bono, G., & Stellingwerf, R. F. 1994, ApJS, 93, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 1974, ApJ, 192, 75 [Google Scholar]
- Chadid, M. 2000, A&A, 359, 991 [NASA ADS] [Google Scholar]
- Chadid, M., & Gillet, D. 1998, A&A, 335, 255 [NASA ADS] [Google Scholar]
- Clem, J. L., VandenBerg, D. A., Grundahl, F., & Bell, R. A. 2004, AJ, 127, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation (Princeton Univ. Press) [Google Scholar]
- Danziger, I. J., & Oke, J. B. 1967, ApJ, 147, 151 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, K. S., & Seggewiss, W. 2008, Stars and Stellar Evolution (EDP Sciences) [Google Scholar]
- de Boer, K. S., Schmidt, J. H. K., & Heber, U. 1995, A&A, 303, 95 [NASA ADS] [Google Scholar]
- de Boer, K. S., Tucholke, H.-J., & Schmidt, J. H. K. 1997, A&A, 317, L23 [NASA ADS] [Google Scholar]
- Fernley, J. 1994, A&A, 284, L16 [NASA ADS] [Google Scholar]
- Fernley, J., Barnes, T. G., Skillen, I., et al. 1998, A&A, 330, 515 [NASA ADS] [Google Scholar]
- Fokin, A. B., Gillet, D., & Chadid, M. 1999, A&A, 344, 930 [NASA ADS] [Google Scholar]
- Gautschy, A., & Saio, H. 1995, ARA&A, 33, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. F. 1998, MNRAS, 296, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Hilker, M. 2000, A&A, 355, 994 [NASA ADS] [Google Scholar]
- Jurcsik, J., Sódor, Á., Szeidl, B., et al. 2009, MNRAS, 400, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C. 1994, AJ, 108, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P., & Walraven, Th. 1958, in Handbook of Physics, LI, 353 [Google Scholar]
- Liu, T., & Janes, K. A. 1989, ApJS, 69, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., & Janes, K. A. 1990, ApJ, 354, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Lub, J. 1977a, Ph.D. Thesis, Univ. Leiden [Google Scholar]
- Lub, J. 1977b, A&AS, 29, 345 [Google Scholar]
- Lub, J. 1979, AJ, 84, 383 [Google Scholar]
- Maintz, G. 2005, A&A, 442, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maintz, G. 2008a, PhD Thesis, Univ. Bonn [Google Scholar]
- Maintz, G. 2008b, BAVSR, 57, 150 [NASA ADS] [Google Scholar]
- Maintz, G., & de Boer, K. S. 2005, A&A, 442, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathias, P., Gillet, D., Fokin, A. B., & Chadid, M. 1995, A&A, 298, 843 [NASA ADS] [Google Scholar]
- McNamara, D. H., & Feltz, K. A. 1977, PASP, 89, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Heber, U., & de Boer, K. S. 1995, A&A, 294, 65 [NASA ADS] [Google Scholar]
- Moehler, S., Heber, U., & Rupprecht, G. 1997, A&A, 319, 109 [NASA ADS] [Google Scholar]
- Oke, J. B. 1966, ApJ, 145, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Bonsack, S. J. 1960, ApJ, 132, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., Giver, L. P., & Searle, L. 1962, ApJ, 136, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Paparó, M., Szabó, R., Benkó, J. M., et al. 2009, in Stellar Pulsation: Challenges for Theory and Observation, ed. J. A. Guzik, & P. Bradley, AIP Conf. Proc., 1170, 240 [Google Scholar]
- Perry, C. L., Olsen, E. H., & Crawford, D. L. 1987, PASP, 99, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, G. W., & Paczynski, B. 1964, ApJ, 140, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Reif, K., Bagschik, K., de Boer, K. S., et al. 1999, Proc. SPIE, 3649, 109 [Google Scholar]
- Renzini, A., Greggio, L., Ritossa, C., & Ferrario, L. 1992, ApJ, 400, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Tamman, G. A. 2006, ARA&A, 44, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, R. F. 1949, ApJ, 109, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt-Kaler, T. 1982, Landolt Börnstein; Mathematics for Engineers; X. Physics and Applied Physics for Engineers, A&A [Google Scholar]
- Siegel, M. J. 1982, PASP, 94, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Sódor, Á., Jurcsik, J., & Szeidl, B. 2009, MNRAS, 394, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Struve, O. 1947, PASP, 59, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, T., Miyamoto, M., & Yoshi, Y. 1998, ApJ, 492, L79 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S., & de Boer, K. S. 1975, A&A, 39, 83 [NASA ADS] [Google Scholar]
- van Hoof, A., & Struve, O. 1953, PASP, 384, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Wesselink, A. J. 1946, Bull. Astr. Inst. Neth., 10, 83 [NASA ADS] [Google Scholar]
Footnotes
- ... photometry
![[*]](/icons/foot_motif.png)
- Original data (photometric indices) for each star are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/520/A46
- ... band
![[*]](/icons/foot_motif.png)
- Since the Cousins I is about 10 times
wider than the bands of the Strömgren-system, the I
measurements were mostly overexposed and have not been used for this
paper. For a few stars we also made some measurements in the H-Balmer
filters H
 W
(wide) and H
W
(wide) and H N
(narrow), which are in the same channel as the Strömgren-b
filter. Since the H
N
(narrow), which are in the same channel as the Strömgren-b
filter. Since the H N
(narrow) filter is yet much narrower than the Strömgren-filters,
exposure times would have to be excessively long and coverage of the
light curves in these filters poor so these data have not been used
either.
N
(narrow) filter is yet much narrower than the Strömgren-filters,
exposure times would have to be excessively long and coverage of the
light curves in these filters poor so these data have not been used
either.
All Tables
Table 1: The stars with basic information, the J.D. of the observations, and the phase ranges covered.
Table 2: Cycle averages of several RR Lyr star parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14030f1.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg27.png)
|
Figure 1: Lightcurves of the RR Lyrae stars in y. Data from subsequent cycles have been combined (see Table 1 for observing dates). The curves have been shifted arbitrarily in y to fit them into one panel. For the stars lower in the figure, the lightcurve coverage is incomplete. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg28.png)
|
Figure 2: Lightcurves of RR Gem and SY Ari observed with BUSCA in the Strömgren-system. Note the different brightness amplitude of the two stars. At the bottom, the instrumental brightness of the mean of two comparison stars (selected in the field of each variable) is shown. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Plot of the amplitude in y versus period of our stars showing that they are fundamental mode RRa-type pulsators. The band between the dotted lines marks the zone of RRa and RRb pulsators (see Ledoux & Walraven 1958). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14030f4.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg39.png)
|
Figure 4: Lightcurves in the calibrated Strömgren-indices of the stars RR Gem, SY Ari, and BR Tau. The phase coverage of the photometry can be reconstructed from the information given in Table 1 (for BR Tau the coverage is only 70%) and can be recognised in Fig. 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f5-1.ps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14030f5-2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg42.png)
|
Figure 5:
Colour loops in b-y,c1
(at left) and in b-y,m1
(at right) of several stars. The data points of
the brightening phase are marked with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg59.png)
|
Figure 6:
For four RR Lyrae (TW Lyn, RR Gem, AS
Cnc, and SY Ari), the run of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14030f7.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg77.png)
|
Figure 7:
Run of the parameters |
| Open with DEXTER | |
| In the text | |
| |
Figure 8:
For RR Gem and TZ Aur, the run of the equivalent
widths W of the spectral lines Ca II K
and H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{fig9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg88.png)
|
Figure 9:
The change in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14030-10/Timg102.png)
|
Figure 10:
Run of the two aspects of |
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Three examples of Strömgren-photometry light curves of RR Lyrae stars near the possible ``bump'' in brightness. TW Lyn either does not show a bump or its bump is rather extended in phase; there is no or little effect on the colour indices. SY Ari does exhibit a bump in y but there are no effects in its colour indices. For AS Cnc, the colour indices u-b and u-v clearly change before y changes, indicating a change in the Balmer jump before a brightness change. The index b-y (representing temperature) changes somewhat later. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.







