| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913227 | |
| Published online | 06 October 2010 | |
Magnetic structures of an emerging flux region in the solar photosphere and chromosphere
Z. Xu1,2 - A. Lagg1 - S. K. Solanki1,3
1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
2
- Yunnan Astronomical Observatory/National Astronomical Observatories,
Chinese Academy of Science, Kunming 650011, PR China
3 - School of Space Research, Kyung Hee University, Yongin,
Gyeonggi 446-701, Korea
Received 2 September 2009 / Accepted 19 March 2010
Abstract
Aims. We investigate the vector magnetic field and Doppler
velocity in the photosphere and upper chromosphere of a young emerging
flux region of the sun close to disk center.
Methods. Spectropolarimetric scans of a young active region made
using the second generation Tenerife Infrared Polarimeter (TIP II)
on the German Vacuum Tower Telescope (VTT) are analyzed. The scanned
area contained multiple sunspots and an emerging flux region. An
inversion based on the Milne-Eddington approximation was performed on
the full Stokes vector of the chromospheric He I
10 830 Å and the photospheric Si I 10 827.1 Å
lines. This provided the magnetic vector and line-of-sight velocity at
each spatial point in both atmospheric layers.
Results. A clear difference is seen between the complex magnetic
structure of the emerging flux region (EFR) in the photosphere and
the much simpler structure in the upper chromosphere. The upper
chromospheric structure is consistent with a set of emerging loops
following elongated dark structures seen in the He I
10 830 Å triplet, similar to arch filament
systems (AFS), while in the photosphere we infer the presence of
U-loops within the emergence zone. Nonetheless, in general the upper
chromospheric field has a similar linear relationship between
inclination angle and field strength as the photospheric field: the
field is weak (![]() 300 G)
and horizontal in the emergence zone, but strong (up to 850 G) and
more vertical near its edges. The field strength decreases from the
photosphere to the upper chromosphere by approximately
0.1-0.2 G km-1 (or even less) within the emergence zone and by 0.3-0.6 G km-1
in sunspots located at its edge. We reconstructed the magnetic field in
3D based on the chromospheric vector field under the assumption
that the He I 10 830 Å triplet forms along the magnetic
field loops. The reconstructed loops are quite flat with supersonic
downflows at both footpoints. Arguments and evidence for an enhanced
formation height of He I 10 830 Å in arch-filaments seen
in this line are provided, which support the validity of the
reconstructed loops.
300 G)
and horizontal in the emergence zone, but strong (up to 850 G) and
more vertical near its edges. The field strength decreases from the
photosphere to the upper chromosphere by approximately
0.1-0.2 G km-1 (or even less) within the emergence zone and by 0.3-0.6 G km-1
in sunspots located at its edge. We reconstructed the magnetic field in
3D based on the chromospheric vector field under the assumption
that the He I 10 830 Å triplet forms along the magnetic
field loops. The reconstructed loops are quite flat with supersonic
downflows at both footpoints. Arguments and evidence for an enhanced
formation height of He I 10 830 Å in arch-filaments seen
in this line are provided, which support the validity of the
reconstructed loops.
Conclusions. The main chromospheric properties of EFRs
previously deduced for a single region NOAA 9451 are shown to be
valid for another region as well, suggesting that the main original
results may have a wider application. The main exception is that only
the first region displayed a current sheet in the chromosphere. We
propose a scenario in which the relatively complex photospheric
structure evolves into the simpler chromospheric one.
Key words: Magnetic fields - Sun: chromosphere - Sun: infrared
1 Introduction
The solar magnetic field forming active regions is generated by
means of a dynamo mechanism in the tachocline at the base of the
solar convection zone around
![]() (where r is
the radial axis starting from the Sun's center, and
(where r is
the radial axis starting from the Sun's center, and ![]() is the
solar radius). Strong magnetic flux tubes escape from there due to
magnetic buoyancy (Parker instability), travel through the
convection zone, and finally emerge at the solar surface
(Schüssler et al. 1994; Caligari et al.
1995; 1998; Fan 2004). The emerging
field normally appears at the surface in the form of a bipolar
region known as an emerging flux region (EFR), whose polarities,
understood to be the footpoints of a loop system rising into the
corona, separate at the photospheric level at speeds of less than 1 km s-1 (Strous et al. 1996; Strous & Zwaan
1999; Schmieder et al. 2004). Previous
ground-based measurements of magnetic fields of EFRs focused mainly
on the photosphere. Early observations using only Stokes I and V(Brants 1985a,b; Zwaan & Brants
1985) indicated that the emerging field has a strength of a
few hecto-Gauss, while modern full Stokes vector observations (Lites
et al. 1998; Martínez Pillet et al. 1998;
Kubo et al. 2003) find that during emergence the magnetic
field is close to horizontal. A small-scale (less than 2
is the
solar radius). Strong magnetic flux tubes escape from there due to
magnetic buoyancy (Parker instability), travel through the
convection zone, and finally emerge at the solar surface
(Schüssler et al. 1994; Caligari et al.
1995; 1998; Fan 2004). The emerging
field normally appears at the surface in the form of a bipolar
region known as an emerging flux region (EFR), whose polarities,
understood to be the footpoints of a loop system rising into the
corona, separate at the photospheric level at speeds of less than 1 km s-1 (Strous et al. 1996; Strous & Zwaan
1999; Schmieder et al. 2004). Previous
ground-based measurements of magnetic fields of EFRs focused mainly
on the photosphere. Early observations using only Stokes I and V(Brants 1985a,b; Zwaan & Brants
1985) indicated that the emerging field has a strength of a
few hecto-Gauss, while modern full Stokes vector observations (Lites
et al. 1998; Martínez Pillet et al. 1998;
Kubo et al. 2003) find that during emergence the magnetic
field is close to horizontal. A small-scale (less than 2
![]() )
flux emergence event in quiet-sun internetwork was observed by the
Hinode/Solar Optical Telescope (SOT) (e.g., Centeno et al.
2007) confirming the previous results of Martínez
González et al. (2007) that flux emergence in the
internetwork as small-scale loops is common. In the Hinode event,
the authors found that the horizontal magnetic field appeared before
any significant amount of vertical field become visible. A
systematic analysis of these events was carried out by Martínez
González & Bellot Rubio (2009). In addition,
bipolar magnetic features are detected in the central part of EFRs
near young sunspots. They were first reported by Bernasconi et al.
(2002), who named them moving dipolar features (MDFs)
to distinguish them from moving magnetic features (MMFs). Both types
of features move horizontally at an average speed of around 0.3-0.5 km s-1.
However, MDFs flow toward sunspots and supergranule boundaries, in
contrast to MMFs, which move away from sunspots (Harvey & Harvey 1973; Lee 1992; Zhang et al.
2003). Both 3D MHD simulations and Hinode observations
reveal an intricate pattern of often compact bipolar magnetic
features between the two main magnetic polarities of the EFR (e.g.,
Cheung et al. 2007; 2008). The MDFs may
be a special form of these bipolar features recorded by Hinode and
seen in simulations.
)
flux emergence event in quiet-sun internetwork was observed by the
Hinode/Solar Optical Telescope (SOT) (e.g., Centeno et al.
2007) confirming the previous results of Martínez
González et al. (2007) that flux emergence in the
internetwork as small-scale loops is common. In the Hinode event,
the authors found that the horizontal magnetic field appeared before
any significant amount of vertical field become visible. A
systematic analysis of these events was carried out by Martínez
González & Bellot Rubio (2009). In addition,
bipolar magnetic features are detected in the central part of EFRs
near young sunspots. They were first reported by Bernasconi et al.
(2002), who named them moving dipolar features (MDFs)
to distinguish them from moving magnetic features (MMFs). Both types
of features move horizontally at an average speed of around 0.3-0.5 km s-1.
However, MDFs flow toward sunspots and supergranule boundaries, in
contrast to MMFs, which move away from sunspots (Harvey & Harvey 1973; Lee 1992; Zhang et al.
2003). Both 3D MHD simulations and Hinode observations
reveal an intricate pattern of often compact bipolar magnetic
features between the two main magnetic polarities of the EFR (e.g.,
Cheung et al. 2007; 2008). The MDFs may
be a special form of these bipolar features recorded by Hinode and
seen in simulations.
In the chromosphere, the early research into EFRs concentrated on
dynamic arch filament systems (AFS) in H![]() (Bruzek
1967, 1969, cf. the review by Chou
1993). At that time, the magnetic field could only be
inferred morphologically from the line core observations of typical
chromospheric lines such as H
(Bruzek
1967, 1969, cf. the review by Chou
1993). At that time, the magnetic field could only be
inferred morphologically from the line core observations of typical
chromospheric lines such as H![]() ,
or Ca II H and K. It is not
straightforward to derive the physical conditions in the
chromosphere from their profiles (e.g., SocasxNavarro &
Uitenbroek 2004). The first direct measurement of
magnetic vectors in an EFR in the upper chromosphere was presented
by Solanki et al. (2003) and Lagg et al.
(2004; 2007) based on full Stokes I, Q,
U, and V profiles of the He I 10 830 Å
triplet. The
observations of NOAA 9451 detected two magnetic features: a set of
rising magnetic loops and an electric current sheet. So far
NOAA 9451, observed in 2001, is the only EFR whose chromospheric
magnetic
field has been analyzed.
,
or Ca II H and K. It is not
straightforward to derive the physical conditions in the
chromosphere from their profiles (e.g., SocasxNavarro &
Uitenbroek 2004). The first direct measurement of
magnetic vectors in an EFR in the upper chromosphere was presented
by Solanki et al. (2003) and Lagg et al.
(2004; 2007) based on full Stokes I, Q,
U, and V profiles of the He I 10 830 Å
triplet. The
observations of NOAA 9451 detected two magnetic features: a set of
rising magnetic loops and an electric current sheet. So far
NOAA 9451, observed in 2001, is the only EFR whose chromospheric
magnetic
field has been analyzed.
The He I 10 830 Å triplet is a unique tool for investigating the
magnetic structures of the upper chromosphere (e.g., see the reviews
by Lagg 2007; Trujillo Bueno 2009). It
originates from the transition between the two lowest metastable
energy levels of Orthohelium, 1s2s
![]() -1s2p
-1s2p
![]() (de Jager et al. 1966). The lower levels of the transition are understood to be populated primarily by
recombination of singly ionized helium previously ionized by the EUV
irradiance from the corona (Pozhalova 1988; Avrett et al. 1994; Andretta & Jones 1997; Centeno et al. 2008). Penn & Kuhn (1995), Rüedi et al. (1995; 1996) and Lin et al. (1998)
pointed out that because of its sensitivity to the Zeeman effect and
that it is narrow compared to other chromospheric lines, it is
feasible to use He I 10 830 Å to investigate the full magnetic
vector in the upper chromosphere. Furthermore, Trujillo Bueno et al.
(2002) showed that in weakly magnetized plasma structures
the linear polarization of the He I triplet is dominated by atomic
level polarization, even in forward scattering geometry. In the
presence of a magnetic field inclined with respect to the local
solar vertical direction, this atomic level polarization (and the
ensuing emergent Stokes Q and U profiles) is modified by the
Hanle effect, which, together with the Stokes V signals that the
Zeeman effect induces, has been used to infer the magnetic field in
chromospheric spicules (Trujillo Bueno et al. 2005)
and in a polar crown prominence (Merenda et al. 2006). As
shown below, the upper chromosphere of the emergence zone (i.e.,
between the footpoints of EFRs) is usually pervaded by weak and
horizontal magnetic fields, which tend to produce linear
polarization profiles with shapes similar to those investigated by
Trujillo Bueno et al. (2002) in a coronal filament at the
solar disk center. However, as shown by Trujillo Bueno & Asensio
Ramos (2007), for magnetic field strengths
100 < B < 2000 G the linear polarization of the He I triplet is
generally caused by the joint actions of atomic level polarization
and the transverse Zeeman effect, while the circular polarization is
always dominated by the longitudinal Zeeman effect. For stronger
fields, the linear polarization of the He I triplet is dominated by
the transverse Zeeman effect.
(de Jager et al. 1966). The lower levels of the transition are understood to be populated primarily by
recombination of singly ionized helium previously ionized by the EUV
irradiance from the corona (Pozhalova 1988; Avrett et al. 1994; Andretta & Jones 1997; Centeno et al. 2008). Penn & Kuhn (1995), Rüedi et al. (1995; 1996) and Lin et al. (1998)
pointed out that because of its sensitivity to the Zeeman effect and
that it is narrow compared to other chromospheric lines, it is
feasible to use He I 10 830 Å to investigate the full magnetic
vector in the upper chromosphere. Furthermore, Trujillo Bueno et al.
(2002) showed that in weakly magnetized plasma structures
the linear polarization of the He I triplet is dominated by atomic
level polarization, even in forward scattering geometry. In the
presence of a magnetic field inclined with respect to the local
solar vertical direction, this atomic level polarization (and the
ensuing emergent Stokes Q and U profiles) is modified by the
Hanle effect, which, together with the Stokes V signals that the
Zeeman effect induces, has been used to infer the magnetic field in
chromospheric spicules (Trujillo Bueno et al. 2005)
and in a polar crown prominence (Merenda et al. 2006). As
shown below, the upper chromosphere of the emergence zone (i.e.,
between the footpoints of EFRs) is usually pervaded by weak and
horizontal magnetic fields, which tend to produce linear
polarization profiles with shapes similar to those investigated by
Trujillo Bueno et al. (2002) in a coronal filament at the
solar disk center. However, as shown by Trujillo Bueno & Asensio
Ramos (2007), for magnetic field strengths
100 < B < 2000 G the linear polarization of the He I triplet is
generally caused by the joint actions of atomic level polarization
and the transverse Zeeman effect, while the circular polarization is
always dominated by the longitudinal Zeeman effect. For stronger
fields, the linear polarization of the He I triplet is dominated by
the transverse Zeeman effect.
In the present paper, we present the analysis of data from another
young emerging flux region NOAA 10917 observed in 2006. A comparison
with the results obtained from NOAA 9451 may help us to distinguish
between features peculiar to each region and common to the
chromospheric magnetic field of EFRs. The present set of
observations display distinct advantages compared with the data of
NOAA 9451 due to the improved spatial sampling and coverage provided
by the second generation Tenerife Infrared Polarimeter (TIP II,
Collados et al. 2007), and that different parts of an
emerging loop were recorded nearly simultaneously. Other
improvements are the inclusion of the Paschen-Back effect in the
inversion and the resolution of the 180![]() azimuth ambiguity
problem, for which we here use the non-potential magnetic field
calculation (NPFC) method of Georgoulis (2005).
azimuth ambiguity
problem, for which we here use the non-potential magnetic field
calculation (NPFC) method of Georgoulis (2005).
The interpretation favored by Solanki et al. (2003) of the height at which the young loop-like structures are sampled by the He I line was questioned by Judge (2009). He proposed instead that the field in these structures be measured at a nearly constant height. In this paper, we provide arguments that support the original interpretation of Solanki et al. (2003, see Sect. 6.3).
The following is an outline of the present paper: in Sect. 2, the observations are presented, while Sect. 3 introduces the inversion code and the atmospheric model used for the data analysis. The main features of the retrieved magnetic field in the local solar frame and the LOS velocity field are presented and analyzed by comparing the photosphere and upper chromosphere in Sect. 4. In Sect. 5, we reconstruct magnetic loops in 3 dimensions based on the retrieved chromospheric vector field and the assumption that the He I triplet forms along magnetic field loops. Finally, the results are discussed in Sect. 6 and conclusions are given in Sect. 7.
2 Observations
The active region NOAA 10917 first appeared on 20 October 2006 as a
simple pore with a positive polarity. The pore grew considerably in
the following 24 h, developing a penumbra and becoming a
sunspot. Several pairs of pores with mutually opposite polarities
began to emerge on 21 Oct., when the region was located at 05![]() S,
30
S,
30![]() W, which corresponds to
W, which corresponds to
![]() (
(![]() is the heliocentric angle, i.e., the angle between the local solar
surface normal direction and the line-of-sight direction). Three of
these newly emerged pores went on to become sunspots as well. The
development of this region on this date is illustrated in Fig. 1,
showing parts of full-disk continuum images recorded by
SOHO/Michelson Doppler Imager (MDI, Scherrer et al.
1995).
is the heliocentric angle, i.e., the angle between the local solar
surface normal direction and the line-of-sight direction). Three of
these newly emerged pores went on to become sunspots as well. The
development of this region on this date is illustrated in Fig. 1,
showing parts of full-disk continuum images recorded by
SOHO/Michelson Doppler Imager (MDI, Scherrer et al.
1995).
Spectropolarimetric observations were carried out using TIP II
(Collados et al. 2007) at the German Vacuum Tower
Telescope (VTT), and by performing digital slit-jaw filter
recordings in H![]() and
Ca II K from 13:24 UT to 16:51 UT on 21 Oct.
2006. In attempting to simultaneously observe the different
parts of freshly emerged loops, the spectrograph entrance slit was
placed parallel to the dark fibrils seen in the H
and
Ca II K from 13:24 UT to 16:51 UT on 21 Oct.
2006. In attempting to simultaneously observe the different
parts of freshly emerged loops, the spectrograph entrance slit was
placed parallel to the dark fibrils seen in the H![]() slit-jaw
images. The slit was 78
slit-jaw
images. The slit was 78
![]() long and the pixel size was
0.175
long and the pixel size was
0.175
![]() .
The whole active region was scanned with a 0.35
.
The whole active region was scanned with a 0.35
![]() step size. The slit orientation and scan direction are indicated in
Fig. 1
(lower right panel). At each scan position, the full
Stokes vector was recorded with a spectral resolution of 11 mÅ.
The 11 Å wide spectral window contained the chromospheric
He I
10 830 Å triplet as well as the photospheric
Si I 10 827.1 Å line. Both are sensitive to the
Zeeman effect. Having spectra of
both lines allows us to study the magnetic vector co-spatially and
co-temporally in two different atmospheric layers.
step size. The slit orientation and scan direction are indicated in
Fig. 1
(lower right panel). At each scan position, the full
Stokes vector was recorded with a spectral resolution of 11 mÅ.
The 11 Å wide spectral window contained the chromospheric
He I
10 830 Å triplet as well as the photospheric
Si I 10 827.1 Å line. Both are sensitive to the
Zeeman effect. Having spectra of
both lines allows us to study the magnetic vector co-spatially and
co-temporally in two different atmospheric layers.
Panels a-d of Fig. 2 display the observed region viewed in
the infrared continuum (10 825 Å), Ca II K line core, H![]() line
core and intensity integrated over the He I 10 830 Å
triplet around 16:28 UT. Two main features of EFRs can be clearly
seen: compact bright plages in Ca II K and an arch filament
system
(AFS) with bright points near the footpoints in H
line
core and intensity integrated over the He I 10 830 Å
triplet around 16:28 UT. Two main features of EFRs can be clearly
seen: compact bright plages in Ca II K and an arch filament
system
(AFS) with bright points near the footpoints in H![]() .
Structures resembling the AFS are seen in the He I line, the three
filaments being oriented nearly parallel to the slit showing a good
correspondence to those detected in H
.
Structures resembling the AFS are seen in the He I line, the three
filaments being oriented nearly parallel to the slit showing a good
correspondence to those detected in H![]() .
The rightmost
structure (more inclined relative to the slit) is seen as a strong
absorption feature only in the He I line. These structures were
present during the whole sequence of observation from 13:24 to 16:51
UT. The transition region and coronal context of NOAA 10917 is
presented in Figs. 2e and f, which show images in the 304 Å and
171 Å channels of the SOHO/Extreme-ultraviolet Imaging Telescope
(EIT, Delaboudinière et al. 1995). The 304 Å channel is chosen since it is dominated by emission from He II,
while the 171 Å channel is selected because it represents the
cool corona and may show more similarities to the He I line than the
hotter 195 Å and 284 Å channels. We find that this is an
isolated active region, in which the spots, pores (indicated by the
yellow contour from MDI), and most of the plage are located within
the scanned area. In addition, the loops visible in 171 Å as
bright ridges terminate mainly in the footpoints located within the
scanned region.
.
The rightmost
structure (more inclined relative to the slit) is seen as a strong
absorption feature only in the He I line. These structures were
present during the whole sequence of observation from 13:24 to 16:51
UT. The transition region and coronal context of NOAA 10917 is
presented in Figs. 2e and f, which show images in the 304 Å and
171 Å channels of the SOHO/Extreme-ultraviolet Imaging Telescope
(EIT, Delaboudinière et al. 1995). The 304 Å channel is chosen since it is dominated by emission from He II,
while the 171 Å channel is selected because it represents the
cool corona and may show more similarities to the He I line than the
hotter 195 Å and 284 Å channels. We find that this is an
isolated active region, in which the spots, pores (indicated by the
yellow contour from MDI), and most of the plage are located within
the scanned area. In addition, the loops visible in 171 Å as
bright ridges terminate mainly in the footpoints located within the
scanned region.
Two different sets of observations of NOAA 10917 on 21 Oct. 2006
were performed. We first made 15 scans of a subregion with a
field-of-view of 15 Mm ![]() 55 Mm, the time series of which
spans 74 min from 13:24 to 14:38 UT. We then performed a single
long scan, covering a field-of-view of 50 Mm
55 Mm, the time series of which
spans 74 min from 13:24 to 14:38 UT. We then performed a single
long scan, covering a field-of-view of 50 Mm ![]() 55 Mm and
lasting from 16:28 to 16:51 UT. The exposure time per scan position
was 7 s, resulting in a noise level of typically
55 Mm and
lasting from 16:28 to 16:51 UT. The exposure time per scan position
was 7 s, resulting in a noise level of typically
![]() I
I![]() .
The estimated spatial resolution of the
image was limited by the seeing to roughly 1.5
.
The estimated spatial resolution of the
image was limited by the seeing to roughly 1.5
![]() .
We applied
the standard TIP data reduction routines, which include dark current
subtraction, flat-fielding, and polarimetric correction including an
automated cross-talk removing algorithm (Beck et al. 2005).
An accurate continuum correction was performed by comparing the
average flat field profile with the FTS spectrum. The quiet-Sun
Stokes I profile, computed by averaging 100 profiles with the
lowest polarization signal in the observed map, was used to
determine the wavelength calibration by assuming that the core
position of the photospheric spectral lines correspond to the
laboratory wavelengths. To enhance the signal-to-noise ratio, we
applied a 5-pixel binning along the wavelength axis, resulting in a
wavelength resolution of 55 mÅ per pixel. In addition, a 2-pixel
binning along the slit direction was applied, resulting in a
quadratic pixel size of 0.35 arcsec2.
.
We applied
the standard TIP data reduction routines, which include dark current
subtraction, flat-fielding, and polarimetric correction including an
automated cross-talk removing algorithm (Beck et al. 2005).
An accurate continuum correction was performed by comparing the
average flat field profile with the FTS spectrum. The quiet-Sun
Stokes I profile, computed by averaging 100 profiles with the
lowest polarization signal in the observed map, was used to
determine the wavelength calibration by assuming that the core
position of the photospheric spectral lines correspond to the
laboratory wavelengths. To enhance the signal-to-noise ratio, we
applied a 5-pixel binning along the wavelength axis, resulting in a
wavelength resolution of 55 mÅ per pixel. In addition, a 2-pixel
binning along the slit direction was applied, resulting in a
quadratic pixel size of 0.35 arcsec2.
| Figure 1: Development of the active region NOAA 10917 on 21 October 2006 seen in continuum radiation (SOHO/MDI). The solar coordinates and the disk center position are indicated in the top-left panel. The slit orientation (a stick marked ``slit'') and the scan direction of the spectropolarimetric observations (an arrow) are indicated in the bottom-right panel. |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height = 12cm]{13227fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg26.png)
|
Figure 2:
a): morphology of NOAA 10917 on 21 Oct. 2006 viewed in infrared continuum radiation at 10 825 Å, b): the Ca II K line core, c): the H |
| Open with DEXTER | |
3 Data analysis
Full Stokes I, Q, U, and V profiles of both Si I and He I
lines were fitted using the HeLIx code (Lagg et al.
2004), which is based on the Unno-Rachkowsky analytic
solution of the radiative transfer equation for polarized radiation
in a Milne-Eddington model atmosphere. The code obtains the best fit
of the observed profiles by varying eight free parameters for a
given atmospheric component: the strength of the magnetic field
vector (B), its inclination (![]() )
and azimuth angle (
)
and azimuth angle (![]() ),
line-of-sight velocity (
),
line-of-sight velocity (
![]() ), Doppler width (
), Doppler width (![]()
![]() ), damping constant (a), slope of the source
function (S1), and the opacity ratio between line-center and
continuum (
), damping constant (a), slope of the source
function (S1), and the opacity ratio between line-center and
continuum (![]() ). The code allows the parameters to be
retrieved for more than one atmospheric component simultaneously, to
treat the presence of unresolved structures within a spatial
resolution element, or light scattered into it from outside the
resolution element. An additional free parameter, the filling
factor, f, is used to fix the relative weight of each component,
where
). The code allows the parameters to be
retrieved for more than one atmospheric component simultaneously, to
treat the presence of unresolved structures within a spatial
resolution element, or light scattered into it from outside the
resolution element. An additional free parameter, the filling
factor, f, is used to fix the relative weight of each component,
where
![]() (i indicating each component to be
considered).
(i indicating each component to be
considered).
For the Si I line, we used a two-component atmospheric model composed of a magnetic component and a field-free one. The latter represents both the contribution to Stokes I from the field-free material in the resolution element and the straylight induced contamination of the Stokes I originating in the surrounding regions.
At the formation level of the He I line in the upper chromosphere,
we can safely assume that the magnetic field fills the resolution
element completely due to the strong expansion of the field in the
lower chromosphere (e.g. Solanki & Steiner 1990),
so we generally used a one-magnetic-component atmospheric model.
However, to fit the profiles at some locations two magnetic
components were needed because of the presence of multiple
line-profile components within one resolution element, each with a
different Doppler shift (Lagg et al. 2007; Aznar
Cuadrado et al. 2007). We used the following approach.
First we applied a one-component inversion to the whole observed
region, followed by the two-component model inversion. We then
compared their fit quality, which is represented by a
fitnessparameter (see
Eqs. (1) and (2) of Lagg et al. 2007, for the definition)
provided by the Pikaia genetic algorithm (Charbonneau
1995). The two-component model was considered to be
necessary only when the quality of the fit, i.e., the fitness
parameter, was increased by at least 20% with respect to the
one-component fit. For our data, the fraction of pixels for which a
2-component model was needed is about 12.5%. In the two-component
model, we initially kept the S1,
![]() ,
and the
magnetic field vector (B,
,
and the
magnetic field vector (B, ![]() ,
and
,
and ![]() )
the same in both
atmospheric components. Whenever the quality of the fit was
compromised by this, which was the case for only a few pixels, we
employed a two-component model with independent magnetic field
strength (B) to obtain a good fit. An example is displayed in Fig. 3. In this pixel, the same magnetic field strength in both
magnetic components was unable to reproduce the Stokes V profile
around 10831.5 Å very well. The difference in the quality of the
fits when we assume independent or identical field strengths for the
two components is similar to that shown in Fig. 4 of Lagg et al.
(2007). In Fig. 3, one component displays
subsonic flows (sound speed
)
the same in both
atmospheric components. Whenever the quality of the fit was
compromised by this, which was the case for only a few pixels, we
employed a two-component model with independent magnetic field
strength (B) to obtain a good fit. An example is displayed in Fig. 3. In this pixel, the same magnetic field strength in both
magnetic components was unable to reproduce the Stokes V profile
around 10831.5 Å very well. The difference in the quality of the
fits when we assume independent or identical field strengths for the
two components is similar to that shown in Fig. 4 of Lagg et al.
(2007). In Fig. 3, one component displays
subsonic flows (sound speed ![]() 10 km s-1 in the
chromosphere), the other exhibits supersonic redshifts. This agrees
with the results of Aznar Cuadrado et al. (2005), who
found that supersonic downflows are rather common in the solar upper
chromosphere. We therefore refer to the two components as the
subsonic (or rest) and the supersonic ones.
10 km s-1 in the
chromosphere), the other exhibits supersonic redshifts. This agrees
with the results of Aznar Cuadrado et al. (2005), who
found that supersonic downflows are rather common in the solar upper
chromosphere. We therefore refer to the two components as the
subsonic (or rest) and the supersonic ones.
![\begin{figure}
\par\includegraphics[height = 6cm, width = 8cm]{13227fg3.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg34.png)
|
Figure 3:
Stokes profiles of the pixel located at X = 28, Y = 42 in the coordinates of Fig. 2a. Two atmospheric
components coexist and cause the partial overlap of line profiles of
the He I triplet and the telluric line at 10 832 Å. The observed
profile is shown in black (solid line), the best fit is shown in red
(filled circles). Three vertical dotted lines indicate the
line-center rest positions of the He I triplet. The fit is the sum
of two components: the one nearly at rest is plotted in green (B =220 G,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height = 10cm, width = 8cm]{13227fg4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg35.png)
|
Figure 4:
Stokes profiles of three-pixel average at X = 18, Y = 27 in the coordinates of Fig. 2a.
A combination of the Hanle and Zeeman effects acting in a single
atmospheric component reproduce both the linear and circular
polarization profiles in He I
line. We perform a Hanle-slab inversion for this point and the
inferred magnetic field vector in the local solar frame is B = 360 G,
|
| Open with DEXTER | |
![\begin{figure*}
\par\includegraphics[scale = 0.7]{f5.eps}
\end{figure*}](/articles/aa/full_html/2010/12/aa13227-09/Timg37.png)
|
Figure 5:
Retrieved atmospheric parameters of active region NOAA 10917 (21 Oct. 2006, 16:28-16:51 UT) in the photosphere (left column) and the upper chromosphere (right column). I: the
infrared continuum intensity, with the direction toward solar disk
center, S
|
| Open with DEXTER | |
The version of HeLIx employed here takes into account the incomplete
Paschen-Back effect (SocasxNavarro et al.
2004; Sasso et al. 2006) and Hanle
effect when calculating the He I triplet. The Hanle effect is
treated with a simplified approach in a forward scattering geometry
(Collados et al. 2003; Lagg et al. 2004). We
believe that this simplification is reasonable to interpret our
observation of NOAA 10917, even though the line-of-sight corresponds
to ![]() (cf., the curves with
(cf., the curves with ![]() in Fig. 9 of Asensio
Ramos et al. 2008). An example of linear polarization
caused by the scattering polarization and its modification due to
the Hanle effect is shown in Fig. 4. Here the Stokes Uprofile is clearly influenced by both the Zeeman and Hanle effects,
but the signal produced by atomic level polarization fully
dominates.
in Fig. 9 of Asensio
Ramos et al. 2008). An example of linear polarization
caused by the scattering polarization and its modification due to
the Hanle effect is shown in Fig. 4. Here the Stokes Uprofile is clearly influenced by both the Zeeman and Hanle effects,
but the signal produced by atomic level polarization fully
dominates.
![\begin{figure}
\par\includegraphics[scale = 0.8]{13227fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg41.png)
|
Figure 6:
Horizontal movement of the sunspots and pores in the course
of the observation. Left: continuum image of the whole
active region. The solid-line rectangle outlines the field of view
of the 15 successive short scans from 13:24 to 14:38 UT. The arrow
points to disk center. The dotted square displays the area shown in
Fig. 9. Middle: the flow field derived from the
displacement of sunspots and pores inside the rectangle of the left
panel (overplotted arrows). The length of the arrow above this frame
corresponds to a speed of 1 km s-1. The continuum image was
obtained halfway through the time series (14:00 UT) and the position
of sunspots and pores at that time is marked by contours.
Right: the pixel-averaged longitudinal magnetic field flux
|
| Open with DEXTER | |
Finally, we resolve the 180![]() ambiguity in the magnetic
azimuth for the magnetic field in the photosphere and upper
chromosphere. By using the non-potential magnetic field calculation
method, NPFC (Georgoulis 2005 - see also Metcalf et al. (2006) for a comparative evaluation with other
disambiguation codes), we convert the magnetic field vector into the
local reference frame. The algorithm self-consistently calculates
the potential and non-potential magnetic field vectors whose
superimposition most precisely describes the studied vector magnetic
field observations.
ambiguity in the magnetic
azimuth for the magnetic field in the photosphere and upper
chromosphere. By using the non-potential magnetic field calculation
method, NPFC (Georgoulis 2005 - see also Metcalf et al. (2006) for a comparative evaluation with other
disambiguation codes), we convert the magnetic field vector into the
local reference frame. The algorithm self-consistently calculates
the potential and non-potential magnetic field vectors whose
superimposition most precisely describes the studied vector magnetic
field observations.
4 Results
By inverting the Si I and He I profiles of the whole observed region, we obtained the atmospheric parameters for each spatial point, in both the photosphere and upper chromosphere. The retrieved maps of the parameters in the active region NOAA 10917 are shown in Fig. 5. In addition to the infrared continuum and He I line core intensity, we plot the LOS velocity and the magnetic vector in the photosphere and upper chromosphere, respectively.
The plotted magnetic vectors have been transformed into the local
solar frame and are represented as if viewed from radially above.
Despite considerable effort being invested in solving the
180![]() ambiguity, we remain unsure whether we have obtained
the correct solution for the whole field of view in both layers. In
particular in the upper chromosphere, where the retrieved magnetic
vectors are more noisy in the LOS frame, we found some artifacts
(e.g., around x=30, y=30 in Fig. 5_VIII). However, we
believe that at worst the ambiguity was incorrectly resolved mainly
at the edge of the EFR. This should not affect our conclusions.
ambiguity, we remain unsure whether we have obtained
the correct solution for the whole field of view in both layers. In
particular in the upper chromosphere, where the retrieved magnetic
vectors are more noisy in the LOS frame, we found some artifacts
(e.g., around x=30, y=30 in Fig. 5_VIII). However, we
believe that at worst the ambiguity was incorrectly resolved mainly
at the edge of the EFR. This should not affect our conclusions.
The plotted LOS velocity in the photosphere corresponds to that of
the magnetic component. In the upper chromosphere, when a
two-magnetic-component model is employed, the plotted LOS velocity
is weighted by the filling factor of each component (i.e.
![]() ).
).
Sunspots in this region are identified in Fig. 5_I. One day before our observation only sunspot d was present. Sunspot a, b, and c formed in the intervening time. The young sunspots a, b, and their surrounding pores appear to be connected in the upper chromosphere by a series of long dark fibrils seen in the He I line core image (Fig. 5_V). The recently formed sunspots a, b and c are footpoints of relatively freshly emerged flux loops. They roughly encircle the so-called emerging flux zone.
4.1 Velocity field in the photosphere and upper chromosphere
The LOS velocity in the upper chromosphere is presented in Fig. 5_VI. Upflows of up to 4 km s-1 are found between spot a and b, i.e. at a place where we expect the tops of the freshly emerged magnetic loops to lie. Redshifts are present on both sides of this central stripe of blueshifts, i.e. where we expect the loop legs. Redshifts smoothly increase with distance along the legs, and become supersonic at some locations. For instance, supersonic downflows with a maximum value exceeding 30 km s-1 are found around the preceding sunspot b. These supersonic downflows can have a filling factor as high as 0.8. Both the intensity image and the magnetic field structure support the conclusion that the supersonic downflows very likely end within this sunspot. The photospheric velocity map is shown in Fig. 5_II. The flow field does not resemble the chromospheric one. However, in contrast to the findings of Lagg et al. (2007) for NOAA 9451, we observe photospheric downflows of 1.5 km s-1 below the supersonic chromospheric downflows. The positions of these photospheric flows are marked by dotted boxes in Fig. 5_II and VI. In some regions, the supersonic downflows are present in an atmospheric component with only a small filling factor. These locations appear unremarkable in this plot, which shows a filling-factor-weighted LOS velocity.We also determined the transversal motion (to the LOS) of dark features in the photosphere based on 15 repeated scans over 74 min covering a limited FOV. The field of view of these repeated scans is marked by a solid rectangle in the left panel of Fig. 6. The flow field is derived from the displacement of dark objects (sunspots and pores) by local correlation tracking (LCT, November & Simon 1988) and is indicated in the middle panel of Fig. 6 by red arrows. The opposite polarity spots and pores obviously appear to be separating away from each other (see middle & right panel of Fig. 6), but not radially. The presence of a shear component to their motion is evident. The transversal velocity of sunspot b reaches 0.4 km s-1. Unfortunately, the field-of-view is insufficiently large to cover the following sunspot a, hence our knowledge of the transversal motion of this active region remains incomplete.
![\begin{figure}
\par\includegraphics[scale = 0.9]{f7.eps}\vspace*{2.85mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg43.png)
|
Figure 7: Scatter plots of pixel-averaged inclination angle versus magnetic field strength in the photosphere (left) and the upper chromosphere (right) for the region shown in Fig. 5. Red symbols represent the sunspot (or pores) and black symbols the emergence zone encircled by sunspots and pores. |
| Open with DEXTER | |
| Figure 8: a)-c): pixel-averaged vertical magnetic field, field inclination with respect to the solar surface (see text), and LOS velocities in the photosphere. d): pixel-averaged vertical magnetic field in the upper chromosphere. In panels a) and d), white (dark) shading refers to the positive (negative) polarity. In panel b) dark (white) patches indicate that the field is parallel (inclined) to the solar surface. In panel c), downflows are positive. The coordinates are the same as in Fig. 5. |
|
| Open with DEXTER | |
4.2 Magnetic field in the photosphere and upper chromosphere
A comparison of Fig.5_III with 5_IV and of
Fig. 5_VII with 5_VIII appears to show that
there is a correlation between the inclination and strength of the
4-pixel averaged magnetic field in both the photosphere and the
chromosphere. This is shown more quantitatively in Fig. 7,
in which the field inclination angle is plotted as a function of the
field strength of sunspots (here including pores) and the emergence
zone in both layers. We distinguish the sunspots by red and the
emergence zone by black plus symbols. Points lying within the outer
contour in Fig. 5_I are assigned to sunspots, while the
emergence zone is the area encircled by the sunspots or pores. We
find the following:
(1) Both the photosphere and upper chromosphere exhibit a weak,
horizontal magnetic field in the emergence zone. Field strength and
inclination are roughly linearly related in both atmospheric layers,
the strongest, nearly vertical fields being found in sunspot umbrae.
In the sunspots (indicated by red plus signs in Fig. 7),
the chromospheric field is more horizontal than the photospheric
one. Comparing the two panels of Fig. 7, we note that the
chromospheric and photospheric fields display a qualitatively
similar behavior, but with the data points shifted to the weaker
fields in the chromosphere. Regression lines placed separately
through the points with inclination ![]()
![]() and those with
inclination >
and those with
inclination >
![]() are also shown in the figure. The average
unsigned slope to the chromospheric points, 0.088, is a factor of
1.76 larger than the corresponding photospheric quantity. In
addition, the magnetic azimuth angle in both layers is similar
(compare Fig. 5_IV and 5_VIII). In both
layers, the magnetic azimuth roughly follows the absorption features
seen in the line cores of He I and H
are also shown in the figure. The average
unsigned slope to the chromospheric points, 0.088, is a factor of
1.76 larger than the corresponding photospheric quantity. In
addition, the magnetic azimuth angle in both layers is similar
(compare Fig. 5_IV and 5_VIII). In both
layers, the magnetic azimuth roughly follows the absorption features
seen in the line cores of He I and H![]() ,
pointing mainly from
sunspot a to sunspot b.
,
pointing mainly from
sunspot a to sunspot b.
(2) The magnetic field strength decreases with height, with
B
![]() /B
/B
![]() .
In the photosphere, the
field strength within the emergence zone is between 300 G and 700 G,
and exceeds 1800 G in sunspots. However, in the upper chromosphere,
the field strength decreases to 850 G in the sunspots and declines
to between 200 G (close to the detection threshold) and 400 G in the
emergence zone.
.
In the photosphere, the
field strength within the emergence zone is between 300 G and 700 G,
and exceeds 1800 G in sunspots. However, in the upper chromosphere,
the field strength decreases to 850 G in the sunspots and declines
to between 200 G (close to the detection threshold) and 400 G in the
emergence zone.
| Figure 9: Spatial maps of the Si I line Stokes V blue wing area, recorded at different times. The starting time of the plotted scans are 13:30 UT, 14:10 UT, 14:15 UT, and 14:20 UT, respectively. White (dark) patches indicate positive (negative) polarity. A number of MBFs are highlighted by white rectangles. The brightness of each panel is normalized to the maximum of the whole sequence. The field of view context is indicated by a dotted square in Fig. 6. |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[scale=0.6]{f10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg50.png)
|
Figure 10:
a): intensity image of the He I line at 10 830.3 Å. The dashed square outlines the region in which the parameter |
| Open with DEXTER | |
(3) The magnetic structure in the emergence zone is more complex in
the photosphere than in the upper chromosphere. Small patches of
opposite polarity within the emergence zone are present in the
photosphere (see Fig. 5_IV), whereas the transition from
one polarity to the other is quite smooth in the chromosphere (Fig. 5_VIII). Figure 8a-c displays blowups
of the emergence zone in the photosphere, showing the pixel-averaged
vertical flux (
![]() ), absolute value of the magnetic
field's inclination relative to the solar surface (
), absolute value of the magnetic
field's inclination relative to the solar surface (
![]() ), and LOS velocity, respectively. The boxes mark the
locations of features identified with fluctuations in the
inclination angle are indicative of bipolar structures. They appear
similar to the moving dipolar features studied by Bernasconi et al.
(2002) and features that are often found in EFRs
studied by Hinode (e.g. Fig. 12 of Cheung et al. 2008).
Here we prefer to refer to these features by their more general term
magnetic bipolar features (MBFs). The polarity of an MBF close to a
sunspot is found to always be opposite to that of the sunspot
itself. The field of both polarities is inclined on average by
20
), and LOS velocity, respectively. The boxes mark the
locations of features identified with fluctuations in the
inclination angle are indicative of bipolar structures. They appear
similar to the moving dipolar features studied by Bernasconi et al.
(2002) and features that are often found in EFRs
studied by Hinode (e.g. Fig. 12 of Cheung et al. 2008).
Here we prefer to refer to these features by their more general term
magnetic bipolar features (MBFs). The polarity of an MBF close to a
sunspot is found to always be opposite to that of the sunspot
itself. The field of both polarities is inclined on average by
20![]() with respect to the solar surface. We cannot isolate
MBFs from their surroundings based on LOS flows, although there is a
tendency for there to be an upflow in one polarity and possibly a
downflow in the other. The vertical magnetic field component in the
upper chromosphere is plotted in Fig. 8d. It displays no
sign of MBFs, indicating that MBFs are a purely photospheric
phenomenon. They are indeed prominent features in the emergence
site, Fig. 9 presenting a sequence of Stokes V images in
which particularly prominent examples of MBFs are outlined by white
rectangles. Many similar, but somewhat less distinctive MBFs, can
also be detected in these and other similar images. The field of
view of Fig. 9 is indicated by the 15 Mm
with respect to the solar surface. We cannot isolate
MBFs from their surroundings based on LOS flows, although there is a
tendency for there to be an upflow in one polarity and possibly a
downflow in the other. The vertical magnetic field component in the
upper chromosphere is plotted in Fig. 8d. It displays no
sign of MBFs, indicating that MBFs are a purely photospheric
phenomenon. They are indeed prominent features in the emergence
site, Fig. 9 presenting a sequence of Stokes V images in
which particularly prominent examples of MBFs are outlined by white
rectangles. Many similar, but somewhat less distinctive MBFs, can
also be detected in these and other similar images. The field of
view of Fig. 9 is indicated by the 15 Mm ![]() 15 Mm
dotted square in Fig. 6.
The MBFs are elongated and aligned
parallel to the absorption structures seen in the He I
10 830 Å line core. No distinct separating motion between the
two polarities
of an MBF is observed during the 74 min over which the time series
was recorded. If we track a particular MBF at the right-bottom
corner of Fig. 9, we can roughly infer that the lifetime of
MBFs can reach up to 45 min and the transversal motion is about
0.3 km s-1. This result is comparable to the typical speed
given by Bernasconi et al. (2002) using a 3.5 h
long series of filtergrams. This speed is very close to the speed of
sunspot b (
15 Mm
dotted square in Fig. 6.
The MBFs are elongated and aligned
parallel to the absorption structures seen in the He I
10 830 Å line core. No distinct separating motion between the
two polarities
of an MBF is observed during the 74 min over which the time series
was recorded. If we track a particular MBF at the right-bottom
corner of Fig. 9, we can roughly infer that the lifetime of
MBFs can reach up to 45 min and the transversal motion is about
0.3 km s-1. This result is comparable to the typical speed
given by Bernasconi et al. (2002) using a 3.5 h
long series of filtergrams. This speed is very close to the speed of
sunspot b (![]() 0.4 km s-1, see Sect. 4.1), so that the
motion of MBFs relative to that sunspot in our observation is too
small to be detected.
0.4 km s-1, see Sect. 4.1), so that the
motion of MBFs relative to that sunspot in our observation is too
small to be detected.
5 Reconstruction of young loops in the upper chromosphere
| Figure 11: Magnetic field structure of the loops reconstructed in an emerging flux region within NOAA 10917, based on the direct measurement of the magnetic vector in the upper chromosphere. Left: viewed directly from above. The chromospheric magnetic inclination map is overlaid by traced loops projected onto the solar disk. Right: the same, but viewed obliquely. The strength of the field along the traced field lines is color coded (upper color bar). The LOS velocity along the magnetic loop is color coded in the projection of the field lines onto the Y-Z plane (lower color bar). Note that the Z-axis is stretched. Areas in dark-blue around the edge of the field of view are the regions where the polarization signals are below our fitting threshold. |
|
| Open with DEXTER | |
We present the results of magnetic flux loops reconstructed
following the method described by Solanki et al.
(2003). The underlying assumption is that the He
absorption follows a particular set of field lines produced by the
high density of chromospheric material freshly emerging along the
field indicated by the dark stripes in Fig. 5_V. It is
evident that the He I line becomes optically thick along the
loop-like structures. In Fig. 10a and b, we compare the
maps of the intensity in the He I line core and the parameter
![]() ,
which is the ratio of the line core to continuum
absorption coefficient. We find that
,
which is the ratio of the line core to continuum
absorption coefficient. We find that ![]() becomes larger in
the He dark loop-like structures, confirming a larger opacity there.
The He line is also optically thick everywhere in the region where
the loops are reconstructed. If we consider the area within the red
trapezium in Fig. 10a, where the one-component model is
valid and that cuts across the
topsof various loops, we find that the magnetic
field strength is anti-correlated with the optical thickness,
becomes larger in
the He dark loop-like structures, confirming a larger opacity there.
The He line is also optically thick everywhere in the region where
the loops are reconstructed. If we consider the area within the red
trapezium in Fig. 10a, where the one-component model is
valid and that cuts across the
topsof various loops, we find that the magnetic
field strength is anti-correlated with the optical thickness,
![]() ,
as quantitatively shown in Fig. 10d (We note
that sunspot c lies outside the red trapezium). We note that
,
as quantitatively shown in Fig. 10d (We note
that sunspot c lies outside the red trapezium). We note that
![]() for all the considered points, which implies that the
He line core is optically thick. Since the field strength generally
decreases with height, and we cannot ``see'' through the loop
structures because of their large optical thickness, we infer that the
loop structures are
located higher than their surroundings. In addition, we point out
(without plotting) that there is no clear relationship between the
field strength and optical thickness in the photosphere, also not,
e.g., in sunspots in the chromosphere.
for all the considered points, which implies that the
He line core is optically thick. Since the field strength generally
decreases with height, and we cannot ``see'' through the loop
structures because of their large optical thickness, we infer that the
loop structures are
located higher than their surroundings. In addition, we point out
(without plotting) that there is no clear relationship between the
field strength and optical thickness in the photosphere, also not,
e.g., in sunspots in the chromosphere.
The loop is reconstructed by starting at one footpoint and tracking the direction of the magnetic vector there to determine the 3D coordinates of the field in the next pixel and so on, until the other footpoint is reached. In the present work, loops are traced based on the vector magnetic field in the local solar frame. In Fig. 11, we illustrate the traced loops as viewed from above (i.e., projected on the solar disk) and obliquely. The bundle of lines in the left panel, representing the traced magnetic field lines, follow the elongated absorption structures visible in He I (Fig. 5_V) relatively closely. In the right panel, the variation in LOS velocity and magnetic field strength along the traced field lines are represented by colors. The highest traced magnetic loops reach a height of almost 4 Mm from their footpoints at the normallevel of He I 10 830 Å line formation. We note that the z-axis scale in Fig. 11 is stretched and the loops are actually very shallow, as can be better judged from Fig. 12a, although the Z-axis is somewhat stretched even there.
The variation in atmospheric parameters along a typical loop is
displayed in Fig. 12. The X-axis is the distance measured
along the solar surface from the limb-side footpoint (having
coordinates at X =18, Y =15 in the left panel of Fig. 11)
to the other footpoint (X=22, Y=42). This loop is 25 Mm long and 3.5 Mm high. The magnetic field strength shows an asymmetric
distribution and decreases by roughly a factor of 2 from loop
footpoint to loop top (i.e. from 800 G /600 G to 300 G). The
inclination angle changes smoothly along the loop, the field at the
(chromospheric) footpoints still being rather inclined to the
vertical. The azimuth exhibits a maximum deviation of 25![]() from the direction at the loop's apex (an azimuth angle of
90
from the direction at the loop's apex (an azimuth angle of
90![]() refers to the direction parallel to the Y-axis of Fig. 11). The LOS velocity is asymmetric, an upflow with a peak
value of nearly 3.8 km s-1 is found around the apex of the
loop, the peak upflow being shifted to the disk-centerward side of
the apex. The loop legs harbor stronger downflows, the faster
downflow being seen along the limbside leg, where the field is
weaker but also more aligned with the LOS. Co-existing supersonic
and subsonic velocities (red and blue plus signs) are present along
both loop legs. One can clearly see that the supersonic downflow
speeds progressively increase toward the loop footpoints. The Stokes
profiles along all the reconstructed loops mostly were well
described by a single magnetic component, even where two velocity
components were required. The reliability of the reconstructed
magnetic structure is discussed in Sect. 6.3
refers to the direction parallel to the Y-axis of Fig. 11). The LOS velocity is asymmetric, an upflow with a peak
value of nearly 3.8 km s-1 is found around the apex of the
loop, the peak upflow being shifted to the disk-centerward side of
the apex. The loop legs harbor stronger downflows, the faster
downflow being seen along the limbside leg, where the field is
weaker but also more aligned with the LOS. Co-existing supersonic
and subsonic velocities (red and blue plus signs) are present along
both loop legs. One can clearly see that the supersonic downflow
speeds progressively increase toward the loop footpoints. The Stokes
profiles along all the reconstructed loops mostly were well
described by a single magnetic component, even where two velocity
components were required. The reliability of the reconstructed
magnetic structure is discussed in Sect. 6.3
6 Discussion
We have presented direct measurements of the vector magnetic field of an emerging flux region in the photosphere and upper chromosphere by the inverting Stokes profiles of the Si I and He I lines near 10 830 Å. This work is an extension of the analysis of Solanki et al. (2003) and Lagg et al. (2004, 2007) in that a second EFR is analyzed, which allows us, by comparing the properties, to judge which properties of the chromospheric field are common to EFRs and which are specific to a given region. It also extends those first results by employing the TIP II spectropolarimeter, which provides higher spectral and spatial resolution and a larger field of view than the original TIP. During the observations analyzed here, the slit also scanned the active region parallel to the AFS visible in HIn the following, we discuss some of the main results of in this paper.
6.1 Velocity field
In the upper chromosphere, the Doppler velocities are consistent
with the expected motion in emerging flux loops, i.e. the material
inside is draining along the loop, while the loop is ascending.
Combining our repeated scans, we find that this motion lasts for
more than 3 h, i.e. the length of time of the entire observation
of long, dark structures in the He I line (13:24-16:51 UT). The
long duration of the up- and down-flows implies that in the course
of the observations we are witnessing different field lines passing
through the upper chromosphere. Estimates of the drain time and rise
time are given in Sect. 6.3. The Doppler velocity obtained from the
He I line is rather similar to the velocities in AFS observed in
H![]() (Bruzek 1967; Chou and Zirin 1988;
Spadaro et al. 2004). Spadaro et al. (2004) studied the dynamic evolution of an AFS in a young active region (
(Bruzek 1967; Chou and Zirin 1988;
Spadaro et al. 2004). Spadaro et al. (2004) studied the dynamic evolution of an AFS in a young active region (
![]() ). They find 3-9 km s-1 upflows at the tops of the AFS, and downflows of up to 17 km s-1 at the ends.
). They find 3-9 km s-1 upflows at the tops of the AFS, and downflows of up to 17 km s-1 at the ends.
Significant supersonic downflows in the chromosphere, but only
gentle subsonic flows in the photosphere, indicates that there has
been a shock between the two layers, which agrees with the
conclusion reached by Lagg et al. (2007)
for NOAA 9451.
In contrast to that region, however, no signs of emission in the
He I lines is observed here, indicating that any heating due to
the
shock is restricted to layers below the formation level of the
He I
line. In the photosphere, the transversal velocity of the preceding
sunspot b is ![]() 0.4 km s-1. If we were to assume that the
other footpoint is moving at the same speed, then the transversal
motion would be a factor of 10 smaller than the upflows measured at
the loop tops, which suggests that the emerging loops expand much
more rapidly in the vertical direction than in the horizontal.
0.4 km s-1. If we were to assume that the
other footpoint is moving at the same speed, then the transversal
motion would be a factor of 10 smaller than the upflows measured at
the loop tops, which suggests that the emerging loops expand much
more rapidly in the vertical direction than in the horizontal.
6.2 Magnetic fields
The freshly emerged magnetic field has a similar inclination-field
strength relationship in the photosphere and upper chromosphere. In
both layers, the vector field is weak and horizontal within the
emergence zone. It becomes stronger and more vertical when moving
toward the edges of this zone. A linear relation is found between
field strength and inclination to the vertical. For the photosphere,
this agrees with the results of Lites et al. (1998), but
also Stanchfield et al. (1997) and Solanki
(2003) for sunspots. The magnetic field strength
decreases with height. The photospheric field strength within the
emergence zone lies between 300 G and 700 G, and exceeds 1800 G in
sunspots. Brants (1985b) and Lites et al. (1998)
obtained similar field strength from the Fe I 6302.5 Å and
6301.5 Å/6302.5 Å line pair, respectively. In the upper
chromosphere, the field strength decreases to 850 G in the sunspots
or pores and even falls to 200 G in the emergence zone, which is
compatible with the first measurement by Solanki et al.
(2003). Assuming that the average distance between the
normal Si I and He I formation heights is
![]() -1500 km
(Schmidt et al. 1995; Centeno et al. 2006;
Bloomfield et al. 2007), the vertical gradient of
spatially averaged field strength dB/dZ is in the range 0.1-0.2 G km-1 within the emergence zone and around 0.3-0.6 G km-1within the sunspots at the loop footpoints. The average vertical
gradient inside sunspots is similar to other measurements for a
large sunspot (Rüedi et al. 1995; Orozco et al.
2005), who found that
-1500 km
(Schmidt et al. 1995; Centeno et al. 2006;
Bloomfield et al. 2007), the vertical gradient of
spatially averaged field strength dB/dZ is in the range 0.1-0.2 G km-1 within the emergence zone and around 0.3-0.6 G km-1within the sunspots at the loop footpoints. The average vertical
gradient inside sunspots is similar to other measurements for a
large sunspot (Rüedi et al. 1995; Orozco et al.
2005), who found that
![]() varies from 0.4-0.6 G km-1 in the umbra to 0.1-0.3 G km-1 in the outer penumbra. The authors used the same lines as us and assumed an equivalent
height range. We note that here we obtained these gradients for
sunspots without taking into account the older sunspot d and newly
born sunspot c. It is of interest that the older sunspot d, present
already before the new flux started to emerge, is clearly visible as
a strong azimuth center in the photosphere (Fig. 5_III),
but not in the upper chromosphere (Fig. 5_VII). This is
also true prior to the conversion to local solar coordinates, so
that it cannot be an artifact of the 180
varies from 0.4-0.6 G km-1 in the umbra to 0.1-0.3 G km-1 in the outer penumbra. The authors used the same lines as us and assumed an equivalent
height range. We note that here we obtained these gradients for
sunspots without taking into account the older sunspot d and newly
born sunspot c. It is of interest that the older sunspot d, present
already before the new flux started to emerge, is clearly visible as
a strong azimuth center in the photosphere (Fig. 5_III),
but not in the upper chromosphere (Fig. 5_VII). This is
also true prior to the conversion to local solar coordinates, so
that it cannot be an artifact of the 180![]() ambiguity. The
field strength in sunspot d falls from 1600 G in the photosphere to
400 G in the upper chromosphere, the
ambiguity. The
field strength in sunspot d falls from 1600 G in the photosphere to
400 G in the upper chromosphere, the
![]() almost reaching 0.8 G km-1 (for a
almost reaching 0.8 G km-1 (for a
![]() km). It appears that the freshly
emerging loops have expanded strongly sideways and partly overlie
the previously present sunspot. Given the strength of the field of
other sunspots in the chromosphere, this is a surprising result and
indicates that the field in the chromosphere above this sunspot is
measured at a considerable height since the field strength above
this sunspot is not significantly higher than in its surroundings,
quite unlike sunspots a and b. The field above sunspot c is
similarly weak in the chromosphere. In this case, He I filaments are
clearly seen to cross this spot, supporting the idea that the weak
fields seen above this spot are caused by the filaments crossing it.
km). It appears that the freshly
emerging loops have expanded strongly sideways and partly overlie
the previously present sunspot. Given the strength of the field of
other sunspots in the chromosphere, this is a surprising result and
indicates that the field in the chromosphere above this sunspot is
measured at a considerable height since the field strength above
this sunspot is not significantly higher than in its surroundings,
quite unlike sunspots a and b. The field above sunspot c is
similarly weak in the chromosphere. In this case, He I filaments are
clearly seen to cross this spot, supporting the idea that the weak
fields seen above this spot are caused by the filaments crossing it.
![\begin{figure}
\par\includegraphics[scale = 0.5]{13227fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg59.png)
|
Figure 12:
a)-d): variation in the atmospheric parameters along a typical reconstructed loop. The X-axis is the distance measured along the solar surface below the loop from one footpoint (located at X =18, Y = 15) to the other footpoint (X=22, Y =42). a): height of the loop vs. distance (note the stretched Z axis). b): magnetic field strength. c): field direction. The inclination is given in red and the azimuth in blue. The dotted-line represents the 90 |
| Open with DEXTER | |
All vertical field strength gradients determined here must be considered with some caution, since 1500 km represents a upper limit to the vertical height separation - see Sects. 5 and 6.3. The gradient is also affected by the straylight. Because of the far greater inhomogeneity of the field in the photosphere than in the chromosphere, straylight has a stronger influence on the spatial distribution of the photospheric field strength than on that of in the chromosphere. This means that in general the gradient will be lower in regions of strong field, such as sunspot umbrae. The effect of straylight in sunspots is greater because the sunspots appear dark in the photosphere, but not particularly so in the chromosphere. Hence the influence of straylight from their bright surroundings is enhanced, making the field strength appear lower in the photosphere.
A rough and grossly simplified sketch of the magnetic structure of
the EFR inferred from the present work is given in Fig. 13.
It illustrates the difference between the complex magnetic
structures in the photosphere and the comparatively simple
structures in the upper chromosphere. Solanki et al.
(2003) noted a similar difference in the complexity of
the fields in the photosphere and chromosphere. Thus, they observed
localized patches of opposite-polarity fields within the larger
scale unipolar regions . The higher resolution of the present work
identifies many of these feature to be bipolar. Small magnetic
bipolar features (MBFs) are only present in the photosphere and
clearly do not reach the upper chromosphere. The polarity of an MBF
close to the nearest sunspot is always opposite to that of the
sunspot itself. The field is close to being horizontal to the solar
surface, the angle being on average 20![]() .
The appearance of
these features is in good qualitative agreement with the observation
of emerging flux regions by Hinode (e.g. Fig. 12 of Cheung et al.
2008; Fig. 2 of Magara 2008), and is
reflected in the most realistic MHD simulations (Cheung et al.
2007). In addition, our observation indicates that the
two parts of MBFs remain connected for the duration of our 74 min
observation. These features may be related to the moving dipolar
features (MDFs) that were first reported and named by Bernasconi et al. (2002), but it is difficult to determine the
relative motion of MBFs toward the nearest sunspot from our
observations. Our data support the proposal of Bernasconi et al.
(2002) that the magnetic configuration of these
features corresponds to U-loops. This explanation is consistent with
the absence of MBFs in the upper chromosphere. U-loops also explain
the continuing proximity of the two poles over the full life time of
an MBF, which varys from tens of minutes to hours according to
Bernasconi et al. (2002). If we try to reconcile the
chromospheric and photospheric magnetic structures with
simplechromospheric loops
constantly rising and becoming replenished while the photospheric
field maintains its convolved structure, we must find a way for the
magnetic field to remove the U-loops before it rises into the
chromosphere and eventually into the corona. One possibility is that
magnetic reconnection at the top of the U-loop forms an O-loop and
an overlaying
.
The appearance of
these features is in good qualitative agreement with the observation
of emerging flux regions by Hinode (e.g. Fig. 12 of Cheung et al.
2008; Fig. 2 of Magara 2008), and is
reflected in the most realistic MHD simulations (Cheung et al.
2007). In addition, our observation indicates that the
two parts of MBFs remain connected for the duration of our 74 min
observation. These features may be related to the moving dipolar
features (MDFs) that were first reported and named by Bernasconi et al. (2002), but it is difficult to determine the
relative motion of MBFs toward the nearest sunspot from our
observations. Our data support the proposal of Bernasconi et al.
(2002) that the magnetic configuration of these
features corresponds to U-loops. This explanation is consistent with
the absence of MBFs in the upper chromosphere. U-loops also explain
the continuing proximity of the two poles over the full life time of
an MBF, which varys from tens of minutes to hours according to
Bernasconi et al. (2002). If we try to reconcile the
chromospheric and photospheric magnetic structures with
simplechromospheric loops
constantly rising and becoming replenished while the photospheric
field maintains its convolved structure, we must find a way for the
magnetic field to remove the U-loops before it rises into the
chromosphere and eventually into the corona. One possibility is that
magnetic reconnection at the top of the U-loop forms an O-loop and
an overlaying ![]() -loop. This process is illustrated in Fig. 14. The overlying
simpleloop then expands into the chromosphere and
eventually into the corona, while the O-loop dissipates. If this
scenario is correct then some of the MBFs many actually be O-loops
that developed out of U-loops.
-loop. This process is illustrated in Fig. 14. The overlying
simpleloop then expands into the chromosphere and
eventually into the corona, while the O-loop dissipates. If this
scenario is correct then some of the MBFs many actually be O-loops
that developed out of U-loops.
6.3 The reconstructed magnetic loops
The emerging young magnetic loops are reconstructed in the upper
chromosphere in the local solar frame. They are morphologically well
aligned with long dark structures visible in the He I 10 830 Å and H![]() lines (the arch filaments). Compared with loops
previously traced by Solanki et al. (2003), the
present loops are more shallow and horizontal. On average, they have
a footpoint separation of 25 Mm and are 3 Mm high, while the
reconstructed loops in NOAA 9541 had a footpoint separation of 20 Mm
and were 10 Mm high. In the present EFR, we do not find any evidence
of a current sheet.
lines (the arch filaments). Compared with loops
previously traced by Solanki et al. (2003), the
present loops are more shallow and horizontal. On average, they have
a footpoint separation of 25 Mm and are 3 Mm high, while the
reconstructed loops in NOAA 9541 had a footpoint separation of 20 Mm
and were 10 Mm high. In the present EFR, we do not find any evidence
of a current sheet.
Judge (2009) estimated the drain time of the loops studied
by Solanki et al. (2003), using the measured
dimensions and Doppler velocities. He argued that it is probable
that these loops had been almost completely drained by the time of
the observations. We now perform a similar order-of-magnitude
estimation for the loop system studied in this paper. Since the
loops are nearly horizontal, the arc length of the loops is roughly
equal to the distance between the two footpoints, L = 25 Mm. The
mean draining velocity, ![]() ,
is around 10 km s -1. Assuming
that mass is conserved, we have
,
is around 10 km s -1. Assuming
that mass is conserved, we have
![]() km
/20 km s-1
km
/20 km s-1 ![]() 1200 s
1200 s ![]() 20 min. This is
consistent with the observation that the lifetime of individual AF
in H
20 min. This is
consistent with the observation that the lifetime of individual AF
in H![]() is about 10-30 min (Chou 1993). Given the
loop height of 3 Mm, the rise time is around
is about 10-30 min (Chou 1993). Given the
loop height of 3 Mm, the rise time is around
![]() km / 4 km s-1
km / 4 km s-1 ![]() 750 s (h = loop height, vu = rise
speed). Thus the magnetic loops still carry excess material and
hence they can appear as regions of excess absorption in He I (i.e.
as an AFS). We note that the strength of the He line in the loops
may be only partly related to a higher density. It may also be
caused by the loop being immersed in the hot corona. The stronger
irradiation by EUV flux (coming from all sides) leads to higher
ionization and greater recombination of He, so that the He 10 830 Å triplet becomes stronger.
750 s (h = loop height, vu = rise
speed). Thus the magnetic loops still carry excess material and
hence they can appear as regions of excess absorption in He I (i.e.
as an AFS). We note that the strength of the He line in the loops
may be only partly related to a higher density. It may also be
caused by the loop being immersed in the hot corona. The stronger
irradiation by EUV flux (coming from all sides) leads to higher
ionization and greater recombination of He, so that the He 10 830 Å triplet becomes stronger.
The observed loop reflects the asymmetric distribution of both the
magnetic field and LOS velocity. Since we scanned the region with
the slit parallel to the AFS seen in H![]() ,
we can exclude this
result being caused by observing different sides of loops at
different times. We explain the LOS velocity asymmetry as follows.
Firstly, we found that the upflow peak is in the disk-centerward
side as shown in Fig. 12d, which is consistent with a loop
that is expanding as it rises (indicated by the 3 blue arrows in
Fig. 13). Secondly, the loop-leg LOS velocity on the limb
side is almost a factor of 2 larger than on the disk-centerward
side. We assume that the true velocity is along the direction of the
local magnetic field, hence
,
we can exclude this
result being caused by observing different sides of loops at
different times. We explain the LOS velocity asymmetry as follows.
Firstly, we found that the upflow peak is in the disk-centerward
side as shown in Fig. 12d, which is consistent with a loop
that is expanding as it rises (indicated by the 3 blue arrows in
Fig. 13). Secondly, the loop-leg LOS velocity on the limb
side is almost a factor of 2 larger than on the disk-centerward
side. We assume that the true velocity is along the direction of the
local magnetic field, hence
![]() (here
V is the true velocity at the footpoints,
(here
V is the true velocity at the footpoints, ![]() is the angle
between the LOS and the magnetic field, and we neglect the motion of
the field itself). We note that the angle between the local vertical
and the LOS is about 30
is the angle
between the LOS and the magnetic field, and we neglect the motion of
the field itself). We note that the angle between the local vertical
and the LOS is about 30![]() according to the heliocentric
position of this EFR. From Fig. 12, we therefore inferred
that the
according to the heliocentric
position of this EFR. From Fig. 12, we therefore inferred
that the ![]() on the disk-centerward side is about 75
on the disk-centerward side is about 75![]() (= 45
(= 45![]() + 30
+ 30![]() )
and about 170
)
and about 170![]() (=140
(=140![]() +30
+30![]() )
on the limb side. Hence the fast
component of
)
on the limb side. Hence the fast
component of
![]() is about 16 km s-1 on the
disk-centerward side and 36 km s-1 on the limb side. We infer
that the true velocity in the disk-centerward side can reach 60 km s-1 and is higher than that in the limb side by a factor of 1.7.
is about 16 km s-1 on the
disk-centerward side and 36 km s-1 on the limb side. We infer
that the true velocity in the disk-centerward side can reach 60 km s-1 and is higher than that in the limb side by a factor of 1.7.
![\begin{figure}
\par\includegraphics[scale=0.5]{13227fg13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg65.png)
|
Figure 13: Sketch of the magnetic field structure in an emerging flux region, summarizing the main observed features. The lower plane represents a cut at the photospheric level, the upper plane at the average chromospheric level. The white (dark) points signify positive (negative) polarity. The green arch connecting the opposite polarities represents an emerging magnetic loop going though the photosphere into the upper chromosphere. The color of the arch indicates the magnetic field strength (deep color corresponds to a strong magnetic field). The arrows in blue and red represent the upflows and downflows detected in the upper chromosphere, respectively. In the photosphere, the footpoints with opposite polarity move apart from each other, as indicated by the yellow arrows. The MBFs, present in the emergence zone, are represented by small pairs of white/black patches. A U-type loop represents the MBF magnetic field configuration. An isolated white patch represents the old sunspot, present already before the new flux started to emerge. It is partly covered by loops of freshly emerging flux. Solid (dotted) lines represent the magnetic field lines above (under) the photosphere. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[scale=0.4,clip]{13227fg14.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg66.png)
|
Figure 14:
Sketch of the evolution of a pair of emerging magnetic loops connected
below the surface by a U-loop. As the loops rise, they can reconnect
above the U-loop, leaving an O-loop and an
overlying |
| Open with DEXTER | |
Judge (2009) questioned that the He I 10 830 Å can be used to reconstruct the loop geometry. He argued that the field in these structures is measured at a nearly constant height, instead of along a magnetic loop. However, there are strands of evidence that support the interpretation put forward by Solanki et al. (2003) and in this paper:
- (a) From the intensity image, we observe a general similarity
between the AFS seen in the H
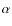 and He I 10 830 Å lines. In particular, the He I absorption structures are smooth and elongated, like the H
and He I 10 830 Å lines. In particular, the He I absorption structures are smooth and elongated, like the H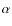 arch filaments (see Figs. 2c and d), and rather distinct
from the more mottled character of the structures seen in, e.g., the
Ca II K line, strongly indicating that the He I absorption indeed
follows individual emerging flux loops (like H
arch filaments (see Figs. 2c and d), and rather distinct
from the more mottled character of the structures seen in, e.g., the
Ca II K line, strongly indicating that the He I absorption indeed
follows individual emerging flux loops (like H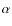 ), rather than
sampling only their footpoints (like Ca II K). Even Ca II K reveals
elongated filaments in plage if observed at sufficiently high
resolution (Pietarila et al. 2009), suggesting that its
emission also follows magnetic field lines to some extent.
), rather than
sampling only their footpoints (like Ca II K). Even Ca II K reveals
elongated filaments in plage if observed at sufficiently high
resolution (Pietarila et al. 2009), suggesting that its
emission also follows magnetic field lines to some extent.
- (b) The chromospheric field strength above sunspot c (which
has very recently emerged) is excessively small, implying that there is
either a much higher dB/dZ than above other spots, or that we
measure the field at a greater height than above the spots a and b.
The second interpretation is consistent with the presence of dark He
filaments passing over spot c. The magnetic field there is more or
less horizontal i.e. inclined by 70-80
 on average with
respect to the local vertical direction.
on average with
respect to the local vertical direction.
- (c) In the emergence zone, the He I line becomes optically thick in the loop-like structures and the magnetic field strength is anti-correlated with the opacity. This suggests that we observe higher layers in the loops since the field strength decreases with height.
- (d) An example of scattering polarization in Stokes Q and Ulocated around the loop top is shown in Fig. 4. The
combined amplitude of
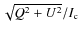 is 0.22%.
Scattering polarization signals of such a large amplitude are found
only around loop tops. The scattering polarization signal is
enhanced when the anisotropy of the radiation field increases, i.e.
with height. Asensio Ramos et al. (2008) pointed out that
it is possible to retrieve reliable height information and the full
magnetic vector simultaneously if one parameter of the magnetic
field vector is known beforehand. For example, if one such parameter
can be constrained by the Zeeman effect, then the height information
can be retrieved. In Fig. 4, we clearly see the joint
action of Zeeman and Hanle effects and perform a HeLIx+inversion (Lagg et al. 2009) to infer the height of
formation of the He I scattering polarization at this location.
HeLIx+ is an upgraded version of HeLIx (Lagg et al.
2004) that includes the forward modeling calculation core
of the computer program HAZEL of Asensio Ramos et al.
(2008), which is based on the quantum theory of the Hanle
and Zeeman effects (see Landi DegI'Innocenti & Landolfi
2004). We employed a one-component, constant-property
slab atmosphere (Trujillo Bueno et al. 2005; Asensio
Ramos et al. 2008) with the free parameters of magnetic
field strength B, inclination and azimuth angle,
is 0.22%.
Scattering polarization signals of such a large amplitude are found
only around loop tops. The scattering polarization signal is
enhanced when the anisotropy of the radiation field increases, i.e.
with height. Asensio Ramos et al. (2008) pointed out that
it is possible to retrieve reliable height information and the full
magnetic vector simultaneously if one parameter of the magnetic
field vector is known beforehand. For example, if one such parameter
can be constrained by the Zeeman effect, then the height information
can be retrieved. In Fig. 4, we clearly see the joint
action of Zeeman and Hanle effects and perform a HeLIx+inversion (Lagg et al. 2009) to infer the height of
formation of the He I scattering polarization at this location.
HeLIx+ is an upgraded version of HeLIx (Lagg et al.
2004) that includes the forward modeling calculation core
of the computer program HAZEL of Asensio Ramos et al.
(2008), which is based on the quantum theory of the Hanle
and Zeeman effects (see Landi DegI'Innocenti & Landolfi
2004). We employed a one-component, constant-property
slab atmosphere (Trujillo Bueno et al. 2005; Asensio
Ramos et al. 2008) with the free parameters of magnetic
field strength B, inclination and azimuth angle, 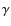 and
and
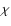 ,
Doppler velocity
,
Doppler velocity
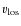 ,
the damping constant a,
the optical thickness of slab
,
the damping constant a,
the optical thickness of slab
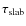 ,
and the height of the
slab above the solar surface
,
and the height of the
slab above the solar surface
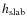 .
To obtain reliable error
estimates for the retrieved atmospheric parameters, we repeated the
inversion of this particular pixel 100 times. Due to the random walk
convergence of the Pikaia algorithm (Charbonneau
1995), the variations in the retrieved parameter
values for the individual runs contain all possible sources of
errors during the inversion process, including those caused by the
degeneracy between some parameters. Comparisons of these error
estimates with those of the Bayesian technique described by Asensio
Ramos et al. (2007) showed good agreement. The standard
deviation of the field direction is very small,
.
To obtain reliable error
estimates for the retrieved atmospheric parameters, we repeated the
inversion of this particular pixel 100 times. Due to the random walk
convergence of the Pikaia algorithm (Charbonneau
1995), the variations in the retrieved parameter
values for the individual runs contain all possible sources of
errors during the inversion process, including those caused by the
degeneracy between some parameters. Comparisons of these error
estimates with those of the Bayesian technique described by Asensio
Ramos et al. (2007) showed good agreement. The standard
deviation of the field direction is very small,
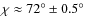 ,
,
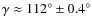 ,
the optical depth in the red-blended component being
,
the optical depth in the red-blended component being
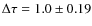 .
From the set of 100 inversions, we
deduced
.
From the set of 100 inversions, we
deduced
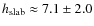 arcsec from the solar
surface. Hence, the loop top should be higher than 3.6 Mm above the
photosphere (1
arcsec from the solar
surface. Hence, the loop top should be higher than 3.6 Mm above the
photosphere (1 ).
The average height of the loop obtained
from our geometrical reconstruction is around 3 Mm above the
normal
He formation height of 1-1.5 Mm, resulting in a total height of
4-4.5 Mm above the solar surface, which is consistent with the
scattering polarization diagnostics. However, the reliability of the
inferred height information using this technique needs to be
discussed further. More details on this technique and more evidence
of the greater height of the loops compared to the claims of Judge
(2009) are presented by Merenda et al. (in preparation).
).
The average height of the loop obtained
from our geometrical reconstruction is around 3 Mm above the
normal
He formation height of 1-1.5 Mm, resulting in a total height of
4-4.5 Mm above the solar surface, which is consistent with the
scattering polarization diagnostics. However, the reliability of the
inferred height information using this technique needs to be
discussed further. More details on this technique and more evidence
of the greater height of the loops compared to the claims of Judge
(2009) are presented by Merenda et al. (in preparation).
7 Conclusions
After NOAA 9451 studied by Solanki et al. (2003) and
Lagg et al. (2004; 2007),
NOAA 10917 is only
the second EFR whose velocity and vector magnetic field have been
investigated in both the solar photosphere and chromosphere. Both
regions display considerable similarities. Their images in He I
10 830 Å exhibit arch filament systems comparable to those
seen in
H![]() .
The magnetic field is found to follow the He filaments in
the shape of a loop. These chromospheric loops are relatively low
lying, having a lower apex height than the chromospheric loops in
NOAA 9451.
.
The magnetic field is found to follow the He filaments in
the shape of a loop. These chromospheric loops are relatively low
lying, having a lower apex height than the chromospheric loops in
NOAA 9451.
Both active regions exhibit a remarkable difference in the complexity of their photospheric and chromospheric magnetic structures. Whereas the chromospheric structure is comparatively simple, being dominated by the low-lying loops and the fields of spots and pores, in the photosphere a considerable amount of additional magnetic structures are found in the middle of the EFR. We identify these features with compact bipolar features and interpret them as being U- or possibly O-loops. They are similar to structures seen by Hinode/SOT/SP in EFRs.
AcknowledgementsThe data used in this paper were obtained with the German Vacuum Tower Telescope in the Teide Observatory of Spain. The authors thank A. Pietarila, T. Wiegelmann, and C. Sasso for very helpful discussions and comments, which led to improvements of the work. This work was partly supported by the National Natural Science Foundation grant 10933003 of China, and by WCU grant No. R31-10016 funded by the Korean Ministry of Education, Science and Technology.
References
- Andretta, V., & Jones, H. P. 1997, ApJ, 489, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Asensio Ramos, A., & Martínez Gonaález, M. J. & Rubiño-Martin, J. A. 2007, A&A, 476, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., Trujillo Bueno, J., & Landi Degl'Innocenti, E. 2008, ApJ, 683, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., Fontenla, J. M. & Loeser, R. 1994, in Infrared Solar Physics, ed. D. M. Rabin (Dordrecht:Kluwer), IAU Symp., 154, 35 [Google Scholar]
- Aznar Cuadrado, R., Solanki, S. K., & Lagg, A. 2005, in Chromosphere and Coronal Magneitc Fields, ed. D. E. Innes, A. Lagg, & S. K. Solanki, ESA SP-56, 49 [Google Scholar]
- Aznar Cuadrado, R., Solanki, S. K., & Lagg, A. 2007, in Modern Solar Facilities-Advance Solar Science, ed. F. Kneer, K. G. Puschmann, & A. D. Wittmann (Universitäsverlag Göttingen), 173 [Google Scholar]
- Beck, C., Schlichenmaier, R., Collados, M., Bellot Rubio, L., & Kentischer, T. 2005, A&A, 443, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernasconi, P. N., Rust, D. M., & Georgoulis, M. K., et al. 2002, Sol. Phys., 209, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Bloomfield, D. S., Lagg, A., & Solanki, S. K. 2007, ApJ, 671, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Brants, J. J. 1985a, Sol. Phys., 95, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Brants, J. J. 1985b, Sol. Phys., 98, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzek, A. 1967, Sol. Phys., 2, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzek, A. 1969, Sol. Phys., 8, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995, ApJ, 441, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Caligari, P., Schüssler, M., & Moreno-Insertis, F. 1998, ApJ, 502, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Centeno, R., Socas-Navarro, H., & Lites, B., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Trujillo Bueno, J., Uitenbroek, H., & Collados, M. 2008, ApJ, 677, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C., Schüssler, M., Tarbell, T. D., & Title, A. M. 2008, ApJ, 687, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, D. Y. 1993, in The Magnetic and Velocity Fields of Solar Active Regions, ASP Conf. Ser. 46, ed. H. Zirin, G. Ai, & H. Wang, IAU Colloq., 141, 471 [Google Scholar]
- Chou, D. Y., & Zirin, H. 1988, ApJ, 333, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Collados, M., Trujillo Bueno, J., & Asensio Ramos, A. 2003, in Solar Polarization 3, ed. J. Trujillo Bueno, & J. Sánchez Almeida, ASP Conf. Ser., 307, 468 [Google Scholar]
- Collados, M., Lagg, A., & Díaz García, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- Delaboudinière, J. -P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2004, Living Rev. Solar Phys., 1 http://solarphysics.livingreviews.org/Articles/lrsp-2004-1/ [Google Scholar]
- Georgoulis, M. K. 2005, ApJ, 629, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, K., & Harvey, J. 1973, Sol. Phys., 28, 61 [NASA ADS] [CrossRef] [Google Scholar]
- De Jager, C., Namba, O., & Neven, L. 1966, Bull. Astron. Inst. Netherlands, 18, 128 [NASA ADS] [Google Scholar]
- Judge, P. G. 2009, A&A, 493, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubo, M., Shimizu, T., & Lites, B. W. 2003, ApJ, 595, 465 [CrossRef] [Google Scholar]
- Landi Degl'Innocenti, E. 1982, Sol. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl'Innocenti, E., & Landofi, M. 2004a, Polarization in Spectral lines (Dordrecht: Kluwer) [Google Scholar]
- Lagg, A. 2007, Adv. Space Res., 39, 1734 [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Woch, J., Solanki, S. K., & Krupp, N. 2007, A&A, 462, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Ishikawa, R., & Merenda, L., et al. 2009, in Second Hinode Science meeting: Beyond Discovery-Toward Understanding, ed. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 327 [Google Scholar]
- Lee, J. W. 1992, Sol. Phys., 139, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Penn, M. J., & Kuhn, J. R. 1998, ApJ, 493, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Skumanich, A., & Martínez Pillet, V. 1998, A&A, 333, 1053 [NASA ADS] [Google Scholar]
- Magara, T. 2008, ApJ, 685, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., & Bellot Rubio, L. R. 2009, ApJ, 700, 1391 [CrossRef] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Solanki, S. K. 2007, A&A, 469, 39 [Google Scholar]
- Martínez Pillet, V., Lites, B. W., & Skumanich, A. 1998, in Crossroads for European Solar and Heliospheric Physics, ed. R. Harris, F. Moreno Insertis, & E. Priest, ESA SP-417, 259 [Google Scholar]
- Merenda, L., Trujillo Bueno, J., Landi Degl'Innocenti, E., & Collados, M. 2006, ApJ, 642, 554 [Google Scholar]
- Metcalf, T. R., Leka, K. D., Barnes, G., et al. 2006, Sol. Phys., 237, 267 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Orozco Suárez, D., Lagg, A., & Solanki, S. K. 2005, Chromosphere and coronal magnetic field, ed. D. E. Innes, A. Lagg, S. K. Solanki, & D. Danesy, ESA-SP-596, 51 [Google Scholar]
- Penn, M. J., & Kuhn, J. R. 1995, ApJ, 441, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Pietarila, A., Hirzberger, J., Zakharov, V., & Solanki, S. K. 2009, A&A, 502, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozhalova, Z. A. 1988, Soviet Ast., 65, 1037 [Google Scholar]
- Rüedi, I., Solanki, S. K., & Livingston, W. C. 1995, A&A, 293, 252 [NASA ADS] [Google Scholar]
- Rüedi, I., Keller, C. U., & Solanki, S. K. 1996, Sol. Phys., 164, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sasso, C., Lagg, A., & Solanki, S. K. 2006, A&A, 456, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, A&A, 162, 129 [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., & Moreno-Insertis, F. 1994, A&A, 281, 69 [Google Scholar]
- Schmidt, W., Knölker, M., & Westendorp-Plaza, C. 1995, A&A, 287, 299 [Google Scholar]
- Schmieder, B., Rust, D. M., Georgoulis, M. K., Démoulin, P., & Bernasconi, P. N. 2004, ApJ, 601, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., & Uitenbroek, H. 2004, ApJ, 603, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Landi Degl'Innocenti, E. 2004, A&A, 612, 1175 [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Solanki, S. K., & Steiner, O. 1990, A&A, 234, 519 [NASA ADS] [Google Scholar]
- Solanki, S. K., Lagg, A., Woch, J., Krupp, N., & Collados, M. 2003, Nature, 425, 692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spadaro, D., Billotta, S., Contarino, L., Romano, P., & Zuccarello, F. 2004, A&A, 425, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanchfield, D. C. H., Thomas, J. H., & Lites, B. W. 1997, ApJS, 477, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Strous, L. H., & Zwaan, C. 1999, ApJ, 527, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Strous, L. H., Scharmer, G., Tarbell, T. D., Title, A. M., & Zwaan, C. 1996, A&A, 306, 947 [NASA ADS] [Google Scholar]
- Trujillo Bueno, J. 2009, in Magnetic Coupling between the Interior and the Atmosphere of the Sun, ed. S. S. Hasan, & R. J. Rutten, Astrophys. Space Sci. (Berlin: Spring-Verlag), in press [Google Scholar]
- Trujillo Bueno, J., & Asensio Ramos, A. 2007, ApJ, 655, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Landi Degl'Innocenti, E., Collados, M., Merenda, L., & Manso Sainz, R. 2002, Nature, 415, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trujillo Bueno, J., Merenda, L., Centeno, R., Collados, M., & Landi Degl'Innocenti, E. 2005, ApJ, 691, 191 [Google Scholar]
- Zhang, J., Solanki, S. K., & Wang, J. X. 2003, A&A, 399, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwaan, C., & Brants, J. J. 1985, Sol. Phys., 95, 3 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
| |
Figure 1: Development of the active region NOAA 10917 on 21 October 2006 seen in continuum radiation (SOHO/MDI). The solar coordinates and the disk center position are indicated in the top-left panel. The slit orientation (a stick marked ``slit'') and the scan direction of the spectropolarimetric observations (an arrow) are indicated in the bottom-right panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height = 12cm]{13227fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg26.png)
|
Figure 2:
a): morphology of NOAA 10917 on 21 Oct. 2006 viewed in infrared continuum radiation at 10 825 Å, b): the Ca II K line core, c): the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height = 6cm, width = 8cm]{13227fg3.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg34.png)
|
Figure 3:
Stokes profiles of the pixel located at X = 28, Y = 42 in the coordinates of Fig. 2a. Two atmospheric
components coexist and cause the partial overlap of line profiles of
the He I triplet and the telluric line at 10 832 Å. The observed
profile is shown in black (solid line), the best fit is shown in red
(filled circles). Three vertical dotted lines indicate the
line-center rest positions of the He I triplet. The fit is the sum
of two components: the one nearly at rest is plotted in green (B =220 G,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height = 10cm, width = 8cm]{13227fg4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg35.png)
|
Figure 4:
Stokes profiles of three-pixel average at X = 18, Y = 27 in the coordinates of Fig. 2a.
A combination of the Hanle and Zeeman effects acting in a single
atmospheric component reproduce both the linear and circular
polarization profiles in He I
line. We perform a Hanle-slab inversion for this point and the
inferred magnetic field vector in the local solar frame is B = 360 G,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[scale = 0.7]{f5.eps}
\end{figure*}](/articles/aa/full_html/2010/12/aa13227-09/Timg37.png)
|
Figure 5:
Retrieved atmospheric parameters of active region NOAA 10917 (21 Oct. 2006, 16:28-16:51 UT) in the photosphere (left column) and the upper chromosphere (right column). I: the
infrared continuum intensity, with the direction toward solar disk
center, S
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale = 0.8]{13227fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg41.png)
|
Figure 6:
Horizontal movement of the sunspots and pores in the course
of the observation. Left: continuum image of the whole
active region. The solid-line rectangle outlines the field of view
of the 15 successive short scans from 13:24 to 14:38 UT. The arrow
points to disk center. The dotted square displays the area shown in
Fig. 9. Middle: the flow field derived from the
displacement of sunspots and pores inside the rectangle of the left
panel (overplotted arrows). The length of the arrow above this frame
corresponds to a speed of 1 km s-1. The continuum image was
obtained halfway through the time series (14:00 UT) and the position
of sunspots and pores at that time is marked by contours.
Right: the pixel-averaged longitudinal magnetic field flux
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale = 0.9]{f7.eps}\vspace*{2.85mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg43.png)
|
Figure 7: Scatter plots of pixel-averaged inclination angle versus magnetic field strength in the photosphere (left) and the upper chromosphere (right) for the region shown in Fig. 5. Red symbols represent the sunspot (or pores) and black symbols the emergence zone encircled by sunspots and pores. |
| Open with DEXTER | |
| In the text | |
| |
Figure 8: a)-c): pixel-averaged vertical magnetic field, field inclination with respect to the solar surface (see text), and LOS velocities in the photosphere. d): pixel-averaged vertical magnetic field in the upper chromosphere. In panels a) and d), white (dark) shading refers to the positive (negative) polarity. In panel b) dark (white) patches indicate that the field is parallel (inclined) to the solar surface. In panel c), downflows are positive. The coordinates are the same as in Fig. 5. |
| Open with DEXTER | |
| In the text | |
| |
Figure 9: Spatial maps of the Si I line Stokes V blue wing area, recorded at different times. The starting time of the plotted scans are 13:30 UT, 14:10 UT, 14:15 UT, and 14:20 UT, respectively. White (dark) patches indicate positive (negative) polarity. A number of MBFs are highlighted by white rectangles. The brightness of each panel is normalized to the maximum of the whole sequence. The field of view context is indicated by a dotted square in Fig. 6. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.6]{f10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg50.png)
|
Figure 10:
a): intensity image of the He I line at 10 830.3 Å. The dashed square outlines the region in which the parameter |
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Magnetic field structure of the loops reconstructed in an emerging flux region within NOAA 10917, based on the direct measurement of the magnetic vector in the upper chromosphere. Left: viewed directly from above. The chromospheric magnetic inclination map is overlaid by traced loops projected onto the solar disk. Right: the same, but viewed obliquely. The strength of the field along the traced field lines is color coded (upper color bar). The LOS velocity along the magnetic loop is color coded in the projection of the field lines onto the Y-Z plane (lower color bar). Note that the Z-axis is stretched. Areas in dark-blue around the edge of the field of view are the regions where the polarization signals are below our fitting threshold. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale = 0.5]{13227fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg59.png)
|
Figure 12:
a)-d): variation in the atmospheric parameters along a typical reconstructed loop. The X-axis is the distance measured along the solar surface below the loop from one footpoint (located at X =18, Y = 15) to the other footpoint (X=22, Y =42). a): height of the loop vs. distance (note the stretched Z axis). b): magnetic field strength. c): field direction. The inclination is given in red and the azimuth in blue. The dotted-line represents the 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.5]{13227fg13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg65.png)
|
Figure 13: Sketch of the magnetic field structure in an emerging flux region, summarizing the main observed features. The lower plane represents a cut at the photospheric level, the upper plane at the average chromospheric level. The white (dark) points signify positive (negative) polarity. The green arch connecting the opposite polarities represents an emerging magnetic loop going though the photosphere into the upper chromosphere. The color of the arch indicates the magnetic field strength (deep color corresponds to a strong magnetic field). The arrows in blue and red represent the upflows and downflows detected in the upper chromosphere, respectively. In the photosphere, the footpoints with opposite polarity move apart from each other, as indicated by the yellow arrows. The MBFs, present in the emergence zone, are represented by small pairs of white/black patches. A U-type loop represents the MBF magnetic field configuration. An isolated white patch represents the old sunspot, present already before the new flux started to emerge. It is partly covered by loops of freshly emerging flux. Solid (dotted) lines represent the magnetic field lines above (under) the photosphere. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.4,clip]{13227fg14.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13227-09/Timg66.png)
|
Figure 14:
Sketch of the evolution of a pair of emerging magnetic loops connected
below the surface by a U-loop. As the loops rise, they can reconnect
above the U-loop, leaving an O-loop and an
overlying |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


