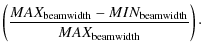| Issue |
A&A
Volume 520, September-October 2010
Pre-launch status of the Planck mission
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 15 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912999 | |
| Published online | 15 September 2010 | |
Pre-launch status of the Planck mission
Planck pre-launch status: HFI beam expectations from the optical optimisation of the focal plane
B. Maffei1
- F. Noviello2,3 - J. A. Murphy3
- P. A. R. Ade4 - J.-M. Lamarre5
- F. R. Bouchet12 - J. Brossard7,6
- A. Catalano5 - R. Colgan3
- R. Gispert2 - E. Gleeson3
- C. V. Haynes1 - W. C. Jones8,10
- A. E. Lange8,
![]() - Y. Longval2
- I. McAuley3 - F. Pajot2
- T. Peacocke3 - G. Pisano1
- J.-L. Puget2 - I. Ristorcelli6
- G. Savini94 - R. Sudiwala4
- R. J. Wylde13 - V. Yurchenko311
- Y. Longval2
- I. McAuley3 - F. Pajot2
- T. Peacocke3 - G. Pisano1
- J.-L. Puget2 - I. Ristorcelli6
- G. Savini94 - R. Sudiwala4
- R. J. Wylde13 - V. Yurchenko311
1 - The University of Manchester, JBCA, School of Physics and
Astronomy, Manchester M13 9PL, UK
2 - Institut d'Astrophysique Spatiale, CNRS & Université Paris
11, Bâtiment 121, 91405 Orsay, France
3 - NUI Maynooth, Department of Experimental Physics, Maynooth, Co.
Kildare, Ireland
4 - Cardiff University, School of Physics and Astronomy, The Parade,
Cardiff CF24 3AA, UK
5 - LERMA, CNRS, Observatoire de Paris, 61 Avenue de l'Observatoire,
75014 Paris, France
6 - CESR, CNRS-Université, 9 Av. du colonel Roche, BP44346, 31038
Toulouse Cedex 4, France
7 - Laboratoire de l'Accélérateur Linéaire, CNRS & Université
Paris 11, Bâtiment 200, 91898 Orsay, France
8 - Caltech/JPL, Caltech Observational Cosmology, Mail code: 59-33,
Pasadena, CA 91125, USA
9 - Optical Science Laboratory, Dept. of Physics and Astronomy, UCL,
London, WC1E 6BT, UK
10 - Princeton University, Dept. of Physics, Princeton, NJ 08544, USA
11 - Institute of Radiophysics and Electronics, NAS of Ukraine, 12
Proskura St., 61085, Kharkov, Ukraine
12 - Institut d'Astrophysique de Paris, CNRS & Université Paris
6, 98bis Bd Arago, 75014 Paris, France
13 - School of Physics and Astronomy, North Haugh, St Andrews, Fife
KY16 9SS, UK
Received 27 July 2009 / Accepted 26 January 2010
Abstract
Planck is a European Space Agency (ESA) satellite,
launched in May 2009, which will map the cosmic microwave background
anisotropies in
intensity and polarisation with unprecedented detail and sensitivity.
It
will also provide full-sky maps of astrophysical foregrounds. An
accurate knowledge of the telescope beam patterns is an essential
element for a correct analysis of the acquired astrophysical data. We
present a detailed
description of the optical design of the High Frequency Instrument
(HFI)
together with some of the optical performances measured during the
calibration
campaigns. We report on the evolution of the knowledge of the
pre-launch HFI beam patterns when coupled to ideal telescope elements,
and on their significance for the HFI data analysis procedure.
Key words: space vehicles: instruments - submillimeter: general - telescopes - cosmic microwave background - instrumentation: polarimeters - instrumentation: detectors
1 Introduction
The primary objective of the Planck mission![]() (Tauber et al. 2010b) is to
measure the temperature fluctuations of the cosmic microwave background
(CMB) with an accuracy limited only by astrophysical processes. This
will greatly improve constraints on the values of fundamental
cosmological parameters, such as the density parameter
(Tauber et al. 2010b) is to
measure the temperature fluctuations of the cosmic microwave background
(CMB) with an accuracy limited only by astrophysical processes. This
will greatly improve constraints on the values of fundamental
cosmological parameters, such as the density parameter ![]() ,
the Hubble parameter H0 and
the cosmological constant
,
the Hubble parameter H0 and
the cosmological constant ![]() .
In addition, Planck will deliver a wealth of
information on the polarisation properties of the CMB. Because of its
extended frequency coverage (30-857 GHz), Planck
will improve our understanding of foreground emissions from both
Galactic and extragalactic sources.
.
In addition, Planck will deliver a wealth of
information on the polarisation properties of the CMB. Because of its
extended frequency coverage (30-857 GHz), Planck
will improve our understanding of foreground emissions from both
Galactic and extragalactic sources.
The Planck payload is equipped with two focal plane instruments, the Low Frequency Instrument (LFI) operating in three frequency bands at 30, 44 and 70 GHz (Bersanelli et al. 2010), and the High Frequency Instrument (HFI) operating in six frequency bands centred at 100, 143, 217, 353, 545 and 857 GHz (Lamarre et al. 2003, 2010). While all the detectors of LFI are dual-linearly-polarised, HFI contains both un-polarised (total intensity) and dual-linearly-polarised pixels. The detectors of these two instruments are optically coupled to an off-axis dual-mirror telescope through corrugated feedhorns (Tauber et al. 2010a). The primary mirror has a projected diameter of 1.5 m, which constitutes a dimensioning parameter of the satellite. The angular resolution of Planck, ranging from 4.5 to 30 arcmin, results from an under-illumination of the primary reflector that minimize the spillover (see Sect. 3.2). Since the observed signal arriving from an astronomical source (such as the CMB) will be convolved with the beam response of the observing instrument, it is of paramount importance to acquire the best possible knowledge of the instrument.
We will focus on the HFI optical design performances.
Section 2 describes the optical concept of the focal plane
unit (FPU) based on experience gained from previous instruments.
Section 3 reviews the optical requirements based on the
scientific goals. Sections 4 and 5 describe the design of the
FPU and the solutions adopted to reach the specifications defined by
the requirements. In Sect. 6 we set out our best prediction of
the pre-launch HFI optical performances deduced from the various
calibration campaigns. Section 7 is then dedicated to the beam
simulations performed for the single and multi-mode channels assuming
an ideal telescope![]() .
.
2 Focal plane unit concept
The Planck-HFI detection system is based on highly sensitive bolometers. A specific detection assembly configuration was developed for Planck-HFI drawing upon the heritage from previous CMB experiments.
The detectors are feedhorn coupled in order to meet the requirements on beam shape definition and straylight control. Notwithstanding recent progress in antenna coupled bolometer performances, when Planck-HFI was designed, the only choice was to use corrugated feedhorns. Moreover, it has been shown (Maffei et al. 2008) that locating quasi-optical components in front of the horn aperture will impact its beam characteristics. When cryogenically cooled detectors are used (such as bolometers), ground based and balloon borne experiments need to have quasi-optical components such as a dewar window and interference filters (Ade et al. 2006) in front of the cold optics. This inevitably results in main beam distortion and an overall increase in sidelobe levels. Because HFI is in space, it is possible to avoid the use of quasi-optical components in front of the the horn. In order to do so and taking thermo-mechanical constraints into consideration, a triple horn configuration has been adopted, where the filters are located between a back-to-back horn and the detector horn. In this position, the filters will have a smaller impact on the beam shape.
This configuration was first used as a 90 GHz radiometer prototype (Church et al. 1996), and subsequently in the experiment BOOMERanG (de Bernardis et al. 2000). It was then optimised for Planck-HFI and operated in the Archeops experiment (Benoit et al. 2002), the balloon borne version of HFI.
| Figure 1: Drawing of an HFI detection assembly chain. The back-to-back horn (front and back horns) couples the incoming radiation from the telescope to a detector horn which then couples the radiation to the bolometric detector. Filters are located in between the two horn assemblies in order to define the spectral band. A lens refocusses the radiation from the back horn to the detector horn. |
|
| Open with DEXTER | |
The thermo-mechanical purpose of this triple horn configuration, forming the detection assembly (or pixel - Fig. 1), is presented in detail in a joint paper (Ade et al. 2010). Here we explain how the optical optimisation has been performed and also compare the theoretical modelling with the measured results.
3 Optical requirements
The scientific goals of Planck-HFI (Tauber et al. 2010b) dictate the instrumental specifications such as the sensitivity, the frequency coverage or the spatial resolution. Taking into account the constraints of a space mission, these specifications are translated into a set of optical requirements that are listed below.
3.1 Spatial resolution
The size of the Planck primary mirror results from a trade-off between the desired resolution and the size and weight limits which can be flown on-board a medium size space mission. The diffraction limit dictates that for frequencies above 300 GHz, a resolution of a few arcminutes can be reached. However, calculations (Planck community 2005) have shown that point source contamination would be too high to extract useful information at high multipoles in the CMB power spectrum. Also, in order to be compliant with a correct sampling of the sky (due to data acquisition rate and speed of rotation of the satellite), a maximum resolution of 5 arcmin has been set (Table 1). To do so, two techniques can be used: either under-illuminating the telescope, resulting in a smaller effective aperture diameter, or alternatively making use of multi-mode optics. We have chosen to slightly under-illuminate the telescope for the 353 GHz band and to use multi-mode channels (Murphy et al 2001) for the two highest frequency spectral bands (545 GHz and 857 GHz). The latter technique has the advantage of increasing the sensitivity of the detection assembly, each mode bringing its contribution to the power detected, but has the drawback of resulting in a beam which is more complicated to model and less predictable than single-mode channels.
Table 1: Summary of optical requirements for each spectral band.
We will describe in this paper the general principles of the optical optimisation, valid for all the HFI channels, and defer a more detailed description and discussion on the design of the multi-mode channels to a specific paper to follow later (2010).
3.2 Spillover, straylight and sidelobe rejection
Since the signal from the CMB anisotropies is weak, it is crucial to reduce unwanted signals to a minimum. These parasitic signals will come not only from the instrument self-emission surrounding the focal plane, as well as from potential bright objects (such as the Earth, the Moon or bright stars for example). The off-axis emission of these bright objects within the spectral bands of observation can reach the detector through the antenna far-sidelobes, through multiple scattering on the baffles and instrument or through the part of the horn beam looking directly at the sky.
The fraction of the horn beam coupling to the telescope will create the antenna main beam through which the CMB and foreground signals will be observed. The remaining part of the horn beam couples either to the sky via sidelobes or to to the instrument through absorption or multiple reflections. The spillover can be defined as the overall radiative power that does not intercept the telescope reflectors, thus directly reaching the detector antennas. This will result in an unwanted signal not directly originating from the source of interest. It is therefore an important parameter in assessing straylight control.
The reduction of the spillover and the maximisation of the power concentrated in the horn main beam is of great importance: not only the horn beam sidelobes have to be reduced, but the main beam has to be as close to a Gaussian profile as possible, as a Gaussian beam does not change its shape or develop sidelobes as it propagates (at least for single-mode case).
In order to be consistent with the science requirements, the spillover has to be maintained to within one percent. A more detailed requirement per band is given in Table 1. An equivalent parameter defining the telescope illumination and the potential straylight contamination is called edge taper. Assuming a Gaussian illumination of the secondary (M2) and primary (M1) mirrors by the horns, the edge taper defines the value of the illumination (in dB) at the edges of the mirrors. The further off-axis the horn is with respect to the axis of the mirror, the less symmetrical the edge taper value is for such a feedhorn position. An average edge taper requirement corresponding to the spillover requirement is given in Table 1 for each spectral band.
Thus, with a fixed telescope diameter, we need to make a trade-off between maximum resolution and spillover reduction.
3.3 Optical efficiency
Assuming that we are observing the CMB radiation as a source and that
the field of view of the detection assemblies is filled with this
radiation (extended source), the power absorbed by each detector from
the CMB source is:
The throughput, ![]() ,
is given by
,
is given by ![]() ,
where
,
where ![]() for a single-mode channel (A being the effective
aperture area of the front horn,
for a single-mode channel (A being the effective
aperture area of the front horn, ![]() the horn beam solid angle and
the horn beam solid angle and ![]() the wavelength). In the case of the multi-mode channels
the wavelength). In the case of the multi-mode channels ![]() is adjusted to produce the required
is adjusted to produce the required ![]() to match the telescope aperture. This will be addressed further in a
future paper (2010).
to match the telescope aperture. This will be addressed further in a
future paper (2010).
In this equation, ![]() ,
the optical efficiency, is the only parameter remaining which can
affect the amount of power received by the detector from the source.
This will then directly impact the instrumental sensitivity.
,
the optical efficiency, is the only parameter remaining which can
affect the amount of power received by the detector from the source.
This will then directly impact the instrumental sensitivity.
The optical efficiency takes into account several parameters
associated with the performance of each component forming the cold
optics. It includes the detector efficiency ![]() which is set by the detector design and manufacture. One of the major
tasks was to optimise the optical efficiency in order to reach a
requirement of
which is set by the detector design and manufacture. One of the major
tasks was to optimise the optical efficiency in order to reach a
requirement of ![]() when averaged over the spectral bandwidth and with a goal of
when averaged over the spectral bandwidth and with a goal of ![]() .
.
3.4 Focal surface curvature
The chosen off-axis Gregorian telescope configuration is designed to accommodate the relatively large size of the focal plane formed by both instruments given the optical and mechanical constraints. The optimisation performed by Thales Alenia Space to reduce the averaged cross-polarisation (Dragone-Mitsugushi criteria) and minimise the straylight pickup as well as the aberration effects for each pixel resulted in an aplanatic configuration consisting of two ellipsoidal reflectors giving a curved focal surface with an off-centre apex (Fargant et al. 2000). This shape has a pronounced slope across the focal plane and with different orthogonal curvatures. This curved focal surface (Fig. 2) is computed assuming an ideal telescope. Each individual front horn has been designed such that its phase centre is located on this theoretical focal surface (on each cross of Fig. 2) and oriented in such a way that its main beam aims at the centre of the primary mirror.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{aa12999-09-fig2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg21.png)
|
Figure 2: Curvature of Planck focal surface from Thales study resulting from simulation of a perfect telescope. Each cross represents the theoretical location of the phase center of a front horn. |
| Open with DEXTER | |
Additionally many of the single-mode detection assemblies are sensitive to polarisation (Table 7). The detectors (PSB, see Sect. 5.2) are oriented so that the telescope depolarisation effect is corrected.
The real mirror surfaces, misalignments (within tolerances) and thermal effects will lead to perturbations in the focal surface shape, resulting in a de-focusing of the feedhorns (Tauber et al. 2010a).
3.5 Shadowing constraints on design
Because the focal surface is not planar, potential shadowing of one of the horn beam by an adjacent front horn could occur. This is a possibility not only between horns of the same instrument, but also between LFI and HFI. Studies on horn mutual coupling and shadowing within Planck focal plane instruments by Thales (internal report) and then by the LFI team (D'Arcangelo et al. 2005) have shown that clearing each horn beam by +/-45 degrees respectively to its boresight axis is enough to make any shadowing effects on a given horn main beam pattern unnoticeable (within 1% error of the measurement system used).
To meet the required overall sensitivity HFI needs to have eight detection assemblies for each single-mode band dedicated to CMB measurements (100, 143, 217 and 353 GHz). In order to fit this number of assemblies within the focal plane, two rows of pixels for the first three spectral bands are needed. This arrangement was also constrained by the sky sampling requirements (Ade et al. 2010). Because of the focal surface curvature, the optical requirements summarised in Table 1 and the constraints due to shadowing, two different horn designs were required per frequency band (100, 143 and 217 GHz channels) depending on their location within the focal plane. The high frequency channels are located close to the centre of the focal plane where aberration effects are less pronounced.
4 Horn design and beam optimisation
Section 2 gives the reasons behind our detection assembly concept and our decision to use cold optics based on corrugated feedhorns. The front horns are coupled directly to the telescope. They define the resolution, the antenna beam shape (main beam and some of the sidelobes) and the spillover of the instrument. Thus, a careful design and an accurate characterisation of each feedhorn are crucial. This section describes the theoretical modelling involved in the horn design leading to the focal instrument shown in Figs. 4 and 5. We also present some results of the horn beam measurement campaign together with an analysis of the horn performances.
4.1 Effects to take into consideration
The back and detector horns couple the radiation from the front horn to the detector through the spectral filters. It is essentially true for the single-mode channels (100, 143, 217 and 353 GHz - CMB channels) that for a given frequency, the filters at this location will not impact the beam shape although they do affect the detection assembly transmission. However, the coupling between the back and detector horns as well as the filter transmission will affect the optical efficiency of the detection assembly non-uniformly with frequency (Ade et al. 2010). Since the beam shape of the horn depends on the specific frequency within the spectral band of the channel (see Sect. 4.6), this frequency dependent transmission will not only affect the sensitivity but also the overall beam shape of the detection assemblies (i.e. for the broad-band beam the beam shape is integrated over the whole bandwidth of the channel).
On the other hand, for the high frequency multi-mode horns (545 and 857 GHz dedicated to high frequency foregrounds removal) the balance between the modes that can propagate through the waveguide filter determines the beam illuminating the telescope and thus the resolution, spillover and edge taper. This balance depends ultimately on how these modes couple to the detector. The beam shapes will then be affected by the detailed nature of the coupling to the detector cavity via the horn-waveguide filter relay system, resulting in a beam modification. The beam will vary to a larger extent compared to single-mode channels. The filter transmission as well as the gap between the back-to-back horn and the detector horn, due to the filter stack thickness located in-between, will affect each mode transmission to the detector in a different way.
| Figure 3: Section view of one of Planck-HFI back-to-back horns. The close-up on the waveguide shows the sequence of cylindrical sections of alternating radii r0 and r1. |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig4a.ps}\vspace*...
...hics[angle=180,width=6cm,clip]{aa12999-09-fig4b.ps}\hspace*{1cm}}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg23.png)
|
Figure 4: Top: HFI focal plane layout. Empty circles represent the location of the front horn of each total intensity pixel. The crosses within the circles give the axis orientation of the dual-polarised detectors a and b of the PSBs. Bottom: top-view of the flight model 4 K focal plane array. |
| Open with DEXTER | |
4.2 Computation of corrugated horn beam patterns
Two main modelling techniques can be used for horn beam predictions. With the finite model analysis method, the horn and its surrounding is divided into small cells and Maxwell equations are solved within and at the boundaries of each cell. Software packages such as Ansoft HFSS (www.ansoft.com) or CST microwave studio (www.cst.com) are based on this technique. While accurate, they are usually very time consuming to run and need fairly high computation capabilities.
After cross-checks between various modelling techniques and validation with experimental data, we decided to use a second technique which has been used for many years in the field of radio and microwave technology development: the modal-matching technique.
In the modal-matching model, a corrugated horn, such as those employed by HFI, is regarded as a sequence of cylindrical waveguide sections with alternating radii as shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{aa12999-09-fig5a.ps}\vspac...
...ludegraphics[width=6.2cm,clip]{aa12999-09-fig5b.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg24.png)
|
Figure 5: Side-view pictures of the 4 K cold plate showing both curvatures of the focal surface. |
| Open with DEXTER | |
For each horn segment the natural modes of propagation are the usual TEn,l and TMn,l modes of a cylindrical waveguide (Olver et al. 1994; Murphy et al 2001; Colgan 2001; Gleeson 2004). For each value of n>0 and l, two orthogonal modal fields exist independently because of cylindrical symmetry.
In the single-mode corrugated horn antennas, the waveguide section is designed to filter out all but the TE11 and TM11 modes to propagate between the wider sections of the horn.
The term single-mode is somewhat misleading, but can be understood within the context of the hybrid mode model. In this model, it is assumed that there are a sufficient number of corrugations along the guide walls to mimic a continuous surface impedance. This assumption is valid if there are several corrugations per wavelength and if there is no abrupt change in the waveguide profile: four corrugations per free space wavelength are usually sufficient (Clarricoats & Olver 1984). Within this framework, each hybrid mode propagating in the horn can be considered as a combination of TE and TM scattering matrix modes (Gleeson 2004; Noviello 2008). For instance, the combination of the TE11 and TM11 scattering matrix modes is called an HE11 hybrid mode. The HE11 fundamental hybrid mode is then the only one actually propagating along the full length of a single-mode horn, although other modes, such as the EH11, will also propagate, but will then subsequently get cut off (evanescent mode).
Several channels of Planck-HFI are also dual-polarised (100, 143, 217 and 353 GHz). In order to limit the cold optics cross-polarisation, the resulting beam needs to be the same for any polarisation of the incoming radiation.
A horn radiation beam pattern gives the variation of the
electromagnetic field amplitude (or intensity in this case, as
bolometers are power sensitive detectors) as a function of the polar
angle ![]() respectively to the boresight (horn axis of symmetry).
respectively to the boresight (horn axis of symmetry). ![]() is the azimuthal angle relating to a cut of the beam. By convention,
the E field is aligned along the axis for which
is the azimuthal angle relating to a cut of the beam. By convention,
the E field is aligned along the axis for which ![]() deg,
while the H field is associated with
deg,
while the H field is associated with ![]() deg.
For this reason a cut of the beam in the
deg.
For this reason a cut of the beam in the ![]() deg plane is
referred as the H-plane cut (or H
plane) while a cut in the
deg plane is
referred as the H-plane cut (or H
plane) while a cut in the ![]() deg plane will be
the E-plane cut (E plane). The
difference between these two cuts will give an indication of the
cross-polarisation level of the horn. Figure 6 shows the two
cuts (both measured and simulated) and also the simulated
cross-polarisation beam of the horn.
deg plane will be
the E-plane cut (E plane). The
difference between these two cuts will give an indication of the
cross-polarisation level of the horn. Figure 6 shows the two
cuts (both measured and simulated) and also the simulated
cross-polarisation beam of the horn.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig6.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg29.png)
|
Figure 6: Typical back-to-back horn beam pattern at 100 GHz. The 2 co-polarisation beams (model and experimental data) are shown (E and H planes) as well as the model of the cross-polarisation beam. |
| Open with DEXTER | |
It has been shown that the easiest way to achieve low level of cross-polarisation is to use single-mode corrugated horns selecting only the HE11 fundamental hybrid mode (Clarricoats & Olver 1984).
In the case of multi-mode horns, a larger number of higher order modes above the TE11 or the TM11 modes can propagate. These give rise effectively to hybrid modes of order higher than the HE11 mode discussed above for the single-mode case. These hybrid fields can be derived using the same scattering matrix mode-matching techniques used for single-mode horns (except that we include modes of all necessary azimuthal orders, n, not just those with n=1). The number of modes propagating through the waveguide filters ultimately needs to be adjusted to produce the correct illumination beam on the telescope. These modes are independent of each other, so there is no phase relationship between them. Thus, these modes will contribute independently (i.e. incoherently) to the beam on the sky. In a single-mode horn only one pair of orthogonal coherent fields makes it through the waveguide filter to the horn aperture. In a multi-mode horn many independent pairs of orthogonal coherent fields will be present. Each of these has to be independently propagated through the Planck telescope to form the independent sum, taking into account a weighting factor for each mode corresponding to the coupling efficiency through the cold optics chain.
4.3 Waveguide definition
A circular corrugated waveguide is described by its radius and by the depth of the corrugations giving two parameters r0 and r1 (Fig. 3). These two radii will define the cut-on frequency of the modes that can propagate. In the case of the single-mode channels, we want to transmit only the fundamental HE11 hybrid mode through the detection assembly, which has a very low cross-polarisation and well defined Gaussian beam. On the other hand, in order to obtain a high sensitivity we need a large bandwidth. The maximum bandwidth with only the fundamental mode transmitted is about 33%. Above this a second mode will be transmitted compromising the polarisation purity. The high frequency cut-off is then defined by the interference filter stack located between the back and detector horns (Ade et al. 2010). Note however that in the case of the multi-mode pixels, the waveguide section does not determine the low frequency cut-off, rather both spectral band edges are determined by the interference filter stack.
4.4 Horn geometry
The front horn geometry controls the instrumental beam shape definition. The task is to be able to illuminate as efficiently as possible the mirrors of the telescope so that the final resolution on the sky meets the requirement. At the same time we need to keep the illumination at the edge of the mirrors below the required edge taper in order to limit the spillover. The idea is then to get a Gaussian horn beam for which the illumination drops quickly once outside the telescope edge.
Based on a previous geometry (del Rio et al. 1999), a profiled-flared horn geometry (Fig. 3) has been developed for Planck and used for Archeops (Maffei et al. 2000). A profiled horn can produce a Gaussian beam and has the advantage of being shorter than a classic conical horn, but the main beam will be surrounded by sidelobes whose level is too high for our instrument. Lengthening the horns would not be an efficient way to reduce the sidelobes because of the mass restrictions in a space mission. The addition of a well matched Gaussian flare at the aperture of the horn reduces the sidelobe levels but also broadens the main beam resulting in higher spillover compared to a pure Gaussian beam. Both effects increase with the length of the flare and a compromise has to be reached between sidelobe reduction, beam Gaussianity and shadowing effect as explained earlier.
While the phase centre of a profiled horn is located close to its aperture, the addition of the flare moves it away from the aperture further inside the horn. This location will depend on the length and the shape of this flare. This effect had to be taken into account when designing horns that will meet all the optical requirements, while being at the right location with respect to the focal surface.
The corrugated horns were manufactured using an electro-deposition technique, and consist mainly of electroformed copper. The thermal-contraction factor of this copper from 300 K to 4 K is taken to be 0.99674. The largest horns (100 GHz) being 62 mm long with an aperture diameter of 15 mm, the length variation will be 200 microns with a diameter variation of 50 microns. The horns have been designed in order to have optical predictions at the operating temperature. The length contraction has been taken into account so that the horn phase centres are positioned at the right location in the cold focal plane to avoid de-focusing effects. All the beam modelling that we present in this paper are performed taking into account the dimensions at the operating temperature of 4 K.
After several iterations between horn designs and GRASP (Pontoppidan 2005) simulations (see Sect. 7), each front horn was designed to meet all the requirements, resulting in the focal plane unit shown in Fig. 4. Pictures in Figs. 5 show the curved surface formed by the horn apertures (the horn phase centres are located only a few millimeters from the apertures) matching the focal surface shown in Fig. 2. An example of model of one of the horn beam patterns is given in Fig. 6 together with the experimental measured data.
4.5 Horn beam pattern measurements
All the back-to-back horns of HFI went through qualification and characterisation tests at single component level. While the result of their transmission measurements is reported in a companion paper (Ade et al. 2010), the relevant results concerning the beam definition are presented here.
The horn beams have been measured with a bolometric test system. This detector type is not sensitive to phase, thus only the power versus off-axis angle (with respect to boresight) has been recorded. However it has been shown (Maffei et al. 2000) that a close match can be achieved between predicted and measured horn phase patterns. For practical reasons, the bolometric detector used during these tests was not identical to those used in the real HFI focal plane. However, these test procedures in conjunction with spectral measurements (Ade et al. 2010) have been proven to give an accurate characterisation of the single-mode channel beams for previous prototypes. Concerning the multi-mode horns, these first tests allowed us to check that the horns meet the requirements. Additional measurements were needed in order to determine the beam shapes of the full detection assemblies and are presented in Murphy et al. (2010).
All horns show very little difference from the ideal pattern
(model prediction) at the level of their main beam (+/-25 deg
corresponding to the edge taper). The difference between the model and
the experimental measurements has been computed on the worst cases
defined in Eq. (2)
where
![\begin{figure}
\par\begin{tabular}{cc}
{\includegraphics[angle=0, scale=0.23]{aa...
...raphics[angle=0,scale=0.25]{aa12999-09-fig7d.ps} }\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg31.png)
|
Figure 7: Comparison between measured and modelled horn beam patterns. Plots are of E or H plane cuts: red line - experimental data, black line - model and blue line - difference. Top plots: E and H cuts corresponding to the pixel 100-4, the same as in Fig. 6. Lower section: worst pixel (217-3) measured at 240 GHz. |
| Open with DEXTER | |
Table 2: Beam pattern measurement results for a typical single-mode back-to-back horn.
The lower plots of Fig. 7 represent the beams for the worst case amongst all of the pixels, 217-3. Even in this case, the impact on the telescope main beam is minimal. The main effect will result in an increased spillover as shown in the next section.
4.6 Horn beam variation with frequency
The horn beam pattern will vary with frequency across the spectral bandwidth of the detection assembly. An example of such variation for one of the 100 GHz front horns (corresponding to the horn in position 100-2) is given in Fig. 8. For clarity, only one type of cut is shown (H field plane cut). As shown in Fig. 6, in the case of a single-mode corrugated horn all cuts of the main beam (E and H for example) are very similar for a given frequency.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg32.png)
|
Figure 8: 100-2 HFI horn beam pattern variation with frequency across the spectral band. Only one cut (H field plane cut) is shown for each of the five frequencies. |
| Open with DEXTER | |
5 Optical coupling within a detection assembly
To increase the sensitivity of the detection assemblies, the optical efficiency had to be optimised, and the cross-polarisation introduced by the optics had to be kept to a minimum. The results of modelling are presented below together with some experimental results performed on prototypes.
5.1 Coupling between the back-to-back and detector horns
Because of the thermal break created between the back-to-back horn and
the detector, the radiation has to propagate in free space over this
gap as well as through the filters. Moreover, the effective thickness
of the spectral filters (dielectric-constant-based) located in between
the horn apertures creates an even larger gap between the horns.
According to the Gaussian beam propagation from a horn, the radius of
the beam w(z) along the axis of
propagation z (horn axis) has its minimum value w0
(beam waist) at the phase center of the horn. From there, the beam
propagates and spreads following an Gaussian angular distribution with
a beam radius given by the equation:
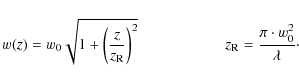
|
(3) |
Figure 9a shows that without a coupling element located between the two horns, a large fraction of the radiation will not be collected by the second horn. A typical conical horn will have its phase center located well inside the horn. By using profiled horns, the phase center can be located close to the aperture, leading to better coupling efficiencies. However, due to the minimum gap needed between the horn apertures, a lens is needed to refocus the beam (Fig. 9b). As an example, for the 143 GHz detection assemblies, the separation between the back and detector horns is about 16 mm. The 143 GHz horns far-field distance is 20 cm thus they are in the near-field of each other. Starting from a simple Gaussian beam approximation model up to a full HFSS analysis of the horn coupling, simulations and experimental data have been compared in order to find the best optical configuration.
A Gaussian beam model can reproduce fairly well the experimental data of simple optical configurations (such as two horns coupled by a central lens), provided that some interactions between the components, such as multiple reflections, are negligible. To model more complex and realistic configurations, including filters and the metallic structures (filter holders at the horn apertures), a much more sophisticated analysis is required. The finite-element analysis approach we used (HFSS) naturally takes into account the multiple reflections between all the components. An example of the HFSS model is shown in Figs. 10. Figure 10a shows how the 143 GHz horn coupling has been modelled to match as closely as possible a real detection assembly shown in Fig. 1. Figure 10b shows the resulting electromagnetic field inside the optical structure.
Anti-reflection coated lenses have been modelled both with a Gaussian beam approximation and with HFSS simulation as explained previously in order to cross-check the predictions. The coupling performance using a lens was first confirmed through the development of a prototype detection assembly before being adopted and used within the real instrument. Polypropylene, with a refractive index of 1.49 for the frequency range of interest has been used to manufacture the lenses. A material with refractive index of approximatively 1.2 was then needed for the anti-reflection coating. Polytetrafluoroethylene (PTFE) with 50% porosity has shown to give very good optical and cryo-mechanical performances. The radius of curvature of the lenses for each spectral band has been optimised in order to reach the highest coupling efficiency. The best results (both from model and experimental data) show that a maximum value of 90% can be reached. This includes the losses through the lens.
Modelling for the multi-mode channels has been more challenging. We did not find a unique lens that will couple all the modes in an optimal way. As confirmed through experimental measurements, we have not been able to design a lens that will improve the coupling efficiency, because the gain for some modes is counter-balanced by the losses through the lens for other modes. Since no solution was found on time, it has then been decided not to use any lens for the multi-mode channels at 545 and 857 GHz. It has to be noted that these channels will be used for high-frequency foreground removal and points source observations for which sensitivity is less of an issue.
Maximum efficiency will be strongly dependent on the accuracy achieved in the respective alignment of the optical components. Modelling of efficiency losses due to misalignment is a lengthy procedure even with single-mode channels. It is even more complicated for few and multi-mode channels. We have adopted an experimental approach in order to define these relative positioning requirements. Experimental measurements have been performed on a 143 GHz detection assembly. Using a blackbody as a source and changing the spectral band of operation, we have been able to operate this detection assembly with various numbers of transmitted modes, thus in various regimes from single-mode to few- and then multi-mode operation.
| Figure 9: Gaussian beam propagation between two horns, a) without lens, potentially a large fraction of the power can be lost; b) with a lens the beam is re-focused onto the second horn aperture. |
|
| Open with DEXTER | |
| Figure 10: HFI 143 GHz channel horn coupling model with HFSS. a) Model reproducing the pixel shown in Fig. 1. b) Simulated electromagnetic field inside the structure. |
|
| Open with DEXTER | |
Measurements made on each configuration have shown that a maximum
transversal misalignment of +/-0.3![]() (x-y plane in Fig. 9), where
(x-y plane in Fig. 9), where ![]() is the central frequency of operation, will allow the horn coupling
efficiency to be maintained within 95% of its maximum value when
operated with only one or a few modes. A maximum misalignment of +/-0.4
is the central frequency of operation, will allow the horn coupling
efficiency to be maintained within 95% of its maximum value when
operated with only one or a few modes. A maximum misalignment of +/-0.4![]() is possible when operated with several modes. Extrapolating these
results for the worst cases of the 545 GHz detection assembly
for few-mode optics and 857 GHz detection assembly for
multi-mode optics, we then found a maximum misalignment value of
+/-150 microns in the x-y
plane of the horn apertures to maintain the horn coupling efficiency
within 95% of its maximum value. Similar experimental measurements have
shown that the position tolerance between the components along the z
axis (along the detection assembly) is not as stringent. We found that
a position tolerance of +/-350 microns in the worst case
scenario has to be achieved for these optical components in order to
stay within 95% of the optical efficiency maximum value.
is possible when operated with several modes. Extrapolating these
results for the worst cases of the 545 GHz detection assembly
for few-mode optics and 857 GHz detection assembly for
multi-mode optics, we then found a maximum misalignment value of
+/-150 microns in the x-y
plane of the horn apertures to maintain the horn coupling efficiency
within 95% of its maximum value. Similar experimental measurements have
shown that the position tolerance between the components along the z
axis (along the detection assembly) is not as stringent. We found that
a position tolerance of +/-350 microns in the worst case
scenario has to be achieved for these optical components in order to
stay within 95% of the optical efficiency maximum value.
Cooling down the instrument to the operating temperature will mainly affect the relative alignment of the three thermal stages (4 K, 1.6 K and 0.1 K) along the z axis of the detection assembly. Thermo-mechanical predictions of the whole instrument ensures that the position of these optical elements are known within +/-350 microns.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{aa12999-09-fig11a.ps}\vspace...
...degraphics[width=8.5cm,clip]{aa12999-09-fig11b.eps}\vspace*{-0.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg36.png)
|
Figure 11:
Top left: HE11 waveguide aperture electric
field. Top right: horn corrugated waveguide with
re-expansion for optimum matching with PSB in |
| Open with DEXTER | |
5.2 Detector horn coupling to bolometer
The bolometric detectors used in HFI (Holmes et al. 2008)
are located in a ![]() cavity at the exit of the detector horn waveguide. For the spider-web
bolometers (SWB - Bock et
al. 1995; Yun et
al. 2004), used for the unpolarised channels,
cross-polarisation is not an issue and efficiency optimisation of the
radiation coupling between the horn and the detector is the main
concern. Polarisation sensitive bolometers (PSB - Jones et al. 2003)
are used for the polarised channels. PSBs are made of two superposed
linear grids orientated at 90 degrees respectively to each
other, so that the incoming radiation is decomposed into two orthogonal
linear polarisation directions (designated as detectors a
and b). In this case, the EM field properties at
the PSB had to be modelled carefully in
order to minimise the cross-polarisation.
cavity at the exit of the detector horn waveguide. For the spider-web
bolometers (SWB - Bock et
al. 1995; Yun et
al. 2004), used for the unpolarised channels,
cross-polarisation is not an issue and efficiency optimisation of the
radiation coupling between the horn and the detector is the main
concern. Polarisation sensitive bolometers (PSB - Jones et al. 2003)
are used for the polarised channels. PSBs are made of two superposed
linear grids orientated at 90 degrees respectively to each
other, so that the incoming radiation is decomposed into two orthogonal
linear polarisation directions (designated as detectors a
and b). In this case, the EM field properties at
the PSB had to be modelled carefully in
order to minimise the cross-polarisation.
Figure 11 shows the concept adopted to couple the radiation from the waveguide to the PSB. The white arrows inside the waveguide (on the left of the figure) represent a polarised electric field of the HE11 mode. We can see that these lines are curved when reaching the edge of the waveguide. When this field will be intercepted by the PSB, this curvature will create cross-polarisation. Limitation of this effect can be achieved by having a PSB diameter slightly smaller that the waveguide diameter. A trade-off has thus to occur between PSB illumination (efficiency) and cross-polarisation. Again, we have used the software HFSS in order to optimise the design of the re-expansion of the horn waveguide (such as Jones et al. 2003; and shown in Fig. 11 bottom). An example of the results obtained for the 100 GHz horn-to-PSB coupling is summarised in Table 3. Of course better values could be achieved if the design were optimised for a small range of frequencies. This horn to detector coupling had to be optimised for a 33% bandwidth in a similar manner to the horn coupling discussed in the previous sub-section. These cross-polarisation and efficiency results are obtained assuming perfect components. We will see in the next section that these values can be very sensitive to real hardware imperfections.
Table 3: HFSS simulation results for the horn-to-PSB coupling for the 100 GHz polarised channel (Fig. 11).
No such detailed optimisation has been performed on the multi-mode channels. For the 545 and 857 GHz detector to horn coupling a simpler model has been used: we assumed that the cavity in which the detector is located behaves like a black-body, thus, all modes are equally excited in power (Murphy et al. 2010).
6 FPU test results and analysis
Extensive test and calibration campaigns have been performed at JPL/Caltech and Cardiff University at the component level, then on each detection assembly and finally as an integrated instrument at IAS. In this section we report on the relevant results and on the optical performances.
6.1 Optical efficiency
The optical efficiency is determined by measuring a known
emission from a source such as a blackbody (Sudiwala et al. 2000;
Woodcraft et al. 2002).
The detection assembly is operated in flight-like conditions, and the
laboratory source radiates like the CMB (blackbody at ![]() K).
The radiative power received at the aperture of the front horn is
calculated using Eq. (1).
The effective detected power is calculated from previous calibration of
the detector. The overall optical efficiency is the ratio between
detected and received powers. Because this measurement is performed on
the overall detection assembly chain, the optical efficiency of each
component of the chain cannot be exactly known from this measurement
alone. Combinations of modelling and component level characterisation
can give a better picture of the various contributions. Table 4 summarises the
best estimates of the optical efficiency for each component when
assumed to be perfect. We see that in the best case scenario, with such
an optical configuration, the overall optical efficiency cannot be
larger than 56%. Some of these estimates are fairly robust. That is the
case for the horn return loss which can be modelled and measured
accurately as well as the filter stacks transmission (Ade et al. 2010). Other
values cannot be known as accurately due to the non-ideality of the
components. This is the case of the back and detector horns coupling
efficiency, the detector horn to bolometer coupling efficiency and the
detector efficiency. In this case the values given in Table 4 is the result of
simulations on perfect components.
K).
The radiative power received at the aperture of the front horn is
calculated using Eq. (1).
The effective detected power is calculated from previous calibration of
the detector. The overall optical efficiency is the ratio between
detected and received powers. Because this measurement is performed on
the overall detection assembly chain, the optical efficiency of each
component of the chain cannot be exactly known from this measurement
alone. Combinations of modelling and component level characterisation
can give a better picture of the various contributions. Table 4 summarises the
best estimates of the optical efficiency for each component when
assumed to be perfect. We see that in the best case scenario, with such
an optical configuration, the overall optical efficiency cannot be
larger than 56%. Some of these estimates are fairly robust. That is the
case for the horn return loss which can be modelled and measured
accurately as well as the filter stacks transmission (Ade et al. 2010). Other
values cannot be known as accurately due to the non-ideality of the
components. This is the case of the back and detector horns coupling
efficiency, the detector horn to bolometer coupling efficiency and the
detector efficiency. In this case the values given in Table 4 is the result of
simulations on perfect components.
Table 4: Break-down of the optical efficiencies of each component of a detection assembly.
Table 5: Optical efficiencies (in %) obtained from the various calibration campaigns (Catalano 2008).
Table 5 summarises the measured optical efficiency of each detection assembly deduced from the calibration campaigns. It is important to note that these measured values have been calculated assuming top-hat like channel spectral transmissions with nominal bandwidth edges. Spectral measurements are still being processed and a better analysis of the real optical efficiencies will be performed and presented in a future post-launch dedicated paper. A preliminary analysis of these spectral data shows that some of the bandwidths are actually narrower than the ones predicted. This will result in a lower power received by the detector in comparison to the one assumed with Eq. (1) with a top-hat like bandwidth and nominal band edges. A more accurate analysis should then lead to slightly better optical efficiency values than the one presented in Table 5. The discrepancies between the measured (Table 5) and ideal (Table 4) optical efficiencies are probably due to hardware imperfections affecting the horn-to-horn optical coupling though the lens, the horn-to-bolometer coupling efficiency and detector efficiency. Moreover, it has to be noted that in some cases, absorber geometries and surface impedances optimised for coupling to the cavities of a specific frequency band have been used in other spectral channels. For example the 100 GHz polarised pixels make use of PSBs optimised for the 143 GHz spectral band. Here the decision represents a design tradeoff between the speed of response, which for some devices proved slower than desired, and the coupling efficiency which is high enough still to meet the sensitivity requirement. In the case of the 217 and 353 GHz devices, the programmatic benefits of using a common design outweighed the slight decrease in efficiency. Finally, another parameter affecting the optical efficiency is the surface impedance of the bolometer (Jones et al. 2003). This is controlled by the thickness of the gold coating on the absorber. Table 3 gives an example of maximum horn to PSB optical coupling one might get, if the absorber layer thickness is perfectly tuned and fabricated. For many of the devices, especially the 353 GHz PSBs, this is not at all likely as the thickness tolerance increases with frequency.
However, it is important to note that even with these under-estimated measured values, the requirement of 25% is achieved in all single-mode pixels except the 353 GHz channel and that the optical efficiency is above the goal of 30% in several cases.
In the case of multi-mode channels the optical efficiency will also depend on the number of modes being transmitted (in other words the throughput of the system). The analysis of the performance of the multi-mode horns is still under investigation and will be reported in Murphy et al. (2010).
Ultimately, the calibration of the values of the optical efficiencies will rely on a combination of ground data and in-flight calibration on the dipole and point sources.
6.2 Polarisation property results
It is important to note too that some of these hardware imperfections will not only have an impact on the optical efficiency, but also on the cross-polarisation of the entire detection assembly. Table 3 gives a typical value of the cross-polarisation for an ideal case (simulation on perfect hardware). A specific paper, describing in details the polarisation properties of HFI, gives the measured values of the detection assemblies cross-polarisation integrated over the spectral band ranging from 1.9% up to 9.2% for the worst case, leading to a polarisation efficiency ranging from 96.2% to 83.2% (Rosset et al. 2010).
7 Simulation of HFI beam patterns through the Planck telescope
The motivation for computing telescope beam patterns on the sky with a
high accuracy can be summarised with a simple example. The signal given
for each pixel of our map (at a single frequency), will be (Dodelson 2003)
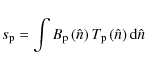
here
In the following simulations, except when stated otherwise, we consider an ideal telescope as specified in Sect. 1. The telescope baffles were not included in these simulations since the radiation intercepted by them does not contribute to the main beam power pattern.
Accurate measurements of the beam characteristics on the ground require the use of compact test ranges (CTR - Brossard 2001), but cannot be performed in exact flight-like conditions. These CTRs are not suited to carry out a large number of measurements, although they can be used to validate simulations of a few representative horns at specific frequencies. A set of such measurements were taken in a system-level validation campaign at 30, 70, 100 and 320 GHz (Tauber et al. 2010a). For this reason the pre-launch beam knowledge relies on accurate simulations.
The antenna beam patterns of the horns at the operating temperature of 4 K were computed with the commercial CORRUG (S.M.T. Consultancies Ltd) and the NUI Maynooth SCATTER software packages (Colgan 2001; Gleeson 2004). These patterns were then propagated through the telescope optics with the TICRA GRASP (versions 8 and 9) reflector antenna analysis software package (Pontoppidan 2005), unless otherwise stated.
7.1 Single-mode main beam predictions
In this section we discuss results obtained in our simulation campaign. As previously written in Sect. 4.2, the HE11 hybrid mode can be viewed as a combination of TE11 and TM11 scattering matrix modes. Also, the TE11 and TM11 modes entering a corrugated horn will both have scattered their power into TE1l and TM1l modes (same azimuthal order) upon exiting the horn aperture. From a computational point of view it is therefore convenient to perform calculations with only one input scattering matrix mode (for instance a TE11). The patterns resulting from both input modes will essentially exit the system as an HE11 (a mixture of TE11 and TM11 - although with different power contents). This approach has the obvious advantage of halving the required computation time. Figure 12 shows one such horn far-field pattern (HFI 100-1x back-to-back) which has the same shape (HE11) whether we use a TE11 or a TM11 mode as input. In Table 6 we compare the respective peak values for the co and cross-polarisation powers.
| Figure 12:
Co-polar (left) and cross-polarisation (right) HFI 100-1x back-to-back horn far-field beam intensity
pattern at 100 GHz also corresponding to the horn beam cuts of
Fig. 6.
The feed power has been normalised to emit 4 |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm]{aa12999-09-fig13.ps} %
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg44.png)
|
Figure 13: Electric field polarisation directions of the 100-1x back-to-back horn beam in the far-field. The reference direction is 0 degrees. The x-axis is in u-coordinates while the y-axis is expressed in v-coordinates. The units on the colourbar are degrees. |
| Open with DEXTER | |
Table 6: Co and cross-polarisation peak values for the 100-1 horn beam intensity patterns.
These results tell us that, not only do the TE11 and TM11 far-field intensity patterns (actually HE11) appear identical, but their co and cross-polar peak values also both scale by the same factor (-5 dB) when going from the TE11 to the TM11 field patterns (as they must). The HE11 horn patterns are linearly polarised over a wide angular range, as shown in Fig. 13. This is a highly desirable feature for fields coupling to PSBs, as in the HFI polarised channels. For the unpolarisd HFI single-mode channels, the two orthogonal HE11 modal fields are propagated independently through the telescope (since there is no phase relationship between them) and are then added in quadrature in the far-field. This approach is also used for multi-mode horns, where a number of independent HE and EH modes of different orders can propagate (see Sect. 7.3).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig14a.ps}\vspace*{1mm}
\includegraphics[width=8cm,clip]{aa12999-09-fig14b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg46.png)
|
Figure 14:
Q polarisation beam relative to the
100-1a&b PSB detectors for Gaussian ( top)
and modal matching ( bottom) horn. The |
| Open with DEXTER | |
One might ask whether the effect of approximating a realistic feed
model with a simpler one (Gaussian approximation) gives rise to
observable effects in the telescope beams on the sky. A relevant
difference was seen when computing Q Stokes
parameter polarisation beam patterns, such as the ones shown in
Figs. 14
for the 100-1 detectors. The Q Stokes parameter is
defined as
where Ia and Ib are the respective intensities on the sky of the two beam patterns corresponding to the two detectors a and b of the same PSB.
Not only are the Q polarisation patterns for the two different feed models visually different, but the ratio between the (absolute) values of the Q pattern peaks and those of the original beam patterns is nearly 4.5 times higher when using our SCATTER fields. A proper appraisal of these effects is of utmost importance for an experiment such as Planck, that will also measure with high accuracy the E-mode (and possible the B-mode) CMB polarisation power spectrum (Rosset et al. 2007).
For the same reason, the angular orientations of the polarised bolometers must be determined and optimised with high accuracy in order to obtained the specified polarisation angles to be measured on the sky. This was achieved through an iterative procedure using GRASP modelling of the beam patterns on the sky. This was undertaken for all a and b dual-polarised detectors at 143, 217 and 353 GHz. A comparative analysis using another commercialy available software package (ZEMAX) led to a good agreement, with a maximum discrepancy of 0.18 deg and 0.04 deg rms. The assumption is that the telescope projects the orientation of the PSB onto the sky. The polarisation angles on the sky for the HFI pixels (assuming an ideal telescope) are given in Table 7.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg47.png)
|
Figure 15: Composite projection of the focal plane on the sky, including all predicted main beams. The third row from the top shows the previous multi-mode channels beam simulations (545 and 857 GHz) which are being re-computed for better predictions (Murphy et al. 2010). |
| Open with DEXTER | |
Table 7: Telescope beam performances: from simulations assuming perfect optical components.
Several iterations have led to previous beam calculations with
other beam parameters (broad-band beams computed across the spectral
bands, elliptical Gaussian fitting), using different software (Brossard et al. 2004;
Yurchenko et al. 2004a;
Yurchenko et al. 2004b).
A full set of simulated beam patterns, for all HFI single-mode pixels,
was computed for the first full-scale test of the HFI data processing
centre (DPC) software pipeline. Important physical parameters, such as
the beam widths, polarisation angles and beam centroid positions on the
sky were also recovered for this data set. The results of these
computations assuming ideal optical components (mirrors and horns) are
summarised in Table 7.
The beam width and ellipticity of each detection assembly has been
computed
with the GRASP post-processor following the equations:
All main beams are shown on the composite projection of the focal plane on the sky given in Fig. 15 and a sub-set of co and cross-polarisation beam maps are given for each of the polarised channel in Figs. 16, 20, 21, and 22. The color scale of the map represents the gain, while the contours are given in dB respectively to the maximum (-1, -3, -5, -10, -15, -20, -25, -30, -40, -50 and -60 dB)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig16a.ps}\vspace*{2mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig16b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg52.png)
|
Figure 16: Top: co-polarisation; bottom: cross-polarisation main beam intensity maps for the polarised detector 100-2a. Simulations performed using ideal telescope and horns at the central frequency of 100 GHz. Color scale: gain. Contours in dB respectively to maximum. |
| Open with DEXTER | |
It is important to note that the cross-polarisation beams computed here do not take into account the cross-polarisation of the full detection assemblies which is dominated by the horn to PSB coupling as mentioned in the previous section (few % typically). In the beam simulation only the polarisation effects of perfect horns and mirrors (about -40 dB level) are taken into account.
Similarly we have assumed perfectly aligned PSBs in the focal plane. Measurements of the real polarisation angles (Rosset et al. 2010) show that there are variations of 0.4 deg up to 2 deg between theoretical and real angles in the focal plane reference system.
The pre-launch HFI main beam pattern predictions including the real mirrors (measured surfaces) and measured telescope alignment can be found in Tauber et al. (2010a). A limited number of beam patterns on the sky were also computed using measured horn patterns. Since only the horn power patterns (but not the phases) were measured, an algorithm combining the measured power with the theoretical (model) phases was developed. The term worst-case denotes the maximum discrepancy between the ideal horn patterns and the measurements. These limited discrepancies do not affect the main beam region of the beam on the sky, but can have some influence on the spillover performance of the telescope.
7.2 Beam width variation with frequency
Theoretical horn beam patterns computed for five frequencies within each spectral band (see for example Fig. 8 for the 100 GHz horn beams) have been used as GRASP inputs to model the variation of the main beam with frequency. Figure 17 shows the instrument beam width variation for each single-mode channel. The same inputs have been used by TICRA in order to compute the averaged beam patterns across the each spectral band (broad-band beams) using the real mirror surfaces of the telescope (Tauber et al. 2010a).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig17.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg53.png)
|
Figure 17: Beam width variation with frequency across each of the single-mode channel computed with measured telescope alignments and reflector surfaces. |
| Open with DEXTER | |
7.3 Multi-mode main beam predictions
For the multi-mode channels the fields are incoherent sums of all modes present. The number of modes transmitted through the detection assemblies that reach the bolometer varies with frequency, giving a non-constant number of modes across each spectral band. Therefore the main beam structure will vary with frequency. Since the main beam will not be Gaussian, a classic full width half maximum (FWHM) used on a typical quasi-Gaussian main beam becomes an inappropriate measure of the beam width here. An example of such a beam is shown in Fig. 18. This is the beam pattern of one of the 857 GHz detection assemblies (857-1) computed as an average across the whole spectral bandwidth (broad-band) in which the main beam is clearly non-Gaussian and the usual value of the FWHM becomes very sensitively dependent on the on-axis gain. A better definition is the half power beam width (HPBW). The power in the beam is integrated within a beam radius of 6 arcmin (the normalised intensity is about -40 dB at +/-6 arcmin). This gives half the included power in the beam at a diameter of 3.55 arcmin. Shown also are two beam power contour plots, one for 857-1 (also corresponding to Fig. 18) and one for 545-2 (Fig. 19). The XY scales are in degrees, and the plots are dB contours normalised to the maximum. The 857 plot is constructed from fifty two frequencies, the 545 from sixty eight.
![\begin{figure}
\par {\hspace*{0.75cm}\includegraphics[width=7.5cm,clip]{aa12999-...
...includegraphics[width=9cm,clip]{aa12999-09-fig18b.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg54.png)
|
Figure 18: Broad-band (52 frequencies) beam pattern of the 857-1 multi-mode pixel. Top: beam power map. Color scale: un-normalised gain. Contours in dB respectively to maximum. Bottom: two perpendicular beam cuts through the beam centroid (as shown in top figure). Red: widest beam cut. Blue: narrowest beam cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig19a.eps}\vspac...
...width=7cm,clip]{aa12999-09-fig19b.eps}\vspace*{-1.5mm}
\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg55.png)
|
Figure 19: Broad-band (68 frequencies) 545-2 multi-mode power beam. Bottom figure is on a different X-Y scale (both in degrees). Color scale: un-normalised gain. Contours in dB respectively to maximum. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig20a.ps}\vspace*{1.3mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig20b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg56.png)
|
Figure 20: Main beam intensity maps for the polarised detector 143-1a at the central frequency of 143 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig21a.ps}\vspace*{1.3mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig21b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg57.png)
|
Figure 21: Main beam intensity maps for the polarised detector 217-5a at the central frequency of 217 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig22a.ps}\vspace...
...ncludegraphics[width=7cm,clip]{aa12999-09-fig22b.ps}
\vspace{-4.5mm}\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg58.png)
|
Figure 22: Main beam intensity maps for the polarised detector 353-3a at the central frequency of 353 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
Note that these beams are not weighted to include filter transmissions, pixel coupling etc. Table 8 gives FWHM and HPBW estimates for three of the 545 and 857 GHz multi-mode pixels based on broad-band simulations.
Table 8: FWHM and HPBW estimated from two beam cuts through the centroid of the unweighted beams of some of the multi-mode pixels.
7.4 Spillover calculations
Measured horn beam patterns have been integrated in GRASP simulations of the spillover calculations, still using theoretical mirror surfaces. We compared spillover performance between ideal and worst-case horns for all single-mode HFI horn types, employing a representative sample of HFI pixels. Results are given in Table 9 only for cases showing discrepancies between the ideal model and the experimental data.
Table 9: Single-mode channels spillover calculations (in %).
Table 10: Spillover calculations (in %) of the high frequency channels assuming theoretical horn beam patterns.
These spillover values show that the original design goals (in Table 1) have been met to within approximately 0.1%, except for the 217-3 case. We must stress that these values represent an upper bound on the overall spillover performance of the focal plane since, for each frequency band and detector type, we chose to analyze the pixel with the largest discrepancy between model and experimental values.
Table 10 gives the current results (theoretical horn beam patterns) of the high frequency channels.
8 Conclusions
We have described the design optimisation of the cold optics and of the focal plane unit of Planck-HFI. The measured optical performances of the resulting instrument flight model are presented, together with beam simulations based on the perfect optical system.
Much original research both in terms of modelling and experimental verification was required to develop horns that could match the very demanding optical performance requirements of Planck (angular resolution, edge taper and spillover) while at the same time minimizing the length of the long wavelength horns. This required the development of complex theoretical tools and approaches to achieve an acceptable solution. The relevant results from the calibration campaigns have been summarised and show that most of the optical requirements are met.
Concerning the single-mode channels, the optical efficiency requirement is met for all but some of the 353 GHz detection assemblies, and analysis is still ongoing in order to get a better understanding of these. Most of the lower frequency pixels exceed the goals. It is important to note (Lamarre et al. 2010) that the measured NETs show that the overall sensitivities exceed the goal in most cases. Simulations show that only the 100 GHz beams have a slightly larger beam width than required (9.6 arcmin instead of 9.2), and that all but one detection assembly has a larger spillover than required (1% instead of 0.5%).
In this paper we also described in broad terms the development and performance of the unique multi-mode channels for HFI, specially designed to have higher throughput than the CMB channels in order to increase the sensitivity, while matching the desired non-diffraction limited resolution. In particular the 857 GHz horns, although challenging to manufacture (the corrugation period is of the order of 60 microns), were shown to have predicted beam patterns that match the resolution and edge taper requirements with significantly improved throughput over a single-mode design. The details of the design and predicted performance of these channels (at 545 GHz and 857 GHz) will be presented in a future paper (Murphy et al. 2010). Because these channels are mainly dedicated to point source detections and high frequency foreground removal, the lower measured efficiencies (Table 5), still within the scientific requirements, are less of an issue.
Some of the ground calibration data are still being analysed and the results will be combined with in-flight calibration in order to get a more accurate knowledge of the instrument. Further post-launch publications will then be available.
AcknowledgementsThe authors would like to acknowledge the support from STFC, CNRS, CNES, NASA, Enterprise Ireland and Science Foundation Ireland.
The authors extend their gratitude to numerous engineers and scientists who have contributed to the design, development, construction or evaluation of HFI.
References
- Ade, P. A. R., Pisano, G., Tucker, C., et al. 2006, Proc. SPIE, 6275 [Google Scholar]
- Ade, P. A. R., Savini, G., Sudiwala, R., et al. 2010, A&A, 520, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benoit, A., Ade, P. A. R., Amblard, A., et al. 2002, Astropart. Phys., 17, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N. Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bock, J. J., Chen, D., Mauskopf, P. D., et al. 1995, Space Sci. Rev., 74, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Brossard, J. 2001, Ph.D. Thesis [Google Scholar]
- Brossard, J., Yurchenko, V., Gleeson, E., et al. 2004, Proc. 5th ICSO, ESA SP-554, 333 [Google Scholar]
- Catalano, A. 2008, Ph.D. Thesis [Google Scholar]
- Church, S. E., Philhour, B. J., Lange, A. E., et al. 1996, Proc. 30th ESLAB symposium on Submillimetre and Far-Infrared Space Instrumentation, ESA-ESTEC, 77 [Google Scholar]
- Clarricoats, P. J. B., & Olver, A. D. 1984, Corrugated horns for microwave antennas, ed. Peregrinus [Google Scholar]
- Colgan, R. 2001, Electromagnetic and Quasi-Optical Modelling of Horn Antennas for Far-IR Space Applications, Ph.D. Thesis, NUI Maynooth [Google Scholar]
- D'Arcangelo, O., Garavalia, S., Simonetto, A., et al. 2005, Experimental Astronomy, 16, 165 [NASA ADS] [CrossRef] [Google Scholar]
- de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- del Rio Bocio, C., Gonzalo, R., Sorolla Ayza, M., et al. 1999, IEEE Trans. Antennas Propag., 47, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S. 2003, Modern Cosmology (Amsterdam: Academic Press) [Google Scholar]
- Fargant, G., Dubruel, D., Cornut, M., et al. 2000, SPIE Proc., 4013, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Gleeson, E. 2004, Single and Multi-moded Corrugated Horn Design for Cosmic Microwave Background Experiments, Ph.D. Thesis, NUI Maynooth [Google Scholar]
- Huffenberger, K. M., Eriksen, H. K., Hansen, F. K., et al. 2008, ApJ, 688, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Holmes, W. A., Bock, J. J., Crill, B. P., et al. 2008, Appl. Opt., 47, 5996 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jones, W. C., Bhatia, R., Bock, J. J., et al. 2003, Proc. SPIE, 4855, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J. M., Puget, J. L., Bouchet, F., et al. 2003, New Astr. Rev., 47, 1017 [Google Scholar]
- Lamarre, J. M., Puget, J. L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maffei, B., Ade, P. A. R., Tucker, C. E., et al. 2000, Int. J. Infrared and Millimetre waves, 21, 2023 [Google Scholar]
- Maffei, B., Pisano, G., Haynes, V., et al. 2008 Proc. SPIE, 7020 [Google Scholar]
- Murphy, J. A., Colgan, R., O'Sullivan, C., et al. 2001, Infrared Phys. Technol., 42, 515 [Google Scholar]
- Murphy, J. A., et al. 2010, Journal of Instrumentation, submitted [Google Scholar]
- Noviello, F. 2008, Optical Performance of the ESA Planck Surveyor and Techniques for the Study of the Cosmic Microwave Background, Ph.D. Thesis, NUI Maynooth [Google Scholar]
- Olver, A. D., Clarricoats, P. J. B., Kishk, A. A., et al. 1994, Microwave Horns and Feeds (IEEE Press) [Google Scholar]
- The Planck community, Blue Book: Planck the Scientific Programme, www.rssd.esa.int/SA/PLANCK/docs/Bluebook-ESA-SCI(2005)1_V2.pdf [Google Scholar]
- Pontoppidan, K. 2005, GRASP9 Technical Description, TICRA Engineering Consultants [Google Scholar]
- Rosset, C. 2004, Conference: XXXIXth Rencontres de Moriond, Exploring the Universe, La Thuile [Google Scholar]
- Rosset, C., Yurchenko, V., Delabrouille, J., et al. 2007, A&A, 464, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosset, C., Tristam, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schroeder, D. J. 2000, Astronomical Optics (San Diego: Academic Press) [Google Scholar]
- Sudiwala, R. V., Maffei, B., Griffin, M. J., et al. 2000, Nucl. Instr. Methods Phys. Res., Sect. A, 444, 408 [Google Scholar]
- Tauber, J. A., Norgaard-Nielsen, H. U., Ade, P. A. R., et al. 2010a, A&A, 520, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010b, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodcraft, A. L., Sudiwala, R. V., Griffin, M. J., et al. 2002, Int. J. Infrared and Millimeter Waves, 23, 575 [CrossRef] [Google Scholar]
- Yun, M., Bock, J. J., Holmes, W., et al. 2004, J. Vac. Sci. Technol. B, 22, 220 [CrossRef] [Google Scholar]
- Yurchenko, V. B., Murphy, J. A., & Lamarre, J. M., et al. 2004a, Proc. SPIE, 5487, 542 [Google Scholar]
- Yurchenko, V. B., Murphy, J. A., Lamarre, J. M., et al. 2004b, Int. J. Infrared and Millimeter Waves, 25, 601 [Google Scholar]
Footnotes
- ... mission
![[*]](/icons/foot_motif.png)
- Planck (http://www.esa.int/Planck) is an ESA project with instruments provided by two scientific Consortia funded by ESA member states (in particular the lead countries: France and Italy) with contributions from NASA (USA), and telescope reflectors provided in collaboration between ESA and a scientific Consortium led and funded by Denmark.
- ... telescope
![[*]](/icons/foot_motif.png)
- In the context of this paper, ``ideal telescope'' must be understood as a telescope model with design alignments and smooth mirror theoretical surfaces.
All Tables
Table 1: Summary of optical requirements for each spectral band.
Table 2: Beam pattern measurement results for a typical single-mode back-to-back horn.
Table 3: HFSS simulation results for the horn-to-PSB coupling for the 100 GHz polarised channel (Fig. 11).
Table 4: Break-down of the optical efficiencies of each component of a detection assembly.
Table 5: Optical efficiencies (in %) obtained from the various calibration campaigns (Catalano 2008).
Table 6: Co and cross-polarisation peak values for the 100-1 horn beam intensity patterns.
Table 7: Telescope beam performances: from simulations assuming perfect optical components.
Table 8: FWHM and HPBW estimated from two beam cuts through the centroid of the unweighted beams of some of the multi-mode pixels.
Table 9: Single-mode channels spillover calculations (in %).
Table 10: Spillover calculations (in %) of the high frequency channels assuming theoretical horn beam patterns.
All Figures
| |
Figure 1: Drawing of an HFI detection assembly chain. The back-to-back horn (front and back horns) couples the incoming radiation from the telescope to a detector horn which then couples the radiation to the bolometric detector. Filters are located in between the two horn assemblies in order to define the spectral band. A lens refocusses the radiation from the back horn to the detector horn. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{aa12999-09-fig2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg21.png)
|
Figure 2: Curvature of Planck focal surface from Thales study resulting from simulation of a perfect telescope. Each cross represents the theoretical location of the phase center of a front horn. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Section view of one of Planck-HFI back-to-back horns. The close-up on the waveguide shows the sequence of cylindrical sections of alternating radii r0 and r1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig4a.ps}\vspace*...
...hics[angle=180,width=6cm,clip]{aa12999-09-fig4b.ps}\hspace*{1cm}}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg23.png)
|
Figure 4: Top: HFI focal plane layout. Empty circles represent the location of the front horn of each total intensity pixel. The crosses within the circles give the axis orientation of the dual-polarised detectors a and b of the PSBs. Bottom: top-view of the flight model 4 K focal plane array. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{aa12999-09-fig5a.ps}\vspac...
...ludegraphics[width=6.2cm,clip]{aa12999-09-fig5b.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg24.png)
|
Figure 5: Side-view pictures of the 4 K cold plate showing both curvatures of the focal surface. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig6.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg29.png)
|
Figure 6: Typical back-to-back horn beam pattern at 100 GHz. The 2 co-polarisation beams (model and experimental data) are shown (E and H planes) as well as the model of the cross-polarisation beam. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
{\includegraphics[angle=0, scale=0.23]{aa...
...raphics[angle=0,scale=0.25]{aa12999-09-fig7d.ps} }\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg31.png)
|
Figure 7: Comparison between measured and modelled horn beam patterns. Plots are of E or H plane cuts: red line - experimental data, black line - model and blue line - difference. Top plots: E and H cuts corresponding to the pixel 100-4, the same as in Fig. 6. Lower section: worst pixel (217-3) measured at 240 GHz. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg32.png)
|
Figure 8: 100-2 HFI horn beam pattern variation with frequency across the spectral band. Only one cut (H field plane cut) is shown for each of the five frequencies. |
| Open with DEXTER | |
| In the text | |
| |
Figure 9: Gaussian beam propagation between two horns, a) without lens, potentially a large fraction of the power can be lost; b) with a lens the beam is re-focused onto the second horn aperture. |
| Open with DEXTER | |
| In the text | |
| |
Figure 10: HFI 143 GHz channel horn coupling model with HFSS. a) Model reproducing the pixel shown in Fig. 1. b) Simulated electromagnetic field inside the structure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{aa12999-09-fig11a.ps}\vspace...
...degraphics[width=8.5cm,clip]{aa12999-09-fig11b.eps}\vspace*{-0.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg36.png)
|
Figure 11:
Top left: HE11 waveguide aperture electric
field. Top right: horn corrugated waveguide with
re-expansion for optimum matching with PSB in |
| Open with DEXTER | |
| In the text | |
| |
Figure 12:
Co-polar (left) and cross-polarisation (right) HFI 100-1x back-to-back horn far-field beam intensity
pattern at 100 GHz also corresponding to the horn beam cuts of
Fig. 6.
The feed power has been normalised to emit 4 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm]{aa12999-09-fig13.ps} %
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg44.png)
|
Figure 13: Electric field polarisation directions of the 100-1x back-to-back horn beam in the far-field. The reference direction is 0 degrees. The x-axis is in u-coordinates while the y-axis is expressed in v-coordinates. The units on the colourbar are degrees. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig14a.ps}\vspace*{1mm}
\includegraphics[width=8cm,clip]{aa12999-09-fig14b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg46.png)
|
Figure 14:
Q polarisation beam relative to the
100-1a&b PSB detectors for Gaussian ( top)
and modal matching ( bottom) horn. The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa12999-09-fig15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg47.png)
|
Figure 15: Composite projection of the focal plane on the sky, including all predicted main beams. The third row from the top shows the previous multi-mode channels beam simulations (545 and 857 GHz) which are being re-computed for better predictions (Murphy et al. 2010). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig16a.ps}\vspace*{2mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig16b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg52.png)
|
Figure 16: Top: co-polarisation; bottom: cross-polarisation main beam intensity maps for the polarised detector 100-2a. Simulations performed using ideal telescope and horns at the central frequency of 100 GHz. Color scale: gain. Contours in dB respectively to maximum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12999-09-fig17.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg53.png)
|
Figure 17: Beam width variation with frequency across each of the single-mode channel computed with measured telescope alignments and reflector surfaces. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{0.75cm}\includegraphics[width=7.5cm,clip]{aa12999-...
...includegraphics[width=9cm,clip]{aa12999-09-fig18b.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg54.png)
|
Figure 18: Broad-band (52 frequencies) beam pattern of the 857-1 multi-mode pixel. Top: beam power map. Color scale: un-normalised gain. Contours in dB respectively to maximum. Bottom: two perpendicular beam cuts through the beam centroid (as shown in top figure). Red: widest beam cut. Blue: narrowest beam cut. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig19a.eps}\vspac...
...width=7cm,clip]{aa12999-09-fig19b.eps}\vspace*{-1.5mm}
\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg55.png)
|
Figure 19: Broad-band (68 frequencies) 545-2 multi-mode power beam. Bottom figure is on a different X-Y scale (both in degrees). Color scale: un-normalised gain. Contours in dB respectively to maximum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig20a.ps}\vspace*{1.3mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig20b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg56.png)
|
Figure 20: Main beam intensity maps for the polarised detector 143-1a at the central frequency of 143 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig21a.ps}\vspace*{1.3mm}
\includegraphics[width=7cm,clip]{aa12999-09-fig21b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg57.png)
|
Figure 21: Main beam intensity maps for the polarised detector 217-5a at the central frequency of 217 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa12999-09-fig22a.ps}\vspace...
...ncludegraphics[width=7cm,clip]{aa12999-09-fig22b.ps}
\vspace{-4.5mm}\end{figure}](/articles/aa/full_html/2010/12/aa12999-09/Timg58.png)
|
Figure 22: Main beam intensity maps for the polarised detector 353-3a at the central frequency of 353 GHz. Same caption than for Fig. 16. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.