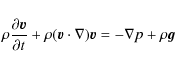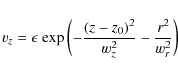| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912996 | |
| Published online | 08 October 2010 | |
Acoustic waves in a stratified atmosphere
IV. Three-dimensional nonlinear hydrodynamics
W. Kalkofen1,2 - P. Rossi3 - G. Bodo3 - S. Massaglia4
1 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
2 - Kiepenheuer-Institute for Solar Physics, Schöneckstr. 6, 79104 Freiburg, Germany
3 - INAF Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy
4 - Università di Torino Dipartimento di Fisica Generale, via Pietro Giuria 1, 10125 Torino, Italy
Received 27 July 2009 / Accepted 8 March 2010
Abstract
Context. The quiet solar chromosphere in the interior of
supergranulation cells is believed to be heated by the dissipation of
acoustic waves that originate with a typical period of 3 min in the
photosphere.
Aims. We investigate how the horizontal expansion with height of
acoustic waves traveling upward into an isothermal, gravitationally
stratified atmosphere depends on the size of the source region.
Methods. We have solved the three-dimensional, nonlinear,
time-dependent hydrodynamic equations for impulsively-generated,
upward-propagating acoustic waves, assuming cylindrical symmetry.
Results. When the diameter of the source of acoustic waves is
small, the pattern of the upward-propagating waves is that of a point
source, for which the energy travels upward in a vertical cone,
qualitatively matching the observed pattern of bright-point expansion
with height. For the largest plausible size of a source region, i.e.,
with granular size of 1 Mm, wave propagation in the low
chromosphere is approximately that of plane waves, but in the middle
and upper chromosphere it is also that of a point source. The
assumption of plane-wave propagation is not a good approximation in the
solar chromosphere. The upward-directed energy flux is larger than that
of the solar chromosphere, at least in the middle and upper
chromosphere, and probably throughout.
Conclusions. Simulations of impulsively generated acoustic waves
emitted from source regions with diameters that are small compared to
the pressure scale height of the atmosphere qualitatively reproduce the
upward expansion observed in chromospheric bright points. The emission
features in the cores of the H and K lines are predicted to be
blueshifted for a pulse and redshifted for the waves in its wake. The
contribution of internal gravity waves to the upward energy flux is
small and decreases with increasing size of the source region.
Key words: hydrodynamics - stars: late-type - waves - Sun: chromosphere
1 Introduction
Why is the solar chromosphere hotter than the photosphere? This question was first posed more than half a century ago (Biermann 1946; Schwarzschild 1948). While some progress has been made in answering the question, current research is still pursuing a complete explanation.The chromosphere supports several wave types that may play a role in the dynamics and heating of the atmosphere. In the interior of supergranulation cells, where magnetic fields are weak, the possible types are acoustic waves and internal gravity waves. On the boundary of cells, where magnetic fields are strong and typically organized in magnetic flux tubes, they are longitudinal and transverse (kink) as well as torsional waves.
In the supergranulation cell interior, where the physics of the medium is the simplest, the magnetic field is weak and mainly horizontal (Lites et al. 2008). So it may be ignored in a discussion of chromospheric heating. Therefore, in the cell interior, acoustic waves and internal gravity waves are the only wave types that may be important. However, observations from space with the Transition Region And Coronal Explorer (Fossum & Carlsson 2005) and Hinode (Carlsson et al. 2007) have not found acoustic waves with sufficient energy flux to cover the observed radiation losses of the chromosphere. But internal gravity waves have been detected, possibly with sufficient energy flux to heat the internetwork chromosphere to the observed temperature (Straus et al. 2008).
It is not known, however, how these waves dissipate their energy. The
heating of the solar chromosphere in the supergranulation cell interior
is therefore an open problem. The dynamics, on the other hand, have
been successfully simulated by Carlsson & Stein (1995, 1997)
on the basis of acoustic waves with a one-dimensional
radiation-hydrodynamic code where the driver at the lower boundary of
the computational domain was the observed velocity field in a
photospheric Fe I line (Lites et al. 1993).
The simulations show conclusively that bright points are caused by
acoustic shocks. But they also show two significant defects in the
theoretical model: the simulated time-average emission in the H![]() emission peak in the H line of Ca II fell short by a factor of 3
of the corresponding emission from the coolest of the empirical models
of Fontenla et al. (1993), called FALA (cf. Carlsson & Stein 1995, Fig. 3),
and, at the same time, the amplitude of the simulated temperature
fluctuations exceeded the temperature difference between model FALA and
the average model, FALC, by an order of magnitude - with a still
greater difference in the corresponding H line intensities. Thus, the
simulated time-average intensity of the Ca II emission from the
middle chromosphere was much lower than observed, and the simulated
maximal instantaneous intensity was much higher than observed.
emission peak in the H line of Ca II fell short by a factor of 3
of the corresponding emission from the coolest of the empirical models
of Fontenla et al. (1993), called FALA (cf. Carlsson & Stein 1995, Fig. 3),
and, at the same time, the amplitude of the simulated temperature
fluctuations exceeded the temperature difference between model FALA and
the average model, FALC, by an order of magnitude - with a still
greater difference in the corresponding H line intensities. Thus, the
simulated time-average intensity of the Ca II emission from the
middle chromosphere was much lower than observed, and the simulated
maximal instantaneous intensity was much higher than observed.
Is it conceivable that a single explanation covers both the very low time-average emission and the very high instantaneous emission? The low time-average intensity in the theoretical model is consistent with the low flux of acoustic waves measured in space. But the high instantaneous intensity, as well as the large amplitude of its oscillations, requires a different explanation. The topology of wave propagation could, in principle, address both discrepant features of the simulations.
Our explanation of the large wave amplitude of the simulated chromospheric oscillations was in terms of the topology of wave propagation, where we assumed that the photospheric source region of the acoustic waves could be idealized as a point. The analytic solution of the hydrodynamic equations in three-dimensional (3D) space was for an isothermal, stratified atmosphere (Bodo et al. 2000) and for a perturbed atmosphere (Bodo et al. 2001). The solutions showed that the geometry of the space in which most of the wave energy propagated could be approximated by a cone, with its apex at the point source. The horizontal spreading of the wave front in upward propagation led to a more gradual growth of the wave amplitude than in one-dimensional (1D) propagation, with reduced dissipation at lower heights and more energy available for heating at greater heights (Kalkofen 2004). This would thus allow more acoustic energy to reach higher levels in the chromosphere and might explain the reduced emission in the h and k lines of Mg II that is found in the numerical solution of the 1D hydrodynamic equations for the chromospheres of late-type stars (Fawzy et al. 2002).
The aim of the present paper is to solve the 3D hydrodynamic equations numerically and to determine the geometry of the upward-propagating waves as a function of the size of the source region, varying it from the point source dealt with in our earlier, analytic, investigations, to the granular size that was investigated by Skartlien et al. (2000). In Sect. 2 we consider observational support for the proposition that the waves in the solar chromosphere behave like 3D waves emanating from a point source, in Sect. 3 we describe the numerical procedure, and in Sect. 4 we illustrate the numerical results for acoustic and internal gravity waves. In Sect. 5 we discuss the results in connection with the observed line shifts, and in Sect. 6 we draw conclusions.
2 Observations
The quiet, nonmagnetic solar chromosphere shows evidence of propagating acoustic waves in the form of spherical (3D) waves, both in the dynamics of 3 min oscillations and, less directly, in the heating. In the dynamics there are three indicators of 3D wave propagation: 1. the increase with height of individual regions oscillating with large amplitude at the acoustic cutoff period of 3 min; 2. the corresponding increase with height of the fractional area in the interior of supergranulation cells that oscillates with large amplitude; and 3. the relatively low shock strength compared to shocks of plane waves. In detail:
- 1.
- In a typical supergranulation cell, which has a diameter of
ca. 20 Mm, there are 10 to 20 bright features seen in the blue
emission peaks in the cores of the H and K lines of Ca II, called H
 and K
and K bright points, respectively (Brandt et al. 1992).
Most of the H
bright points, respectively (Brandt et al. 1992).
Most of the H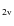 bright points, which have a diameter of up to 2 Mm (Cram & Damé 1983)
and are formed at a height of about 1 Mm in the chromosphere, are
found above intergranular lanes in the photosphere (Sivaraman
et al. 1990). The lanes have a width of 100 to 200 km. In the upper chromosphere, the oscillating regions have increased
in size to 5 to 6 Mm (cf. Table 1).
Although there are no simultaneous observations linking the oscillating
regions in the middle layers of the chromosphere directly to those in
the upper layers, the wave periods as well as the density of bright
points observed or inferred in the two layers appear to be the same,
which suggests that the oscillating regions refer to the same
phenomenon (Kalkofen 2003).
The height dependence of the diameter of bright points implies propagation channels in the shape of
cones with an opening angle of about
bright points, which have a diameter of up to 2 Mm (Cram & Damé 1983)
and are formed at a height of about 1 Mm in the chromosphere, are
found above intergranular lanes in the photosphere (Sivaraman
et al. 1990). The lanes have a width of 100 to 200 km. In the upper chromosphere, the oscillating regions have increased
in size to 5 to 6 Mm (cf. Table 1).
Although there are no simultaneous observations linking the oscillating
regions in the middle layers of the chromosphere directly to those in
the upper layers, the wave periods as well as the density of bright
points observed or inferred in the two layers appear to be the same,
which suggests that the oscillating regions refer to the same
phenomenon (Kalkofen 2003).
The height dependence of the diameter of bright points implies propagation channels in the shape of
cones with an opening angle of about 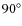 .
.
- 2.
- In the middle layers of the chromosphere, at a height of 1 Mm, the filling factor of K
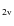 bright points is 5% to 10% of the area of the cell interior (von Uexküll & Kneer 1995);
and in the upper layers, the fractional area of bright points, as
observed in lines of neutral C, N, and O at a formation height of
bright points is 5% to 10% of the area of the cell interior (von Uexküll & Kneer 1995);
and in the upper layers, the fractional area of bright points, as
observed in lines of neutral C, N, and O at a formation height of 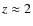 Mm, has increased to 50% (Carlsson et al. 1997).
Mm, has increased to 50% (Carlsson et al. 1997).
- 3.
- The observed temperature fluctuations at the acoustic cutoff
period amount to only a few percent of the ambient temperature. For
example, in the top layers of the chromosphere where the Lyman
continuum is formed (
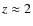 Mm), the temperature fluctuations are about 100 K
(Wilhelm & Kalkofen 2003), and even the strongest K
Mm), the temperature fluctuations are about 100 K
(Wilhelm & Kalkofen 2003), and even the strongest K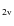 bright points are observed to have shocks with peak brightness
temperatures that are less than 30% above the ambient temperature (Liu 1974, Fig. 2). On the other hand, numerical simulations with plane acoustic waves by Carlsson & Stein (1995)
show a temperature excursion at a height of 1.4 Mm from
3000 K to 16 000 K, and, at the top of the chromosphere,
the temperature fluctuates maximally between 2000 K and
25 000 K (Carlsson & Stein 1994).
Although their more recent calculations have a lower level of
fluctuations because of a different boundary condition, the high
simulated temperature excursions as compared to those observed
highlight the effect of the assumed plane-wave propagation on shock
strength. A plausible explanation of this difference between simulated
and observed temperature variations is that the acoustic waves are not
plane, but three-dimensional, and therefore spread the wave energy in
the horizontal direction as they propagate in the vertical direction
(Ulmschneider et al. 2005).
bright points are observed to have shocks with peak brightness
temperatures that are less than 30% above the ambient temperature (Liu 1974, Fig. 2). On the other hand, numerical simulations with plane acoustic waves by Carlsson & Stein (1995)
show a temperature excursion at a height of 1.4 Mm from
3000 K to 16 000 K, and, at the top of the chromosphere,
the temperature fluctuates maximally between 2000 K and
25 000 K (Carlsson & Stein 1994).
Although their more recent calculations have a lower level of
fluctuations because of a different boundary condition, the high
simulated temperature excursions as compared to those observed
highlight the effect of the assumed plane-wave propagation on shock
strength. A plausible explanation of this difference between simulated
and observed temperature variations is that the acoustic waves are not
plane, but three-dimensional, and therefore spread the wave energy in
the horizontal direction as they propagate in the vertical direction
(Ulmschneider et al. 2005).
Table 1: Upward expansion of bright areas.
In chromospheric heating, the geometrical properties of the
upward-propagating acoustic waves are not directly constrained by
observations. Nevertheless, the relatively low level of temperature
fluctuations implied by the fluctuations in the observed intensity of K![]() emission at random locations in the supergranulation cell interior (von Uexküll & Kneer 1995, Fig. 3) suggests 3D wave propagation and appears to exclude 1D wave propagation.
emission at random locations in the supergranulation cell interior (von Uexküll & Kneer 1995, Fig. 3) suggests 3D wave propagation and appears to exclude 1D wave propagation.
Thus, observations of phenomena in the nonmagnetic chromosphere that
are associated with both the dynamics and the heating imply that the
acoustic waves propagate upward as 3D waves, emanating from point-like
sources in the photosphere. This 3D geometry of the dynamics of bright
points is not surprising in view of the location of most wave sources
in intergranular lanes. But for chromospheric heating, which we might
imagine being caused by the emission of short-period acoustic waves by
the Lighthill-Stein mechanism (Musielak et al. 1994), where the sources in the photosphere might then have granular size, i.e., with diameters of ![]() 1 Mm,
this finding of 3D wave propagation is unexpected. But it might be
consistent with the low value of the acoustic flux measured by Fossum
& Carlsson (2005) and the very low value of the flux of high-frequency waves.
1 Mm,
this finding of 3D wave propagation is unexpected. But it might be
consistent with the low value of the acoustic flux measured by Fossum
& Carlsson (2005) and the very low value of the flux of high-frequency waves.
The wave generation discussed in previous work with plane waves indicated that impulsive excitation had the property of emitting a pulse that was followed by a wake at the acoustic cutoff period. The decay of the wave amplitude in the linear calculations resembled that of the solar phenomenon (Kalkofen et al. 1994; Sutmann & Ulmschneider 1995), but the nonlinear calculations showed decay that was faster than observed and, in addition, gave a very large wave amplitude for the first wave after the pulse, indicating again a problem with the plane-wave assumption or with the impulsive-excitation model.
An attempt to model nonplanar wave propagation was made by Skartlien et al. (2000)
who assumed that the wave excitation was due to collapsing granules. Since the diameter of a
granule, about 1 Mm, is comparable to the height at which the radiation in H![]() is formed, also 1 Mm, the departure from plane-wave propagation
was minimal and essentially justified the plane-wave assumption. But,
as explained above, solar observations suggest source regions with an
area that is smaller than that of a granule by two orders of magnitude.
We can therefore expect a calculation with a ``point-like'' source
region to give the desired reduction in the wave amplitude as a
function of height. At the same time, it should tell us whether
impulsive wave excitation is a plausible mechanism.
is formed, also 1 Mm, the departure from plane-wave propagation
was minimal and essentially justified the plane-wave assumption. But,
as explained above, solar observations suggest source regions with an
area that is smaller than that of a granule by two orders of magnitude.
We can therefore expect a calculation with a ``point-like'' source
region to give the desired reduction in the wave amplitude as a
function of height. At the same time, it should tell us whether
impulsive wave excitation is a plausible mechanism.
3 The basic equations and numerical results
The hydrodynamic equations expressing the conservation of mass,
momentum, and internal energy for a gravitationally stratified, isothermal
atmosphere can be written as


where p,

where p00 and
The numerical integration of the system (1) has been carried out using a PPM code (piecewise-parabolic-Method, Colella & Woodward 1984) in cylindrical coordinates, with the vertical axis ranging from -10 to 35 in units of the scale height and a uniform vertical grid of 2000 points (spacing of 2.25 km). The horizontal axis has a uniform grid from the central axis to a radial distance corresponding to 15 scale heights (spacing of 5 km), and then is stretched by a factor of 1.02 for consecutive grid points, up to a total width corresponding to 80 scale heights, for 500 grid points. We discuss the results between 0 and 20 scale heights in the vertical direction and 15 in the horizontal direction, although the actual calculation is spatially more extended to avoid reflection problems in the region of interest.
We consider a disturbance by a vertical velocity pulse of Gaussian shape
with variable horizontal width,
excited at the base of the atmosphere, in the form
where
The velocities vz and
We consider three different values of wr with
the condition that the perturbation energy
be the same, i.e.,
For 3D waves, the energy is partitioned between acoustic waves and internal gravity waves, whereas for 1D waves, which propagate only in the vertical direction, all energy goes into acoustic waves. In addition, for 3D waves, we have to consider the geometrical decrease of the wave amplitude as
3.1 Acoustic waves
Figure 1 shows the gray-scale spatial distribution of the thermal pressure, in units of the initial values, for the case wr=0.05H and at the instant when the wave front has reached 15 scale heights. We see that the maximum value of the pressure is attained at the apex of the wave front, on the vertical axis, and that it declines off axis.

|
Figure 1: Spatial distribution of the thermal pressure for wr=0.05H, in units of the values at t=0, at the instant when the wave front has reached 15H. |
| Open with DEXTER | |

|
Figure 2: Spatial behavior of the vertical velocity vz versus height at the instant when the wave fronts have reached 15H. |
| Open with DEXTER | |
|
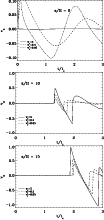
Figure 3:
Temporal behavior of the pulse amplitude vz versus time relative to the acoustic cutoff period, |
| Open with DEXTER | |
Figure 2 compares three waves in 3D having different radial extensions and amplitudes (but the same energy). The waves are excited by pulses and are seen at the time when the pulses have reached a height of 15 scale heights, which occurs at different times since the waves have different velocity amplitudes and therefore travel at different speeds. The first feature to note is that, going from extended to point source excitation, the wave shortens, i.e., the vertical distance between the pulse and the first maximum or minimum decreases. The separation between consecutive wave peaks in the wr = 5H case, which approaches the 1D limit, is nearly twice that of our most extreme 3D case, where wr=0.05H. This effect is related to the fact that in the former case, the first shock is stronger (at z = 15 H) and so the downflow is stronger and, as a consequence, the following shock stays far behind. Furthermore, looking at vertical velocity versus time at three different heights (Fig. 3), we see that at z = 0 the amplitude of the oscillation with wr = 0.05H is the highest but, with increasing height in the atmosphere, the wakes weaken. This effect comes from internal gravity waves (Bodo et al. 2000), which are not excited in 1D since they do not propagate in the vertical direction. At greater height (z/H=10 and 15) the internal gravity waves disappear completely. The much more rapid decay with height and time of the wave from the ``point-source'' excitation, where wr = 0.05H, is due to the more pronounced horizontal spreading in the vertical propagation of the wave.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12996fig6.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12996-09/Timg30.png)
|
Figure 4:
Horizontal size of the perturbation for different wr's. The size corresponds to
|
| Open with DEXTER | |
The behavior of the wave velocity and amplitude may be easier to
understand by looking, at given times, along the wavefront of the pulse
to the radius where
![]() .
One could compute a similar ratio at given heights but for different times (Bodo et al. 2001, Fig. 7). In Fig. 4, the thick solid line represents a propagation cone with an opening angle of
.
One could compute a similar ratio at given heights but for different times (Bodo et al. 2001, Fig. 7). In Fig. 4, the thick solid line represents a propagation cone with an opening angle of ![]() ,
i.e., the linear solution for a pulse perturbation emanating from a
point source. The dot-dashed line is the horizontal size of a pulse
with
wr = 0.05H. It shows the immediate flaring in 3D of the perturbation propagating
up in the atmosphere, implying effectively a dilution of the energy from the beginning.
Note that the feature visible within 2 H for this case is not an artifact, but comes from the
initial perturbation amplitude that is nonlinear and focuses the propagation cone before the
conical dilution of the wave can take place. Between 2 and 7 scale heights, the cases wr=0.05H and wr=0.5H
(dashed line) maintain the same behavior, since their wave amplitudes
are close in that height range. In contrast, in the case closest to the
1D case (solid, for wr = 5H), the perturbation propagates essentially as a plane wave up to 5H
but, when the shock-overtaking process becomes effective, starts to
flare, however, never reaching the fully 3D transverse size.
We can conclude that with the 3D approach the wake is strongly damped
by the horizontal spreading of the wave energy. The impulsive
excitation that seemed viable from 1D simulation is excluded by the 3D
results since we no longer observe the wake. Our results give
information on the wave propagation in an undisturbed medium: the
extension of the perturbed region roughly follows a cone with a fixed
opening angle. Starting from a perturbation with a horizontal size of
more than 5H
the 3D effects are negligible, at least up to the beginning of the
shock-overtaking process, at which point the 3D case presents a
flaring, with a consequent dilution, that does not occur in the 1D
treatment.
,
i.e., the linear solution for a pulse perturbation emanating from a
point source. The dot-dashed line is the horizontal size of a pulse
with
wr = 0.05H. It shows the immediate flaring in 3D of the perturbation propagating
up in the atmosphere, implying effectively a dilution of the energy from the beginning.
Note that the feature visible within 2 H for this case is not an artifact, but comes from the
initial perturbation amplitude that is nonlinear and focuses the propagation cone before the
conical dilution of the wave can take place. Between 2 and 7 scale heights, the cases wr=0.05H and wr=0.5H
(dashed line) maintain the same behavior, since their wave amplitudes
are close in that height range. In contrast, in the case closest to the
1D case (solid, for wr = 5H), the perturbation propagates essentially as a plane wave up to 5H
but, when the shock-overtaking process becomes effective, starts to
flare, however, never reaching the fully 3D transverse size.
We can conclude that with the 3D approach the wake is strongly damped
by the horizontal spreading of the wave energy. The impulsive
excitation that seemed viable from 1D simulation is excluded by the 3D
results since we no longer observe the wake. Our results give
information on the wave propagation in an undisturbed medium: the
extension of the perturbed region roughly follows a cone with a fixed
opening angle. Starting from a perturbation with a horizontal size of
more than 5H
the 3D effects are negligible, at least up to the beginning of the
shock-overtaking process, at which point the 3D case presents a
flaring, with a consequent dilution, that does not occur in the 1D
treatment.
3.2 Internal gravity waves
A point source perturbation impressed at the bottom of a stratified atmosphere gives rise to two kinds of waves: acoustic waves and internal gravity waves (Bray & Loughhead 1974). Following the linear analysis of Bodo et al. (2000), the two kinds of waves have the dispersion relations:![\begin{displaymath}\omega_\pm^2=\frac{1}{2}\left[(k^2+1) \pm \sqrt{(k^2+1)^2-16\frac{\gamma-1}{\gamma^2}k_x^2}\right]
\end{displaymath}](/articles/aa/full_html/2010/12/aa12996-09/img31.png)
where
![\begin{displaymath}(\vec{v}_{\rm g})_z=\frac{\partial \omega_\pm}{\partial k_z}=...
...^2+1}{\sqrt{(k^2+1)^2-16k_x^2(\gamma-1)/\gamma^2}}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/12/aa12996-09/img37.png)
If one considers a propagation direction close to the vertical axis, one can compute the ratio of group velocities of gravity to acoustic modes. For example, setting kx=0.1 and kz=1, one derives a velocity ratio of about 5%. One can then conclude that the energy flux of gravity waves in the upward direction is small compared to the acoustic flux.
4 Discussion of the results
The aim of this paper is to study the topology of the wave propagation channel as a function of the size of the wave source. We chose three sizes, defined by the diameter of the source at the height at which the wave amplitude has dropped to half the peak value, i.e., the value on the symmetry axis: a ``small'' size of d1=10 km at the height corresponding to unit optical depth in the continuum at 500 nm, z=0; an ``intermediate" size, of d2=100 km at z=0; and a ``large'' size, of d3=1 Mm.
Interesting heights at which to determine the expansion of the propagation channel are the height corresponding to the base of the chromosphere, at z=0.5 Mm, and the height of z=1 Mm in the middle chromosphere, which is the approximate height of formation of the emission features of the blue peaks in the H and K lines of Ca II. We find that for the two smaller sizes, with d= 10 km and 100 km, the diameter of the propagation channel at z=0.5 Mm has expanded by an order of magnitude, to 0.8 Mm; and for the largest source diameter, of 1 Mm, the channel has broadened by 20%, to 1.2 Mm. At the height of z=1.1 Mm, all three channels have broadened to 1.5 Mm; and above 1.1 Mm, the three channels broaden together at a rate corresponding to that of a point source.
The width of the propagation channel is observationally defined
not by the shape of the wave front at a given time, but by the passage
of the wave through a given layer and, therefore, by optical depth, or
height, in the atmosphere. Since we have shown in this paper that above
z=1.1 Mm the
propagation channel resembles that of a point source, we can use the
analytic results of Fig. 8 of Bodo et al. (2000)
for a point source to estimate the increase in the diameter of a bright
point and the corresponding reduction in the upward-directed wave flux.
We find that, at a height of 1.5 Mm, the opening angle of the
propagation cone for all three initial source diameters is about 130![]() ,
leading to the diameter of a bright point of 6 Mm at a height of
1.5 Mm in the upper chromosphere, with a corresponding reduction
in the upward wave flux by a factor of 20 relative to the flux at
1 Mm height. It is interesting that the SUMER observations
analyzed by Carlsson et al. (1997) show a bright point size in lines of neutral C, N, and O in the upper chromosphere of up to 8
,
leading to the diameter of a bright point of 6 Mm at a height of
1.5 Mm in the upper chromosphere, with a corresponding reduction
in the upward wave flux by a factor of 20 relative to the flux at
1 Mm height. It is interesting that the SUMER observations
analyzed by Carlsson et al. (1997) show a bright point size in lines of neutral C, N, and O in the upper chromosphere of up to 8
![]() ,
which agrees with the size we have estimated from our numerical solutions.
,
which agrees with the size we have estimated from our numerical solutions.
For a range of plausible sizes of bright points in the source layer, of 10 km to 100 km for a point source (Bodo et al. 2000), or for an extended, plane-wave source of 1 Mm (Skartlien et al. 2000), the solution in the middle to upper chromosphere resembles that of a point source, independent of the initial source size; and the substantial reduction in wave flux by the expansion of the propagation cone in large measure explains the large energy flux in the 1D numerical solutions of Carlsson & Stein (1994, 1995) and others as compared to the energy flux in actual bright points.
A pulse launched in an undisturbed atmosphere travels upward, generating a strong downflow in its wake. Profiles of lines emitted by the pulse may exhibit a blueshift; the wave due to the wake will be strongly redshifted. However, in the solar chromosphere, the medium is not quiescent but in motion. A pulse could therefore show a redward or a blueward shift. But the wake should still result in a strong downflow. Profiles of lines emitted in the downflow will be strongly redshifted. We therefore expect that the most luminous bright points have the highest redshifts.
5 Conclusions
We
have investigated the geometrical properties of acoustic-wave
propagation in a stratified atmosphere with cylindrical symmetry and a
constant scale height of 100 km. The waves were excited at the
origin of the stationary medium by an energy pulse of constant value.
The source region was described by a Gaussian shape with a diameter of
![]() ,
measured in units of the scale height, and thus the diameter
corresponded to 10 km, 100 km and 1000 km, respectively.
These cases range from the width of intergranular lanes to the diameter
of photospheric granules.
The acoustic waves generated in the photosphere travel upward into the
chromosphere in a propagation channel whose geometrical properties
depend on the size of the source region, the initial wave amplitude,
and the radiative losses due to the perturbation of the medium by the
wave.
,
measured in units of the scale height, and thus the diameter
corresponded to 10 km, 100 km and 1000 km, respectively.
These cases range from the width of intergranular lanes to the diameter
of photospheric granules.
The acoustic waves generated in the photosphere travel upward into the
chromosphere in a propagation channel whose geometrical properties
depend on the size of the source region, the initial wave amplitude,
and the radiative losses due to the perturbation of the medium by the
wave.
When the diameter of the source region is small compared to the
thickness of the chromosphere and the initial wave amplitude is small
compared to the sound speed, the waves travel in a cone whose opening
angle is about ![]() for a cone defined by a decrease of 50% of the pressure amplitude along
the wave front. When the diameter of the source region is of granular
size (1 Mm), wave propagation in the lower chromosphere resembles
that of plane waves, with effects at the edge of the perturbed region
playing a minor role, but in the middle and upper chromosphere, it
resembles that of a point source. For the solar chromosphere, which has
a thickness of 2 Mm, a wave with a value of the width parameter of
wr=5H,
corresponding to the diameter of a large granule with a diameter of
about 1 Mm, would be well represented by a plane wave in the lower
chromosphere, but with increasing corrections in upper layers. The
observations discussed in this paper imply however that the acoustic
waves responsible for bright points are best represented by waves
emanating from small sources.
for a cone defined by a decrease of 50% of the pressure amplitude along
the wave front. When the diameter of the source region is of granular
size (1 Mm), wave propagation in the lower chromosphere resembles
that of plane waves, with effects at the edge of the perturbed region
playing a minor role, but in the middle and upper chromosphere, it
resembles that of a point source. For the solar chromosphere, which has
a thickness of 2 Mm, a wave with a value of the width parameter of
wr=5H,
corresponding to the diameter of a large granule with a diameter of
about 1 Mm, would be well represented by a plane wave in the lower
chromosphere, but with increasing corrections in upper layers. The
observations discussed in this paper imply however that the acoustic
waves responsible for bright points are best represented by waves
emanating from small sources.
The generation of acoustic waves is accompanied by the emission
of internal gravity waves (IGWs), whose contribution to the wave flux
depends on the size of the source region. In a1D medium, IGWs are
entirely absent. Hence their contribution for a large source region
with 2wr=1 Mm
is very small. For small source regions, idealized as point sources,
the contribution to the energy budget of the solar atmosphere may be
significant. However, their properties do not make it appear likely
that they might be important for the wave flux in the middle and upper
chromosphere. But the work of Straus et al. (2008)
has shown that the energy flux in IGWs can dominate the one in acoustic
waves and match the radiative losses in the lower chromosphere (up to ![]() 600 km).
Thus, while they might be important for heating the low chromosphere
(where most of the energy is dissipated), their contribution to the
dynamics and heating of the middle and upper chromosphere is likely to
be small, and still needs to be investigated.
600 km).
Thus, while they might be important for heating the low chromosphere
(where most of the energy is dissipated), their contribution to the
dynamics and heating of the middle and upper chromosphere is likely to
be small, and still needs to be investigated.
References
- Biermann, L. 1946, Naturwissenschaften, 33, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Kalkofen, W., Massaglia, S., & Rossi, P. 2000, A&A, 354, 296 [NASA ADS] [Google Scholar]
- Bodo, G., Kalkofen, W., Massaglia, S., & Rossi, P. 2001, A&A, 370, 1088 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandt, P. N., Rutten, R. J., Shine, R. A., & Trujillo Bueno 1992, in Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. M. S. Giampapa, & J. A. Bookbinder (San Francisco: ASP), ASP Conf. Ser., 26 161 [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1974, The Solar Atmosphere (London: Chapman and Hall) [Google Scholar]
- Carlsson, M., & Stein, R. F. 1994, in Proc. Mini-Workshop on Chromosph. Dynamics, ed. M. Carlsson (Oslo: Inst. Theor. Astroph.), 47 [Google Scholar]
- Carlsson, M., & Stein, R. F. 1995, ApJ, 440, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [Google Scholar]
- Carlsson, M., Judge, P. G., & Wilhelm, K. 1997, ApJ, 486, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., de Pontieu, B., et al. 2007, PASJ, 59, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, JCoPh, 54, 174 [Google Scholar]
- Cram, L., & Damé, L. 1983, ApJ, 272, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fawzy, D., Ulmschneider, P., Stepien, K., Musielak, Z. S., & Rammacher, W. 2002, A&A, 386, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B., & Bonnet, R. M. 1984, ApJ, 279, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Fossum, A., & Carlsson, M. 2005, Nature, 435, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalkofen, W. 2003, Current Theor. Models and High-Res. Obs.: Preparing for ATST, ed. A. A. Pevtsov, & H. Uitenbroek, ASP Conf. Ser., 286, 443 [Google Scholar]
- Kalkofen, W. 2004, ed. A. K. Dupree, & A. O. Benz, IAU Symp., 219, 115 [Google Scholar]
- Kalkofen, W., Rossi, P., Bodo, G., & Massaglia, S. 1994, A&A, 284, 976 [NASA ADS] [Google Scholar]
- Lites, B. W., Rutten, R. J., & Kalkofen, W. 1993, ApJ, 414, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, 1237, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S.-Y. 1974, ApJ, 189, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Musielak, Z. E., Rosner, R., Stein, R. F., & Ulmschneider, P. 1994, ApJ, 423, 474 [Google Scholar]
- Rammacher, W., & Ulmschneider, P. 1992, A&A, 253, 586 [NASA ADS] [Google Scholar]
- Schwarzschild, M. 1948, ApJ, 107, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sivaraman, K. R., Bagare, S. P., & November, L. J. 1990, in Basic Plasma Processes on the Sun (Dordrecht: Kluwer), 102 [Google Scholar]
- Skartlien, R., Stein, R. F., & Nordlund, Å 2000, Apj, 541, 468 [Google Scholar]
- Straus, T., Fleck, B., Jefferies, S. M., et al. 2008, ApJ, 681, 125 [Google Scholar]
- Sutmann, G., & Ulmschneider, P. 1995, A&A, 294, 232 [NASA ADS] [Google Scholar]
- Ulmschneider, P., Rammacher, W., Musielak, Z. E., & Kalkofen, W. 2005, ApJ, 631, L115 [NASA ADS] [Google Scholar]
- von Uexküll, M., & Kneer, F. 1995, A&A, 294, 252 [NASA ADS] [Google Scholar]
- Wilhelm, K., & Kalkofen, W. 2003, 1137, A&A, 408, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Table 1: Upward expansion of bright areas.
All Figures

|
Figure 1: Spatial distribution of the thermal pressure for wr=0.05H, in units of the values at t=0, at the instant when the wave front has reached 15H. |
| Open with DEXTER | |
| In the text | |

|
Figure 2: Spatial behavior of the vertical velocity vz versus height at the instant when the wave fronts have reached 15H. |
| Open with DEXTER | |
| In the text | |

|
Figure 3:
Temporal behavior of the pulse amplitude vz versus time relative to the acoustic cutoff period, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12996fig6.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12996-09/Timg30.png)
|
Figure 4:
Horizontal size of the perturbation for different wr's. The size corresponds to
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.