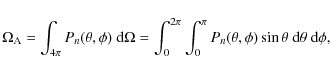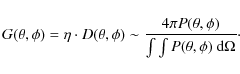EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A7 Full HTML
Issue
A&A
Volume 520, September-October 2010
Pre-launch status of the Planck mission
Article Number A7
Number of page(s) 12
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200912891
Published online 15 September 2010
A&A 520, A7 (2010)

Pre-launch status of the Planck mission

Planck pre-launch status: Low Frequency Instrument optics

M. Sandri1 - F. Villa1 - M. Bersanelli2 - C. Burigana1 - R. C. Butler1 - O. D'Arcangelo3 - L. Figini3 - A. Gregorio4,5 - C. R. Lawrence6 - D. Maino2 - N. Mandolesi1 - M. Maris4 - R. Nesti7 - F. Perrotta8 - P. Platania3 - A. Simonetto3 - C. Sozzi3 - J. Tauber9 - L. Valenziano1

1 - INAF-IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
2 - Università degli Studi di Milano, via Celoria 16, 20133 Milano, Italy
3 - IFP-CNR, via Cozzi 53, Milano, Italy
4 - INAF-OATS, via Tiepolo 11, 34143 Trieste, Italy
5 - University of Trieste, Department of Physics, via Valerio 2, 34127 Trieste, Italy
6 - Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena CA 91109, USA
7 - Osservatorio Astrofisico di Arcetri, INAF, Largo E. Fermi 5, 50125 Florence, Italy
8 - SISSA, via Beirut 4, 34014 Trieste, Italy
9 - ESA ESTEC, PO Box 299, 2200 AG Noordwijk, The Netherlands

Received 14 July 2009 / Accepted 1 October 2009

Abstract
We describe the optical design and optimisation of the Low Frequency Instrument (LFI), one of two instruments onboard the Planck satellite, which will survey the cosmic microwave background with unprecedented accuracy. The LFI covers the 30-70 GHz frequency range with an array of cryogenic radiometers. Stringent optical requirements on angular resolution, sidelobes, main beam symmetry, polarization purity, and feed orientation have been achieved. The optimisation process was carried out by assuming an ideal telescope according to the Planck design and by using both physical optics and multi-reflector geometrical theory of diffraction. This extensive study led to the flight design of the feed horns, their characteristics, arrangement, and orientation, while taking into account the opto-mechanical constraints imposed by complex interfaces in the Planck focal surface.

Key words: cosmic microwave background - space vehicles: instruments - instrumentation: detectors - submillimeter: general - telescopes

1 Introduction

The Planck[*] Satellite was developed to measure the temperature and polarization of the cosmic microwave background (CMB) over the entire sky with unprecedented sensitivity and angular resolution. The Low Frequency Instrument (LFI), operating in the 30-70 GHz frequency range, is an array of cryogenic pseudo-correlation radiometers (Bersanelli et al. 2010) sharing the focal surface of a 1.5 m off-axis dual reflector telescope with the High Frequency Instrument (HFI) (see Lamarre et al. 2010). This unique optical layout, with one instrument (LFI) surrounding the other (HFI), leads to potentially significant off-axis aberrations in the LFI beams that must be accurately controlled in the telescope and instrument design optimization phases. The requirements on the LFI beams were originally set in terms of angular resolution (33$^\prime $, 24$^\prime $, and 14$^\prime $, respectively at 30 GHz, 44 GHz, and 70 GHz) and straylight contamination (lower than 3 $\mu$K). The aim of this paper is to describe the complex process of design and optimization of the LFI optics, leading to the current flight configuration, which in some cases achieves angular resolutions superior to the requirements.

A CMB experiment should ideally have an optical system producing symmetric Gaussian beam responses to avoid distortion effects, and without spillover, to avoid straylight entering the detectors through the sidelobes producing signals that may be indistinguishable from fluctuations in the CMB. In real systems, however, residual non-idealities in the optical system may introduce serious limitations to the scientific return if not well understood and controlled. The systematic effects induced by the optics can be divided into two main areas: (i) the aberrations of the main beam, which degrade the angular resolution and increase the uncertainty in the measurements at high multipoles (particularly for polarization) as the texture of the cosmic signal is smeared and distorted; (ii) the sidelobes in the feed/telescope radiation pattern, which contribute to the straylight induced noise, i.e., the unwanted power reaching the detectors and not coupled through the main beam. These introduce contamination mainly at large and intermediate angular scales, typically at multipoles less than $\simeq$100.

In this paper, we present the definition, optimization, and characterization of the LFI optical interfaces. The work involved here has been carried out by means of electromagnetic simulations devoted to maximizing the angular resolution and at the same time minimizing systematic effects. The starting point of the optimization activity was the Planck telescope, which is an off-axis Gregorian telescope satisfying the Mizuguchi-Dragone condition. Initially, the LFI focal surface configuration included (in addition to the frequency channels at 30, 44 and, 70 GHz), also a channel at 100 GHz comprising seventeen horns distributed around the HFI front-end. The LFI 100 GHz channel was subsequently removed, but it was part of the initial study and much of the analysis was completed for this channel and applied to the lower frequencies. The position and orientation of each horn was determined by taking into account the mechanical constraints imposed by the LFI interfaces and 4 K reference loads attached to the HFI instrument (see Mandolesi et al. 2010) and assuming a Gaussian model. We emphasize that the simulations discussed in this paper were carried out by assuming a radio frequency model composed of the ideal telescope, the baffle, and the coldest V-groove thermal radiator (see Sandri et al 2002b). The current most suitable model of the detailed beams for both LFI and HFI, taking into account a realistic model of the telescope, are given in Tauber et al. (2010).

The assumed Planck telescope design and the focal surface layout are described in Sects. 2 and 3, respectively. In Sect. 4, edge-taper degradation of the horns is presented. The edge-taper was degraded to improve the angular resolution while maintaining straylight rejection to within the requirements. Section 5 presents the feedhorn alignment process, complete so that CMB polarization measurements can be made. In Sect. 6, given the edge-taper values and the location and orientation of the feeds detemined in the previous sections, each horn design was then optimized in terms of sidelobe level, cross polarization response, and beamwidth. This optimization was first carried out at 100 GHz, i.e., the most critical channel for LFI, and the results were extrapolated to lower frequencies, taking care to check the consistency at the end of the activity. Finally, the fully optimized performance of the LFI beams is reported in Sect. 7.

2 Telescope optical design

The Planck telescope was designed to comply with the following high level opto-mechanical requirements: wide frequency coverage (about two decades), 100 squared degrees of field of view, wide focal region ( $400 \times 600$ mm), and a cryogenic operational environment (40- 65 K). These unique characteristics for an experimental cosmology telescope have never been previously implemented. The Planck telescope represents a challenge for telescope technology and optical design (Villa et al. 2002; Tauber et al. 2010).

The telescope optical layout is based on a dual reflector off-axis Gregorian design. This configuration allows it to have a small overall focal ratio (and thus small feeds), an unobstructed field of view, and low diffraction effects from the secondary reflector and struts. It allows, at the same time, the secondary reflector to be appropriately oversized. To improve the image quality, the design has been optimized by changing the conic constants, the radius of curvature, the distance between the mirrors, and the tilting of both mirrors, using the spillover level and the wave front error as optimization parameters (Dubruel et al. 2000). The primary mirror is elliptical in shape (but nearly parabolic since the conic constant is about -0.9) as in aplanatic configurations (Wilson 1996), and the size of the rim is $1.9\times 1.5$ m. The offset of the primary reflector, i.e., the distance between its center and its major axis, is 1.04 m, while the secondary reflector offset is 0.3 m. The secondary mirror is elliptical with a nearly circular rim about 1 m in diameter. The overall focal ratio, $F_\char93 $, equals 1.1, and the projected aperture is circular with a diameter of 1.5 m. The telescope field of view is $\pm$5$^\circ$ centered on the line of sight (LOS), which is tilted at about 3.7$^\circ$ relative to the main reflector axis, and forms an angle of 85$^\circ$ with the satellite spin axis, which is typically oriented in the anti-Sun direction during the survey (Dupac 2008). The Planck telescope as a complete satellite subsystem is shown in Fig. 1 and a detailed description is reported in Tauber et al. (2010).

\begin{figure} \par\includegraphics[width=21pc,clip]{images/12891fg1.eps} \end{figure} Figure 1:

Lateral and top view of the telescope unit consisting of the reflectors and the support structure; the hexagonal support structure is readily seen as well as the field of view (in gray) (left panel). The telescope unit allocated into Planck satellite (right panel). The vertical axis is the spin axis of the satellite and the line of sight is tilted by $85^\circ $ with respect to the spin axis. The baffle around the telescope is not shown.

Open with DEXTER
\begin{figure} \par\begin{tabular}{c} \includegraphics[height=7.5cm,clip]{images... ...ncludegraphics[height=6.3cm,clip]{images/12891fg3.eps}\end{tabular} \end{figure} Figure 2:

A CAD model of the Planck focal plane, which is located directly below the telescope primary mirror. It comprises the HFI bolometric detector array (small feed horns on golden circular base) and the LFI radio receiver array (larger feed horns around the HFI). The box holding the feedhorns appears to be transparent in this view, to also show the elements inside and behind it ( top panel). The HFI and LFI feed horns are seen reflected in the primary mirror of the Planck telescope in the clean room at Kourou, French Guiana ( bottom panel). © ESA/Thales.

Open with DEXTER

3 LFI optical interfaces

In its flight configuration, LFI is coupled to the telescope by eleven dual-profiled, corrugated, conical horns (Villa et al. 2010): six feed horns at 70 GHz (FH18 - FH23), three feed horns at 44 GHz (FH24 - FH26), and two feed horns at 30 GHz (FH27 and FH28). Figure 2 shows the arrangement of the horns inside the LFI main frame. It should be noted that the feed position in the focal surface is axisymmetric (for instance, FH27 is symmetric to FH28 at 30 GHz), a natural design choice based on the symmetry of the telescope and satellite. As a consequence, only six different feed elements have been considered in the optimisation analysis: one feed at 30 GHz, two at 44 GHz, and three at 70 GHz (Villa et al. 2010). The center of the focal surface is occupied by the HFI horns. This optical layout, with one instrument (LFI) around the other (HFI), required that aberration effects in the LFI beams be accurately controlled in the telescope and instrument design optimization phases. Corrugated horns were selected as the most suitable solution in terms of cross polarization levels, sidelobes levels, return and insertion loss. Dual-profiled corrugation shaping was chosen for the control of the main lobe shape, the phase centre location, and compactness (Clarricoats 1984; Olver & Xiang 1988). The corrugation profile of each horn was designed to achieve a trade-off between angular resolution and straylight rejection. Each feed horn is connected to an orthomode transducer (OMT) to divide the field propagating into the horn into two orthogonal linear polarization components, X and Y (D'Arcangelo et al. 2010).

The feeds and corresponding OMTs are adjusted in the focal surface so that the main beam polarization directions of the two symmetrically located feed horns in the focal plane unit (FPU) are at an angle of 45 degrees when observed in the same direction in the sky. This configuration permits measurement of the Q and U Stokes parameters and thus the linear polarization of the CMB. The location and orientation of each horn is reported in Table 1, with respect to the reference detector plane (RDP) coordinate system, placed in the center of the FPU and with the $Z_{\rm RDP}$ axis aligned along the chief ray of the telescope.

The focal plane configuration is a result of a long iteration process. Apart from the horn aperture definition, which is the result of edge-taper optimization (see Sect. 4), the location, the orientation, and the length of the feed horns were determined on the basis of the mechanical interfaces, feed mutual obscuration, and pointing direction as derived form the telescope characteristics. The horn pointing was obtained from the optical study of the telescope and the tilting angles were derived by means of ray tracing simulations. This study was addressed at the end of the telescope optimization process when the focal plane design was not frozen. However, this was sufficient to derive analytical formulae for pointing that have been used in additional focal plane optimizations, ending with the final design. We consider the reference detector plane coordinate system $\left({X_{\rm RDP}}, {Y_{\rm RDP}}, {Z_{\rm RDP}}\right)$ as a starting point to define horn pointing. The horn pointing depends only on the $\left(X_{\rm RDP}, Y_{\rm RDP}\right)$ coordinates, while $Z_{\rm RDP}$ defines the phase centre location only. We also define the two rotation angles as $\alpha$ the rotation angle around ${Y_{\rm RDP}}$, and $\beta$ the rotation around ${X_{\rm RDP}}$ axis. For the Planck telescope, and in the region where the LFI feeds are located (i.e., outside the centre of the focal plane), the two angles were derived from a linear fit to the optical simulation results:

                $\displaystyle \alpha$ = $\displaystyle a_x \cdot X_{\rm RDP} + b_x,$ (1)
$\displaystyle \beta$ = $\displaystyle b_x \cdot Y_{\rm RDP} + b_y.$ (2)

The lengths of the horns were chosen to satisfy the following constraints: (i) to guarantee the interface specifications of the 4 K reference load (which are attached to the HFI instrument, and are thus a driver on the LFI focal plane interface design); (ii) to guarantee matching with both the focal surface and the obscuration criterion of the LFI horns. These criteria fixed the clearance as a cone of $45^\circ$ from the horn aperture rim. It was set after measurements performed by the LFI team (Ocleto et al 2009) and simulations performed by the industrial contractor[*]. In this way, it was possible to optimize the focal plane with the LFI CAD solid model without performing time consuming electromagnetic computations. Once the horn location and orientation were frozen, the phase centre position and the edge-taper were used as inputs to the corrugation design.

Table 1:   Location and orientation of the LFI feed horns.

4 Edge-taper evaluation

The angular resolution (expressed here in terms of full width half maximum, FWHM) of the beam in the sky depends on the illumination, g(x,y), of the primary mirror. For an aperture-type antenna (such as a reflecting telescope), the far field is the Fourier transform of the aperture illumination function. If a Gaussian illumination is assumed, the main beam shape is Gaussian too. The flatter the illumination, the narrower the resulting pattern; in contrast, if the illumination is more centrally peaked, then the angular resolution of the pattern is degraded. For a dual reflector telescope, the illumination function g(x,y) is produced by the feed-horn pattern, reflected and diffracted by the subreflector, and distorted by aberrations mainly due to the off-axis position of the feeds. This is the case for the LFI focal plane configuration. The trade-off between the angular resolution (which impacts the instrument's ability to reconstruct the anisotropy power spectrum of the cosmic microwave background radiation at high multipoles) and the edge-taper (which controls the systematic effect of straylight radiation) was identified as a critical design step. A preliminary analysis was carried out at the beginning of the optimization activity. The sidelobe level is determined by the edge-taper, which is defined to be the ratio of the power per unit area incident on the centre of the mirror (if the illumination is symmetrical, otherwise the maximum illumination is considered) to that incident at the edge. A strong taper (or a high value of the edge-taper) means a strong illumination beneath the reflector, which has a negative impact on the angular resolution. In contrast, increasing the illumination of the telescope (low values of the edge-taper) improves the angular resolution and degrades the straylight rejection of the telescope. The edge-taper can be modified by changing the feed-horn design, which controls the way in which the horn illuminates the telescope. The dependence of the angular resolution improvement on the edge-taper degradation is almost linear until a threshold is achieved, when increasing the illumination on the primary mirror no longer produces further improvement in the angular resolution. This is because a strong illumination of the mirrors increases the aberrations of the main beam. Obviously, the amount of improvement depends on the feed-horn location, since the primary mirror is illuminated in a different way.

\begin{figure} \par\includegraphics[height=9cm,angle=90,clip]{images/12891fg4.ps} \end{figure} Figure 3:

Simulated co-polar pattern, in the E- plane, of the FM feed horns at 70 (FH21, FH22, and FH23), 44 (FH24 and FH25), and 30 (FH27) GHz assuming the designed profile.

Open with DEXTER

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=3.9cm,height=3cm,... ...s[width=3.9cm,height=3cm,clip]{images/12891fg6.ps}\\ \end{tabular} \end{figure} Figure 4:

10 dB contour of all horn patterns on the sub (left panel) and main (right panel) reflectors: the contours corresponding to the 30 GHz patterns are pink, the 44 GHz contours are blue, and those at 70 GHz are green.

Open with DEXTER
A preliminary study of the primary mirror edge-taper of the Planck telescope baseline configuration was performed by computing the field distribution on the primary mirror for each feed horn. The simulations was carried out in the transmitting mode (i.e., the horn was treated as a source) using GRASP8[*]. The model of the feed that we used is a X-axis polarized Gaussian horn with an edge-taper of 30 dB at an angle of 22 degrees. The contour plots of the total amplitude field incident on the main reflector were produced for each feed horn considered. Geometrical optics (GO) and the geometrical theory of diffraction (GTD) were used on the sub-reflector to calculate the total amplitude of the field incident on the surface of the primary mirror, in the reference system of the main beam. The resulting contour plots showned that, as expected, the illumination of the primary mirror is roughly elliptical. As a consequence, the field amplitude on the primary mirror rim is not constant. The amplitudes of the field on the main reflector contour were used to set the requirements on the edge-taper values for all the LFI feed-horn illuminations. The field amplitude on the mirror contour is a function of the angle $\varphi$ ( $E = E(\varphi)$), defined in the reference system of the main beam ( $\varphi = 0$ in the direction of the top edge of the main reflector, in an anti-clockwise direction). The edge-taper of each feed, at a reference angle (22$^\circ$ or 24$^\circ$), was chosen by comparing the field amplitude, $E(\varphi)$, with that corresponding to a worst reference case, $\tilde{E}(\varphi)$. A full straylight analysis was performed for this worst case and measured acceptable contamination levels from the Galactic emission (Burigana et al. 2001). The edge-taper correction of each feed horn, to ensure a straylight rejection analogous to the reference case, was calculated by computing the lowest difference between the edge-taper curve of each feed and the reference edge-taper curve ( $min\vert E(\varphi)- \tilde{E}(\varphi)\vert$). We then decrease by this difference the horn's edge-taper at the reference angle. In this way, for each LFI feed horn, no single point on the main reflector rim has an edge-taper value lower than that of the reference case. Figure 5 compares the field distribution on the Planck mirrors for a 70 GHz Gaussian feed horn and for the flight model case, nominal edge-tapers being equal. Figure 6 shows the difference between the fields in the two cases, and Fig. 7 reports the edge-taper curves defined on the primary mirror. From the latter figure, it can be inferred that a first optimization of the feed horn edge-taper carried out using a Gaussian approximation is sufficient for the edge-taper definition, and it allows time to be saved since it is independent of the internal corrugation profile of the horns being study.

\begin{figure} \par\begin{tabular}{cc} \includegraphics[width=3.9cm,clip]{images... ...udegraphics[width=4.2cm,clip]{images/12891fg10.ps}\\ \end{tabular} \end{figure} Figure 5:

Field distribution on Planck mirrors (the sub-reflector is on the left and the main reflector is on the right) for a 70 GHz feed horn assuming a Gaussian feed approximation ( $E_{\rm GM}(\theta ,\varphi )$, first row) and the flight model feed horn ( $E_{\rm FM}(\theta ,\varphi )$, second row).

Open with DEXTER

\begin{figure} \par\begin{tabular}{l l} \includegraphics[width=3.6cm,clip]{image... ...cludegraphics[width=4cm,clip]{images/12891fg12.ps}\\ \end{tabular} \end{figure} Figure 6:

Difference in the field distribution on the Planck mirrors between computations with the flight model feed and the Gaussian approximation. Differences data are in percent (( $E_{\rm FM}(\theta ,\varphi )-E_{\rm GM}(\theta ,\varphi ))/E_{\rm GM}(\theta ,\varphi )$). The color scale goes from black (minimum value) to red (maximum value). For the sub-reflector, the color scale goes from 0 to 200% and the white region on the lower part of the reflector is off the of scale since the differences are enormous. For the main reflector, the colour scale goes from 0 to the maximum value, i.e., 37.56%.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{images/12891fg13.ps} \end{figure} Figure 7:

Edge-taper curve on the primary mirror computed assuming a Gaussian illumination (red curve) and a realistic illumination (blue curve). The nominal edge-taper of the two feeds is the same: 17 dB at 22 degrees.

Open with DEXTER

5 Polarization alignment

The main beams were computed in UV-spherical polar grids, in which $u = \sin \theta_{\rm bf} \cdot \cos \phi_{\rm bf}$ and $v = \sin \theta_{\rm bf} \cdot \sin \phi_{\rm bf}$ and the subscript bf means beam frame to indicate that each main beam was computed in its own coordinate system. These frames are defined starting from considerations, described below, that are related to the main beam polarization. In each point of the UV-grid, the far field was computed in the co- and cross-polar basis according to Ludwig's third definition (Ludwig 1973). Although the simulated beams are computed as the far-field angular transmission function of a highly polarized radiating element in the focal plane, the far-field pattern is in general no longer linearly polarized, but a spurious component, induced by the optics, is present. The co-polar pattern is interpreted as the response of the linearly polarized detector to radiation from the sky that is linearly polarized in the direction defined as co-polar, and the same is true for the cross-polar pattern, where the cross-polar direction is orthogonal to the co-polar one. Therefore, the main beams can be shown with a contour plot of the co-polar pattern ( $E_{\rm cp}$), a contour plot of the cross-polar pattern ( $E_{\rm xp}$), or a contour plot of the total field ( $E_{\rm far}$). The adopted beam frame reference, in which each main beam was computed, implies that: i) the power peak of the co-polar component lies in the center of the UV-grid; and ii) a minimum in the cross-polar component appears at the same point (i.e., the major axis of the polarization ellipse is along the U-axis). This means that, very close to the beam pointing direction, the main beam can be assumed to be linearly polarized, and the X- axis of the beam frame can be assumed to be the main beam polarization direction.

\begin{figure} \par\includegraphics[width=8cm,clip]{images/12891fg14.eps} \end{figure} Figure 8:

Footprint of the LFI focalplane on the sky as seen by an observer looking towards the satellite along its optical axis. The origin of a right-handed uv-coordinate system is at the center of the focalplane (LOS). The z-axis is along the line-of-sight and points towards the observer. Labels from 18 to 23 refer to 70 GHz horns, from 24 to 26 refer to 44 GHz horns, and 27 and 28 refer to 30 GHz horns. Each beam has its own coordinate system as shown in the figure. The focalplane scans the sky as the satellite spins. The scanning direction is indicated by an arrow. The +u axis points to the spin axis of the satellite. The centers of the 30 GHz beams sweep about 1 degree from the ecliptic poles when the spin axis is in the ecliptic plane.

Open with DEXTER

The LFI radiometers are intrinsically linearly polarized, and by combining the signal received by several detectors it is possible to retrieve the Stokes parameters, U and Q, with particularly high sensitivity in the regions close to the ecliptic poles. LFI polarization properties were optimized by rotating the feed horns (and the connected OMTs) about their axes to compensate for the offset introduced by the Planck telescope optics and to obtain the desired orientation of the beams' polarization. The rotation of the spacecraft around its spin axis was considered, and the orientation of the polarization direction of each beam in the sky was taken into account such that the main beam polarization of two symmetrically located feed horns are at 45 degrees to each other when observing the same direction in the sky. Polarization orientations of the LFI horns are reported in Table 1 ( $\psi_{\rm RDP}$ angle), polarization orientations of the corresponding main beams in the sky are reported in Table 2 ( $\psi_{\rm MB}$ angle), and the rotation angle of the polarization ellipse computed along the line of sight of each beam (i.e., in the center of the UV-grid) is reported in Table 3 ($\tau$ angle, ranges from -90$^\circ$ to 90$^\circ$).

6 Trade-off between angular resolution and straylight

The final trade-off between angular resolution and straylight has been a long and complex process throughout the project development. For each LFI feed horn, several beams have been computed for the radiation patterns corresponding to different geometries (i.e. inner corrugation profile) of the horn itself (Sandri et al. 2004). Then, each beam was convolved with the microwave sky (CMB and foregrounds), taking into account the Planck scanning strategy in the (nominal) fifteen months observational time, and the straylight noise induced by the Galaxy, which has been derived (Burigana et al. 2004). From the comparison between these straylight values, and taking into account the beam characteristics, the optimal horn design was selected for the flight models. In this framework, the inadequacy of a pure Gaussian feed model in realistic far beam predictions has been demonstrated: relevant features in the beam are related to the sidelobes in the feed horn pattern. Not only does the realistic pattern need to be considered, but the details of the corrugation design could also affect the beam characteristics. The edge-taper being equal, different corrugation profiles involve differences of about 3% in the main beam size and about 40% in the straylight signal. It has been demonstrated that not only the spillover level is crucial, but also how the spillover radiation is distributed in the sky, and thus sophisticated pattern simulations are required to accurately quantify the beam aberrations and the straylight contamination.

Finally, while the main beam is highly polarized (greater than 99% linearly polarized, i.e., the cross-polar component is always 25 dB below that of the co-polar component), the computed 4$\pi $ beams have shown that the co- and cross-polar components in the sidelobe region may have the same intensity. Therefore, the cross-polar component will contaminate the co-polar component of the orthogonal polarization. This is particularly important at lower frequencies where the Galactic emission is strongly polarized. In other words, the strongly polarized Galactic emission collected through the sidelobes into the two polarized detectors is added to the slightly polarized CMB field entering the feed horn from the main beam direction. However, because of the rapid spatial variability in both the sky polarized emission and the polarized pattern, the polarized sidelobe contribution will probably average out to a significant degree.

7 LFI main beams

Table 2:   Main beam frames.

Table 3:   Main beam characteristics at the central frequency.

Once the location and orientation of the feed horns, as well as their inner corrugation profile, had been properly defined, we carried out a full characterisation of the optical performance using electromagnetic simulations devoted to computing the LFI beams. The beam solid angle, $\Omega_{\rm A}$, of an antenna is given by

\begin{displaymath}\Omega_{\rm A} = \int_{4\pi} P_n(\theta, \phi) \mbox{ d}\Omeg... ...i P_n(\theta, \phi) \sin \theta \mbox{ d}\theta \mbox{ d}\phi, \end{displaymath} (3)

where $P_n(\theta, \phi)$ is the normalized power pattern and the field computed by GRASP is normalised to a total power of 4$\pi $ watt, i.e.,

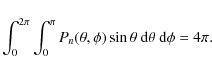
\begin{displaymath}\int_0^{2\pi} \int_0^\pi P_n(\theta, \phi) \sin \theta \mbox{ d}\theta \mbox{ d}\phi = 4\pi. \end{displaymath}

For most antennas, the normalized power pattern has considerably larger values for a certain range of both $\theta$ and $\phi$ than for the remaining part of the sphere. This range is called the main beam and the remainder is called the sidelobes or back lobes. Obviously the quality of an antenna as a directional measuring device depends on how well the power pattern is concentrated in the main beam. The received power originating in region outside the main beam is called straylight, and it is one of the major sources of systematic effects in the Planck observations and for CMB experiments in general. In the next section, the sidelobes of the LFI beams are presented, together with the straylight-induced noise evaluated from these beams. The separation of the power pattern into a main beam and sidelobes can be somewhat arbitrary and is basically governed by convention. Different definitions of these regions could in principle be used: electromagnetic definitions, science-related definitions, and simulation-related definitions. In the framework of the present simulations, the main beam region was defined by taking care that not only the relevant main beam characteristics are computed (angular resolution, ellipticity, directivity, cross polar discrimination factor, and so on), but also that the main beam distortion, at a level of about -60 dB (mainly due to the off-axis location of the LFI feed horns), can be evaluated. This involves longer computational times but ensures a superior knowledge of the systematic effects related to the LFI main beams. The main beam simulations are performed by considering the feed as a source, and by computing the pattern scattered by both reflectors onto the far field with GRASP8 using physical optics (PO) and physical theory of diffraction (PTD) for both reflectors. We assumed an ideal telescope and computed main beam and sidelobe properties for each channel, taking into account the effects of the surrounding structures.

7.1 LFI main beam characterisation

Far field radiation patterns were computed on the co- and cross-polar basis according to Ludwig's third definition in UV-spherical grids. We computed the main beam angular resolution of each feed model analysed, as well as all major electromagnetic characteristics reported in Tables 2 and 3. U ( $\sin\theta \times \cos\phi$) and V ( $\sin\theta \times \sin\phi$) range from -0.026 to 0.026 ( $\theta \leq 1.5^\circ$) for the 30 and 44 GHz channels, and from -0.015 to 0.015 ( $\theta \leq 0.9^\circ$) for the 70 GHz channel. Each grid has been sampled with $301 \times 301$ points, therefore $\Delta U = \Delta V \simeq 1.7 \times 10^{-4}$ for the 30 and 44 GHz channels and 10-4 for the 70 GHz channel. In Table 2, the coordinate systems in which each main beam was computed are reported: $U_{\rm MB}$ and $V_{\rm MB}$ correspond to the centre of the UV-grids shown in this section. In Table 3, relevant main beam characteristics computed at the central frequency are summarized, such as the full width half maximum, the cross polar discrimination factor, and the main beam depolarization parameter. In Fig. 9, the contour plot in the UV-plane of the co- and cross-polar components is shown for the main beam #27 and #28 (Y-polarized). The lines in the contour plots, normalized with respect to the power peak (the directivity reported in Table 3 for the co-polar plot and the directivity minus the XPD for the cross- polar plot), are at -3, -10, -20, -30, -40, -50, and -60. The colour scales goes from -90 to 0 dB. Figure 10 shows the differences between the two polarization X- and Y- for the main beam #27, which are imperceptible below -40 dB. In Figs. 11 and 12, the contour plot in the UV-plane of the co- and cross-polar components is shown for the main beam #24, #26, #21, #22, and #23 (Y-polarized), respectively.

The cross-polar response of the OMT affects the beam pattern in a significant way below the -40 dB contour since the co-polar component is a linear combination of the co- and cross-polar pattern with coefficients of about 1 and 10-4. A detailed study of the LFI polarization capability is reported in Leahy et al. (2010).

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg18.ps}\\ \end{tabular} \end{figure} Figure 9:

Contour plot in the UV-plane ( -0.026 < U,V < 0.026) of the main beam co-polar (left side) and cross-polar (right side) component computed for the 30 GHz feed horns #27 (first row) and #28 (second row), assuming an ideal telescope. The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 32.58$^\prime $ in both cases. The two beams are perfectly symmetric with respect to the U-axis because of the symmetry of the Planck LFI optics. The lines in the contour plots represent levels of at -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg20.ps}\\ \end{tabular} \end{figure} Figure 10:

Contour plot in the UV-plane of the differences between the main beam #27 computed assuming the X-polarized feed and the main beam computed assuming the Y-polarized feed. The differences in the co- (left side) and cross- (right side) polar components are normalized to the local amplitude and expressed in dB. Table 3 quantitatively shows the differences between the two polarizations of the same feed.

Open with DEXTER

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg24.ps}\\ \end{tabular} \end{figure} Figure 11:

Contour plot in the UV- plane ( -0.026 < U,V < 0.026) of the main beam co- (left side) and cross- (right side) polar components computed for the feed horns #24 (first row) and #26 (second row). The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 22.82 and 28.90, respectively. The lines in the contour plots represent levels of -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=10pc,clip]{images... ...ludegraphics[width=10pc,clip]{images/12891fg30.ps}\\ \end{tabular} \end{figure} Figure 12:

Contour plot in the UV-plane ( -0.015 < U,V < 0.015) of the main beam co- (left side) and cross- (right side) polar components computed for the feed horns #21 (third row), #22 (fourth), and #23 (fifth row). The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 12.49, 12.71, and 13.05 arcmin, respectively. The lines in the contour plots represent levels of -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER

8 LFI sidelobes

Power that does not originate in sources located in the main beam direction (i.e, the straylight) enters detectors through the sidelobes of the radiation pattern generating a signal that may be indistinguishable from signals induced by CMB fluctuations in the main beam. More than the spurious signal itself, fluctuations in the straylight signal contaminate the measurements mainly on large and intermediate angular scales (i.e., at multipoles $\ell$ less than $\approx$100), and must be kept below a level of few $\mu$K (the required straylight rejection levels must be at about 10-9, 10-7, and 10-6 for the Sun, Earth, and Galactic plane, respectively). The control of this systematic effect was achieved by accurate predictions of the LFI beams.

In principle, Physical optics is the most accurate method for predicting beams and may be used in all regions surrounding the reflector antenna system. Neverthless, as the frequency increases the reflectors need to be more precisely sampled. In addition, a finer integration grid is required because in the sidelobe region, the PO integrand becomes increasingly oscillatory. For a two-reflector antenna system such as Planck, the computation time increases as the fourth power of the frequency, and sidelobe simulations would be impractical for LFI. Although a full PO computation would be required to predict accurately the antenna pattern of the telescope, this is not feasible for the full spacecraft simulations since the PO approach cannot be applied correctly within a reasonable time when multiple diffractions and reflections between scatterers are involved. For this reason, the GRASP8 multi-reflector GTD (MrGTD) was used to compute 4$\pi $ beam. MrGTD computes the scattered field from the reflectors performing a backward ray tracing, and represents a suitable method for predicting the full-sky radiation pattern of complex mm-wavelength optical systems in which the computational time is frequency-independent.

8.1 LFI sidelobe characterisation

\begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg32.ps}\end{tabular}\end{figure} Figure 13:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 30 GHz (feed horn #27 Y polarized) computed with MrGTD. The maximum level of the main spillover is about -4.6 dBi at $\phi \simeq 17^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and about -8.0 dBi at $\phi \simeq 18^\circ $ and $\theta \simeq 86^\circ $ for the cross-polar component.

Open with DEXTER

To first approximation, the efficiency of an optical system in rejecting external straylight contamination is quantified by the fractional amount of power entering far from the main beam in the case of an isotropic signal. We provide here this information for all LFI beams in terms of relative (percent) contributions from the intermediate and far beam to the beam $4\pi$ integral. The intermediate beam includes here the region at angles between $0.8^\circ$ ($1^\circ$, $1.2^\circ$, respectively) and $5^\circ$ from the beam centre for the beams at 70 (resp. 44, 30) GHz, while the far beam includes the regions at angles greater than $5^\circ$ from the beam centre. The main, intermediate, and far beams are known in tabulated form and with different resolutions. Thus, the accuracy in the computations of their integrals cannot be extremely high. We exploited three different numerical methods and compared the corresponding results: (i) a 2D quadrature in $\theta$ and $\phi$, performed with the routine D01DAF of the Mark 21 version of the NAG numerical library; (ii) a combination of two 1D quadratures, a Gaussian quadrature (adapted in double precision and with 2048 grid points) from Press et al. (1992) for the integral in $\theta$ and the NAG routine D01AJF for the (more difficult) integral in $\phi$; (iii) a summation over the relevant pixels of the beam responses projected into a map at $n_{\rm side} = 256$ or 1024 in the HEALPix[*] scheme (Gorski et al. 2005) for the far beam or for the intermediate and main beam, respectively. A robust bilinear interpolation is adopted to estimate the beam response between tabulated points. Methods (ii) and (iii) give consistent (i.e., with relative differences always less than 0.08%) results for the far beams and we report here their average (while method (i) provides only a rough estimate, in agreement with the others only within a factor of $\sim$2, because of its relatively poorer sampling of the 2D function). All methods give very consistent results for the main beams (agreement level always superior to 0.04% for methods (i) and (ii) and better than 2.3% for methods (i) - or (ii) - and (iii)). For the intermediate beams, the level of agreement between the results obtained with the three methods depends significantly on the beam considered and ranges from 0.1% to 15%, being on average several percent. We report here the results based on method (ii), which samples the 2D function more effectively and allows good control of integration accuracy. Obviously, the true accuracy depends on the beam sampling

The results are summarized in Table 4, where we also provide predictions for the Galactic straylight contamination. For each (normalized to the maximum power measured in the field, i.e., the main beam power peak) LFI FM beam (Cols. 1 and 2) we report: the $4\pi$ integral as the sum (the global integral GI, Col. 3) of the contributions from the main, intermediate, and far beam and the relative (percent) contributions to it from the intermediate ( IB, Col. 4) and far ( FB, Col. 7) beam. The transition between intermediate and far beam was adopted here at $0.8^\circ$, $1^\circ$, and $1.2^\circ$ from the beam centre, respectively, at 70 GHz, 44 GHz, and 30 GHz. Columns 5 and 6 (respectively, 8 and 9) report the Galactic straylight contamination ( GSC, in $\mu$K RMS and peak-to-peak antenna temperature) evaluated considering the intermediate (respectively, far) pattern region. The RMS and peak-to-peak values reported in the table were estimated by a proper rescaling of the results presented in Burigana et al. (2004) considering the fractional contributions to the $4\pi$ integrated antenna pattern from intermediate and far beams and the frequency behaviour of the considered foreground components (diffuse dust, free-free, and synchrotron emission, and HII regions).

In principle, the straylight contamination from the CMB dipole is important only for the even multipoles, where it is expected to dominate over the Galactic one at frequencies greater or equal to 44 GHz (Burigana et al. 2006). Given the fractional contributions from the far sidelobes to the $4\pi$ integrated antenna pattern reported in Table 4, we expect that dipole straylight will not significantly affect the recovery of the angular power spectrum at low multipoles and the analysis of large-scale anomalies (Gruppuso et al. 2007), provided that the relative uncertainty in the modelling of the far sidelobes is $\la $20%.

Table 4:   Galactic straylight contamination.

\begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg34.ps}\end{tabular}\end{figure} Figure 14:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 44 GHz (feed horn #24 Y polarized) computed with MrGTD. The maximum level of the main spillover is about -5.4 dBi at $\phi = 0^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and the cross-polar component is down to -15 dBi everywhere.

Open with DEXTER

\begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg36.ps}\end{tabular}\end{figure} Figure 15:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 70 GHz (feed horn #23 FM, Y polarized) computed with MrGTD. The maximum level of the main spillover is about -1.8 dBi at $\phi \simeq 10^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and the cross-polar component is, in the main spillover region, at about -4.8 dBi.

Open with DEXTER

9 Conclusions

From the beginning of the Phase A study to the current flight configuration, we have reported reported the history of the optimization of the LFI optical interface. The definition, optimization, and characterization of the LFI feed horns coupled the Planck telescope have been derived by means of electromagnetic simulations devoted to maximizing the angular resolution and at the same time minimizing systematic effects produced by the sidelobes of the radiation pattern. The position and orientation of each horn was set taking into account the mechanical constraints imposed by the LFI interfaces and the 4 K reference loads. The feeds and corresponding OMTs have been adjusted in the focal surface in such a way that the main beam polarization directions of the two symmetrically located feed horns in the FPU are at an angle of 45 degrees when they observe the same direction in the sky, in order to measure the Q and U Stokes parameters and thus the linear polarization of the CMB. Finally, the LFI optical performance computed with the ideal telescope has been presented. The requirements have been met and in some cases exceeded. Typical LFI main beams have angular resolutions of about 33$^\prime $, 24$^\prime $, and 13$^\prime $, respectively, at 30 GHz, 44 GHz, and 70 GHz, slightly exceeding the requirements for the cosmological 70 GHz channel. The beams have been delivered to the LFI data processing center and they are the current baseline data used in the testing of the data reduction pipeline. Of course, the performance in-flight will be different owing to the true telescope and focal surface alignment, the surface roughness, and the distortion of the reflectors caused by the cooldown. However, simulations on the Planck radio frequency flight model (Tauber et al. 2010) have shown that the LFI performance is quite similar to the ideal case, so values reported in the tables of this paper (beam characteristics and straylight contamination) are presumably not far from the true values.

Acknowledgements

Planck is a project of the European Space Agency with instruments funded by ESA member states, and with special contributions from Denmark and NASA (USA). The Planck-LFI project is developed by an International Consortium lead by Italy and involving Canada, Finland, Germany, Norway, Spain, Switzerland, UK, USA. The Italian contribution to Planck is supported by the Italian Space Agency (ASI). We wish to thank people of the Herschel/Planck Project of ESA, ASI, THALES Alenia Space Industries, and the LFI Consortium that are involved in activities related to optical simulations. Some of the results in this paper have been derived using the HEALPix (Górski, Hivon, and Wandelt 1999). Special thanks to Denis Dubruel (THALES Alenia Space), for his professional collaboration in all these years. We warmly thank David Pearson for constructive comments and suggestions, and for the careful reading of the first version of this work.

Appendix A: Main beam descriptive parameters

Owing to the telescope configuration and the feed horn off-axis location on the focal surface, the main beams are strongly distorted and their shape differs from a Gaussian. In other words, the main beams cannot be mathematically represented by a single parameter (for instance, the full width half maximum) and by a simple formula (Gaussian function, polynomial function) because aberrations prevail at power levels lower than -10 dB. However, it is indispensable to characterize the main beams as precisely as possible, and several descriptive parameters have been evaluated: the angular resolution (FWHM), the ellipticity (e), the main beam directivity ($\cal D$), the cross polar discrimination factor (XPD), the depolarization parameter (d), the rotation angle of the polarization ellipse ($\tau$), and the main spillover ($\cal S$).

A.1 Angular resolution

For CMB anisotropy measurements, an effective angular resolution can be defined as the FWHM of a perfect (symmetric Gaussian) beam, which produces the same signal as the distorted beam when the CMB field is observed (Burigana et al. 1998). Nevertheless, this definition involves astrophysical simulations taking into account the scanning strategy and the CMB expected anisotropy map (or the WMAP results). Owing to the large computation time, this approach is not practical for the optimization activity of the LFI feed horns.

Main beam aberrations degrade its angular resolution. Instead of the effective FWHM, the angular resolution can be evaluated by taking the average FWHM of the distorted beam. The average FWHM has been computed in three different ways, using the minimum and maximum values:

  • arithmetic average: by taking the average value between the maximum and minimum of the FWHM of the distorted beam:

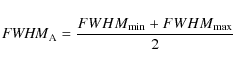
    \begin{displaymath}{{\it FWHM}}_{\rm A} = \frac{{{FWHM}}_{\rm min}+ {{FWHM}}_{\rm max}}{2}\end{displaymath}

  • quadratic average: by taking the quadratic mean between the maximum and minimum of the FWHM of the distorted beam:

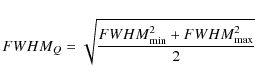
    \begin{displaymath}{{FWHM}}_Q = \sqrt{\frac{{{FWHM}}_{\rm min}^2+ {{FWHM}}_{\rm max}^2}{2}}\end{displaymath}

  • equal area average[*]: the distorted beam exhibits the same beam area of a symmetric beam with a FWHM defined as:

    \begin{displaymath}{{\it FWHM}}_E = \sqrt{{{\it FWHM}}_{\rm min} \cdot {{\it FWHM}}_{\rm max}}.\end{displaymath}

The differences between the three average values are about 2.8% at 30 GHz, 2.5% at 44 GHz, and less than 1.3% at 70 GHz. It is noticed that the arithmetical average value is in-between the other two values, and small differences exist between the FWHM$_{\rm A}$ and the arithmetic mean of FWHMQ and FWHME. The average can be written as a function of the ellipticity (e, computed as the ratio of the maximum to minumum values of the beam width at -3 dB) in the following way:

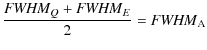
    $\displaystyle \frac{{{\it FWHM}}_Q + {{\it FWHM}}_E}{2} = {{\it FWHM}}_{\rm A}$  
    $\displaystyle \qquad-\left[ \frac{1}{2} \cdot {{\it FWHM}}_{\rm min} \cdot \left( 1 + e - \sqrt{e} - \frac{\sqrt{2}}{2} \sqrt{1+e^2} \right) \right]$ (A.1)

or alternatively:
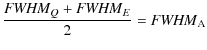
    $\displaystyle \frac{{{\it FWHM}}_Q + {{\it FWHM}}_E}{2} = {{\it FWHM}}_{\rm A}$  
    $\displaystyle \quad -\left[ \frac{1}{2} \cdot {{\it FWHM}}_{\rm max} \cdot \lef... ...t{\frac{1}{e}} - \frac{\sqrt{2}}{2} \sqrt{1+\frac{1}{e^2}} \right) \right]\cdot$ (A.2)

The term between the inner brackets is small ($\simeq$10-4-10-5), and it is zero in the case of perfect symmetric beam (e = 1). Although it is important to include in the data analysis the detailed information of the beam shape, these small differences are not a concern for the angular resolution requirements, and the adopted angular resolution is the FWHM computed arithmetically (FWHM$_{\rm A}$).

A.2 Directivity and gain

Directivity is the ability of an antenna to focus energy in a particular direction when transmitting, or when receiving to receive energy preferentially from a particular direction. In a realistic, but lossless antenna (i.e., of efficiency $\eta \sim 1$), the directivity D $(\theta,\phi)$ is essentially equal to the gain G $(\theta,\phi)$:

\begin{displaymath}{G}(\theta,\phi) = \eta \cdot {D}(\theta,\phi) \sim \frac{4\pi P(\theta,\phi)}{\int\int P(\theta,\phi) \mbox{ d}\Omega}\cdot \end{displaymath} (A.3)

Thus, gain or directivity is also a normalized power pattern similar to Pn in Eq. (3) with the difference that the normalizing factor is $\int P(\theta,\phi) \mbox{d}\Omega/4\pi$. Substituting Eq. (3) into Eq. (A.3), it is easy to see that the maximum directive gain $G_{\rm max}$, improperly called directivity $\cal D$, can be expressed as

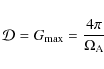
\begin{displaymath}{\cal D} = {G}_{\rm max} = \frac{4 \pi}{\Omega_{\rm A}} \end{displaymath} (A.4)

where $G_{\rm max}$ is the maximum value of the far field amplitude radiation pattern computed by GRASP8

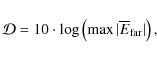
\begin{displaymath}{\cal D} = 10 \cdot \log \left( \max \vert\overline E_{\rm far}\vert \right), \end{displaymath} (A.5)

and $\overline E_{\rm far} = (\vert E_{\rm cp}\vert^2 + \vert E_{\rm xp}\vert^2)$, and $\cal D$ is defined in dBi, which is decibels referenced to an isotropic radiator.

A.3 Cross polar discrimination factor

The cross polar discrimination factor (XPD, usually expressed in dB) was computed as the ratio of the directivity to the co- and cross-polar components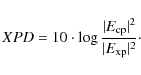

\begin{displaymath}XPD = 10 \cdot \log \frac{\vert E_{\rm cp}\vert^2}{\vert E_{\rm xp}\vert^2}\cdot \end{displaymath} (A.6)

A.4 Depolarization parameter

The depolarization parameter (d) was obtained by computing the Stokes parameters in each point of the regular UV- grid:

                                 SI(u,v) = $\displaystyle E_{\rm cp}(u,v)^2 + E_{\rm xp}(u,v)^2$ (A.7)
SQ(u,v) = $\displaystyle E_{\rm cp}(u,v)^2 - E_{\rm xp}(u,v)^2$ (A.8)
SU(u,v) = $\displaystyle 2 \cdot E_{\rm cp}(u,v) \cdot E_{\rm xp}(u,v) \cdot \cos [\delta \phi (u,v)]$ (A.9)
SV(u,v) = $\displaystyle 2 \cdot E_{\rm cp}(u,v) \cdot E_{\rm xp}(u,v) \cdot \sin [\delta \phi (u,v)]$ (A.10)

in which $E_{\rm cp}$ and $E_{\rm xp}$ are the amplitude field of the co-polar and cross-polar components, respectively, and $\delta \phi$ is the phase difference between the co-polar and cross-polar fields. Then, over the whole UV-plane, each parameter was summed:
$\displaystyle S_N = \sum_{(u,v)} S_N(u,v) \cdot \Delta u \Delta v \mbox{\hspace{1cm} where}\quad N=I,Q,U,V$     (A.11)

and, finally
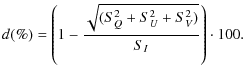
$\displaystyle {d(\%)} = \left( 1 - \frac{\sqrt{(S_Q^2+S_U^2+S_V^2)}}{S_I} \right) \cdot 100.$     (A.12)

A.5 Rotation angle

The rotation angle of the polarization ellipse ($\tau$, ranges from -90$^\circ$ to 90$^\circ$) is computed as

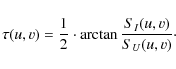
\begin{displaymath}\tau(u,v) = \frac{1}{2} \cdot \arctan \frac{S_I(u,v)}{S_U(u,v)}\cdot \end{displaymath} (A.13)

In Fig. A.1, the rotation angles of the 70 GHz main beam #21 and the 44 GHz main beam #24 (both X-polarized) are shown and it should be noted that the main beam is mainly linear polarized close to the main beam pointing direction, as discussed in Sect. 5.

\begin{figure} \par\begin{tabular}{c c} \includegraphics[width=4.2cm,bb=100 368 ... ...dth=4.2cm,bb=100 368 510 793]{images/12891fg38.ps}\\ \end{tabular} \end{figure} Figure A.1:

Polarization angle of the main beam #21 at 70 GHz (left side) and main beam #24 at 44 GHz (right side).

Open with DEXTER

A.6 Spillover

By means of simple ray-tracing, the main beam spillover (which points towards the Galactic plane) can be evaluated quickly for each feed model, taking into account the radiation pattern of the feed and the geometry of the optical system. This is a first approximation to the true spillover since it takes into account only the rays reflected by the subreflector that do not hit the main reflector.

A more precise but time-consuming computation of the spillover was performed using physical optics and the results are very similar. With PO, the spillover was computed as 1 - W, where W is the relative power hitting the main reflector. The power contained in the incident field on the main reflector is computed by integrating Poynting's vector P over the surface:

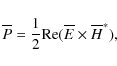
\begin{displaymath}\overline P = \frac{1}{2} {\rm Re} (\overline E \times \overline H^*), \end{displaymath} (A.14)

where Re denotes the real part and * the complex conjugate. The power $\Delta W$ hitting a surface element with area $\Delta s$ becomes

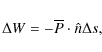
\begin{displaymath}\Delta W = - \overline P \cdot \hat{n} \Delta s, \end{displaymath} (A.15)

where $\overline P$ is the Poynting vector of the incident field and $\hat{n}$ is the unit surface normal pointing towards the illuminated side of the surface. The total power W on the surface becomes

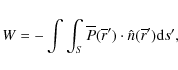
\begin{displaymath}W = - \int \int_S \overline P(\overline r^\prime) \cdot \hat{n} (\overline r^\prime) {\rm d}s^\prime, \end{displaymath} (A.16)

which is a surface integral with the integration variable $(\overline r^\prime)$.



References

  1. Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Burigana, C., Maino, D., Mandolesi, N., et al. 1998, A&AS., 130, 551 [Google Scholar]
  3. Burigana, C., Maino, D., Górski, K. M., et al. 2001, A&A, 373, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Burigana, C., Sandri, M., Villa, F., et al. 2004, A&A, 428, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Burigana, C., Gruppuso, A., & Finelli, F. 2006, MNRAS, 371, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  6. Clarricoats, P. J. B., & Olver, A. D. 1984, Corrugated horns for microwave antennas, IEE, London [Google Scholar]
  7. D'Arcangelo, O., Figini, L., Simonetto, A., et al. 2010, JINST, 4, T12007 [Google Scholar]
  8. Dubruel, D., Cornut, M., Fargant, et al. 2000, ESA Conf. Proc. SP-444, ed. D. Danesy, & H. Sawaya, CD-ROM [Google Scholar]
  9. Dupac, X. Baseline observation strategy definition document, Planck/PSO/2006-030, Rev 2 [Google Scholar]
  10. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gruppuso, A., Burigana, C., & Finelli, F. 2007, MNRAS, 376, 907 [NASA ADS] [CrossRef] [Google Scholar]
  12. Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Leahy, J. P., Bersanelli, M., D'Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Ludwig, A. C. 1973, The Definition of Cross Polarization, IEEE Transactions on Antennas and Propagation, 116 [Google Scholar]
  15. Maino, D., Burigana, C., Górski, K. M., Mandolesi, N., & Bersanelli, M. 2002, A&A, 387, 356 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
  17. Nielsen, P. H., RF Effect of Core Print-through Distortion on the Planck Telescope, PL-COM-DRI-AN-MIR012 [Google Scholar]
  18. Olver, A. D., & Xiang, J. 1988, IEEE Trans. On Antenna Propagation, 36, 936 [NASA ADS] [CrossRef] [Google Scholar]
  19. Pontoppidan, K. 1999, Technical Description of GRASP8, TICRA [Google Scholar]
  20. Press, W. H., Flannery, B. P., Teukolski, S. A., & Vetterling, W. T. 1992, Numerical Recipes (Cambridge University Press) [Google Scholar]
  21. Sandri, M., & Villa, F 2002, Int. Rep. INAF-IASFBO/342/2002, May [Google Scholar]
  22. Sandri, M., Villa, F., Bersanelli, M., et al. 2002, 25th ESA Antenna Workshop on Satellite Antenna Technology ESA Conf. Proc. WPP-202, 621 [Google Scholar]
  23. Sandri, M., Villa, F., Burigana, C., et al. 2004, A&A, 428, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Tauber J. A., Norgaard-Nielsen H. U., Ade, P. A. R., et al. 2010, A&A, 520, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Villa, F., Bersanelli, M., Burigana, C., et al. 2002, AIP Conf. proc. 616, ed. M. De Petris, & M. Gervasi, 224 [NASA ADS] [CrossRef] [Google Scholar]
  26. Villa, F., Terenzi, L., Sandri, M., et al. 2010, A&A, 520, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Wilson, R. N. 1996, Reflecting Telescope Optics I, Springer Astron. Astrophys. Library [Google Scholar]

Footnotes

...Planck[*]
Planck (http://www.esa.int/Planck) is an ESA project with instruments provided by two scientific Consortia funded by ESA member states (in particular the lead countries: France and Italy) with contributions from NASA (USA), and telescope reflectors provided in a collaboration between ESA and a scientific Consortium led and funded by Denmark.
... contractor[*]
Thales Alenia Space - France, formerly Alcatel Space.
... GRASP8[*]
The GRASP software was developed by TICRA (Copenhagen, DK) for analysing general reflector antennas.
... HEALPix[*]
http://healpix.jpl.nasa.gov
... average[*]
The meaning of equal area is derived from Maino et al. (2002). For Gaussian elliptical beams, FWHM $_{\rm eff}$ = FWHME.

All Tables

Table 1:   Location and orientation of the LFI feed horns.

Table 2:   Main beam frames.

Table 3:   Main beam characteristics at the central frequency.

Table 4:   Galactic straylight contamination.

All Figures

  \begin{figure} \par\includegraphics[width=21pc,clip]{images/12891fg1.eps} \end{figure} Figure 1:

Lateral and top view of the telescope unit consisting of the reflectors and the support structure; the hexagonal support structure is readily seen as well as the field of view (in gray) (left panel). The telescope unit allocated into Planck satellite (right panel). The vertical axis is the spin axis of the satellite and the line of sight is tilted by $85^\circ $ with respect to the spin axis. The baffle around the telescope is not shown.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c} \includegraphics[height=7.5cm,clip]{images... ...ncludegraphics[height=6.3cm,clip]{images/12891fg3.eps}\end{tabular} \end{figure} Figure 2:

A CAD model of the Planck focal plane, which is located directly below the telescope primary mirror. It comprises the HFI bolometric detector array (small feed horns on golden circular base) and the LFI radio receiver array (larger feed horns around the HFI). The box holding the feedhorns appears to be transparent in this view, to also show the elements inside and behind it ( top panel). The HFI and LFI feed horns are seen reflected in the primary mirror of the Planck telescope in the clean room at Kourou, French Guiana ( bottom panel). © ESA/Thales.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=9cm,angle=90,clip]{images/12891fg4.ps} \end{figure} Figure 3:

Simulated co-polar pattern, in the E- plane, of the FM feed horns at 70 (FH21, FH22, and FH23), 44 (FH24 and FH25), and 30 (FH27) GHz assuming the designed profile.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=3.9cm,height=3cm,... ...s[width=3.9cm,height=3cm,clip]{images/12891fg6.ps}\\ \end{tabular} \end{figure} Figure 4:

10 dB contour of all horn patterns on the sub (left panel) and main (right panel) reflectors: the contours corresponding to the 30 GHz patterns are pink, the 44 GHz contours are blue, and those at 70 GHz are green.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{cc} \includegraphics[width=3.9cm,clip]{images... ...udegraphics[width=4.2cm,clip]{images/12891fg10.ps}\\ \end{tabular} \end{figure} Figure 5:

Field distribution on Planck mirrors (the sub-reflector is on the left and the main reflector is on the right) for a 70 GHz feed horn assuming a Gaussian feed approximation ( $E_{\rm GM}(\theta ,\varphi )$, first row) and the flight model feed horn ( $E_{\rm FM}(\theta ,\varphi )$, second row).

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{l l} \includegraphics[width=3.6cm,clip]{image... ...cludegraphics[width=4cm,clip]{images/12891fg12.ps}\\ \end{tabular} \end{figure} Figure 6:

Difference in the field distribution on the Planck mirrors between computations with the flight model feed and the Gaussian approximation. Differences data are in percent (( $E_{\rm FM}(\theta ,\varphi )-E_{\rm GM}(\theta ,\varphi ))/E_{\rm GM}(\theta ,\varphi )$). The color scale goes from black (minimum value) to red (maximum value). For the sub-reflector, the color scale goes from 0 to 200% and the white region on the lower part of the reflector is off the of scale since the differences are enormous. For the main reflector, the colour scale goes from 0 to the maximum value, i.e., 37.56%.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{images/12891fg13.ps} \end{figure} Figure 7:

Edge-taper curve on the primary mirror computed assuming a Gaussian illumination (red curve) and a realistic illumination (blue curve). The nominal edge-taper of the two feeds is the same: 17 dB at 22 degrees.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{images/12891fg14.eps} \end{figure} Figure 8:

Footprint of the LFI focalplane on the sky as seen by an observer looking towards the satellite along its optical axis. The origin of a right-handed uv-coordinate system is at the center of the focalplane (LOS). The z-axis is along the line-of-sight and points towards the observer. Labels from 18 to 23 refer to 70 GHz horns, from 24 to 26 refer to 44 GHz horns, and 27 and 28 refer to 30 GHz horns. Each beam has its own coordinate system as shown in the figure. The focalplane scans the sky as the satellite spins. The scanning direction is indicated by an arrow. The +u axis points to the spin axis of the satellite. The centers of the 30 GHz beams sweep about 1 degree from the ecliptic poles when the spin axis is in the ecliptic plane.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg18.ps}\\ \end{tabular} \end{figure} Figure 9:

Contour plot in the UV-plane ( -0.026 < U,V < 0.026) of the main beam co-polar (left side) and cross-polar (right side) component computed for the 30 GHz feed horns #27 (first row) and #28 (second row), assuming an ideal telescope. The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 32.58$^\prime $ in both cases. The two beams are perfectly symmetric with respect to the U-axis because of the symmetry of the Planck LFI optics. The lines in the contour plots represent levels of at -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg20.ps}\\ \end{tabular} \end{figure} Figure 10:

Contour plot in the UV-plane of the differences between the main beam #27 computed assuming the X-polarized feed and the main beam computed assuming the Y-polarized feed. The differences in the co- (left side) and cross- (right side) polar components are normalized to the local amplitude and expressed in dB. Table 3 quantitatively shows the differences between the two polarizations of the same feed.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=9pc,clip]{images/... ...cludegraphics[width=9pc,clip]{images/12891fg24.ps}\\ \end{tabular} \end{figure} Figure 11:

Contour plot in the UV- plane ( -0.026 < U,V < 0.026) of the main beam co- (left side) and cross- (right side) polar components computed for the feed horns #24 (first row) and #26 (second row). The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 22.82 and 28.90, respectively. The lines in the contour plots represent levels of -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=10pc,clip]{images... ...ludegraphics[width=10pc,clip]{images/12891fg30.ps}\\ \end{tabular} \end{figure} Figure 12:

Contour plot in the UV-plane ( -0.015 < U,V < 0.015) of the main beam co- (left side) and cross- (right side) polar components computed for the feed horns #21 (third row), #22 (fourth), and #23 (fifth row). The fit bivariate Gaussian contours are superimposed with dotted lines and the resulting averaged FWHM is 12.49, 12.71, and 13.05 arcmin, respectively. The lines in the contour plots represent levels of -3, -10, -20, -30, -40, -50, and -60. The colour scales go from -90 to 0 dB.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg32.ps}\end{tabular}\end{figure} Figure 13:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 30 GHz (feed horn #27 Y polarized) computed with MrGTD. The maximum level of the main spillover is about -4.6 dBi at $\phi \simeq 17^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and about -8.0 dBi at $\phi \simeq 18^\circ $ and $\theta \simeq 86^\circ $ for the cross-polar component.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg34.ps}\end{tabular}\end{figure} Figure 14:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 44 GHz (feed horn #24 Y polarized) computed with MrGTD. The maximum level of the main spillover is about -5.4 dBi at $\phi = 0^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and the cross-polar component is down to -15 dBi everywhere.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c} \includegraphics[width=11pc, angle=90,clip... ...hics[width=11pc, angle=90,clip]{images/12891fg36.ps}\end{tabular}\end{figure} Figure 15:

Co- (top panel) and cross- (bottom panel) polar components of the 4$\pi $ beam at 70 GHz (feed horn #23 FM, Y polarized) computed with MrGTD. The maximum level of the main spillover is about -1.8 dBi at $\phi \simeq 10^\circ $ and $\theta \simeq 85^\circ $ for the co-polar component, and the cross-polar component is, in the main spillover region, at about -4.8 dBi.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{c c} \includegraphics[width=4.2cm,bb=100 368 ... ...dth=4.2cm,bb=100 368 510 793]{images/12891fg38.ps}\\ \end{tabular} \end{figure} Figure A.1:

Polarization angle of the main beam #21 at 70 GHz (left side) and main beam #24 at 44 GHz (right side).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.