| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201014702 | |
| Published online | 14 September 2010 | |
Helium in first and second-generation stars in globular clusters from
spectroscopy of red giants![[*]](/icons/foot_motif.png)
A. Bragaglia1 - E. Carretta1 - R. Gratton2 - V. D'Orazi2 - S. Cassisi3 - S. Lucatello2,4,5
1 -
INAF-Osservatorio Astronomico di Bologna, Via Ranzani 1, 40127 Bologna, Italy
2 -
INAF-Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 -
INAF-Osservatorio Astronomico di Collurania, via M. Maggini, 64100 Teramo, Italy
4 -
Excellence Cluster Universe, Technische Universität München, Boltzmannstr. 2, 85748 Garching, Germany
5 -
Max-Planck-Institut für Astrophysik, 85741 Garching, Germany
Received 1 April 2010 / Accepted 11 May 2010
Abstract
The stars in a globular cluster (GC) have always been considered
coeval and of the same metallicity. Recently, this assumption has been
challenged on the basis of spectroscopic and photometric observations,
which show various generations of stars in GCs, differing in the
abundances of products of H-burning at high temperatures. The main
final product of this burning is He. It is then important to study the
connections between stars properties and He content. We consider here
the nearly 1400 stars on the red giant branch (RGB) observed with
FLAMES@VLT in 19 Galactic Globular Clusters (GCs) in the course of our
project on the Na-O anticorrelation. Stars with different He are
expected to have different temperatures (i.e., different colours),
slightly different metallicities [Fe/H], and different luminosity
levels of the RGB bump. All these differences are small, but our study
has the necessary precision, good statistics, and homogeneity to detect
them. Besides considering the observed colours and the temperatures and
metallicities determined in our survey, we computed suitable sets of
stellar models - fully consistent with those present in the BaSTI
archive - for various assumptions about the initial He content. We find
that differences in observable quantities that can be attributed to
variations in He content are generally detectable between stars of the
primordial (P, first-generation) and extreme (E, second-generation)
populations, but not between the primordial and intermediate ones (I).
The only exception, where differences are also significant between P
and I populations, is the cluster NGC 2808, where three
populations are clearly separated also on the main sequence and
possibly on the horizontal branch. The average enhancement in the He
mass fraction Y between P and E stars is about 0.05-0.11, depending on the assumptions. The differences in Y,
for NGC 2808 alone, are about 0.11-0.14 between P and I stars, and
about 0.15-0.19 between P and E stars, again depending on the
assumptions. When we consider the RGB bump luminosity of first and
second-generation stars we find different levels; the implied Y difference is more difficult to quantify, but agrees with the other determinations.
Key words: stars: atmospheres - stars: Population II - globular clusters: general - stars: abundances
1 Introduction
Recent progress has indicated that large star-to-star variations exist in the He content among
stars in globular clusters (GCs), in spite of difficulties in directly deriving He abundances (see however Moehler et al. 2007; Villanova et al. 2009). The first clear evidence has been obtained from
observations of multiple main sequences in ![]() Cen (Bedin et al. 2004)
and NGC 2808 (Piotto et al. 2007; D'Antona et al. 2005). In
Cen (Bedin et al. 2004)
and NGC 2808 (Piotto et al. 2007; D'Antona et al. 2005). In ![]() Cen,
stars on the bluest main sequence (MS) are more metal-rich than those of the
reddest one (Piotto et al. 2005), a fact that can only be explained by an
He content higher by about 0.10 to 0.15 in the mass fraction
Y (as originally suggested by Norris 2004)
with respect to a canonical (primordial) He content of about 0.245
commonly adopted for the bulk of the stellar population in this
cluster. The small scatter found in NGC 2808 among red giant
branch (RGB) stars also implies a larger He content for the bluer MS,
by roughly
the same amount. Two other clusters have been found to have wide MSs:
47 Tuc (Anderson et al. 2009) and NGC 6752 (Milone et al. 2010, who also suggest a possible split)
Cen,
stars on the bluest main sequence (MS) are more metal-rich than those of the
reddest one (Piotto et al. 2005), a fact that can only be explained by an
He content higher by about 0.10 to 0.15 in the mass fraction
Y (as originally suggested by Norris 2004)
with respect to a canonical (primordial) He content of about 0.245
commonly adopted for the bulk of the stellar population in this
cluster. The small scatter found in NGC 2808 among red giant
branch (RGB) stars also implies a larger He content for the bluer MS,
by roughly
the same amount. Two other clusters have been found to have wide MSs:
47 Tuc (Anderson et al. 2009) and NGC 6752 (Milone et al. 2010, who also suggest a possible split)![]() .
.
A star-to-star spread in the He abundance may explain many aspects of the
horizontal branches (HBs) of GCs, as extensively discussed in
Gratton et al. (2010), but we are aware that the case for a null spread of He in GCs is also maintained in the literature (e.g., Catelan 2009).
Internal variations in He are likely to be connected with
other chemical signatures found in GCs, related to H burning
occurring at high temperatures. This has been first proposed in a modern way
by D'Antona et al. (2002), who noticed that the lower masses of He-rich stars may
naturally explain the correlation between the presence of stars at the blue
extreme of the HB, and of stars extremely depleted in O in
various clusters. Lee et al. (2005) suggest that a super-He rich population could
explain the extreme HB stars in GCs, specifically presenting the cases of ![]() Cen and NGC 2808 (where they had predicted a spread or a split of the MS, just before it
was actually found). Kaviraj et al. (2007) suggest that the far-UV properties of
GCs in the Virgo elliptical M87 could be explained by a super-He rich population
similar to the one in
Cen and NGC 2808 (where they had predicted a spread or a split of the MS, just before it
was actually found). Kaviraj et al. (2007) suggest that the far-UV properties of
GCs in the Virgo elliptical M87 could be explained by a super-He rich population
similar to the one in ![]() Cen. D'Antona & Caloi (2008)
try to explain the whole distribution of stars along the HB of various
clusters (including NGC 2808, M 13, and M 3) as due to
star-to-star variations in the He content (but see also Castellani et al. 2005).
In a companion paper (Gratton et al. 2010),
we make a more
systematic comparison of the extremes of the distribution of stars
along
the HB and of the Na-O anticorrelation. We find that median HB colours
are reproduced quite well by a combination of metallicity, age, and a
simple mass loss proportional to metallicity.
However, the low-mass extreme of the HB is clearly correlated with the
extension
of the Na-O anticorrelation (see also Carretta et al. 2009a) which, in turn,
seems to be linked with the cluster absolute magnitude, a proxy for cluster mass.
Cen. D'Antona & Caloi (2008)
try to explain the whole distribution of stars along the HB of various
clusters (including NGC 2808, M 13, and M 3) as due to
star-to-star variations in the He content (but see also Castellani et al. 2005).
In a companion paper (Gratton et al. 2010),
we make a more
systematic comparison of the extremes of the distribution of stars
along
the HB and of the Na-O anticorrelation. We find that median HB colours
are reproduced quite well by a combination of metallicity, age, and a
simple mass loss proportional to metallicity.
However, the low-mass extreme of the HB is clearly correlated with the
extension
of the Na-O anticorrelation (see also Carretta et al. 2009a) which, in turn,
seems to be linked with the cluster absolute magnitude, a proxy for cluster mass.
These correlations suggest that the multiple-generation scenario needed to
explain the Na-O anticorrelation![]() is able to explain many peculiarities of GCs. As we have seen, a crucial datum
in this scenario is the He content of second-generation stars. While the most
spectacular evidence of a variation in the He content comes from the HB and the
MS, the RGB stars are also very useful because chemical
composition (but -alas- not He content) can be determined easily enough for
these stars using spectroscopy, unlike faint MS stars. This allows us to cross
correlate the abundances of various elements, providing significant constraints on
the properties of the He producer, which have not been clearly identified yet.
(Two main possible mechanisms have been proposed, intermediate/massive
asymptotic giant stars - AGB - and fast-rotating massive stars - FRMS -
see e.g., D'Antona & Ventura 2007; Decressin et al. 2007, respectively.)
Various properties of RGB stars
are affected by the variable He abundances:
is able to explain many peculiarities of GCs. As we have seen, a crucial datum
in this scenario is the He content of second-generation stars. While the most
spectacular evidence of a variation in the He content comes from the HB and the
MS, the RGB stars are also very useful because chemical
composition (but -alas- not He content) can be determined easily enough for
these stars using spectroscopy, unlike faint MS stars. This allows us to cross
correlate the abundances of various elements, providing significant constraints on
the properties of the He producer, which have not been clearly identified yet.
(Two main possible mechanisms have been proposed, intermediate/massive
asymptotic giant stars - AGB - and fast-rotating massive stars - FRMS -
see e.g., D'Antona & Ventura 2007; Decressin et al. 2007, respectively.)
Various properties of RGB stars
are affected by the variable He abundances:
- 1.
- The temperature (at a given luminosity) of He-rich RGB stars is slightly warmer than for He-poor ones (see e.g., D'Antona et al. 2002). The difference is not large (only a few tens of K), and very accurate relative determinations are required. However, both colours and line excitation can be used to show that this really occurs.
- 2.
- The gravity (again at a given luminosity) is also different, owing to both the lower mass and higher temperature of He-rich stars. The He-rich stars have slightly lower gravity, but this effect is very small, and difficult to show, because of several complications (for instance, the greater molecular weight and reduced continuum opacity simulate a higher gravity, offsetting most of the effect expected on, e.g., ionisation equilibrium), so we will not consider it here.
- 3.
- The [Fe/H] value is different, because of the different H content (broadly speaking, if Y increases, X decreases, hence [Fe/H] increases; things are of course more complicated, see Sec. 2.3): this difference is small but not negligible. We already noticed this effect in NGC 2808 (Carretta et al. 2006, Paper I).
- 4.
- Finally, the luminosity of the RGB bump is also different: the RGB bump
is more luminous for He-rich stars (Salaris et al. 2006; Iben 1968), even if also in this case
the situation is more complex (see Sect. 3). We showed
that possible evidence of this effect can be traced in the run of Na
abundances along the RGB of NGC 6218 (=M 12) and NGC 6752
(Carretta et al. 2007b, Paper IV).
Table 1: Difference in colour and metallicity between different populations in the 19 GCs.
Beside observations, determining the impact of different He abundances requires appropriate modelling. To this purpose we used a set of BaSTI evolutionary models (Pietrinferni et al. 2009,2006,2004) purposely computed for this paper and employing two sets of heavy-element mixtures (see Sects. 2 and 3 for details and relations).
The structure of this paper is as follows. In Sect. 2 we present the observed differences in colour, temperature, and metallicity and derive the implied differences in He content; in Sect. 3 we compare the RGB bumps of first and second-generation stars, also deducing a different He abundance. Finally, we summarise and discuss our results in Sect. 4.
2 Difference in Helium from RGB stars
We may find different He values for the three populations using various
indicators. To actually compute the implied Y (as in the definition X+Y+Z=1 for
the chemical composition of stellar models on mass fraction), we used relations
based on the BaSTI stellar evolutionary models. We have computed an extended set
of low-mass stellar models for various assumptions about the initial He content.
All the stellar model predictions adopted in the present analysis have been obtained
exactly in the same physical framework used for the BaSTI![]() stellar model
library (Pietrinferni et al. 2006,2004). Thus, they are fully consistent with
the predictions corresponding to a ``canonical'' assumption about the
initial He abundance (
stellar model
library (Pietrinferni et al. 2006,2004). Thus, they are fully consistent with
the predictions corresponding to a ``canonical'' assumption about the
initial He abundance (
![]() ).
In particular, we used two
assumptions for the heavy element mixtures (others may be valid, but these
represent two extremes):
).
In particular, we used two
assumptions for the heavy element mixtures (others may be valid, but these
represent two extremes):
- (a)
- one where the second-generation I, E stars have the same heavy-element
distribution of the first-generation P stars, both
 -enhanced
(for more details see Pietrinferni et al. 2006) and without peculiarities in the
distribution of C, N, O, and Na (a simplified approach);
-enhanced
(for more details see Pietrinferni et al. 2006) and without peculiarities in the
distribution of C, N, O, and Na (a simplified approach);
- (b)
- a second one where the I, E stars have a peculiar distribution of metals (i.e., showing a signature of the Na-O anticorrelation) and different from the standard one of the P stars. In particular, we adopted the ``CNONa-extreme'' chemical composition accounted for by Pietrinferni et al. (2009), which has the C+N+O sum enhanced by a factor of two.
2.1  Y from difference in colours
Y from difference in colours
For all stars in our 19 GCs we have Johnson V magnitudes. The photometry
was obtained as described in Papers I to VIII of our series![]() :
Carretta et al. (2009a,2007b,c,a,2009b,2006)
and Gratton et al. (2007,2006), where the interested
reader can find references to the original papers or description for the
unpublished data. We retrieved K magnitudes from the R2MASS
:
Carretta et al. (2009a,2007b,c,a,2009b,2006)
and Gratton et al. (2007,2006), where the interested
reader can find references to the original papers or description for the
unpublished data. We retrieved K magnitudes from the R2MASS![]() Point Source Catalog (Skrutskie et al. 2006) for almost all stars.
Distance moduli and colour excesses E(B-V) were
taken from the on-line version of the GC catalogue by Harris (1996).
Point Source Catalog (Skrutskie et al. 2006) for almost all stars.
Distance moduli and colour excesses E(B-V) were
taken from the on-line version of the GC catalogue by Harris (1996).
In our series of papers devoted to the study of Na and O abundances for RGB stars, we derived the temperatures of the stars using the Alonso et al. (1999) relations and the photometry. In particular, to decrease the internal error, we derived the temperatures not directly from the (V-K)colours, but from relations of temperature with the V or K magnitude (see Papers II to VIII; the exception is NGC 2808, the first cluster analysed, for which we used the classical relation between colour and temperature). In the present paper we used the unreddened (V-K) colours. The second step provided the necessary elimination of offsets between the photometries: in each cluster we selected stars belonging to the P component, computed the average offset in colour between (V-K) observed and derived from the colour-temperature relations, and used it to define the zero point for the P stars (so that they have zero colour by definition).
Only after this normalisation did we compute the offsets in colours
between the three populations. We have 319, 587, and 39 stars in the P,
I, E components, respectively. We only considered stars fainter than MK=-3.5 because for brighter stars the different sequences for different He are too close and become indistinguishable![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14702f1.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg15.png)
|
Figure 1: Mean differences in (V-K) colours between the I and P components in the 19 GCs as a function of the metallicity difference (I - P). The two are well-correlated, as indicated by the Pearson and Spearman coefficients. |
| Open with DEXTER | |
Results for the 19 GCs are given in Table 1, where we
indicate the cluster, the metallicity (Col. 2, taken from Paper VIII),
the number of stars in the P component (Col. 3), their
average colour
![]() and rms (Cols. 4, 5), the number of stars in the
I component (Col. 6), and their average offset with respect to the P stars, with
rms (Cols. 7, 8). Columns 9 to 12 show the average metallicities of the P and
I components with their rms, and Col. 13 shows the difference in [Fe/H]
(see next section). We did not evaluate the corresponding individual cluster values
for the E component since the number of E stars is very small, and they
would not be significant. Figure 1
shows that differences in colours and in metallicity are anticorrelated
well as indicated by the Pearson and Spearman rank coefficients, and
this
is significant at better than the 99.9% level.
and rms (Cols. 4, 5), the number of stars in the
I component (Col. 6), and their average offset with respect to the P stars, with
rms (Cols. 7, 8). Columns 9 to 12 show the average metallicities of the P and
I components with their rms, and Col. 13 shows the difference in [Fe/H]
(see next section). We did not evaluate the corresponding individual cluster values
for the E component since the number of E stars is very small, and they
would not be significant. Figure 1
shows that differences in colours and in metallicity are anticorrelated
well as indicated by the Pearson and Spearman rank coefficients, and
this
is significant at better than the 99.9% level.
To see whether there is a difference in colour among the different populations,
we summed up the P, I, and E components in all clusters and obtained the following weighted means![]() :
:

We see that
A complication may arise from the presence of CO bands in the K filter. They
are stronger in P stars than in O-depleted I and E ones, and may depress the
flux in the K filter by about 1-2%, making the P stars to appear bluer, hence
decreasing the difference in (V-K) among populations. From simulations based on
the CO index by Cohen et al. (1978) we have estimated that the
(V-K) of P stars should be about 0.013 mag redder than they appear. That means
that the corrected
![]() between E and P is about -0.05;
this corresponds to
between E and P is about -0.05;
this corresponds to ![]() of about 0.06 or 0.10, for the two mixtures.
of about 0.06 or 0.10, for the two mixtures.
This is a global result, averaged over the 19 GCs; it is interesting to consider NGC 2808 separately, the only cluster in our sample for which large differences in He have been deduced on the basis of the multiple MSs (Piotto et al. 2007). We find for NGC 2808

For this cluster both the I - P difference and the E - P one are significant at about the 2.5
Table 2: Summary of differences in colour and metallicity between populations.
Table 3: Summary of differences in Y between first and second-generation stars.
2.2  Y from difference in d
Y from difference in d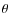
As an alternative to the use of temperatures derived from colours, we may also use
information derived from excitation to find (small) temperature differences
between the three populations![]() .
This is possible because we did not derive
.
This is possible because we did not derive
![]() 's from the excitation
equilibrium (i.e. the spectroscopic route) but from the photometry.
From the excitation equilibrium we derived the d
's from the excitation
equilibrium (i.e. the spectroscopic route) but from the photometry.
From the excitation equilibrium we derived the d![]() values for all the
programme stars; recalling that d
values for all the
programme stars; recalling that d![]() means that the star is warmer than
expected from its luminosity, we found the following weighted average values:
means that the star is warmer than
expected from its luminosity, we found the following weighted average values:
![]() using the 39 E stars and the 207 P stars with more than 25 lines measured.
The result improves to
using the 39 E stars and the 207 P stars with more than 25 lines measured.
The result improves to
![]() if we relax the request on the number of lines and use the 61 E stars and the
315 P stars with more than 15 lines measured. This difference is significant at 2.5
if we relax the request on the number of lines and use the 61 E stars and the
315 P stars with more than 15 lines measured. This difference is significant at 2.5![]() and corresponds to a difference in temperature of
and corresponds to a difference in temperature of ![]() K
(in the sense of E stars being warmer than P ones) at 4500 K, the
mean temperature of the stars considered. This implies a
K
(in the sense of E stars being warmer than P ones) at 4500 K, the
mean temperature of the stars considered. This implies a ![]() of about 0.06 between E and P stars (an average between results for the cases a) and b) discussed above). Since in this case we have averaged stars of all magnitudes and the sequences
tend to converge at brighter luminosity, the average difference is smaller than
the one implied by colours.
of about 0.06 between E and P stars (an average between results for the cases a) and b) discussed above). Since in this case we have averaged stars of all magnitudes and the sequences
tend to converge at brighter luminosity, the average difference is smaller than
the one implied by colours.
Once again, the difference between the P and I populations is not significant;
the corresponding differences are
![]() and
and
![]() considering stars with at least 25 or 15 lines measured, respectively.
considering stars with at least 25 or 15 lines measured, respectively.
2.3  Y from difference in [Fe/H]
Y from difference in [Fe/H]
Grossly speaking, given the definition X+Y+Z=1, for a fixed global metallicity Z, an increase in He (Y) has to be associated to a decrease of the H abundance, so that [Fe/H] increases. Of course, the issue is more complex, since a change in the H to He ratio has effects on the star structure, which are taken into account by the evolutionary models used in the present paper.
We noticed this feature in NGC 2808 (Carretta et al. 2006) when, dividing stars in a way different from the one adopted here, we found slightly different (and increasing) values of [Fe/H] for ``O-normal'', intermediate, and very O-poor stars (i.e., with canonical, intermediate, and enhanced He in the usual interpretation of Na-O anti-correlation). We explore here the whole sample of our programme clusters.
In this case we have to proceed in a slightly different way. As mentioned in
Sect. 2.1, in our series of papers (Papers II to VII, but notably not in
Paper I on NGC 2808), we derived the temperatures used to obtain [Fe/H] and other
abundance ratios from a calibration between magnitude and colour-based
temperature. This reduced the effect of errors (since magnitudes are more
reliably measured than colours) and allowed to have smaller internal errors, but
also effectively collapsed all possible differences in metallicity due to
different He, which would have shown up as different colours, hence temperatures.
Before comparing [Fe/H] values of the different populations, we then applied
a correction to transform the metallicities to the values they would have had,
had we used the colour-based
![]() 's directly.
's directly.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{14702f2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg46.png)
|
Figure 2: Individual differences I - P of metallicity ( upper panel) and colours ( lower panel) versus [Fe/H], with Spearman and Pearson coefficients indicated (in the lower panel, values in parenthesis are obtained excluding NGC 6388 and NGC 6441). |
| Open with DEXTER | |
When we apply the same procedure adopted for colours, i.e. normalising to the P population of each cluster (for a total of 320 stars), we obtain the following weighted means:
![\begin{eqnarray*}&& \rm [Fe/H]_{\rm I} - [Fe/H]_{\rm P} = 0.000\pm0.003 ~~({\rm ...](/articles/aa/full_html/2010/11/aa14702-10/img47.png)
with 587 stars in the I and 38 stars in the E component, respectively. If we eliminate NGC 3201 because of its differential reddening, things do not change much: these two numbers become
Also in this case we may separate NGC 2808, and we obtain
![\begin{eqnarray*}\rm [Fe/H]_{\rm I} - [Fe/H]_{\rm P} &=& 0.046\pm0.020 ~~({\rm r...](/articles/aa/full_html/2010/11/aa14702-10/img52.png)
Both values are significant and imply
![\begin{figure}
\par\includegraphics[scale=0.35,clip]{14702f3a.ps}\par\includegraphics[scale=0.35,clip]{14702f3b.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg57.png)
|
Figure 3: Cumulative distributions for difference in colour ( upper panel) and metallicity ( lower panel) for individual stars in the three populations. |
| Open with DEXTER | |
2.4 Differences among the three populations
Even if this is part of our global study of the
anticorrelations in GCs, we have to remember that ![]() is not a direct
synonym of anticorrelation and that the same extension of the anticorrelations
(as measured, e.g. from the interquartile range IQR[O/Na], see
Carretta et al. 2007d,2006), may be reached for different values of
is not a direct
synonym of anticorrelation and that the same extension of the anticorrelations
(as measured, e.g. from the interquartile range IQR[O/Na], see
Carretta et al. 2007d,2006), may be reached for different values of ![]() .
We have an indication of that from Fig. 2:
in the lower panel we plot the difference in metallicity and colour
between I and P stars as a function of cluster metallicity, while in
the upper panel we do the same for differences in metallicity. The
individual values have large errors (so we considered only the averages
over the whole sample); however, there is a hint that the effects of
differences in He content (as inferred from the difference in
metallicity or colour) are less evident for the metal-poor clusters.
Only in the metal-richer clusters are the I stars bluer and
metal-richer than the P ones. This could suggest that, for the same
production of proton-capture elements (e.g., destruction of O and
production of
Na), more He is produced in metal-richer clusters. In other words, in
the
metal-poor GCs a smaller
.
We have an indication of that from Fig. 2:
in the lower panel we plot the difference in metallicity and colour
between I and P stars as a function of cluster metallicity, while in
the upper panel we do the same for differences in metallicity. The
individual values have large errors (so we considered only the averages
over the whole sample); however, there is a hint that the effects of
differences in He content (as inferred from the difference in
metallicity or colour) are less evident for the metal-poor clusters.
Only in the metal-richer clusters are the I stars bluer and
metal-richer than the P ones. This could suggest that, for the same
production of proton-capture elements (e.g., destruction of O and
production of
Na), more He is produced in metal-richer clusters. In other words, in
the
metal-poor GCs a smaller ![]() is required to produce an effect on the shape
of the Na-O anticorrelation, i.e., on the classification of a star in the I or
even E population.
is required to produce an effect on the shape
of the Na-O anticorrelation, i.e., on the classification of a star in the I or
even E population.
While the effect discussed above needs corroboration, a solid conclusion is that,
with the exception of NGC 2808, the differences in colour and
metallicity are only significant between the extremes of the GC populations.
This can be immediately visualised using the cumulative distributions of the differences in colour
and metallicity for the individual stars (i.e., the difference between each star and the
average of the P population). Figure 3 shows these cumulative distributions,
separated for P, I, and E stars. The P and I distributions look very similar in both panels,
while the E stars show a distinct behaviour. (The probability that they are taken from the
same parent distribution of the P stars is very low:
![]() and 0.015 for colour and metallicity, respectively.) As a whole, they are bluer and metal-richer.
and 0.015 for colour and metallicity, respectively.) As a whole, they are bluer and metal-richer.
3 Helium from the luminosity function of Na-poor and Na-rich stars
With the intent of finding additional evidence supporting our scenario for the correlation between Na-rich stars and their initial helium content, we also tested the possibility of detecting any brightness difference between the RGB bumps corresponding to the two distinct stellar populations. In fact, canonical stellar evolution predicts that the RGB bump brightness increases when the initial He content increases (see, for instance Salaris & Cassisi 2005). As a consequence, one should expect to observe this occurrence when comparing the primordial stellar component with the intermediate/extreme one (e.g., Salaris et al. 2006).
Table 4:
Adopted values of
![]() .
.
However, the possibility of detecting this observational signature in the
luminosity function (LF) of a given GC is generally strongly hampered by the
inadequate statistics. (The number of RGB stars in the various LF bins is not
large enough.) We made a first explorative attempt (Paper IV), combining the
samples in NGC 6218 and NGC 6752 to improve the statistics. Here, in order to
better overcome this problem, we decided to combine the data for the LFs
corresponding to the various GCs in our database. We took the values for
![]() from the literature (see Table 4) but could only apply the test
to 14 of the 19 GCs. We did not reach the level of the bump in some of our
target clusters, either because they were very far, like NGC 6388 and NGC 6441, or
because they were so rich, like NGC 104 and NGC 2808, that we had enough target in
the upper RGB and did not need to reach down along the RGB. (Our original goal
was to obtain good spectra to measure Na and O abundances for about 100 stars
per cluster, so we selected preferentially bright targets.) Finally, we did not
find a
from the literature (see Table 4) but could only apply the test
to 14 of the 19 GCs. We did not reach the level of the bump in some of our
target clusters, either because they were very far, like NGC 6388 and NGC 6441, or
because they were so rich, like NGC 104 and NGC 2808, that we had enough target in
the upper RGB and did not need to reach down along the RGB. (Our original goal
was to obtain good spectra to measure Na and O abundances for about 100 stars
per cluster, so we selected preferentially bright targets.) Finally, we did not
find a
![]() value for NGC 7099. Since it has the same metallicity as
NGC 7078, we could have adopted the value for the latter, taking
the distance moduli into account, but we would have introduced an additional uncertainty,
given also the slight difference in age (Carretta et al. 2009c; these
two GCs have the same age in Marín-Franch et al. 2009).
value for NGC 7099. Since it has the same metallicity as
NGC 7078, we could have adopted the value for the latter, taking
the distance moduli into account, but we would have introduced an additional uncertainty,
given also the slight difference in age (Carretta et al. 2009c; these
two GCs have the same age in Marín-Franch et al. 2009).
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{14702f4a.ps}\par\includegraphics[width=5.5cm,clip]{14702f4b.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg60.png)
|
Figure 4:
Upper panel: histogram of the difference in magnitude between
individual V and
|
| Open with DEXTER | |
We have in total 1368 stars in the 14 GCs with a measured Na abundance. To
separate P stars from I and E ones we used [Na/Fe]
![]() (see Carretta et al. 2009a); we have 438 P stars and 930 I, E ones. (We sum the
second-generation populations, since the E stars are a minority.) We computed
for each cluster the residuals between the individual V values and
(see Carretta et al. 2009a); we have 438 P stars and 930 I, E ones. (We sum the
second-generation populations, since the E stars are a minority.) We computed
for each cluster the residuals between the individual V values and
![]() ,
to eliminate the dependence on metallicity and cluster age. We produced
histograms both for the whole sample and for the P and I/E stars separately.
The upper panel of Fig. 4 shows the resulting luminosity
functions. Since we have only the stars here for which we obtained a spectrum
and not the entire RGB, the part below the bump is strongly incomplete, and we do
not see the usual increase going towards fainter stars found in photometric
works on the RGB luminosity function. However, the bump is visible both in the
whole sample and in the two subsamples that show slightly different peak
values. The small offset from zero in the histograms is due to the different
photometries adopted in the definition of
,
to eliminate the dependence on metallicity and cluster age. We produced
histograms both for the whole sample and for the P and I/E stars separately.
The upper panel of Fig. 4 shows the resulting luminosity
functions. Since we have only the stars here for which we obtained a spectrum
and not the entire RGB, the part below the bump is strongly incomplete, and we do
not see the usual increase going towards fainter stars found in photometric
works on the RGB luminosity function. However, the bump is visible both in the
whole sample and in the two subsamples that show slightly different peak
values. The small offset from zero in the histograms is due to the different
photometries adopted in the definition of
![]() and in our programme (see below).
and in our programme (see below).
To help appreciate this, we present a zoom in the bump region in the lower panels of
Fig. 4, separating the three
components. Fitting a Gaussian to the bumps we derive a difference in magnitude
between P and I, E stars of 0.044 mag, in the direction expected from theory,
with I, E stars presenting a brighter RGB bump than P stars. Unfortunately, the
significance is low, because of the errors on the position of the peaks. A first
source of error is the statistics: the bump peak (i.e., above the background) is
produced by only about 150 stars, with two thirds in the I, E population and
one third in the P one. To halve the errors in the position of the two separate
peaks we should increase the number of stars by at least 3 times, but this is not
an immediate possibility because of the large amount of telescope time and
analysis implied. Other sources of errors come from the photometry: i)
![]() is measured at best with an uncertainty of 0.05 mag, ii) the
magnitudes we use have a small attached error, and iii) we did use a different
photometry from the one on which
is measured at best with an uncertainty of 0.05 mag, ii) the
magnitudes we use have a small attached error, and iii) we did use a different
photometry from the one on which
![]() was determined (although the
possible offsets should be amply accommodated within the uncertainty on
was determined (although the
possible offsets should be amply accommodated within the uncertainty on
![]() ). However, even if we tried to re-determine the bump positions in our
photometric data, the situation would not become significantly better. We note
in fact that the bump has an intrinsic width of the order of 0.2 mag
(Salaris et al. 2002) and that we have already reached that level: the FWHM of the
Gaussian used to fit the P population (the one with a single Y value) is 0.21 mag (while the FWHM of the second-generation stars, with varying Y content, is
larger, about 0.28 mag).
). However, even if we tried to re-determine the bump positions in our
photometric data, the situation would not become significantly better. We note
in fact that the bump has an intrinsic width of the order of 0.2 mag
(Salaris et al. 2002) and that we have already reached that level: the FWHM of the
Gaussian used to fit the P population (the one with a single Y value) is 0.21 mag (while the FWHM of the second-generation stars, with varying Y content, is
larger, about 0.28 mag).
To estimate the average difference in the initial He content between the P stellar population and the I/E one, from the measured RGB bump brightness difference, we used the extended set of low-mass stellar models for various assumptions about the initial He content described in Sect. 2.
As a first step, it was assumed that the P and I/E stellar populations have
exactly the same heavy elements distribution (case a). Then for a fixed age of
![]() 12.5 Gyr and iron content [Fe/H] = -1.31, we computed the synthetic
LF
12.5 Gyr and iron content [Fe/H] = -1.31, we computed the synthetic
LF![]() for the P population by using a canonical He abundance (Y=0.248), whereas for
the I/E population various synthetic LFs were computed by using various
He-enhanced abundances in the range from 0.26 to 0.40. By using these
theoretical LFs, we estimated the brightness difference between the RGB
bump of the P population and that of the I/E one as a function of the difference
in the initial He contents of the two populations. The results of this analysis
are shown in Fig. 5. The comparison between the model predictions
and the estimated empirical difference suggests a difference in the mean He
content between the P and the I/E sub-populations of about
for the P population by using a canonical He abundance (Y=0.248), whereas for
the I/E population various synthetic LFs were computed by using various
He-enhanced abundances in the range from 0.26 to 0.40. By using these
theoretical LFs, we estimated the brightness difference between the RGB
bump of the P population and that of the I/E one as a function of the difference
in the initial He contents of the two populations. The results of this analysis
are shown in Fig. 5. The comparison between the model predictions
and the estimated empirical difference suggests a difference in the mean He
content between the P and the I/E sub-populations of about
![]() .
.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14702f5.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg64.png)
|
Figure 5:
The V-band RGB
bump brightness difference between the P sub-population and the I/E one
as a function of the He abundance difference between the two
sub-populations. In this case, for both sub-populations it has been
assumed the
same normal, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14702f6.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg65.png)
|
Figure 6: As in Fig. 5, but taking into account that the I/E sub-population is characterised by a peculiar chemical pattern with a CNONa anticorrelation (case b). |
| Open with DEXTER | |
Case b should represent a more significant comparison between theory and
observations, because the adopted heavy elements distribution corresponds to a mixture
where the sum (C+N+O) is enhanced by about a factor of 2 with respect to the
reference, ![]() -enhanced mixture. This value is consistent - although
it represents an upper limit - with the results of the spectroscopical analysis
performed by Carretta et al. (2005) for the extreme values of the chemical
anti-correlations observed in GCs. The RGB bump brightness difference between
the P sub-population and the I/E one, when a CNONa peculiar
mixture is assumed for the latter, is shown in Fig. 6 as a function of the He
abundance difference. This figure deserves some comments. The RGB bump
brightness of the I/E sub-population is fainter than that of the P
sub-population for an He content difference lower than about 0.045. This
occurs because when comparing
-enhanced mixture. This value is consistent - although
it represents an upper limit - with the results of the spectroscopical analysis
performed by Carretta et al. (2005) for the extreme values of the chemical
anti-correlations observed in GCs. The RGB bump brightness difference between
the P sub-population and the I/E one, when a CNONa peculiar
mixture is assumed for the latter, is shown in Fig. 6 as a function of the He
abundance difference. This figure deserves some comments. The RGB bump
brightness of the I/E sub-population is fainter than that of the P
sub-population for an He content difference lower than about 0.045. This
occurs because when comparing ![]() -enhanced stellar
models with those accounting for a CNONa peculiar pattern, we are considering
the same iron content [Fe/H], and this means that the global metallicity of the
stellar models with the peculiar heavy elements distribution is higher than for
the reference models. Therefore, as discussed by
Pietrinferni et al. (2009), the RGB bump - at fixed age and [Fe/H] value - is
expected to be fainter in those sub-populations characterised by a peculiar
chemical pattern (see also Salaris et al. 2006). However, for the increasing
difference in the He content, the effect of the He abundance on the RGB bump
brightness overcomes the one associated to the higher metallicity, and the bump in
the I/E sub-population becomes brighter with respect the P sub-population.
Theoretical models shown in Fig. 6 suggest an average difference
between the P and the I/E sub-population of
-enhanced stellar
models with those accounting for a CNONa peculiar pattern, we are considering
the same iron content [Fe/H], and this means that the global metallicity of the
stellar models with the peculiar heavy elements distribution is higher than for
the reference models. Therefore, as discussed by
Pietrinferni et al. (2009), the RGB bump - at fixed age and [Fe/H] value - is
expected to be fainter in those sub-populations characterised by a peculiar
chemical pattern (see also Salaris et al. 2006). However, for the increasing
difference in the He content, the effect of the He abundance on the RGB bump
brightness overcomes the one associated to the higher metallicity, and the bump in
the I/E sub-population becomes brighter with respect the P sub-population.
Theoretical models shown in Fig. 6 suggest an average difference
between the P and the I/E sub-population of ![]()
![]() .
This agrees more
closely with the estimates obtained in previous sections from
independent indicators, even if lower. We consider, however, that NGC 2808 is not in
the sample and that this cluster brings a strong signature of Y enhancement.
.
This agrees more
closely with the estimates obtained in previous sections from
independent indicators, even if lower. We consider, however, that NGC 2808 is not in
the sample and that this cluster brings a strong signature of Y enhancement.
As stated above, all the stellar models used in this analysis were
computed by assuming a constant [Fe/H] value regardless of the
adopted initial He content. It is in fact expected that both candidate polluters
(AGB and FRMS) do not alter the
initial iron content. However, it could be worthwhile to check to what extent - if any -
the present results are affected by this assumption. For this purpose, we
computed suitable stellar models for selected initial He contents, keeping the iron
content fixed. We found that the magnitude difference between the RGB bump
of the I/E sub-population and that of the P one
is increased by a negligible 0.01 mag for an He difference between the two
sub-populations equal to
![]() and about 0.09 mag for
and about 0.09 mag for
![]() .
From Figs. 5 and 6, it is clear that
this change does not affect our previous estimates of the He
content difference.
.
From Figs. 5 and 6, it is clear that
this change does not affect our previous estimates of the He
content difference.
Finally, we wish to draw attention to a possible test: clusters with larger
![]() should also display broader RGB bumps. From Figs. 5 and 6 we estimate that a
should also display broader RGB bumps. From Figs. 5 and 6 we estimate that a
![]() should correspond to a visible
broadening of the bump (since first and second-generation stars should display
differences of about 0.20-0.35 mag between their respective bumps). The precise
photometry of all their RGB stars should be used. An ideal pair for this
comparison are the two GCs NGC 2808 and NGC 6121, which have similar metallicity
but very different extensions of the Na-O anticorrelation (Carretta et al., Paper VII) and very different implied
should correspond to a visible
broadening of the bump (since first and second-generation stars should display
differences of about 0.20-0.35 mag between their respective bumps). The precise
photometry of all their RGB stars should be used. An ideal pair for this
comparison are the two GCs NGC 2808 and NGC 6121, which have similar metallicity
but very different extensions of the Na-O anticorrelation (Carretta et al., Paper VII) and very different implied ![]() (Gratton et al. 2010).
(Gratton et al. 2010).
4 Discussion and summary
Recently, spreads and splits in GC RGBs have been presented other than the ones (in V-K, metallicity and temperature) considered here. They most probably stem from the same phenomenon we are seeing here, since the He-enhanced stars should also show other chemical signatures. For instance, the correlated N-enhancement should be responsible for the effects seen in the colour-magnitude diagrams involving the Johnson U or Strömgren u filters (Yong et al. 2008; Marino et al. 2008). On the other hand, the effect seen in hk photometry, attributed to a spread in calcium by Lee et al. (2009) and demonstrated not to be so by Carretta et al. (2010), still awaits a definite explanation.
We have used information on RGB stars in GCs to infer the plausible He
differences implied by the existence of two generations of stars. This is a new
approach, since the different methods used in the past to deduce the He content
of GCs generally involve the HB, which is the evolutionary phase more sensitive to even
small He variations (the two exceptions being ![]() Cen and NGC 2808 with
their multiple MSs).
Cen and NGC 2808 with
their multiple MSs).
Apart from the information coming from photometric data, He can be deduced from
the spectra of HB stars, where He lines are visible for temperatures hotter than
about 8500 K. Villanova et al. (2009) studied seven HB stars in NGC 6752, using UVES
spectra at high resolution and very high S/N. For the four stars where they were
able to measure the He line, they obtained a value similar to the cosmological
one (Y=0.245).
However, these four are all O-rich, Na-poor, while Villanova
et al. could not measure He for the only Na-rich, O-poor star, the
one that
should also be He-enhanced, so the case is not yet settled. However,
the
photospheric abundances of HB stars hotter than about
11 500 K are altered by
atomic diffusion processes and cannot be used directly to measure the
original
values. For instance, Behr (2003) finds a depletion in moderately hot
HB stars
in several GCs. In a series of papers
(e.g., Moehler et al. 2007), Moehler et al. concentrated instead on the hottest part of the HB
(and blue-hook stars in the two GCs - ![]() Cen and NGC 2808 - where they are
present) and found He-enhancement. This can be attributed either to pollution
from a previous generation or to He flash-induced mixing occurring in hot
He-flashers, i.e. those stars experiencing the He flash not at the RGB tip but
along the white dwarf cooling sequence (see Castellani & Castellani 1993). A further
discussion of this problem in
Cen and NGC 2808 - where they are
present) and found He-enhancement. This can be attributed either to pollution
from a previous generation or to He flash-induced mixing occurring in hot
He-flashers, i.e. those stars experiencing the He flash not at the RGB tip but
along the white dwarf cooling sequence (see Castellani & Castellani 1993). A further
discussion of this problem in ![]() Cen can be found in Cassisi et al. (2009).
Cen can be found in Cassisi et al. (2009).
In a companion paper (Gratton et al. 2010), we studied the effect of (even a small) difference in He content on the morphology of HBs, and found that He is most probably the third parameter governing the HB, after metallicity and age. We refer the reader to that paper for a long and detailed discussion of the effects of He variations, of methods to measure He content (e.g., the R-method: Iben 1968), and of comparison between results obtained through different approaches. In the present paper we limited our analysis to the differences in He that can be deduced from RGB stars.
May we use the present analysis, combined with the previous work on the Na-O and other (anti)correlations to try to distinguish between AGB and FRMS as the polluters of the second-generation stars? We need to consider that He is essentially produced in MS for both classes of polluters, while there is a difference for the other ``peculiar'' elements (O, Na, Mg, Al, Si), produced during hot bottom burning or in MS, respectively. However, we still lack important details of stellar evolution (e.g., how much He is dredged up in AGB stars or the dependence on metallicity - via rotation - of FRMS), the numbers are still small, and the inferences are not conclusive. We need to further investigate the dependencies of variations in He and those other elements on the stars and cluster properties.
In summary, with the present work we have seen that
- i)
- it is possible to also deduce variations of He from RGB stars in GCs when using large samples treated homogeneously;
- ii)
- these variations are generally measurable from colour (here V-K) and [Fe/H] only between first-generation (P) and extreme second-generations (E) stars;
- iii)
- the variations implied for the average of the 19 GCs considered range between
0.05-0.10 (
 ); however, the heavy-elements mixture
assumed for the second-generation stars has to be taken into account (and we
have presented two extreme cases);
); however, the heavy-elements mixture
assumed for the second-generation stars has to be taken into account (and we
have presented two extreme cases);
- iv)
- NGC 2808 is a notable exception because, in this cluster, differences in
colour and metallicity are also seen between P and the intermediate (I)
component of second-generation stars. This is perfectly in line with
NGC 2808 presenting clear evidence of three He levels also in the MS. For
NGC 2808 the deduced
 values are higher (see Table 3) than
for the average of all GCs;
values are higher (see Table 3) than
for the average of all GCs;
- v)
- similar results can also be obtained when considering the luminosity of the
RGB bump. We could only test this method for 14 GCs; unluckily, NGC 2808 is not
among them. Within the limits of the rather poor statistics, we found that the implied
 values are in reasonable agreement with those found from colour and metallicity;
values are in reasonable agreement with those found from colour and metallicity;
- vi)
- the absolute calibration of the
 in GCs still needs to be
defined.
in GCs still needs to be
defined.
This work was partially funded by the grant INAF 2005 ``Experimenting nucleosynthesis in clean environments'' and the PRIN MIUR 2007 ``Multiple stellar populations in Globular Clusters''. S.L. is grateful to the DFG cluster of excellence ``Origin and Structure of the Universe'' for support. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA's Astrophysical Data System. We thank the referee for her/his comments, useful for improving the presentation.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, D. R., & Sarajedini, A. 1999, ApJ, 511, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., Piotto, G., King, I. R., Bedin, L. R., & Guhathakurta, P. 2009, ApJ, 697 L58 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & de Mink, S. 2009, MNRAS, 398, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Gratton R. G., Lucatello, S., Bragaglia, A., & Bonifacio, P. 2005, A&A, 433, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton R. G., et al. 2006, A&A, 450, 523 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton R. G., Lucatello, S., & Momany, Y. 2007a, A&A, 464, 927 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007b, A&A, 464, 967 (Paper VI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007c, A&A, 464, 939 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Recio-Blanco, A., Gratton, R. G., Piotto, G., & Bragaglia, A. 2007d, ApJ, 671, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 (Paper VII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 (Paper VIII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D'Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, ApJ, 712, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Anderson, J., et al. 2009, ApJ, 702, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, M., Castellani, V., & Cassisi, S. 2005, A&A, 437, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M. 2009, IAU Symp., 258, 209 [NASA ADS] [Google Scholar]
- Cohen, J. G., Persson, S. E., & Frogel, J. A. 1978, ApJ, 222, 165 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., & Ventura, P. 2007, MNRAS, 379, 1431 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., & Caloi, V. 2008, MNRAS, 390, 693 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel C., Prantzos, N., & Ekstrom, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraro, F. R., Messineo, M., Fusi Pecci, F., et al. 1999, AJ, 118, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Glatt, K., Grebel, E. K., Sabbi, E., et al. 2008, AJ, 136, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2006, A&A, 455, 271(Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953(Paper V) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D'Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Iben., I. Jr. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kaviraj, S., Sohn, S. T., O'Connell, R. W., et al. 2007, MNRAS, 377, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., Joo, S.-J., Han, S.-I., et al. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-W., Kang, Y.-W., Lee, J., & Lee, Y.-W. 2009, Nature, 462, 480 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mackey, A. D., Broby Nielsen, P., Ferguson, A. M. N., & Richardson, J. C. 2008, ApJ, 681, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A., et al. 2008, ApJ, 637, 241 [CrossRef] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., & Anderson, J. 2009, A&A, 497, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Piotto, G., King, I. R., et al. 2010, ApJ, 709, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Dreizler, S., Lanz, T., et al. 2007, A&A, 475, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., Percival, S., & Ferguson, J. W. 2009, ApJ, 697, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations, ISBN 0-470-09220-3. Wiley-VCH [Google Scholar]
- Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Weiss, A., Ferguson, J. W., & Fusilier, D. J. 2006, ApJ, 645, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., & D'Antona, F. 2009, A&A, 499, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Piotto, G., & Gratton, R. G. 2009, A&A, 499, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Braun, K., & Mateo, M. 2001, AJ, 121, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008, ApJ, 684, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Cassisi, S., Piotto, G., Bono, G., & Salaris, M. 1999, ApJ, 518, L49 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... giants
![[*]](/icons/foot_motif.png)
- Based on observations collected at ESO telescopes under programmes 072.D-507 and 073.D-0211.
- ... split)
![[*]](/icons/foot_motif.png)
- The split subgiant branches (SGB, e.g., NGC 6388: Moretti et al. 2009; NGC 1851: Milone et al. 2008) seem more related to differences in age or CNO content. A spread in ages is probably the cause of the spread/split MS turn-offs found in many intermediate-age Magellanic Cloud GCs (Mackey et al. 2008; Milone et al. 2009, in LMC; Glatt et al. 2008, in SMC) even if for them - but notably not for the old Galactic GCs - there is an alternative physical interpretation based on the observational effects associated to the occurrence of stellar rotation as discussed by Bastian & de Mink (2009).
- ... anticorrelation
![[*]](/icons/foot_motif.png)
- It is generally assumed that first-generation stars have a chemical composition similar to field stars of similar age and metallicity (i.e., high O and Mg, low Na and Al, etc.), while second-generation stars, formed from material polluted by matter lost from the primordial population, show the abundance patterns (e.g., Na-O anticorrelation) that are unique to GCs.
- ... BaSTI
![[*]](/icons/foot_motif.png)
- The whole set of stellar models used in present work, as well as additional predictions for He-enhanced models can be retrieved from the URL site: http://www.oa-teramo.inaf.it/BASTI
- ... series
![[*]](/icons/foot_motif.png)
- In particular: in Paper I for NGC 2808, Paper II for NGC 6752, Papers III, V for NGC 6441, Paper IV for NGC 6218, Paper VI for NGC 6838, Paper VII for NGC 104, NGC 288, NGC 1904, NGC 3201, NGC 4590, NGC 5904, NGC 6121, NGC 6171, NGC 6254, NGC 6397, NGC 6809, NGC 6838, NGC 7078, and NGC 7099.
- ... R2MASS
![[*]](/icons/foot_motif.png)
- The Two Micron All Sky Survey is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
- ... indistinguishable
![[*]](/icons/foot_motif.png)
- This has also the effect of minimising the possible
contamination of AGB stars, since the separation between RGB and
AGB is clear at that magnitude level. As an example, in the case of
NGC 6752 , MK=-3.5 means
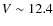 (see
Carretta et al. 2007a).
From Fig. 1 of that paper, the separation in colour (B-V)
between the two sequences is then about 0.1 mag, i.e., much
more than the photometric error.
(see
Carretta et al. 2007a).
From Fig. 1 of that paper, the separation in colour (B-V)
between the two sequences is then about 0.1 mag, i.e., much
more than the photometric error.
- ... means
![[*]](/icons/foot_motif.png)
- The values would become
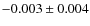 and
and 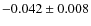 had we eliminated
NGC 3201, a cluster with differential reddening (which we
corrected for anyway, using the maps by von
Braun & Mateo 2001). Its potential influence on the
global properties of our sample
is greater than the one by, e.g., NGC 6388 or
NGC 6441 because we have many more stars. Even so, the results
are indistinguishable.
had we eliminated
NGC 3201, a cluster with differential reddening (which we
corrected for anyway, using the maps by von
Braun & Mateo 2001). Its potential influence on the
global properties of our sample
is greater than the one by, e.g., NGC 6388 or
NGC 6441 because we have many more stars. Even so, the results
are indistinguishable.
- ...
respectively
![[*]](/icons/foot_motif.png)
- The small difference in
 between
the average of 19 GCs and NGC 2808 alone comes from
the latter making
a strong contribution to the global E population.
between
the average of 19 GCs and NGC 2808 alone comes from
the latter making
a strong contribution to the global E population.
- ... populations
![[*]](/icons/foot_motif.png)
- The definition is
 .
Since
.
Since 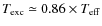 ,
we
have
,
we
have  .
By differentiating the equation,
we have the relation between d
.
By differentiating the equation,
we have the relation between d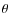 and d
and d
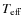 .
.
- ...
LF
![[*]](/icons/foot_motif.png)
- To consider the observational errors that can
affect the photometric data for each GC in our sample, when computing
the
synthetic LFs we have considered a photometric error of
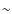 0.02 mag.
0.02 mag.
All Tables
Table 1: Difference in colour and metallicity between different populations in the 19 GCs.
Table 2: Summary of differences in colour and metallicity between populations.
Table 3: Summary of differences in Y between first and second-generation stars.
Table 4:
Adopted values of
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14702f1.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg15.png)
|
Figure 1: Mean differences in (V-K) colours between the I and P components in the 19 GCs as a function of the metallicity difference (I - P). The two are well-correlated, as indicated by the Pearson and Spearman coefficients. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{14702f2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg46.png)
|
Figure 2: Individual differences I - P of metallicity ( upper panel) and colours ( lower panel) versus [Fe/H], with Spearman and Pearson coefficients indicated (in the lower panel, values in parenthesis are obtained excluding NGC 6388 and NGC 6441). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.35,clip]{14702f3a.ps}\par\includegraphics[scale=0.35,clip]{14702f3b.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg57.png)
|
Figure 3: Cumulative distributions for difference in colour ( upper panel) and metallicity ( lower panel) for individual stars in the three populations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{14702f4a.ps}\par\includegraphics[width=5.5cm,clip]{14702f4b.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg60.png)
|
Figure 4:
Upper panel: histogram of the difference in magnitude between
individual V and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14702f5.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg64.png)
|
Figure 5:
The V-band RGB
bump brightness difference between the P sub-population and the I/E one
as a function of the He abundance difference between the two
sub-populations. In this case, for both sub-populations it has been
assumed the
same normal, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14702f6.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14702-10/Timg65.png)
|
Figure 6: As in Fig. 5, but taking into account that the I/E sub-population is characterised by a peculiar chemical pattern with a CNONa anticorrelation (case b). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


