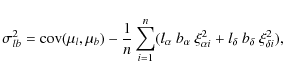| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201014353 | |
| Published online | 15 September 2010 | |
Insights on the Milky Way bulge formation
from the correlations
between kinematics and metallicity![[*]](/icons/foot_motif.png)
C. Babusiaux1 - A. Gómez1 - V. Hill2 - F. Royer1 - M. Zoccali3 - F. Arenou1 - R. Fux4 - A. Lecureur1 - M. Schultheis5 - B. Barbuy6 - D. Minniti3,8 - S. Ortolani7
1 - GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5
Place Jules Janssen, 92190 Meudon, France
2 - Laboratoire CASSIOPEE, University of Nice Sophia Antipolis, CNRS,
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
3 - P. Universidad Católica de Chile, Departamento de Astronomía y
Astrofísica, Casilla 306, Santiago 22, Chile
4 - Observatoire de Genève, Université de Genève, 51 Ch des Maillettes,
1290 Sauverny, Switzerland
5 - Observatoire de Besançon, CNRS UMR6091, BP 1615, 25010 Besançon,
France
6 - Universidade de São Paulo, IAG, Rua do Matão 1226, São Paulo
05508-900, Brazil
7 - Universita di Padova,Vicolo dell'Osservatorio 5, 35122 Padova,
Italy
8 - Vatican Observatory, V00120 Vatican City State, Italy
Received 4 March 2010 / Accepted 12 May 2010
Abstract
Context. Two main scenarios for the formation of the
Galactic bulge are invoked, the first one through gravitational
collapse or hierarchical merging of subclumps, the second through
secular evolution of the Galactic disc.
Aims. We aim to constrain the formation of the
Galactic bulge through studies of the correlation between kinematics
and metallicities in Baade's Window (
![]() ,
,
![]() )
and two other fields along the bulge minor axis (
)
and two other fields along the bulge minor axis (
![]() ,
,
![]() and
and
![]() ).
).
Methods. We combine the radial velocity and the
[Fe/H] measurements obtained with FLAMES/GIRAFFE at the VLT with a
spectral resolution of R=20 000, plus for
the Baade's Window field the OGLE-II proper motions, and compare these
with published N-body simulations of the Galactic
bulge.
Results. We confirm the presence of two distinct
populations in Baade's Window found in Hill et al. (2010,
A&A, submitted): the metal-rich population presents bar-like
kinematics while the metal-poor population shows kinematics
corresponding to an old spheroid or a thick disc. In this context the
metallicity gradient along the bulge minor axis observed by Zoccali
et al. (2008, A&A, 486, 177), visible also in the
kinematics, can be related to a varying mix of these two populations as
one moves away from the Galactic plane, alleviating the apparent
contradiction between the kinematic evidence of a bar and the existence
of a metallicity gradient.
Conclusions. We show evidence that the two main
scenarios for the bulge formation co-exist within the Milky Way bulge.
Key words: Galaxy: bulge - Galaxy: formation - Galaxy: abundances - Galaxy: kinematics and dynamics
1 Introduction
Although the Milky Way bulge is our closest opportunity to study in detail such a complex chemo-dynamical system, its formation and evolution is still poorly understood. Indeed the high extinction, the crowding, and the superposition of multiple structures along the line of sight make studies of the inner Galactic regions challenging. Two main scenarios have been invoked for bulge formation. The first is gravitational collapse (Eggen et al. 1962) or hierarchical merging of subclumps (Aguerri et al. 2001; Noguchi 1999). There the bulge formed before the disc and the star-formation time-scale was very short. The resulting stars are old (>10 Gyr) and have enhancements ofChemo-dynamical modelling of disc galaxy formation in a Cold
Dark Matter (CDM) universe stresses that both types of bulges can
coexist in the same galaxy. In the Samland
& Gerhard (2003) simulation the bulge contains two
stellar populations, an old population formed during the collapse phase
and a younger bar population, differing in the [![]() /Fe] ratio. Nakasato & Nomoto (2003)
suggest that the Galactic bulge may consist of two chemically different
components: one rapidly formed through subgalactic clump merger in the
proto-Galaxy, and the other one formed later in the inner region of the
disc. The [Fe/H] abundance of the merger component tends to be smaller
than that of the second component. Recently Rahimi
et al. (2010) simulated bulges formed through
multiple mergers and analysed the chemical and dynamical properties of
accreted stars with respect to locally formed stars: accreted stars
tend to form in early epochs and have lower [Fe/H] and higher [Mg/Fe]
ratios, as expected.
/Fe] ratio. Nakasato & Nomoto (2003)
suggest that the Galactic bulge may consist of two chemically different
components: one rapidly formed through subgalactic clump merger in the
proto-Galaxy, and the other one formed later in the inner region of the
disc. The [Fe/H] abundance of the merger component tends to be smaller
than that of the second component. Recently Rahimi
et al. (2010) simulated bulges formed through
multiple mergers and analysed the chemical and dynamical properties of
accreted stars with respect to locally formed stars: accreted stars
tend to form in early epochs and have lower [Fe/H] and higher [Mg/Fe]
ratios, as expected.
Exploring correlations of abundances and kinematics in Baade's Window, Soto et al. (2007) suggest a transition in the kinematics of the bulge, from an isotropic oblate spheroid to a bar, at [Fe/H] = -0.5 dex. Their study was based on 315 K and M giants with proper motions of Spaenhauer et al. (1992), radial velocities of Sadler et al. (1996) and low-resolution abundances of Terndrup et al. (1995) re-calibrated with the iron abundances scale of Fulbright et al. (2006). Similar conclusions were obtained earlier by Zhao et al. (1994) using a sample of 62 K giants who pointed out the triaxiality of the bulge from kinematics in Baade's Window and that the metal-poor and metal-rich populations were not drawn from the same distribution.
We here analyse the correlations between kinematics and
metallicity along three different minor-axis fields: Baade's Window (
![]() ),
),
![]() and
and ![]() ,
for which [Fe/H] abundances (Zoccali
et al. 2008, hereafter Paper I; and Hill et al. 2010,
hereafter Paper III) and radial velocities data for about
700 stars have been determined. Paper II obtained
[Fe/H] and [Mg/H] metallicity distributions for red clump stars in
Baade's Window and showed that the sample seems to be separated into
two different populations in the metallicity distributions. We here use
the kinematic properties of the samples to confirm and constrain the
nature of these two populations in Baade's Window and study their
relative proportion change along the bulge minor axis fields of
Paper I. The paper is organized as follows: Sect. 2
summarizes the data used in this study. In Sect. 3 we analyse
Baade's Window by combining our spectroscopic data with OGLE proper
motion data. In Sect. 4 we analyse the radial velocity versus
metallicity trend along the bulge minor axis. In Sect. 5 we
compare our data with some published N-body models.
Section 6 discusses our results.
,
for which [Fe/H] abundances (Zoccali
et al. 2008, hereafter Paper I; and Hill et al. 2010,
hereafter Paper III) and radial velocities data for about
700 stars have been determined. Paper II obtained
[Fe/H] and [Mg/H] metallicity distributions for red clump stars in
Baade's Window and showed that the sample seems to be separated into
two different populations in the metallicity distributions. We here use
the kinematic properties of the samples to confirm and constrain the
nature of these two populations in Baade's Window and study their
relative proportion change along the bulge minor axis fields of
Paper I. The paper is organized as follows: Sect. 2
summarizes the data used in this study. In Sect. 3 we analyse
Baade's Window by combining our spectroscopic data with OGLE proper
motion data. In Sect. 4 we analyse the radial velocity versus
metallicity trend along the bulge minor axis. In Sect. 5 we
compare our data with some published N-body models.
Section 6 discusses our results.
2 Data
The different samples are described in detail in Papers I
and II. Only a brief summary is given here. Paper I
samples consist of K giants (called RGB samples
below) observed in the following fields: Baade's Window (
![]() ,
,
![]() :
194 stars);
:
194 stars); ![]() (
(
![]() ,
,
![]() :
201 stars) and
:
201 stars) and
![]() (
(
![]() ,
,
![]() :
99 stars). All stars have photometric V,
I data coming from different sources (for details
see Paper I and Paper II) and 2MASS J,
H, K data. The spectra
have been obtained with VLT/FLAMES-GIRAFFE spectrograph in Medusa mode
at a resolution of about 20 000. The sample of
Paper II, observed in the same conditions, contains 219 red
clump stars (called RC data in what follows) in Baade's Window
(
:
99 stars). All stars have photometric V,
I data coming from different sources (for details
see Paper I and Paper II) and 2MASS J,
H, K data. The spectra
have been obtained with VLT/FLAMES-GIRAFFE spectrograph in Medusa mode
at a resolution of about 20 000. The sample of
Paper II, observed in the same conditions, contains 219 red
clump stars (called RC data in what follows) in Baade's Window
(
![]() ,
,
![]() ).
Iron abundances have been obtained with a mean accuracy of about
0.2 dex, depending on the value of [Fe/H], more metal-rich
stars have the largest errors. In order to increase the statistics, we
combined the two samples of Baade's Window (RC sample of
Paper II and RGB sample of Paper I). Due to a
difference in the reduction process, the two original MDs were not
totally compatible. We therefore used in this combination the new
reduction of the RGB sample made with the Paper II automatic
reduction process (see Sect. 5.1.4 of Paper II),
which lead to two compatible MDs, which we can therefore combine in
Sect. 3
of this study. However, we note that according to the Besançon model (Robin et al. (2003), see
Fig. 9 of Paper II and Fig. 10 of
Paper I), the two selections have slightly different mean
distance and contamination. In Sect. 4 the other
minor axis fields at
).
Iron abundances have been obtained with a mean accuracy of about
0.2 dex, depending on the value of [Fe/H], more metal-rich
stars have the largest errors. In order to increase the statistics, we
combined the two samples of Baade's Window (RC sample of
Paper II and RGB sample of Paper I). Due to a
difference in the reduction process, the two original MDs were not
totally compatible. We therefore used in this combination the new
reduction of the RGB sample made with the Paper II automatic
reduction process (see Sect. 5.1.4 of Paper II),
which lead to two compatible MDs, which we can therefore combine in
Sect. 3
of this study. However, we note that according to the Besançon model (Robin et al. (2003), see
Fig. 9 of Paper II and Fig. 10 of
Paper I), the two selections have slightly different mean
distance and contamination. In Sect. 4 the other
minor axis fields at ![]() and
and ![]() are compared with the Baade's Window data and, to be consistent, we
will use only the original RGB data of Baade's Window computed in
Paper I in this comparison.
are compared with the Baade's Window data and, to be consistent, we
will use only the original RGB data of Baade's Window computed in
Paper I in this comparison.
Radial velocities were obtained with the cross-correlation
tool available in the GIRAFFE reduction pipeline (Royer
et al. 2002). The individual spectra were
cross-correlated with a box-shaped template corresponding to a K0 giant
star. For each target, the barycentric radial velocities derived for
each exposure were combined into an average velocity, and the standard
deviation was used as an error estimate. The median error of the
combined velocities range from 0.26 to 0.43 km s-1
for the different fields. Throughout this paper, ![]() stands for the heliocentric radial velocity.
stands for the heliocentric radial velocity.
OGLE-II proper motions (Sumi et al. 2004) are only available for the Baade's Window field. We removed stars with less than 100 data points used in the proper motion computation. Those removed stars are either near the edge of the CCD image or CCD defects or affected by blending. In the present paper the mas/yr has been converted in km s-1 assuming a distance to the Galactic Centre of 8 kpc (1 mas/yr = 37.9 km s-1). The mean error on the proper motions of our sample is 1.24 mas/yr, i.e. 47 km s-1. We worked on the relative values of the proper motions as provided in the catalogue. Section 6 of Sumi et al. (2004) details how one can transform the catalogue into an inertial frame based on the measured proper motions for the Galactic Centre (GC). Our data cover fields BUL_SC45 and BUL_SC46, which do not show any difference in the proper motions of the GC (Table 3 of Sumi et al. 2004) so that the relative zero-points from these two fields do not need to be taken into account.
Throughout this paper errors will be computed from a bootstrap analysis using 1000 samplings of the datasets.
3 Analysis of Baade's Window
Our sample of 340 stars in Baade's Window is at present the largest one
that has proper motions, radial velocities and homogeneous iron
abundances determinations. This sample combines both the Baade's Window
dataset of Paper I (RGB sample) and the dataset of
Paper II (RC sample) with metallicities derived in an
homogeneous way by Paper II.
We computed the proper motion dispersions following the equations in Spaenhauer et al. (1992):
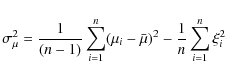
|
(1) |
with
The covariance ![]() ,
used in the computation of correlations between the different velocity
components and in the velocity ellipsoid angles, also needs to be
corrected from measurement errors due to the transformation from image
coordinates to galactic proper motions. Indeed we have
,
used in the computation of correlations between the different velocity
components and in the velocity ellipsoid angles, also needs to be
corrected from measurement errors due to the transformation from image
coordinates to galactic proper motions. Indeed we have
with the errors in the equatorial proper motions un-correlated (Sumi 2010, private communication), which implies
with
Our Baade's Window radial velocity measurements
![]() km s-1,
km s-1,
![]() km s-1
excellently agree with previous studies: Howard
et al. (2008):
km s-1
excellently agree with previous studies: Howard
et al. (2008):
![]() km s-1,
km s-1,
![]() km s-1,
Rangwala et al. (2009):
km s-1,
Rangwala et al. (2009):
![]() km s-1,
km s-1,
![]() km s-1,
and other measurements listed in Rangwala
et al. (2009).
The proper motion dispersions
km s-1,
and other measurements listed in Rangwala
et al. (2009).
The proper motion dispersions
![]() mas/yr
and
mas/yr
and ![]() mas/yr
also excellently agree with the high-accuracy HST
measurements of Kozowski
et al. (2006):
mas/yr
also excellently agree with the high-accuracy HST
measurements of Kozowski
et al. (2006):
![]() ,
,
![]() mas/yr.
mas/yr.
3.1 Kinematics versus metallicity
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14353Fig1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg41.png)
|
Figure 1:
Dispersion of the radial (
|
| Open with DEXTER | |
Figure 1
plots the dispersion of velocity components along the line-of-sight (
![]() ), the galactic longitude (
), the galactic longitude (
![]() )
and the galactic latitude (
)
and the galactic latitude (
![]() )
as a function of [Fe/H]. The figure shows that
)
as a function of [Fe/H]. The figure shows that
![]() increases with metallicity, while
increases with metallicity, while
![]() decreases. No significant variation of
decreases. No significant variation of
![]() is seen. To quantify if these variations are indeed significant, we
used the F-test to compare the variances of the velocity distributions
for the first and last 33% quantiles ([Fe/H]<-0.14 and
[Fe/H]>0.30):
is seen. To quantify if these variations are indeed significant, we
used the F-test to compare the variances of the velocity distributions
for the first and last 33% quantiles ([Fe/H]<-0.14 and
[Fe/H]>0.30): ![]() and
and ![]() are indeed significantly different (p-value = 0.04
and 0.01 respectively), while the variation in
are indeed significantly different (p-value = 0.04
and 0.01 respectively), while the variation in
![]() is not significant (p-value = 0.2). These results do
not confirm those of Soto
et al. (2007). Their study, based on a compiled
sample of proper motions, radial velocities and low-resolution
abundances, showed only a rather shallow variation in
is not significant (p-value = 0.2). These results do
not confirm those of Soto
et al. (2007). Their study, based on a compiled
sample of proper motions, radial velocities and low-resolution
abundances, showed only a rather shallow variation in
![]() ,
in the sense that the more metal-poor stars have a higher
,
in the sense that the more metal-poor stars have a higher
![]() value. The discrepancies with the study of Soto
et al. (2007) may partly come from the sample
itself. Our results are based on more accurate and homogeneous
spectroscopic data. The different contamination of the sample by
foreground objects may also be another source of discrepancy. Recently,
Clarkson et al. (2008)
constructed the {l,b} velocity
ellipse as a function of line-of-sight distance from HST
proper motions and estimated photometric parallaxes in the Sagittarius
Window and demonstrated that its properties are sensitive to the
distance to the considered objects. They concluded that the
depth-integrated velocity ellipsoid of a small population of objects
should be treated with caution. Half of our sample are red clump stars,
while Soto et al. (2007)
studied M giants, so we expect our sample to be less biased towards
closer stars.
value. The discrepancies with the study of Soto
et al. (2007) may partly come from the sample
itself. Our results are based on more accurate and homogeneous
spectroscopic data. The different contamination of the sample by
foreground objects may also be another source of discrepancy. Recently,
Clarkson et al. (2008)
constructed the {l,b} velocity
ellipse as a function of line-of-sight distance from HST
proper motions and estimated photometric parallaxes in the Sagittarius
Window and demonstrated that its properties are sensitive to the
distance to the considered objects. They concluded that the
depth-integrated velocity ellipsoid of a small population of objects
should be treated with caution. Half of our sample are red clump stars,
while Soto et al. (2007)
studied M giants, so we expect our sample to be less biased towards
closer stars.
Table 1: Baade's Window velocity ellipsoid parameters.
Below we analyse the shape and the orientation of the velocity
ellipsoid for the data sets quoted in Table 1. From the whole
sample, the observed anisotropy in
![]() agrees well with the results of Spaenhauer
et al. (1992), Feltzing
& Johnson (2002), Kuijken
& Rich (2002) and Kozowski
et al. (2006). We also detected an anisotropy in
agrees well with the results of Spaenhauer
et al. (1992), Feltzing
& Johnson (2002), Kuijken
& Rich (2002) and Kozowski
et al. (2006). We also detected an anisotropy in
![]() and not a significant one in
and not a significant one in
![]() .
Because the kinematic properties of the whole sample is an average of
the properties of distinct populations, we analyse the shape of the
velocity ellipsoid of the two metallicity samples.
.
Because the kinematic properties of the whole sample is an average of
the properties of distinct populations, we analyse the shape of the
velocity ellipsoid of the two metallicity samples.
The metal-poor sample ([Fe/H]<-0.14) shows a
![]() higher than the other components,
higher than the other components,
![]() ,
and an anisotropy in
,
and an anisotropy in
![]() (confirmed by an F-test with a 98% confidence) and in
(confirmed by an F-test with a 98% confidence) and in
![]() (an F-test cannot be performed here due to the large difference in the
errors in the proper motion and radial velocity measurements).
Following Zhao et al.
(1996), the observed anisotropies for the metal-poor sample (
(an F-test cannot be performed here due to the large difference in the
errors in the proper motion and radial velocity measurements).
Following Zhao et al.
(1996), the observed anisotropies for the metal-poor sample (
![]() )
may be interpreted in terms of rotation broadening: as Baade's Window
passes close to the minor axis of the bulge, only
)
may be interpreted in terms of rotation broadening: as Baade's Window
passes close to the minor axis of the bulge, only
![]() should be broadened by the rotation, which is indeed what is observed.
However, a possible contamination with foreground thick disc stars
higher than expected would also contribute to an increase in
should be broadened by the rotation, which is indeed what is observed.
However, a possible contamination with foreground thick disc stars
higher than expected would also contribute to an increase in ![]() .
.
For the metal-rich sample ([Fe/H]>0.30) the shape of
the velocity ellipsoid is significantly different from the metal-poor
sample. We observe for the metal-rich population
![]() ,
and that
,
and that ![]() is higher (with 96% confidence) and
is higher (with 96% confidence) and ![]() is lower (with 99% confidence) than the observed values for the
metal-poor sample. In the case of a bar, the velocity dispersion along
the bar major axis is expected to be much larger than its azimuthal
dispersion, which is itself smaller than its vertical dispersion. If
the bar was pointing nearly end-on, that would mean
is lower (with 99% confidence) than the observed values for the
metal-poor sample. In the case of a bar, the velocity dispersion along
the bar major axis is expected to be much larger than its azimuthal
dispersion, which is itself smaller than its vertical dispersion. If
the bar was pointing nearly end-on, that would mean
![]() ,
which is what we observe. The anisotropy in
,
which is what we observe. The anisotropy in
![]() observed for the metal-rich sample may be explained by the flattening
of the bar-driven population.
observed for the metal-rich sample may be explained by the flattening
of the bar-driven population.
The Baade's Window velocity ellipsoid shows the
characteristics of a non-axisymmetric system. We now analyse the
orientation of the velocity ellipsoid. We first examine the
correlations between the different velocity components. The obtained
cross-correlation terms (
![]() ,
,
![]() being
the covariance) are given in Table 1.
being
the covariance) are given in Table 1.
Clb
is higher than the results of Kozowski
et al. (2006) (
![]() )
and Rattenbury et al.
(2007) (
)
and Rattenbury et al.
(2007) (
![]() ).
We note that Rattenbury
et al. (2007) used the same OGLE-II data but
selected only stars with errors in the proper motion smaller than
1 mas/yr, introducing a bias towards closer stars, but
reducing the impact of the correction described in Eq. (2).
).
We note that Rattenbury
et al. (2007) used the same OGLE-II data but
selected only stars with errors in the proper motion smaller than
1 mas/yr, introducing a bias towards closer stars, but
reducing the impact of the correction described in Eq. (2).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg72.png)
|
Figure 2:
|
| Open with DEXTER | |
A decrease with metallicity of the correlations between the velocity
components seems to be present in our sample. We now quantify the
observed correlations in terms of velocity ellipsoid angles in
Table 1
with

|
(3) |
Below we will call the vertex deviation
Our derived value of
![]() is consistent with the results of Clarkson
et al. (2008) (
is consistent with the results of Clarkson
et al. (2008) (
![]() )
and Kozowski et al. (2006)
(
)
and Kozowski et al. (2006)
(
![]() ).
It shows a significant variation with metallicity. The Pearson's
correlation test indicates a correlation with 99% confidence for the
metal-rich sample, while the metal-poor sample correlation is not
significant (p-value = 0.1).
).
It shows a significant variation with metallicity. The Pearson's
correlation test indicates a correlation with 99% confidence for the
metal-rich sample, while the metal-poor sample correlation is not
significant (p-value = 0.1).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg80.png)
|
Figure 3: Vertex deviation lv in Baade's Window as a function of metallicity by bins of 0.4 dex. |
| Open with DEXTER | |
We measured ![]() for the first time. The Pearson's correlation test does not show a
significant correlation between
for the first time. The Pearson's correlation test does not show a
significant correlation between ![]() and
and ![]() for the metal-poor sample (p-value = 0.3), while it
finds the correlation to be significant for the metal-rich sample with
99.9% confidence.
for the metal-poor sample (p-value = 0.3), while it
finds the correlation to be significant for the metal-rich sample with
99.9% confidence.
Following Paper II, we applied the SEMMUL Gaussian
components decomposition algorithm (Celeux
& Diebolt 1986) to the [Fe/H] distribution of the
full Baade's Window sample and find a decomposition fully compatible
with the Paper II results (which were based on the red clump
sample only): the decomposition clearly identifies two populations, in
roughly equal proportions, a metal-poor component (46 ![]() 3%
of the sample,
3%
of the sample, ![]() Fe/H
Fe/H
![]() )
with a large dispersion (0.23
)
with a large dispersion (0.23 ![]() 0.01 dex) and a metal-rich
component (54
0.01 dex) and a metal-rich
component (54 ![]() 3%
of the sample,
3%
of the sample, ![]() Fe/H
Fe/H
![]() )
with a small dispersion (0.11
)
with a small dispersion (0.11 ![]() 0.01 dex). The variation of
the kinematic properties between the metal-rich and the metal-poor
parts of the sample studied here suggests different formation scenarii
for those populations. The metal-poor component of our sample shows
0.01 dex). The variation of
the kinematic properties between the metal-rich and the metal-poor
parts of the sample studied here suggests different formation scenarii
for those populations. The metal-poor component of our sample shows
![]() higher than
higher than ![]() and
and ![]() ,
,
![]() ,
a strong anisotropy in
,
a strong anisotropy in ![]() and
and ![]() and no correlations between the velocity components. This population
can be interpreted as a spheroidal population with the velocity
anisotropy due mostly to rotation that broadens the observed
and no correlations between the velocity components. This population
can be interpreted as a spheroidal population with the velocity
anisotropy due mostly to rotation that broadens the observed
![]() component. The metal-rich population shows significant anisotropy and
correlation between all the velocity components. In particular the
strong vertex deviation indicates that it can be interpreted as a
bar-driven population.
component. The metal-rich population shows significant anisotropy and
correlation between all the velocity components. In particular the
strong vertex deviation indicates that it can be interpreted as a
bar-driven population.
3.2 Kinematics versus distance
We used our red clump stars sample to probe the kinematics against distance. Red clump stars should indeed allow to measure the velocity shift between the two bar streams (Mao & Paczynski 2002; Rangwala et al. 2009). As the stars form, the bar streams in the same sense as the Galactic rotation, and because the bar is in the first quadrant, the stars on the near side of the bar are expected to go towards us, while stars on the far side should move away from us. The actual velocity shifts between these two streams constrains the bar orientation angle.
The Besançon model confirms that our red clump sample should
be nicely centred around the Galactic Centre (see Fig. 9 of
Paper II). The magnitude I is less
sensitive than magnitude K to both the metallicity
and the age for ages older than ![]() 4 Gyr (Salaris
& Girardi 2002). Moreover the I magnitude
is more sensitive to the extinction, which itself increases with
distance, leading the I magnitude to be
much more sensitive to distance than K. No
differential extinction pattern is seen in the region of our sample (Sumi 2004).
4 Gyr (Salaris
& Girardi 2002). Moreover the I magnitude
is more sensitive to the extinction, which itself increases with
distance, leading the I magnitude to be
much more sensitive to distance than K. No
differential extinction pattern is seen in the region of our sample (Sumi 2004).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig4.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg88.png)
|
Figure 4:
Distribution of the I magnitude and |
| Open with DEXTER | |
Table 2: Baade's Window red clump mean velocities for the faint and bright stars in magnitude I (first and the last 25% quantiles) for stars with [Fe/H] >-0.09 (33% quantile of the [Fe/H] distribution).
Table 3:
Summary of the bulge minor axis fields (Paper I)
characteristics. ![]() is the height of the field along the bulge minor axis, assuming a
distance Sun - Galactic Centre of 8 kpc.
is the height of the field along the bulge minor axis, assuming a
distance Sun - Galactic Centre of 8 kpc.
We cut our sample into bright and faint stars on the first and
last 25% quantile of our I magnitude distribution
(Fig. 4)
and computed the mean velocities. Without selection in metallicity, the
Welch Two Sample t-test does not indicate that the mean values between
the bright and the faint samples are significant (p-value
= 0.1 for ![]() ,
0.1 for
,
0.1 for ![]() and 0.8 for
and 0.8 for ![]() ).
By removing the metal-poor stars (selecting [Fe/H]>-0.09, which
corresponds to the 66% quantile of the [Fe/H] distribution), the Welch
Two Sample t-test becomes significant on the radial velocities (p-value
= 0.02 for
).
By removing the metal-poor stars (selecting [Fe/H]>-0.09, which
corresponds to the 66% quantile of the [Fe/H] distribution), the Welch
Two Sample t-test becomes significant on the radial velocities (p-value
= 0.02 for ![]() ,
0.2 for
,
0.2 for ![]() and 0.4 for
and 0.4 for ![]() ).
The resulting values are presented in Table 2. The numbers
go in the expected direction, which is a negative
).
The resulting values are presented in Table 2. The numbers
go in the expected direction, which is a negative ![]() and a positive
and a positive ![]() for the near stream and a positive
for the near stream and a positive ![]() with a negative
with a negative ![]() for the far stream. Note that the mean proper motions quoted in
Table 2
are relative. By removing the metal-rich stars from the sample
(selecting [Fe/H]<0.33, which corresponds to the 66% quantile of
the [Fe/H] distribution), the Welch Two Sample t-test does not
distinguish differences between the faint and the bright sample (p-value
= 0.5 for
for the far stream. Note that the mean proper motions quoted in
Table 2
are relative. By removing the metal-rich stars from the sample
(selecting [Fe/H]<0.33, which corresponds to the 66% quantile of
the [Fe/H] distribution), the Welch Two Sample t-test does not
distinguish differences between the faint and the bright sample (p-value
= 0.5 for ![]() ,
0.2 for
,
0.2 for ![]() and 0.9 for
and 0.9 for ![]() ).
This again confirms our interpretation of the metal-rich population of
Baade's Window being associated to the bar and the metal-poor
population to a spheroidal population.
).
This again confirms our interpretation of the metal-rich population of
Baade's Window being associated to the bar and the metal-poor
population to a spheroidal population.
This shift was not seen in the radial velocities of Rangwala et al. (2009). They argue that this may be because Baade's Window population is the superposition of an old spheroidal population and a bar population, which we here confirm.
No correlation of the kinematics with the magnitude I
can be seen for the RGB sample. We note that the RGB sample is biased
towards closest stars. According to the Besançon model, the median
distance difference between the RC and the RGB sample is
expected to be 1 kpc (see Fig. 9 of Paper II
for the RC and Fig. 10 of Paper I for the
RGB sample). This bias in distance is not significant in the mean
kinematics of the RGB sample (
![]() km s-1,
km s-1,
![]() mas/yr,
mas/yr,
![]() mas/yr).
mas/yr).
4 Radial velocity versus metallicity along the bulge minor axis
We now wonder whether the two distinct stellar populations found in the
previous section are present all along the
bulge minor axes. We analyse the radial velocity distribution behaviour
of the fields of Paper I, presented in Table 3. To be
consistent with the ![]() and
and ![]() metallicity distribution, we will use only the RGB sample of Baade's
Window with the original metallicity distribution function of
Paper I. Paper I showed a variation of the
metallicity distribution with height z above the
Galactic mid-plane (Fig. 5). In this
section we combine the metallicity data with radial velocity data.
Figure 6
shows the radial velocity dispersion as a function of metallicity.
metallicity distribution, we will use only the RGB sample of Baade's
Window with the original metallicity distribution function of
Paper I. Paper I showed a variation of the
metallicity distribution with height z above the
Galactic mid-plane (Fig. 5). In this
section we combine the metallicity data with radial velocity data.
Figure 6
shows the radial velocity dispersion as a function of metallicity.
We first compare the kinematic behaviour along the bulge minor
axis (Table 3)
with previous results from the literature. We saw in Sect. 3
that our Baade's Window radial velocity dispersion excellently agrees
with previous measurements. At
![]() our radial velocity dispersion is lower than the BRAVA measure (
our radial velocity dispersion is lower than the BRAVA measure (
![]() km s-1,
Howard et al. 2008).
The decrease of the radial velocity dispersion with galactic latitude
we observe is consistent with the SiO maser measurements of Izumiura et al. (1995).
km s-1,
Howard et al. 2008).
The decrease of the radial velocity dispersion with galactic latitude
we observe is consistent with the SiO maser measurements of Izumiura et al. (1995).
All fields show a negligible skew, while the kurtosis is
different. This variation of the kurtosis was not detected in Howard et al. (2008). At
![]() the
distribution is significantly pointy (with 99.3% confidence according
to the Anscombe-Glynn kurtosis test), indicating that the kinematics
are significantly affected by the disc. At
the
distribution is significantly pointy (with 99.3% confidence according
to the Anscombe-Glynn kurtosis test), indicating that the kinematics
are significantly affected by the disc. At
![]() the kurtosis becomes consistent with zero. In Baade's Window the
distribution is significantly flattened (with 93% confidence in the RGB
sample and 99.8% in the red clump sample). Sharples
et al. (1990) and Rangwala
et al. (2009) also measured a skew consistent with
zero and kurtosis significantly negative in Baade's Window, indicating
that the distributions are flat-topped rather than peaked. Rangwala et al. (2009)
concludes that this seems to be consistent with a model of the bar with
stars in elongated orbits forming two streams at different mean radial
velocities, broadening and flattening the total distribution.
the kurtosis becomes consistent with zero. In Baade's Window the
distribution is significantly flattened (with 93% confidence in the RGB
sample and 99.8% in the red clump sample). Sharples
et al. (1990) and Rangwala
et al. (2009) also measured a skew consistent with
zero and kurtosis significantly negative in Baade's Window, indicating
that the distributions are flat-topped rather than peaked. Rangwala et al. (2009)
concludes that this seems to be consistent with a model of the bar with
stars in elongated orbits forming two streams at different mean radial
velocities, broadening and flattening the total distribution.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig5.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg103.png)
|
Figure 5: Distribution of the metallicity for the different galactic latitudes of Paper I. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig6.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg104.png)
|
Figure 6: Dispersion of the radial velocity for the different galactic latitudes as a function of metallicity by bins of 0.4 dex. |
| Open with DEXTER | |
We now analyse kinematic data versus metallicity. The mean radial
velocities do not show significant variation with metallicity in any of
our fields. Figure 6
shows that the velocity dispersion at the rich end decreases
significantly with latitude. However, the velocity dispersion on the
metal-poor end does not vary significantly with latitude. Summing all
stars with [Fe/H] < -0.5 dex in all fields leads to
![]() km s-1.
km s-1.
The field ![]() is close enough to Plaut's Window (
is close enough to Plaut's Window (
![]() ,
,
![]() )
so that we can compare our results to the proper motion study of Vieira et al. (2007).
The Besançon model indicates a mean distance of our selected bulge
stars to be 6.5 kpc, compatible with the Vieira et al. (2007)
selection. Their metallicity distribution is compatible with ours. They
do not find any change in the proper motion dispersion as a function of
metallicity either. They found
)
so that we can compare our results to the proper motion study of Vieira et al. (2007).
The Besançon model indicates a mean distance of our selected bulge
stars to be 6.5 kpc, compatible with the Vieira et al. (2007)
selection. Their metallicity distribution is compatible with ours. They
do not find any change in the proper motion dispersion as a function of
metallicity either. They found
![]() km s-1
and
km s-1
and ![]() km s-1
at
km s-1
at ![]() ,
we obtain
,
we obtain ![]() km s-1
at
km s-1
at ![]() ,
leading to a full picture coherent with the predictions of the model of
Zhao (1996) of
,
leading to a full picture coherent with the predictions of the model of
Zhao (1996) of
![]() and
and ![]() at these latitudes (see the bottom of Fig. 6 of Zhao 1996).
at these latitudes (see the bottom of Fig. 6 of Zhao 1996).
We have seen in the previous section that Baade's Window kinematic behaviour as a function of metallicity can be interpreted as a mix of two populations, a metal-poor component with kinematics that can be associated to an old spheroid population and a metal-rich component with bar-driven kinematics. In this light we can interpret the variation with galactic latitude of both the metallicity distribution function (Fig. 5) and the kinematics as a function of metallicity (Fig. 6) as the bar population disappearing while moving away from the plane. At high latitudes the foreground disc component dominates the metal-rich part of the kinematic behaviour. The metal-poor component associated with the old spheroid stays present along the bulge minor axis.
We obtained an estimation of the variation of the populations
with latitude by using the SEMMUL Gaussian components decomposition in
the metallicity distribution of the Paper I samples.
Table 4
gives the decomposition of the Baade's Window RGB sample. The
proportion of the metal-rich component is higher than in the red clump
sample of Paper II and its spread in metallicity is also
higher, most probably due to a difference in the sample selection,
which is biased towards stars closer to the Sun in the RGB sample.
Although both samples are not exactly on the same scale at the
high-metallicity end (cf. Sect. 5.1.4 of Paper II), the mean
metallicities for the metal-poor population is extremely similar in
both samples (see also the decomposition of the full Baade's Window
sample on the same metallicity scale at the end of Sect. 3.1).
At ![]() the Wilks' test allows us to keep a solution with three components
presented in Table 5
rather than the two components. Population A and population B could
correspond to the population A and B observed in Baade's Window. The
mean metallicities are coherent although their spread is smaller. The
radial velocity dispersions of population A are identical. The radial
velocity dispersion of population B decreases at
the Wilks' test allows us to keep a solution with three components
presented in Table 5
rather than the two components. Population A and population B could
correspond to the population A and B observed in Baade's Window. The
mean metallicities are coherent although their spread is smaller. The
radial velocity dispersions of population A are identical. The radial
velocity dispersion of population B decreases at
![]() as expected for a bar-like kinematic behaviour (see Fig. 8 and
associated text). Population C represents only
as expected for a bar-like kinematic behaviour (see Fig. 8 and
associated text). Population C represents only ![]() % of the sample with a low
mean metallicity of
% of the sample with a low
mean metallicity of ![]() dex and a high-velocity dispersion of
dex and a high-velocity dispersion of ![]() km s-1,
which could therefore be associated to the halo. The Besançon model
prediction of only
km s-1,
which could therefore be associated to the halo. The Besançon model
prediction of only ![]() %
of halo star in the sample could therefore have been underestimated.
This population could also have been hidden in the population A at
%
of halo star in the sample could therefore have been underestimated.
This population could also have been hidden in the population A at
![]() .
Selecting all stars with [Fe/H]<-0.9 in our three fields we
obtain 16 stars with a radial velocity dispersion of
.
Selecting all stars with [Fe/H]<-0.9 in our three fields we
obtain 16 stars with a radial velocity dispersion of
![]() km s-1,
which is coherent with the solar neighbourhood velocity dispersions
measured in this metallicity range (e.g. Chiba
& Beers 2000:
km s-1,
which is coherent with the solar neighbourhood velocity dispersions
measured in this metallicity range (e.g. Chiba
& Beers 2000:
![]() km s-1)
containing both thick disc and halo stars. We are not in a position to
clearly associate this population either to the halo or to a metal-poor
thick disc in our inner galactic samples. SEMMUL did not converge on
the
km s-1)
containing both thick disc and halo stars. We are not in a position to
clearly associate this population either to the halo or to a metal-poor
thick disc in our inner galactic samples. SEMMUL did not converge on
the ![]() field due to the smaller number of stars and the higher contamination
with thin, thick discs and halo stars expected in this field. At
field due to the smaller number of stars and the higher contamination
with thin, thick discs and halo stars expected in this field. At
![]() the metal-rich component present at
the metal-rich component present at
![]() and
and ![]() seems to have fully disappeared. The metal-rich velocity part of the
velocity dispersion corresponds to a disc-like component (see next
section), while the metal-poor part shows a velocity dispersion still
coherent with the metal-poor population of
seems to have fully disappeared. The metal-rich velocity part of the
velocity dispersion corresponds to a disc-like component (see next
section), while the metal-poor part shows a velocity dispersion still
coherent with the metal-poor population of
![]() and
and ![]() ,
although we cannot distinguish a spheroid and a thick disc
contribution.
,
although we cannot distinguish a spheroid and a thick disc
contribution.
Table 4:
SEMMUL Gaussian components decomposition of field
![]() ,
RGB sample only.
,
RGB sample only.
Table 5:
SEMMUL Gaussian components decomposition of field
![]() .
.
5 Comparison with dynamical models
In this section we combine the full Baade's Window sample of
Sect. 3 with the b=-6![]() and b=-12
and b=-12![]() fields of Sect. 4.
fields of Sect. 4.
We first compared our kinematics with the model of Zhao (1996) in Baade's Window (Table 1) and along the minor axis (Fig. 7). The model of Zhao (1996) is a 3D steady-state stellar model using a generalized Schwarzschild technique consisting of orbital building blocks within a bar and a disc potential. We find a very good agreement between our data and this model. Figure 7 also shows the very good agreement of our radial velocity distribution along the minor axis with the BRAVA data (Howard et al. 2009,2008). These comparisons are done on global kinematics, while we have shown here that several populations are present in these data.
The N-body dynamical model of Fux (1999) allows us to compare the
kinematic properties of the particles that were originally in the disc
to those in the old spheroid. This model is a 3D self-consistent,
symmetry-free N-body and smooth particle
hydrodynamics code. It contains 3.8 million particles: a dark
halo, a disc, a spheroid, and a gas component. Following Howard et al. (2009) we
used the model c10t2066 described in Fux
(1999), which assumes a bar angle of 20![]() and a distance to the Sun of 8 kpc. We selected
particles at a distance from the Sun 6<r<10 kpc
in a cone selection of 0.5 degree radius for
and a distance to the Sun of 8 kpc. We selected
particles at a distance from the Sun 6<r<10 kpc
in a cone selection of 0.5 degree radius for
![]() and in a cone selection of 1 degree for
and in a cone selection of 1 degree for
![]() to permit us to work with a sample away from the plane large enough
(this larger cone leads to 209 particles at
to permit us to work with a sample away from the plane large enough
(this larger cone leads to 209 particles at
![]() ).
We computed statistical uncertainties of the model by bootstrap of
2-3 km s-1 in the velocity
dispersions and 5
).
We computed statistical uncertainties of the model by bootstrap of
2-3 km s-1 in the velocity
dispersions and 5
![]() in the velocity ellipsoid
angles for the disc/bar, 20
in the velocity ellipsoid
angles for the disc/bar, 20
![]() for the spheroid.
for the spheroid.
Table 1
shows the predictions of the model of Fux
(1999) in Baade's Window. In this field the model contains
50% of stars from the spheroid and 50% from the disc/bar population,
equivalent to the SEMMUL Gaussian components decomposition we obtained
for the red clump sample in Paper II. The velocity dispersions
of the model are slightly higher than our observed ones and the
velocity component correlations are lower. The velocity
dispersions of the metal-rich population correspond to the disc/bar
particles except for ![]() ,
which is higher in the model. Both metal-rich observations and disc/bar
particles show a correlation of the velocity components, but the
correlations in the observations are higher. The vertex deviation is
however identical in the model and the observations. The metal-poor
component show smaller velocity dispersions in
,
which is higher in the model. Both metal-rich observations and disc/bar
particles show a correlation of the velocity components, but the
correlations in the observations are higher. The vertex deviation is
however identical in the model and the observations. The metal-poor
component show smaller velocity dispersions in
![]() and
and ![]() than the spheroid model particles. As expected the model does not show
any correlations in the velocity components of the spheroid particles,
in line with our metal-poor sample.
than the spheroid model particles. As expected the model does not show
any correlations in the velocity components of the spheroid particles,
in line with our metal-poor sample.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{14353Fig7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg132.png)
|
Figure 7: Radial velocity dispersion along the bulge minor axis compared to the BRAVA data (; Howard et al. 2008) and the model of Zhao (1996). |
| Open with DEXTER | |
Figure 8
shows the strong decrease in radial velocity dispersion predicted by
the Fux model for the disc/bar population while moving away from the
plane. In the plane the predicted dispersion is larger for the disc/bar
than the spheroid one, due to the influence of the bar driven orbits.
At high latitude the ![]() dispersion is small for the bar/disc component, following a disc-like
behaviour. The spheroid population keeps the same velocity dispersion
along the minor axis. In Fig. 8 we
over-plotted the Fux model radial velocity dispersions with our data
for the full sample, the metal-rich and the metal-poor parts, as
defined by the 33% and 66% quantiles in the [Fe/H] distribution. For
the metal-rich part we observe a strong decrease of the metallicity
dispersion while going away from the plane, which is coherent with the
behaviour of the disc/bar particles of Fux model. For the metal-poor
part we observe a constant velocity dispersion, similar to the spheroid
particles of the Fux model, but with a mean velocity dispersion of
about 20 km s-1 lower than the
model. It is this difference of velocity dispersion for the metal-poor
component which leads to a too high global velocity dispersion of the
Fux model compared to the BRAVA data, which in turn lead Howard et al. (2009) to
an interpretation different from ours: at
dispersion is small for the bar/disc component, following a disc-like
behaviour. The spheroid population keeps the same velocity dispersion
along the minor axis. In Fig. 8 we
over-plotted the Fux model radial velocity dispersions with our data
for the full sample, the metal-rich and the metal-poor parts, as
defined by the 33% and 66% quantiles in the [Fe/H] distribution. For
the metal-rich part we observe a strong decrease of the metallicity
dispersion while going away from the plane, which is coherent with the
behaviour of the disc/bar particles of Fux model. For the metal-poor
part we observe a constant velocity dispersion, similar to the spheroid
particles of the Fux model, but with a mean velocity dispersion of
about 20 km s-1 lower than the
model. It is this difference of velocity dispersion for the metal-poor
component which leads to a too high global velocity dispersion of the
Fux model compared to the BRAVA data, which in turn lead Howard et al. (2009) to
an interpretation different from ours: at
![]() the radial velocity distribution is compatible with the disc/bar
component of the Fux model without the need for an old spheroid
component. However, with a velocity dispersion for the spheroid of
the radial velocity distribution is compatible with the disc/bar
component of the Fux model without the need for an old spheroid
component. However, with a velocity dispersion for the spheroid of ![]() 100 km s-1
instead of
100 km s-1
instead of ![]() 120 km s-1
the global velocity dispersion would be coherent with the full Fux
model (spheroid+disc). The use of the Besançon model adds support to
the interpretation that the decrease in
120 km s-1
the global velocity dispersion would be coherent with the full Fux
model (spheroid+disc). The use of the Besançon model adds support to
the interpretation that the decrease in
![]() with latitude, seen in disc/bar particles of Fux
(1999) and in our metal-rich samples, can be due to the disc
replacing the bar in the sample: according to the Besançon model, the
thin disc contamination of our sample at
with latitude, seen in disc/bar particles of Fux
(1999) and in our metal-rich samples, can be due to the disc
replacing the bar in the sample: according to the Besançon model, the
thin disc contamination of our sample at
![]() was expected to be of 10% with a
was expected to be of 10% with a
![]() km s-1
and 19% at
km s-1
and 19% at ![]() with
with ![]() km s-1.
km s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg135.png)
|
Figure 8: Radial velocity dispersion along the bulge minor axis compared with the model of Fux (1999). The metal-poor and metal-rich population are defined by the 33% and 66% quantile of the [Fe/H] distribution. |
| Open with DEXTER | |
6 Discussion
Our analysis of the kinematics as a function of metallicity in Baade's Window shows that our sample can be decomposed into two distinct populations, for which we suggest different formation scenarii. The metal-poor component does not show any correlation between its velocity components and is therefore consistent with an isotropic rotating population. Paper II showed that this component is enriched in [Mg/Fe]. We interpret this population as an old spheroid with a rapid time-scale formation. The metal-rich component shows a vertex deviation consistent with that expected from a population with orbits supporting a bar. Paper II showed that this component has a [Mg/Fe] near solar. We interpret this population as a pseudo-bulge formed over a long time-scale through disc secular evolution under the action of a bar. This pseudo-bulge is gradually disappearing when moving away from the Galactic plane.
In this context we can give a new consistent interpretation of
the metallicity gradient in the bulge. A metallicity gradient is indeed
visible in the bulge when observing further away from the plane than
Baade's Window (Frogel et al.
1999 and Paper I), while in the inner regions (
![]() )
no gradient in metallicity has been found (Ramírez
et al. 2000; and Rich
et al. 2007). This can be understood if the bar as
well as the old spheroid population are both present in the inner
regions, leading to a constant metallicity at
)
no gradient in metallicity has been found (Ramírez
et al. 2000; and Rich
et al. 2007). This can be understood if the bar as
well as the old spheroid population are both present in the inner
regions, leading to a constant metallicity at
![]() ,
while the bar influence gradually fades further away from the plane
than Baade's Window. At high latitudes only the old spheroid remains:
the mean metallicity of the outer bulge measured by Ibata & Gilmore (1995)
of [Fe/H
,
while the bar influence gradually fades further away from the plane
than Baade's Window. At high latitudes only the old spheroid remains:
the mean metallicity of the outer bulge measured by Ibata & Gilmore (1995)
of [Fe/H![]() dex
corresponds very well to our metal-poor population. This scenario is
also consistent with the distribution of bulge globular clusters of Valenti et al. (2009)
who found no evidence for a metallicity gradient but all their clusters
with [Fe/H]>-0.5 dex are located within (
dex
corresponds very well to our metal-poor population. This scenario is
also consistent with the distribution of bulge globular clusters of Valenti et al. (2009)
who found no evidence for a metallicity gradient but all their clusters
with [Fe/H]>-0.5 dex are located within (
![]() ).
).
Concerning the age of the two populations, we expect the
spheroid component to be old, while the pseudo-bulge component may
contain both the old stars of the inner disc redistributed by the bar
and younger stars whose formation has been triggered by the bar gas
flow. van Loon
et al. (2003) found that although the bulk of the
bulge population is old, a fraction of the stars are of intermediate
age (1 to 7 Gyr). Groenewegen
& Blommaert (2005) observed Mira stars of ages 1-3
Gyr at all latitudes from -1.2 to -5.8 in the OGLE-II data.
Uttenthaler et al. (2007)
found four bulge stars with ages lower than 3 Gyr at a
latitude of ![]() .
Bensby et al. (2010)
found three microlensed bulge dwarfs with ages lower than
5 Gyr. 87% of the variable stars detected by Kouzuma & Yamaoka (2009)
are distributed within
.
Bensby et al. (2010)
found three microlensed bulge dwarfs with ages lower than
5 Gyr. 87% of the variable stars detected by Kouzuma & Yamaoka (2009)
are distributed within
![]() ,
and most of them should be large-amplitude and long-period variables
such as Mira variables or OH/IR stars. This intermediate age population
has been shown to trace the Galactic bar (Groenewegen &
Blommaert 2005; Izumiura et al. 1995;
Kouzuma
& Yamaoka 2009; van Loon et al. 2003),
although providing a larger bar angle (
,
and most of them should be large-amplitude and long-period variables
such as Mira variables or OH/IR stars. This intermediate age population
has been shown to trace the Galactic bar (Groenewegen &
Blommaert 2005; Izumiura et al. 1995;
Kouzuma
& Yamaoka 2009; van Loon et al. 2003),
although providing a larger bar angle (![]()
![]() )
than studies based on older tracers such as red clump stars (
)
than studies based on older tracers such as red clump stars (![]()
![]() ,
Stanek
et al. 1994; Babusiaux & Gilmore 2005).
This discrepancy in the bar angle could well be explained if the old
tracers probed a mix of spheroid and bar structures, while the young
tracers only probe the bar (although biases on the longitude area
surveyed also need to be taken into account, see Nishiyama et al. 2005).
If this intermediate age population were associated to a part of the
bar component, their presence in the CMDs would decrease while going
away from the plane as the main bar component and would therefore be a
small fraction of the CMD of Zoccali
et al. (2003) at
,
Stanek
et al. 1994; Babusiaux & Gilmore 2005).
This discrepancy in the bar angle could well be explained if the old
tracers probed a mix of spheroid and bar structures, while the young
tracers only probe the bar (although biases on the longitude area
surveyed also need to be taken into account, see Nishiyama et al. 2005).
If this intermediate age population were associated to a part of the
bar component, their presence in the CMDs would decrease while going
away from the plane as the main bar component and would therefore be a
small fraction of the CMD of Zoccali
et al. (2003) at
![]() .
Clarkson et al. (2008)
obtained a proper motion decontaminated CMD with a well defined old
turn-off in an inner field (
.
Clarkson et al. (2008)
obtained a proper motion decontaminated CMD with a well defined old
turn-off in an inner field (
![]() ,
,
![]() ).
However, we would expect an intermediate age population associated with
the bar to be metal-rich, which, due to the age-metallicity degeneracy,
would imply that this population could be hidden in the CMD of Clarkson et al. (2008)
if its contribution is small enough compared to the bulk of the bulge
population. The new filter combination proposed by the ACS Bulge
Treasury Programme to break the age-metallicity-temperature degeneracy (Brown et al. 2009) should
provide new insights into this issue.
).
However, we would expect an intermediate age population associated with
the bar to be metal-rich, which, due to the age-metallicity degeneracy,
would imply that this population could be hidden in the CMD of Clarkson et al. (2008)
if its contribution is small enough compared to the bulk of the bulge
population. The new filter combination proposed by the ACS Bulge
Treasury Programme to break the age-metallicity-temperature degeneracy (Brown et al. 2009) should
provide new insights into this issue.
We note that in Baade's Window neither the kinematics nor the chemistry allow us to distinguish what we call the old spheroid to the thick disc. The mean metallicity of the solar neighbourhood thick disc is however lower (e.g. Fuhrmann 2008 derived [Fe/H] =-0.6 and [Mg/H] =-0.2) than the mean metallicity of our metal-poor population ([Fe/H]= -0.27 dex and [Mg/H]=-0.04, Paper II). Meléndez et al. (2008), Ryde et al. (2010), Bensby et al. (2010) and Alves-Brito et al. (2010) observed similarities between the metallicity of the bulge and the metallicity of thick disc stars for metal-poor stars. The sample of Ryde et al. (2010) contains 11 of our stars all with less than solar metallicity. Simulations of the formation of thick stellar discs by rapid internal evolution in unstable, gas-rich, clumpy discs (Bournaud et al. 2009) show that thick discs and classical bulges form together in a time-scale shorter than 1 Gyr, which explains the observed abundance similarities.
The coexistence of classical and pseudo bulge has been
observed in external galaxies (Prugniel et al. 2001; Erwin 2008;
Peletier
et al. 2007) and obtained by N-body
simulations (Samland
& Gerhard 2003; Athanassoula 2005). The
chemical and dynamical model of Nakasato
& Nomoto (2003) suggests the presence of two
chemically different components in the bulge as we found, one formed
quickly through the subgalactic clump merger in the proto-Galaxy, and
the other formed gradually in the inner disc. But they do not have a
bar in their model. They fitted the kinematics of Minniti (1996) well who observed
at ![]() ,
,
![]() a
decrease of
a
decrease of ![]() with metallicity, which is coherent with what we observed at
with metallicity, which is coherent with what we observed at
![]() and that Nakasato & Nomoto
(2003) defined the bulge radius as R<2 kpc.
The chemo-dynamical model of Samland
& Gerhard (2003) predicts the different
characteristics of our sample: their total bulge population contains
two stellar populations: a metal-rich population ([Fe/H]>0.17)
with [
and that Nakasato & Nomoto
(2003) defined the bulge radius as R<2 kpc.
The chemo-dynamical model of Samland
& Gerhard (2003) predicts the different
characteristics of our sample: their total bulge population contains
two stellar populations: a metal-rich population ([Fe/H]>0.17)
with [![]() /Fe]<0
associated with the bar, and an old population that formed during the
proto-galactic collapse, with a high [
/Fe]<0
associated with the bar, and an old population that formed during the
proto-galactic collapse, with a high [![]() /Fe] and a [Fe/H]
corresponding to the ``thick disc'' component. Their model also
predicts the resulting apparent metallicity gradient along the bulge
minor axis (their Fig. 13).
/Fe] and a [Fe/H]
corresponding to the ``thick disc'' component. Their model also
predicts the resulting apparent metallicity gradient along the bulge
minor axis (their Fig. 13).
Our study highlights the importance to combine metallicity to 3D-kinematic information to disentangle the different bulge populations. This approach needs to be extended to various galactic longitudes. Gaia will not only provide those, but also allow us to determine the distances (probing the different structures along the line of sight and removing distance induced biases) and work on an impressively large sample of un-contaminated bulge stars.
AcknowledgementsM.Z. and D.M. are supported by FONDAP Center for Astrophysics 15010003, the BASAL Center for Astrophysics and Associated Technologies PFB-06, the FONDECYT 1085278 and 1090213, and the MIDEPLAN MilkyWay Millennium Nucleus P07-021-F.
References
- Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001, A&A, 367, 428 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alard, C. 2001, A&A, 379, L44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2000, ApJ, 541, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Alves-Brito, A., Melendez, J., Asplund, M., Ramirez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., & Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., Johnson, J. A., et al. 2010, A&A, 512, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sahu, K., Zoccali, M., et al. 2009, AJ, 137, 3172 [NASA ADS] [CrossRef] [Google Scholar]
- Celeux, G., & Diebolt, J. 1986, Rev. Stat. Appl., 34, 35 [Google Scholar]
- Chiba, M., & Beers, T. C. 2000, AJ, 119, 2843 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., & Sanders, R. H. 1981, A&A, 96, 164 [NASA ADS] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- de Vaucouleurs, G. 1964, in The Galaxy and the Magellanic Clouds, IAU Symp., 20, 195 [Google Scholar]
- Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P. 2008, in IAU Symposium, ed. M. Bureau, E. Athanassoula, & B. Barbuy, IAU Symp., 245, 113 [Google Scholar]
- Feltzing, S., & Gilmore, G. 2000, A&A, 355, 949 [NASA ADS] [Google Scholar]
- Feltzing, S., & Johnson, R. A. 2002, A&A, 385, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frogel, J. A., Tiede, G. P., & Kuchinski, L. E. 1999, AJ, 117, 2296 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Fux, R. 1999, A&A, 345, 787 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T., & Blommaert, J. A. D. L. 2005, A&A, 443, 143 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Habing, H. J., Sevenster, M. N., Messineo, M., van de Ven, G., & Kuijken, K. 2006, A&A, 458, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2010, A&A, submitted, Paper III [Google Scholar]
- Howard, C. D., Rich, R. M., Reitzel, D. B., et al. 2008, ApJ, 688, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., & Gilmore, G. F. 1995, MNRAS, 275, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Izumiura, H., Deguchi, S., Hashimoto, O., et al. 1995, ApJ, 453, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kouzuma, S., & Yamaoka, H. 2009, AJ, 138, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Koz▯owski, S., Wozniak, P. R., Mao, S., et al. 2006, MNRAS, 370, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Rich, R. M. 2002, AJ, 124, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., Mahoney, T. J., et al. 2007, AJ, 133, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S., & Paczynski, B. 2002, MNRAS, 337, 895 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Merrifield, R. M. 1996, in Barred Galaxies, ed. R. Buta, D. A. Crocker, & B. C. Elmegreen (San Francisco: ASP), IAU Colloq., 157, 179 [Google Scholar]
- Minniti, D. 1996, ApJ, 459, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Nakasato, N., & Nomoto, K. 2003, ApJ, 588, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Baba, D., et al. 2005, ApJ, 621, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Norman, C. A., Sellwood, J. A., & Hasan, H. 1996, ApJ, 462, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Peletier, R. F., Falcón-Barroso, J., Bacon, R., et al. 2007, MNRAS, 379, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., Maubon, G., & Simien, F. 2001, A&A, 366, 68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahimi, A., Kawata, D., Brook, C. B., & Gibson, B. K. 2010, MNRAS, 401, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Stephens, A. W., Frogel, J. A., & DePoy, D. L. 2000, AJ, 120, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Rangwala, N., Williams, T. B., & Stanek, K. Z. 2009, ApJ, 691, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Debattista, V. P., et al. 2007, MNRAS, 378, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2007, ApJ, 665, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Royer, F., Blecha, A., North, P., et al. 2002, in SPIE Conf. Ser., 4847, ed. J.-L. Starck, & F. D. Murtagh, 184 [Google Scholar]
- Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadler, E. M., Rich, R. M., & Terndrup, D. M. 1996, AJ, 112, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Girardi, L. 2002, MNRAS, 337, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Samland, M., & Gerhard, O. E. 2003, A&A, 399, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharples, R., Walker, A., & Cropper, M. 1990, MNRAS, 246, 54 [NASA ADS] [Google Scholar]
- Soto, M., Rich, R. M., & Kuijken, K. 2007, ApJ, 665, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Spaenhauer, A., Jones, B. F., & Whitford, A. E. 1992, AJ, 103, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Mateo, M., Udalski, A., et al. 1994, ApJ, 429, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T. 2004, MNRAS, 349, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Wu, X., Udalski, A., et al. 2004, MNRAS, 348, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Terndrup, D. M., Sadler, E. M., & Rich, R. M. 1995, AJ, 110, 1774 [NASA ADS] [CrossRef] [Google Scholar]
- Uttenthaler, S., Hron, J., Lebzelter, T., et al. 2007, A&A, 463, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2009, MNRAS, 402, 1729 [Google Scholar]
- van Loon, J. T., Gilmore, G. F., Omont, A., et al. 2003, MNRAS, 338, 857 [Google Scholar]
- Vieira, K., Casetti-Dinescu, D. I., Méndez, R. A., et al. 2007, AJ, 134, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. S. 1996, MNRAS, 283, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Spergel, D. N., & Rich, R. M. 1994, AJ, 108, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Rich, R. M., & Biello, J. 1996, ApJ, 470, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177, Paper I [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... metallicity
![[*]](/icons/foot_motif.png)
- Based on ESO-VLT observations 71.B-0617, 73.B-0074, and Paris Observatory GTO 71.B-0196.
All Tables
Table 1: Baade's Window velocity ellipsoid parameters.
Table 2: Baade's Window red clump mean velocities for the faint and bright stars in magnitude I (first and the last 25% quantiles) for stars with [Fe/H] >-0.09 (33% quantile of the [Fe/H] distribution).
Table 3:
Summary of the bulge minor axis fields (Paper I)
characteristics. ![]() is the height of the field along the bulge minor axis, assuming a
distance Sun - Galactic Centre of 8 kpc.
is the height of the field along the bulge minor axis, assuming a
distance Sun - Galactic Centre of 8 kpc.
Table 4:
SEMMUL Gaussian components decomposition of field
![]() ,
RGB sample only.
,
RGB sample only.
Table 5:
SEMMUL Gaussian components decomposition of field
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14353Fig1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg41.png)
|
Figure 1:
Dispersion of the radial (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg72.png)
|
Figure 2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg80.png)
|
Figure 3: Vertex deviation lv in Baade's Window as a function of metallicity by bins of 0.4 dex. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14353Fig4.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg88.png)
|
Figure 4:
Distribution of the I magnitude and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig5.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg103.png)
|
Figure 5: Distribution of the metallicity for the different galactic latitudes of Paper I. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig6.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg104.png)
|
Figure 6: Dispersion of the radial velocity for the different galactic latitudes as a function of metallicity by bins of 0.4 dex. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{14353Fig7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg132.png)
|
Figure 7: Radial velocity dispersion along the bulge minor axis compared to the BRAVA data (; Howard et al. 2008) and the model of Zhao (1996). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14353Fig8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14353-10/Timg135.png)
|
Figure 8: Radial velocity dispersion along the bulge minor axis compared with the model of Fux (1999). The metal-poor and metal-rich population are defined by the 33% and 66% quantile of the [Fe/H] distribution. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.