| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014065 | |
| Published online | 08 September 2010 | |
On the effect of cosmic rays in bolometric cosmic microwave background measurements from the stratosphere
S. Masi1,2 - E. Battistelli1,2 - P. de Bernardis1,2 - L. Lamagna1,2 - F. Nati1,2 - L. Nati1,2 - P. Natoli3 - G. Polenta4,5 - A. Schillaci1,2
1 - Dipartimento di Fisica, Università di Roma ``La Sapienza'', Roma, Italy
2 - INFN Sezione di Roma 1, Roma, Italy
3 - Dipartimento di Fisica, Università di ``Tor Vergata'', Roma, Italy
4 - Agenzia Spaziale Italiana - ASI Science Data Center, Frascati, Italy
5 - INAF - Osservatorio Astronomico di Roma, Monte Porzio Catone, Italy
Received 14 January 2010 / Accepted 11 May 2010
Abstract
Context. Precision measurements of the anisotropy of the
cosmic microwave background (CMB) are able to detect low-level
non-Gaussian features caused by either topological defects or the
inflation process. These measurements are becoming feasable with the
development of large arrays of ultra-sensitive bolometric detectors and
their use in balloon-borne or satellite missions. However, the space
environment includes a population of cosmic rays (CRs), which produce
spurious spikes in bolometric signals.
Aims. We analyze the effect of CRs on the measurement of
CMB anisotropy maps and the estimate of cosmological
non-Gaussianity and angular power spectra of the CMB.
Methods. Using accurate simulations of noise and CR events
in bolometric detectors, and de-spiking techniques, we produce
simulated measured maps and analyze the Gaussianity and power spectrum
of the maps for different levels and rates of CR events.
Results. We find that a de-spiking technique based on outlier
removal in the detector signals contributing to the same sky pixel is
effective in removing CR events larger than the noise. However, low
level events hidden in the noise produce a positive shift of the
average power signal measured by a bolometer, and increase its
variance. If the number of hits per pixel is large enough, the
data distribution for each sky pixel is approximately Gaussian, but the
skewness and the kurtosis of the temperatures of the pixels indicate
the presence of some low-level non-Gaussianity. The standard noise
estimation pipeline produces a positive bias in the power spectrum at
high multipoles.
Conclusions. In the case of a typical balloon-borne survey, the
CR-induced non-Gaussianity will be marginally detectable in the
membrane bolometer channels, but be negligible in the spider-web
bolometer channels. In experiments with detector sensitivity better
than 100
![]() ,
in an environment less favorable than the earth stratosphere,
the CR-induced non-Gaussianity is likely to significantly affect
the results.
,
in an environment less favorable than the earth stratosphere,
the CR-induced non-Gaussianity is likely to significantly affect
the results.
Key words: cosmic background radiation - instrumentation: detectors - space vehicles - methods: data analysis
1 Introduction
Information about the early Universe is encoded in the primary anisotropy of the CMB. While the Gaussian fluctuations expected in the adiabatic inflationary scenario beautifully fit the available power spectrum data (see e.g. Nolta et al. 2009; and Komatsu et al. 2010), non-Gaussian signals are also expected at a lower level in the maps, due to non-linearities in the inflation potential (see e.g. Verde et al. 2000) and/or the presence of topological defects (see e.g. Kaiser & Stebbins 1984). In addition, non-Gaussian secondary anisotropies are imprinted in the post-recombination universe because of the interaction of CMB photons with the large-scale structures present in the Universe, and the emission of Galactic and extragalactic sources. The study of primordial non-Gaussianity can in principle allow to confirm and select an inflation model, but the signal to be detected is very small. For this reason, it is essential to ensure that the measurement system does not introduce non-Gaussian features into the data.
Arrays of microwave detectors feature high mapping speed and are now starting to operate at the focus of large telescopes (see e.g. Sayers et al. 2009; Siringo et al. 2009; Carlstrom et al. 2009; Wilson et al. 2008; Swetz et al. 2008) or in CMB polarimeters (see e.g. Hinderks et al. 2009; Yoon et al. 2006; Kuo et al. 2006; Samtleben et al. 2007). Transition edge superconducting (TES) bolometric detectors, involving only litographic fabrication techniques, are easier to replicate in large arrays, and extremely sensitive.
To fully exploit their sensitivity, the radiative background has to be minimized. In this sense, the optimal solution is to use bolometric detectors in space, possibly feeding them by means of a cryogenic telescope or optical system. The bolometers of the HFI instrument on the Planck mission (Holmes et al. 2008) and those of the PACS and SPIRE instruments on the Herschel mission (Billot et al. 2009; Schultz et al. 2008) represent a first step in this direction.
Being extremely sensitive to any form of energy deposited on their
absorber and thermistors, bolometers are also sensitive to
cosmic rays. The energy deposited by a single MeV proton in a
cryogenic bolometer is much higher than the typical level of the noise
(see e.g. Caserta et al. 1990): if an amount of energy ![]() is deposited in a bolometer in a time much shorter than the bolometer
time constant, the temperature rise of the bolometer will be
is deposited in a bolometer in a time much shorter than the bolometer
time constant, the temperature rise of the bolometer will be
![]() ,
where C
is the heat capacity of the detector. This peak level will be achieved
sooner than one time constant; the subsequent decay, instead, will be
regulated by the time constant. The typical noise of a bolometer
corresponds to physical temperature fluctuations much lower than
,
where C
is the heat capacity of the detector. This peak level will be achieved
sooner than one time constant; the subsequent decay, instead, will be
regulated by the time constant. The typical noise of a bolometer
corresponds to physical temperature fluctuations much lower than
![]() ,
so most CR-induced spikes will be evident in the bolometer time-ordered-data.
,
so most CR-induced spikes will be evident in the bolometer time-ordered-data.
To allow the operation of bolometers in unprotected environments (such as sub-orbital or orbital space instruments), special low cross-section bolometers have been developed (spider-webs: Mauskopf et al. 1997; wire-grids: Jones et al. 2003). An additional benefit of these low-cross-section detectors is the reduced heat capacity with respect to solid-absorber or membrane-absorber ones, resulting in a shorter time constant.
In a polar stratospheric balloon flight, the rate of cosmic-ray events in low cross-section (spider-web) bolometers cooled to 0.3 K is on the order of 0.1 Hz (Masi et al. 2006), which is about 20 times less than the rate of events for solid/membrane-absorber bolometers at the same temperature in the same environment. The events are produced either by primary CR interacting with the detectors, or by secondary particles, including showers of electrons and bremmstrahlung-produced gammas, resulting from the interactions of primary cosmic rays with the metal surrounding the bolometric detector. Lower temperature detectors of basically the same geometry are affected by lower noise, such that the rate of CR events above the noise level is even higher; this effect is in part mitigated by their more rapid response. Rates between 0.02 Hz and 0.3 Hz have been measured for spider-web bolometers cooled to 0.1 K in similar stratospheric conditions (see Macias-Perez et al. 2007). The promising kinetic inductance detectors (KIDs), currently under development, are also sensitive to CRs, at least if the substrate is solid Si or sapphire. Anyway, their very fast response reduces significantly the fraction of contaminated data. Moreover, their sensitivity to CRs can be strongly reduced by depositing the KID resonator on a membrane. Coherent radiometers, using macroscopic thermally stable components, are much less prone to CR glitches.
Balloon-borne missions, using bolometer arrays, currently under development, include among others the EBEX CMB polarimeter (Oxley et al. 2004), the SPIDER experiment to detect CMB polarization at larger angular scales (Crill et al. 2008), the OLIMPO telescope, mainly devoted to high frequency observations of the Sunyaev-Zeldovich effect (Nati et al. 2007), and the BLAST/BLASTPOL telescope devoted to far infrared cosmological and Galactic studies (Pascale et al. 2008; Marsden et al. 2008). Given the high mapping speed of large arrays of bolometers and the efficient and relatively cheap access to space provided by stratospheric balloons, we expect these efforts to continue in the future. It is thus relevant to focus on the stratospheric case.
The data from a bolometric detector can be cleaned by detecting the spikes and flagging the corresponding section of data as unusable for additional analysis. For filtering purposes, the masked data can be filled with constrained realizations of noise with the same properties as the surrounding data (see e.g. Masi et al. 2006). However, in the absence of independent cosmic rays monitors, a number of low level events will remain unidentified, hidden in the noise. If the bolometer is non-ideal, and features an additional long time constant, the effect of CR can be an increase in 1/f noise. In this paper, we focus on the undetected cosmic rays hits and study how they can affect the analysis of data aimed at measuring CMB anisotropy and non-Gaussianity.
2 Simulation of bolometer time-ordered data
To study the effect of CR events, we simulated first time-streams of
bolometer data in the absence of sky signals, i.e., we added
CR events to a Gaussian realization of noise G(t) with a given standard deviation ![]() and null average. The time-ordered samples of bolometer noise are built
as a Gaussian realization, filtered with a first-order low-pass filter
simulating the thermal response of the detector.
and null average. The time-ordered samples of bolometer noise are built
as a Gaussian realization, filtered with a first-order low-pass filter
simulating the thermal response of the detector.
We considered two reference cases with different bolometer time constants and CR rates: case R1 has a rate of 2 Hz for a slow, membrane absorber bolometer at 0.3 K (
![]() ), and case R2 is a low-cross-section bolometer (spider-web) with a rate of 0.1 Hz and a time constant of
), and case R2 is a low-cross-section bolometer (spider-web) with a rate of 0.1 Hz and a time constant of
![]() .
.
The waiting times for CR events follow an exponential distribution of rate R
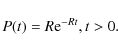
|
(1) |
The amplitudes A of the pulses induced by CRs are assumed to follow an exponential distribution with average
The shape of each pulse is modeled as a sudden level jump of amplitude A, followed by an exponential decay with a time constant ![]() :
:

|
(2) |
For 10 time constants after the CR event, the simulated data are obtained as S(t) = D(t) + G(t), whereas elsewhere the simulated data are simply G(t). In our initial tests, we do not include sky signals in the simulation.
We simulated chunks of 10 h of data, to obtain a sufficient number of events: we have an average of 72 000 (3600) events per chunk in case R1 (R2). Our full set of simulations includes 10 000 simulated chunks.
In Figs. 1 and 2, we show sample subsections of simulated data. Large CR spikes are evident, but smaller ones remain hidden in the noise.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg01.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg30.png)
|
Figure 1:
Top line: sample subsection of simulated bolometer data S(t) (converted in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg33.png)
|
Figure 2:
Same as Fig. 1, with
|
| Open with DEXTER | |
3 Despiking the time-ordered data
Evident CR events (with amplitudes larger than say 4![]() )
can be easily identified and removed. To remove smaller CR spikes,
one can take advantage of the peculiar shape of these signals. The
exact shape depends on the bolometer configuration (single or double
time constant, or even more complex response) and on the details of the
front-end electronics, amplifying the nV-level bolometer signals. In
our simulations, we used a simple exponential decay, but it would not
be difficult to extend our analysis to more complex shapes, once the
impulsive response of the system is known from calibrations.
)
can be easily identified and removed. To remove smaller CR spikes,
one can take advantage of the peculiar shape of these signals. The
exact shape depends on the bolometer configuration (single or double
time constant, or even more complex response) and on the details of the
front-end electronics, amplifying the nV-level bolometer signals. In
our simulations, we used a simple exponential decay, but it would not
be difficult to extend our analysis to more complex shapes, once the
impulsive response of the system is known from calibrations.
In the simulations described in this section, we did not
include any sky signal. With a typical 200 Hz sampling rate and
100
![]() NET, the standard deviation in the bolometer noise is on the order of 1400
NET, the standard deviation in the bolometer noise is on the order of 1400 ![]() ,
while the standard deviation in the CMB anisotropy is on the order of 100
,
while the standard deviation in the CMB anisotropy is on the order of 100 ![]() .
It is thus very unlikely that CMB signals can affect the
performance of any despiking procedure. Diffuse Galactic emission can
reach levels on the order of or higher than 1000
.
It is thus very unlikely that CMB signals can affect the
performance of any despiking procedure. Diffuse Galactic emission can
reach levels on the order of or higher than 1000 ![]() only in the Galactic plane, which is not useful for CMB studies. Point sources are also masked in sensitive CMB searches.
only in the Galactic plane, which is not useful for CMB studies. Point sources are also masked in sensitive CMB searches.
A standard method for identifying events embedded in noise is to search
for correlations between the noisy time ordered data and an event
template. To estimate the correlation, we computed the
normalized convolution
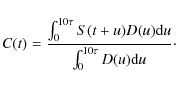
|
(3) |
In the absence of noise, this correlation is positive for all times t where a CR event contaminates the signal. Noise induces fluctuations in C(t) that, however, are smaller than the fluctuations in S(t), so there is some advantage in using this estimator. We defined a positive threshold T and assumed that all the samples with C(t)>T are contaminated by CR events. To analyze the efficiency and accuracy of this CR detection method, we considered the contaminated samples as a function of the threshold level T, and computed the fractions ft and ff. The parameter ft is the fraction of events that have C(t)> T and
Owing to the noise, we found that the convolution-based method fails
to identify a number of contaminated samples, and introduces a large
number of false detections (see Table 1 for
![]() ).
To avoid a large number of false detections, we found that one has
to raise the threshold level, although many CR events are then
missed. The situation is even worse if the ratio
).
To avoid a large number of false detections, we found that one has
to raise the threshold level, although many CR events are then
missed. The situation is even worse if the ratio
![]() is lowered.
is lowered.
Table 1:
Fraction of true detections (![]() )
and false detections (
)
and false detections (![]() )
versus threshold level T for the convolution-based despiking method, for the two reference cases (R1 and R2) (see text). Here
)
versus threshold level T for the convolution-based despiking method, for the two reference cases (R1 and R2) (see text). Here
![]() .
.
4 Pixel-space despiking
In addition to the problems listed in the previous section, removing CR pulses directly from the time-ordered data is inadvisable, because of the risk of removing true sky signals (for example, fast signals produced by scans over point sources, such as planets used as calibrators).
A more effective strategy is to analyze the set of data samples contributing to the same sky pixel: for all of these samples, the sky signal is the same, so outliers must be caused by either detector noise or CR events. This is true in the absence of pointing errors. In areas with steep brightness gradients (for example near the Galactic plane), the combination of pixelization and pointing errors can lead to spurious glitches. We neglect these effects here, since they are not relevant to CMB studies.
We used a simple iterative procedure to remove outliers. For a given pixel p, the average
![]() and the standard deviation
and the standard deviation ![]() ,
in all the contributing time-ordered signals Sk were computed. For sample k, if the difference
,
in all the contributing time-ordered signals Sk were computed. For sample k, if the difference
![]() was larger than
was larger than ![]() ,
the sample was classified as an outlier, and removed. Detection of
outliers was therefore performed in pixel space, but outliers were
removed in the time domain. New values of both the average and variance
were computed from the remaining samples of
the set, and new outliers were identified and removed. This procedure
was repeated until the average and the variance no longer changed
(no or few new outliers are found).
,
the sample was classified as an outlier, and removed. Detection of
outliers was therefore performed in pixel space, but outliers were
removed in the time domain. New values of both the average and variance
were computed from the remaining samples of
the set, and new outliers were identified and removed. This procedure
was repeated until the average and the variance no longer changed
(no or few new outliers are found).
In general, only a few iterations are needed to achieve convergence. We found that after 6 iterations the efficiency of this removal method is similar to that of the convolution-based one, yet with this method we do not remove true sky signals.
The despiked timelines are very similar to the noise-only time-lines, and their spectrum (in frequency domain) closely resembles the noise spectrum, as shown in Fig. 3 for our worst-case R1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg03.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg51.png)
|
Figure 3: Power spectrum of the data for case R1 (top line), of the despiked data, and of the original noise-only data (middle lines). The despiking procedure does not introduce spectral features in the data, as is evident from the difference between the despiked spectrum and the original noise-only spectrum (bottom line). |
| Open with DEXTER | |
The average in each pixel converges to a positive value, while according to detector noise only it would be very close to zero. This is due to CR hits of amplitude smaller than the noise: these remain undetected and produce a positive bias. They also increase the standard deviation in the data contributing to the same pixel.
For this reason, the 1-point distribution of temperatures in pixels obtained after the averaging and the outlier-removal processes will be shifted towards positive values, and be broader than expected from instrument noise only.
After a CR event, the data are contaminated for a certain amount of time, depending on both the spike amplitude and the time constants of the system. Some of these data might be recovered by removing a best-fit spike profile from the timeline. However, due to noise, the fit will not be perfect. We prefer to be conservative, and flag as unusable all the data after a spike, for a period of 5 time constants. The fraction of flagged data is plotted in Fig. 4 for different CR rates and bolometer time constants. The obvious effect of CR events is thus a significant decrease in the redundancy of the maps. Only the use of fast detectors mitigates this problem. In the following, we focus on the second effect, i.e. the introduction of bias and non-Gaussian features in the maps.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg04.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg52.png)
|
Figure 4: Fraction of data flagged
as contaminated by CR events, versus average CR rate, in a
bolometric experiment. A detector noise of 100
|
| Open with DEXTER | |
We study two different cases. The first case is a targeted observation of a small map (about ![]()
![]()
![]() in size, with a 4
in size, with a 4![]() FWHM resolution) for a relatively short time (10 h of
integration for a single detector), such as the maps observed by the
OLIMPO experiment to measure the Sunyaev-Zeldovich effect in well known
clusters (Nati et al. 2007). The second is the observation of a large (about
FWHM resolution) for a relatively short time (10 h of
integration for a single detector), such as the maps observed by the
OLIMPO experiment to measure the Sunyaev-Zeldovich effect in well known
clusters (Nati et al. 2007). The second is the observation of a large (about ![]()
![]()
![]() in size) deep survey of a clean region, with 7 days of
integration. This is similar to the blind deep survey of CMB and
undetected SZ clusters carried out by OLIMPO. We assume the same
angular resolution for this survey as well.
in size) deep survey of a clean region, with 7 days of
integration. This is similar to the blind deep survey of CMB and
undetected SZ clusters carried out by OLIMPO. We assume the same
angular resolution for this survey as well.
In Fig. 5, we plot the 1-point distributions versus the iteration number in the case of observations of 4320 independent pixels (small map case), in our two reference cases, for a total integration time on the map of 10 h. The results for the moments of these distributions are reported in Table 2.
| Figure 5:
Left: one-point distributions of pixel temperatures estimates
|
|
| Open with DEXTER | |
It is clear that the outlier removal process is effective, since the 1-point distribution approaches a Gaussian distribution after a few iterations. The skewness and kurtosis of the 1-point distribution return to values consistent with zero, after the despiking process. This means that the number of low level spikes averaged in each pixel is large enough to produce a more Gaussian distribution, at least at the level of sensitivity considered here.
However, the positive bias and the increase in the variance in the estimated pixel temperatures caused by undetected CR persist, as is evident from Fig. 5 and Table 2.
Table 2: Parameters of the 1-point distribution of pixel temperature estimates, versus iteration of the pixel-based despiking, for cases R1 and R2 (observations of small maps, same conditions as in Fig. 5).
If the average rate of CR hits is not constant during the observations of different pixels, this positive bias varies accordingly, introducing fake structures in the measured maps. A modulation of the CR rate can be introduced by the scanning strategy of the instrument, which induces variations in the absorbing material in-between the CR flux and the bolometers, thus producing scan-synchronous systematic effects. For example, an asymmetric satellite spinning in the solar wind could introduce spurious dipole or higher order anisotropy (depending on the structure of the satellite) aligned to the solar wind direction. It would be very useful to include in the instrumental setup an independent CR flux monitor, as close as possible to the focal plane bolometers. The level of the spurious signal depends on the CR composition, flux and spectrum, on the cross-section of the bolometers, and on the structure of the instrument; this can be quantified only by focusing on the specific case.
Even if the CR flux is perfectly steady, the increase in the variance of the detected data for each pixel can bias the noise estimates, which are needed to estimate the power spectra. In the standard analysis procedure for CMB maps one estimates the noise from the data, assuming Gaussian noise, and then uses Gaussian Monte Carlo simulations to assess the bias in the power spectrum (see e.g. Hivon et al. 2002; Polenta et al. 2005).
In principle, this can bias the noise estimates, and, at a lower level, might affect the non-Gaussianity parameters relevant to cosmology.
These effects are studied in the following paragraphs, where we
focus on observations of the larger survey, which is most useful to
minimizing cosmic variance and measuring the power spectrum of
the CMB and non-Gaussianity parameters. This ![]() square degrees map contains
N = 86 070
square degrees map contains
N = 86 070
![]() pixels. A total integration time of 1 week is assumed.
pixels. A total integration time of 1 week is assumed.
We define a data timeline contaminated by spikes for the cases R1 and R2 described above (70 and 10 ms detector time constant, respectively). These are, respectively, a hard case and a mild case, from the point of view of CR contamination. We thus perform iterative despiking as described above, and analyze the resulting large maps.
5 Tests of Gaussianity
Primordial CMB anisotropies are known to have Gaussian distributions to leading order (see e.g. Komatsu et al. 2003; De Troia et al. 2003; Natoli et al. 2010). Small deviations from Gaussianity have however been predicted and, if observed, may be used to constrain inflationary models (see Bartolo et al. 2004, for a review).
Measurements of this non-Gaussian component are however hampered by several sources of instrumental or non instrumental (e.g., foreground contamination) systematic effects, which may induce spurious non-Gaussian signatures in the data.
In particular, undetected cosmic-ray hits add a non-Guassian contribution to detector noise, which is usually assumed to be otherwise normally distributed. Furthermore, the despiking procedures described above are based on clipping and may also alter the statistics of the dataset.
We first perform a Kolmogorov-Smirnov (KS) test on the pixel values for (1) five iteration despiking for the R1 and R2
and (2) no CR contamination, the latter to be used as the
reference purely Gaussian dataset. The KS test (see Press et al. 1992)
is a standard test to quantify the probability that a sample can be
ascribed to a given distribution. It can also be used to reject
the null hypothesis that two different samples are drawn from the same
distribution. For each map, we compute the KS measure
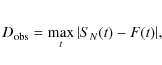
where t is the map temperature value, F the cumulative of the Gaussian distribution function, and SN the empirical distribution function of a simulated noise map. We also define
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg06.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg65.png)
|
Figure 6: Histogrammed probabilities of the KS test, for the R1 ( top) and R2 ( bottom) cases. The hatched histograms refer to the reference Gaussian sets. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg07.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg66.png)
|
Figure 7:
Same as Fig. 6 but for the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg8T.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{14065fg8B.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg67.png)
|
Figure 8: Empirical observed probabilities for skewness (S3) and kurtosis (S4), sampled from 140 Monte Carlo noise maps (red). Shown are again the R1 (top) and R2 cases. The reference Gaussian sets are shown hatched. When comparing to the values reported in Table 2 it should be noted that the histograms here are computed over a considerably larger number of pixels. |
| Open with DEXTER | |
To quantify our detection of non-Gaussianity, we define two simple NG estimators: the normalized skewness (S3) and kurtosis (S4) of each map. The corresponding histograms are shown in Fig. 8, again for the cases R1, R2, and their respective reference Gaussian sets (hatched). We note how the R2 case
also exhibits deviation from Gaussianity in the case of the kurtosis.
The empirical (histogrammed) distribution functions can themselves be
subject to a KS test against their Gaussian reference sets:
in this case, one simply measures the distance between the
empirical cumulative distribution functions. This test rejects at high
significance (
![]() )
the null hypothesis that the distribution of S3 and S4 is Gaussian for the R1 case. For R2, the Gaussianity of S4 is also rejected with similar confidence, but the null hypothesis is accepted (
)
the null hypothesis that the distribution of S3 and S4 is Gaussian for the R1 case. For R2, the Gaussianity of S4 is also rejected with similar confidence, but the null hypothesis is accepted (![]() )
for the S3 case.
)
for the S3 case.
In conclusion, the non-Gaussianity level induced by
CR contamination in the large noise maps is weak and cannot be
detected with high statistical significance even in the R1 case, while the R2 maps are, taken one at a time, indistinguishable from Gaussian maps, at least for the tests
employed here. However, the situation changes when a set
of maps is considered: our Monte Carlo analysis shows that, when a
moderate number (140 in our case) are analyzed jointly,
non-Gaussian signatures are detected even for R2.
As a consequence, an experiment that uses a similar
detector but gathers significantly more data than considered here, may
be prone to CR-induced non-Gaussianity, especially when high precision
measurements are sought. This is especially critical for high
sensitivity measurements of the
![]() parameter that quantifies
the level of non-Gaussianity in the primordial perturbations (Bartolo et al. 2004). In particular, Planck (The Planck Collaboration 2006) is expected to tighten existing constraints on
parameter that quantifies
the level of non-Gaussianity in the primordial perturbations (Bartolo et al. 2004). In particular, Planck (The Planck Collaboration 2006) is expected to tighten existing constraints on
![]() by roughly an order of magnitude. We leave a detailed study of the level of contamination by residual CR on
by roughly an order of magnitude. We leave a detailed study of the level of contamination by residual CR on
![]() estimates to a future paper.
estimates to a future paper.
6 Biasing of power spectra
The angular power spectrum of the CMB is a most valuable cosmological observable, which can be used to extract information about the underlying physical model. Thus, it is critical to assess the effect of contamination from residual, undetected spikes.
We thus estimate the angular power spectrum using cROMAster, a pseudo-![]() estimator based on MASTER (Hivon et al. 2002), which was originally developed for (and applied to) BOOMERanG-B03 (Jones et al. 2006; Piacentini et al. 2006; Montroy et al. 2006; Masi et al. 2006)
and later improved for PLANCK data analysis. cROMAster can estimate
both auto- and cross-power spectra, where the former are more efficient
but require noise removal and the latter are less efficient but are
naturally unbiased (Polenta et al. 2005),
therefore residual bias is not expected in the pure cross-spectrum
case. We verified this assertion using simulations. The case of
auto-spectra is more delicate since they require a companion
Monte Carlo dataset to estimate and remove residual noise.
estimator based on MASTER (Hivon et al. 2002), which was originally developed for (and applied to) BOOMERanG-B03 (Jones et al. 2006; Piacentini et al. 2006; Montroy et al. 2006; Masi et al. 2006)
and later improved for PLANCK data analysis. cROMAster can estimate
both auto- and cross-power spectra, where the former are more efficient
but require noise removal and the latter are less efficient but are
naturally unbiased (Polenta et al. 2005),
therefore residual bias is not expected in the pure cross-spectrum
case. We verified this assertion using simulations. The case of
auto-spectra is more delicate since they require a companion
Monte Carlo dataset to estimate and remove residual noise.
To verify the effect of the spikes, we firstly generated a Monte Carlo dataset that ignores the presence of residual spikes themselves, and only relies on the nominal detector noise level. When using this dataset as a noise estimate, the resulting power spectrum is heavily biased, as shown in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg09.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg72.png)
|
Figure 9: Simulated measurement of the power spectrum of CMB anisotropy in a bolometric experiment affected by CR hits as in case R1. The noise estimate neglects the presence of CR spikes. As a result, the spectrum is heavily biased (black crosses show this residual). |
| Open with DEXTER | |
Thus taking into account the effect of spikes in the Monte Carlo dataset is important. This can be done in two ways: the first and in principle more precise method is to process the Monte Carlo timelines by adding simulated spike signal with the same properties of the spikes seen in real data. When this is performed, a bias free auto-spectrum can be obtained as shown in Fig. 10.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg73.png)
|
Figure 10: Same as Fig. 9. Here the noise estimate accounts for CR spikes, assuming that their distribution is known a-priori. As a result, the spectrum is not biased. |
| Open with DEXTER | |
However, this procedure relies on the knowledge of the underlying spike's rate and distribution. The spike characteristics and statistics can in principle be extrapolated from the data themselves, relying on the observed events. This procedure, however, significantly complicates the noise estimation and Monte Carlo generation pipeline of the experiment. Moreover, this approach is prone to biases, since the estimated statistics are derived from the most energetic CR events, which are detected above the noise, while the low energy ones, which contaminate the data, are not detected: their distribution can only be estimated by means of analytic extrapolation of the high energy distribution. The reliability is thus unknown. The variance produced by the extrapolated low-energy part of the distribution can be used to guess the importance of the problem. The only way to obtain robust estimates is to perform detailed and extensive Monte Carlo simulations (using packages such as GEANT-4, see Agostinelli et al. 2003) of the interaction of the full instrument with the cosmic environment. If the high-energy part of the simulated spectrum fits the data, the low energy part of the simulated spectrum can be used to estimate the noise bias from undetected spikes. This procedure is certainly complex and computationally very intensive.
We thus verified wether a simpler approach would produce sufficiently accurate results for power spectrum estimation. For this second scheme, we estimated the noise properties from the data that are contaminated by spikes but, in the timeline simulation, we avoided modeling the spike contribution and despiking procedure. In practice, we first measured the noise properties of the despiked timeline, after subtracting the signal contribution by means of standard iterative techniques (Ferreira & Jaffe 2000), and used this dataset to estimate the noise power spectrum. Since a timeline contaminated by spikes exhibits some level of non-Gaussianity, the noise power spectrum does not encode all the information about our noise properties. However, we ignored this complication, and used the estimated spectrum information to generate stationary Gaussian realization of noise. Since the spike residual is probably non-Gaussian, this procedure is not strictly correct. However, as shown in Fig. 11, the residual bias we obtain is - visually - very small.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg11.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg74.png)
|
Figure 11: Same as Fig. 9. Here the noise estimate has been performed from the dataset using a standard pipeline, i.e. subtracting the best fit signal contribution from the data timelines. The non-Gaussian nature of the residual spikes has been neglected. The residual bias in the power spectrum is small, and appears to be limited to the highest multipoles. |
| Open with DEXTER | |
To quantify this statement, we performed the Hausman test (Polenta et al. 2005)
on the band power we obtain from our simulations. The Hausman test is a
powerful procedure to assess
the significance of a residual noise bias in the spectrum. It uses
both cross-spectra and auto-spectra estimates. We restrict ourselves to
the R1 and R2 cases described above. As in
Polenta et al. (2005), we define three test statistics to detect a bias in the noise estimation,
![]() ,
,
![]() ,
and
,
and
![]() ,
where BL(r) is a random process defined as
,
where BL(r) is a random process defined as
![\begin{displaymath}%
B_{L}(r)=\frac{1}{\sqrt{L}}\sum_{\ell =1}^{[Lr]}H_{\ell }, r\in \lbrack 0,1],
\end{displaymath}](/articles/aa/full_html/2010/11/aa14065-10/img78.png)
|
(4) |
where [.] denotes integer part, L is the maximum multipole used in the harmonic analysis, and
Table 3: Confidence level for bias detection with the Hausman test in cases R1 (top three lines) and R2 (bottom three lines), with a naively simulated noise estimation pipeline (see text).
We note that, despite being small, the bias can always be detected at a high statistical significance. This is a strong indication that the noise estimation pipeline for an high precision experiment must account for the presence of spikes in a more accurate way than the simple procedure set forth above, at least if auto spectra are desired.
While we do not explicitly simulate an experiment capable of measuring polarization spectra, it is clear that the same conclusions hold, a fortiori, when linear polarization can be measured. On the other hand, a spectral pipeline that relies only on cross-spectra is very robust to the effect of spikes.
Hence, cross-spectra, while being less efficient than auto-spectra, are certainly more adequate for an experiment contaminated by cosmic rays, at least as long as correlated events between different detectors are excluded.
7 Conclusions
Bolometric observations carried out from space are affected by cosmic rays. The data must be despiked to be used efficiently and avoid serious biases in the results. Pixel-based outliers removal works well: the power spectra of the despiked timelines closely resemble the original Gaussian noise used in the simulation. However, low-level events remain hidden in the noise, resulting in a positive shift of the average signal measured in each pixel, and increasing its variance.
The maps obtained from despiked data are non-Gaussian. The level of non-Gaussianity depends on the rate of the spikes, on the deposited energy and on the time constant and noise of the detectors. Using the skewness and the kurtosis of the pixel temperatures as simple non-Gaussianity indicators, we have found that, in the case of the 100 square degree survey, the CR-induced non-Gaussianity is unlikely to be detected if spider-web bolometers are used, but would be marginally detectable for slow membrane detectors. For experiments with longer integration times and/or lower noise detectors, the CR-induced non-Gaussianity will be significant. This will probably affect the constraints on the primordial non-Gaussianity expected by present space-borne missions. Detailed studies need to be performed in these cases.
Using the standard analysis pipeline on the map produced by the despiked timeline, we have found that the residual hidden events produce a positive bias in the angular power spectrum of the map at high multipoles. In the specific example of the 100 square degree survey, the expected bias is negligible for spider-web bolometers, but can be important for slow membrane detectors. However, since all modern experiments use bolometer arrays, cross-spectra can be computed in place of auto-spectra. These spectra are virtually unaffected by the CR-induced bias problem. The only unavoidable problem however is a significant decrease in the effective integration time and redundancy of the maps, in the case of slow membrane detectors.
This work has been supported by Italian Space Agency contracts ``COFIS'', ``Planck-HFI'' and ``OLIMPO'' and by PRIN 2006 ``Cosmologia Millimetrica con Grandi Mosaici di Rivelatori'' of the Ministero dell'Istruzione, dell'Università e della Ricerca.
References
- Agostinelli, S., Allison, J., Amako, K., et al. 2003, Nucl. Inst. and Methods A, 506, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Bartolo, N., Komatsu, E., Matarrese, S., & Riotto, A. 2004, Phys. Rep., 402, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Billot, N., Rodriguez, L., Okumura, K., Sauvage, M., & Agnèse, P. 2009, Astrophysics Detector Workshop 2008, ed. P. Kern, EAS Publ. Ser., 37, 119 [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2009, PASP, submitted [arXiv:0907.4445] [Google Scholar]
- Caserta, A., de Bernardis, P., Masi, S., & Mattioli, M. 1990, Nuclear Instrumentation and Methods in Physics Research A294, 328 [Google Scholar]
- Crill, B. P., Ade, P. A. R., Battistelli, E. S., et al. 2008, Space Telescopes and Instrumentation 2008: Optical, Infrared, and Millimeter, ed. J. M. Oschmann, Jr., M. W. M. de Graauw, & H. A. MacEwen, Proc. SPIE, 7010, [arXiv:0807.1548] [Google Scholar]
- De Troia, G., Ade, P. A. R., Bock, J. J., et al. 2003, MNRAS, 343, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, P. G., & Jaffe, A. H. 2000, MNRAS, 312, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Hinderks, J. R., Ade, P., Bock, J., et al. 2009, ApJ, 692, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Hivon, E., Górski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Holmes, W. A., Bock, J. J., Crill, B. P., et al. 2008, Appl. Opt., 47, 5996 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jones, W. C., Bhatia, R. S., Bock, J. J., & Lange, A. E. 2003, Proc. SPIE, 4855, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, W. C., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., & Stebbins, A. 1984, Nature, 310, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJS, submitted [arXiv:1001.4538] [Google Scholar]
- Kuo, C. L. 2006, Nuclear Instruments and Methods in Physics Research A, 559, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Kogut, A., Nolta, M. R., et al. 2003, ApJS, 148, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Macias-Perez, J. F., Lagache, G., Maffei, B., et al. 2007, A&A, 467, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, G., Ade, P. A. R., Benton, S., et al. 2008, SPIE Conf. Proc. [arXiv:0805.4420] [Google Scholar]
- Masi, S., Ade, P. A. R., Bock, J. J., et al. 2006, A&A, 458, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauskopf, P. D., Bock, J. J., Del Castillo, H., Holzapfel, W. L., & Lange, A. E. 1997, Appl. Opt., 36, 4 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Montroy, T. E., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Nati, F., Ade, P., Boscaleri, A., et al. 2007, New Astron. Rev., 51, 385 [Google Scholar]
- Natoli, P., De Troia, G., Hikage, C., et al. 2010, MNRAS, in press [arXiv:0905.4301] [Google Scholar]
- Nolta, M. R., Dunkley, J., Hill, R. S., et al. 2009, ApJS, 180, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Oxley, P., Ade, P. A., Baccigalupi, C., et al. 2004, Proc. SPIE Int. Soc. Opt. Eng., 5543, 320 [Google Scholar]
- Pascale, E., Ade, P. A. R., Bock, J. J., et al. 2008, ApJ, 681, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Piacentini, F., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Polenta, G., Marinucci, D., Balbi, A., et al. 2005, JCAP, 0511, 001 [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1992, Numerical Recipes in FORTRAN, The Art of Scientific Computing, 2nd edn (Cambridge: Cambridge University Press) [Google Scholar]
- Samtleben, D. 2007, Nuovo Cimento, 122B, 1353 [NASA ADS] [Google Scholar]
- Sayers, J., Golwala, S. R., Rossinot, P., et al. 2009, ApJ, 690, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Schultz, B., Bock, J. J., Lu, N., et al. 2008, in Millimeter and Submillimeter Detectors and Instrumentation for Astronomy IV, ed. W. D. Duncan, W. S. Holland, S. Withington, & J. Zmuidzinas, Proc. SPIE, 7020, 52 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swetz, D. S., Ade, P. A. R., Allen, C., et al. 2008, Proc. SPIE, 7020, 6 [NASA ADS] [Google Scholar]
- The PLANCK Collaboration 2006, unpublished, [arXiv:astro-ph/0604069] [Google Scholar]
- Verde, L., Wang, L., Heavens, A. F., & Kamionkowski, M. 2000, MNRAS, 313, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G. W., et al. 2008, MNRAS, 385, 2225 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, K. W., Ade, P. A. R., Barkats, D., et al. 2006, in Millimeter and Submillimeter Detectors and Instrumentation for Astronomy III, Proc. SPIE, 6275, [arXiv:astro-ph/0606278] [Google Scholar]
Footnotes
- ... variance
![[*]](/icons/foot_motif.png)
- The reference Gaussian dataset is different in the two cases because the noise realizations are different and their variances are corrected to account for the increase in noise caused by despiking; see the next section for further details.
All Tables
Table 1:
Fraction of true detections (![]() )
and false detections (
)
and false detections (![]() )
versus threshold level T for the convolution-based despiking method, for the two reference cases (R1 and R2) (see text). Here
)
versus threshold level T for the convolution-based despiking method, for the two reference cases (R1 and R2) (see text). Here
![]() .
.
Table 2: Parameters of the 1-point distribution of pixel temperature estimates, versus iteration of the pixel-based despiking, for cases R1 and R2 (observations of small maps, same conditions as in Fig. 5).
Table 3: Confidence level for bias detection with the Hausman test in cases R1 (top three lines) and R2 (bottom three lines), with a naively simulated noise estimation pipeline (see text).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg01.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg30.png)
|
Figure 1:
Top line: sample subsection of simulated bolometer data S(t) (converted in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg33.png)
|
Figure 2:
Same as Fig. 1, with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg03.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg51.png)
|
Figure 3: Power spectrum of the data for case R1 (top line), of the despiked data, and of the original noise-only data (middle lines). The despiking procedure does not introduce spectral features in the data, as is evident from the difference between the despiked spectrum and the original noise-only spectrum (bottom line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg04.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg52.png)
|
Figure 4: Fraction of data flagged
as contaminated by CR events, versus average CR rate, in a
bolometric experiment. A detector noise of 100
|
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
Left: one-point distributions of pixel temperatures estimates
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg06.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg65.png)
|
Figure 6: Histogrammed probabilities of the KS test, for the R1 ( top) and R2 ( bottom) cases. The hatched histograms refer to the reference Gaussian sets. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg07.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg66.png)
|
Figure 7:
Same as Fig. 6 but for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg8T.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{14065fg8B.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg67.png)
|
Figure 8: Empirical observed probabilities for skewness (S3) and kurtosis (S4), sampled from 140 Monte Carlo noise maps (red). Shown are again the R1 (top) and R2 cases. The reference Gaussian sets are shown hatched. When comparing to the values reported in Table 2 it should be noted that the histograms here are computed over a considerably larger number of pixels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg09.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg72.png)
|
Figure 9: Simulated measurement of the power spectrum of CMB anisotropy in a bolometric experiment affected by CR hits as in case R1. The noise estimate neglects the presence of CR spikes. As a result, the spectrum is heavily biased (black crosses show this residual). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg73.png)
|
Figure 10: Same as Fig. 9. Here the noise estimate accounts for CR spikes, assuming that their distribution is known a-priori. As a result, the spectrum is not biased. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14065fg11.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14065-10/Timg74.png)
|
Figure 11: Same as Fig. 9. Here the noise estimate has been performed from the dataset using a standard pipeline, i.e. subtracting the best fit signal contribution from the data timelines. The non-Gaussian nature of the residual spikes has been neglected. The residual bias in the power spectrum is small, and appears to be limited to the highest multipoles. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


