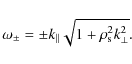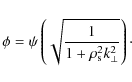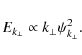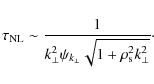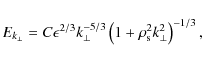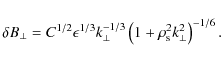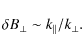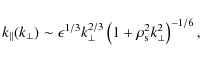| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014048 | |
| Published online | 21 September 2010 | |
Parallel electric field generation by Alfvén wave turbulence
N. H. Bian - E. P. Kontar - J. C. Brown
Department of Physics & Astronomy, University of Glasgow, G12 8QQ, UK
Received 12 January 2010 / Accepted 4 June 2010
Abstract
Aims. This work aims to investigate the spectral structure
of the parallel electric field generated by strong anisotropic and
balanced Alfvénic turbulence in relation with the problem of electron
acceleration from the thermal population in solar flare plasma
conditions.
Methods. We consider anisotropic Alfvénic fluctuations in the
presence of a strong background magnetic field. Exploiting this
anisotropy, a set of reduced equations governing non-linear, two-fluid
plasma dynamics is derived. The low-![]() limit of this model is used to follow the turbulent cascade of the
energy resulting from the non-linear interaction between kinetic Alfvén
waves, from the large magnetohydrodynamics (MHD) scales with
limit of this model is used to follow the turbulent cascade of the
energy resulting from the non-linear interaction between kinetic Alfvén
waves, from the large magnetohydrodynamics (MHD) scales with
![]() down to the small ``kinetic'' scales with
down to the small ``kinetic'' scales with
![]() ,
,
![]() being the ion sound gyroradius.
being the ion sound gyroradius.
Results. Scaling relations are obtained for the magnitude of the turbulent electromagnetic fluctuations, as a function of ![]() and
and
![]() ,
showing that the electric field develops a component parallel to the magnetic field at large MHD scales.
,
showing that the electric field develops a component parallel to the magnetic field at large MHD scales.
Conclusions. The spectrum we derive for the parallel electric
field fluctuations can be effectively used to model stochastic resonant
acceleration and heating of electrons by Alfvén waves in solar flare
plasma conditions
Key words: Sun: corona - Sun: flares - Sun: X-rays, gamma rays - turbulence
1 Introduction
Solar flares provide many challenges
for crucial aspects of high energy astrophysics, including
energy release, particle acceleration and transport
in magnetized plasmas (e.g. Aschwanden 2002; Brown et al. 2006, as recent reviews).
The impulsive phase of a flare marks the rapid
release and conversion of a large amount of magnetic energy, stored
in the solar corona, into the kinetic energy of particles.
In the standard thick-target model, (Brown 1971; Syrovatskii & Shmeleva 1972; Lin & Hudson 1976),
reviewed by (Brown & Kontar 2005; Brown et al. 2003), the stream of fast electrons which
emits bremsstrahlung hard X-rays heats the dense chromospheric plasma collisionally,
is produced first in the tenuous corona by electron acceleration from thermal
energies (![]() 1 keV) to deka-keV and MeV energies.
This standard geometry of flare electron acceleration and transport is consistent with a variety of spatially resolved
observations (Kontar et al. 2008; Emslie et al. 2003; Krucker & Lin 2008; Aschwanden et al. 2002) and by electron time of flight effects in Hard X-ray light curves (Aschwanden 2002). However, an electron beam undergoing solely collisional energy loss, as in the standard thick target model, gives
up around 105 times energy to heat than to bremsstrahlung and demands (Brown 1971) a very high electron production rate to yield observed hard X-ray fluxes.
Furthermore the electron beam and hard X-ray source anisotropies
in the standard thick target model (Brown 1972) are much higher than inferred
from the flare hard X-ray data (Kontar & Brown 2006). Brown et al. (2009) have proposed
that if fast electrons, on reaching the chromosphere, undergo re-acceleration by current sheets
there, their enhanced lifetimes increase the hard X-ray yield per electron, so reducing
the injection rate needed for hard X-ray production, while greatly reducing the fast
electron anisotropy in the main hard X-ray source. Therefore, any mechanism that can
re-accelerate electrons in the chromosphere is also of interest.
1 keV) to deka-keV and MeV energies.
This standard geometry of flare electron acceleration and transport is consistent with a variety of spatially resolved
observations (Kontar et al. 2008; Emslie et al. 2003; Krucker & Lin 2008; Aschwanden et al. 2002) and by electron time of flight effects in Hard X-ray light curves (Aschwanden 2002). However, an electron beam undergoing solely collisional energy loss, as in the standard thick target model, gives
up around 105 times energy to heat than to bremsstrahlung and demands (Brown 1971) a very high electron production rate to yield observed hard X-ray fluxes.
Furthermore the electron beam and hard X-ray source anisotropies
in the standard thick target model (Brown 1972) are much higher than inferred
from the flare hard X-ray data (Kontar & Brown 2006). Brown et al. (2009) have proposed
that if fast electrons, on reaching the chromosphere, undergo re-acceleration by current sheets
there, their enhanced lifetimes increase the hard X-ray yield per electron, so reducing
the injection rate needed for hard X-ray production, while greatly reducing the fast
electron anisotropy in the main hard X-ray source. Therefore, any mechanism that can
re-accelerate electrons in the chromosphere is also of interest.
Various acceleration mechanisms have been proposed for energetic solar particles (Aschwanden 2002), including acceleration by a large scale parallel electric field (Holman 1985), electric fields inside current sheets (Wood & Neukirch 2005; Litvinenko 2003; Bian & Tsiklauri 2008; Siversky & Zharkova 2009), collapsing trap acceleration (Bogachev & Somov 2007) as well as turbulent non-resonant (Bykov & Fleishman 2009), and resonant acceleration by waves (see the reviews by Petrosian 1999; Miller et al. 1997). Parallel acceleration between electrons and the parallel electric field produced by turbulent Alfvén waves is the subject of the present study.
The resonant coupling between a given electromagnetic mode
characterized by its dispersion relation ![]() and an electron gyrating
at the gyrofrequency
and an electron gyrating
at the gyrofrequency
![]() while streaming at the speed
while streaming at the speed
![]() along the magnetic field, is given by the Doppler resonance condition,
along the magnetic field, is given by the Doppler resonance condition,
![]() .
In this expression,
.
In this expression,
![]() is the parallel wavenumber of the wave,
is the parallel wavenumber of the wave,
![]() is the Lorentz factor and s is the harmonic number of
is the Lorentz factor and s is the harmonic number of
![]() .
Basically, the resonance condition specifies under which condition
this electron experiences an electromagnetic force which is
stationary. Therefore, if a broad spectrum of the electromagnetic field
fluctuations associated with a particular mode is present,
and moreover, if the resonance condition with this mode is satisfied
for thermal electrons, then
it is possible for these electrons to achieve a large energy gain, only
limited by the
final energy which corresponds to the last resonance with this mode.
Within quasilinear theory, this resonant acceleration process is a
diffusion in velocity space, from the
thermal velocity
.
Basically, the resonance condition specifies under which condition
this electron experiences an electromagnetic force which is
stationary. Therefore, if a broad spectrum of the electromagnetic field
fluctuations associated with a particular mode is present,
and moreover, if the resonance condition with this mode is satisfied
for thermal electrons, then
it is possible for these electrons to achieve a large energy gain, only
limited by the
final energy which corresponds to the last resonance with this mode.
Within quasilinear theory, this resonant acceleration process is a
diffusion in velocity space, from the
thermal velocity
![]() up to the final velocity
up to the final velocity ![]() .
The most straightforward way of producing a stream of fast electrons
accelerated along the magnetic field lines is through wave resonance satisfying the condition
.
The most straightforward way of producing a stream of fast electrons
accelerated along the magnetic field lines is through wave resonance satisfying the condition
either by the parallel electric force
Many people starting from (Fermi 1949) considered stochastic
acceleration of particles. Miller et al. (1996) have developed a model
of thermal electron acceleration during flares based on the Landau resonance
between these electrons and the fluctuating parallel mirror force produced by
the compressive magnetic field component of turbulent magnetoacoustic waves.
The mechanism being the magnetic analog of Landau damping is called transit-time damping.
Since magnetoacoustic waves have similar speeds as Alfvén waves,
their frequency being given by
![]() they indeed can resonate with a population
of thermal electrons, i.e.
they indeed can resonate with a population
of thermal electrons, i.e.
![]() .
Under typical plasma conditions in the solar
corona (e.g. Kontar et al. 2008; Emslie et al. 2003),
i.e. magnetic field
.
Under typical plasma conditions in the solar
corona (e.g. Kontar et al. 2008; Emslie et al. 2003),
i.e. magnetic field
![]() G, plasma
density
G, plasma
density
![]() cm-3, and electron
temperature
cm-3, and electron
temperature
![]() K, the Alfvén velocity
(
K, the Alfvén velocity
(
![]() cm/s)
is close to the electron thermal speed (
cm/s)
is close to the electron thermal speed (
![]() cm/s).
In the model by Miller et al. (1996), the broad spectrum of magnetic fluctuations
is produced by isotropic MHD turbulence.
cm/s).
In the model by Miller et al. (1996), the broad spectrum of magnetic fluctuations
is produced by isotropic MHD turbulence.
As stated above, the Landau resonance (1) is well satisfied between
thermal electrons and shear-Alfvén waves with frequency given by
![]() .
However, it is often assumed in the literature that
the shear-Alfvén mode lacks the parallel electric field necessary to accelerate the particles.
This is only true if non-MHD effects are ignored in the range of wavenumbers where the wave
has a frequency
.
However, it is often assumed in the literature that
the shear-Alfvén mode lacks the parallel electric field necessary to accelerate the particles.
This is only true if non-MHD effects are ignored in the range of wavenumbers where the wave
has a frequency
![]() .
In this study, we reconsider the possibility of electron acceleration through the
Landau resonance with the fluctuating parallel electric force produced by Alfvénic turbulence. This is done
by investigating the spectral structure of the parallel electric field fluctuation resulting from
kinetic Alfvén wave (KAW) turbulence, the KAW mode having a frequency given by
.
In this study, we reconsider the possibility of electron acceleration through the
Landau resonance with the fluctuating parallel electric force produced by Alfvénic turbulence. This is done
by investigating the spectral structure of the parallel electric field fluctuation resulting from
kinetic Alfvén wave (KAW) turbulence, the KAW mode having a frequency given by
![]() where
where
![]() is the ion-sound gyro radius. Following the same lines as the Goldreich-Sidhrar theory for Alfvénic
turbulence (Goldreich & Sridhar 1995),
we derive an expression for the parallel electric field spectrum,
for strong anisotropic KAW
turbulence, from the large MHD scales with
is the ion-sound gyro radius. Following the same lines as the Goldreich-Sidhrar theory for Alfvénic
turbulence (Goldreich & Sridhar 1995),
we derive an expression for the parallel electric field spectrum,
for strong anisotropic KAW
turbulence, from the large MHD scales with
![]() down to the small ``kinetic'' scales with
down to the small ``kinetic'' scales with
![]() .
It is shown that the magnitude of the
the parallel electric field fluctuation, being an increasing function
of wave number in the MHD regime but a decreasing function of the wave number in the ``kinetic'' regime, it reaches a maximum
at the boundary, where the Alfvén wave becomes dispersive. This means that the condition
.
It is shown that the magnitude of the
the parallel electric field fluctuation, being an increasing function
of wave number in the MHD regime but a decreasing function of the wave number in the ``kinetic'' regime, it reaches a maximum
at the boundary, where the Alfvén wave becomes dispersive. This means that the condition
![]() does not have to be satisfied
for stochastic acceleration by Alfvén waves to be effective.
does not have to be satisfied
for stochastic acceleration by Alfvén waves to be effective.
2 Two-fluid plasma dynamics
The starting point is a reduced set of equations,
describing anisotropic two-fluid plasma dynamics in a
strong magnetic field. Under the assumption of quasi-neutrality and
considering that the bulk plasma electrons have negligibly
small inertia, the fluid equations of motion
for the ions and the electrons are
where n is the plasma number density,
These equations are made dimensionless by introducing a typical length scale
L0, density n0, a typical value for the magnetic field B0,
corresponding to the Alfvén velocity
![]() ,
a time scale
,
a time scale
![]() and the pressures are normalized to the magnetic
pressure
and the pressures are normalized to the magnetic
pressure
![]() .
Equations (1)-(2) are then combined
to give an ion equation of motion
.
Equations (1)-(2) are then combined
to give an ion equation of motion
with
with
Ohm's law (5) involves the non-dimensional
parameter ![]() which is the normalized ion skin depth
which is the normalized ion skin depth
![]() with
with
![]() .
The expression for its magnetic field aligned component,
.
The expression for its magnetic field aligned component,
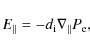
|
(6) |
shows that a parallel electric field can be produced by the electron pressure gradient along the magnetic field lines. We emphasize that this electric field is parallel to the total magnetic field, comprising the background plus its perturbation.
The existence of a strong background magnetic field
![]() makes the plasma dynamics anisotropic with
makes the plasma dynamics anisotropic with
![]() .
We can write the normalized magnetic field as
.
We can write the normalized magnetic field as
![]() and make
the following ordering
and make
the following ordering
![]() for its perturbation. The solenoidal condition for
the magnetic field perturbation allows its perpendicular
component to be written in term of a flux
function:
for its perturbation. The solenoidal condition for
the magnetic field perturbation allows its perpendicular
component to be written in term of a flux
function:
![]() .
In the same way, the perpendicular velocity is written
in term of a stream function:
.
In the same way, the perpendicular velocity is written
in term of a stream function:
![]() with the ordering
with the ordering
![]() .
Following the same standard procedure as is employed to obtain reduced
magnetohydrodynamics (RMHD) from the MHD
equations (Strauss 1976; Kadomtsev & Pogutse 1974), the two-fluid Eqs. (4)-(5) yield, to
order
.
Following the same standard procedure as is employed to obtain reduced
magnetohydrodynamics (RMHD) from the MHD
equations (Strauss 1976; Kadomtsev & Pogutse 1974), the two-fluid Eqs. (4)-(5) yield, to
order
![]() in the asymptotic expansion,
in the asymptotic expansion,
where the notation
with p the normalized pressure perturbation. The plasma pressure parameter is defined as
In the limit
![]() ,
it can be seen from (11) that the plasma
flow becomes incompressible,
,
it can be seen from (11) that the plasma
flow becomes incompressible,
![]() ,
and hence,
the above system is equivalent to the incompressible reduced Hall-MHD equations derived,
for instance, by Gómez et al. (2008).
For
,
and hence,
the above system is equivalent to the incompressible reduced Hall-MHD equations derived,
for instance, by Gómez et al. (2008).
For
![]() ,
the classical reduced-MHD equations are recovered with
Eqs. (7) and (9) forming an independent system
describing the non-linear dynamics of shear Alfvén waves.
,
the classical reduced-MHD equations are recovered with
Eqs. (7) and (9) forming an independent system
describing the non-linear dynamics of shear Alfvén waves.
Assuming ![]() in the previous model leads to the reduced
electron-MHD (EMHD) equations which conserve the magnetic
energy
in the previous model leads to the reduced
electron-MHD (EMHD) equations which conserve the magnetic
energy
![]() Its linear modes are the whistler
waves with
Its linear modes are the whistler
waves with
![]()
![]() .
Some key properties of the EMHD turbulence have been investigated
both numerically and theoretically, suggesting that the Kolmogorov type arguments
work fine (Cho & Lazarian 2004,2009; Ng et al. 2003; Biskamp et al. 1999). A calculation along the lines
of the one below for KAWs, shows that the energy spectrum for whistler wave
turbulence is
.
Some key properties of the EMHD turbulence have been investigated
both numerically and theoretically, suggesting that the Kolmogorov type arguments
work fine (Cho & Lazarian 2004,2009; Ng et al. 2003; Biskamp et al. 1999). A calculation along the lines
of the one below for KAWs, shows that the energy spectrum for whistler wave
turbulence is
![]() .
.
Relaxing the assumption of a large ![]() ,
we can allow for the effect
of a finite plasma compressibility. Since the perpendicular pressure balance,
,
we can allow for the effect
of a finite plasma compressibility. Since the perpendicular pressure balance,
![]() ,
is satisfied to order
,
is satisfied to order
![]() in the expansion of the ion equation of motion, the compression
term
in the expansion of the ion equation of motion, the compression
term
![]() can be eliminated from (11) and (8) using
the fact that
can be eliminated from (11) and (8) using
the fact that
![]() .
Therefore, defining
.
Therefore, defining
![]() ,
,
![]() and
and
![]() ,
the following model
is obtained:
,
the following model
is obtained:
The system conserves the total energy
3 Kinetic Alfvén turbulence
Forwith
Notice that this model is very similar to the EMHD system when
This shows that the low-frequency Alfvén wave, with a frequency much smaller that the ion cyclotron frequency
From Eqs. (16)-(17), a theory for KAW turbulence is now constructed
along the same lines as the Goldreich-Sidrar theory (Goldreich & Sridhar 1995)
for Alfvén wave turbulence (Kraichnan 1965). Some form of dissipation at small
scales, balancing the energy input at large scales, is necessary for a steady cascade of energy to take place.
It is assumed that the turbulent
fluctuations are composed of KAWs, hence,
Focusing first on the perpendicular cascade, we can express the energy per wave number
Moreover, we adopt the standard assumption that the flux of turbulent energy at a given scale is determined by the turbulence at that scale and is a constant equal to the energy injection rate
with the non-linear time scale being given by
Combining relations (21)-(23) yields the scaling law for the energy spectrum:
where C is a constant of the order of unity (Kraichnan 1965). This expression recovers the spectrum of Alfvenic turbulence, in the limit
Now, we recall a fundamental ordering used in the derivation of the two-fluid reduced MHD system (16)-(17):
This ordering is not restrictive in the sense that we are interested in the inertial range and not in the outer scale of the Alfvenic turbulence, where
which recovers the original Goldreich-Sridhar critical balance relation
In fact, it would have been equivalent to argue, following Goldreich & Sridhar (1995), that the anisotropy
of the turbulence is fixed by the so-called critical balance condition,
i.e. to assume that the characteristic non-linear decorrelation time
is of the order of the inverse KAW frequency, i.e.
![]() ,
with
,
with ![]() given by Eq. (19). The scaling relations
obtained for the energy spectrum and anisotropy in the dispersive scales
of kinetic Alfvén wave turbulence (Cranmer & van Ballegooijen 2003; Howes et al. 2008; Schekochihin et al. 2009)
are similar to the ones of EMHD turbulence (Cho & Lazarian 2004,2009; Ng et al. 2003; Biskamp et al. 1999).
Notice however that for an EMHD Ohm's law given by
given by Eq. (19). The scaling relations
obtained for the energy spectrum and anisotropy in the dispersive scales
of kinetic Alfvén wave turbulence (Cranmer & van Ballegooijen 2003; Howes et al. 2008; Schekochihin et al. 2009)
are similar to the ones of EMHD turbulence (Cho & Lazarian 2004,2009; Ng et al. 2003; Biskamp et al. 1999).
Notice however that for an EMHD Ohm's law given by
![]() ,
whistlers
do not have a parallel electric field.
,
whistlers
do not have a parallel electric field.
Before concluding this section, few comments are due. In deriving the energy spectrum for kinetic Alfvén wave turbulence we are relying on the existing theory developed by (Goldreich & Sridhar 1995) for strong anisotropic and balanced Alfvén turbulence. The same approach was followed by (Schekochihin et al. 2009) based on a compressible EMHD model to describe the dispersive range of Alfvén turbulence, see also (Cranmer & van Ballegooijen 2003). It is our framework to investigate the spectral structure of the turbulent parallel electric field. This should however not suggest that there is one universal cascade of Alfvenic fluctuations. Indeed, the previous arguments are based on the assumption that the turbulence is non cross-helical. In the MHD range, the effect of cross-helicity on the cascade of the two Elsasser energies, i.e. imbalanced turbulence, was investigated by (Lithwick et al. 2007; Beresnyak & Lazarian 2008; Perez & Boldyrev 2009; Chandran 2008). Imbalanced turbulence is a more general situation but it is not yet clear how the imbalance affects the dispersive range. Moreover it should be mentioned that MHD and EMHD turbulence can also be dominated by weak fluctuations, see (Galtier & Bhattacharjee 2003; Galtier et al. 2002), weak Alfvén turbulence producing different spectra and anisotropy than the case studied here. Also, it has been argued that ``dynamic alignment'' of velocity and magnetic fields result in spectra that are flatter than Kolmogorov (Boldyrev 2006; Mason et al. 2006; Beresnyak & Lazarian 2006). With these restrictions in mind we can now discuss the parallel electric field spectrum of Alfvén turbulence, a potentially important issue, which to the best of our knowledge has not been investigated so-far.
4 Parallel electric field spectrum
As stated above, the dispersive nature of the dynamics of KAWs involves the production of an electric field perturbation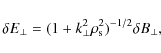
|
(28) |
for the perpendicular component and
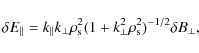
|
(29) |
for the parallel component. Using the scaling (25) for

|
(30) |
and
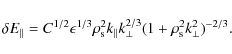
|
(31) |
These equations, together with Eq. (27), determine the magnitude of the electric field fluctuations produced by strong anisotropic and balanced kinetic Alfvén wave turbulence as a function of wavenumber
![\begin{figure}
\par\includegraphics[width=8cm,clip]{electric_k.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14048-10/Timg132.png)
|
Figure 1:
Parallel electric field,
|
| Open with DEXTER | |
5 Discussion and conclusions
There exists an extensive literature on stochastic acceleration by resonant interaction
between waves and particles. However, to our knowledge, a scenario
for field-aligned acceleration of electrons by the parallel electric field
produced by Alfvenic turbulence has not been
considered so-far. The reason is that it is generally assumed
that the MHD Alfvén mode, whose frequency is given by
![]() when
when
![]() ,
lacks the parallel electric field to accelerate
the particles. A main objective of the present work is to emphasize that, on the contrary,
the role of the parallel electric field intrinsic to the Alfvén wave
dynamics in a warm plasma should not be ignored, even at the scales of standard MHD.
We believe that while a scenario based on Alfvén waves for electron
acceleration during solar flares remains a conjecture, as is any
other acceleration mechanism proposed so far, it is particulary attractive. The reason is due to the
body of observational evidences on the role played by these waves in controlling many aspects of the
dynamics of astrophysical plasmas.
,
lacks the parallel electric field to accelerate
the particles. A main objective of the present work is to emphasize that, on the contrary,
the role of the parallel electric field intrinsic to the Alfvén wave
dynamics in a warm plasma should not be ignored, even at the scales of standard MHD.
We believe that while a scenario based on Alfvén waves for electron
acceleration during solar flares remains a conjecture, as is any
other acceleration mechanism proposed so far, it is particulary attractive. The reason is due to the
body of observational evidences on the role played by these waves in controlling many aspects of the
dynamics of astrophysical plasmas.
In plasma conditions typical of solar flares, values of the fluctuating parallel electric field
can be significant. We consider a range of solar plasma parameters:
guiding magnetic field B0=100 Gauss, plasma density
![]() cm-3,
plasma temperature 1 MK, and the loop length scale L0. Normalizing the wavenumber
by
cm-3,
plasma temperature 1 MK, and the loop length scale L0. Normalizing the wavenumber
by
![]() ,
the amplitude of the
parallel electric field is presented in Fig. (1). For solar flare
parameters
,
the amplitude of the
parallel electric field is presented in Fig. (1). For solar flare
parameters
![]() cm, the maximum electric fields
cm, the maximum electric fields
![]() V m-1appears at the scales
V m-1appears at the scales
![]() cm.
The maximum values of the electric field and the characteristic scales can be derived
explicitly from the results of the previous section. The maximum of the electric field amplitude
cm.
The maximum values of the electric field and the characteristic scales can be derived
explicitly from the results of the previous section. The maximum of the electric field amplitude
is reached at
These are dependent on the magnitude of the magnetic perturbation
Our estimate for the maximum electric electric field fluctuation
produced by Alfvén wave
turbulence show that the latter can be rather strong.
Indeed, for the adopted solar flares plasma parameters, the Dreicer electric field
is ![]() 0.02 V m-1, and the maximum amplitude of the fluctuating field
can exceed this values.
0.02 V m-1, and the maximum amplitude of the fluctuating field
can exceed this values.
The parallel electric force associated with the Alfvén wave dynamics could play an important role in a number
of cases. First, as the primary source
of thermal electron acceleration, where waves and turbulence are triggered
by the reconnection process (Longcope & Priest 2007; Bellan 1998) or as a result of the
twisting of the field lines anchored in the photosphere. It has also been proposed that part
of the energy released during magnetic reconnection is transported by Alfvén waves to the chromosphere (Fletcher & Hudson 2008; Emslie & Sturrock 1982).
Therefore, in a situation where Alfvenic turbulence fills the loop,
the waves will affect the transport of the energetic
electrons to the chromosphere. Acceleration occurs along the field lines which are perturbed by the
Alfvén dynamics, hence the pace
of the acceleration along
![]() also controls the cross-
also controls the cross-
![]() transport.
Finally, as already mentioned in the Introduction, we note that if the
electric field produced by Alfvén turbulence
can re-accelerate non-thermal electrons injected into the chromosphere
this revision of the standard Thick Target Model may resolve existing
problems with it. Whether this is really the case depends on
the detailed nature of the interaction between the parallel electric
field and the electrons which requires a kinetic description, the
subject of a future publication.
transport.
Finally, as already mentioned in the Introduction, we note that if the
electric field produced by Alfvén turbulence
can re-accelerate non-thermal electrons injected into the chromosphere
this revision of the standard Thick Target Model may resolve existing
problems with it. Whether this is really the case depends on
the detailed nature of the interaction between the parallel electric
field and the electrons which requires a kinetic description, the
subject of a future publication.
This work is supported by a STFC rolling grant (N.H.B., E.P.K., J.C.B.) and an STFC Advanced Fellowship (EPK). Financial support by the Leverhulme Trust grant (F/00179/AY) and by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484) is gratefully acknowledged.
References
- Aschwanden, M. J. 2002, Space Sci. Rev., 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Brown, J. C., & Kontar, E. P. 2002, Sol. Phys., 210, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Bellan, P. M. 1998, Phys. Plasmas, 5, 3081 [NASA ADS] [CrossRef] [Google Scholar]
- Beresnyak, A., & Lazarian, A. 2006, ApJ, 640, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Beresnyak, A., & Lazarian, A. 2008, ApJ, 682, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N., & Tsiklauri, D. 2008, A&A, 489, 1291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, N. H., & Tsiklauri, D. 2009, Phys. Plasmas, 16, 064503 [NASA ADS] [CrossRef] [Google Scholar]
- Biskamp, D., Schwarz, E., Zeiler, A., Celani, A., & Drake, J. F. 1999, Phys. Plasmas, 6, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Bogachev, S. A., & Somov, B. V. 2007, Astron. Lett., 33, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Boldyrev, S. 2006, Phys. Rev. Lett., 96, 115002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1972, Sol. Phys., 26, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & Kontar, E. P. 2005, Adv. Space Res., 35, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Emslie, A. G., & Kontar, E. P. 2003, ApJ, 595, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Emslie, A. G., Holman, G. D., et al. 2006, ApJ, 643, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bykov, A. M., & Fleishman, G. D. 2009, ApJ, 692, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Chandran, B. D. G. 2008, ApJ, 685, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2004, ApJ, 615, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2009, ApJ, 701, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & van Ballegooijen, A. A. 2003, ApJ, 594, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., & Sturrock, P. A. 1982, Sol. Phys., 80, 99 [Google Scholar]
- Emslie, A. G., Kontar, E. P., Krucker, S., & Lin, R. P. 2003, ApJ, 595, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., & Hudson, H. S. 2008, ApJ, 675, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Galtier, S., & Bhattacharjee, A. 2003, Phys. Plasmas, 10, 3065 [NASA ADS] [CrossRef] [Google Scholar]
- Galtier, S., Nazarenko, S. V., Newell, A. C., & Pouquet, A. 2002, ApJ, 564, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, D. O., Mahajan, S. M., & Dmitruk, P. 2008, Phys. Plasmas, 15, 102303 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D. 1985, ApJ, 293, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Howes, G. G., Cowley, S. C., Dorland, W., et al. 2008, J. Geophys. Res. (Space Physics), 113, 5103 [Google Scholar]
- Kadomtsev, B. B., & Pogutse, O. P. 1974, Soviet Journal of Experimental and Theoretical Physics, 38, 283 [Google Scholar]
- Kontar, E. P., & Brown, J. C. 2006, ApJ, 653, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Hannah, I. G., & MacKinnon, A. L. 2008, A&A, 489, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraichnan, R. H. 1965, Phys. Fluids, 8, 1385 [Google Scholar]
- Krucker, S., & Lin, R. P. 2008, ApJ, 673, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., Goldreich, P., & Sridhar, S. 2007, ApJ, 655, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 2003, Adv. Space Res., 32, 2385 [NASA ADS] [Google Scholar]
- Longcope, D. W., & Priest, E. R. 2007, Phys. Plasmas, 14, 122905 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, J., Cattaneo, F., & Boldyrev, S. 2006, Phys. Rev. Lett., 97, 255002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., Cargill, P. J., Emslie, A. G., et al. 1997, J. Geophys. Res., 102, 14631 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. S., Bhattacharjee, A., Germaschewski, K., & Galtier, S. 2003, Phys. Plasmas, 10, 1954 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, J. C., & Boldyrev, S. 2009, Phys. Rev. Lett., 102, 025003 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Petrosian, V. 1999, in Plasma Turbulence and Energetic Particles in Astrophysics, Proceedings of the International Conference, Cracow (Poland), 5-10 September, Obserwatorium Astronomiczne, Uniwersytet Jagiellonski, Kraków 1999, ed. M. Ostrowski & R. Schlickeiser, 135 [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Dorland, W., et al. 2009, ApJS, 182, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Siversky, T. V., & Zharkova, V. V. 2009, J. Plasma Phys., 75, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, H. R. 1976, Phys. Fluids, 19, 134 [Google Scholar]
- Syrovatskii, S. I., & Shmeleva, O. P. 1972, AZh, 49, 334 [NASA ADS] [Google Scholar]
- Waelbroeck, F. L., Hazeltine, R. D., & Morrison, P. J. 2009, Phys. Plasmas, 16, 032109 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, P., & Neukirch, T. 2005, Sol. Phys., 226, 73 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{electric_k.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14048-10/Timg132.png)
|
Figure 1:
Parallel electric field, |
| Open with DEXTER | |
In the text
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



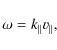
![\begin{displaymath}
\partial_{\rm t}\psi=\partial_{z}(\phi-d_{\beta}Z)+ [\phi-d_{\beta}Z,
\psi]
\end{displaymath}](/articles/aa/full_html/2010/11/aa14048-10/img89.png)
![\begin{displaymath}
\partial_{\rm t} Z=\partial_{z}(c_{\beta}v_{z}-d_{\beta}j_{z})+[c_{\beta}v_{z}-d_{\beta}j_{z},\psi]+[\phi,Z]
\end{displaymath}](/articles/aa/full_html/2010/11/aa14048-10/img90.png)
![\begin{displaymath}
\partial_{\rm t} v_{z}=c_{\beta}\partial _{z}Z+[\phi, v_{z}]+c_{\beta}[Z,\psi].
\end{displaymath}](/articles/aa/full_html/2010/11/aa14048-10/img92.png)
![\begin{displaymath}
\partial_{\rm t}\psi=\partial_{z}(\phi+\rho^{2}_{\rm s}\omega_{z})+ [\phi+\rho^{2}_{\rm s}\omega_{z},
\psi],
\end{displaymath}](/articles/aa/full_html/2010/11/aa14048-10/img96.png)
![\begin{displaymath}
E=\int {\rm d}^{3}r\left[(\nabla\phi)^{2}+(\nabla \psi)^{2}+\rho_{\rm s}^{2}\omega^{2}_{z}\right].
\end{displaymath}](/articles/aa/full_html/2010/11/aa14048-10/img99.png)