| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913886 | |
| Published online | 08 September 2010 | |
Study of star-forming galaxies in SDSS up to redshift 0.4
II. Evolution from the fundamental parameters: mass, metallicity and star formation rate
M. A. Lara-López1,2 - A. Bongiovanni1,2 - J. Cepa1,2 - A. M. Pérez García1,2 - M. Sánchez-Portal4 - H. O. Castañeda1,3 - M. Fernández Lorenzo1,2 - M. Povic1,2
1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Spain
2 - Departamento de Astrofísica, Universidad de la Laguna, Spain
3 - Departamento de Física, Escuela Superior de Física y Matemática,
IPN, México D.F., Mexico
4 - Herschel Science Center, INSA/ESAC, Madrid, Spain
Received 16 December 2009 / Accepted 24 March 2010
Abstract
Context. To understand the formation and evolution
of galaxies, it is important to have a full comprehension of
the role played by metallicity, star formation rate (SFR), morphology,
and color. The interplay of these parameters at different redshifts
will substantially affect the evolution of galaxies and, as a
consequence, their evolution provides important clues and constraints
for the galaxy evolution models.
Aims. In this work we focus on the evolution of the
SFR, metallicity of the gas, and morphology of galaxies at low redshift
in search of signs of evolution. We analyzed the evolution of the SFR,
metallicity, and morphology, through the mass-metallicity,
luminosity-metallicity, SFR-stellar mass, and SFR-metallicity
relationships of star-forming galaxies from SDSS-DR5 (Sloan Digital Sky
Survey-Data Release 5), using redshift intervals in bins
of 0.1 from ![]() 0 to 0.4.
0 to 0.4.
Methods. We used data processed with the STARLIGHT
spectral synthesis code, correcting the fluxes for dust extinction, and
estimating metallicities using the R23 method.
We used the S2N2 (log(H![]() /[S II]) vs.
log(H
/[S II]) vs.
log(H![]() /[N II]))
diagnostic diagram as a tool to classify star-forming, composite, and
AGN galaxies. We analyzed the evolution of the three principal
BPT diagrams, estimating the SFR and specific SFR (SSFR) for
our samples of galaxies, studying the luminosity and mass-metallicity
relations, and analyzing the morphology of our sample of galaxies
through the g-r color,
concentration index, and SSFR.
/[N II]))
diagnostic diagram as a tool to classify star-forming, composite, and
AGN galaxies. We analyzed the evolution of the three principal
BPT diagrams, estimating the SFR and specific SFR (SSFR) for
our samples of galaxies, studying the luminosity and mass-metallicity
relations, and analyzing the morphology of our sample of galaxies
through the g-r color,
concentration index, and SSFR.
Results. We found that the S2N2 is a reliable
diagram for classifying star-forming, composite, and AGNs galaxies. We
demonstrate that the three principal BPT diagrams show an
evolution toward higher values of [O III]
![]() 5007/H
5007/H![]() due to a metallicity decrement. We found an evolution in the
mass-metallicity relation of
due to a metallicity decrement. We found an evolution in the
mass-metallicity relation of ![]() 0.2 dex for the
redshift range 0.3 < z
< 0.4 compared to our local one. From the analysis of the
evolution of the SFR and SSFR as a function of the stellar mass and
metallicity, we discovered a group of galaxies with higher SFR and SSFR
at all redshift samples, whose morphology is consistent with those of
late-type galaxies. Finally, the comparison of our local (
0.04<z<0.1)
with our higher redshift sample (0.3<z<0.4)
shows that the metallicity, the SFR, and morphology evolve toward lower
values of metallicity, higher SFRs, and late-type morphologies for the
redshift range 0.3<z<0.4.
0.2 dex for the
redshift range 0.3 < z
< 0.4 compared to our local one. From the analysis of the
evolution of the SFR and SSFR as a function of the stellar mass and
metallicity, we discovered a group of galaxies with higher SFR and SSFR
at all redshift samples, whose morphology is consistent with those of
late-type galaxies. Finally, the comparison of our local (
0.04<z<0.1)
with our higher redshift sample (0.3<z<0.4)
shows that the metallicity, the SFR, and morphology evolve toward lower
values of metallicity, higher SFRs, and late-type morphologies for the
redshift range 0.3<z<0.4.
Key words: galaxies: abundances - galaxies: evolution - galaxies: starburst - galaxies: spiral - galaxies: star formation
1 Introduction
Baldwin et al. (1981,
hereafter BPT) were the first to propose diagnostic diagrams for
classifying galaxies into starburst or active galactic nucleus (AGN),
based on the dominant energy source in emission-line galaxies, since
AGNs have a much harder ionizing spectrum than hot stars. Revised and
refined by Veilleux & Osterbrock (1987),
the three BPT empirical diagnostic diagrams use the
optical line ratios [O I] ![]() 6300/H
6300/H![]() ,
[S II]
,
[S II] ![]()
![]() 6717, 6731/H
6717, 6731/H![]() ,
[N II]
,
[N II] ![]() 6583/H
6583/H![]() ,
and [O III]
,
and [O III] ![]() 5007/H
5007/H![]() (hereafter [N II] will refer to
[N II]
(hereafter [N II] will refer to
[N II] ![]() 6583, and
[S II] to [S II]
6583, and
[S II] to [S II] ![]()
![]() 6717, 6731).
The BPT diagrams are the most widely used method of
segregating between star-forming (SF) galaxies and AGNs, since the
lines in SF galaxies are emitted by H II regions,
which are ionized by massive stars, while AGNs are ionized by a harder
radiation field.
6717, 6731).
The BPT diagrams are the most widely used method of
segregating between star-forming (SF) galaxies and AGNs, since the
lines in SF galaxies are emitted by H II regions,
which are ionized by massive stars, while AGNs are ionized by a harder
radiation field.
Kewley et al. (2001,
hereafter Kew01) used a combination of stellar population synthesis
models and detailed self-consistent photoionization models to create a
theoretical maximum starburst line on the three BPT diagrams. Kauffmann
et al. (2003a,
hereafter Kauf03) has shifted this starburst limit to a lower and more
precise one in the [N II]/H![]() diagram, excluding Seyfert-H II
composite objects whose spectra contain significant contributions from
both AGN and star formation, from pure SF galaxies. Galaxies
between the Kauf03 and Kew01 divisions are considered as composite
galaxies.
diagram, excluding Seyfert-H II
composite objects whose spectra contain significant contributions from
both AGN and star formation, from pure SF galaxies. Galaxies
between the Kauf03 and Kew01 divisions are considered as composite
galaxies.
There are more division criteria between SF galaxies and AGNs
in the [N II]/H![]() vs.
[O III]
vs.
[O III] ![]() 5007/H
5007/H![]() BPT diagram, such as the one of Stasinska
et al. (2006),
which used a lower limit than that of Kauf03, based on a more rigorous
criterion, and the one of Lee et al. (2007a), which used
an intermediate empirical line between the Kauf03 and
Kew01 divisions. It is possible, however,
to classify SF galaxies and AGNs using only the
[N II]/H
BPT diagram, such as the one of Stasinska
et al. (2006),
which used a lower limit than that of Kauf03, based on a more rigorous
criterion, and the one of Lee et al. (2007a), which used
an intermediate empirical line between the Kauf03 and
Kew01 divisions. It is possible, however,
to classify SF galaxies and AGNs using only the
[N II]/H![]() ratio,
as discussed in Stasinska et al. (2006), since the
left arm of the [N II]/H
ratio,
as discussed in Stasinska et al. (2006), since the
left arm of the [N II]/H![]() diagram
(see for example Fig. 2) is a measure of the
combination of the metallicity and the ionization parameter. Then,
higher values of this ratio indicate that the galaxy hosts an AGN.
Stasinska et al. (2006)
classify as SF galaxies those with log([N II]/H
diagram
(see for example Fig. 2) is a measure of the
combination of the metallicity and the ionization parameter. Then,
higher values of this ratio indicate that the galaxy hosts an AGN.
Stasinska et al. (2006)
classify as SF galaxies those with log([N II]/H![]() )
) ![]() -0.4,
composite galaxies those with -0.4 < log([N II]/H
-0.4,
composite galaxies those with -0.4 < log([N II]/H![]() )
) ![]() -0.2, and as AGNs those galaxies with log([N II]/H
-0.2, and as AGNs those galaxies with log([N II]/H![]() ) > -0.2.
) > -0.2.
Following with the objective of segregating SF from composite
and AGNs galaxies, in this work we study the
S2N2 diagram as a reliable segregator of galaxies. This log(H![]() /[S II]) vs.
log(H
/[S II]) vs.
log(H![]() /[N II]) diagram
was introduced by Sabbadin et al. (1977) as a useful
tool for separating galactic planetary nebula (PNe),
H II regions, and
supernova remnants (SNRs). This diagram was later applied to
Herbig-Haro objects (Cantó 1981),
Galactic PNe (García-Lario et al. 1991; Riesgo
& López 2005),
and extragalactic PNe (Magrini et al. 2003). The
S2N2 diagram has also been used as a metallicity and
ionization parameter indicator for extragalactic H II regions
by Viironen et al. (2007).
/[N II]) diagram
was introduced by Sabbadin et al. (1977) as a useful
tool for separating galactic planetary nebula (PNe),
H II regions, and
supernova remnants (SNRs). This diagram was later applied to
Herbig-Haro objects (Cantó 1981),
Galactic PNe (García-Lario et al. 1991; Riesgo
& López 2005),
and extragalactic PNe (Magrini et al. 2003). The
S2N2 diagram has also been used as a metallicity and
ionization parameter indicator for extragalactic H II regions
by Viironen et al. (2007).
The S2N2 diagram has been also applied to galaxies by some
authors. For example, Moustakas & Kennicutt (2006) studied
whether there was a difference between integrated spectra of galaxies
and the spectra of individual H II regions.
Dopita et al. (2006)
used the S2N2 diagram, among others, for abundance
diagnostics using photoionization models. Nevertheless,
the [S II] flux
always shows deficiences when generated by photoionization models
(e.g. Levesque et al. 2010). Also,
Lamareille et al. (2009)
and Pérez-Montero et al. (2009) used the S2N2 diagram
as a segregator of SF from Seyfert 2 galaxies, but using
different ratios: log([N II]/H![]() ) vs.
log([S II]/H
) vs.
log([S II]/H![]() ). However, in their
division, Lamareille et al. (2009) do not
distinguish between SF and composite galaxies; also, they use
equivalent widths instead of emission line fluxes, which could affect
the results (Kobulnicky & Kewley 2004).
). However, in their
division, Lamareille et al. (2009) do not
distinguish between SF and composite galaxies; also, they use
equivalent widths instead of emission line fluxes, which could affect
the results (Kobulnicky & Kewley 2004).
The formation and evolution of galaxies at different
cosmological epochs are driven mainly by two linked processes: the star
formation history and the metal enrichment. Thus, from an observational
point of view, the star formation rate (SFR), the metallicity, and the
stellar mass of the galaxies at different epochs will give us important
clues to the evolution of galaxies. The first quantitative SFRs were
derived from evolutionary synthesis models of galaxy colors (Tinsley 1968, 1972; Searle
et al. 1973),
confirming the trends in SFRs and star formation histories along the
Hubble sequence and giving the first predictions of the evolution of
the SFR with cosmic lookback time. The development of more precise
direct SFR diagnostics includes the integrated emission-line
fluxes (Cohen 1976;
Kennicutt 1983), near-ultraviolet continuum fluxes (Donas &
Deharveng 1984),
and infrared continuum fluxes (Harper & Low 1973; Rieke
& Lebofsky 1978;
Telesco & Harper 1980);
see Kennicutt (1998)
for a review. The hydrogen Balmer line H![]() is currently the most reliable tracer of star formation, since in
H II regions and
star-forming galaxies, the Balmer emission-line luminosity
scales directly with the total ionizing flux of the embedded stars.
A widely known calibration of the H
is currently the most reliable tracer of star formation, since in
H II regions and
star-forming galaxies, the Balmer emission-line luminosity
scales directly with the total ionizing flux of the embedded stars.
A widely known calibration of the H![]() line as
SFR tracer is the one devised by Kennicutt (1998). However,
it is important to take corrections for stellar absorption and
reddening into account to obtain SFRs in agreement with the ones
derived using other wavelengths (e.g. Rosa-González
et al. 2002; Charlot et al. 2002; Dopita
et al. 2002).
In parallel, other diagnostics have been developed using the
oxygen doublet [O II]
line as
SFR tracer is the one devised by Kennicutt (1998). However,
it is important to take corrections for stellar absorption and
reddening into account to obtain SFRs in agreement with the ones
derived using other wavelengths (e.g. Rosa-González
et al. 2002; Charlot et al. 2002; Dopita
et al. 2002).
In parallel, other diagnostics have been developed using the
oxygen doublet [O II] ![]() 3726,
3729 for the redshift range
3726,
3729 for the redshift range ![]() (e.g. Gallagher et al. 1989; Kennicutt 1998; Rosa-González
et al. 2002; Kewley et al. 2004). Moreover,
this diagnostic is useful when the H
(e.g. Gallagher et al. 1989; Kennicutt 1998; Rosa-González
et al. 2002; Kewley et al. 2004). Moreover,
this diagnostic is useful when the H![]() line is not easily
observed at higher redshifts (
line is not easily
observed at higher redshifts (![]() in the optical). However, the [O II]
doublet presents problems in reddening and abundance dependence (Jansen
et al. 2001;
Charlot et al. 2002).
Alternatively, it is possible to estimate the SFR from the
soft X-ray luminosity, which is comparable to the one determined from
the H
in the optical). However, the [O II]
doublet presents problems in reddening and abundance dependence (Jansen
et al. 2001;
Charlot et al. 2002).
Alternatively, it is possible to estimate the SFR from the
soft X-ray luminosity, which is comparable to the one determined from
the H![]() luminosity
(Rosa González et al. 2009;
Rovilos et al. 2009).
luminosity
(Rosa González et al. 2009;
Rovilos et al. 2009).
A strong dependence on the SFR and the stellar mass and its evolution with redshift has been found, with the bulk of star formation occurring first in massive galaxies, and later in less massive systems (e.g. Guzmán et al. 1997; Brinchmann & Ellis 2000; Juneau et al. 2005; Bauer et al. 2005; Bell et al. 2005; Pérez-Gonzalez et al. 2005; Feulner et al. 2005; Papovich et al. 2006; Caputi et al. 2006; Reddy et al. 2006; Erb et al. 2006a; Noeske et al. 2007a; Buat et al. 2008). In the local universe, several studies have illustrated a relationship between the SFR and stellar mass, identifying two populations: galaxies on a star-forming sequence, and ``quenched'' galaxies, with little or no detectable star formation (Brinchmann et al. 2004; Salim et al. 2005; Lee 2006; Lee et al. 2007b). At higher redshift, Noeske et al. (2007a) shows the existence of a ``main sequence'' (MS) for SF galaxies in the SFR-stellar mass relation over the redshift range 0.2 < z < 1.1. From the galaxies considered in this study, the range of log(SFR) remains constant to z>1, while the MS as a whole moves to higher SFR as z increases.
Metallicity is another important property of galaxies, and its study is crucial for a deep understanding of galaxy formation and evolution, since it is related to the whole past history of the galaxy. Metallicity is a tracer of the fraction of baryonic mass already converted into stars and is sensitive to the metal losses due to stellar winds, supernovae, and active nuclei feedbacks. A detailed description of the different metallicity methods and calibrations are given in Lara-López et al. (2009a,b).
Stellar mass and metallicity are strongly correlated in SF
galaxies, with massive galaxies showing higher metallicities than less
massive galaxies. This relationship provides essential insight into
galaxy formation and evolution. The mass-metallicity (M-Z) relation
first observed by Lequeux et al. (1979) has been
intensively studied (Skillman et al. 1989; Brodie
& Huchra 1991;
Zaritsky et al. 1994;
Richer & McCall 1995;
Garnett et al. 1997;
Pilyugin & Ferrini 2000,
López-Sánchez 2010;
López-Sánchez & Esteban 2010,
among others), and it is well established by the work of Tremonti
et al. (2004,
hereafter T04) for the local universe (z ![]() 0.1)
using SDSS data. The study of the redshift evolution of the M-Z relation
has provided us with basic information on the cosmic evolution of star
formation.
0.1)
using SDSS data. The study of the redshift evolution of the M-Z relation
has provided us with basic information on the cosmic evolution of star
formation.
Regarding the evolution of the M-Z relation
for SF galaxies at z < 1,
Savaglio et al. (2005)
have investigated the mass-metallicity relations using galaxies at
0.4 < z < 1,
finding that metallicity is lower at higher redshift by ![]() 0.15 dex.
Moreover, Maier et al. (2005),
Hammer et al. (2005),
and Liang et al. (2006)
find that emission line galaxies are poorer in metals at z
0.15 dex.
Moreover, Maier et al. (2005),
Hammer et al. (2005),
and Liang et al. (2006)
find that emission line galaxies are poorer in metals at z ![]() 0.7
than present-day spirals. A study of Lamareille
et al. (2009)
focused on the evolution of the M-Z relation
up to z
0.7
than present-day spirals. A study of Lamareille
et al. (2009)
focused on the evolution of the M-Z relation
up to z ![]() 0.9, suggesting that
the M-Z relation is
flatter at higher redshifts. However, Carollo & Lilly (2001), from
emission-line ratios of 15 galaxies in a range of
0.5 < z < 1,
find that their metallicities appear to be remarkably similar to those
of local galaxies selected with the same criteria. Also, Lilly
et al. (2003)
used a sample of 66 SF galaxies with
0.47 < z < 0.92 to
claim a smaller variation in metallicity of
0.9, suggesting that
the M-Z relation is
flatter at higher redshifts. However, Carollo & Lilly (2001), from
emission-line ratios of 15 galaxies in a range of
0.5 < z < 1,
find that their metallicities appear to be remarkably similar to those
of local galaxies selected with the same criteria. Also, Lilly
et al. (2003)
used a sample of 66 SF galaxies with
0.47 < z < 0.92 to
claim a smaller variation in metallicity of ![]() 0.08 dex compared
with the metallicity observed locally, showing only modest evolutionary
effects (for more details about the M-Z relation,
see Lara-López et al. 2009b).
0.08 dex compared
with the metallicity observed locally, showing only modest evolutionary
effects (for more details about the M-Z relation,
see Lara-López et al. 2009b).
In a recent study, Calura et al. (2009) have demonstrated the importance of the morphology of galaxies when deriving the M-Z relation since, at any redshift, elliptical galaxies present the highest stellar masses and the highest metallicities, whereas the irregulars are the least massive galaxies, characterized by the lowest O abundances.
In this paper, we consistently approach several topics, starting with introducing the S2N2 as a reliable diagram for classifying galaxies, analyzing of the metallicity evolution of galaxies in the three BPT diagrams, and, for a better understanding of the processes involved in the observed evolution of galaxies at low redshift, studying the mass, metallicity and SFR relations, such as the M-Z, metallicity-SFR, and mass-SFR relations. We also point out that the morphology of galaxies play an important role when deriving conclusions, since late-type galaxies will result in lower metallicity estimates and higher SFRs than early-type (Calura et al. 2009).
This paper is structured as follows. In Sect. 2 we give the data used for this study, the dust extinction correction, and the metallicity estimates for our sample of galaxies. In Sect. 3 we introduce the S2N2 as a reliable diagram for segregating SF, composite, and AGNs galaxies. In Sect. 4 we analyze the evolution of the BPT diagrams. In Sect. 5 we investigate the evolution of the mass-metallicity and luminosity-metallicity relations, whereas in Sect. 6 we discuss the relations between the SFR and SSFR with stellar mass and metallicity, as well as the morphology of our galaxies using colors, concentration index, and SSFRs. Finally, conclusions are given in Sect. 7.
2 Data processing and sample selection
We selected emission line galaxies from SDSS-DR5 (Adelman-McCarthy
et al. 2007).
Data were taken with a 2.5 m telescope located at Apache Point
Observatory (Gunn et al. 2006).
The SDSS spectra were obtained using 3 arcsec
diameter fibres, covering a wavelength range of 3800-9200 Å,
and with a mean spectral resolution ![]() /
/
![]()
![]() 1800.
The SDSS-DR5 spectroscopy database contains spectra for
1800.
The SDSS-DR5 spectroscopy database contains spectra for ![]()
![]() objects over
objects over ![]() 5700
5700
![]() .
Further technical details can be found in Stoughton et al. (2002).
.
Further technical details can be found in Stoughton et al. (2002).
We used the SDSS-DR5 spectra from the STARLIGHT database![]() , which were processed with
the STARLIGHT spectral synthesis code, developed by Cid Fernandes and
collaborators (Cid Fernandes et al. 2005, 2007; Mateus
et al. 2006;
Asari et al. 2007).
From the spectra, the STARLIGHT code subtracts the continuum,
obtaining the emission lines flux measurements for each galaxy.
For each emission line, the STARLIGHT code returns
the rest frame flux and its associated equivalent width, linewidth,
velocity displacement relative to the rest-frame wavelength, and the
signal-to-noise ratio (S/N) of the fit. For Balmer lines, the
underlying stellar absorption was corrected by the STARLIGHT code using
synthetic spectra obtained by fitting an observed spectrum with a
combination of 150 simple stellar populations (SSPs) from the
evolutionary synthesis models of Bruzual & Charlot (2003).
, which were processed with
the STARLIGHT spectral synthesis code, developed by Cid Fernandes and
collaborators (Cid Fernandes et al. 2005, 2007; Mateus
et al. 2006;
Asari et al. 2007).
From the spectra, the STARLIGHT code subtracts the continuum,
obtaining the emission lines flux measurements for each galaxy.
For each emission line, the STARLIGHT code returns
the rest frame flux and its associated equivalent width, linewidth,
velocity displacement relative to the rest-frame wavelength, and the
signal-to-noise ratio (S/N) of the fit. For Balmer lines, the
underlying stellar absorption was corrected by the STARLIGHT code using
synthetic spectra obtained by fitting an observed spectrum with a
combination of 150 simple stellar populations (SSPs) from the
evolutionary synthesis models of Bruzual & Charlot (2003).
From the full set of galaxies, we only consider galaxies whose
spectra show the H![]() ,
H
,
H![]() ,
[N II], [O II]
,
[N II], [O II]
![]() 3727,
[O III]
3727,
[O III] ![]() 4959, [O III]
4959, [O III]
![]() 5007,
[O I]
5007,
[O I] ![]() 6300, and [S II] lines
in emission. We selected galaxies with a S/N higher
than 3
6300, and [S II] lines
in emission. We selected galaxies with a S/N higher
than 3![]() for the H
for the H![]() ,
H
,
H![]() ,
and [N II] lines.
,
and [N II] lines.
To identify any evolution of galaxy parameters or relations,
we divided our sample in four redshift intervals as follows: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
The lower limit of z0
corresponds to an aperture covering fraction of 20
.
The lower limit of z0
corresponds to an aperture covering fraction of 20![]() ,
which is the minimum required to avoid domination of the spectrum by
aperture effects (Kewley et al. 2005). This
classification give us 85 931 galaxies for z0,
48 888 galaxies for z1,
3278 galaxies for z2,
and 199 galaxies for z3.
,
which is the minimum required to avoid domination of the spectrum by
aperture effects (Kewley et al. 2005). This
classification give us 85 931 galaxies for z0,
48 888 galaxies for z1,
3278 galaxies for z2,
and 199 galaxies for z3.
We selected galaxies with an apparent Petrosian r magnitude of 14.5 < r < 17.77 in the redshift samples z0, z1, and z2, which yields 82 884, 44 763, and 1802 galaxies, respectively, corresponding to the magnitude completeness at these redshifts (see Fig. 1). Galaxies of the z3 sample have a different completeness range 16.9 < r < 18.8, as observed in Fig. 1, giving 119 galaxies. We used the z0 and z1 sample of galaxies with its respective completeness, but for galaxies of samples z2 and z3 we used both those in the completeness range and those out of the completeness range. The reason for this was to improve the galaxy statistics by increasing their number. As we show in the next sections, the main results are similar using galaxies in the magnitude completeness and galaxies of the total sample.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg1.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg20.png)
|
Figure 1: Normalized histogram of the apparent Petrosian r magnitudes in the four redshift bins. The dark solid line represents galaxies at z0, the dashed line the galaxies at z1, dot-dashed lines the galaxies at z2, and the clear solid line the galaxies at z3. The black arrow shows the completeness limit for the samples z0, z1, and z2, and the clear arrow points to the same for z3. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
2.1 Sample selection for Sect. 3
In Sect. 3, to study the S2N2 diagram as a segregator of different types of galaxies, we adopt the ``main galaxy sample'' (e.g. Strauss et al. 2002) with Petrosian r magnitudes in the range 14.5 < r < 17.77, and the redshift interval z0, taking all the emission lines into account and the S/N mentioned above, which yields 82 884 galaxies. In this section, we used AGN, composite, and SF galaxies.
2.2 Sample selection for Sect. 4
In Sect. 4, we study the evolution of the three BPT diagrams using the four redshift intervals, magnitude intervals, and the S/N restrictions mentioned above. In this section, we used AGN, composite, and SF galaxies. Also, to study the metallicity evolution of the SF galaxies of the BPT diagrams (see Fig. 6), we used the sample of Sects. 5 and 6, mentioned below.
2.3 Sample selection for Sects. 5 and 6
For Sects. 5 and 6, we selected SF galaxies following
the criterion given by Kauf03 in the BPT empirical diagnostic
diagram: log[O III] ![]() 5007/H
5007/H![]()
![]() 0.61/
0.61/![]() log([N II]/H
log([N II]/H![]() )-0.05
)-0.05![]() + 1.3,
the same used by Veilleux & Osterbrock (1987), Kewley
et al. (2001,
2006), and
Stasinska et al. (2006),
among others. After all these selections, the number of galaxies of
each redshift bin is reduced to
61 921 SF galaxies for z0,
27 853 for z1,
1671 for z2,
and 67 H II galaxies
for z3.
+ 1.3,
the same used by Veilleux & Osterbrock (1987), Kewley
et al. (2001,
2006), and
Stasinska et al. (2006),
among others. After all these selections, the number of galaxies of
each redshift bin is reduced to
61 921 SF galaxies for z0,
27 853 for z1,
1671 for z2,
and 67 H II galaxies
for z3.
The extinction correction and metallicity estimates were
calculated as in Lara-López et al. (2009b). Our
extinction correction was derived using the Balmer decrements in order
to obtain the reddening coefficient C(H![]() ). We used the Cardelli
et al. (1989)
law, with Rv =
Av/E(B
-V) = 3.1, assuming case
B recombination with a density of 100 cm-3
and a temperature of 104 K, with H
). We used the Cardelli
et al. (1989)
law, with Rv =
Av/E(B
-V) = 3.1, assuming case
B recombination with a density of 100 cm-3
and a temperature of 104 K, with H![]() /H
/H![]() = 2.86
(Osterbrock 1989).
= 2.86
(Osterbrock 1989).
We estimated metallicities using the R23
relation introduced by Pagel et al. (1979), R23 =
([O II] ![]() 3727+[O III]
3727+[O III]
![]() 4959, 5007)/H
4959, 5007)/H![]() ,
and adopted the calibration given by Tremonti et al. (2004),
,
and adopted the calibration given by Tremonti et al. (2004), ![]() ,
where x = log R23.
We selected the upper branch of the double-valued R23,
in which the Tremonti et al. (2004) calibration is
valid, taking
12 + log(O/H) > 8.4 and
log([N II]/[O II]
,
where x = log R23.
We selected the upper branch of the double-valued R23,
in which the Tremonti et al. (2004) calibration is
valid, taking
12 + log(O/H) > 8.4 and
log([N II]/[O II]![]() 3727) > -1.2,
since the upper and lower branches of the R23 calibration
bifurcates at those values (see Kewley & Ellison 2008).
3727) > -1.2,
since the upper and lower branches of the R23 calibration
bifurcates at those values (see Kewley & Ellison 2008).
After applying this final criterion, we end with 58866
galaxies for z0,
24 385 for z1,
1631 for z2 (from
which 712 galaxies are in their completeness magnitude
interval), and 62 galaxies for z3
(from which 41 galaxies are in their completeness magnitude
interval), all of them in the upper branch of the R23 relation,
corresponding to the ![]() 99
99![]() to the H II classified galaxies.
Then, we are not introducing a bias when selecting the upper branch for
this samples.
to the H II classified galaxies.
Then, we are not introducing a bias when selecting the upper branch for
this samples.
3 The S2N2 diagnostic diagram as a star-forming, composite, and AGN galaxy segregator
As mentioned in Sect. 1, BPT diagrams are the most
used method of segregating star-forming and AGN galaxies. From the
three BPT diagrams ([N II]/H![]() ,
[S II]/H
,
[S II]/H![]() ,
and [O I]
,
and [O I] ![]() 6300/H
6300/H![]() vs.
[O III]
vs.
[O III] ![]() 5007/H
5007/H![]() ), the most used one
is the [N II]/H
), the most used one
is the [N II]/H![]() vs.
[O III]
vs.
[O III] ![]() 5007/H
5007/H![]() ,
since it is the only one that can segregate pure SF and composite
galaxies, as demonstrated by Kewley et al. (2006) and
Pérez-Montero et al. (2009). The two other
BPT diagrams are not useful for segregating SF from composite
objects.
,
since it is the only one that can segregate pure SF and composite
galaxies, as demonstrated by Kewley et al. (2006) and
Pérez-Montero et al. (2009). The two other
BPT diagrams are not useful for segregating SF from composite
objects.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg26.png)
|
Figure 2:
Log([N II]/H |
| Open with DEXTER | |
Commonly known as the S2N2, the log(H![]() /[S II]) vs.
log(H
/[S II]) vs.
log(H![]() /[N II]) diagram
has been used to separate planetary nebulae (PNe), H II regions,
and supernova remnants (SNRs, see Sabbadin et al. 1977; Riesgo
& López 2006;
Viironen et al. 2007).
We propose the S2N2 diagram for classifying SF,
composite, and AGN galaxies, something until now only possible
with the [N II]/H
/[N II]) diagram
has been used to separate planetary nebulae (PNe), H II regions,
and supernova remnants (SNRs, see Sabbadin et al. 1977; Riesgo
& López 2006;
Viironen et al. 2007).
We propose the S2N2 diagram for classifying SF,
composite, and AGN galaxies, something until now only possible
with the [N II]/H![]() vs.
[O III]
vs.
[O III] ![]() 5007/H
5007/H![]() diagram.
However, the S2N2 diagram use only the H
diagram.
However, the S2N2 diagram use only the H![]() ,
[N II], and [S II] emission
lines, all of them close in wavelength, avoiding reddening corrections,
and making possible its use for surveys limited in the spectral range.
,
[N II], and [S II] emission
lines, all of them close in wavelength, avoiding reddening corrections,
and making possible its use for surveys limited in the spectral range.
From the ``main galaxy sample'', we consider SF galaxies as
those lying below the Kauf03 division, composite galaxies as
those lying between the Kauf03 and Kew01 lines, and
AGN galaxies those above the Kew01 division
(see Fig. 2).
From the total sample (82 884 galaxies, see
Sect. 2), the 71.4![]() ,
19
,
19![]() ,
and 9.6
,
and 9.6![]() correspond to SF, composite, and AGN galaxies, respectively.
Taking this classification as a reference, we plotted the
S2N2 diagram with the three classifications of galaxies
(see Figs. 3
and 4).
correspond to SF, composite, and AGN galaxies, respectively.
Taking this classification as a reference, we plotted the
S2N2 diagram with the three classifications of galaxies
(see Figs. 3
and 4).
| Figure 3:
Contour plots for star-forming, composite, and AGN galaxies.
a) Star-forming, darker (blue) contour, and
composite, lighter (orange) contour, enclosing the |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13886fg4.ps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{13886fg5.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg28.png)
|
Figure 4:
a) log(H |
| Open with DEXTER | |
To establish division lines to separate SF, composite and
AGN galaxies in the S2N2 diagram, we generated
contour plots for each category of galaxies (see Fig. 3). Because our sample
of galaxies is larger for the SF and composite galaxies, we used
contours enclosing ![]() 90
90![]() for those galaxies. However, as AGN galaxies are less
numerous, we used contours enclosing
for those galaxies. However, as AGN galaxies are less
numerous, we used contours enclosing ![]() 75
75![]() for composite and AGNs. The contour plots shown in Fig. 3a delimit two tangent
parallel lines, generating with this criterium division lines defined
by Eqs. (1) and (2). To define a division
line between composite and AGN galaxies, we sampled the plot
area with parallel lines of Eq. (1) in bins of
0.02 dex, in this way generating histograms for composite and
AGN galaxies, where Eq. (3) corresponds to the
intersection of both histograms.
for composite and AGNs. The contour plots shown in Fig. 3a delimit two tangent
parallel lines, generating with this criterium division lines defined
by Eqs. (1) and (2). To define a division
line between composite and AGN galaxies, we sampled the plot
area with parallel lines of Eq. (1) in bins of
0.02 dex, in this way generating histograms for composite and
AGN galaxies, where Eq. (3) corresponds to the
intersection of both histograms.
- (i)
- Pure star-forming galaxies are
separated by
![\begin{displaymath}%
{\rm log}({\rm {H\alpha}}/[${N~\textsc{ii}}$ ]) > -0.28 \times {\rm log({H\alpha}}/[${S~\textsc{ii}}$ ])+0.51,
\end{displaymath}](/articles/aa/full_html/2010/11/aa13886-09/img29.png)
(1)
and 98.8 of galaxies above this line are SF galaxies and correspond to
88
of galaxies above this line are SF galaxies and correspond to
88 of the SF sample.
of the SF sample.
- (ii)
- Star-forming and composite galaxies
are divided by
![\begin{displaymath}%
{\rm log}({\rm {H\alpha}}/[${N~\textsc{ii}}$ ]) > -0.28 \times {\rm log({H\alpha}}/[${S~\textsc{ii}}$ ])+0.40,
\end{displaymath}](/articles/aa/full_html/2010/11/aa13886-09/img30.png)
(2)
where 99.8 of the SF sample lay above this line. However, from all
galaxies above this line, 8
of the SF sample lay above this line. However, from all
galaxies above this line, 8 will correspond to composite galaxies, and the remaining 91
will correspond to composite galaxies, and the remaining 91 to SF galaxies.
to SF galaxies.
- (iii)
- Composite and AGN galaxies are divided
by
![\begin{displaymath}%
{\rm log}({\rm {H\alpha}}/[${N~\textsc{ii}}$ ]) > -0.28 \times {\rm log({H\alpha}}/[${S~\textsc{ii}}$ ])+0.25,
\end{displaymath}](/articles/aa/full_html/2010/11/aa13886-09/img31.png)
(3)
In Table 1
we compare the N2 ratio, considering the Stasinska limits, with the
S2N2 diagram in order to test their respective ability for
segregating SF, composite, and AGN galaxies. This table shows
the percentage of galaxies classified according to each division line,
as well as its corresponding contamination and the percentage
of missed galaxies, taking as a reference the classification of the
log([N II]/H![]() ) vs. log([O III]
) vs. log([O III] ![]() 5007/H
5007/H![]() ) diagram.
Labels S2N2(1&3) and S2N2(2) refer to galaxies taking
as a reference Eqs. (1&3) and (2),
respectively. The SF block indicates for the
S2N2(2) division, for example, that by taking all
galaxies above Eq. (2), 91
) diagram.
Labels S2N2(1&3) and S2N2(2) refer to galaxies taking
as a reference Eqs. (1&3) and (2),
respectively. The SF block indicates for the
S2N2(2) division, for example, that by taking all
galaxies above Eq. (2), 91![]() will correspond to
SF galaxies, and the 8
will correspond to
SF galaxies, and the 8![]() remaining to composite galaxies; also, we have missed 0.2
remaining to composite galaxies; also, we have missed 0.2![]() of the original SF sample. As can be appreciated for
the SF segregation, the N2 division misses
the highest percentage of SF galaxies, while our pure
star-forming division (Eq. (1)) misses less
SF galaxies, although with the same contamination from
composite galaxies. Moreover, our SF limit (Eq. (2))
encloses almost all SF galaxies with a small contamination
from composite galaxies. This provides the additional advantage over
the N2 diagram, i.e., that the user can choose
between the possibilities of selecting either most SF galaxies
or galaxies with the least contamination from composite galaxies. The
composite division for the N2 ratio shows a similar percentage
of composite and SF galaxies. However,
the S2N2 division allows obtaining a higher
percentage of composite galaxies, missing less composite galaxies, with
a lower contamination of SF galaxies and with only a quite
small increment of AGN contamination. For segregating
AGNs, while the S2N2 diagram provides a lower contamination
from composite galaxies, miss
of the original SF sample. As can be appreciated for
the SF segregation, the N2 division misses
the highest percentage of SF galaxies, while our pure
star-forming division (Eq. (1)) misses less
SF galaxies, although with the same contamination from
composite galaxies. Moreover, our SF limit (Eq. (2))
encloses almost all SF galaxies with a small contamination
from composite galaxies. This provides the additional advantage over
the N2 diagram, i.e., that the user can choose
between the possibilities of selecting either most SF galaxies
or galaxies with the least contamination from composite galaxies. The
composite division for the N2 ratio shows a similar percentage
of composite and SF galaxies. However,
the S2N2 division allows obtaining a higher
percentage of composite galaxies, missing less composite galaxies, with
a lower contamination of SF galaxies and with only a quite
small increment of AGN contamination. For segregating
AGNs, while the S2N2 diagram provides a lower contamination
from composite galaxies, miss ![]() 6
6![]() more AGNs than using the N2 ratio.
more AGNs than using the N2 ratio.
Table 1: Comparison between the S2N2 diagram and the N2 ratio to segregate SF, composite, and AGN galaxies.
In Fig. 4, we overplot the pre-run photoionization grids of Dopita et al. (2000) and Kew01 for an instantaneous burst model and for a continuous starburst model. The best grid to our SF galaxies for the S2N2 diagram is the one corresponding to an instantaneous burst model, with an electronic density of 10 cm-3, using the PEGASE code (see Fig. 4a). As explained in Dopita et al. (2000), the high surface-brightness, isolated extragalactic H II regions are in general excited by young clusters of OB; in this case, the ionizing EUV spectra and H II region emission-line spectra predicted by the PEGASE and STARBURST99 codes for an instantaneous, zero-age star formation model are essentially identical.
In their work, Dopita et al. (2000) and Kew01
model a large sample of infrared starburst galaxies using both the
PEGASE v2.0 (Fioc & Rocca-Volmerange 1997) and the
STARBURST99 (Leitherer et al. 1999) codes to
generate the spectral energy distribution. In both cases,
MAPPINGS III code was used to compute photoionization models.
The pre-run grids use photoionization models with ionization
parameters q (cm s-1)
in the range 5 ![]()
![]()
![]() 108, and metallicities from Z=0.05
to 3
108, and metallicities from Z=0.05
to 3 ![]() ;
moreover, two values for electronic density were used,
10 and 350 cm-3.
;
moreover, two values for electronic density were used,
10 and 350 cm-3.
For starburst galaxies, it is expected to have a continuous star formation on at least a galactic dynamical timescale, at which point the assumption of a continuous rather than an instantaneous burst of star formation would be more accurate. We generated the PEGASE grid of Kew01 for a continuous starburst model and found, as expected, that this corresponds to SF and composite objects (see Fig. 4b), since this is the limit used by Kew01 to parametrize an extreme starburst line in the BPT diagrams.
The photoionization grids generated with the STARBURST99 code were not hard enough to produce the needed [S II] flux to enclose all galaxies in the S2N2 diagram. The BPT diagrams are most sensitive to the spectral index of the ionizing radiation field in the 1-4 ryd interval, and the PEGASE ionizing stellar continuum is harder in this range than that of STARBURST99, therefore PEGASE are the only models that encompass nearly all of the observed starburst on all three of the BPT diagrams. We also tried the grids of Levesque et al. (2010), which use the STARBURST99 code, but these grids comprise an insufficiently hard ionizing radiation field, leading to deficiencies in the [S II] fluxes produced by the models.
In galaxy surveys there are at least three methods commonly
used to deal with AGNs. The first one consists of removing galaxies
hosting AGNs by cross-correlating the sample with published
AGN catalogs (e.g. Condon et al. 2002; Serjeant
et al. 2002).
The second one deals with the identification of the galaxies through
the so-called BPT diagram. Nevertheless, at z ![]() 0.5,
the H
0.5,
the H![]() line
is redshifted out of the optical range. The third method consists of
subtracting AGNs in a statistical manner, used when no other methods
are applicable (e.g. Tresse & Maddox 1998).
line
is redshifted out of the optical range. The third method consists of
subtracting AGNs in a statistical manner, used when no other methods
are applicable (e.g. Tresse & Maddox 1998).
In addition to those methods, we propose the use of the
S2N2 diagram, which has demonstrated the ability of accurately
segregate SF from composite and AGN galaxies. The
S2N2 diagram has the following advantages:
an extinction correction is not necessary, since all the
emission lines are close in wavelength. It requires only a
narrow spectral range, making it suitable for surveys of limited
spectral coverage. The SF and composite divisions of the
S2N2 diagram offer less contamination in all cases, with
respectively a higher number of galaxies for SF and composites than
using only the N2 ratio. Additionally, the user can
choose any of the SF galaxy divisions provided for the
S2N2 diagram, either when the low contamination from composite
galaxies (Eq. (1)) or when selection of the most
SF galaxies (Eq. (2)) is required. Finally,
the use of the [S II] lines
does not reduce the number of galaxies, since those lines for
AGN galaxies are ![]() 1.3 times
stronger than the [O III] line
used in the BPT diagrams. Then, comparing the number of
galaxies of all the types, the S2N2 diagram has 1
1.3 times
stronger than the [O III] line
used in the BPT diagrams. Then, comparing the number of
galaxies of all the types, the S2N2 diagram has 1![]() more galaxies than the log([N II]/H
more galaxies than the log([N II]/H![]() ) vs.
log([O III]/H
) vs.
log([O III]/H![]() ) diagram. Although
this diagram has been used in the past for galaxies, it is the
first time that it is presented as a diagnostic diagram for classifying
galaxies. Given its advantages, we propose it as an alternative to the
BPT diagrams and N2 ratio for classifying galaxies.
) diagram. Although
this diagram has been used in the past for galaxies, it is the
first time that it is presented as a diagnostic diagram for classifying
galaxies. Given its advantages, we propose it as an alternative to the
BPT diagrams and N2 ratio for classifying galaxies.
4 Evolutionary effects on the BPT diagrams
As explained in Sect. 3, the BPT and other optical emission lines diagnostic diagrams have become important in the classification of galaxies. In this section, our aim is to investigate the effects of the evolution of galaxies from the three BPT diagrams. For this purpose, and with the objective of increasing our number of galaxies, we did not allow any restriction in magnitude, as detailed in the sample selection.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg6.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg36.png)
|
Figure 5: Evolution of line ratios from the BPT diagrams. Black dots show galaxies in the redshift range z0, blue dots galaxies in the z1 range, big red triangles represent galaxies in the completeness of the z2 range, while small red triangles galaxies out of the completeness, yellow big circles represent galaxies in the completeness of the z3 range, and small circles galaxies out of the completeness. The black solid line shows the Kauf03 limit for SF galaxies, and the red solid line shows the Kew01 limit for starburst galaxies in the three BPT diagrams. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13886fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg37.png)
|
Figure 6:
Evolution with redshift of the log([O III] |
| Open with DEXTER | |
In Fig. 5
we show the three BPT diagrams for the four redshift samples.
As redshift increases, we observe that [O III] ![]() 5007/H
5007/H![]() goes toward higher values. To explain this shift, we plotted
the ratio [O III]
goes toward higher values. To explain this shift, we plotted
the ratio [O III] ![]() 5007/H
5007/H![]() versus
redshift and metallicity in Fig. 6 only for
SF galaxies selected with the Kauf03 criterion. The
gap observed around z
versus
redshift and metallicity in Fig. 6 only for
SF galaxies selected with the Kauf03 criterion. The
gap observed around z ![]() 0.145
(see Figs. 6a,c)
comes from the H
0.145
(see Figs. 6a,c)
comes from the H![]() line
falling nearby the 5577 Å sky line, because the residuals are
significant and, as a consequence, measurements of H
line
falling nearby the 5577 Å sky line, because the residuals are
significant and, as a consequence, measurements of H![]() around this redshift were lost. As shown in Fig. 6b, there is a clear
tendency of the [O III]
around this redshift were lost. As shown in Fig. 6b, there is a clear
tendency of the [O III] ![]() 5007/H
5007/H![]() ratio
towards higher values with redshift, which is explained by examining
the same ratio against 12 + log(O/H). The ratio
[O III]
ratio
towards higher values with redshift, which is explained by examining
the same ratio against 12 + log(O/H). The ratio
[O III] ![]() 5007/H
5007/H![]() has been demonstrated to correlate linearly with metallicity
(see, for example, Liang et al. 2006). Then, a
decrement in 12 + log(O/H) will result in higher
values of [O III]
has been demonstrated to correlate linearly with metallicity
(see, for example, Liang et al. 2006). Then, a
decrement in 12 + log(O/H) will result in higher
values of [O III] ![]() 5007/H
5007/H![]() (see Fig. 6b).
We observe a decrement of
(see Fig. 6b).
We observe a decrement of ![]() 0.2 dex
in [O III]
0.2 dex
in [O III] ![]() 5007/H
5007/H![]() and a decrement of
and a decrement of ![]() 0.1 dex
in 12 + log(O/H) for the z3 redshift
range with respect to the z0 range.
0.1 dex
in 12 + log(O/H) for the z3 redshift
range with respect to the z0 range.
In previous papers (Lara-López et al. 2009a,b), we
reported a decrement in 12 + log(O/H) of ![]() 0.1 dex
for the redshift range 0.3
< z < 0.4 when comparing galaxies in
the same range of luminosity at different redshift intervals. Since the
possible bias, such as the luminosity, mass, and aperture
effects of those samples, was carefully studied, we demonstrated there
that this decrement in metallicity stems from an intrinsic evolution of
the galaxies.
0.1 dex
for the redshift range 0.3
< z < 0.4 when comparing galaxies in
the same range of luminosity at different redshift intervals. Since the
possible bias, such as the luminosity, mass, and aperture
effects of those samples, was carefully studied, we demonstrated there
that this decrement in metallicity stems from an intrinsic evolution of
the galaxies.
Although our z3
sample corresponds to luminous galaxies, if we compare galaxies with
the same luminosity taking our previous papers as a reference,
the metallicity decrement will again be of ![]() 0.1 dex,
and as consequence, the effects on the BPT diagrams will be
the same. Therefore, the evolution observed in the [O III]
0.1 dex,
and as consequence, the effects on the BPT diagrams will be
the same. Therefore, the evolution observed in the [O III] ![]() 5007/H
5007/H![]() lines
ratio toward higher values in the three BPT diagrams could be
attributed to evolution in metallicity.
lines
ratio toward higher values in the three BPT diagrams could be
attributed to evolution in metallicity.
On the other hand, we analyzed the [N II]/H![]() ratio
against redshift and metallicity (see Figs. 6c,d). The [N II]/H
ratio
against redshift and metallicity (see Figs. 6c,d). The [N II]/H![]() ratio
is also a metallicity index, commonly known as N2, and it has
been widely studied since it is not severely affected by dust
extinction (see Pettini & Pagel 2004). Among the
calibrations of the N2 index, we have for example those of
Raimann et al. (2000),
Denicoló et al. (2002),
and Liang et al. (2006).
In Fig. 6d
we observe a clear increasing trend of metallicity following the
increase in the N2 index up to 12 + log(O/H)
ratio
is also a metallicity index, commonly known as N2, and it has
been widely studied since it is not severely affected by dust
extinction (see Pettini & Pagel 2004). Among the
calibrations of the N2 index, we have for example those of
Raimann et al. (2000),
Denicoló et al. (2002),
and Liang et al. (2006).
In Fig. 6d
we observe a clear increasing trend of metallicity following the
increase in the N2 index up to 12 + log(O/H) ![]() 9.0.
The galaxies with
12 + log(O/H) > 9 show a
flattening and a slightly decrease in the N2 index with
metallicity (see Fig. 6d). This trend was
explained by Kewley et al. (2002) using photoionization models
as follows. When the secondary production of nitrogen dominates at
somewhat higher metallicity, the [N II]/H
9.0.
The galaxies with
12 + log(O/H) > 9 show a
flattening and a slightly decrease in the N2 index with
metallicity (see Fig. 6d). This trend was
explained by Kewley et al. (2002) using photoionization models
as follows. When the secondary production of nitrogen dominates at
somewhat higher metallicity, the [N II]/H![]() line
ratio continues to increase, despite the decreasing electron
temperature. Eventually, at still higher metallicities,
nitrogen becomes the dominant coolant in the nebula, and the electron
temperature falls enough to ensure that the nitrogen line weakens with
increasing metallicity. Using SDSS galaxies with redshifts
0.04 < z < 0.25, Liang
et al. (2006)
observed a small decrement of the N2 index against
metallicity; this turnover of the N2 index is more evident for
the higher redshifts z2
and z3 in our sample
(see Fig. 6d).
The turnover of the N2 ratio will produce, in the
[O III]
line
ratio continues to increase, despite the decreasing electron
temperature. Eventually, at still higher metallicities,
nitrogen becomes the dominant coolant in the nebula, and the electron
temperature falls enough to ensure that the nitrogen line weakens with
increasing metallicity. Using SDSS galaxies with redshifts
0.04 < z < 0.25, Liang
et al. (2006)
observed a small decrement of the N2 index against
metallicity; this turnover of the N2 index is more evident for
the higher redshifts z2
and z3 in our sample
(see Fig. 6d).
The turnover of the N2 ratio will produce, in the
[O III] ![]() 5007/H
5007/H![]() vs. [N II]/H
vs. [N II]/H![]() BPT diagram, the turnover zone around N2
BPT diagram, the turnover zone around N2 ![]() -0.4,
which is more evident in a density plot (see Fig. 2).
-0.4,
which is more evident in a density plot (see Fig. 2).
Regarding the two left hand BPT diagrams in Figs. 5b and c,
since they share the ratio [O III] ![]() 5007/H
5007/H![]() ,
the evolutionary effects due to a decrement in metallicity
will be the same as discussed above. The ratio [S II]/H
,
the evolutionary effects due to a decrement in metallicity
will be the same as discussed above. The ratio [S II]/H![]() has never been used before as a metallicity indicator because it is far
more sensitive to ionization than to metallicity (Liang et al.
2006).
Moreover, it is double-valued with metallicity
(see Fig. 4),
whereas the ratio [OI]/H
has never been used before as a metallicity indicator because it is far
more sensitive to ionization than to metallicity (Liang et al.
2006).
Moreover, it is double-valued with metallicity
(see Fig. 4),
whereas the ratio [OI]/H![]() is not a metallicity indicator.
is not a metallicity indicator.
Therefore, after analyzing all the ratios involved in the
three BPT diagrams, we concluded that the evolution of
galaxies in the three BPT diagrams is shown through the
[O III] ![]() 5007/H
5007/H![]() ratio.
Since this ratio is a metallicity indicator, any decrement in
metallicity will result in higher values of the [O III]
ratio.
Since this ratio is a metallicity indicator, any decrement in
metallicity will result in higher values of the [O III] ![]() 5007/H
5007/H![]() ratio.
ratio.
5 Evolution of the mass-metallicity and luminosity-metallicity relations
It has been demonstrated that the metallicity and mass of
SF galaxies are strongly correlated, with massive and luminous
galaxies showing higher metallicities than less massive galaxies
(see Sect. 1). The masses of our galaxies were
estimated using the STARLIGHT code, which fit an observed
spectrum with a combination of 150 SSPs from the evolutionary
synthesis models of Bruzual & Charlot (2003), computed
using a Chabrier (2003)
initial mass function between 0.1 and 100 ![]() ,
and ``Padova 1994'' evolutionary tracks. The 150 base elements
span 25 ages between 1 Myr and 18 Gyr, and
six metallicities from Z=0.005 to 2.5
,
and ``Padova 1994'' evolutionary tracks. The 150 base elements
span 25 ages between 1 Myr and 18 Gyr, and
six metallicities from Z=0.005 to 2.5 ![]() .
As argued by Mateus et al. (2006), including
very low Z SSPs in the base inevitably
leads to higher stellar masses. A comparison with the
Kauffmann et al. (2003b)
mass estimates, which are based on a library of model galaxies
constructed with Z > 0.25
.
As argued by Mateus et al. (2006), including
very low Z SSPs in the base inevitably
leads to higher stellar masses. A comparison with the
Kauffmann et al. (2003b)
mass estimates, which are based on a library of model galaxies
constructed with Z > 0.25 ![]() ,
results in systematic discrepancies of about 0.1 dex
(for details see Mateus et al. 2006). The masses of
our galaxies were corrected for aperture effects based on the
differences between the total galaxy magnitude in the r band,
and the magnitude inside the fiber, assuming that the mass-to-light
ratio does not depend on the radius (see Mateus et al. 2006, for details).
,
results in systematic discrepancies of about 0.1 dex
(for details see Mateus et al. 2006). The masses of
our galaxies were corrected for aperture effects based on the
differences between the total galaxy magnitude in the r band,
and the magnitude inside the fiber, assuming that the mass-to-light
ratio does not depend on the radius (see Mateus et al. 2006, for details).
A histogram of our mass estimates is shown in Fig. 7, where a larger fraction of massive galaxies are observed at highest redshifts. In Fig. 8 we derived the M-Z and L-Z relations for the galaxies of our sample. As explained in previous sections, galaxies of the z0 and z1 samples are complete in luminosity, while for the z2 and z3 samples, the completeness criterium is not taken into account.
The M-Z relation of
T04, which is valid over the range 8.5 < log(
![]() /
/![]() ) < 11.5,
shows a steep M-Z relation
for masses from 108.5 to
) < 11.5,
shows a steep M-Z relation
for masses from 108.5 to ![]() that flattens at higher masses. In this study,
T04 analyzed galaxies with redshift ranges
0.005 < z < 0.3. It is
important to notice that in our M-Z relation,
a flatness is not observed for masses
that flattens at higher masses. In this study,
T04 analyzed galaxies with redshift ranges
0.005 < z < 0.3. It is
important to notice that in our M-Z relation,
a flatness is not observed for masses ![]() 1010.5 for the redshift
range z0,
(see Fig. 8a),
but this flatness is observed for the higher redshift samples. Then,
the flatness observed by T04 depends on the redshift range observed.
To establish the bias-free M-Z relation
for local galaxies, Kewley & Ellison (2008) recalibrated
the M-Z relation of T04
with galaxies at 0.04 < z < 0.1,
since 0.04 is the minimum redshift to avoid fibers effects
(Kewley et al. 2005).
1010.5 for the redshift
range z0,
(see Fig. 8a),
but this flatness is observed for the higher redshift samples. Then,
the flatness observed by T04 depends on the redshift range observed.
To establish the bias-free M-Z relation
for local galaxies, Kewley & Ellison (2008) recalibrated
the M-Z relation of T04
with galaxies at 0.04 < z < 0.1,
since 0.04 is the minimum redshift to avoid fibers effects
(Kewley et al. 2005).
In Fig. 8
(M-Z and L-Z
relations) the metallicity decrement for the z3 redshift
sample discussed in our previous articles (Lara-López et al. 2009a,b) is also
evident. To fit our local M-Z relation,
we estimated the mode of the metallicity of the galaxies in mass bins
of 0.1 dex and fit them with a second-order polynomial (
y=a0+a1x+a2x2),
with a0=-0.467,
a1=1.611, a2=-0.067.
We also fit a second-order polynomial to our M-Z relation
for galaxies at z3,
with a0=-0.632,
a1=1.557, a2=-0.063.
All the fits are shown in Fig. 9. According to them,
our M-Z relation for
the galaxies at z3
is ![]() 0.2 dex
lower than our local galaxy sample. Additionally,
in Fig. 9
we compare the M-Z fits
from literature at different redshifts with our results. At
0.2 dex
lower than our local galaxy sample. Additionally,
in Fig. 9
we compare the M-Z fits
from literature at different redshifts with our results. At
![]() we represent the calibration of T04, at
we represent the calibration of T04, at ![]() the T04 recalibration of Kewley & Ellison (2008), as well as
our fit for the local (z0)
M-Z relation.
At higher redshift, we represent our fit to the M-Z relation
for galaxies at z3,
as well as the fit of Erb et al. (2006a) at z
the T04 recalibration of Kewley & Ellison (2008), as well as
our fit for the local (z0)
M-Z relation.
At higher redshift, we represent our fit to the M-Z relation
for galaxies at z3,
as well as the fit of Erb et al. (2006a) at z ![]() 2.2
scaled to the T04 metallicity calibration. Due to
their high redshift, Erb et al. (2006a) used the
N2 method and the calibration of Pettini & Pagel (2004) to estimate
their metallicities. We converted their N2 metallicities to
the R23 calibration
of T04 with the metallicity conversions given in Kewley &
Ellison (2008).
Even with the dispersion of our local sample, our M-Z fit
is a little lower, but in a good agreement with those of T04 and Kewley
& Ellison (2008).
Since we are using the T04 calibration of the R23
method to estimate metallicities, the main differences with the fit of
T04 are the redshift ranges, as discussed above, and the mass
estimates, since T04 and Kewley & Ellison (2008) adopted a
Kroupa et al. (2001) IMF, while we are using a Chabrier (2003) IMF.
2.2
scaled to the T04 metallicity calibration. Due to
their high redshift, Erb et al. (2006a) used the
N2 method and the calibration of Pettini & Pagel (2004) to estimate
their metallicities. We converted their N2 metallicities to
the R23 calibration
of T04 with the metallicity conversions given in Kewley &
Ellison (2008).
Even with the dispersion of our local sample, our M-Z fit
is a little lower, but in a good agreement with those of T04 and Kewley
& Ellison (2008).
Since we are using the T04 calibration of the R23
method to estimate metallicities, the main differences with the fit of
T04 are the redshift ranges, as discussed above, and the mass
estimates, since T04 and Kewley & Ellison (2008) adopted a
Kroupa et al. (2001) IMF, while we are using a Chabrier (2003) IMF.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg8.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg41.png)
|
Figure 7: Normalized mass histogram for all our samples. Dark solid line represent galaxies at z0, dashed line galaxies at z1, point dashed line galaxies at z3, and clear solid line galaxies at z3. The histograms were constructed not taking the completeness for galaxies at z2 and z3 into account. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg9.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg42.png)
|
Figure 8:
a) Relation between the stellar mass and
12 + log(O/H) (M-Z relation).
b) Relation between the absolute
Petrosian r magnitude and
12 + log(O/H) (L-Z relation)
for our sample of galaxies. The cut observed in Fig.
b) for the z1 sample
comes from the 5577 Å sky line (see the text). In
both relations, white contours represent from outside to
inside, 15, 30, 50, 70, and 90 |
| Open with DEXTER | |
Although redshift ranges are different, the comparison of our fit for
the z3 sample with
the Erb et al. (2006a)
data at z ![]() 2.2, which also use
a Chabrier IMF, are similar in 12 + log(O/H)
(see Fig. 9).
As will be explained in the next sections, our z3 sample
is composed mainly of spiral galaxies, while the Erb et al. (2006a) sample
corresponds to a mix of morphological types. A possible
explanation for the high metallicities of Erb et al. (2006a) or to the
lower metallicities of our sample is given by Calura et al. (2009), who use
models that distinguish among different morphological types through the
use of different infall, outflow, and star formation to reproduce the
mass-metallicity relation in galaxies of all morphological types,
taking the observational M-Z relations
of Kewley & Ellison (2008),
Savaglio et al. (2005),
Erb et al. (2006a),
and Maiolino et al. (2008)
as a reference. In his work Calura et al. (2009) predicts that,
at any redshift, elliptical galaxies will present the highest stellar
masses and the highest metallicities, whereas the irregulars are the
least massive and metallic galaxies, with spiral galaxies being at an
intermediate stage.
2.2, which also use
a Chabrier IMF, are similar in 12 + log(O/H)
(see Fig. 9).
As will be explained in the next sections, our z3 sample
is composed mainly of spiral galaxies, while the Erb et al. (2006a) sample
corresponds to a mix of morphological types. A possible
explanation for the high metallicities of Erb et al. (2006a) or to the
lower metallicities of our sample is given by Calura et al. (2009), who use
models that distinguish among different morphological types through the
use of different infall, outflow, and star formation to reproduce the
mass-metallicity relation in galaxies of all morphological types,
taking the observational M-Z relations
of Kewley & Ellison (2008),
Savaglio et al. (2005),
Erb et al. (2006a),
and Maiolino et al. (2008)
as a reference. In his work Calura et al. (2009) predicts that,
at any redshift, elliptical galaxies will present the highest stellar
masses and the highest metallicities, whereas the irregulars are the
least massive and metallic galaxies, with spiral galaxies being at an
intermediate stage.
This means that, because our z3
sample is composed only of spiral galaxies, our metallicities will be
lower than if our sample were composed of a mix of morphological types.
The observed metallicities and SFRs for the Erb et al. (2006a) sample at z ![]() 2.2,
according to the study of Calura et al. (2009), indicate that
their galaxies are likely to represent a morphological mix, partly
composed of spirals (or proto-spirals) and partly of
ellipticals (or proto-ellipticals). Calura et al. (2009) predicts lower
metallicities (
2.2,
according to the study of Calura et al. (2009), indicate that
their galaxies are likely to represent a morphological mix, partly
composed of spirals (or proto-spirals) and partly of
ellipticals (or proto-ellipticals). Calura et al. (2009) predicts lower
metallicities (![]() 0.3 dex)
for the Erb et al. (2006a)
galaxies at z
0.3 dex)
for the Erb et al. (2006a)
galaxies at z ![]() 2.2 if the sample
were composed of spiral galaxies. Then, the similarities in
12 + log(O/H) of our M-Z relation
at z3 with the one
of Erb et al. (2006a)
at z
2.2 if the sample
were composed of spiral galaxies. Then, the similarities in
12 + log(O/H) of our M-Z relation
at z3 with the one
of Erb et al. (2006a)
at z ![]() 2.2, could be
explained by the morphological selection in each case: lower
metallicities in our M-Z relation
can be addressed to the prominence of spiral galaxies, whereas higher
metallicities in the M-Z relation
of the Erb et al. (2006a)
is a consequence of a sample formed by a mix of morphological types.
In other words, the morphology of the galaxies is crucial in
deriving and comparing the metallicity and the M-Z relation.
2.2, could be
explained by the morphological selection in each case: lower
metallicities in our M-Z relation
can be addressed to the prominence of spiral galaxies, whereas higher
metallicities in the M-Z relation
of the Erb et al. (2006a)
is a consequence of a sample formed by a mix of morphological types.
In other words, the morphology of the galaxies is crucial in
deriving and comparing the metallicity and the M-Z relation.
An additional point is that our samples plotted in Fig. 9 are selected with different magnitude completeness, then, our z3 redshift sample is more luminous and massive than our local one. This must be taken into account when comparing both M-Z relations. Unfortunately, our z0 sample does not have enough galaxies in the same absolute magnitude range of the z3 sample, making it imposible to generate a local M-Z relation comparable in luminosity to the z3 one.
Comparing our M-Z
relation with that of high-z samples in the
literature, we have the M-Z relation
of Savaglio et al. (2005)
at ![]() .
In their study, they only find a slight decrement in
metallicity for galaxies at
.
In their study, they only find a slight decrement in
metallicity for galaxies at ![]() compared with the local one of T04, which is inconsistent with the
compared with the local one of T04, which is inconsistent with the ![]() dex
decrement found in our z3
M-Z relation.
Nevetheless, as pointed out by Rodrigues et al. (2008),
the sample of Savaglio et al. (2005) have spectra
with a low S/N and spectral resolution, as well as
extinction problems. With a more consistent result, Rodrigues
et al. (2008)
generated the M-Z relation
for galaxies at
dex
decrement found in our z3
M-Z relation.
Nevetheless, as pointed out by Rodrigues et al. (2008),
the sample of Savaglio et al. (2005) have spectra
with a low S/N and spectral resolution, as well as
extinction problems. With a more consistent result, Rodrigues
et al. (2008)
generated the M-Z relation
for galaxies at ![]() ,
finding a decrement in metallicity of
,
finding a decrement in metallicity of ![]() 0.3 dex compared with
the local one of T04. Unfortunately, given the narrow range in
their stellar masses, it was impossible to constrain the
evolution of the shape of their M-Z relation.
0.3 dex compared with
the local one of T04. Unfortunately, given the narrow range in
their stellar masses, it was impossible to constrain the
evolution of the shape of their M-Z relation.
There are two main ways to explain the origin of the M-Z relation.
The first one is related to the well-known effect of downsizing
(e.g. Cowie et al. 1996; Gavazzi
& Scodeggio 1996),
in which lower mass galaxies form their stars later and on longer time
scales than more massive systems, implying low star formation
efficiencies in low-mass galaxies (Efstathiou 2000; Brooks
et al. 2007;
Mouhcine et al. 2008;
Tassis et al. 2008;
Scannapieco et al. 2008;
Ellison et al. 2008).
Therefore, low-mass galaxies are expected to show lower metallicities.
Supporting this scenario, Calura et al. (2009) have
reproduced the M-Z relation
with chemical evolution models for ellipticals, spirals, and irregular
galaxies by means of an increasing efficiency of star formation with
mass in galaxies of all morphological types, without the need for
outflows favoring the loss of metals in the less massive galaxies.
In a recent study that supports this result for
massive galaxies, Vale Asari et al. (2009) model the time
evolution of stellar metallicity using a closed-box chemical evolution
picture. They suggest that the M-Z relation
for galaxies in the mass range from 109.8
to
![]() is mainly driven by the star formation history and not by inflows
or outflows.
is mainly driven by the star formation history and not by inflows
or outflows.
A second scenario to explain the M-Z relation is attributed to metal and baryon loss from gas outflow, where low-mass galaxies eject large amounts of metal-enriched gas by supernovae winds before high metallicities are reached, while massive galaxies have deeper gravitational potentials that help to retain their gas, thus reaching higher metallicities (Larson 1974; Dekel & Silk 1986; MacLow & Ferrara 1999; Maier et al. 2004; T04; De Lucia et al. 2004; Kobayashi et al. 2007; Finlator & Dave 2008). As pointed out in the high-resolution simulations of Brooks et al. (2007), supernovae feedback plays a crucial role in lowering the star formation efficiency in low-mass galaxies. Without energy injection from supernovae to regulate the star formation, gas that remains in galaxies rapidly cools, forms stars, and increases its metallicity too early, producing a M-Z relation that is too flat compared to observations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg46.png)
|
Figure 9:
Evolution of the mass-metallicity relation observed at different
redshifts. The point-dashed line represents the curve of T04 at z |
| Open with DEXTER | |
An additional interpretation of the M-Z relation is linked to some properties of star formation, for instance, the IMF. Köppen et al. (2007) suggest that the M-Z relation can be explained by a higher upper-mass cutoff in the IMF in more massive galaxies.
Finally, we also generated the L-Z relation for our redshift samples (see Fig. 8b). Nevertheless, our z3 sample is restricted to a narrow range in luminosity, making it impossible to fit a curve. The local L-Z relation is well established by T04, then, due to our small luminosity range at z3 we cannot conclude anything about the L-Z relation. Nevertheless, the M-Z relation has shown itself to be stronger and tighter than the L-Z relation, confirming that stellar mass is a more meaningful physical parameter than luminosity when both are compared with gas metallicity (Savaglio et al. 2005).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg11.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg47.png)
|
Figure 10:
Mass versus Petrosian absolute k-corrected
magnitude for all our redshift samples. White contours represent, going
from outside to inside, 10, 25, 50, and 80 |
| Open with DEXTER | |
5.1 Evolution of the mass-to-light ratio
As explained by Erb et al. (2006a), at higher redshifts, the M-Z relation is clearly more physically meaningful than the L-Z relation. A corollary is that the local L-Z relation is simply the result of the strong correlation between mass and luminosity at low redshift.
We also analyzed the evolution of the mass-to-light (M/L)
ratio (see Fig. 10).
For a given mass, we observed higher luminosities for the z3 sample
compared with the local one, which means lower M/L ratios
as redshift increases. To observe this evolution, we fit a line (
y=a0+a1x)
to the z0 and z3 redshift
samples (see Fig. 10),
obtaining a0=-0.924
and a1=-0.544
for z0, and a0=-18.686
and a1=-1.304
for z3. The
variation in M/L at a
given rest frame optical luminosity can be as much as a factor of ![]() 70 (Shapley
et al. 2005),
which means that an extended range of stellar masses exists for any
range in luminosity. This large variation in M/L
explains the lack of correlation in the L-Z relation
for the z3 sample
compared to the local relation. For a narrow range of absolute
magnitudes in the z3 sample,
we have a wide range of masses, making it possible to generate an M-Z relation.
At higher redshifts, the effect is the same,
as pointed out by Erb et al. (2006a), finding a
wide range of stellar mass in a narrow range of luminosity for
star-forming galaxies at z
70 (Shapley
et al. 2005),
which means that an extended range of stellar masses exists for any
range in luminosity. This large variation in M/L
explains the lack of correlation in the L-Z relation
for the z3 sample
compared to the local relation. For a narrow range of absolute
magnitudes in the z3 sample,
we have a wide range of masses, making it possible to generate an M-Z relation.
At higher redshifts, the effect is the same,
as pointed out by Erb et al. (2006a), finding a
wide range of stellar mass in a narrow range of luminosity for
star-forming galaxies at z ![]() 2.2.
2.2.
6 Morphology indicators and SFR
The variation in SFR activity and young stellar content along the Hubble sequence is one of the most recognizable features of galaxies. In fact, this variation in stellar content is part of the basis of the Hubble classification itself (Hubble 1926), and understanding its physical nature and origin is fundamental to comprehending the galaxy evolution (for reviews see Kennicutt 1998; Kennicutt et al. 1994). The general picture, presented by Roberts (1963), Searle et al. (1973), Larson & Tinsley (1978), and Kennicutt et al. (1994), shows that early-type galaxies (types S0-Sb) represent systems that formed most of their gas into stars on timescales much less than the Hubble time, while the disks of late-type systems (Sc-Im) have formed stars at a roughly constant rate since they formed.
For most of the 20th century, catalogs of morphologically classified galaxies were compiled by individuals or small teams of astronomers (e.g. Sandage 1961; de Vaucouleurs 1991). Nowadays, selection criteria are based on galaxy properties such as color, concentration index, spectral features, surface brightness profile, other structural parameters, or some combination of these (e.g. Strateva et al. 2001; Abraham et al. 2003; Kauffmann et al. 2004; Conselice 2006; Scarlata et al. 2007). With the advent of modern surveys, such as the SDSS, and with the participation of thousands of volunteers, it has been possible to develop the Galaxy Zoo project (e.g. Lintott et al. 2008), providing visual morphological classification for more than 107 galaxies.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg12.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg48.png)
|
Figure 11:
Metallicity and mass versus log(SFR). Contours correspond to the z0 sample
in both plots. White contours represent, from outside to inside, in
panel a): 15, 30, 50, 70, and 90 |
| Open with DEXTER | |
In this section, we focus on the relations at different redshifts between the SFR, metallicity, mass, and morphology of SF galaxies selected with the Kauffmann et al. (2003a) criteria, as explained in Sect. 2.
6.1 Evolution of the SFR
We estimate the SFR with the H![]() emission line flux following the Kennicutt (1998) expression:
emission line flux following the Kennicutt (1998) expression:
![\begin{displaymath}%
{\it SFR}[{{M}_{\odot}}\;{\rm yr}^{-1}]=7.9 \times 10^{-42}~{L ({\rm H\alpha}})\; [{\rm erg}\;{\rm s}^{-1}],
\end{displaymath}](/articles/aa/full_html/2010/11/aa13886-09/img49.png)
|
(4) |
where
Recent studies have explored the relationship between the stellar mass and the SFR in galaxies at different redshifts. It has been shown that SFR critically depends on the galaxy mass both at low and high redshifts (e.g. Gavazzi et al. 2002; Brinchmann et al. 2004; Dickinson et al. 2004; Feulner et al. 2005; Papovich et al. 2006).
In our sample, galaxies with high SFRs are more abundant at
higher redshifts (see Fig. 11),
a fact already observed in non biased samples
(e.g. Noeske et al. 2007a). In
Fig. 11a,
we show 12 + log(O/H) against log(SFR). Although our z3 sample
of galaxies is biased to the most luminous and massive galaxies, the
observed decrement of ![]() 0.1 dex
in 12 + log(O/H) found in Lara-López et al. (2009a,b) is also
present. Regarding the z0 sample
of galaxies, there is a clear sequence with galaxies going toward
higher values of SFR as metallicity increases. This tendency can be
explained from the z0 sample
in the M-Z relation of
Fig. 8,
where massive galaxies correspond to the highest metallicity galaxies,
and for more massive galaxies, we expect higher SFRs (see Fig. 11). Also, we can
slightly appreciate a population of galaxies with higher SFR (see
Fig. 11a).
This population will form a tail when the
mass is taken into account, as will be shown in Fig. 11b. As redshift
increases, we appreciate a flattening of the SFR vs.
12 + log(O/H) relation in Fig. 11a for galaxies at z2
and z3, with most of the
galaxies showing log(SFR) between 1 and 2.
0.1 dex
in 12 + log(O/H) found in Lara-López et al. (2009a,b) is also
present. Regarding the z0 sample
of galaxies, there is a clear sequence with galaxies going toward
higher values of SFR as metallicity increases. This tendency can be
explained from the z0 sample
in the M-Z relation of
Fig. 8,
where massive galaxies correspond to the highest metallicity galaxies,
and for more massive galaxies, we expect higher SFRs (see Fig. 11). Also, we can
slightly appreciate a population of galaxies with higher SFR (see
Fig. 11a).
This population will form a tail when the
mass is taken into account, as will be shown in Fig. 11b. As redshift
increases, we appreciate a flattening of the SFR vs.
12 + log(O/H) relation in Fig. 11a for galaxies at z2
and z3, with most of the
galaxies showing log(SFR) between 1 and 2.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg13.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg52.png)
|
Figure 12:
Metallicity and mass versus log(SSFR). Contours correspond to the z0 sample
in both plots. White contours represent, from outside to inside, in
panel a): 10, 20, 40, 60, and 90 |
| Open with DEXTER | |
In Fig. 11b,
we show the log(
![]() /
/![]() )
versus log(SFR) plot. Galaxies at z0
show a main sequence, where massive galaxies have higher SFRs. This
main sequence was identified by Noeske et al. (2007a), when
studying galaxies with redshifts from 0.2 to 1.1,
finding that this main sequence moves as a whole to higher SFR as
redshift increases. The SSFR, defined as the total SFR divided by the
stellar mass, reflects the strength of the current burst of star
formation relative to the underlying galaxy mass. Deep galaxy surveys
have consistently found that the SSFR depends strongly on both
)
versus log(SFR) plot. Galaxies at z0
show a main sequence, where massive galaxies have higher SFRs. This
main sequence was identified by Noeske et al. (2007a), when
studying galaxies with redshifts from 0.2 to 1.1,
finding that this main sequence moves as a whole to higher SFR as
redshift increases. The SSFR, defined as the total SFR divided by the
stellar mass, reflects the strength of the current burst of star
formation relative to the underlying galaxy mass. Deep galaxy surveys
have consistently found that the SSFR depends strongly on both ![]() and redshift, with the bulk of star formation occurring earlier in
massive galaxies than in less massive systems (Guzmán et al. 1997; Brinchmann
& Ellis 2000;
Juneau et al. 2005;
Bauer et al. 2005;
Bell et al. 2005;
Pérez-González et al. 2005;
Feulner et al. 2005;
Papovich et al. 2006;
Caputi et al. 2006;
Reddy et al. 2006).
and redshift, with the bulk of star formation occurring earlier in
massive galaxies than in less massive systems (Guzmán et al. 1997; Brinchmann
& Ellis 2000;
Juneau et al. 2005;
Bauer et al. 2005;
Bell et al. 2005;
Pérez-González et al. 2005;
Feulner et al. 2005;
Papovich et al. 2006;
Caputi et al. 2006;
Reddy et al. 2006).
We also analyzed the evolution of the SSFR as a function of the metallicity and the stellar mass. Interestingly, in the 12 + log(O/H) vs. SSFR diagram (Fig. 12a), the observed population of Fig. 11a at z0 is more evident, showing a higher SSFR (SSFR > -10) than the other galaxies at the same redshift. We are going to investigate this tail in more detail in the next subsection.
In Fig. 12b,
we show the log(
![]() /
/![]() ) versus
log(SSFR) plot. The SSFR increase with redshift, showing for
more massive galaxies a tendency toward lower SSFR values, which agrees
with the results of Noeske et al. (2007b), for
galaxies with z > 0.2.
Massive galaxies shows lower SSFR because they probably have low gas
fractions so have nearly finished assembling their stellar mass (Erb
et al. 2006b;
Reddy et al. 2006).
On the other hand, the presence of dust has demonstrated to play an
important role when deriving the SSFR, as shown by Pannella
et al. (2009),
who obtain a flat SSFR for dust free galaxies for redshift bins
centered on
) versus
log(SSFR) plot. The SSFR increase with redshift, showing for
more massive galaxies a tendency toward lower SSFR values, which agrees
with the results of Noeske et al. (2007b), for
galaxies with z > 0.2.
Massive galaxies shows lower SSFR because they probably have low gas
fractions so have nearly finished assembling their stellar mass (Erb
et al. 2006b;
Reddy et al. 2006).
On the other hand, the presence of dust has demonstrated to play an
important role when deriving the SSFR, as shown by Pannella
et al. (2009),
who obtain a flat SSFR for dust free galaxies for redshift bins
centered on ![]() and 2.1, instead of a drop with increasing mass. In our
samples, the SFR and SSFR were derived through the dust-corrected H
and 2.1, instead of a drop with increasing mass. In our
samples, the SFR and SSFR were derived through the dust-corrected H![]() flux,
showing that this flatness is absent for redshifts below 0.4.
flux,
showing that this flatness is absent for redshifts below 0.4.
We found also evidence of two populations in Fig. 12b, one at
redshift z0, which
concentrate in a square delimited by the contour plots, and another one
showing SSFR > -10, which
is more evident for the higher redshifts samples, but is also evident
in the z0 sample.
In a forthcoming paper (Lara-López et al. 2010), we
have shown that the SFR, metallicity, and stellar mass of SF galaxies
form a fundamental plane (FP) in a 3D space, obtaining a 1![]() error of 0.16 dex in the mass estimates through the FP. This
population of galaxies will be explained in the next section as a
consequence of the morphology of the galaxies.
error of 0.16 dex in the mass estimates through the FP. This
population of galaxies will be explained in the next section as a
consequence of the morphology of the galaxies.
6.2 The SSFR as a morphology indicator
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg14.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg54.png)
|
Figure 13:
Principal morphological classifiers. In panels a)-
c), we show the log(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13886fg15.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg55.png)
|
Figure 14: Metallicity and mass versus log(SSFR). Black dots and yellow circles represent galaxies at z0 and z3, respectively, while green dots, represent late-type galaxies at z0 selected with log( SSFR) > -10. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
In this section, we investigate the morphology of the galaxies in our sample with the aim of clarify whether the tail observed in Figs. 11 and 12, with higher SFR and SSFR in the z0 sample, respectively, is related to specific morphological types. We focus on samples z0 and z3 because those samples show their galaxies uniformly distributed on mass. Galaxies of samples z1 and z2 show systematic problems due to sky lines and to incompleteness, respectively. We used the g-r color, the concentration index c=R90/R50 (e.g. Park & Choi 2005), and the SSFR (e.g. Salim et al. 2009), which are the most common indexes to segregate early from late-type galaxies (see Fig. 13). We used k-corrected fiber colors for all the galaxies samples.
The color index has been commonly used as an early and late
type morphological classifier (Baldry et al. 2004; Faber
et al. 2007;
Wang et al. 2007;
Lee et al. 2007a).
Strateva et al. (2001)
find that the integrated observed frame u-r
shows a bimodal distribution; however, they show that, when divided at u-r=2.22,
the early and late type subsets have significant contamination,
reaching about 30![]() for a sample with visually identified morphological types. Because the u band
shows large errors for the SDSS galaxies, we decided to use
for a sample with visually identified morphological types. Because the u band
shows large errors for the SDSS galaxies, we decided to use ![]() (e.g. Schawinski et al. 2009; Masters
et al. 2009),
which allows separation of early from late-type galaxies.
As observed in Fig. 13a,
(e.g. Schawinski et al. 2009; Masters
et al. 2009),
which allows separation of early from late-type galaxies.
As observed in Fig. 13a,
![]() 97
97![]() of the z3 sample of
galaxies corresponds to a late-type morphology.
of the z3 sample of
galaxies corresponds to a late-type morphology.
The concentration index c=R90/R50
has been successfully used in segregating late (c < 2.86)
from early-type (c ![]() 2.86) subsets (e.g. Shimasaku
et al. 2001;
Strateva et al. 2001;
Goto et al. 2002;
Nakamura et al. 2003;
Deng et al. 2009).
Nevertheless, contamination in the early and late-type subsets
separated using the concentration index, is typically about 20
2.86) subsets (e.g. Shimasaku
et al. 2001;
Strateva et al. 2001;
Goto et al. 2002;
Nakamura et al. 2003;
Deng et al. 2009).
Nevertheless, contamination in the early and late-type subsets
separated using the concentration index, is typically about 20![]() (Yamauchi et al. 2005; Shimasaku et al. 2001). Using both
color and concentration indices, Park & Choi (2005) used the
color-color space u-r versus
(Yamauchi et al. 2005; Shimasaku et al. 2001). Using both
color and concentration indices, Park & Choi (2005) used the
color-color space u-r versus
![]() and the concentration index c-1 =
R50/R90
and the concentration index c-1 =
R50/R90 ![]() 0.35 as a reliable morphological classifier. In Fig. 13b, we show the
concentration index c vs. g-r
for galaxies at z0 and z3,
with the
0.35 as a reliable morphological classifier. In Fig. 13b, we show the
concentration index c vs. g-r
for galaxies at z0 and z3,
with the ![]() 95
95![]() of the z3 galaxies
corresponding to late-type (c < 2.86)
galaxies.
of the z3 galaxies
corresponding to late-type (c < 2.86)
galaxies.
Finally, the SSFR has been used as an indicator of early and
late-type morphology (e.g. Wolf et al. 2009; Salim
et al. 2009)
since late-types have blue colors and high SSFRs, while early-types
have red colors and low SSFRs. For our z3 sample,
![]() 89
89![]() of the galaxies have log(SSFR) > -10
(see Fig. 13c),
and as reported by Salim et al. (2009), blue actively
star-forming galaxies have log(SSFR) > -10,
while lower values would correspond to the green valley
and red-sequence galaxies. As argued by Weinmann
et al. (2006),
the use of the SSFR would give us important clues for determining the
morphological galaxy type, since for example, a genuine
SF disk galaxy may appear red owing to strong extinction (e.g.
when seen edge-on), and thus be classified as early-type based on its
color, while the SFR and morphology quantifiers would classify it as a
late-type galaxy.
of the galaxies have log(SSFR) > -10
(see Fig. 13c),
and as reported by Salim et al. (2009), blue actively
star-forming galaxies have log(SSFR) > -10,
while lower values would correspond to the green valley
and red-sequence galaxies. As argued by Weinmann
et al. (2006),
the use of the SSFR would give us important clues for determining the
morphological galaxy type, since for example, a genuine
SF disk galaxy may appear red owing to strong extinction (e.g.
when seen edge-on), and thus be classified as early-type based on its
color, while the SFR and morphology quantifiers would classify it as a
late-type galaxy.
Our sample of galaxies at z3
is mainly composed by late-type galaxies, as indicated by any of the
morphological classifiers discussed above. We decided to take these
galaxies as a reference to delimit the late-type zone. After trying all
the discussed methods, in order to obtain a reliable
morphological classification, and following the location of the z3 galaxies
in Fig. 13c,
we conclude that the best method is to use both log(SSFR) >
-10 and a color g-r < 0.6.
After applying this criterion to our z0 sample,
we end with 7967 galaxies classified as late-type,
corresponding to ![]() 13
13![]() of the original sample. If we repeat the comparative analysis
between SFR and metallicity, and SFR against stellar mass (see
Fig. 14)
for galaxies at z0 and z1,
the tail with higher SFR identified in previous
sections corresponds to late-type galaxies. The separation between late
and early-type in the stellar mass versus SFR is a straight border (see
Fig. 14b),
because the separation criterion is the SSFR.
of the original sample. If we repeat the comparative analysis
between SFR and metallicity, and SFR against stellar mass (see
Fig. 14)
for galaxies at z0 and z1,
the tail with higher SFR identified in previous
sections corresponds to late-type galaxies. The separation between late
and early-type in the stellar mass versus SFR is a straight border (see
Fig. 14b),
because the separation criterion is the SSFR.
To alternatively assess this statement, we compared our
results with selected mock galaxy samples from the Millennium
simulations (Springel et al. 2005). We used the
Bower2006a catalog (Bower et al. 2006), which gives
us redshift, SDSS k-corrected colors, stellar mass,
and H![]() luminosity,
among other information. From the original catalog, we randomly
selected 35 000 galaxies at z=0
and z=0.4 with the H
luminosity,
among other information. From the original catalog, we randomly
selected 35 000 galaxies at z=0
and z=0.4 with the H![]() line in emission to
be able to compare with our galaxies. As shown in Fig. 15, there is a clean
separation between a red sequence, formed by galaxies with g-r
line in emission to
be able to compare with our galaxies. As shown in Fig. 15, there is a clean
separation between a red sequence, formed by galaxies with g-r ![]() 0.8,
the green valley with 0.6
0.8,
the green valley with 0.6 ![]() g-r
g-r ![]() 0.8,
and the blue cloud with g-r
0.8,
and the blue cloud with g-r ![]() 0.6.
It can be observed how galaxies move towards late-type
galaxies as redshift increases. Then, these results are consistent with
mainly observing late-type galaxies at redshift z3.
0.6.
It can be observed how galaxies move towards late-type
galaxies as redshift increases. Then, these results are consistent with
mainly observing late-type galaxies at redshift z3.
7 Summary and conclusions
We analyzed a sample of emission line galaxies selected in four
redshift intervals from ![]() 0
to 0.4 in bins of 0.1, taking the magnitude
completeness of every redshift interval into account. In this paper we
introduced the S2N2 diagram as a star-forming, composite, and
AGN galaxy classifier, estimated metallicities using the R23 method,
and analyzed the evolutive effects of galaxies from the three
BPT diagrams. Additionally, we studied the evolution of the M-Z
and L-Z relations and
analyzed the evolution and implications of the galaxy morphology in the
SFR-mass and metallicity relations. From these analyses we conclude the
following.
0
to 0.4 in bins of 0.1, taking the magnitude
completeness of every redshift interval into account. In this paper we
introduced the S2N2 diagram as a star-forming, composite, and
AGN galaxy classifier, estimated metallicities using the R23 method,
and analyzed the evolutive effects of galaxies from the three
BPT diagrams. Additionally, we studied the evolution of the M-Z
and L-Z relations and
analyzed the evolution and implications of the galaxy morphology in the
SFR-mass and metallicity relations. From these analyses we conclude the
following.
- Using the Kew01 photoionization grids, the Kauf03 and Kew01
SF, and starburst limit respectively, in the [N II]/H
 vs.
[O III]
vs.
[O III] 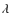 5007/H
5007/H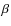 diagram,
we demonstrated that the S2N2 is a well-behaved diagnostic diagram
efficiently classifying star-forming, composite, and AGN galaxies.
diagram,
we demonstrated that the S2N2 is a well-behaved diagnostic diagram
efficiently classifying star-forming, composite, and AGN galaxies.
- We analyzed the galaxy evolution using the three main BPT
diagrams: [N II]/H
 ,
[S II]/H
,
[S II]/H ,
and [O I]
,
and [O I] 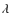 6300/H
6300/H vs.
[O III]
vs.
[O III] 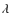 5007/H
5007/H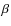 in our four redshift bins, observing an evolution toward higher values
of the [O III]
in our four redshift bins, observing an evolution toward higher values
of the [O III] 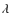 5007/H
5007/H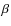 ratio. This evolution is a consequence of the metallicity evolution as
redshift increases, reflected in the three BPT diagrams,
because the ratio [O III]
ratio. This evolution is a consequence of the metallicity evolution as
redshift increases, reflected in the three BPT diagrams,
because the ratio [O III] 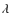 5007/H
5007/H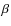 is a good metallicity indicator. As a result,
a metallicity decrement will be reflected in higher values of
this ratio.
is a good metallicity indicator. As a result,
a metallicity decrement will be reflected in higher values of
this ratio.
- We analyzed the evolution of the M-Z
and L-Z relations, observing
that at higher redshift values, both relations evolve towards lower
values of metallicity. We discovered that the flat zone of the M-Z relation
reported by Tremonti et al. (2004) for galaxies
with log(
 /
/ )
)  10.5, is mainly constituted by galaxies at z
> 0.1 (samples at z1,
z2 and z3).
Galaxies at z0 redshift
could be fitted with a linear function. Our M-Z relation
at redshift z3 is
10.5, is mainly constituted by galaxies at z
> 0.1 (samples at z1,
z2 and z3).
Galaxies at z0 redshift
could be fitted with a linear function. Our M-Z relation
at redshift z3 is 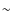 0.2 dex
lower than our local one.
0.2 dex
lower than our local one.
- Our fit to the M-Z
relation for sample z3
agrees with the one of Erb et al. (2006a) at
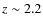 .
We attribute this similarity to the galaxy morphology in the different
samples, since our z3 sample
conforms to late-type galaxies, while the sample of Erb et al.
is composed of a mix of early and late-type galaxies. According to
Calura et al. (2009),
the M-Z relation of
late-type galaxies will have systematically lower metallicities than an
M-Z relation
composed of a mix of early and late-type galaxies.
.
We attribute this similarity to the galaxy morphology in the different
samples, since our z3 sample
conforms to late-type galaxies, while the sample of Erb et al.
is composed of a mix of early and late-type galaxies. According to
Calura et al. (2009),
the M-Z relation of
late-type galaxies will have systematically lower metallicities than an
M-Z relation
composed of a mix of early and late-type galaxies.
- We analyzed the evolution of the mass-to-light ratio, observing lower M/L ratios as redshift increases. For a narrow range of absolute magnitudes in the z3 sample, we have a wide range of mass, making it possible to generate the M-Z relation, but difficult to generate the L-Z relation.
- The decrement in metallicity observed in previous papers for galaxies at redshift z3 (Lara-López et al. 2009a,b) is also observed, even though in this study we are not restricting our galaxy luminosities as in our previous studies.
- We estimated the SFR and SSFR for our sample of galaxies
and analyzed its relation with 12 + log(O/H) and log(
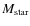 /
/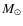 ), confirming the existence of
the MS reported by Noeske et al. (2007) in the
log(SFR) vs. log(
), confirming the existence of
the MS reported by Noeske et al. (2007) in the
log(SFR) vs. log(
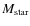 /
/ )
plot. Consistently, we found that higher SFRs and SSFRs increase with
redshift.
)
plot. Consistently, we found that higher SFRs and SSFRs increase with
redshift.
- We analyzed the morphology of our galaxies through the g-r color, the concentration index R90/R50, and the SSFR, concluding that the best method of determining the morphology was by combining both a color of g-r < 0.6 and a log(SSFR) > 10 for selecting late-type galaxies.
- Our z3 sample of galaxies is mainly formed by late-type galaxies, which helped us to classify morphological types at lower redshift. That at higher redshift the fraction of late-type galaxies is greater, was confirmed by using mock galaxy catalogs from Millennium simulations.
- At the higher redshift, we found a population with higher SFR and SSFR than the galaxies in the z0 sample. After classifying late and early-type galaxies in the z0 sample, we realized that the observed tail showing higher SFR and SSFR is formed by late-type galaxies, demonstrating the connection of the galaxy morphology with the SFR in a new fashion.
This work was supported by the Spanish Plan Nacional de Astronomía y Astrofísica under grant AYA2008-06311-C02-01. The Sloan Digital Sky Survey (SDSS) is a joint project of The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Max-Planck-Institute for Astronomy, Princeton University, the United States Naval Observatory, and the University of Washington. Apache Point Observatory, site of the SDSS, is operated by the Astrophysical Research Consortium. Funding for the project has been provided by the Alfred P. Sloan Foundation, the SDSS member institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, and Monbusho. The official SDSS web site is www.sdss.org. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. We thank the Starlight Project Team (UFSC, Brazil), especially William Schoenell, who helped us downloads the whole data set. We thank Romano Corradi for giving us the idea of using the S2N2 diagram in galaxies. We thank Kerttu Viironen for providing us the lines and metallicity data for several H II and PNe to test the efficiency of the S2N2 diagram. We also thank the anonymous referee for his/her constructive comments. Maritza A. Lara-López is supported by a CONACyT and SEP Mexican fellowships.
References
- Abraham, R. G., van den Bergh, S., & Nair, P. 2003, ApJ, 588, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Asari, N. V., Cid Fernandes, R., Stasinska, G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldwin, J., Phillips, M., & Terlevich, R. 1981, PASP, 93, 5 (BPT) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, A. E., Drory, N., Hill, G. J., & Feulner, G. 2005, ApJ, 621, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., & Ellis, R. S. 2000, ApJ, 536, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brodie, J. P., & Huchra, J. P. 1991, ApJ, 379, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Boissier, S., Burgarella, D., et al. 2008, A&A, 483, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantó, J. 1981, in Investigating the Universe, ed. Z. Kopal, & F. D. Kahn (Dordrecht: Reidel), 95 [Google Scholar]
- Caputi, K. I., Dole, H., Lagache, G., et al. 2006, ApJ, 637, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., & Lilly, S. J. 2001, ApJ, 548, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., Kauffmann, G., Longhetti, M., et al. 2002, MNRAS, 330, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasinska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Asari, N. V., Sodré, L., et al. 2007, MNRAS, 375, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G. 1976, ApJ, 203, 587 [Google Scholar]
- Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, MNRAS, 373, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- De Lucia, G., Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, X., He, J., Wu, P., & Ding, Y. 2009, ApJ, 699, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, M., Stern, D., Giavalisco, M., et al. 2004, ApJ, 600, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Donas, J., & Deharveng, J. M. 1984, A&A, 140, 325 [NASA ADS] [Google Scholar]
- Dopita, M. A., Kewley, L. J., Heisler, C. A., & Sutherland, R. S. 2000, ApJ, 542, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Periera, L., Kewley, L. J., & Capacciolo, M. 2002, ApJS, 143, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Fischera, J., Sutherland, R. S., et al. 2006, ApJS, 167, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 2000, MNRAS, 317, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, ApJ, 672, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006a, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006b, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Feulner, G., Gabasch, A., Salvato, M., et al. 2005, ApJ, 633, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 329, 950 [NASA ADS] [Google Scholar]
- Gallagher, J. S., Hunter, D. A., & Bushouse, H. 1989, AJ, 97, 700 [NASA ADS] [CrossRef] [Google Scholar]
- García-Lario, O., Manchado, A., Riera, A., Mampaso, A., & Pottasch, S. R. 1991, A&A, 249, 223 [NASA ADS] [Google Scholar]
- Garnett, D. R., Shields, G. A., Skillman, E. D., Sagan, S. P., & Dufour, R. J. 1997, ApJ, 489, 36 [Google Scholar]
- Gavazzi, G., & Scodeggio, M. 1996, A&A, 312, L29 [NASA ADS] [Google Scholar]
- Gavazzi, G., Bonfanti, C., Sanvito, G., Boselli, A., & Scodeggio, M. 2002, ApJ, 576, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Okamura, S., McKay, T. A., et al. 2002, PASJ, 54, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, R., Gallego, J., Koo, D. C., et al. 1997, ApJ, 489, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Harper, D. A., & Low, F. J. 1973, ApJ, 182, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubble, E. 1926, ApJ, 64, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, R. A., Franx, M., & Fabricant, D. 2001, ApJ, 551, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Juneau, S., Glazebrook, K., Crampton, D., et al. 2005, ApJ, 619, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 (Kauf03) [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D., et al. 2003b, MNRAS, 341, 54 [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., & Kent, S. M. 1983, AJ, 88, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Tamblin, P., & Congdon, C. 1994, 435, 22 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 (Kew01) [Google Scholar]
- Kewley, L. J., Geller, M. J., & Jansen, R. A. 2004, AJ, 127, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Springel, V., & White, S. D. M. 2007, MNRAS, 376, 1465 [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 204 [Google Scholar]
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lamareille, F., Brinchmann, J., Contini, T., et al. 2009, A&A, 495, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2009a, A&A, 493, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2009b, A&A, 505, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, submitted [arXiv:1005.0509] [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., & Tinsley, B. M. 1978, ApJ, 219, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C. 2006, Ph.D. Thesis, Univ. Arizona [Google Scholar]
- Lee, J. H., Lee, M. G., Kim, T., et al. 2007a, ApJ, 663, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Kennicutt, R. C., Funes, S. J., et al. 2007b, ApJ, 671, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Levesque, E. M., Kewley, L. J., & Larson, K. L. 2010, ApJ, 139, 712 [Google Scholar]
- Liang, Y. C., Yin, S. Y., Hammer, F., et al. 2006, ApJ, 652, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Carollo, C. M., & Stockton, A. 2003, ApJ, 597, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C. J., Schawinski, K., Slosar, A., et al. 2008, MNRAS, 389, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, A. R. 2010, A&A, accepted [arXiv:1005.0659] [Google Scholar]
- López-Sánchez, A. R., & Esteban, C. 2010, A&A, 517, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacLow, M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Perinotto, M., Corradi, R. L. M., & Mampaso, A. 2003, A&A, 400, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maier, C., Meisenheimer, K., & Hippelein, H. 2004, A&A, 418, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maier, C., Lilly, S., Carollo, C. M., Stockton, A., & Brodwin, M. 2005, ApJ, 634, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, K. L., Mosleh, M., Romer, A. K., et al. 2010, MNRAS, 405, 783 [NASA ADS] [Google Scholar]
- Mateus, A., Sodré, L., Cid Fernandes, R., et al. 2006, MNRAS, 370, 721 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., & Kennicutt, R. C. Jr. 2006, ApJ, 651, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Mouhcine, M., Gibson, B. K., Renda, A., & Kawata, D. 2008, A&A, 486, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, O., Fukugita, M., Yasuda, N., et al. 2003, AJ, 125, 1682 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007a, ApJ, 660, L43 [Google Scholar]
- Noeske, K. G., Faber, S. M., Weiner, B. J., et al. 2007b, ApJ, 660, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. R. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley CA: University Science Books) [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009, ApJ, 698, L116 [Google Scholar]
- Papovich, C., Moustakas, L. A., Dickinson, M., et al. 2006, ApJ, 640, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Park, C., & Choi, Y. 2005, ApJ, 635, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Montero, E., & Contini, T. 2009, MNRAS, 398, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., & Ferrini, F. 2000, A&A, 358, 72 [NASA ADS] [Google Scholar]
- Raimann, D., Storchi-Bergmann, T., Bica, E., Melnick, J., & Schmitt, H. 2000, MNRAS, 316, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, M. G., & McCall, M. L. 1995, ApJ, 445, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1978, ApJ, 220, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Riesgo, H., & López, J. A. 2005, Rev. Mex. Astron. Astrofis., 41, 57 [NASA ADS] [Google Scholar]
- Riesgo, H., & López, J. A. 2006, Rev. Mex. Astron. Astrofis., 42, 47 [NASA ADS] [Google Scholar]
- Roberts, M. S. 1963, ARA&A, 1, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosa-González, D., Terlevich, E., & Terlevich, R. 2002, MNRAS, 332, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Rosa González, D., Terlevich, E., Jiménez Bailón, E., et al. 2009, MNRAS, 399, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Rovilos, E., Georgantopoulos, I., Tzanavaris, P., et al. 2009, A&A, 502, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbadin, F., Minello, S., & Bianchini, A. 1977, A&A, 60, 174 [Google Scholar]
- Salim, S., Charlot, S., Rich, M., et al. 2005, ApJ, 619, L39 [Google Scholar]
- Salim, S., Dickinson, M., Rich, R. M., et al. 2009, ApJ, 700, 161 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sandage, A. R. 1961, The Hubble Atlas of Galaxies, Carnegie Institute of Washington, Washington [Google Scholar]
- Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2008, MNRAS, 389, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, C., Carollo, C. M., Lilly, S., et al. 2007, ApJS, 172, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Virani, S., Simmons, B., et al. 2009, ApJ, 692, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L., Sargent, W. L. W., & Bagnuolo, W. G. 1973, ApJ, 179, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Serjeant, S., Gruppioni, C., & Oliver, S. 2002, MNRAS, 330, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Erb, D. K., et al. 2005, ApJ, 626, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Shimasaku, K., Fukugita, M., Doi, M., et al. 2001, AJ, 122, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., Kennicutt, R. C., Jr., & Hodge, P. W. 1989, ApJ, 347, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stasinska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I., Ivezic, Z., Knapp, G. R., et al. 2001, AJ, 122, 1861 [Google Scholar]
- Tassis, K., Kravtsov, A. V., & Gnedin, N. Y. 2008, ApJ, 672, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Telesco, C. M., & Harper, D. A. 1980, ApJ, 235, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1968, ApJ, 151, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1972, A&A, 20, 383 [NASA ADS] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 (T04) [NASA ADS] [CrossRef] [Google Scholar]
- Tresse, L., & Maddox, S. J. 1998, ApJ, 495, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vale Asari, N., Cid Fernandes, R., Gomes, J. M., et al. 2009, MNRAS, 396, L71 [NASA ADS] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference Catalog of Bright Galaxies (New York: Springer-Verlag) [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Viironen, K., Delgado-Inglada, G., Mampaso, A., Magrini, L., & Corradi, R. L. M. 2007, MNRAS, 381, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Yang, X., Mo, H. J., & van den Bosch, F. C. 2007, ApJ, 664, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, A. M., van den Bosch, F. C., Yang, X., & Mo, H. J. 2006, MNRAS, 366, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Aragón-Salamanca, A., & Balogh, M. 2009, MNRAS, 393, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Yamauchi, C., & Goto, T. 2005, MNRAS, 359, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... database
![[*]](/icons/foot_motif.png)
- http://www.starlight.ufsc.br
All Tables
Table 1: Comparison between the S2N2 diagram and the N2 ratio to segregate SF, composite, and AGN galaxies.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg1.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg20.png)
|
Figure 1: Normalized histogram of the apparent Petrosian r magnitudes in the four redshift bins. The dark solid line represents galaxies at z0, the dashed line the galaxies at z1, dot-dashed lines the galaxies at z2, and the clear solid line the galaxies at z3. The black arrow shows the completeness limit for the samples z0, z1, and z2, and the clear arrow points to the same for z3. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg26.png)
|
Figure 2:
Log([N II]/H |
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
Contour plots for star-forming, composite, and AGN galaxies.
a) Star-forming, darker (blue) contour, and
composite, lighter (orange) contour, enclosing the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13886fg4.ps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{13886fg5.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg28.png)
|
Figure 4:
a) log(H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg6.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg36.png)
|
Figure 5: Evolution of line ratios from the BPT diagrams. Black dots show galaxies in the redshift range z0, blue dots galaxies in the z1 range, big red triangles represent galaxies in the completeness of the z2 range, while small red triangles galaxies out of the completeness, yellow big circles represent galaxies in the completeness of the z3 range, and small circles galaxies out of the completeness. The black solid line shows the Kauf03 limit for SF galaxies, and the red solid line shows the Kew01 limit for starburst galaxies in the three BPT diagrams. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13886fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg37.png)
|
Figure 6:
Evolution with redshift of the log([O III] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg8.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg41.png)
|
Figure 7: Normalized mass histogram for all our samples. Dark solid line represent galaxies at z0, dashed line galaxies at z1, point dashed line galaxies at z3, and clear solid line galaxies at z3. The histograms were constructed not taking the completeness for galaxies at z2 and z3 into account. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg9.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg42.png)
|
Figure 8:
a) Relation between the stellar mass and
12 + log(O/H) (M-Z relation).
b) Relation between the absolute
Petrosian r magnitude and
12 + log(O/H) (L-Z relation)
for our sample of galaxies. The cut observed in Fig.
b) for the z1 sample
comes from the 5577 Å sky line (see the text). In
both relations, white contours represent from outside to
inside, 15, 30, 50, 70, and 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg46.png)
|
Figure 9:
Evolution of the mass-metallicity relation observed at different
redshifts. The point-dashed line represents the curve of T04 at z |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg11.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg47.png)
|
Figure 10:
Mass versus Petrosian absolute k-corrected
magnitude for all our redshift samples. White contours represent, going
from outside to inside, 10, 25, 50, and 80 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg12.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg48.png)
|
Figure 11:
Metallicity and mass versus log(SFR). Contours correspond to the z0 sample
in both plots. White contours represent, from outside to inside, in
panel a): 15, 30, 50, 70, and 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg13.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg52.png)
|
Figure 12:
Metallicity and mass versus log(SSFR). Contours correspond to the z0 sample
in both plots. White contours represent, from outside to inside, in
panel a): 10, 20, 40, 60, and 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13886fg14.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg54.png)
|
Figure 13:
Principal morphological classifiers. In panels a)-
c), we show the log(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13886fg15.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg55.png)
|
Figure 14: Metallicity and mass versus log(SSFR). Black dots and yellow circles represent galaxies at z0 and z3, respectively, while green dots, represent late-type galaxies at z0 selected with log( SSFR) > -10. (See the electronic edition of the Journal for a color version of this figure.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13886fg16.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13886-09/Timg60.png)
|
Figure
15: Mass versus g-r color for Millennium galaxies. Black and yellow dots represent galaxies at z0 and z3, respectively. (See the electronic edition of the Journal for a color version of this figure.) |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


