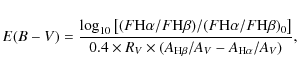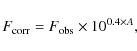| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 31 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913774 | |
| Published online | 09 September 2010 | |
Nearby early-type galaxies with ionized gas
IV. Origin and powering mechanism of the ionized gas![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
F. Annibali1 - A. Bressan1,2,3 - R. Rampazzo1 - W. W. Zeilinger4 - O. Vega3 - P. Panuzzo5
1 - INAF - Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5, 35122 Padova, Italy
2 - SISSA/ISAS, via Beirut 2-4, 34151 Trieste, Italy
3 -
INAOE, Luis Enrique Erro 1, 72840 Tonantzintla, Puebla, Mexico
4 -
Institut für Astronomie der Universität Wien, Türkenschanzstra![]() e 17, 1180 Wien, Austria
e 17, 1180 Wien, Austria
5
- CEA Saclay/Service d'Astrophysique, Laboratoire AIM,
CEA/DSM/IRFU-CNRS-Université Paris Diderot, 91191 Gif-sur-Yvette Cedex,
France
Received 30 November 2009 / Accepted 8 April 2010
Abstract
Aims. A significant fraction of early-type galaxies (ETGs)
exhibit emission lines in their optical spectra. We attempt to identify
the producing the emission mechanism and the ionized gas in ETGs, and
its connection with the host galaxy evolution.
Methods. We analyzed intermediate-resolution optical spectra of
65 ETGs, mostly located in low density environments and exhibiting
spectros-copic diagnostic lines of ISM from which we had previously
derived stellar population properties. To extract the emission lines
from the galaxy spectra, we developed a new fitting procedure that
accurately subtracts the underlying stellar continuum, and accounts for
the uncertainties caused by the age-metallicity degeneracy.
Results. Optical emission lines are detected in 89% of the
sample. The incidence and strength of emission correlate with neither
the E/S0 classification, nor the fast/slow rotator classification. By
means of the classical [OIII]/H![]() versus [NII]/H
versus [NII]/H![]() diagnostic diagram, the nuclear galaxy activity is classified such that
72% of the galaxies with emission are LINERs, 9% are Seyferts, 12% are
composite/transition objects, and 7% are non-classified. Seyferts have
young luminostiy-weighted ages (
diagnostic diagram, the nuclear galaxy activity is classified such that
72% of the galaxies with emission are LINERs, 9% are Seyferts, 12% are
composite/transition objects, and 7% are non-classified. Seyferts have
young luminostiy-weighted ages (![]() 5 Gyr),
and appear, on average, significantly younger than LINERs and
composites. Excluding the Seyferts from our sample, we find that the
spread in the ([OIII], H
5 Gyr),
and appear, on average, significantly younger than LINERs and
composites. Excluding the Seyferts from our sample, we find that the
spread in the ([OIII], H![]() ,
or [NII]) emission strength increases with the galaxy central velocity dispersion
,
or [NII]) emission strength increases with the galaxy central velocity dispersion
![]() .
Furthermore, the [NII]/H
.
Furthermore, the [NII]/H![]() ratio tends to increase with
ratio tends to increase with
![]() .
The [NII]/H
.
The [NII]/H![]() ratio decreases with increasing galactocentric distance, indicative of
either a decrease in the nebular metallicity, or a progressive
``softening'' of the ionizing spectrum. The average nebular oxygen
abundance is slightly less than solar, and a comparison with the
results obtained in Paper III from Lick indices shows that it is
ratio decreases with increasing galactocentric distance, indicative of
either a decrease in the nebular metallicity, or a progressive
``softening'' of the ionizing spectrum. The average nebular oxygen
abundance is slightly less than solar, and a comparison with the
results obtained in Paper III from Lick indices shows that it is ![]() 0.2 dex lower than that of stars.
0.2 dex lower than that of stars.
Conclusions. The nuclear (
![]() )
emission can be attributed to photoionization by PAGB stars alone only for
)
emission can be attributed to photoionization by PAGB stars alone only for ![]() 22%
of the LINER/composite sample. On the other hand, we cannot exclude an
important role of PAGB star photoionization at larger radii. For the
major fraction of the sample, the nuclear emission is consistent with
excitation caused by either a low-accretion rate AGN or fast shocks
(200-500 km s-1) in a relatively gas poor environment (
22%
of the LINER/composite sample. On the other hand, we cannot exclude an
important role of PAGB star photoionization at larger radii. For the
major fraction of the sample, the nuclear emission is consistent with
excitation caused by either a low-accretion rate AGN or fast shocks
(200-500 km s-1) in a relatively gas poor environment (
![]() cm-3),
or both. The derived [SII]6717/6731 ratios are consistent with the low
gas densities required by the shock models. The derived nebular
metallicities are indicative of either an external origin of the gas,
or an overestimate of the oxygen yields by SN models.
cm-3),
or both. The derived [SII]6717/6731 ratios are consistent with the low
gas densities required by the shock models. The derived nebular
metallicities are indicative of either an external origin of the gas,
or an overestimate of the oxygen yields by SN models.
Key words: galaxies: elliptical and lenticular, cD - galaxies: ISM - galaxies: active - galaxies: abundances
1 Introduction
Early-type galaxies (ETGs) have long been considered to be inert stellar systems,
essentially devoid of gas and dust. However, this view has radically changed
since a number of imaging and spectroscopy studies from both
the ground and space have revealed the presence of a multiphase
interstellar medium (ISM):
a hot (
![]() K), X-ray emitting halo (Forman & Jones 1985;
Fabbiano et al. 1992; O'Sullivan et al. 2001); a warm (
K), X-ray emitting halo (Forman & Jones 1985;
Fabbiano et al. 1992; O'Sullivan et al. 2001); a warm (
![]() K) gas (often referred to as ``ionized gas'')
(e.g., Phillips et al. 1986; Sadler & Gerhard 1985;
see also Goudfrooij 1999 for a review);
and colder components detected in the mid and far infrared, CO and HI
(for reviews see Sadler et al. 2002;
Temi et al. 2004; Bressan et al. 2006; Sage & Welch 2006; Morganti et al. 2006; Helmboldt 2007; Oosterloo et al. 2007;
Panuzzo et al. 2007).
The hot gas component dominates the ISM in E/S0 galaxies,
and only comparatively small quantities are detected in the warm and cold
phases (Bregman et al. 1992). The derived masses of the warm ISM range from
K) gas (often referred to as ``ionized gas'')
(e.g., Phillips et al. 1986; Sadler & Gerhard 1985;
see also Goudfrooij 1999 for a review);
and colder components detected in the mid and far infrared, CO and HI
(for reviews see Sadler et al. 2002;
Temi et al. 2004; Bressan et al. 2006; Sage & Welch 2006; Morganti et al. 2006; Helmboldt 2007; Oosterloo et al. 2007;
Panuzzo et al. 2007).
The hot gas component dominates the ISM in E/S0 galaxies,
and only comparatively small quantities are detected in the warm and cold
phases (Bregman et al. 1992). The derived masses of the warm ISM range from ![]() 103 to
103 to ![]()
![]() (Phillips et al. 1986; Trinchieri & di Serego Alighieri 1991; Macchetto et al. 1996;
Goudfrooij et al. 1994a,1994b,1994c; Goudfrooij & de Jong 1995),
orders of magnitude below the X-ray emitting hot ISM and the stellar
mass. Ionized gas is detected in 40-80% of early-type galaxies from
their optical emission lines (Caldwell 1984; Phillips et al. 1986; Macchetto et al. 1996; Sarzi et al. 2006,2009; Yan et al. 2006; Serra et al. 2008). The ionized gas is also usually morphologically associated with dust (Kim 1989; Goudfrooij et al. 1994c).
(Phillips et al. 1986; Trinchieri & di Serego Alighieri 1991; Macchetto et al. 1996;
Goudfrooij et al. 1994a,1994b,1994c; Goudfrooij & de Jong 1995),
orders of magnitude below the X-ray emitting hot ISM and the stellar
mass. Ionized gas is detected in 40-80% of early-type galaxies from
their optical emission lines (Caldwell 1984; Phillips et al. 1986; Macchetto et al. 1996; Sarzi et al. 2006,2009; Yan et al. 2006; Serra et al. 2008). The ionized gas is also usually morphologically associated with dust (Kim 1989; Goudfrooij et al. 1994c).
Despite the number of studies, several issues remain open. The
first problem is the origin of the ISM in ETGs.
Narrow-band imaging centered around H![]() [NII]
[NII]![]() 6584
shows that the ionized gas has a variety of morphologies, from regular,
disk-like structures, to filamentary structures
(Demoulin-Ulrich et al. 1984; Buson et al. 1993; Macchetto et al. 1996;
Zeilinger et al. 1996; Martel et al. 2004; Sarzi et al. 2006).
Evidence of the acquisition of external gas comes from
kinematical studies showing that the angular momentum
of the gas is often decoupled from that of the stars
(Bertola et al. 1992; van Dokkum & Franx 1995; Caon et al. 2000),
even if according to Sarzi et al. (2006) the angular
momenta are inconsistent with a purely external origin for the gas.
That the ionized gas emission is always associated with dust
(e.g. Tran et al. 2001) tends to exclude ``cooling flows'' as the origin of the warm gas in E/S0
galaxies (Goudfrooij 1999). In the scenarios proposed by
Sparks et al. (1989) and de Jong et al. (1990),
the dusty filaments can arise from
the interaction of a small gas-rich galaxy with the giant elliptical,
or from a tidal accretion event in which the gas and dust are stripped
from a passing spiral (see e.g. Domingue et al. 2003; Tal et al. 2009).
6584
shows that the ionized gas has a variety of morphologies, from regular,
disk-like structures, to filamentary structures
(Demoulin-Ulrich et al. 1984; Buson et al. 1993; Macchetto et al. 1996;
Zeilinger et al. 1996; Martel et al. 2004; Sarzi et al. 2006).
Evidence of the acquisition of external gas comes from
kinematical studies showing that the angular momentum
of the gas is often decoupled from that of the stars
(Bertola et al. 1992; van Dokkum & Franx 1995; Caon et al. 2000),
even if according to Sarzi et al. (2006) the angular
momenta are inconsistent with a purely external origin for the gas.
That the ionized gas emission is always associated with dust
(e.g. Tran et al. 2001) tends to exclude ``cooling flows'' as the origin of the warm gas in E/S0
galaxies (Goudfrooij 1999). In the scenarios proposed by
Sparks et al. (1989) and de Jong et al. (1990),
the dusty filaments can arise from
the interaction of a small gas-rich galaxy with the giant elliptical,
or from a tidal accretion event in which the gas and dust are stripped
from a passing spiral (see e.g. Domingue et al. 2003; Tal et al. 2009).
The history of star formation and evolution leaves its chemical signature in the ISM of ETGs. Historically, X-ray abundance measurements of the hot ISM have been problematic, as typified by the so-called Fe discrepancy (Arimoto et al. 1997). Chandra and XMM measurements of X-ray bright galaxies at the center of groups have inferred roughly solar or even slightly supersolar abundances for the ISM (e.g. Gastaldello & Molendi 2002; Buote et al. 2003; Tamura et al. 2003) and claimed no evidence of very subsolar Fe abundances (Humphrey & Buote 2006; Ji et al. 2009). These studies also report anomalously low oxygen abundances compared to iron and magnesium. This is in conflict with results from SN stellar yields if one assumes that the source of ISM is the material injected into interstellar space by evolved stars. Until now, the only study of metallicity in the warm ISM has been that of Athey & Bregman (2009), who derived oxygen abundances for seven ETGs from optical emission lines. The authors find on average a solar metallicity, favoring an internal origin of the warm ISM. However, this study is limited by the small sample. Determining the metallicity of the warm ISM is fundamental to creating a link between the hot gas phase and the galaxy stellar population, and discriminating between an internal and an external origin of the interstellar matter in E/S0 galaxies.
The second open issue concerns the ionizing source of the warm gas. Optical spectroscopic studies show that ETGs are typically classified as LINERs (Low-Ionization Nuclear Emission-line Regions, Heckman 1980) according to their emission line ratios (e.g. Phillips et al. 1986; Yan et al. 2006). However, there is a strong debate about the ionization mechanism in LINERs. At present, the most viable excitation mechanisms are: a low accretion-rate AGN (e.g., Ho 1999b; Kewley et al. 2006; Ho 2009a), photoionization by old post-asymptotic giant branch (PAGB) stars (e.g. Trinchieri & di Serego Alighieri 1991; Binette et al. 1994; Stasinska et al. 2008), and fast shocks (Koski & Osterbrock 1976; Heckman 1980; Dopita & Sutherland 1995; Allen et al. 2008). The AGN mechanism is strongly supported by the detection of broad emission lines in optical spectra (e.g. Ho et al. 1997a; Wang & Wei 2008), by the properties of the X-ray emission (Terashima et al. 2000; Flohic et al. 2006; Gonzalez-Martin et al. 2009), by the presence of UV and X-ray variability (e.g Maoz et al. 2005, Pian et al. 2010), and by the evidence that massive black holes (BHs) appear to be a generic component of galaxies with a bulge (Magorrian et al. 1998; Ho 1999a; Kormendy 2004). PAGB stars are good candidates because their radiation, much harder than that from young stars, is able to reproduce the observed emission-line ratios in LINERs (Trinchieri & di Serego Alighieri 1991; Binette et al. 1994; Stasinska et al. 2008). The most compelling evidence in support of the PAGB mechanism is the finding that the emission-line flux correlates very well with the host galaxy stellar luminosity within the emission-line region (Macchetto et al. 1996), and that the emission-line flux distribution follows that of the stellar continuum (Sarzi et al. 2006,2009). These correlations suggest that the source of ionizing photons is distributed in the same way as the stellar population. LINERs emission has also been observed in extranuclear regions associated with large-scale outflows and related shocks (Lípari et al. 2004), or regions shocked by radio jets (Cecil et al. 2000).
Evidence is growing that more than one mechanism may operate in LINERs.
Sarzi et al. (2009) showed that the role of AGN activity
is confined to the central regions, whereas at larger radii the stellar and
nebular fluxes correlate with each other, which is indicative of a stellar ionizing source.
Eracleous et al. (2010) showed that low accretion-rate AGNs do not
produce enough ionizing photons to explain the observed H![]() luminosities within a
luminosities within a
![]() aperture, so that other mechanisms are needed.
aperture, so that other mechanisms are needed.
To help us understand the formation history of ETGs, and the connection between the stellar populations and the ionized gas, we analyzed intermediate-resolution optical spectra for a sample of 65 field E/S0 galaxies (Rampazzo et al. 2005, hereafter Paper I; Annibali et al. 2006, hereafter Paper II). The stellar population properties (i.e., ages, metallicities, and elements abundance ratios) were derived at different radii in Annibali et al. (2007, hereafter Paper III) by means of the analysis of the Lick indices. In this paper, we present the study of the optical emission lines in annuli of increasing galactocentric distance. The purpose is to characterize the properties of the ionized gas, its origin, and the possible excitation mechanisms at different radii.
The paper is organized as it follows. In Sect. 2, we provide a brief overview of the sample. In Sect. 3, we describe the method used to extract the emission-line fluxes from the optical spectra. In Sect. 4, we provide a spectral classification inferred from standard diagnostic diagrams, and investigate possible correlations with the host galaxy properties. In Sect. 5, we determine the oxygen metallicity. In Sect. 6, we compare our data with the models. A summary and the conclusions are given in Sect. 7.
Table 1: Sample overview.
2 Sample overview
The Rampazzo et al. (2005) + Annibali et al. (2006) sample (hereafter R05+A06 sample) was selected from a compilation of ETGs exhibiting evidence of an
ISM in at least one of the following bands:
IRAS 100 ![]() m, X-ray, radio, HI, and CO (Roberts et al. 1991). All galaxies belong to the Revised Shapley Ames Catalog of
Bright Galaxies (RSA) (Sandage & Tammann 1987) and have
a redshift lower than
m, X-ray, radio, HI, and CO (Roberts et al. 1991). All galaxies belong to the Revised Shapley Ames Catalog of
Bright Galaxies (RSA) (Sandage & Tammann 1987) and have
a redshift lower than ![]() 5500 km s-1.
Because of the selection criteria, the sample is biased toward the presence
of emission lines.
Table 1 summarizes the main characteristics of the sample.
Column (1) gives the galaxy identification name;
Cols. (2) and (3) provide the galaxy morphological classification
according to RSA (Sandage & Tammann 1987) and
RC3 (de Vaucouleurs et al. 1991), respectively: only in few cases
do the two catalogues disagree in the distinction between E and S0 classes;
Col. (4) provides the central velocity dispersion from HYPERLEDA
5500 km s-1.
Because of the selection criteria, the sample is biased toward the presence
of emission lines.
Table 1 summarizes the main characteristics of the sample.
Column (1) gives the galaxy identification name;
Cols. (2) and (3) provide the galaxy morphological classification
according to RSA (Sandage & Tammann 1987) and
RC3 (de Vaucouleurs et al. 1991), respectively: only in few cases
do the two catalogues disagree in the distinction between E and S0 classes;
Col. (4) provides the central velocity dispersion from HYPERLEDA
![]() ;
Col. (5) gives the effective radius
;
Col. (5) gives the effective radius ![]() from RC3;
Col. (6) gives the galaxy systemic velocity,
from RC3;
Col. (6) gives the galaxy systemic velocity,
![]() ,
which is lower
than
,
which is lower
than ![]() 5000 km s-1; Col. (7) provides the richness
parameter
5000 km s-1; Col. (7) provides the richness
parameter
![]() (Tully 1988), which represents the density of
galaxies brighter than apparent B-mag of -16 in the vicinity of the entry, in galaxies
(Tully 1988), which represents the density of
galaxies brighter than apparent B-mag of -16 in the vicinity of the entry, in galaxies ![]() Mpc-3. Columns (8)-(10) list the age,
metallicity, and [
Mpc-3. Columns (8)-(10) list the age,
metallicity, and [![]() /Fe] ratios derived in Paper III.
/Fe] ratios derived in Paper III.
The galaxies of the R05+A06 sample are mainly located in low
density environments. The local density of the galaxies varies from
![]() Mpc-3, typical of very isolated galaxies, to
Mpc-3, typical of very isolated galaxies, to
![]() Mpc-3, characteristic of denser regions in the
Virgo cluster. For comparison, in the Tully (1988) catalogue objects such as NGC 1399
and NGC 1389, members of the Fornax cluster, have
Mpc-3, characteristic of denser regions in the
Virgo cluster. For comparison, in the Tully (1988) catalogue objects such as NGC 1399
and NGC 1389, members of the Fornax cluster, have
![]() =1.59
and 1.50 Mpc-3, respectively. Thus, the R05+A06 sample, even though biased towards low
density environments, contains a fraction of galaxies in relatively
dense environments. The sample spans a wide range in central velocity dispersion, from
=1.59
and 1.50 Mpc-3, respectively. Thus, the R05+A06 sample, even though biased towards low
density environments, contains a fraction of galaxies in relatively
dense environments. The sample spans a wide range in central velocity dispersion, from ![]() 115 to 340 km s-1 (see Papers I and II for details).
115 to 340 km s-1 (see Papers I and II for details).
Following the RC3 classification, the sample is composed of ![]() 70% ellipticals and
70% ellipticals and ![]() 30%
lenticulars. However, if we classify the galaxies according to their
amount of rotation (see Appendix A), we end up with
30%
lenticulars. However, if we classify the galaxies according to their
amount of rotation (see Appendix A), we end up with ![]() 70% fast rotators (F) and
70% fast rotators (F) and ![]() 30% slow rotators (S).
30% slow rotators (S).
Intermediate resolution (
![]() Å at 5550 Å) spectra in the 3700-7250 Å wavelength range were acquired with the
1.5 m ESO-La Silla telescope for the 65 galaxies of the sample.
The spectra were extracted for 7 apertures of increasing radius
(1.5
Å at 5550 Å) spectra in the 3700-7250 Å wavelength range were acquired with the
1.5 m ESO-La Silla telescope for the 65 galaxies of the sample.
The spectra were extracted for 7 apertures of increasing radius
(1.5
![]() ,
2.5
,
2.5
![]() ,
10
,
10
![]() ,
,
![]() /10,
/10, ![]() /8,
/8, ![]() /4, and
/4, and ![]() /2),
corrected for the galaxy ellipticity, and 4 adjacent annulii
(
/2),
corrected for the galaxy ellipticity, and 4 adjacent annulii
(
![]() ,
,
![]() ,
and
,
and
![]() ).
The data reduction and the computation of the Lick indices are described
in Papers I and II. In Paper III, we derived ages, metallicities,
and [
).
The data reduction and the computation of the Lick indices are described
in Papers I and II. In Paper III, we derived ages, metallicities,
and [![]() /Fe] ratios by comparing the data with our new
simple stellar population (SSP) models.
No stellar population parameters are derived for IC 5063, since
line emission is too strong to allow a measurement of the Lick indices.
Summarizing the results of Paper III, we derive a large age spread, with SSP-equivalent ages
ranging from a few Gyrs to a Hubble time.
The galaxies have metallicities and [
/Fe] ratios by comparing the data with our new
simple stellar population (SSP) models.
No stellar population parameters are derived for IC 5063, since
line emission is too strong to allow a measurement of the Lick indices.
Summarizing the results of Paper III, we derive a large age spread, with SSP-equivalent ages
ranging from a few Gyrs to a Hubble time.
The galaxies have metallicities and [![]() /Fe] ratios above solar.
Both the total metallicity and the [
/Fe] ratios above solar.
Both the total metallicity and the [![]() /Fe]
exhibit a positive correlation with the central velocity
dispersion, indicating that the chemical enrichment was more efficient
and the duration of the star formation shorter in more massive
galaxies.
We also find that the youngest objects in our sample are all located in
the lowest density environments (
/Fe]
exhibit a positive correlation with the central velocity
dispersion, indicating that the chemical enrichment was more efficient
and the duration of the star formation shorter in more massive
galaxies.
We also find that the youngest objects in our sample are all located in
the lowest density environments (
![]() Mpc-3).
We suggest that the young galaxies in the lowest density environments underwent
secondary episodes of star formation, which we call ``rejuvenation episodes''.
Within the individual galaxies, the stellar metallicity tends
to decrease from the center outwards.
We derive an average metallicity gradient of
Mpc-3).
We suggest that the young galaxies in the lowest density environments underwent
secondary episodes of star formation, which we call ``rejuvenation episodes''.
Within the individual galaxies, the stellar metallicity tends
to decrease from the center outwards.
We derive an average metallicity gradient of
![]() .
.
3 Emission lines
3.1 Starlight subtraction and measurement of line intensities
There are a number of emission lines that we expect to detect
within the wavelength range 3700-7250 Å sampled by our spectra:
[OII] ![]() 3727, [NeIII]
3727, [NeIII] ![]() 3869, H
3869, H![]()
![]() 4861,
[OIII]
4861,
[OIII]
![]() 4959, 5007, [OI]
4959, 5007, [OI] ![]() 6300, H
6300, H![]()
![]() 6563,
[NII]
6563,
[NII]
![]() 6548, 6584, and [SII]
6548, 6584, and [SII]
![]() 6717, 6731.
6717, 6731.
The emission line fluxes were measured in residual spectra
obtained after subtracting the stellar population contribution from the
observed galaxy spectra.
The starlight subtraction is a crucial step in correctly determining the
emission line properties, in particular for H![]() and H
and H![]() ,
which are superimposed on the Balmer absorption features of the
underlying stellar population.
The H
,
which are superimposed on the Balmer absorption features of the
underlying stellar population.
The H![]() emission, which is much fainter than that of
H
emission, which is much fainter than that of
H![]() (FH
(FH
![]() FH
FH![]() in the absence of extinction),
is the most difficult to measure.
With only a few exceptions, we never see in our spectra
a true emission feature in H
in the absence of extinction),
is the most difficult to measure.
With only a few exceptions, we never see in our spectra
a true emission feature in H![]() ,
but rather
an infilling of the stellar absorption line.
It follows that a reliable measurement of this
line rests on the appropriate modeling of the
underlying starlight contribution.
,
but rather
an infilling of the stellar absorption line.
It follows that a reliable measurement of this
line rests on the appropriate modeling of the
underlying starlight contribution.
To subtract the underlying stellar population from the galaxy spectra,
we used new SSPs (Bressan, unpublished, see also
Clemens et al. 2009; Chavez et al. 2009).
The SSPs were computed from the isochrones of Padova 94
(Bertelli et al. 1994) with the revision of Bressan et al. (1998),
including a new AGB mass-loss treatment calibrated on LMC cluster colors.
These SSPs are particularly suited to our analysis because they use the MILES spectral library
(Sánchez-Blázquez et al. 2006). MILES consists of 2.3 Å
![]() optical spectra of
optical spectra of ![]() 1000 stars spanning a large range of atmospheric parameters,
and represents a substantial improvement over previous libraries used in population synthesis models.
1000 stars spanning a large range of atmospheric parameters,
and represents a substantial improvement over previous libraries used in population synthesis models.
For our study, we considered the galaxy spectra extracted in 4 concentric annulii
(
![]() ,
,
![]() ,
and
,
and
![]() ),
as described in Sect. 2.
The galaxy continua were fitted with the new SSPs,
previously smoothed to match the instrumental resolution and the galaxy velocity dispersion,
by means of a
),
as described in Sect. 2.
The galaxy continua were fitted with the new SSPs,
previously smoothed to match the instrumental resolution and the galaxy velocity dispersion,
by means of a ![]() criterion.
In the fit, we considered selected spectral regions chosen to be particularly
sensitive to either age or to metallicity.
For each SSP of a given age and metallicity,
and E(B-V) ranging from the Galactic foreground value to
criterion.
In the fit, we considered selected spectral regions chosen to be particularly
sensitive to either age or to metallicity.
For each SSP of a given age and metallicity,
and E(B-V) ranging from the Galactic foreground value to
![]() ,
the
,
the ![]() is
is
|
(1) |
where Nr is the number of selected spectral regions,
Because of the degeneracy between age, metallicity, and extinction,
fits with similarly good ![]() values
can produce significantly different residual spectra, in
particular around H
values
can produce significantly different residual spectra, in
particular around H![]() .
Thus, to obtain a statistically meaningful determination of the emission lines, we considered all the N fits with
.
Thus, to obtain a statistically meaningful determination of the emission lines, we considered all the N fits with
![]() ,
and computed the emission lines in the corresponding residual spectra.
,
and computed the emission lines in the corresponding residual spectra.
For each line, we adopted the average emission flux ![]() computed as
computed as
|
(2) |
where FZ,t,AV is the line flux obtained by subtracting the SSP of metallicity Z, age t, and reddening AV to the observed galaxy spectrum, and
The error in the average emission flux is
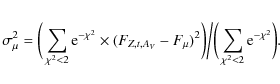
|
(3) |
This error takes into account the uncertainty caused by the intrinsic degeneracy of the stellar populations. Because of the high signal-to-noise ratio (S/N) of our spectra, this is actually the largest source of error in the measure of the emission fluxes.
The use of a single SSP in the fitting procedure may lead to
spurious effects where recent star formation is present in some
amounts. We showed in Paper III that some galaxies in our sample
have very young luminosity-weighted ages (<4 Gyr), possibly as
a consequence of ``rejuvenation'' episodes. Therefore, we repeated the
fitting procedure using, instead of one SSP, a combination of a young (t < 8 Gyr) and an old (t > 8 Gyr) SSP. This approach guarantees a more reliable spectral
subtraction from the Balmer lines for the ``rejuvenated'' galaxies.
The two-SSP fitting procedure results in some differences for the galaxies with faint H![]() emission.
This may be important when discriminating between LINERs and Seyfert
through the [OIII]/H
emission.
This may be important when discriminating between LINERs and Seyfert
through the [OIII]/H![]() ratio (see Sect. 4). On the other hand, we checked that there are no significant differences between
the resulting emission lines for galaxies randomly selected among those without signs of recent star formation.
ratio (see Sect. 4). On the other hand, we checked that there are no significant differences between
the resulting emission lines for galaxies randomly selected among those without signs of recent star formation.
![\begin{figure}
\par\includegraphics[width=17cm]{13774fg1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg85.png)
|
Figure 1:
Central (
|
| Open with DEXTER | |
In Fig. 1, we show the
stellar continuum subtraction procedure for two illustrative examples:
IC 1459, with relatively strong emission lines, and NGC 5813,
with weak emission lines. We note that in the figure the subtracted
stellar continuum is an SSP of age, metallicity, and extinction equal
to the average of all the N solution with
![]() .
This is slightly different from our procedure,
where we have subtracted the individual solutions
N times from the same galaxy spectrum, and have computed the final emission lines to be average of the
N emission fluxes.
In Fig. 1, the emission features are easily visible in IC 1459. The errors in the emission line fluxes
introduced by the uncertainties in the stellar continuum subtraction are thus relatively small.
In the case of NGC 5813, instead, the determination of the emissions is dominated by
starlight subtraction effects, in particular for H
.
This is slightly different from our procedure,
where we have subtracted the individual solutions
N times from the same galaxy spectrum, and have computed the final emission lines to be average of the
N emission fluxes.
In Fig. 1, the emission features are easily visible in IC 1459. The errors in the emission line fluxes
introduced by the uncertainties in the stellar continuum subtraction are thus relatively small.
In the case of NGC 5813, instead, the determination of the emissions is dominated by
starlight subtraction effects, in particular for H![]() and H
and H![]() .
The errors in the emission lines are consequently quite large.
.
The errors in the emission lines are consequently quite large.
We provide in Table 2 the emission line fluxes in units of
![]() erg s-1 cm-2 arcsec-2 derived for the R05+A06 sample in 4 annuli of increasing galactocentric distance
(
erg s-1 cm-2 arcsec-2 derived for the R05+A06 sample in 4 annuli of increasing galactocentric distance
(
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ).
In Table 3, we provide the equivalent width (EW) of each line, derived as
).
In Table 3, we provide the equivalent width (EW) of each line, derived as
![]() ,
where
,
where
![]() is the flux computed in a continuum band adjacent to the line of interest.
The large errors in H
is the flux computed in a continuum band adjacent to the line of interest.
The large errors in H![]() are due
to its intrinsic faintness, accompanied by a strong
dependence of the H
are due
to its intrinsic faintness, accompanied by a strong
dependence of the H![]() absorption line on age.
The values given in Tables 2 and 3 are not corrected for reddening.
The extinction-corrected emissions can be easily derived from the E(B-V) values given
in Col. 3 of Table 2, and computed as described in the next paragraph.
absorption line on age.
The values given in Tables 2 and 3 are not corrected for reddening.
The extinction-corrected emissions can be easily derived from the E(B-V) values given
in Col. 3 of Table 2, and computed as described in the next paragraph.
3.2 Extinction
The extinction in the lines was derived from the relative observed strengths of the Balmer lines.
The intrinsic flux ratio
![]() is
is ![]() 2.85 for HII regions and
2.85 for HII regions and ![]() 3.1
for AGN-like objects (Osterbrock 1989).
Values larger than these are due to absorption
from an intervening medium.
3.1
for AGN-like objects (Osterbrock 1989).
Values larger than these are due to absorption
from an intervening medium.
More specifically, given an observed
![]() ratio,
the reddening is computed to be
ratio,
the reddening is computed to be
where
![]() is the magnitude attenuation at a given wavelength,
and
is the magnitude attenuation at a given wavelength,
and
![]() ,
,
![]() ,
and
RV = AV / E(B-V),
depend on the adopted extinction curve.
We adopted the Cardelli et al. (1989) extinction law, where
RV = 3.05. We also assumed
,
and
RV = AV / E(B-V),
depend on the adopted extinction curve.
We adopted the Cardelli et al. (1989) extinction law, where
RV = 3.05. We also assumed
![]() ,
since all the galaxies in the R05+A06 sample display AGN - like emission-line ratios (see Sect. 4). The assumption of
,
since all the galaxies in the R05+A06 sample display AGN - like emission-line ratios (see Sect. 4). The assumption of
![]() does not significantly change our results.
does not significantly change our results.
In Fig. 2, we plot the H![]() versus H
versus H![]() fluxes derived in a central
fluxes derived in a central
![]() region.
The majority of the galaxies have
E(B-V) < 0.3.
Some galaxies exhibit instead very strong extinction, as high as
region.
The majority of the galaxies have
E(B-V) < 0.3.
Some galaxies exhibit instead very strong extinction, as high as
![]() or even more.
They have very faint H
or even more.
They have very faint H![]() intensities,
accompanied by relatively strong H
intensities,
accompanied by relatively strong H![]() emission.
Vice versa, a few objects fall below the
E(B-V) =0 line, in the
region of ``negative reddening''. In these cases, the emission derived in
H
emission.
Vice versa, a few objects fall below the
E(B-V) =0 line, in the
region of ``negative reddening''. In these cases, the emission derived in
H![]() is incompatible (too large) with the derived H
is incompatible (too large) with the derived H![]() .
An obvious explanation is that the underlying continuum was not
subtracted properly. More specifically, that we underestimate the
H
.
An obvious explanation is that the underlying continuum was not
subtracted properly. More specifically, that we underestimate the
H![]() /H
/H![]() ratio suggests that we have subtracted populations
that are systematically too young or too metal poor.
To verify this hypothesis, we simulated the situation in which a too-young population
is subtracted from the galaxy spectrum in the following way.
We created a synthetic spectrum by adding H
ratio suggests that we have subtracted populations
that are systematically too young or too metal poor.
To verify this hypothesis, we simulated the situation in which a too-young population
is subtracted from the galaxy spectrum in the following way.
We created a synthetic spectrum by adding H![]() and H
and H![]() emission lines
(in the ratio
emission lines
(in the ratio
![]() )
to an old SSP.
We then rederived the emission intensities by subtracting from the
synthetic spectrum increasingly younger SSPs.
We found that the
)
to an old SSP.
We then rederived the emission intensities by subtracting from the
synthetic spectrum increasingly younger SSPs.
We found that the
![]() ratio
decreases as the
ratio
decreases as the ![]() age increases.
The effect is much stronger when the initial emission
intensities are weaker, because of a combination of
the stronger dependence of the H
age increases.
The effect is much stronger when the initial emission
intensities are weaker, because of a combination of
the stronger dependence of the H![]() absorption line on age,
and of the intrinsic faintness of the H
absorption line on age,
and of the intrinsic faintness of the H![]() emission line relative to H
emission line relative to H![]() .
.
Finally, there are some galaxies
whose H![]() and H
and H![]() emissions are both
consistent with zero within a 3
emissions are both
consistent with zero within a 3 ![]() errorbar (NGC 1366, NGC 1389, NGC 1407, NGC 1426,
NGC 5638, NGC 5812, and NGC 5831).
These galaxies also exhibit no emission in the other lines, and are classified as no emission (N) galaxies.
errorbar (NGC 1366, NGC 1389, NGC 1407, NGC 1426,
NGC 5638, NGC 5812, and NGC 5831).
These galaxies also exhibit no emission in the other lines, and are classified as no emission (N) galaxies.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg101.png)
|
Figure 2:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg102.png)
|
Figure 3:
E(B-V) distribution derived for our sample from the
|
| Open with DEXTER | |
The derived E(B-V) values at different
galactocentric distances are given in Col. 3 of Table 2.
For the galaxies with ``negative reddening'', and galaxies with E(B-V) lower than
the Galactic foreground extinction, the E(B-V) was set to
the foreground value.
Very large E(B-V) values are derived for
NGC 777, NGC 1521, NGC 3136, NGC 3557, NGC 6776, NGC 7007,
and NGC 3489. These strong extinction values, not observed in the
continuum, suggest that the distribution of the dust is patchy.
We note however that the errors in the derived E(B-V) values are quite large,
due to the large uncertainty in the H![]() emission.
The reddening distributions for the E and S0 classes
are shown in Fig. 3. The median E(B-V) values for the two classes are
0.11 and 0.26, respectively. However, a Mann-Withney U test shows that
there is no significant difference between the two distributions.
emission.
The reddening distributions for the E and S0 classes
are shown in Fig. 3. The median E(B-V) values for the two classes are
0.11 and 0.26, respectively. However, a Mann-Withney U test shows that
there is no significant difference between the two distributions.
After computing the E(B-V) values, we corrected the observed emission fluxes to be
where
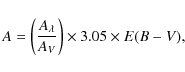
|
(6) |
3.3 Results
The galaxies are classified in Table 4 according to the intensity of their nuclear emission lines.
We identify three categories: no emission galaxies (N), where no emission lines are detected within a 3![]() error; weak emission-line galaxies (W), with EW(H
error; weak emission-line galaxies (W), with EW(H![]() + [NII]6584) <3 Å;
and strong emission-line galaxies (H), with EW(H
+ [NII]6584) <3 Å;
and strong emission-line galaxies (H), with EW(H![]() + [NII]6584) >3 Å.
+ [NII]6584) >3 Å.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13774fg4.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg106.png)
|
Figure 4:
H |
| Open with DEXTER | |
Emission lines are detected in 58 of 65 galaxies (![]() 89% of the sample), while strong emission is present in 57% of the sample.
In the central
89% of the sample), while strong emission is present in 57% of the sample.
In the central
![]() region, we derive median EWs of
region, we derive median EWs of ![]() 0.51, 0.72, 1.4, and 1.8
for H
0.51, 0.72, 1.4, and 1.8
for H![]() ,
[OIII]
,
[OIII]
![]() ,
H
,
H![]() ,
and [NII]
,
and [NII]![]() 6584, respectively. For the same lines, the median percentage errors amount to
6584, respectively. For the same lines, the median percentage errors amount to
![]() 31%, 11% , 6% , and , 1%.
31%, 11% , 6% , and , 1%.
We investigated possible differences in the emission intensity between
the E and S0 subsamples, and between the fast (F) and slow (S) rotators
subsamples. The distributions and the relative median values are shown
in Fig. 4.
An appreciable difference is observed only between F and S for the
median [NII] value. However, Mann-Whitney U tests provide
![]() (for a two-tailed test) for all the distributions,
indicating that there is no significant difference between the E, S0, F, and S subsamples.
(for a two-tailed test) for all the distributions,
indicating that there is no significant difference between the E, S0, F, and S subsamples.
To quantify the importance of the emission with respect to the underlying stellar continuum at
increasing galactocentric distance, we studied the behavior of the
[NII]
![]() and the H
and the H![]() lines in the 4 annuli defined in Sect. 2. We note that the
use of adjacent annuli instead of ``apertures'' allows us to isolate
the true emission contribution from different regions within the
galaxy.
The [NII]
lines in the 4 annuli defined in Sect. 2. We note that the
use of adjacent annuli instead of ``apertures'' allows us to isolate
the true emission contribution from different regions within the
galaxy.
The [NII]
![]() line is stronger than the other lines, and thus
more easily measured also in the external annuli. Furthermore, it is also very poorly affected
by uncertainties in the underlying stellar population subtraction, and has the lowest percentage error.
On the other hand, the H
line is stronger than the other lines, and thus
more easily measured also in the external annuli. Furthermore, it is also very poorly affected
by uncertainties in the underlying stellar population subtraction, and has the lowest percentage error.
On the other hand, the H![]() line
has the advantage that, being a recombination line, it directly
reflects the ionizing photon flux, but its measure is far more affected
than the [NII] by uncertainties in the underlying population
subtraction. The behaviors of the observed [NII]/([NII]
line
has the advantage that, being a recombination line, it directly
reflects the ionizing photon flux, but its measure is far more affected
than the [NII] by uncertainties in the underlying population
subtraction. The behaviors of the observed [NII]/([NII]
![]() /16) and H
/16) and H![]() /(H
/(H
![]() /16) ratios
with increasing galactocentric distances are shown in Fig. 5.
Negative values are consistent with no emission.
The plotted values were not corrected for reddening, but
extinction may affect the EWs if the
nebular emission were more reddened than the continuum.
Tran et al. (2001) indeed showed that the presence of emission lines in ETGs tends to be associated with the presence of clumpy dust.
/16) ratios
with increasing galactocentric distances are shown in Fig. 5.
Negative values are consistent with no emission.
The plotted values were not corrected for reddening, but
extinction may affect the EWs if the
nebular emission were more reddened than the continuum.
Tran et al. (2001) indeed showed that the presence of emission lines in ETGs tends to be associated with the presence of clumpy dust.
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg5.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg112.png)
|
Figure 5:
Emission EW derived in annuli of increasing galactocentric distance (
|
| Open with DEXTER | |
Figure 5 shows that, with
some exceptions (NGC 3489, NGC 5898, NGC 7007,
NGC 7079, NGC 7192, NGC 7377), the emission EWs tend to
decrease from the center outwards.
The average decrease in the [NII] EW is ![]() 0.7, 0.5, and 0.4 of the central value at
0.7, 0.5, and 0.4 of the central value at ![]() 0.1
0.1 ![]() ,
,
![]() 0.2
0.2 ![]() ,
and
,
and ![]() 0.4
0.4 ![]() ,
while the H
,
while the H![]() EW decreases more gently
(
EW decreases more gently
(![]() 0.8, 0.7, and 0.6 at the same radii). The steeper decrease in the [NII] relative to the H
0.8, 0.7, and 0.6 at the same radii). The steeper decrease in the [NII] relative to the H![]() is indicative of a progressive softening of the ionizing spectrum from the galaxy center to more
external regions. The decrease in the H
is indicative of a progressive softening of the ionizing spectrum from the galaxy center to more
external regions. The decrease in the H![]() EW implies that the ionizing flux decrease more rapidly than the stellar continuum around
EW implies that the ionizing flux decrease more rapidly than the stellar continuum around ![]() 6500 Å. However, given the uncertainties, we can consider
significant only the decrease from the center to
6500 Å. However, given the uncertainties, we can consider
significant only the decrease from the center to ![]() 0.1
0.1 ![]() .
Deeper observations are needed to trace with higher confidence
the EW behavior out to larger radii.
.
Deeper observations are needed to trace with higher confidence
the EW behavior out to larger radii.
The galaxies NGC 7079, NGC 3489, NGC 7007, NGC 7192, NGC 7377, and NGC 5898 deviate from
the average decreasing trend, exhibiting flat or increasing emission EWs (although the H![]() of NGC 3489, NGC 5898, and NGC 7079 drops in the most
external annulus).
NGC 3489 and NGC 7007 have large reddenings, thus their
increasing trend may be caused by stronger extinction toward the galaxy
center. Unfortunately, the errors in the derived E(B-V)
values are large, and it is difficult to establish from our data if
indeed the reddening decreases with galacto-centric distance.
On the other hand, the other galaxies (NGC 7079, NGC 7192,
NGC 7377, and NGC 5898) show very little or almost null
extinction, thus the observed trends are likely to be intrinsic.
of NGC 3489, NGC 5898, and NGC 7079 drops in the most
external annulus).
NGC 3489 and NGC 7007 have large reddenings, thus their
increasing trend may be caused by stronger extinction toward the galaxy
center. Unfortunately, the errors in the derived E(B-V)
values are large, and it is difficult to establish from our data if
indeed the reddening decreases with galacto-centric distance.
On the other hand, the other galaxies (NGC 7079, NGC 7192,
NGC 7377, and NGC 5898) show very little or almost null
extinction, thus the observed trends are likely to be intrinsic.
4 Spectral classification
4.1 Diagnostic diagrams
Galaxies were classified by means of the standard [OIII]![]() 5007/ H
5007/ H![]() versus
[NII]
versus
[NII]![]() 6584/ H
6584/ H![]() diagnostic diagram (Baldwin, Phillips and Terlevich (1981; hereafter BPT).
Using a combination of stellar population synthesis models and photoionization models,
Kewley et al. (2001) identified a ``maximum starburst line'' in the BPT diagram.
Galaxies lying above this line are likely to be dominated by an AGN.
Kauffmann et al. (2003) later revised the Kewley et al. (2001) classification scheme
introducing an empirical line to divide
pure star-forming galaxies from AGN-HII composite objects (also called ``transition objects''),
which may have a significant contribution from both AGN and star formation
(see also Stasinska et al. 2006).
The optical spectra of composite objects may be produced by either
1) a combination of star formation and a Seyfert nucleus, or 2) a combination of star formation
and LINER emission (Kewley et al. 2006).
diagnostic diagram (Baldwin, Phillips and Terlevich (1981; hereafter BPT).
Using a combination of stellar population synthesis models and photoionization models,
Kewley et al. (2001) identified a ``maximum starburst line'' in the BPT diagram.
Galaxies lying above this line are likely to be dominated by an AGN.
Kauffmann et al. (2003) later revised the Kewley et al. (2001) classification scheme
introducing an empirical line to divide
pure star-forming galaxies from AGN-HII composite objects (also called ``transition objects''),
which may have a significant contribution from both AGN and star formation
(see also Stasinska et al. 2006).
The optical spectra of composite objects may be produced by either
1) a combination of star formation and a Seyfert nucleus, or 2) a combination of star formation
and LINER emission (Kewley et al. 2006).
From the distribution in the BPT diagram of the galaxies from the Sloan Digital Sky Survey,
Kewley et al. (2006) introduced an empirical horizontal line to separate ``Seyfert'' and LINERs.
Even though LINERs exhibit [NII]/ H![]() ratios higher than the star-forming galaxies, indicating a harder ionization continuum,
it remains debated wether they are powered by active galactic nuclei or not (see Sect. 1).
ratios higher than the star-forming galaxies, indicating a harder ionization continuum,
it remains debated wether they are powered by active galactic nuclei or not (see Sect. 1).
The BPT diagram for the R05+A06 sample is shown in Fig. 6.
The [NII]![]() 6584/ H
6584/ H![]() line ratio was preferred to the
[SII](
line ratio was preferred to the
[SII](![]() 6717 +
6717 + ![]() 6731)/ H
6731)/ H![]() and
[OI]
and
[OI]![]() 6300/ H
6300/ H![]() ratios because
of the larger signal-to-noise ratio of the [NII] line in our spectra.
Emission-line ratios were corrected for extinction adopting the E(B-V) values
derived in Sect. 3.2 and reported in Col. 3 of Table 2, even though the BPT
diagram is almost insensitive to reddening.
The galaxies with negative reddening, or reddening lower than the foreground value, were
corrected by adopting the Galactic foreground reddening from NED.
ratios because
of the larger signal-to-noise ratio of the [NII] line in our spectra.
Emission-line ratios were corrected for extinction adopting the E(B-V) values
derived in Sect. 3.2 and reported in Col. 3 of Table 2, even though the BPT
diagram is almost insensitive to reddening.
The galaxies with negative reddening, or reddening lower than the foreground value, were
corrected by adopting the Galactic foreground reddening from NED.
According to their nuclear (
![]() )
emission, the majority of our galaxies are classified as LINERs.
A few galaxies (NGC 3258, NGC 4552, NGC 5193,
NGC 5328, NGC 6721, NGC 6876, and IC 2006) fall in
the region of ``composites'', and possibly contain a combined
contribution
from both star formation and AGN. The galaxies IC 5063,
NGC 777, NGC 3489, NGC 7007, and NGC 6958, fall in
the Seyfert region. Among them, only IC 5063 can be classified as
a bona fide Seyfert galaxy.
The others all have very large uncertainties in their [OIII]/ H
)
emission, the majority of our galaxies are classified as LINERs.
A few galaxies (NGC 3258, NGC 4552, NGC 5193,
NGC 5328, NGC 6721, NGC 6876, and IC 2006) fall in
the region of ``composites'', and possibly contain a combined
contribution
from both star formation and AGN. The galaxies IC 5063,
NGC 777, NGC 3489, NGC 7007, and NGC 6958, fall in
the Seyfert region. Among them, only IC 5063 can be classified as
a bona fide Seyfert galaxy.
The others all have very large uncertainties in their [OIII]/ H![]() ratios, due to their low H
ratios, due to their low H![]() emission (nuclear
EW < 0.3 Å), and are consistent with a LINER classification within the errors.
These galaxies also exhibit very large reddenings (
emission (nuclear
EW < 0.3 Å), and are consistent with a LINER classification within the errors.
These galaxies also exhibit very large reddenings (
![]() ).
In contrast, NGC 3136 and NGC 6776 are LINERs, but are consistent with being Seyferts within the errors.
Among the Seyferts, a spectral classification is provided in the literature only for
NGC 3489 (Ho et al. 1997b; Sarzi et al. 2006), NGC 777 (Ho et al. 1997b),
and NGC 6958 (Saraiva et al. 2001). These studies classify
the first two galaxies as Seyferts, and the last one as LINER.
).
In contrast, NGC 3136 and NGC 6776 are LINERs, but are consistent with being Seyferts within the errors.
Among the Seyferts, a spectral classification is provided in the literature only for
NGC 3489 (Ho et al. 1997b; Sarzi et al. 2006), NGC 777 (Ho et al. 1997b),
and NGC 6958 (Saraiva et al. 2001). These studies classify
the first two galaxies as Seyferts, and the last one as LINER.
The final spectral classification obtained from the nuclear (
![]() /16) lines is given in Col. 3 of Table 4.
/16) lines is given in Col. 3 of Table 4.
4.2 Gradients
We investigated how the distribution of the galaxies in the BPT diagram changes at annuli of increasing
galactocentric distance
(
![]() /16,
/16,
![]() /16
/16
![]() /8,
/8, ![]() /
/
![]() /4, and
/4, and ![]() /4
/4
![]() /2).
This emerges by comparing the four panels of Fig. 6.
Only a few galaxies have sufficiently high S/N ratios that allows us to
measure the emission line ratios in the most external annuli.
/2).
This emerges by comparing the four panels of Fig. 6.
Only a few galaxies have sufficiently high S/N ratios that allows us to
measure the emission line ratios in the most external annuli.
The clear result is that, from the center outwards, the bulk of the galaxies
moves left and down in the BPT diagram. An increasing number of galaxies move from
being LINERs to ``composite'' objects as the emission lines are measured at larger
galactocentric distances. This effect would probably not have been observed
by considering apertures instead of annuli,
since the central emission almost always predominates.
The effect is more accurately quantified in Fig. 7, where we plot
the distribution of the [NII]/H![]() and [OIII]/H
and [OIII]/H![]() ratios over the
central
ratios over the
central
![]() /16 values (C) for the different annuli.
The peak of the ([NII]/H
/16 values (C) for the different annuli.
The peak of the ([NII]/H![]() )/([NII]/H
)/([NII]/H![]() )C distribution
moves from 1 to values <1 at larger radii. The average ([NII]/H
)C distribution
moves from 1 to values <1 at larger radii. The average ([NII]/H![]() )/([NII]/H
)/([NII]/H![]() )Cvalues are
)Cvalues are ![]() 0.85, 0.73, and 0.69 at
0.85, 0.73, and 0.69 at
![]() /
/
![]() /8,
/8, ![]() /
/
![]() /4, and
/4, and ![]() /4
/4
![]() /2,
respectively. These correspond to horizontal shifts of
/2,
respectively. These correspond to horizontal shifts of ![]() -0.07,
-0.14, and -0.16 dex in the BPT diagram.
However, given the large errors in the emission-line measures in the
most external annulus, we consider this result significant only out to
-0.07,
-0.14, and -0.16 dex in the BPT diagram.
However, given the large errors in the emission-line measures in the
most external annulus, we consider this result significant only out to
![]() /4. The ([OIII]/H
/4. The ([OIII]/H![]() )/([OIII]/H
)/([OIII]/H![]() )C distribution is less peaked, in part also because of the large errors in the derived [OIII]/H
)C distribution is less peaked, in part also because of the large errors in the derived [OIII]/H![]() ratios. The average values are 0.92, 0.77, and 0.64, for the three annuli, corresponding to vertical shifts of
ratios. The average values are 0.92, 0.77, and 0.64, for the three annuli, corresponding to vertical shifts of ![]() -0.04,
-0.11, and -0.19 dex in the BPT diagram. However, given the
intrinsic faintness and large errors of the [OIII] and H
-0.04,
-0.11, and -0.19 dex in the BPT diagram. However, given the
intrinsic faintness and large errors of the [OIII] and H![]() lines compared to [NII] and H
lines compared to [NII] and H![]() ,
none of our conclusions will be based on the spatial behavior of the [OIII]/H
,
none of our conclusions will be based on the spatial behavior of the [OIII]/H![]() ratio.
ratio.
![\begin{figure}
\par\includegraphics[width=17cm]{13774fg6.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg115.png)
|
Figure 6:
Extinction-corrected BPT
diagnostic diagram for the galaxy sample in annuli of increasing galacto-centric distance
(
|
| Open with DEXTER | |
When the galaxies are inspected individually, we see that for the majority of
them the [NII]/H![]() ratio decreases monotonically with galactocentric distance.
The only exceptions are:
IC 5063, NGC 1521, NGC 3136, NGC 3489, NGC 5813, NGC 5898,
NGC 6721, NGC 6876, NGC 7135, and NGC 7192.
In all these galaxies, the [NII]/H
ratio decreases monotonically with galactocentric distance.
The only exceptions are:
IC 5063, NGC 1521, NGC 3136, NGC 3489, NGC 5813, NGC 5898,
NGC 6721, NGC 6876, NGC 7135, and NGC 7192.
In all these galaxies, the [NII]/H![]() ratio does not exhibit a clear trend.
In NGC 3489, the ratio increases from the center outwards.
The [NII]/H
ratio does not exhibit a clear trend.
In NGC 3489, the ratio increases from the center outwards.
The [NII]/H![]() ratio decreases very steeply in IC 1459, IC 4296,
NGC 3607, NGC 4374, NGC 4697, NGC 5090, and
NGC 5266.
We show in Fig. 8 the individual BPT diagrams in different annuli for some galaxies of the sample.
The [NII]/H
ratio decreases very steeply in IC 1459, IC 4296,
NGC 3607, NGC 4374, NGC 4697, NGC 5090, and
NGC 5266.
We show in Fig. 8 the individual BPT diagrams in different annuli for some galaxies of the sample.
The [NII]/H![]() and [OIII]/H
and [OIII]/H![]() ratios in the four annuli for the whole sample are shown in Appendix B.
ratios in the four annuli for the whole sample are shown in Appendix B.
Summarizing, the hardness of the ionizing continuum decreases with galactocentric distance.
4.3 Central correlations with galaxy properties
We investigated possible correlations between the emission-line properties and the galaxy properties. Our results are summarized in Fig. 9.
In the top panels of Fig. 9, we plotted the central (
![]() )
H
)
H![]() and [NII]
and [NII]![]() 6584 equivalent widths versus the central velocity dispersion
6584 equivalent widths versus the central velocity dispersion
![]() ,
the age, the metallicity, and
the
,
the age, the metallicity, and
the ![]() /Fe enhancement. The H
/Fe enhancement. The H![]() and [NII] EWs quantify the strength of the emission with respect
to the stellar continuum. However, the [NII] line is much less affected than the H
and [NII] EWs quantify the strength of the emission with respect
to the stellar continuum. However, the [NII] line is much less affected than the H![]() by uncertainties or systematics caused by the stellar continuum subtraction.
The scatter in both the H
by uncertainties or systematics caused by the stellar continuum subtraction.
The scatter in both the H![]() and [NII] EW increases with
and [NII] EW increases with
![]() .
This remains true if the
[OIII] emission is considered. If we exclude the Seyfert galaxy IC 5063, strong emission is observed only for galaxies with
.
This remains true if the
[OIII] emission is considered. If we exclude the Seyfert galaxy IC 5063, strong emission is observed only for galaxies with
![]() km s-1. The galaxies with the strongest emission tend to be fast rotators. All the low
km s-1. The galaxies with the strongest emission tend to be fast rotators. All the low
![]() galaxies are also fast rotators.
For the stellar population parameters, the trend is preserved only for the [NII] line versus
the [
galaxies are also fast rotators.
For the stellar population parameters, the trend is preserved only for the [NII] line versus
the [![]() /Fe] ratio (it is barely present in the H
/Fe] ratio (it is barely present in the H![]() versus [
versus [![]() /Fe] plane). We note that this trend could be driven by the contamination of the Mgb index by the [NI]
/Fe] plane). We note that this trend could be driven by the contamination of the Mgb index by the [NI]![]() 5199 line, which causes larger [
5199 line, which causes larger [![]() /Fe] values for galaxies with stronger emission (Goudfrooij & Emsellem 1996). The lack of a trend between the EW and metallicity is rather surprising in the light of the well know metallicity-
/Fe] values for galaxies with stronger emission (Goudfrooij & Emsellem 1996). The lack of a trend between the EW and metallicity is rather surprising in the light of the well know metallicity-![]() relation for ETGs.
relation for ETGs.
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg117.png)
|
Figure 7:
Distribution of emission line ratios over the central
|
| Open with DEXTER | |
In the third row panels of Fig. 9, we show the central (
![]() )
[NII]
)
[NII]![]() 5684/H
5684/H![]() ratio, which is a measure of the hardness of the ionizing spectrum.
When examining possible correlations between this emission line ratio
and the galaxy properties, we separated the sample into high emission
galaxies (H) and weak emission ones (W) (see Sect. 3.3 and
classification in Table 4). The determination of the H
ratio, which is a measure of the hardness of the ionizing spectrum.
When examining possible correlations between this emission line ratio
and the galaxy properties, we separated the sample into high emission
galaxies (H) and weak emission ones (W) (see Sect. 3.3 and
classification in Table 4). The determination of the H![]() emission may indeed be strongly affected by systematic errors in the
underlying continuum subtraction in the W galaxies. To investigate the
presence of correlations, it is thus safer to consider only the H
subsample.
The first panel in the third row shows that there is a positive
correlation between the central [NII]/H
emission may indeed be strongly affected by systematic errors in the
underlying continuum subtraction in the W galaxies. To investigate the
presence of correlations, it is thus safer to consider only the H
subsample.
The first panel in the third row shows that there is a positive
correlation between the central [NII]/H![]() and
and
![]() .
The Spearman correlation coefficient rs is 0.31 (with 36 data points),
implying that there is a 6% probability that the variables are not correlated
for a two-tailed test. However, if we restrict the analysis to the galaxies with
EW([NII]) >3, the probability that there is no correlation drops to 4%.
This result agrees with Phillips et al. (1986), who derived a positive trend between the
[NII]/ H
.
The Spearman correlation coefficient rs is 0.31 (with 36 data points),
implying that there is a 6% probability that the variables are not correlated
for a two-tailed test. However, if we restrict the analysis to the galaxies with
EW([NII]) >3, the probability that there is no correlation drops to 4%.
This result agrees with Phillips et al. (1986), who derived a positive trend between the
[NII]/ H![]() ratio and the galaxy absolute magnitude.
On the other hand, Spearman tests show that there is no strong correlation between [NII]/ H
ratio and the galaxy absolute magnitude.
On the other hand, Spearman tests show that there is no strong correlation between [NII]/ H![]() and either the age, the metallicity, or the
and either the age, the metallicity, or the ![]() /Fe enhancement of the galaxy stellar population.
/Fe enhancement of the galaxy stellar population.
In the fourth row panels of Fig. 9, we show the central
[OIII]/H![]() ratio, which is related to the ionization
parameter. No clear trend is observed with
ratio, which is related to the ionization
parameter. No clear trend is observed with
![]() ,
age, metallicity, and [
,
age, metallicity, and [![]() /Fe]. We note only that
the highest [OIII]/H
/Fe]. We note only that
the highest [OIII]/H![]() values are associated with the youngest galaxy ages.
values are associated with the youngest galaxy ages.
The relation between the nuclear emission spectral class (Seyfert,
LINERs, composite), and the stellar population properties is show in
Figs. 10 and 11. Seyfert galaxies tend to have ages younger than ![]() 4 Gyr.
``Composite'' galaxies have ages older than 5 Gyr. LINERs cover
the whole age range from a few Gyrs to a Hubble time.
For the three classes, the average ages are 3.8, 7.5, and
9 Gyr, respectively. The average metallicities are
4 Gyr.
``Composite'' galaxies have ages older than 5 Gyr. LINERs cover
the whole age range from a few Gyrs to a Hubble time.
For the three classes, the average ages are 3.8, 7.5, and
9 Gyr, respectively. The average metallicities are
![]() ,
0.29, and 0.22, respectively. No significant difference is observed in the [
,
0.29, and 0.22, respectively. No significant difference is observed in the [![]() /Fe] ratio.
/Fe] ratio.
It emerges that Seyferts tend to have luminosity-weighted ages significantly younger than LINERs, probably because of recent star formation episodes. The only caveat in this statement is that the only bona fide Seyfert in our sample (IC 5063), does not have an age determination.
5 Oxygen abundance
When the ionizing source is known, one can derive the element abundance of the warm gas. In their nuclear (
![]() )
region,
the majority of the galaxies in our sample are classified as LINERs, a
few are classified as ``composites'', and only IC 5063 is
classified as a bona fide Seyfert galaxy.
We also noticed a progressive increase in the fraction of
``composites'' with respect to pure LINERs moving from the galaxy
center to more external regions. As discussed in Sect. 1, the
ionizing mechanism in LINERs/composites is still far from being
understood.
For this reason, we derived the oxygen metallicity for the R05+A06
sample in the two extreme assumptions of 1) photoionization by hot
stars; and 2) AGN excitation.
A calibration in the case of shock heating is not provided in the
literature.
)
region,
the majority of the galaxies in our sample are classified as LINERs, a
few are classified as ``composites'', and only IC 5063 is
classified as a bona fide Seyfert galaxy.
We also noticed a progressive increase in the fraction of
``composites'' with respect to pure LINERs moving from the galaxy
center to more external regions. As discussed in Sect. 1, the
ionizing mechanism in LINERs/composites is still far from being
understood.
For this reason, we derived the oxygen metallicity for the R05+A06
sample in the two extreme assumptions of 1) photoionization by hot
stars; and 2) AGN excitation.
A calibration in the case of shock heating is not provided in the
literature.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13774fg8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg119.png)
|
Figure 8:
BPT diagrams of some galaxies representing the general trends of the whole sample in the four annuli:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13774fg9.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg120.png)
|
Figure 9:
H |
| Open with DEXTER | |
| Figure 10:
Age, metallicity, and [ |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13774fg11.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg122.png)
|
Figure 11: BPT diagnostic diagram for Seyfert galaxies ( left panel), ``composites'' ( center), and LINERs ( right panel). The data were color-coded according to the galaxy age as derived in Paper III: blue stars are for ages younger than 4 Gyr, green squares for ages between 4 and 8 Gyr, and red circles for ages older than 8 Gyr. |
| Open with DEXTER | |
Table 4:
Classification from optical lines in the nuclear (
![]() /16) region.
/16) region.
Table 5:
Electron densities ![]() derived from [SII]6716/6731 assuming T=10 000 K.
derived from [SII]6716/6731 assuming T=10 000 K.
5.1 HII region calibration
In HII regions, the oxygen metallicity is determined by means of the standard
![]() parametrization, first introduced by Pagel et al. (1979), and then revised by other authors
(Edmund & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; McGaugh 1991; Zaritsky et al. 1994).
The main problem with this calibration is that the relationship between R23 and
the oxygen abundance is double valued, requiring some a priori knowledge of a galaxy's
metallicity to determine its correct location in the upper or lower branch of the curve. A good discriminator is the [OIII]
parametrization, first introduced by Pagel et al. (1979), and then revised by other authors
(Edmund & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; McGaugh 1991; Zaritsky et al. 1994).
The main problem with this calibration is that the relationship between R23 and
the oxygen abundance is double valued, requiring some a priori knowledge of a galaxy's
metallicity to determine its correct location in the upper or lower branch of the curve. A good discriminator is the [OIII]![]() 5007/ [NII]
5007/ [NII]![]() 6584 ratio, which is usually less then
6584 ratio, which is usually less then ![]() 100 for galaxies with
100 for galaxies with ![]() (O/H) > 8.3, on the metal-rich branch
(Edmunds & Pagel 1984; Kobulnicky et al. 1999). The various calibrations, based on different photoionization models and HII region data, show a dispersion of
(O/H) > 8.3, on the metal-rich branch
(Edmunds & Pagel 1984; Kobulnicky et al. 1999). The various calibrations, based on different photoionization models and HII region data, show a dispersion of ![]() 0.2 dex in the metal-rich branch. Kobulnicky et al. (1999)
report analytic expressions based on a set of photoionization models
that fit the empirical calibrations within less than 0.05 dex, and
that include the effect of the ionization parameter through
0.2 dex in the metal-rich branch. Kobulnicky et al. (1999)
report analytic expressions based on a set of photoionization models
that fit the empirical calibrations within less than 0.05 dex, and
that include the effect of the ionization parameter through
![]() .
.
We computed the oxygen abundance for our sample adopting the calibration in Kobulnicky et al. (1999,
hereafter Kob99). Because of the lack of star-forming regions in ETGs,
this calibration is valid if: 1) the gas is photoionized by hot old
stars, probably PAGB stars; and 2) the calibration is still valid
even though PAGB stars have different spectral shapes than high-mass
main sequence stars. The same approach was adopted by Athey &
Bregman (2009) to determine
oxygen abundances in a sample of 7 ETGs.
We computed the R23 and O32 values using the emission line fluxes in
Table 2, and correcting for reddening using the values in Col 3 of Table 2.
The derived oxygen metallicities at
![]() /16 are given in Col. 2 of Table 6. The errors were computed by combining the intrinsic uncertainty in the calibration (
/16 are given in Col. 2 of Table 6. The errors were computed by combining the intrinsic uncertainty in the calibration (![]() 0.15 dex, see Kob99),
with the uncertainty in the emission line fluxes.
We could not determine the oxygen abundance in 13 galaxies,
namely IC 5063, NGC 777, NGC 1297, NGC 1521,
NGC 1947, NGC 2749 , NGC 3136, NGC 3489, NGC 3557, NGC 5011,
NGC 6776, NGC 6958, and NGC 7007, since R23 is larger than 10, and falls outside the valid calibration range for HII regions.
0.15 dex, see Kob99),
with the uncertainty in the emission line fluxes.
We could not determine the oxygen abundance in 13 galaxies,
namely IC 5063, NGC 777, NGC 1297, NGC 1521,
NGC 1947, NGC 2749 , NGC 3136, NGC 3489, NGC 3557, NGC 5011,
NGC 6776, NGC 6958, and NGC 7007, since R23 is larger than 10, and falls outside the valid calibration range for HII regions.
Table 6: [O/H] values obtained with the Kobulnicky et al. (1999) calibration (Kob99), and the Storchi-Bergmann et al. (1998) calibration (SB98).
There are 6 galaxies in common with the sample of
Athey and Bregman (2009): NGC 3489, NGC 3607, NGC 4374, NGC 4636, NGC 5044,
and NGC 5846.
Excluding NGC 3489, we derived for the other galaxies
central
![]() values of
values of
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
For the same galaxies, they derived
.
For the same galaxies, they derived
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
With the exception of NGC 3607, our and their results are in agreement
within the errors.
.
With the exception of NGC 3607, our and their results are in agreement
within the errors.
The oxygen metallicity distribution is shown in the top panel of Fig. 13.
The
![]() values were computed adopting a solar abundance of
values were computed adopting a solar abundance of
![]() from Caffau et al. (2008).
The average metallicity is
from Caffau et al. (2008).
The average metallicity is
![]() .
Some values are as low as
.
Some values are as low as
![]() 0.25 times solar, while the highest derived metallicity is
0.25 times solar, while the highest derived metallicity is ![]() twice solar.
twice solar.
5.2 AGN calibration
Storchi-Bergmann et al. (1998) (hereafter SB98) derived oxygen metallicity calibrations
from a grid of models assuming photoionization by a typical AGN continuum
(the segmented power law of Mathews & Ferland 1987).
The first calibration (hereafter SB1) is in terms of
[OIII]
![]() 4959,5007/H
4959,5007/H![]() and [NII]
and [NII]
![]() 6548,6584/H
6548,6584/H![]() (Eq. (2) in SB98), while the second calibration (hereafter SB2) is in terms of [OII]
(Eq. (2) in SB98), while the second calibration (hereafter SB2) is in terms of [OII]![]() 3727/ [OIII]
3727/ [OIII]![]() 4959,5007 and [NII]
4959,5007 and [NII]
![]() 6548,6584/H
6548,6584/H![]() (Eq. (3) in SB98). The fitted calibrations are within
(Eq. (3) in SB98). The fitted calibrations are within ![]() 0.05 dex of the models. The models were computed assuming a gas density
0.05 dex of the models. The models were computed assuming a gas density
![]() cm-3.
The correction required because of deviations from this density is
cm-3.
The correction required because of deviations from this density is
![]() ,
valid for 100 cm
,
valid for 100 cm
![]() cm-3.
cm-3.
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg12.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg146.png)
|
Figure 12:
Oxygen abundance at
|
| Open with DEXTER | |
We derived oxygen metallicities for the R05+A06 sample using both SB1 and SB2. The electron densities ![]() were calculated from the [SII]
were calculated from the [SII]
![]() 6717, 31 line ratios
using the temden task within IRAF/STSDAS (Shaw & Dufour 1995), and assuming an electronic temperature
6717, 31 line ratios
using the temden task within IRAF/STSDAS (Shaw & Dufour 1995), and assuming an electronic temperature
![]() K.
This was possible only for some galaxies in our sample (see Table 5),
because the quality of our spectra is significantly poorer redward of
K.
This was possible only for some galaxies in our sample (see Table 5),
because the quality of our spectra is significantly poorer redward of ![]() 6600 Å, and telluric absorption lines around 6800 Å prevent in many cases a reliable
fit to the [SII] doublet. The derived electron densities are given in Table 5. As evident from the [SII] fluxes given in Table 2, both increasing and decreasing density profiles are present within our sample.
The oxygen metallicities were then corrected for the density dependence assuming
6600 Å, and telluric absorption lines around 6800 Å prevent in many cases a reliable
fit to the [SII] doublet. The derived electron densities are given in Table 5. As evident from the [SII] fluxes given in Table 2, both increasing and decreasing density profiles are present within our sample.
The oxygen metallicities were then corrected for the density dependence assuming
![]() .
Because of the limited range of validity for the density correction, we discarded the galaxies with
.
Because of the limited range of validity for the density correction, we discarded the galaxies with
![]() cm-3.
The [O/H] values obtained with SB1 and SB2 are compared in Fig. 12.
The metallicities obtained with SB2 are on average
cm-3.
The [O/H] values obtained with SB1 and SB2 are compared in Fig. 12.
The metallicities obtained with SB2 are on average ![]() 0.09 dex higher than those obtained with SB1, in agreement with SB98 who derived a shift of
0.09 dex higher than those obtained with SB1, in agreement with SB98 who derived a shift of ![]() 0.11 dex
between the two calibrations. The final metallicities are computed to
be the average between the two values. The results are given in
Col. 3 of Table 6.
0.11 dex
between the two calibrations. The final metallicities are computed to
be the average between the two values. The results are given in
Col. 3 of Table 6.
![\begin{figure}
\par\includegraphics[width=8.8cm]{13774fg13.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg151.png)
|
Figure 13:
Top panel: oxygen abundance distributions (
|
| Open with DEXTER | |
We compare the results obtained with the Kob99 and with the SB98 calibrations in Fig. 13. The SB98 calibration provides an average oxygen
abundance ![]() 0.04 dex higher than that obtained with Kob99.
In addition, Kob99 infers a broader metallicity range than SB98.
0.04 dex higher than that obtained with Kob99.
In addition, Kob99 infers a broader metallicity range than SB98.
5.3 Abundance gradients
We studied the behavior of the oxygen metallicity as function of galactocentric distance.
The [O/H] distributions obtained with Kob99 and SB98 in the three more internal annuli (
![]() /16,
/16, ![]() /16
/16
![]() /8,
/8, ![]() /
/
![]() /4)
are shown in Fig. 14. The samples are not very large
because of the increased difficulty in measuring the emission lines in the more external annuli.
Emission lines are too faint to allow a reliable abundance measurement in
the more external annulus (
/4)
are shown in Fig. 14. The samples are not very large
because of the increased difficulty in measuring the emission lines in the more external annuli.
Emission lines are too faint to allow a reliable abundance measurement in
the more external annulus (![]() /
/
![]() /2).
The results obtained with the Kob99 and SB98 calibrations are
inconsistent:
in the first case, the oxygen metallicity tends to increase from the
galaxy center outwards. In the second case, the opposite behavior is
observed. The latter trend is more consistent with the negative
metallicity gradients of the stellar populations.
/2).
The results obtained with the Kob99 and SB98 calibrations are
inconsistent:
in the first case, the oxygen metallicity tends to increase from the
galaxy center outwards. In the second case, the opposite behavior is
observed. The latter trend is more consistent with the negative
metallicity gradients of the stellar populations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13774fg14.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg152.png)
|
Figure 14:
Oxygen abundance distributions in the three more internal annuli (
|
| Open with DEXTER | |
5.4 Comparison with stellar metallicities
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg15.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg153.png)
|
Figure 15:
Nebular oxygen abundance versus star oxygen abundance. The latter was derived from the Z and [ |
| Open with DEXTER | |
To understand the origin of the warm gas in ETGs, it is important
to compare the nebular metallicities with those of the stellar populations.
We already derived the (total) stellar metallicities (Z) and the [![]() /Fe] ratios for the R05+A06 sample using the Lick indices in Paper III.
The comparison with the nebular metallicities is not straightforward,
since the emission lines provide a direct measure of the oxygen abundance, while the Lick indices
depend on a mixture of different elements.
In this paper, we compute the oxygen stellar metallicities from
the Z and [
/Fe] ratios for the R05+A06 sample using the Lick indices in Paper III.
The comparison with the nebular metallicities is not straightforward,
since the emission lines provide a direct measure of the oxygen abundance, while the Lick indices
depend on a mixture of different elements.
In this paper, we compute the oxygen stellar metallicities from
the Z and [![]() /Fe] values derived in Paper III, assuming
that O belongs to the
/Fe] values derived in Paper III, assuming
that O belongs to the ![]() -enhanced group
(Ne, Na, Mg, Si, S, Ca, Ti, and also N).
The comparison between gas and stellar metallicities is shown in Fig. 15.
The clear result is that, irrespective of the adopted calibration
(Kob99 or SB98), the gas metallicity tends to be lower than
the stellar metallicity. The effect is more severe for the galaxies
with the highest stellar metallicities. A Spearman test shows that in
both cases the stellar and gas metallicities are poorly correlated.
-enhanced group
(Ne, Na, Mg, Si, S, Ca, Ti, and also N).
The comparison between gas and stellar metallicities is shown in Fig. 15.
The clear result is that, irrespective of the adopted calibration
(Kob99 or SB98), the gas metallicity tends to be lower than
the stellar metallicity. The effect is more severe for the galaxies
with the highest stellar metallicities. A Spearman test shows that in
both cases the stellar and gas metallicities are poorly correlated.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg16.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg154.png)
|
Figure 16:
Oxygen abundances derived with the Kob99 ( top)
and SB98 ( bottom) calibration
at
|
| Open with DEXTER | |
We plot the central (
![]() /16) nebular metallicities obtained with Kob99 and SB98
versus the galaxy stellar velocity dispersions
in Fig. 16.
Linear square fits provide an increasing trend of
/16) nebular metallicities obtained with Kob99 and SB98
versus the galaxy stellar velocity dispersions
in Fig. 16.
Linear square fits provide an increasing trend of
![]() with
with
![]() in both cases.
However, the Spearman correlation coefficients are low (
rs = 0.25 with N=39 degrees of freedom
for Kob99, top panel, and
rs = 0.08 with N=22 degrees of freedom for SB98, bottom panel),
indicating that the correlations are weak.
For comparison, we plot in Fig. 16 the stellar metallicity-
in both cases.
However, the Spearman correlation coefficients are low (
rs = 0.25 with N=39 degrees of freedom
for Kob99, top panel, and
rs = 0.08 with N=22 degrees of freedom for SB98, bottom panel),
indicating that the correlations are weak.
For comparison, we plot in Fig. 16 the stellar metallicity-
![]() relations derived by ourselves in Paper III (A07) and by Thomas et al. (2005) for low density environment ETGs. The A07 relation was appropriately rescaled to account for the solar
metallicity adopted in this paper
relations derived by ourselves in Paper III (A07) and by Thomas et al. (2005) for low density environment ETGs. The A07 relation was appropriately rescaled to account for the solar
metallicity adopted in this paper![]() .
In Fig. 16, the fits provide
.
In Fig. 16, the fits provide
![]() and
and
![]() at
at
![]() km s-1 for Kob99 and SB98, respectively.
For comparison, the A07 relation gives a stellar metallicity of
km s-1 for Kob99 and SB98, respectively.
For comparison, the A07 relation gives a stellar metallicity of ![]() 0.18 dex at the same
0.18 dex at the same ![]() ,
i.e., 0.26 dex and 0.21 dex higher than those obtained for the warm gas with Kob99 and SB98,
respectively.
The discrepancy is even larger if we consider the Thomas et al. (2005) relation, which provides a metallicity of 0.34 dex at
,
i.e., 0.26 dex and 0.21 dex higher than those obtained for the warm gas with Kob99 and SB98,
respectively.
The discrepancy is even larger if we consider the Thomas et al. (2005) relation, which provides a metallicity of 0.34 dex at
![]() km s-1,
i.e.
km s-1,
i.e. ![]() 0.4 dex higher than the nebular metallicity.
We notice that the discrepancy between gas and stars persists (and is even more significant)
if we consider only the strong emission-line (H) galaxies (see classification in Table 4).
0.4 dex higher than the nebular metallicity.
We notice that the discrepancy between gas and stars persists (and is even more significant)
if we consider only the strong emission-line (H) galaxies (see classification in Table 4).
6 Comparison with models
The ionizing source in LINERs remains poorly understood. Among the proposed mechanisms, we recall sub-Eddington accretion onto a supermassive black hole (e.g., Ho 1999b; Kewley et al. 2006; Ho 2009a), photoionization by old PAGB stars (e.g. Trinchieri & di Serego Alighieri 1991; Binette et al. 1994; Stasinska et al. 2008), and fast shocks (Koski & Osterbrock 1976; Heckman 1980; Dopita & Sutherland 1995; Allen et al. 2008).
The first hypothesis is strongly supported by our current knowledge of the demography of central
BHs based on direct dynamical searches (Magorrian et al. 1998; Ho 1999a; Kormendy 2004), according to which massive BHs appear to be a generic component of galaxies with a bulge.
As shown by Ho et al. (1997c), local stellar mass loss can supply the fuel necessary for accretion rates of
![]() .
Thus, radiatively inefficient accretion flows onto a central BH
(see Quataert 2001 for a review) provide an attractive solution for explaining the origin of LINERs.
Additional evidence of AGN activity come from X-ray and radio observations,
which have detected compact nuclear X-ray and radio
sources, sometimes exhibiting variability, in a significant fraction of LINERs
(see e.g. Terashima 1999; Flohic et al. 2006; Filho et al. 2006;
Gonzalez-Martin et al. 2009; Pian et al. 2010).
On the other hand, some LINERs lack evidence of a central AGN, leaving space for
alternative explanations of the observed emission lines.
X-ray and radio studies are available in the literature for a few galaxies in our sample.
Compact nuclear X-ray and/or radio sources have been detected in
IC 5063 (Koyama et al. 1992), NGC 777 (Ho & Ulvestad 2001), NGC 1052, NGC 4374, IC 1459 (Gonzalez-Martin et al. 2009), NGC 5363 (Gonzalez-Martin et al. 2009;
Filho et al. 2006), NGC 1553 (Blanton et al. 2001),
NGC 3557 (Balmaverde et al. 2006), NGC 5090 (Grützbauch et al. 2007),
IC 4296 (Pellegrini et al. 2003), NGC 5077, (Filho et al. 2006), and NGC 4552 (Nagar et al. 2002; Filho et al. 2004). Other galaxies observed in X-ray and/or radio lack evidence of AGN activity:
NGC 3607, NGC 4636, NGC 5813, (Gonzalez-Martin et al. 2009; Filho et al. 2006),
NGC 4696, NGC 5846 (Gonzalez-Martin et al. 2009), and NGC 6876 (Machacek et al. 2005).
High quality X-ray imaging of NGC 4636 revealed the signature of
shocks, probably driven by energy deposited off-center by jets (Jones et al. 2002; Baldi et al. 2009).
.
Thus, radiatively inefficient accretion flows onto a central BH
(see Quataert 2001 for a review) provide an attractive solution for explaining the origin of LINERs.
Additional evidence of AGN activity come from X-ray and radio observations,
which have detected compact nuclear X-ray and radio
sources, sometimes exhibiting variability, in a significant fraction of LINERs
(see e.g. Terashima 1999; Flohic et al. 2006; Filho et al. 2006;
Gonzalez-Martin et al. 2009; Pian et al. 2010).
On the other hand, some LINERs lack evidence of a central AGN, leaving space for
alternative explanations of the observed emission lines.
X-ray and radio studies are available in the literature for a few galaxies in our sample.
Compact nuclear X-ray and/or radio sources have been detected in
IC 5063 (Koyama et al. 1992), NGC 777 (Ho & Ulvestad 2001), NGC 1052, NGC 4374, IC 1459 (Gonzalez-Martin et al. 2009), NGC 5363 (Gonzalez-Martin et al. 2009;
Filho et al. 2006), NGC 1553 (Blanton et al. 2001),
NGC 3557 (Balmaverde et al. 2006), NGC 5090 (Grützbauch et al. 2007),
IC 4296 (Pellegrini et al. 2003), NGC 5077, (Filho et al. 2006), and NGC 4552 (Nagar et al. 2002; Filho et al. 2004). Other galaxies observed in X-ray and/or radio lack evidence of AGN activity:
NGC 3607, NGC 4636, NGC 5813, (Gonzalez-Martin et al. 2009; Filho et al. 2006),
NGC 4696, NGC 5846 (Gonzalez-Martin et al. 2009), and NGC 6876 (Machacek et al. 2005).
High quality X-ray imaging of NGC 4636 revealed the signature of
shocks, probably driven by energy deposited off-center by jets (Jones et al. 2002; Baldi et al. 2009).
Shock heating was initially proposed as a viable excitation mechanism to solve the so-called ``temperature problem'' of Seyferts and LINERs, in which the electron temperatures observed were found to be systematically higher than predicted by photoionization models. Koski & Osterbrock (1976) and Fosbury et al. (1978) argued that shocks are essential for explaining the observed [OIII] line ratios of the prototypical LINER NGC 1052. Dopita & Sutherland (1995) and Allen et al. (2008) presented extensive grids of high velocity shock models, and showed that the emission line ratios observed in LINERs can be modeled in terms of fast shocks (150-500 km s-1) in a relatively gas poor environment.
The findings that the emission-line flux correlates with the host galaxy stellar luminosity
within the emission-line region (Macchetto et al. 1996), and that the line flux distribution
closely follows that of the stellar continuum (Sarzi et al. 2006,2009),
have been presented as evidences in support of the PAGB scenario. These
results suggest that the sources of ionizing photons are distributed in
the same way as the stellar population.
Sarzi et al. (2009) tried to model the H![]() EW spatial distribution based on the assumption that the ionizing photons originate in an underlying old stellar population.
They showed that to obtain an almost constant EW it is necessary to assume that the gas radial profile
decreases more gently than the ionizing radiation, or alternatively that the ionizing photons are more concentrated
than the bulk of the stellar populations. The presence of negative metallicity gradients in ETGs
(e.g., Annibali et al. 2007) may explain this effect, because in general the ionizing
flux from old populations is stronger for higher metallicities.
The Stasinska et al. (2008) models are able to reproduce the emission line ratios
of LINERs provided that the ionization parameter is sufficiently high (
EW spatial distribution based on the assumption that the ionizing photons originate in an underlying old stellar population.
They showed that to obtain an almost constant EW it is necessary to assume that the gas radial profile
decreases more gently than the ionizing radiation, or alternatively that the ionizing photons are more concentrated
than the bulk of the stellar populations. The presence of negative metallicity gradients in ETGs
(e.g., Annibali et al. 2007) may explain this effect, because in general the ionizing
flux from old populations is stronger for higher metallicities.
The Stasinska et al. (2008) models are able to reproduce the emission line ratios
of LINERs provided that the ionization parameter is sufficiently high (
![]() ). Binette et al. (1994) and Cid Fernandes et al. (2009) demonstrated that photoionization
by PAGB stars can only explain LINERs with relatively weak emission lines.
Binette et al. (1994) estimated that the H
). Binette et al. (1994) and Cid Fernandes et al. (2009) demonstrated that photoionization
by PAGB stars can only explain LINERs with relatively weak emission lines.
Binette et al. (1994) estimated that the H![]() equivalent width produced by a 8 Gyr old and a 13 Gyr old
simple stellar populations is 0.6 Å and 1.7 Å, respectively.
Stronger emission lines require far more ionizing photons than old
stars can provide.
equivalent width produced by a 8 Gyr old and a 13 Gyr old
simple stellar populations is 0.6 Å and 1.7 Å, respectively.
Stronger emission lines require far more ionizing photons than old
stars can provide.
A first-order test of the validity of the PAGB scenario consists of a comparison
of the observed and predicted EWs. Following the computations of Binette et al. (1994), we
assume that photoionization by old stars produce a typical emission of 1 Å in H![]() .
Comparing this value with our measured central (
.
Comparing this value with our measured central (
![]() )
EWs, we find that
PAGB photoionization alone can explain the observed nuclear emission
in only 11 out of the 49 galaxies classified as LINERs/composites in our sample (i.e. in
)
EWs, we find that
PAGB photoionization alone can explain the observed nuclear emission
in only 11 out of the 49 galaxies classified as LINERs/composites in our sample (i.e. in ![]() 22% of the LINERs/Comp sample).
This implies that, for the majority of the cases, some mechanism other than PAGB stars must operate
in the central regions of LINERs.
On the other hand, as we progressively move toward larger radii, an increasing number of LINERs enter the EW(H
22% of the LINERs/Comp sample).
This implies that, for the majority of the cases, some mechanism other than PAGB stars must operate
in the central regions of LINERs.
On the other hand, as we progressively move toward larger radii, an increasing number of LINERs enter the EW(H
![]() Å transition
region, where the emission strength is compatible with photoionization
by PAGB stars alone. Thus, while our computations exclude PAGB
stars playing a significant role in the central galaxy regions, we
cannot exclude them from being an important excitation source at larger
radii. Interestingly, Sarzi et al. (2009)
quote a 3'' radius for the maximum extent of central activity, which
for their sample galaxies corresponds on average to 0.11
Å transition
region, where the emission strength is compatible with photoionization
by PAGB stars alone. Thus, while our computations exclude PAGB
stars playing a significant role in the central galaxy regions, we
cannot exclude them from being an important excitation source at larger
radii. Interestingly, Sarzi et al. (2009)
quote a 3'' radius for the maximum extent of central activity, which
for their sample galaxies corresponds on average to 0.11 ![]() .
.
One of the arguments presented in support of the PAGB photoionization scenario is that
the emission flux closely follows the stellar continuum.
In disagreement with other results (e.g. Sarzi et al. 2009), we have shown in Sect. 3.3 that the
EW (emission flux over continuum flux) decreases with radius.
Is this incompatible with the PAGB scenario? Answering this question is not straightforward.
First of all, we have shown that the strongest decrease in EW occurs from the nuclear to the second (![]() /
/
![]() /8)
annulus, the decrease with radius being much gentler at larger radii.
Unfortunately, our data lack the depth necessary to reliably trace the
emission strength beyond
/8)
annulus, the decrease with radius being much gentler at larger radii.
Unfortunately, our data lack the depth necessary to reliably trace the
emission strength beyond
![]() .
Second, a well established decreasing trend in EW would not be per se
incompatible with the PAGB scenario: because of the presence of
age/metallicity gradients in the stellar population, the ratio of the
ionizing flux to the optical continuum is not necessarily constant. A
reliable radial prediction of the ionizing photon budget stems from a
detailed analysis of the combined effect of age and metallicity on the
PAGB population, which is beyond the aims of this paper.
.
Second, a well established decreasing trend in EW would not be per se
incompatible with the PAGB scenario: because of the presence of
age/metallicity gradients in the stellar population, the ratio of the
ionizing flux to the optical continuum is not necessarily constant. A
reliable radial prediction of the ionizing photon budget stems from a
detailed analysis of the combined effect of age and metallicity on the
PAGB population, which is beyond the aims of this paper.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13774fg17.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg166.png)
|
Figure 17:
BPT diagram for our galaxies at
|
| Open with DEXTER | |
Since the nuclear emission requires a different mechanism from PAGB photoionization, we compare in Fig. 17 our (
![]() /16) data, corrected for reddening, with the dusty AGN models of Groves et al. (2004), and the fast shock models
of Allen et al. (2008).
Among the data points, we identify objects with compact nuclear
X-ray and/or radio source detections, probably hosting an AGN, and objects with equivalent width in H
/16) data, corrected for reddening, with the dusty AGN models of Groves et al. (2004), and the fast shock models
of Allen et al. (2008).
Among the data points, we identify objects with compact nuclear
X-ray and/or radio source detections, probably hosting an AGN, and objects with equivalent width in H
![]() Å
, compatible with sole ionization from PAGBs. We note that three
galaxies (NGC 777, NGC 4552, and NGC 3557) exhibit AGN
activity in X ray or radio observations, and at the same time have
EW(H
Å
, compatible with sole ionization from PAGBs. We note that three
galaxies (NGC 777, NGC 4552, and NGC 3557) exhibit AGN
activity in X ray or radio observations, and at the same time have
EW(H
![]() .
Comparing dusty models with reddening-corrected data is not completely self-consistent;
however, the effect of extinction in the BPT diagram is negligible.
.
Comparing dusty models with reddening-corrected data is not completely self-consistent;
however, the effect of extinction in the BPT diagram is negligible.
Both the AGN and shock models were developed using the code MAPPINGS III (Dopita et al. 1982; Sutherland & Dopita 1993), implemented with dust and radiation pressure (Groves et al. 2004).
The AGN models were developed for different metallicities,
and assuming a power law with slope ![]() between -1.2 and -2.0 for the ionizing spectrum.
For the AGN models in Fig. 17,
between -1.2 and -2.0 for the ionizing spectrum.
For the AGN models in Fig. 17,
![]() ,
,
![]() and 2
and 2 ![]() ,
,
![]() cm-3, and
cm-3, and ![]() between -4 and 0. LINERs and Seyferts are both explainable with being AGNs, provided that the former
have much lower ionization parameters than the latter.
According to these models,
the galaxies in our sample should have gas metallicities much above solar. This disagrees
with the oxygen metallicities derived in Sect. 5 with the Storchi-Bergmann et al. (1998) calibration. The discrepancy arises from the use of a power law in the Groves et al. (2004) models
compared to the typical AGN continuum of Mathews & Ferland (1987) adopted by SB98. Indeed, SB98 noticed that models obtained with power-law ionizing continua yield systematically higher
(up to 0.5 dex) metallicities than models that adopt a typical AGN continuum.
between -4 and 0. LINERs and Seyferts are both explainable with being AGNs, provided that the former
have much lower ionization parameters than the latter.
According to these models,
the galaxies in our sample should have gas metallicities much above solar. This disagrees
with the oxygen metallicities derived in Sect. 5 with the Storchi-Bergmann et al. (1998) calibration. The discrepancy arises from the use of a power law in the Groves et al. (2004) models
compared to the typical AGN continuum of Mathews & Ferland (1987) adopted by SB98. Indeed, SB98 noticed that models obtained with power-law ionizing continua yield systematically higher
(up to 0.5 dex) metallicities than models that adopt a typical AGN continuum.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13774fg18.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg173.png)
|
Figure 18:
Distribution of
|
| Open with DEXTER | |
Based on the assumption that all the central LINERs activity is powered by a sub-Eddington accretion AGN,
we can determine the accretion rate from the
![]() ratio (where
ratio (where
![]() is the extinction-corrected [OIII] luminosity), which is proportional to
is the extinction-corrected [OIII] luminosity), which is proportional to
![]() (Heckman et al. 2004).
The result is shown in Fig. 18.
The accretion rate increases systematically along the sequence composite
(Heckman et al. 2004).
The result is shown in Fig. 18.
The accretion rate increases systematically along the sequence composite
![]() LINERs
LINERs
![]() Seyferts (left panel) in agreement with the findings of Ho (2009a).
Galaxies with compact nuclear X-ray/ radio sources, likely hosting an AGN, also tend to have
higher accretion rates than non-AGN galaxies (right panel).
We note that since
Seyferts (left panel) in agreement with the findings of Ho (2009a).
Galaxies with compact nuclear X-ray/ radio sources, likely hosting an AGN, also tend to have
higher accretion rates than non-AGN galaxies (right panel).
We note that since
![]() ,
and
,
and
![]() in the sub-Eddington accretion regime,
the AGN luminosity can vary significantly for a fixed
in the sub-Eddington accretion regime,
the AGN luminosity can vary significantly for a fixed ![]() depending on the accretion
depending on the accretion ![]() .
This implies that it is necessary to assume a maximum, sub-Eddington,
accretion rate to reproduce the observed trend between the emission
strength and
.
This implies that it is necessary to assume a maximum, sub-Eddington,
accretion rate to reproduce the observed trend between the emission
strength and ![]() .
.
The Allen et al. (2008) shock models are dust free, and were computed for different chemical abundances, pre-shock densities n from 0.01 to 1000 cm-3, velocities up to 1000 km s-1,
and magnetic parameters B/n1/2 from 10-4 to 10 ![]() G cm3/2, where B is the
pre-shock transverse magnetic field.
In Fig. 17, we plot the models with solar metallicity and B =1.
With these parameters, the bulk of LINERs in our sample is well reproduced by pre-shock densities
n=0.01-10 cm-3, and shock velocities
v=200-500 km s-1. Using a stronger magnetic field implies higher densities for our sample. For instance, for
G cm3/2, where B is the
pre-shock transverse magnetic field.
In Fig. 17, we plot the models with solar metallicity and B =1.
With these parameters, the bulk of LINERs in our sample is well reproduced by pre-shock densities
n=0.01-10 cm-3, and shock velocities
v=200-500 km s-1. Using a stronger magnetic field implies higher densities for our sample. For instance, for
![]() G, our data
are consistent with pre-shock densities as high as
G, our data
are consistent with pre-shock densities as high as
![]() cm-3. This range in B is typical of the ISM (e.g., Rand & Kulkarni 1989).
cm-3. This range in B is typical of the ISM (e.g., Rand & Kulkarni 1989).
Are these densities consistent with those derived from the observed [SII](6717)/[SII](6731) ratios? As shown in Table 5, the majority of our galaxies have ratios >1, implying
![]() cm-3
for an assumed T=10 000 K. A significant fraction of galaxies have ratios around 1.45, which is the saturation limit for
cm-3
for an assumed T=10 000 K. A significant fraction of galaxies have ratios around 1.45, which is the saturation limit for
![]() .
These values are consistent with pre-shock densities
as low as n < 10 cm-3. Indeed, as the density of the material passing through the shock increases,
the density indicated by the [SII] ratio also increases. However, the amount of compression
depends critically upon the magnetic parameter (Dopita & Sutherland 1995). In the Allen et al. (2008) models, [SII](6717)/[SII](6731)
.
These values are consistent with pre-shock densities
as low as n < 10 cm-3. Indeed, as the density of the material passing through the shock increases,
the density indicated by the [SII] ratio also increases. However, the amount of compression
depends critically upon the magnetic parameter (Dopita & Sutherland 1995). In the Allen et al. (2008) models, [SII](6717)/[SII](6731) ![]() 0.7 and
0.7 and ![]() 1 for a pre-shock density
n = 10 cm-3, and B = 1 and 10
1 for a pre-shock density
n = 10 cm-3, and B = 1 and 10 ![]() G, respectively.
G, respectively.
In the fast shock scenario, where does the mechanical energy come from? Dopita & Sutherland (1995) distinguish between two possible types of gas dynamical flows: jet-driven and accretion-driven flows. Evidence of jets in LINERs comes from observations that detect low-luminosity AGNs associated with radio sources with a high brightness temperature and/or elongated radio morphology (e.g., Nagar et al. 2001). In accretion-driven flows, the shock is either the result of the collision of cool clouds that have dropped out of a cooling flow into the potential of the galaxy (e.g. Crawford & Fabian 1992) or have been accreted from a companion galaxy. Shocks may also occur in the outer accretion disk about the central object either by means of the dissipation of turbulence, dynamical instabilities, or spiral shocks (e.g. Dopita et al. 1997). We suppose that the mechanical energy may also come from turbulent motion of gas clouds, either injected by stellar mass loss or accreted, within the potential well of the galaxy.
Figure 17 shows that the shock velocities required
to reproduce the distribution of LINERs in the BPT diagram
range between 200 and 500 km s-1. Are the before mentioned mechanisms able
to account for these high shock velocities?
It seems that jet-driven flows or accretion onto a central massive BH
may well do (e.g., Nagar et al. 2005, Dopita et al. 1997).
On the other hand, it is difficult to establish whether, in the absence
of these sources, pure gravitational motion of clouds within the
potential well of the galaxy can produce collision at the required
velocities.
Close to the center of a relaxed stellar system, the gas should quickly
relax into a disk-like configuration and orbit at a velocity close to
the circular one, even though not necessarily in the same direction of
stars. This is indeed confirmed by observations, showing regular
gaseous disk structures and coherent gas motions (see e.g. Zeilinger
et al. 1996; Sarzi et al. 2006).
If most of the clouds were to rotate in the same direction, it would then be rather
difficult for them to collide at the high speed required.
On the other hand, observations detect an additional gaseous component
of high gas velocity dispersion, in the range
150-250 km s-1 (Bertola et al. 1995; Zeilinger et al. 1996; Emsellem et al. 2003).
Sarzi et al. (2006) found that
![]() is generally
smaller than the stellar velocity dispersion
is generally
smaller than the stellar velocity dispersion
![]() ,
but in some cases
,
but in some cases
![]() ,
either only in the central regions or over most of the field. For a
sample of 345 galaxies, with Hubble type from E to Sbc, Ho (2009b) found
that the gas dispersions strongly correlate with the stellar dispersions over the velocity dispersion range of
,
either only in the central regions or over most of the field. For a
sample of 345 galaxies, with Hubble type from E to Sbc, Ho (2009b) found
that the gas dispersions strongly correlate with the stellar dispersions over the velocity dispersion range of
![]() -350 km s-1, such that
-350 km s-1, such that
![]() /
/
![]() ,
with an average value of 0.80.
All these observations suggest that random motions are crucial for the dynamical support of the gas.
Projected velocity dispersions in the range 150-250 km s-1 translate, based on the assumption of isotropy,
into intrinsic 3D velocity dispersions in the range 260-430 km s-1
,
with an average value of 0.80.
All these observations suggest that random motions are crucial for the dynamical support of the gas.
Projected velocity dispersions in the range 150-250 km s-1 translate, based on the assumption of isotropy,
into intrinsic 3D velocity dispersions in the range 260-430 km s-1 ![]() . This is a crude estimate of the intrinsic velocity dispersions since
studies indicate deviation from isotropy (e.g. Merrifield et al. 2001).
Given these values, collisions at a speed between 200 and 500 km s-1 cannot be excluded.
. This is a crude estimate of the intrinsic velocity dispersions since
studies indicate deviation from isotropy (e.g. Merrifield et al. 2001).
Given these values, collisions at a speed between 200 and 500 km s-1 cannot be excluded.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13774fg19.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg192.png)
|
Figure 19:
Shock models of Allen et al. (2008) compared with our
|
| Open with DEXTER | |
We compare the shock models of Allen et al. (2008) with our data in a luminosity versus velocity plane
in Fig. 19. For the data, we adopted a velocity of
![]() ,
which is a first-order approximation for the shock velocity based on
the assumption that the shocks are caused by motions of gas clouds in
the galaxy potential well.
The models are plotted for four density values
(
n=0.01, 1, 10, 100 cm-3), and for three values of the transverse magnetic field (
B=0.1, 1, 10
,
which is a first-order approximation for the shock velocity based on
the assumption that the shocks are caused by motions of gas clouds in
the galaxy potential well.
The models are plotted for four density values
(
n=0.01, 1, 10, 100 cm-3), and for three values of the transverse magnetic field (
B=0.1, 1, 10 ![]() G).
The shock luminosity increases significantly with both the shock
velocity and the gas density. The dependence on the magnetic parameter
is almost null in H
G).
The shock luminosity increases significantly with both the shock
velocity and the gas density. The dependence on the magnetic parameter
is almost null in H![]() (and modest in [NII]).
The observed nuclear H
(and modest in [NII]).
The observed nuclear H![]() luminosities were corrected for reddening in terms of
the values derived in Table 2.
Some galaxies have very large reddening, associated with large uncertainties, and have quite
high luminosities once corrected for extinction (NGC 777, NGC 1521, NGC 7007, NGC 3557).
Their
luminosities were corrected for reddening in terms of
the values derived in Table 2.
Some galaxies have very large reddening, associated with large uncertainties, and have quite
high luminosities once corrected for extinction (NGC 777, NGC 1521, NGC 7007, NGC 3557).
Their
![]() should be interpreted with caution.
Figure 19 shows that, for almost all the galaxies in our sample,
the observed luminosities are well reproduced by models with
pre-shock densities
should be interpreted with caution.
Figure 19 shows that, for almost all the galaxies in our sample,
the observed luminosities are well reproduced by models with
pre-shock densities
![]() cm-3.
This does not prove that shocks are the excitation mechanism in LINERs, but
indicates that this scenario is compatible with the data.
We note that shocks could provide a natural explanation of the observed
half-cone-shaped distribution in the line luminosity/EW versus
cm-3.
This does not prove that shocks are the excitation mechanism in LINERs, but
indicates that this scenario is compatible with the data.
We note that shocks could provide a natural explanation of the observed
half-cone-shaped distribution in the line luminosity/EW versus ![]() plane (see also Fig. 9).
They could also explain the observed [NII]/H
plane (see also Fig. 9).
They could also explain the observed [NII]/H![]() versus
versus
![]() correlation
(Fig. 9). The shock models predict an increase in the [NII]/H
correlation
(Fig. 9). The shock models predict an increase in the [NII]/H![]() line ratio with the shock velocity. This is because higher velocity shocks result in harder and more luminous ionizing spectra.
It is interesting that the weak emission galaxies in our sample, compatible with pure
photoionization by PAGB stars at their center, are those deviating from the [NII]/H
line ratio with the shock velocity. This is because higher velocity shocks result in harder and more luminous ionizing spectra.
It is interesting that the weak emission galaxies in our sample, compatible with pure
photoionization by PAGB stars at their center, are those deviating from the [NII]/H![]() vs
vs
![]() relation in Fig.9.
Phillips et al. (1986) also found that the [NII]/H
relation in Fig.9.
Phillips et al. (1986) also found that the [NII]/H![]() ratio increases with the galaxy absolute magnitude in a sample of
LINERs. They interpreted this behavior as being caused by differences
in metallicities or differing ionization conditions.
ratio increases with the galaxy absolute magnitude in a sample of
LINERs. They interpreted this behavior as being caused by differences
in metallicities or differing ionization conditions.
7 Summary and conclusions
We have detected optical emission lines in 89% of the galaxies in
our sample. This large fraction is somehow expected, since our sample
was selected among a compilation of galaxies showing traces of ISM, and
it is thus biased toward spectra containing emission lines. This
fraction is higher than that derived by Phillips et al. (1986) (55%-60%),
Macchetto et al. (1996) (72%-85%), Sarzi et al. (2006) (75%), Yan et al. (2006) (52%), and Serra et al. (2008) (60%) for other samples of early-type galaxies. If we consider only the galaxies in our sample with EW(H![]() + [NII]6584) > 3 Å, the detection fraction drops to 57%.
+ [NII]6584) > 3 Å, the detection fraction drops to 57%.
The incidence and the strength of emission in our sample is
independent of their elliptical or lenticular morphological classes.
These results agree with Phillips et al. (1986), while on the other hand Macchetto et al. (1996) and Sarzi et al. (2006) found a higher incidence of emission in lenticular than in elliptical galaxies.
Following the studies of Cappellari et al. (2007) and Emsellem et al. (2007), we attempted a classification between fast and slow rotators in our sample. Fast and slow rotators account for ![]() 70% and
70% and ![]() 30% of the sample, respectively. This is interesting given that the sample is composed of
30% of the sample, respectively. This is interesting given that the sample is composed of ![]() 70% ellipticals and
70% ellipticals and ![]() 30% lenticulars. Emission does not depend on the fast and slow rotator classification in our sample.
30% lenticulars. Emission does not depend on the fast and slow rotator classification in our sample.
The EW of the lines tends to decrease from the center outwards. The [NII] line declines more steeply than the H![]() .
However, given the uncertainties, we consider only
the decrease from the center to
.
However, given the uncertainties, we consider only
the decrease from the center to ![]() 0.1
0.1 ![]() to be significant. Deeper observations are needed to trace with higher
confidence the EW out to larger radii. Some galaxies deviate from the
general trend, either because they have a flatter emission profile
(NGC 3489, NGC 7007, NGC 7377, NGC 5898), or
because their emission is nuclear concentrated (IC 4296,
NGC 4374, NGC 5090).
Previous narrow-band imaging and integral field spectroscopy studies
have revealed extended distribution for the ionized gas (Caldwell 1984; Goudfrooij et al. 1994b; Macchetto et al. 1996; Sarzi et al. 2006,2009).
to be significant. Deeper observations are needed to trace with higher
confidence the EW out to larger radii. Some galaxies deviate from the
general trend, either because they have a flatter emission profile
(NGC 3489, NGC 7007, NGC 7377, NGC 5898), or
because their emission is nuclear concentrated (IC 4296,
NGC 4374, NGC 5090).
Previous narrow-band imaging and integral field spectroscopy studies
have revealed extended distribution for the ionized gas (Caldwell 1984; Goudfrooij et al. 1994b; Macchetto et al. 1996; Sarzi et al. 2006,2009).
Extinction was derived from the observed H![]() /H
/H![]() flux ratio,
assuming an intrinsic value of
flux ratio,
assuming an intrinsic value of ![]() 3.1 for AGN-like objects (Osterbrock 1989). This choice was driven by our galaxies having AGN-like [NII]/H
3.1 for AGN-like objects (Osterbrock 1989). This choice was driven by our galaxies having AGN-like [NII]/H![]() ratios.
For the majority of the galaxies, the derived E(B-V) values are lower than 0.3. Some galaxies however have very large reddenings, up to
ratios.
For the majority of the galaxies, the derived E(B-V) values are lower than 0.3. Some galaxies however have very large reddenings, up to
![]() or even more.
Since the observed continuum is incompatible with these large values, our result suggests
that in these galaxies the dust has a patchy distribution. This is consistent with narrow-band
imaging studies that have detected dust lanes and patches in early-type galaxies (e.g. Goudfrooij et al. 1994b).
or even more.
Since the observed continuum is incompatible with these large values, our result suggests
that in these galaxies the dust has a patchy distribution. This is consistent with narrow-band
imaging studies that have detected dust lanes and patches in early-type galaxies (e.g. Goudfrooij et al. 1994b).
We performed a spectral classification for our sample using the classical [OIII]/H![]() versus [NII]/H
versus [NII]/H![]() diagnostic diagram (BPT diagram). The classification based on the central
diagnostic diagram (BPT diagram). The classification based on the central
![]() /16 emission lines is provided in Table 4. About 72% of the galaxies exhibit a central LINER emission activity. Seyferts account for
/16 emission lines is provided in Table 4. About 72% of the galaxies exhibit a central LINER emission activity. Seyferts account for ![]() 9%
of the emission sample.
However, only IC 5063 can be classified as a bona fide Seyfert
galaxy. The other 4 Seyferts (NGC 3489, NGC 777,
NGC 7007, and NGC 6958),
have very large errors in [OIII]/H
9%
of the emission sample.
However, only IC 5063 can be classified as a bona fide Seyfert
galaxy. The other 4 Seyferts (NGC 3489, NGC 777,
NGC 7007, and NGC 6958),
have very large errors in [OIII]/H![]() (because of the faint emission in H
(because of the faint emission in H![]() ),
and the classification is less robust. We note however that
NGC 3489 and NGC 777 were also classified as Seyferts by
other authors (Ho et al. 1997b, Sarzi et al. 2006).
Seven galaxies (
),
and the classification is less robust. We note however that
NGC 3489 and NGC 777 were also classified as Seyferts by
other authors (Ho et al. 1997b, Sarzi et al. 2006).
Seven galaxies (![]() 12% of the emission line sample) are ``composites'' (or transition objects):
NGC 3258, NGC 4552, NGC 5193, NGC 5328, NGC 6721, NGC 6876, and IC 2006.
They have [NII]/H
12% of the emission line sample) are ``composites'' (or transition objects):
NGC 3258, NGC 4552, NGC 5193, NGC 5328, NGC 6721, NGC 6876, and IC 2006.
They have [NII]/H![]() ratios intermediate between HII regions and LINERs/Seyferts. In our
sample, these galaxies exhibit the weakest emission lines. For the
remaining 7% of the emission-line galaxies, we cannot provide a
classification, either because the lines are too weak, or because the
spectra are too noisy.
ratios intermediate between HII regions and LINERs/Seyferts. In our
sample, these galaxies exhibit the weakest emission lines. For the
remaining 7% of the emission-line galaxies, we cannot provide a
classification, either because the lines are too weak, or because the
spectra are too noisy.
We derive spatial trends in the emission line ratios:
moving from the center toward annuli of increasing galactocentric distance, we detect a clear decrease in the
[NII]/H![]() ratio. The decrease in [OIII]/H
ratio. The decrease in [OIII]/H![]() is
less clear.
It implies that galaxies classified as LINERs on the basis of their
nuclear line ratios,
would shift toward the region of ``composites'' if one were to consider
the emission from more external regions.
This could be interpreted as either a decrease in the nebular
metallicity, or a progressive ``softening'' of the ionizing spectrum.
is
less clear.
It implies that galaxies classified as LINERs on the basis of their
nuclear line ratios,
would shift toward the region of ``composites'' if one were to consider
the emission from more external regions.
This could be interpreted as either a decrease in the nebular
metallicity, or a progressive ``softening'' of the ionizing spectrum.
We have investigated possible relations between the central line emission properties and the host galaxy properties. The main results are:
- 1.
- Seyferts have young luminosity weighted ages (
 5 Gyr),
and are on average younger than LINERs. LINERs span a wide age range,
from a few Gyrs to a Hubble time. ``Composites'' have ages older than
5 Gyr, at variance with the idea that they may originate from the
combined contribution of AGN and star formation.
5 Gyr),
and are on average younger than LINERs. LINERs span a wide age range,
from a few Gyrs to a Hubble time. ``Composites'' have ages older than
5 Gyr, at variance with the idea that they may originate from the
combined contribution of AGN and star formation.
- 2.
- Excluding the Seyferts, the spread in the emission equivalent width ([NII], H
 ,
or [OIII])
increases with the galaxy central velocity dispersion. Low-
,
or [OIII])
increases with the galaxy central velocity dispersion. Low-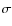 galaxies have weak emission lines, while high-
galaxies have weak emission lines, while high-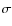 galaxies exhibit both weak and strong emission lines. Equivalent widths of [NII]
galaxies exhibit both weak and strong emission lines. Equivalent widths of [NII]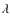 6584 stronger than
6584 stronger than 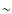 5 Å are found only in galaxies with
5 Å are found only in galaxies with
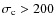 km s-1.
km s-1.
- 3.
- If we consider only the high-emission subsample (H) (see Table 4), where the emission line ratios are more reliable, a positive correlation exists between the [NII]/H
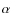 ratio and
ratio and
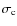 .
.
- 4.
- Excluding the Seyferts, which have higher [OIII]/H
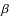 and younger ages, no relation between the emission line ratios and the galaxy age, metallicity, or
and younger ages, no relation between the emission line ratios and the galaxy age, metallicity, or 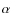 /Fe enhancement is found.
/Fe enhancement is found.
7.1 The AGN-starburst connection in Seyferts
The first result agrees with previous findings that LINERs are older than Seyferts
(e.g., Kewley et al. 2006), and supports the idea that the star formation and the AGN phenomena coexist (Terlevich et al. 1990; Cid Fernandes & Terlevich 1995; Heckman et al. 1997; González Delgado et al. 2001; Kauffmann et al. 2003; Cid Fernandes et al. 2005; Davies et al. 2007; Riffel et al. 2009).
The young luminosity-weighted ages in the Seyferts of our sample are probably caused by recent star formation
episodes superimposed on a several Gyr old stellar population (see Paper III).
Davies et al. (2007)
provide evidence for a delay of 50-100 Myr between the onset of
star formation and the subsequent fueling of the black hole. Given the
short duration of the AGN phenomenon (![]() 100 Myr), this suggests that star formation has occurred a few hundreds Myr ago in the Seyfert galaxies of our sample.
Because of the short duration of the AGN phase, we also expect to observe galaxies with relatively young
luminosity-weighted ages but no signatures of current Seyfert activity.
This agrees with the LINERs spanning a wide luminosity-weighted age range, from a few Gyr to a Hubble time.
100 Myr), this suggests that star formation has occurred a few hundreds Myr ago in the Seyfert galaxies of our sample.
Because of the short duration of the AGN phase, we also expect to observe galaxies with relatively young
luminosity-weighted ages but no signatures of current Seyfert activity.
This agrees with the LINERs spanning a wide luminosity-weighted age range, from a few Gyr to a Hubble time.
7.2 The ionization mechanism in LINERs
Several studies have demonstrated that a minimum level of ionizing photons are produced
in any evolved stellar systems. Thus, if cold gas is present, some level of
nebular emission is always expected in early-type galaxies.
However, the critical question is: can PAGB stars provide all
the ionization observed in early-type galaxies? In answering this
question, we should first of all distinguish between the central LINER
activity and the more extended LINER-like emission. By means of the BPT
classification carried out in annuli of increasing galactocentric
distance, we have demonstrated that ETGs have both a central and an
extended LINER-like emission. When comparing the stronger nuclear
![]() /16 emission with the results of the
photoionization models from Binette et al. (1994), we have found
that only 11 of the 49 galaxies classified as LINERs/composites in our sample (i.e. in
/16 emission with the results of the
photoionization models from Binette et al. (1994), we have found
that only 11 of the 49 galaxies classified as LINERs/composites in our sample (i.e. in ![]() 22%
of the LINER/comp sample) can be explained with photoionization by old
stars alone. Of these 11 galaxies, 6 are classified as LINERs
and 5 as composites.
22%
of the LINER/comp sample) can be explained with photoionization by old
stars alone. Of these 11 galaxies, 6 are classified as LINERs
and 5 as composites.
For the other 78% of LINERs/composites, some mechanism other than photoionization by PAGB stars must operate. We caution however that this fraction is very uncertain, since there is no precise description yet for the evolution and number of PAGB stars (e.g., Brown et al. 2008).
On the other hand, we cannot exclude the importance of hot old stars as a photoionization source at larger radii. The emission strength indeed progressively decreases toward larger galactocentric distances, so that an increasing number of LINERs become compatible with pure PAGB star photoionization.
Summarizing, we cannot exclude a scenario in which more than a source of ionizing photons are present, with different roles at different radii. We can think of a transition region from the center, where PAGB stars fail in accounting alone for the ionizing photon budget, to more extended regions, where they may do well the job, in agreement with the findings of Sarzi et al. (2009) and Eracleous et al. (2010).
Studies of LINERs based on large sample, such as the SDSS, were presented by Stasinska et al. (2008) and Cid Fernandes et al. (2009). However, we warn against direct comparisons of our findings with the results from SDSS for at least two reasons: the 3''-wide aperture of the SDSS usually encompasses large kpc-scale regions where diffuse emission contribute to the nebular fluxes; and our sample is biased toward the presence of emission lines.
After ascertaining the limited role of PAGB stars in the nuclear LINER region,
we investigated other possible scenarios, more specifically
photoionization by sub-Eddington accretion rate AGN and fast shocks.
Direct evidence of AGNs comes from the detection of compact nuclear X-ray/ radio sources.
High resolution X-ray and/or radio data are available for 18 galaxies in our sample, 16 of which are classified as LINERs.
Among the 16 LINERs, evidence of an AGN is found in 10.
Even if the statistics are small, this result suggests that there is a low accretion rate AGNs in ![]() 62%
of LINERs. However, the presenceof an AGN does not exclude the
coexistence of shock heating:
indeed, jet-driven flows and dissipative accretion disks in active
galaxies with strongly sub-Eddington accretion have been proposed as
possible sources of shocks (Dopita & Sutherland 1995; Dopita et al. 1997), and bubbles probably produced by an AGN outburst
have been observed in LINERs (e.g. Baldi et al. 2009).
62%
of LINERs. However, the presenceof an AGN does not exclude the
coexistence of shock heating:
indeed, jet-driven flows and dissipative accretion disks in active
galaxies with strongly sub-Eddington accretion have been proposed as
possible sources of shocks (Dopita & Sutherland 1995; Dopita et al. 1997), and bubbles probably produced by an AGN outburst
have been observed in LINERs (e.g. Baldi et al. 2009).
Both AGN and shock models reproduce the central emission line ratios in
our sample. In the dusty AGN models of Groves et al. (2004), LINERs require a ionization parameter
![]() ,
significantly lower than for Seyferts.
This is consistent with a scenario in which LINERs are AGNs accreting at a much lower rate
than Seyferts.
LINERs can also be modeled in terms of fast shocks
(200-500 km s-1) in a relatively gas poor environment
(pre-shock densities
,
significantly lower than for Seyferts.
This is consistent with a scenario in which LINERs are AGNs accreting at a much lower rate
than Seyferts.
LINERs can also be modeled in terms of fast shocks
(200-500 km s-1) in a relatively gas poor environment
(pre-shock densities
![]() cm-3, depending on the
magnetic field), with gas metallicity
cm-3, depending on the
magnetic field), with gas metallicity ![]() solar.
These low pre-shock densities are consistent with the observed [SII]6717/[SII]6731 ratios.
A critical point concerns the high shock velocities required to explain the
emission-line spectrum in LINERs. Jet-driven flows or accretion onto a massive BH may well produce
these velocities (Nagar et al. 2005; Dopita et al. 1997).
We suppose that an alternative source of
mechanical energy comes from turbulent motion of gas clouds,
either injected by stellar mass loss or accreted, within the potential well of the galaxy.
This scenario cannot be excluded since several studies have found
a gaseous component of high velocity dispersion, in the range
150-250 km s-1, in the center of early-type galaxies (e.g. Bertola et al. 1995; Zeilinger et al. 1996;
Sarzi et al. 2006),
which translates into higher intrinsic 3D velocity dispersions. This
scenario is very appealing since it would naturally explain the
observed trends between the emission strength, and the [NII]/H
solar.
These low pre-shock densities are consistent with the observed [SII]6717/[SII]6731 ratios.
A critical point concerns the high shock velocities required to explain the
emission-line spectrum in LINERs. Jet-driven flows or accretion onto a massive BH may well produce
these velocities (Nagar et al. 2005; Dopita et al. 1997).
We suppose that an alternative source of
mechanical energy comes from turbulent motion of gas clouds,
either injected by stellar mass loss or accreted, within the potential well of the galaxy.
This scenario cannot be excluded since several studies have found
a gaseous component of high velocity dispersion, in the range
150-250 km s-1, in the center of early-type galaxies (e.g. Bertola et al. 1995; Zeilinger et al. 1996;
Sarzi et al. 2006),
which translates into higher intrinsic 3D velocity dispersions. This
scenario is very appealing since it would naturally explain the
observed trends between the emission strength, and the [NII]/H![]() ratio, with the
galaxy stellar central velocity dispersion.
ratio, with the
galaxy stellar central velocity dispersion.
A solid result from our study is that the [NII]/H![]() ratio decreases with increasing galacto-centric distance. This trend
may reflect metallicity gradients in the gas, similarly to what is
observed for the stars. However, this is difficult to reproduce in a
scenario in which the gas has an external origin (see Sect. 7.3).
If not caused by metallicity variations, the [NII]/H
ratio decreases with increasing galacto-centric distance. This trend
may reflect metallicity gradients in the gas, similarly to what is
observed for the stars. However, this is difficult to reproduce in a
scenario in which the gas has an external origin (see Sect. 7.3).
If not caused by metallicity variations, the [NII]/H![]() gradient should reflect variations in the properties of the ionization mechanism.
In the shock scenario, this requires decreasing shock velocities with increasing galactocentric distances.
Unfortunately, we lack the spectral resolution necessary to determine the gas velocity dispersion and,
ultimately, to ascertain the presence of a radial gradient in the shock velocity.
gradient should reflect variations in the properties of the ionization mechanism.
In the shock scenario, this requires decreasing shock velocities with increasing galactocentric distances.
Unfortunately, we lack the spectral resolution necessary to determine the gas velocity dispersion and,
ultimately, to ascertain the presence of a radial gradient in the shock velocity.
A large fraction (40/65) of our sample was observed with Spitzer-IRS. In a forthcoming paper, we will use MIR ionic and molecular emission lines, and polycyclic aromatic hydrocarbon features, to investigate the powering mechanism in LINERs, and more clearly distinguish the contributions from AGN photoionization and shock heating.
7.3 Origin of the gas
We derived the oxygen abundance using two calibrations present in the literature: the Kobulnicky et al. (1999) calibration, valid for HII regions, and the Storchi-Bergmann et al. (1998) calibration, based on the assumption of photoionization by a typical AGN continuum (Mathews & Ferland 1987). The first approach was also adopted by Athey & Bregman (2009)
to derive nebular metallicities in 7 early-type galaxies, and is
probably reasonable in the case of photoionization by PAGB stars.
The second calibration is valid in the case of AGN excitation, and may
be reasonable if LINERs are low-accretion rate AGNs.
Our result is the following: irrespective of the adopted calibration,
the nebular oxygen metallicities are significantly lower than the
stellar ones. The main caveat is that power-law ionizing spectra tend
to provide abundances up to ![]() 0.5 dex
higher than a typical AGN continuum.
A calibration in the case of shock heating is not available in the
literature. However, we can see that shock models indicate nebular
metallicities not higher than solar in our sample, in agreement with
the results obtained with the Kobulnicky et al. (1999) and Storchi-Bergmann et al. (1998) calibrations.
0.5 dex
higher than a typical AGN continuum.
A calibration in the case of shock heating is not available in the
literature. However, we can see that shock models indicate nebular
metallicities not higher than solar in our sample, in agreement with
the results obtained with the Kobulnicky et al. (1999) and Storchi-Bergmann et al. (1998) calibrations.
Our result has an important implication for the origin of the gas, suggesting that it may be at least in part of external origin (e.g., from either a cooling flow or accretion from a companion galaxy). This is in agreement with photometric and kinematical studies in ETGs showing in many cases gas/star misalignment and gas/star angular momentum decoupling (Bertola et al. 1992; van Dokkum & Franx 1995; Caon et al. 2000; Sarzi et al. 2006). Kinematical and morphological peculiarities are present in 50% of our sample, suggesting that accretion is frequent. Accretion of fresh gas can feed the central supermassive BH, and activate the AGN emission. This is consistent with a major fraction of our galaxies studied in the X-ray and/or radio containing nuclear compact sources.
Finally, we cannot exclude that the low oxygen abundance is
unrelated to the gas origin, and reflects that oxygen does not vary on
lockstep with the other ![]() -elements. In a survey of 27 Milky Way bulge giants, Fulbright et al. (2006) found that,
although Mg appears to be enhanced at all [Fe/H], [O/Fe] declines with increasing [Fe/H] and is solar or
mildly sub-solar at [Fe/H]
-elements. In a survey of 27 Milky Way bulge giants, Fulbright et al. (2006) found that,
although Mg appears to be enhanced at all [Fe/H], [O/Fe] declines with increasing [Fe/H] and is solar or
mildly sub-solar at [Fe/H] ![]() .
X-ray studies have also derived
subsolar [O/Fe] values, but supersolar [Mg/Fe] values, in the hot gas of elliptical galaxies
(e.g., Humphrey & Buote 2006; Ji et al. 2009).
This may be evidence of an overestimate of O yield by SNII models,
which do not consider significant mass loss at the late evolutionary stages of massive progenitor stars
(Ji et al. 2009).
.
X-ray studies have also derived
subsolar [O/Fe] values, but supersolar [Mg/Fe] values, in the hot gas of elliptical galaxies
(e.g., Humphrey & Buote 2006; Ji et al. 2009).
This may be evidence of an overestimate of O yield by SNII models,
which do not consider significant mass loss at the late evolutionary stages of massive progenitor stars
(Ji et al. 2009).
We acknowledge a financial contribution from contract ASI-INAF I/016/07/0. F. A. thanks R. van der Marel for useful suggestions. We thank the anonymous referee for having carefully read the manuscript, and for his/her useful comments and suggestions that helped to improve significantly the paper.
References
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20
- Annibali, F., Bressan, A., Rampazzo, R., & Zeilinger, W. W. 2006, A&A, 445, 79
- Annibali, F., Bressan, A., Rampazzo, R., Zeilinger, W. W., & Danese, L. 2007, A&A, 463, 455
- Arimoto, N., Matsushita, K., Ishimaru, Y., Ohashi, T., & Renzini, A. 1997, ApJ, 477, 128
- Athey, A. E., & Bregman, J. N. 2009, ApJ, 696, 681
- Baldi, A., Forman, W., Jones, C., et al. 2009, [arXiv:0909.2942]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5
- Balmaverde, B., & Capetti, A. 2006, A&A, 447, 97
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275
- Bertola, F., Buson, L. M., & Zeilinger, W. W. 1992, ApJ, 401, L79
- Bertola, F., Cinzano, P., Corsini, E. M., Rix, H.-W., & Zeilinger, W. W. 1995, ApJ, 448, L13
- Binette, L., Magris, C. G., Stasinska, G., & Bruzual, A. G. 1994, A&A, 292, 13
- Blanton, E. L., Sarazin, C. L., & Irwin, J. A. 2001, ApJ, 552, 106
- Bregman, J. N., Hogg, D. E., & Roberts, M. S. 1992, ApJ, 387, 484
- Bressan, A., Granato, G. L., & Silva, L. 1998, A&A, 332, 135
- Bressan, A., Panuzzo, P., Buson, L., et al. 2006, ApJ, 639, L55
- Brown, T. M., Smith, E., Ferguson, H. C., et al. 2008, ApJ, 682, 319
- Buote, D. A., Lewis, A. D., Brighenti, F., & Mathews, W. G. 2003, ApJ, 595, 151
- Buson, L. M., Sadler, E. M., Zeilinger, W. W., et al. 1993, A&A, 280, 409
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031
- Caffau, E., Maiorca, E., Bonifacio, P., et al. 2009, A&A, 498, 877
- Caldwell, N. 1984, PASP, 96, 287
- Caon, N., Macchetto, D., & Pastoriza, M. 2000, ApJS, 127, 39
- Cappellari, M., Emsellem, E., Bacon, R., Bureau, M., & Davies, R. L. 2008, MNRAS, 379, 418
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245
- Cecil, G., Greenhill, L. J., DePree, C. G., et al. 2000, ApJ, 536, 675
- Chavez, M., Bertone, E., Morales-Hernandez, J., & Bressan, A. 2009, ApJ, 700, 694
- Cid Fernandes, R. J., & Terlevich, R. 1995, MNRAS, 272, 423
- Cid Fernandes, R., González Delgado, R. M., Storchi-Bergmann, T., Martins, L. P., & Schmitt, H. 2005, MNRAS, 356, 270
- Cid Fernandes, R., Schlickmann, M., Stasinska, G., et al. 2009, ASP Conf. Ser., 408, 122
- Clemens, M. S., Bressan, A., Nikolic, B., & Rampazzo, R. 2009, MNRAS, 392, L35
- Corsini, E. M., & Bertola, F. 1998, Journal of the Korean Physical Society, 33, 574
- Crawford, C. S., & Fabian, A. C. 1992, MNRAS, 259, 265
- Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41
- Davies, R. I., Sánchez, F. M., Genzel, R., et al. 2007, ApJ, 671, 1388
- de Jong, T., Norgaard-Nielsen, H. U., Jorgensen, H. E., & Hansen, L. 1990, A&A, 232, 317
- Demoulin-Ulrich, M.-H., Butcher, H. R., & Boksenberg, A. 1984, ApJ, 285, 527
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, S&T, 82, 621
- Domingue, D. L., Sulentic, J. W., Xu, C., et al. 2003, AJ, 125, 555
- Dopita, M. A., & Evans, I. N. 1986, ApJ, 307, 431
- Dopita, M. A., & Sutherland, R. S. 1995, ApJ, 455, 468
- Dopita, M. A., Binette, L., & Schwartz, R. D. 1982, ApJ, 261, 183
- Dopita, M. A., Koratkar, A. P., Allen, M. G., et al. 1997, ApJ, 490, 202
- Edmunds, M. G., & Pagel, B. E. J. 1984, MNRAS, 211, 507
- Emsellem, E., Goudfrooij, P., & Ferruit, P. 2003, MNRAS, 345, 1297
- Emsellem, E., Cappellari, M., Peletier, R. F., McDermid, R. M., & Bacon, R. 2004, MNRAS, 352, 721
- Emsellem, E., Cappellari, M., Krajnovic, D., van de Ven, G., Bacon, R., et al. 2007, MNRAS, 379, 401.
- Eracleous, M., Hwang, J. A., & Flohic, H. M. L. G. 2010, ApJ, 711, 796
- Fabbiano, G., Kim, D.-W., & Trinchieri, G. 1992, ApJS, 80, 531
- Filho, M. E., Fraternali, F., Markoff, S., et al. 2004, A&A, 418, 429
- Filho, M. E., Barthel, P. D., & Ho, L. C. 2006, A&A, 451, 71
- Forman, W., & Jones, C. 1985, BAAS, 17, 586
- Fosbury, R. A. E., Mebold, U., Goss, W. M., & Dopita, M. A. 1978, MNRAS, 183, 549
- Flohic, H. M. L. G., Eracleous, M., Chartas, G., Shields, J. C., & Moran, E. C. 2006, ApJ, 647, 140
- Fulbright, J. P., Rich, R. M., & McWilliam, A. 2006, Chemical Abundances and Mixing in Stars in the Milky Way and its Satellites, ESO Astrophys. Symp. (Springer-Verlag), 93, 93
- Gastaldello, F., & Molendi, S. 2002, ApJ, 572, 160
- González Delgado, R. M., Heckman, T., & Leitherer, C. 2001, ApJ, 546, 845
- Gonzalez-Martin, O., Masegosa, J., Marquez, I., Guainazzi, M., & Jimenez-Bailon, E. 2009, A&A, 506, 1107
- Goudfrooij, P. 1999, Star Formation in Early Type Galaxies, 163, 55
- Goudfrooij, P., & de Jong, T. 1995, A&A, 298, 784
- Goudfrooij, P., & Emsellem, E. 1996, A&A, 306, L45
- Goudfrooij, P., Hansen, L., Jorgensen, H. E., et al. 1994a, A&AS, 104, 179
- Goudfrooij, P., Hansen, L., Jorgensen, H. E., & Norgaard-Nielsen, H. U. 1994b, A&AS, 105, 341
- Goudfrooij, P., de Jong, T., Hansen, L., & Norgaard-Nielsen, H. U. 1994c, MNRAS, 271, 833
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 9
- Grützbauch, R., Trinchieri, G., Rampazzo, R., et al. 2007, AJ, 133, 220
- Heckman, T. M. 1980, A&A, 87, 152
- Heckman, T. M., Gonzalez-Delgado, R., Leitherer, C., et al. 1997, ApJ, 482, 114
- Heckman, T. M., Kauffmann, G., Brinchmann, J., et al. 2004, ApJ, 613, 109
- Helmboldt, J. F. 2007, MNRAS, 379, 1227
- Ho, L. 1999a, Observational Evidence for the Black Holes in the Universe, 234, 157
- Ho, L. C. 1999b, Adv. Space Res., 23, 813
- Ho, L. C. 2009a, ApJ, 699, 626
- Ho, L. C. 2009b, ApJ, 699, 638
- Ho, L. C., & Ulvestad, J. S. 2001, ApJS, 133, 77
- Ho, L. C., Filippenko, A. V., Sargent, W. L. W., & Peng, C. Y. 1997a, ApJS, 112, 391
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997b, ApJS, 112, 315
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997c, ApJ, 487, 591
- Humphrey, P. J., & Buote, D. A. 2006, ApJ, 639, 136
- Ji, J., Irwin, J. A., Athey, A., Bregman, J. N., & Lloyd-Davies, E. J. 2009, ApJ, 696, 2252
- Jones, C., Forman, W., Vikhlinin, A., et al. 2002, ApJ, 567, L115
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961
- Kim, D.-W. 1989, ApJ, 346, 653
- Kobulnicky, H. A., Kennicutt, R. C., Jr., Pizagno, & James, L. 1999, ApJ, 514, 544 (Kob99)
- Kormendy, J. 2004, Coevolution of Black Holes and Galaxies, 1
- Koski, A. T., & Osterbrock, D. E. 1976, ApJ, 203, L49
- Koyama, K., Awaki, H., Iwasawa, K., & Ward, M. J. 1992, ApJ, 399, L129
- Lípari, S., Mediavilla, E., Garcia-Lorenzo, B., et al. 2004, MNRAS, 355, 641
- Macchetto, F., Pastoriza, M., Caon, N., et al. 1996, A&AS, 120, 463
- Machacek, M. E., Nulsen, P., Stirbat, L., Jones, C., & Forman, W. R. 2005, ApJ, 630, 280
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285
- Malin, D. F., & Carter, D. 1983, ApJ, 274, 534
- Maoz, D., Nagar, N. M., Falcke, H., & Wilson, A. S. 2005, ApJ, 625, 699
- Martel, A. R., Ford, H. C., Bradley, L. D., et al. 2004, AJ, 128, 2758
- Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1
- McGaugh, S. S. 1991, ApJ, 380, 140
- Merrifield, M. R., Gerssen, J., & Kuijken, K. 2001, Galaxy Disks and Disk Galaxies, 230, 221
- Morganti, R., de Zeeuw, P. T., Oosterloo, T. A., et al. 2006, MNRAS, 371, 157
- Nagar, N. M., Wilson, A. S., & Falcke, H. 2001, ApJ, 559, L87
- Nagar, N. M., Falcke, H., Wilson, A. S., & Ulvestad, J. S. 2002, A&A, 392, 53
- Nagar, N. M., Falcke, H., & Wilson, A. S. 2005, A&A, 435, 521
- Osterbrock, D. E. 1989, S&T, 78, 491
- Oosterloo, T. A., Morganti, R., Sadler, E. M., van der Hulst, T., & Serra, P. 2007, A&A, 465, 787
- O'Sullivan, E., Forbes, D. A., & Ponman, T. J. 2001, MNRAS, 328, 461
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95
- Panuzzo, P., Vega, O., Bressan, A., et al. 2007, ApJ, 656, 206
- Pellegrini, S., Venturi, T., Comastri, A., et al. 2003, ApJ, 585, 677
- Phillips, M. M., Jenkins, C. R., Dopita, M. A., Sadler, E. M., & Binette, L. 1986, AJ, 91, 1062
- Pian, E., Romano, P., Maoz, D., et al. 2010, MNRAS, 401, 677
- Pierfederici, F., & Rampazzo, R. 2004, AN, 325, 359
- Quataert, E. 2001, Probing the Physics of Active Galactic Nuclei, 224, 71
- Rampazzo, R., Annibali, F., Bressan, A., et al. 2005, A&A, 433, 497
- Rand, R. J., & Kulkarni, S. R. 1989, ApJ, 343, 760
- Riffel, R. A., Storchi-Bergmann, T., Dors, O. L., & Winge, C. 2009, MNRAS, 393, 783
- Roberts, M. S., Hogg, D. E., Bregman, J. N., Forman, W. R., & Jones, C. 1991, ApJS, 75, 751
- Sadler, E. M., & Gerhard, O. E. 1985, MNRAS, 214, 177
- Sadler, E. M., Oosterloo, T., & Morganti, R. 2002, The Dynamics, Structure & History of Galaxies: A Workshop in Honour of Professor Ken Freeman, ASP Conf. Proc., 273, ed. G. S. Da Costa, & H. Jerjen
- Sage, L. J., & Welch, G. A. 2006, ApJ, 644, 850
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703
- Sandage, A., & Tammann, G. A. 1987, Carnegie Institution of Washington Publication, Washington: Carnegie Institution, 2nd edn
- Saraiva, M. F., Bica, E., Pastoriza, M. G., & Bonatto, C. 2001, A&A, 376, 43
- Sarzi, M., F.-B., Jesùs, Davies, R. L., et al. 2006, MNRAS, 366, 1151
- Sarzi, M., et al. 2009 [arXiv:0912.0275]
- Serra, P., Trager, S. C., Oosterloo, T. A., & Morganti, R. 2008, A&A, 483, 57
- Shaw, R. A., & Dufour, R. J. 1995, PASP, 107, 896
- Sparks, W. B., Macchetto, F., & Golombek, D. 1989, ApJ, 345, 153
- Stasinska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972
- Stasinska, G., Vale Asari, N., Cid Fernandes, R., et al. 2008, MNRAS, 391, L29
- Storchi-Bergmann, T., Schmitt, H. R., Calzetti, D., & Kinney, A. L. 1998, AJ, 115, 909 (SB98)
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253
- Tal, T., van Dokkum, P. G., Nelan, J., & Bezanson, R. 2009, AJ, 138 1417
- Tamura, T., Kaastra, J. S., Makishima, K., & Takahashi, I. 2003, A&A, 399, 497
- Temi, P., Brighenti, F., Mathews, W. G., & Bregman, J. D. 2004, ApJS, 151, 237
- Terashima, Y. 1999, Adv. Space Res., 23, 851
- Terashima, Y., Ho, L. C., & Ptak, A. F. 2000, ApJ, 539, 161
- Terlevich, E., Díaz, A. I., & Terlevich, R. 1990, Rev. Mex. Astron. Astrofis, 21, 21, 218
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673
- Tran, H. D., Tsvetanov, Z., Ford, H. C., et al. 2001, AJ, 121, 2928
- Trinchieri, G., & di Serego Alighieri, S. 1991, AJ, 101, 1647
- Tully, R. B. 1988, Nearby Galaxy Catalog (Cambridge University Press)
- Yan, R., Newman, J. A., Faber, S. M. 2006, ApJ, 648, 281
- Zaritsky, D., Kennicutt, R. C. Jr., & Huchra, J. P. 1994, ApJ, 420, 87
- Zeilinger, W. W., Pizzella, A., Amico, P., Bertin, G., et al. 1996, A&AS, 120, 257
- van Dokkum, P. G., & Franx, M. 1995, AJ, 110, 2027
- Wang, J., & Wei, J. Y. 2008, ApJ, 679, 86
Online Material
Table 2:
Observed emission line fluxes in units of
![]() .
.
Table 3: Observed emission line equivalent widths.
Appendix A: Short description of morphological and kinematic characteristics and peculiarities of the galaxy sample (Paper I+Paper II)
We collect in Table A1 the morphological and kinematic characteristics, as well as the peculiarities, of the complete R05+A06 sample. The morphological and kinematic properties in Table A1 are derived from the literature, and were in part already described in the Appendix (provided as on-line material) of Paper I and Paper II.
We list in Cols. 3 and 4 the galaxy ellipticity, ![]() ,
and the
(
,
and the
(![]() )
)
![]() .
The latter is computed from slit spectroscopy measurements
through the relation provided by Cappellari et al. (2007),
(
.
The latter is computed from slit spectroscopy measurements
through the relation provided by Cappellari et al. (2007),
(![]() )
)
![]() (V/
(V/
![]() .
It should
be a reasonable approximation of the (
.
It should
be a reasonable approximation of the (![]() )
)![]() ,
computed on a luminosity weighted spectrum within
,
computed on a luminosity weighted spectrum within ![]() .
For the eight galaxies in common with the SAURON
sample, i.e. NGC 2974, NGC 3489, NGC 4374, NGC 4552, NGC 5813,
NGC 5831, NGC 5846 and NGC 7332, the
.
For the eight galaxies in common with the SAURON
sample, i.e. NGC 2974, NGC 3489, NGC 4374, NGC 4552, NGC 5813,
NGC 5831, NGC 5846 and NGC 7332, the ![]() and
and ![]() values are those derived through integral field spectroscopy.
Cappellari et al. (2007) noticed that there is
a good agreement between
values are those derived through integral field spectroscopy.
Cappellari et al. (2007) noticed that there is
a good agreement between ![]() values derived in the literature
with different methods.
values derived in the literature
with different methods.
Emsellem et al. (2007) defined a new parameter,
![]() ,
where R is the galacto-centric distance, and V and
,
where R is the galacto-centric distance, and V and ![]() are
luminosity weighted averages over the two-dimensional kinematic field.
This parameter is a proxy to quantify the observed projected stellar angular momentum per unit mass,
and can be used to classify ETGs into slow or fast rotators.
In the
are
luminosity weighted averages over the two-dimensional kinematic field.
This parameter is a proxy to quantify the observed projected stellar angular momentum per unit mass,
and can be used to classify ETGs into slow or fast rotators.
In the ![]() vs. (
vs. (![]() )
)![]() plane, Cappellari et al. (2007) identified a region (0.0
plane, Cappellari et al. (2007) identified a region (0.0
![]() ,
,
![]() 0.13)
where slow- rotators are generally found.
Lacking the 2D V and
0.13)
where slow- rotators are generally found.
Lacking the 2D V and ![]() information for most of our galaxies,
we used (
information for most of our galaxies,
we used (![]() )
)
![]() to identify in the
to identify in the ![]() vs. (
vs. (![]() )
)![]() plane the fast and slow rotators.
The derived classification is provided in Col. 5 of Table A1
(F = fast rotator; S = slow rotator).
We obtain that
plane the fast and slow rotators.
The derived classification is provided in Col. 5 of Table A1
(F = fast rotator; S = slow rotator).
We obtain that ![]() 68% (36/53) of our sample is fast rotator
(to be compared with 75% fast rotators in the SAURON sample).
Less than 1/3 of our galaxies are slow rotators
(vs. 25% in the SAURON sample).
68% (36/53) of our sample is fast rotator
(to be compared with 75% fast rotators in the SAURON sample).
Less than 1/3 of our galaxies are slow rotators
(vs. 25% in the SAURON sample).
In Cols. 6 and 7 of Table A1 we provide the kinematic and morphological peculiarities, respectively. A large fraction, approximately 50% of our ETGs, displays kinematic peculiarities, like counter-rotation, or peculiar faint features, like shells, tails, or decoupled gas distributions with respect to the stars.
Table A.1: Kinematic and morphological overview.
Appendix B: Emission line ratios for the total sample in annuli of increasing galacto-centric distance
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig20.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg228.png)
|
Figure B.1:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig21.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg229.png)
|
Figure B.2:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig22.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg231.png)
|
Figure B.3:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig23.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg232.png)
|
Figure B.4:
|
| Open with DEXTER | |
Footnotes
- ... gas
![[*]](/icons/foot_motif.png)
- Based on observations obtained at the European Southern Observatory, La Silla, Chile.
- ...
![[*]](/icons/foot_motif.png)
- Appendix and Tables 2 and 3 are only available in electronic form at http://www.aanda.org
- ... HYPERLEDA
![[*]](/icons/foot_motif.png)
- http://leda.univ-lyon1.fr
- ... paper
![[*]](/icons/foot_motif.png)
-
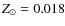 in A07, while we adopt
in A07, while we adopt
 from
Caffau et al. (2009) in this paper. This implies a correction term of
from
Caffau et al. (2009) in this paper. This implies a correction term of
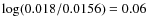 dex
to be applied to the A07 relation.
dex
to be applied to the A07 relation.
- ...
![[*]](/icons/foot_motif.png)
- The total 3D velocity dispersion
satisfies
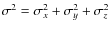 ,
because of the Pythagoras theorem and basic statistics of the second moments. If the dispersion is isotropic,
,
because of the Pythagoras theorem and basic statistics of the second moments. If the dispersion is isotropic,
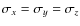 by definition, and
by definition, and
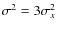 .
.
All Tables
Table 1: Sample overview.
Table 4:
Classification from optical lines in the nuclear (
![]() /16) region.
/16) region.
Table 5:
Electron densities ![]() derived from [SII]6716/6731 assuming T=10 000 K.
derived from [SII]6716/6731 assuming T=10 000 K.
Table 6: [O/H] values obtained with the Kobulnicky et al. (1999) calibration (Kob99), and the Storchi-Bergmann et al. (1998) calibration (SB98).
Table 2:
Observed emission line fluxes in units of
![]() .
.
Table 3: Observed emission line equivalent widths.
Table A.1: Kinematic and morphological overview.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm]{13774fg1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg85.png)
|
Figure 1:
Central (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg101.png)
|
Figure 2:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg102.png)
|
Figure 3:
E(B-V) distribution derived for our sample from the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13774fg4.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg106.png)
|
Figure 4:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg5.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg112.png)
|
Figure 5:
Emission EW derived in annuli of increasing galactocentric distance (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{13774fg6.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg115.png)
|
Figure 6:
Extinction-corrected BPT
diagnostic diagram for the galaxy sample in annuli of increasing galacto-centric distance
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg117.png)
|
Figure 7:
Distribution of emission line ratios over the central
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13774fg8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg119.png)
|
Figure 8:
BPT diagrams of some galaxies representing the general trends of the whole sample in the four annuli:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13774fg9.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg120.png)
|
Figure 9:
H |
| Open with DEXTER | |
| In the text | |
| |
Figure 10:
Age, metallicity, and [ |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13774fg11.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg122.png)
|
Figure 11: BPT diagnostic diagram for Seyfert galaxies ( left panel), ``composites'' ( center), and LINERs ( right panel). The data were color-coded according to the galaxy age as derived in Paper III: blue stars are for ages younger than 4 Gyr, green squares for ages between 4 and 8 Gyr, and red circles for ages older than 8 Gyr. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg12.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg146.png)
|
Figure 12:
Oxygen abundance at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{13774fg13.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg151.png)
|
Figure 13:
Top panel: oxygen abundance distributions (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13774fg14.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg152.png)
|
Figure 14:
Oxygen abundance distributions in the three more internal annuli (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{13774fg15.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg153.png)
|
Figure 15:
Nebular oxygen abundance versus star oxygen abundance. The latter was derived from the Z and [ |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13774fg16.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg154.png)
|
Figure 16:
Oxygen abundances derived with the Kob99 ( top)
and SB98 ( bottom) calibration
at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13774fg17.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg166.png)
|
Figure 17:
BPT diagram for our galaxies at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13774fg18.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg173.png)
|
Figure 18:
Distribution of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13774fg19.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg192.png)
|
Figure 19:
Shock models of Allen et al. (2008) compared with our
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig20.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg228.png)
|
Figure B.1:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig21.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg229.png)
|
Figure B.2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig22.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg231.png)
|
Figure B.3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{annibali.fig23.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13774-09/Timg232.png)
|
Figure B.4:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.