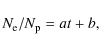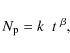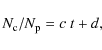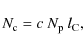EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A112 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A112
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200913668
Published online 21 September 2010
A&A 519, A112 (2010)

Dynamical evolution of escaped plutinos, another source of Centaurs

R. P. Di Sisto - A. Brunini - G. C. de Elía

Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata and Instituto de Astrofísica de La Plata, CCT La Plata-CONICET-UNLP Paseo del Bosque S/N, 1900 La Plata, Argentina

Received 13 November 2009 / Accepted 13 May 2010

Abstract
Context. Weakly chaotic orbits that diffuse very slowly have been found to exist in the plutino population. These orbits correspond to long-term plutino escapers and represent the plutinos presently escaping from the resonance.
Aims. We perform numerical simulations to explore the dynamical evolution of plutinos that have recently escaped from the resonance.
Methods. The numerical simulations were divided into two parts. In the first, we evolved 20 000 test particles in the resonance to detect and select the long-term escapers. In the second, we numerically integrated the selected escaped plutinos to study their dynamical post escaped behavior.
Results. We characterize the escape routes of plutinos and their evolution in the Centaur zone. We derive a present rate of escape of plutinos of between 1 and 10 every 10 years. The escaped plutinos would have a mean lifetime in the Centaur zone of 108 Myr and their contribution to the Centaur population would be a fraction of smaller than $6\%$ of the total Centaur population. In this way, escaped plutinos would be a secondary source of Centaurs.

Key words: methods: numerical - Kuiper Belt

1 Introduction

In the past few years, the number of observed transneptunian objects has grown enormously thanks to progress in astronomical observations. This has allowed us to define, in a more rigorous way, the different dynamical classes previously identified in the first years of discoveries. The objects in the transneptunian region (TNR) can be divided into 4 dynamical classes (Chiang et al. 2007). The resonant objects are those in mean motion resonance with Neptune, the classical objects are non-resonant objects with semimajor axes a greater than $\sim$42 AU and low eccentricity orbits, the scattered disk objects (SDOs) have perihelion distances q > 30 AU and high eccentricities, and the Centaurs objects. This last group has perihelion distances that are inside the orbit of Neptune and represents transitory object descendants of the other 3 classes, mainly of SDOs, recently dislodged from the transneptunian zone by planetary perturbations (Levison & Duncan 1997; Tiscareno & Malhotra 2003; Di Sisto & Brunini 2007).

Centaurs are sometimes defined in terms of either their aphelion distance or semimajor axis (a), as in for example the nomenclature of Gladman et al. (2008) that uses $a < a_{\rm N}$ (where $a_{\rm N}$ is Neptune's semimajor axis), objects then being entirely in the giant planet zone. Nevertheless, it is generally accepted that they are objects that enter the planetary region from the TNR, evolve in the giant planetary zone, and a fraction of which enter the zone interior to the Jupiter's orbit becoming Jupiter family comets (JFCs).

The resonant transneptunian population most densely populated are the plutinos, which are trapped into the 2:3 mean motion resonance with Neptune, Pluto being its most representative member. Some of the plutinos cross Neptune's orbit, hence one might think they would be sensitive to strong perturbations during close encounters with that planet. However, conjunctions occur near plutinos's aphelions and then close encounters do not occur. This provides a stable configuration of the resonance, with the critical angle $\sigma = 3 \lambda - 2 \lambda_{\rm N} - \varpi$ librating around  $180^{\circ}$, where $\lambda$ and $\varpi$ are the mean longitude and the longitude of perihelion of the plutino, and  $\lambda_{\rm N}$ is the mean longitude of Neptune.

Duncan et al. (1995) analyzed the dynamical structure of the transneptunian region using numerical simulations. They numerically integrated thousands of test transneptunian bodies to study their dynamical behavior and determine which regions are potential sources of the Jupiter family comets that we see today. For the Plutinos, Duncan et al. showed that the boundaries of this long-lived mean motion resonance have a timescale for instability of the order of the age of the Solar System, and therefore that the long-term erosion of the particles is rather gradual and must continue until the current epoch. The existence of these currently unstable orbits may be related to the origin of the observed Jupiter family comets.

Morbidelli (1997) studied the dynamical structure of the 2:3 resonance with Neptune to analyze possible diffusive phenomena and their relation to the existence of long-term escape trajectories. He performed numerical simulations integrating the evolution of 150 test particles initially covering the 2:3 resonance with eccentricities up to e = 0.3 and inclinations less than $i = 5 ^ {\circ }$, for 4 byr. The author found regular orbits that never escaped from the resonance present only at moderate eccentricity and a small amplitude of libration, and a strong chaotic region at large amplitude of libration, which is quickly depleted and seems to be generated for the interaction between the $\nu_{18}$ and kozai resonances. Morbidelli (1997) showed the existence of weakly chaotic orbits that diffuse very slowly and finally dive into the strong chaotic region. They are long-term escapers and thus plutinos that have recently escaped from the resonance. The source zone of those particles produce Neptune-encountering bodies at the current epoch of the Solar System and should be an active source of Centaurs and comets at present. He found that 10$\%$ of the bodies initially in that weakly chaotic zone have been delivered to Neptune in the past 109 years.

The first attempt to include the gravitational influence of Pluto into numerical models of the dynamics of plutinos was developed by Yu & Tremaine (1999). These authors suggested that the effect of Pluto, ejecting objects from the 2:3 resonance to Neptune-crossing orbits, may contribute to or even dominate the flux of JFCs. At the same time, Nesvorný et al. (2000) analyzed the effect of Pluto on the 2:3 resonant orbits. They found that Pluto produces a large excitation of the libration amplitudes in the 2:3 resonance. However, they estimated that the flux rate that contributes to the flux of short period comets is about 1$\%$ of the 2:3 resonant population per 108 years, which is about the same value as the flux obtained by Morbidelli (1997) without Pluto.

Melita & Brunini (2000) developed a comparative study of mean motion resonances in the transneptunian region. These authors used the frequency-map-analysis method (Laskar 1993) to describe the dynamical structure of the 2:3, 3:5, and 1:2 Neptune resonances, at 39.5, 42.3, and 47.7 AU, respectively. In particular, Melita & Brunini (2000) showed that the 2:3 resonance presents a very robust stable zone primarily at low inclinations, where a great number of the observed plutinos are distributed. They suggested that the existence of plutinos in very unstable regions can be explained by physical collisions or gravitational encounters with other plutinos.

De Elía et al. (2008) performed a collisional evolution of plutinos and obtained a plutino removal by their collisional evolution of 2 plutinos with R>1 km every 10 000 years or a flux rate of escape of 0.5$\%$ of plutinos in 1010 years.

Tiscareno & Malhotra (2009) carried out 1-Gyr numerical integrations to study the characteristics of the 2:3 and 1:2 mean motion resonances with Neptune. Their main results include maps of resonance stability for a whole range of eccentricities and inclinations. They performed integrations with and without Pluto, and concluded that it has only modest effects on the Plutino population. They calculated the fraction of remaining plutinos in the resonance as a function of time and extrapolated this fraction after 4 Gyr and also evaluated the fate of escaped particles.

From those previous works, plutino removal by dynamical evolution is much greater than plutino removal by collisions. We refer to as ``dynamical'', numerical simulations that take into account the gravitational forces that follow the evolution of a particle and occasionally cause the removal. In this work, we then present ``dynamical'' numerical simulations to describe and characterize the routes of escape of plutinos and their contribution to the other minor body populations of the Solar System, especially Centaurs.

2 The numerical runs

We attempted to characterize the post-escaped evolution of plutinos and the presence of plutinos among other small body populations in the current Solar System. We therefore needed to identify the plutinos that had recently escaped from the resonance. Morbidelli (1997) studied the dynamical structure of the 2:3 mean motion resonance with Neptune to analyze possible diffusive phenomena and their relation to the existence of long-term escape trajectories from the 2:3 resonance. The author showed the existence of weakly chaotic orbits that diffuse very slowly, finally diving into a strong chaotic region. These orbits correspond to long-term escapers, i.e., plutinos that have recently escaped from the resonance. We divided our numerical simulations into two parts. At first, we developed a numerical simulation of plutinos in the resonance to detect those plutinos that had recently escaped from the resonance. Secondly, we performed a numerical simulation of the selected escaped plutinos to study their dynamical post-escape behavior. In the following subsections, we describe both types of integrations.

2.1 Pre-runs: the integration in the resonance

To detect the long-term escapers from the plutino population, we performed a numerical integration following the study of Morbidelli (1997). We integrated the evolution of 20 000 test particles under the gravitational influence of the Sun and the four giant planets over 4.5 Gyr with an integration step of 0.5 years, using the hybrid integrator EVORB (Fernández et al. 2002).

We defined the initial orbital elements to be such that they cover the present observational range of orbital elements of plutinos. The initial semimajor axis of the particles was set equal to the exact value of the resonance $a_{\rm i} = 39.5$ AU. The initial argument of perihelion $\omega$, longitude of node $\Omega$ and the mean anomaly M were chosen at random from the range of  $[0^{\circ},360^{\circ}]$ in such a way that the critical angle $\sigma$ remains between  $180^{\circ}$ and  $330^{\circ}$. Since $\sigma$ librates about  $180^{\circ}$, and given the relation between a and $\sigma$ in the resonance, the choice of $\sigma > 180^{\circ}$ and $a_{\rm i} = 39.5$ AU covers the 2:3 mean motion resonance (see Morbidelli 1997, for a complete explanation). We assumed the maximum limit of $\sigma$ to be $330^{\circ}$, in accordance with Malhotra (1996), Morbidelli (1997) and Nesvorný & Roig (2000), who collectively indicate that orbits starting at large amplitude of libration ( $A_{\sigma}$) are in a strong chaotic region, very unstable, and rapidly driven to the borders of the resonance. In the present paper, we study the long-term escapers from the plutino population, and because particles with large initial  $A_{\sigma}$ escape at the beginning of the integration they do not contribute to the long-term escaper flux.

The initial eccentricity and inclination of the particles were randomly chosen from the intervals [0, 0.35] and [ $0^{\circ}, 45^{\circ}$], respectively. The test particles were integrated up to the first encounter within the Hill sphere of a giant planet collision onto a planet or ejection. Those cut-off conditions imply that plutinos moved from the stable zone of the resonance, after experiencing an encounter with a planet, and then no longer belonged to the resonant population. They therefore represent the escape conditions of plutinos.

2.2 Selection of the long-term escapers

From the 20 000 initial particles, 17 577 ($87.9 \%$) were left out of the integration at a given time either because of an encounter with a planet or an ejection. We found that 21 particles are ejected from the Solar System, and that 17 556 encounter Neptune or Uranus. The remaining 2423 particles ($12.1 \%$) keep inside the resonance until the end of the integration. We refer to the particles that leave the resonance, either because of an encounter or ejection, as ``escaped plutinos''. From our simulation, we can calculate the rate of escape of particles from the resonance. In Fig. 1, we plot the cumulative number of escape particles from the resonance ($N_{\rm e}$) with respect to the number of the remaining particles $N_{\rm p}$, where $N_{\rm p} = 20~000-N_{\rm e}$, as a function of time. It can be seen that the number of escaped particles increases quickly at the beginning up to $t \sim 1.5$ Gyr. At this point, the slope of the curve changes and behaves roughly as a linear relation. This change of slope was already noticed by Morbidelli (1997) and is related to the time when the strongly chaotic region is completely depleted and the weakly chaotic region begins to be the dominant source of Neptune-encountering bodies. For t > 1.5 Gyr, we fit to the plot a linear relation given by

\begin{displaymath}% N_{\rm e}/N_{\rm p} = a t + b, \end{displaymath} (1)

where a=9.00713 $\times$ 10-10 $\pm$ 4.735 $\times$ $10 ^{-13}~{\rm yr}^{-1} $ and b = 3.28079 $\pm$ 0.001347.

Morbidelli (1997) defined the slow diffusion region to be the only active source of the 2:3 mean motion resonance producing Neptune-encountering bodies at present; then the slope of the linear relation, a, represents the present rate of escape of the particles from the 2:3 mean motion resonance. We note that there are very few particles for which the semimajor axis diverges from the resonant value before they have an encounter with a planet or even if they never have an encounter with a planet. But this behavior does not change the previous calculated rate of escape from the resonance.

On the other hand, we plot in Fig. 2, the number of remaining plutinos ($N_{\rm p}$) as a function of time. A change of slope can be seen at $t \sim 100$ Myr, which was also already noticed by Morbidelli (1997) and Tiscareno & Malhotra (2009). We can fit a power law to the number of surviving plutinos versus time for t > 100 Myr that is given by

\begin{displaymath}% N_{\rm p} = k ~~t~^{\beta}, \end{displaymath} (2)

where k=7 560 950 $\pm$ 34 600 and $\beta = -0.362672$ $\pm$ 0.0002372.

Previous works have used power laws to describe the number of surviving particles in the 2:3 mean motion resonance (Morbidelli 1997; Tiscareno & Malhotra 2009). In particular, when analyzing Morbidelli (1997) data (see his Fig. 12) for t>100 Myr, one can obtain $\beta = -0.32$. This is a value very close to our value of $\beta = -0.36$. Tiscareno & Malhotra (2009) obtained a somewhat steeper slope, although they fitted the number of remaining particles versus time for the past 0.5 Gyr of their integration (from 500 Myr to 1 Gyr).

The number of small objects in the plutino population has not been accurately determined, since the present observational surveys are unable to cover all the small-sized objects. The size distribution of plutinos is therefore calculated from different surveys up to a given size, typically a radius of $R \sim 30$ km. For objects of radius smaller than this size, the power-law size distribution could have a break (Kenyon et al. 2008; Bernstein et al. 2004; Elliot et al. 2005). Theoretical models have also been developed to account for accretion and fragmentation of planetesimals in the Kuiper belt and to predict a broken power-law size distribution at a given radius (Kenyon et al. 2008).

De Elía et al. (2008) analyzed the size distribution of plutinos, taking into account the suggested mass of the population and the possible existence of a break in the power-law distribution. By means of the collisional evolution of plutinos, they concluded that the existence of a break in the plutino size distribution should be a primordial feature. By considering the analysis of de Elía et al. (2008) and the three plutino size distributions proposed, we calculated the present number of plutinos with radius R > 1 km as $N_{\rm p} \sim 10^8{-}10^9$, depending on the existence of the break. We then inferred the present rate of escape to be from 1 to 10 plutinos with R > 1 km every 10 years.

We found that 1183 particles escape from the resonance after t = 1.5 Gyr and so originate in the slow diffusion region of the resonance. Since those particles would represent the present escaped plutinos, we identified their original orbital elements from our second integration, as we explain in the following subsection.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg1.ps} \end{figure} Figure 1:

Cumulative number of escaped particles ($N_{\rm e}$) with respect to the number of the surviving particles $N_{\rm p}$, versus the time t in Myr. The fit to the plot for t > 1.5 Gyr is also shown.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg2.ps} \end{figure} Figure 2:

Number of remaining plutinos ($N_{\rm p}$) versus the time t in Myr. A power-law fit to the plot for t > 100 Myr is also showed.

Open with DEXTER

2.3 The post-escape integration

We repeated the numerical integration again from t = 0 for the 1183 particles that escape at t > 1.5 Gyr, to obtain their post-escape evolution. We integrated those particles with the same computing conditions as in the previous integration. We used the EVORB code under the gravitational influence of the Sun and the four giant planets, the same step of integration of 0.5 years, but followed the integration instead for 10 Gyr. The particles were removed from the simulation when they either collided with a planet or the Sun, reached a semimajor axis greater than 1000 AU or entered the region inside Jupiter's orbit (r < 5.2) where the perturbations of the terrestrial planets are not negligible. We recorded the orbital elements of the particles and the planets every 104 years. In the following sections, we describe the results of this simulation.

3 Escaped plutinos: general results

The vast majority of escaped plutinos have encounters with Neptune, so this planet is primarily responsible for their post-escape evolution. We registered the encounters with the major planets at a distance of less than 3 Hill's radii. We found 1 945 643 encounters with Neptune, 534 557 encounters with Uranus, 88 947 encounters with Saturn, and 1309 with Jupiter. However, the encounters with Jupiter in particular were reduced by the removal of objects at a distance of Jupiter.

From the 1183 initial particles, 1179 were removed from and 4 particles remained within the integration. Those four particles have encounters with Uranus or Neptune or both including short incursions to the Centaur zone, and afterwards they are quickly transferred to a mean motion resonance in the SD, remaining there until the end of the integration. Among the 1179 particles removed from the integration at some time, 790 ($67\%$) are ejected, 385 ($32.7\%$) reach the zone interior to Jupiter's orbit (r < 5.2), and 4 ($0.3\%$) have collisions with the planets: 1 with Saturn, 1 with Uranus, and 2 with Neptune. These numbers can be compared with those obtained in the numerical simulation performed by Di Sisto & Brunini (2007); in particular, the number of escaped plutinos that reach the orbit of Jupiter and the number of ejections are similar to these numbers for SDOs with low semimajor axes and perihelion distances smaller than 35 AU. We can also compare our results with those of Tiscareno & Malhotra (2009). They found that $27\%$ of escaped particles reach the zone of r < 5.2 AU. This is a slightly smaller number than ours, but this may be because the result of Tiscareno & Malhotra (2009) was obtained from the escaped particles from their 1 Gyr integration.

When a plutino escapes from the resonance, it is transferred to the scattered disk (SD) zone (q>30 AU) or to the centaur zone (q<30 AU). This is also noticed by Tiscareno & Malhotra (2009). The mean time scale for reaching the Centaur zone is 670 000 years and for reaching the SD zone is about 6 Myr.

3.1 Distribution of orbital elements

In Fig. 3, we plot the time-weighted distribution of escaped plutinos in the orbital element space. We present the probability distribution of finding an escaped plutino in the orbital element space. These plots assume time-invariability, so do not represent reality in which plutinos are continuously leaving the resonance, passing through a certain zone out of the resonance and leaving the solar system, but they help us to identify both the densest and emptiest regions. As we can see, Neptune is the planet that mainly governs the post-escape evolution of escaped plutinos. This behavior can be seen in Fig. 3 as the densest zone near Neptune's perihelion. The densest zone in the orbital element space of escaped plutinos corresponds to the ranges of 30 < a < 100 AU and $5^{\circ} < i < 40^{\circ}$. Several densely populated mean motion resonances, can also be seen corresponding to the blue lines denoted in the a versus i plot.

As mentioned in the previous section, escaped plutinos occupy both the Centaur zone and the SDO zone. In general, they switch each of those populations during its dynamical evolution until it ends like one of them. This is obviously caused by the presence of Neptune and leads to the dynamical evolution of escaped plutinos. In particular, it is notable that when escaped plutinos are transferred to the SD they are quickly locked into a mean motion resonance with Neptune. This behavior is similar to the behavior of SDOs analyzed by Fernández et al. (2004) and Gallardo (2006). The most densely populated mean motion resonances are 2:3N, 4:7N, 4:11N, 1:3N, 1:6U, and 1:5N, where ``N'' means ``with Neptune'' and U means ``with Uranus''.

The distribution of escaped plutinos in the Centaur zone is similar to that obtained for SDOs by Di Sisto & Brunini (2007). We analyze this contribution in the next section.

\begin{figure} \par\includegraphics[width=8.3cm,clip]{13668fg3.eps} \end{figure} Figure 3:

Time-weighed distribution of escaped plutinos in the orbital element space.

Open with DEXTER

4 Contribution to the Centaur population

4.1 Mean lifetime

From the 1183 particles that escape from plutinos, 1179 particles enter the Centaur zone. The four remaining escaped plutinos are ejected by the first encounter with a planet (Neptune in all these cases) within 1 Hill's radii. The escaped plutinos have a mean lifetime in the Centaur zone of $l_{\rm C} = 108$ Myr. This is greater than the mean lifetime of Centaurs from the SD of 72 Myr (Di Sisto & Brunini 2007). In Fig. 4, we plot the normalized fraction of escaped plutinos against intervals of lifetime in the Centaur zone. We also plott, for a comparison, the distribution of lifetimes in the Centaur zone for objects from the SD. As we can see, Centaurs from plutinos have longer lifetimes than Centaurs from SDOs, and the most plutino lifetimes in the Centaur zone are longer than 1 Myr. Escaped plutinos therefore spend a long time in the Centaur zone, from 1 Myr to 1000 Myr. From our numerical simulations, we noticed that the mean lifetime of plutinos in the Centaur zone, as a function of the initial inclination, has nearly the same behavior as for Centaurs from SDOs (see Fig. 5 in Di Sisto & Brunini 2007), but have higher values at each bin of initial inclination. The difference between the mean lifetimes of plutino-Centaurs and SDO-Centaurs is therefore independent of the initial inclinations.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg4.ps} \end{figure} Figure 4:

Normalized fraction of escaped plutinos against lifetime in the Centaur zone (filled line) and normalized fraction of SDOs that enter the Centaur zone against lifetime there (dashed line).

Open with DEXTER

In Fig. 5, we plot the lifetimes of plutinos in the Centaur zone with perihelion distances q smaller than a given value and also the mean lifetimes of SDOs in the Centaur zone, as a comparison. In compiling this plot, for each particle (i) we count the time that it spends at perihelion distance q smaller than a given value q0, ( ${\rm d}t_i (q<q_0)$). We also count the number N of particles that remain for a certain time with q < q0. The mean lifetime of the particles with q<q0 should then be $l_{\rm C} ({<}q_0) = \frac{\sum_{i=1}^N {\rm d}t_i (q~<~q_0)}{N}$.

We can see a stronger dependence of Centaur lifetime on their perihelion distance for plutino-Centaurs than for SDO-Centaurs. However, the greatest differences are found for large perihelion distances, and for perihelion distances smaller than ${\sim}15$ AU both populations have similar lifetimes. Escaped-plutinos thus live longer than SDOs in the greater-perihelion Centaur zone, causing a slower diffusion to the inner Solar System of escaped-plutino orbits than SDO orbits. We suggest that this is due to the difference in the relative encounter velocities with the major planets of SDOs and plutinos. In Fig. 6, we show the distribution of the relative encounter velocities of escaped plutinos (solid line) and SDOs (dotted line) with the four giant planets. It is clearly seen that SDOs have smaller encounter velocities than plutinos. The mode of the encounter velocities is equal to 3.22 km s-1 for plutinos and 1.86 km s-1 for SDOs, and the mean values are equal to 2.92 km s-1 for plutinos and 2.45 km s-1 for SDOs. Orbits with smaller relative encounter velocities experience larger changes in both velocity and orbital energy. Successive encounters with the major planets cause the objects to evolve into the inner Solar System or to the transneptunian region up to ejection. Thus, larger changes in the orbits accelerate the rate of these transitions. We conclude that this explains why SDOs have a shorter mean lifetime than escaped plutinos.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg5.ps} \end{figure} Figure 5:

Mean lifetime of Plutinos (filled line) and of SDOs (dashed line) in the Centaur zone with perihelion distances less than a given value.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg6.ps} \end{figure} Figure 6:

Normalized distribution of encounter velocities with the major planets of SDOs (dashed line) and escaped plutinos (solid line).

Open with DEXTER

4.2 Number of plutino-Centaurs

To calculate the number of escaped plutinos located at present in the Centaur population, we calculate the present rate of injection of escaped plutinos into the Centaur zone. As we have mentioned, we assume that the long-term escapers of the plutino population, i.e., those that escape after t = 1.5 Gyr, represent the present plutino espapers. In Fig. 7, we plot the cumulative number of escaped plutinos injected into the Centaur zone ($N_{\rm c}$) with respect to the number of the remaining plutinos ($N_{\rm p}$), as a function of time. We have taken into account that a plutino escapes from the population when it has an encounter with a planet or is ejected, so the number of remaining plutinos depends on the plutinos injected into the Centaur zone but also on the escaped plutinos that are permanently or transitorily injected into the SD zone. As Fig. 7 shows, the ratio  $N_{\rm c}/N_{\rm p}$ is well fitted by a linear relation, given by

\begin{displaymath}% N_{\rm c}/N_{\rm p} = c ~ t + d, \end{displaymath} (3)

where: c=1.62076 $\times$ 10-10 $\pm$ 8.502 $\times$ $10 ^{-14}~{\rm yr}^{-1}$ and d = -0.228442 $\pm$ 0.000242.

The slope of the linear relation, c, represents the present rate of injection of plutinos from the 2:3 mean motion resonance into the Centaur zone.

The present number of escaped plutinos in the Centaur population can be calculated by differentiating Eq. (2), i.e.,  ${\rm d}N_{\rm C} / {\rm d}t = c N_{\rm p}$, where we have assumed that $N_{\rm p}$ is constant during an interval of time ${\rm d}t$. To calculate the present number of plutino-Centaurs, we assume that ${\rm d}t = l_{\rm C}$ and that $N_{\rm p}$ is constant during the lifetime of plutino-Centaurs, i.e.,

\begin{displaymath}% N_{\rm c} = c ~ N_{\rm p} ~ l_{\rm C}, \end{displaymath} (4)

where $l_{\rm C}$ is the mean lifetime in the Centaur zone.

Taking from de Elía et al. (2008) the present number of plutinos with radius R > 1 km as $N_{\rm p} \sim 10^8{-}10^9$, the rate of injection of plutinos with radii greater than 1 km into the Centaur zone should be between 1.6 to 16 plutinos every 100 years. This is between 250 and 25 times less than the rate of injection of SDOs into the Centaur zone obtained by Di Sisto & Brunini (2007). Thus the present number of plutino-Centaurs of radius greater than 1 km should be between 1.8 $\times$  106-1.8 $\times$ 107.

Di Sisto & Brunini (2007) estimated the number of Centaurs with R>1 km coming from the SD to be ${\sim}2.8$ $\times$ 108, hence Centaurs coming from plutinos should represent a fraction smaller than $6\%$ of the total Centaur population. That is to say that the plutino population is a secondary source of Centaurs, comparable to the contribution of the low eccentricity transneptunian objects, according to the estimations of Levison & Duncan (1997) of 1.2 $\times$ 107.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg7.ps} \end{figure} Figure 7:

Cumulative number of escaped plutinos injected into the Centaur zone ($N_{\rm c}$) with respect to the number of the remaining plutinos $N_{\rm p}$, as a function of time. The dashed line is the fitting to the data.

Open with DEXTER

4.3 Orbital evolution of escaped plutinos in the Centaur zone

Di Sisto & Brunini (2007) analyzed the dynamical behavior of the SDOs that enter the Centaur zone, and identified four classes of dynamical evolution. The Centaurs behaves as one of the classes or as a combination of them. For reasons ofcompleteness, we briefly describe the four classes here. The first type is characterized by the conservation of the perihelion distance into a range of values between that of Saturn and Neptune's orbit, the conservation of or the very slow variation in the perihelion longitude, and eccentricities greater than ${\sim}0.8$. The characteristics of this evolution make the orbit go into a ``pseudo-stable'' state during which the encounters with the planets are avoided or very weak, causing a very slow variation in the orbit orientation. The second type of objects represents those that exhibit ``resonance hopping'' (in which objects move quickly from one resonance, in this case with Neptune, to another) combined with a behavior similar to the first but with less constant eccentricity values and constant perihelion distances for shorter intervals of time (Tiscareno & Malhotra 2003). These objects also transfer between mean motion resonances and Kozai resonances. A Kozai resonance occurs when the argument of pericentre, w, librates about a constant value. For low inclinations, it is possible for w to librate about $w = 0 ^{\circ}$ and $w = 180^{\circ}$, and for large inclinations about $w = 90 ^{\circ}$ and $w = 270 ^{\circ}$. The semimajor axis of the object remains constant but the eccentricity and the inclination of the orbit are coupled in such a way that e is a maximum when i is a minimum, and vice versa. In these two first types, the objects have casual encounters with Neptune and Uranus, sometimes also with Saturn, but they are not strong enough to drastically change their orbit causing a kind of stable orbit in the Centaur zone. Into the third type of objects, we group those that have the behaviors of the first and second types, but they have perihelion distances near Neptune. These objects are therefore continuously entering and leaving the Centaur zone. The last type of objects represent those that enter a mean motion resonance or Kozai resonance for almost all their lifetime as a Centaur.

Bailey & Malhotra (2009) analyzed the chaotic behavior of the known Centaurs. Their analysis revealed that two types of chaotic evolution are quantitatively distinguishable. One random walk-type behavior and an orbital evolution dominated by intermittent resonance sticking. These two dynamical classes embrace the four already found by Di Sisto & Brunini (2007). Bailey & Malhotra (2009) also found that these two types of behavior are correlated with Centaur dynamical lifetimes.

In this paper, we have analyzed the orbital evolution of escaped plutinos in the Centaur zone, and have found that they can be grouped into the four dynamical classes proposed by Di Sisto & Brunini (2007). There are more particles that have the dynamical behaviors of the so-called second class. We note the high frequency of Kozai resonances in all the four classes. In the Centaur zone, mean motion resonances and Kozai resonances are more frequent for semimajor axes between 30 AU and 50 AU. For example in Fig. 8, we show the dynamical evolution of one plutino-Centaur of the second class for which there are transfers between mean motion resonances and Kozai resonances most of the time. Some particles once they escape, return to a plutino state for some time before evolving to their final state. There are also particles that exhibit a ``hand-off'' from the gravitational control of one planet to another until crossing Jupiter's orbit. The scale time of this hand-off is either as short as few Myr or as long as some hundreds of Myr. The particles that have shorter lifetimes (of about Myr) carry out short incursions into the Centaur zone, or transfer from the gravitational control of a Jovian planet to that of the next inside, eventually passing through mean motion resonances, or undergoing a quick diffusion through all the inter giant-planetary zone, until ejection from or injection into Jupiter's orbit.

\begin{figure} \par\includegraphics[width=8cm,clip]{13668fg8.ps} \end{figure} Figure 8:

Dynamical evolution of the orbital elements of an escaped plutino injected into the Centaur zone.

Open with DEXTER

5 Conclusions

We have performed two numerical simulations to produce particles that are representative of the plutinos escaping at present from the resonance and to describe their dynamical post-escape evolution. In the first simulation, we integrated 20 000 initial particles in the 2:3 resonance and found that ${\sim}88\%$ of the particles were left out of the integration while, the rest remained in it. Considering a plutino population of radius greater than 1 km of $N_{\rm p} \sim 10^8{-}10^9$, we obtained a present rate of escape of plutinos of between 1 and 10 every 10 years. From this integration, we selected the particles that are representative of the present escape plutinos and performed a second integration. From this last integration, we obtained the dynamical evolution of plutinos once they escape from the resonance. From the 1183 initial particles, 1179 were removed from the integration and 4 remained within. From the 1179 removed particles, 787 were ejected, 385 reached the Jupiter's zone, and 4 collided with the planets.

We found that the vast majority of escaped plutinos have encounters with Neptune, and that this planet governs their dynamical evolution. When a plutino escapes from the resonance, it is transferred to either the SD zone (q>30 AU) or the Centaur zone (q<30 AU), but eventually switches from Centaurs to SDOs or viceversa because of the dynamical influence of Neptune.

The densest zone in the orbital element space of escaped plutinos corresponds to the ranges 30 < a < 100 AU and $5^{\circ} < i < 40^{\circ}$ and perihelions close to the orbit of Neptune. When escaped plutinos are transferred to the SD, they are quickly locked into a mean motion resonance with Neptune in a similar way to the SDOs analyzed by Fernández et al. (2004) and Gallardo (2006). In the Centaur zone (the zone for which q < 30 AU), the distribution of escaped plutinos is similar to that of SDOs in the Centaur zone obtained by Di Sisto & Brunini (2007).

The orbital evolution of escaped plutinos in the Centaur zone can be grouped into the four dynamical classes proposed by Di Sisto & Brunini (2007). There are more particles that have the dynamical behavior of the second class, and the high frequency of Kozai resonances in all the four classes is remarkable. There are also several mean motion resonances densely populated in the ranges of 30 < a < 50 AU.

The escaped plutinos have a mean lifetime in the Centaur zone of 108 Myr, which is longer than that of Centaurs from SD of 72 Myr. Escaped-plutinos live longer than SDOs in the greater-perihelion Centaur zone, causing a slower diffusion to the inner Solar System of escaped-plutino orbits than of SDO orbits.

The present rate of injection of plutinos with radius greater than 1 km to the Centaur zone is between 1.6 and 16 plutinos every 100 years and the number of plutino-Centaurs with radius greater than 1 km would be between 1.8 $\times$ 106-1.8 $\times$ 107. Both the rate of injection and the number of Centaurs from plutinos are much lower than the contribution from the SD obtained by Di Sisto & Brunini (2007). Plutinos appear to represent a secondary source of Centaurs and contribute a fraction of less than $6\%$ to the total Centaur population.

Acknowledgements
We thank Matthew S. Tiscareno who, as referee, made valuable comments that helped to improve this manuscript.

References

  1. Bailey, B. L., & Malhotra, R. 2009, Icarus, 203, 155 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  3. Chiang, E., Lithwick, Y., Murray-Clay, R., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson, USA: University of Arizona Press), 895 [Google Scholar]
  4. de Elía, G. C., Brunini, A., & Di Sisto, R. P. 2008, A&A, 490, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Di Sisto, R. P., & Brunini, A. 2007, Icarus, 190, 224 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Di Sisto, R. P., Fernández, J. A., & Brunini, A. 2009, Icarus, 203, 140 [NASA ADS] [CrossRef] [Google Scholar]
  7. Duncan, M. J., Levison, H. F., & Budd, S. M. 1995, AJ, 110, 3073 [NASA ADS] [CrossRef] [Google Scholar]
  8. Elliot, J. L., Kern, S. D., Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fernández, J. A., Gallardo, T., & Brunini, A. 2002, Icarus, 159, 358 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fernández, J. A., Gallardo, T., & Brunini, A. 2004, Icarus, 172, 372 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gallardo, T. 2006, Icarus, 184, 29 [Google Scholar]
  12. Gladman, B., Marsden, B. G., & Vanlaerhoven, C. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, et al. (Tucson, USA: University of Arizona Press), 293 [Google Scholar]
  13. Kenyon, S. J., Bromley, B. C., O'Brien, D. P., & Davis, D. R. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, et al. (Tucson, USA: University of Arizona Press), 293 [Google Scholar]
  14. Laskar, J. 1993, Physica D, 67, 257 [Google Scholar]
  15. Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [Google Scholar]
  16. Malhotra, R. 1996, AJ, 111, 504 [NASA ADS] [CrossRef] [Google Scholar]
  17. Melita, M. D., & Brunini, A. 2000, Icarus, 147, 205 [NASA ADS] [CrossRef] [Google Scholar]
  18. Morbidelli, A. 1997, Icarus, 127, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  19. Nesvorný, D., & Roig, F. 2000, Icarus, 148, 282 [NASA ADS] [CrossRef] [Google Scholar]
  20. Nesvorný, D., Roig, F., & Ferraz-Mello, S. 2000, AJ, 119, 953 [NASA ADS] [CrossRef] [Google Scholar]
  21. Tiscareno, M. S., & Malhotra, R. 2003, AJ, 126, 3122 [NASA ADS] [CrossRef] [Google Scholar]
  22. Tiscareno, M. S., & Malhotra, R. 2009, AJ, 138, 827 [NASA ADS] [CrossRef] [Google Scholar]
  23. Yu, Q., & Tremaine, S. 1999, AJ, 118, 1873 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg1.ps} \end{figure} Figure 1:

Cumulative number of escaped particles ($N_{\rm e}$) with respect to the number of the surviving particles $N_{\rm p}$, versus the time t in Myr. The fit to the plot for t > 1.5 Gyr is also shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg2.ps} \end{figure} Figure 2:

Number of remaining plutinos ($N_{\rm p}$) versus the time t in Myr. A power-law fit to the plot for t > 100 Myr is also showed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{13668fg3.eps} \end{figure} Figure 3:

Time-weighed distribution of escaped plutinos in the orbital element space.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg4.ps} \end{figure} Figure 4:

Normalized fraction of escaped plutinos against lifetime in the Centaur zone (filled line) and normalized fraction of SDOs that enter the Centaur zone against lifetime there (dashed line).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg5.ps} \end{figure} Figure 5:

Mean lifetime of Plutinos (filled line) and of SDOs (dashed line) in the Centaur zone with perihelion distances less than a given value.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg6.ps} \end{figure} Figure 6:

Normalized distribution of encounter velocities with the major planets of SDOs (dashed line) and escaped plutinos (solid line).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13668fg7.ps} \end{figure} Figure 7:

Cumulative number of escaped plutinos injected into the Centaur zone ($N_{\rm c}$) with respect to the number of the remaining plutinos $N_{\rm p}$, as a function of time. The dashed line is the fitting to the data.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13668fg8.ps} \end{figure} Figure 8:

Dynamical evolution of the orbital elements of an escaped plutino injected into the Centaur zone.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.