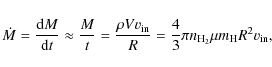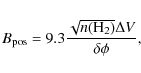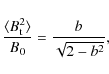| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200811137 | |
| Published online | 09 September 2010 | |
G30.79 FIR 10: a gravitationally bound infalling high-mass star-forming clump
P. C. Cortes1,3 - R. Parra2 - J. R. Cortes3 - E. Hardy3
1 - Departamento de Astronomía y Astrofísica, Pontificia Universidad
Católica de Chile, Casilla 306, Santiago 22, Chile
2 - European Southern Observatory, Alonso de Cordova 3107, Vitacura,
Casilla 19001, Santiago, Chile
3 - National Radio Astronomy Observatory, Joint ALMA Office, Apoquindo
3846 piso 19, Las Condes, Santiago, Chile
Received 13 October 2008 / Accepted 10 June 2010
Abstract
Context. The process of high-mass star formation is
still shrouded in controversy. Models are still tentative and current
observations are just beginning to probe the densest inner regions of
giant molecular clouds.
Aims. The study of high-mass star formation requires
the observation and analysis of high-density gas. This can be achieved
by the detection of emission from higher rotational transitions of
molecules in the sub-millimeter. Here, we studied the high-mass clump
G30.79 FIR 10 by observing molecular emission in the 345 GHz
band. The goal is to understand the gravitational state of this clump,
considering turbulence and magnetic fields, and to study the kinematics
of dense gas.
Methods. We approached this region by mapping the
spatial distribution of HCO
![]() ,
H13CO
,
H13CO
![]() ,
CS
,
CS
![]() ,
12CO
,
12CO
![]() ,
and 13CO
,
and 13CO
![]() molecular emission by using the ASTE telescope and by observing the 12C18O
molecular emission by using the ASTE telescope and by observing the 12C18O
![]() ,
HCN
,
HCN
![]() ,
and H13CN
,
and H13CN
![]() molecular transitions with the APEX telescope.
molecular transitions with the APEX telescope.
Results. Infalling motions were detected and modeled
toward this source. A mean infall velocity of 0.5 kms-1
with an infall mass rate of ![]()
![]() yr-1
was obtained. Also, a previously estimated value for the magnetic field
strength in the plane of the sky was refined to be 855
yr-1
was obtained. Also, a previously estimated value for the magnetic field
strength in the plane of the sky was refined to be 855 ![]() G which we
used to calculate a mass-to-magnetic flux ratio,
G which we
used to calculate a mass-to-magnetic flux ratio, ![]() ,
or super-critical. The virial mass from turbulent motions was also
calculated finding
,
or super-critical. The virial mass from turbulent motions was also
calculated finding ![]() ,
which gives a ratio of
,
which gives a ratio of ![]() /
/
![]() .
Both values strongly suggest that this clump must be in a state of
gravitational collapse. Additionally, we estimated the HCO+
abundance, obtaining X(HCO
.
Both values strongly suggest that this clump must be in a state of
gravitational collapse. Additionally, we estimated the HCO+
abundance, obtaining X(HCO
![]() .
.
Key words: magnetic fields - stars: formation - ISM: individual objects: G30.79 FIR 10
1 Introduction
It is well known that massive stars (![]() 10
10 ![]() )
form in giant
molecular clouds (GMCs), the largest molecular gas and dust complexes
in our galaxy. The amount of gas involved in this process is several
orders
of magnitude larger than in the low-mass star formation scenario, which
significantly increases the uncertainties that makes its study
difficult. In contrast to
the low-mass star formation case, where theory and observations have
established clear evolutionary steps (McKee
& Ostriker 2007), there are no
well defined stages for the evolution of proto-massive stars.
Presently, two different mechanisms are proposed as the dominant
process involved in the formation of massive stars. One mechanism is
the coalescence of small fragments
(Bonnell
et al. 2004,1998; Stahler et al. 2000).
The other is accretion
directly onto a massive protostellar object, which is
supported by accumulating evidence for disks around proto-massive stars
(McKee
& Ostriker 2007; Beuther & Sridharan 2007).
)
form in giant
molecular clouds (GMCs), the largest molecular gas and dust complexes
in our galaxy. The amount of gas involved in this process is several
orders
of magnitude larger than in the low-mass star formation scenario, which
significantly increases the uncertainties that makes its study
difficult. In contrast to
the low-mass star formation case, where theory and observations have
established clear evolutionary steps (McKee
& Ostriker 2007), there are no
well defined stages for the evolution of proto-massive stars.
Presently, two different mechanisms are proposed as the dominant
process involved in the formation of massive stars. One mechanism is
the coalescence of small fragments
(Bonnell
et al. 2004,1998; Stahler et al. 2000).
The other is accretion
directly onto a massive protostellar object, which is
supported by accumulating evidence for disks around proto-massive stars
(McKee
& Ostriker 2007; Beuther & Sridharan 2007).
The rate of formation of massive stars can be up to several orders of magnitude lower than low-mass stars, and they appear to be born in clusters. The process is highly energetic and dynamic, a massive star will quickly perturb and ionize its surrounding medium, which makes its study quite challenging (Wood & Churchwell 1989; Hoare et al. 2007). Therefore, it is crucial to probe the densest regions in high massive star forming clumps to understand their physical and chemical conditions. In this regard, high rotational levels from molecules emitting in the sub-millimeter windows are the ideal tracers to go for. The combination of optically thick and optically thin isotopomers of the same molecular species can be used to infer physical properties from star formation sites.
The magnetic field is likely the least known physical
parameter
in star formation. While its presence seems to be ubiquitous within the
ISM, with strengths ranging from a few ![]() G to mG
(Crutcher et al. 1999),
there are surprisingly few observations.
Moreover, while it is still unclear what role is played by
the magnetic field in the formation of low-mass stars, the degree of
uncertainty is even higher for high-mass star formation owing to the
lack of observations. However, we can say with certainty that magnetic
fields have been observed towards high-mass star forming regions
(Girart
et al. 2009; Cortes & Crutcher 2006).
Therefore, it is
important to incorporate it as a relevant physical parameter in
observations and models of high-mass start formation.
G to mG
(Crutcher et al. 1999),
there are surprisingly few observations.
Moreover, while it is still unclear what role is played by
the magnetic field in the formation of low-mass stars, the degree of
uncertainty is even higher for high-mass star formation owing to the
lack of observations. However, we can say with certainty that magnetic
fields have been observed towards high-mass star forming regions
(Girart
et al. 2009; Cortes & Crutcher 2006).
Therefore, it is
important to incorporate it as a relevant physical parameter in
observations and models of high-mass start formation.
In this paper we present a multi-line study of the high-mass star forming region G30.79 FIR 10. The aim of this paper is to understand the gravitational state of this clump as well as to study the kinematics of the dense gas. We also use previous inteferometric observations of polarized dust emission to include information about the magnetic field toward this region. The paper is organized as follows, Sect. 1 is the introduction, Sect. 2 presents the source, Sect. 3 the observational procedure. In Sect. 4 we present the results, while in Sect. 5 we discuss the abundance of HCO+. The kinematics of the gas is studied in Sect. 5, where we present evidence for infall motions and discuss the likelihood of outflows. Additionally, we refined a previous estimation of the magnetic field strength in the plane of the sky for this source (Cortes & Crutcher 2006), and use it to evaluate the gravitational state of this clump. Finally, Sect. 6 presents the summary and conclusions.
2 The source
G30.79 FIR 10 (hereafter G30.79) is a massive molecular complex
located within the W 43 region. It involves an H II
region-molecular
cloud complex near ![]() ,
with several far-infrared sources, of which G30.79 is the most massive
and densest
component. Figure 1
presents an overview of our observations
superposed over the 350
,
with several far-infrared sources, of which G30.79 is the most massive
and densest
component. Figure 1
presents an overview of our observations
superposed over the 350 ![]() m continuum map from Motte
et al. (2003).
Liszt (1995) observed
G30.79 in HCO+ and 13CO
concluding
that the presence of several rings and shells in the dense molecular
gas was a disturbance product of star formation. Vallée & Bastien (2000)
observed the dust continuum emission in this source at 760
m continuum map from Motte
et al. (2003).
Liszt (1995) observed
G30.79 in HCO+ and 13CO
concluding
that the presence of several rings and shells in the dense molecular
gas was a disturbance product of star formation. Vallée & Bastien (2000)
observed the dust continuum emission in this source at 760 ![]() m
using JCMT. They found linear polarization of about 1.9% with a
position angle (PA) of 160
m
using JCMT. They found linear polarization of about 1.9% with a
position angle (PA) of 160![]() .
Mooney et al. (1995)
observed this source at 1.3 mm using the IRAM 30 m
telescope,
detecting a total flux density of 13.6 Jy; their wide field
map shows
the clump and the extended H II region in the G30.79 complex. H2O
masers have been observed toward this region (Cesaroni
et al. 1988), which
are within a half arc-second of the peak in the Mooney et al. (1995)
map.
Additionally, Ellingsen (2007)
detected 6.7 GHz methanol masers
in the proximity of G30.79, which is considered to be a
signature for massive star formation. No centimeter radio-continuum
emission seems to be associated with FIR 10, suggesting that
the
source could be in an early stage of evolution. However, the maser
emission
already indicates that star formation has started and outflows may be
present. Motte et al. (2003)
mapped the
W43 main complex in dust continuum emission at 1.3 mm and
350
.
Mooney et al. (1995)
observed this source at 1.3 mm using the IRAM 30 m
telescope,
detecting a total flux density of 13.6 Jy; their wide field
map shows
the clump and the extended H II region in the G30.79 complex. H2O
masers have been observed toward this region (Cesaroni
et al. 1988), which
are within a half arc-second of the peak in the Mooney et al. (1995)
map.
Additionally, Ellingsen (2007)
detected 6.7 GHz methanol masers
in the proximity of G30.79, which is considered to be a
signature for massive star formation. No centimeter radio-continuum
emission seems to be associated with FIR 10, suggesting that
the
source could be in an early stage of evolution. However, the maser
emission
already indicates that star formation has started and outflows may be
present. Motte et al. (2003)
mapped the
W43 main complex in dust continuum emission at 1.3 mm and
350 ![]() m
with the IRAM 30 m and CSO telescopes, respectively. They also
mapped the
HCO+
m
with the IRAM 30 m and CSO telescopes, respectively. They also
mapped the
HCO+ ![]() line and measured H13CO+
line and measured H13CO+
![]() towards prominent dust maxima. One of the maxima,
W43-MM1, corresponds to G30.79 and is the compact fragment we
observed with ASTE. Motte
et al. (2003) found
towards prominent dust maxima. One of the maxima,
W43-MM1, corresponds to G30.79 and is the compact fragment we
observed with ASTE. Motte
et al. (2003) found ![]() km s-1,
km s-1,
![]() km s-1
(from
H13CO+),
km s-1
(from
H13CO+), ![]() K,
K,
![]()
![]() ,
and
,
and ![]() cm-3.
They estimated the virial mass to be
cm-3.
They estimated the virial mass to be ![]()
![]() ,
suggesting that this compact fragment
should be in a state of gravitational collapse unless there are other
sources of support in addition to kinetic energy. Cortes & Crutcher (2006)
mapped G30.79 in dust polarized emission at 1.3 mm using the
BIMA interferometer founding a polarization pattern, which suggests an
hour-glass morphology for the field. They also estimated the magnetic
field strength in the plane of the sky to be
,
suggesting that this compact fragment
should be in a state of gravitational collapse unless there are other
sources of support in addition to kinetic energy. Cortes & Crutcher (2006)
mapped G30.79 in dust polarized emission at 1.3 mm using the
BIMA interferometer founding a polarization pattern, which suggests an
hour-glass morphology for the field. They also estimated the magnetic
field strength in the plane of the sky to be ![]() 1.7 mG, which gave
a statistically corrected mass-to-magnetic flux ratio of 0.9 or
critical, where by critical we mean the equilibrium value between
self-gravitation and magnetic field support for the cloud.
1.7 mG, which gave
a statistically corrected mass-to-magnetic flux ratio of 0.9 or
critical, where by critical we mean the equilibrium value between
self-gravitation and magnetic field support for the cloud.
3 Observations
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11137fg1.eps}\par\psfrag{C...
... }
\par\psfrag{12CO32}[m][c][0.5]{$^{12}$ CO$(J=3\rightarrow 2)$ }\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg42.png)
|
Figure 1:
Overview of the G30.79FIR10 massive star forming region. The main panel
represents the 350 |
| Open with DEXTER | |
3.1 ASTE observations
G30.79 FIR 10 was observed during September 2006 using the Atacama Sub-millimeter Telescope Experiment (ASTE) from the National Astronomical Observatory of Japan (NAOJ) (Kohno 2005). The telescope is located at Pampa la bola in the Chilean Andes plateau reserve for Astronomical research at 4900 m of altitude. ASTE is a 10 m diameter antenna equipped with a 345 GHz double side band SIS-mixer receiver. We simultaneously observed 12CO3.2 APEX observations
Observations were performed during the first week of August 2008 using the Swedish Heterodyne Facility Instrument (SHFI) mounted on the Atacama Pathfinder Experiment telescope (APEX) (Güsten et al. 2006), located at llano de Chajnantor inthe Chilean Andes. We tuned SHFI at 329.3 GHz in order to detect the 12C18OTable 1: Line parameters.
4 Results
4.1 12CO, 13CO, and 12C18O
 results
results
The 12CO
![]() line was detected all over
the sampled region, covering an area of
line was detected all over
the sampled region, covering an area of
![]() around the peak from the dust
emission at 1.3 mm (see Fig. 1) The velocity
integrated emission
map is presented in Fig. 2
where the 12CO emission was
integrated over the complete available velocity range (43 to
154 kms-1). The peak in the map
corresponds to 317 K kms-1
located at about
around the peak from the dust
emission at 1.3 mm (see Fig. 1) The velocity
integrated emission
map is presented in Fig. 2
where the 12CO emission was
integrated over the complete available velocity range (43 to
154 kms-1). The peak in the map
corresponds to 317 K kms-1
located at about
![]() to the south-west from the reference position, while the peak
at the reference position is 234 K kms-1.
Overall we see most of
the emission clustered in a south-west to north-east elongated
pattern, which is consistent with the morphology of the dust emission
seen in the maps from Motte
et al. (2003) and
Mooney et al. (1995).
However, the peak in our 12CO map does not
coincide with the peak in dust emission (located at our reference
position). Figure 3
shows velocity channel maps binned every
5 kms-1 (or 50 channels) with a
resolution of 5.4 kms-1 for each
map with respect to the original resolution of 0.1 kms-1.
The channel maps
are presented in increasing velocity from 84 to 106 kms-1
covering
the most intense features in the 12CO emission.
By examining
Fig. 3, a
velocity gradient from the south-west to north-east
can be seen with each successive channel where the peaks in emission
are
at 89 and 95 kms-1 and at almost
opposite spatial
locations. Particularly interesting is the intense emission seen at
the south-west part of the map. According to Motte
et al. (2003, see Fig. 3 and
also our Fig. 1#, the giant H
II region produced
by a Wolf-Rayet cluster of massive stars has not yet reached the G30.79
clump. However, the Mooney
et al. (1995) maps put the H II region at an
interface with the clump. Because we could not sample beyond
105
to the south-west from the reference position, while the peak
at the reference position is 234 K kms-1.
Overall we see most of
the emission clustered in a south-west to north-east elongated
pattern, which is consistent with the morphology of the dust emission
seen in the maps from Motte
et al. (2003) and
Mooney et al. (1995).
However, the peak in our 12CO map does not
coincide with the peak in dust emission (located at our reference
position). Figure 3
shows velocity channel maps binned every
5 kms-1 (or 50 channels) with a
resolution of 5.4 kms-1 for each
map with respect to the original resolution of 0.1 kms-1.
The channel maps
are presented in increasing velocity from 84 to 106 kms-1
covering
the most intense features in the 12CO emission.
By examining
Fig. 3, a
velocity gradient from the south-west to north-east
can be seen with each successive channel where the peaks in emission
are
at 89 and 95 kms-1 and at almost
opposite spatial
locations. Particularly interesting is the intense emission seen at
the south-west part of the map. According to Motte
et al. (2003, see Fig. 3 and
also our Fig. 1#, the giant H
II region produced
by a Wolf-Rayet cluster of massive stars has not yet reached the G30.79
clump. However, the Mooney
et al. (1995) maps put the H II region at an
interface with the clump. Because we could not sample beyond
105
![]() west, we can only speculate about the nature of
this intense 12CO
west, we can only speculate about the nature of
this intense 12CO
![]() emission and whether it is related to an interface between this clump
and the H II region without further observations.
emission and whether it is related to an interface between this clump
and the H II region without further observations.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg2.eps}
\par\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg75.png)
|
Figure 2:
Velocity integrated 12CO
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg76.png)
|
Figure 3:
Channel maps for the 12CO line emission. Maps
are shown as averages of 50 channels giving a velocity
resolution of 5.4 kms-1 for each map.
The average velocity in each plot is shown by the box in lower left
corner of each map. Both |
| Open with DEXTER | |
To study the velocity structure at selected locations in the
integrated emission map, we present 12CO
spectra
from three positions in the map in Fig. 4. These positions
correspond to
averages over nine pointings centered at
![]() ,
(-90, -40) and (30, 40)arcsec. The (0, 0) offset plot corresponds to
the spectrum
over the reference position and had superposed 13CO
and
12C18O spectra as well.
The emission is strong with a peak
of 16 K for the 12CO, 8.5 K
for 13CO, and 3.1 K for
12C18O, obtained by
fitting Gaussian profiles. The
remaining spectra correspond only to 12CO and
are taken from the
maxima seen at 89 and 95 km s-1
velocity channel maps.
We did not obtain data from the other CO isotopomers
at these positions. We immediately appreciate that the 12CO
line
profiles are complex and have many components with the emission
appearing to
be optically thick. But owing to the large angular extension of the
whole W43 region, we did not find a suitable off position in our
observations. This is clearly seen in the dip features at the line
wings of our spectra (see Fig. 4
upper panel). While the emission at the off position is weak compared
to the peak
of the line, it is strong enough to disrupt the line-wings.
In principle this does not affect the
integrated intensity map, but it will prevent us from concluding about
possible outflow motions from the CO line-wings. We also see that all
spectra show blue-shifted peaks relative to
,
(-90, -40) and (30, 40)arcsec. The (0, 0) offset plot corresponds to
the spectrum
over the reference position and had superposed 13CO
and
12C18O spectra as well.
The emission is strong with a peak
of 16 K for the 12CO, 8.5 K
for 13CO, and 3.1 K for
12C18O, obtained by
fitting Gaussian profiles. The
remaining spectra correspond only to 12CO and
are taken from the
maxima seen at 89 and 95 km s-1
velocity channel maps.
We did not obtain data from the other CO isotopomers
at these positions. We immediately appreciate that the 12CO
line
profiles are complex and have many components with the emission
appearing to
be optically thick. But owing to the large angular extension of the
whole W43 region, we did not find a suitable off position in our
observations. This is clearly seen in the dip features at the line
wings of our spectra (see Fig. 4
upper panel). While the emission at the off position is weak compared
to the peak
of the line, it is strong enough to disrupt the line-wings.
In principle this does not affect the
integrated intensity map, but it will prevent us from concluding about
possible outflow motions from the CO line-wings. We also see that all
spectra show blue-shifted peaks relative to ![]() kms-1.
The
associated peak velocities are 94.24 kms-1
for (0, 0), 89.69 kms-1 for (-90, -40),
and 95.00 kms-1 for (30, 40). All
spectra show broad
line-wings, particularly at offset (-90, -40), and a high velocity
component at v=115 kms-1.
This peculiar emission may indicate
outflow motions, but as mentioned before, it is difficult to be
decisive due to contamination from the off position.
kms-1.
The
associated peak velocities are 94.24 kms-1
for (0, 0), 89.69 kms-1 for (-90, -40),
and 95.00 kms-1 for (30, 40). All
spectra show broad
line-wings, particularly at offset (-90, -40), and a high velocity
component at v=115 kms-1.
This peculiar emission may indicate
outflow motions, but as mentioned before, it is difficult to be
decisive due to contamination from the off position.
In mapping 13CO
![]() ,
we were only able to cover
an area of
,
we were only able to cover
an area of ![]() around the reference
position. The maximum is found at 124.7 K kms-1
located at
30
around the reference
position. The maximum is found at 124.7 K kms-1
located at
30
![]() west from the center. The emission also seems to
follow a south-west to north-east orientation like 12CO
do. Yet,
we cannot confirm the correlation due the lack of equal coverage for
our 13CO. Figure 4, first panel, shows a
spectrum
corresponding to the nine central pointings, or 30
west from the center. The emission also seems to
follow a south-west to north-east orientation like 12CO
do. Yet,
we cannot confirm the correlation due the lack of equal coverage for
our 13CO. Figure 4, first panel, shows a
spectrum
corresponding to the nine central pointings, or 30
![]() ,
in 12C18O and 13CO
overlaid
on the 12CO spectrum. The same complex features
seen in
12CO are seen in the 13CO
line profile, particularly the
high velocity component at 115 kms-1.
Signs of self-absorption near
the center of the line seem to be present, but not the strong
absorption seen in the 12CO profile at the
edges of the line
wings. From these features, it is likely that the 13CO
emission
that we detected towards the center is also optically thick. In
contrast, 12C18O is
single-peaked, with an almost Gaussian profile, showing no trace of
self-absorption, which suggests a likely optically thin emission.
,
in 12C18O and 13CO
overlaid
on the 12CO spectrum. The same complex features
seen in
12CO are seen in the 13CO
line profile, particularly the
high velocity component at 115 kms-1.
Signs of self-absorption near
the center of the line seem to be present, but not the strong
absorption seen in the 12CO profile at the
edges of the line
wings. From these features, it is likely that the 13CO
emission
that we detected towards the center is also optically thick. In
contrast, 12C18O is
single-peaked, with an almost Gaussian profile, showing no trace of
self-absorption, which suggests a likely optically thin emission.
| Figure 4:
Spectra from 12CO
|
|
| Open with DEXTER | |
An additional feature of the CO data is a consistent blue-shifted peak
emission. It has been suggested that optically thick lines with a
blue-shifted profile may indicate infall motions
(Leung & Brown 1977).
Both 12CO and 13CO
emission are similar
in complexity showing the same gradient in velocity from south-west to
north-east, broad line wings, and blue asymmetry in the line profile
(
![]() kms-1).
Particularly interesting is that
the line profiles in addition to their blue-shifted peak are both
self-absorbed,
which is also often seen in infall candidates (Klaassen & Wilson 2007).
Considering that our offset (0, 0) corresponds to the peak in dust
emission at both 1.3 mm and 350
kms-1).
Particularly interesting is that
the line profiles in addition to their blue-shifted peak are both
self-absorbed,
which is also often seen in infall candidates (Klaassen & Wilson 2007).
Considering that our offset (0, 0) corresponds to the peak in dust
emission at both 1.3 mm and 350 ![]() m, which covers most of the
continuum spectrum from pre-stellar cores, it is likely that the
condensation
we are seeing is actively forming stars. Unfortunately, we cannot
resolve the number of fragments due to the coarse
m, which covers most of the
continuum spectrum from pre-stellar cores, it is likely that the
condensation
we are seeing is actively forming stars. Unfortunately, we cannot
resolve the number of fragments due to the coarse ![]() beam of the
ASTE telescope. Our APEX observations, with their
beam of the
ASTE telescope. Our APEX observations, with their
![]() resolution will not help either because previous
interferometric, 4
resolution will not help either because previous
interferometric, 4
![]() resolution,
observations also did
not resolve the core (Cortes
& Crutcher 2006). However and due to the
expected multiplicity in high-mass star forming cores, it is unlikely
that we are seeing only a single object.
resolution,
observations also did
not resolve the core (Cortes
& Crutcher 2006). However and due to the
expected multiplicity in high-mass star forming cores, it is unlikely
that we are seeing only a single object.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg5.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg82.png)
|
Figure 5:
Velocity integrated emission map for HCO
|
| Open with DEXTER | |
4.2 HCO
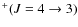 and H13CO
and H13CO
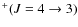 results
results
We observed HCO
![]() )
simultaneously with 12CO
)
simultaneously with 12CO
![]() ,
which also covered an area of
,
which also covered an area of
![]() .
The velocity integrated emission
map is presented in Fig. 5.
The morphology of the emission
follows the same orientation south-west to north-east as the 12CO observations,
but without the extension of 12CO. Clearly, the
strongest emission is clustered at the center of the map, to the
north-east, while some hint of emission over
.
The velocity integrated emission
map is presented in Fig. 5.
The morphology of the emission
follows the same orientation south-west to north-east as the 12CO observations,
but without the extension of 12CO. Clearly, the
strongest emission is clustered at the center of the map, to the
north-east, while some hint of emission over ![]() seems to appear
at the south-west, roughly at (
seems to appear
at the south-west, roughly at (
![]() ,
,
![]() ),
where the strongest 12CO
emission is located. The map morphology is also consistent with the
HCO
),
where the strongest 12CO
emission is located. The map morphology is also consistent with the
HCO
![]() map of Motte et al. (2003,
see Fig. 2).
Figure 6,
central panel, shows the spectrum from the
reference position for both HCO+ and H13CO+.
The line profile is clearly non-Gaussian, showing
evident self-absorption. It is likely that the HCO+
emission is
optically thick. No hint of emission is seen at the off position, which
is same
off position used for 12CO. Superposed in thick
lines is the H13CO
map of Motte et al. (2003,
see Fig. 2).
Figure 6,
central panel, shows the spectrum from the
reference position for both HCO+ and H13CO+.
The line profile is clearly non-Gaussian, showing
evident self-absorption. It is likely that the HCO+
emission is
optically thick. No hint of emission is seen at the off position, which
is same
off position used for 12CO. Superposed in thick
lines is the H13CO
![]() spectrum with a peak brightness temperature of
1.2 K at V=98.1 kms-1.
The H13CO+ emission is
only significant (over the 3
spectrum with a peak brightness temperature of
1.2 K at V=98.1 kms-1.
The H13CO+ emission is
only significant (over the 3![]() level)
at the reference position. The velocity associated with the peak can
be considered to be at the
level)
at the reference position. The velocity associated with the peak can
be considered to be at the ![]() within the boundaries of
the bin. The emission is also coincident with the strong absorption dip
in HCO+, suggesting self-absorption.
Additionally, because
the line profile appears to be Gaussian in shape, it
is likely that the H13CO+
emission is optically thin.
within the boundaries of
the bin. The emission is also coincident with the strong absorption dip
in HCO+, suggesting self-absorption.
Additionally, because
the line profile appears to be Gaussian in shape, it
is likely that the H13CO+
emission is optically thin.
| Figure 6:
High density molecular gas spectra from the G30.79 FIR 10 clump.
The upper panel presents the HCN
|
|
| Open with DEXTER | |
4.3 CS
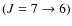 results
results
The integrated velocity map for CS
![]() is presented
in Fig. 7.
As for H13CO+, the CS
emission is fairly compact, arising only from the center of the map,
which
suggests that most of the activity is coincident with the peak of
the dust emission. The spectra from the
central 30
is presented
in Fig. 7.
As for H13CO+, the CS
emission is fairly compact, arising only from the center of the map,
which
suggests that most of the activity is coincident with the peak of
the dust emission. The spectra from the
central 30
![]() are shown in Fig. 6
in
the lower panel. The CS emission presents a peak brightness temperature
of 3.6 K at
V=98.1 kms-1 with
some excess emission in its line-wings,
which may be due to outflowing motions. Note that the CS emission is
not self-absorbed as seen
with HCO+ and HCN. It is possible that the
molecule is not abundant enough to become self-absorbed. However,
another possibility is
that the CS gas is bound inside the dense core, which would explain why
its emission is not widespread (as indicated by our map).
are shown in Fig. 6
in
the lower panel. The CS emission presents a peak brightness temperature
of 3.6 K at
V=98.1 kms-1 with
some excess emission in its line-wings,
which may be due to outflowing motions. Note that the CS emission is
not self-absorbed as seen
with HCO+ and HCN. It is possible that the
molecule is not abundant enough to become self-absorbed. However,
another possibility is
that the CS gas is bound inside the dense core, which would explain why
its emission is not widespread (as indicated by our map).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg90.png)
|
Figure 7:
Velocity integrated emission map for CS
|
| Open with DEXTER | |
4.4 HCN
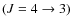 and H13CN
and H13CN
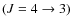 results
results
The HCN
![]() was observed in position-switching mode over and area of
was observed in position-switching mode over and area of
![]() to sample
the same region as HCO+. We looked for emission
only in
the most significant areas within the region.
The H13CN
to sample
the same region as HCO+. We looked for emission
only in
the most significant areas within the region.
The H13CN
![]() was only observed over the
central
was only observed over the
central ![]() ,
where we expected to find most of the emission.
Figure 8
presents the velocity integrated emission map
for HCN. While the emission is mostly concentrated at the center, there
is a hint
for a gradient along the south-west to north east direction as with HCO+
and CO.
The extent of the emission appears to be midway between the HCO+
,
where we expected to find most of the emission.
Figure 8
presents the velocity integrated emission map
for HCN. While the emission is mostly concentrated at the center, there
is a hint
for a gradient along the south-west to north east direction as with HCO+
and CO.
The extent of the emission appears to be midway between the HCO+
![]() and the CS
and the CS
![]() where the CS map presents the most compact
morphology.
Figure 6
shows in its upper panel the HCN
where the CS map presents the most compact
morphology.
Figure 6
shows in its upper panel the HCN
![]() overlaid by the H13CN
overlaid by the H13CN
![]() spectrum
in red. The HCN emission
is clearly opticaly thick with a self-absorption feature as indicated
by the optically thin H13CN. The double peaked
HCN
spectrum has a stronger blue peak at 93.8 kms-1;
while
the H13CN is peaked at 98.3 kms-1,
both taken from Gaussian fits.
This type of spectrum is often seen toward infall candidates
like the well-studied source B335 (Zhou
et al. 1993).
spectrum
in red. The HCN emission
is clearly opticaly thick with a self-absorption feature as indicated
by the optically thin H13CN. The double peaked
HCN
spectrum has a stronger blue peak at 93.8 kms-1;
while
the H13CN is peaked at 98.3 kms-1,
both taken from Gaussian fits.
This type of spectrum is often seen toward infall candidates
like the well-studied source B335 (Zhou
et al. 1993).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11137fg8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg91.png)
|
Figure 8:
Velocity integrated emission map for HCN
|
| Open with DEXTER | |
5 Analysis and discussion
5.1 The HCO+ abundance
In the current paradigm, it is suggested that carbon bearing molecules
will freeze onto grain surfaces, forming ices, in cold and dense cores
(see e.g. Bergin & Tafalla
2007); while some other molecular abundances,
like HCO+, might get enhanced by non-thermal
motions such as
outflows and/or infall (Rawlings
et al. 2004). In order to investigate
the abundance of HCO+ toward this region, we
estimate the
physical parameters associated with this molecule. The optical depth
for
HCO+ is estimated by the ratio between the
optically thick and
optically thin brightness temperatures by using (Choi
et al. 1993)
where
To obtain the column density for the upper rotational level,
we use
(Goldsmith & Langer 1999)
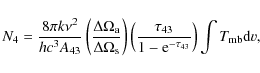
|
(2) |
where
where Z is the partition function, g=2J + 1 is the statistical weight of the upper level,
5.2 An outflow in G30.79 FIR 10?
One of the signatures of high-mass star formation are the powerful
molecular outflows observed toward these regions
(Bourke
et al. 1997; Shepherd et al. 2007).
Because FIR 10 is a massive core, it
is likely that outflowing motions are present or will develop over
time.
However, to untangle the outflow motions from our molecular emission
observations is certainly not trivial. The
choice of sub-millimeter emission lines as a tool to study this region
allow us to separate the most dense components from the rest of the
molecular core. Particularly, 12CO
![]() has been
successfully used to trace outflowing motion from star forming regions
(Choi et al. 1993).
However, our 12CO
has been
successfully used to trace outflowing motion from star forming regions
(Choi et al. 1993).
However, our 12CO
![]() results are
inconclusive because of emission at the off position, which affected
the line wings in our spectra. Also, the
high velocity component seen at V=115 kms-1,
which is
results are
inconclusive because of emission at the off position, which affected
the line wings in our spectra. Also, the
high velocity component seen at V=115 kms-1,
which is ![]() 20 kms-1
over
the
20 kms-1
over
the ![]() and is only seen in 12CO and 13CO
but not observed either in HCO+, HCN, or CS. It
is
likely that this component is not dense enough to excite either of
these
lines; indeed, this high velocity component might be optically
thin. Although it could be interpreted as high velocity outflow
emission, its widespread spatial distribution makes this
interpretation un-likely. Another possibility is that this component
corresponds to a foreground object, or cloud, which is not associated
with
this clump. Additionally, it is difficult to accelerate the gas to
such high velocities without dissociation.
and is only seen in 12CO and 13CO
but not observed either in HCO+, HCN, or CS. It
is
likely that this component is not dense enough to excite either of
these
lines; indeed, this high velocity component might be optically
thin. Although it could be interpreted as high velocity outflow
emission, its widespread spatial distribution makes this
interpretation un-likely. Another possibility is that this component
corresponds to a foreground object, or cloud, which is not associated
with
this clump. Additionally, it is difficult to accelerate the gas to
such high velocities without dissociation.
Outflows are discovered through their signature in the
line-wings of
molecular emission lines. Figure 9
shows the HCO+ and CS spectra with their
corresponding Gaussian fittings and the residual
emission in their line-wings. Between 100 and 110 kms-1
we
found some significant emission over the ![]() level, with
level, with
![]() K, in both CS and HCO+
spectrum. However,
the blue-shifted part of the emission, for velocities lower
than 95 kms-1, does not show
significant traces of residual emission.
Even though the red-shifted excess emission may be due to non-thermal
motions, the bipolar nature of an outflow must be clearly stated,
which we cannot do with these data.
Therefore, we cannot yet come to a conclusion about the presence of
a bipolar outflow towards this source. Our lack of spatial resolution
due to the distance to G30.79 FIR 10 might be the reason behind this.
However, outflows are ubiquitous in the high-mass star forming regions,
so it is likely that they
are present or will develop over time. Additional observations of
shocked excited chemistry, such as SiO, SO, or SO2
may help confirming
an outflow in this clump.
K, in both CS and HCO+
spectrum. However,
the blue-shifted part of the emission, for velocities lower
than 95 kms-1, does not show
significant traces of residual emission.
Even though the red-shifted excess emission may be due to non-thermal
motions, the bipolar nature of an outflow must be clearly stated,
which we cannot do with these data.
Therefore, we cannot yet come to a conclusion about the presence of
a bipolar outflow towards this source. Our lack of spatial resolution
due to the distance to G30.79 FIR 10 might be the reason behind this.
However, outflows are ubiquitous in the high-mass star forming regions,
so it is likely that they
are present or will develop over time. Additional observations of
shocked excited chemistry, such as SiO, SO, or SO2
may help confirming
an outflow in this clump.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11137fg9.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg114.png)
|
Figure 9:
Residual emission after Gaussian substraction is shown in both panels.
The lower panel shows the HCO
|
| Open with DEXTER | |
5.3 Infall motions
It is not clear whether high-mass stars
forms through accretion or through a different process such as
coalescence of less massive fragments. This situation is difficult to
distinguish due to the physical complexities involved in the evolution
of
high density gas and dust. The study of the kinematics and dynamics at
the earliest phases, along with the detection of accretion disks,
could clarify this uncertainty. In this scope, the determination of
infalling motions is a first step toward the identification of
collapsing pre-stellar objects. The characterization of these motions
is a challenging topic, the current avenue towards investigating
infalling is the
study of asymmetries in molecular line profiles. Leung & Brown (1977)
suggested that an asymmetry in the line profile toward the blue may
indicate the presence of infalling motions.
Thus, the low excitation, red-shifted
infalling layers of gas in the front part of the cloud absorbs
some of the emission from the rest of the gas. This red-shifted
self-absorption is what makes the spectrum present a brighter blue
peak.
To quantify this asymmetry, the calculation of the normalized
line velocity difference has been used by many authors (Wu et al.
2007; Fuller
et al. 2005; Szymczak et al. 2007).
where
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11137fg10.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg120.png)
|
Figure 10:
The central |
| Open with DEXTER | |
The main terms in this equation are the Planck excitation temperature given by
| |
= | ![$\displaystyle \tau_{0} \exp{\left[ \frac{-(v - v_{{\rm f}} - v_{{\rm lsr}})^2}
{2\sigma^2} \right]}$](/articles/aa/full_html/2010/11/aa11137-08/img133.png)
|
(6) |
| = | ![$\displaystyle \tau_{0} \exp{\left[ \frac{-(v + v_{{\rm r}} - v_{{\rm lsr}})^2}
{2\sigma^2} \right]},$](/articles/aa/full_html/2010/11/aa11137-08/img135.png)
|
(7) |
where
Table 2: Parameters from the model fit.
| Figure 11: Central HCN spectrum from G30.79 FIR 10. Overlaid in thick lines is the best fit for the infalling model. |
|
| Open with DEXTER | |
The infalling velocity for both slabs is estimated by the infalling
model
to be ![]() kms-1
and
kms-1
and ![]() kms-1.
A simple estimation can also be done by using the analytical model
derived by Myers et al.
(1996) for a contracting cloud.
By using Eq. (9), from their model, we
estimated an infalling velocity of 0.5 kms-1.
This result is in good agreement with the the values obtained by
adjusting the model to our data. The next step is to estimate the mass
infall rate, which we do by following (Klaassen
& Wilson 2007)
kms-1.
A simple estimation can also be done by using the analytical model
derived by Myers et al.
(1996) for a contracting cloud.
By using Eq. (9), from their model, we
estimated an infalling velocity of 0.5 kms-1.
This result is in good agreement with the the values obtained by
adjusting the model to our data. The next step is to estimate the mass
infall rate, which we do by following (Klaassen
& Wilson 2007)
where
Table 3: Normalized velocity difference.
5.4 Dynamical state of G30.79
5.4.1 The magnetic field
The dynamical state of high-mass star forming cores is difficult to establish. The accumulation of a large amount of molecular gas is still poorly understood, as is what triggers the gravitational collapse. Moreover, it is known that magnetic fields are present in these regions with strengths substantially larger than in low-mass star forming regions (Lai 2001; Cortes & Crutcher 2006). Thus, the magnetic field can have a profound effect on the dynamical evolution of the gas as postulated by ambipolar diffusion theories (Ciolek & Mouschovias 1993). Our object of study is not an exception to the above. Magnetic fields have been observed through polarized emission from dust towards this core (Vallée & Bastien 2000; Cortes & Crutcher 2006). However, it is not yet clear how important the field is with respect to turbulence in the high-mass star forming process, but its presence alone is a reason to consider its effects.
From the interferometric observations of polarized dust
emission,
Cortes & Crutcher (2006)
found a smooth polarimetric pattern centered at
the G30.79 FIR 10 clump. Assuming magnetic alignment of dust grains,
they proposed
an hourglass morphology for the field. Additionally, they
estimated the magnetic field strength on the plane
of the sky using the Chandrasekhar-Fermi method (Chandrasekhar & Fermi 1953),
finding a value of ![]() mG.
In this way,
the mass-to-magnetic flux ratio was calculated to be
mG.
In this way,
the mass-to-magnetic flux ratio was calculated to be ![]() or critical.
In this work, we refined the previously described
estimation by considering our molecular line observations. Before
stating this improvement, we will briefly introduce the
Chandrasekhar-Fermi method by the following equation.
or critical.
In this work, we refined the previously described
estimation by considering our molecular line observations. Before
stating this improvement, we will briefly introduce the
Chandrasekhar-Fermi method by the following equation.
where
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11137fg12.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg165.png)
|
Figure 12: The polarization position angle dispersion function is shown here in closed circles along with its respective error bars. The dispersion function points are join with thick lines, while superposed is the fit for Eq. (10) to the first 3 points. |
| Open with DEXTER | |
While the polarization pattern observed by Cortes
& Crutcher (2006) is smooth,
it is unclear how distorted by turbulence the field might be. This
source
is 5.5 kpc away which gives 0.03 pc/1
![]() or 0.1 pc/beamsize.
This length scale is larger than the predicted turbulence length scale
of
1 mpc (Yan
et al. 2004; Li & Houde 2008).
Therefore, the dispersion in the
field lines, or the turbulent component of the field, cannot be
directly
seen from the polarization pattern.
Hildebrand et al. (2009)
developed an approximation to calculate the plane of the sky dispersion
function
for the magnetic field in turbulent molecular clouds. By using
polarized
emission from dust, they calculated a dispersion function for the
polarization
position angle as a quadratic function of
the length scale. Two main assumptions are made in this calculation.
The length scale is larger
than the turbulence, or correlation length scale, and smaller than the
length scale associated with large scale variations of the field.
Our BIMA polarization data satisfy both assumptions, the
interferometric
observations have a length scale on the order of 0.1 pc while
the field varies
over 1 pc distances (as seen from the polarization
pattern). This approximation is stated in Eq. (2) in Hildebrand et al. (2009).
From this approximation, the ratio between the turbulent component of
the
field on the plane of the sky and the main magnetic field strength can
be estimated as
or 0.1 pc/beamsize.
This length scale is larger than the predicted turbulence length scale
of
1 mpc (Yan
et al. 2004; Li & Houde 2008).
Therefore, the dispersion in the
field lines, or the turbulent component of the field, cannot be
directly
seen from the polarization pattern.
Hildebrand et al. (2009)
developed an approximation to calculate the plane of the sky dispersion
function
for the magnetic field in turbulent molecular clouds. By using
polarized
emission from dust, they calculated a dispersion function for the
polarization
position angle as a quadratic function of
the length scale. Two main assumptions are made in this calculation.
The length scale is larger
than the turbulence, or correlation length scale, and smaller than the
length scale associated with large scale variations of the field.
Our BIMA polarization data satisfy both assumptions, the
interferometric
observations have a length scale on the order of 0.1 pc while
the field varies
over 1 pc distances (as seen from the polarization
pattern). This approximation is stated in Eq. (2) in Hildebrand et al. (2009).
From this approximation, the ratio between the turbulent component of
the
field on the plane of the sky and the main magnetic field strength can
be estimated as
where b is the turbulent contribution to the dispersion function,
5.4.2 The gravitational equilibrium in G30.79 FIR 10
This source is one of the few where information about the magnetic
field and
turbulence is present. Thus, we should be able to characterize with
confidence
the state of gravitational equilibrium in this source. In order to
quantify this,
we will follow the analysis as stated by McKee
& Zweibel (1992) and Bertoldi
& McKee (1992):
| (11) |
where
Motte et al. (2003)
estimated the virial mass without knowing the
magnetic field, stating that G30.79 FIR 10 is likely to be bound. To
estimate
the virial mass they used ![]() from
Bertoldi & McKee (1992),
which we refined by deriving our own values for
R=0.3 pc (obtained from the interferometric
map
of dust emission from Cortes
& Crutcher 2006 as half the size of
the continuum core or
from
Bertoldi & McKee (1992),
which we refined by deriving our own values for
R=0.3 pc (obtained from the interferometric
map
of dust emission from Cortes
& Crutcher 2006 as half the size of
the continuum core or ![]() ),
and
),
and ![]() m s-1
from our
H13CO+ observations (
m s-1
from our
H13CO+ observations (![]() is not the FWHM value), obtaining
is not the FWHM value), obtaining
![]()
![]() .
Comparing this with the mass of the
clump taken to be
.
Comparing this with the mass of the
clump taken to be ![]() (Cortes & Crutcher 2006)
we obtained the ratio of the virial mass to the
dust mass to be
(Cortes & Crutcher 2006)
we obtained the ratio of the virial mass to the
dust mass to be ![]() /
/
![]() .
Values of
.
Values of
![]() /
/
![]() are considered to remain
gravitationally bound according to Pound
& Blitz (1993). At the same time,
we recall our previous calculation of the mass-to-magnetic flux
ratio, which was found to be super-critical. This means that there is
not enough energy in the turbulence and/or in the magnetic field to
balance gravity. Therefore and even though the uncertainties involved
in the total mass estimations for this object, the results
suggest that G30.79 FIR 10 is bound and must be undergoing
gravitational collapse. The whole picture appears to be
self-consistent,
we have detected infalling motions into the clump where neither
turbulence or
the magnetic field have enough energy to counterbalance gravity.
are considered to remain
gravitationally bound according to Pound
& Blitz (1993). At the same time,
we recall our previous calculation of the mass-to-magnetic flux
ratio, which was found to be super-critical. This means that there is
not enough energy in the turbulence and/or in the magnetic field to
balance gravity. Therefore and even though the uncertainties involved
in the total mass estimations for this object, the results
suggest that G30.79 FIR 10 is bound and must be undergoing
gravitational collapse. The whole picture appears to be
self-consistent,
we have detected infalling motions into the clump where neither
turbulence or
the magnetic field have enough energy to counterbalance gravity.
6 Summary and conclusions
We mapped the G30.79 FIR 10 molecular clump embedded in the W43
mini-starburst by mapping the molecular emission from 12CO
![]() ,
13CO
,
13CO
![]() ,
C18O
,
C18O
![]() ,
CS
,
CS
![]() ,
HCO
,
HCO
![]() ,
H13CO
,
H13CO
![]() ,
HCN
,
HCN
![]() ,
and H13CN
,
and H13CN
![]() .
Emission from 12CO is
extended presenting a gradient
from south-west to north-east, consistent with the dust morphology of
the core. Even though we mapped 13CO from a
smaller region
surrounding the center, its emission appears to follow 12CO,
which is
also optically thick. The C18O emission was also
mapped at the
central
.
Emission from 12CO is
extended presenting a gradient
from south-west to north-east, consistent with the dust morphology of
the core. Even though we mapped 13CO from a
smaller region
surrounding the center, its emission appears to follow 12CO,
which is
also optically thick. The C18O emission was also
mapped at the
central ![]() .
Its line
profile is almost Gaussian without any of the complex features seen in
the previous CO isotopomers and is likely optically thin. We found a
high
velocity component at 115 kms-1, which
was also present all over our sampled
region. We interpreted this emission as a foreground cloudlet not
associated with our clump. The emission from HCO+
is optically thick, with an optical depth
.
Its line
profile is almost Gaussian without any of the complex features seen in
the previous CO isotopomers and is likely optically thin. We found a
high
velocity component at 115 kms-1, which
was also present all over our sampled
region. We interpreted this emission as a foreground cloudlet not
associated with our clump. The emission from HCO+
is optically thick, with an optical depth ![]() ,
but more compact
than 12CO. This is expected due to the higher
densities required
to excite this molecule. Additionally, both CS and H13CO+are
even more compact, with the emission coming mostly from the central
,
but more compact
than 12CO. This is expected due to the higher
densities required
to excite this molecule. Additionally, both CS and H13CO+are
even more compact, with the emission coming mostly from the central
![]() and consistent with the
position of the dust maxima obtained by others. By using our
observations, we estimated the HCO+ abundance X(HCO
and consistent with the
position of the dust maxima obtained by others. By using our
observations, we estimated the HCO+ abundance X(HCO
![]() ,
a depletion factor
,
a depletion factor ![]() ,
which is consistent with estimations done toward other high-mass star
forming regions (Purcell
et al. 2006).
,
which is consistent with estimations done toward other high-mass star
forming regions (Purcell
et al. 2006).
Outflows were looked for in the line-wings of the observed
molecular
lines toward the center of G30.79 FIR 10. All HCO+,
HCN, and CS
profiles present excess emission in their line wings. However, the
bipolar nature of this emission is inconclusive at the ![]() level.
Infalling motions were also looked for by studying the profile
asymmetry
of our molecular observations. The blue asymmetry was estimated by
calculating
the normalized velocity difference (see Table 3). The clearest
evidence for infall is
given by the HCN spectra. Toward the center and surroundings pointings,
the emission is double peaked with the blue peak
stronger than the red peak (see Figs. 6 and 10). By using the Myers et al. (1996)
improved model by Di Francesco
et al. (2001),
we estimated an infall velocity of 0.5 kms-1
with an infall rate of
level.
Infalling motions were also looked for by studying the profile
asymmetry
of our molecular observations. The blue asymmetry was estimated by
calculating
the normalized velocity difference (see Table 3). The clearest
evidence for infall is
given by the HCN spectra. Toward the center and surroundings pointings,
the emission is double peaked with the blue peak
stronger than the red peak (see Figs. 6 and 10). By using the Myers et al. (1996)
improved model by Di Francesco
et al. (2001),
we estimated an infall velocity of 0.5 kms-1
with an infall rate of ![]()
![]() yr-1.
yr-1.
We refined a previous estimate for the magnetic field strength
on the
plane of sky in this region. Interferometric observations of polarized
emission from dust from Cortes
& Crutcher (2006) estimated a magnetic field
of ![]() mG,
by using the Chandrashekar-Fermi technique. The
estimation needs a reliable tracer for the gas turbulent motions from
the
region traced by the dust emission. By using the line-width from our
ion optically thin molecule H13CO
mG,
by using the Chandrashekar-Fermi technique. The
estimation needs a reliable tracer for the gas turbulent motions from
the
region traced by the dust emission. By using the line-width from our
ion optically thin molecule H13CO
![]() ,
,
![]() kms-1,
we were able to obtained an improved
estimation of
kms-1,
we were able to obtained an improved
estimation of ![]()
![]() G for the
magnetic field,
which also refined the mass-to-magnetic flux ratio to
G for the
magnetic field,
which also refined the mass-to-magnetic flux ratio to ![]() or
super-critical. Along with
or
super-critical. Along with ![]() ,
we calculated the contribution
from turbulence to the virial mass, getting a value of
,
we calculated the contribution
from turbulence to the virial mass, getting a value of
![]() /
/
![]() .
These two results suggest
that neither the magnetic field nor the turbulence have enough energy
to
counterbalance gravity. Therefore, the G30.79 FIR 10 clump must be
bound and
undergoing gravitational collapse. This also reinforce the core as an
infall candidate.
.
These two results suggest
that neither the magnetic field nor the turbulence have enough energy
to
counterbalance gravity. Therefore, the G30.79 FIR 10 clump must be
bound and
undergoing gravitational collapse. This also reinforce the core as an
infall candidate.
P. C. Cortés and R. Parra acknowledges support by the FONDECYT grants 3085039 and 3085032 respectively. J. R. Cortés and E. Hardy acknowledge support from the National Radio Astronomy Observatory of the United States. The National Radio Astronomy Observatory is a facilityof the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Barnes, P. J., Yonekura, Y., Ryder, S. D., et al. 2010, MNRAS, 402, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Ungerechts, H., Goldsmith, P. F., et al. 1997, ApJ, 482, 267 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bertoldi, F. & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Sridharan, T. K. 2007, ApJ, 668, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., & Zinnecker, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Bourke, T. L., Garay, G., Lehtinen, K. K., et al. 1997, ApJ, 476, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Palagi, F., Felli, M., et al. 1988, A&AS, 76, 445 [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, M., Evans, II, N. J., & Jaffe, D. T. 1993, ApJ, 417, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., & Mouschovias, T. C. 1993, ApJ, 418, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Cortes, P., & Crutcher, R. M. 2006, ApJ, 639, 965 [Google Scholar]
- Crutcher, R. M., Troland, T. H., Lazareff, B., Paubert, G., & Kazès, I. 1999, ApJ, 514, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Defrees, D. J., Loew, G. H., & McLean, A. D. 1982, ApJ, 257, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Myers, P. C., Wilner, D. J., Ohashi, N., & Mardones, D. 2001, ApJ, 562, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Ellingsen, S. P. 2007, MNRAS, 377, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. I. 2003, in SFChem 2002: Chemistry as a Diagnostic of Star Formation, ed. C. L. Curry, & M. Fich, 157 [Google Scholar]
- Fuller, G. A., Williams, S. J., & Sridharan, T. K. 2005, A&A, 442, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H., Kirby, L., Dotson, J. L., Houde, M., & Vaillancourt, J. E. 2009, ApJ, 696, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Hiramatsu, M., Hayakawa, T., Tatematsu, K., et al. 2007, ApJ, 664, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Hoare, M. G., Kurtz, S. E., Lizano, S., Keto, E., & Hofner, P. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 181 [Google Scholar]
- Klaassen, P. D., & Wilson, C. D. 2007, ApJ, 663, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Kohno, K. 2005, in The Cool Universe: Observing Cosmic Dawn, ed. C. Lidman, & D. Alloin, ASP Conf. Ser., 344, 242 [Google Scholar]
- Lai, S. P. 2001, Ph.D. Thesis, University of Illinois at Urbana - Champaign, Urbana, IL 61801, available at the Astronomy library at the Astronomy building [Google Scholar]
- Leung, C. M., & Brown, R. L. 1977, ApJ, 214, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H.-B., & Houde, M. 2008, ApJ, 677, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H., & Lucas, R. 2000, A&A, 355, 333 [NASA ADS] [Google Scholar]
- Liszt, H. S. 1995, AJ, 109, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Zweibel, E. G. 1992, ApJ, 399, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Mooney, T., Sievers, A., Mezger, P. G., et al. 1995, A&A, 299, 869 [NASA ADS] [Google Scholar]
- Motte, F., Schilke, P., & Lis, D. C. 2003, ApJ, 582, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Mardones, D., Tafalla, M., Williams, J. P., & Wilner, D. J. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Pound, M. W., & Blitz, L. 1993, ApJ, 418, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H. 2002, Numerical recipes in C++: the art of scientific computing, ed. W. H. Press [Google Scholar]
- Purcell, C. R., Balasubramanyam, R., Burton, M. G., et al. 2006, MNRAS, 367, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, J. M. C., Redman, M. P., Keto, E., & Williams, D. A. 2004, MNRAS, 351, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, C., Apponi, A. J., Ziurys, L. M., & Wyckoff, S. 2002, ApJ, 578, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, D. S., Povich, M. S., Whitney, B. A., et al. 2007, ApJ, 669, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, Y. L., Evans, II, N. J., Young, K. E., Knez, C., & Jaffe, D. T. 2003, ApJS, 149, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Palla, F., & Ho, P. T. P. 2000, Protostars and Planets IV, 327 [Google Scholar]
- Szymczak, M., Bartkiewicz, A., & Richards, A. M. S. 2007, A&A, 468, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vallée, J. P., & Bastien, P. 2000, ApJ, 530, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, A. J., & Burton, M. G. 2006, MNRAS, 365, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Henkel, C., Xue, R., Guan, X., & Miller, M. 2007, ApJ, 669, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Lazarian, A., & Draine, B. T. 2004, ApJ, 616, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S., Evans, II, N. J., Koempe, C., & Walmsley, C. M. 1993, ApJ, 404, 232 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table 1: Line parameters.
Table 2: Parameters from the model fit.
Table 3: Normalized velocity difference.
All Figures
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11137fg1.eps}\par\psfrag{C...
... }
\par\psfrag{12CO32}[m][c][0.5]{$^{12}$ CO$(J=3\rightarrow 2)$ }\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg42.png)
|
Figure 1:
Overview of the G30.79FIR10 massive star forming region. The main panel
represents the 350 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg2.eps}
\par\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg75.png)
|
Figure 2:
Velocity integrated 12CO
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg3.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg76.png)
|
Figure 3:
Channel maps for the 12CO line emission. Maps
are shown as averages of 50 channels giving a velocity
resolution of 5.4 kms-1 for each map.
The average velocity in each plot is shown by the box in lower left
corner of each map. Both |
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Spectra from 12CO
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg5.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg82.png)
|
Figure 5:
Velocity integrated emission map for HCO
|
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
High density molecular gas spectra from the G30.79 FIR 10 clump.
The upper panel presents the HCN
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11137fg7.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg90.png)
|
Figure 7:
Velocity integrated emission map for CS
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11137fg8.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg91.png)
|
Figure 8:
Velocity integrated emission map for HCN
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11137fg9.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg114.png)
|
Figure 9:
Residual emission after Gaussian substraction is shown in both panels.
The lower panel shows the HCO
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11137fg10.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg120.png)
|
Figure 10:
The central |
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Central HCN spectrum from G30.79 FIR 10. Overlaid in thick lines is the best fit for the infalling model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11137fg12.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa11137-08/Timg165.png)
|
Figure 12: The polarization position angle dispersion function is shown here in closed circles along with its respective error bars. The dispersion function points are join with thick lines, while superposed is the fit for Eq. (10) to the first 3 points. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




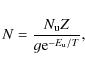
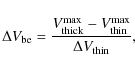
![\begin{displaymath}
\Delta T_{{\rm B}} = (J_{{\rm f}} - J_{{\rm C}})[1 - {\rm e}...
...{\rm cmb}})[1 - {\rm e}^{-(\tau_{{\rm r}} + \tau_{{\rm f}})}].
\end{displaymath}](/articles/aa/full_html/2010/11/aa11137-08/img121.png)