EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) L16 Full HTML
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number L16
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201014685
Published online 16 July 2010
A&A 518, L16 (2010)

Herschel: the first science highlights

LETTER TO THE EDITOR

First detection of the Sunyaev Zel'dovich effect increment at 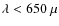$\lambda < 650~{\sf\mu}$m[*]

M. Zemcov1,2 - M. Rex3 - T. D. Rawle3 - J. J. Bock1,2 - E. Egami3 - B. Altieri4 - A. W. Blain1 - F. Boone5,7 - C. R. Bridge1 - B. Clement6 - F. Combes7 - C. D. Dowell1,2 - M. Dessauges-Zavadsky8 - D. Fadda9 - O. Ilbert6 - R. J. Ivison10,11 - M. Jauzac6 - J.-P. Kneib6 - D. Lutz12 - R. Pelló5 - M. J. Pereira3 - P. G. Pérez-González13,3 - J. Richard14 - G. H. Rieke3 - G. Rodighiero15 - D. Schaerer8,5 - G. P. Smith16 - I. Valtchanov4 - G. L. Walth3 - P. van der Werf17 - M. W. Werner2

1 - California Institute of Technology, Pasadena, CA 91125, USA
2 - Jet Propulsion Laboratory, Pasadena, CA 91109, USA
3 - Steward Observatory, University of Arizona, 933 N. Cherry Ave, Tucson, AZ 85721, USA
4 - Herschel Science Centre, ESAC, ESA, PO Box 78, Villanueva de la Cañada, 28691 Madrid, Spain
5 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 Av. Edouard Belin, 31400 Toulouse, France
6 - Laboratoire d'Astrophysique de Marseille, CNRS - Université Aix-Marseille, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
7 - Observatoire de Paris, LERMA, 61 Av. de l'Observatoire, 75014 Paris, France
8 - Geneva Observatory, University of Geneva, 51, Ch. des Maillettes, 1290 Versoix, Switzerland
9 - NASA Herschel Science Center, California Institute of Technology, MS 100-22, Pasadena, CA 91125, USA
10 - UK Astronomy Technology Centre, Science and Technology Facilities Council, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
11 - Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
12 - Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
13 - Departamento de Astrofísica, Facultad de CC. Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
14 - Institute for Computational Cosmology, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
15 - Department of Astronomy, University of Padova, Vicolo dell'Osservatorio 3, 35122 Padova, Italy
16 - School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
17 - Sterrewacht Leiden, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands

Received 31 March 2010 / Accepted 10 May 2010

Abstract
The Sunyaev-Zel'dovich (SZ) effect is a spectral distortion of the cosmic microwave background as observed through the hot plasma in galaxy clusters. This distortion is a decrement in the CMB intensity for $\lambda > 1.3~$mm, an increment at shorter wavelengths, and small again by $\lambda \sim 250~\mu$m. As part of the Herschel Lensing Survey (HLS) we have mapped 1E0657-56 (the Bullet cluster) with SPIRE with bands centered at 250, 350 and 500 $\mu $m and have detected the SZ effect at the two longest wavelengths. The measured SZ effect increment central intensities are $\Delta I_{0} = 0.097 \pm 0.019$ MJy sr-1 at 350 $\mu $m and $\Delta I_{0} = 0.268 \pm 0.031$ MJy sr-1 at 500 $\mu $m, consistent with the SZ effect spectrum derived from previous measurements at 2 mm. No other diffuse emission is detected. The presence of the finite temperature SZ effect correction is preferred by the SPIRE data at a significance of 2.1$\sigma$, opening the possibility that the relativistic SZ effect correction can be constrained by SPIRE in a sample of clusters. The results presented here have important ramifications for both sub-mm measurements of galaxy clusters and blank field surveys with SPIRE.

Key words: cosmic background radiation - galaxies: clusters: individual: 1E0657-56

1 Introduction

The Sunyaev-Zel'dovich (SZ) effect is a distortion of the spectral shape of the cosmic microwave background (CMB) due to inverse Compton scattering in the ubiquitous, hot ( $T_{{\rm e}} \sim 10^{7}$ K) intracluster medium (ICM) of galaxy clusters (Sunyaev & Zeldovich 1972). The canonical thermal SZ spectrum is a decrement in the brightness of the CMB as measured through galaxy clusters at mm wavelengths and an increment at sub-mm wavelengths which passes though a null at $\lambda \approx 1.3$ mm. To correctly describe the SZ spectral distortion when relativistic electrons are present or the cluster is moving with respect to the CMB additional correction terms, usually termed ``relativistic'' (or ``finite temperature'') corrections and ``kinetic'' SZ effect, are required. Measurement of these corrections is only possible using observations at multiple wavelengths, and is expedited by measurement at wavelengths where the expected modifications to the thermal SZ effect are largest. In the case of the finite temperature corrections, the largest changes expected in the SZ increment are at wavelengths shorter than 1 $\mu $m.

Decrements in emission are rare astrophysically and can be ascribed to the SZ effect with little ambiguity; this has lead to measurements of the SZ effect at $\lambda \gtrsim 2~$mm becoming almost routine. In comparison, measurements of the SZ effect increment are complicated by the presence of the dusty, high redshift galaxies which constitute the sub-mm cosmic background. Additionally, the individual sources comprising the sub-mm background are gravitationally lensed by galaxy clusters, the effect of which is to preferentially correlate increases in sub-mm emission with clustering. This correlation makes unambiguous detection of the SZ increment difficult, though successful measurements do exist (Lamarre et al. 1998; Komatsu et al. 1999; Zemcov et al. 2003; Zemcov et al. 2007; Nord et al. 2009). Moreover, the presence of the sub-mm background may contaminate measurements of the SZ effect for $\lambda > 1~$mm in less massive galaxy clusters (Aghanim et al. 2005). A better understanding of the sub-mm emission associated with galaxy clusters is required.

\begin{figure} \par\includegraphics[width=16cm,clip]{14685fig1.ps} \vspace{-3mm}\end{figure} Figure 1:

Source subtracted maps at 250, 350 and 500 $\mu $m; these figures show the same regions defined by the 7$^\prime $ $\times 7 $$^\prime $green boxes in Fig. 1 of Egami et al. (2010). All three maps are shown on the colour scale shown at right; units are mJy beam-1. The left most panel shows the source-subtracted 250 $\mu $m map; the confused sub-mm background is most clearly evident in this band. The center and rightmost panels are respectively the 350 and 500 $\mu $m source removed and masked maps; their construction is discussed in the text. The cross hairs show the best fitting SZ effect centroid from Halverson et al. (2009); the emission visible at 500 $\mu $m but not in the other maps is consistent with the position, shape and flux from the SZ effect expected at this wavelength.

Open with DEXTER

Heretofore, systematic far infrared (FIR) surveys of many galaxy clusters to large radii have been technically challenging so a complete census of sub-mm emission from clusters has been difficult to obtain. The advent of SPIRE (Griffin et al. 2010) on Herschel (Pilbratt et al. 2010) has, for the first time, provided the capability to make deep maps of clusters to large angles on the sky and to use colour information to separate the different sources of sub-mm emission present in galaxy clusters. In addition to gravitationally lensed background sources (Rex et al. 2010), emission in clusters above the confused sub-mm background may also comprise emission from galaxies in the cluster itself (Rawle et al. 2010), as well as truly diffuse emission from the SZ effect and possibly even cold dust in the ICM. SPIRE's ability to separate sources of emission based both on spatial and spectral information allows the demographics of the sub-mm emission to be measured.

In this paper, we use deep SPIRE maps of the z = 0.3 Bullet cluster (1E0657-56) taken as part of the Herschel Lensing Survey (HLS, P.I. Egami) at 250, 350, and 500 $\mu $m with 18, 25 and 36 arcsec resolution to measure the SZ effect and constrain other diffuse emission associated with the cluster.

2 Analysis and results

The HLS is a programme to observe 40 massive clusters in the range 0.1 < z < 1.0; during Herschel's science demonstration phase 1E0657-56 was observed to full depth. The specific observation strategy, low level data reduction and map making processes are summarized in Egami et al. (2010); here we begin with the calibrated flux and noise maps at 250, 350 and 500 $\mu $m (Fig. 1 of Egami et al. 2010).

Measurement of dim, extended emission is complicated by the presence of background sub-mm galaxies the confusion noise from which, at SPIRE's resolution, is measured to be $\sim$6 mJy in all three bands for blank fields (Nguyen et al. 2010). Indeed, in these maps we measure an rms noise of $\{6.0,6.0,7.5\}~$mJy/beam at 250, 350, 500 $\mu $m, consistent with the combination of confusion noise and instrument noise expected from the integration time. Obviously, care must be taken to disentangle extended emission from confused sources. To do this, we employ the approach discussed below, the fundamental tenet of which is to account for and remove all 250 $\mu $m emission from the two longer wavelength channels.

To generate a 250 $\mu $m source catalog, sources are detected in the 250 $\mu $m map using the StarFinder algorithm (Diolaiti et al. 2000). The detection threshold is set to 2.5$\sigma$and is run iteratively using SPIRE's 250 $\mu $m point response function (PRF) to account for blending; as the purpose here is not to generate a catalog of real sources but rather to remove all potential sources of emission resolved in the shortest wavelength band, an aggressive source detection level is desirable. Because the confusion noise in these maps is already a factor of $\sim$3 above the instrument noise level, lowering the source detection threshold does not substantially increase the number of identified sources. The 250 $\mu $m selected sources are then subtracted from the 250 $\mu $m map to produce the source-subtracted map shown in Fig. 1. In order to remove 250 $\mu $m emission that is correlated with 350 and 500 $\mu $m emission we employ a very conservative approach. The first step in this process is to use the 250 $\mu $m source candidate catalog to determine the possible positions of counterparts in the other two channels. The algorithm described below is performed independently on both the 350 and 500 $\mu $m maps; no direct comparison between the catalogs for the two longer wavelengths is performed or necessary. For each 250 $\mu $m candidate source position, the relevant PRF is fit to the position in the longer wavelength channel. In the fit, the position, flux and width of the source are allowed to vary. The resulting list of long wavelength candidate source counterparts is then compared to the 250 $\mu $m candidate source catalog. All those fits where the best fit flux is different by >50% at 350 $\mu $m or >90% at 500 $\mu $m, whose best fit width differs from the nominal PRF by >20%, or whose best fitting position is different by a total distance of 2 map pixels or more are deemed ``unsuccessful''. The catalog consisting of the successful fits is then subtracted from the long wavelength map to produce a source subtracted map at that wavelength.

Table 1:   Best fitting and expected SZ effect parameters at 350 and 500 $\mu $m.

Since the angular resolution of the two longer wavelength channels is significantly larger than that at 250 $\mu $m, it is common to have a large fraction of the fits be unsuccessful. As this is due to the effects of confusion rather than an actual lack of a long wavelength counterpart source, to be conservative we need to account for these unsubtracted sources; this process is performed in two steps. First, we generate a 250 $\mu $m map which is the sum of the 250 $\mu $m source subtracted map (shown in Fig. 1) and all those 250 $\mu $m selected sources for which the longer wavelength fit was unsuccessful. This corresponds to the 250 $\mu $m map which would arise if all those sources detected and removed at the longer wavelength were also removed from the 250 $\mu $m input map. This map is then convolved up to the longer wavelength's resolution using the relevant PRF and rebinned to the longer wavelength map's resolution. This map - which is equivalent to the long wavelength source free 250 $\mu $m counterpart map - is then pixel-wise fit to the long wavelength map to determine the scaling between them. Bright sources tend to make such scalings difficult in SPIRE data because such sources have individual colours which make pixel-wise colour comparisons have large variance. However, by construction such bright sources have been removed from the comparison so the scaling between the colours is well described by a linear model with coefficients of 0.76 at 350 $\mu $m and 0.40 at 500 $\mu $m. The scaled 250 $\mu $m bright source removed map is then subtracted from the equivalent long wavelength map. This has the effect of subtracting out both the $250~\mu$m sources undetected in the longer wavelength map and the component of the confused background present in the 250 $\mu $m map.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14685fig2.ps} \vspace*{-3mm}\end{figure} Figure 2:

Radial averages of the source subtracted and masked maps shown in Fig. 1. As the absolute mean of the maps are not measured by SPIRE, the points for each band are scattered about 0 MJy sr-1. Also plotted are the best fitting isothermal $\beta $ models using the parameters in Halverson et al. (2009) in the two SPIRE bands in which the SZ effect is expected to be non-zero, 350 and 500 $\mu $m; Table 1 gives the numerical values of the central increments brightnesses at both wavelengths. As the 250 $\mu $m radial bins are not correlated, each point should be compared to the (dashed) line $\Delta I = 0$ MJy sr-1, while in 350 and 500 $\mu $m the dashed line shows the inferred zero level of the SZ effect.

Open with DEXTER

As a further step, the 250 $\mu $m sources whose long wavelength fits were unsuccessful are binned into a map using their 250 $\mu $m flux and position, but the PRF of the longer wavelength channel. This undetected source model map is then threshold cut; all pixels with values greater than the threshold are deemed possible contaminants to the longer wavelength maps and a pixel mask is generated based on the positions of the cut sources. The center and right most panels of Fig. 1 show the resulting 250 $\mu $m source removed and masked maps for the 350 and 500 $\mu $m channels.

The 500 $\mu $m map shown in Fig. 1 features an extended source coincident with the measured center of the SZ effect in this cluster Halverson et al. (2009). If this signal is due to extended, roughly azimuthally symmetric emission as expected from the SZ effect then taking radial averages of the masked maps will enhance the signal to noise ratio of this detection. As the signal to noise ratio per map pixel is small, here we assume azimuthal symmetry and average the maps in simple radial bins of constant 18 arcsec width; the results of this are shown in Fig. 2. Interestingly, both the 350 and 500 $\mu $m data exhibit extended emission at the center of the cluster; to constrain this, we fit these data to the best fitting isothermal $\beta $ model from Halverson et al. (2009) which has a characteristic angular size of a few arcminutes. The resulting fits are plotted in Fig. 2; Table 1 lists the best fitting central SZ increment brightnesses at 350 and 500 $\mu $m. For the Halverson et al. (2009) model parameters the probability to exceed the measured $\chi^{2}$ for the fit at 350 $\mu $m is 0.21; for 500 $\mu $m it is 0.25. The isothermal $\beta $ model is a poor statistical description of the radial average at 250 $\mu $m. In addition to the statistical uncertainties associated with the errors on the data output from the fit, the uncertainties in the Halverson et al. (2009) model contribute a further 1.2 MJy sr-1at 350 $\mu $m and 1.9 MJy sr-1 at 500 $\mu $m. We have not included the contribution of these in the uncertainties listed in Table 1.

In order to compare the SZ effect increments measured here with the signal expected from previous measurements, we compile the results of Andreani et al. (1999), Halverson et al. (2009) and Plagge et al. (2010). As all of these measurements were performed with instruments working at 2 mm, they can be averaged to create a best estimate for the central Comptonization parameter using the X-ray determined cluster temperature of $T_{{\rm e}} = 13.9$ keV. Including relativistic corrections, the uncertainty weighted average y0 is $3.46 \pm 0.16 \times 10^{-4}$. Table 1 lists the expected brightness of the SZ distortion in the SPIRE bands including the effect of the actual filter bandpasses; Fig. 3 shows the spectral distortion of the CMB brightness for these y0and $T_{{\rm e}}$ values with the SPIRE bandpasses for reference. Good agreement is found between the expected results given the fiducial y0 and $T_{{\rm e}}$ and the SPIRE results at both 350 and 500 $\mu $m.

The relativistic SZ effect corrections required in the presence of a relativistic electron population have the largest effect at both the peaks of the SZ effect and the very shortest wavelengths. Nozawa et al. (2000) has calculated analytic fitting formulae for these corrections for $\lambda \gtrsim 250~\mu$m; in the calculations above we use these formulae to correct the purely thermal SZ effect spectrum for the presence of relativistic electrons. To determine the change in the SPIRE result if these finite temperature corrections were absent, we also compute the SZ spectrum without the relativistic electron correction and central Comptonization parameter which leaves the brightness at 2 mm constant, $y_{0} = 3.16 \times 10^{-4}$. Figure 3 shows this pure thermal SZ effect spectrum and Table 1 lists the corresponding 350 and 500 $\mu $m SPIRE band weighted intensities.

\begin{figure} \par\includegraphics[width=8.8cm]{14685fig3.ps} \vspace{-1.5mm}\end{figure} Figure 3:

The SZ effect spectrum in 1E0657-56. The 2 mm uncertainty weighted average of the measurements of Andreani et al. (1999), Halverson et al. (2009) and Plagge et al. (2010) (purple asterisk) leads to the SZ spectrum shown (solid black curve). The best fitting SPIREmeasurements at 350 and 500 $\mu $m (green and red diamonds) and the normalized SPIRE bandpasses (blue, green, red solid lines) are shown for reference. The SZ effect spectrum which is consistent with the 2 mm measurements but excludes the relativistic SZ effect correction is also shown (black dotted line). Though both SZ effect curves are well matched in the decrement, the finite temperature SZ effect corrections change the results by as much as 70% of the expected signal in the SPIRE bands.

Open with DEXTER

Table 1 also lists the ratio of the 350 to 500 $\mu $m SZ effect intensities for the SPIRE measurement presented here, the finite temperature SZ effect corrected spectrum, and the pure thermal SZ spectrum. The SPIRE and relativistic SZ effect corrected spectrum are consistent at the 1$\sigma$ level, while the SPIRE measurement and the purely thermal SZ spectrum are different by 2.1$\sigma$. This is the strongest evidence for the presence of the relativistic corrections to date, though not a detection of their effect on the SZ spectrum.

3 Discussion and conclusions

The possibility of detecting the SZ effect significantly shortward of its positive peak is a testament to the extraordinary capabilities of SPIRE. However, works like Zemcov et al. (2007) show that in large galaxy cluster survey samples, significant contamination to the SZ signal from bright, gravitationally lensed background sources is common. Though the properties of this particular cluster have not precluded measurement of the SZ effect - 1E0657-56 has fewer bright, lensed sources close to its SZ effect center than typical clusters which have been observed in the sub-mm and is relatively bright and broad in the SZ effect - based on this single example it is difficult to determine whether gravitational lensing of the sub-mm background will make measurements similar to this one more challenging in more typical clusters at these and other wavelengths. Data from surveys like the HLS will allow us to understand whether typical clusters are suitable for SZ effect increment detection, and how the lensed sub-mm background will affect measurements at other wavelengths.

The possibility of diffuse emission from cold dust in the ICM has been discussed in the past (e.g. Stickel et al. 2002). It is expected that, due to sputtering by energetic photons, such dust would have a very short lifetime in the ICM environment (Draine & Salpeter 1979). Based on the radial averages of the 250 $\mu $msource subtracted maps, where for ICM dust with reasonable temperatures the brightest thermal emission would occur, we find no evidence for this type of diffuse emission in this cluster. Because in any reasonable scenario such dust emission would be faint in a z > 0.1 cluster, we expect that targeted searches of local clusters will be more successful for this science, though the HLS and similar surveys can provide useful constraints.

Given the statistical uncertainties, the 350 $\mu $m SZ effect increment measured here is slightly less than 2$\sigma$ larger than would be expected from the 2 mm measurements. This may point to residual problems with the source subtraction procedure. More data will allow tuning of the confused sub-mm background removal algorithm and checks on whether biases arising from poor background removal are endemic in a large cluster sample.

Given the presence of the SZ effect in clusters, it seems that care must be taken with photometry of 500 $\mu $m sources within an arcminute or so of the cluster center; such sources will be positioned on a diffuse background so their fluxes will be biased by a small amount (Rex et al. 2010).

As the peak of the FIR emission of dusty sources is redshifted to progressively longer wavelengths, high redshift sources are expected to have exceptionally red spectral energy distributions. The results of this work show that care must be taken when searching for sources based on their presence in the 500 $\mu $m band alone; galaxy clusters whose SZ effects are relatively bright and compact could well masquerade as such sources. Due to the well known problem of determining counterparts to sub-mm sources at other wavelengths, such SZ effect contamination may not be immediately obvious, particularly as cluster fields are crowded and many possible counterparts may be present. As a corollary, searching for very red sources in confusion limited SPIRE surveys may turn up compact clusters based on the presence of strong 500 $\mu $m emission. The search for such extremely red SPIRE sources in the HLS and other programmes is underway now.

Acknowledgements
This work is based in part on observations made with Herschel, a European Space Agency Cornerstone Mission with significant participation by NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech.

References

  1. Aghanim, N., Hansen, S. H., & Lagache, G. 2005, A&A, 439, 901 Andreani, P., Böhringer, H., dall'Oglio, G., et al. 1999, ApJ, 513, 23 [NASA ADS] [CrossRef] [Google Scholar]
  2. Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
  4. Egami, E., et al. 2010, A&A, 518, L12 [CrossRef] [EDP Sciences] [Google Scholar]
  5. Griffin, M. J., et al. 2010, A&A, 518, L3 [Google Scholar]
  6. Halverson, N. W., Lanting, T., Ade, P. A. R., et al. 2009, ApJ, 701, 42 [NASA ADS] [CrossRef] [Google Scholar]
  7. Komatsu, E., Kitayama, T., Suto, Y., et al. 1999, ApJ, 516, L1 [NASA ADS] [CrossRef] [Google Scholar]
  8. Lamarre, J. M., Giard, M., Pointecouteau, E., et al.1998, ApJ, 507, L5 [Google Scholar]
  9. Nguyen, H. T., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Nord, M., Basu, K., Pacaud, F., et al. 2009, A&A, 506, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Nozawa, S., Itoh, N., Kawana, Y., & Kohyama, Y. 2000, ApJ, 536, 31 [NASA ADS] [CrossRef] [Google Scholar]
  12. Pilbratt, G. L., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  13. Plagge, T., Benson, B. A., Ade, P. A. R., et al. 2010, ApJ, 716, 1118 [NASA ADS] [CrossRef] [Google Scholar]
  14. Rawle, T. D., et al. 2010, A&A, 518, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Rex, M., et al. 2010, A&A, 518, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Stickel, M., Klaas, U., Lemke, D., & Mattila, K. 2002, A&A, 383, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments on Astrophysics and Space Physics, 4, 173 [Google Scholar]
  18. Zemcov, M., Borys, C., et al. 2007, MNRAS, 376, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  19. Zemcov, M., Halpern, M., Borys, C., et al. 2003, MNRAS, 346, 1179 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

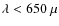...$\lambda < 650~{\sf\mu}$m[*]
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA. It is open for proposals for observing time from the worldwide astronomical community. Data presented in this paper were analyzed using ``The Herschel interactive processing environment (HIPE)'', a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia.

All Tables

Table 1:   Best fitting and expected SZ effect parameters at 350 and 500 $\mu $m.

All Figures

  \begin{figure} \par\includegraphics[width=16cm,clip]{14685fig1.ps} \vspace{-3mm}\end{figure} Figure 1:

Source subtracted maps at 250, 350 and 500 $\mu $m; these figures show the same regions defined by the 7$^\prime $ $\times 7 $$^\prime $green boxes in Fig. 1 of Egami et al. (2010). All three maps are shown on the colour scale shown at right; units are mJy beam-1. The left most panel shows the source-subtracted 250 $\mu $m map; the confused sub-mm background is most clearly evident in this band. The center and rightmost panels are respectively the 350 and 500 $\mu $m source removed and masked maps; their construction is discussed in the text. The cross hairs show the best fitting SZ effect centroid from Halverson et al. (2009); the emission visible at 500 $\mu $m but not in the other maps is consistent with the position, shape and flux from the SZ effect expected at this wavelength.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14685fig2.ps} \vspace*{-3mm}\end{figure} Figure 2:

Radial averages of the source subtracted and masked maps shown in Fig. 1. As the absolute mean of the maps are not measured by SPIRE, the points for each band are scattered about 0 MJy sr-1. Also plotted are the best fitting isothermal $\beta $ models using the parameters in Halverson et al. (2009) in the two SPIRE bands in which the SZ effect is expected to be non-zero, 350 and 500 $\mu $m; Table 1 gives the numerical values of the central increments brightnesses at both wavelengths. As the 250 $\mu $m radial bins are not correlated, each point should be compared to the (dashed) line $\Delta I = 0$ MJy sr-1, while in 350 and 500 $\mu $m the dashed line shows the inferred zero level of the SZ effect.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{14685fig3.ps} \vspace{-1.5mm}\end{figure} Figure 3:

The SZ effect spectrum in 1E0657-56. The 2 mm uncertainty weighted average of the measurements of Andreani et al. (1999), Halverson et al. (2009) and Plagge et al. (2010) (purple asterisk) leads to the SZ spectrum shown (solid black curve). The best fitting SPIREmeasurements at 350 and 500 $\mu $m (green and red diamonds) and the normalized SPIRE bandpasses (blue, green, red solid lines) are shown for reference. The SZ effect spectrum which is consistent with the 2 mm measurements but excludes the relativistic SZ effect correction is also shown (black dotted line). Though both SZ effect curves are well matched in the decrement, the finite temperature SZ effect corrections change the results by as much as 70% of the expected signal in the SPIRE bands.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.