| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201014680 | |
| Published online | 16 July 2010 | |
Herschel: the first science highlights
LETTER TO THE EDITOR
HerMES: The SPIRE confusion limit![[*]](/icons/foot_motif.png)
H. T. Nguyen1,2 - B. Schulz2,3 - L. Levenson2 - A. Amblard4 - V. Arumugam5 - H. Aussel6 - T. Babbedge7 - A. Blain2 - J. Bock1,2 - A. Boselli8 - V. Buat8 - N. Castro-Rodriguez9 - A. Cava9 - P. Chanial7 - E. Chapin10 - D.L. Clements7 - A. Conley11 - L. Conversi12 - A. Cooray4,2 - C. D. Dowell1,2 - E. Dwek13 - S. Eales14 - D. Elbaz6 - M. Fox7 - A. Franceschini15 - W. Gear14 - J. Glenn11 - M. Griffin14 - M. Halpern10 - E. Hatziminaoglou16 - E. Ibar17 - K. Isaak14 - R. J. Ivison17,5 - G. Lagache18 - N. Lu2,3 - S. Madden6 - B. Maffei19 - G. Mainetti15 - L. Marchetti15 - G. Marsden10 - J. Marshall2,1 - B. O'Halloran7 - S. J. Oliver20 - A. Omont21 - M.J. Page22 - P. Panuzzo6 - A. Papageorgiou14 - C. P. Pearson23,24 - I. Perez Fournon9 - M. Pohlen14 - N. Rangwala11 - D. Rigopoulou23,25 - D. Rizzo7 - I. G. Roseboom20 - M. Rowan-Robinson7 - D. Scott10 - N. Seymour22 - D. L. Shupe2,3 - A. J. Smith20 - J. A. Stevens26 - M. Symeonidis22 - M. Trichas7 - K. E. Tugwell22 - M. Vaccari15 - I. Valtchanov12 - L. Vigroux21 - L. Wang20 - R. Ward20 - D. Wiebe10 - G. Wright17 - C. K. Xu2,3 - M. Zemcov2
1 - Jet Propulsion Laboratory, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
2 - California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
3 - Infrared Processing and Analysis Center, MS 100-22, California Institute of Technology, JPL, Pasadena, CA 91125, USA
4 - Dept. of Physics & Astronomy, University of California, Irvine, CA 92697, USA
5 - Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
6
- Laboratoire AIM-Paris-Saclay, CEA/DSM/Irfu - CNRS - Université Paris
Diderot, CE-Saclay, pt courrier 131, 91191 Gif-sur-Yvette, France
7 - Astrophysics Group, Imperial College London, Blackett Laboratory, Prince Consort Road, London SW7 2AZ, UK
8
- Laboratoire d'Astrophysique de Marseille, OAMP, Université
Aix-marseille, CNRS, 38 rue Frédéric Joliot-Curie, 13388 Marseille
Cedex 13, France
9 - Institute de Astrofisica de Canarias, C/via Lactea s/n, 38200 La Laguna, Spain
10
- Department of Physics & Astronomy, University of British
Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1,
Canada
11 - Dept. of Astrophysical and Planetary Sciences, CASA 389-UCB, University of Colorado, Boulder, CO 80309, USA
12 - Herschel Science Centre, European Space Astronomy Centre, Villanueva de la Cañada, 28691 Madrid, Spain
13 - Observational Cosmology Lab, Code 665, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
14 - Cardiff School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff CF24 3AA, UK
15 - Dipartimento di Astronomia, Università di Padova, vicolo Osservatorio 3, 35122 Padova, Italy
16 - ESO, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
17 - UK Astronomy Technology Centre, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
18 - Institut d'Astrophysique Spatiale (IAS), bâtiment 121, Université Paris-Sud 11 and CNRS (UMR 8617), 91405 Orsay, France
19 - School of Physics and Astronomy, The University of Manchester, Alan Turing Building, Oxford Road, Manchester M13 9PL, UK
20 - Astronomy Centre, Dept. of Physics & Astronomy, University of Sussex, Brighton BN1 9QH, UK
21 - Institut d'Astrophysique de Paris, UMR 7095, CNRS, UPMC Univ. Paris 06, 98bis boulevard Arago, 75014 Paris, France
22 - Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
23 - Space Science & Technology Department, Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire OX11 0QX, UK
24 - Institute for Space Imaging Science, University of Lethbridge, Lethbridge, Alberta, T1K 3M4, Canada
25 - Astrophysics, Oxford University, Keble Road, Oxford OX1 3RH, UK
26 - Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield, Hertfordshire AL10 9AB, UK
Received 31 March 2010 / Accepted 20 April 2010
Abstract
We report on the sensitivity of SPIRE photometers on the Herschel
Space Observatory. Specifically, we measure the confusion noise from
observations taken during the science demonstration phase of the Herschel
Multi-tiered Extragalactic Survey. Confusion noise is defined to be the
spatial variation of the sky intensity in the limit of infinite
integration time, and is found to be consistent among the different
fields in our survey at the level of 5.8, 6.3 and 6.8 mJy/beam at
250, 350 and 500 ![]() m,
respectively. These results, together with the measured instrument
noise, may be used to estimate the integration time required for
confusion limited maps, and provide a noise estimate for maps obtained
by SPIRE.
m,
respectively. These results, together with the measured instrument
noise, may be used to estimate the integration time required for
confusion limited maps, and provide a noise estimate for maps obtained
by SPIRE.
Key words: space vehicules: instruments - surveys - submillimeter: diffuse background - submillimiter: galaxies
1 Introduction
The Spectral and Photometric Imaging REceiver (SPIRE) (Griffin et al. 2010) onboard the Herschel Space Observatory (Pilbratt et al. 2010) has opened a new window on the Universe at far-infrared (FIR) wavelengths. The sensitivity of SPIRE detectors combined with Herschel's 3.5 m aperture allow astronomers to observe the FIR sky with unprecedented efficiency. With 18.1'', 24.9'', 36.6'' (FWHM) beams at 250, 350 and 500 microns, respectively, we expect SPIRE maps to be dominated by confused sources. It is therefore useful to determine the key characteristics, both of the instrument and the sky, that would allow observers to optimize their observing plans, and/or to make sky surveys that probe as deep and as wide as possible for allocated observing time. In this letter we report measurements in SPIRE maps of the following: i) instrument noise, i.e. noise from the detectors, readout electronics and photon noise from the telescope; ii) confusion noise, that is, the variance in the sky map due to the presence of unresolved sources; and iii) cosmic variance, arising from underlying large-scale fluctuations in the galaxy number density.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{14680fig1-1.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg13.png)
|
Figure 1:
The GOODS-N field at 250, 350 and 500 |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm,clip]{14680fig2Left-1.eps} \...
...udegraphics[width=9cm,clip]{14680fig2Right-1.eps} }\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg14.png)
|
Figure 2:
Left: variance of SPIRE map pixels at 250, 350 and 500 |
| Open with DEXTER | |
The confusion noise due to sources below a given flux cutoff, ![]() ,
is derived in
Condon (1974)
to be the second moment of the measured flux distribution:
,
is derived in
Condon (1974)
to be the second moment of the measured flux distribution:
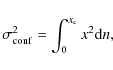
|
(1) |
where x is the measured flux,
In Sect. 2, we describe the observations, followed by the analysis details and results in Sect. 3. In Sect. 4 we provide the number of ``repeats'' required to achieve confusion limited maps. A repeat, as defined by the Herschel science planning and observing tool (HSPOT), contains two orthogonal scans of the entire field. At nominal scan speed, a single repeat averages to 16, 29 and 28 samples/pixel, or an integration time of 0.9, 1.6 and 1.5 s/pixel. In addition, we discuss the often-used (albeit, model-dependent) definition of confusion limit in terms of the source density or number of sources per 30 to 40 beams.
2 Data sets
The Herschel Multi-tiered Extragalactic Survey (HerMES![]() ) science demonstration phase (SDP) observations are detailed in Table 1 of Oliver et al. (2010).
In this letter we have measured the noise properties of SPIRE maps of
three of the five fields, GOODS-N, Lockman-North and Lockman-SWIRE. The
GOODS-N field is
) science demonstration phase (SDP) observations are detailed in Table 1 of Oliver et al. (2010).
In this letter we have measured the noise properties of SPIRE maps of
three of the five fields, GOODS-N, Lockman-North and Lockman-SWIRE. The
GOODS-N field is
![]() and was covered by 30 map repeats. The Lockman-North field is
and was covered by 30 map repeats. The Lockman-North field is
![]() covered by 7 repeats. These fields were observed in nominal scan
mode with the spacecraft scanning at 30''/s with an angle of
covered by 7 repeats. These fields were observed in nominal scan
mode with the spacecraft scanning at 30''/s with an angle of ![]() 42.4 degrees with respect to the spacecraft y-axis (see SPIRE observers' manual 2010). Lockman-SWIRE is
42.4 degrees with respect to the spacecraft y-axis (see SPIRE observers' manual 2010). Lockman-SWIRE is
![]() wide and was observed in SPIRE fast scan with a 60''/s scan speed, and
was covered by 2 repeats. Standard SPIRE pipeline maps (see Oliver
et al., in prep.) were used. These maps are calibrated
in mJy/beam and have pixel dimensions of 6'', 10'' and 14' at 250,
350 and 500
wide and was observed in SPIRE fast scan with a 60''/s scan speed, and
was covered by 2 repeats. Standard SPIRE pipeline maps (see Oliver
et al., in prep.) were used. These maps are calibrated
in mJy/beam and have pixel dimensions of 6'', 10'' and 14' at 250,
350 and 500 ![]() m, respectively.
m, respectively.
The two remaining HerMES SDP fields, FLS and Abell 2218 were not used in this analysis. The FLS was contaminated by Galactic cirrus which is clearly seen in the measured pixel variance. Abell 2218 is a small cluster field with lensing effects. Both of these fields are strongly biased to higher confusion noise.
The central
![]() of the GOODS-N field are shown in Fig. 1 at 250, 350 and 500
of the GOODS-N field are shown in Fig. 1 at 250, 350 and 500 ![]() m,
clearly demonstrates the effect of confusion in SPIRE maps. We note
that the confusion noise according to Eq. (1) is defined with some
cutoff flux,
m,
clearly demonstrates the effect of confusion in SPIRE maps. We note
that the confusion noise according to Eq. (1) is defined with some
cutoff flux, ![]() ,
which is set by the brightest sources in these maps. We will discuss
the effect of these cutoffs to the determination of the confusion
noise.
,
which is set by the brightest sources in these maps. We will discuss
the effect of these cutoffs to the determination of the confusion
noise.
3 Analysis
Fundamentally, spatial fluctuations in a map arise due to two
sources: instrument noise and the presence of sources on the sky. The
instrument component,
![]() ,
will be reduced with integration time, while fluctuations due to the convolution of the sky with the instrument beam,
,
will be reduced with integration time, while fluctuations due to the convolution of the sky with the instrument beam,
![]() ,
will remain. Since the sources of noise are uncorrelated, and if
low-frequency correlated noise has been properly accounted for in the
low level data reduction, the total variance in the map is simply,
,
will remain. Since the sources of noise are uncorrelated, and if
low-frequency correlated noise has been properly accounted for in the
low level data reduction, the total variance in the map is simply,
![]() ,
where t is the integration time. Note that
,
where t is the integration time. Note that
![]() has unit of surface brightness in mJy/beam, while
has unit of surface brightness in mJy/beam, while
![]() in mJy/beam
in mJy/beam
![]() .
A straight line fit of the variance vs. inverse integration time has a slope that determines the instrument variance,
.
A straight line fit of the variance vs. inverse integration time has a slope that determines the instrument variance,
![]() ,
and a non-zero intercept that determines the variance of the sky intensity,
,
and a non-zero intercept that determines the variance of the sky intensity,
![]() (Jarosik et al. 2003).
(Jarosik et al. 2003).
Table 1: Measured SPIRE noise.
In our analysis we begin by selecting all map pixels with a total integration time between
![]() ,
where dt is 0.5 times the integration time per sample (i.e.
0.054 s/sample in nominal scan mode). We then measure the
variance,
,
where dt is 0.5 times the integration time per sample (i.e.
0.054 s/sample in nominal scan mode). We then measure the
variance,
![]() ,
of the pixel values in that subset. Figure 2 shows
,
of the pixel values in that subset. Figure 2 shows
![]() vs. t-1 at 250, 350 and 500
vs. t-1 at 250, 350 and 500 ![]() m
in the fields observed in nominal and fast scan mode. GOODS-N pixel
sets are shown in black, Lockman-North in green and the shallow
Lockman-SWIRE field in red. The black line shows a simultaneous linear
fit to all three fields and traces a component proportional to t-1
and a non-zero intercept. The data from the three included fields
clearly show that the noise properties of the SPIRE instrument and the
SPIRE observed sky are independent of the SPIRE scanning speed and
stable from shallow to deep fields. The consistency of the result in
deep and shallow fields confirms that this method of noise
characterization measures the confusion noise in maps that, themselves,
are not confusion limited. In fact, the large area shallow field (red
points) in Fig. 2 show far
less scatter about the fit than the fewer pixels in the deep fields
since there are many more pixels, providing a larger statistical
ensemble.
m
in the fields observed in nominal and fast scan mode. GOODS-N pixel
sets are shown in black, Lockman-North in green and the shallow
Lockman-SWIRE field in red. The black line shows a simultaneous linear
fit to all three fields and traces a component proportional to t-1
and a non-zero intercept. The data from the three included fields
clearly show that the noise properties of the SPIRE instrument and the
SPIRE observed sky are independent of the SPIRE scanning speed and
stable from shallow to deep fields. The consistency of the result in
deep and shallow fields confirms that this method of noise
characterization measures the confusion noise in maps that, themselves,
are not confusion limited. In fact, the large area shallow field (red
points) in Fig. 2 show far
less scatter about the fit than the fewer pixels in the deep fields
since there are many more pixels, providing a larger statistical
ensemble.
The right side of Fig. 2 shows the same data in a different graphical representation. The square root of the variance in all three fields (now all in black) is plotted vs. the integration time along with the derived instrument noise (red line) and confusion noise (blue line). If the sky were dark, the noise would integrate down to zero following the red line, while for the real sky the noise can not get below the confusion floor.
The measured noise is presented in Table 1. The confusion noise values in Table 1 are equivalent to the 1![]() point source sensitivities, in mJy, in confusion limited maps. The
two rightmost columns are included for observation planning and show
the instrument noise scaled from mJy/beam
point source sensitivities, in mJy, in confusion limited maps. The
two rightmost columns are included for observation planning and show
the instrument noise scaled from mJy/beam
![]() to mJy/beam
to mJy/beam
![]() for
nominal and fast scan mode, respectively, by averaging the total
integration time per pixel in a map for a given number of map repeats.
Fast scan mode is
for
nominal and fast scan mode, respectively, by averaging the total
integration time per pixel in a map for a given number of map repeats.
Fast scan mode is ![]() higher since it has half the samples in a sky pixel for a given number of map repeats.
higher since it has half the samples in a sky pixel for a given number of map repeats.
We have made 10 simulated realizations of our survey fields by constructing timestreams with known instrument noise and injecting sources drawn from the number counts determined by BLAST (Patachon et al. 2009). These simulations are used to check for biases due to the non- Gaussian nature of the pixel distribution or correlated noise and to provide better estimated uncertainties in our measurement. These simulated timestreams (Glenn et al., in prep.) are then processed through the mapping pipeline, and the above variance analysis is run on the simulated maps. The confusion and instrument noise measured in the simulated maps agree with the analytically computed input noise in all three bands, indicating that any bias is insignificant. The consistency of our results in the deep and shallow fields further indicates an absence of measurement bias due to non-Gaussianity. The scatter in the instrument and confusion noise determined in these simulations about the known inputs indicates that the statistical uncertainty on the instrument noise is 5% and on the confusion noise 6%, with no significant bias in the recovered values.
The agreement among the three fields of varying depth and solid angle
also indicate that an additional uncertainty due to cosmic variance is
unnecessary. Cosmic variance, often negligible in relatively large
surveys, can become a significant source of uncertainties in deep
pencil-beam surveys for high redshift studies. As a check, we re-ran
the variance analysis on sub-fields of the GOODS-N field to estimate
the field size at which the noise estimates diverge from those made
from the full dataset. That analysis shows that the confusion noise
reported here is unaffected by cosmic variance in fields larger than
![]() ,
,
![]() and
and
![]() at 250, 350 and 500
at 250, 350 and 500 ![]() m. As our smallest map is
m. As our smallest map is
![]() ,
we include no uncertainty due to cosmic variance.
,
we include no uncertainty due to cosmic variance.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14680fig3.eps}\vspace*{-2mm}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg35.png)
|
Figure 3:
Histogram of the 250 |
| Open with DEXTER | |
Figure 4 shows the equivalent of left column of Fig. 2
for the jackknife map of GOODS-N. As expected, the instrument noise
remains in the jackknife map, and with the sources removed the
intercept is now consistent with zero. Specifically, intercepts from
jackknife map give noise estimates of
![]() ,
-
,
-
![]() and -0.4 mJy/beam
and -0.4 mJy/beam ![]() 0.5 at 250, 350 and 500
0.5 at 250, 350 and 500 ![]() m. Instrument noise measured using the same method in the jackknife map is
m. Instrument noise measured using the same method in the jackknife map is
![]() ,
,
![]() and
and
![]() mJy/beam
mJy/beam
![]() which agrees with the values determined from the full maps.
which agrees with the values determined from the full maps.
![\begin{figure}
\par\includegraphics[width=8.5cm]{14680fig4-1.eps}\vspace*{-2mm}\vspace*{-3mm}\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg43.png)
|
Figure 4: Variance plot for jackknife map of GOODS-N. As expected, the null map gives a linear fit with the similar slope or instrument noise as the full map, and the intercept or confusion noise is consistent with zero since sky contribution has been removed. |
| Open with DEXTER | |
4 Discussion
We have made a precision measurement of the confusion and instrument
noise in the HerMES SDP SPIRE scan maps. The various checks presented,
including simulated datasets with known noise properties and a repeat
of the analysis on null map or jackknife, demonstrate the robustness of
the analysis and give good consistency in the values of the confusion
and instrument noise. Our simulations indicate that the statistical
error of the confusion noise is about 5%. We note that the
systematic error is largely dependent on the calibration and map-making
process, currently estimated to be ![]() 15% (Griffin et al. 2010). Table 1
can be used as a guide for achieving confusion limited maps with SPIRE.
In particular, to make maps in which the instrument noise is comparable
to the confusion, it will take a minimum of 3 map repeats in
nominal scan mode or 5 map repeats in fast scan mode. Longer
integration time will result in maps in which confusion is the dominant
source of uncertainty in measurements of source flux and position.
15% (Griffin et al. 2010). Table 1
can be used as a guide for achieving confusion limited maps with SPIRE.
In particular, to make maps in which the instrument noise is comparable
to the confusion, it will take a minimum of 3 map repeats in
nominal scan mode or 5 map repeats in fast scan mode. Longer
integration time will result in maps in which confusion is the dominant
source of uncertainty in measurements of source flux and position.
The noise values reported in Table 1
make no significant source cut and, accounting for the possibility that
even bright sources are confused, measure the variance in HerMES maps
due to all sources up to 10
![]() or
80 mJy (more than 99% of data). It may be interesting to
systematically remove bright sources and study how confusion noise
might change accordingly. We have determined the confusion noise using
the same method presented in Sect. 3, after removing pixels within
a beam FWHM of any pixel brighter than a given flux cut. (Since the
maps are calibrated such that the source flux is given by the flux in
the pixel at the peak of the PSF,i.e., mJy/beam, this method is
equivalent to removal of sources. Removing pixels within a FWHM is
conservative and ensures that any
extended emission is completely removed.) The results of this analysis
are shown in Fig. 5. The vertical lines indicate 5
or
80 mJy (more than 99% of data). It may be interesting to
systematically remove bright sources and study how confusion noise
might change accordingly. We have determined the confusion noise using
the same method presented in Sect. 3, after removing pixels within
a beam FWHM of any pixel brighter than a given flux cut. (Since the
maps are calibrated such that the source flux is given by the flux in
the pixel at the peak of the PSF,i.e., mJy/beam, this method is
equivalent to removal of sources. Removing pixels within a FWHM is
conservative and ensures that any
extended emission is completely removed.) The results of this analysis
are shown in Fig. 5. The vertical lines indicate 5
![]() as measured in the full map. The residual noise estimates are 3.8, 4.6 and 5.2 mJy with a 3
as measured in the full map. The residual noise estimates are 3.8, 4.6 and 5.2 mJy with a 3
![]() cut and 4.8, 5.5 and 6.1 mJy with a 5
cut and 4.8, 5.5 and 6.1 mJy with a 5
![]() cut.
cut.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14680fig5.eps}
\vspace*{-3.5mm}\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg45.png)
|
Figure 5:
Confusion noise as a function of pixel flux cut at 250/350/500 |
| Open with DEXTER | |
The confusion limit is often quoted in terms of the flux, at which
the source density in a map reaches 30 to 50 beams per source.
This quantity requires a measurement or a model of the density of
sources, and often is derived assuming a power law source distribution
with a 3-4
![]() (Franceschini 1982).
BLAST (Devlin et al. 2009) predicts confusion limits corresponding
to 40 beams per source for SPIRE of 22, 22 and 18 mJy at 250,
350 and 500
(Franceschini 1982).
BLAST (Devlin et al. 2009) predicts confusion limits corresponding
to 40 beams per source for SPIRE of 22, 22 and 18 mJy at 250,
350 and 500 ![]() m,
respectively. The best source counts available at the SPIRE wavelengths
are probably the HerMES counts themselves, as reported
by Oliver et al. (2010). The HerMES counts reach 1 source per 40 beams at
m,
respectively. The best source counts available at the SPIRE wavelengths
are probably the HerMES counts themselves, as reported
by Oliver et al. (2010). The HerMES counts reach 1 source per 40 beams at
![]() ,
,
![]() ,
and
,
and
![]() mJy at 250, 350 and 500
mJy at 250, 350 and 500 ![]() m, corresponding to 3.29, 2.81, and
2.60
m, corresponding to 3.29, 2.81, and
2.60
![]() ,
and in rough agreement with BLAST's prediction.
,
and in rough agreement with BLAST's prediction.
SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC (UK); and NASA (USA).
References
- Condon, J. J. 1974, ApJ, 188, 279
- Devlin, M. J., Ade, P. A. R., Aretxaga, I., et al. 2009, Nature, 458, 737
- Franceschini, A. 1982, AP&SS, 86, 3F
- Griffin, M. J., et al. 2010, A&A, 518, L3
- Jarosik, N., Barnes, C., Bennett, C. L., et al. 2003, ApJ, 148, 29
- Oliver, S. J., et al. 2010, A&A, 518, L21
- Patanchon, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1750
- Pilbratt, G. L., et al. 2010, A&A, 518, L1
- SPIRE observers' manual 2010, HERSCHEL-HSC-DOC-0789, version TBD, Date, Website, ESA
Footnotes
- ... limit
![[*]](/icons/foot_motif.png)
- Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
- ... (HerMES
![[*]](/icons/foot_motif.png)
- http://hermes.sussex.ac.uk
All Tables
Table 1: Measured SPIRE noise.
All Figures
![\begin{figure}
\par\includegraphics[width=18cm,clip]{14680fig1-1.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg13.png)
|
Figure 1:
The GOODS-N field at 250, 350 and 500 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm,clip]{14680fig2Left-1.eps} \...
...udegraphics[width=9cm,clip]{14680fig2Right-1.eps} }\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg14.png)
|
Figure 2:
Left: variance of SPIRE map pixels at 250, 350 and 500 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14680fig3.eps}\vspace*{-2mm}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg35.png)
|
Figure 3:
Histogram of the 250 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14680fig4-1.eps}\vspace*{-2mm}\vspace*{-3mm}\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg43.png)
|
Figure 4: Variance plot for jackknife map of GOODS-N. As expected, the null map gives a linear fit with the similar slope or instrument noise as the full map, and the intercept or confusion noise is consistent with zero since sky contribution has been removed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14680fig5.eps}
\vspace*{-3.5mm}\end{figure}](/articles/aa/full_html/2010/10/aa14680-10/Timg45.png)
|
Figure 5:
Confusion noise as a function of pixel flux cut at 250/350/500 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


