| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | L64 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201014588 | |
| Published online | 16 July 2010 | |
Herschel: the first science highlights
LETTER TO THE EDITOR
The central region of spiral galaxies as seen by Herschel![[*]](/icons/foot_motif.png)
M 81, M 99, and M 100
M. Sauvage1 - N. Sacchi2 - G. J. Bendo3 - A. Boselli4 - M. Pohlen5 - C. D. Wilson6 - R. Auld5 - M. Baes7 - M. J. Barlow8 - J. J. Bock9 - M. Bradford9 - V. Buat4 - N. Castro-Rodriguez10 - P. Chanial1 - S. Charlot11 - L. Ciesla4 - D. L. Clements3 - A. Cooray12 - D. Cormier1 - L. Cortese5 - J. I. Davies5 - E. Dwek13 - S. A. Eales5 - D. Elbaz1 - M. Galametz1 - F. Galliano1 - W. K. Gear5 - J. Glenn14 - H. L. Gomez5 - M. Griffin5 - S. Hony1 - K. G. Isaak515 - L. R. Levenson9 - N. Lu9 - S. C. Madden1 - B. O'Halloran3 - K. Okumura1 - S. Oliver16 - M. J. Page17 - P. Panuzzo1 - A. Papageorgiou5 - T. J. Parkin6 - I. Perez-Fournon10 - N. Rangwala14 - E. E. Rigby18 - H. Roussel11 - A. Rykala5 - B. Schulz19 - M. R. P. Schirm6 - M. W. L. Smith5 - L. Spinoglio2 - J. A. Stevens20 - S. Srinivasan11 - M. Symeonidis17 - M. Trichas3 - M. Vaccari21 - L. Vigroux11 - H. Wozniak22 - G. S. Wright23 - W. W. Zeilinger24
1 - CEA, Laboratoire AIM, Irfu/SAp, Orme des Merisiers, 91191 Gif-sur-Yvette, France
2 -
Istituto di Fisica dello Spazio Interplanetario, INAF, via del Fosso
del Cavaliere 100, 00133 Roma, Italy
3 -
Astrophysics Group, Imperial College, Blackett Laboratory, Prince
Consort Road, London SW7 2AZ, UK
4 -
Laboratoire d'Astrophysique de Marseille, UMR6110 CNRS, 38 rue F.
Joliot-Curie, 13388 Marseille France
5 -
School of Physics and Astronomy, Cardiff University, Queens
Buildings The Parade, Cardiff CF24 3AA, UK
6 -
Dept. of Physics & Astronomy, McMaster University, Hamilton,
Ontario, L8S 4M1, Canada
7 -
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9,
9000 Gent, Belgium
8 -
Department of Physics and Astronomy, University College London,
Gower Street, London WC1E 6BT, UK
9 -
Jet Propulsion Laboratory, Pasadena, CA 91109, United States;
Department of Astronomy, California Institute of Technology, Pasadena,
CA 91125, USA
10 -
Instituto de Astrofísica de Canarias, vía Láctea S/N, 38200 La
Laguna, Spain
11 -
Institut d'Astrophysique de Paris, UMR7095 CNRS, Université Pierre
& Marie Curie, 98 bis Boulevard Arago, 75014 Paris, France
12 -
Department of Physics & Astronomy, University of California, Irvine,
CA 92697, USA
13 -
Observational Cosmology Lab, Code 665, NASA Goddard Space Flight
Center Greenbelt, MD 20771, USA
14 -
Department of Astrophysical and Planetary Sciences, CASA CB-389,
University of Colorado, Boulder, CO 80309, USA
15 -
ESA Astrophysics Missions Division, ESTEC, PO Box 299, 2200 AG
Noordwijk, The Netherlands
16 -
Astronomy Centre, Department of Physics and Astronomy, University of
Sussex, UK
17 -
Mullard Space Science Laboratory, University College London,
Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
18 -
School of Physics & Astronomy, University of Nottingham, University
Park, Nottingham NG7 2RD, UK
19 -
Infrared Processing and Analysis Center, California Institute of
Technology, Mail Code 100-22, 770 South Wilson Av, Pasadena, CA 91125,
USA
20 -
Centre for Astrophysics Research, Science and Technology Research
Centre, University of Hertfordshire, College Lane, Herts AL10 9AB, UK
21 -
University of Padova, Department of Astronomy, Vicolo Osservatorio
3, 35122 Padova, Italy
22 -
Observatoire Astronomique de Strasbourg, UMR 7550 Université de
Strasbourg - CNRS, 11 rue de l'Université, 67000 Strasbourg, France
23 -
UK Astronomy Technology Center, Royal Observatory Edinburgh,
Edinburgh, EH9 3HJ, UK
24 -
Institut für Astronomie, Universität Wien, Türkenschanzstr. 17,
1180 Wien, Austria
Received 30 March 2010 / Accepted 20 April 2010
Abstract
With appropriate spatial resolution, images of spiral
galaxies in thermal infrared (![]() 10
10 ![]() m and beyond) often
reveal a bright central component, distinct from the stellar bulge,
superimposed on a disk with prominent spiral arms. ISO and
Spitzer studies have shown that much of the scatter in the
mid-infrared colors of spiral galaxies is related to changes
in the relative importance of these two components, rather than to
other modifications, such as the morphological type or star
formation rate, that affect the properties of the galaxy as a
whole. With the Herschel imaging capability from 70 to
500
m and beyond) often
reveal a bright central component, distinct from the stellar bulge,
superimposed on a disk with prominent spiral arms. ISO and
Spitzer studies have shown that much of the scatter in the
mid-infrared colors of spiral galaxies is related to changes
in the relative importance of these two components, rather than to
other modifications, such as the morphological type or star
formation rate, that affect the properties of the galaxy as a
whole. With the Herschel imaging capability from 70 to
500 ![]() m, we revisit this two-component approach at longer
wavelengths, to see if it still provides a working description of the
brightness distribution of galaxies, and to determine its
implications on the interpretation of global far-infrared
properties of galaxies.
m, we revisit this two-component approach at longer
wavelengths, to see if it still provides a working description of the
brightness distribution of galaxies, and to determine its
implications on the interpretation of global far-infrared
properties of galaxies.
We quantify the luminosity of the central component by both a
decomposition of the radial surface brightness profile and a direct
extraction in 2D. We find the central component contribution is
variable within the three galaxies in our sample, possibly
connected more directly to the presence of a bar than to the
morphological type. The central component's relative contribution is at its
maximum in the mid-infrared range and drops around 160 ![]() m to
reach a constant value beyond 200
m to
reach a constant value beyond 200 ![]() m. The central component
contains a greater fraction of hot dust than the disk component, and
while the colors of the central components are scattered,
colors of the disk components are more homogenous from one galaxy to
the next.
m. The central component
contains a greater fraction of hot dust than the disk component, and
while the colors of the central components are scattered,
colors of the disk components are more homogenous from one galaxy to
the next.
Key words: infrared: galaxies - submillimeter: galaxies - galaxies: spiral - galaxies: nuclei - galaxies: fundamental parameters
1 Introduction
The central region of spiral galaxies hosts a number of processes that have little or no counterpart in the disks. A nuclear starburst, triggered by bar instabilities and associated or not with an active galactic nucleus (AGN) can often be found. The stellar density is also enhanced with respect to the disk, leading to an increase in the interstellar radiation field (ISRF) intensity. It is thus no surprise that in the mid-infrared (MIR), spiral galaxies can often be seen as the sum of a central component, hereafter referred to as the core component as distinct from the bulge, and a disk component (see e.g. Bendo et al. 2007). Extraction of the core component from MIR brightness profiles have revealed that it can contribute up to 90% of the total MIR luminosity and that the distribution of core/total luminosity ratio is evenly spread between 0 and 1 (Roussel et al. 2001a). This study also showed that much of the scatter in the MIR global properties of spiral galaxies came from changes in the relative contribution of the core component and of its spectral energy distribution (SED), while disk components formed a much more homogenous group. In short, the scatter affecting the global MIR colors of galaxies is caused by a very local effect, i.e., the importance of the core component, rather than by a change in any single property of galaxies such as the ISRF throughout the disk. Taking this into account, Roussel et al. (2001b) shows that the MIR luminosity of galaxies could be turned into an accurate tracer of the star-formation rate, provided it was corrected for the core contribution. More recently, Chanial et al. (2007) extends this analysis by showing that the dispersion in the correlation between the infrared luminosity of galaxies and the dust temperature could be reduced by considering a compactness parameter, again related to the relative contribution of the core and disk components.
Care must therefore be taken when extrapolating locally established
relations, such as the correlation of star-formation tracers in
galactic disks, to global studies where galaxies are no longer
resolved. One first needs to verify that the total luminosity of
galaxies is indeed dominated by the component where these correlations
have been established, or to design methods to correct for the existence
of multiple contributors to the total luminosity. With its
unprecedented sensitivity and spatial resolution, Herschel
(Pilbratt et al. 2010) now allows us to carry this very investigation over
the full thermal infrared peak, by combining the PACS instrument
(Poglitsch et al. 2010), delivering spatial resolutions of
![]() ,
,
![]() ,
and 11'' (FWHM) at 70, 100, and 160
,
and 11'' (FWHM) at 70, 100, and 160 ![]() m, and the SPIRE
instrument (Griffin et al. 2010) delivering spatial resolutions of
m, and the SPIRE
instrument (Griffin et al. 2010) delivering spatial resolutions of
![]() ,
,
![]() ,
and
,
and
![]() (FWHM) in its three
photometric bands at 250, 350, and 500
(FWHM) in its three
photometric bands at 250, 350, and 500 ![]() m.
m.
2 The objects and data reduction methods
Galaxies studied here are part of the Herschel Reference Survey (Boselli et al. 2010), a SPIRE volume-limited imaging survey of 323 galaxies. Out of the 4 noninteracting spirals observed during the science demonstration phase, NGC 3683 and NGC 3982 are too small in apparent size for the present study, leaving M 99 and M 100 (see also Pohlen et al. 2010), to which we add M 81, which was observed as part of the Very Nearby Galaxies program (Bendo et al. 2010b). The properties of the objects that are relevant to this study are in Table 1.
Details of the SPIRE data reduction can be found in Pohlen et al. (2010) and
Bendo et al. (2010b), while the PACS data reduction of M 81 is described
in Bendo et al. (2010b). Photometric uncertainties are quoted at ![]() 15%
for all SPIRE bands and at
15%
for all SPIRE bands and at ![]() 10/20% for the PACS
70/160
10/20% for the PACS
70/160 ![]() m bands by the instrument teams. We also use Spitzer MIPS maps at 24, 70, and 160
m bands by the instrument teams. We also use Spitzer MIPS maps at 24, 70, and 160 ![]() m (see Clements et al. 2010; Bendo et al. 2010a, for data reduction details). The SPIRE maps are
calibrated in Jy/Beam, and we used a beam size of
m (see Clements et al. 2010; Bendo et al. 2010a, for data reduction details). The SPIRE maps are
calibrated in Jy/Beam, and we used a beam size of
![]() ,
,
![]() ,
and
,
and
![]() sr
at 250, 350, and 500
sr
at 250, 350, and 500 ![]() m, respectively, to convert these into more
conventional brightness units. The MIPS maps are calibrated in MJy/sr,
and the PACS maps in Jy/pixel, with a pixel size of 1
m, respectively, to convert these into more
conventional brightness units. The MIPS maps are calibrated in MJy/sr,
and the PACS maps in Jy/pixel, with a pixel size of 1
![]() 4 and
2
4 and
2
![]() 85 for the 70 and 160
85 for the 70 and 160 ![]() m bands.
m bands.
Table 1: Relevant data for the galaxies studied here, as well as the images used (M: MIPS, P: PACS, S: SPIRE).
3 Extraction of the core components
Our first approach uses radial surface brightness profiles measured
inside concentric ellipses. For all maps of a given galaxy, we
used the same parameters to build the integrating ellipses, namely the
central coordinate, the ellipse axis ratio, and the position angle;
i.e., these parameters are not fit to the data but obtained from
NED![]() . This is a
coarser approach than the one used by Pohlen et al. (2010), where the ellipse
parameters are first fitted to the maps before the profile integration
is made. A simpler approach is justified here since we are not searching
for the most accurate structural description of the surface brightness
distribution in galaxies, but rather for a method to systematically
measure the contribution of the central region to the total galaxy
luminosity. Errors in the computed average surface brightness are the
quadratic sum of the error on the mean brightness, of the error
derived by accounting for the corresponding error map on the same
ellipses, and of the error on the background level. Generally, the total
errors are much smaller than the computed brightness except close to
the background. For all maps, we intentionally went significantly
beyond the D25 diameter. To obtain the galaxy's brightness
profile, we determined the background brightness as the mean of the
brightness measured typically about 100'' beyond the point where the
galaxy emission ceased to be detected.
. This is a
coarser approach than the one used by Pohlen et al. (2010), where the ellipse
parameters are first fitted to the maps before the profile integration
is made. A simpler approach is justified here since we are not searching
for the most accurate structural description of the surface brightness
distribution in galaxies, but rather for a method to systematically
measure the contribution of the central region to the total galaxy
luminosity. Errors in the computed average surface brightness are the
quadratic sum of the error on the mean brightness, of the error
derived by accounting for the corresponding error map on the same
ellipses, and of the error on the background level. Generally, the total
errors are much smaller than the computed brightness except close to
the background. For all maps, we intentionally went significantly
beyond the D25 diameter. To obtain the galaxy's brightness
profile, we determined the background brightness as the mean of the
brightness measured typically about 100'' beyond the point where the
galaxy emission ceased to be detected.
To search for and extract the core component, we obtained the best (in
the least-square sense) combination of Gaussian or exponential
functions that represent the measured radial profiles. Expressed
in units of surface brightness as a function of radius, we fit the
following function to the data:
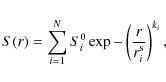
|
(1) |
with S0 the central surface brightness,
The use of either Gaussian or exponential functions is a result of the fit, but that some of the disk profiles prefer a Gaussian to an exponential must not be overinterpreted because the presence of prominent spiral arms can create a distinctive bump in the disk part of the profile that is represented by a Gaussian better than by an exponential. In either case we did not use the fit parameters that describe the ``disk'' component in the rest of the analysis. The central component is almost always represented by a Gaussian profile very well, with the disk component also adequately fit at the location where the core profile merges into the disk profile (see Fig. 1). We then decomposed the luminosity of the galaxies in the following way. The total luminosity was obtained by integrating the measured radial profile up to the background radius, the total luminosity of the core component was obtained by integrating the fitted profile of the core, and the disk luminosity is simply the difference between these two quantities. In Table 2 we list the core components' scalelength and contribution to the total luminosity derived from the fits.
In a second approach, we performed 2D fitting on M 81 (chosen because of the level of details available and the existence of a point-like component in the center), using the GALFIT code (Peng et al. 2002). Galactic structure (arms, bars, rings) is much more complex to represent mathematically in 2D, thus this method converges on the extraction of unresolved components. This provides a cross-check to the radial profile approach since, when the central component is resolved in the profile, the 2D method should underestimate it, but both methods should agree when it is unresolved. This is what we observe (see below).
Table 2: Scale-lengths and relative contributions of the core component.
4 Discussion
In general, we observe that the same family of functions provides the best-fit models to a given galaxy, regardless of the wavelength. This is mostly because the same morphological features dominate the profile of galaxies over the explored spectral domain, a fact worth noting given the quite drastic changes in the thermodynamical state and physical nature of the mid to far IR-emitting grains, from out-of-equilibrium, nearly molecular-sized grains to thermalized sub-micron grains (but see Pohlen et al. 2010, for a discussion of the full profiles properties). However, the profiles already show that the relative importance of the core component is variable from one galaxy to the next (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14588fg1.eps}
\vspace{-3mm}\end{figure}](/articles/aa/full_html/2010/10/aa14588-10/Timg18.png)
|
Figure 1:
The surface brightness radial profiles at 250 |
| Open with DEXTER | |
M 81 - This is the closest galaxy and thus its central region
is observable with a high level of detail (see Bendo et al. 2010b). The core is compact, possibly the IR counterpart of the Seyfert
nucleus, on which a bright arc, presumably the start of one of the
spiral arms, connects. Moving away from the center, the brightness of
the arm diminishes until it increases again to form a bright, almost
ring-like structure. Thus all profiles, except the 24 ![]() m one, show
a first local minimum at
m one, show
a first local minimum at
![]() radius (1.4 kpc at 3.65 Mpc).
With high enough resolution, the double nature of the core component
(central unresolved source and spiral arm) is visible in the
profile as a break in the slope of the core profile. The interplay
between the resolved and unresolved parts of the core is clear in the
comparison of the GALFIT and profile-fitting core-fraction
estimates: as the former preferentially extracts the unresolved
component, while the latter is able to extract both the
unresolved and resolved components as a single structure
departing from the disk, we expect both methods to agree, for a
given band, when either the unresolved source is dominant or the
whole core structure is unresolved. This is indeed observed for MIPS
24
radius (1.4 kpc at 3.65 Mpc).
With high enough resolution, the double nature of the core component
(central unresolved source and spiral arm) is visible in the
profile as a break in the slope of the core profile. The interplay
between the resolved and unresolved parts of the core is clear in the
comparison of the GALFIT and profile-fitting core-fraction
estimates: as the former preferentially extracts the unresolved
component, while the latter is able to extract both the
unresolved and resolved components as a single structure
departing from the disk, we expect both methods to agree, for a
given band, when either the unresolved source is dominant or the
whole core structure is unresolved. This is indeed observed for MIPS
24 ![]() m (where the unresolved component dominates) and for MIPS
160, SPIRE 350, and 500
m (where the unresolved component dominates) and for MIPS
160, SPIRE 350, and 500 ![]() m (where the whole core structure is not,
or barely, resolved). In the other bands, the unresolved component is
less dominant, and GALFIT computes core fractions that are a
factor of 3 below those coming from the profile fitting. However,
inspection of the corresponding images clearly shows the unresolved
component sitting on a core structure distinct in brightness from the
disk. The core contribution derived with the profile fitting method is
also very compatible with what can be measured naively from the
profile itself, inside the 80'' radius. The core component is
generally well represented by Gaussians and, when resolved, the
derived scalelengths are compatible with one another, given
typical uncertainties of 10%. We note a severe disagreement between the
two 160
m (where the whole core structure is not,
or barely, resolved). In the other bands, the unresolved component is
less dominant, and GALFIT computes core fractions that are a
factor of 3 below those coming from the profile fitting. However,
inspection of the corresponding images clearly shows the unresolved
component sitting on a core structure distinct in brightness from the
disk. The core contribution derived with the profile fitting method is
also very compatible with what can be measured naively from the
profile itself, inside the 80'' radius. The core component is
generally well represented by Gaussians and, when resolved, the
derived scalelengths are compatible with one another, given
typical uncertainties of 10%. We note a severe disagreement between the
two 160 ![]() m core fraction measurements, but inspection of the
profiles clearly shows that this stems from dilution of the barely
resolved central component in the disk emission at the low resolution
of Spitzer, thereby pointing to the intrinsic limitations of the
MIPS 160
m core fraction measurements, but inspection of the
profiles clearly shows that this stems from dilution of the barely
resolved central component in the disk emission at the low resolution
of Spitzer, thereby pointing to the intrinsic limitations of the
MIPS 160 ![]() m band as the way to perform these decomposition studies. At
increasing SPIRE wavelengths, we observe as well that the central
component becomes gradually unresolved.
m band as the way to perform these decomposition studies. At
increasing SPIRE wavelengths, we observe as well that the central
component becomes gradually unresolved.
M 99 - Although this galaxy clearly shows a bright center and
spiral arms in all available IR bands (see Pohlen et al. 2010), our fit
of the profiles is usually adequate with a single exponential
function; however: (1) an exponential does not accurately represent
the disk profile that has a distinct break (at
![]() in
Fig. 1, see Pohlen et al. 2010, for a discussion of this feature),
and (2) the 24
in
Fig. 1, see Pohlen et al. 2010, for a discussion of this feature),
and (2) the 24 ![]() m image is sharp enough to reveal a barely resolved Gaussian component in the center
(
m image is sharp enough to reveal a barely resolved Gaussian component in the center
(
![]() )
contributing less than 0.5% of the total 24
)
contributing less than 0.5% of the total 24 ![]() m flux.
m flux.
M 100 - The barred nature of the galaxy clearly shows up as a bump
in the high-resolution profiles (e.g. 24 ![]() m and 250
m and 250 ![]() m,
see also Pohlen et al. 2010), and as a result, the fitting function favors a
double Gaussian profile, with very good fits of the central
component achieved from 24
m,
see also Pohlen et al. 2010), and as a result, the fitting function favors a
double Gaussian profile, with very good fits of the central
component achieved from 24 ![]() m to 500
m to 500 ![]() m.
Table 2, however, shows the central component is unresolved at 160, 350, and 500
m.
Table 2, however, shows the central component is unresolved at 160, 350, and 500 ![]() m, while for the other wavelengths a
scale-length of
m, while for the other wavelengths a
scale-length of
![]() is indicated by the fits. When the
central component is unresolved, our capacity to accurately measure
its contribution will depend on how bright it is compared to the disk
component. Thus it is possible that the core fraction we compute at
160
is indicated by the fits. When the
central component is unresolved, our capacity to accurately measure
its contribution will depend on how bright it is compared to the disk
component. Thus it is possible that the core fraction we compute at
160 ![]() m (the band with the worst resolution) is in fact a lower
limit to the actual core fraction, pointing again to the limited
ability of the MIPS 160
m (the band with the worst resolution) is in fact a lower
limit to the actual core fraction, pointing again to the limited
ability of the MIPS 160 ![]() m band to accurately measure core
contributions.
m band to accurately measure core
contributions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14588fg2.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14588-10/Timg23.png)
|
Figure 2:
Top panel: colors as a function of wavelength. Colors are
displayed at an abscissa in-between the band wavelengths used, e.g.,
the [24]/[70] color is plotted at 50 |
| Open with DEXTER | |
The necessity to account for a core component to represent the surface brightness profile already appears weakly related to the morphological type: it is on the intermediate type galaxy M 100 that we observe the largest core fraction. It is quite tempting, and probably logical, to relate that to the presence of a weak bar in M 100, but this can only be asserted on a reasonable sample, as the presence of a bar does not guarantee there is a strong MIR core component (Roussel et al. 2001a).
Interestingly, even though M 81 and M 100 have significantly
different core fractions (by a factors >2), we observe in
Fig. 2 the same trend in the evolution of this
fraction with wavelength: it is maximum at the shorter wavelengths
and nearly constant beyond 200 ![]() m, with the transition occurring
in the 70-200
m, with the transition occurring
in the 70-200 ![]() m range. The evolution of the core fraction can be
interpreted by inspecting the component's colors. We show in
Fig. 2 the colors of the core and disk components
built from neighboring bands. This figure first shows quite clearly
that all the disk colors are very similar for the
three galaxies studied here, even when the core component represents a
substantial fraction of the emission (10-20% at
m range. The evolution of the core fraction can be
interpreted by inspecting the component's colors. We show in
Fig. 2 the colors of the core and disk components
built from neighboring bands. This figure first shows quite clearly
that all the disk colors are very similar for the
three galaxies studied here, even when the core component represents a
substantial fraction of the emission (10-20% at
![]() ). It also shows that only the
[70]/[160]
). It also shows that only the
[70]/[160]![]() core colors, and to
a lesser extent [160]/[250], significantly differ from the disk
colors. The [70]/[160] core colors are systematically higher than
those of disks, showing the core emission as coming from hotter dust
than the disk emission. If the dust is hotter in the core than in the
disk, then it will represent a larger fraction of the emission at
shorter wavelengths. In the SPIRE range, we reach the Rayleigh-Jeans
regime, where colors have no dependence on temperature. That
color differences are more prominent in the 70-250
core colors, and to
a lesser extent [160]/[250], significantly differ from the disk
colors. The [70]/[160] core colors are systematically higher than
those of disks, showing the core emission as coming from hotter dust
than the disk emission. If the dust is hotter in the core than in the
disk, then it will represent a larger fraction of the emission at
shorter wavelengths. In the SPIRE range, we reach the Rayleigh-Jeans
regime, where colors have no dependence on temperature. That
color differences are more prominent in the 70-250 ![]() m range is
simply because this is where the peak of the thermal emission of dust
in galaxies occur, showing that this range is key to properly
understanding the infrared emission of galaxies.
m range is
simply because this is where the peak of the thermal emission of dust
in galaxies occur, showing that this range is key to properly
understanding the infrared emission of galaxies.
To reconcile the small [24]/[70] color variation between disks and
cores with the larger core fractions at 24 ![]() m, we suggest that it
is because the 24
m, we suggest that it
is because the 24 ![]() m and some of the 70
m and some of the 70 ![]() m emission come from transiently heated grains, i.e., show little
spectral variation with the ISRF intensity or hardness. A harder ISRF
in the core could then explain the larger core fractions observed at
24
m emission come from transiently heated grains, i.e., show little
spectral variation with the ISRF intensity or hardness. A harder ISRF
in the core could then explain the larger core fractions observed at
24 ![]() m by boosting the emission from transiently heatedgrains
without significantly affecting their emission spectrum. The small AGN
in M 81 is a natural explanation for this, as is a possible
bar-driven starburst in the center of M 100. We also tested an
alternative explanation in M 81, namely a direct contribution of bulge
stars in the 24
m by boosting the emission from transiently heatedgrains
without significantly affecting their emission spectrum. The small AGN
in M 81 is a natural explanation for this, as is a possible
bar-driven starburst in the center of M 100. We also tested an
alternative explanation in M 81, namely a direct contribution of bulge
stars in the 24 ![]() m band, as suggested by Bendo et al. (2008), by
correcting the MIPS image using IRAC data (a correction to the
total flux of
m band, as suggested by Bendo et al. (2008), by
correcting the MIPS image using IRAC data (a correction to the
total flux of ![]() ). The ``dust-only'' core fraction is almost
unchanged, revealing that bulge stars are not responsible for the FIR
core structure.
). The ``dust-only'' core fraction is almost
unchanged, revealing that bulge stars are not responsible for the FIR
core structure.
5 Conclusions
In this small set of galaxies, the core fractions are small
(![]() 20%), therefore the correction to the full SED of the
galaxies introduced by accounting for the different core properties
would be minimum. Nevertheless we already observe both a significant
variation in the core component contribution from one galaxy to the
next and a systematic decrease with wavelength. We also find
that the galactic disks studied here show remarkable color homogeneity
over the 24-500
20%), therefore the correction to the full SED of the
galaxies introduced by accounting for the different core properties
would be minimum. Nevertheless we already observe both a significant
variation in the core component contribution from one galaxy to the
next and a systematic decrease with wavelength. We also find
that the galactic disks studied here show remarkable color homogeneity
over the 24-500 ![]() m range, while the core components are notably
hotter as shown by their higher [70]/[160] color value. This opens the
possibilities that (i) across the Herschel wavelength range, the
global SED of a galaxy may be influenced as much by the relative
importance of the core and disk components as by a global property,
such as the star formation rate or the morphological type, and (ii) that
this may depend on the observed wavelength. We shall thus examine this
in larger samples such as the HRS set of resolved spiral galaxies.
m range, while the core components are notably
hotter as shown by their higher [70]/[160] color value. This opens the
possibilities that (i) across the Herschel wavelength range, the
global SED of a galaxy may be influenced as much by the relative
importance of the core and disk components as by a global property,
such as the star formation rate or the morphological type, and (ii) that
this may depend on the observed wavelength. We shall thus examine this
in larger samples such as the HRS set of resolved spiral galaxies.
SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, OAMP (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech/JPL, IPAC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); Stockholm Observatory (Sweden); STFC (UK); and NASA (USA).
PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/AOT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICT/MCT (Spain).
This research has made use of HIPE, a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia, and of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, Caltech, under contract with NASA.
References
- Boselli, A., Eales, S., Cortese, L., et al. 2010, PASP, 122, 261 Bendo, G., Calzetti, D., Engelbracht, C. W., et al. 2007, MNRAS, 380, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G., Draine, B. T., Engelbracht, C. W., et al. 2008, MNRAS, 389, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Wilson, C. D., Warren, B. E., et al. 2010a, MNRAS, 402, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., et al. 2010b, A&A, 518, L65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chanial, P., Flores, H., Guiderdoni, B., et al. 2007, A&A, 462, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clements, D. L., et al. 2010, A&A, 518, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., et al. 2010, A&A, 518, L3 [Google Scholar]
- Ho, L. C., Filipenko, A. V., & Sargent, W. L. W. 1997, ApJ, 112, 315 [NASA ADS] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A. et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M. et al. 2010, A&A, 518, L72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H., Sauvage, M., Vigroux, L., et al. 2001a, A&A, 372, 406 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H., Sauvage, M., Vigroux, L., & Bosma, A. 2001b, A&A, 372, 427 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Footnotes
- ...Herschel
![[*]](/icons/foot_motif.png)
- Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with significant participation from NASA.
- ...
NED
![[*]](/icons/foot_motif.png)
- http://nedwww.ipac.caltech.edu/.
- ... functions
![[*]](/icons/foot_motif.png)
- In the
case of a Gaussian, we have
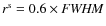 .
.
- ...
[70]/[160]
![[*]](/icons/foot_motif.png)
Shorthand for![$\log
\left[f_{\nu}(70~\mbox{$\mu$ m})/f_{\nu}(160~\mbox{$\mu$ m})\right]$](/articles/aa/full_html/2010/10/aa14588-10/img25.png) .
.
All Tables
Table 1: Relevant data for the galaxies studied here, as well as the images used (M: MIPS, P: PACS, S: SPIRE).
Table 2: Scale-lengths and relative contributions of the core component.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14588fg1.eps}
\vspace{-3mm}\end{figure}](/articles/aa/full_html/2010/10/aa14588-10/Timg18.png)
|
Figure 1:
The surface brightness radial profiles at 250 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14588fg2.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14588-10/Timg23.png)
|
Figure 2:
Top panel: colors as a function of wavelength. Colors are
displayed at an abscissa in-between the band wavelengths used, e.g.,
the [24]/[70] color is plotted at 50 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


