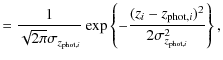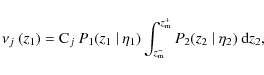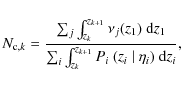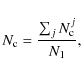| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014236 | |
| Published online | 24 August 2010 | |
Spectro-photometric close pairs in GOODS-S: major and minor companions of intermediate-mass galaxies
C. López-Sanjuan1,2,3,4 - M. Balcells1,2,5 - P. G. Pérez-González3,6 - G. Barro3 - J. Gallego3 - J. Zamorano3
1 - Instituto de Astrofísica de Canarias, Calle vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
2 - Departamento de Astrofísica, Universidad de La Laguna, 38200 La Laguna, Tenerife, Spain
3
- Departamento de Astrofísica y Ciencias de la Atmósfera, Facultad de
C.C. Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
4
- Laboratoire d'Astrophysique de Marseille, Pôle de l'Étoile Site de
Château-Gombert, 38 rue Frédéric Joliot-Curie, 13388 Marseille, France
5 - Isaac Newton Group of Telescopes, Aptdo. Correos 321, 38700 Santa Cruz de La Palma, Tenerife, Spain
6 - Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
Received 10 February 2010 / Accepted 6 April 2010
Abstract
Aims. Recent work has shown that major mergers of disc galaxies can only account for ![]() 20% of the growth of the galaxy red sequence between z=1 and z=0.
Our goal here is to provide merger frequencies that encompass both
major and minor mergers, derived from close pair statistics. We aim to
show that reliable close pair statistics can be derived from galaxy
catalogues with mixed spectroscopic and photometric redshifts.
20% of the growth of the galaxy red sequence between z=1 and z=0.
Our goal here is to provide merger frequencies that encompass both
major and minor mergers, derived from close pair statistics. We aim to
show that reliable close pair statistics can be derived from galaxy
catalogues with mixed spectroscopic and photometric redshifts.
Methods. We use B-band luminosity- and mass-limited samples from a Spitzer/IRAC-selected catalogue of GOODS-S. We present a new methodology for computing the number of close companions, ![]() ,
when spectroscopic redshift information is partial. The methodology
extends the one used in spectroscopic surveys to make use of
photometric redshift information. We select as close companions those
galaxies separated by
,
when spectroscopic redshift information is partial. The methodology
extends the one used in spectroscopic surveys to make use of
photometric redshift information. We select as close companions those
galaxies separated by
![]() kpc
kpc
![]() kpc in the sky plane and with a difference
kpc in the sky plane and with a difference
![]() km s-1 in redshift space.
km s-1 in redshift space.
Results. We provide ![]() for four different B-band-selected
samples. It increases with luminosity, in good agreement with previous
estimations from spectroscopic surveys. The evolution of
for four different B-band-selected
samples. It increases with luminosity, in good agreement with previous
estimations from spectroscopic surveys. The evolution of ![]() with redshift is faster in more luminous samples. We provide
with redshift is faster in more luminous samples. We provide ![]() of
of
![]() galaxies, finding that the number including minor companions (
galaxies, finding that the number including minor companions (
![]() ,
mass ratio
,
mass ratio
![]() )
is roughly two times the number of major companions alone (
)
is roughly two times the number of major companions alone (
![]() ,
mass ratio
,
mass ratio
![]() )
in the range
)
in the range
![]() .
We compare the major merger rate derived by close pairs with the one
computed by morphological criteria, finding that both approaches
provide similar merger rates for field galaxies when the progenitor
bias is taken into account. Finally, we estimate that the total
(major+minor) merger rate is
.
We compare the major merger rate derived by close pairs with the one
computed by morphological criteria, finding that both approaches
provide similar merger rates for field galaxies when the progenitor
bias is taken into account. Finally, we estimate that the total
(major+minor) merger rate is ![]() 1.7 times the major merger rate.
1.7 times the major merger rate.
Conclusions. Only 30% to 50% of the
![]() early-type (E/S0/Sa) galaxies that appear between z=1 and z=0 may have undergone a major or a minor merger. Half of the red sequence growth since z=1 is therefore unrelated to mergers.
early-type (E/S0/Sa) galaxies that appear between z=1 and z=0 may have undergone a major or a minor merger. Half of the red sequence growth since z=1 is therefore unrelated to mergers.
Key words: galaxies: interactions - galaxies: evolution - galaxies: formation
1 Introduction
How important are galaxy mergers on the mass assembly history of red
sequence (i.e., passive early-type) galaxies? This is one of the most
challenging questions in galaxy evolution studies, one that is
motivated by both theory and observations. In the former, popular
hierarchical ![]() -CDM
models predict that the more massive dark matter haloes, inhabited by
red-sequence galaxies, are the final stage of successive mergers of
less massive haloes. However, the behaviour of the baryonic component
is still unclear. Only with many ad-hoc ingredients can the latest
models, which include radiative cooling, star formation, and AGN and
supernova feedback, reproduce the observational trends better (see Bower et al. 2006; De Lucia & Blaizot 2007; Hopkins et al. 2009c; Stewart et al. 2009b, and references therein). On the other hand, N-body simulations suggest that gas-rich mergers can produce intermediate-mass spheroidal systems (e.g., Bournaud et al. 2005; Naab & Burkert 2003; Hopkins et al. 2008), while dissipationless mergers can explain the more massive spheroids (e.g., Naab et al. 2006b; González-García & van Albada 2003; González-García & Balcells 2005). Observationally, merger remnants in the local Universe can evolve into elliptical galaxies (Rothberg & Joseph 2006b,a). In addition, the size (van der Wel et al. 2008; Daddi et al. 2005; Buitrago et al. 2008; Trujillo et al. 2007) and velocity-dispersion (Cenarro & Trujillo 2009) evolution of massive galaxies with redshift, and the luminosity density evolution of red sequence galaxies since
-CDM
models predict that the more massive dark matter haloes, inhabited by
red-sequence galaxies, are the final stage of successive mergers of
less massive haloes. However, the behaviour of the baryonic component
is still unclear. Only with many ad-hoc ingredients can the latest
models, which include radiative cooling, star formation, and AGN and
supernova feedback, reproduce the observational trends better (see Bower et al. 2006; De Lucia & Blaizot 2007; Hopkins et al. 2009c; Stewart et al. 2009b, and references therein). On the other hand, N-body simulations suggest that gas-rich mergers can produce intermediate-mass spheroidal systems (e.g., Bournaud et al. 2005; Naab & Burkert 2003; Hopkins et al. 2008), while dissipationless mergers can explain the more massive spheroids (e.g., Naab et al. 2006b; González-García & van Albada 2003; González-García & Balcells 2005). Observationally, merger remnants in the local Universe can evolve into elliptical galaxies (Rothberg & Joseph 2006b,a). In addition, the size (van der Wel et al. 2008; Daddi et al. 2005; Buitrago et al. 2008; Trujillo et al. 2007) and velocity-dispersion (Cenarro & Trujillo 2009) evolution of massive galaxies with redshift, and the luminosity density evolution of red sequence galaxies since ![]() (Faber et al. 2007; Bell et al. 2004)
rule out the passive-evolution hypothesis and suggest galaxy mergers
are an important process in galaxy formation and growth.
(Faber et al. 2007; Bell et al. 2004)
rule out the passive-evolution hypothesis and suggest galaxy mergers
are an important process in galaxy formation and growth.
The merger fraction, ![]() ,
defined as the ratio between the number of merger events in a
sample and the total number of sources in the same sample, is a useful
observational quantity to explore the role of mergers in the growth of
the red sequence and thus to constraint cosmological models. Many
studies have determined the merger fraction and its evolution with
redshift up to
,
defined as the ratio between the number of merger events in a
sample and the total number of sources in the same sample, is a useful
observational quantity to explore the role of mergers in the growth of
the red sequence and thus to constraint cosmological models. Many
studies have determined the merger fraction and its evolution with
redshift up to ![]() ,
usually parametrized as
,
usually parametrized as
![]() ,
using different
sample selections and methods, such as morphological criteria (Cassata et al. 2005; Jogee et al. 2009; López-Sanjuan et al. 2009a; Kampczyk et al. 2007; Heiderman et al. 2009; Conselice et al. 2009,2003; Bridge et al. 2007; Lotz et al. 2008a; Lavery et al. 2004; Darg et al. 2010; Conselice et al. 2008),
kinematic close companions (Patton et al. 2002; De Propris et al. 2007; Patton et al. 2000; Lin et al. 2004,2008; De Propris et al. 2005; Patton & Atfield 2008), spatially close pairs (Bridge et al. 2007; Hsieh et al. 2008; Bluck et al. 2009; Bundy et al. 2004; Le Fèvre et al. 2000; Bundy et al. 2009; Kartaltepe et al. 2007), or the correlation function (Bell et al. 2006; Masjedi et al. 2006). In these studies the value of the merger index m at redshift
,
using different
sample selections and methods, such as morphological criteria (Cassata et al. 2005; Jogee et al. 2009; López-Sanjuan et al. 2009a; Kampczyk et al. 2007; Heiderman et al. 2009; Conselice et al. 2009,2003; Bridge et al. 2007; Lotz et al. 2008a; Lavery et al. 2004; Darg et al. 2010; Conselice et al. 2008),
kinematic close companions (Patton et al. 2002; De Propris et al. 2007; Patton et al. 2000; Lin et al. 2004,2008; De Propris et al. 2005; Patton & Atfield 2008), spatially close pairs (Bridge et al. 2007; Hsieh et al. 2008; Bluck et al. 2009; Bundy et al. 2004; Le Fèvre et al. 2000; Bundy et al. 2009; Kartaltepe et al. 2007), or the correlation function (Bell et al. 2006; Masjedi et al. 2006). In these studies the value of the merger index m at redshift
![]() varies in the range m = 0-4.
varies in the range m = 0-4. ![]() -CDM models predict
-CDM models predict ![]() 2-3 (Governato et al. 1999; Kolatt et al. 1999; Fakhouri & Ma 2008; Gottlöber et al. 2001) for dark matter haloes, while suggesting a weaker evolution,
2-3 (Governato et al. 1999; Kolatt et al. 1999; Fakhouri & Ma 2008; Gottlöber et al. 2001) for dark matter haloes, while suggesting a weaker evolution, ![]() -2, for the galaxy merger fraction (Berrier et al. 2006; Stewart et al. 2009a).
-2, for the galaxy merger fraction (Berrier et al. 2006; Stewart et al. 2009a).
In this paper we study the number of close companions (
![]() )
in a Spitzer/IRAC-selected catalogue of the GOODS-S area and explore its dependence on redshift, B-band luminosity, and stellar mass. A robust methodology for measuring
)
in a Spitzer/IRAC-selected catalogue of the GOODS-S area and explore its dependence on redshift, B-band luminosity, and stellar mass. A robust methodology for measuring ![]() in spectroscopic surveys was developed by Patton et al. (2000),
and we adapt it in present paper to exploit all the available redshift
information in spectro-photometric catalogues, obtaining reliable
values when compared with those from fully spectroscopic samples. In
addition, work with close companions gives us useful information about
the galaxies involved in the mergers, such as their mass ratio. Thanks
to that, and taking advantage of our new methodology, we report an
estimation of the number of minor companions (stellar mass ratio 1:10)
and their relation with major companions (mass ratio higher than 1:3)
for intermediate mass galaxies (see Jogee et al. 2009; Lotz et al. 2008a, for a morphological determination of the minor merger fraction).
in spectroscopic surveys was developed by Patton et al. (2000),
and we adapt it in present paper to exploit all the available redshift
information in spectro-photometric catalogues, obtaining reliable
values when compared with those from fully spectroscopic samples. In
addition, work with close companions gives us useful information about
the galaxies involved in the mergers, such as their mass ratio. Thanks
to that, and taking advantage of our new methodology, we report an
estimation of the number of minor companions (stellar mass ratio 1:10)
and their relation with major companions (mass ratio higher than 1:3)
for intermediate mass galaxies (see Jogee et al. 2009; Lotz et al. 2008a, for a morphological determination of the minor merger fraction).
The paper is organized as follows. In Sect. 2 we summarize the GOODS-S data set we used, and in Sect. 3 we develop the methodology for determining the number of companions in spectro-photometric catalogues. Then, in Sect. 4.1 we study the number of close companions in B-band selected samples, while mass-selected samples are analysed in Sect. 4.2. We compare our inferred major merger rates with those from morphological criteria in Sect. 5. We discuss the implications of our results in Sect. 6, and in Sect. 7 we present our conclusions. We use
![]() ,
,
![]() ,
and
,
and
![]() throughout. All magnitudes are Vega unless otherwise noted.
throughout. All magnitudes are Vega unless otherwise noted.
2 GOODS-S catalogue
We worked with the galaxy catalogue from the Great Observatories Origins Deep Survey South (GOODS-S)![]() field by the Spitzer Legacy Team (Giavalisco et al. 2004). We used the Version 1.0 catalogues
field by the Spitzer Legacy Team (Giavalisco et al. 2004). We used the Version 1.0 catalogues![]() and reduced mosaics in
the F435W (B435), F606W (V606), F775W (i775), and F850LP(z850) HST/ACS bands. These catalogues were cross-correlated using a
and reduced mosaics in
the F435W (B435), F606W (V606), F775W (i775), and F850LP(z850) HST/ACS bands. These catalogues were cross-correlated using a
![]() search radius with the GOODS-S IRAC selected sample in the
Rainbow cosmological database
search radius with the GOODS-S IRAC selected sample in the
Rainbow cosmological database![]() published in Pérez-González et al. (2008, see also Pérez-González et al. 2005 and Barro et al., in prep.#, which provided us with spectral energy
distributions (SEDs) in the UV-to-MIR range, well-calibrated and with reliable
photometric redshifts, stellar masses, star formation rates, and rest-frame
absolute magnitudes. We worked with a Spitzer/IRAC selected catalogue in [3.4] and [4.5] filters to ensure completeness in stellar mass. Although the PSF of Spitzer/IRAC is
published in Pérez-González et al. (2008, see also Pérez-González et al. 2005 and Barro et al., in prep.#, which provided us with spectral energy
distributions (SEDs) in the UV-to-MIR range, well-calibrated and with reliable
photometric redshifts, stellar masses, star formation rates, and rest-frame
absolute magnitudes. We worked with a Spitzer/IRAC selected catalogue in [3.4] and [4.5] filters to ensure completeness in stellar mass. Although the PSF of Spitzer/IRAC is ![]()
![]() (Fazio et al. 2004), we were able of resolve sources with
(Fazio et al. 2004), we were able of resolve sources with ![]()
![]() separation (see Pérez-González et al. 2008 for details about the deblending process of Spitzer/IRAC sources). We used this
separation (see Pérez-González et al. 2008 for details about the deblending process of Spitzer/IRAC sources). We used this
![]() separation to fix the minimum radius when searching for close companions (Sect. 3.1).
separation to fix the minimum radius when searching for close companions (Sect. 3.1).
We refer the reader to these papers for a more detailed description of
the data included in the SEDs and the analysis procedure. Here, we
briefly summarize the main characteristics of the data set. The Rainbow
database contains consistent aperture photometry in several UV,
optical, NIR, and MIR bands with the method described in Pérez-González et al. (2008). The UV-to-MIR SEDs were built for 4927 IRAC sources in the GOODS-S region down to a 75% completeness magnitude
[3.6] =23.5 mag
(AB). These SEDs were fitted to stellar population and dust emission models to
obtain estimates of the photometric redshift (
![]() ), the stellar
mass (
), the stellar
mass (![]() ), and the rest-frame B-band absolute magnitude (MB).
), and the rest-frame B-band absolute magnitude (MB).
Rest-frame absolute B-band magnitudes were
estimated for each source by convolving the templates fitting the SED with the
transmission curve of a typical Bessel-B filter, taking the
redshift of each source into account. This procedure provided accurate interpolated
B-band magnitudes including a robustly estimated k-correction. Stellar
masses were estimated using the exponential star formation PEGASE01 models with
a Salpeter (1955) IMF, and various ages, metallicities, and dust contents (Calzetti et al. 2000) were included. The typical uncertainties in the stellar masses are a factor of ![]() 2, which is
typical of most stellar population studies (see, e.g., Fontana et al. 2006; Papovich et al. 2006).
2, which is
typical of most stellar population studies (see, e.g., Fontana et al. 2006; Papovich et al. 2006).
In the catalogue, ![]() 40% of the sources have spectroscopic redshift (
40% of the sources have spectroscopic redshift (
![]() ), and we rely on
), and we rely on
![]() for the other
for the other ![]() 60%. Because of this, we refer to our catalogue as spectro-photometric hereafter. The median accuracy of the photometric redshifts at z < 1.5 is
60%. Because of this, we refer to our catalogue as spectro-photometric hereafter. The median accuracy of the photometric redshifts at z < 1.5 is
![]() ,
with a fraction <5% of catastrophic
outliers (Pérez-González et al. 2008, Fig. B2). In the present paper we use
,
with a fraction <5% of catastrophic
outliers (Pérez-González et al. 2008, Fig. B2). In the present paper we use
![]() as
as
![]() error, where
error, where
![]() is the standard deviation in the distribution of the
variable
is the standard deviation in the distribution of the
variable
![]() ,
which is described by a Gaussian well with mean
,
which is described by a Gaussian well with mean
![]() and
standard deviation
and
standard deviation
![]() (see López-Sanjuan et al. 2009a, for details).
We take
(see López-Sanjuan et al. 2009a, for details).
We take
![]() for
for
![]() sources and
sources and
![]() for z > 0.9 sources.
for z > 0.9 sources.
Finally, we remove those sources in the catalogue within
![]() of the centre of the most prominent large-scale structure (LSS) in GOODS-S, located at z = 0.735 (López-Sanjuan et al. 2010; Rawat et al. 2008; Ravikumar et al. 2007).
This is because the relative velocity of two galaxies located in a
cluster is representative not of the dynamical state of the pair, but
of the cluster potential, and we cannot apply the Sect. 3 methodology. For that reason, the present results are mainly refer to field galaxies.
of the centre of the most prominent large-scale structure (LSS) in GOODS-S, located at z = 0.735 (López-Sanjuan et al. 2010; Rawat et al. 2008; Ravikumar et al. 2007).
This is because the relative velocity of two galaxies located in a
cluster is representative not of the dynamical state of the pair, but
of the cluster potential, and we cannot apply the Sect. 3 methodology. For that reason, the present results are mainly refer to field galaxies.
Table 1: B-band luminosity and mass function parameters.
3 Methodology
In this section we recall the methodology developed by Patton et al. (2000), which has been used extensively on spectroscopic samples (De Propris et al. 2007; de Ravel et al. 2009; Patton et al. 2000; De Propris et al. 2010; Lin et al. 2004,2008; Patton et al. 2002; De Propris et al. 2005; Patton & Atfield 2008). Then, we extend that methodology to use all the available information in spectro-photometric samples, paying attention to different bias as luminosity/mass (Sect. 3.1) and spectroscopic (Sect. 4.1.1) completeness of the samples, the border effects in redshift space and images limits (Sect. 3.5), and the treatment of multiple systems (Sect. 3.4).
3.1 Close pair statistics in spectroscopic samples
The linear distance between two sources can be obtained from their projected separation,
![]() ,
and their rest-frame relative velocity along the line of sight,
,
and their rest-frame relative velocity along the line of sight,
![]() ,
where zi and zl are the redshift of the primary (more luminous/massive galaxy in the pair) and secondary galaxy, respectively;
,
where zi and zl are the redshift of the primary (more luminous/massive galaxy in the pair) and secondary galaxy, respectively; ![]() is the angular separation, in arcsec, of the two galaxies on the sky plane; and dA(z) is the angular scale, in kpc/arcsec, at redshift z. Two galaxies are defined as a close pair if
is the angular separation, in arcsec, of the two galaxies on the sky plane; and dA(z) is the angular scale, in kpc/arcsec, at redshift z. Two galaxies are defined as a close pair if
![]() and
and
![]() .
The lower limit in
.
The lower limit in ![]() is imposed to avoid identifying bright star-forming regions of the primary galaxy as close companions. Common limits are
is imposed to avoid identifying bright star-forming regions of the primary galaxy as close companions. Common limits are
![]() kpc,
kpc,
![]() kpc, and
kpc, and
![]() km s-1. With these constraints 50%-70% of the selected close pairs will finally merge (Bell et al. 2006; Patton et al. 2000; Lin et al. 2004; Patton & Atfield 2008). We used the same limit in velocity but slightly different
km s-1. With these constraints 50%-70% of the selected close pairs will finally merge (Bell et al. 2006; Patton et al. 2000; Lin et al. 2004; Patton & Atfield 2008). We used the same limit in velocity but slightly different ![]() limits:
limits:
![]() kpc and
kpc and
![]() kpc. First, the minimum distance for which we are able to resolve two separate sources in our catalogue is
kpc. First, the minimum distance for which we are able to resolve two separate sources in our catalogue is
![]() (Sect. 2), which corresponds to
(Sect. 2), which corresponds to ![]() 8.5 kpc (6
8.5 kpc (6
![]() kpc) in our cosmology at the minimum of the function dA(z). This confusion limit fixes the value of
kpc) in our cosmology at the minimum of the function dA(z). This confusion limit fixes the value of
![]() .
Second, we imposed
.
Second, we imposed
![]() kpc. This condition comes from the study of Bell et al. (2006). They find that the merger fraction is proportional to the radial range under study, so we kept the
kpc. This condition comes from the study of Bell et al. (2006). They find that the merger fraction is proportional to the radial range under study, so we kept the
![]() kpc range used widely in the literature.
kpc range used widely in the literature.
To compute close pairs we defined a primary and a secondary sample. The primary sample contains the more luminous source of the pair, and we looked for those galaxies in the secondary sample that fulfil the close pair criterion for each galaxy of the primary sample.
If we work with B-band luminosity-selected samples, the primary sample comprises the galaxies in the catalogue with
![]() ,
while the secondary comprises
,
while the secondary comprises
![]() galaxies, where
galaxies, where
![]() is an upper limit in luminosity to avoid the different clustering properties of the most luminous galaxies (Patton et al. 2000). In every case,
is an upper limit in luminosity to avoid the different clustering properties of the most luminous galaxies (Patton et al. 2000). In every case,
![]() .
If we work with mass-selected samples, primary sample comprises
.
If we work with mass-selected samples, primary sample comprises
![]() sources, and secondary comprises
sources, and secondary comprises
![]() sources. In this case,
sources. In this case,
![]() .
With the previous definitions the number of companions (
.
With the previous definitions the number of companions (![]() )
per primary galaxy is
)
per primary galaxy is
where N1 is the number of sources in the primary sample, and
where
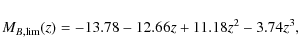
|
(3) |
defined as the third quartile in MB distribution at each redshift (Pérez-González et al. 2008). With this definition, the catalogue is complete for galaxies brighter than MB = -19.5 up to
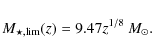
|
(4) |
With this definition the catalogue is complete for galaxies more massive than
We parametrize the luminosity/mass function in Eq. (2) with a Schechter function:
where M = MB or
Finally, and following Patton et al. (2000), the number of companions normalized to a volume-limited sample is
where the index l covers all the close companions of the primary galaxy i.
3.2 Close pair statistics in spectro-photometric samples
The main problem in close pair studies with photometric samples is to constrain the redshift space condition. For example, the
![]() km s-1 condition at
km s-1 condition at
![]() implies
implies
![]() .
This condition is
.
This condition is ![]() 15 times less than the typical
15 times less than the typical
![]() error at that redshift in our catalogue,
error at that redshift in our catalogue,
![]() .
When one or both galaxies in a close spatial pair have photometric
redshift, we therefore cannot apply the methodology in Sect. 3.1. To date a few works have used photometric catalogues to determine pair statistics: Kartaltepe et al. (2007) and Bundy et al. (2009)
tackle the problem using a projection correction calculated in random
samples on the plane of the sky, but keeping the redshift information
of the sources. Hsieh et al. (2008) redefine the velocity criterion to
.
When one or both galaxies in a close spatial pair have photometric
redshift, we therefore cannot apply the methodology in Sect. 3.1. To date a few works have used photometric catalogues to determine pair statistics: Kartaltepe et al. (2007) and Bundy et al. (2009)
tackle the problem using a projection correction calculated in random
samples on the plane of the sky, but keeping the redshift information
of the sources. Hsieh et al. (2008) redefine the velocity criterion to
![]() and apply a conventional projection correction. Finally, Ryan et al. (2008) also redefine the redshift criterion to
and apply a conventional projection correction. Finally, Ryan et al. (2008) also redefine the redshift criterion to
![]() ,
but no projection correction is applied. In this paper we present a new
approximation to determine close pairs in spectro-photometric samples
based on the methodology of Patton et al. (2000) and other previous photometric works.
,
but no projection correction is applied. In this paper we present a new
approximation to determine close pairs in spectro-photometric samples
based on the methodology of Patton et al. (2000) and other previous photometric works.
We use the following procedure to define a close pair system: first we
search for close spatial companions of a primary galaxy, with redshift z1 and uncertainty
![]() ,
assuming that the galaxy is located at
,
assuming that the galaxy is located at
![]() .
This defines the maximum
.
This defines the maximum ![]() possible for a given
possible for a given
![]() in the first instance. If we find a secondary galaxy with redshift z2 and uncertainty
in the first instance. If we find a secondary galaxy with redshift z2 and uncertainty
![]() in the range
in the range
![]() and with a given luminosity/mass with respect to the primary galaxy,
then we study both galaxies in redshift space. For convenience, we
assume below that every primary galaxy has, at most, one close
companion in the secondary sample. In this case, our two galaxies could
be a close pair in the redshift range
and with a given luminosity/mass with respect to the primary galaxy,
then we study both galaxies in redshift space. For convenience, we
assume below that every primary galaxy has, at most, one close
companion in the secondary sample. In this case, our two galaxies could
be a close pair in the redshift range
![\begin{displaymath}[z^{-},z^{+}]= [z_1 - 2\sigma_{z_1}, z_1 + 2\sigma_{z_1}] \cap [z_2- 2\sigma_{z_2}, z_2 + 2\sigma_{z_2}].
\end{displaymath}](/articles/aa/full_html/2010/10/aa14236-10/img124.png)
|
(7) |
Because of variation in the range [z-,z+] of the function dA(z), a sky pair at
The next step is to define the number of companions associated at each close pair system j. For this, we suppose in the following that a galaxy i in whatever sample is described in redshift space by a probability distribution
![]() ,
where zi is the source's redshift and
,
where zi is the source's redshift and ![]() are the parameters that define the distribution. If the source i has a photometric redshift, we assume that
are the parameters that define the distribution. If the source i has a photometric redshift, we assume that
while if the source has a spectroscopic redshift
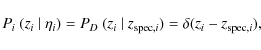
|
(9) |
where
where
| (11) | |||
| (12) |
the subindex 1 [2] refers to the primary [secondary] galaxy in j system, and the constant
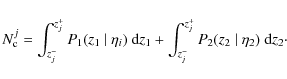
|
(13) |
Note that
With previous definitions, the number of companions per primary galaxy in the interval
zr,k = [zk,zk+1] is
where the index k spans the redshift intervals defined over the redshift range under study. If we integrate over the whole redshift space,
where
The definition of function ![]() in Eq. (10) is general, and we can find four different cases in our spectro-photometric samples:
in Eq. (10) is general, and we can find four different cases in our spectro-photometric samples:
- 1.
- Primary and secondary galaxies have
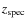 . In this case
. In this case 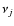 is
is
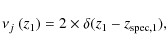
(16)
where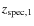 is the spectroscopic redshift of the more luminous/massive galaxy in the close pair. With this definition,
is the spectroscopic redshift of the more luminous/massive galaxy in the close pair. With this definition, 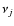 is not zero only at
is not zero only at
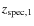 .
If all galaxies in the sample have
.
If all galaxies in the sample have
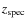 ,
Eq. (15) is equivalent to Eq. (1). These systems provide
,
Eq. (15) is equivalent to Eq. (1). These systems provide
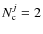 companions in Eq. (15).
companions in Eq. (15).
- 2.
- The primary galaxy has
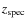 and the secondary
and the secondary
 . Replacing the corresponding distributions of probability in Eq. (10) we obtain
. Replacing the corresponding distributions of probability in Eq. (10) we obtain
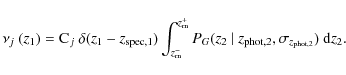
(17)
As in the previous case,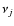 is not zero only at
is not zero only at
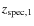 .
These systems provide
.
These systems provide
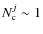 companions in Eq. (15).
companions in Eq. (15).
- 3.
- The primary galaxy has
 and the secondary
and the secondary
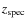 . In this case Eq. (10) becomes
. In this case Eq. (10) becomes
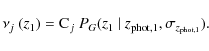
(18)
Function is nonzero in the range
is nonzero in the range
![\begin{displaymath}\bigg[\frac{z_{{\rm spec},2} - \Delta v^{\rm max}/c}{1+\Delta...
...pec},2} + \Delta v^{\rm max}/c}{1-\Delta v^{\rm max}/c}\bigg].
\end{displaymath}](/articles/aa/full_html/2010/10/aa14236-10/img152.png)
(19)
This interval is imposed by the secondary galaxy, and spans those redshifts of the primary galaxy in which the secondary fulfils the condition .
As in the previous case, these systems provide
.
As in the previous case, these systems provide
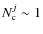 companions in Eq. (15).
companions in Eq. (15).
- 4.
- Primary and secondary galaxies have
 . In this case the function
. In this case the function 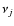 is
is
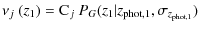
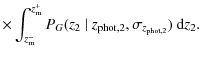
(20)
The main difference between this approach and, for example, the one in Ryan et al. (2008) is that we use the probability distributions of the photometric redshifts to weight the number of companions in each system,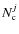 ,
and to minimize projection effects. To illustrate how the weight process works, we show three examples in Fig. 1. In all these cases, the primary galaxy has
,
and to minimize projection effects. To illustrate how the weight process works, we show three examples in Fig. 1. In all these cases, the primary galaxy has
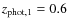 and
and
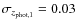 .
In the panel (a), the secondary galaxy has
.
In the panel (a), the secondary galaxy has
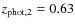 and
and
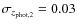 .
With these values the function
.
With these values the function 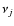 is symmetric and not zero at
[zj-,zj+] = [0.57,0.66]. The integral of the function
is symmetric and not zero at
[zj-,zj+] = [0.57,0.66]. The integral of the function 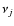 over the redshift space gives us the number of companions in the system, which is
over the redshift space gives us the number of companions in the system, which is
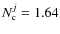 .
In the panel (b) we increase the redshift of the secondary galaxy to
.
In the panel (b) we increase the redshift of the secondary galaxy to
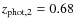 and keep its previous error. In this example the function
and keep its previous error. In this example the function 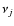 is nonzero at
[zj-,zj+] = [0.62,0.66], a narrower range than in the previous case. Because of this, the number of companions in this system is only
is nonzero at
[zj-,zj+] = [0.62,0.66], a narrower range than in the previous case. Because of this, the number of companions in this system is only
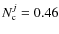 .
Finally, in the panel (c) we keep the previous redshift of the secondary and increase its error to
.
Finally, in the panel (c) we keep the previous redshift of the secondary and increase its error to
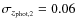 .
In this case, the function
.
In this case, the function 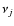 is not symmetric and not zero at
[zj-,zj+] = [0.56,0.66], a similar range to the one in the panel (a). However, the secondary galaxy is more extended in redshift space, and the number of companions is lower,
is not symmetric and not zero at
[zj-,zj+] = [0.56,0.66], a similar range to the one in the panel (a). However, the secondary galaxy is more extended in redshift space, and the number of companions is lower,
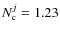 .
.
|
Figure 1:
Probability distributions in redshift space of a primary galaxy (back
solid line), a secondary galaxy (black dashed line), and the function |
| Open with DEXTER | |
The last step involves normalizing our results to volume-limited samples, by applying the SN function (Eq. (2)),
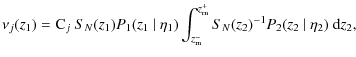
|
(21) |
while the final number of companions is
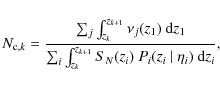
|
(22) |
In order to estimate the error of
3.3 Testing the method in a local, volume-limited sample
We tested that our new methodology is able to statistically recover the
number of companions in a spectroscopic survey from a photometric one.
For this, we study ![]() in the Millennium Galaxy Catalogue (MGC
in the Millennium Galaxy Catalogue (MGC![]() , Liske et al. 2003). This survey comprises 10 095 galaxies with
, Liske et al. 2003). This survey comprises 10 095 galaxies with
![]() over 37.5
over 37.5 ![]() ,
with a spectroscopic completeness of 96% (Driver et al. 2005). De Propris et al. (2007) use the MGC to study the number of companions in a volume-limited sample (
0.01 < z < 0.123,
,
with a spectroscopic completeness of 96% (Driver et al. 2005). De Propris et al. (2007) use the MGC to study the number of companions in a volume-limited sample (
0.01 < z < 0.123,
![]() ,
N = 3183 sources), obtaining
,
N = 3183 sources), obtaining
![]() for
for
![]() and
and
![]() kpc (see also De Propris et al. 2005).
We used this volume-limited sample in the present test. In addition,
the MGC area had been observed by the Sloan Digital Sky Survey (SDSS
kpc (see also De Propris et al. 2005).
We used this volume-limited sample in the present test. In addition,
the MGC area had been observed by the Sloan Digital Sky Survey (SDSS![]() , Adelman-McCarthy et al. 2006), so every galaxy in the sample also has a photometric redshift. Comparing the
, Adelman-McCarthy et al. 2006), so every galaxy in the sample also has a photometric redshift. Comparing the
![]() 's from MGC with the
's from MGC with the
![]() 's from SDSS, we obtained
's from SDSS, we obtained
![]() .
We take this uncertainty as representative of SDSS photometric redshifts.
.
We take this uncertainty as representative of SDSS photometric redshifts.
We defined
![]() as the fraction of the sample's sources with spectroscopic redshift. The MGC sample has
as the fraction of the sample's sources with spectroscopic redshift. The MGC sample has
![]() ,
while the SDSS sample has
,
while the SDSS sample has
![]() .
To test our method at intermediate
.
To test our method at intermediate
![]() and for different
and for different
![]() ,
we assigned a
,
we assigned a
![]() to
to
![]() )
random sources of the MGC sample, as drawn for a Gaussian distribution (Eq. (8)) with median
)
random sources of the MGC sample, as drawn for a Gaussian distribution (Eq. (8)) with median
![]() and a given
and a given
![]() .
Then we measured
.
Then we measured
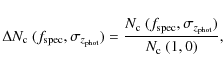
|
(23) |
where
- When we only have spectroscopic information, we obtain the same number of companions as De Propris et al. (2007),
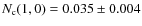 .
This implies that our methodology is equivalent to those used in spectroscopic samples when
.
This implies that our methodology is equivalent to those used in spectroscopic samples when
 ,
as we hoped.
,
as we hoped.
- When we only have photometric information, our method recovers the initial number of companions (Fig. 2) within error bars where the photometric redshift errors are small (
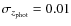 ). On the other hand, the method overestimates the number of companions for
). On the other hand, the method overestimates the number of companions for
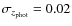 and 0.03. This implies that we need small photometric redshift
errors to avoid projection effects if only photometric information is
available.
and 0.03. This implies that we need small photometric redshift
errors to avoid projection effects if only photometric information is
available.
- If we use the measured
 's of MGC sources from SDSS instead of the spectroscopic ones, the number of companions is higher than expected (
's of MGC sources from SDSS instead of the spectroscopic ones, the number of companions is higher than expected (
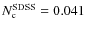 )
and agrees with that from random samples with
)
and agrees with that from random samples with
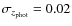 ;
that is, our random samples are representative of the observational ones, and we can use them to explore
;
that is, our random samples are representative of the observational ones, and we can use them to explore
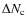 at intermediate values of
at intermediate values of
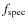 .
.
- When our observational errors are not small enough, we need to increase
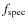 to obtain reliable
to obtain reliable 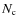 values (Fig. 2). That fixes the redshift of
values (Fig. 2). That fixes the redshift of
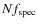 galaxies,
and we use the photometric information to minimize projection effects.
The higher the photometric redshift errors, the higher
galaxies,
and we use the photometric information to minimize projection effects.
The higher the photometric redshift errors, the higher
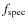 must be to obtain reliable results. In this test we need
must be to obtain reliable results. In this test we need
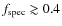 for
for
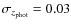 and
and
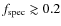 for
for
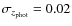 .
.
Table 2:
Number of companions in random samples in units of that in the spectroscopic MGC sample,
![]() .
.

|
Figure 2:
|
| Open with DEXTER | |
3.4 Number of companions as a function of r
In this section we use the methodology developed in Sect. 3.2 to studying the variation in ![]() with
with
![]() .
This is a consistency test of our method because
.
This is a consistency test of our method because
![]() (Patton et al. 2002; de Ravel et al. 2009; Lin et al. 2008), where
(Patton et al. 2002; de Ravel et al. 2009; Lin et al. 2008), where ![]() is the exponent in the correlation function,
is the exponent in the correlation function,
![]() .
The
.
The ![]() values in the literature are consistent with
values in the literature are consistent with
![]() (e.g., Le Fèvre et al. 2005), so we expect
(e.g., Le Fèvre et al. 2005), so we expect
![]() .
.
In this test we define two samples: one comprises all the galaxies in our catalogue with
![]() and
and
![]() ,
named
,
named
![]() ,
while another comprises only the galaxies of
,
while another comprises only the galaxies of
![]() with
with
![]() ,
named
,
named
![]() .
We take these two samples as primary and secondary, and we do not
impose any difference in luminosity between both galaxies when
searching for close companions. We vary
.
We take these two samples as primary and secondary, and we do not
impose any difference in luminosity between both galaxies when
searching for close companions. We vary
![]() from
from
![]() kpc to
kpc to
![]() kpc in
kpc in
![]() kpc steps, and include the radius
kpc steps, and include the radius
![]() kpc. In all cases we use
kpc. In all cases we use
![]() kpc.
kpc.
When we increase the radius of search, we start to find two or more secondary galaxies close to each primary galaxy. We treat these multiple systems with two different approaches:
- 1.
- We study all the possible pairs as independent systems; that is, in a multiple system that comprises the galaxies A, B, and C; we study the subsystems A-B, A-C, and B-C.
- 2.
- We only study the most massive pair, that is, the one with the lowest difference in luminosity/mass between the primary and the secondary galaxies. If this spatial pair is not a close pair in redshift space, we study the next more representative pair, and so on.
- The trends obtained in the
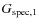 and
and
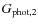 cases agree with the expected
cases agree with the expected
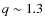 ;
however, the value of q in the
;
however, the value of q in the
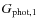 case is higher than expected, reflecting the increased contamination by projection effects when the search area increases.
case is higher than expected, reflecting the increased contamination by projection effects when the search area increases.
Table 3: Number of companions as a function of
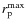 for approaches 1 (independent pairs) and 2 (more representative pair) in the multiple-system treatment.
for approaches 1 (independent pairs) and 2 (more representative pair) in the multiple-system treatment. - For a given
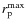 ,
one expects that
,
one expects that
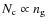 ,
where
,
where 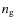 is the number of galaxies in the sample (Lin et al. 2008); in our case,
is the number of galaxies in the sample (Lin et al. 2008); in our case,
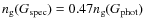 ,
so we can predict the expected number of companions in the
,
so we can predict the expected number of companions in the
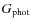 sample from the obtained in the
sample from the obtained in the
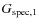 (Fig. 3). We see that the expected number is in excellent agreement with the
(Fig. 3). We see that the expected number is in excellent agreement with the
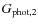 number of companions.
This implies that our methodology is able to recover statistically, from the GOODS-S spectro-photometric sample, the same
number of companions.
This implies that our methodology is able to recover statistically, from the GOODS-S spectro-photometric sample, the same 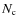 that in a fully spectroscopic one, as we hoped (see also Sects. 3.3 and 4.1.1).
that in a fully spectroscopic one, as we hoped (see also Sects. 3.3 and 4.1.1).
- The number of companions at
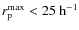 kpc in the
kpc in the
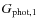 and
and
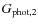 cases are the same. This implies that projection effects start to be important at
cases are the same. This implies that projection effects start to be important at
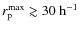 kpc.
kpc.

|
Figure 3:
Number of companions vs.
|
| Open with DEXTER | |
3.5 Border effects in redshift and in the sky plane
Table 4: Number of companions in B-band luminosity-selected samples.
When we search for a primary source companion, we define a volume in
the sky plane-redshift space. If the primary source is near the
boundaries of the survey, a fraction of the search volume lies outside
of the effective volume of the survey. To account for this, we use a
correction factor fb, the fraction of the area
![]() around the primary galaxy that lies in the survey area. This factor is positive and depends on z
because the projected distance in the sky is function of primary source
redshift. We studied how this factor affects the previous section
results, finding that border effects are representative (i.e.,
around the primary galaxy that lies in the survey area. This factor is positive and depends on z
because the projected distance in the sky is function of primary source
redshift. We studied how this factor affects the previous section
results, finding that border effects are representative (i.e., ![]() discrepancy) only at
discrepancy) only at
![]() kpc.
kpc.
We avoid the redshift incompleteness by including in the samples not
only the sources inside the redshift range under study, but also those
sources with
![]() and
and
![]() (see Sects. 3.4 and 4.1). This implies that our samples comprise sources with
(see Sects. 3.4 and 4.1). This implies that our samples comprise sources with
![]() .
.
![\begin{figure}
\par\mbox{\includegraphics[width = 8.5cm,clip]{14236fg4a.eps}\inc...
...\includegraphics[width = 8.5cm,clip]{14236fg4d.eps} }
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14236-10/Timg289.png)
|
Figure 4:
Number of companions vs. redshift for different B-band luminosity selections: panel a) for -
|
| Open with DEXTER | |
4 Results
4.1 Number of close companions in B-band luminosity-selected samples
In this section we study the number of companions as a function of z and MB. For this, we define three luminosity-selected samples,
![]() ,
,
![]() ,
and
,
and
![]() ,
and study
,
and study ![]() in two redshift ranges, named
zr,1 = [0.2,0.65) and
zr,2 = [0.65,1.1). We chose these redshift
ranges to ensure good statistics in our study. In addition, we take the
three previous luminosity-selected samples as primary and secondary,
and do not impose any limit in primary to secondary luminosity ratio.
We apply the same luminosity selections and search parameters to the
MGC sample described in Sect. 3.3 to obtain consistent data points at z = 0.092. We summarize our results with those from previous spectroscopic studies in literature in Table 4 and show them in Fig. 4.
We find that our results from spectro-photometric samples are in
excellent agreement with those from fully spectroscopic ones when
similar search parameters (i.e., luminosity selection and radius range)
are applied.
in two redshift ranges, named
zr,1 = [0.2,0.65) and
zr,2 = [0.65,1.1). We chose these redshift
ranges to ensure good statistics in our study. In addition, we take the
three previous luminosity-selected samples as primary and secondary,
and do not impose any limit in primary to secondary luminosity ratio.
We apply the same luminosity selections and search parameters to the
MGC sample described in Sect. 3.3 to obtain consistent data points at z = 0.092. We summarize our results with those from previous spectroscopic studies in literature in Table 4 and show them in Fig. 4.
We find that our results from spectro-photometric samples are in
excellent agreement with those from fully spectroscopic ones when
similar search parameters (i.e., luminosity selection and radius range)
are applied.
The dependence of ![]() on z can be parametrized with a power-law function,
on z can be parametrized with a power-law function,
The least-squares fits of Eq. (24) to the data are summarized in Table 5. We find that the number of companions evolves faster for more luminous galaxies. The index m decreases from
In the near universe (
![]() ), Patton & Atfield (2008) study the dependence of
), Patton & Atfield (2008) study the dependence of ![]() on r-band luminosity in an SDSS sample. They find a nearly constant value over the range
-22 < Mr < -18 for
on r-band luminosity in an SDSS sample. They find a nearly constant value over the range
-22 < Mr < -18 for
![]() kpc and
kpc and
![]() kpc close companions,
kpc close companions,
![]() ,
in contrast to our measured evolution with luminosity of
,
in contrast to our measured evolution with luminosity of
![]() .
However, they only account for major companions (
.
However, they only account for major companions (
![]() ),
while we do not impose any luminosity constraint. This implies that we
are sensitive to minor companions, more numerous than major (see
Sect. 4.2), in the lower luminosity sample, that lead to an increase in
),
while we do not impose any luminosity constraint. This implies that we
are sensitive to minor companions, more numerous than major (see
Sect. 4.2), in the lower luminosity sample, that lead to an increase in ![]() .
On the other hand, de Ravel et al. (2009) measure the evolution of the major merger fraction (
.
On the other hand, de Ravel et al. (2009) measure the evolution of the major merger fraction (
![]() )
in the VIMOS-VLT Deep Survey (VVDS
)
in the VIMOS-VLT Deep Survey (VVDS![]() , Le Fèvre et al. 2005) up to
, Le Fèvre et al. 2005) up to ![]() ,
finding that the index m
is lower in more luminous samples, an opposite trend to what we find.
This discrepancy can be explained again by the different definition of
companion: we lose major companions near the selection luminosity, but
gain the minor ones of the more luminous galaxies. These two examples
point out that similar definitions of companion are needed to compare
results from different studies and surveys.
,
finding that the index m
is lower in more luminous samples, an opposite trend to what we find.
This discrepancy can be explained again by the different definition of
companion: we lose major companions near the selection luminosity, but
gain the minor ones of the more luminous galaxies. These two examples
point out that similar definitions of companion are needed to compare
results from different studies and surveys.
Lin et al. (2008) study the evolution of ![]() at
0 < z < 1.2 from
at
0 < z < 1.2 from ![]() 35 000 spectroscopic sources, finding
35 000 spectroscopic sources, finding
![]() and
and
![]() ,
a low value that is incompatible with those in the present work. However, Lin et al. (2008) galaxies have
,
a low value that is incompatible with those in the present work. However, Lin et al. (2008) galaxies have
![]() ,
where
,
where
![]() ,
a different selection than ours. To explore whether this can be the origin of the discrepancy in m value, as suggested by Kartaltepe et al. (2007), we mimic the Lin et al. (2008) selection in the literature and in present work as close as possible. In the latter, the Lin et al. (2008) selection at z = 0.425 is
,
a different selection than ours. To explore whether this can be the origin of the discrepancy in m value, as suggested by Kartaltepe et al. (2007), we mimic the Lin et al. (2008) selection in the literature and in present work as close as possible. In the latter, the Lin et al. (2008) selection at z = 0.425 is
![]() and is
and is
![]() at z = 0.875. We summarize the data in Table 6 and show them in the panel (d) of Fig. 4. We obtain
at z = 0.875. We summarize the data in Table 6 and show them in the panel (d) of Fig. 4. We obtain
![]() ,
a low value compatible with the Lin et al. (2008) result: the selection of the sample is a key issue in determining m, and must be taken into account when one compares different works. Finally, the models of Berrier et al. (2006) predict
m = 0.4-1.0, in good agreement with our result.
,
a low value compatible with the Lin et al. (2008) result: the selection of the sample is a key issue in determining m, and must be taken into account when one compares different works. Finally, the models of Berrier et al. (2006) predict
m = 0.4-1.0, in good agreement with our result.
4.1.1 Dependence on the spectroscopic completeness of the sample
In previous section we show that our methodology provides reliable ![]() values,
compatible with those obtained in fully spectroscopic samples, from
GOODS-S spectro-photometric samples. As we show in Sect. 3.3, this can stem from either i) small photometric redshift errors or ii) enough spectroscopic completeness. The
values,
compatible with those obtained in fully spectroscopic samples, from
GOODS-S spectro-photometric samples. As we show in Sect. 3.3, this can stem from either i) small photometric redshift errors or ii) enough spectroscopic completeness. The
![]() sample has
sample has
![]() ,
where
,
where
![]() is the fraction of sources with
is the fraction of sources with
![]() in the sample, the
in the sample, the
![]() sample has
sample has
![]() ,
and the
,
and the
![]() sample has
sample has
![]() .
This means that our methodology works at least for
.
This means that our methodology works at least for
![]() samples. To check that photometric redshift errors in GOODS-S catalogue
are small enough to skip spectroscopic information, we repeat the study
in the previous section but using
samples. To check that photometric redshift errors in GOODS-S catalogue
are small enough to skip spectroscopic information, we repeat the study
in the previous section but using
![]() for all the sources, although some have
for all the sources, although some have
![]() (i.e.,
(i.e.,
![]() ). Unfortunately, we obtain higher values of
). Unfortunately, we obtain higher values of ![]() than expected. This implies (i) that we need
than expected. This implies (i) that we need
![]() in the current GOODS-S samples to avoid an overestimation in
in the current GOODS-S samples to avoid an overestimation in ![]() because of projection effects and (ii) that lower
because of projection effects and (ii) that lower
![]() are needed in order to apply our methodology to
are needed in order to apply our methodology to
![]() catalogues up to
catalogues up to ![]() (e.g., the COSMOS
(e.g., the COSMOS![]() survey, where
survey, where
![]() ,
Ilbert et al. 2009).
,
Ilbert et al. 2009).
Table 5:
Fit parameters of the function
![]() to the data.
to the data.
Table 6:
Number of companions for
![]() galaxies.
galaxies.
4.2 Number of close companions in mass-selected samples
In this section we study the number of major and minor companions of primary galaxies with
![]() .
As in previous sections, we define two redshift ranges, named
zr,1 = [0.2,0.65) and
zr,2 = [0.65,1.1). In the following we denote the galaxy mass ratio as
.
As in previous sections, we define two redshift ranges, named
zr,1 = [0.2,0.65) and
zr,2 = [0.65,1.1). In the following we denote the galaxy mass ratio as
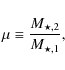
|
(25) |
where
We summarize our results in Table 7 and show them in Fig. 5. We find that (i) the number of close companions decreases with redshift for every ![]() .
Combining all the
.
Combining all the ![]() values, this evolution is described by
values, this evolution is described by
![]() well. This evolution agrees with the finding by de Ravel et al. (2009) for the major merger (
well. This evolution agrees with the finding by de Ravel et al. (2009) for the major merger (
![]() )
fraction of
)
fraction of
![]() galaxies in VVDS-Deep survey, m = 2.04. And (ii), the number of close companions grows when
galaxies in VVDS-Deep survey, m = 2.04. And (ii), the number of close companions grows when ![]() decreases. Combining both redshift ranges, we obtain
decreases. Combining both redshift ranges, we obtain
![]() ;
that is, the number of minor companions is roughly twice the number of major companions.
;
that is, the number of minor companions is roughly twice the number of major companions.
Table 7:
Number of close companions of
![]() galaxies as a function of mass ratio
galaxies as a function of mass ratio ![]() .
.
Only a few works have studied minor mergers statistically. Jogee et al. (2009) report the minor merger (
![]() /10) fraction in Galaxy Evolution from Morphology and SEDs (GEMS
/10) fraction in Galaxy Evolution from Morphology and SEDs (GEMS![]() , Rix et al. 2004) for
, Rix et al. 2004) for
![]() galaxies (Salpeter 1955 IMF), and estimate that minor mergers are three times major (
galaxies (Salpeter 1955 IMF), and estimate that minor mergers are three times major (
![]() /4) mergers. Lotz et al. (2008a) use G-M20 morphological indices to determine the minor merger (
/4) mergers. Lotz et al. (2008a) use G-M20 morphological indices to determine the minor merger (
![]() /9, Lotz et al. 2009) fraction in All-Wavelength Extended Groth Strip International Survey (AEGIS
/9, Lotz et al. 2009) fraction in All-Wavelength Extended Groth Strip International Survey (AEGIS![]() , Davis et al. 2007). Their values are in good agreement with the Jogee et al. (2009) results, but they do not estimate the major merger fraction. In the local Universe, Darg et al. (2010) estimate that minor mergers are twice major mergers in Galaxy Zoo
, Davis et al. 2007). Their values are in good agreement with the Jogee et al. (2009) results, but they do not estimate the major merger fraction. In the local Universe, Darg et al. (2010) estimate that minor mergers are twice major mergers in Galaxy Zoo![]() (Lintott et al. 2008); the latter is based on the visual classification of SDSS galaxies by internet users. Finally, Woods & Geller (2007) study the different properties of major (
(Lintott et al. 2008); the latter is based on the visual classification of SDSS galaxies by internet users. Finally, Woods & Geller (2007) study the different properties of major (
![]() )
and minor (
)
and minor (
![]() )
close pairs in SDSS, which corresponds to
)
close pairs in SDSS, which corresponds to
![]() .
Unfortunately, they do not attempt to derive merger fractions, but the
influence of close companions on galaxy properties (see also Ellison et al. 2008). Summarizing, literature values are consistent with
.
Unfortunately, they do not attempt to derive merger fractions, but the
influence of close companions on galaxy properties (see also Ellison et al. 2008). Summarizing, literature values are consistent with
![]() .
The different methodologies (close pair vs. morphology) and sample
selections make quantitative comparisons difficult (see also Sect. 6.1), but the qualitative agreement is remarkable.
.
The different methodologies (close pair vs. morphology) and sample
selections make quantitative comparisons difficult (see also Sect. 6.1), but the qualitative agreement is remarkable.
The observed dependence of ![]() on
on ![]() is parametrized well as
is parametrized well as
![]() ,
as predicted by the simulations of Maller et al. (2006). Fitting a power-law function to the data we obtain
,
as predicted by the simulations of Maller et al. (2006). Fitting a power-law function to the data we obtain
![]() at z = 0.875, and
at z = 0.875, and
![]() at z = 0.475. However, the observed evolution in s is not significant: if we impose s = -0.6 in the range zr,1,
the observational values are also described well within the
uncertainties. The highest difference between the model with fixed s = -0.6 and the observations occurs at
at z = 0.475. However, the observed evolution in s is not significant: if we impose s = -0.6 in the range zr,1,
the observational values are also described well within the
uncertainties. The highest difference between the model with fixed s = -0.6 and the observations occurs at
![]() ,
i.e., for minor companions. This suggests that
,
i.e., for minor companions. This suggests that
![]() galaxies have accreted satellite galaxies between
galaxies have accreted satellite galaxies between
![]() and
and
![]() .
Since most of these low-mass satellites are expected to be gas-rich,
this accretion could explain the residual star formation observed in
early-types galaxies at
.
Since most of these low-mass satellites are expected to be gas-rich,
this accretion could explain the residual star formation observed in
early-types galaxies at
![]() (Kaviraj et al. 2010).
Studies with larger samples are needed to constraint the differential
evolution with redshift, if any, of the number of major and minor
companions.
(Kaviraj et al. 2010).
Studies with larger samples are needed to constraint the differential
evolution with redshift, if any, of the number of major and minor
companions.

|
Figure 5:
Number of companions vs. mass ratio |
| Open with DEXTER | |
5 Major merger rate: close pairs vs. morphological criteria
The local study (
![]() )
of De Propris et al. (2007)
shows that merger fractions by close pairs and by morphological
criteria (i.e., taking highly distorted galaxies as major merger
remnants) give similar merger rates when samples are compared
carefully. However, in the range
0.2 < z < 1.2 both methods yield different merger rates, some times by an order of magnitude (e.g., Lin et al. 2004). In this section we compare the major merger rate inferred by our close pair study,
)
of De Propris et al. (2007)
shows that merger fractions by close pairs and by morphological
criteria (i.e., taking highly distorted galaxies as major merger
remnants) give similar merger rates when samples are compared
carefully. However, in the range
0.2 < z < 1.2 both methods yield different merger rates, some times by an order of magnitude (e.g., Lin et al. 2004). In this section we compare the major merger rate inferred by our close pair study,
![]() ,
with that from López-Sanjuan et al. (2009b, L09 hereafter) by morphological criteria,
,
with that from López-Sanjuan et al. (2009b, L09 hereafter) by morphological criteria,
![]() .
In L09 gas-rich major merger remnants are selected as those galaxies with high values of the asymmetry index (A, Abraham et al. 1996; Conselice 2003). L09 determine the morphological merger fraction of
.
In L09 gas-rich major merger remnants are selected as those galaxies with high values of the asymmetry index (A, Abraham et al. 1996; Conselice 2003). L09 determine the morphological merger fraction of
![]() galaxies in the same GOODS-S catalogue that we use in the present
paper, and lead with three important sources of systematics: (i) they
avoid morphological K-corrections by measuring the asymmetries in the rest-frame B-band;
(ii) the deal with the loss of information with redshift (i.e., spatial
resolution descent and cosmological dimming) by artificially
redshifting all the galaxies to a unique and representative redshift,
galaxies in the same GOODS-S catalogue that we use in the present
paper, and lead with three important sources of systematics: (i) they
avoid morphological K-corrections by measuring the asymmetries in the rest-frame B-band;
(ii) the deal with the loss of information with redshift (i.e., spatial
resolution descent and cosmological dimming) by artificially
redshifting all the galaxies to a unique and representative redshift,
![]() ;
and (iii) they take the effect of observational errors in z and A into account by maximum likelihood techniques developed in López-Sanjuan et al. (2008). To obtain
;
and (iii) they take the effect of observational errors in z and A into account by maximum likelihood techniques developed in López-Sanjuan et al. (2008). To obtain
![]() from the merger fraction, they assume Pérez-González et al. (2008) mass functions, as in the present paper, and a typical timescale of
from the merger fraction, they assume Pérez-González et al. (2008) mass functions, as in the present paper, and a typical timescale of
![]() Gyr (Conselice 2009,2006; Lotz et al. 2009,2008b).
Gyr (Conselice 2009,2006; Lotz et al. 2009,2008b).
Following Lin et al. (2004), we define the major merger rate by close pairs as
where the factor 1/2 is for obtaining the number of merger systems from the number of close companions, the factor 4/3 takes the lost companions in the inner
Although L09 determine
![]() for
for
![]() galaxies, we cannot compare their merger rate with that from
galaxies, we cannot compare their merger rate with that from
![]() because of the progenitor bias (Bell et al. 2006; Lotz et al. 2008a). In morphological studies we are sensitive to the high distorted remnant phase of a major merger (
because of the progenitor bias (Bell et al. 2006; Lotz et al. 2008a). In morphological studies we are sensitive to the high distorted remnant phase of a major merger (
![]() ,
Conselice 2006; Lotz et al. 2009),
while in pair studies we see the pre-merger stage; that is, the mass of
the future remnant is the sum of the two galaxies' masses in the pair.
This also was noted by Genel et al. (2009),
who compare the merger rate per progenitor (i.e., close pairs) and
descendant (i.e., morphological criteria) dark matter halo in the
Millennium Simulation (Springel et al. 2005).
They find that these two merger rates are different quantities, so
close pairs and morphological studies do not measure the same merger
rate. We therefore compare the morphological merger rate of
,
Conselice 2006; Lotz et al. 2009),
while in pair studies we see the pre-merger stage; that is, the mass of
the future remnant is the sum of the two galaxies' masses in the pair.
This also was noted by Genel et al. (2009),
who compare the merger rate per progenitor (i.e., close pairs) and
descendant (i.e., morphological criteria) dark matter halo in the
Millennium Simulation (Springel et al. 2005).
They find that these two merger rates are different quantities, so
close pairs and morphological studies do not measure the same merger
rate. We therefore compare the morphological merger rate of
![]() galaxies with that from
galaxies with that from
![]() obtained with
obtained with
![]() ,
,
![]() ,
and
,
and
![]() .
With this definition, the merger of two galaxies with limiting masses is
.
With this definition, the merger of two galaxies with limiting masses is
![]() ,
a mass that could increase owing to the induced star formation in gas-rich mergers (e.g., Robaina et al. 2009; Knapen & James 2009; Lin et al. 2007; Li et al. 2008). Finally, we apply a
,
a mass that could increase owing to the induced star formation in gas-rich mergers (e.g., Robaina et al. 2009; Knapen & James 2009; Lin et al. 2007; Li et al. 2008). Finally, we apply a
![]() Gyr
delay to the close pairs data points to mimic the redshifts at which
the highly distorted remnants of these close pairs systems could be
observed. The higher redshift point at z = 0.875 becomes z = 0.725, while the point at z = 0.4 becomes z = 0.335. In summary, both morphological and close pair studies now provide the rate of major merger remnants with
Gyr
delay to the close pairs data points to mimic the redshifts at which
the highly distorted remnants of these close pairs systems could be
observed. The higher redshift point at z = 0.875 becomes z = 0.725, while the point at z = 0.4 becomes z = 0.335. In summary, both morphological and close pair studies now provide the rate of major merger remnants with
![]() (i.e., per descendant galaxy), and we can compare each of them.
(i.e., per descendant galaxy), and we can compare each of them.
We summarize the final values of
![]() from this work and those of
from this work and those of
![]() from L09 in Table 8, and show them in Fig. 6.
We see that both methodologies provide similar merger rates within the
error bars in the range under study, as expected if we are observing
two different phases of the same physical process in the same field
(i.e., we minimize the field-to-field variance between both
measurements). This reconciles the morphological merger rates with
those from pair statistics and lends credibility to the asymmetry
index A as a major merger indicator.
from L09 in Table 8, and show them in Fig. 6.
We see that both methodologies provide similar merger rates within the
error bars in the range under study, as expected if we are observing
two different phases of the same physical process in the same field
(i.e., we minimize the field-to-field variance between both
measurements). This reconciles the morphological merger rates with
those from pair statistics and lends credibility to the asymmetry
index A as a major merger indicator.
We parametrize the merger rate evolution with a power-law function,
The fit to all the data in Table 8 yields
These parameters are substantially different from those in L09, who find
|
Figure 6:
Major merger rate vs. redshift for
|
| Open with DEXTER | |
In the previous discussion we do not consider that the close pair
methodology is sensitive to gas-rich (wet + mixed) and
spheroidal-spheroidal (dry) mergers, while the morphological merger
rate only refers to gas-rich major mergers (Conselice 2006; Lotz et al. 2009; López-sanjuan et al., in prep.). However, at
![]() the fraction of dry mergers with respect to the total is
the fraction of dry mergers with respect to the total is ![]() 10% (Lin et al. 2008, see also de Ravel et al. 2009), increasing their importance at z < 0.2 and being
10% (Lin et al. 2008, see also de Ravel et al. 2009), increasing their importance at z < 0.2 and being ![]() 25% of the total at
25% of the total at
![]() (Lin et al. 2008). This implies that
(Lin et al. 2008). This implies that
![]() must be similar to
must be similar to
![]() in the range under study, but higher at low redshifts, when dry mergers
become more important. We can compare the gas-rich merger rate at z = 0.04 from the previous fit,
in the range under study, but higher at low redshifts, when dry mergers
become more important. We can compare the gas-rich merger rate at z = 0.04 from the previous fit,
![]() Mpc-3 Gyr-1, with the total major merger rate inferred from the number of companions (
Mpc-3 Gyr-1, with the total major merger rate inferred from the number of companions (
![]() )
observed by Domingue et al. (2009) at that redshift and stellar mass,
)
observed by Domingue et al. (2009) at that redshift and stellar mass,
![]() Mpc-3 Gyr-1 (black square in Fig. 6). The latter is higher than the former and suggests that
Mpc-3 Gyr-1 (black square in Fig. 6). The latter is higher than the former and suggests that ![]() 35% of the mergers at z = 0.04 are dry, in agreement with the expected tendency (see Wen et al. 2009 for an estimation of the dry merger rate of luminous early-type galaxies at
35% of the mergers at z = 0.04 are dry, in agreement with the expected tendency (see Wen et al. 2009 for an estimation of the dry merger rate of luminous early-type galaxies at
![]() ).
).
Table 8:
Major merger rate of
![]() galaxies in GOODS-S.
galaxies in GOODS-S.
6 The role of mergers in the evolution of intermediate-mass early types
In a previous work, López-Sanjuan et al. (2010) have studied the number density evolution of early-type (ET, E/S0/Sa) galaxies of
![]() at
at ![]() ,
finding that these galaxies increase their comoving number density (
,
finding that these galaxies increase their comoving number density (
![]() )
by a factor of 5 from z = 1 to the present. Comparing the evolution of the early-type population between
)
by a factor of 5 from z = 1 to the present. Comparing the evolution of the early-type population between
![]() and
and
![]() ,
named
,
named
![]() ,
against the gas-rich major merger rate in the same redshift range, we can define
,
against the gas-rich major merger rate in the same redshift range, we can define
![]() ,
the fraction of new early types that appear between
,
the fraction of new early types that appear between
![]() and
and
![]() because of gas-rich major mergers:
because of gas-rich major mergers:
where
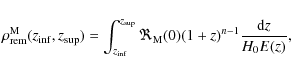
|
(30) |
where
Using the L09 gas-rich major merger rate, López-Sanjuan et al. (2010) infer that
![]() % for early-type galaxies of
% for early-type galaxies of
![]() .
As we have shown in Sect. 5,
when we join the major merger rate by close pairs statistics from this
work with the one in L09, derived from morphological criteria, the
merger rate parameters change substantially from those derived
by L09 using morphological information alone. However, the number
density of major merger remnants remains similar in the two
determinations, varying from
.
As we have shown in Sect. 5,
when we join the major merger rate by close pairs statistics from this
work with the one in L09, derived from morphological criteria, the
merger rate parameters change substantially from those derived
by L09 using morphological information alone. However, the number
density of major merger remnants remains similar in the two
determinations, varying from
![]() Mpc-3 with L09 parameters to
Mpc-3 with L09 parameters to
![]() Mpc-3 with the parameters from the present paper (Eq. (28)), which implies
Mpc-3 with the parameters from the present paper (Eq. (28)), which implies
![]() %. Both morphologies (López-Sanjuan et al. 2010)
and close pairs (this work) therefore agree in yielding consistently
low values for the fraction of early types that appear between
redshifts 1 and 0 due to major mergers.
%. Both morphologies (López-Sanjuan et al. 2010)
and close pairs (this work) therefore agree in yielding consistently
low values for the fraction of early types that appear between
redshifts 1 and 0 due to major mergers.
6.1 Estimating the minor merger rate
Since gas-rich major mergers cannot explain the rise in
![]() early-type galaxies since
early-type galaxies since ![]() ,
López-Sanjuan et al. (2010) suggest
minor mergers and secular processes (e.g., bars, disc instabilities,
gas exhaustion, or morphological quenching) as the main path in that
evolution (see also Oesch et al. 2010; Bundy et al. 2010). In Sect. 4.2 we find that the number of minor companions (
,
López-Sanjuan et al. (2010) suggest
minor mergers and secular processes (e.g., bars, disc instabilities,
gas exhaustion, or morphological quenching) as the main path in that
evolution (see also Oesch et al. 2010; Bundy et al. 2010). In Sect. 4.2 we find that the number of minor companions (
![]() )
is roughly twice the number of major companions (
)
is roughly twice the number of major companions (
![]() ). This implies that
). This implies that
![]() ,
so we can estimate the minor merger rate (
,
so we can estimate the minor merger rate (
![]() ), defined as the merger rate of galaxies with
), defined as the merger rate of galaxies with
![]() .
We denote
.
We denote
![]() as the total (major + minor) merger rate.
as the total (major + minor) merger rate.
We apply Eq. (26) to obtain
![]() .
We assume that parameters for minor companions are similar to those for major companions, except for the merger time scale
.
We assume that parameters for minor companions are similar to those for major companions, except for the merger time scale
![]() .
From N-body hydrodynamical simulations, Lotz et al. (2009) find
.
From N-body hydrodynamical simulations, Lotz et al. (2009) find
![]() for
for
![]() kpc <
kpc <
![]() kpc close pairs. With the previous assumptions we infer that
kpc close pairs. With the previous assumptions we infer that
![]() ,
and
,
and
![]() .
The latest cosmological models (e.g., Hopkins et al. 2010; Stewart et al. 2009a; González-García et al. 2009) predict
.
The latest cosmological models (e.g., Hopkins et al. 2010; Stewart et al. 2009a; González-García et al. 2009) predict ![]() ,
similar to our estimation
,
similar to our estimation
![]() .
However, simulations refer to minor mergers selected by baryonic (gas + stellar) mass, while our estimation is from minor mergers selected by stellar
mass. Although baryonic masses are more uncertain than stellar ones, it
is interesting to compare the baryonic and the stellar merger rates,
which could be quite different (Stewart et al. 2009b). Moreover, the baryonic merger rate can be compared to the fraction of galaxies with distorted kinematics at
.
However, simulations refer to minor mergers selected by baryonic (gas + stellar) mass, while our estimation is from minor mergers selected by stellar
mass. Although baryonic masses are more uncertain than stellar ones, it
is interesting to compare the baryonic and the stellar merger rates,
which could be quite different (Stewart et al. 2009b). Moreover, the baryonic merger rate can be compared to the fraction of galaxies with distorted kinematics at
![]() (Neichel et al. 2008), which are described well by merger simulations (
(Neichel et al. 2008), which are described well by merger simulations (
![]() ,
Hammer et al. 2009).
,
Hammer et al. 2009).
6.2 Mergers vs. secular processes in the evolution of early-type galaxies
Following the Sect. 6 steps with the combined major and minor merger rates estimated in the previous section, we infer that ![]() 30%, and up to
30%, and up to ![]() 50%, of the early-type (E/S0/Sa) galaxies of
50%, of the early-type (E/S0/Sa) galaxies of
![]() that appear since
that appear since ![]() may have undergone a major or minor merger event. This is an upper
limit because a single minor merger does not transform a late-type
galaxy into an early type (Hopkins et al. 2009b), but increases the Sérsic index of the galaxy (Bournaud et al. 2007; Eliche-Moral et al. 2006). This result suggests that the other
may have undergone a major or minor merger event. This is an upper
limit because a single minor merger does not transform a late-type
galaxy into an early type (Hopkins et al. 2009b), but increases the Sérsic index of the galaxy (Bournaud et al. 2007; Eliche-Moral et al. 2006). This result suggests that the other ![]() 50% of the new early types appear due to secular processes (see also Bundy et al. 2010).
50% of the new early types appear due to secular processes (see also Bundy et al. 2010).
That a large fraction of S0-Sb discs host pseudo-bulges (Kormendy & Kennicutt 2004) also points to secular processes for the growth of the red sequence at z < 1. And the strong similarity of disc and nuclear colours in disc galaxies up to
![]() (Domínguez-Palmero & Balcells 2008)
likewise argues for a fading process that does not destroy the disc.
The process leading to such an evolution may be suggested by the
mentioned colour similarity of (the inner parts of the) disc and
nucleus/bulge. Both star formation and the subsequent fading must be to
some degree coordinated throughout the galaxy, so the quenching of star
formation may simply be due to gas exhaustion (Bauermeister et al. 2009; Zheng et al. 2007).
Interestingly, the star formation in the galaxy, leading to the growth
of the central bulge component, may lead to this fading as the growth
of the central potential stabilizes the gas component preventing disc
fragmentation (morphological quenching, Martig et al. 2009).
Disc fragmentation contributes both to star formation and to the growth
of the central bulge, as shown by the evolution of chain and tadpole
galaxies (Elmegreen et al. 2008; Bournaud et al. 2009; Ceverino et al. 2010).
(Domínguez-Palmero & Balcells 2008)
likewise argues for a fading process that does not destroy the disc.
The process leading to such an evolution may be suggested by the
mentioned colour similarity of (the inner parts of the) disc and
nucleus/bulge. Both star formation and the subsequent fading must be to
some degree coordinated throughout the galaxy, so the quenching of star
formation may simply be due to gas exhaustion (Bauermeister et al. 2009; Zheng et al. 2007).
Interestingly, the star formation in the galaxy, leading to the growth
of the central bulge component, may lead to this fading as the growth
of the central potential stabilizes the gas component preventing disc
fragmentation (morphological quenching, Martig et al. 2009).
Disc fragmentation contributes both to star formation and to the growth
of the central bulge, as shown by the evolution of chain and tadpole
galaxies (Elmegreen et al. 2008; Bournaud et al. 2009; Ceverino et al. 2010).
These results refer to intermediate-mass galaxies (
![]() )
at
)
at
![]() ,
but the picture is different at higher stellar masses. On the one hand,
,
but the picture is different at higher stellar masses. On the one hand,
![]() galaxies have higher pair fractions than less
massive ones (de Ravel et al. 2009; Bundy et al. 2009), and red pairs are more common at these masses (Bundy et al. 2009). This suggests that dry mergers are an important process in the evolution of massive
galaxies since
galaxies have higher pair fractions than less
massive ones (de Ravel et al. 2009; Bundy et al. 2009), and red pairs are more common at these masses (Bundy et al. 2009). This suggests that dry mergers are an important process in the evolution of massive
galaxies since ![]() (e.g., Ilbert et al. 2010; Bell et al. 2004; Lin et al. 2008). On the other hand, the size
(van Dokkum et al. 2010; van der Wel et al. 2008; Buitrago et al. 2008; Trujillo et al. 2007) and velocity
dispersion evolution (Cenarro & Trujillo 2009) of
(e.g., Ilbert et al. 2010; Bell et al. 2004; Lin et al. 2008). On the other hand, the size
(van Dokkum et al. 2010; van der Wel et al. 2008; Buitrago et al. 2008; Trujillo et al. 2007) and velocity
dispersion evolution (Cenarro & Trujillo 2009) of
![]() early-type galaxies since
early-type galaxies since ![]() also supports the importance of mergers, especially
the impact of minor mergers on the evolution of these systems
(Hopkins et al. 2009a; Naab et al. 2009; Bezanson et al. 2009). In addition, residual star formation in early-type (E/S0) galaxies at
also supports the importance of mergers, especially
the impact of minor mergers on the evolution of these systems
(Hopkins et al. 2009a; Naab et al. 2009; Bezanson et al. 2009). In addition, residual star formation in early-type (E/S0) galaxies at
![]() can also be explained by minor merging (Kaviraj et al. 2009,2010). This problem has also been analysed by Eliche-Moral et al. (2010a), who have modelled the evolution of luminosity function backwards in time for
can also be explained by minor merging (Kaviraj et al. 2009,2010). This problem has also been analysed by Eliche-Moral et al. (2010a), who have modelled the evolution of luminosity function backwards in time for
![]() galaxies, selected according to their colours (red/blue/total) and
their morphologies. They find that the observed luminosity function
evolution can be explained naturally by the observed gas-rich and dry
major merger rates and that 50-60% of
today's E/S0 in this mass range were formed by major mergers at
0.8 < z < 1, with a small number evolution since z = 0.8 (see also Cristóbal-Hornillos et al. 2009; Eliche-Moral et al. 2010b; Ilbert et al. 2010; van der Wel et al. 2009). The gas-rich major merger fractions assumed by Eliche-Moral et al. (2010a) are those
from L09 for B-band selected galaxies (
galaxies, selected according to their colours (red/blue/total) and
their morphologies. They find that the observed luminosity function
evolution can be explained naturally by the observed gas-rich and dry
major merger rates and that 50-60% of
today's E/S0 in this mass range were formed by major mergers at
0.8 < z < 1, with a small number evolution since z = 0.8 (see also Cristóbal-Hornillos et al. 2009; Eliche-Moral et al. 2010b; Ilbert et al. 2010; van der Wel et al. 2009). The gas-rich major merger fractions assumed by Eliche-Moral et al. (2010a) are those
from L09 for B-band selected galaxies (
![]() ), which were obtained in a similar way than the morphological merger fractions used through present paper.
), which were obtained in a similar way than the morphological merger fractions used through present paper.
This makes
![]() (Pérez-González et al. 2008) a transition mass at
(Pérez-González et al. 2008) a transition mass at
![]() :
at higher masses mergers are an important process in the evolution of
early-type galaxies, while other mechanisms dominate the observed
evolution at lower masses.
:
at higher masses mergers are an important process in the evolution of
early-type galaxies, while other mechanisms dominate the observed
evolution at lower masses.
7 Conclusions
In this paper we have developed a new method, which is based on the
one used widely over spectroscopic surveys, to determine the mean
number of companions per galaxy (![]() )
over current spectro-photometric surveys. We tested our method in a
local, volume-limited sample from MGC spectroscopic catalogue. We find
that the method provides reliable
)
over current spectro-photometric surveys. We tested our method in a
local, volume-limited sample from MGC spectroscopic catalogue. We find
that the method provides reliable ![]() values when either photometric redshift errors are smaller than
values when either photometric redshift errors are smaller than
![]() or the spectroscopic completeness of the sample is higher than
or the spectroscopic completeness of the sample is higher than
![]() ,
with these limits depending on the sample under study. For typical SDSS samples with
,
with these limits depending on the sample under study. For typical SDSS samples with
![]() ,
we find
,
we find
![]() ,
while we find
,
while we find
![]() for our GOODS-S catalogue.
for our GOODS-S catalogue.
We studied the number of companions in B-band luminosity-selected samples, finding that:
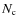 depends on search radius as expected from correlation function,
depends on search radius as expected from correlation function,
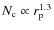 ,
and their values are similar to those expected from a spectroscopic sample.
,
and their values are similar to those expected from a spectroscopic sample.
- The values of
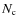 for different luminosity selections are in excellent agreement with
those in the literature when the same selection criteria and pair
definition are applied. We find that the number of companions decreases
when luminosity increase and that the
for different luminosity selections are in excellent agreement with
those in the literature when the same selection criteria and pair
definition are applied. We find that the number of companions decreases
when luminosity increase and that the 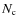 of
of
 galaxies evolves faster (m = 2.5) than for
galaxies evolves faster (m = 2.5) than for
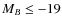 galaxies (m = 1.6). In addition, this evolution becomes slower, m = 0.7, when luminosity evolution is taken into account.
galaxies (m = 1.6). In addition, this evolution becomes slower, m = 0.7, when luminosity evolution is taken into account.
Finally, we compared the merger rates derived by close pairs with those by morphological criteria for
![]() galaxies,
finding that both are similar when the progenitor bias is taken into
account. We estimate that the total (major + minor) merger rate is
galaxies,
finding that both are similar when the progenitor bias is taken into
account. We estimate that the total (major + minor) merger rate is ![]() 1.7
times the major merger rate. After comparing the merger rate with the
observed structural evolution of GOODS-S galaxies, we infer that up to
1.7
times the major merger rate. After comparing the merger rate with the
observed structural evolution of GOODS-S galaxies, we infer that up to ![]() 50% of the new early-type galaxies appeared since
50% of the new early-type galaxies appeared since ![]() could have undergone a merger event (major or minor), and we refer to
star formation fading in the disc of spiral galaxies to explain the
other
could have undergone a merger event (major or minor), and we refer to
star formation fading in the disc of spiral galaxies to explain the
other ![]() 50%.
50%.
Our new methodology can be applied to extensive spectro-photometric surveys such as AEGIS, COSMOS, or VVDS, which have an order of magnitude more galaxies than the present catalogue. This will allow better determination of the number of major and minor companions and their dependence on redshift and other galactic properties, such as luminosity, mass, colour, or environment.
AcknowledgementsWe dedicate this paper to the memory of our six IAC colleagues and friends who met with a fatal accident in Piedra de los Cochinos, Tenerife, in February 2007. With a special thanks to Maurizio Panniello, whose teachings of python were so important for this paper.We thank the anonymous referee for his/her pertinent comments that have improved the original manuscript. We also thank Ignacio Trujillo, Carmen Eliche-Moral, and Rubén Sanchez-Janssen for useful discussions and suggestions.
This work was supported by the Spanish Programa Nacional de Astronomía y Astrofísica through project number AYA2006-12955, AYA2006-02358, and AYA 2006-15698-C02-02. This work was partially funded by the Spanish MEC under the Consolider-Ingenio 2010 Programme grant CSD2006-00070: First Science with the GTC (http://www.iac.es/consolider-ingenio-gtc/).
This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, Caltech under NASA contract 1407.
This work uses the Millennium Galaxy Catalogue, which consists of imaging data from the Isaac Newton Telescope and spectroscopic data from the Anglo Australian Telescope, the ANU 2.3 m, the ESO New Technology Telescope, the Telescopio Nazionale Galileo, and the Gemini North Telescope. The survey was supported through grants from the Particle Physics and Astronomy Research Council (UK) and the Australian Research Council (AUS). The data and data products are publicly available from http://www.eso.org/ jliske/mgc/ or on request from J. Liske or S.P. Driver.
P.G.P.G. acknowledges support from the Ramón y Cajal Programme financed by the Spanish Government and the European Union.
References
- Abraham, R. G., van den Bergh, S., Glazebrook, K., et al. 1996, ApJS, 107, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2006, ApJS, 162, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Bauermeister, A., Blitz, L., & Ma, C.-P. 2009, ApJ, 717, 323 [Google Scholar]
- Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Berrier, J. C., Bullock, J. S., Barton, E. J., et al. 2006, ApJ, 652, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bezanson, R., van Dokkum, P. G., Tal, T., et al. 2009, ApJ, 697, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Bluck, A. F. L., Conselice, C. J., Bouwens, R. J., et al. 2009, MNRAS, 394, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2005, A&A, 437, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Bridge, C. R., Appleton, P. N., Conselice, C. J., et al. 2007, ApJ, 659, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Conselice, C. J., et al. 2008, ApJ, 687, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Fukugita, M., Ellis, R. S., Kodama, T., & Conselice, C. J. 2004, ApJ, 601, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Fukugita, M., Ellis, R. S., et al. 2009, ApJ, 697, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Scarlata, C., Carollo, C. M., et al. 2010, ApJ, 719, 1969 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Cimatti, A., Franceschini, A., et al. 2005, MNRAS, 357, 903 [Google Scholar]
- Cenarro, A. J., & Trujillo, I. 2009, ApJ, 696, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., Dekel, A., & Bournaud, F. 2010, MNRAS, 404, 2151 [NASA ADS] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2009, MNRAS, 399, L16 [NASA ADS] [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Rajgor, S., & Myers, R. 2008, MNRAS, 386, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Yang, C., & Bluck, A. F. L. 2009, MNRAS, 361 [Google Scholar]
- Cristóbal-Hornillos, D., Aguerri, J. A. L., Moles, M., et al. 2009, ApJ, 696, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Darg, D. W., Kaviraj, S., Lintott, C. J., et al. 2010, MNRAS, 401, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Liske, J., Driver, S. P., Allen, P. D., & Cross, N. J. G. 2005, AJ, 130, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Conselice, C. J., Liske, J., et al. 2007, ApJ, 666, 212 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Driver, S. P., Colless, M., et al. 2010, AJ, 139, 794 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domingue, D. L., Xu, C. K., Jarrett, T. H., & Cheng, Y. 2009, ApJ, 695, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez-Palmero, L., & Balcells, M. 2008, A&A, 489, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Driver, S. P., Liske, J., Cross, N. J. G., De Propris, R., & Allen, P. D. 2005, MNRAS, 360, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Efron, B. 1982, CBMS-NSF Reg. Conf. Ser. in Applied Mathematics, Philadelphia (SIAM) [Google Scholar]
- Eliche-Moral, M. C., Balcells, M., Aguerri, J. A. L., & González-García, A. C. 2006, A&A, 457, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eliche-Moral, M. C., Prieto, M., Gallego, J., et al. 2010a, A&A, in press [arXiv:1002.3537] [Google Scholar]
- Eliche-Moral, M. C., Prieto, M., Gallego, J., & Zamorano, J. 2010b, ApJ, submitted [arXiv:1003.0686] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, AJ, 135, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., & Ma, C.-P. 2008, MNRAS, 386, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Ashby, M. L. N., Barmby, P., et al. 2004, ApJS, 154, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fontana, A., Salimbeni, S., Grazian, A., et al. 2006, A&A, 459, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genel, S., Genzel, R., Bouché, N., Naab, T., & Sternberg, A. 2009, ApJ, 701, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- González-García, A. C., & Balcells, M. 2005, MNRAS, 357, 753 [NASA ADS] [CrossRef] [Google Scholar]
- González-García, A. C., Oñorbe, J., Domínguez-Tenreiro, R., & Gómez-Flechoso, M. Á. 2009, A&A, 497, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-García, A. C., & van Albada, T. S. 2003, MNRAS, 342, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlöber, S., Klypin, A., & Kravtsov, A. V. 2001, ApJ, 546, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Gardner, J. P., Stadel, J., Quinn, T., & Lake, G. 1999, AJ, 117, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Puech, M., et al. 2009, A&A, 507, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiderman, A., Jogee, S., Marinova, I., et al. 2009, ApJ, 705, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Dutta, S. N., & Rothberg, B. 2008, ApJ, 679, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Hernquist, L., Wuyts, S., & Cox, T. J. 2009a, MNRAS, 1635 [Google Scholar]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009b, ApJ, 691, 1168 [Google Scholar]
- Hopkins, P. F., Somerville, R. S., Cox, T. J., et al. 2009c, MNRAS, 397, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, B. C., Yee, H. K. C., Lin, H., Gladders, M. D., & Gilbank, D. G. 2008, ApJ, 683, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc'h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Jogee, S., Miller, S. H., Penner, K., et al. 2009, ApJ, 697, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Kampczyk, P., Lilly, S. J., Carollo, C. M., et al. 2007, ApJS, 172, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kartaltepe, J. S., Sanders, D. B., Scoville, N. Z., et al. 2007, ApJS, 172, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Kaviraj, S., Peirani, S., Khochfar, S., Silk, J., & Kay, S. 2009, MNRAS, 394, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Kaviraj, S., Tan, K., Ellis, R. S., & Silk, J. 2010, MNRAS, submitted [arXiv:1001.2141] [Google Scholar]
- Khochfar, S., & Burkert, A. 2001, ApJ, 561, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 391, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. H., & James, P. A. 2009, ApJ, 698, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Kolatt, T. S., Bullock, J. S., Somerville, R. S., et al. 1999, ApJ, 523, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Lavery, R. J., Remijan, A., Charmandaris, V., Hayes, R. D., & Ring, A. A. 2004, ApJ, 612, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Abraham, R., Lilly, S. J., et al. 2000, MNRAS, 311, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Guzzo, L., Meneux, B., et al. 2005, A&A, 439, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, C., Kauffmann, G., Heckman, T. M., Jing, Y. P., & White, S. D. M. 2008, MNRAS, 385, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Koo, D. C., Willmer, C. N. A., et al. 2004, ApJ, 617, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Koo, D. C., Weiner, B. J., et al. 2007, ApJ, 660, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C. J., Schawinski, K., Slosar, A., et al. 2008, MNRAS, 389, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Liske, J., Lemon, D. J., Driver, S. P., Cross, N. J. G., & Couch, W. J. 2003, MNRAS, 344, 307 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., García-Dabó, C. E., & Balcells, M. 2008, PASP, 120, 571 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Balcells, M., García-Dabó, C. E., et al. 2009a, ApJ, 694, 643 [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2009b, A&A, 501, 505 [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2010, ApJ, 710, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Davis, M., Faber, S. M., et al. 2008a, ApJ, 672, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2008b, MNRAS, 391, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2010, MNRAS, 404, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Maller, A. H., Katz, N., Keres, D., Davé, R., & Weinberg, D. H. 2006, ApJ, 647, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Bournaud, F., Teyssier, R., & Dekel, A. 2009, ApJ, 707, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Masjedi, M., Hogg, D. W., Cool, R. J., et al. 2006, ApJ, 644, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Burkert, A. 2003, ApJ, 597, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Jesseit, R., & Burkert, A. 2006a, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Khochfar, S., & Burkert, A. 2006b, ApJ, 636, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oesch, P. A., Carollo, C. M., Feldmann, R., et al. 2010, ApJ, 714, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Moustakas, L. A., Dickinson, M., et al. 2006, ApJ, 640, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., & Atfield, J. E. 2008, ApJ, 685, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Pritchet, C. J., Carlberg, R. G., et al. 2002, ApJ, 565, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Villar, V., et al. 2008, ApJ, 675, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Ravikumar, C. D., Puech, M., Flores, H., et al. 2007, A&A, 465, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawat, A., Hammer, F., Kembhavi, A. K., & Flores, H. 2008, ApJ, 681, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Robaina, A. R., Bell, E. F., Skelton, R. E., et al. 2009, ApJ, 704, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Rothberg, B., & Joseph, R. D. 2006a, AJ, 131, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Rothberg, B., & Joseph, R. D. 2006b, AJ, 132, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, Jr., R. E., Cohen, S. H., Windhorst, R. A., & Silk, J. 2008, ApJ, 678, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stewart, K. R., Bullock, J. S., Barton, E. J., & Wechsler, R. H. 2009a, ApJ, 702, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, K. R., Bullock, J. S., Wechsler, R. H., & Maller, A. H. 2009b, ApJ, 702, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Holden, B. P., Zirm, A. W., et al. 2008, ApJ, 688, 48 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Rix, H., Holden, B. P., Bell, E. F., & Robaina, A. R. 2009, ApJ, 706, L120 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Whitaker, K. E., Brammer, G., et al. 2010, ApJ, 709, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Liu, F. S., & Han, J. L. 2009, ApJ, 692, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, D. F. & Geller, M. J. 2007, AJ, 134, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, X. Z., Bell, E. F., Papovich, C., et al. 2007, ApJ, 661, L41 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... (GOODS-S)
![[*]](/icons/foot_motif.png)
- http://www.stsci.edu/science/goods/
- ... catalogues
![[*]](/icons/foot_motif.png)
- http://archive.stsci.edu/prepds/goods/
- ... database
![[*]](/icons/foot_motif.png)
- http://guaix.fis.ucm.es/ pgperez/Proyectos/ucmcsdatabase.en.html
- ... (MGC
![[*]](/icons/foot_motif.png)
- http://eso.org/ jliske/mgc/
- ... (SDSS
![[*]](/icons/foot_motif.png)
- http://sdss.org/
- ... (VVDS
![[*]](/icons/foot_motif.png)
- http://www.oamp.fr/virmos/vvds.htm
- ... COSMOS
![[*]](/icons/foot_motif.png)
- Cosmological Evolution Survey, Scoville et al. 2007 (http://cosmos.astro.caltech.edu/index.html).
- ... (GEMS
![[*]](/icons/foot_motif.png)
- http://www.mpia.de/GEMS/gems.htm
- ... (AEGIS
![[*]](/icons/foot_motif.png)
- http://aegis.ucolick.org/
- ... Zoo
![[*]](/icons/foot_motif.png)
- http://www.galaxyzoo.org
All Tables
Table 1: B-band luminosity and mass function parameters.
Table 2:
Number of companions in random samples in units of that in the spectroscopic MGC sample,
![]() .
.
Table 3:
Number of companions as a function of
![]() for approaches 1 (independent pairs) and 2 (more representative pair) in the multiple-system treatment.
for approaches 1 (independent pairs) and 2 (more representative pair) in the multiple-system treatment.
Table 4: Number of companions in B-band luminosity-selected samples.
Table 5:
Fit parameters of the function
![]() to the data.
to the data.
Table 6:
Number of companions for
![]() galaxies.
galaxies.
Table 7:
Number of close companions of
![]() galaxies as a function of mass ratio
galaxies as a function of mass ratio ![]() .
.
Table 8:
Major merger rate of
![]() galaxies in GOODS-S.
galaxies in GOODS-S.
All Figures

|
Figure 1:
Probability distributions in redshift space of a primary galaxy (back
solid line), a secondary galaxy (black dashed line), and the function |
| Open with DEXTER | |
| In the text | |

|
Figure 2:
|
| Open with DEXTER | |
| In the text | |

|
Figure 3:
Number of companions vs.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width = 8.5cm,clip]{14236fg4a.eps}\inc...
...\includegraphics[width = 8.5cm,clip]{14236fg4d.eps} }
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14236-10/Timg289.png)
|
Figure 4:
Number of companions vs. redshift for different B-band luminosity selections: panel a) for -
|
| Open with DEXTER | |
| In the text | |

|
Figure 5:
Number of companions vs. mass ratio |
| Open with DEXTER | |
| In the text | |

|
Figure 6:
Major merger rate vs. redshift for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



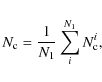
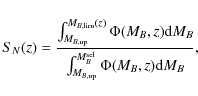
![\begin{displaymath}N_{\rm c} = \frac{\sum^{N_1}_{i} \big[S_N(z_i) \sum_{l}S_N(z_l)^{-1} \big]}{\sum^{N_{1}}_{i} S_N(z_i)},
\end{displaymath}](/articles/aa/full_html/2010/10/aa14236-10/img114.png)