| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014147 | |
| Published online | 31 August 2010 | |
Triaxial collapse and virialisation of dark-matter haloes
C. Angrick - M. Bartelmann
Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
Received 27 January 2010 / Accepted 13 May 2010
Abstract
We reconsider the ellipsoidal-collapse model and extend it in two
ways: we modify the treatment of the external gravitational shear
field, introducing a hybrid model in between linear and non-linear
evolution, and we introduce a virialisation criterion derived from the
tensor virial theorem to replace the ad hoc criterion employed so
far. We compute the collapse parameters
![]() and
and
![]() and find that they increase with ellipticity e and decrease with prolaticity p. We marginalise them over the appropriate distribution of e and p
and show the marginalised results as functions of halo mass and
virialisation redshift. While the hybrid model for the external shear
gives results very similar to those obtained from the non-linear model,
ellipsoidal collapse changes the collapse parameters typically by
and find that they increase with ellipticity e and decrease with prolaticity p. We marginalise them over the appropriate distribution of e and p
and show the marginalised results as functions of halo mass and
virialisation redshift. While the hybrid model for the external shear
gives results very similar to those obtained from the non-linear model,
ellipsoidal collapse changes the collapse parameters typically by
![]() ,
in a way increasing with decreasing halo mass and decreasing
virialisation redshift. We qualitatively confirm the dependence on mass
and virialisation redshift of a fitting formula for
,
in a way increasing with decreasing halo mass and decreasing
virialisation redshift. We qualitatively confirm the dependence on mass
and virialisation redshift of a fitting formula for
![]() ,
but find noticeable quantitative differences in particular at low mass
and high redshift. The derived mass function is in good agreement with
mass functions recently proposed in the literature.
,
but find noticeable quantitative differences in particular at low mass
and high redshift. The derived mass function is in good agreement with
mass functions recently proposed in the literature.
Key words: cosmology: theory - methods: analytical - dark matter - cosmological parameters - galaxies: clusters: general
1 Introduction
The spherical-collapse model (e.g. Mota & van de Bruck 2004; Schäfer & Koyama 2008; Engineer et al. 2000; Bartelmann et al. 2006; Wang & Steinhardt 1998)
is a fundamental ingredient in the theory of cosmic structure
formation. Following the collapse of a slightly overdense, homogeneous
sphere, it allows the derivation of two essential parameters; the
overdensity
![]() of a virialised halo compared to the mean or the critical cosmic density, and the critical linear density contrast
of a virialised halo compared to the mean or the critical cosmic density, and the critical linear density contrast
![]() .
The former is important because it allows relating sizes to masses of
virialised structures, and the latter because it establishes a link
between linear structure formation and the population statistics of
collapsed haloes. Despite fundamental doubts as to the validity of such
a simplified model for accurate cosmological predictions, the
parameters derived from the spherical-collapse model or variants
thereof allow surprisingly far-reaching predictions such as the halo
mass function or the correlation properties of haloes, which are
confirmed by numerical simulations.
.
The former is important because it allows relating sizes to masses of
virialised structures, and the latter because it establishes a link
between linear structure formation and the population statistics of
collapsed haloes. Despite fundamental doubts as to the validity of such
a simplified model for accurate cosmological predictions, the
parameters derived from the spherical-collapse model or variants
thereof allow surprisingly far-reaching predictions such as the halo
mass function or the correlation properties of haloes, which are
confirmed by numerical simulations.
The statistics of a Gaussian random field implies that
spherical collapse should not occur. In fact, the probability
distribution for the eigenvalues ![]() of the Zel'dovich deformation tensor (Doroshkevich 1970) shows that spherical collapse has a vanishing probability,
of the Zel'dovich deformation tensor (Doroshkevich 1970) shows that spherical collapse has a vanishing probability,
because it requires
Ellipsoidal collapse was analysed many times before (see Bond & Myers 1996; Eisenstein & Loeb 1995; Bartelmann et al. 1993, for examples). Several authors have worked with the model by Bond & Myers (1996), generalising it for different cosmologies and introducing the scale factor a as a time variable (Monaco 1998; Sheth et al. 2001; Ohta et al. 2004; Monaco 1997,1995; Sheth & Tormen 2002). We are reconsidering it here for two reasons.
First, we want to analyse how different assumptions on the treatment of the environment of a halo impact on the parameters
![]() and
and
![]() .
Previous assumptions have been that the principal-axis system of the
homogeneous ellipsoid is either identical with that of the external
gravitational shear field, or that the two eigensystems do not
coincide, introducing rotation and a deviation from the homogeneous
mass profile. We introduce another assumption here, letting the
eigensystems of the collapsing ellipsoid and its surrounding shear
field follow each other until turn-around of the major principal axis
and then decoupling both.
.
Previous assumptions have been that the principal-axis system of the
homogeneous ellipsoid is either identical with that of the external
gravitational shear field, or that the two eigensystems do not
coincide, introducing rotation and a deviation from the homogeneous
mass profile. We introduce another assumption here, letting the
eigensystems of the collapsing ellipsoid and its surrounding shear
field follow each other until turn-around of the major principal axis
and then decoupling both.
Second, we want to stop the collapse along any of the principal
axes according to a physically motivated virialisation condition.
Virialisation must be invoked to prevent the axes from collapsing to
zero, and thus to be able to follow the entire collapse of an
ellipsoid, i.e. the collapse of its three principal axes.
Conventionally, the collapse of each axis is stopped when
ai(a)=0.177a, where ai is the scale factor of the ith axis and a is the background scale factor (Sheth et al. 2001; Bond & Myers 1996). In this way,
![]() for spherical collapse in an Einstein-de Sitter universe at the time
when the third axis virialises. However, the value 0.177 has no
fundamental physical motivation, and there is no guarantee for it not
to be different for ellipsoidal rather than spherical collapse, or
whencosmologies other than EdS are to be considered. We introduce a
general virialisation condition based on the tensor virial theorem that avoids introducting such an uncalibrated factor. We find substantial changes on both
for spherical collapse in an Einstein-de Sitter universe at the time
when the third axis virialises. However, the value 0.177 has no
fundamental physical motivation, and there is no guarantee for it not
to be different for ellipsoidal rather than spherical collapse, or
whencosmologies other than EdS are to be considered. We introduce a
general virialisation condition based on the tensor virial theorem that avoids introducting such an uncalibrated factor. We find substantial changes on both
![]() and
and
![]() from both modifications and point out several discrepancies of our results with earlier studies.
from both modifications and point out several discrepancies of our results with earlier studies.
We introduce the ellipsoidal-collapse model including our modifications in Sect. 2, present our results in Sect. 3 and conclude in Sect. 4.
2 The model
in this section, we shall briefly review the ellipsoidal-collapse model of Bond & Myers (1996) for cosmologies with a cosmological constant introducing the scale factor a as time variable. Furthermore, we shall present a physically motivated virialisation condition to stop the collapse of each axis, and show how to find the proper initial ellipticity and prolaticity as a function of mass and virialisation redshift.
2.1 The evolution equations
Let
![]() be the dimension-less principal axes of the ellipsoid, where Ri with
be the dimension-less principal axes of the ellipsoid, where Ri with
![]() are its dimensional semi-major axes, and
are its dimensional semi-major axes, and
![]() the size of a spherical top-hat corresponding to a mass
the size of a spherical top-hat corresponding to a mass
![]() with the cosmological background density
with the cosmological background density
![]() .
The evolution of the three principal axes ai with time t in a cosmology with a cosmological constant
.
The evolution of the three principal axes ai with time t in a cosmology with a cosmological constant
![]() is given by
is given by
(Bond & Myers 1996), where G is the gravitational constant and c the speed of light. The density contrast of the ellipsoid with respect to the background density is
while the external shear can be approximated by
where D+ is the linear growth factor, and the
In linear approximation, the environment into which the ellipsoid is embedded evolves completely independently of it, whereas in the non-linear approximation it is tightly coupled to the ellipsoid. In Sect. 3.1 we shall introduce the hybrid model as a third approximation for the external shear.
We can rewrite Eq. (2) by using the scale factor a as time variable using Friedmann's equation
![]() ,
where H0 is Hubble's constant. The expansion function of the universe, E(a), introduces the dimension-less density parameters of matter and dark energy today,
,
where H0 is Hubble's constant. The expansion function of the universe, E(a), introduces the dimension-less density parameters of matter and dark energy today,
![]() and
and
![]() ,
respectively. This gives
,
respectively. This gives
where a prime denotes differentiation with respect to a, and
since
In the following, we shall assume that the eigenvalues ![]() of the Zel'dovich tensor are ordered as
of the Zel'dovich tensor are ordered as
![]() ,
which implies that the ellipsoid first collapses along the direction 1,
,
which implies that the ellipsoid first collapses along the direction 1,
![]() first. At that time
first. At that time
![]() ,
and the collapse of the remaining two axes can no longer be followed so
that we have to add a virialisation condition for each axis preventing
their collapse to zero.
,
and the collapse of the remaining two axes can no longer be followed so
that we have to add a virialisation condition for each axis preventing
their collapse to zero.
2.2 The virialisation condition
Conventionally, the collapse of each axis is stopped when
ai(a)=0.177a, where ai is the scale factor of the ith axis and a the background scale factor (e.g. Sheth et al. 2001; Bond & Myers 1996). In this way,
![]() for
spherical collapse in an Einstein-de Sitter (EdS) universe at the time
when the third axis is assumed to virialise. However, the value 0.177
has no fundamental motivation in the physics of the collapse, and there
is no guarantee that it remain unchanged in the case of ellipsoidal
instead of spherical collapse, or in other cosmologies than Einstein-de
Sitter.
for
spherical collapse in an Einstein-de Sitter (EdS) universe at the time
when the third axis is assumed to virialise. However, the value 0.177
has no fundamental motivation in the physics of the collapse, and there
is no guarantee that it remain unchanged in the case of ellipsoidal
instead of spherical collapse, or in other cosmologies than Einstein-de
Sitter.
We shall thus follow a different approach and present a
physically well-motivated virialisation condition in the following to
stop the collapse of each axis individually. We start from the tensor virial theorem (see Binney & Tremaine 1987, p. 213, 280),
where
and
where
We now specialise to the case of a homogeneous ellipsoid. For a stable mass configuration, the left-hand side of Eq. (8)
has to vanish for each component of the inertial tensor individually.
Since the ellipsoid is assumed to be at rest and the ellipsoid's
eigensystem is chosen as a reference frame,
![]() so that Kij=0 and
so that Kij=0 and
![]() ,
with the Kronecker symbol
,
with the Kronecker symbol
![]() .
Note again that in this framework the eigensystems of the overdense
ellipsoid and the gravitational tidal field are identical. For a
homogeneous ellipsoid
.
Note again that in this framework the eigensystems of the overdense
ellipsoid and the gravitational tidal field are identical. For a
homogeneous ellipsoid
![]() ,
thus
,
thus
with the mass M of the ellipsoid. The sum Wij+Vij can be evaluated using
Requiring that Eq. (8) is fulfilled for each axis separately and introducing the scale factor a as time variable yields the virialisation conditions for the three axes ai,
When this condition is fulfilled for an axis together with
We emphasise that the former equation is consistent with the
virialisation condition for spherical collapse in the EdS universe,
where
![]() .
The subscripts ``v'' and ``ta'' denote the time of virialisation and
turn-around, respectively. For the special case of EdS, Eq. (13) becomes
.
The subscripts ``v'' and ``ta'' denote the time of virialisation and
turn-around, respectively. For the special case of EdS, Eq. (13) becomes
with
(Engineer et al. 2000) together with the relations
For bound objects in the ![]() CDM model, the virialisation condition is
CDM model, the virialisation condition is
where
with
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig1.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg95.png)
|
Figure 1: Comparison of the virialisation conditions from the scalar and tensor virial theorems. The curves differ slightly because they refer to different times. While the tensor virial theorem was evaluated at virialisation, the scaler virial theorem was evaluated at collapse. If we choose the collapse of the dark-matter halo as reference for z, both yield exactly the same result. |
| Open with DEXTER | |
2.3 The initial ellipticity and prolaticity
Equations (6), (7)
imply that one has to choose initial values for the Zel'dovich
deformation tensor to define the initial deviation of the principal
axes and their time derivatives from the background. We shall show how
they are chosen appropriately so that they comply with the assumed
Gaussian nature of the Universe's initial conditions and represent a
statistical average of haloes with the same mass M and virialisation redshift ![]() but different shapes.
but different shapes.
| Figure 2:
Evolution of the principal axes and the external shear for a
|
|
| Open with DEXTER | |
Starting from the probability distribution for the eigenvalues of the Zel'dovich deformation tensor, Eq. (1), the conditional probability distribution for the ellipticity ![]() and the prolaticity
and the prolaticity
![]() ,
defined as
,
defined as
![]() and
and
![]() ,
respectively, was derived by Sheth et al. (2001) to be
,
respectively, was derived by Sheth et al. (2001) to be
To compute a statistical average of any quantity
However, a Taylor expansion of
where
Since the variances are
Generally, the eigenvalues ![]() are related to e and p by (see e.g. Bardeen et al. 1986; Bond & Myers 1996)
are related to e and p by (see e.g. Bardeen et al. 1986; Bond & Myers 1996)
where we have set
3 Results
In this Section, we show the results of the ellipsoidal-collapse model for the parameters
![]() and
and
![]() for three different cosmologies and discuss how they are affected by the choice of the external-shear model.
for three different cosmologies and discuss how they are affected by the choice of the external-shear model.
3.1 Influence of the external shear
Figure 2 shows the evolution of the three principal axes and the eigenvalues of the external shear for a reference ![]() CDM model with
CDM model with
![]() ,
,
![]() ,
and
,
and
![]() for three different models of the external shear and
for three different models of the external shear and
![]() ,
p=0. The shear in the linear approximation evolves completely smoothly over the entire collapse time. The evolution of each eigenvalue is given by D+(a) so that according to Eq. (4),
,
p=0. The shear in the linear approximation evolves completely smoothly over the entire collapse time. The evolution of each eigenvalue is given by D+(a) so that according to Eq. (4),
![]() ,
,
![]() ,
and
,
and
![]() at all times.
at all times.
This is different in the non-linear approximation: At early times, the evolution of the
![]() is the same, but soon thereafter they start evolving non-linearly and
is the same, but soon thereafter they start evolving non-linearly and
![]() becomes slightly negative. Noticeably there are steps in the evolution
of the external shear whenever an axis virialises because
becomes slightly negative. Noticeably there are steps in the evolution
of the external shear whenever an axis virialises because
![]() ,
and the evolution of this volume factor changes after virialisation of each axis. In the right panel, we introduce the hybrid approximation: Initially, the evolution of
,
and the evolution of this volume factor changes after virialisation of each axis. In the right panel, we introduce the hybrid approximation: Initially, the evolution of
![]() is described by the non-linear model. When one of the axes turns
around, however, the corresponding eigenvalue of the external shear
continues evolving linearly, i.e. its value at turn-around is then
scaled by
is described by the non-linear model. When one of the axes turns
around, however, the corresponding eigenvalue of the external shear
continues evolving linearly, i.e. its value at turn-around is then
scaled by
![]() .
.
We believe that the hybrid model is the preferred model for the evolution of the external shear since it takes into account that the evolution of the ellipsoid itself and its vicinity should be tightly coupled in the beginning. At turn-around, however, they are definitely decoupled so that choosing this moment to switch from non-linear to linear evolution seems appropriate. Hence, we will use the hybrid model for the evolution of the external shear in the following.
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig3a}\hspace...
...[width=4.3cm,clip]{figures/14147fig3d}\vspace*{-1mm}
\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg136.png)
|
Figure 3:
|
| Open with DEXTER | |
The influence of the external-shear model on the parameters
![]() and
and
![]() is shown in Fig. 3. For a given mass and a given virialisation redshift
is shown in Fig. 3. For a given mass and a given virialisation redshift ![]() ,
the initial overdensity is chosen such that the third axis of the ellipsoid finally virialises at
,
the initial overdensity is chosen such that the third axis of the ellipsoid finally virialises at ![]() .
Both parameters can then be calculated by
.
Both parameters can then be calculated by
In this case,
Using
![]() as a function of virialisation redshift and p=0 (top panels of Fig. 3), the dependence of
as a function of virialisation redshift and p=0 (top panels of Fig. 3), the dependence of
![]() and
and
![]() on
on ![]() is
almost the same for the non-linear and the hybrid models. However, both
differ from the linear model, showing that the external shear is most
important at the beginning of the ellipsoid's evolution. At that time,
the non-linear and the hybrid models agree. While
is
almost the same for the non-linear and the hybrid models. However, both
differ from the linear model, showing that the external shear is most
important at the beginning of the ellipsoid's evolution. At that time,
the non-linear and the hybrid models agree. While
![]() is always smaller in the linear compared to the other two models, the curves for
is always smaller in the linear compared to the other two models, the curves for
![]() cross. This reflects the circumstance that the initial overdensity in
the linear model is different from that in the two other models,
leading to a different initial ellipticity and therefore to a
completely different evolution history. This can be seen in the bottom
panels of Fig. 3, for which we have chosen e=0.2 independently of
cross. This reflects the circumstance that the initial overdensity in
the linear model is different from that in the two other models,
leading to a different initial ellipticity and therefore to a
completely different evolution history. This can be seen in the bottom
panels of Fig. 3, for which we have chosen e=0.2 independently of ![]() .
They also clearly show that a varying initial ellipticity drives primarily the evolution of
.
They also clearly show that a varying initial ellipticity drives primarily the evolution of
![]() ,
whereas
,
whereas
![]() also strongly varies for fixed e. In this case, both
also strongly varies for fixed e. In this case, both
![]() and
and
![]() are smaller in the linear-shear model compared to the non-linear and the hybrid models.
are smaller in the linear-shear model compared to the non-linear and the hybrid models.
3.2 Parameters as function of mass and redshift
Before we present general results for the parameters
![]() and
and
![]() ,
we should comment on a subtle but very important issue: Whenever we
want to compare our results with the ordinary spherical-collapse model,
we have to keep in mind that we calculate all quantities at the time
when the third axis virialises.
Thus, we also have to compare these quantities those from the
spherical-collapse model that are also calculated at the time of
virialisation and not of collapse, i.e. when
,
we should comment on a subtle but very important issue: Whenever we
want to compare our results with the ordinary spherical-collapse model,
we have to keep in mind that we calculate all quantities at the time
when the third axis virialises.
Thus, we also have to compare these quantities those from the
spherical-collapse model that are also calculated at the time of
virialisation and not of collapse, i.e. when
![]() and not R=0 for EdS. This leads to slightly lower reference values of
and not R=0 for EdS. This leads to slightly lower reference values of
![]() and
and
![]() since
since
![]() .
Here the subscript ``col'' denotes collapse. Using the parametric solutions of Ohta et al. (2004) for the linear and the non-linear overdensity,
.
Here the subscript ``col'' denotes collapse. Using the parametric solutions of Ohta et al. (2004) for the linear and the non-linear overdensity,
respectively, and
The top panels of Fig. 4 show
![]() and
and
![]() for three different cosmologies for e=p=0, i.e. spherical systems. The OCDM cosmology is the same as our reference
for three different cosmologies for e=p=0, i.e. spherical systems. The OCDM cosmology is the same as our reference ![]() CDM model except that
CDM model except that
![]() .
For the EdS model we set
.
For the EdS model we set
![]() and
and
![]() .
Indeed, for the EdS universe the constant values derived analytically are also reproduced by solving Eq. (5) numerically. This demonstrates again that Eqs. (5), (13) are fully consistent with the well-known spherical-collapse model. Note that the qualitative behaviour of
.
Indeed, for the EdS universe the constant values derived analytically are also reproduced by solving Eq. (5) numerically. This demonstrates again that Eqs. (5), (13) are fully consistent with the well-known spherical-collapse model. Note that the qualitative behaviour of
![]() is the same as
is the same as
![]() (compare e.g. with Bartelmann et al. 2006). However, there is a difference for the critical linear overdensity whose shape as a function of
(compare e.g. with Bartelmann et al. 2006). However, there is a difference for the critical linear overdensity whose shape as a function of ![]() differs substantially from the shape as a function of
differs substantially from the shape as a function of
![]() .
This should illustrate that the time chosen in the model when virialisation actually occurs (
.
This should illustrate that the time chosen in the model when virialisation actually occurs (![]() or
or
![]() )
can already have substantial impact on the qualitative behaviour of
relevant quantities as a function of redshift, hence it is not
necessarily a consequence of ellipsoidal collapse alone.
)
can already have substantial impact on the qualitative behaviour of
relevant quantities as a function of redshift, hence it is not
necessarily a consequence of ellipsoidal collapse alone.
The bottom panels of Fig. 4 show
![]() and
and
![]() for a triaxial halo with e=0.2 and p=-0.1. Also in this case both parameters are independent of
for a triaxial halo with e=0.2 and p=-0.1. Also in this case both parameters are independent of ![]() for the EdS universe, although
for the EdS universe, although
![]() changes from 1.583 to 2.058, while
changes from 1.583 to 2.058, while
![]() stays
almost the same, 148 instead of 147. Interestingly, the most drastic
changes in the shapes of both parameters occur for the OCDM model, for
which the total density is only approximately a third of the critical
density, while for the
stays
almost the same, 148 instead of 147. Interestingly, the most drastic
changes in the shapes of both parameters occur for the OCDM model, for
which the total density is only approximately a third of the critical
density, while for the ![]() CDM model their changes are small.
CDM model their changes are small.
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig4a}\hspace...
...pace*{1.5mm}
\includegraphics[width=4.3cm,clip]{figures/14147fig4d}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg149.png)
|
Figure 4:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig5a}\hspace...
...ace*{1.5mm}
\includegraphics[width=4.3cm,clip]{figures/14147fig5d}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg151.png)
|
Figure 5:
|
| Open with DEXTER | |
The influence of the halo mass M and the virialisation redshift ![]() on both
on both
![]() and
and
![]() are illustrated in Fig. 5. For both decreasing mass and decreasing redshift,
are illustrated in Fig. 5. For both decreasing mass and decreasing redshift,
![]() is a monotonically decreasing function, approaching the reference
values from the spherical-collapse model in the EdS universe for large
masses and high virialisation redshifts, the situation for
is a monotonically decreasing function, approaching the reference
values from the spherical-collapse model in the EdS universe for large
masses and high virialisation redshifts, the situation for
![]() is much more complicated. For all three models, it has a minimum at redshifts 4-5 and at a mass of
is much more complicated. For all three models, it has a minimum at redshifts 4-5 and at a mass of ![]()
![]() .
For smaller values of mass and redshift, it is a monotonically decreasing function of both M and
.
For smaller values of mass and redshift, it is a monotonically decreasing function of both M and ![]() for the OCDM and EdS models. It is also monotonically decreasing as a function of M in the
for the OCDM and EdS models. It is also monotonically decreasing as a function of M in the ![]() CDM model, but reaches a maximum at
CDM model, but reaches a maximum at
![]() .
This is a direct result of the definition of
.
This is a direct result of the definition of
![]() with respect to the critical density. If it was defined with respect to the background density, the factor
with respect to the critical density. If it was defined with respect to the background density, the factor
![]() would not appear in Eq. (26), and all three curves would increase with decreasing
would not appear in Eq. (26), and all three curves would increase with decreasing ![]() .
.
In Fig. 5 one can clearly see that the intervals that are covered for both
![]() and
and
![]() are the largest for the EdS model, indicating that there is a stronger
dependence of the ellipsoid's evolution on the total amount of matter
in the Universe compared to the size of the cosmological constant if
varying initial ellipticities are taken into account.
are the largest for the EdS model, indicating that there is a stronger
dependence of the ellipsoid's evolution on the total amount of matter
in the Universe compared to the size of the cosmological constant if
varying initial ellipticities are taken into account.
For either
![]() or
or
![]() ,
both
,
both
![]() and
and
![]() must reach the reference values for spherical collapse in the EdS universe since the initial ellipticity
must reach the reference values for spherical collapse in the EdS universe since the initial ellipticity
![]() and
and ![]() both decrease with increasing mass, and
both decrease with increasing mass, and ![]() has to be higher the earlier the structure is required to collapse. This expected behaviour can be clearly seen for
has to be higher the earlier the structure is required to collapse. This expected behaviour can be clearly seen for
![]() ,
whereas for
,
whereas for
![]() this happens finally for very large M and
this happens finally for very large M and ![]() .
We should stress again in this context that a crucial portion of the
dependence on mass and virialisation redshift is driven by the change
in the initial ellipticity, comparing Figs. 4 and 5.
.
We should stress again in this context that a crucial portion of the
dependence on mass and virialisation redshift is driven by the change
in the initial ellipticity, comparing Figs. 4 and 5.
| Figure 6:
Comparison of the fitting formula of Sheth et al. (2001) for
|
|
| Open with DEXTER | |
We compare in Fig. 6 the results of this work for
![]() as a function of mass and redshift with the fitting formula of Sheth et al. (2001) given by
as a function of mass and redshift with the fitting formula of Sheth et al. (2001) given by
where
The right panel of Fig. 6 shows a similar behaviour for
![]() as
a function of redshift. The differences between the fitting formula and
the result of our work again occur due to the different virialisation
time and condition, and the difference between the most probable and
the expectation value of e.
as
a function of redshift. The differences between the fitting formula and
the result of our work again occur due to the different virialisation
time and condition, and the difference between the most probable and
the expectation value of e.
For applications, fitting formulae for both
![]() and
and
![]() may be useful. We provide expressions here which are inspired by Eq. (28) of Sheth et al. (2001). For
may be useful. We provide expressions here which are inspired by Eq. (28) of Sheth et al. (2001). For
![]() we suggest
we suggest
where b=0.6536, c=0.6387, and both
A similar functional dependence can be found for
![]() .
Only a small correction term has to be added to arrive at a satisfactory accuracy. We find
.
Only a small correction term has to be added to arrive at a satisfactory accuracy. We find
with a=0.3819, b=0.5379, c=0.7589, and
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig7}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg174.png)
|
Figure 7:
Influence of the initial ellipticity e and prolaticity p on the parameters
|
| Open with DEXTER | |
3.3 Influence of initial ellipticity and prolaticity
In Fig. 7 we plot both
![]() and
and
![]() as a function of the initial ellipticity e and prolaticity p centered around their expectation values given by Eq. (21) for three different cosmologies. For increasing e and decreasing p, both parameters grow qualitatively in the same way as already reported by Sheth et al. (2001, cf. their Fig. 1). Quantitative deviations arise from the differences in the applied algorithm as discussed in Sect. 3.2. For a given mass and virialisation redshift, the initial overdensity for the EdS universe is larger compared to both
as a function of the initial ellipticity e and prolaticity p centered around their expectation values given by Eq. (21) for three different cosmologies. For increasing e and decreasing p, both parameters grow qualitatively in the same way as already reported by Sheth et al. (2001, cf. their Fig. 1). Quantitative deviations arise from the differences in the applied algorithm as discussed in Sect. 3.2. For a given mass and virialisation redshift, the initial overdensity for the EdS universe is larger compared to both ![]() CDM and OCDM due to a shorter physical time interval that corresponds to the same redshift interval, resulting in a larger
CDM and OCDM due to a shorter physical time interval that corresponds to the same redshift interval, resulting in a larger
![]() and
and ![]() ,
but also in larger curvatures of
,
but also in larger curvatures of
![]() and
and
![]() with respect to e and p. These are the sources of the larger error in the approximation
with respect to e and p. These are the sources of the larger error in the approximation
![]() discussed in Sect. 2.3. Since the redshift-time relation is not very different between
discussed in Sect. 2.3. Since the redshift-time relation is not very different between ![]() CDM and OCDM, the dependences of
CDM and OCDM, the dependences of
![]() and
and
![]() on e and p are comparable.
on e and p are comparable.
3.4 Mass function
Using Eq. (29), we are able to construct the mass function of dark-matter haloes using the extended Press-Schechter formalism developed by Bond et al. (1991) and Lacey & Cole (1993), which is based on the first-upcrossing distribution of the density contrast ![]() as a function of the ``time variable''
as a function of the ``time variable''
![]() .
We shall proceed similarly as Sheth & Tormen (1999,2002) and define the scaled variable
.
We shall proceed similarly as Sheth & Tormen (1999,2002) and define the scaled variable
![]() to derive the mass function for our standard
to derive the mass function for our standard ![]() CDM cosmology.
CDM cosmology.
As Sheth & Tormen (2002) pointed out, expressing the first-upcrossing distribution f as a function of ![]() has the advantage that it is only necessary to calculate
has the advantage that it is only necessary to calculate ![]() for a barrier of height
for a barrier of height ![]() at one arbitrary redshift to infer the mass function n(M) at any other redshift by a simple rescaling. For a given first-upcrossing distribution
at one arbitrary redshift to infer the mass function n(M) at any other redshift by a simple rescaling. For a given first-upcrossing distribution ![]() ,
the differential mass function can be calculated using the relation
,
the differential mass function can be calculated using the relation
where
First, we want to find an accurate fit to the first-upcrossing
distribution of a moving barrier which is given by the mass-dependent
linear overdensity parameter of the ellipsoidal collapse,
(see Eq. (29)). The parameter
thus, our suggested fitting formula is a mixture of the functional forms proposed by Sheth & Tormen (1999) and Sheth & Tormen (2002). The remaining best-fit parameters are A=0.357, p=0.212 and a=1.171. The result is shown in Fig. 8.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig8}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg187.png)
|
Figure 8: Comparison between the first-upcrossing distribution of the moving barrier, Eq. (32), inferred from an ensemble of one million random walks, and the fitting formula, Eq. (33). |
| Open with DEXTER | |
Second, to find a viable mass function from the first-upcrossing distribution, we proceed as Sheth & Tormen (1999) and Sheth et al. (2001), normalise ![]() to unity and rescale the variable a such that we are in agreement with the standard Sheth & Tormen mass function and a mass function based on N-body simulations proposed by Courtin et al. (2010). The latter is based on a first-upcrossing distribution that has the same functional form as that proposed by Sheth & Tormen (1999), but slightly different best-fit parameters,
to unity and rescale the variable a such that we are in agreement with the standard Sheth & Tormen mass function and a mass function based on N-body simulations proposed by Courtin et al. (2010). The latter is based on a first-upcrossing distribution that has the same functional form as that proposed by Sheth & Tormen (1999), but slightly different best-fit parameters,
with
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig9}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg194.png)
|
Figure 9: Comparison of the Sheth & Tormen and the Courtin et al. mass functions with the mass function derived from the rescaled upcrossing distribution, Eq. (33), based on our treatment of the ellipsoidal-collapse dynamics. |
| Open with DEXTER | |
4 Conclusions
We have reconsidered the collapse of a homogeneous, triaxial ellipsoid in an expanding background universe and extended the treatment of Bond & Myers (1996) in two ways:
- We have introduced a physically motivated criterion for the onset of virialisation along each principal axis of a collapsing ellipsoid. We derive this criterion from the tensor virial theorem, demanding that the inertial tensor stabilises and its second time derivative vanishes. This approach is a generalisation of the usual virialisation condition for the spherical-collapse scenario and thus fully consistent with it. It replaces the conventional requirement that virialisation is assumed along an axis i when the dimension-less semi-major axis ai of the ellipsoid along that axis reaches ai(a)=0.177a.
- We have introduced a hybrid model for the influence of the external gravitational shear field acting on the ellipsoid, supplementing the two different models of Bond & Myers (1996). The principal axes of the shear field evolve with those of the halo before it turns around and decouples from the background expansion, and then continues to evolve linearly while the halo evolves non-linearly and collapses. We have shown that the differences between the hybrid and the non-linear model are relatively small.
Our main results are as follows:
- The collapse parameters
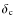 and
and
 depend only weakly on the model for the external gravitational shear. The hybrid model and the non-linear model by Bond & Myers (1996) give approximately the same results.
depend only weakly on the model for the external gravitational shear. The hybrid model and the non-linear model by Bond & Myers (1996) give approximately the same results.
- When supplied with our virialisation condition derived
from the tensor virial theorem, the ellipsoidal-collapse model returns
values
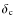 and
and
 that differ substantially from those obtained with the
spherical-collapse model. Depending on halo mass and redshift,
deviations of order
that differ substantially from those obtained with the
spherical-collapse model. Depending on halo mass and redshift,
deviations of order
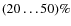 are common. After marginalisation over e and p,
are common. After marginalisation over e and p,
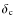 and
and
 increase with decreasing halo mass and with decreasing virialisation redshift.
increase with decreasing halo mass and with decreasing virialisation redshift.
- Both parameters increase with increasing initial ellipticity e and decrease with increasing prolaticity p, as already suggested by Sheth et al. (2001).
- Our results for
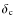 qualitatively confirm the dependence on halo mass and virialisation redshift given by a fitting formula by Sheth et al. (2001).
Deviations in particular at low mass and high redshift occur due to the
differences in the virialisation condition, the model for the external
shear, and the marginalisation over e.
qualitatively confirm the dependence on halo mass and virialisation redshift given by a fitting formula by Sheth et al. (2001).
Deviations in particular at low mass and high redshift occur due to the
differences in the virialisation condition, the model for the external
shear, and the marginalisation over e.
- The mass function based on our refined treatment of the ellipsoidal-collapse model is in good agreement with those proposed by Sheth & Tormen (1999) for low redshifts and Courtin et al. (2010) for high redshifts. This suggests that differences between the Sheth & Tormen mass function and results from N-body simulations at large redshifts may occur due to an imprecise treatment of the ellipsoidal-collapse dynamics.
C.A. wants to thank Francesco Pace for fruitful discussions, and the Deutsche Forschungsgemeinschaft for financial support under grant number BA 1369/12-1, the Heidelberg Graduate School of Fundamental Physics, and the IMPRS for Astronomy & Cosmic Physics at the University of Heidelberg.
Appendix A: Comparison to a previous study
Here we compare our results for the evolution equations of the collapsing ellipsoid with those presented by Monaco (1997) for a flat ![]() CDM and an OCDM model.
CDM and an OCDM model.
Starting from Eq. (5), we can replace E(a) and E'(a) for a flat ![]() CDM model using
CDM model using
since
This equation differs from Eq. (B11) of Monaco (1997) in the second and third term: a factor a2 in the denominator of both terms was omitted. Additionally, the vacuum term
For an OCDM model, we have
since
Equation (B12) of Monaco (1997) is again slightly different: the factor 3 in the last term was omitted.
There is one last difference concerning the initial conditions: Comparing Eq. (B17) of Monaco (1997) with Eq. (6) of this paper, one can find an additional factor a0 in front of
![]() which should be dropped.
which should be dropped.
References
- Angrick, C., & Bartelmann, M. 2009, A&A, 494, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., Ehlers, J., & Schneider, P. 1993, A&A, 280, 351 [NASA ADS] [Google Scholar]
- Bartelmann, M., Doran, M., & Wetterich, C. 2006, A&A, 454, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics, ed. J. P. Ostriker, Princeton Series in Astrophysics (Princeton, NJ: Princeton University Press) [Google Scholar]
- Bond, J. R., & Myers, S. T. 1996, ApJS, 103, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. R., Cole, S., Efstathiou, G., & Kaiser, N. 1991, ApJ, 379, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Courtin, J., Rasera, Y., Alimi, J., et al. 2010, MNRAS, submitted,[arXiv:1001.3425] [Google Scholar]
- Doroshkevich, A. G. 1970, Astrophysics, 6, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Loeb, A. 1995, ApJ, 439, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Engineer, S., Kanekar, N., & Padmanabhan, T. 2000, MNRAS, 314, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O., Lilje, P. B., Primack, J. R., & Rees, M. J. 1991, MNRAS, 251, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S., & Ng, K. 2009, [arXiv:0910.0126] [Google Scholar]
- Monaco, P. 1995, ApJ, 447, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, P. 1997, MNRAS, 287, 753 [NASA ADS] [Google Scholar]
- Monaco, P. 1998, Fundamentals of Cosmic Physics, 19, 157 [NASA ADS] [Google Scholar]
- Mota, D. F., & van de Bruck, C. 2004, A&A, 421, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohta, Y., Kayo, I., & Taruya, A. 2004, ApJ, 608, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Schäfer, B. M., & Koyama, K. 2008, MNRAS, 385, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 2002, MNRAS, 329, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, L., & Steinhardt, P. J. 1998, ApJ, 508, 483 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig1.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg95.png)
|
Figure 1: Comparison of the virialisation conditions from the scalar and tensor virial theorems. The curves differ slightly because they refer to different times. While the tensor virial theorem was evaluated at virialisation, the scaler virial theorem was evaluated at collapse. If we choose the collapse of the dark-matter halo as reference for z, both yield exactly the same result. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Evolution of the principal axes and the external shear for a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig3a}\hspace...
...[width=4.3cm,clip]{figures/14147fig3d}\vspace*{-1mm}
\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg136.png)
|
Figure 3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig4a}\hspace...
...pace*{1.5mm}
\includegraphics[width=4.3cm,clip]{figures/14147fig4d}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg149.png)
|
Figure 4:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{figures/14147fig5a}\hspace...
...ace*{1.5mm}
\includegraphics[width=4.3cm,clip]{figures/14147fig5d}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg151.png)
|
Figure 5:
|
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Comparison of the fitting formula of Sheth et al. (2001) for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig7}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg174.png)
|
Figure 7:
Influence of the initial ellipticity e and prolaticity p on the parameters
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig8}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg187.png)
|
Figure 8: Comparison between the first-upcrossing distribution of the moving barrier, Eq. (32), inferred from an ensemble of one million random walks, and the fitting formula, Eq. (33). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figures/14147fig9}
\end{figure}](/articles/aa/full_html/2010/10/aa14147-10/Timg194.png)
|
Figure 9: Comparison of the Sheth & Tormen and the Courtin et al. mass functions with the mass function derived from the rescaled upcrossing distribution, Eq. (33), based on our treatment of the ellipsoidal-collapse dynamics. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
b_i(t)= a_1(t)a_2(t)a_3(t)\int_0^\infty\frac{{\rm d}\tau}{[a_i^2(t)+1]\prod_{k=1}^3[a_k^2(t)+1]^{1/2}}-\frac{2}{3},
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img38.png)
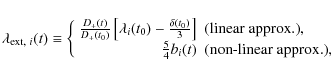
![\begin{displaymath}
\frac{{\rm d}^2a_i}{{\rm d}a^2}+\left[\frac{1}{a}+\frac{E'(a...
...5 E^2(a)}C_i(a)-\frac{\Omega_\Lambda}{a^2 E^2(a)}\right]a_i=0,
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img43.png)
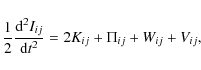
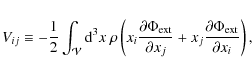
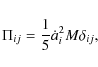
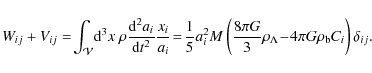
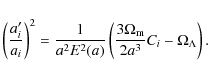
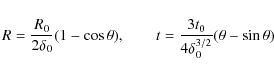
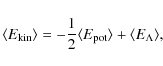
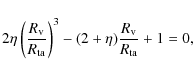
![\begin{displaymath}
g(e,p\vert\delta)=\frac{1125}{\sqrt{10\pi}}e(e^2-p^2)\left(\...
...{5}{2}\left(\frac{\delta}{\sigma}\right)^2(3e^2+p^2)\right]\!.
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img102.png)
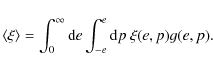
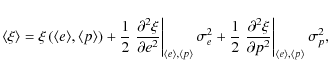
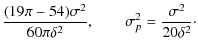
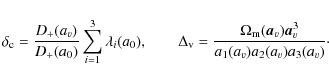
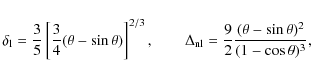
![\begin{displaymath}
\delta_{\rm c}(M,z)=\delta_{\rm c,sph}(z)\left\{1+0.47\left[...
...sigma^2(M,z)}{\delta_{\rm c,sph}^2(z)}\right]^{0.615}\right\},
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img160.png)
![\begin{displaymath}
\delta_{\rm c}(M,z)=\delta_{\rm c,sph}(z_{\rm v})\left\{1+b\...
...z_{\rm v})}{\delta_{\rm c,sph}^2(z_{\rm v})}\right]^c\right\},
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img165.png)
![$\displaystyle \Delta_{\rm v}(M,z)=\Delta_{\rm v,sph}(z_{\rm v})\left[a\!+\!b~\sigma^{2c}(M,z_{\rm v})\!+\!d(1+z_{\rm v})^{2/5}\log^{9/4}(M)\right]](/articles/aa/full_html/2010/10/aa14147-10/img171.png)
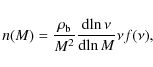
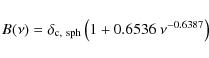
![\begin{displaymath}
\nu f(\nu)=A\left[1+(a\nu)^{-p}\right]\sqrt{\frac{a\nu}{2\pi...
...left(-\frac{a\nu}{2}
\frac{B(\nu)}{\delta_{\rm c,sph}}\right),
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img186.png)
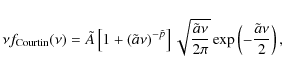
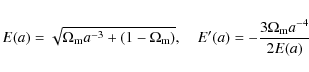
![\begin{displaymath}
\frac{{\rm d}^2 a_i}{{\rm d}a^2}\mathbf{-}\frac{1\!-\!2(\Ome...
...^2\left[1\!+\!(\Omega_{\rm m}^{-1}\!-\!1)a^3\right]}a_i\!=\!0.
\end{displaymath}](/articles/aa/full_html/2010/10/aa14147-10/img199.png)
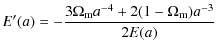
![$\displaystyle \frac{{\rm d}^2 a_i}{{\rm d}a^2}-\left\{2a\left[1+(\Omega_{\rm m}...
...}a}
+3\left\{2a^2\left[1+(\Omega_{\rm m}^{-1}-1)a\right]\right\}^{-1}C_i a_i=0.$](/articles/aa/full_html/2010/10/aa14147-10/img205.png)