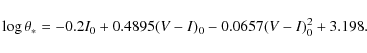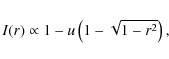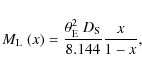| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201014053 | |
| Published online | 02 September 2010 | |
OGLE 2008-BLG-290: an accurate measurement of the limb darkening of a galactic bulge K Giant spatially resolved by microlensing
P. Fouqué1,44
- D. Heyrovský48 - S. Dong2,7
- A. Gould2,7 - A. Udalski3,27
- M. D. Albrow1,8 -
V. Batista1,11 - J.-P. Beaulieu1,11
- D. P. Bennett1,4,15 -
I. A. Bond4,30 -
D. M. Bramich1,5,10 -
S. Calchi Novati50 -
A. Cassan1,12 - C. Coutures1,11
- S. Dieters1,11 - M. Dominik1,5,6,13,![]() -
D. Dominis Prester1,17 -
J. Greenhill1,19 - K. Horne1,5,13
- U. G. Jørgensen6,45 -
S. Koz
-
D. Dominis Prester1,17 -
J. Greenhill1,19 - K. Horne1,5,13
- U. G. Jørgensen6,45 -
S. Koz![]() owski2,7
- D. Kubas1,9 - C.-H. Lee46,61
- J.-B. Marquette1,11 -
M. Mathiasen6,45 - J. Menzies1,22
- L. A. G. Monard2,26
- S. Nishiyama59 - I. Papadakis2,31
- R. Street1,5,39,43 - T. Sumi4,31
- A. Williams1,21 -
J. C. Yee2,7 -
S. Brillant9 -
J. A. R. Caldwell15 -
A. Cole19 - K. H. Cook16
- J. Donatowicz18 - N. Kains5,13
- S. R. Kane20 -
R. Martin21 -
K. R. Pollard8 -
K. C. Sahu23 -
Y. Tsapras5,39,60 -
J. Wambsganss6,12 - M. Zub6,12
(The PLANET Collaboration)1 -
D. L. DePoy7 -
B. S. Gaudi7 - C. Han24
- C.-U. Lee25 - B.-G. Park25
- R. W. Pogge7(The
owski2,7
- D. Kubas1,9 - C.-H. Lee46,61
- J.-B. Marquette1,11 -
M. Mathiasen6,45 - J. Menzies1,22
- L. A. G. Monard2,26
- S. Nishiyama59 - I. Papadakis2,31
- R. Street1,5,39,43 - T. Sumi4,31
- A. Williams1,21 -
J. C. Yee2,7 -
S. Brillant9 -
J. A. R. Caldwell15 -
A. Cole19 - K. H. Cook16
- J. Donatowicz18 - N. Kains5,13
- S. R. Kane20 -
R. Martin21 -
K. R. Pollard8 -
K. C. Sahu23 -
Y. Tsapras5,39,60 -
J. Wambsganss6,12 - M. Zub6,12
(The PLANET Collaboration)1 -
D. L. DePoy7 -
B. S. Gaudi7 - C. Han24
- C.-U. Lee25 - B.-G. Park25
- R. W. Pogge7(The ![]() FUN
Collaboration)2 - M. Kubiak27
- M. K. Szymanski27 -
G. Pietrzynski27,28 -
I. Soszynski27 - O. Szewczyk27,28
- K. Ulaczyk27 -
FUN
Collaboration)2 - M. Kubiak27
- M. K. Szymanski27 -
G. Pietrzynski27,28 -
I. Soszynski27 - O. Szewczyk27,28
- K. Ulaczyk27 - ![]() . Wyrzykowski29
(The OGLE Collaboration)3 - F. Abe31
- A. Fukui31 - K. Furusawa31
- A. C. Gilmore8 -
J. B. Hearnshaw8 -
Y. Itow31 - K. Kamiya31
- P. M. Kilmartin29 -
A. V. Korpela38 -
W. Lin8 - C. H. Ling18
- K. Masuda31 - Y. Matsubara31
- N. Miyake31 - Y. Muraki33
- M. Nagaya31 - K. Ohnishi34
- T. Okumura31 - Y. Perrott35
- N. J. Rattenbury5,35 -
To. Saito36 - T. Sako31
- S. Sato37 - L. Skuljan8
- D. Sullivan38 - W. Sweatman8
- P. J. Tristram29 -
P. C. M. Yock35 (The
MOA Collaboration)4 - A. Allan41
- M. F. Bode40 -
M. J. Burgdorf6,57,58 -
N. Clay40 -
S. N. Fraser40 -
E. Hawkins39 - E. Kerins32
- T. A. Lister39 -
C. J. Mottram40 -
E. S. Saunders39,41 -
C. Snodgrass6,9 -
I. A. Steele40 -
P. J. Wheatley42 (The
RoboNet-II Collaboration)5 - T. Anguita12
- V. Bozza50 - K. Harpsøe45
- T. C. Hinse45,51 -
M. Hundertmark53 - P. Kjærgaard45
- C. Liebig12 - L. Mancini50
- G. Masi49 - S. Rahvar52
- D. Ricci54 - G. Scarpetta50
- J. Southworth55 - J. Surdej54
- C. C. Thöne45,56 (The
MiNDSTEp Consortium)6 - A. Riffeser46
- S. Seitz46,47 - R. Bender46,47
(The WeCAPP collaboration)61
. Wyrzykowski29
(The OGLE Collaboration)3 - F. Abe31
- A. Fukui31 - K. Furusawa31
- A. C. Gilmore8 -
J. B. Hearnshaw8 -
Y. Itow31 - K. Kamiya31
- P. M. Kilmartin29 -
A. V. Korpela38 -
W. Lin8 - C. H. Ling18
- K. Masuda31 - Y. Matsubara31
- N. Miyake31 - Y. Muraki33
- M. Nagaya31 - K. Ohnishi34
- T. Okumura31 - Y. Perrott35
- N. J. Rattenbury5,35 -
To. Saito36 - T. Sako31
- S. Sato37 - L. Skuljan8
- D. Sullivan38 - W. Sweatman8
- P. J. Tristram29 -
P. C. M. Yock35 (The
MOA Collaboration)4 - A. Allan41
- M. F. Bode40 -
M. J. Burgdorf6,57,58 -
N. Clay40 -
S. N. Fraser40 -
E. Hawkins39 - E. Kerins32
- T. A. Lister39 -
C. J. Mottram40 -
E. S. Saunders39,41 -
C. Snodgrass6,9 -
I. A. Steele40 -
P. J. Wheatley42 (The
RoboNet-II Collaboration)5 - T. Anguita12
- V. Bozza50 - K. Harpsøe45
- T. C. Hinse45,51 -
M. Hundertmark53 - P. Kjærgaard45
- C. Liebig12 - L. Mancini50
- G. Masi49 - S. Rahvar52
- D. Ricci54 - G. Scarpetta50
- J. Southworth55 - J. Surdej54
- C. C. Thöne45,56 (The
MiNDSTEp Consortium)6 - A. Riffeser46
- S. Seitz46,47 - R. Bender46,47
(The WeCAPP collaboration)61
1 - Probing Lensing Anomalies Network, http://planet.iap.fr
2 - Microlensing Follow Up Network, http://www.astronomy.ohio-state.edu/ microfun
3 - The Optical Gravitational Lensing Experiment, http://ogle.astrouw.edu.pl
4 - Microlensing Observations in Astrophysics, http://www.phys.canterbury.ac.nz/moa
5 - Robotic Telescope Network, http://robonet.lcogt.net
6 - Microlensing Network for the Detection of Small Terrestrial
Exoplanets, http://www.mindstep-science.org
7 - Department of Astronomy, Ohio State University, 140 West 18th
Avenue, Columbus, OH 43210, USA
8 - University of Canterbury, Department of Physics &
Astronomy, Private Bag 4800, Christchurch 8020, New Zealand
9 - European Southern Observatory (ESO), Casilla 19001, Vitacura 19,
Santiago, Chile
10 - European Southern Observatory (ESO), Karl-Schwarzschild-Straße 2,
85748 Garching bei Munchen, Germany
11 - Institut d'Astrophysique de Paris, CNRS, Université Pierre
& Marie Curie, 98bis Bd Arago, 75014 Paris, France
12 - Astronomisches Rechen-Institut (ARI), Zentrum für Astronomie der
Universität Heidelberg (ZAH), Mönchhofstrasse 12-14, 69120 Heidelberg,
Germany
13 - Scottish Universities Physics Alliance, School of Physics
& Astronomy, University of St Andrews, North Haugh, St Andrews,
KY16 9SS, UK
14 - University of Notre Dame, Department of Physics, 225 Nieuwland
Science Hall, Notre Dame, IN 46556, USA
15 - University of Texas, McDonald Observatory, 16120 St Hwy Spur 78,
Fort Davis TX 79734, USA
16 - Institute of Geophysics and Planetary Physics (IGPP), L-413,
Lawrence Livermore National Laboratory, PO Box 808, Livermore, CA
94551, USA
17 - Physics Department, Faculty of Arts and Sciences, University of
Rijeka, Omladinska 14, 51000 Rijeka, Croatia
18 - Technical University of Vienna, Dept. of Computing, Wiedner
Hauptstrasse 10, Vienna, Austria
19 - School of Mathematics and Physics, University of Tasmania, Private
Bag 37, Hobart, Tasmania 7001, Australia
20 - NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South
Wilson Avenue, Pasadena, CA 91125, USA
21 - Perth Observatory, Walnut Road, Bickley, Perth 6076, Australia
22 - South African Astronomical Observatory, PO Box 9 Observatory 7925,
South Africa
23 - Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
24 - Department of Physics, Institute for Basic Science Research,
Chungbuk National University, Chongju 361-763, Korea
25 - Korea Astronomy and Space Science Institute, 61-1, Whaam-Dong,
Youseong-Gu, Daejeon 305-348, Korea
26 - Bronberg Observatory, Pretoria, South Africa
27 - Warsaw University Observatory. Al. Ujazdowskie 4, 00-478 Warszawa,
Poland
28 - Universidad de Concepción, Departamento de Física, Astronomy
Group, Casilla 160-C, Concepción, Chile
29 - Institute of Astronomy, University of Cambridge, Madingley Road,
Cambridge CB3 0HA, UK
30 - Institute of Information and Mathematical Sciences, Massey
University, Private Bag 102-904, North Shore Mail Centre, Auckland, New
Zealand
31 - Solar-Terrestrial Environment Laboratory, Nagoya University,
Nagoya, 464-8601, Japan
32 - Jodrell Bank Centre for Astrophysics, University of Manchester,
Manchester M13 9PL, UK
33 - Department of Physics, Konan University, Nishiokamoto 8-9-1, Kobe
658-8501, Japan
34 - Nagano National College of Technology, Nagano 381-8550, Japan
35 - Department of Physics, University of Auckland, Private Bag 92019,
Auckland 1142, New Zealand
36 - Tokyo Metropolitan College of Industrial Technology, Tokyo
116-0003, Japan
37 - Department of Physics and Astrophysics, Faculty of Science, Nagoya
University, Nagoya 464-8602, Japan
38 - Mount John Observatory, PO Box 56, Lake Tekapo 8770, New Zealand
39 - Las Cumbres Observatory, 6740B Cortona Dr, suite 102, Goleta, CA
93117, USA
40 - Astrophysics Research Institute, Liverpool John Moores University,
Twelve Quays House, Egerton Wharf, Birkenhead CH41 1LD, UK
41 - School of Physics, University of Exeter, Stocker Road, Exeter EX4
4QL, UK
42 - Department of Physics, University of Warwick, Coventry,
CV4 7AL, UK
43 - Department of Physics, Broida Hall, University of California,
Santa Barbara CA 93106-9530, USA
44 - LATT, Université de Toulouse, CNRS, 14 avenue Edouard Belin, 31400
Toulouse, France
45 - Dark Cosmology Centre, Københavns Universitet, Juliane Maries Vej
30, 2100 København, Denmark
46 - University Observatory Munich, Scheinerstrasse 1, 81679 München,
Germany
47 - Max Planck Institute for Extraterrestrial Physics,
Giessenbachstrasse, 85748 Garching, Germany
48 - Institute of Theoretical Physics, Charles University, V
Holesovickách 2, 18000 Prague, Czech Republic
49 - Bellatrix Observatory, via Madonna de Loco 47, 03023 Ceccano,
Italy
50 - Dipartimento di Fisica, Universita' di Salerno and INFN, sez. di
Napoli, Italy
51 - Armagh Observatory, College Hill, Armagh, BT61 9DG, Ireland
52 - Department of Physics, Sharif University of Technology, PO Box
11155-9161, Tehran, Iran
53 - Institut für Astrophysik, Georg-August Universität,
Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
54 - Institut d'Astrophysique et de Géophysique, Allée du 6 Août, Sart
Tilman, Bât. B5c, 4000 Liège, Belgium
55 - Astrophysics Group, Keele University, Newcastle-under-Lyme, ST5
5BG, UK
56 - INAF, Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807
Merate (LC), Italy
57 - Deutsches SOFIA Institut, Universität Stuttgart, Pfaffenwaldring
31, 70569 Stuttgart, Germany
58 - SOFIA Science Center, NASA Ames Research Center, Mail Stop N211-3,
Moffett Field CA 94035, USA
59 - Department of Astronomy, Kyoto University, Kyoto 606-8502, Japan
60 - School of Mathematical Sciences, Queen Mary University of London,
Mile End Road, London E1 4NS, UK
61 - The Wendelstein Calar Alto Pixellensing Project, http://www.usm.uni-muenchen.de/people/arri/wecapp.html
Received 13 January 2010 / Accepted 5 May 2010
Abstract
Context. Not only is gravitational microlensing a
successful tool for discovering distant exoplanets, but it also enables
characterization of the lens and source stars involved in the lensing
event.
Aims. In high-magnification events, the lens caustic
may cross over the source disk, which allows determination of the
angular size of the source and measurement of its limb darkening.
Methods. When such extended-source effects appear
close to maximum magnification, the resulting light curve differs from
the characteristic Paczynski point-source curve. The exact shape of the
light curve close to the peak depends on the limb darkening of the
source. Dense photometric coverage permits measurement of the
respective limb-darkening coefficients.
Results. In the case of the microlensing event
OGLE 2008-BLG-290, the K giant source star reached a peak
magnification at about 100. Thirteen different telescopes have covered
this event in eight different photometric bands. Subsequent light-curve
analysis yielded measurements of linear limb-darkening coefficients of
the source in six photometric bands. The best-measured coefficients
lead to an estimate of the source effective temperature of about
4700+100-200 K.
However, the photometric estimate from colour-magnitude diagrams
favours a cooler temperature of
![]() K.
K.
Conclusions. Because the limb-darkening
measurements, at least in the CTIO/SMARTS2 ![]() - and
- and ![]() -bands, are among the most
accurate obtained, the above disagreement needs to be understood. A
solution is proposed, which may apply to previous events where such a
discrepancy also appeared.
-bands, are among the most
accurate obtained, the above disagreement needs to be understood. A
solution is proposed, which may apply to previous events where such a
discrepancy also appeared.
Key words: gravitational lensing: micro - techniques: high angular resolution - stars: atmospheres - stars: individual: OGLE 2008-BLG-290
1 Introduction
Astrophysical opportunities for measuring stellar limb darkening are very scarce. Moreover, they are often limited to very specific types of stars. Until recently, most measurements had been based on analyses of eclipsing-binary light curves (Popper 1984), requiring large amounts of high-precision photometric data but only rarely yielding useful constraints on the recovered limb-darkening parameters (e.g. Southworth et al. 2005; Popper & Etzel 1981).
Resolving stellar surfaces by interferometry is a promising technique, limited nevertheless at present to nearby giants and supergiants. For most of the sufficiently well-resolved stars it has been shown that a fixed model-atmosphere-based limb-darkening profile agrees with the observations better than a uniform or fully limb-darkened stellar disk. Only a limited number of cases have been used to actually measure limb darkening from interferometric data (e.g., Wittkowski et al. 2006; Burns et al. 1997; Perrin et al. 2004; Aufdenberg et al. 2006). The same is true for observations of lunar occultation of stars, which only rarely yield limb-darkening measurements (Richichi & Lisi 1990).
An alternative method that permits accurate limb-darkening measurement practically independent of stellar type is based on gravitational microlensing. In a stellar gravitational microlensing event the flux from an observed source star is temporarily amplified by the gravitational field of another object passing in the foreground and acting as a gravitational lens (Paczynski 1996). The lensing object may be a single star, a binary star, or a star with one or several planetary companions. A particularly interesting situation occurs in so-called caustic-crossing events, in which the caustic of the lens directly crosses the projected disk of the source star, typically on a timescale of a fraction of a day to a few days. The very high angular resolution provided by the caustic presents a unique opportunity to measure the source star's limb darkening from photometric observations or the centre-to-limb variation of spectral features from spectroscopic observations of the crossing (e.g. Heyrovský et al. 2000; Heyrovský 2003; Witt 1995).
The first well-documented source-resolving, caustic-crossing microlensing event was MACHO Alert 95-30 (Alcock et al. 1997), in which an M4 III giant source star was scanned by the point-like caustic of a single lens. The observations permitted measurement of the source size and detection of its limb darkening. Precise measurement of the limb darkening was not possible due to low-amplitude variability of the source (Heyrovský 2003). The first limb-darkening measurement came from the analysis of binary-lens event MACHO 97-BLG-28 (Albrow et al. 1999), producing V- and I-band coefficients of the linear and square-root limb-darkening laws for the K2 III giant source. By the time of writing, six further binary-lens caustic-crossing events yielded limb-darkening measurements of their source stars: MACHO 97-BLG-41 (Albrow et al. 2000), MACHO 98-SMC-1 (Afonso et al. 2000), OGLE 1999-BUL-23 (Albrow et al. 2001), EROS 2000-BLG-5 (Fields et al. 2003; An et al. 2002), MOA 2002-BLG-33 (Abe et al. 2003), and OGLE 2002-BLG-069 (Kubas et al. 2005; Cassan et al. 2004).
Limb-darkening measurements are also available from four single-lens, caustic-crossing events: OGLE 2003-BLG-262 (Yoo et al. 2004), OGLE 2003-BLG-238 (Jiang et al. 2004), OGLE 2004-BLG-254 (Heyrovský 2008; Cassan et al. 2006), and OGLE 2004-BLG-482 (Zub et al. 2009). In addition, there are a comparable number of events that required including limb darkening in their analysis (such as MACHO Alert 95-30), but for which a sufficiently accurate limb-darkening measurement was not (and often could not be) performed. These include two other single-lens events (Batista et al. 2009; Yee et al. 2009), as well as all ten published planetary microlensing events, in which a star with a planet acted as the lens (Bennett et al. 2008; Beaulieu et al. 2006; Dong et al. 2009; Gould et al. 2006; Janczak et al. 2010; Gaudi et al. 2008; Udalski et al. 2005; Bond et al. 2004; Sumi et al. 2010).
In this paper we report the results of the analysis of OGLE 2008-BLG-290, a microlensing event in which the caustic of a single lens crossed the disk of a K giant in the galactic bulge. In Sect. 2 we describe the obtained data and their reduction. We discuss the properties of the source star in detail in Sect. 3. The data modelling in Sect. 4 is followed in Sect. 5 by a description of the limb-darkening measurements in six photometric bands and their comparison with model atmospheres. We devote Sect. 6 to the study of the properties of the lens. We explore the possibility of deviations caused by a potential planetary companion to the lens in Sect. 7 and consider other potential systematics in Sect. 8. The main results are summarized in Sect. 9.
2 Data sets: observations and data reductions
The OGLE-III early warning system (EWS) (Udalski
2003) alerted the Bulge
event OGLE 2008-BLG-290 (
![]() ,
,
![]() (J2000.0)
and
(J2000.0)
and ![]() ,
,
![]() )
on May 15, 2008, from observations carried out with
the 1.3 m Warsaw Telescope at the Las Campanas Observatory
(Chile).
Independently, the MOA-II 1.8 m telescope at Mount John
Observatory (New Zealand)
discovered the same event under name MOA 2008-BLG-241 on May
31, 2008.
)
on May 15, 2008, from observations carried out with
the 1.3 m Warsaw Telescope at the Las Campanas Observatory
(Chile).
Independently, the MOA-II 1.8 m telescope at Mount John
Observatory (New Zealand)
discovered the same event under name MOA 2008-BLG-241 on May
31, 2008.
A few days later, it was clear that this event had the
potential to become one
of the rare high-magnification events discovered each year, and
follow-up
observations were undertaken on PLANET, ![]() FUN, RoboNet/LCOGT and
MiNDSTEp telescopes available at that time. In total, 13 telescopes
covered the
event in different photometric bands: OGLE 1.3 m (I-band),
MOA-II 1.8 m (wide
MOA-red band), SAAO 1.0 m at Sutherland (South Africa) (V-
and I-bands),
Canopus 1.0 m at Hobart (Australia) (I-band),
Perth/Lowell 0.6 m at Bickley
(Australia) (I-band), CTIO 1.3 m at Cerro
Tololo (Chile) (
FUN, RoboNet/LCOGT and
MiNDSTEp telescopes available at that time. In total, 13 telescopes
covered the
event in different photometric bands: OGLE 1.3 m (I-band),
MOA-II 1.8 m (wide
MOA-red band), SAAO 1.0 m at Sutherland (South Africa) (V-
and I-bands),
Canopus 1.0 m at Hobart (Australia) (I-band),
Perth/Lowell 0.6 m at Bickley
(Australia) (I-band), CTIO 1.3 m at Cerro
Tololo (Chile) (![]() -,
-,
![]() - and
H-bands), LOAO 1.0 m at Mount Lemmon
(Arizona) (I-band), Bronberg 0.36 m at
Pretoria (South Africa) (unfiltered), Skinakas 1.3 m at Mount
Ida (Greece)
(I-band), Faulkes North 2.0 m at
Haleakala (Hawaii) (Bessell R-band),
Faulkes South 2.0 m at Siding Spring (Australia) (Bessell R-band),
Liverpool
2.0 m at La Palma (Spain) (SDSS r-band),
and Danish 1.5 m at La Silla (Chile)
(I-band). The CTIO/SMARTS2 bandpasses are close to
standard Bessell
V and I, but sufficiently
distinct to be treated separately
(Gould et al. 2010).
We mark them here by
- and
H-bands), LOAO 1.0 m at Mount Lemmon
(Arizona) (I-band), Bronberg 0.36 m at
Pretoria (South Africa) (unfiltered), Skinakas 1.3 m at Mount
Ida (Greece)
(I-band), Faulkes North 2.0 m at
Haleakala (Hawaii) (Bessell R-band),
Faulkes South 2.0 m at Siding Spring (Australia) (Bessell R-band),
Liverpool
2.0 m at La Palma (Spain) (SDSS r-band),
and Danish 1.5 m at La Silla (Chile)
(I-band). The CTIO/SMARTS2 bandpasses are close to
standard Bessell
V and I, but sufficiently
distinct to be treated separately
(Gould et al. 2010).
We mark them here by ![]() and
and ![]() .
.
Thanks to the public availability of data from the different
groups, real-time
modelling efforts then showed that the light curve was deviating from a
normal
Paczynski curve (Paczynski 1986),
exhibiting evidence of extended-source
effects. The event peaked on that same night (June 15).
Because such events are
reasonably sensitive to Jupiter-mass planets, as recently shown by
Dong et al. (2009),
amateur telescopes from the ![]() FUN
network were
alerted, resulting in an excellent coverage of the peak region from 9
different
telescopes.
FUN
network were
alerted, resulting in an excellent coverage of the peak region from 9
different
telescopes.
Data reduction has been done using both PSF photometry based
on a customized
DoPhot package and image subtraction. ![]() FUN telescope images were first
reduced using DoPhot. RoboNet/LCOGT data were reduced using an
automatic image
subtraction package, and reduced again off-line. PLANET telescopes also
use image subtraction: at telescope an on-line version called WISIS,
based on
Alard's ISIS package, then off-line version 3.0 of pySIS (Albrow et al. 2009),
based on a numerical kernel (Bramich
2008). SAAO I photometry obtained
with pySIS has been checked independently using a DIA package. However,
even then the SAAO I data were found to exhibit
correlated noise at the peak.
Its effect was found to be strong enough to skew the recovered lensing
parameters (see Sect. 4).
For this reason we decided to omit the light
curve from the final event analysis, even though we include it when
testing for
a potential planetary companion in Sect. 7. SAAO V
images were
taken well after the light curve peak and therefore do not bring
constraints on
the event parameters. Bronberg images were re-reduced using the same
DIA package. Looking at stars of similar colours as the target, a clear
airmass effect is generally detected in Bronberg data because there
is no filter on the camera. However, in the case of this event, only a
clear trend with time was present in the data, instead of the expected
airmass
trend. As the origin of this trend is unexplained, we could not correct
for it
and as a result we did not use Bronberg data in the following analysis.
CTIO
FUN telescope images were first
reduced using DoPhot. RoboNet/LCOGT data were reduced using an
automatic image
subtraction package, and reduced again off-line. PLANET telescopes also
use image subtraction: at telescope an on-line version called WISIS,
based on
Alard's ISIS package, then off-line version 3.0 of pySIS (Albrow et al. 2009),
based on a numerical kernel (Bramich
2008). SAAO I photometry obtained
with pySIS has been checked independently using a DIA package. However,
even then the SAAO I data were found to exhibit
correlated noise at the peak.
Its effect was found to be strong enough to skew the recovered lensing
parameters (see Sect. 4).
For this reason we decided to omit the light
curve from the final event analysis, even though we include it when
testing for
a potential planetary companion in Sect. 7. SAAO V
images were
taken well after the light curve peak and therefore do not bring
constraints on
the event parameters. Bronberg images were re-reduced using the same
DIA package. Looking at stars of similar colours as the target, a clear
airmass effect is generally detected in Bronberg data because there
is no filter on the camera. However, in the case of this event, only a
clear trend with time was present in the data, instead of the expected
airmass
trend. As the origin of this trend is unexplained, we could not correct
for it
and as a result we did not use Bronberg data in the following analysis.
CTIO
![]() and
and ![]() and LOAO I images were re-reduced off-line using
pySIS 3.0, with a slight improvement over DoPhot. CTIO H
images were of poor
quality and thus discarded. Danish images were reduced using
pySIS 3.0; they
were also reduced with the DIAPL package from Pych & Wozniak
(Wozniak 2000), with very
similar results. Finally, OGLE images were
re-reduced with the OGLE pipeline, but with a better resolution
reference image
and a correctly adjusted centroid.
and LOAO I images were re-reduced off-line using
pySIS 3.0, with a slight improvement over DoPhot. CTIO H
images were of poor
quality and thus discarded. Danish images were reduced using
pySIS 3.0; they
were also reduced with the DIAPL package from Pych & Wozniak
(Wozniak 2000), with very
similar results. Finally, OGLE images were
re-reduced with the OGLE pipeline, but with a better resolution
reference image
and a correctly adjusted centroid.
The final data set before rejection of outliers contains 4389
data
points from 11 different telescopes (OGLE I:
1065, CTIO ![]() :
252,
LOAO I: 159, CTIO
:
252,
LOAO I: 159, CTIO ![]() :
12, MOA-red: 2555, Canopus I: 44,
Perth I: 13, Skinakas I: 28,
Faulkes North R: 12, Faulkes South R:
27,
Liverpool r: 59, Danish I:
163).
:
12, MOA-red: 2555, Canopus I: 44,
Perth I: 13, Skinakas I: 28,
Faulkes North R: 12, Faulkes South R:
27,
Liverpool r: 59, Danish I:
163).
The shape of the light curve depends on the limb darkening of
the source which
is different for each photometric band. In the following two figures we
plot by
solid lines only those that are distinguishable at the peak: the I-
and
![]() -band light
curves in Fig. 1,
and the I-,
-band light
curves in Fig. 1,
and the I-,
![]() - and r-band
light curves in Fig. 2.
The curves
correspond to the best-fit limb-darkened extended-source model
described
further and specified in Table 2. The
residuals in the lower
panels are computed and displayed for their respective light-curve
solutions.
Dashed lines in these figures correspond to a point-source light curve
with the
same timescale and impact parameter.
- and r-band
light curves in Fig. 2.
The curves
correspond to the best-fit limb-darkened extended-source model
described
further and specified in Table 2. The
residuals in the lower
panels are computed and displayed for their respective light-curve
solutions.
Dashed lines in these figures correspond to a point-source light curve
with the
same timescale and impact parameter.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig1.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg25.png)
|
Figure 1:
Upper panel: photometry of microlensing event
OGLE 2008-BLG-290 in terms of source-flux amplification, as
observed by OGLE (olive), MOA (blue), two PLANET sites (Canopus: grey;
Perth: wine), three |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig2.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg26.png)
|
Figure 2: Zoom of the event peak (June 15, 2008) from Fig. 1. Amplification is plotted in the upper panel; relative residuals in the lower panel. Colours and lines have the same meaning as in Fig. 1, with the added SDSS r-band light curve (solid red). |
| Open with DEXTER | |
3 Source properties
3.1 Near-infrared colour-magnitude diagram
The distance to the source and the amount of reddening along the line of sight are uncertainties which always affect the final determination of the properties of the lens-source system. We want to dedicate a short discussion to these issues to justify our adopted values and associated uncertainties and to serve as a reference in our future papers.
Due to the geometry of the galactic bulge with a bar embedded
in it, the
galactic coordinates of the target give an estimate of the relative
position of
the source with respect to the galactic centre, if we assume that the
source is
at the same distance as the majority of the stars in the field. The
galactic
centre distance itself is adopted from Eisenhauer
et al. (2005) as
![]() kpc
or
kpc
or ![]() .
Rattenbury et al. (2007)
give the relative positions of the OGLE-II fields with
respect to the field BUL_SC45, which contains Baade's Window
(
.
Rattenbury et al. (2007)
give the relative positions of the OGLE-II fields with
respect to the field BUL_SC45, which contains Baade's Window
(
![]() ,
,
![]() ). As shown by Paczynski & Stanek (1998),
it is
safe to assume that the mean distance of stars seen in Baade's Window
is
similar to the galactic centre distance. Our target's position lies
outside of
any OGLE-II fields, but close to field BUL_SC20, and this field is at
about
the same distance as BUL_SC45. We therefore adopt the galactic centre
distance
modulus as the source distance modulus, but with an increased
uncertainty due
to the additional involved assumptions, namely
). As shown by Paczynski & Stanek (1998),
it is
safe to assume that the mean distance of stars seen in Baade's Window
is
similar to the galactic centre distance. Our target's position lies
outside of
any OGLE-II fields, but close to field BUL_SC20, and this field is at
about
the same distance as BUL_SC45. We therefore adopt the galactic centre
distance
modulus as the source distance modulus, but with an increased
uncertainty due
to the additional involved assumptions, namely ![]() .
.
Table 1: Coordinates and magnitudes of the two stars close to the target position and the 2MASS blend.
There are several estimates of the reddening in the ![]() -band at
about the
position of our target. They range from AKs=
0.28 (Schultheis et al.
1999) to
AKs=
0.46 (Dutra et al. 2003).
Part of the disagreement may come from the
patchiness of dust structure, but unfortunately different assumptions
about the
reddening law also play a role.
-band at
about the
position of our target. They range from AKs=
0.28 (Schultheis et al.
1999) to
AKs=
0.46 (Dutra et al. 2003).
Part of the disagreement may come from the
patchiness of dust structure, but unfortunately different assumptions
about the
reddening law also play a role.
Our own estimate is based on IRSF/Sirius photometry of a ![]() field
containing our target. We use isochrones from Bonatto
et al. (2004) based
on Padova group models, but directly calibrated for the 2MASS
bandpasses. The
IRSF/Sirius photometric system, similar to the MKO system (Tokunaga et al. 2002),
is close to the 2MASS system, but we calibrated the photometry using
2MASS
stars in the same field to ensure coherence.
field
containing our target. We use isochrones from Bonatto
et al. (2004) based
on Padova group models, but directly calibrated for the 2MASS
bandpasses. The
IRSF/Sirius photometric system, similar to the MKO system (Tokunaga et al. 2002),
is close to the 2MASS system, but we calibrated the photometry using
2MASS
stars in the same field to ensure coherence.
We restrict the fitting region to 300 pixels around the target
(
![]() )
to avoid differential extinction. This is large enough to form
well-defined colour-magnitude diagrams (hereafter CMD), where the red
giant clump (hereafter RC) is easily identified. This is not the case
when using only 2MASS, because the brighter limiting magnitude cuts off
part of
the clump. An example of such a CMD is displayed in Fig. 3.
)
to avoid differential extinction. This is large enough to form
well-defined colour-magnitude diagrams (hereafter CMD), where the red
giant clump (hereafter RC) is easily identified. This is not the case
when using only 2MASS, because the brighter limiting magnitude cuts off
part of
the clump. An example of such a CMD is displayed in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig3.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg44.png)
|
Figure 3:
Colour-magnitude diagram in J and H
from IRSF/Sirius stars in a |
| Open with DEXTER | |
Although the position of the clump could in principle give an estimate
of its
distance, in practice variations in age and metallicity do not allow an
accurate determination. Adopting a 10 Gyr isochrone and a
solar metallicity, we
get the following estimates of the near-infrared extinction and
reddening law:
| AKs= 0.44 | (1) |
Note that the corresponding reddening law in J differs from what Nishiyama et al. (2006) found based on the IRSF/Sirius galactic bulge survey (
The target, which appears as a double star in the OGLE finding chart, is well separated by PSF photometry of the IRSF/Sirius image. The accurate coordinates and magnitudes of the two components are given in Table 1, together with the corresponding values for the single object in the 2MASS catalogue.
Although the 2MASS flags do not indicate any blending, the coordinates and magnitudes correspond well to the blend of the two stars. The microlensed target is the fainter southwestern component and, after extinction correction and conversion to the Bessell & Brett photometric system (Bessell & Brett 1988), it has K0= 13.05 and typical colours of a K4 giant star ( (J-K)0=0.87, (H-K)0=0.13). Such a star is predicted to have colours of (V-I)0=1.50 and (V-K)0=3.26, so we expect V0=16.3 and I0=14.8.
Estimating the uncertainties of the measured near-infrared extinctions is not straightforward, because the present method mixes hypotheses about distance, age, metallicity with actual measurements by isochrone fitting. In the next paper of this series (Fouqué, in prep.) on MOA 2009-BLG-411, a refined method will be introduced, using reddening law, clump absolute magnitudes and distance hypothesis to simultaneously fit isochrones to near-infrared and visible CMDs and derive a coherent source size. We applied this new technique to the present data set to estimate the uncertainties in our measured extinctions. We found differences of 0.06, 0.13 and 0.05 in AJ, AH and AKs, respectively. We therefore adopt an uncertainty of 0.1 in the extinction measurement for each near-infrared band.
3.2 Visible CMD
A colour-magnitude diagram allows an estimate of the dereddened
magnitude and
colour of the source, by comparison with the observed position of the
red giant
clump, if one assumes that both suffer the same amount of extinction.
The
CTIO 1.3 m telescope obtained the uncalibrated
colour-magnitude diagram
displayed in Fig. 4
(instrumental magnitudes), from which we read a
magnitude shift in I of ![]() for the source compared to the RC, and a
colour shift of
for the source compared to the RC, and a
colour shift of ![]() .
.
Table 2: Main parameters of the best-fitting point-lens limb-darkened source model, using the linear limb-darkening law.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig4.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg66.png)
|
Figure 4:
Colour-magnitude diagram in |
| Open with DEXTER | |
For the mean absolute magnitude of the clump, we adopt the Hipparcos
value as
given by Stanek & Garnavich
(1998), ![]() and for the mean colour
and for the mean colour
![]() .
With our adopted distance to the field,
.
With our adopted distance to the field,
![]() ,
this gives
,
this gives ![]() .
So our source is
predicted to have
.
So our source is
predicted to have ![]() and
and ![]() ,
in good agreement with the values obtained before from the
near-infrared CMD.
,
in good agreement with the values obtained before from the
near-infrared CMD.
From magnitude and colour, and using the recent revision of
surface-brightness-colour relations (hereafter SBC) in I,
(V-I) published by
Kervella & Fouqué (2008),
we get an estimate of the angular source radius ![]() in
in
![]() of:
of:
The uncertainty of this estimate is 0.0238, so adding quadratically the uncertainty in magnitude and colour gives
However, this source is probably a giant star, and these SBC relations
have
been calibrated for dwarfs and sub-giants. In order to check if this
introduces
a systematic uncertainty in our measurement of the angular radius, we
use the
Groenewegen (2004)
SBC relation specifically designed for giants:
The uncertainty of this estimate is similar at 0.024, so adding quadratically the uncertainty in the magnitude
Using the dereddened colours and, for instance, Houdashelt et al. (2000)
tables, we estimate the effective temperature of the source star to be
about 4200 K, corresponding to a K3 giant. In order to
estimate an
uncertainty of this value, we repeated the whole procedure adopting
plausible
different values for the clump distance, its colour and absolute
magnitude,
and measured the shift in colour and magnitude of the source with
respect to
the centroid of the clump using the OGLE-III photometric catalogue. The
difference in colours that we get using these new values corresponds to
a
difference in temperature of about 100 K. We therefore adopt ![]() K
as our estimate of the photometric temperature of the source star.
K
as our estimate of the photometric temperature of the source star.
Using this value, we looked at Marigo
et al. (2008) isochrones for a model star
with similar characteristics to ours. Two routes are used to derive the
star's
luminosity: on one hand, from K0=
13.05, distance modulus (14.4)
and model bolometric correction in K
(2.36), we get ![]() and
and
![]() ;
on another hand, we use
;
on another hand, we use ![]() and our estimate of the
star's radius, to get
and our estimate of the
star's radius, to get ![]() .
We note that different modelers
still use different values of the bolometric magnitude of the Sun
(4.72 for Houdashelt
et al. 2000; vs. 4.77 for Marigo
et al. 2008). We
find that an old star (12.7 Gyr), slightly metal-rich (Z=0.03)
gives a red
giant of 1 solar mass and
.
We note that different modelers
still use different values of the bolometric magnitude of the Sun
(4.72 for Houdashelt
et al. 2000; vs. 4.77 for Marigo
et al. 2008). We
find that an old star (12.7 Gyr), slightly metal-rich (Z=0.03)
gives a red
giant of 1 solar mass and ![]() ,
with such characteristics.
,
with such characteristics.
4 Data modelling: noise model
From the original data set, we remove data points in OGLE and MOA older than date 4490 or newer than 4770. This corresponds to selecting the whole 2008 observing season. We verified that this does not change the resulting fit parameters. The reason for this cut is two-fold: the planetary deviation search is very demanding in terms of CPU time, so reducing the number of useful points helps; moreover, the number of data points in the baseline before 4490 is quite large, and any slight error in the photometric error estimate may bias the fit.
We then proceed to remove outliers and rescale photometric
error bars in a
consistent way: the rescaling factor is computed by forcing ![]() for each telescope data set independently, and after rescaling,
any point lying at more than
for each telescope data set independently, and after rescaling,
any point lying at more than ![]() is removed. This slightly changes
the estimate of
is removed. This slightly changes
the estimate of ![]() and thus the rescaling factor. After a few iterations,
the process converges. Care was taken not to remove any potential
planet-caused
outliers. The number of outliers varies between 1
and 6 per telescope.
and thus the rescaling factor. After a few iterations,
the process converges. Care was taken not to remove any potential
planet-caused
outliers. The number of outliers varies between 1
and 6 per telescope.
We return briefly to the SAAO I-band light curve. Inspecting the residuals of the microlensing fit, we find they are mutually correlated rather than randomly distributed, as mentioned earlier in Sect. 2. Near the event peak clusters of points with positive residuals alternate with negative-residual clusters. Despite its small amplitude, the effect is strong enough to influence the recovered lensing parameters. Adding the SAAO light curve to the twelve other curves results in a lower impact parameter and shorter source-radius crossing time, both of which in turn influence the limb-darkening measurement. The small-amplitude abrupt shifts in the SAAO residuals during the crossing are most probably a systematic artifact in the data (see also Sects. 7 and 8). We therefore decided not to include this light curve in the subsequent event analysis.
In the case of MOA data, several measurements close to the peak were saturated and therefore were eliminated. For this particular telescope, 51 data points were removed a priori or as outliers. For OGLE data, we quadratically added 0.003 mag to all photometric errors, in order to avoid too small errors at the peak, which correspond to Poisson noise at these bright magnitudes, but do not reflect systematic errors.
The final total number of fitted data points amounts to 2049 in 12 light curves observed in 6 different photometric bands (see Fig. 1).
5 Limb darkening of the source star
5.1 Limb-darkening measurement
As expected, a single-lens point-source model results in a high
![]() ,
which obviously rejects this simple model. A uniform
extended-source model provides us with a first working set of
parameters; however, the fit still has a high
,
which obviously rejects this simple model. A uniform
extended-source model provides us with a first working set of
parameters; however, the fit still has a high ![]() At
this stage the residuals of the fit show a symmetric pattern around
the peak of the light curve, the signature of limb darkening. We thus
add
linear limb darkening to the source model. This is described here by
At
this stage the residuals of the fit show a symmetric pattern around
the peak of the light curve, the signature of limb darkening. We thus
add
linear limb darkening to the source model. This is described here by
where r is a radial coordinate running from 0 at disk centre to 1 at limb, and u is the linear limb-darkening coefficient (hereafter LLDC, e.g., Claret 2000).
The adopted event parametrization involves the following microlensing
quantities: t0 (time of
closest approach), u0
(impact parameter
in units of the Einstein ring radius ![]() ),
), ![]() (crossing time of
(crossing time of ![]() ),
),
![]() (source radius in units of
(source radius in units of ![]() )
and two annual parallax
parameters
)
and two annual parallax
parameters ![]() and
and ![]() (see Sect. 6)
common to all
data sets; plus light-curve-specific parameters: baseline and
blending fluxes, as well as the LLDC u for the
respective photometric band.
The main parameters of the set best fitting the data (
(see Sect. 6)
common to all
data sets; plus light-curve-specific parameters: baseline and
blending fluxes, as well as the LLDC u for the
respective photometric band.
The main parameters of the set best fitting the data (
![]() )
and their errors are given in Table 2. The
limb-darkening coefficients correspond to the involved six distinct
photometric
bands: CTIO/SMARTS2
)
and their errors are given in Table 2. The
limb-darkening coefficients correspond to the involved six distinct
photometric
bands: CTIO/SMARTS2 ![]() ,
SDSS r, R, MOA-red,
CTIO/SMARTS2
,
SDSS r, R, MOA-red,
CTIO/SMARTS2 ![]() ,
and I,
in order of increasing effective wavelength.
,
and I,
in order of increasing effective wavelength.
Based on the final model, we find that the source-radius
transit time
is ![]() d;
the time (in terms of
d;
the time (in terms of ![]() )
at which the lens starts to transit the source disk
)
at which the lens starts to transit the source disk ![]() d,
while the exit time is
d,
while the exit time is ![]() d.
The
peak magnification achieved in the I-band is
d.
The
peak magnification achieved in the I-band is ![]() 97, in the
97, in the ![]() -band
-band
![]() 102. The
source I-band magnitude in the OGLE-III photometric
database
is 17.26, so the source star temporarily brightened to
magnitude 12.3 due to
the lens passing in the foreground.
102. The
source I-band magnitude in the OGLE-III photometric
database
is 17.26, so the source star temporarily brightened to
magnitude 12.3 due to
the lens passing in the foreground.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig5n.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg100.png)
|
Figure 5:
Linear limb-darkening coefficients in the I-band
for 4 different telescopes when fitting the limb darkening
independently for each data set. We determine the I-band
measurement as the weighted mean of these values, |
| Open with DEXTER | |
Individual telescopes constrain the measured limb darkening unequally,
because of their different coverage of the caustic-crossing peak. As a
result,
Perth, Skinakas and Faulkes-North do not contribute, Faulkes-South very
weakly
(closest points to the peak are just outside the limb) and Liverpool
only
weakly. Hence, the obtained limb darkening in the R-band
(Faulkes telescopes)
and the r-band (Liverpool) is poorly constrained.
In the ![]() -
and
-
and ![]() -bands,
the LLDCs rely on the respective CTIO light curves. With the MOA-red
band result determined by MOA data, only the I-band
result is constrained by
4 different telescope data sets (Danish, LOAO, OGLE, Canopus).
-bands,
the LLDCs rely on the respective CTIO light curves. With the MOA-red
band result determined by MOA data, only the I-band
result is constrained by
4 different telescope data sets (Danish, LOAO, OGLE, Canopus).
In order to test for consistency we fit the event data again,
using
common lensing parameters but leaving the limb darkening independent
for each
of the 12 data sets. Checking the I-band LLDCs
shown in Fig. 5,
we find that even though the Canopus value is consistent with the
others at the
3-![]() level, the scatter of the values exceeds individual errors as well
as the error obtained from the straightforward fit in Table 2.
In the light of this finding, the small error on uI
in
Table 2
is not really the result of an excellent agreement
between individual light curves. Rather, it is a statistical artifact
obtained
by the competing higher-u-value Canopus and the
lower-u-value-favouring
others. Possible causes of this discrepancy include slightly different
filters,
detector or atmosphere response, light curve coverage, secondary
amendments of
the source or lens models, but also noise models for each telescope. To
get a
more realistic result under these circumstances, we determine the I-band
LLDC
from the values in Fig. 5. The
weighted mean of the individual
values with the statistical error given by their scatter yields
level, the scatter of the values exceeds individual errors as well
as the error obtained from the straightforward fit in Table 2.
In the light of this finding, the small error on uI
in
Table 2
is not really the result of an excellent agreement
between individual light curves. Rather, it is a statistical artifact
obtained
by the competing higher-u-value Canopus and the
lower-u-value-favouring
others. Possible causes of this discrepancy include slightly different
filters,
detector or atmosphere response, light curve coverage, secondary
amendments of
the source or lens models, but also noise models for each telescope. To
get a
more realistic result under these circumstances, we determine the I-band
LLDC
from the values in Fig. 5. The
weighted mean of the individual
values with the statistical error given by their scatter yields
![]() .
.
5.2 Comparison with model atmospheres
We obtain the response functions of the individual telescopes by
combining their filter transmission curves and their CCD quantum
efficiency
curves. We then use the response functions to compute theoretical
values of
the LLDCs, based on Kurucz's ATLAS9 atmosphere models
(Kurucz
1993b,1994,1993a).
To get the LLDC for a
particular theoretical limb-darkening profile we use the radially
integrated
fit method described in Heyrovský
(2007) rather than the 11-point fit from
Claret (2000), for reasons
described in the former reference. We compute
the LLDC values for a sub-grid of Kurucz's model grid based on the
source
properties inferred in Sect. 3, with
effective temperature ![]() ranging from
4000 K to 5000 K, metallicity [Fe/H] from 0 to +0.3,
surface
gravity
ranging from
4000 K to 5000 K, metallicity [Fe/H] from 0 to +0.3,
surface
gravity ![]() from 2.0 to 3.0, and microturbulent velocity fixed at
from 2.0 to 3.0, and microturbulent velocity fixed at
![]() km s-1.
km s-1.
![\begin{figure}
\includegraphics[width=8.5cm]{14053fig6n.eps} \end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg105.png)
|
Figure 6:
Linear limb-darkening coefficients of the K-giant source star
in CTIO/SMARTS2 |
| Open with DEXTER | |
The comparison of the measured LLDC in the 6 bands to theoretical model
predictions is presented in Fig. 6.
Judging first the
agreement between the bands, we point out that the obtained values
decrease
with increasing effective wavelength, in agreement with theoretical
expectations. Second, we note that within each band the measured values
point
to a similar effective temperature of the source, with all measurements
being
mutually compatible within their error bars. This leads to an
LLDC-based
initial estimate of the effective temperature of the source star, with
the most accurate ![]() and
and ![]() measurements indicating 4750 K. The value is
in rather poor agreement with the photometric estimate 4200 K
derived in
Sect. 3.2.
We note that the theoretical Claret
(2000) coefficients
would lead to an even larger discrepancy, with the I-band
measurement
indicating an effective temperature higher than 5500 K.
measurements indicating 4750 K. The value is
in rather poor agreement with the photometric estimate 4200 K
derived in
Sect. 3.2.
We note that the theoretical Claret
(2000) coefficients
would lead to an even larger discrepancy, with the I-band
measurement
indicating an effective temperature higher than 5500 K.
Comparing measured LLDCs with corresponding values computed from model atmospheres has its potential pitfalls (Heyrovský 2007,2003). Simple analytical limb-darkening laws, and the linear law in particular, often do not describe theoretical limb-darkening profiles sufficiently accurately. Such analytical approximations do not even conserve the flux of the approximated profile with the required precision. To avoid this problem at least partly, we compare our measured LLD profiles directly with the theoretical profiles of the Kurucz models rather than with their linear limb-darkening approximations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig7an.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14053fig7bn.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg106.png)
|
Figure 7:
Comparison of the measured |
| Open with DEXTER | |
We denote by ![]() our measured intensity profile given by
Eq. (6)
with the measured LLDC u, normalizing it to unit
rms intensity. For each theoretical profile from the considered
sub-grid we
then compute a scale factor yielding the best agreement with
our measured intensity profile given by
Eq. (6)
with the measured LLDC u, normalizing it to unit
rms intensity. For each theoretical profile from the considered
sub-grid we
then compute a scale factor yielding the best agreement with ![]() and mark the
rescaled theoretical profile
and mark the
rescaled theoretical profile ![]() .
In
Fig. 7
we plot the obtained difference curves
.
In
Fig. 7
we plot the obtained difference curves
![]() as a function of radial position on the stellar
disk for our most precise measurements, i.e., the
as a function of radial position on the stellar
disk for our most precise measurements, i.e., the ![]() - and
- and ![]() -band
limb darkening. From the plot one can already distinguish by eye the
agreement
with Kurucz profiles of different effective temperature, metallicity,
and
surface gravity. For instance, all the 4750 K profiles agree
with the
measured
-band
limb darkening. From the plot one can already distinguish by eye the
agreement
with Kurucz profiles of different effective temperature, metallicity,
and
surface gravity. For instance, all the 4750 K profiles agree
with the
measured ![]() profile within 1.3% of the rms intensity from disk centre
out to the limb. Nevertheless, in the case of the measured
profile within 1.3% of the rms intensity from disk centre
out to the limb. Nevertheless, in the case of the measured ![]() profile it is
hard to judge by eye which group of model profiles agrees better. The
4500 K
models are preferred near the centre, but closer to the limb their
accuracy
drops earlier than that of the 4750 K models.
profile it is
hard to judge by eye which group of model profiles agrees better. The
4500 K
models are preferred near the centre, but closer to the limb their
accuracy
drops earlier than that of the 4750 K models.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig8an.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14053fig8bn.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg107.png)
|
Figure 8:
Agreement between the measured |
| Open with DEXTER | |
To obtain a quantitative measure of agreement we compute the relative
residual
![]() ,
defined as the rms difference in units of rms intensity. The values of
,
defined as the rms difference in units of rms intensity. The values of
![]() corresponding
to the profiles in Fig. 7 are
presented
graphically in Fig. 8.
Each point in the left (right)
grid corresponds to a Kurucz
corresponding
to the profiles in Fig. 7 are
presented
graphically in Fig. 8.
Each point in the left (right)
grid corresponds to a Kurucz ![]() -band (
-band (![]() -band) profile with the
corresponding
-band) profile with the
corresponding ![]() ,
[Fe/H], and
,
[Fe/H], and ![]() values as the coordinates.
The colour of the point indicates the value of
values as the coordinates.
The colour of the point indicates the value of ![]() as shown in the
colour bar. The black point singles out the best agreeing model with
the
relative residual
as shown in the
colour bar. The black point singles out the best agreeing model with
the
relative residual ![]() given above the grid. Clearly
given above the grid. Clearly
![]() K is strongly
favoured in both bands, validating our previous
finding. As for the other parameters, there is a weaker preference for
higher
[Fe/H] and higher
K is strongly
favoured in both bands, validating our previous
finding. As for the other parameters, there is a weaker preference for
higher
[Fe/H] and higher ![]() .
.
In order to get an error bar estimate on ![]() ,
we perform a similar
analysis for profiles with LLDC values given by the upper and lower
error bars
in either band from Table 2. We
find that the lower limits on
,
we perform a similar
analysis for profiles with LLDC values given by the upper and lower
error bars
in either band from Table 2. We
find that the lower limits on
![]() and
and ![]() both agree best with 4750 K models, while the upper
limits on both agree best with 4500 K models. Based on these
results and the
change of
both agree best with 4750 K models, while the upper
limits on both agree best with 4500 K models. Based on these
results and the
change of ![]() with
with ![]() in Fig. 8
we conclude that our
limb-darkening measurement yields a temperature estimate of the source
star
in Fig. 8
we conclude that our
limb-darkening measurement yields a temperature estimate of the source
star
![]() K,
obtained by comparison with the limb darkening of
Kurucz's models.
K,
obtained by comparison with the limb darkening of
Kurucz's models.
The LLDC measured from our analysis for the I-band is presented in Table 3 and compared to model LLDC predictions for the given stellar parameters, together with values for similar giants resolved by microlensing, namely EROS 2000-BLG-5 from Fields et al. (2003) as reported in Yoo et al. (2004), OGLE 2003-BLG-238 from Jiang et al. (2004) and OGLE 2004-BLG-254 from revised fits in Heyrovský (2008), which solve discrepancies noted in Cassan et al. (2006). Unfortunately, the listed effective temperatures are based on photometric estimates for all events but OGLE 2004-BLG-254, for which the spectroscopic measurement (4100 K) disagrees with the photometric one (4500 K) given in the Table. OGLE 2008-BLG-290 appears to be a twin of EROS 2000-BLG-5, while OGLE 2003-BLG-238 and OGLE 2004-BLG-254 are slightly hotter.
Table 3: Photometric temperatures and I-band limb-darkening coefficients of K Bulge giants for OGLE 2008-BLG-290 and other published microlensing events with source stars of similar spectral type.
For the present event, the agreement between temperatures
estimated from
colours and from limb-darkening coefficients is not satisfactory
(
![]() vs. 4700+100-200 K,
respectively). Unfortunately, we do
not have a spectroscopic estimate of
vs. 4700+100-200 K,
respectively). Unfortunately, we do
not have a spectroscopic estimate of ![]() ,
but it is not unusual that
photometric and spectroscopic estimates disagree by several hundred K
in cool
giants. We refer to Affer
et al. (2005) and Fulbright
et al. (2006) for detailed
discussions about this discrepancy.
,
but it is not unusual that
photometric and spectroscopic estimates disagree by several hundred K
in cool
giants. We refer to Affer
et al. (2005) and Fulbright
et al. (2006) for detailed
discussions about this discrepancy.
One way to solve the disagreement is to assume that our target
suffers more
extinction than the red clump in the same region. Let us check what it
would
imply if the source star suffers 0.1 mag more
extinction in the ![]() -band
than
the clump. According to our adopted reddening law in the near-infrared
(Eqs. (2)
and (3)),
the source star would be at
-band
than
the clump. According to our adopted reddening law in the near-infrared
(Eqs. (2)
and (3)),
the source star would be at ![]() and (J-H)0=0.66,
inside the red clump. Adopting typical reddening law ratios of
10 and 5.6 between respectively AV
and AI on
one side, and AKs
on the
other side, the source star brightens by 0.56 mag in I
and becomes bluer by
0.44 mag in (V-I),
explaining the observed shifts in the visible CMD with
respect to the red clump centroid not because the star is redder and
fainter,
but because it suffers more extinction.
and (J-H)0=0.66,
inside the red clump. Adopting typical reddening law ratios of
10 and 5.6 between respectively AV
and AI on
one side, and AKs
on the
other side, the source star brightens by 0.56 mag in I
and becomes bluer by
0.44 mag in (V-I),
explaining the observed shifts in the visible CMD with
respect to the red clump centroid not because the star is redder and
fainter,
but because it suffers more extinction.
As the typical temperature of Bulge red clump giants is about 4750 K (Hill, personal communication), this would approximately reconcile the effective temperature deduced from the LD measurements with the photometric temperature.
Obviously, this would slightly decrease (by about 5%) the angular radius of the source obtained from the surface brightness colour relations (Eqs. (4) and (5)) and accordingly all the dependent parameters, but the exact change depends on the visible to near-infrared extinction ratios, which are not well known (e.g. Nishiyama et al. 2008).
6 Lens properties
With the angular Einstein radius being related to the angular source
radius
![]() as
as ![]() ,
we find
,
we find ![]() .
This
enables us to calculate the relative lens-source proper motion:
.
This
enables us to calculate the relative lens-source proper motion:
![]() mas/yr.
The relative transverse velocity
mas/yr.
The relative transverse velocity
![]() between lens
and source at the lens distance then follows from
between lens
and source at the lens distance then follows from
![]() .
.
From the value of ![]() in mas and
in mas and ![]() in kpc, we obtain a constraint on the
lens mass
in kpc, we obtain a constraint on the
lens mass ![]() in solar mass units as
(Dominik 1998):
in solar mass units as
(Dominik 1998):
where
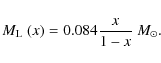
|
(8) |
In principle, a measurement of the source size in both Einstein radius and physical units, as well as the measurement of parallax parameters completely determine the lens location (given the source distance
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig9.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg132.png)
|
Figure 9:
Probability densities for the lens mass |
| Open with DEXTER | |
We then use estimates of the physical parameters, following
Dominik (2006) and
assuming his adopted Galaxy model. The event
time-scale ![]() and the angular Einstein radius
and the angular Einstein radius
![]() mas
provide us with probability densities for the lens mass
mas
provide us with probability densities for the lens mass ![]() and the lens
distance
and the lens
distance ![]() ,
which are shown in Fig. 9.
,
which are shown in Fig. 9.
From these, we find a median lens mass ![]() ,
a median
projected relative velocity
,
a median
projected relative velocity ![]() ,
and
a median lens distance
,
and
a median lens distance ![]() for an adopted source
distance of
for an adopted source
distance of ![]() .
The lens is inferred to reside in the
galactic bulge, with
.
The lens is inferred to reside in the
galactic bulge, with ![]() probability.
probability.
7 Possible planetary deviations
In this section we include even the 120 points of the SAAO I-band
data in the analysis to test whether the overall residuals may harbour
the weak
signature of a planetary companion of the lens. The single-lens
extended-source model with fitted limb-darkening coefficients then has
a ![]() of 2485.7 for 2169 data points (after rescaling error bars). We
will now test if a binary lens fit may improve this
of 2485.7 for 2169 data points (after rescaling error bars). We
will now test if a binary lens fit may improve this ![]() by more than some
threshold level. If this were the case, then a planet signal is
probably buried
in the small residuals, similarly to the MOA 2007-BLG-400 (Dong et al. 2009) and
MOA 2008-BLG-310 (Janczak
et al. 2010) events.
by more than some
threshold level. If this were the case, then a planet signal is
probably buried
in the small residuals, similarly to the MOA 2007-BLG-400 (Dong et al. 2009) and
MOA 2008-BLG-310 (Janczak
et al. 2010) events.
Our exploration of the parameter space uses the ![]() parameterization
introduced and justified by Dong
et al. (2009). q is the
mass
ratio between the two components of the lens system (q
< 1), w is the width
of the central caustic as defined by Chung
et al. (2005) (given there by their
Eq. (12), and called vertical width or short diameter) and
parameterization
introduced and justified by Dong
et al. (2009). q is the
mass
ratio between the two components of the lens system (q
< 1), w is the width
of the central caustic as defined by Chung
et al. (2005) (given there by their
Eq. (12), and called vertical width or short diameter) and ![]() is the
trajectory angle with respect to the line joining the two components.
is the
trajectory angle with respect to the line joining the two components.
In order to choose the limits of the grid in ![]() and
and ![]() ,
we
note that any planetary deviation would be strongly smeared out by the
extended-source effect when the caustic width
,
we
note that any planetary deviation would be strongly smeared out by the
extended-source effect when the caustic width ![]() .
Han & Kim (2009)
argue that a 5% deviation can be detected even when the central
caustic width w is larger than a quarter of the
source
diameter (
.
Han & Kim (2009)
argue that a 5% deviation can be detected even when the central
caustic width w is larger than a quarter of the
source
diameter (
![]() ).
Indeed, with adequate photometric accuracy,
Dong et al. (2009)
clearly detect a planetary deviation in MOA 2007-BLG-400 at
).
Indeed, with adequate photometric accuracy,
Dong et al. (2009)
clearly detect a planetary deviation in MOA 2007-BLG-400 at
![]() ,
and Batista et al. (2009)
find some sensitivity even down
to
,
and Batista et al. (2009)
find some sensitivity even down
to ![]() .
.
We therefore use a grid with w between 10-3
and 10-2 and q
between
10-4 and 10-2. We find a
marginal improvement of 55 in ![]() in a
region centred around
in a
region centred around ![]() ,
,
![]() and
and ![]() rad,
corresponding to
rad,
corresponding to ![]() .
However, the corresponding residuals
do not show any improvement over the single lens case, so we conclude
that any
possible planetary deviation is not detectable in this event, given the
large
source size.
.
However, the corresponding residuals
do not show any improvement over the single lens case, so we conclude
that any
possible planetary deviation is not detectable in this event, given the
large
source size.
A similar conclusion can be drawn even for the presence of multiple planetary companions. Just like in the single-planet case, in a high-magnification event such as ours lens companions would in effect change the point-like caustic of the single lens to a small cusped caustic at the same position. On the light curve this would produce symmetrically placed perturbations at the times of entering and exiting the limb of the source, a region where we see no significant systematic residuals.
8 Other potential systematics
In order to affect our limb-darkening measurement and the subsequent
![]() estimate, any potential modelling systematic uncertainty would have to
influence the light-curve shape in the narrow region corresponding to
the
caustic crossing. In our case the region is limited to the
estimate, any potential modelling systematic uncertainty would have to
influence the light-curve shape in the narrow region corresponding to
the
caustic crossing. In our case the region is limited to the ![]() 1-day-wide
interval around the peak. Having already tested negatively for the
presence of a planetary companion, we turn here to potential
uncertainties
related to the source, and to the limb-darkening treatment.
1-day-wide
interval around the peak. Having already tested negatively for the
presence of a planetary companion, we turn here to potential
uncertainties
related to the source, and to the limb-darkening treatment.
Two relevant source-related uncertainties that could influence the result are the presence of star spots and the presence of low-level variability of the source star. The microlensing influence of a star spot would be temporally limited to the spot-crossing time, and the maximum photometric effect is given approximately by the fractional radius of the spot (Heyrovský & Sasselov 2000). Judging by the amplitude of the residuals in the peak region, our event could potentially permit spots with radii <0.01 stellar radii. Nevertheless, any such a spot, in addition to being obscured by light-curve noise, would affect only 0.01 of the source-crossing time. For a longer duration small-amplitude effect one would be limited to the option of a very low-contrast larger spot possibly positioned off the projected lens path. However, such a weak perturbation would be unlikely to affect our results significantly.
Potential low-level variability of the source should always be
considered, especially because it could go undetected in the absence of
the
lens if there is substantial blended light from other stars. In the
presence of
the lens it should be noticeable in the residuals near the light-curve
peak,
which should also be mutually correlated in the different light curves
as seen
in the MACHO Alert 95-30 case (Alcock et al. 1997; Heyrovský 2003).
However, only a
source varying significantly on timescales ![]() the source-crossing time
could potentially affect the limb-darkening measurement. Checking our
residuals
in the peak region, we find that they stay below the 1% level and the
residuals from individual curves do not exhibit a clear correlated
pattern.
the source-crossing time
could potentially affect the limb-darkening measurement. Checking our
residuals
in the peak region, we find that they stay below the 1% level and the
residuals from individual curves do not exhibit a clear correlated
pattern.
The results could be potentially affected also by the adopted
limb-darkening treatment. For our measurement we have chosen the linear
limb-darkening law primarily because it is the most widely used
single-parameter law. In addition, it is reasonably accurate for
broadband
photometry in the optical part of the spectrum of a wide range of
stars. For
the sub-grid of Kurucz models tested in the paper and the relevant
photometric
bands, the accuracy of the linear law stays better than its average
value for
the full Kurucz grid (Heyrovský
2007). Within the tested range, the
accuracy is best in the ![]() -band
and decreases with effective wavelength to
the I-band. Nevertheless, our
-band
and decreases with effective wavelength to
the I-band. Nevertheless, our ![]() -band and
-band and ![]() -band
measurements gave us
compatible results. Moreover, in order to compensate for the potential
inadequacy of the law, we compared the measured limb darkening not only
with
the LLDCs of the Kurucz models but also directly with their
unapproximated
limb-darkening profiles. In principle, one could test more advanced
limb-darkening laws such as the PCA description
(Heyrovský
2008,2003)
or higher-order analytical laws with more
free parameters. However, non-negligible inadequacy of the linear law
would be
exhibited by a centre-to-limb pattern in the residuals, something we do
not see
in our results given the level of light-curve noise. Based on the above
we do
not expect the limb-darkening treatment to change our conclusions on
the
measured limb darkening and the derived effective temperature of the
source
star.
-band
measurements gave us
compatible results. Moreover, in order to compensate for the potential
inadequacy of the law, we compared the measured limb darkening not only
with
the LLDCs of the Kurucz models but also directly with their
unapproximated
limb-darkening profiles. In principle, one could test more advanced
limb-darkening laws such as the PCA description
(Heyrovský
2008,2003)
or higher-order analytical laws with more
free parameters. However, non-negligible inadequacy of the linear law
would be
exhibited by a centre-to-limb pattern in the residuals, something we do
not see
in our results given the level of light-curve noise. Based on the above
we do
not expect the limb-darkening treatment to change our conclusions on
the
measured limb darkening and the derived effective temperature of the
source
star.
Finally, it should be noted that inaccuracies may arise on the model-atmosphere side of the comparison. The Kurucz ATLAS9 models used in our analysis involve various simplifications, such as 1-D radiative transfer in a plane-parallel atmosphere, the assumption of local thermodynamic equilibrium, or the mixing-length treatment of convection. Such approximations may affect the predicted limb-darkening profiles, which reflect the change of physical conditions in the atmosphere with depth. Accurate measurement of limb darkening thus provides an opportunity to test the depth structure of model atmospheres and, hence, the appropriateness of their underlying physical assumptions.
9 Summary and conclusion
We have performed dense photometric monitoring of the microlensing
event
OGLE 2008-BLG-290, a short duration and very small impact
parameter
microlensing event generated by a point-like lens transiting a giant
star. The
peak magnification was about ![]() ,
effectively multiplying
the diameter of our network telescopes by a factor
,
effectively multiplying
the diameter of our network telescopes by a factor ![]() 10. Using a
calibrated
colour-magnitude diagram analysis and isochrones, we find a source
angular radius
10. Using a
calibrated
colour-magnitude diagram analysis and isochrones, we find a source
angular radius ![]() ,
and a physical radius
,
and a physical radius
![]() at the adopted source distance
at the adopted source distance ![]() kpc.
A
Galaxy model together with the event time-scale
kpc.
A
Galaxy model together with the event time-scale ![]() and
the angular Einstein radius
and
the angular Einstein radius ![]() mas
yielded statistically inferred
median parameters, namely a lens mass
mas
yielded statistically inferred
median parameters, namely a lens mass ![]() ,
a lens distance
,
a lens distance
![]() ,
and a relative velocity
,
and a relative velocity
![]() .
.
From our photometric data, we have derived accurate
measurements of the
linear limb-darkening coefficients of the source for the ![]() ,
SDSS
r, R, MOA-red,
,
SDSS
r, R, MOA-red, ![]() ,
and I broadband filters. The obtained
limb-darkening profiles lead to a source-star temperature estimate of
,
and I broadband filters. The obtained
limb-darkening profiles lead to a source-star temperature estimate of
![]() K
when compared with the limb-darkening profiles of
Kurucz's ATLAS9 atmosphere models. This result is in marginal
disagreement with
the corresponding estimate based on measured colours, a finding that
has
already been noted for several previous events measured by the
microlensing
technique, which also parallels the known discrepancies in temperature
estimates based on photometry vs. spectroscopy of similar cool giants
(Fulbright et al. 2006).
Possible explanations involve reddening corrections
which may lead to wrong colour estimates, or inaccuracies in model
atmosphere
physics.
K
when compared with the limb-darkening profiles of
Kurucz's ATLAS9 atmosphere models. This result is in marginal
disagreement with
the corresponding estimate based on measured colours, a finding that
has
already been noted for several previous events measured by the
microlensing
technique, which also parallels the known discrepancies in temperature
estimates based on photometry vs. spectroscopy of similar cool giants
(Fulbright et al. 2006).
Possible explanations involve reddening corrections
which may lead to wrong colour estimates, or inaccuracies in model
atmosphere
physics.
We express our gratitude to ESO for a two months invitation at Santiago headquarters, Chile, where part of this work was achieved. We are very grateful to the observatories that support our science (Bronberg, Canopus, CTIO, ESO, IRSF, LCOGT, Liverpool, LOAO, MOA, OGLE, Perth, SAAO, Skinakas) via the generous allocation of time that makes this work possible. The operation of Canopus Observatory is in part supported by a financial contribution from David Warren. The OGLE project is partially supported by the Polish MNiSW grant N20303032/4275 to AU. Allocation of the Holmes grant from the French Agence Nationale de la Recherche has been indispensable to finance observing trips and meeting travels, and is gratefully acknowledged here. D.H. was supported by Czech Science Foundation grant GACR 205/07/0824 and by the Czech Ministry of Education project MSM0021620860. C.H. was supported by the grant 2009-0081561 of National Research Foundation of Korea. T.C.H. was financed for his astronomical research at the Armagh Observatory by the Department for Culture, Arts and Leisure, Northern Ireland, UK. D.R. and J.S. acknowledge support from the Communauté française de Belgique - Actions de recherche concertées - Académie universitaire Wallonie-Europe. The Dark Cosmology Centre is funded by the Danish National Research Council. P.F. wishes to thank Noriyuki Matsunaga for discussions about the interplay between adopted distance and derived extinction, David Nataf for measuring the red giant clump in the recently released OGLE-III photometric catalogue, and Etienne Bachelet for checking the whole chain from extinction to source size using a refined method. We are grateful to the anonymous referee for constructive comments that helped us improve the manuscript.This publication makes use of data products from the 2MASS project, as well as the SIMBAD database, Aladin and Vizier catalogue operation tools (CDS Strasbourg, France). The Two Micron All Sky Survey is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Abe, F., Bennett, D., Bond, I., et al. 2003, A&A, 411, L493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Affer, L., Micela, G., Morel, T., Sanz-Forcada, J., & Favata, F. 2005, A&A, 433, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Afonso, C., Alard, C., Albert, J. N., et al. 2000, ApJ, 532, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Albrow, M. D., Beaulieu, J.-P., Caldwell, J. A. R., et al. 1999, ApJ, 522, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Albrow, M. D., Beaulieu, J.-P., Caldwell, J. A. R., et al. 2000, ApJ, 534, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Albrow, M. D., An, J., Beaulieu, J.-P., et al. 2001, ApJ, 549, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Albrow, M. D., Horne, K., Bramich, D. M., et al. 2009, MNRAS, 397, 2099 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allen, W. H., Allsman, R. A., et al. 1997, ApJ, 491, 436 [NASA ADS] [CrossRef] [Google Scholar]
- An, J. H., Albrow, M. D., Beaulieu, J.-P., et al. 2002, ApJ, 572, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Batista, V., Dong, S., Gould, A., et al. 2009, A&A, 508, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beaulieu, J.-P., Bennett, D. P., Fouqué, P., et al. 2006, Nature, 439, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bennett, D. P., Bond, I. A., Udalski, A., et al. 2008, ApJ, 684, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., Bica, E., & Girardi, L. 2004, A&A, 415, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, I. A., Udalski, A., Jaroszynski, M., et al. 2004, ApJ, 606, L155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bramich, D. M. 2008, MNRAS, 386, L77 [Google Scholar]
- Burns, D., Baldwin, J. E., Boysen, R. C., et al. 1997, MNRAS, 290, L11 [NASA ADS] [Google Scholar]
- Cassan, A., Beaulieu, J. P., Brillant, S., et al. 2004, A&A, 419, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassan, A., Beaulieu, J.-P., Fouqué, P., et al. 2006, A&A, 460, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chung, S.-J., Han, C., Park, B.-G., et al. 2005, ApJ, 630, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Dominik, M. 1998, A&A, 329, 361 [NASA ADS] [Google Scholar]
- Dominik, M. 2006, MNRAS, 367, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., Bond, I. A., Gould, A., et al. 2009, ApJ, 698, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Dutra, C. M., Santiago, B. X., Bica, E. L. D., & Barbuy, B. 2003, MNRAS, 338, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, D. L., Albrow, M. D., An, J., et al. 2003, ApJ, 596, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudi, B. S., Bennett, D. P., Udalski, A., et al. 2008, Science, 319, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gould, A., Udalski, A., An, D., et al. 2006, ApJ, 644, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Dong, S., Bennett, D. P., et al. 2010, ApJ, 710, 1800 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2004, MNRAS, 353, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Kim, D. 2009, ApJ, 693, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Heyrovský, D. 2003, ApJ, 594, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Heyrovský, D. 2007, ApJ, 656, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Heyrovský, D. 2008, in Proceedings of the Manchester Microlensing Conference, ed. E. Kerins, S. Mao, N. Rattenbury, & ▯. Wyrzykowski, Manchester, Univ. of Manchester, Proceedings of Science (GMC8) 028 [Google Scholar]
- Heyrovský, D., & Sasselov, D. 2000, ApJ, 529, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Heyrovský, D., Sasselov, D., & Loeb, A. 2000, ApJ, 543, 406 [Google Scholar]
- Houdashelt, M. L., Bell, R. A., & Sweigart, A. V. 2000, AJ, 119, 1448 [Google Scholar]
- Janczak, J., Fukui, A., Dong, S., et al. 2010, ApJ, 711, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 617, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., & Fouqué, P. 2008, A&A, 491, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubas, D., Cassan, A., Beaulieu, J., et al. 2005, A&A, 435, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993a, Limbdarkening for 2 km s-1 grid (No. 13): [+1.0] to [-1.0], Kurucz CD-ROM No. 16, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 16 [Google Scholar]
- Kurucz, R. 1993b, Limbdarkening for 2 km s-1 grid (No. 13): [+0.0] to [-5.0], Kurucz CD-ROM No. 17, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 17 [Google Scholar]
- Kurucz, R. 1994, Solar abundance model atmospheres for 0, 1, 2, 4, 8 km s-1. Kurucz CD-ROM No. 19, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 19 [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1996, ARA&A, 34, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B., & Stanek, K. Z. 1998, ApJ, 494, L219 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, G., Ridgway, S. T., Coudé du Foresto, V., et al. 2004, A&A, 418, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popper, D. M. 1984, AJ, 89, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Sumi, T., & Smith, M. C. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Richichi, A., & Lisi, F. 1990, A&A, 230, 355 [NASA ADS] [Google Scholar]
- Schultheis, M., Ganesh, S., Simon, G., et al. 1999, A&A, 349, L69 [NASA ADS] [Google Scholar]
- Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., & Garnavich, P. M. 1998, ApJ, 503, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Bennett, D. P., Bond, I. A., et al. 2010, ApJ, 710, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Tokunaga, A. T., Simons, D. A., & Vacca, W. D. 2002, PASP, 114, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Udalski, A., Jaroszynski, M., Paczynski, B., et al. 2005, ApJ, 628, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J. 1995, ApJ, 449, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., Driebe, T., et al. 2006, A&A, 460, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wozniak, P. R. 2000, Acta Astron., 50, 421 [NASA ADS] [Google Scholar]
- Yee, J. C., Udalski, A., Sumi, T., et al. 2009, ApJ, 703, 2082 [NASA ADS] [CrossRef] [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
- Zub, M., Cassan, A., Heyrovský, D., et al. 2009, A&A, submitted [arXiv:0912.2312] [Google Scholar]
Footnotes
All Tables
Table 1: Coordinates and magnitudes of the two stars close to the target position and the 2MASS blend.
Table 2: Main parameters of the best-fitting point-lens limb-darkened source model, using the linear limb-darkening law.
Table 3: Photometric temperatures and I-band limb-darkening coefficients of K Bulge giants for OGLE 2008-BLG-290 and other published microlensing events with source stars of similar spectral type.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig1.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg25.png)
|
Figure 1:
Upper panel: photometry of microlensing event
OGLE 2008-BLG-290 in terms of source-flux amplification, as
observed by OGLE (olive), MOA (blue), two PLANET sites (Canopus: grey;
Perth: wine), three |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig2.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg26.png)
|
Figure 2: Zoom of the event peak (June 15, 2008) from Fig. 1. Amplification is plotted in the upper panel; relative residuals in the lower panel. Colours and lines have the same meaning as in Fig. 1, with the added SDSS r-band light curve (solid red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig3.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg44.png)
|
Figure 3:
Colour-magnitude diagram in J and H
from IRSF/Sirius stars in a |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14053fig4.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg66.png)
|
Figure 4:
Colour-magnitude diagram in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig5n.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg100.png)
|
Figure 5:
Linear limb-darkening coefficients in the I-band
for 4 different telescopes when fitting the limb darkening
independently for each data set. We determine the I-band
measurement as the weighted mean of these values, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm]{14053fig6n.eps} \end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg105.png)
|
Figure 6:
Linear limb-darkening coefficients of the K-giant source star
in CTIO/SMARTS2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig7an.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14053fig7bn.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg106.png)
|
Figure 7:
Comparison of the measured |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig8an.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{14053fig8bn.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg107.png)
|
Figure 8:
Agreement between the measured |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14053fig9.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14053-10/Timg132.png)
|
Figure 9:
Probability densities for the lens mass |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.