EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A22 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A22
Number of page(s) 9
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913722
Published online 25 August 2010
A&A 518, A22 (2010)

Open and closed boundaries in large-scale convective dynamos

P. J. Käpylä1,2 - M. J. Korpi1,2 - A. Brandenburg2,3

1 - Department of Physics, Gustaf Hällströmin katu 2a, PO Box 64, 00014 University of Helsinki, Finland
2 - NORDITA, Roslagstullsbacken 23, 10691 Stockholm, Sweden
3 - Department of Astronomy, Stockholm University, 10691 Stockholm, Sweden

Received 23 November 2009 / Accepted 26 May 2010

Abstract
Context. Earlier work has suggested that large-scale dynamos can reach and maintain equipartition field strengths on a dynamical time scale only if magnetic helicity of the fluctuating field can be shed from the domain through open boundaries.
Aims. Our aim is to test this scenario in convection-driven dynamos by comparing results for open and closed boundary conditions.
Methods. Three-dimensional numerical simulations of turbulent compressible convection with shear and rotation are used to study the effects of boundary conditions on the excitation and saturation of large-scale dynamos. Open (vertical-field) and closed (perfect- conductor) boundary conditions are used for the magnetic field. The shear flow is such that the contours of shear are vertical, crossing the outer surface, and are thus ideally suited for driving a shear-induced magnetic helicity flux.
Results. We find that for given shear and rotation rate, the growth rate of the magnetic field is larger if open boundary conditions are used. The growth rate first increases for small magnetic Reynolds number, ${\rm Rm}$, but then levels off at an approximately constant value for intermediate values of ${\rm Rm}$. For large enough ${\rm Rm}$, a small-scale dynamo is excited and the growth rate of the field in this regime increases as ${\rm Rm}^{1/2}$. Regarding the nonlinear regime, the saturation level of the energy of the total magnetic field is independent of ${\rm Rm}$ when open boundaries are used. In the case of perfect-conductor boundaries, the saturation level first increases as a function of ${\rm Rm}$, but then decreases proportional to ${\rm Rm}^{-1}$ for ${\rm Rm}\ga 30$, indicative of catastrophic quenching. These results suggest that the shear-induced magnetic helicity flux is efficient in alleviating catastrophic quenching when open boundaries are used. The horizontally averaged mean field is still weakly decreasing as a function of ${\rm Rm}$ even for open boundaries.

Key words: magnetohydrodynamics - convection - turbulence - magnetic fields - stars: magnetic field - magnetic fields

1 Introduction

The classical view of the effect of shear in large-scale dynamos is that it promotes the generation of magnetic fields, and that it is instrumental in exciting oscillatory solutions (e.g. Parker 1955; Steenbeck & Krause 1969). While these aspects remain unchanged, a much more subtle effect of shear has been discovered in studies of the saturation mechanism of the large-scale dynamo. If the saturation of the dynamo occurs due to magnetic helicity conservation, a fully periodic or closed system experiences catastrophic quenching with the energy of the large-scale magnetic field decreasing in inverse proportion to the magnetic Reynolds number (Vainshtein & Cattaneo 1992; Cattaneo & Hughes 1996; Brandenburg 2001). A way to avoid catastrophic quenching is to allow magnetic helicity fluxes to escape from the system through open boundaries, thus allowing the large-scale fields to saturate at equipartition strength in a dynamical time scale (Blackman & Field 2000; Kleeorin et al. 2000). One of the most promising mechanisms, introduced by Vishniac & Cho (2001), operates by driving a flux of magnetic helicity along the isocontours of shear. Forced turbulence simulations with shear have confirmed that the quenching of the $\alpha$-effect is up to 30 times weaker when closed boundaries are replaced by open ones (Brandenburg & Sandin 2004).

Recent numerical experiments with forced turbulence (Brandenburg 2005; Yousef et al. 2008a,b; Brandenburg et al. 2008) and convection (Käpylä et al. 2008, hereafter Paper I; Hughes & Proctor 2009; see also Käpylä et al. 2010) with imposed large-scale shear flows have established the existence of a robust large-scale dynamo. The origin of this dynamo is still under debate (shear-current versus incoherent $\alpha$-shear effects). This is discussed in detail elsewhere (e.g. Brandenburg et al. 2008; Käpylä et al. 2009b). In forced turbulence simulations with fully periodic boundaries, that do not allow magnetic helicity fluxes, large-scale magnetic fields show slow saturation on a diffusive timescale (Brandenburg 2001). Earlier results from convection also suggest that no appreciable large-scale magnetic fields are seen if magnetic helicity fluxes are suppressed (Paper I).

In most of the simulations of Paper I the isocontours of shear were vertical and thus intersecting the boundaries. However, the boundary conditions (bc) imposed on the magnetic field on the vertical borders would either allow (open vertical-field bc) or inhibit (closed perfect-conductor bc) a net flux out of the domain. It was shown that when the flux is suppressed, only weak large-scale magnetic fields occur in the saturated state at large ${\rm Rm}$. Conversely, allowing a flux produced a significant large-scale field. Furthermore, using a similar setup as in Tobias et al. (2008), where the isocontours of shear are horizontal, a similar effect was found. Thus it would appear that the shear-induced flux plays a critical role in exciting a large-scale dynamo in turbulent convection. This has given rise to the impression that the dynamos seen in Paper I are solely due to the magnetic helicity flux and thus inherently nonlinear (Hughes & Proctor 2009). In the present paper we argue that this interpretation is incorrect and that the lack of appreciable large-scale magnetic fields in some of our earlier cases with vanishing helicity flux is due to the fact that the critical dynamo number for the excitation of the dynamo is larger in that case. We also note that, more recently, large-scale dynamos have been found in turbulent convection without shear (Käpylä et al. 2009a), irrespective of the presence of magnetic helicity fluxes.

The origin of the dynamos reported in Paper I was interpreted in the context of turbulent dynamo theory in Käpylä et al. (2009b). An important feature of turbulent dynamos is that according to standard mean-field theory neither the turbulent transport coefficients nor the growth rate of the field should depend on the microscopic resistivity. The former prediction was confirmed by Käpylä et al. (2009b), but the latter has not yet been studied in detail in direct simulations. This is one of the goals of the present paper.

Another aim is to study the saturation behaviour of the large-scale dynamo with both open and closed boundary conditions. Firstly, in homogeneous systems, i.e. where the turbulent transport coefficients do not vary in space, full saturation is expected to occur on a slow diffusive time scale with closed boundaries whereas with open boundaries the saturation is expected to happen on a dynamical time scale if a helicity flux is present (Brandenburg 2001). However, in inhomogeneous systems the situation is likely to be more complex (e.g. Mitra et al. 2010). Furthermore, simulations of helically forced isotropic turbulence have shown that, in the absence of shear, the saturation level of the magnetic field scales as $\overline{\bm B}^2/B_{\rm eq}^2\propto{\rm Rm}^{-1}$ for open boundaries (Fig. 2 of Brandenburg & Subramanian 2005a). When shear is present, the shear-induced magnetic helicity flux should alleviate the ${\rm Rm}$-dependence of the saturation level. Preliminary results in Paper I indicate that this might indeed be true, but the results are not fully conclusive because other parameters, such as the Rayleigh number and the fluid Reynolds number changed when ${\rm Rm}$ was varied. In the present paper we perform a more detailed study where only ${\rm Rm}$ is varied.

2 Model and methods

2.1 Setup and boundary conditions

We use the same setup as in Paper I in which a small rectangular portion of a star is modelled by a box situated at colatitude $\theta$. The coordinate system is such that (x,y,z) correspond to $(\theta,\phi,r)$ in a spherical coordinate system. The dimensions of the domain are (Lx, Ly, Lz) = (4,4,2)d, where d is the depth of the convectively unstable layer, which is also used as our unit length. The box is divided into three layers, an upper cooling layer, a convectively unstable layer, and a lower stable overshoot layer. Gravity points in the negative z direction, g=(0,0,-g), rotation is in the positive z direction, $\bm{\Omega}=(0,0,\Omega)$, i.e. $\theta=0$ corresponding to the north pole, and shear is in the y direction, with $\overline{\bm U}=(0,Sx,0)$, where S is the shear rate.

The values (z1, z2, z3, z4) = (-0.85, 0, 1, 1.15)d give the vertical positions of the bottom of the box, the bottom and top of the convectively unstable layer, and the top of the box, respectively. We use a heat conductivity profile such that the associated hydrostatic reference solution is piecewise polytropic with indices (m1, m2, m3)=(3, 1, 1). We apply a cooling term in the thin uppermost layer which makes this region nearly isothermal and hence stably stratified. The bottom layer is also stably stratified, and the middle layer is convectively unstable.

At the vertical boundaries we use stress-free boundary conditions for the velocity,

Ux,z = Uy,z = Uz = 0. (1)

For the magnetic field either vertical-field or perfect-conductor boundary conditions are used. Occasionally we refer to them also as open and closed, respectively. Thus, we have
Bx = By = $\displaystyle 0 \quad\mbox{(vertical-field, VF, or open)},$ (2)
         Bx,z = By,z = Bz = $\displaystyle 0 \quad\mbox{(perfect-conductor, PC, closed)},$ (3)

the former allowing magnetic helicity flux while the latter one does not. This also motivates the usage of the names ``open'' and ``closed'' for the two boundary conditions. The y-direction is periodic and shearing-periodic conditions are used in the x-direction (e.g. Wisdom & Tremaine 1988). A constant temperature gradient is maintained at the base which leads to a steady influx of heat due to the constant heat conductivity.

The simulations were performed with the P ENCIL C ODE[*], which uses sixth-order explicit finite differences in space and third-order accurate time stepping method. Resolutions of up to 5123 mesh points were used.

Table 1:   Summary of the runs with varying ${\rm Pm}$.

2.2 Units, nondimensional quantities, and parameters

Dimensionless quantities are obtained by setting

$\displaystyle d = g = \rho_0 = c_{\rm P} = \mu_0 = 1 ,$     (4)

where g is the constant acceleration due to gravity, $\rho_0$ is the density at z2, $c_{\rm P}$ is the heat capacity at constant pressure, and $\mu_0$ is the vacuum permeability. The units of length, time, velocity, density, specific entropy, and magnetic field are then
                           [x] = $\displaystyle d,\;\; [t] = \sqrt{d/g},\;\; [U]=\sqrt{dg},\;\; [\rho]=\rho_0 ,$  
$\displaystyle \left[s\right]$ = $\displaystyle c_{\rm P},\;\; [B]=\sqrt{dg\rho_0\mu_0} .$ (5)

The system is controlled by the Prandtl, Reynolds, and Rayleigh numbers,
                          $\displaystyle {\rm Pr}$ = $\displaystyle \frac{\nu}{\chi_0},\;\; {\rm Pm}=\frac{\nu}{\eta},$ (6)
$\displaystyle {\rm Re}$ = $\displaystyle \frac{u_{\rm rms}}{\nu k_{\rm f}},\;\; {\rm Rm}=\frac{u_{\rm rms}}{\eta k_{\rm f}}\equiv{\rm Pm}~{\rm Re}, \;\;$ (7)
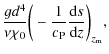
$\displaystyle {\rm Ra}$ = $\displaystyle \frac{gd^4}{\nu \chi_0} \bigg(-\frac{1}{c_{\rm P}} \frac{{\rm d}s}{{\rm d}z} \bigg)_{z_{\rm m}} ,$ (8)

where $\nu$ is the kinematic viscosity, $\chi_0 = K/(\rho_{\rm m} c_{\rm P})$ is the thermal diffusivity with $\rho_{\rm m}$ the density at the middle of the convectively unstable layer at $z_{\rm m}={\textstyle{1\over2}}(z_3-z_2)$, $\eta $ is the magnetic diffusivity, $u_{\rm rms}$ the root mean square velocity, and $k_{\rm f}=2\pi/d$ is an estimate of the wavenumber of the energy-carrying eddies. The entropy gradient, measured at $z_{\rm m}$ in the non-convecting initial state, is given by
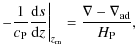
$\displaystyle -\frac{1}{c_{\rm P}}\frac{{\rm d}s}{{\rm d}z}\bigg\vert _{z_{\rm m}} = \frac{\nabla-\nabla_{\rm ad}}{H_{\rm P}} ,$   (9)

with $\nabla_{\rm ad} = 1-1/\gamma$ and $\nabla = (\partial\ln T/\partial\ln p)_{z_{\rm m}}$, where $\gamma=c_{\rm P}/c_{\rm V}=5/3$ is the ratio of the heat capacities at constant pressure and volume, respectively, and $H_{\rm P}$ is the pressure scale height, also at $z=z_{\rm m}$. The differentials of logarithmic temperature and entropy are related via ${\rm d}s/c_{\rm P}={\rm d}\ln T-\nabla_{\rm ad}{\rm d}\ln p$, and  ${\rm d}\ln p={\rm d}\ln T+{\rm d}\ln\rho$.

The degree of stratification is controlled by the parameter

$\displaystyle \xi_0 = \frac{(\gamma-1) e_0}{gd} ,$   (10)

where e0 is the internal energy at z=z4. The internal energy is related to the temperature via $e=c_{\rm V}T$. We use $\xi_0=1/3$ in all models, which yields a density contrast of about 27 over the whole domain.

The strengths of rotation and shear are quantified by the Coriolis and shear numbers

$\displaystyle {\rm Co}= \frac{2\Omega}{u_{\rm rms}k_{\rm f}},\;\; {\rm Sh}= \frac{S}{u_{\rm rms}k_{\rm f}},$   (11)

where $(u_{\rm rms}k_{\rm f})^{-1}$ gives an estimate of the convective turnover time.

2.3 Characterization of the simulation data

Our runs can be characterized using the following quantities. We express the rms velocity in the unit of (gd)1/2, which is related to the Mach number, and thus define

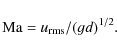
\begin{displaymath}\mbox{Ma}=u_{\rm rms}/(gd)^{1/2}. \end{displaymath} (12)

The normalized growth rate of magnetic field is expressed as

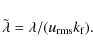
\begin{displaymath}\tilde\lambda=\lambda/(u_{\rm rms}k_{\rm f}). \end{displaymath} (13)

The typical wavenumber of the energy-carrying eddies and the relative kinetic helicity are given by

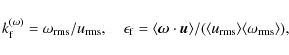
\begin{displaymath}k_{\rm f}^{(\omega)}=\omega_{\rm rms}/u_{\rm rms}, \quad \eps... ...langle u_{\rm rms} \rangle \langle \omega_{\rm rms} \rangle), \end{displaymath} (14)

where $\bm\omega=\vec{\nabla} \times \bm{u}$ is the vorticity and the angular brackets denote volume averaging. The normalized rms magnetic field strength is given by

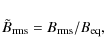
\begin{displaymath}\tilde B_{\rm rms}=B_{\rm rms}/B_{\rm eq}, \end{displaymath} (15)

where $B_{\rm eq}=\sqrt{\mu_0 \langle \rho \bm{U}^2 \rangle}$ is the equipartition value of the field. Corresponding values for the horizontally averaged (denoted by an overbar) horizontal components of the field are given by

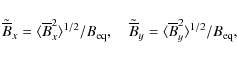
\begin{displaymath}\tilde{\overline{B}}_x=\langle \overline{B}_x^2\rangle^{1/2}/... ...erline{B}}_y=\langle \overline{B}_y^2\rangle^{1/2}/B_{\rm eq}, \end{displaymath} (16)

and $\tilde{\overline{B}}=(\tilde{\overline{B}}_x^2+\tilde{\overline{B}}_y^2)^{1/2}$, is referred to as the total mean field.

Error bars are estimated by dividing the time series into three equally long parts and computing a mean value individually for each of these. The largest deviation from the average over the full time series is taken to represent the error.

Table 2:   Summary of the runs with varying ${\rm Co}$ and ${\rm Sh}$.

3 Results

In order to study the effects of different boundary conditions and magnetic helicity fluxes on the excitation and saturation of convective dynamos, we perform a number of simulations with perfect-conductor and vertical-field boundary conditions. We follow two lines in parameter space where we either vary ${\rm Pm}$ and ${\rm Rm}$, keeping all other parameters fixed, or we fix both Reynolds numbers and vary ${\rm Co}$ and ${\rm Sh}$. The runs are listed in Tables 1 and 2.

3.1 Dynamo excitation

We begin by investigating the linear regime where the magnetic field is still weak. In that case the values of $u_{\rm rms}$ are not yet quenched by the field, and so the resulting values of ${\rm Rm}$ are somewhat larger than in the saturated case. Turbulent dynamo theory predicts that large-scale dynamo action is possible if the magnetic Reynolds number and a relevant dynamo number exceed critical values that depend on the details of the system in question (e.g. Moffatt 1978; Krause & Rädler 1980; Rüdiger & Hollerbach 2004). Furthermore, boundary conditions also influence the excitation of large-scale dynamos (e.g. Choudhuri 1984; Jouve et al. 2008). In order to study these effects, we determine the critical ${\rm Rm}$ and the critical dynamo number, here implicitly described by the strengths of rotation and shear, needed to excite the dynamo with both open and closed boundary conditions.

3.1.1 Dependence on Rm

From the perspective of mean-field dynamo theory a, large-scale dynamo should operate if ${\rm Rm}\ga1$. We start the simulations with a random small-scale magnetic field of the order of $10^{-4}B_{\rm eq}$ and monitor the time evolution of the total magnetic field quantified by $B_{\rm rms}$. We indeed find that in runs with vertical-field boundary conditions the dynamo is excited for ${\rm Rm}\ga1$, whereas in the case of perfectly conducting boundaries, the critical value is about five times higher (see Table 1 and Fig. 1).

As a consistency check we use a one-dimensional mean-field model written in terms of the vector potential

$\displaystyle \dot{\overline{A}}_i=-\overline{U}_{j,i}\overline{A}_j+\alpha_{ij}\overline{B}_j -(\eta_{ij}+\eta\delta_{ij})\mu_0\overline{J}_j$     (17)

where $\dot{\overline{A}}_i$ denotes a time derivative and $\overline{U}_{j,i}\overline{A}_j=(S\overline{A}_y,0,0)$ is the shear term. The mean magnetic field is given by $\overline{\bm{B}}=(-\overline{A}_y',\overline{A}_x',0)$, the mean current density is given by $\mu_0\overline{J}_i=-\overline{A}_i''$, and primes denote z-derivatives. The coefficients $\alpha_{ij}$ and $\eta_{ij}$, describing the turbulent transport coefficients relevant for z-dependent large-scale fields, are taken from a test field calculation (Run D4 of Käpylä et al. 2009b; see their Fig. 13) which is the same as our run VF7, but with ${\rm Pm}=5$ instead of 2.5 used here. We then use either VF or PC boundary conditions, defined by Eq. (3), and determine the marginal value of $\eta $ that allows dynamo action. This is quantified by a Reynolds number ${\rm Rm}_{\rm c}=u_{\rm rms}/(\eta_{\rm c} k_{\rm f})$, where $u_{\rm rms}$ is taken from the same run as the turbulent transport coefficients and $\eta_{\rm c}$ is the marginal value of the microscopic magnetic diffusivity.

We find a marginal value ${\rm Rm}_{\rm c}\approx 1.0$ for the vertical-field boundary conditions, whereas in the case of perfect-conductor boundaries ${\rm Rm}_{\rm c}\approx4.1$ is obtained. These values are very close to those obtained from direct simulations, although one must bear in mind that the ${\rm Rm}$-dependence of $\alpha_{ij}$ and $\eta_{ij}$ at small values of ${\rm Rm}$ (Käpylä et al. 2009b) is not taken into account in our mean-field modelling. However, the qualitative result that the dynamo is harder to excite when perfect-conductor boundaries are used is consistent with the direct simulations.

We measure the growth rate, $\lambda $, of the rms magnetic field as

\begin{displaymath}\lambda = \left\langle{\rm d} \ln B_{\rm rms}/{\rm d}t\right\rangle_{\rm t}, \end{displaymath} (18)

where $\langle \ldots \rangle_{\rm t}$ denotes a time average over the kinematic range where $B_{\rm rms}$ grows exponentially. We find that, for Reynolds numbers close to the marginal value, $\lambda $increases roughly proportional to ${\rm Rm}$ (see Fig. 1) in accordance with theoretical considerations. However, soon this increase ceases and $\lambda $levels off to a roughly constant value for intermediate values of ${\rm Rm}$. For ${\rm Rm}\ga60$ the growth rate is consistent with $\lambda\propto{\rm Rm}^{1/2}$. This behaviour can be understood as follows: for small ${\rm Rm}$ the large-scale dynamo is excited, but the growth rate is still affected by the relatively large value of the microscopic magnetic diffusivity $\eta $. In the present system the small-scale dynamo is excited when ${\rm Rm}\ga 30$, but this contribution begins to dominate over the growth rate of the large-scale field only for ${\rm Rm}\ga60$ where our data for $\lambda $ is consistent with an ${\rm Rm}^{1/2}$ scaling. This is in accordance with findings of Schekochihin et al. (2004) and Haugen et al. (#HBD04<#766) for forced isotropic turbulence.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg1.eps} \end{figure} Figure 1:

Growth rate $\lambda $ of the magnetic field as a function of ${\rm Rm}$ from the runs listed in Table 1. Solid (dashed) line with closed (open) symbols shows the results for the VF (PC) boundary conditions. Dotted lines proportional to ${\rm Rm}$ and ${\rm Rm}^{1/2}$ are shown for reference.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg2.eps} \end{figure} Figure 2:

Growth rate $\lambda $ of the magnetic field as a function of ${\rm Co}$ with open (VF, solid line) and closed (PC, dashed line) boundary conditions for the runs listed in Table 2.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg3.eps} \end{figure} Figure 3:

Dynamo numbers according to Eq. (23) as functions of rotation for the runs listed in Table 2. The solid (dashed) curve shows the results for vertical-field (perfect-conductor) boundary conditions. The horizontal dash-dotted and dash-triple-dotted lines indicate the critical dynamo number in the case of open and closed boundaries, respectively. Power law proportional to ${\rm Co}^2$ is shown for reference.

Open with DEXTER

3.1.2 Dependence on shear and rotation

In addition to the dependence on the magnetic Reynolds number, we study the influence of shear on the excitation of the dynamo. We use a setup where ${\rm Rm}\approx35$ in the case ${\rm Co}={\rm Sh}=0$, in which case the small-scale dynamo is marginal. We then introduce shear and rotation into the system and keep the quantity $q=-S/\Omega=1$ fixed in all cases. Our results for the growth rate of the magnetic field in the range ${\rm Co}\approx0.07\ldots1.5$ are shown in Fig. 2. We find that for a given ${\rm Co}$ the growth rate is always greater in the simulations with open boundaries (see also Table 2). The case ${\rm Co}\approx0.07$ (Run VF11) is very close to marginal in the case of open boundaries, but clearly subcritical when perfectly conducting boundaries are used (Run PC9). The critical value of ${\rm Co}$ in the perfect-conductor case seems to be roughly twice as large as the corresponding value in the vertical-field runs. To be more precise, we estimate the relevant dynamo numbers as

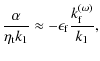
                 $\displaystyle C_\alpha$ $\textstyle \equiv$ $\displaystyle \frac{\alpha}{\eta_{\rm t}k_1}\approx -\epsilon_{\rm f}\frac{k_{\rm f}^{(\omega)}}{k_1},$ (19)
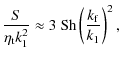
$\displaystyle C_{\rm S}$ $\textstyle \equiv$ $\displaystyle \frac{S}{\eta_{\rm t}k_1^2}\approx 3~{\rm Sh}\left(\frac{k_{\rm f}}{k_1}\right)^2,$ (20)

where $k_1=\pi/L_z$ is the wavenumber of the leading decay mode for both boundary conditions. Here we approximate the $\alpha$ effect and turbulent diffusivity by
$\displaystyle \alpha \approx -{\textstyle{1\over3}}\tau_{\rm c} \langle \bm\ome... ...gle,\quad \eta_{\rm t} \approx {\textstyle{1\over3}}\tau_{\rm c} u_{\rm rms}^2.$   (21)

Furthermore, we assume the Strouhal number,
$\displaystyle {\rm St}=\tau_{\rm c}u_{\rm rms}k_{\rm f},$   (22)

of unity (as found by Brandenburg & Subramanian 2005b) so that $\tau_{\rm c}=(u_{\rm rms}k_{\rm f})^{-1}$. The fractional helicity is defined via $\epsilon_{\rm f}=\langle \bm\omega\cdot\bm{u} \rangle/(u_{\rm rms}\omega_{\rm rms})$, where $\omega_{\rm rms}=k_{\rm f}^{(\omega)} u_{\rm rms}$. We can now define the dynamo number as

\begin{displaymath}D\equiv C_\alpha C_{\rm S}. \end{displaymath} (23)

For the marginal open-field Run VF11 we find a critical dynamo number $D_{\rm crit}^{\rm (VF)} \approx0.1$. The dynamo numbers for the perfect-conductor Runs PC9 and PC10 are 0.7 and 3.5, respectively. Linear interpolation of the magnetic field growth rates give a critical value of $D_{\rm crit}^{\rm (PC)}\approx0.3$ which is roughly three times greater than in the vertical-field case (see Fig. 3). We find that the dynamo number is approximately proportional to ${\rm Co}^2$ in the range of parameters studied here. This dependence can be understood qualitatively as follows: the $\alpha$ effect, and hence $C_\alpha$, increases approximately proportional to ${\rm Co}$ in the range of parameters studied here (see Käpylä et al. 2009b). Furthermore, as we keep the ratio $S/\Omega$ constant, shear and $C_{\rm S}$ also increase proportionally to ${\rm Co}$.

In the preceding simplified analysis we have estimated $\alpha$ and $\eta_{\rm t}$ using volume averages that are not ideally suited for the present case (see, e.g. Käpylä et al. 2009b). Furthermore, we have assumed here that the dynamo is of pure $\alpha$-shear type and have neglected all other possible induction effects (shear-current, $\bm\Omega\times\overline{\bm J}$, and incoherent $\alpha$-shear effects) that can assist in dynamo action (Käpylä et al. 2009b). This means that the quantitative results should be taken with some amount of caution.

In Paper I, the only case where open and closed boundaries were compared was the one where only shear was present, i.e. ${\rm Sh}\neq0$, whereas ${\rm Co}=0$ (Run C with vertical-field boundary conditions versus Run C' with perfect-conductor boundary conditions). In Paper I we also showed that, in the absence of rotation, the growth rate of the magnetic field is reduced in comparison to the case where both shear and rotation are present. Furthermore, our present results suggest that the large-scale dynamo is harder to excite in the case of perfect-conductor boundaries. Thus, a reasonable explanation to the slow growth of the large-scale field in Run C' of Paper I is that the system is close to being marginally excited, and not, as suggested by Hughes & Proctor (2009), the result of some nonlinear effect arising from magnetic helicity flux out of the system. A straightforward quantitative analysis in terms of a classical $\alpha$-shear dynamo described above is, however, not useful in the non-rotating case. This is shown by the results of Käpylä et al. (2009b): the main contribution to dynamo action in this case is due to the incoherent $\alpha$-shear process which relies on the fluctuations of $\alpha$ (e.g. Vishniac & Brandenburg 1997; Sokolov 1997; Silant'ev 2000; Proctor 2007).

\begin{figure} \par\includegraphics[width=17cm,clip]{13722fg4.eps} \end{figure} Figure 4:

Magnetic field component By from runs with vertical-field ( left column) and perfect-conductor ( right column) boundary conditions. Three different cases with low ( top), intermediate ( middle) and high ( bottom) ${\rm Rm}$ are shown. The sides of the boxes show the By field at the periphery of the domain whereas the top and bottom panels show the field at z=z3 and z=z2, respectively.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16cm,clip]{13722fg5.eps} \vspace{-2mm}\end{figure} Figure 5:

Horizontally averaged magnetic field components Bx and By from the same six runs as in Fig. 4. Those runs and the corresponding values of ${\rm Rm}$ are also highlighted in Table 1 in bold face. The dotted white lines at z=0 and z=d denote the bottom and top of the convectively unstable layer, respectively. The runs on the left are for open boundaries and those on the right are for closed ones. The magnetic Reynolds number increases downwards.

Open with DEXTER

3.2 Nonlinear regime

We find that in all cases where a dynamo is excited, large-scale magnetic fields are also generated. In the low-${\rm Rm}$ runs the large-scale contribution is substantial, i.e. $\overline{\bm B}/B_{\rm rms}$ is close to unity already in the kinematic regime. In the cases where also the fluctuation dynamo is excited, a large-scale pattern is discernible only once the dynamo has reached saturation. This feature is common to all known large-scale dynamos and was already seen in simulations of Brandenburg (2001). Figure 4 shows visualizations of the streamwise component of the field in the saturated state for three Reynolds numbers, representing low, intermediate, and high ${\rm Rm}$, with open and closed boundaries (see Table 1). The runs depicted in Fig. 4 are indicated in boldface in the table. Although an increasing amount of small-scale features is seen with increasing ${\rm Rm}$, a large-scale pattern is clearly visible in all cases.

Unlike the case with just rotation and no shear, where the mean field shows variations in the horizontal directions (Käpylä et al. 2009a), here the kx=ky=0 mode dominates the large-scale field and thus horizontal averages are suitable. Space-time diagrams of the horizontally averaged magnetic field components, $\overline{B}_x$ and $\overline{B}_y$, are shown in Fig. 5 for the same runs as in Fig. 4. We find that the large-scale field is non-oscillatory in all cases, which is in agreement with earlier results (Paper I; Hughes & Proctor 2009; Käpylä et al. 2010). In most cases, regardless of the boundary conditions, the field changes sign near the base of the convectively unstable layer, with the exception of the runs with vertical-field boundary conditions (VF runs) with the lowest values of ${\rm Rm}$. (The solutions are invariant under sign reversal, $\bm{B}\to-\bm{B}$, and both realizations of the large-scale field are found in Figs. 4 and 5, depending just on the initial conditions.) In the perfect-conductor runs (PC runs), the field near the top of the domain has a different sign than in the bulk of the convection zone, whereas in the VF runs such behaviour is not seen. We find that in the PC runs the layer of oppositely directed field becomes progressively thinner as ${\rm Rm}$ is increased, leading to strong gradients near the boundary (see Fig. 5). This can possibly explain the numerical problems encountered in the ${\rm Rm}\approx239$ simulation (Run PC9) with perfect-conductor boundary conditions. The saturated state of Run PC9 is significantly shorter than that of the other runs due to numerical instability that prevented running the simulation further.

It turns out that the emergence of the large-scale field occurs progressively earlier as ${\rm Rm}$ is increased. This can be seen most clearly in Fig. 5, which shows that the large-scale field has reached saturation in less than 200 turnover times for ${\rm Rm}=222$ (Run VF10), while for Runs VF7 and VF4 with ${\rm Rm}=34$ and 3.7, the saturation times exceed 300 and 400 turnover times, respectively. A similar trend is seen also in the PC runs. In an earlier study we found that the mean values of the turbulent transport coefficients relevant for the generation of large-scale magnetic fields, $\alpha_{yy}$ and $\eta_{\rm t}$, remain constant within the errors given that ${\rm Rm}\ga8$; see Fig. 5 of Käpylä et al. (2009b). However, as the magnetic Reynolds number is increased, the fluctuations of $\alpha$ tend to increase as well. Such fluctuations can contribute to the incoherent $\alpha$-shear process which can possibly explain the faster saturation of the large-scale field when ${\rm Rm}$ is increased.

The saturation level of the total and mean magnetic fields for runs with open and closed boundary conditions are shown in Fig. 6. We find that the total magnetic field in the runs with open boundary conditions is roughly consistent with an ${\rm Rm}$-independent value. In the perfect-conductor case the total magnetic energy first increases up to ${\rm Rm}\approx30$ and then decreases proportionally to ${\rm Rm}^{-1}$ for ${\rm Rm}\ga60$. Mean-field models taking into account magnetic helicity evolution can also produce a maximum for the saturation level at some intermediate ${\rm Rm}$ (e.g. Brandenburg et al. 2007). We note that an ${\rm Rm}^{-1}$ dependence for the mean field energy is indicative of catastrophic quenching. This would indeed be the expected result for closed boundaries. However, in our case only the total field energy shows the ${\rm Rm}^{-1}$ behaviour whereas the mean field exhibits a much steeper (at least ${\rm Rm}^{-1.6}$) dependence. The explanation for such a steep trend is as yet unclear. The data for the mean magnetic field in the case of open boundaries also show a weak decreasing trend consistent with a power law ${\rm Rm}^{-0.25}$ as opposed to the expectation that the saturation level is independent of ${\rm Rm}$. However, the unexpected behaviour of the saturation level could simply be related to the fact that in mean-field models true asymptotic behaviour may only commence at much larger values of ${\rm Rm}$(Brandenburg et al. 2009).

Our simulations with the highest magnetic Reynolds numbers and closed boundaries apparently do not show a slow saturation behaviour; e.g. as in Fig. 7 where the mean magnetic field and a saturation predictor (Brandenburg 2001) proportional to $1-{\rm e}^{-2\eta k^2(t-t_{\rm sat})}$ are shown for Runs PC6-PC8. Here we use $k=2\pi /L_z$ and $t_{\rm sat}$ is the time at which the small-scale dynamo has saturated. In the runs with intermediate ${\rm Rm}$ (PC6 and PC7) the saturation predictor is in fairly good agreement with the simulation results, whereas for Run PC8 this is no longer the case. This might be caused by additional contributions to  $\overline {\bm {B}}$whose effective value of k is larger. In fact, earlier simulations of forced turbulence with perfect-conductor boundary conditions (Brandenburg & Dobler 2002) showed that the final configuration of the mean field can be established in steps, but the time between different steps can still be resistively long. This could explain why, in the highest-${\rm Rm}$ simulations, the saturation level of the mean magnetic field is lower than expected. Whether this is also the case in the present simulations remains an open question.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13722fg6.eps} \end{figure} Figure 6:

Upper panel: rms-value of the total magnetic field in the saturated regime for runs with perfect-conductor (solid line) and vertical-field (dashed) boundaries. Lower panel: same as above but for the horizontally averaged mean magnetic field $\overline {\bm {B}}$. In both panels power laws fitting to the data at high ${\rm Rm}$ are shown for reference.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13722fg7.eps} \end{figure} Figure 7:

Mean magnetic field as a function of time from Runs PC6 (solid line), and PC7 (dashed). The inset shows the same for Run PC8. The dotted lines show a saturation predictor according to Brandenburg (2001) with the microscopic values of $\eta $ and $k=2\pi /L_z$.

Open with DEXTER

4 Conclusions

We have studied the effects of magnetic boundary conditions on the excitation and saturation of large-scale dynamos driven by turbulent convection, shear, and rotation by means of numerical simulations. We find that the critical magnetic Reynolds number is greater ( ${\rm Rm}\approx5$) in the case of closed boundaries (perfect-conductor) compared to simulations with open (vertical-field) boundaries where the large-scale dynamo is excited already for ${\rm Rm}\approx1$. A similar result is obtained from mean-field models operating in the same parameter regime. Furthermore, the relevant dynamo number is roughly three times greater with closed boundaries. These effects are likely to explain the weak large-scale dynamo action seen in the perfect-conductor runs in Paper I.

The measured growth rate of the magnetic field is independent of the microscopic resistivity when ${\rm Rm}$ is sufficiently above the critical value. This is manifested by the approximately constant growth rate in the intermediate ${\rm Rm}$ range in Fig. 1. For ${\rm Rm}\ga 30$, the small-scale dynamo is excited, and for ${\rm Rm}\ga60$ it becomes dominant. The growth rate of the magnetic field is then consistent with $\lambda\propto{\rm Rm}^{1/2}$ scaling, which is in accordance with the results of Schekochihin et al. (2004) and Haugen et al. (#HBD04<#916). The fact that the qualitative behaviour of the growth rate of the magnetic field is similar for both boundary conditions suggests that the origin of the large-scale dynamo is not likely to be a process that is essentially nonlinear, as suggested by Hughes & Proctor (2009), but that it can be understood within the framework of classical kinematic mean-field theory.

In the saturated state the energy of the total magnetic field remains independent of ${\rm Rm}$ for open boundaries and decreases as ${\rm Rm}^{-1}$ for closed boundaries. The latter result is consistent with catastrophic quenching while the former result suggests that magnetic helicity fluxes are efficiently driven out of the system. On the other hand, the energy of the mean field, taken here to be represented by horizontal averages, decreases approximately as ${\rm Rm}^{-0.25}$ for open and as ${\rm Rm}^{-1.6}$ for closed boundaries. It is not yet clear why the mean fields tend to show a steeper decline than the total field. It is possible that this declining trend levels off at a higher ${\rm Rm}$ and that the magnetic Reynolds numbers in our simulations are still not large enough (cf. Brandenburg et al. 2009). A similarly weak ${\rm Rm}$-dependence has been observed in the cycle period of $\alpha$-shear dynamos with isotropically forced turbulence (Käpylä & Brandenburg 2009).

We find that, for intermediate values of ${\rm Rm}$, the large-scale magnetic field saturates on a resistive time scale when closed boundaries are used. However, with the largest ${\rm Rm}$ no clear signs of slow saturation are observed. Earlier results using perfect-conductor boundaries have shown that the mean field can evolve in steps (Brandenburg & Dobler 2002; see also Brandenburg et al. 2007) which are associated with a change of the large-scale magnetic field configuration. We have not seen such a behaviour in our current simulations but the existence of such events at a later stage cannot be ruled out. Another possible explanation is that there are magnetic helicity fluxes occurring inside the domain which arise from the spatial gradients of magnetic helicity (e.g. Covas et al. 1998; Kleeorin et al. 2000; Mitra et al. 2010). However, a quantitative study of these effects requires more detailed knowledge of the helicity fluxes and possibly an anisotropic formulation of the magnetic $\alpha$ effect. These issues merit further investigation and are beyond the scope of the present paper.

Acknowledgements
The authors thank Anvar Shukurov for his detailed comments on the paper. The computations were performed on the facilities hosted by the CSC - IT Center for Science in Espoo, Finland, administered by the Finnish ministry of education. We also wish to acknowledge the DECI - DEISA network for granting computational resources to the CONVDYN project. Financial support from the Academy of Finland grants No. 121431 (PJK) and 112020 (MJK), as well as the Swedish Research Council grant 621-2007-4064 and the European Research Council AstroDyn Research Project 227952 (AB) are acknowledged. The authors acknowledge the hospitality of Nordita during the program ``Solar and stellar dynamos and cycles''.

References

  1. Blackman, E. G., & Field, G. B. 2000, ApJ, 534, 984 [NASA ADS] [CrossRef] [Google Scholar]
  2. Brandenburg, A. 2001, ApJ, 550, 824 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brandenburg, A. 2005, ApJ, 625, 539 [Google Scholar]
  4. Brandenburg, A., & Dobler, W. 2002, Comp. Phys. Comm., 147, 471 [Google Scholar]
  5. Brandenburg, A., & Sandin, C. 2004, A&A, 427, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Brandenburg, A., & Subramanian, K. 2005a, AN, 326, 400 [Google Scholar]
  7. Brandenburg, A., & Subramanian, K. 2005b, A&A, 439, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brandenburg, A., Käpylä, P. J., Mitra, D., Moss, D., & Tavakol, R. 2007, AN, 328, 1118 [NASA ADS] [Google Scholar]
  9. Brandenburg, A., Rädler, K.-H., Rheinhardt, M., & Käpylä, P. J. 2008, ApJ, 676, 740 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brandenburg, A., Candelaresi, S., & Chatterjee, P. 2009, MNRAS, 398, 1414 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cattaneo, F., & Hughes, D. W. 1996, PhRvE, 54, R4532 [Google Scholar]
  12. Choudhuri, A. R. 1984, ApJ, 281, 846 [NASA ADS] [CrossRef] [Google Scholar]
  13. Covas, E., Tavakol, R., Tworkowski, A., & Brandenburg, A. 1998, A&A, 329, 350 [NASA ADS] [Google Scholar]
  14. Haugen, N. E. L., Brandenburg, A., & Dobler, W. 2004, PhRvE, 70, 016308 [NASA ADS] [Google Scholar]
  15. Hughes, D. W., & Proctor, M. R. E. 2009, PhRvL, 102, 044501 [Google Scholar]
  16. Jouve, L., Brun, A. S., Arlt, R., et al. 2008, A&A, 483, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Käpylä, P. J., & Brandenburg, A. 2009, ApJ, 699, 1059 [NASA ADS] [CrossRef] [Google Scholar]
  18. Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2008, A&A, 491, 353 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009a, ApJ, 697, 1153 [NASA ADS] [CrossRef] [Google Scholar]
  20. Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009b, A&A, 500, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2010, MNRAS, 402, 1458 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kleeorin, N., Moss, D., Rogachevskii, I., &Sokoloff, D. 2000, A&A, 361, L5 [NASA ADS] [Google Scholar]
  23. Krause, F., & Rädler, K.-H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
  24. Mitra, D., Candelaresi, S., Chatterjee, P., Tavakol, R., & Brandenburg, A. 2010, AN, 331, 130 [Google Scholar]
  25. Moffatt, H. K. 1978, Magnetic field generation in electrically conducting fluids (Cambridge: Cambridge Univ. Press) [Google Scholar]
  26. Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
  27. Parker, E. N. 1979, Cosmical Magnetic Fields: Their Origin and Their Activity (Oxford & NY: Clarendon Press) [Google Scholar]
  28. Proctor, M. R. E. 2007, MNRAS, 382, 39 [NASA ADS] [CrossRef] [Google Scholar]
  29. Rüdiger, G., & Hollerbach, R. 2004, The Magnetic Universe (Weinheim: Wiley-VCH) [Google Scholar]
  30. Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., & McWilliams, J. C. 2004, ApJ, 612, 276 [NASA ADS] [CrossRef] [Google Scholar]
  31. Silant'ev, N. A.. 2000, A&A, 364, 339 [NASA ADS] [Google Scholar]
  32. Sokolov, D. D. 1997, Astron. Rep., 41, 68 [NASA ADS] [Google Scholar]
  33. Steenbeck, M., & Krause, F. 1969, AN, 291, 49 [Google Scholar]
  34. Tobias, S. M., Cattaneo, F., & Brummell, N. H. 2008, ApJ, 685, 596 [NASA ADS] [CrossRef] [Google Scholar]
  35. Vainshtein, S. I., & Cattaneo, F. 1992, ApJ, 393, 165 [NASA ADS] [CrossRef] [Google Scholar]
  36. Vishniac, E. T., & Brandenburg, A. 1997, ApJ, 475, 263 [NASA ADS] [CrossRef] [Google Scholar]
  37. Vishniac, E. T., & Cho, J. 2001, ApJ, 550, 752 [NASA ADS] [CrossRef] [Google Scholar]
  38. Wisdom, J., & Tremaine, S. 1988, AJ, 95, 925 [NASA ADS] [CrossRef] [Google Scholar]
  39. Yousef, T. A., Heinemann, T., Schekochihin, A. A., et al. 2008a, PhRvL, 100, 184501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  40. Yousef, T. A., Heinemann, T., Rincon, F., et al. 2008b, AN, 329, 737 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... ODE[*]
http://pencil-code.googlecode.com/

All Tables

Table 1:   Summary of the runs with varying ${\rm Pm}$.

Table 2:   Summary of the runs with varying ${\rm Co}$ and ${\rm Sh}$.

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg1.eps} \end{figure} Figure 1:

Growth rate $\lambda $ of the magnetic field as a function of ${\rm Rm}$ from the runs listed in Table 1. Solid (dashed) line with closed (open) symbols shows the results for the VF (PC) boundary conditions. Dotted lines proportional to ${\rm Rm}$ and ${\rm Rm}^{1/2}$ are shown for reference.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg2.eps} \end{figure} Figure 2:

Growth rate $\lambda $ of the magnetic field as a function of ${\rm Co}$ with open (VF, solid line) and closed (PC, dashed line) boundary conditions for the runs listed in Table 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13722fg3.eps} \end{figure} Figure 3:

Dynamo numbers according to Eq. (23) as functions of rotation for the runs listed in Table 2. The solid (dashed) curve shows the results for vertical-field (perfect-conductor) boundary conditions. The horizontal dash-dotted and dash-triple-dotted lines indicate the critical dynamo number in the case of open and closed boundaries, respectively. Power law proportional to ${\rm Co}^2$ is shown for reference.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13722fg4.eps} \end{figure} Figure 4:

Magnetic field component By from runs with vertical-field ( left column) and perfect-conductor ( right column) boundary conditions. Three different cases with low ( top), intermediate ( middle) and high ( bottom) ${\rm Rm}$ are shown. The sides of the boxes show the By field at the periphery of the domain whereas the top and bottom panels show the field at z=z3 and z=z2, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{13722fg5.eps} \vspace{-2mm}\end{figure} Figure 5:

Horizontally averaged magnetic field components Bx and By from the same six runs as in Fig. 4. Those runs and the corresponding values of ${\rm Rm}$ are also highlighted in Table 1 in bold face. The dotted white lines at z=0 and z=d denote the bottom and top of the convectively unstable layer, respectively. The runs on the left are for open boundaries and those on the right are for closed ones. The magnetic Reynolds number increases downwards.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13722fg6.eps} \end{figure} Figure 6:

Upper panel: rms-value of the total magnetic field in the saturated regime for runs with perfect-conductor (solid line) and vertical-field (dashed) boundaries. Lower panel: same as above but for the horizontally averaged mean magnetic field $\overline {\bm {B}}$. In both panels power laws fitting to the data at high ${\rm Rm}$ are shown for reference.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13722fg7.eps} \end{figure} Figure 7:

Mean magnetic field as a function of time from Runs PC6 (solid line), and PC7 (dashed). The inset shows the same for Run PC8. The dotted lines show a saturation predictor according to Brandenburg (2001) with the microscopic values of $\eta $ and $k=2\pi /L_z$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.