EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A46 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A46
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911834
Published online 01 September 2010
A&A 518, A46 (2010)

The energy spectrum of anomalous X-ray pulsars and soft gamma-ray repeaters

J. E. Trümper1 - A. Zezas2,3 - Ü. Ertan4 - N. D. Kylafis2,3

1 - Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
2 - University of Crete, Physics Department, 71003 Heraklion, Crete, Greece
3 - Foundation for Research and Technology-Hellas, 71110 Heraklion, Crete, Greece
4 - Faculty of Engineering and Natural Sciences, Sabanci University, 34956, Orhanli, Tuzla, Istanbul, Turkey

Received 12 February 2009 / Accepted 16 April 2010

Abstract
Context. Anomalous X-ray pulsars (AXPs) and soft gamma-ray repeaters (SGRs) exhibit characteristic X-ray luminosities (both soft and hard) of around 1035 erg s-1 and characteristic power-law, hard X-ray spectra extending to about 200 keV. Two AXPs also exhibit pulsed radio emission.
Aims. Assuming that AXPs and SGRs accrete matter from a fallback disk, we attempt to explain both the soft and the hard X-ray emission as the result of the accretion process. We also attempt to explain their radio emission or the lack of it.
Methods. We test the hypothesis that the power-law, hard X-ray spectra are produced in the accretion flow mainly by bulk-motion Comptonization of soft photons emitted at the neutron star surface. Fallback disk models invoke surface dipole magnetic fields of 10 12 - 1013 G, which is what we assume here.
Results. Unlike normal X-ray pulsars, for which the accretion rate is highly super-Eddington, the accretion rate is approximately Eddington in AXPs and SGRs and thus the bulk-motion Comptonization operates efficiently. As an illustrative example we reproduce both the hard and the soft X-ray spectra of AXP 4U 0142+61 well using the XSPEC package compTB.
Conclusions. Our model seems to explain both the hard and the soft X-ray spectra of AXPs and SGRs, as well as their radio emission or the lack of it, in a natural way. It might also explain the short bursts observed in these sources. On the other hand, it cannot explain the giant X-ray outbursts observed in SGRs, which may result from the conversion of magnetic energy in local multipole fields.

Key words: pulsars: individual: 1E 1841-045 - pulsars: individual: 1RXS J1708-4009 - pulsars: individual: 4U 0142+61 - X-rays: stars - stars: magnetic fields

1 Introduction

Anomalous X-ray pulsars (AXPs) and soft gamma-ray repeaters (SGRs) constitute a special population of young neutron stars distinguished by much higher X-ray luminosities than their rotational powers and spin periods clustered in a narrow range (2-12 s). The AXPs and SGRs are now believed to belong to the same class of objects, since short bursts that were once believed to be a distinctive property of the SGRs were observed from some of the AXPs as well (Gavriil et al. 2002; Kaspi et al. 2003). They are all spinning down with spin-period derivatives in the 10-13 - 10-11 s s-1 range (Woods & Thompson 2006; Kaspi 2007; Mereghetti 2008, for recent reviews on AXPs and SGRs).

In addition to these main properties, broad-band observations have revealed many other peculiarities of these sources, which provide constraints for the models. In particular, some of these sources are persistent with soft X-ray luminosities of $L_{{\rm x,soft}} \sim 10^{34} {-} 10^{36}$ erg s-1, while others, discovered in recent years, are transients with $L_{{\rm x,soft}} \sim ~10^{33}$ erg s-1 in quiescence (see Table 1 of Mereghetti 2008). Both transient and persistent sources show occasional X-ray enhancements lasting from months to more than years and are correlated, in the long term, with infrared (IR) luminosities (Tam et al. 2004). The transient AXPs have been discovered in such X-ray outbursts (enhancements) when their $L_{{\rm x,soft}}$ levels were about two orders of magnitude higher than when in quiescence (Torii et al. 1998; Kouveliotou et al. 2003; Gotthelf et al. 2004; Ibrahim et al. 2004; Mereghetti et al. 2006; Israel et al. 2007; Muno et al. 2007). There are both similarities and systematic differences in the X-ray outburst light-curve morphologies of transient and persistent sources. Other constraints on models come from the properties of AXPs and SGRs in the optical to mid-IR bands and their relations with the X-ray luminosities.

These sources are widely believed to be magnetars mainly 1) because they account for the energetics of the super-Eddington soft gamma-ray bursts and 2) because the P and $\dot{P}$measurements lead to large magnetic dipole strengths based on the assumption that these sources spin down by magnetic dipole radiation. Magnetar models (Duncan & Thompson 1992; Thompson & Duncan 1993, 1995) do explain the super-Eddington bursts of SGRs. However, the quantitative explanation of the persistent soft X-ray luminosity by magnetic field decay, the optical and IR properties during persistent states, the X-ray and the accompanying IR enhancements, and the period clustering of AXP and SGRs all seem to meet difficulties within the original frame of the magnetar model.

On the other hand, fallback disk models (Chatterjee et al. 2000; Alpar 2001) can account for these observational facts. They have been developed in a series of connected, self-consistent ideas by means of detailed quantitative models (Eksi & Alpar 2003; Ertan & Alpar 2003; Ertan & Cheng 2004; Ertan et al. 2006, 2007, 2009; Ertan & Çaliskan 2006; Ertan & Erkut 2008). These models do not explain the super-Eddington bursts. Nevertheless, they are compatible with the presence of magnetar fields provided that these fields are in higher multipoles rather than in the dipole component. In these models, the strength of the dipole magnetic field is found to be less than $\sim 10^{13}$ G to account for the observations. The first direct observational support for the presence of fallback disks around these systems came from SPITZER observations of AXP 4U 0142+61 in mid-IR bands by Wang et al. (2006). The same source has also been detected in optical and near-IR bands. Through model fits, Wang et al. (2006) show that the mid-IR data can be reproduced by an irradiated disk model. These authors propose that the near-IR and the optical luminosities have a magnetic origin, while the mid-IR flux originates in a passive and irradiated disk. Later it was shown that all the data sets from optical to mid-IR can be accounted for by a single disk model that is active and irradiated by X-rays, which themselves are produced by accretion of disk matter onto the neutron star (Ertan et al. 2007). Recently, AXP 1E 2259+586 was also detected in the SPITZER bands. The combined overall spectrum, including the earlier IR detections of this source, is similar to that of AXP 4U 0142+61 (Kaplan et al. 2009).

In recent years, some of the AXPs, namely AXP 1E 1841-045 (Molkov et al. 2004; Kuiper et al. 2004), AXP 1RXS J1708-40 (Revnivtsev et al. 2004; den Hartog et al. 2008a) and AXP 4U 0142+61 (Kuiper et al. 2006; den Hartog et al. 2008b), have been found to emit pulsed hard X-rays up to 150 keV or more with isotropic luminosities close to the soft X-ray luminosities (see den Hartog et al. 2008b and Mereghetti 2008).

Detailed discussions of the magnetar models trying to explain the hard X-ray emission properties of AXPs can be found in (Heyl & Hernquist 2005; Heyl 2007; Beloborodov & Thompson 2007; Baring & Harding 2007). The advantages and disadvantages of the different magnetar models are summarized in den Hartog et al. (2008b).

The main aim of this paper is to discuss how the hard and the soft X-ray components can be produced in the framework of accretion from a fallback disk. In doing so, we treat AXPs and SGRs as a class with the following representative properties:

1)
luminosities are 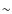$\sim $1035 erg s-1;

2)
soft (<10 keV) and hard (>10 keV) luminosities are similar;

3)
dipolar magnetic field strengths are 1012 - 1013 G;

4)
rotational periods are 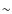$\sim $5 s.

We find that we can explain the observations very naturally by considering the bulk-motion Comptonization (BMC) that takes place in the accretion flow above the polar cap. The seed photons for this Comptonization are provided by the polar cap, while the observed soft X-ray emission comes from both the polar cap and an extended region around it.

As an illustrative example, we fit the observed X-ray spectrum (both soft and hard) of AXP 4U 0142+61 using the XSPEC package compTB (Farinelli et al. 2008). The fit is extremely good and the resulting parameters are very reasonable.

The BMC model is presented in Sect. 2. In Sect. 3 we present the X-ray data of AXP 4U 0142+61 and the fit to them using the XSPEC package compTB. In Sect. 4 we discuss our model, and in Sect. 5 we present the relation of AXPs and SGRs to other source classes. Finally in Sect. 6 we give our conclusions.

2 Bulk-motion Comptonization model

2.1 Soft X-ray emission

The soft X-ray spectra of AXPs below 10 keV can be fitted by two-component models composed of two blackbody spectra or a blackbody plus a steep power-law spectrum (Mereghetti 2008). As pointed out by Gotthelf & Halpern (2005), the double blackbodies are more physically motivated. The hotter component may represent photospheric radiation from a small hot polar cap (area $A_{\rm hot}$), while the cooler component is photospheric emission from a large fraction of the neutron star surface (area $A_{\rm cool}$). Actually, such a combination of spectra is also found for young energetic radio pulsars and for isolated neutron stars showing purely thermal emission.

For an accreting neutron star, whose magnetic axis is inclined with respect to the fallback disk, the emitting region $A_{\rm hot}$ at the base of the accretion flow will not have radial symmetry around the magnetic pole, but will assume the bow-shaped configuration discussed by Basko & Sunyaev (1976) and confirmed by the MHD calculations of Romanova et al. (2004; see also Bachetti et al. 2010). This region is heated by the infall of accreting matter and the produced soft X-ray photons either escape unscattered, and are observed as such, or get upscattered in the accretion flow and produce the hard X-ray spectrum.

2.2 Hard X-ray emission

The equation describing upscattering of soft photons in a converging, ionized, fluid flow was first introduced and solved by Blandford & Payne (1981a,b) and Payne & Blandford (1981). Their Comptonization equation (bulk-motion Comptonization) was solved in the case of spherical accretion onto a neutron star by Mastichiadis & Kylafis (1992), who assumed a reflective neutron-star surface. This last work was generalized by Titarchuk et al. (1996, 1997), who examined the general case of a partially reflecting inner boundary and also included a second order term in the flow velocity (see also Psaltis & Lamb 1997; Psaltis 2001).

The idea in the bulk-motion Comptonization (BMC) model, as applied to the AXP X-ray spectra, is the following. Soft X-ray photons, emitted by the polar cap region, where the accretion occurs, find themselves in the accretion flow. For accretion rates comparable to the Eddington rate, the optical depth to electron scattering in the accretion flow is close to unity or more. Thus, a fraction of the emitted soft photons get trapped in the flow and after several, nearly head-on collisions with the accreting electrons acquire significant amounts of energy. As a result, a power-law, hard X-ray spectrum is produced.

Torrejon et al. (2004) have applied the BMC model to the wind-accreting, slowly spinning, neutron star 4U 2206+54, which has similar properties to our sources ( $L_{\rm x} \sim 10^{35}$ erg s-1, $L_{\rm soft} \sim L_{\rm hard}$, $kT_{\rm bb} \sim 1.2$ keV, and a hard spectral tail extending up to $\buildrel > \over \sim 90$ keV). The BMC model was also used to fit hard X-ray tails observed in neutron star sources by Paizis et al. (2006), and it was significantly improved by Farinelli et al. (2008).

3 Application to AXP 4U 0142+61

The AXP 4U 0142+61 is one of the brightest known AXPs. Therefore its spectrum can provide one of the most stringent tests of the applicability of the BMC model to the X-ray spectra of AXPs. It has been extensively observed with the Chandra, XMM-Newton, and INTEGRAL X-ray missions.

To constrain the low-energy (0.5-10.0 keV) spectrum of 4U 0142+61, we opted for the available Chandra high-energy transmission grating (HETG) spectra. These data are least affected by pile-up, while they do cover the desired energy band. There are also Chandra data obtained in continuous clocking mode (previously analyzed by Patel et al. 2003); however, the calibration of this mode for spectral analysis is still uncertain, as is indicated by the differences between the published analysis of the HETG and the continuous clocking mode data (Juett et al. 2006; Patel et al. 2003). For the high-energy spectrum of 4U 0142+61, we use the extensive ISGRI INTEGRAL data, which cover the 20-200 keV band. The spectral analysis has been performed with the XSPEC v12.0 package (Arnaud 1996). All cited errors are at the 90% confidence level for one interesting parameter unless otherwise specified.

3.1 Chandra data

4U 0142+61 has been observed with the Chandra High-Energy Transmission Grating for 25 ksec in May 2001 (OBSID 1018; PI C. Canizares). We used the reduced spectra available from the Chandra Grating Data Archive and Catalog (TGCat; http://tgcat.mit.edu/). Since even the 0th order spectrum is affected by pile up, we used the positive and negative 1st order of the Medium Energy Transmission Grating and the High Energy Transmission Grating. The individual spectra were binned in order to have at least 50 counts per bin. The four spectra were fitted simultaneously using the relevant response matrices (rmfs) and ancillary responce matrices (arfs) for each order.

A fit of the HETG data with a two component blackbody and power-law model, affected by photoelectric absorption by cold gas (PHABS model in XPSEC) gives a blackbody temperature of 0.42+0.03-0.02 keV, a power-law slope of $\Gamma=3.66^{+0.25}_{-0.29}$, and an absorbing $\rm {H}{\textsc i}$ column density of $0.95^{+0.10}_{-0.12}\times10^{22}$ cm-2. These parameters are almost identical to the parameters derived by Juet et al. (2002) from the analysis of the same data ( $kT=0.418 \pm 0.013$ keV; $\Gamma=3.3 \pm 0.4$, $N_{\rm H} = (0.88 \pm 0.13) \times 10^{22}$ cm-2). However, they are slightly different from the parameters derived by Patel et al. ( $kT=0.470 \pm 0.008$ keV; $\Gamma = 3.40 \pm 0.06$, $N_{\rm H}= (0.93 \pm 0.02)\times10^{22}$ cm-2) from the spectral fits of the continuous clocking mode data. Given the uncertainties in the calibration of the latter mode, we consider that the HETG data provide a more accurate representation of the low-energy spectrum of 4U 0142+61.

3.2 INTEGRAL ISGRI data

4U 0142+61 has been extensively observed by INTEGRAL. We downloaded all public pointed observations from the INTEGRAL archive, which are longer than 3 ks and the source falls within 10 degrees from the pointing direction. The data were analyzed with the OSA v8.0[*] data analysis software provided by the Integral Science Data Analysis Center. We used version 8.0.1 of the instrument characteristics database (which provides the latest calibration data) and version 30.0 of the reference catalog (which provides a list of known sources used for the source detection and spectral extraction processes). First, we produced an image of the observed region in the 4 standard ISGRI bands (20-40 keV, 40-60 keV, 80-100 keV, 100-200 keV) following the standard procedures described in the IBIS analysis user manual[*]. 4U 0142+61 has been clearly detected in all four bands. Next we extracted a spectrum of 4U 0142+61, again following the standard procedures for IBIS data analysis. As recommended, we added 2% systematic errors to the spectrum to account for calibration uncertainties.

We fitted the spectrum with a power-law model, using the latest arf and rmf files. We find an energy slope of $\Gamma=0.94\pm0.10$, consistent with the slope of $\Gamma=1.05\pm0.11$ reported by Kuiper et al. (2006). We also fitted the spectrum with older arf files available in the instrument characteristics database in order to assess the effect of different calibration data on the measured spectral parameters. We did not find any statistically significant difference between the estimated spectral parameters.

3.3 Joint Chandra and INTEGRAL ISGRI fits

In the previous paragraphs, we have shown that our analysis of the archival Chandra and INTEGRAL ISGRI data of 4U 0142+61 nicely reproduces the canonical model consisting of an absorbed blackbody and power-law model in the soft X-ray band (0.5-10.0 keV) and a hard power-law above 20.0 keV. Next we investigated whether the same spectrum can be reproduced with a bulk-motion Comptonization model. For this reason we used the model of Farinelli et al. (2008) provided as an external XSPEC model (model COMPTB[*]). This model includes a self-consistent treatment of the seed blackbody spectrum and the thermal and/or bulk-motion Comptonization of its photons. Therefore we did not include an ad-hoc blackbody component. The seed spectrum is described by a modified blackbody function $S(E) \propto E^{\gamma-1} / [\exp(E/kT_{\rm s}) -1]$, where $kT_{\rm s}$ is the characteristic temperature of the blackbody, and $E^{\gamma}$ is a power-law component that modifies the blackbody. For $\gamma=3$ this component simplifies to a pure blackbody. Since this model includes both bulk-motion and thermal Comptonization, an important parameter is the relative efficiency of the two components defined as $\delta = <E_{\rm bulk}>)/\!\!\!<E_{\rm th}>$. For $\delta=0$ we have a pure thermal Comptonization spectrum. Other parameters of this model are the energy index of the Comptonization spectrum ($\alpha$; for more details see Farinelli et al. 2008), the temperature of the Comptonizing electrons ( $kT_{\rm e}$), a factor describing the ratio between the observed Compton scattered spectrum and the observed seed blackbody spectrum (A), and the normalization of the seed photon spectrum ($C_{\rm N}$). To model photoelectric absorption by cold gas, we included the XSPEC PHABS model component.

The results of this fit are presented in Table 1 and Figs. 1 and 2. The first figure shows the data and the best-fit model (top panel). It also shows the ratio of the data to the best-fit model (bottom panel). Figure 2 shows the model and the data corrected for instrumental effects (unfolded spectrum) in E2f(E) space. It is evident from this figure that the model gives a very good fit to the broad band spectrum of 4U 0142+61 ( $\chi_{\nu}^{2}=166.7/248$). The temperature of the seed photons (kT=0.72 keV) is slightly higher than the temperature estimated from the blackbody fit of the Chandra data alone. However, the parameter $\gamma=0.95$, which modifies the seed blackbody spectrum indicates that it is not a pure blackbody. Furthermore, we find that the bulk-motion Comptonization dominates over thermal Comptonization ( $\delta=2.32$) and that only 0.3% of the observed photons have been Compton scattered [ $\log(A)=-2.3$]. These results show that the spectrum of 4U 0142+61 can be reproduced equally well with a self-consistent BMC model with very reasonable parameters.

Table 1:   Fits of the ISGRI and Chandra data with the COMPTB model.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11834fg1.ps} \end{figure} Figure 1:

Top panel: The Chandra HEG and MEG (first positive order shown with red and green points respectively) and INTEGRAL ISGRI data (shown in black) along with the best-fit COMPTB model. Bottom panel: Ratio between the data and the best-fit model.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11834fg2.ps} \end{figure} Figure 2:

The best-fit COMPTB model, along with the data corrected for instrumental effects shown in E2f(E) space.

Open with DEXTER

4 Discussion

The advantage of the bulk-motion Comptonization model is that it uses a proven concept, which has been applied to many cases including the slowly pulsating source 4U 2206+54, which in turn shows a low-luminosity (1035 erg s-1) and a hard X-ray tail like the AXPs (Torrejon et al. 2004). Another advantage is that the whole spectrum, from the soft thermal component to the hard X-ray tail, is explained by a single, well-understood mechanism using as few parameters as possible. The accreting matter both heats the polar cap, which emits the seed photons for Comptonization, and provides the high-energy electrons, which do the Comptonization. Depending on detailed conditions, both the soft and the hard X-ray components have luminosities that are within the same order of magnitude as observed. Since the soft and hard components come from the same place at the neutron star surface, their maxima occur at basically the same rotational phase. This agrees well with the observational fact that these sources show a very slow change in pulse profile with energy (Kaspi 2007). On the other hand, there are fine structures in the energy-dependent pulse profiles, which can be explained by cyclotron resonance effects, as in the case of normal X-ray pulsars having dipole magnetic fields of similar strengths to the ones postulated by our model for AXPs and SGRs.

The radio emission observed in two of the AXPs (1E 1547-54 (Camilo et al. 2007) and XTE J1810-197 (Halpern et al. 2005; Camilo et al. 2006)) can also be explained by the BMC model. Usually, it is thought that the radio emission of a neutron star is quenched by the accretion, but there may be little or no overlap in our model between the circumpolar zone of radio emission and the bow-shaped accretion zone (Romanova et al. 2004). Indeed, according to the canonical expression, the size of the radio-active polar cap is $r_{\rm pc} = 10^4 P^{-1/2} \sim 5 \times 10^3$ cm. It seems likely that the bow-shaped accretion region is farther from the magnetic pole. Therefore, both radio and X-ray emission may coexist.

A necessary requirement for a detectable radio flux is that the magnetic dipole power $\dot E$ is strong enough. Comparing $\dot E = (1/6 c^3) B^2 R^6 (2\pi/P)^4$, where B is the surface magnetic field, R the radius of the neutron star, P the rotational period and c the speed of light, with the observed radio luminosities of the two pulsars, we estimate the radio emission efficiencies to be $\sim $10-4 and $\ga$0.03 for 1E 1547-54 and XTE J1810-197, respectively, when assuming a polar magnetic field of 1013 G. A lower magnetic field strength is also allowed in our model, because the observed radio luminosity is not isotropic. These efficiencies are quite large, but comparable to those of the most efficient normal radio pulsars with periods >2 s, taken from the ATNF catalog http://www.atnf.csiro.au/research/pulsar/psrcat/ (Manchester et al. 2005).

The fact that most AXPs and SGRs have remained undetected in the radio band despite deep searches (Burgay et al. 2007) may be due to their long periods, which may place them beyond the death line. Another reason could be that long-period radio pulsars have narrow beams with widths scaling with P-1/3 (Lyne & Manchester 1988). For a period of 6 s, the full beam is then only $\sim $7 degrees. Therefore the probability of detecting the radio beam of an AXP is only a few percent.

5 Relation to other source classes

The main point of this paper is to explain the hard X-ray spectra of AXPs and SGRs as a result of accretion from a fallback disk. In addition, we attribute the soft X-ray spectra of AXPs and SGRs to thermal, photospheric radiation from the polar cap (hotter component) and from the bulk surface of the neutron star (cooler component). This latter point leads us to the following thoughts:

The class of isolated neutron stars showing purely thermal emission that was discovered by ROSAT (XDINS, Magnificent Seven) exhibits blackbody emission as well, though at lower temperatures (by a factor $\sim $10) and lower luminosities (by $\sim $104) compared with AXPs. Like the latter, the XDINs have long periods and strong magnetic fields ($\ge $1013 G, Haberl 2007). Their period derivatives and proper motion data indicate ages of a few hundred thousand years, and they are not associated with supernova remnants. All these facts show that XDINs are older than AXPs, supporting the idea that some (or possibly all) XDINs have been AXPs before they exhausted their residual disk and have subsequently cooled down.

Another young neutron-star population, namely the central compact objects (CCOs, see review by Pavlov et al. 2004), are probably related to AXPs, SGRs, and XDINs as well. It was originally proposed by Alpar (2001) that similarities and differences in these neutron star classes could be explained if fallback disks with different properties are included in the initial parameters of the evolution models in addition to initial spin period and the magnetic moment of the neutron star.

6 Conclusions

Contrary to common belief, AXPs and SGRs may not be that different from normal accreting X-ray pulsars. The major differences between the two classes of X-ray sources are the extent of the hard X-ray spectrum and the X-ray luminosity, which is lower for AXPs/SGRs by two to three orders of magnitude. The hard X-ray power-law spectral index is essentially the same for both classes, but the spectrum of normal X-ray pulsars extends to about 20 keV, while that of the anomalous X-ray pulsars extends to about 200 keV. In our model, this difference is caused by the normalized (to the Eddington value) accretion rate being near unity in AXPs/SGRs, and bulk-motion Comptonization takes place and produces the hard X-ray tail, which extends to $\sim $200 keV.

Our model naturally explains the $\sim $100% pulsations observed at $\sim $100 keV, because they come from the accretion flow above the polar cap. It also explains the similarity between AXPs/SGRs and XDINS, which has often been noted. It may be that XDINS are evolved AXPs with no remaining accretion disk. The absence of cyclotron lines in the observed X-ray spectra is a natural consequence of our model. For a dipole magnetic field of $\sim $1013 G, the electron cyclotron line would appear at E > 100 keV, where the photon statistics are not good enough. On the other hand, a proton cyclotron line would appear at $E \sim 0.05$ keV, where interstellar absorption is huge.

Our model could in principle explain the short bursts observed from AXPs and SGRs as the result of infalling lumps of matter with appropriate mass. We defer an analysis of this process to another paper. On the other hand, our model does not explain the giant bursts observed from AXPs and SGRs. These may indeed require very strong, magnetar-type magnetic fields. Our model does not exclude the existence of such super strong magnetic fields if they reside in multipole components.

Last but not least, we feel that the detection of a fallback disk around the neutron stars in AXP 4U 0142+61 and AXP 1E 2259+586 gives strong observational support to our model.

Acknowledgements
Ü.E. and J.T. thank the Astrophysics Group of the University of Crete and FORTH for their hospitality. This research has been supported in part by EU Marie Curie project no. 39965, EU REGPOT project number 206469 and by EU FPG Marie Curie Transfer of Knowledge Project ASTRONS, MKTD-CT-2006-042722. Ü.E. acknowledges research support from TÜBITAK (The Scientific and Technical Research Council of Turkey) through grant 107T013 and support from the Sabanci University Astrophysics and Space Forum.

References

  1. Alpar, M. A. 2001, ApJ, 554, 1245 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, ed. G. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  3. Bachetti, M., Romanova, M., Kulkarni, A., Burderi, L., & di Salvo, T. 2010, MNRAS, 403, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baring, M. G., & Harding, A. K. 2007, Ap&SS, 308, 109 [NASA ADS] [CrossRef] [Google Scholar]
  5. Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
  6. Beloborodov, A. M., & Thompson, C. 2007, ApJ, 657, 967 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blandford, R. D., & Payne, D. G. 1981a, MNRAS, 194, 1033 [NASA ADS] [Google Scholar]
  8. Blandford, R. D., & Payne, D. G. 1981b, MNRAS, 194, 1041 [NASA ADS] [Google Scholar]
  9. Burgay, M., Rea, N., Israel , G., et al. 2007, Ap&SS, 308, 531B [NASA ADS] [CrossRef] [Google Scholar]
  10. Camilo, F., Ransom, S. M., Halpern, J. P., et al. 2006, Nature, 442, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Camilo, F., Ransom, S. M., Halpern, J. P., & Reynolds, J. 2007, ApJ, 666, L93 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chatterjee, P., Hernquist, L., & Narayan, R. 2000, ApJ, 534, 373 [NASA ADS] [CrossRef] [Google Scholar]
  13. den Hartog, P. R., Kuiper, L., & Hermsen, W. 2008a, A&A, 489, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. den Hartog, P. R., Kuiper, L., Hermsen, W., et al. 2008b, A&A, 489, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Duncan, R. A., & Thompson, C. 1992, ApJ, 392, 9 [Google Scholar]
  16. Eksi, K. Y., & Alpar, M. A. 2003, ApJ, 599, 450 [NASA ADS] [CrossRef] [Google Scholar]
  17. Ertan, Ü., & Alpar, M. A. 2003, ApJ, 593, L93 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ertan, Ü., & Çaliskan, S. 2006, ApJ, 649, L87 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ertan, Ü., & Cheng, K. S. 2004, ApJ, 605, 840 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ertan, Ü., & Erkut, M. H. 2008, ApJ, 673, 1062 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ertan, Ü., Gögüs, E., & Alpar, M. A. 2006, ApJ, 640, 435 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ertan, Ü., Erkut, M. H., Eksi, K. Y., & Alpar, M. A. 2007, ApJ, 657, 441 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ertan, Ü., Eksi, K. Y., Erkut, M. H., & Alpar, M. A. 2009, ApJ, 702, 1309 [NASA ADS] [CrossRef] [Google Scholar]
  24. Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gavriil, F. P., Kaspi, V. M., & Woods, P. M. 2002, Nature, 419, 142 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. Gotthelf, E. V., & Halpern, J. P. 2005, ApJ, 632, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gotthelf, E. V., Halpern, J. P., Buxton, M., & Bailyn, C. 2004, ApJ, 605, 368 [NASA ADS] [CrossRef] [Google Scholar]
  28. Haberl, F. 2007, Ap&SS, 308, 181 [NASA ADS] [CrossRef] [Google Scholar]
  29. Halpern, J. P., Gotthelf, E. V., Becker, R. H., Helfand, D. J., & White, R. L. 2005 ApJ, 632, L29 [Google Scholar]
  30. Heyl, J. S. 2007, Ap&SS, 308, 101 [NASA ADS] [CrossRef] [Google Scholar]
  31. Heyl, J. S., & Hernquist, L. 2005, ApJ, 618, 463 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ibrahim, A. I., Markwardt, C. B., Swank, J. H., et al. 2004, ApJ, 609, 21 [Google Scholar]
  33. Israel, G. L., Campana, S., Dall'Osso, et al. 2007, ApJ, 664, 448 [NASA ADS] [CrossRef] [Google Scholar]
  34. Juett, A. M., Marshall, H. L., Chakrabarty, D., & Schulz, N. S. 2002, ApJ, 568, L31 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kaplan, D. L., Chakrabarty, D., Wang, Z., & Wachter, S. 2009, ApJ, 700, 149 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kaspi, V. M., 2007, Ap&SS, 308, 1 [Google Scholar]
  37. Kaspi, V. M., Gavriil, F. P., Woods, P. M., et al. 2003, ApJ, 588, L93 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kouveliotou, C., Eichler, D., Woods, P. M., et al. 2003, ApJ, 596, 79 [Google Scholar]
  39. Kuiper, L., Hermsen, W., & Mendez, M. 2004, ApJ, 613, 1173 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kuiper, L., Hermsen, W., den Hartog, R. P., & Collmar, W. 2006, ApJ, 645, 556 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lyne, A. G., & Manchester, R. N. 1988, MNRAS, 234, 477 [NASA ADS] [CrossRef] [Google Scholar]
  42. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mastichiadis, A., & Kylafis, N. D. 1992, ApJ, 384, 136 [NASA ADS] [CrossRef] [Google Scholar]
  44. Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mereghetti, S., Esposito, P., Tiengo, A., et al. 2006, A&A, 450, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Molkov, S. V., Cherepashchuk, A. M., Lutovinov, A. A., et al. 2004, Astron. Lett., 30, 534 [NASA ADS] [CrossRef] [Google Scholar]
  47. Muno, M. P., Gaensler, B. M., Clark, J. S., et al. 2007, MNRAS, 378, L44 [NASA ADS] [Google Scholar]
  48. Paizis, A., Farinelli, R., Titarchuk, L., et al. 2006, A&A, 459, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Patel, S. K., Kouveliotou, C., Woods, P. M., et al. 2003, ApJ, 587, 367 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pavlov, G. G., Sanwal, D., & Teter, M. A. 2004, in Young Neutron Stars and Their Environments, ed. F. Camilo, & B. M. Gaensler, IAU Symp., 218, 239 [Google Scholar]
  51. Payne, D. G., & Blandford, R. D. 1981, MNRAS, 196, 781 [NASA ADS] [Google Scholar]
  52. Psaltis, D. 2001, ApJ, 555, 786 [NASA ADS] [CrossRef] [Google Scholar]
  53. Psaltis, D., & Lamb, F. K. 1997, ApJ, 488, 881 [NASA ADS] [CrossRef] [Google Scholar]
  54. Revnitsev , M. G., Sunyaev, R. A., Varshalovich, D. A., et al. 2004, Astron. Lett., 30, 382 [NASA ADS] [CrossRef] [Google Scholar]
  55. Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2004, ApJ, 610, 920 [NASA ADS] [CrossRef] [Google Scholar]
  56. Tam, C. R., Kaspi, V. M., van Kerkwijk, M. H., & Durant, M. 2004, ApJ, 617, L53 [NASA ADS] [CrossRef] [Google Scholar]
  57. Thompson, C., & Duncan, R. C. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef] [Google Scholar]
  58. Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255 [NASA ADS] [CrossRef] [Google Scholar]
  59. Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1996, A&AS, 120, C171 [Google Scholar]
  60. Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
  61. Torii, K., Kinugasa, K., Katayama, K., et al. 1998, ApJ, 503, 843 [NASA ADS] [CrossRef] [Google Scholar]
  62. Torrejon, J. M., Kreykenbohm, I., Orr, A., Titarchuk, L., & Negueruela, I. 2004, A&A, 423, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Wang, Z., Chakrabarty, D., & Kaplan, D. L. 2006, Nature, 440, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  64. Woods, P. M., & Thompson, C. 2006, in Compact Stellar X-ray Sources, ed. W. H. G. Lewin, & M. van der Klis (Cambridge Univ. Press.), 547 [arXiv:astro-ph/0406133] [Google Scholar]

Footnotes

... v8.0[*]
http://www.isdc.unige.ch/integral/download/osa_sw
... manual[*]
http://isdcul3.unige.ch/Soft/download/osa/osa_doc/osa_doc-8.0/osa_um_ibis-7.0.pdf
... COMPTB[*]
http://heasarc.gsfc.nasa.gov/xanadu/xspec/models/comptb.html

All Tables

Table 1:   Fits of the ISGRI and Chandra data with the COMPTB model.

All Figures

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11834fg1.ps} \end{figure} Figure 1:

Top panel: The Chandra HEG and MEG (first positive order shown with red and green points respectively) and INTEGRAL ISGRI data (shown in black) along with the best-fit COMPTB model. Bottom panel: Ratio between the data and the best-fit model.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11834fg2.ps} \end{figure} Figure 2:

The best-fit COMPTB model, along with the data corrected for instrumental effects shown in E2f(E) space.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.