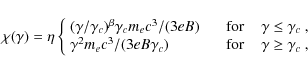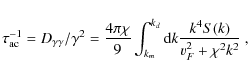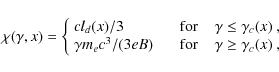EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) L4 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number L4
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201015169
Published online 30 July 2010
A&A 517, L4 (2010)

LETTER TO THE EDITOR

Lepton models for TeV emission from SNR RX J1713.7-3946

Z. H. Fan1 - S. A. Liu2 - Q. Yuan3 - L. Fletcher2

1 - Department of Physics, Yunnan University, Kunming 650091, Yunnan, PR China
2 - Department of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK
3 - Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, PR China

Received 8 June 2010 / Accepted 4 July 2010

Abstract
Aims. SNR RX J1713.7-3946 is perhaps one of the best observed shell-type supernova remnants with emissions dominated by energetic particles accelerated near the shock front. The nature of the TeV emission, however, is an issue still open to investigation.
Methods. We carried out a systematic study of four lepton models for the TeV emission with the Markov chain Monte Carlo method.
Results. It is shown that current data already give good constraints on the model parameters. Two commonly used parametric models do not appear to fit the observed radio, X-ray, and $\gamma$-ray spectra. Models motivated by diffusive shock acceleration and by stochastic acceleration by compressive waves in the shock downstream give comparably good fits. The former has a sharper spectral cutoff in the hard X-ray band than the latter. Future observations with the HXMT and NuSTAR may distinguish these two models.

Key words: acceleration of particles - plasmas - shock waves - turbulence

1 Introduction

Energetic particles produce radiations over a broad energy range under typical astrophysical circumstances. To study the energetic particle population in high-energy astrophysical sources, observations over a broad spectral range are needed. Multi-wavelength observations of individual sources usually give sparse spectral data points, which can be fitted reasonably well with a simple power-law or broken power-law function. A featureless power-law distribution implies the lack of characteristic scales or distinct processes in the system. The nature of particle acceleration processes are still a matter of debate nearly a century after the discovery of high-energy particles from the outer space (Butt 2009).

Recent progress in observations of high-energy astrophysical sources has resulted in more detailed spectral coverage, and spectral features start to emerge. These features are produced by the underlying physical processes with well-defined characteristic scales in space, time, and/or energy, and they play essential roles in advancing our understanding of the acceleration mechanism (Berezhko & Krymsky 1988). Diffusive astrophysical shocks are considered as one of the most important particle accelerators (Berezhko 1996; Drury 1983; Toptygin 1980). The acceleration of particles by compressive motions of astrophysical flows is also a very generic process (Ptuskin 1988). Both processes may be important in the acceleration of particles dominating the radiative characteristics of the shock associated with SNR RX J1713.7-394 (Fan et al. 2010). Detailed X-ray and $\gamma$-ray observations of this source have revealed several features: 1) the X-ray and $\gamma$-ray emissions are well correlated in space (Plaga 2008; Aharonian et al. 2006); 2) the emission spectrum shows a clear high-energy cutoff in both the X-ray and TeV bands (Aharonian et al. 2007), and the cutoff in hard X-rays appears to be sharp (Tanaka et al. 2008), implying a sharp cutoff in the electron distribution producing the observed radio to X-ray spectrum through the synchrotron process; 3) the $\gamma$-ray spectrum has a broad convex shape (Funk 2009); 4) there are bright X-ray filaments with a width of $\sim$0.1 light year varying on a timescale of about a year (Uchiyama et al. 2007). Liu et al. (2008) showed that these emissions may be attributed to a single population of electrons with the $\gamma$-rays produced via the inverse Compton scattering of the background photons by relativistic electrons.

In light of recent high-resolution observations with Suzaku and Fermi, we use the Markov chain Monte Carlo (MCMC) method to constrain parameters of four possible lepton models. It is shown that simple models with a power-law electron distribution, which cuts off at TeV energies, give a poor fit to either the X-ray or $\gamma$-ray spectrum. Motivated by the mechanism of diffusive shock acceleration (DSA) and stochastic acceleration (SA) by compressive motions, we introduce two alternative models, both of which give acceptable fits to the observed spectra (Sect. 2). In Sect. 3, we discuss the implications of these results and future work needed to improve these models. Conclusions are drawn in Sect. 4.

2 Spectral fits with lepton models

In the lepton scenario, the radio to X-ray emissions are produced through the synchrotron process of relativistic electrons, and the $\gamma$-ray emission is produced through the inverse Compton scattering of the background radiation fields by the same electron population. If the background magnetic fields are relatively uniform, similar to the background radiation fields, the model can naturally explain the spatial correlation between the X-rays and $\gamma$-rays (Plaga 2008). As pointed out by Liu et al. (2008), the magnetic field required to produce the X-ray flux agrees with what is required to produce an X-ray spectral cutoff by an electron population cutting off in the TeV energy range (Ellision et al. 2010; Aharonian et al. 2007).

There are at least four parameters in a specific model. In this work we employ an MCMC technique suitable for multi-parameter determination to search all the model parameters. The Metropolis-Hastings sampling algorithm is adopted when determining the jump probability from one point to the next in the parameter space (MacKay 2003). The MCMC approach, which is based on the Bayesian statistics, is superior to the grid approach with a more efficient sampling of the parameter space of interest, especially for high dimensions. The algorithm ensures that the probability density functions (PDF) of model parameters can be asymptotically approached with the number density of samples. Starting with an initial parameter set $\vec{P_0}$, which should lie in a reasonable parameter space, one obtains the likelihood function of $\vec{P_0}$: $\mathcal{L}_0(\vec {P_0})\propto \exp \left(-{\chi^2(\vec{P_0})}/{2}\right)$. Then another parameter set $\vec{P_1}$ is randomly selected with the corresponding likelihood function $\mathcal{L}_1$. This parameter set is accepted with the probability $\alpha=\min\{1,{\mathcal{L}_1}/{\mathcal{L}_0}\}$. If the new point is accepted, it becomes the starting point for the next step, otherwise, we reset $\vec{P_1}=\vec{P_0}$. This procedure is repeated to derive a parameter chain that determines the PDF of model parameters. More details of this procedure can be found in Neil (1993), Gamerman (1997), and MacKay (2003).

I: Without detailed modeling of the particle acceleration processes, a power-law electron distribution with an exponential high-energy cutoff is often assumed to fit the observed spectrum:

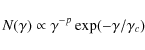
\begin{displaymath}N(\gamma)\propto \gamma^{-p}\exp({-\gamma/\gamma_c}) \end{displaymath} (1)

where p is the spectral index, $\gamma_c$ the Lorentz factor of the high-energy cutoff $E_c=\gamma_c m_ec^2$, me and c are the electron mass and the speed of light, respectively. The integration of $N(\gamma)$ over the Lorentz factor $\gamma$ gives the particle number density. It has been shown that this model gives a sufficient fit to previous observations of SNR RX J1713.7-3946 when the interstellar radiation field is considered (Porter et al. 2006); however, more detailed studies suggest that such a model systematically underestimates the photon flux at the low-energy end of HESS observations (Tanaka et al. 2008; Zirakashvili & Aharonian 2010). In this paper, we adopt the interstellar radiation field spectrum of Porter et al. (2006). There are then four model parameters. Besides the magnetic field B, p, and $\gamma_c$, we need a normalization for the relativistic electrons $E_{\rm {tot}}$, which is the total energy of electrons with $\gamma>10$. Figures 1 and 2 give the best fit of this model to the data and the probability density of the model parameters. All four model parameters are well constrained. However, detailed examination of residuals of the spectral fit shows that there are several data points below 1 and near 10 TeV with normalized residuals significantly greater than 3.

II: Liu et al. (2008) suggested that the fit to the $\gamma$-ray spectrum can be improved by considering a more gradual cutoff in the electron distribution:

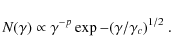
\begin{displaymath}N(\gamma)\propto \gamma^{-p}\exp{-(\gamma/\gamma_c)^{1/2}}~. \end{displaymath} (2)

Several mechanisms can cause variations in the shape of the high-energy cutoff (Blasi 2010; Zirakashvili & Aharonian 2007; Becker et al. 2006; Berezhko & Krymsky 1988). However, given the sharp cutoff of the X-ray spectrum, Tanaka et al. (2008) claim that the electron distribution must have a very steep cutoff. Indeed, by using their data and performing the MCMC fit, we obtain radio fluxes nearly one order of magnitude below the observed values. The model also significantly overestimates the hard X-ray fluxes. To increase the weight of the radio and $\gamma$-ray data in the model fit, we artificially increase the errors of the X-ray data from Suzaku by a factor of 2[*] (Figs. 1 and 2). The normalized residuals are indeed improved significantly with a reduced $\chi ^2$ of 1.2, in agreement with Liu et al. (2008), where cruder X-ray data from ASCA observations were used. However, as emphasized by Tanaka et al. (2008), the sharp cutoff in the X-ray spectrum is significant and the error estimate of the Suzaku observation appears to be robust (Takahashi et al. 2008). This simple model therefore cannot fit the X-ray spectrum.

III: The particle distribution is determined by the injection process and the spatial diffusion coefficient $\chi$ in the DSA model. The time-dependent electron distribution with a constant injection rate may be approximated as (Drury 1991; Berezhko & Krymsky 1988; Forman & Drury 1983)

\begin{displaymath}N(\gamma)\propto \gamma^{-p} \exp [-9\chi (\gamma)/U^2{T_{\rm life}}]~, \end{displaymath} (3)

where $T_{\rm life}$ is the supernova lifetime since the onset of particle acceleration and U the shock speed. A very sharp high-energy cutoff can be produced when gyro-radii of high-energy particles exceed the characteristic length of the magnetic field in the background plasma ld. Particles at such high energies do not perform gyro-motions around the chaotic magnetic field and instead interact randomly with the background fields. The spatial diffusion coefficient of these particles increases as the square of the relativistic Lorentz factor in the absence of waves on scales greater than ld. Consequently, they can readily cross the acceleration site without interactions. We assume a spatial diffusion coefficient

\begin{displaymath}\chi(\gamma) = \eta \left\{ \begin{array}{ll} {(\gamma/\gamma... ...rm for}\;\;\;\; \gamma \geq \gamma_c ~,\\ \end{array}\right. \end{displaymath} (4)

where e is the elementary charge, $\eta>1$ depends on the turbulence intensity, $\beta=1/2$ and 1/3 for particle interactions with a spectrum of plasma waves following the Kraichnan (1965) and Kolmogorov (1941) phenomenology for the turbulence spectral evolution, respectively. The characteristic length of the magnetic field is then given by the gyro-radius of electrons at $\gamma_c$: $l_d= \gamma_c m_e c^2/e B$.

Compared with the previous two models, an extra parameter is introduced here: $\eta/T_{\rm life}U^2$, which is proportional to the electron acceleration timescale. Figures 1 and 2 show the results with $\beta=1/2$. The probability density of $\eta(1.6~{\rm kyr}/T_{\rm life})(4\; {\rm Mm\ s}^{-1}/U)^2$peaks near a typical value of 12. Since $\eta$ has to be greater than 1, we have $T_{\rm life}U^2>0.02 c$ lyr. The gyro-radius of electrons at the cutoff Lorentz factor $\gamma_c \sim 2\times 10^8$ is $\sim$0.01 pc comparable to the width of the observed highly variable X-ray filaments. The X-ray variability may then be attributed to spatial diffusion of X-ray emitting electrons from a high-density region formed presumably via an intermittent process. It is interesting to note that the best fit spectral index p=1.92 is less than 2, implying acceleration by multiple shocks or strong nonlinear effects (Zirakashvili & Aharonian 2010). The model with $\beta=1/3$ gives a similar fit with a slightly higher value of $\eta$ and sharper hard X-ray cutoff.

IV: Fan et al. (2010) have carried out detailed modeling of electron acceleration by compressive motions in the shock downstream and argued that it might also explain these observations. Here we follow the same treatment and also consider the effect of incompressive motions, which can dominate the spatial diffusion and therefore the escape of energetic electrons from the acceleration region. The acceleration rate is given by (Bykov & Toptygin 1993)

\begin{displaymath}\tau_{\rm ac}^{-1}= D_{\gamma\gamma}/\gamma^2 = {4\pi \chi\over 9}\int_{k_m}^{k_d}{\rm d}k {k^4 S(k)\over v_F^2+ \chi^2k^2}~, \end{displaymath} (5)

where $\chi$, k, vF, and S are the spatial diffusion coefficient, the wave-number, speed, and intensity of compressive waves, respectively. The overall wave intensity $\int S(k) 4\pi k^2{\rm d}k= \xi v_F^2$ with $\xi<1$ for subsonic turbulence[*]. The turbulence is generated on a scale L near the shock front, and ld corresponds to the scale where the turbulence speed is comparable to the Alfvén speed $v_{\rm A}$. Relativistic electrons with a gyro-radius less than ld have a mean-free path comparable to ld since waves on smaller scales are subject to strong transit time damping by thermal background ions. We then have the diffusion coefficient

\begin{displaymath}\chi(\gamma,x) = \left\{ \begin{array}{ll} {cl_d(x)/3}\ \ \ \... ...for}\;\;\;\; \gamma \geq \gamma_c(x) ~,\\ \end{array}\right. \end{displaymath} (6)

where x indicates the spatial location in the downstream, $l_{\rm d} = \gamma_c m_ec^2/eB$, and we have assumed Bohm diffusion for $\gamma>\gamma_c$. Due to gradual decay of the turbulence intensity, related quantities evolve with x in the downstream. Equation (6) is quite different from Eq. (4), where particle scattering by the background turbulence is parameterized without considering details of the turbulence structure. Considering the presence of strong turbulence with $u>v_{\rm A}$ between the scales of ld and L, Bohm diffusion may be appropriate, and as we show below, faster diffusion may not be able to accelerate electrons efficiently to account for the observations. The intensity of the incompressive motions T(k) can be determined from the energy conservation: $\int [2T(k)+S(k)]4\pi k^2dk=3u^2$, where 3u2/2 is the total turbulence energy density per unit mass. Further downstream, where vF is high ($\ge$61/2 u), the incompressive motions vanish completely. To derive the escape time $T_{\rm esc}$ of electrons from the acceleration region, we need to consider the enhancement of the spatial diffusion coefficient by the turbulence motions. According to Eq. (4.30) in Bykov & Toptygin (1993), the effective diffusion coefficient $\chi_*$ can be derived from
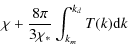
                                    $\displaystyle \chi_*$ = $\displaystyle \chi + \frac{8\pi}{3\chi_*}\int_{k_m}^{k_d} T(k) {\rm d}k$ (7)
  $\textstyle \quad +$ $\displaystyle \frac{4\pi \chi_*}{3}\int_{k_m}^{k_d} \left[\frac{1}{k^2\chi_*^2+... ...}-\frac{2(k^2\chi_*^2-v_F^2)} {(k^2\chi_*^2+v_F^2)^2}\right]k^2 S(k) {\rm d}k~,$  

where we have ignored the decay of incompressive motions. Then we have

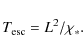
\begin{displaymath}T_{\rm esc} = L^2/\chi_*. \end{displaymath} (8)

With the above treatment, we can study particle acceleration by compressive motions all the way to the shock front, which is different from the case studied by Fan et al. (2010), where only the subsonic phase with vF>u is considered. Near the shock front, we assume $\xi =1/2$ so that Eq. (5) is applicable. Since the compressive wave intensity is lower than in Fan et al. (2010) and the acceleration timescale of TeV electrons becomes comparable to the supernova lifetime, a time-dependent treatment is necessary[*]. Both the acceleration and escape timescale explicitly depend on the diffusion coefficient $\chi$, which is independent of $\gamma$ for $\gamma<\gamma_c$. Assuming that electrons are injected at the Lorentz factor $\gamma_{\rm inj}=10$ with a constant rate, the time-dependent results of Becker et al. (2006; see also Park & Petrosion 1995; Cowsik & Sarkar 1984) can be used to describe the evolution of the electron distribution function at energies below $\gamma_c$. Near the cutoff energy $\gamma_c$, the nontrivial dependence of the acceleration and escape timescales on the Lorentz factor demand numerical solutions. We assume the time-dependent distribution function has a high-energy cutoff given by $\exp[-(\tau_{\rm ac}/T_{\rm esc})^{1/2}]$ (For details, see Fan et al. 2010). Figures 1 and 2 show the results for U=4000 km s-1 with the Kraichnan phenomenology. The quality of this fit is comparable to the DSA model. The deduced model parameters also agree with those obtained in Fan et al. (2010).

\begin{figure} \par\includegraphics[width=9cm,clip]{15169fg1.eps} \vspace*{4mm} \end{figure} Figure 1:

Model fit to the spectrum of SNR RX J1713.7-3946. The TeV data is from Aharonian et al. (2007), the Fermi data is from Funk (2009), and the X-ray data is from Tanaka et al. (2008) (Thanks to Jun Fang). The thick solid, dashed line and the thin solid, dashed line in the upper panel correspond to the diffusive shock, stochastic acceleration model, and the model with an exponential, more gradual cutoff in the electron distribution, respectively. The low and high-energy spectral hump are produced by relativistic electrons through the synchrotron and inverse Comptonization process, respectively. The lower panels show the normalized residuals. From top to bottom, they are for the model with an exponential and more gradual cutoff, the DSA, and SA model. For the model with a gradual cutoff, the X-ray errors have been artificially increased by a factor of 2 to improve the fit. The reduced $\chi ^2$ of these fits are indicated in the top-left corner. See the text for details. The instrumental sensitivity of NuSTAR and HXMT are indicated by the dotted and dot-dashed lines, respectively.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{15169fg2.eps} \vspace*{3mm} \end{figure} Figure 2:

Probability density function of model parameters normalized at the peak value. Different line types correspond to different models as explained in Fig. 1 and the text.

Open with DEXTER


3 Discussion

The SA model (Fig. 1) predicts a higher hard X-ray flux than the DSA model since the diffusion coefficient of the DSA model has a stronger dependence on the electron energies leading to a sharper high-energy cutoff. The electron distribution in the SA model includes contributions from broad regions in the downstream, which also makes the overall electron distribution broader. Future observations with NuSTAR and HXMT may be able to distinguish these two models.

In actual turbulent astrophysical shocks, both the DSA and SA mechanisms may contribute to the electron acceleration (Bykov & Toptygin 1993; Achterberg 1990). The distinction between the two resides in the dissipation structure (Berezhko & Krymsky 1988). Supersonic shock fronts dominate the acceleration in the DSA model. The SA model dominates in the subsonic phase. It is possible that the shock downstream of SNR RX 1713.7-3946 has both a supersonic and subsonic phase turbulence with the former closer to the shock front. The electron acceleration is therefore a continuous process in the turbulent downstream. In the SA model of this paper, we intentionally remove the DSA by requiring that the compressive waves be subsonic in the downstream. A self-consistent treatment of the turbulence evolution in the shock downstream is needed for particle acceleration near astrophysical shock fronts.

All the models appear to systematically underproduce $\gamma$-ray flux in the Fermi energy band and overproduce flux near 10 TeV. The latter could be caused by inhomogeneities of the background magnetic field, which implies lower cutoff energy of the electron distribution and less high-energy $\gamma$-ray flux (Tanaka et al. 2008). The former requires a broader electron distribution from the GeV to TeV energy range. A combination of DSA and SA model with the former dominating the higher energy particle acceleration and the latter enhancing the lower energy ones may address this issue. Such a scenario is possible if both supersonic and subsonic turbulence are produced by the supernova shock (Bykov & Toptygin 1993; Berezhko & Krymsky 1988). Contributions to GeV-TeV emission from decay of neutral pions produced by inelastic collisions of relativistic protons with the background ions may also explain these residuals. However, as shown by Ellision et al. (2010) and Katz & Waxman (2008), relativistic protons can not be the dominant TeV emission component (Zirakashvili & Aharonian 2010). Including this component is beyond the scope of the current investigation but may give a good constraint on the relative acceleration efficiency of relativistic electrons and protons (Katz & Waxman 2008).

4 Conclusions

With recent high spectral-resolution observations of SNR RX 1713.7-3946 in X-rays and $\gamma$-rays, we show that, in general, models with simple parametric descriptions of energetic particle distribution give a poor fit to the broadband spectrum. Details of relativistic electron acceleration may be probed with advanced models. Although both the DSA and SA model give acceptable fits to the spectrum, the SA model predicts a higher hard X-ray flux than the DSA model, which may be tested by future observations. The spatial distribution of energetic electrons in the SA and DSA models is also different, and the source structure can be used to distinguish these two models as well. The results agree with the scenario where energetic electrons are accelerated by interacting diffusively with a turbulent electromagnetic field and produce nearly all of the observed emissions from the shell of SNR RX 1713.7-3946. Turbulence evolution at astrophysical shocks appears to play a key role in advancing our understanding of particle acceleration processes.

Acknowledgements
This work is supported in part by the SOLAIRE research and training network at the University of Glasgow (MTRN-CT-2006-035484), the National Science Foundation of China (grants 10963004 and 10778702), Yunnan Provincial Science Foundation of China (grant 2008CD061) and SRFDP of China (grant 20095301120006). S.L. thanks Eduard Kontar for helpful discussion. Q.Y. thanks Jie Liu for helping to develop the MCMC code adapted from the COSMOMC code of Lewis & Bridle (2002).

References

  1. Achterberg, A. 1990, A&A, 231, 251 [NASA ADS] [Google Scholar]
  2. Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 449, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, A&A, 464, 235 [Google Scholar]
  4. Becker, P. A., Le, T., & Demer, C. D. 2006, ApJ, 647, 539B [Google Scholar]
  5. Berezhko, E. G. 1996, Astropart. Phys., 5, 367 [NASA ADS] [CrossRef] [Google Scholar]
  6. Berezhko, E. G., & Krymsky, G. F. 1988, Sov. Phys. Usp., 31, 27 [Google Scholar]
  7. Blasi, P. 2010, MNRAS, 402, 2807 [NASA ADS] [CrossRef] [Google Scholar]
  8. Butt, Y. M. 2009, Nature, 460, 701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Bykov, A. M., & Toptygin, I. N. 1993, Phys. Usp., 36, 1020 [Google Scholar]
  10. Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 427, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cowsik, R., & Sarkar, S. 1984, MNRAS, 207, 745 [NASA ADS] [Google Scholar]
  12. Drury, L. 1983, SSRv, 36, 57 [Google Scholar]
  13. Drury, L. 1991, MNRAS, 251, 340 [NASA ADS] [Google Scholar]
  14. Ellison, D. C., Patnaude, D. J., Slane, P., & Raymond, J. 2010, ApJ, 712, 287 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fan, Z. H., Liu, S. M., & Fryer, C. L. 2010, MNRAS, 406, 1337 [NASA ADS] [Google Scholar]
  16. Forman, M. A., & Drury, L. O. 1983, ICRC, 2, 267 [Google Scholar]
  17. Funk, S. 2009, Fermi Symp. [Google Scholar]
  18. Gamerman, D. 1997, Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference (London: Chapman and Hall) [Google Scholar]
  19. Katz, B., & Waxman, E. 2008, JCAP, 01, 018 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kolmogorov A. 1941, Dokl. Akad. Nauk SSSR, 30, 301 [Google Scholar]
  21. Kraichnan 1965, Phys. Fluids, 8, 1385 [Google Scholar]
  22. Lewis, A., & Bridle, S. 2002, Phys. Rev. D 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
  23. Liu, S. M., Fan, Z. H., Fryer, C. L., Wang, J. M., & Li, H. 2008, ApJ, 683, L163 [NASA ADS] [CrossRef] [Google Scholar]
  24. MacKay, D. 2003 Information Theory, Inference, and Learning Algorithms, (Cambridge University Press) [Google Scholar]
  25. Neal, R. M. 1993 Probabilistic Inference Using Markov Chain Monte Carlo Methods, Technical Report CRG-TR-93-1, Department of Computer Science, University of Toronto [Google Scholar]
  26. Park, B. T., & Petrosian, V. 1995, ApJ, 446, 699 [NASA ADS] [CrossRef] [Google Scholar]
  27. Plaga, R. 2008, NewA, 13, 73 [Google Scholar]
  28. Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ptuskin, V. S. 1988, Soviet Astron. Lett., 14, 255 [NASA ADS] [Google Scholar]
  30. Takahashi, T., Tanaka, T., Uchiyama, Y., et al. 2008, PASJ, 60, 131 [Google Scholar]
  31. Tanaka, T., Uchiyama, Y., Aharonian, F. A., et al. 2008, ApJ, 685, 988 [NASA ADS] [CrossRef] [Google Scholar]
  32. Toptygin, I. N. 1980, SSRv, 26, 157 [Google Scholar]
  33. Uchiyama, Y., Aharonian, F. A., Tanaka, T., et al. 2007, Nature, 449, 576 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  34. Zirakashvili, V. N., & Aharonian, F. A. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 2[*]
Given the complexity of the instrumental background and calibration, and unknowns, such as the estimated cosmic X-ray background, such an artificial increase may well be reasonable.
... turbulence[*]
Here we adopt the formula given by Bykov & Toptygin (1993), which gives an acceleration rate a factor of 2 lower than that of Ptuskin (1988).
... necessary[*]
At the point, where vF=u, the compressive wave intensity used here is 3 times lower than in Fan et al. (2010).
Copyright ESO 2010

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{15169fg1.eps} \vspace*{4mm} \end{figure} Figure 1:

Model fit to the spectrum of SNR RX J1713.7-3946. The TeV data is from Aharonian et al. (2007), the Fermi data is from Funk (2009), and the X-ray data is from Tanaka et al. (2008) (Thanks to Jun Fang). The thick solid, dashed line and the thin solid, dashed line in the upper panel correspond to the diffusive shock, stochastic acceleration model, and the model with an exponential, more gradual cutoff in the electron distribution, respectively. The low and high-energy spectral hump are produced by relativistic electrons through the synchrotron and inverse Comptonization process, respectively. The lower panels show the normalized residuals. From top to bottom, they are for the model with an exponential and more gradual cutoff, the DSA, and SA model. For the model with a gradual cutoff, the X-ray errors have been artificially increased by a factor of 2 to improve the fit. The reduced $\chi ^2$ of these fits are indicated in the top-left corner. See the text for details. The instrumental sensitivity of NuSTAR and HXMT are indicated by the dotted and dot-dashed lines, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{15169fg2.eps} \vspace*{3mm} \end{figure} Figure 2:

Probability density function of model parameters normalized at the peak value. Different line types correspond to different models as explained in Fig. 1 and the text.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.