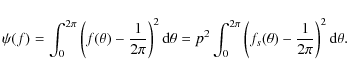EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) L9 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number L9
Number of page(s) 3
Section Letters
DOI https://doi.org/10.1051/0004-6361/201014362
Published online 13 August 2010
A&A 517, L9 (2010)

LETTER TO THE EDITOR

The H-test probability distribution revisited: improved sensitivity

O. C. de Jager1,3 - I. Büsching1,2

1 - Unit for Space Physics, School of Physics, North-West University, 2520 Potchefstroom, South Africa
2 - Centre for High Performance Computing (CHPC), CSIR Campus, 15 Lower Hope St. Rosebank, Cape Town, South Africa
3 - South African Department of Science & Technology and National Research Foundation Reseach Chair: Astrophysics & Space Science, South Africa

Received 5 March 2010 / Accepted 28 May 2010

Abstract
Aims. To provide a significantly improved probability distribution for the H-test for periodicity in X-ray and $\gamma $-ray arrival times, which is already extensively used by the $\gamma $-ray pulsar community. Also, to obtain an analytical probability distribution for stacked test statistics in the case of a search for pulsed emission from an ensemble of pulsars where the significance per pulsar is relatively low, making individual detections insignificant on their own. This information is timely given the recent rapid discovery of new pulsars with the Fermi-LAT t $\gamma $-ray telescope.
Methods. Approximately 1014 realisations of the H-statistic (H) for random (white) noise is calculated from a random number generator for which the repetition cycle is $\gg$1014. From these numbers the probability distribution P(>H) is calculated.
Results. The distribution of H is found to be exponential with parameter $\lambda=0.4$ so that the cumulative probability distribution $P({>}H)=\exp{(-\lambda H)}$. If we stack independent values for H, the sum of K such values would follow the Erlang-K distribution with parameter $\lambda$ for which the cumulative probability distribution is also a simple analytical expression.
Conclusions. Searches for weak pulsars with unknown pulse profile shapes in the Fermi-LAT, Agile or other X-ray data bases should benefit from the H-test since it is known to be powerful against a broad range of pulse profiles, which introduces only a single statistical trial if only the H-test is used. The new probability distribution presented here favours the detection of weaker pulsars in terms of an improved sensitivity relative to the previously known distribution.

Key words: methods: statistical - pulsars: general

1 Introduction

When searching for a periodic signal in X-ray or $\gamma $-ray arrival times dominated by noise, we may either perform a blind search for $\gamma $-ray pulsars as demonstrated by the Fermi-LAT Collaboration (Abdo et al. 2009), or, search for such a signal where the frequency parameters have been prescribed by contemporary radio data (Weltevrede 2010). Following the folding of say N arrival times t1, ...,tN modulo the pulsar spin parameters, we arrive at a set of phases $\theta_i$, i=1, ...N. However, in the case of blind searches, Atwood et al. (2006) introduced a time differencing technique in which case the number of trial periods is significantly reduced.

de Jager et al. (1989, hereafter DSR) reviewed the general class of Beran statistics (Beran 1969), from which the most general test statistics such as Pearson's $\chi^2$, Rayleigh and Z2m statistics are derived, and from within this class they derived the well known H-test for X-ray and $\gamma $-ray Astronomy.

The probability distribution of the H-test statistic as given by DSR was derived from Monte Carlo simulations employing $\sim $108 simulations. The computational power and random number simulators on typical IBM machines during the 1980's had limited ranges of applicability and the H-test suffered accordingly. For values of H<23 we found that the probability distribution was exponential with parameter $\lambda=0.398$ (or 0.4), whereas a hard tail developed for H>23, which resulted in a significant compromise in sensitivity.

The old version of the H-test probability distribution is already extensively used by e.g. the Fermi-LAT Collaboration for pulsar searches (e.g. Abdo et al. 2009; and Weltevrede et al. 2010), and from this paper it will become clear that the significances assigned to pulsar detections (or non-detections) may be too conservative, so that some pulsars may be missed, especially when many trial periods are involved, so that large values of the H-statistic are required for a significant detection. In this Letter we notify the community that all previous published significances from the H-test should be reassessed, based on the new improved distribution presented below. Before we do so, we first briefly review the origin and properties of the H-test.

2 The Beran class of test statistics - towards the H-test

Let $\theta$ be the pulsar phase measured on the interval $[0,2\pi)$, so that a full rotation corresponds to $2\pi$. Assuming noise (e.g. from cosmic rays) are also present such that the pulsed fraction is $p\le 1$. Let $f_s(\theta)$ be the observed line-of-sight pulse profile in the absence of noise. The case p=0 then corresponds to no signal (pure noise), whereas p=1 corresponds to no noise (pure pulsed signal). The observed light curve $f(\theta)$ can then be represented as a mixing of the noise and signal distributions (see Eq. (2) of DSR 1989)

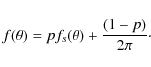
\begin{displaymath}f(\theta)=pf_s(\theta)+\frac{(1-p)}{2\pi}\cdot \end{displaymath} (1)

The general form of the Beran statistic is given by Beran (1969) in the form (see also DSR 1989)

\begin{displaymath} \psi(f)=\int_0^{2\pi}\left(f(\theta)-\frac{1}{2\pi}\right)^... ...2\pi}\left(f_s(\theta)-\frac{1}{2\pi}\right)^2 {\rm d}\theta . \end{displaymath} (2)

It is thus clear that the Beran statistic measures the integrated squared distance between the pulse profile and uniformity, so that if $p \rightarrow 0$, then $\psi \rightarrow 0$ as well, or, if $f_s=1/2\pi$ (i.e. a flat uniform distribution), then $\psi=0$ as well. Thus, we would reject uniformity if $\psi$ exceeds a chosen positive critical value.

It was noted by DSR that by replacing $f(\theta)$ with a density estimator $\hat{f}(\theta)$based on the observed folded phases $\theta_i$, we retrieve test statistics specific to the kernel of the density estimator. Selecting the Fourier series estimator $\hat{f}_m$ with m harmonics (see Eq. (5) of DSR) as representative of the light curve, results in the well-known Z2m given the proper normalisation (Eq. (7) of DSR)

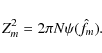
\begin{displaymath}Z^2_m=2\pi N \psi(\hat{f}_m). \end{displaymath} (3)

Since $\psi(f)$ scales with p2 (Eq. ( 2)), it is then clear that the statistic Z2m should scale as p2N. The quantity $X=p\sqrt{N}$ is then also the approximate Gaussian significance of the point source on the skymap if the background level is well known.

The main problem raised by DSR is that we do not know a-priori the optimal number of harmonics to select. In the case of the popular Z2m test, the optimal number of harmonics would depend on X and the pulse profile shape.

The rationale behind the H-test was to find a consistent estimator for $f(\theta)$ where the number of harmonics m is not chosen subjectively by the observer, since selecting a number of m values for Z2m, until a pleasing result is obtained, may lead to a false detection, given the difficulty to keep track of the number of trials involved.

Hart (1985) derived a technique to obtain the optimal number of harmonics M such that the mean integrated squared error (MISE) between the Fourier series estimator $\hat{f}_M(\theta)$ and the true unknown light curve shape is a minimum (see DSR for a review). Thus, $\hat{f}_M(\theta)$would give the best Fourier series representation of the true pulse profile, given the constraints imposed by the statistics and inherent pulsed fraction. Since the minimum of the MISE involves the finding of a maximum quantity over all harmonics m, DSR redefined this maximal (optimal) quantity in terms of the so-called H-test statistic (named after Hart):

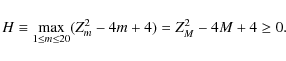
\begin{displaymath}H\equiv \max_{1\le m \le 20}(Z^2_m-4m+4)=Z^2_M-4M+4\ge 0. \end{displaymath} (4)

Uniformity would correspond to low values of M and also low values of H, whereas large values of Z2M (relatively strong pulsed signal) corresponds to large values of H. Subtracting 4M and adding 4 (to ensure positive values of H only) effectively limits the variance of H in the absence of a pulsed signal. It is clear that the H test represents a rescaled version of the Z2m test: if M=1, then we retrieve the well-known Rayleigh test. DSR have shown that this test is powerful against a wide range of alternatives, which makes this test attractive if the pulse profile shape is not known a priori.

To give an example of how H and M depend on the abovementioned significance $X=p\sqrt{N}$given real data, we selected archival photon arrival times from the public Fermi-LAT data base from the Vela pulsar direction, with events selected according to the Fermi-LAT point spread function, but with energies >500 MeV. Folding these phases with the given contemporary spin parameters of Vela reveals a pulsed fraction of $p\sim 0.96$, i.e. nearly 100% and from N=600 events (4 days integration) we already obtain M=20. By adding randomly generated events (i.e. uniformly distributed pulse phases) to the signal events we effectively reduce p and hence X, so that H and M should also decrease accordingly. Figure 1 shows how H and M relates to X: For X>3 (stronger than a $\sim $$ 3 \sigma$ signal) we see that H scales with X2, with H=1.9X2, whereas the optimal M is already >10 for X>7.

\begin{figure} \par\includegraphics[width=8 cm,clip]{psqrtN.EPS} \end{figure} Figure 1:

The dependence of H and M on the approximate skymap significance X for $\gamma $-ray pulse phases above 500 MeV from the Vela pulsar as described in the text. The errors represent standard deviations based on 20 independent Fermi-LAT Vela pulsar data sets, each of length up to $\sim $4 days. The horisontal line represent the upper limit of M=20, whereas the dashed line represent a fit of the form H=1.9X2 for X>3.

Open with DEXTER

This figure is also quite useful to see what typical H and M values we may expect for a typical Vela-like pulsar if we know the strength of the signal as derived from a point source on the skymap, and assuming the excess is due to such a pulsed signal.

3 The revised probability distribution of H for uniformity

The calculations were performed on the Institutional Cluster of the North-West University, Potchefstroom campus. To parallelize the computations, we used the RngStream package (L'Ecuyer 2002), which guarantees independent, non-overlapping substreams of random numbers. The repetition cycle for this random number generator is $3\times 10^{57}$, which is certainly large enough for our purposes. A total of $4\times 10^{14}$ samples were calculated in this way.

In the case of large statistics (N>100) we do not need to simulate individual arrival times directly (see the approximate correction factors in Figs. 1 and 2 of DSR in the case of low statistics - N<100), so that we only need to simulate the Z2m statistics directly: since Z2m is the sum of m $\chi^2_2$-statistics, we can simulate a $\chi^2_2$ statistic directly from a uniformly distributed random number $r\in [0,1)$ by taking the transformation $-2\ln {r}$ and adding these numbers to give Z2m. This speeds up the process considerably. A total of $4\times 10^{14}$ values of H were simulated in this way and the results are shown in Fig. 2. The distribution is everywhere consistent with an exponential distribution with parameter $\lambda=0.398$ (or 0.4), except for H>70 where a downturn relative to the 0.4 index is possibly seen. DSR arrived at the same precise value of $\lambda=0.398$ for small values of H (i.e. less than 23) since the random number generator used by DSR did not yet reach the limit of its random cycle for the number of simulations required to reach $H\sim 23$ (with a relatively small error on the corresponding probability) and should therefore reveal the same result as ours for H<23.

It is thus clear that the probability distribution of the H-statistic can be conservatively described by the simple formula

\begin{displaymath}{\rm Prob}({>}H)=\exp{(-0.4H)}. \end{displaymath} (5)

\begin{figure} \par\includegraphics[width=8 cm,clip]{h-statistic_2.EPS} \end{figure} Figure 2:

The distribution of the H-statistic derived from $4\times 10^{14}$ Monte Carlo simulations with the best fit model for the cumulative probability $P({>}H)=\exp{(-0.4H)}$ (solid line) and the old version of the probability distribution given by DSR shown as a dashed line.

Open with DEXTER

4 Incoherent stacking

Suppose we analysed the data from K pulsars, or, K independent observations of the same pulsar, where the effect of e.g. unrecorded glitches excluded the possibility of analysing all the data as one single coherent set of arrival times. In this case we want to see if there is a net signal represented by K values of the H-statistic. Suppose we arrive at a set of K such values of H, given by Hi, i=1, ...,K.

Since we have shown (to the probability level of $\sim $10-14) that the H-statistic follows that of an exponential distribution with parameter $\lambda=0.4$, we can stack these test statistics through the sum

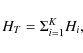
\begin{displaymath}H_T=\Sigma_{i=1}^K H_i, \end{displaymath} (6)

which is known to follow the Erlang-K distribution with parameter $\lambda$, so that the significance (or probability for uniformity) of such stacking is given by the simple analytical expression (see e.g., Leemis & McQueston 2008, on univariate distribution relationships, which includes the Erlang distribution as the sum of independent exponential variables with parameter $\lambda$.)

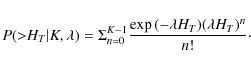
\begin{displaymath}P({>}H_T\vert K,\lambda)=\Sigma_{n=0}^{K-1}\frac{\exp{(-\lambda H_T)}(\lambda H_T)^n}{n!}\cdot \end{displaymath} (7)

5 Conclusions

For M=1 we retrieve the well-known Rayleigh test, with the exception that the parameter for the exponential distribution has been reduced from $\lambda=0.5$ (for the Rayleigh test) to $\lambda=0.4$ for the H-test. This slight loss of sensitivity is the effect of the number of trials taken implicitly into account as a result of the search through m within the H-test.

Finally, it is clear that the corrected distribution of the H-statistic follows a simple exponential with parameter $\lambda=0.4$ and evaluation of results for H>23 (i.e. the 10-4 significance level) would yield more significant results compared to the old distribution presented by DSR. For example, for H=50 a probability of $4\times 10^{-8}$ is typically quoted in the literature, whereas the true probability for uniformity is actually $2\times 10^{-9}$ - already a factor 20 smaller.

A Fermi-LAT example of the Vela pulsar (>500 MeV) shows clearly values for M up to 20 for ``skymap'' significances $X=p\sqrt{N} > 20$, whereas H scales with $H\propto X^2$ as expected for Beran-type tests. The scaling H=1.9X2 can be used to predict H-test statistics for Vela-like pulsars above 500 MeV if we assume the excess on the skymap is all pulsed.

The hard tail of the distribution beyond H>23 presented by DSR probably arose from the repetition cycle of the random number generator used in those days, so that the same fluctuations at large H values were repeated given the finite cycle length of the generator used. In this case we however used a generator with a cycle time much longer than 1014, in which case we did not see the repetition of outliers as a result of a finite cycle length. Confirmation of the possible break (i.e. downturn) in the probability distribution at H>70 requires extensive simulations beyond $4\times 10^{14}$ and is beyond the scope of this paper.

Acknowledgements
The authors are grateful for partial financial support granted to them by the South African National Research Foundation (NRF) and by the Meraka Institute as part of the funding for the South African Centre for High Performance Computing (CHPC).

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 325, 840 [NASA ADS] [CrossRef] [Google Scholar]
  2. Atwood, W. B., Ziegler, M., Johnson, R. P., & Baughman, B. M. 2006, ApJ, 652, L49 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beran, R. J. 1969, Ann. Math. Stat., 40, 1196 [CrossRef] [Google Scholar]
  4. Buccheri, R., & de Jager, O. C. 1989, in NATO ASI Workshop on Timing Neutron Stars, ed. H. Ögelman, & E. P. J. van den Heuvel (Dordrecht: Kluwer), 95 [Google Scholar]
  5. de Jager, O. C., Swanepoel, J. W. H., & Raubenheimer, B. C. 1989, A&A, 221, 180 (DSR) [NASA ADS] [Google Scholar]
  6. Hart, J. D. 1985, J. Statist. Comput. Simul., 21, 95 [CrossRef] [Google Scholar]
  7. Leemis, L. M., & McQueston, J. T. 2008, American Statistician, 62, 45 [Google Scholar]
  8. L'Ecuyer, P., Simard, R., Chen, E. J., & Kelton, W. D. 2002, Operations Res., 50, 1073 [CrossRef] [Google Scholar]
  9. Weltevrede, P., Abdo, A. A., Ackermann, M., et al. 2010, ApJ, 708, 1426 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=8 cm,clip]{psqrtN.EPS} \end{figure} Figure 1:

The dependence of H and M on the approximate skymap significance X for $\gamma $-ray pulse phases above 500 MeV from the Vela pulsar as described in the text. The errors represent standard deviations based on 20 independent Fermi-LAT Vela pulsar data sets, each of length up to $\sim $4 days. The horisontal line represent the upper limit of M=20, whereas the dashed line represent a fit of the form H=1.9X2 for X>3.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8 cm,clip]{h-statistic_2.EPS} \end{figure} Figure 2:

The distribution of the H-statistic derived from $4\times 10^{14}$ Monte Carlo simulations with the best fit model for the cumulative probability $P({>}H)=\exp{(-0.4H)}$ (solid line) and the old version of the probability distribution given by DSR shown as a dashed line.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.