Typical duration of good seeing sequences at Concordia

E. Fossat; E. Aristidi; A. Agabi; E. Bondoux; Z. Challita; F. Jeanneaux; D. Mékarnia

doi:10.1051/0004-6361/201014186

Home

All issues

Volume 517 (July 2010)

A&A, 517 (2010) A69

Full HTML

Free Access

Issue		A&A Volume 517, July 2010


Article Number		A69
Number of page(s)		4
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/201014186
Published online		10 August 2010

A&A 517, A69 (2010)

Typical duration of good seeing sequences at Concordia
(Research Note)

E. Fossat - E. Aristidi - A. Agabi - E. Bondoux - Z. Challita - F. Jeanneaux - D. Mékarnia

Fizeau Laboratory, University of Nice Sophia Antipolis, CNRS, Observatoire Côte d'Azur, Parc Valrose, 06108 Nice Cedex, France

Received 2 February 2010 / Accepted 16 March 2010

Abstract
Context. The winter seeing at Concordia is bimodal, i.e. either excellent or quite poor, depending on the altitude above the snow surface. We study the temporal behavior of the good seeing sequences. Efficient exploitation of extremely good seeing conditions with an adaptive optics system requires long integrations.
Aims. We examine the temporal distribution of time intervals providing excellent seeing at Concordia.
Methods. We create temporal windows of good seeing by applying a simple binary process: good or bad. We correct the autocorrelations of these windows for those of the existing data sets, since these are not continuous, often being interrupted by technical problems in addition to the adverse weather gaps. We infer the typical duration of good seeing sequences from these corrected autocorrelations. This study has to be a little detailed as its results depend on the season, summer or winter.
Results. When we adopt a threshold of 0.5 arcsec to define ``good seeing'', we find that three characteristic numbers describe the temporal evolution of the good seeing windows. The first number is the mean duration of an uninterrupted good seeing sequence, which is $\tau_0=7.5$ h at 8 m above the ground and 15 h at 20 m. These sequences are randomly distributed in time, following a negative exponential law of damping time $\tau_1=29$ h (at elevation 8 m and 20 m), which represents our second number. The third number is the mean time between two 29 h episodes, which is T=10 days at 8 m high (5 days at 20 m).
Conclusions. There is certainly no other site on Earth, except for the few other high altitude Domes on the Antarctic plateau, at which we can achieve these exceptionally high quality seeing conditions.

Key words: site testing - atmospheric effects - methods: statistical

1 Introduction

Regarded as astronomical sites, the highest points of the Antarctica plateau have many obvious advantages over competing sites, due to their climate and remoteness from any polluting civilization. They also benefit from an interestingly unique distribution of turbulence. This has been extensively measured at Dome C since the first winter-over authorised in 2005 by the French-Italian Concordia station operation (Aristidi et al. 2009). During winter and summer very different but both unusual vertical distributions of the turbulent energy are measured. The situation is in general dominated by a surface inversion layer that becomes very turbulent when the temperature gradient is steep in winter, and can completely vanish in summer when this gradient becomes flat. In summer the situation depends on the Sun's elevation, and is then strongly time dependent, having an optimum period of a few hours of excellent seeing every day in the middle of local afternoon (Aristidi et al. 2005). In the other 3 seasons, the mean seeing is almost only altitude dependent above the snow surface. The turbulent layer, which contains, statistically, 95 percent of the total Cn² along the line of sight, has geometrical properties that are statistically independent of the season, within the measurement accuracy. Above this layer, the mean seeing value is also independent of the season, between 0.3 and 0.4 arcsec as soon as the telescope is located above a sharply defined altitude threshold, which fluctuates about a mean value of the order of 25 m. The non summer seeing therefore exhibits a nearly bimodal statistical distribution. It is indeed as good as between 0.3 and 0.4 arcsec 50 percent of the time 25 m above the surface, this fraction of time decreasing to about 40 percent at 20 m and slightly less than 20 percent at 8 m. But it is obviously not equivalent to have 40 percent of the good seeing distributed in many short periods of from seconds to minutes rather than in extended long sequences of hours or days. This paper addresses the temporal distribution of this good seeing percentage. It extends the first analysis of Aristidi et al. (2009), by applying a method to compensate for the gaps in the data.

2 The autocorrelation method

Our analysis is based on the Concordia DIMM data. A DIMM, located about 8 m above the snow surface, has been permanently operating since the end of 2004, after having operated during a summer season one year earlier. A second DIMM was positioned at 20 m high on the roof of the Concordia station for 3 months in 2005. There is also a GSM, consisting of two DIMMs on the snow surface, whose data are not exploited in the present paper.

The DIMM seeing data sets have a sampling rate of 2 min. Their data time series are not continuous, being often interrupted by either adverse weather or by various technical problems such as frost on the optics, electronics or computer shut downs, loss of star tracking. It is then difficult to directly track the continuity of good seeing sequences in the original data files because a gap in a sequence of good seeing data can may be caused by bad seeing or a simple lack of data. Our study must therefore be performed on a statistical basis.

We found that applying the autocorrelation method to data windows was a very efficient tool for that purpose. Two different temporal windows can be defined, by means of a function equal to 1 or 0. The first one is called $w_{\rm e}(t)$ and defines the existence of data at a time t. $w_{\rm e}(t)=1$ if data exist, 0 otherwise. The second one $w_{\rm g}(t)$ defines the seeing quality. It uses a threshold $\sigma_{\rm g}$ so that $w_{\rm g}(t) =1$ if the seeing $\sigma(t)<\sigma_{\rm g}$ and $w_{\rm g}(t)=0$ if $\sigma(t)>\sigma_{\rm g}$ . In this paper, we use $\sigma_{\rm g} = 0.5$ arcsec, a value that is near the minimum of the gap between good and bad seeing in the winter seeing histograms (Aristidi et al. 2009).

This second window function, however, is not directly accessible because many measurements are missing. The only accessible window function is the product of these two windows, which is 1 when the measurement does exist and provides a good seeing value, and 0 when either the seeing is not good or the measurement does not exist. This accessible window function can be given by $w_{\rm ge}(t)=w_{\rm e}(t) w_{\rm g}(t)$ .

It is unfortunately impossible to recover the interesting but unknown window $w_{\rm g}(t)$ because a division by $w_{\rm e}(t)$ which is often zero is not feasible. This, however, is possible in the domain of the autocorrelations, when the data sets are sufficiently long relative to their characteristic time. When $w_{\rm g}$ and $w_{\rm e}$ are statistically independent, the autocorrelation of $w_{\rm ge}(t)$ can be written as

$\displaystyle \Gamma_{\rm ge}(\tau)$	=	$\displaystyle \frac{1}{m_{\rm e}~m_{\rm g}} E[w_{\rm e}(t)~w_{\rm g}(t)~w_{\rm e}(t+\tau)~ w_{\rm g}(t+\tau)]$	(1)
	=	$\displaystyle \frac{1}{m_{\rm e}~m_{\rm g}} E[w_{\rm e}(t)~w_{\rm e}(t+\tau)]\: E[w_{\rm g}(t)~w_{\rm g}(t+\tau)]$
	=	$\displaystyle \Gamma_{\rm e}(\tau)\: \Gamma_{\rm g}(\tau)$

where $\Gamma _{\rm e}(\tau )$ , $\Gamma _{\rm g}(\tau )$ , and $\Gamma_{\rm ge}(\tau)$ are the autocorrelation functions of $w_{\rm e}(t)$ , $w_{\rm g}(t)$ , and $w_{\rm ge}(t)$ , respectively, $m_{\rm e}$ and $m_{\rm g}$ are the mean values of $w_{\rm e}$ and $w_{\rm g}$ (the mean value is here equal to the variance since the functions $w_{\rm e}$ and $w_{\rm g}$ equal 0 or 1), and E[] denotes the expected value. This technique has been extensively used in the past to analyse helioseismic data (Lazrek 1993) and is a method of deconvolution in the Fourier plane. Because we can analyse very long time series, which cover several years of accumulated data, and as there is very little suspicion of dependence between the observation window $w_{\rm e}(t)$ and the good seeing occurrences $w_{\rm g}(t)$ , we can use this mentioned division and thus study the statistical properties of the good seeing sequences by evaluating the autocorrelation $\Gamma _{\rm g}(\tau )$ of the corresponding window $w_{\rm g}(t)$ .

It is now well established that the summer and winter conditions at Concordia drastically differ. We are mostly interested here by the winter conditions. The ``winter'' is defined to be the 6 months during which no significant temperature variation is detected, which is from early April to the end of September. We also qualify and illustrate our method by a summer analysis, the summer data being those taken during the permanent sunlight season, performing from early November to February 10th.

Figures 1 and 2 illustrate the data window function autocorrelation $\Gamma _{\rm e}(\tau )$ . During the first two winters, in 2005 and 2006, only one astronomer was present at the site. It is clear from Fig. 1 that the automation of the instrument has not been successful yet, as indicated by the one-day periodicity of the window function. In 2007 for the first time, two astronomers remained during winter and could then take care of the instrument more permanently. The one-day periodicity of the window function was not found to completely disappear, but almost.

The overall filling factors of the data sets are provided by the asymptotic values of the autocorrelations functions. It is indeed well known (Papoulis 1984) that $\Gamma_{\rm e}(\tau)\rightarrow E[w_{\rm e}(t)]^2/m_{\rm e}=m_{\rm e}$ where $\tau\rightarrow\infty$ , as the quantities $w_{\rm e}(t)$ and $w_{\rm e}(t+\tau)$ become statistically independent. The autocorrelation tends towards the mean value of $w_{\rm e}$ , i.e. the percentage of time with $w_{\rm e}=1$ . This filling factor was found to be about 40 percent during the first two years and only slightly more than 30 percent in 2007, due to a relatively long technical interruption during the first half of that winter season.

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig1.eps}\vspace*{-1.5mm} \end{figure}$	Figure 1: Autocorrelation $\Gamma _{\rm e}(\tau )$ of the existing data window, averaged over the 2005 and 2006 winter seasons. The one-day periodicity is clearly visible.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig2.eps}\vspace*{-2mm} \end{figure}$	Figure 2: Autocorrelation $\Gamma _{\rm e}(\tau )$ of the winter 2007 data window function. A long gap due to an important technical problem occurred during that winter, so that the overall filling factor is a little less, but with two astronomers wintering over instead of only one, the amplitude of the 24-h periodicity is drastically reduced.
Open with DEXTER

3 The summer situation

There are generally a few more observers in summer, but there is also more technical maintenance, so the number of gaps in the data are not shorter than in winter. The overall filling factors are still between 30 and 40 percent but with several people in charge of the data acquisition, the one-day periodicity is almost absent in the window $w_{\rm e}(t)$ (not shown here). However, the seeing itself has a 24-h periodicity because it displays a minimum every day in the afternoon (Aristidi et al. 2005), so that the autocorrelation of the good seeing window function $\Gamma _{\rm g}(\tau )$ , obtained by the division of $\Gamma_{\rm ge}(\tau)$ by $\Gamma _{\rm e}(\tau )$ , is then expected to display a large amplitude one-day periodicity. This is confirmed by the the autocorrelation shown in Fig. 3, which has been averaged over all available summer seasons from 2003/2004 up to 2007/2008 and is therefore statistically very robust.

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig3.eps}\vspace*{-3.5mm} \end{figure}$	Figure 3: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing data window, averaged over all the summer seasons from 2003/2004 up to 2007/2008. This time, the one-day periodicity is not caused by data gaps but by a real daily variability of the seeing.
Open with DEXTER

This figure deserves some comments. The first comment is about the asymptotic behaviour of the autocorrelation, which oscillates between 0.42 and 0.72, about a mean value of 0.57. This means that 57 percent of the time during the 3-month summer season the seeing is better than our threshold $\sigma_{\rm g} = 0.5$ arcsec. Another comment concerns the first 6 h, where the autocorrelation shows an almost exactly linear decrease, which corresponds to a rectangular window function. This therefore means that a significant part of the summer good seeing sequences consist of continuous sequences of 6 h long on average, every day at the same time. This is precisely what we already know about the summer seeing (see Fig. 3 in Aristidi et al. 2005), which has been measured to be better than 0.5 arcsec between 2 and 8 pm every day in summer.

We noted that while 6 h per day represents 25 percent, the total fraction of good seeing data is statistically more than twice this percentage. There are many other episodes of good seeing in summer, which are shorter and more randomly distributed. For instance, the quick decrease in the autocorrelation from 1 to $\sim$ 0.9 in the first few minutes indicates that an order of 10 percent of good or poor seeing events occur as isolated events of one or a very few consecutive 2-min measurements.

Apart from this very last remark, our autocorrelation analysis of summer data does not provide much new information indeed. It does however qualify the method and is used as a reference for understanding the winter data.

4 The winter situation

We consider Fig. 4, which provides the mean autocorrelation function $\Gamma _{\rm g}(\tau )$ of the good seeing windows averaged over 4 winter seasons from 2005 to 2008. This is the seeing measured on the Concordiastro platform at 8 m. Thanks to the 24 months of data exploited here, this autocorrelation is again statistically very robust.

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig4.eps}\vspace*{-2mm} \end{figure}$	Figure 4: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing windows, averaged over 4 winter seasons seasons from 2005 to 2008. The 5 parameters fit described by Eq. (2) is superimposed on the curve.
Open with DEXTER

The asymptotic value of this autocorrelation, which is slightly less than 0.2, is a good approximation of the probability of obtaining good seeing values, i.e. being above the turbulent boundary layer at 8 m high. It confirms the estimation of 18% made by means of the histogram integrals (Aristidi et al. 2009).

The origin drops sharply from 1 to about 0.8. It confirms the existence of very short sequences (typically shorter than 10 mn) where the seeing is either continuously good or bad. These individual events were noticed by the observers, and represent 20% of the data. In addition, the graph of $\Gamma _{\rm g}(\tau )$ shows three main features. A linear decrease in the first 7 h, followed by a negative exponential distribution of characteristic time of a few tens of h, and an horizontal asymptote towards large values of $\tau$ . We converted $\Gamma _{\rm g}(\tau )$ by applying the following 5 parameter fit:

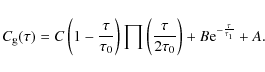
$\begin{displaymath}C_{\rm g}(\tau) = C \left(1 - \frac{\tau}{\tau_0}\right)\prod... ...rac{\tau}{2\tau_0}\right)+B {\rm e}^{- \frac{\tau}{\tau_1}}+A. \end{displaymath}$

(2)

The first term accounts for the linear part and is truncated by the rectangle function $\prod\left( \frac{\tau}{2\tau_0}\right)$ , which equals 0 when $\tau>\tau_0$ . We found that:

the asympotic value A=0.16, which represents the overall probability to observing during a good seeing;
the parameters of the exponential decrease are B=0.52 and 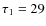$\tau_1=29$ h;
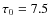the parameters of the linear decrease are C=0.08, $\tau_0=7.5$ h.

The linear part is similar to what is obtained in summer, and is indeed the autocorrelation of a rectangular window function. It shows that many good seeing sequences occur in continuous runs lasting $\tau_0=7.5$ h on average. An important difference, though, is that in summer, these 6 h sequences reoccur every day at the same time, while in winter, no significant daily periodicity is found. The exponential decrease that follows this initial linear behavior is a typical winter feature and must be interpreted.

We propose a model for the temporal window function $w_{\rm g}(t)$ , that depends on several parameters adjusted to ensure so that its autocorrelation correctly reproduces the autocorrelation $C_{\rm g}(\tau)$ of the data. We model $w_{\rm g}(\tau)$ by using well separated episodes including several rectangular functions of width 7.5 h. The mean delay between two consecutive episodes is T=10 days.

During an episode, the rectangular functions begin at times $t_{\rm i}$ , where $t_{\rm i}$ is a random variable with a negative exponential distribution of damping time $\tau_1=29$ h. This implies that most of the windows appear at the beginning of the episode and tend to disappear after a delay of 29 h from the beginning of the episode. The mean number $N_{\rm r}$ of rectangular windows within a 10 day episode is adjusted to account for the value of B in the function $C_{\rm g}(\tau)$ (Eq. (2)). We found that $N_{\rm r}=11$ . These 11 windows are concentrated mostly in the first 29 h of the episode and there can be large overlaps. In our simulation, more than 75% of the good seeing values are concentrated in the first 48 h of a 10-day episode. Figure 5 shows an example of such a 2-day episode.

In addition to these episodes, and to account for the initial quick drop of $\Gamma _{\rm g}(\tau )$ , we simply simulated the initial drop by adding a random number $N_{\rm i}$ of isolated measurements of either good or poor seeing (lasting two minutes). $N_{\rm i}$ is adjusted to be 0.22.

The general figure at 8 m is then that every 10 days on average, there is a two to three day episode during which many nearly uninterrupted runs of good seeing occur with individual durations of 7.5 h.

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig5.eps}\vspace*{-2mm} \end{figure}$	Figure 5: A nice sequence of good seeing data obtained in winter 2005 at 8 m high. During 50 h, there are only a few nearly individual values above the 0.5 arcsec threshold, but also an 11-h gap.
Open with DEXTER

The seeing at 20 m high.

Only a little more than 3 months of data have been collected at this height so that the statistical robustness is not as good as it is at 8 m. Figure 6 shows the autocorrelation function $\Gamma _{\rm g}(\tau )$ of the good seeing windows at 20 m. This curve is clearly not as smooth as the other one, because of its weaker statistical robustness. The one-day periodicity is visible because a large part of this data set (from July, 23rd to October, 31st) originates in spring when the Sun is present, only part of the time but a longer and longer part until the end of the run. However, the same kind of fit can be attempted and works well. Interestingly enough, the 29-h damping time of the exponential decrease is not modified by this higher altitude. This may presumably be explained by it depending mostly on the meteorological general situation, which should not be affected by a few meters difference of altitude. On the other hand, the nearly linear decrease that was explained by uninterrupted runs of 7.5 h is still present, with now a twice longer duration of 15 h. The numbers A and B are fitted to be 0.36 and 0.27, respectively. The value A=0.36 is coherent with the good seeing fraction of 40% derived from the histograms (Aristidi et al. 2009). In our simulations, $N_{\rm r}$ must be adjusted to be between 6 and 7. This is again indicative of plenty of overlaps and a mean fraction of good seeing of about 90 percent during the first 48 h of a simulated episode. The delay T between consecutive episodes is found to be twice as shorter, around 5 days. The two delays between consecutive episodes, 10 and 5 days, imply that during the 100-day winter time (without any sunrise), the mean numbers of such good seeing episodes must be about 10 at 8 m and 20 at 20 m.

This difference can be statistically explained by assuming that half the good seeing episodes at 20 m correspond to a boundary layer upper limit that goes down below 20 m but not as low as 8 m, the other half including situations when it will also spend some time below 8 m. The same 29-h exponential decrease at both altitudes is consistent with our model and its meteorological interpretation.

It would not be realistic to attempt a more rigorous interpretation of that curve, which provides an estimate of what happens at an altitude of 20 m. However, this estimate is important as one has to consider wether an optimal choice for a future high angular resolution instrument at Dome C is to set it at $\sim$ 20 m, together with a well qualified GLAO system. It would then enjoy a statistics of free atmosphere seeing of about 40 percent of the time during all the dark and cold periods, concentrated inside episodes of at least two days with several uninterrupted runs with individual durations of at least 15 h. Approximately 20 of these episodes may occur during all the dark period, which would definitely permit long integrations in very good seeing conditions.

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig6.eps}\vspace*{-2mm} \end{figure}$	Figure 6: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing data window, at 20-m high during 3 months in winter/spring 2005, with the same kind of fit.
Open with DEXTER

5 Discussion and conclusions

Thanks to the very long data sets exploited here, the validity of the autocorrelation division for correcting the data interruptions and the final statistical robustness are well validated by the summer season analysis and results. At least at a height of 8-m. The smaller amount of data available at 20-m high makes the statistical robustness of the numbers visibly weaker, but the general tendency tends to reinforce the interpretation of the 8-m data. The 29-h exponential decay of the distribution of the good runs starting times, assumed to depend on the meteorological situation, is found to be the same at both altitudes. The second characteristic time $\tau_0$ , which can be regarded as the minimum duration of nearly uninterrupted good runs, is found twice as long at 20 m, i.e. 15 h compared to 7.5 h at 8 m. Finally, the number of episodes of excellent seeing is estimated to be twice as frequent at 20 m, 20 times compared to 10 times per winter, which can be understood with a reasonable assumption about the vertical motions of the boundary layer upper limit.

Acknowledgements

We wish to thank the French and Italian Polar Institutes, IPEV and PNRA and the CNRS for the financial and logistical support of this programme. Thanks also to the different logistics teams on the site who helped us to set up the experiments. We are also grateful to our industrial partners ``Optique et Vision'' and ``Astro-Physics'' for technical improvements of the telescopes and their help in finding solutions to critical technical failures on the site. Thanks to our colleagues Max Azouit and François Martin for constant help and ideas since the beginning of the project. Thanks to F. Vakili, the director of Fizeau laboratory, for his support. We thank all the people who gave a hand in setting up the instruments during the summer campaigns since the end of 2003. Finally, thanks to the referee who helped improving the presentation.

References

Aristidi, E., Agabi, A., Fossat, E., et al. 2005, A&A, 444, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Aristidi, E., Fossat, E., Agabi, A., et al. 2009, A&A, 499, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lazrek, M., & Hill, F. 1993, ASP Conf. Ser., 42, 449 [NASA ADS] [Google Scholar]
Papoulis, A. 1984, Probability, random variables and stochastic processes (McGraw-Hill) [Google Scholar]

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig1.eps}\vspace*{-1.5mm} \end{figure}$	Figure 1: Autocorrelation $\Gamma _{\rm e}(\tau )$ of the existing data window, averaged over the 2005 and 2006 winter seasons. The one-day periodicity is clearly visible.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig2.eps}\vspace*{-2mm} \end{figure}$	Figure 2: Autocorrelation $\Gamma _{\rm e}(\tau )$ of the winter 2007 data window function. A long gap due to an important technical problem occurred during that winter, so that the overall filling factor is a little less, but with two astronomers wintering over instead of only one, the amplitude of the 24-h periodicity is drastically reduced.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig3.eps}\vspace*{-3.5mm} \end{figure}$	Figure 3: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing data window, averaged over all the summer seasons from 2003/2004 up to 2007/2008. This time, the one-day periodicity is not caused by data gaps but by a real daily variability of the seeing.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig4.eps}\vspace*{-2mm} \end{figure}$	Figure 4: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing windows, averaged over 4 winter seasons seasons from 2005 to 2008. The 5 parameters fit described by Eq. (2) is superimposed on the curve.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig5.eps}\vspace*{-2mm} \end{figure}$	Figure 5: A nice sequence of good seeing data obtained in winter 2005 at 8 m high. During 50 h, there are only a few nearly individual values above the 0.5 arcsec threshold, but also an 11-h gap.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{14186fig6.eps}\vspace*{-2mm} \end{figure}$	Figure 6: Autocorrelation $\Gamma _{\rm g}(\tau )$ of the good seeing data window, at 20-m high during 3 months in winter/spring 2005, with the same kind of fit.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Homepage

Table of Contents