| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014164 | |
| Published online | 29 July 2010 | |
Mixing of CNO-cycled matter in massive stars![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
N. Przybilla1 - M. Firnstein1 - M. F. Nieva2 - G. Meynet3 - A. Maeder3
1 - Dr. Karl Remeis-Observatory & ECAP,
Astronomical Institute, Friedrich-Alexander University
Erlangen-Nuremberg, Sternwartstr. 7, 96049 Bamberg, Germany
2 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
3 -
Geneva Observatory, University of Geneva, Maillettes 51, 1290 Sauverny, Switzerland
Received 29 January 2010 / Accepted 17 April 2010
Abstract
Aims. We test predictions of evolution models on mixing of
CNO-cycled products in massive stars from a fundamental perspective.
Relative changes within the theoretical C:N:O abundance ratios and the
buildup of helium are compared with observational results.
Methods. A sample of well-studied Galactic massive stars is
presented. High-quality optical spectra are carefully analysed using
improved NLTE line-formation and comprehensive analysis strategies. The
results are put in the context of the existing literature data.
Results. A tight trend in the observed N/C vs. N/O ratios and
the buildup of helium is found from the self-consistent analysis of
main-sequence to supergiant stars for the first time. The catalytic
nature of the CNO-cycles is confirmed quantitatively, though further
investigations are required to derive a fully consistent picture. Our
observational results support the case of strong mixing, as predicted
e.g. by evolution models that consider magnetic fields or by models
that have gone through the first dredge-up in the case of many
supergiants.
Key words: stars: abundances - stars: atmospheres - stars: early-type - stars: evolution - stars: massive - supergiants
1 Introduction
Energy production in massive stars is governed by the CNO-cycles throughout most of their lifetimes. The general correctness of our understanding of the CNO cycles and of the relevant nuclear data (e.g. Maeder 1983) is confirmed impressively by observation: when massive stars enter the Wolf-Rayet phase as WN subtypes, equilibrium CNO-processed material becomes exposed on their surface (see e.g. Crowther 2007).
However, traces of mixing of CNO-cycled products from the stellar core to the stellar surface can already be found much earlier in the lives of massive stars. Observational indications of superficial abundance anomalies for carbon, nitrogen, and oxygen (and the burning product helium) in OB-type stars even on the main sequence (MS) and, more prominently, in the blue supergiants was found early in classification spectrograms (e.g. Walborn 1976). Subsequent analyses provided evidence for a characteristic enrichment of nitrogen - which is the easiest to be detected - and helium in many early-type stars, both near the MS and in blue supergiants (e.g. Herrero et al. 1992; Lyubimkov 1996; Schönberner et al. 1988; McErlean et al. 1999; Gies & Lambert 1992; Kilian 1992; Venn 1995).
A theoretical understanding of early mixing of CNO-processed material to the stellar surface could not be achieved within the framework of evolution calculations for non-rotating stars with mass-loss, which were state-of-the-art at that time (e.g. Chiosi & Maeder 1986). The pollution of the surface layers with CNO-cycled material only occurs when the star reaches the red supergiant phase in such models, via convective dredge-up.
Considered a secondary effect for a long time, stellar rotation has come lately into focus. It turned out that rotationally-induced mixing through meridional circulation and turbulent diffusion in rotating stars provides the means to change all model outputs substantially and to bring theory and observation into much better agreement (Maeder & Meynet 2000; Heger & Langer 2000). The latest step taken in the modelling was to consider the effects from an interplay of rotation and magnetic fields, which - depending on the detailed input physics and approximations made - only provide minor modifications to the surface abundances (Heger et al. 2005) or substantial changes (Maeder & Meynet 2005, henceforth abbreviated as MM05). These differences result mainly from the two groups using different sets of equations for computing the effects of magnetic fields; see in particular, the changes brought to the system of equations given by Spruit (2002) by MM05 in their Sect. 2.
The only means to verify the models is via systematic comparison with observations covering the relevant parts of the Hertzsprung-Russell diagram. Homogeneous analyses of a larger star sample from the main sequence to the supergiant stage have only recently become available. The results in particular for N abundances apparently challenge the concept of rotational mixing in massive stars (Hunter et al. 2009) and thus the present-day evolution models (see, however, Maeder et al. 2009).
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{14164fg1a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm]{14164fg1b.eps} }
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg7.png)
|
Figure 1:
Status of observational constraints on the (magneto-)hydrodynamic
mixing of CNO-burning products in massive stars from previous NLTE
analyses. Mass ratios N/C
over N/O are displayed. Left panel: main-sequence stars.
Circles: Kilian (1992); triangles: Gies & Lambert (1992);
diamonds: Cunha & Lambert (1994), Daflon et al. (2001b,a,1999);
squares: Morel et al. (2008); crosses: Hunter et al. (2009).
Right panel: BA supergiants.
Triangles: Venn (1995), Venn & Przybilla (2003);
circles: Takeda (2000); squares: Crowther et al. (2006); diamonds: Searle et al. (2008).
Error bars are omitted for clarity: uncertainties in the
abundances of the individual elements are typically about a factor 2, such that the
error bars can be larger than the plotting range.
The lines represent predictions from evolution
calculations, for a rotating 15 |
| Open with DEXTER | |
Here, we address the topic of early mixing of CNO-cycled products in massive stars from a fundamental perspective. We compare the model predictions for the relative changes within the C:N:O abundance ratios and the buildup of helium (Sect. 2) with observations. For this we briefly review the status of the literature on CNO abundances and introduce a well-studied Galactic star sample for which high-accuracy analyses of high-quality spectra were performed using improved NLTE modelling and comprehensive analysis techniques (Sect. 3). Conclusions from this comparison are drawn in Sect. 4.
2 Theoretical considerations
Diagnostic plots of an abundance ratio vs. another one, such as N/C vs.
N/O or helium vs. N/O discussed in this paper, depend on both the
changes produced by nuclear reactions and the dilution effects produced
by mixing. Let us estimate the slope
![]() produced
by the nuclear effects at the beginning of CNO burning, with everything
expressed in mass fractions. Apart from the very massive stars (M > 40
produced
by the nuclear effects at the beginning of CNO burning, with everything
expressed in mass fractions. Apart from the very massive stars (M > 40 ![]() ), one may assume that, at the beginning of the burning,
the 14N enhancement comes from the 12C destruction via the
CN cycle, and the oxygen content O remains about constant. Thus, one has
), one may assume that, at the beginning of the burning,
the 14N enhancement comes from the 12C destruction via the
CN cycle, and the oxygen content O remains about constant. Thus, one has
![]() since
14N globally results from the addition of two protons to 12C,
since
14N globally results from the addition of two protons to 12C,
| |
= | ||
| = | ![$\displaystyle \frac{\rm dN}{\rm C} -\frac{\rm N}{\rm C^2} ~ \frac{\rm dC}{\rm d...
... dN}=
\frac{\rm dN}{\rm C}\left[1+ \frac{6}{7}~\frac{\rm N}{\rm C} \right]\cdot$](/articles/aa/full_html/2010/09/aa14164-10/img13.png)
|
(1) |
This gives the slope
always in mass fractions. With initial
This ratio is evidently greater than 1, since as N starts growing, C decreases, while O does not vary much. The relation turns slightly upward as N/C is increasing owing to the term in brackets in Eq. (2). However, at some advanced stage in evolution, corresponding to WN stars not shown here, the curve will saturate and turn down slightly (Maeder 2009, p. 699), since the CN cycle is then at equilibrium, while 16O is still turned to 14N. Dilution mixes a fraction f of N +
The value of f, however, determines the amplitudes of the departures from the cosmic ratios.
Our models with rotational mixing (Meynet & Maeder 2003, MM03;
Ekström et al. 2008, E08) or with rotation and magnetic fields
(MM05), as illustrated e.g. in Fig. 1,
have an initial slope
![]() ,
which is in excellent agreement with Eq. (3).
The amplitude f of the mixing depends on the various model assumptions, in particular
on the treatment of the shear mixing with or without horizontal turbulence.
The models without horizontal turbulence (Meynet & Maeder 2000, MM00)
predict more mixing than models that account for it (MM03).
Models that include both rotation and magnetic field predict a still larger
mixing (MM05).
,
which is in excellent agreement with Eq. (3).
The amplitude f of the mixing depends on the various model assumptions, in particular
on the treatment of the shear mixing with or without horizontal turbulence.
The models without horizontal turbulence (Meynet & Maeder 2000, MM00)
predict more mixing than models that account for it (MM03).
Models that include both rotation and magnetic field predict a still larger
mixing (MM05).
Let us now consider the behaviour of the helium surface content
![]() vs. N/O (as illustrated later).
Strictly and only at the very beginning
of the CN burning, and under the assumption of an initially constant
oxygen, we get
vs. N/O (as illustrated later).
Strictly and only at the very beginning
of the CN burning, and under the assumption of an initially constant
oxygen, we get
![]() ,
since
when 4 units of mass of helium are made, 14 units of mass of nitrogen are produced.
The slope is
,
since
when 4 units of mass of helium are made, 14 units of mass of nitrogen are produced.
The slope is
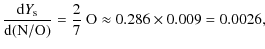
|
(4) |
i.e., it is essentially flat initially. Later in the evolution, both N and O change simultaneously, and one has to rely on numerical models. The resulting slope in the models can vary; e.g., a steeper slope is inferred for the 25
Table 1: Stellar parameters and elemental abundances of the sample stars.
3 Observational constraints
Numerous studies of CNO abundances in massive stars of the Milky Way are available from the literature, mostly for early B-type stars close to the MS and for B and A-type supergiants. We illustrate the results of several key publications in the N/O-N/C diagrams of Fig. 1. Some of the more recent studies (Crowther et al. 2006; Searle et al. 2008; Hunter et al. 2009) are based on NLTE model atmospheres, while the bulk of the data were obtained from NLTE line-formation computations on LTE model atmospheres - which is equivalent to the full NLTE approach in the cases under consideration (Nieva & Przybilla 2007, NP07).
The MS stars show a concentration around the solar ratios of N/C ![]() 0.3 and
N/O
0.3 and
N/O ![]() 0.1. However, overall a wide range of N/O-N/C
combinations has been realised, with the deviations from the predictions
increasing in the supergiants. On the one hand, this leaves room for broad
interpretation - even more so if only one of the elements (like
N) is considered - including the statement that some
observational data points pose
a challenge for the evolution models. On the other hand, most of
the data are nevertheless consistent with the predictions, as the abundance
uncertainties are very large. Typically, the statistical 1
0.1. However, overall a wide range of N/O-N/C
combinations has been realised, with the deviations from the predictions
increasing in the supergiants. On the one hand, this leaves room for broad
interpretation - even more so if only one of the elements (like
N) is considered - including the statement that some
observational data points pose
a challenge for the evolution models. On the other hand, most of
the data are nevertheless consistent with the predictions, as the abundance
uncertainties are very large. Typically, the statistical 1![]() -error in
abundance per element is about a factor
-error in
abundance per element is about a factor ![]() 2, and systematic
uncertainties are often largely underestimated (for a
discussion of this see Nieva & Przybilla 2010)
or even unaccounted for. The error bars in Fig. 1 are
larger than the entire plotting range in many cases. In consequence,
no definite conclusions can be drawn on the quality of the stellar
evolution models from these data.
2, and systematic
uncertainties are often largely underestimated (for a
discussion of this see Nieva & Przybilla 2010)
or even unaccounted for. The error bars in Fig. 1 are
larger than the entire plotting range in many cases. In consequence,
no definite conclusions can be drawn on the quality of the stellar
evolution models from these data.
In past years a number of high-accuracy studies of massive stars in the solar neighbourhood have been published by us. Carefully analysed data are available on 6 slowly-rotating early B-type stars near the MS (Nieva & Przybilla 2007; Przybilla et al. 2008; Nieva & Przybilla 2006,2008, PNB08) and on 14 BA-type supergiants (Przybilla et al. 2006; Schiller & Przybilla 2008; Firnstein 2006).
In brief, high-resolution (R = 40-48 000) and high-S/N
spectra (S/N > 300) with wide wavelength coverage and thorough
continuum normalisation (obtained with FOCES@Calar Alto
Observatory and FEROS@ESO/La Silla) were analysed using a hybrid NLTE approach
(Przybilla et al. 2006; NP07). State-of-the-art atomic input data were
used in the modelling. In contrast to all previous work, multiple hydrogen
lines, the helium lines, multiple metal ionisation
equilibria and the stellar energy distributions were reproduced
simultaneously in an iterative approach to determine the stellar
atmospheric parameters.
Chemical abundances were derived from analysis of practically the entire
observable spectrum per element. The rewards of such a comprehensive,
but time-consuming procedure are unprecedentedly small statistical error margins and largely
reduced systematics. The relevant results - effective temperature
![]() ,
surface gravity
,
surface gravity ![]() ,
projected rotational velocity
,
projected rotational velocity ![]() ,
surface helium abundance
,
surface helium abundance ![]() ,
CNO abundances and their total, and the zero-age MS mass
(derived under the assumption that the objects have evolved
directly from the MS) - are summarised in Table 1
and visualised in Figs. 2-6. We re-ran the
analysis of the supergiant targets for the present work, taking
advantage of improved model grids.
Our new results for these supergiants agree with the earlier ones within the uncertainties but are more accurate.
,
CNO abundances and their total, and the zero-age MS mass
(derived under the assumption that the objects have evolved
directly from the MS) - are summarised in Table 1
and visualised in Figs. 2-6. We re-ran the
analysis of the supergiant targets for the present work, taking
advantage of improved model grids.
Our new results for these supergiants agree with the earlier ones within the uncertainties but are more accurate.
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg174.png)
|
Figure 2:
Sample stars in the
|
| Open with DEXTER | |
The sample is displayed in the
![]() -
-![]() -plane
and compared to evolutionary tracks for rotating
stars
-plane
and compared to evolutionary tracks for rotating
stars![]() in Fig. 2.
The stars have initial masses between about 9 to 25
in Fig. 2.
The stars have initial masses between about 9 to 25 ![]() .
Stars close to the MS are apparently slow rotators, while
the atmospheric expansion has erased any indication of the initial
rotational velocity in the supergiants. There is good qualitative
agreement between the observations and predictions for the N/C ratios,
finding low values close to the initial (solar) ratio
near the MS and enhanced values in the supergiants. However, the
observed N/C ratios reach much higher values than predicted by the models
discussed in Fig. 2,
provided these stars have
recently left the MS and evolve now into red supergiants.
.
Stars close to the MS are apparently slow rotators, while
the atmospheric expansion has erased any indication of the initial
rotational velocity in the supergiants. There is good qualitative
agreement between the observations and predictions for the N/C ratios,
finding low values close to the initial (solar) ratio
near the MS and enhanced values in the supergiants. However, the
observed N/C ratios reach much higher values than predicted by the models
discussed in Fig. 2,
provided these stars have
recently left the MS and evolve now into red supergiants.
The behaviour of light element abundances of the MS sample stars is
shown in Fig. 3.
Theoretical evolutionary tracks are
overplotted. It is striking to see that, regardless of the initial mass and
of the initial rotation, the slope of the theoretical tracks
is always the same and equal to the nuclear effect of the CN cycle as
derived analytically in Sect. 2![]() . Thus the observed slope is
a confirmation of the activity of the CN cycle. It does not depend on the
stellar model but constitutes observational evidence of the nuclear path.
As already indicated before, what is model dependent are the
amplitudes of the departure from the cosmic ratios.
Figure 3 shows that the observed points may be reproduced
from models having differing velocities and masses, with and without
magnetic field;
however, by itself this diagram cannot help in disentangling the
various possibilities.
. Thus the observed slope is
a confirmation of the activity of the CN cycle. It does not depend on the
stellar model but constitutes observational evidence of the nuclear path.
As already indicated before, what is model dependent are the
amplitudes of the departure from the cosmic ratios.
Figure 3 shows that the observed points may be reproduced
from models having differing velocities and masses, with and without
magnetic field;
however, by itself this diagram cannot help in disentangling the
various possibilities.
The same evolutionary tracks are plotted in the N/C vs. ![]() diagram in Fig. 4. We see that, except for the stars HD 61068 and
HD 149438 (
diagram in Fig. 4. We see that, except for the stars HD 61068 and
HD 149438 (![]() Sco, which is a genuine slow rotator with a
rather strong magnetic field
Sco, which is a genuine slow rotator with a
rather strong magnetic field![]() of probably fossil origin, Donati et al. 2006), the other points may
be accounted for by models having low initial rotation. HD 61068 is marginally
compatible with the 15
of probably fossil origin, Donati et al. 2006), the other points may
be accounted for by models having low initial rotation. HD 61068 is marginally
compatible with the 15 ![]() model
at
model
at
![]() = 300 km s-1computed with magnetic field, while
= 300 km s-1computed with magnetic field, while
![]() Sco challenges present stellar models. It has a behaviour
that may be explained by a homogeneous evolution, but this still has
to be confirmed by further computations. This is a very
interesting star that certainly deserves further inspections both from the
observational and theoretical points of view.
Sco challenges present stellar models. It has a behaviour
that may be explained by a homogeneous evolution, but this still has
to be confirmed by further computations. This is a very
interesting star that certainly deserves further inspections both from the
observational and theoretical points of view.
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg176.png)
|
Figure 3:
Comparison of N/C vs. N/O abundance ratios (by mass) for our
six MS sample stars (diamonds) with model predictions for 9 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg177.png)
|
Figure 4:
N/C abundance ratios on the MS as function
of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg178.png)
|
Figure 5:
N/C vs. N/O abundance ratios (by mass) for our sample stars.
B-type MS stars are displayed as diamonds, BA-type supergiants
as circles. The symbol size encodes the stellar mass and error bars
give 1 |
| Open with DEXTER | |
The behaviour of light element abundances in the whole star sample is shown in Fig. 5. In contrast to the literature values (Fig. 1), a clear and tight trend is found, confirming the predicted locus of N/O-N/C abundance ratios. However, as already indicated above, the MM03 models for rotating stars with mass loss evolving towards the red supergiant stage (solid line in Fig. 5) predict mixing that is too low, i.e. too low f (Sect. 2), in particular for most of the supergiants. A combination of five reasons may provide an explanation.
- I)
- Higher than average rotation velocities in the progenitor stars of these supergiants on the MS may reconcile the situation for some objects.
- II)
- Evolution models for rotating stars that also account for the interaction of rotation and a magnetic dynamo (MM05) predict enhanced mixing signatures of the amount required (dotted line).
- III)
- Some stars may have evolved in a close binary, which can also lead to enhanced mixing associated with mass transfer.
- IV)
- Some objects may have been siblings to
 Sco on the
MS, climbing up the N/O-N/C relation even further in their further evolution.
Sco on the
MS, climbing up the N/O-N/C relation even further in their further evolution.
- V)
- Supergiants may already have evolved through the red supergiant phase (e.g., on a blue loop) to expose first dredge-up abundance ratios, which could quantitatively also explain the observations (dashed line).
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg180.png)
|
Figure 6:
Surface helium abundance |
| Open with DEXTER | |
We note, however, that we cannot exclude at present the possibility that the observed helium abundances in the supergiants may be overestimated. A systematic downward shift by a mere 10-15% (which is within the typical systematic uncertainties in our abundance determinations) would be sufficient, e.g., to bring the observations and the magnetic model in Fig. 6 into agreement. All observed lines arise from two energetically close He I levels only (2p 1P, 3P). Model atom shortcomings (such as insufficient ab-initio collisional data), which may become important only in the weak-line limit at the cool temperature border, could therefore remain unnoticed and could give rise to systematics. It would not be the first time that uncertainties in atomic data complicate the statistic equilibrium and radiative transfer calculations needed to interpret the observed He I lines (e.g. Przybilla 2005; Najarro et al. 2006). Further investigations are required before firm conclusions on the evolutionary state of the supergiants are drawn from the helium abundances, and a fully coherent picture can be deduced.
Finally, an inspection of the total of the CNO abundances
(see Table 1) is instructive. Because the CNO cycles are
catalytic, the sum of particles is conserved. Indeed, the sample shows only
a small scatter around the mean
combined abundance, ![]() CNO + 12 = 8.98
CNO + 12 = 8.98![]() 0.05. This
is further (indirect) evidence that chemical inhomogeneities among the massive
star population in the solar neighbourhood are small
(Nieva & Przybilla 2008; PNB08), even at extended distances out to 1-2 kpc from the Sun.
Predictions of a high efficiency of hydrodynamic mixing in the
interstellar medium and consequently of a locally well-mixed
Milky Way (Edmunds 1975; Roy & Kunth 1995) are thus supported as well.
0.05. This
is further (indirect) evidence that chemical inhomogeneities among the massive
star population in the solar neighbourhood are small
(Nieva & Przybilla 2008; PNB08), even at extended distances out to 1-2 kpc from the Sun.
Predictions of a high efficiency of hydrodynamic mixing in the
interstellar medium and consequently of a locally well-mixed
Milky Way (Edmunds 1975; Roy & Kunth 1995) are thus supported as well.
4 Conclusions
Evolution models for massive stars predict very tight relations for
the change-of-surface N/O and N/C abundance ratios and for the
buildup of helium, as a consequence of mixing with CNO-cycled matter
(for given initial chemical composition).
Massive stars in the solar neighbourhood, which supposedly share
a nearly uniform initial composition (PNB08), are
therefore expected to follow the predicted relations, which are
governed by nuclear reactions and the dilution effects
produced by mixing.
A comparison with NLTE spectral analyses from the literature
on CNO abundances in massive stars of ![]() 8-25
8-25 ![]() leaves room for broad interpretation because of large uncertainties.
Observations may even be interpreted as posing a challenge to theory,
in particular when the full set of information is not accounted for
and conclusions are drawn from one indicator alone, e.g. nitrogen.
leaves room for broad interpretation because of large uncertainties.
Observations may even be interpreted as posing a challenge to theory,
in particular when the full set of information is not accounted for
and conclusions are drawn from one indicator alone, e.g. nitrogen.
On the other hand, our high-precision analyses of a sample of Galactic massive stars from the main sequence to the supergiant stage find these tight correlations. Even though further investigations are required to refine the observational constraints on helium abundances before a fully coherent picture can be obtained, the case for strong mixing is clearly supported. It is predicted, e.g., by the models of MM00, by models with magnetic field (MM05), or in cases where the models have gone through the first dredge-up. The separation of the different possibilities may come from studying the evolution of the rotation velocities with time. On the one hand, models with magnetic field predict higher rotational velocities at the end of the MS phase, because the strong internal coupling transmits some of the fast core rotation to the surface. On the other hand, stars on a blue loop should be slower rotators than objects on their first passage from blue to red on average because of the additional angular-momentum loss experienced through strong mass loss during the red supergiant phase. Indeed, some of the slowest rotators show very strong mixing signatures (Table 1).
Finally, we have to point out that some of our results have the
potential of challenging the currently available evolution models.
The star ![]() Sco (HD 149438) stands out in the sample as it shows
characteristics that may be explained by a homogeneous evolution, but
it requires a highly-efficient spin-down mechanism. One may speculate on
magnetic breaking due to angular-momentum losses by a
magnetically confined line-driven stellar wind or magnetic coupling
to the accretion disc during the star-forming process in the case of a fossil field.
Even though the topic is not understood theoretically in a comprehensive
way, spin-down times of the order of 1 Myr (Ud-Doula et al. 2009) or even less
(Mikulásek et al. 2008) are reported for some magnetic massive stars,
possibly leading to the required slow rotation already on the
zero-age MS in this case as well. Then, if the present
helium abundances are confirmed and the supergiants are shown to have
evolved directly from the MS, a different kind of mixing may also be
required.
Sco (HD 149438) stands out in the sample as it shows
characteristics that may be explained by a homogeneous evolution, but
it requires a highly-efficient spin-down mechanism. One may speculate on
magnetic breaking due to angular-momentum losses by a
magnetically confined line-driven stellar wind or magnetic coupling
to the accretion disc during the star-forming process in the case of a fossil field.
Even though the topic is not understood theoretically in a comprehensive
way, spin-down times of the order of 1 Myr (Ud-Doula et al. 2009) or even less
(Mikulásek et al. 2008) are reported for some magnetic massive stars,
possibly leading to the required slow rotation already on the
zero-age MS in this case as well. Then, if the present
helium abundances are confirmed and the supergiants are shown to have
evolved directly from the MS, a different kind of mixing may also be
required.
We conclude that the tight observational constraints that are required for a thorough testing of the stellar evolution models are within reach. Applications of the improved modelling and analysis techniques to high-quality observations of larger star samples in the Milky Way and other galaxies may finally provide the empirical basis to benchmark the models. It may thus become feasible to disentangle the effects of metallicity, rotation, magnetic fields, and binarity on massive star evolution.
AcknowledgementsN.P. and M.F.N. would like to thank the staff at Geneva Observatory for their hospitality. M.F. acknowledges funding by the Deutsche Forschungsgemeinschaft, DFG under project number PR 685/3-1. Travel to the Calar Alto Observatory/Spain was supported by DFG under grant PR 685/1-1.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C., & Maeder, A. 1986, ARA&A, 24, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, K., & Lambert, D. L. 1994, ApJ, 426, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., & Becker, S. R. 1999, ApJ, 522, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., Becker, S. R., & Smith, V. V. 2001a, ApJ, 552, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., Butler, K., & Smith, V. V. 2001b, ApJ, 563, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Edmunds, M. G. 1975, Ap&SS, 32, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 (E08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Firnstein, M. 2006, Diploma Thesis, Univ. Erlangen-Nuremberg [Google Scholar]
- Gies, D. R., & Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. S. Kubono, & T. Kajino, 15 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Hubrig, S., Briquet, M., De Cat, P., et al. 2009, Astron. Nachr., 330, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilian, J. 1992, A&A, 262, 171 [Google Scholar]
- Lyubimkov, L. S. 1996, Ap&SS, 243, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1983, A&A, 120, 113 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin: Springer Verlag) [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2005, A&A, 440, 1041 (MM05) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Meynet, G., Ekström, S., & Georgy, C. 2009, CoAst, 158, 72 [Google Scholar]
- McErlean, N. D., Lennon, D. J., & Dufton, P. L. 1999, A&A, 349, 553 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 (MM00) [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 (MM03) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikulásek, Z., Krticka, J., Henry, G. W., et al. 2008, A&A, 485, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Hubrig, S., & Briquet, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najarro, F., Hillier, D. J., Puls, J., Lanz, T., & Martins, F. 2006, A&A, 456, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2006, ApJ, 639, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2007, A&A, 467, 295 (NP07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2008, A&A, 481, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2010, in ASP Conf. Ser., 425, 146 [Google Scholar]
- Przybilla, N. 2005, A&A, 443, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Butler, K., Becker, S. R., & Kudritzki R. P. 2006, A&A, 445, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Nieva, M. F., & Butler K. 2008, ApJ, 688, L103 (PNB08) [NASA ADS] [CrossRef] [Google Scholar]
- Roy, J.-R., & Kunth, D. 1995, A&A, 294, 432 [NASA ADS] [Google Scholar]
- Schiller, F., & Przybilla, N. 2008, A&A, 479, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönberner, D., Herrero, A., Becker, S. R., et al. 1988, A&A, 197, 209 [NASA ADS] [Google Scholar]
- Searle, S. C., Prinja, R. K., Massa, D., & Ryans, R. 2008, A&A, 481, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2000, PASJ, 52, 113 [NASA ADS] [Google Scholar]
- Ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2009, MNRAS, 392, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A. 1995, ApJ, 449, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A., & Przybilla, N. 2003, in ASP Conf. Ser., 304, 20 [Google Scholar]
- Walborn, N. R. 1976, ApJ, 205, 419 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Based on observations obtained at the European Southern Observatory, proposals 62.H-0176 & 074.B-0455(A).
- ...
![[*]](/icons/foot_motif.png)
- Based on observations collected at the Centro Astronómico Hispano Alemán at Calar Alto, proposals H2001-2.2-011 & H2005-2.2-016.
- ... initial
![[*]](/icons/foot_motif.png)
- The chemical composition of the evolution models is identical to those used in the OPAL opacity tables: the solar mixture of Grevesse & Noels (1993).
- ...
stars
![[*]](/icons/foot_motif.png)
- The metal content (by mass) of the models is Z = 0.020, while a value of 0.014 seems more appropriate for the massive star population in the solar neighbourhood (PNB08). No fundamental changes to our conclusions are expected to arise from this difference. The tracks will shift a bit, in particular the zero-age MS towards higher gravities.
- ...
![[*]](/icons/foot_motif.png)
- The theoretical slope varies
between
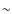 3.0
and 4.2 for typical initial CNO abundances
(e.g. solar values according to Anders & Grevesse 1989; Grevesse &
Sauval 1998; Asplund
et al. 2009, or the cosmic abundance
standard of PNB08), indicated by the grey area in
Fig. 3.
Improved agreement between observation and
theory may be achieved when tailored abundances are used for the
stellar evolution models, see also the previous footnote.
3.0
and 4.2 for typical initial CNO abundances
(e.g. solar values according to Anders & Grevesse 1989; Grevesse &
Sauval 1998; Asplund
et al. 2009, or the cosmic abundance
standard of PNB08), indicated by the grey area in
Fig. 3.
Improved agreement between observation and
theory may be achieved when tailored abundances are used for the
stellar evolution models, see also the previous footnote.
- ... field
![[*]](/icons/foot_motif.png)
- A magnetic field is present also in HD 74575 (Hubrig et al. 2009).
All Tables
Table 1: Stellar parameters and elemental abundances of the sample stars.
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{14164fg1a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm]{14164fg1b.eps} }
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg7.png)
|
Figure 1:
Status of observational constraints on the (magneto-)hydrodynamic
mixing of CNO-burning products in massive stars from previous NLTE
analyses. Mass ratios N/C
over N/O are displayed. Left panel: main-sequence stars.
Circles: Kilian (1992); triangles: Gies & Lambert (1992);
diamonds: Cunha & Lambert (1994), Daflon et al. (2001b,a,1999);
squares: Morel et al. (2008); crosses: Hunter et al. (2009).
Right panel: BA supergiants.
Triangles: Venn (1995), Venn & Przybilla (2003);
circles: Takeda (2000); squares: Crowther et al. (2006); diamonds: Searle et al. (2008).
Error bars are omitted for clarity: uncertainties in the
abundances of the individual elements are typically about a factor 2, such that the
error bars can be larger than the plotting range.
The lines represent predictions from evolution
calculations, for a rotating 15 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg174.png)
|
Figure 2:
Sample stars in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg176.png)
|
Figure 3:
Comparison of N/C vs. N/O abundance ratios (by mass) for our
six MS sample stars (diamonds) with model predictions for 9 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg177.png)
|
Figure 4:
N/C abundance ratios on the MS as function
of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg178.png)
|
Figure 5:
N/C vs. N/O abundance ratios (by mass) for our sample stars.
B-type MS stars are displayed as diamonds, BA-type supergiants
as circles. The symbol size encodes the stellar mass and error bars
give 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14164fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14164-10/Timg180.png)
|
Figure 6:
Surface helium abundance |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle \frac{\rm d(N/C)}{\rm d(N/O)}=
\frac{\rm (N/C)}{\rm (N/O)} \left[1+ \frac{6}{7}~ \frac{\rm N}{\rm C}\right] ,$](/articles/aa/full_html/2010/09/aa14164-10/img14.png)