| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014118 | |
| Published online | 30 July 2010 | |
Spectral optical monitoring of 3C 390.3 in 1995-2007
I. Light curves and flux variation in the continuum and broad
lines![[*]](/icons/foot_motif.png)
A. I. Shapovalova1 - L.C. Popovic2,3 - A. N. Burenkov1 - V. H. Chavushyan4 - D. Ilic3,5 - W. Kollatschny6 - A. Kovacevic3,5 - N. G. Bochkarev7 - L. Carrasco4 - J. León-Tavares8 - A. Mercado9 - J. R. Valdes4 - V. V. Vlasuyk1 - E. de la Fuente10
1 - Special Astrophysical Observatory of the Russian AS,
Nizhnij Arkhyz, Karachaevo-Cherkesia 369167, Russia
2 -
Astronomical Observatory, Volgina 7, 11160 Belgrade 74, Serbia
3 -
Isaac Newton Institute of Chile, Yugoslavia Branch
4 -
Instituto
Nacional de Astrofísica, Óptica y Electrónica, Apartado
Postal 51, CP 72000, Puebla, Pue. México
5 -
Department of Astronomy, Faculty of Mathematics, University
of Belgrade, Studentski trg 16, 11000 Belgrade, Serbia
6 -
Institut
für Astrophysik, Friedrich-Hund-Platz 1, Göttingen, Germany
7 -
Sternberg Astronomical Institute, Moscow, Russia
8 -
Aalto University Metsähovi Radio Observatory, Metsähovintie 114,
02540 Kylmälä, Finland
9 -
Universidad Politécnica de Baja California, Mexicali B.C.,
México
10 -
Instituto de Astronomia y Meteorologia, Dpto. de
Física CUCEI, Universidad de Guadalajara, Av. Vallarta 2602, CP
44130, Guadalajara, Jalisco, México
Received 22 January 2010 / Accepted 8 March 2010
Abstract
Context. We present the results of the long-term (1995-2007)
spectral monitoring of the broad-line radio galaxy
3C 390.3, a well known AGN with double-peaked broad
emission lines, usually assumed to be emitted from an accretion disk.
Aims. To explore dimensions and structure of the BLR, we analyze the light curves of the broad H![]() and H
and H![]() line fluxes and the continuum flux. To detect variations in the BLR, we analyze the H
line fluxes and the continuum flux. To detect variations in the BLR, we analyze the H![]() and H
and H![]() line profiles, as well as the change in the line profiles during the monitoring period.
line profiles, as well as the change in the line profiles during the monitoring period.
Methods. We attempt first to find a periodicity in the continuum and H![]() light curves, finding that there is a high probability of measuring
quasi-periodical oscillations. Using the line shapes and their
characteristics (such as e.g., peak separation and their intensity
ratio, or FWHM) of broad H
light curves, finding that there is a high probability of measuring
quasi-periodical oscillations. Using the line shapes and their
characteristics (such as e.g., peak separation and their intensity
ratio, or FWHM) of broad H![]() and H
and H![]() lines, we discuss the structure of the BLR. We also cross-correlate the continuum flux with H
lines, we discuss the structure of the BLR. We also cross-correlate the continuum flux with H![]() and H
and H![]() lines to determine the dimensions of the BLR.
lines to determine the dimensions of the BLR.
Results. During the monitoring period, we found that the broad emission component of the H![]() and H
and H![]() lines, and the continuum flux varied by a factor of
lines, and the continuum flux varied by a factor of ![]() 4-5. We also detected different structure in the line profiles of H
4-5. We also detected different structure in the line profiles of H![]() and H
and H![]() .
An additional central component appears to be present and superimposed
on the disk emission. In the period of high activity (after 2002), H
.
An additional central component appears to be present and superimposed
on the disk emission. In the period of high activity (after 2002), H![]() became broader than H
became broader than H![]() and red wing of H
and red wing of H![]() was higher than that of H
was higher than that of H![]() .
We detected time lags of
.
We detected time lags of ![]() 95 days between the continuum and H
95 days between the continuum and H![]() flux, and about 120 days between the continuum and H
flux, and about 120 days between the continuum and H![]() flux.
flux.
Conclusions. Variations in the line profiles, as well as
correlation between the line and continuum flux during the monitoring
period, are consistent with a disk origin of the broad lines and the
possible contribution of some additional region and/or some kind of
perturbation in the disk.
Key words: galaxies: active - quasar: individual: 3C 390.3 - line: profiles
1 Introduction
Active galactic nuclei (AGN) often exhibit variability in the broad emission lines. The region where broad lines are formed (hereinafter BLR - broad line region) is close to the central supermassive black hole and may hold basic information about the formation and fueling of AGN.
A long-term spectral monitoring of the nucleus of some AGN has revealed a time lag in the response of the broad emission lines relative to flux changes in the continuum. This lag depends on the size, geometry, and physical conditions of the BLR. Thus, the search for correlations between the nuclear continuum changes and flux variations in the broad emission lines may serve as a tool for mapping the geometrical and dynamical structure of the BLR (see e.g., Peterson 1993, and reference therein).
During the past decade, the study of the BLR in some objects has
achieved considerable success, mainly because of the increasing
number of coordinated multiwavelength monitoring campaigns through
the international ``AGN Watch'' program (see e.g., Peterson 1999).
Most of the objects, included in the AGN Watch, are radio-quiet Sy1
galaxies and only one, 3C 390.3 (z=0.0561), is a well known
broad-line radio galaxy. It is a powerful double-lobed FRII
radio-galaxy with a relatively strong compact core. The two extended
lobes, at a position angle of 144![]() ,
each one with a hot
spot, are separated by about 223
,
each one with a hot
spot, are separated by about 223
![]() (Leahy & Perley 1991). A faint
well-collimated thin jet at
(Leahy & Perley 1991). A faint
well-collimated thin jet at
![]() ,
connecting the
core to the northern lobe, was observed by Leahy & Perley (1995).
The VLBI observations at 5 GHz show evidence of the superluminal
motion (with
,
connecting the
core to the northern lobe, was observed by Leahy & Perley (1995).
The VLBI observations at 5 GHz show evidence of the superluminal
motion (with ![]() )
in this parsec-scale jet (Alef et al. 1988,1996).
)
in this parsec-scale jet (Alef et al. 1988,1996).
In a similar way to about 10% of radio-loud AGN, 3C 390.3 emits
very broad, double-peaked emission lines. A number of possible
models have been suggested to explain double-peaked line profiles:
supermassive binary black holes (Gaskell 1996), outflowing biconical
gas streams (Zheng 1996), or emission from an accretion disk
(Rokaki et al. 1992; Perez et al. 1988). The strong variability of this object, in both
continuum and emission lines is well known (Tao et al. 2008; Barr et al. 1980; Netzer 1982; Veilleux & Zheng 1991; Yee & Oke 1981; Clavel & Wamsteker 1987; Sergeev et al. 2002; Barr et al. 1983; Shapovalova et al. 2001; Wamsteker et al. 1997; Gupta et al. 2009; O'Brien et al. 1998; Dietrich et al. 1998). The
object is also a highly variable X-ray source, which has a spectrum
exhibiting a broad Fe K![]() line (Eracleous et al. 1996; Inda et al. 1994; Wozniak et al. 1998). During a
multiwavelength monitoring campaign in 1995, several,
large-amplitude, X-ray flares were observed in 3C 390.3; in one of
them, the X-ray flux increased by a factor of 3 in a period of 12
days (Leighly et al. 1997). The X-ray flux also varies on scales of several
days (Gliozzi et al. 2003; Gupta et al. 2009), exhibiting greater variation for a smaller
energy range (Gliozzi et al. 2003).
line (Eracleous et al. 1996; Inda et al. 1994; Wozniak et al. 1998). During a
multiwavelength monitoring campaign in 1995, several,
large-amplitude, X-ray flares were observed in 3C 390.3; in one of
them, the X-ray flux increased by a factor of 3 in a period of 12
days (Leighly et al. 1997). The X-ray flux also varies on scales of several
days (Gliozzi et al. 2003; Gupta et al. 2009), exhibiting greater variation for a smaller
energy range (Gliozzi et al. 2003).
In an analysis of IUE spectra of 3C 390.3 obtained during
1978-1986, Clavel & Wamsteker (1987) detected a variability time
lag of 50 and 60 days for the broad C IV ![]() 1549 and
Ly
1549 and
Ly![]() emission lines, relative to the UV-continuum changes.
However, from a reanalysis of the same spectral data, Wamsteker et al. (1997) derived a lag of
emission lines, relative to the UV-continuum changes.
However, from a reanalysis of the same spectral data, Wamsteker et al. (1997) derived a lag of
![]() days for C IV and
days for C IV and
![]() days for Ly
days for Ly![]() .
Furthermore, from the IUE monitoring
data from December 1994 to March 1996, O'Brien et al. (1998)
measured a corresponding lag of 35 days for the C IV
.
Furthermore, from the IUE monitoring
data from December 1994 to March 1996, O'Brien et al. (1998)
measured a corresponding lag of 35 days for the C IV
![]() emission line and 60 days for Ly
emission line and 60 days for Ly![]() .
From the
optical monitoring of 3C 390.3 during 1994-1995, Dietrich et al.
(1998) derived, however, a time lag of about 20 days for the Balmer
lines, i.e., their response with respect to changes in the X-ray
continuum. Furthermore, a temporal lag between the optical and the
UV or X-ray continua was not detected. From the spectrophotometric
monitoring of 3C 390.3 in 1995-1999, Shapovalova et al. (2001)
(Paper I, hereinafter) found that the lag of the H
.
From the
optical monitoring of 3C 390.3 during 1994-1995, Dietrich et al.
(1998) derived, however, a time lag of about 20 days for the Balmer
lines, i.e., their response with respect to changes in the X-ray
continuum. Furthermore, a temporal lag between the optical and the
UV or X-ray continua was not detected. From the spectrophotometric
monitoring of 3C 390.3 in 1995-1999, Shapovalova et al. (2001)
(Paper I, hereinafter) found that the lag of the H![]() emission
line relative to the continuum flux changes was
emission
line relative to the continuum flux changes was ![]() 100 days.
Sergeev et al. (2002) inferred a lag between the continuum and
H
100 days.
Sergeev et al. (2002) inferred a lag between the continuum and
H![]() variations for the centroid CCF of
variations for the centroid CCF of ![]() 89 days. The
UV-bump, usually observed in a large number of Seyfert galaxies, is
very weak or even absent in 3C 390.3 (Wamsteker et al. 1997).
89 days. The
UV-bump, usually observed in a large number of Seyfert galaxies, is
very weak or even absent in 3C 390.3 (Wamsteker et al. 1997).
Studies of the variations in both the continuum and broad
emission-line profiles and their correlations can provide
information about the BLR physics (see e.g., Shapovalova et al. 2009). The
double-peaked broad lines of 3C 390.3 are indicative of accretion
disk emission, therefore long period spectral variation in 3C 390.3
can help us determine the nature of accretion disks. In this paper,
we present the results of the spectral (H![]() and H
and H![]() )
monitoring of 3C 390.3 during the period between 1995 and 2007. This
work proceeds the long-term monitoring program for 3C 390.3 and our
first results were published in 2001 (Paper I). In this paper, we
present spectral data between 1995 and 2007, and we analyze the
continuum and H
)
monitoring of 3C 390.3 during the period between 1995 and 2007. This
work proceeds the long-term monitoring program for 3C 390.3 and our
first results were published in 2001 (Paper I). In this paper, we
present spectral data between 1995 and 2007, and we analyze the
continuum and H
![]() line variations. The paper is
organized as follow: in Sect. 2 we describe our observations and
data reduction, in Sect. 3 we present the analysis of the
observations, in Sect. 4 we discuss our results, and in Sect. 5 we
outline our conclusions.
line variations. The paper is
organized as follow: in Sect. 2 we describe our observations and
data reduction, in Sect. 3 we present the analysis of the
observations, in Sect. 4 we discuss our results, and in Sect. 5 we
outline our conclusions.
2 Observations and data reduction
2.1 Spectral observations
Spectra of 3C 390.3 (during 158 nights) were taken with the
6 m and
1 m telescopes of the SAO RAS (Russia, 1995-2007) and with INAOE's
2.1 m telescope of the ``Guillermo Haro Observatory'' (GHO) at
Cananea, Sonora, México (1998-2007). They were acquired using
long-slit spectrographs, equipped with CCD detector arrays. The
typical wavelength interval covered was from 4000 Å
to 7500 Å, the spectral resolution varied between 5 and
15 Å, and
the S/N ratio was >50 in the continuum near H![]() and
H
and
H![]() .
Spectrophotometric standard stars were observed every
night. The log of spectroscopic observations is given in Table 1 (available electronically only).
.
Spectrophotometric standard stars were observed every
night. The log of spectroscopic observations is given in Table 1 (available electronically only).
The spectrophotometric data reduction was carried out using either the software developed at SAO RAS or the IRAF package for the spectra obtained in México. The image reduction process included bias and flat-field corrections, cosmic ray removal, 2D wavelength linearization, sky spectrum subtraction, addition of the spectra for every night, and relative flux calibration based on standard star observations.
2.2 Absolute calibration (scaling) of the spectra
The standard technique of the flux calibration of spectra (i.e., comparison with stars of known spectral energy distribution) is not precise enough for the study of AGN variability, since even under good photometric conditions, the accuracy of spectrophotometry is not superior to 10%. Therefore we used standard stars only for a relative calibration.
For the absolute calibration, the fluxes of the narrow emission lines are adopted for scaling the AGN spectra, because they are known to remain constant on timescales of tens of years (Peterson 1993).
However, for 3C 390.3 there has been discussion about the
variability of the narrow lines. We considered this in more detail
in Paper I and found that in the case of 3C 390.3 there is no
reliable evidence of the [O III]
![]() 4959+5007
flux variability in timescales of between months and years.
Therefore, spectra were scaled by the [O III]
4959+5007
flux variability in timescales of between months and years.
Therefore, spectra were scaled by the [O III]
![]() 4959+5007 integrated line flux taken to be
4959+5007 integrated line flux taken to be
![]() erg s-1 cm-2 (Veilleux & Zheng 1991). To confirm this, we compared photometric fluxes in the V filter with the spectral fluxes (close to observed
erg s-1 cm-2 (Veilleux & Zheng 1991). To confirm this, we compared photometric fluxes in the V filter with the spectral fluxes (close to observed
![]() Å) obtained from spectra scaled by [OIII]
Å) obtained from spectra scaled by [OIII]
![]() 4959,5007. Spectra and photometric data were obtained using the
aperture
4959,5007. Spectra and photometric data were obtained using the
aperture
![]() ,
and
,
and
![]() ,
respectively.
Both observations were performed in the same, or in nearby nights
(separated by <3 days). The V magnitudes were transformed into
fluxes F(V) using the equation (Alen 1973; Wamsteker 1981; Dietrich et al. 1998)
,
respectively.
Both observations were performed in the same, or in nearby nights
(separated by <3 days). The V magnitudes were transformed into
fluxes F(V) using the equation (Alen 1973; Wamsteker 1981; Dietrich et al. 1998)
| (1) |
Figure 1 shows a correlation between photometric and spectral fluxes in the monitoring period. The regression line corresponds to the equation:
As can be seen from Fig. 1, there is a strong linear relationship between F(V) and F(sp) with the correlation coefficient R=0.99. This indicates that the [OIII] lines do not vary (at least on a level of a few percent) on timescales of
The scaling of the blue spectra was performed using the method of
Van Groningen & Wanders (1992) modified by Shapovalova et al.
(2004)![]() . This
method allowed us to obtain a homogeneous set of spectra with the
same wavelength calibration and the same [OIII]
. This
method allowed us to obtain a homogeneous set of spectra with the
same wavelength calibration and the same [OIII]![]() 5007 flux.
Red spectra were scaled to the constant flux value of the narrow
emission line [OI]
5007 flux.
Red spectra were scaled to the constant flux value of the narrow
emission line [OI]
![]() ,
by also applying the modified
method of Van Groningen & Wanders (1992) (see also Shapovalova
et al. 2004). As a reference, we used a red spectrum obtained with
the
GHAO 2.1 m telescope during a good photometric night, and
accurately
scaled using the [OIII]
,
by also applying the modified
method of Van Groningen & Wanders (1992) (see also Shapovalova
et al. 2004). As a reference, we used a red spectrum obtained with
the
GHAO 2.1 m telescope during a good photometric night, and
accurately
scaled using the [OIII]![]() 5007 line (details of the
procedure are given in Shapovalova et al. 2008).
5007 line (details of the
procedure are given in Shapovalova et al. 2008).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14118f01.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg33.png)
|
Figure 1: The correlation between the photometric - F(V) and spectral - F(sp) fluxes. |
| Open with DEXTER | |
2.3 Unification of the spectral data
To investigate the long-term spectral variability of an AGN, it is necessary to gather a consistent set of spectral data. This requires us, in turn, to correct the line and continuum fluxes for aperture effects (Peterson & Collins 1983), a detailed justification of which is given in Peterson et al. (1995), and will not be repeated here.
The NLR in 3C 390.3 is more compact than for most Sy1 galaxies. In
narrow-band [OIII] images, the object displays compact nuclear
emission without any extended structure (Baum et al. 1988). The results of
panoramic two-dimensional spectrophotometry of the nuclear region of
this object imply that the [OIII]![]() 5007 emission originates
in a zone smaller than r < 2 arsec (Bochkarev et al. 1997). Furthermore,
Osterbrock et al. (1975) obtained a rather low value of the [OIII] F(
5007 emission originates
in a zone smaller than r < 2 arsec (Bochkarev et al. 1997). Furthermore,
Osterbrock et al. (1975) obtained a rather low value of the [OIII] F(![]() 4363)/F(
4363)/F(![]() 5007) line ratio, implying a moderately
high electron density in the NLR (several 106 cm-3).
Therefore, the NLR in 3C 390.3 can be considered to be a point
source, and we did not correct for aperture effects either the ratio
of non-stellar continuum to narrow-line flux or the ratio of the
broad to narrow line flux, as the light losses in the slit are
similar for these components. In addition, our apertures are
5007) line ratio, implying a moderately
high electron density in the NLR (several 106 cm-3).
Therefore, the NLR in 3C 390.3 can be considered to be a point
source, and we did not correct for aperture effects either the ratio
of non-stellar continuum to narrow-line flux or the ratio of the
broad to narrow line flux, as the light losses in the slit are
similar for these components. In addition, our apertures are
![]() or
or
![]() ,
which are
greater than the size of the NLR. However, the light contribution to
the continuum from the host galaxy does depend on the aperture, and
it is necessary to introduce the corresponding corrections. To
accomplish this goal, we adopted the relation (see Peterson et al. 1995)
,
which are
greater than the size of the NLR. However, the light contribution to
the continuum from the host galaxy does depend on the aperture, and
it is necessary to introduce the corresponding corrections. To
accomplish this goal, we adopted the relation (see Peterson et al. 1995)
![\begin{displaymath}F_{\rm con} =F(4959+5007)\left[\frac{F_{\rm
con}}{F(4959+5007)}\right]_{\rm obs} - G,
\end{displaymath}](/articles/aa/full_html/2010/09/aa14118-10/img35.png)
|
(2) |
where F(4959+5007) is the absolute flux in the [OIII] doublet and the value in brackets is the continuum to [OIII] line observed flux ratio, where G is an aperture-dependent correction factor that accounts for the host galaxy flux. Since most of our spectra were obtained with the 6 m telescope through an aperture of
We note here that there is the influence of seeing on G(Sergeev et al. 2002). We estimated that if the seeing changes from 1
![]() to 3
to 3
![]() (that was typical for our observations), the Gwould change at the level of
(that was typical for our observations), the Gwould change at the level of ![]() 5% (see Sergeev et al. 2002). For
standard apertures
5% (see Sergeev et al. 2002). For
standard apertures
![]()
![]() ,
and another aperture
,
and another aperture
![]()
![]() that is also very close to the
standard one, the estimated G is very small
(
that is also very close to the
standard one, the estimated G is very small
(
![]() for
aperture
for
aperture
![]() ,
or 3% of the minimal flux).
Therefore, in our case, the seeing has a small influence on G.
,
or 3% of the minimal flux).
Therefore, in our case, the seeing has a small influence on G.
We did not estimate the contribution of the host galaxy, since it
is constant and does not influence the analysis of variability, but
we mention here that Sergeev et al. (2002) estimated that the host
galaxy contributions (for a seeing of 2.5
![]() )
in the H
)
in the H![]() and H
and H![]() wavelength region are
wavelength region are ![]()
![]() ,
and
,
and ![]()
![]() ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14118f02a.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{14118f02b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg44.png)
|
Figure 2:
An example of the narrow line template for the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f03a.ps}\par\vspace*{...
...}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{14118f03c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg45.png)
|
Figure 3:
An example of the substraction of the narrow lines in
H |
| Open with DEXTER | |
2.4 The narrow emission-line template
To obtain only the broad component of Balmer lines, i.e. to remove
the narrow lines, we created a narrow line template using the blue
and red spectra in the minimum activity state (Sep. 09, 1997 and
Feb. 21, 2002), obtained with a spectral resolution of ![]() 8 Å. In
these spectra, the broad H
8 Å. In
these spectra, the broad H![]() component was very weak, and the
broad component of the higher Balmer line series were absent. To
construct the narrow line template for the H
component was very weak, and the
broad component of the higher Balmer line series were absent. To
construct the narrow line template for the H![]() wavelength band,
we first estimated the broad component (as can be seen in Fig. 2, top) and then subtracted it from the composite spectrum.
The narrow line template is shown in Fig. 2 (bottom).
wavelength band,
we first estimated the broad component (as can be seen in Fig. 2, top) and then subtracted it from the composite spectrum.
The narrow line template is shown in Fig. 2 (bottom).
In the case of H![]() ,
there is a problem of removing the
atmospheric B-band (O2) at
,
there is a problem of removing the
atmospheric B-band (O2) at
![]() Å in the blue wing. In
comparison stars, the B band is very weak due to the shortness of
the exposures, therefore it is not possible to remove it using the
relative flux calibration. To remove this component, we used the
spectra of NGC 4151, taken with long exposures in nights close-by in
time. Using different coefficients, we then subtracted the B-band
from the H
Å in the blue wing. In
comparison stars, the B band is very weak due to the shortness of
the exposures, therefore it is not possible to remove it using the
relative flux calibration. To remove this component, we used the
spectra of NGC 4151, taken with long exposures in nights close-by in
time. Using different coefficients, we then subtracted the B-band
from the H![]() observed spectrum in the minimum activity state
(Sep. 9, 1997). Using this spectrum, we fitted the broad component by
the spline method (Fig. 3, panel A). The narrow line
template for the H
observed spectrum in the minimum activity state
(Sep. 9, 1997). Using this spectrum, we fitted the broad component by
the spline method (Fig. 3, panel A). The narrow line
template for the H![]() line was obtained by subtracting this
broad component from the observed spectrum (Fig. 3, panel A).
line was obtained by subtracting this
broad component from the observed spectrum (Fig. 3, panel A).
In addition, we apply the Gaussian-fitting method to the H![]() wavelength region, after subtracting the B-band (see Fig. 3, panel B). The narrow components are narrow
H
wavelength region, after subtracting the B-band (see Fig. 3, panel B). The narrow components are narrow
H![]() ,
[N II]
,
[N II]
![]() 6548,6584,
[O I]
6548,6584,
[O I]
![]() 6300,6364)
[S II]
6300,6364)
[S II]
![]() 6717,6731, while the broad line
contains 3 components, the broad blue, core, and the broad red
Gaussians (panel B, bottom). In panel B (up) of Fig. 3, the observed spectrum and the sum of all Gaussian
components and their residuals are presented. One can see that the
sum of Gaussian components closely represents the H
6717,6731, while the broad line
contains 3 components, the broad blue, core, and the broad red
Gaussians (panel B, bottom). In panel B (up) of Fig. 3, the observed spectrum and the sum of all Gaussian
components and their residuals are presented. One can see that the
sum of Gaussian components closely represents the H![]() observed
profile, i.e. the residual is very small. In Fig. 3 (panel B, middle), we present the estimated broad component of
H
observed
profile, i.e. the residual is very small. In Fig. 3 (panel B, middle), we present the estimated broad component of
H![]() ,
obtained by subtraction of sum of narrow Gaussian
components, from the observed spectrum (after removing B-band).
,
obtained by subtraction of sum of narrow Gaussian
components, from the observed spectrum (after removing B-band).
We also compare the broad components, obtained by using the spline method and the Gaussian-fitting method (Fig. 3, panel C). As can be seen from Fig. 3 (panel C), there is practically no difference between the broad component obtained with these two different procedures.
2.5 Measurements of the spectra and errors
From the scaled spectra, we determined the average flux in the
continuum at the observed wavelength ![]() 5384 Å (or at
5384 Å (or at ![]() 5100 Å in the rest frame of 3C 390.3, z=0.0556) by means of flux
averages in the frame of 5369-5399 Å. To determine the observed
fluxes of the broad H
5100 Å in the rest frame of 3C 390.3, z=0.0556) by means of flux
averages in the frame of 5369-5399 Å. To determine the observed
fluxes of the broad H![]() and H
and H![]() lines,
it is necessary
to subtract the continuum. To achieve this goal, after subtracting
the narrow components, a linear continuum was fitted at windows
of 30 Å located at 4800 Å
and 5400 Å for the H
lines,
it is necessary
to subtract the continuum. To achieve this goal, after subtracting
the narrow components, a linear continuum was fitted at windows
of 30 Å located at 4800 Å
and 5400 Å for the H![]() wavelength band, and at 6560 Å and 7250 Å for the
H
wavelength band, and at 6560 Å and 7250 Å for the
H![]() wavelength band.
wavelength band.
After the continuum subtraction, we defined the observed fluxes in
the lines in the wavelength intervals 4909-5353 Å for H![]() and 6740-7160 Å for H
and 6740-7160 Å for H![]() .
.
In Table 2 (available electronically only), the fluxes for
the continuum, broad H![]() ,
and H
,
and H![]() lines are given. The
mean error (uncertainty) in the fluxes is for the continuum
lines are given. The
mean error (uncertainty) in the fluxes is for the continuum ![]() 3%, for the broad H
3%, for the broad H![]() line
line ![]() 5% and the broad
H
5% and the broad
H![]() line
line ![]() 10% (see Table 3).
These quantities were estimated by comparing
results from spectra obtained within a time interval shorter
than 3 days. In addition, we measured the line-part fluxes.
To do that, we
divided the H
10% (see Table 3).
These quantities were estimated by comparing
results from spectra obtained within a time interval shorter
than 3 days. In addition, we measured the line-part fluxes.
To do that, we
divided the H![]() and H
and H![]() profiles into three parts: the
blue wing (covering the blue peak), the core, and the red wing. The
intervals adopted were: (i) for H
profiles into three parts: the
blue wing (covering the blue peak), the core, and the red wing. The
intervals adopted were: (i) for H![]() ,
a blue interval of -9004:-1988 km s-1 (4977 Å-5097 Å), a central interval of -1988:+1988 km s-1 (5097 Å-5165 Å), and a red interval of +1988:+8010 km s-1 (5165 Å-5268 Å); (ii) for H
,
a blue interval of -9004:-1988 km s-1 (4977 Å-5097 Å), a central interval of -1988:+1988 km s-1 (5097 Å-5165 Å), and a red interval of +1988:+8010 km s-1 (5165 Å-5268 Å); (ii) for H![]() ,
a
blue interval of -9007:-1992 km s-1 (6720 Å-6882 Å), a
central interval of -1992:+1992 km s-1 (6882 Å-6974 Å), and
a red interval of +1992:+9007 km s-1 (6974 Å-7136 Å).
,
a
blue interval of -9007:-1992 km s-1 (6720 Å-6882 Å), a
central interval of -1992:+1992 km s-1 (6882 Å-6974 Å), and
a red interval of +1992:+9007 km s-1 (6974 Å-7136 Å).
In addition, we measured only the blue and red part of lines by
considering the intervals -9004:0:+8010 km s-1 for H![]() and -9007:0:+9007 km s-1 for H
and -9007:0:+9007 km s-1 for H![]() .
.
In Table 3, we present the estimated mean flux errors in the
H![]() and H
and H![]() lines and their segments. Figure 4
shows the distribution of the flux
error in the H
lines and their segments. Figure 4
shows the distribution of the flux
error in the H![]() line parts against the corresponding fluxes.
There is only a weak regression between the flux error and flux in
the broad H
line parts against the corresponding fluxes.
There is only a weak regression between the flux error and flux in
the broad H![]() line, while we can not detect the regression for
the case of the broad H
line, while we can not detect the regression for
the case of the broad H![]() line.
line.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f04a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{14118f04b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg47.png)
|
Figure 4: The estimated errors in the flux measurements as functions of the corresponding flux, in case we divided lines in 3 parts ( left panels) and 2 parts ( right panels). The correlation coefficient and the p-value are given in the upper right corner. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[origin=rb,angle=-90,width=12cm,clip]{14118f05.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg48.png)
|
Figure 5: The spectra of 3C 390.3 close to maximum ( up - observed in 2007) and minimum ( bottom - observed in 1997). |
| Open with DEXTER | |
Table 3:
The estimated mean flux errors of the H![]() and H
and H![]() lines and
their segments.
lines and
their segments.
3 Data analysis
We analyzed variations in the continuum and lines using a total of 129 spectra covering the H![]() wavelength region, and 48 spectra
covering the H
wavelength region, and 48 spectra
covering the H![]() line. During the monitoring period, we found
that the minimum in the continuum flux occurred during
August-September 1997, and the maximum in May-June 2007. In Fig. 5, the shape of 3C 390.3 spectra around the minimum and
maximum of activity is presented. As can be seen from Fig. 5, the slope of the continuum in the blue part of the
spectrum in the minimum-activity state was significantly flatter
than in the high-activity state. The wings of H
line. During the monitoring period, we found
that the minimum in the continuum flux occurred during
August-September 1997, and the maximum in May-June 2007. In Fig. 5, the shape of 3C 390.3 spectra around the minimum and
maximum of activity is presented. As can be seen from Fig. 5, the slope of the continuum in the blue part of the
spectrum in the minimum-activity state was significantly flatter
than in the high-activity state. The wings of H![]() and H
and H![]() became extremely weak in the minimum state, and those of H
became extremely weak in the minimum state, and those of H![]() and higher Balmer line series could not be detected at
all. These profiles correspond to the Sy 1.8 type and not to Sy 1,
as this AGN usually is classified. The spectral type of this object
therefore changes with time as noted earlier. In April 1984, the
nucleus of 3C 390.3 experienced a very deep minimum, the broad wings
of hydrogen lines became much weaker (they almost completely
vanished in April 1984) and the spectrum of the nucleus was
identified as the Sy 2 (Penston & Perez 1984). Therefore, to compare the
continuum and broad line variability we use the broad H
and higher Balmer line series could not be detected at
all. These profiles correspond to the Sy 1.8 type and not to Sy 1,
as this AGN usually is classified. The spectral type of this object
therefore changes with time as noted earlier. In April 1984, the
nucleus of 3C 390.3 experienced a very deep minimum, the broad wings
of hydrogen lines became much weaker (they almost completely
vanished in April 1984) and the spectrum of the nucleus was
identified as the Sy 2 (Penston & Perez 1984). Therefore, to compare the
continuum and broad line variability we use the broad H![]() and H
and H![]() lines only, and the measured continuum around
lines only, and the measured continuum around ![]() 5100 Å (rest frame). Our measurements are given in Table 2
(available electronically only).
5100 Å (rest frame). Our measurements are given in Table 2
(available electronically only).
3.1 Variability of the emission lines and the optical continuum
As noted above (see e.g. Paper I, Tao et al. 2008; Sergeev et al. 2002; Dietrich et al. 1998, etc.), the
optical flux variability of 3C 390.3 in the line as well as in the
continuum was observed. The light curves of the broad H![]() ,
H
,
H![]() line, and continuum fluxes are illustrated in Fig. 6. In general, the light curve of the continuum is
similar to that of H
line, and continuum fluxes are illustrated in Fig. 6. In general, the light curve of the continuum is
similar to that of H![]() and H
and H![]() ,
but there are some
differences in the sharpness of the peaks (maxima) and also it is
obvious that a lag exists between the continuum and H
,
but there are some
differences in the sharpness of the peaks (maxima) and also it is
obvious that a lag exists between the continuum and H![]() and H
and H![]() light curves.
light curves.
The maximum amplitude of the flux variations during a monitoring
period (1995-2007) corresponds to factors of ![]() 5.2 for the
continuum (at
5.2 for the
continuum (at ![]() 5100 Å in the rest frame),
5100 Å in the rest frame), ![]() 4.7 for
H
4.7 for
H![]() ,
and
,
and ![]() 3.4 for H
3.4 for H![]() (see in Sect. 3.5, Table 5). As one can see in Fig. 6, there are several
maxima (outbursts). They are more prominent in the continuum light
curve than in the H
(see in Sect. 3.5, Table 5). As one can see in Fig. 6, there are several
maxima (outbursts). They are more prominent in the continuum light
curve than in the H![]() and H
and H![]() light curves. In 1995-2002,
an outburst of decreasing amplitude and duration (intervals between
minima) from 1000 days to
light curves. In 1995-2002,
an outburst of decreasing amplitude and duration (intervals between
minima) from 1000 days to ![]() 400 days can be seen. In 2003-2007,
we can discern about
400 days can be seen. In 2003-2007,
we can discern about ![]() 3 outbursts on ascending branch of curves
of durations
3 outbursts on ascending branch of curves
of durations ![]() 600 days,
600 days, ![]() 900 days,
900 days, ![]() 500 days, and a
maximum in 2007. The similar outbursts (oscillations) in the light
curve in B band from 1995 to 2001 are also clearly seen (see Fig. 2
in Paper I). These minima/maxima may be indicative of a periodicity
(or quasi-periodical oscillation) in the continuum and broad-line
light curves.
500 days, and a
maximum in 2007. The similar outbursts (oscillations) in the light
curve in B band from 1995 to 2001 are also clearly seen (see Fig. 2
in Paper I). These minima/maxima may be indicative of a periodicity
(or quasi-periodical oscillation) in the continuum and broad-line
light curves.
3.2 Light curve analysis
Searching for periodicity has been an important part of variability studies of AGN, because the confirmed periodicity would strongly constrain possible physical models and help us to determine the relevant physical parameters of AGN. We therefore applied a wavelet transform with the Morlet wavelet to see if there is periodicity in the continuum light curve. Wavelet analysis involves a transform from one-dimensional time series to a diffuse two-dimensional time-frequency image for detecting localized (pseudo-)periodic fluctuations from subsets of the time series corresponding to a limited time span (Torrence & Compo 1998).
We employed the standard wavelet IDL codes of Torrence & Compo
(1998) to look for periodicities in the 3C 390.3 optical-continuum
and H![]() flux light curves. A Morlet wavelet is particularly
suited to the analysis of time series and has been successfully
applied to study variability in AGN (i.e. Hovatta 2008; Gupta et al. 2009; Lachowicz et al. 2009, etc.).
We therefore employ a Morlet wavelet here, which is defined as
flux light curves. A Morlet wavelet is particularly
suited to the analysis of time series and has been successfully
applied to study variability in AGN (i.e. Hovatta 2008; Gupta et al. 2009; Lachowicz et al. 2009, etc.).
We therefore employ a Morlet wavelet here, which is defined as
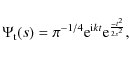
|
(3) |
where t is the time parameter,
The continuous wavelet power spectra is subject to edge artefacts because the wavelet is not completely localized in time. It is useful to introduce a cone of influence (COI) in which the transform suffers from these edge effects (Torrence & Compo 1998). Periods inside the COI are subject to edge effects and might be dubious.
Figure 7 shows the
continuous wavelet power spectra of the long-term light curve in the
optical-continuum and H![]() fluxes, respectively. There are
evidently common features in the wavelet power of the two time
series. Both wavelet spectra have a long-term periodicity (
fluxes, respectively. There are
evidently common features in the wavelet power of the two time
series. Both wavelet spectra have a long-term periodicity (![]() 1.65-2.45 yr) in the late part of the light curve, above the 95%
confidence level, but within the COI (periodicity being too close to
the total signal length).
1.65-2.45 yr) in the late part of the light curve, above the 95%
confidence level, but within the COI (periodicity being too close to
the total signal length).
However, we found a varying timescale of 0.5-0.74 yr around 2004
with a confidence of >![]() that this component does not arise
by chance (significance computed assuming the global wavelet
spectrum as the theoretical background spectrum following Torrence
& Compo 1998) and located above the COI.
that this component does not arise
by chance (significance computed assuming the global wavelet
spectrum as the theoretical background spectrum following Torrence
& Compo 1998) and located above the COI.
Taking into account that this method provides some indication about
periodicity, we performed an analysis assuming that there can be
several reasons for variability, e.g. some kinds of shocks or
flares in the accretion disk. We therefore assumed that the total
flux in the line and continuum can be represented as
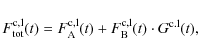
where
Using the above equation and observed light curves of the continuum
and H![]() line, we estimated
line, we estimated
![]() by assuming this function
to be an envelope covering minima on the light curves, and
by assuming this function
to be an envelope covering minima on the light curves, and
![]() to be an envelope covering maxima on the light curves. The
illustration of the decomposition of the continuum and H
to be an envelope covering maxima on the light curves. The
illustration of the decomposition of the continuum and H![]() light curves into three aforementioned functions are given in Figs. 8 and 9.
light curves into three aforementioned functions are given in Figs. 8 and 9.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14118f06.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg60.png)
|
Figure 6:
Light curves of the continuum (top), broad H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14118f07a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{14118f07b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg61.png)
|
Figure 7:
The continuous wavelet power spectra of the
long-term light curve of the optical continuum at 5100 Å ( top) and in the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f08a.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f08c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg62.png)
|
Figure 8:
The decomposition of the continuum light curve: a) the flux
in the continuum and estimation of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f09a.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f09c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg63.png)
|
Figure 9:
The same as in Fig. 8, but for the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f10a.ps}\par\vspace*{2m...
....ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f10d.ps}\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg64.png)
|
Figure 10:
The comparison of different flux components of H |
| Open with DEXTER | |
In Fig. 10 we compare the (rescaled) function ![]() ,
,
![]() ,
and G estimated from the continuum (dashed line, full circles) and
H
,
and G estimated from the continuum (dashed line, full circles) and
H![]() (dotted line, asterisks) light curve. As one can see (Fig. 10, first panel), the shapes of
(dotted line, asterisks) light curve. As one can see (Fig. 10, first panel), the shapes of ![]() seem to be similar
with slight differences, which may be caused by estimation of
minima. In contrast, the shapes of
seem to be similar
with slight differences, which may be caused by estimation of
minima. In contrast, the shapes of ![]() are different (second
panel), which is indicative of a rapidly increasing continuum
are different (second
panel), which is indicative of a rapidly increasing continuum
![]() from 2002, when higher activity of AGN also started.
The
from 2002, when higher activity of AGN also started.
The ![]() component may be quasi-periodical in both the continuum
and H
component may be quasi-periodical in both the continuum
and H![]() ,
i.e. it may contain two peaks separated by about ten years,
that 10-year signal is also visible in the wavelet plot, though
in the COI. Finally, the G(t) exhibits (third and fourth panel)
quasi-periodical oscillations with a period of around 2-4 yr, which is
very close to the period indicated by Morlet wavelet spectral
analysis.
,
i.e. it may contain two peaks separated by about ten years,
that 10-year signal is also visible in the wavelet plot, though
in the COI. Finally, the G(t) exhibits (third and fourth panel)
quasi-periodical oscillations with a period of around 2-4 yr, which is
very close to the period indicated by Morlet wavelet spectral
analysis.
The minima and maxima of the continuum G(t) more closely match those
of the H![]() G(t) after a shift of
G(t) after a shift of ![]() 95 days,
which is close
to the lag obtained from the CCF analysis (see Sect. 3.6). It is
also interesting that quasi-periodical oscillations can be seen
until 2002, before the beginning of the high activity phase
(from 2002 to 2007). In the period 1995-2002, there are three
prominent
maxima. From 2002 to 2004, at the beginning of the activity, a clear
peak cannot be seen, while from 2004 to 2007 two maxima can be
recognized (see Fig. 10, 3rd and 4th panels).
95 days,
which is close
to the lag obtained from the CCF analysis (see Sect. 3.6). It is
also interesting that quasi-periodical oscillations can be seen
until 2002, before the beginning of the high activity phase
(from 2002 to 2007). In the period 1995-2002, there are three
prominent
maxima. From 2002 to 2004, at the beginning of the activity, a clear
peak cannot be seen, while from 2004 to 2007 two maxima can be
recognized (see Fig. 10, 3rd and 4th panels).
3.3 Changes in the broad line profiles
We first inspected the H![]() and H
and H![]() profiles using
spectra with a resolution of 8 Å for different epochs, comparing
H
profiles using
spectra with a resolution of 8 Å for different epochs, comparing
H![]() and H
and H![]() profiles. As one can see in Fig. 11, there are no large differences
between the line profiles of H
profiles. As one can see in Fig. 11, there are no large differences
between the line profiles of H![]() and H
and H![]() .
The lines in
all considered epochs show a blue-boosted and red-tailed peaks,
which are common for emission from a relativistic disk. However,
there are some differences among the H
.
The lines in
all considered epochs show a blue-boosted and red-tailed peaks,
which are common for emission from a relativistic disk. However,
there are some differences among the H![]() and H
and H![]() line
profiles that vary during the monitoring period. For instance,
H
line
profiles that vary during the monitoring period. For instance,
H![]() exhibits a bump in its central part during 1997-1998, which
later disappears (until 2002). From the minimal phase of activity in
2002, the red wing remains stronger in H
exhibits a bump in its central part during 1997-1998, which
later disappears (until 2002). From the minimal phase of activity in
2002, the red wing remains stronger in H![]() than in H
than in H![]() .
During maximum activity, between 2004 and 2007, the H
.
During maximum activity, between 2004 and 2007, the H![]() is also
broader than H
is also
broader than H![]() .
.
As noted above, the first inspection of line profiles identified
differences between H![]() and H
and H![]() line shapes after the
beginning of the phase of activity in 2002. We therefore, decided to
consider the mean profiles of H
line shapes after the
beginning of the phase of activity in 2002. We therefore, decided to
consider the mean profiles of H![]() and H
and H![]() during the
whole monitoring period, and both the mean and root-mean-square
(rms) profiles for the period before March 05, 2002 (period I,
JD 2 452 339.01 according the minimum in H
during the
whole monitoring period, and both the mean and root-mean-square
(rms) profiles for the period before March 05, 2002 (period I,
JD 2 452 339.01 according the minimum in H![]() )
and after that
(period II, see Figs. 12). The mean and rms profiles of
both lines have ``double-peaked'' structure and a full width at zero
intensity of about 20 000 km s-1. The blue bump in the mean
spectrum is located at a radial velocity of about -4000 km s-1relative to the H
)
and after that
(period II, see Figs. 12). The mean and rms profiles of
both lines have ``double-peaked'' structure and a full width at zero
intensity of about 20 000 km s-1. The blue bump in the mean
spectrum is located at a radial velocity of about -4000 km s-1relative to the H![]() and H
and H![]() narrow components, while the
red bump with the flatter peak is located between +2000 and +5000 km s-1. The blue bump in the mean profiles is brighter than the
red one during 1995-2007. The rms profiles show that the variability
of the blue wing is stronger than that of the red (in all periods).
As can also be seen in Fig. 12, in the first period a
central component was present and apart from the variation in two
peaks, there is also a dominant variation in the core of the lines.
We note that the sharp narrow central peak in the H
narrow components, while the
red bump with the flatter peak is located between +2000 and +5000 km s-1. The blue bump in the mean profiles is brighter than the
red one during 1995-2007. The rms profiles show that the variability
of the blue wing is stronger than that of the red (in all periods).
As can also be seen in Fig. 12, in the first period a
central component was present and apart from the variation in two
peaks, there is also a dominant variation in the core of the lines.
We note that the sharp narrow central peak in the H![]() rms and
H
rms and
H![]() rms may be caused by the narrow line substraction.
rms may be caused by the narrow line substraction.
Table 4: The line widths and asymmetry measurements for the whole monitoring period, period I and II.
We measured the full width at half maximum (FWHM) in the rms and
averaged broad line profiles, and we defined an asymmetry parameter
A as the ratio of the red to blue half width at half maximum (HWHM),
i.e.
![]() .
We also
estimated the peak positions and their ratios. The measured values
for the broad H
.
We also
estimated the peak positions and their ratios. The measured values
for the broad H![]() and H
and H![]() lines and their rms values are
given in Table 4. As can be seen from Table 4, the
FWHM of the mean H
lines and their rms values are
given in Table 4. As can be seen from Table 4, the
FWHM of the mean H![]() line (as well as the rms) obtained from
the whole monitoring period is broader than that of H
line (as well as the rms) obtained from
the whole monitoring period is broader than that of H![]() ,
and
line (and rms) profiles exhibit the blue asymmetry on the half
maximum.
,
and
line (and rms) profiles exhibit the blue asymmetry on the half
maximum.
There are also differences between line and rms parameters obtained
from periods I and II. As one can see from Table 4, in
period I, the FWHMs of H![]() and H
and H![]() are practically
identical, while H
are practically
identical, while H![]() exhibits a slightly blue and H
exhibits a slightly blue and H![]() slightly red asymmetry (within the errorbars), i.e. they are almost
symmetric at the half intensity maximum (here measured to be the
blue peak maximum). In contrast, during the phase of flaring
(2002-2007), the FWHM of H
slightly red asymmetry (within the errorbars), i.e. they are almost
symmetric at the half intensity maximum (here measured to be the
blue peak maximum). In contrast, during the phase of flaring
(2002-2007), the FWHM of H![]() remains broader than H
remains broader than H![]() (around 1500 km s-1), and both lines have a significant blue
asymmetry at half intensity maximum. On the other hand, the
separation between peaks is higher in period I than in period II,
which is indicative of some global perturbation in the BLR. This
result agrees with that of Paper I, where it was found that the
difference in the radial velocities of the blue and red peaks is
anticorrelated with the brightness of H
(around 1500 km s-1), and both lines have a significant blue
asymmetry at half intensity maximum. On the other hand, the
separation between peaks is higher in period I than in period II,
which is indicative of some global perturbation in the BLR. This
result agrees with that of Paper I, where it was found that the
difference in the radial velocities of the blue and red peaks is
anticorrelated with the brightness of H![]() and continuum. We
note that the blue to red peak ratio does not differ too
significantly between the two periods, but there is a difference in
the peak ratios and their separations of the mean H
and continuum. We
note that the blue to red peak ratio does not differ too
significantly between the two periods, but there is a difference in
the peak ratios and their separations of the mean H![]() (RP-BP
(RP-BP ![]() 6500
6500
![]() ,
Ib/Ir
,
Ib/Ir ![]() 1.65) and
H
1.65) and
H![]() (RP-BP
(RP-BP ![]() 5600
5600
![]() ,
Ib/Ir
,
Ib/Ir ![]() 1.30) lines, which may reflect a stratification in the BLR, i.e. the
different dimensions of the H
1.30) lines, which may reflect a stratification in the BLR, i.e. the
different dimensions of the H![]() and H
and H![]() emitting regions.
emitting regions.
3.4 Flux variability in the wings and core of the broad H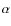 and
H
and
H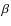 lines and various correlations
lines and various correlations
To determine whether there are any variations in the structure of
the BLR (here probably in the disk geometry), we investigated the
relationships between different parts of H![]() and H
and H![]() .
.
Light curves for the wings and cores of H![]() and H
and H![]() are
presented in Fig. 13. As can be seen, the flux in the wings
and cores of both lines behaved similarly during the monitoring
period. This was also found when we considered only the blue and red
parts of the lines.
are
presented in Fig. 13. As can be seen, the flux in the wings
and cores of both lines behaved similarly during the monitoring
period. This was also found when we considered only the blue and red
parts of the lines.
We found that the flux ratio of different H![]() to H
to H![]() parts varies during the monitoring period. In Fig. 14, we
presented the flux ratios of the red to blue part (asterisk
blue-line), the central to blue (circles black-line), and the red to
blue for when we divided lines into only two parts (triangle
red-line). As one can see from Fig. 14, the blue part remains
more prominent in the phase of higher activity in the period 2002-2007. This also reflects some global changes in the
line-emitting regions.
parts varies during the monitoring period. In Fig. 14, we
presented the flux ratios of the red to blue part (asterisk
blue-line), the central to blue (circles black-line), and the red to
blue for when we divided lines into only two parts (triangle
red-line). As one can see from Fig. 14, the blue part remains
more prominent in the phase of higher activity in the period 2002-2007. This also reflects some global changes in the
line-emitting regions.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14118f11a.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg71.png)
|
Figure 11:
The comparison of the H |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm,clip]{14118f11b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg72.png)
|
Figure 11: continued. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm,clip]{14118f11c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg73.png)
|
Figure 11: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{14118f12a.ps}\hspace*{4mm}...
....ps}\hspace*{4mm}
\includegraphics[width=5.2cm,clip]{14118f12f.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg74.png)
|
Figure 12:
Mean and rms spectra of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f13a.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f13b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg76.png)
|
Figure 13:
JD-fluxes in the blue and red wings, and core and
for H |
| Open with DEXTER | |
We also identified a correlation between the continuum flux and both
the integral flux and flux of different parts of the line (see Fig. 15). In Fig. 16,
we present the relationship between the H![]() and H
and H![]() line
parts. As we see in Figs. 15 and 16, there is a
linear relationship between the fluxes of the broad H
line
parts. As we see in Figs. 15 and 16, there is a
linear relationship between the fluxes of the broad H![]() and H
and H![]() lines, their parts, and continuum fluxes (Fig. 15), as well between the broad line parts themselves (Fig. 16). These linear correlations indicate that for both
lines, both the blue and red wings, and the core originate in the
BLR that is ionized by the AGN source.
lines, their parts, and continuum fluxes (Fig. 15), as well between the broad line parts themselves (Fig. 16). These linear correlations indicate that for both
lines, both the blue and red wings, and the core originate in the
BLR that is ionized by the AGN source.
3.5 Variability analysis
In Table 5, we present various parameters characterizing the
continuum, the integral line, and the line parts, where F is the
mean flux and ![]() is its standard deviation, R(max) is the
ratio of the maximum to the minimum flux in the monitoring period,
F(var) is a measured (uncertainty-corrected) estimate of the
variation amplitude with respect to the mean flux, defined by
O'Brien et al. (1998) to be
is its standard deviation, R(max) is the
ratio of the maximum to the minimum flux in the monitoring period,
F(var) is a measured (uncertainty-corrected) estimate of the
variation amplitude with respect to the mean flux, defined by
O'Brien et al. (1998) to be
![\begin{displaymath}F({\rm var})= \left[\sqrt{\sigma(F)^2 -e^2}\right]/F({\rm mean}), \end{displaymath}](/articles/aa/full_html/2010/09/aa14118-10/img78.png)
where e2 is the mean square value of the individual measurement uncertainty for N observations, i.e.
Table 5: Variability parameters.
3.6 Correlations and cross-correlations(CCF) analysis
To estimate the size and structure of the BLR, one can derive the
cross-correlation function (CCF) of the continuum light curve with
the emission-line light curves. There are several ways to construct
a CCF, and it is always advisable to use two or more methods to
confirm the obtained results. Therefore, we cross-correlated the
5100 Å continuum light curve with both the H![]() and H
and H![]() line (and their parts) light curves using two methods: (i) the
z-transformed discrete correlation function (ZDCF) method introduced
by Alexander (1997), and (ii) the interpolation cross-correlation
function method (ICCF) described by Bischof & Kollatschny (1999).
line (and their parts) light curves using two methods: (i) the
z-transformed discrete correlation function (ZDCF) method introduced
by Alexander (1997), and (ii) the interpolation cross-correlation
function method (ICCF) described by Bischof & Kollatschny (1999).
We choose to apply the CCF method introduced by Alexander (1997),
i.e., the z-transformed discrete correlation function (ZDCF). The
ZDCF approximates the bin distribution using a bi-normal
distribution (see also Shapovalova et al. 2008). In the ZDCF the binning is
performed by ensuring that there are equal population, while the
effect of measurement errors is estimated by performing the Monte
Carlo simulations (usually 100 runs is sufficient) of the averaged
ZDCF of light curves with simulated random errors. Since a priori
models of light curves do not exist, the estimated ZDCF errors may
be extremely large. The Z transforms convergence requires a minimum
of 11 points per bin. Using this method, we obtained a lag of
96
+28-47 with coefficient of correlation of
![]() between the continuum and H
between the continuum and H![]() .
The cross-correlation functions
obtained by ZDCF method are shown in Fig. 17. The lags and CCF coefficients are given in
Table 6. As can be seen for H
.
The cross-correlation functions
obtained by ZDCF method are shown in Fig. 17. The lags and CCF coefficients are given in
Table 6. As can be seen for H![]() ,
the CCF is affected
by noise because of the small amount of observational data, and it
is difficult to reliably determine the lag, there being two peaks in
the CCF curve with estimated lags of 24 days (0.90
+0.070.05)
and 151 days (0.90
+0.06-0.05).
,
the CCF is affected
by noise because of the small amount of observational data, and it
is difficult to reliably determine the lag, there being two peaks in
the CCF curve with estimated lags of 24 days (0.90
+0.070.05)
and 151 days (0.90
+0.06-0.05).
As we mentioned above, we applied in addition the ICCF method to
cross-correlate the flux of the continuum with both the H![]() and
H
and
H![]() fluxes, and found lags of
fluxes, and found lags of ![]() days (CCF = 0.95) for H
days (CCF = 0.95) for H![]() and
and ![]() days (CCF = 0.84) for H
days (CCF = 0.84) for H![]() ,
which agree
with the ZDCF analysis. Both methods indicate that the lag between
the continuum and H
,
which agree
with the ZDCF analysis. Both methods indicate that the lag between
the continuum and H![]() flux is around 95 days. For the H
flux is around 95 days. For the H![]() line, the ICCF method is not applicable (because of the small amount
of observations). To confirm the results obtained we compiled
centroids for H
line, the ICCF method is not applicable (because of the small amount
of observations). To confirm the results obtained we compiled
centroids for H![]() (see Table 6) and measured a lag of
(see Table 6) and measured a lag of
![]() days, which is closer to the larger value obtained from
ZDCF.
days, which is closer to the larger value obtained from
ZDCF.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f14a.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f14b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg86.png)
|
Figure 14:
The variation in the ratio red/blue (asterisk blue-line)
and central/blue (circles black-line) of the H |
| Open with DEXTER | |
We also correlated the continuum and H![]() functions
functions
![]() ,
,
![]() ,
and G(t) described in Sect. 3.2 and found no lag between
the continuum-H
,
and G(t) described in Sect. 3.2 and found no lag between
the continuum-H![]()
![]() ,
while the lag between the
continuum-H
,
while the lag between the
continuum-H![]()
![]() is 574
+12-26 days
(0.74
+0.07-0.06). It is interesting that the lag between
is 574
+12-26 days
(0.74
+0.07-0.06). It is interesting that the lag between
![]() and
and
![]() is close to the lag of the entire line within
the errorbars and is 97
+ 27-46 (0.59
+0.08-0.07). The
CCFs between these three function are presented in Fig. 18.
is close to the lag of the entire line within
the errorbars and is 97
+ 27-46 (0.59
+0.08-0.07). The
CCFs between these three function are presented in Fig. 18.
The calculated lags and CCF between the continuum and different
parts of lines, as well as between different parts of H![]() and
H
and
H![]() using ZDCF method are given in Table 6. The last
two columns of Table 6 indicate the centroid lag and the
90% of the ZDCF maximum, respectively.
using ZDCF method are given in Table 6. The last
two columns of Table 6 indicate the centroid lag and the
90% of the ZDCF maximum, respectively.
In addition, we searched for any linearity between either the
H![]() and continuum flux, or the H
and continuum flux, or the H![]() and continuum flux,
taking different time shifts for the continuum. We assumed that the
continuum is shifted by 0, 30, 100, 200, and 300 days. As shown
Figs. 19 and 20, the
best-fit linear correlation H
and continuum flux,
taking different time shifts for the continuum. We assumed that the
continuum is shifted by 0, 30, 100, 200, and 300 days. As shown
Figs. 19 and 20, the
best-fit linear correlation H![]() versus (vs.) continuum flux is
found when the continuum has a lag of 200 days, but for H
versus (vs.) continuum flux is
found when the continuum has a lag of 200 days, but for H![]() the
clearest linearity is obtained for a continuum shift of 100 days.
This agrees well with the results obtained for the CCF analysis
mentioned above.
the
clearest linearity is obtained for a continuum shift of 100 days.
This agrees well with the results obtained for the CCF analysis
mentioned above.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f15a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{14118f15b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg89.png)
|
Figure 15:
The relationships between the H |
| Open with DEXTER | |
3.6.1 The lines, line-parts, and continuum correlations
We correlated the continuum and line parts, as well as the line
parts with the other line parts, finding that the lag in the
continuum vs. H![]() line parts is 96
+47-28 in all cases
(the CCF coefficient being larger than 0.9). This and a short lag in
the H
line parts is 96
+47-28 in all cases
(the CCF coefficient being larger than 0.9). This and a short lag in
the H![]() line part - line part lag (6
+36-6, practically
around zero within the errorbars) indicate that total line responses
to the continuum vary at the same time. In both cases, there is no
significant lag between the blue and red H
line part - line part lag (6
+36-6, practically
around zero within the errorbars) indicate that total line responses
to the continuum vary at the same time. In both cases, there is no
significant lag between the blue and red H![]() line parts, when
we consider only blue and red part, and in the second case when we
consider the blue, central, and red part.
line parts, when
we consider only blue and red part, and in the second case when we
consider the blue, central, and red part.
For H![]() ,
Table 6 shows that may be same lag between
the blue and red/central part, around 23 days. However, since for
H
,
Table 6 shows that may be same lag between
the blue and red/central part, around 23 days. However, since for
H![]() there are fewer data available for the calculation than
for H
there are fewer data available for the calculation than
for H![]() ,
as well as that there is one peak around zero (with a
slightly smaller CCF value; see values in brackets in Table 6), this should be interpreted with care.
,
as well as that there is one peak around zero (with a
slightly smaller CCF value; see values in brackets in Table 6), this should be interpreted with care.
The CCFs for both H![]() and H
and H![]() in addition to the CCFs
between their parts are shown in Fig. 17. On the left
side of Fig. 17 (from top to bottom), we present the
H
in addition to the CCFs
between their parts are shown in Fig. 17. On the left
side of Fig. 17 (from top to bottom), we present the
H![]() CCFs of the continuum-total line flux, blue-core, blue-red
(three parts), continuum-red, and continuum-blue. On the right side,
we present the same for H
CCFs of the continuum-total line flux, blue-core, blue-red
(three parts), continuum-red, and continuum-blue. On the right side,
we present the same for H![]() line. The CCFs for H
line. The CCFs for H![]() are
clearly noisier than for H
are
clearly noisier than for H![]() because there are fewer
observations of H
because there are fewer
observations of H![]() than H
than H![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f16a.ps}\hspace*{4mm}
\includegraphics[width=8.1cm,clip]{14118f16b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg92.png)
|
Figure 16:
Relationships between the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14118f17.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg93.png)
|
Figure 17:
CCFs for H |
| Open with DEXTER | |
Table 6:
The time lag and CCF coefficient for the
continuum and H
![]() line (total line and parts) using ZDCF
method.
line (total line and parts) using ZDCF
method.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{14118f18a.ps}\par\vspace*{...
...\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14118f18c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg142.png)
|
Figure 18:
CCFs between continuum and line functions |
| Open with DEXTER | |
4 Discussion of results
We have presented and analyzed data of the long-term monitoring of 3C 390.3 (13 years, from 1995 to 2007). In Paper I, we presented the monitoring results for the period 1995-1999, and here we have enlarged our data set for the 8-year period 1999-2007. We now discuss the derived results.
4.1 Continuum and line light curves: possible quasi-periodical oscillation
In the first period (1995-2002), three maxima (outbursts) are
discernible in the H![]() and continuum light curves, after which
in 2002, the activity seems to reach a minimum. Besides these three
maxima, there are several local peaks, even in the minimum state,
which became enhanced during the maximum of activity (2003-2007).
This motivated us to search periodicity in the light curves of both
H
and continuum light curves, after which
in 2002, the activity seems to reach a minimum. Besides these three
maxima, there are several local peaks, even in the minimum state,
which became enhanced during the maximum of activity (2003-2007).
This motivated us to search periodicity in the light curves of both
H![]() and continuum (we did not attempt this for H
and continuum (we did not attempt this for H![]() because there were fewer data than for H
because there were fewer data than for H![]() ). By applying the
two methods, we showed that there is a high probability that in both
the line and continuum light curves some quasi-periodical
oscillations exist, i.e., there is some long-term periodicity over
between 1.65 and 4 years. Tao et al. (2008) constructed a historical
light curve from 1894 to 2004 and identified possible periods of 8.30, 5.37, 3.51, and 2.13 yr.
). By applying the
two methods, we showed that there is a high probability that in both
the line and continuum light curves some quasi-periodical
oscillations exist, i.e., there is some long-term periodicity over
between 1.65 and 4 years. Tao et al. (2008) constructed a historical
light curve from 1894 to 2004 and identified possible periods of 8.30, 5.37, 3.51, and 2.13 yr.
The appearance of quasi-periodic oscillation (QPOs) is often related
to accretion flows around black holes. Chakrabarti et al. (2004)
performed numerical simulations of two-dimensional axisymmetric
accretion flows around both stellar and supermassive black holes and
found that due to both the radial and vertical oscillation of shock
waves in the accretion flow, the quasi-periodic variabilities in the
light curve can be expected. These quasi-periodic variabilities may
be detectable because of the predominance of the interaction between
the winds and the inflow (see Chakrabarti et al. 2004, and references therein).
Chakrabarti et al. (2004) found that the QPO frequency of
supermassive black hole should be approximately 10-6-10-7 Hz, and the frequencies of possible oscillations were found to be ![]() 10-8. These variabilities are consistent with a disk
geometry. Gierlinski et al. (2008) reported that QPO is detected
in X-ray spectra of RE J1034+396 (a narrow-line Seyfert 1 galaxy),
but the QPO does not appear to have a disk origin
(see Middleton et al. 2009).
10-8. These variabilities are consistent with a disk
geometry. Gierlinski et al. (2008) reported that QPO is detected
in X-ray spectra of RE J1034+396 (a narrow-line Seyfert 1 galaxy),
but the QPO does not appear to have a disk origin
(see Middleton et al. 2009).
Harris et al. (2009) also reported the discovery of a X-ray QPO in
the M 87 jet. Arshakian et al. (2010) found a connection
between the
variable optical continuum and the subparsec-scale jet in
3C 390.3,
in addition to a significant correlation (at a confidence level
of >99.99%) between the ejected jet components and optical
continuum flares and that radio events follow the maxima of optical
flares with the mean time delay around ![]() 36 days. Results
obtained in León-Tavares et al. (2010) for the broad-line radio
galaxy 3C 120, confirm the correlations found in Arshakian et al.
(2010) and support the idea that the correlation between optical
flares and kinematics of the jet may be common to all radio-loud
galaxies and quasars. There is therefore, an open question about the
origin of QPOs in 3C 390.3.
36 days. Results
obtained in León-Tavares et al. (2010) for the broad-line radio
galaxy 3C 120, confirm the correlations found in Arshakian et al.
(2010) and support the idea that the correlation between optical
flares and kinematics of the jet may be common to all radio-loud
galaxies and quasars. There is therefore, an open question about the
origin of QPOs in 3C 390.3.
We note that quasi-periodical variations in the observed blue-to-red
line wing flux ratios of H![]() ,
of period about 10 years, have
been reported in several papers (see Veilleux & Zheng 1991;
Shapovalova et al. 1996; Bochkarev et al. 1997), maximum values
occurring at 1975, 1985, and 1995. From our data (Sect. 3.4, Fig. 14), it follows that the maximal ratio F(blue)/F(red) was
observed in 2004-2006. In Figs. 6, 10b,
13, the fluxes of maximal amplitude
clearly occur in the years 1996 and 2006, e.g. they
divide the interval by about 10 years. This
closely agrees with reported quasi-periodical variations of period
,
of period about 10 years, have
been reported in several papers (see Veilleux & Zheng 1991;
Shapovalova et al. 1996; Bochkarev et al. 1997), maximum values
occurring at 1975, 1985, and 1995. From our data (Sect. 3.4, Fig. 14), it follows that the maximal ratio F(blue)/F(red) was
observed in 2004-2006. In Figs. 6, 10b,
13, the fluxes of maximal amplitude
clearly occur in the years 1996 and 2006, e.g. they
divide the interval by about 10 years. This
closely agrees with reported quasi-periodical variations of period
![]() 10 years. This period of 10 years may be connected with the
BLR (disk) rotation period.
10 years. This period of 10 years may be connected with the
BLR (disk) rotation period.
4.2 Dimension of the BLR: CCF analysis
In Table 6, the correlations between the continuum flux
and either H![]() or H
or H![]() give different values, indicating
different sizes of the H
give different values, indicating
different sizes of the H![]() and H
and H![]() emission regions. The
lag measured for H
emission regions. The
lag measured for H![]() is
is ![]() 95 days, while for H
95 days, while for H![]() it
is closer to 100 days. In addition, the coefficient of variability
(see Table 5) is slightly higher for H
it
is closer to 100 days. In addition, the coefficient of variability
(see Table 5) is slightly higher for H![]() than
H
than
H![]() ,
implying that the H
,
implying that the H![]() emitting region may be more
compact than that of H
emitting region may be more
compact than that of H![]() .
.
In Paper I, the time lag in the response of the emission line
relative to flux variations in the continuum, has been found to vary
with time i.e. during 1995-1997 a lag of about 100 days was
detected, while during 1998-1999, a double-valued lag of ![]() 100 days and
100 days and ![]() 35 days is present. It is
interesting that we obtained a similar result from H
35 days is present. It is
interesting that we obtained a similar result from H![]() ,
while
for H
,
while
for H![]() we obtained consistent lag of 95 days using both
methods. This, and also difference in the FWHM may indicate
multicomponent origin of broad lines, as e.g. in the classical
accretion disk, and one disk-like region formed around the accretion
disk.
we obtained consistent lag of 95 days using both
methods. This, and also difference in the FWHM may indicate
multicomponent origin of broad lines, as e.g. in the classical
accretion disk, and one disk-like region formed around the accretion
disk.
We recall the BLR scenario proposed by Arshakian et al. (2010),
where the broad emission lines of a double-peaked structure
originate in two kinematically and physically different regions of
3C 390.3: 1) BLR1 - a traditional BLR (accretion disk (AD) and the
surrounding gas), which is at the distance ![]() 30 light days from
the nuclei; 2) BLR2 - a subrelativistic outflow surrounding the jet
that is in the cone that is within
30 light days from
the nuclei; 2) BLR2 - a subrelativistic outflow surrounding the jet
that is in the cone that is within ![]() 100 light days of the
source, at a distance of
100 light days of the
source, at a distance of ![]() 0.4 pc from the central engine.
During the maximal-brightness periods of the nucleus, most of the
continuum variable radiation is emitted from the jet and ionizes the
surrounding gas, creating the BLR2 that then produces the broad line
emission. During the brightness minima, the jet contribution to the
ionizing continuum diminishes and the main broad-line emission
originates in the ``classical'' BLR1 (AD), ionized by nuclei
continuum related to accretion onto the BH.
0.4 pc from the central engine.
During the maximal-brightness periods of the nucleus, most of the
continuum variable radiation is emitted from the jet and ionizes the
surrounding gas, creating the BLR2 that then produces the broad line
emission. During the brightness minima, the jet contribution to the
ionizing continuum diminishes and the main broad-line emission
originates in the ``classical'' BLR1 (AD), ionized by nuclei
continuum related to accretion onto the BH.
One can speculate that this scenario can be used to explain
different lags of H![]() and H
and H![]() (and difference in the rate
of variation), but there may also be some perturbation in a
``classical'' accretion disk in combination with the different
dimensions of the emitting regions that may explain the observed
results. In a forthcoming paper, we propose to apply disk models to
explore these findings.
(and difference in the rate
of variation), but there may also be some perturbation in a
``classical'' accretion disk in combination with the different
dimensions of the emitting regions that may explain the observed
results. In a forthcoming paper, we propose to apply disk models to
explore these findings.
4.3 The structure of the BLR - disk and perturbations
An accretion disk is usually assumed to produce the double-peaked
line profiles emitted by some AGN. Gezari et al. (2007) found, from
their approximately 20-year long spectral monitoring of the
double-peaked H![]() emission line of seven broad-line radio
galaxies, that their profiles varied on timescales of from months to
years, and double-peaked lines were successfully modeled by emission
of the gas from the outer part of the accretion disk. To explain
variable flux ratios of the line wings, more complex models are
required, such as hot spots (Zheng 1996), two-arm spiral waves in the
accretion disk (Chakrabarti & Wiita 1994), or a relativistic eccentric disk
(Eracleous et al. 1995). Therefore, accretion-disk emission from 3C 390.3 is
probably present, and investigation of the long-term variability in
the spectra (broad lines and continuum) of this object can provide
information about the accretion disk structure.
emission line of seven broad-line radio
galaxies, that their profiles varied on timescales of from months to
years, and double-peaked lines were successfully modeled by emission
of the gas from the outer part of the accretion disk. To explain
variable flux ratios of the line wings, more complex models are
required, such as hot spots (Zheng 1996), two-arm spiral waves in the
accretion disk (Chakrabarti & Wiita 1994), or a relativistic eccentric disk
(Eracleous et al. 1995). Therefore, accretion-disk emission from 3C 390.3 is
probably present, and investigation of the long-term variability in
the spectra (broad lines and continuum) of this object can provide
information about the accretion disk structure.
As mentioned in Paper I (and papers quoted in Sect. 1), the geometry of the BLR of 3C 390.3 probably has a disk-like structure.
From Table 4, we conclude that the distance (in velocity) between the blue and red peaks was smaller in 2002-2007, when the continuum flux was relatively high, while it was larger when the continuum flux was relatively weak. The similar anticorrelation in 1995-1999 was found in Paper I. This can be expected in the case where broad emission lines originate in the AD, i.e., are produced by changes in the dimension of the disk. The velocity difference increases, corresponding to smaller radii (emission from the part of the disk near to the BH), as the continuum flux decreases. When the continuum flux increases the velocity difference decreases, i.e., the contribution of disk parts farther from the BH is more significant.
If the BLR, however, consists of 2 regions - AD and sub-parcsec-jet (Arshakian et al. 2010), then, in the maximum activity state, most radiation is produced by the jet and the velocity difference between blue and red peak decreases (further from BH). Otherwise, in contrast (i.e., in the minimum state of activity) most radiation is caused by AD and the velocity difference increases (near BH). We also note that in blazars, where the emission is dominated by the extremely variable, non-thermal radiation from the jet, the few spectroscopic studies available (since lines are often absent for these objects) have shown that in some cases there is a weak (or no) correlation between the line and continuum emission. This result was also reported by Benitez et al. (2009) on the basis of their spectroscopical monitoring of blazar 3C 454.3 from September 2003 to July 2008. They found that Mg II emission lines respond proportionally to the continuum variations when the source is in a low-activity state. In contrast, close to the optical outbursts detected in 2005 and 2007, the Mg II emission lines showed little response to the continuum flux variations.
In any case, the profile evolution indicates that some additional
emission is present, as seen in the first period 1997-1998 for the
central part of the line, and at the end of the monitoring campaign,
when a difference was measured for the red wings of H![]() and
H
and
H![]() lines. These results could be interpreted by some kind of
two-component model (see also Popovic et al. 2004; Bon et al. 2009) but may also
caused by the perturbations in the disk (due to shock waves),
providing support for a disk model (as noted in Paper I). A pure
disk model would be consistent with the absence of a lag between
flux variations in the red and blue wings of the lines, and the line
shapes of H
lines. These results could be interpreted by some kind of
two-component model (see also Popovic et al. 2004; Bon et al. 2009) but may also
caused by the perturbations in the disk (due to shock waves),
providing support for a disk model (as noted in Paper I). A pure
disk model would be consistent with the absence of a lag between
flux variations in the red and blue wings of the lines, and the line
shapes of H![]() and H
and H![]() (with the blue and red peaks) being
indicative of the relativistic disk emission.
(with the blue and red peaks) being
indicative of the relativistic disk emission.
If one were to propose pure disk geometry (without additional
emission), then the various bumps in line profiles may be caused by
spiral shocks in the disk. As we have shown in Sect. 3.2, the
H![]() and continuum light curves can be decomposed into three
functions
and continuum light curves can be decomposed into three
functions
![]() ,
,
![]() ,
and G(t). As discussed in Sect. 3.5,
the time lag between
,
and G(t). As discussed in Sect. 3.5,
the time lag between
![]() and
and
![]() is zero, while
between
is zero, while
between
![]() and
and
![]() it is around 600 days,
which is close to the bump in CCF curves (see Fig. 17).
The lag between the G(t) functions corresponds to the lag between
the continuum and line fluxes. This may indicate that we have a
complex scenario in which the variability has two distinct periods.
Assuming emission to originate in the disk, if a perturbation
appears close to the black hole, the continuum flux may first
increase, after which (at around 90-100 days) the line flux
increases. This is well described by the lag in the function G(t).
On the other side, one may expect some of the continuum to be
emitted from the line emission region (as e.g. due to free-bound
transitions), which may be described by
it is around 600 days,
which is close to the bump in CCF curves (see Fig. 17).
The lag between the G(t) functions corresponds to the lag between
the continuum and line fluxes. This may indicate that we have a
complex scenario in which the variability has two distinct periods.
Assuming emission to originate in the disk, if a perturbation
appears close to the black hole, the continuum flux may first
increase, after which (at around 90-100 days) the line flux
increases. This is well described by the lag in the function G(t).
On the other side, one may expect some of the continuum to be
emitted from the line emission region (as e.g. due to free-bound
transitions), which may be described by ![]() (lag zero between
continuum and line). It is interesting that we have an additional
lag of around 600 days in the flux (
(lag zero between
continuum and line). It is interesting that we have an additional
lag of around 600 days in the flux (![]() ), which may be caused by
the perturbation seen in the flash, after which the perturbation
spreads through the disk at super-sonic velocities.
), which may be caused by
the perturbation seen in the flash, after which the perturbation
spreads through the disk at super-sonic velocities.
The line profile variations and a possible model of the spiral shocks in the disk will be presented in Paper II of this series.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f19a.eps}\hspace*{4mm...
...*{4cm}\includegraphics[width=7.5cm,clip]{14118f19e.eps}\hspace*{4cm}\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg147.png)
|
Figure 19:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f20a.eps}\hspace*{4mm...
...aphics[width=7.5cm,clip]{14118f20e.eps}\hspace*{4cm}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg148.png)
|
Figure 20:
H |
| Open with DEXTER | |
4.4 Disk versus a bipolar radial outflow
As noted in the Introduction, some models can explain the
double-peaked broad emission line profiles in 3C 390.3. As
aforementioned, a very popular model generates these lines in a
relativistic disk. However, there is some contradiction between this
model and the polarization observations of 3C 390.3. Smith et al.
(2004, 2005) proposed a two-component scattering model to explain
the polarization properties of the optical continuum and H![]() broad emission lines in Sy1 nuclei. They hypothesized that both the
compact equatorial scattering region located inside the torus and
the polar scattering regions are present in all Seyfert galaxies,
and that their polarization properties can be broadly understood in
terms of an orientation effect. On the one hand, Smith et al. (2004)
suggested that the broad emission lines originate in a rotating
emission line disk surrounded by a coplanar scattering region. Thus,
in polarization light a double-peaked profile of H
broad emission lines in Sy1 nuclei. They hypothesized that both the
compact equatorial scattering region located inside the torus and
the polar scattering regions are present in all Seyfert galaxies,
and that their polarization properties can be broadly understood in
terms of an orientation effect. On the one hand, Smith et al. (2004)
suggested that the broad emission lines originate in a rotating
emission line disk surrounded by a coplanar scattering region. Thus,
in polarization light a double-peaked profile of H![]() will be
observed, as in total light, and the degree of polarization will be
maximal in the wings of the line and minimal in the line core. The
position angle (PA) of polarization is aligned with the projected
disk rotation axis and hence with the radio source axis (e.g.
E-vector is parallel to the pc-jet axis). On the other hand, the
polarization is caused by far-field scattering in the polar
illumination cones of the circumnuclear torus (Smith et al. 2004).
In polarization light, the H
will be
observed, as in total light, and the degree of polarization will be
maximal in the wings of the line and minimal in the line core. The
position angle (PA) of polarization is aligned with the projected
disk rotation axis and hence with the radio source axis (e.g.
E-vector is parallel to the pc-jet axis). On the other hand, the
polarization is caused by far-field scattering in the polar
illumination cones of the circumnuclear torus (Smith et al. 2004).
In polarization light, the H![]() profile has only one central
peak and the position angle (PA) of polarization is perpendicular to
the projected disk rotation axis or pc-jet axis (e.g. E-vector is
perpendicular to the pc-jet axis). From spectropolarimetric
observations of 3C 390.3 in H
profile has only one central
peak and the position angle (PA) of polarization is perpendicular to
the projected disk rotation axis or pc-jet axis (e.g. E-vector is
perpendicular to the pc-jet axis). From spectropolarimetric
observations of 3C 390.3 in H![]() region taken at the 4.2 m
Wiliam Herschel telescope in 1995 and 1997, Corbett et al. (1998,
2000) obtained the following main results:
region taken at the 4.2 m
Wiliam Herschel telescope in 1995 and 1997, Corbett et al. (1998,
2000) obtained the following main results:
- a)
- the optical polarization E vector is very closely aligned with the radio source axis, as for the case of equatorial scattering region;
- b)
- in polarized light, the H
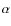 profile has a broad central peak centered
close to the systematic velocity and is also slightly asymmetric,
the blue wing being somewhat less extended than the red.
This result favors polar scattering and is inconsistent with an equatorial
scattering model because a double peak in the polarized line profile is not
observed;
profile has a broad central peak centered
close to the systematic velocity and is also slightly asymmetric,
the blue wing being somewhat less extended than the red.
This result favors polar scattering and is inconsistent with an equatorial
scattering model because a double peak in the polarized line profile is not
observed;
- c)
- The P(
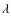 )- the percentage polarization of the continuum
changed significantly between 1995 and 1997, presumably because
there is a variable, intrinsically polarized, synchrotron contribution
to the continuum (from a pc-jet component);
)- the percentage polarization of the continuum
changed significantly between 1995 and 1997, presumably because
there is a variable, intrinsically polarized, synchrotron contribution
to the continuum (from a pc-jet component);
- 1.
- the CCF-analysis for the H
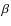 and H
and H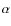 line wings
in 3C 390 did not reveal any significant delay in the variations of the line
wings with respect to the central part of the line, or relative to each
other. The flux in the H
line wings
in 3C 390 did not reveal any significant delay in the variations of the line
wings with respect to the central part of the line, or relative to each
other. The flux in the H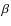 line wings and core also varied simultaneously.
These results are indicative of predominantly circular motions in the BLR and
favor a model in which the main contribution to the broad lines flux originates
in the accretion disk and not the biconical flow (Dietrich et al. 1998; Paper I);
line wings and core also varied simultaneously.
These results are indicative of predominantly circular motions in the BLR and
favor a model in which the main contribution to the broad lines flux originates
in the accretion disk and not the biconical flow (Dietrich et al. 1998; Paper I);
- 2.
- Livio & Xu (1997) demonstrated that the double-peaked lines seen in 3C 390.3 cannot be produced by two line-emitting streams, since the emission region of the far cone jet would be obscured by the optically thick accretion disk. The aforementioned simple scattering models obviously would be unable to explain the available polarimetric and optic observations.
5 Conclusion
We have presented a long-term spectroscopic monitoring campaign of
3C 390.3. We have constructed the continuum and H![]() and
H
and
H![]() light curves, performed cross correlation between the
continuum flux and line fluxes as well as between the line parts. In
addition, we have analyzed any changes in H
light curves, performed cross correlation between the
continuum flux and line fluxes as well as between the line parts. In
addition, we have analyzed any changes in H![]() and H
and H![]() line profiles and compiled mean and rms profiles. From our analysis
and inspection of the observed data, we have reached the following
conclusions:
line profiles and compiled mean and rms profiles. From our analysis
and inspection of the observed data, we have reached the following
conclusions:
- (i)
- During 1995-2007, the H
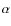 and H
and H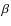 broad emission
lines and continuum varied 3-5 times. The amplitude of variability
F(var) was larger in the continuum (0.46) than in either H
broad emission
lines and continuum varied 3-5 times. The amplitude of variability
F(var) was larger in the continuum (0.46) than in either H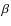 (0.38) or H
(0.38) or H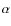 (0.35). The blue H
(0.35). The blue H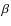 and H
and H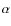 wings
were always brighter and vary slightly more strongly than those in
the red. The H
wings
were always brighter and vary slightly more strongly than those in
the red. The H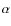 and H
and H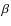 profiles varied in a way similar
to those of Sy 1 type in the maximum activity state and Sy1.8 type
in the minimum activity state.
profiles varied in a way similar
to those of Sy 1 type in the maximum activity state and Sy1.8 type
in the minimum activity state.
- (ii)
- We found that QPOs exist in the H
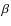 and continuum light
curve, as commonly observed for stellar-mass black holes. The
periodicity of the light curves is probably connected with some
shock waves near the supermassive black hole spreading in the outer
part of the disk, but on the other hand, we cannot exclude the
contribution of either ejection or jets to QPOs. Our results imply
that the QPO variations in the observed flux ratio of the blue to
red H
and continuum light
curve, as commonly observed for stellar-mass black holes. The
periodicity of the light curves is probably connected with some
shock waves near the supermassive black hole spreading in the outer
part of the disk, but on the other hand, we cannot exclude the
contribution of either ejection or jets to QPOs. Our results imply
that the QPO variations in the observed flux ratio of the blue to
red H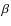 wings, of period
wings, of period  10 years (
10 years (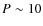 yr),
probably exist, as previously detected by Veilleux & Zheng
(1991).
yr),
probably exist, as previously detected by Veilleux & Zheng
(1991).
- (iii)
- Cross-correlation of the continuum and H
 broad emission
line fluxes shows a lag
broad emission
line fluxes shows a lag  95 days, as in both Paper I (in
1998-1999,
95 days, as in both Paper I (in
1998-1999,  100 days) and Sergeev et al. (2002, lag
100 days) and Sergeev et al. (2002, lag  89 days). There is no significant lag between both the blue and red
wings and the core, which is indicative of predominantly circular
motions in the BLR of 3C 390.3 and a disk-like geometry. For
H
89 days). There is no significant lag between both the blue and red
wings and the core, which is indicative of predominantly circular
motions in the BLR of 3C 390.3 and a disk-like geometry. For
H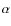 ,
we found a lag of around 120 days. This difference in
lags as well as in the FWHM of H
,
we found a lag of around 120 days. This difference in
lags as well as in the FWHM of H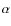 and H
and H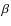 may imply that
there is some stratification in the BLR (disk) of 3C 390.3.
may imply that
there is some stratification in the BLR (disk) of 3C 390.3.
- (iv)
- The H
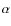 and H
and H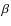 line fluxes and parts of lines are
strongly correlated with the continuum flux, indicating that the
ionizing continuum was a good extrapolation of the optical one.
line fluxes and parts of lines are
strongly correlated with the continuum flux, indicating that the
ionizing continuum was a good extrapolation of the optical one.
- (v)
- By comparing the H
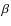 and H
and H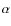 line profiles, we
found that the broad emission region has a disk-like structure,
but there probably exists a non-disk component, or also a disk-like
one of different parameters that contributes to
the line emission. More details about the line shape variation and
any possible disk structure will be given in a forthcoming paper.
line profiles, we
found that the broad emission region has a disk-like structure,
but there probably exists a non-disk component, or also a disk-like
one of different parameters that contributes to
the line emission. More details about the line shape variation and
any possible disk structure will be given in a forthcoming paper.
This work was supported by INTAS (grant N96-0328), RFBR (grants N97-02-17625 N00-02-16272, N03-02-17123, 06-02-16843, and N09-02-01136), State program ``Astronomy'' (Russia), CONACYT research grant 39560-F and 54480 (México), PROMEP/103.5/08/4722 grant and the Ministry of Science and Technological Development of Republic of Serbia through the project Astrophysical Spectroscopy of Extragalactic Objects (146002). L.C.P., W.K. and D.I. are grateful to the Alexander von Humboldt foundation for support in the frame of program ``Research Group Linkage''. We would like to thank to the anonymous referee for very useful comments.
References
- Alef, W., Gotz, M. M. A., Preuss, E., & Kellermann, K. I. 1988, A&A, 192, 53
- Alexander, T. 1997, Astronomical Time Series, ed. D. Maoz, A. Sternberg, & E. M. Leibowitz (Dordrecht: Kluwer), 163
- Alef, W., Wu, S. Y., Preuss, E., Kellermann, K. I., & Qiu, Y. H. 1996, A&A, 308, 376
- Allen, C. W. 1973, Astrophysical Quantities (London: Athlone)
- Arshakian, T. G., León-Tavares, J., Lobanov, A. P., et al. 2010, MNRAS, 401, 1231
- Barr, P., Pollard, G., Sanford, P. W., et al. 1980, MNRAS, 193, 549
- Barr, P., Willis, A. J., & Wilson, R. 1983, MNRAS, 202, 453
- Baum, S. A., Heckman, T., Bridle, A., van Breugel, W., & Miley, G. 1988, ApJS, 68, 643
- Benitez, E., Chavushyan, V. H., Raiteri, C. M., et al. 2009, Proceeding Accretion and Ejection in AGN: A Global View [arXiv:0910.0437]
- Bischoff, K., & Kollatschny, W. 1999, A&A, 345, 49
- Bochkarev, N. G., Burenkov, A. N., & Shapovalova, A. I. 1997, Astron. Astrophys. Trans., 14, 97
- Bon, E., Popovic, L. C., Gavrilovic, N., La Mura, G., & Mediavilla, E. 2009, MNRAS, 400, 924
- Clavel, J. C., & Wamsteker, W. 1987, ApJ, 320, L9
- Chakrabarti, S. K., & Wiita, P. J. 1994, ApJ, 434, 518
- Chakrabarti, S. E., Acharyya, K., & Molteni, D. 2004, A&A, 421, 1
- Corbett, E. A., Robinson, A., Axon, D. J., Young, S., & Hough, J. H. 1998, MNRAS, 296, 721
- Corbett, E. A., Robinson, A., Axon, D. J., & Young, S. 2000, MNRAS, 319, 685
- Dietrich, M., Peterson, B. M., Albrecht, P., et al. 1998, ApJS, 115, 185
- Eracleous, M., Livio, M., Halpern, J. P., & Storchi-Bergmann, T. 1995, ApJ, 438, 610
- Eracleous, M., Halpern, J. P., & Livio, M. 1996, ApJ, 459, 89
- Gaskell, C. M. 1996, ApJ, 464, L107
- Gezari, S., Halpern, J. P., & Eracleous, M. 2007, ApJS, 169, 167
- Gierlinski, M., Middleton, M., Ward, M., & Done, C. 2008, Nature, 455, 369
- Gliozzi, M., Sambruna, R. M., & Eracleous, M. 2003, ApJ, 584, 176
- Gupta, A. C., Srivastava, A. K., & Wiita, P. J. 2009, ApJ, 690, 216
- Harris, D. E., Cheung, C. C., Stawarz, L., Biretta, J. A., & Perlman, E. S. 2009, ApJ, 699, 305
- Hovatta, T., Lehto, H. J., & Tornikoski, M. 2008, A&A, 488, 897
- Inda, M., Makishima, K., Kohmura, Y., et al. 1994, ApJ, 420, 143
- Lachowicz, P., Gupta, A. C., Gaur, H., & Wiita, P. J. 2009, A&A, 506, L17
- Leahy, J. P., & Perley, R. A. 1991, AJ, 102, 537
- Leahy, J. P., & Perley, R. A. 1995, MNRAS, 277,1097
- Leighly, K. M., O'Brien, P. T., Edelson, R., et al. 1997, ApJ, 483, 767
- León-Tavares, J., Lobanov, A. P., Chavushyan, V. H., et al. 2010, ApJ, 715, 355
- Livio, M., & Xu, C. 1997, Apj, 478, L63
- Middleton, M., Done, C., Ward, M., Gierlinski, M., & Schurch, N. 2009, MNRAS, 394, 250
- Netzer, H. 1982, MNRAS, 198, 589
- O'Brien, P. T., Dietrich, M., Leighly, K., et al. 1998, ApJ, 509, 163
- Osterbrock, D. E., Koski, A. T., & Phillips, M. M. 1975, ApJ, 197, L41
- Penston, M. V., & Perez, E. 1984, MNRAS, 211, 13P
- Perez, E., Mediavilla, E., Penston, M. V., Tadhunter, C., & Moles, M. 1988, MNRAS, 230, 353
- Peterson, B. M. 1993, PASP, 105, 207
- Peterson, B. M. 1999, ASPC, 175, 49
- Peterson, B. M., & Collins II, G. W. 1983, ApJ, 270, 71
- Peterson, B. M., Pogge, R. W., Wanders, I., Smith, S. M., & Romanishin, W. 1995, PASP, 107, 579
- Popovic, L. C., Mediavilla, E., Bon, E., & Ilic, D. 2004, A&A, 423, 909
- Rokaki, E., Boisson, C., & Collin-Souffrin, S. 1992, A&A, 253, 57
- Schield, R. E., 1983, PASP, 95, 1021
- Sergeev, S. G., Pronik, V. I., Peterson, B. M., Sergeeva, E. A., & Zheng, W. 2002, ApJ, 576, 660S
- Shapovalova, A. I., Burenkov, A. N., & Bochkarev, N. G. 1996, Bull. Spec. Astrophys. Obs., 41, 28
- Shapovalova, A. I., Burenkov, A. N., Carrasco, L., et al. 2001, A&A, 376, 775
- Shapovalova, A. I., Doroshenko, V. T., Bochkarev, N. G., et al. 2004, A&A, 422, 925
- Shapovalova, A. I., Popovic, L.C., Collin, S., et al. 2008, A&A, 486, 99
- Shapovalova, A. I., Popovic, L.C., Bochkarev, N. G., et al. 2009, NewAR, 53, 191
- Smith, J. E., Robinson, A., Alexander, D. M., et al. 2004, MNRAS, 350, 140
- Smith, J. E., Robinson, A., Young, S., Axon, D. J., & Corbett, E. A. 2005, MNRAS, 359, 846
- Tao, J., Fan, J., Qian, B., & Liu, Y. 2008, AJ, 135, 737
- Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc., 79, 61
- Van Groningen, E., & Wanders, I. 1992, PASP, 104, 700
- Veilleux, S., & Zheng, W. 1991, ApJ, 377, 89
- Wamsteker W. 1981, A&A, 97, 329
- Wamsteker, W., Wang, T.-G., Schartel, N., & Vio, R. 1997, MNRAS, 288, 225
- Wozniak, P. R., Zdziarski, A. A., Smith, D., Madejski, G. M., & Johnson, W. N. 1998, MNRAS, 299, 449
- Yee, H. K., & Oke, J. B. 1981, ApJ, 248, 472
- Zheng, W. 1996, AJ, 111, 1498
Online Material
Table 1: The log of spectroscopic observations.
Table 2:
Observed continuum, the broad H![]() and
H
and
H![]() fluxes, reduced to the 6 m telescope aperture
fluxes, reduced to the 6 m telescope aperture
![]() .
.
Footnotes
- ...
lines
![[*]](/icons/foot_motif.png)
- Tables 1 and 2 are only available in electronic form at http://www.aanda.org
- ...
(2004)
![[*]](/icons/foot_motif.png)
- See Appendix A of Shapovalova et al. (2004).
All Tables
Table 3:
The estimated mean flux errors of the H![]() and H
and H![]() lines and
their segments.
lines and
their segments.
Table 4: The line widths and asymmetry measurements for the whole monitoring period, period I and II.
Table 5: Variability parameters.
Table 6:
The time lag and CCF coefficient for the
continuum and H
![]() line (total line and parts) using ZDCF
method.
line (total line and parts) using ZDCF
method.
Table 1: The log of spectroscopic observations.
Table 2:
Observed continuum, the broad H![]() and
H
and
H![]() fluxes, reduced to the 6 m telescope aperture
fluxes, reduced to the 6 m telescope aperture
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14118f01.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg33.png)
|
Figure 1: The correlation between the photometric - F(V) and spectral - F(sp) fluxes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14118f02a.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{14118f02b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg44.png)
|
Figure 2:
An example of the narrow line template for the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f03a.ps}\par\vspace*{...
...}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{14118f03c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg45.png)
|
Figure 3:
An example of the substraction of the narrow lines in
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f04a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{14118f04b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg47.png)
|
Figure 4: The estimated errors in the flux measurements as functions of the corresponding flux, in case we divided lines in 3 parts ( left panels) and 2 parts ( right panels). The correlation coefficient and the p-value are given in the upper right corner. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[origin=rb,angle=-90,width=12cm,clip]{14118f05.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg48.png)
|
Figure 5: The spectra of 3C 390.3 close to maximum ( up - observed in 2007) and minimum ( bottom - observed in 1997). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14118f06.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg60.png)
|
Figure 6:
Light curves of the continuum (top), broad H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14118f07a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{14118f07b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg61.png)
|
Figure 7:
The continuous wavelet power spectra of the
long-term light curve of the optical continuum at 5100 Å ( top) and in the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f08a.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f08c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg62.png)
|
Figure 8:
The decomposition of the continuum light curve: a) the flux
in the continuum and estimation of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f09a.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f09c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg63.png)
|
Figure 9:
The same as in Fig. 8, but for the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f10a.ps}\par\vspace*{2m...
....ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f10d.ps}\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg64.png)
|
Figure 10:
The comparison of different flux components of H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14118f11a.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg71.png)
|
Figure 11:
The comparison of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm,clip]{14118f11b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg72.png)
|
Figure 11: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm,clip]{14118f11c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg73.png)
|
Figure 11: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{14118f12a.ps}\hspace*{4mm}...
....ps}\hspace*{4mm}
\includegraphics[width=5.2cm,clip]{14118f12f.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg74.png)
|
Figure 12:
Mean and rms spectra of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f13a.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f13b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg76.png)
|
Figure 13:
JD-fluxes in the blue and red wings, and core and
for H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f14a.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{14118f14b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg86.png)
|
Figure 14:
The variation in the ratio red/blue (asterisk blue-line)
and central/blue (circles black-line) of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f15a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{14118f15b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg89.png)
|
Figure 15:
The relationships between the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14118f16a.ps}\hspace*{4mm}
\includegraphics[width=8.1cm,clip]{14118f16b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg92.png)
|
Figure 16:
Relationships between the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14118f17.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg93.png)
|
Figure 17:
CCFs for H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{14118f18a.ps}\par\vspace*{...
...\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{14118f18c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg142.png)
|
Figure 18:
CCFs between continuum and line functions |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f19a.eps}\hspace*{4mm...
...*{4cm}\includegraphics[width=7.5cm,clip]{14118f19e.eps}\hspace*{4cm}\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg147.png)
|
Figure 19:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14118f20a.eps}\hspace*{4mm...
...aphics[width=7.5cm,clip]{14118f20e.eps}\hspace*{4cm}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14118-10/Timg148.png)
|
Figure 20:
H |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


