Scattered Hα emission from a large translucent cloud G294-24

K. Lehtinen; M. Juvela; K. Mattila

doi:10.1051/0004-6361/200913982

Free Access

Issue		A&A Volume 517, July 2010


Article Number		A79
Number of page(s)		7
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/200913982
Published online		11 August 2010

A&A 517, A79 (2010)

Scattered H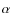 $\alpha$ emission from a large translucent cloud G294-24

K. Lehtinen - M. Juvela - K. Mattila

Observatory, Tähtitorninmäki, PO Box 14, 00014, University of Helsinki, Finland

Received 29 December 2009 / Accepted 25 March 2010

Abstract
Aims. We study an undocumented large translucent cloud, detected by means of its enhanced radiation in the SHASSA (Southern H-Alpha Sky Survey Atlas) survey. We consider whether its excess surface brightness can be explained by light scattered off the dust grains in the cloud, or whether emission from in situ ionized gas is required. In addition, we aim to determine the temperature of dust, the mass of the cloud, and its possible star formation activity.
Methods. We compare the observed H $\alpha$ surface brightness of the cloud with predictions of a radiative transfer model. We use the WHAM (Wisconsin H-Alpha Mapper) survey as a source for the Galactic H $\alpha$ interstellar radiation field illuminating the cloud. Visual extinction through the cloud is derived using 2MASS J, H, and K band photometry. We use far-IR ISOSS (ISO Serendipitous Survey), IRAS, and DIRBE data to study the thermal emission of dust. The LAB (The Leiden/Argentine/Bonn Galactic HI Survey) is used to study 21 cm HI emission associated with the cloud.
Results. Radiative transfer calculations of the Galactic diffuse H $\alpha$ radiation indicate that the surface brightness of the cloud can be explained solely by radiation scattered off dust particles in the cloud. The maximum visual extinction through the cloud is about 1.2 mag. The cloud is found to be associated with 21 cm HI emission at a velocity $\sim$ -9 km s^-1. The total mass of the cloud is about 550-1000 $M_{\odot}$ . There is no sign of star formation in this cloud. The distance of the cloud is estimated from the Hipparcos data to be $\sim$ 100 pc.

Key words: ISM: clouds - dust, extinction - infrared: ISM

1 Introduction

del Burgo & Cambrésy (2006) were the first to report on detection of diffuse H $\alpha$ emission in a molecular cloud. They detected an excess surface brightness over the cloud LDN1780 of intensity $\sim$ 1-4 rayleigh (one rayleigh (R) being equivalent to $2.4\times 10^{-7}$ erg cm^-2 s^-1 sr^-1 at the wavelength of H $\alpha$ emission). They interpreted the surface brightness as a result of enhanced in situ cosmic ray ionization. However, Mattila et al. (2007) showed that the H $\alpha$ surface brightness observed in LDN1780 can be explained solely in terms of scattered H $\alpha$ radiation. In addition, Mattila et al. found several other molecular clouds that had excess H $\alpha$ emission relative to the surroundings of the cloud. In some cases, a cloud was not detected in H $\alpha$ images, although other physically similar clouds do. These observations can be naturally explained in the framework of scattered H $\alpha$ radiation by varying the proportions of general diffuse in situ H $\alpha$ emission either in front of or behind the dust cloud.

While comparing the all-sky H $\alpha$ and 100 $\mu$ m IRAS maps, we noticed a large cloud visible in both maps. The Galactic coordinates of the cloud are $l \approx 294\hbox{$^\circ$ }$ , $b \approx -24\hbox{$^\circ$ }$ . The maximum excess surface brightness of H $\alpha$ is about 2.4 R. With a size of about 1.4 $^\circ$ $\times$ 4.9 $^\circ$ , the cloud is the largest dust cloud visible in the light of scattered H $\alpha$ emission known to us. Hereafter the cloud is called G294-24.

2 Observations and calculations

$\begin{figure} \par\includegraphics[width=15cm,clip]{13982fg1.eps} \end{figure}$

Figure 1:

Map of visual extinction a) map of 644/677 nm continuum intensity, b) map of IRAS 100 $\mu$ m intensity and c) and map of H $\alpha$ intensity d). The value of background at each wavelength was determined within the circle, and then subtracted from the maps. The line in panel c) shows the location of the slew of the ISO Serendipitous Survey (ISOSS). In panel a), dots indicate the Hipparcos stars, while the ellipse delineates the extent of the cloud.

Open with DEXTER

Dust grains in the cloud G294-24 are seen in the light of scattered and emitted radiation. In addition, dust grains cause extinction of light of those stars which are located behind the cloud. Atomic hydrogen gas in the cloud is expected to be seen in the 21 cm spin-flip line. We are studying these components by utilizing different data archives.

2.1 H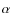 $\alpha$ surface brightness

We obtained the H $\alpha$ data from the SHASSA (Southern H-Alpha Sky Survey Atlas) survey (Gaustad et al. 2001), which is incorporated into the all-sky composite map by Finkbeiner (2003). The data were re-gridded into a regular grid in Galactic coordinate system, using a pixel size of $3.4\hbox{$^\prime$ }\times3.4\hbox{$^\prime$ }$ , which gives the same pixel area as the original HEALPix data. The H $\alpha$ data have a spatial resolution of ${\it FWHM}=6\hbox{$^\prime$ }$ . The intensities are given in units of rayleigh (R).

2.2 644/677 nm surface brightness

The SHASSA survey includes continuum images taken with a dual-band (644 and 677 nm) notch filter. In the original SHASSA survey, these images were used to subtract continuum emission from the H $\alpha$ images. In the case of dust clouds, these continuum images detect diffuse interstellar radiation scattered off the dust clouds. With a pixel size of 47.6 $^{\prime\prime}$ , the low surface brightness of the cloud is superimposed by numerous undersampled stars, which cannot be removed by fitting the stars with the point spread function of the instrument. To remove the stars, we replaced each map pixel with a mean value over a $9\times9$ pixel area around the pixel in question, using only those pixels that occupy the lowest 30% of the intensity histogram. The resolution of the image was then about 7.2 $^\prime$ . Figure 1b shows the continuum image after most of the stars were removed. Some residuals remain in place of the brightest stars. The intensity of the continuum surface brightness in SHASSA for the 644/677 nm filter is given in rayleigh units. This has been scaled for the purpose of background subtraction from the H $\alpha$ filter band. The physical units for the continuum surface brightness are R/ $\AA$ and the value depends on the width of the filter. Thus, we cannot compare the absolute intensities of the 644/677 nm and H $\alpha$ images from the SHASSA survey.

2.3 IRAS/IRIS and ISOSS (ISO Serendipity Survey) far-IR data

We used the 100 $\mu$ m IRIS data and the 170 $\mu$ m ISOSS data to derive equilibrium temperature and column density of the ``big classical'' dust grains in the cloud. IRIS data set (Miville-Deschênes & Lagache 2005) is an improved version of the all-sky IRAS/ISSA data.

The 170 $\mu$ m slew data of the ISOPHOT instrument aboard the ISO satellite were assembled into the ISOPHOT Serendipity Survey data set by Stickel et al. (2007). It covers $\sim$ 15% of the sky, mapped with a grid size of 22 $.\!\!^{\prime\prime}$ 4, and a few slews cover our cloud. The one that we used in our data analysis is shown in Fig. 1c.

2.4 COBE/DIRBE far-IR data

Because of the large size of the cloud, it is resolved in DIRBE data, which have a beam size of about 0.7 $^\circ$ . We thus used DIRBE data at 100 $\mu$ m, 140 $\mu$ m, and 240 $\mu$ m to obtain another estimate of the temperature and column density of the ``big classical'' dust grains.

2.5 Visual extinction

We compiled an extinction map of the cloud by applying the NICER (Near Infrared Color Excess Revised) method of Lombardi & Alves (2001), which is an optimized color excess technique using data in three bands simultaneously. Our data comprise J, H, and $K_{\rm s}$ band magnitudes from the 2MASS archive. The intrinsic colors of stars were determined in an area having a local minimum in the 100 $\mu$ m IRIS map, located at $l=292.0\hbox{$^\circ$ }$ , $b=-22.3\hbox{$^\circ$ }$ .

The grid used in the extinction map is the same as that of the H $\alpha$ map. The extinction value at each grid point is a weighted mean of the individual extinctions of stars obtained by using a Gaussian with a width of ${\it FWHM}=6\hbox{$^\prime$ }$ as a weighting function.

2.6 Hipparcos data

Owing to the large size and low extinction of the cloud, the Hipparcos data (ESA 1997) enable us to estimate the distance of the cloud. We collected Hipparcos data over $5\hbox{$^\circ$ }\times5\hbox{$^\circ$ }$ area towards the cloud. The intrinsic colors of stars as a function of spectral and luminosity class were used to derive a color excess E(B-V) for each Hipparcos star in the area.

2.7 Hydrogen 21 cm line emission data

The ``The Leiden/Argentine/Bonn (LAB) Survey of Galactic HI'' dataset (Kalberla et al. 2005; Bajaja et al. 2005) was used to search for hydrogen emission related to the cloud. The angular resolution of the LAB survey is $HPBW\approx0.6\hbox{$^\circ$ }$ .

2.8 Subtraction of background sky

When studying extinction, scattering and emission associated solely with the cloud G294-24, we need to subtract the background, determined in the immediate vicinity of G294-24. Figure 1 shows the circular area that was used to estimate the background for each dataset. The background values of 100 $\mu$ m intensity, extinction A_V, and H $\alpha$ brightness are about 4.1 MJy sr^-1, 0.5 mag, and 1.0 R, respectively.

3 Results

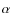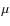3.1 Comparison of H $\alpha$ , I(100 $\mu$ m), A_V, and 644/677 nm maps

Inspection of Fig. 1 shows that the oval cloud at the center of the images is visible in extinction (panel a), in scattered light caused by dust (panel b), and in thermal emission by dust (panel c). The same cloud is also seen in the light of the H $\alpha$ line (panel d). The maximum excess H $\alpha$ surface brightness of the cloud above the background is about 2.0 rayleighs (R), which is similar to the brightness of the other H $\alpha$ scattering clouds, 1-3 R, as discovered by Mattila et al. (2007). We show in Sect. 3.8 that the detected H $\alpha$ radiation can be explained solely in terms of scattered radiation.

In addition to the central oval and the SW leg that are seen in the A_V data, the H $\alpha$ map shows a blob-like structure at coordinates $l=295\hbox{$^\circ$ }$ , $b=-26\hbox{$^\circ$ }$ , which is not seen in any of the other maps. The maximum surface brightness of the blob is about 7 R, and thus the blob cannot be scattered light (see Sect. 3.8). The emission must instead be in situ emission from hot, ionized gas, possibly unconnected to the G294-24 dust cloud. Similar small size ( $\la$ $1\hbox{$^\circ$ }$ ) H $\alpha$ enhancements at latitudes $\vert b\vert\ge10\hbox{$^\circ$ }$ were reported by Reynolds et al. (2005) in the northern sky. Many of them have no obvious embedded or associated ionizing star. This is also the case for our H $\alpha$ blob. This H $\alpha$ enhancement could be associated with a planetary nebula, or be ionized by either a O or early B type star, or a hot evolved low-mass star (Reynolds et al. 2005). The SIMBAD database does not list any of these kinds of objects within a distance of 1 $^\circ$ from the center of the blob. The nearest O or early B type star in SIMBAD is the B2 type star CD-80 228 ( $l=292.58\hbox{$^\circ$ }$ , $b=-27.43\hbox{$^\circ$ }$ ), identified as EC 06387-8045, at a distance of 4.4 kpc (Kilkenny et al. 1995). Association of the blob with the star CD-80 228 would mean that the blob is located much further away than G294-24 (see Sect. 3.5).

The correlation plots between H $\alpha$ , $I(100~\mu$ m), I(644 nm/677 nm), and A_V data are shown in Fig. 2, after subtracting the background values from each dataset. To correlate data sets produced in a compatible way, both sets of data in panel Fig. 2c are from the original SHASSA survey (Gaustad et al. 2001), and analyzed as described above in Sect. 2.2. The absolute intensity calibration performed by our analysis method in Fig. 2c is inaccurate, as indicated by a calibration difference of a factor of two between the Finkbeiner's (2003) (WHAM calibrated) H $\alpha$ data (panels a and b) and H $\alpha$ data in panel c. However, the linear relation in panel c supports the idea that the H $\alpha$ intensity is also mainly scattered light. In the following, our analysis of the H $\alpha$ surface brightness is based solely on Finkbeiner's (2003) data, because its calibration is based on the accurately calibrated WHAM survey (Haffner et al. 2003).

3.2 Temperature and column density of dust

Equilibrium temperature of dust particles along the ISOSS slew was derived from the ISOSS and IRIS far-IR data, after subtracting an estimate of the background intensity, assumed to be a mean value over the circular region shown in Fig. 1c. We assume a frequency dependence of $\nu^{2}$ for the emissivity index. The ISOSS data were convolved to the resolution of the IRIS data, which is given by a Gaussian ${\it FWHM}=4\hbox{$^\prime$ }$ . The temperature along the ISOSS slew (see Fig. 1c) is plotted in Fig. 3 as a solid line, showing that the temperature decreases from about 18.7 K at the northern edge of the cloud to a minimum of about 17.5 K at the center.

The 100 $\mu$ m optical depth, derived with the formula

$\begin{displaymath}\tau(100~\mu{\rm m})=I_{\nu}(100~\mu{\rm m})/B_{\nu}(T_{{\rm dust}}) \end{displaymath}$

(1)

is shown in Fig. 3 as a dotted line. The maximum optical depth is $\tau$ (100 $\mu$ m $)\approx2\times10^{-3}$ . The distribution of A_Valong the same slew is shown in Fig. 3 as a dash-dotted line. The maximum of $\tau$ (100 $\mu$ m) is located to the south of the 100 $\mu$ m surface brightness maximum, at a position where A_Vhas its maximum.

To determine the dust temperature from the DIRBE maps, we first subtracted the estimated background intensities from the DIRBE maps, derived in the circular area shown in Fig. 1. The dust temperature was then derived by fitting the 100 $\mu$ m, 140 $\mu$ m, and 240 $\mu$ m intensities with a modified black body having a $\nu^{2}$ emissivity law. The minimum temperature of the cloud is $\sim$ $16.6\pm1.5$ K, in agreement with the minimum temperature derived from ISOSS and IRAS data. It is obvious that we are unable to resolve any possible colder condensations in the cloud due to the low resolution of DIRBE data. Figure 4 shows a map of the 100 $\mu$ m optical depth based on DIRBE data, derived using Eq. (1).

The total mass (gas plus dust) of the cloud was calculated with the formula

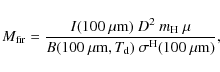
$\begin{displaymath}M_{{\rm fir}} = \frac{ I({\rm 100~\mu{\rm m}})~ D^{2}~ m_{\r... ...0~\mu {\rm m}, T_{\rm d})~ \sigma^{\rm H}(100~\mu {\rm m}) }, \end{displaymath}$

(2)

where $I_{\rm 100~\mu m}$ is the observed flux density, D is the distance, $m_{\rm H}$ is the mass of a hydrogen atom, $\mu$ is the mean molecular weight (1.4) with respect to the mass of hydrogen atom, accounting for 10% helium by number, B(100 $\mu$ m, $T_{\rm d}$ ) is the black-body emission at temperature $T_{\rm d}$ , and $\sigma^{\rm H}$ is the absorption cross section per H-nucleus for which we used the value $2.4\times 10^{-25}$ cm² (Lehtinen et al. 2007, the case L1642 C in Table 1). The total mass of the cloud is about 1000 $M_{\odot}$ for the distance of 100 pc.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg2.eps} \end{figure}$	Figure 2: The observed H $\alpha$ surface brightness as a function of IRAS 100 $\mu$ m intensity a), visual extinction b) and 644/677 nm intensity c). The background values have been subtracted from each dataset. Note that the H $\alpha$ data in panels a) and b) are from Finkbeiner (2003), while in panel c) the data are from Gaustad et al. (2001).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{13982fg3.eps} \end{figure}$

Figure 3:

Solid line: temperature of dust, $T_{\rm d}$ , along the ISOSS slew shown in Fig. 1c, derived from 100 $\mu$ m IRAS and 170 $\mu$ m ISOSS data. Dotted line: 100 $\mu$ m optical depth, $\tau(100~\mu$ m), along the same slew. Dashed line: 100 $\mu$ m surface brightness, $I(100~\mu$ m), along the same slew, divided by $1.4\times 10^4$ . Dash-dotted: visual extinction, A_V, along the same slew, divided by $7\times 10^2$ .

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{13982fg4.eps} \end{figure}$	Figure 4: 100 $\mu$ m optical depth, derived from 100 $\mu$ m, 140 $\mu$ m, and 240 $\mu$ m DIRBE data. The ellipse, which is the same as in Fig. 1, delineates the area that was used to determine the total mass of the cloud.
Open with DEXTER

3.3 Visual extinction

The visual extinction map is shown in Fig. 1a. Maximum visual extinction is $\sim$ 1.2 mag over the background. The typical error in the extinction map is 0.2 mag.

We can use the visual extinction to estimate the total hydrogen column density, $N({\rm H}) \equiv N({\rm HI})+2N({\rm H}_2)$ . As a starting point, we adopt the value $N({\rm H})/E(B-V)=5.8\times 10^{21}$ cm^-2 mag^-1 for diffuse clouds (Bohlin et al. 1978), together with A_V/E(B-V)=3.1 (``diffuse dust'') to obtain $N({\rm H})/A_V\equiv\beta=1.9\times 10^{21}$ cm^-2 mag^-1.

The total cloud mass can then be derived with the formula

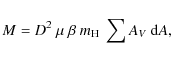
$\begin{displaymath}M = D^2~ \mu~ \beta~ m_{\rm H}~ \sum A_V~ {\rm d}A, \end{displaymath}$

(3)

where D is the cloud distance, $m_{\rm H}$ is the hydrogen mass, dA is the area of one pixel in the A_V map in steradian, and the summation is evaluated over the whole cloud (inside the ellipse in Fig. 1a). This procedure gives a total mass of $\sim$ $550~M_{\odot}$ .

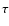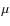3.4 A_V versus $\tau$ (100 $\mu$ m)

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg7.eps} \end{figure}$	Figure 5: Relation between 100 $\mu$ m optical depth and visual extinction. Typical 1- $\sigma$ errors are shown.
Open with DEXTER

Figure 5 shows the relation between visual extinction and 100 $\mu$ m optical depth, after the A_V map has been convolved to the resolution of the DIRBE data. The slope of the fit gives the emissivity $\epsilon=1.5\pm0.3\times 10^{-3}$ mag^-1. For a $\nu^{-2}$ emissivity law, the emissivity at 200 $\mu$ m is $4.0 \pm 0.8\times 10^{-4}$ mag^-1. The observed value agrees with theoretical values of $\epsilon(200~\mu$ m) for diffuse interstellar matter (Désert et al. 1990; Dwek et al. 1997; Cambrésy et al. 2001; Li & Draine 2001; see Lehtinen et al. 2007 for a compilation of values of $\epsilon(200~\mu$ m)).

3.5 Distance based on Hipparcos data

Figure 6 shows E(B-V) versus distance for the stars shown in Fig. 1a. Color excess E(B-V) has been converted into A_V by assuming a normal reddening law, A_V/E(B-V)=3.1. For stars that are within the cloud area and have E(B-V)>0.1, the minimum distance is $\sim$ 100 pc. Thus, we adopt a distance of 100 pc for G294-24, which is less than the distance of 150 pc to the adjacent Chamaeleon region (Knude & Høg 1998).

3.6 HI emission line data

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg5.eps} \end{figure}$	Figure 6: The reddening E(B-V) of Hipparcos stars as a function of their distances for the stars marked in Fig. 1a. The stars that are shown as filled circles are within the ellipse in Fig. 1a. The vertical line is at a distance of 100 pc.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg8.eps} \end{figure}$	Figure 7: Spectrum of 21 cm hydrogen line at the position $l=294.0\hbox {$^\circ $ }$ , $b=-24.5\hbox {$^\circ $ }$ . Histogram shows the observed spectrum, the three Gaussian functions fitted to the observed spectrum are shown as dotted lines, while the solid line shows the combination of the three Gaussians. The brightest component is related to the cloud G294-24.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg9.eps} \end{figure}$	Figure 8: Map of line area ([K km s^-1]) of 21 cm HI emission from the cloud G294-24. The ellipse, which is the same as in Fig. 1, delineates the area used to determine the atomic hydrogen mass of the cloud.
Open with DEXTER

Figure 7 shows a HI spectrum from the LAB survey towards the position $l=294.0\hbox {$^\circ $ }$ , $b=-24.5\hbox {$^\circ $ }$ . Velocity-longitude diagrams show that the strength of the narrow component at $\sim$ -9 km s^-1 follows the intensity of the far-IR emission of G294-24. The component at $\sim$ 4 km s^-1 is from gas in the Galactic plane. We fit the spectrum in Fig. 7 with three Gaussian functions, and use the fit as a template for fits at other Galactic coordinates; the width of the narrow line at $\sim$ -9 km s^-1 is kept constant, and the velocities of the narrow components at $\sim$ -9 km s^-1 and $\sim$ 4 km s^-1are allowed to vary by $\pm$ 3 km s^-1. Figure 8 shows a map of the line area of the narrow component at $\sim$ -9 km s^-1. The oval G294-24 cloud and the SW leg are seen. The blob, seen at coordinates $l=295.0\hbox{$^\circ$ }$ , $b=-26\hbox{$^\circ$ }$ on the H $\alpha$ map, cannot be seen as a separate entity in the LAB data, lending support to the idea that the blob is ionized gas. The maximum of line area is located on the eastern side of the cloud, in contrast to the maximum of 100 $\mu$ m optical depth, which is located on the western side.

The column density (atoms per cm^-2) of atomic hydrogen can be obtained from (see e.g., Verschuur 1974)

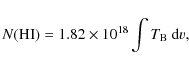
$\begin{displaymath}N({\rm HI}) = 1.82\times 10^{18} \int T_{\rm B}~ {\rm d}v, \end{displaymath}$

(4)

where $T_{\rm B}$ is the brightness temperature and the integral is line area in units of K km s^-1, and low optical depth is assumed. The total atomic hydrogen mass of the cloud, integrated over the ellipse in Fig. 8, is about 41 $M_{\odot}$ . Thus, the atomic hydrogen mass of the cloud is 4%-7% of the total mass of the cloud.

The large-scale ¹²CO(J=1-0) survey of the Chamaeleon region by Mizuno et al. (2001) shows a weak, isolated region near the center of G294-24, seen only in the velocity range 2-6 km s^-1. The integrated intensity of ¹²CO(J=1-0) emission towards the cloud is estimated to be $\sim$ 2 K km s^-1(Fig. 1 of Mizuno et al.). The possible relation of the CO emission with the cloud G294-24 has to be studied with observations of higher angular resolution.

3.7 IRAS or 2MASS point sources

We checked the IRAS point source catalog for objects that have spectral energy distribution typical of young stellar objects. There are several 100 $\mu$ m only sources in the cloud. They are probably small cirrus structures seen as points sources by IRAS at 100 $\mu$ m, and we do not consider them further here. The only source that has fluxes measured at least at the two longest IRAS wavelengths is IRAS 08048-8211, which was identified as a galaxy by Buta (1995).

We compiled a color-color diagram (J-H versus H-K magnitudes) for all the stars with magnitude errors smaller than 0.05 mag at J, H, and K band. There is no star within the cloud area that exhibits a significant infrared excess above the color indices that can be explained by interstellar reddening.

Based on the non-existence of IRAS point sources and 2MASS objects with colors characteristic of young stellar objects, we conclude that the cloud is devoid of star formation.

3.8 Radiative transfer calculations

The maximum possible surface brightness of any Galactic dust cloud, due to scattering, is limited by the average all-sky H $\alpha$ surface brightness of $\sim$ 8 R. Since the H $\alpha$ excess surface brightness of G294-24 of $\sim$ 2.4 R is well below this value, we conclude that it can be explained solely by scattered radiation. To verify this assumption, we simulated scattered H $\alpha$ radiation with Monte Carlo radiative transfer calculations (Mattila 1970; Juvela & Padoan 2003; Juvela 2005). We used the WHAM Northern Sky Survey (Haffner 2003) to derive the intensity of the northern H $\alpha$ background sky illuminating the model cloud. The missing southern sky was recreated by assuming symmetry about the Galactic latitude and longitude. The physical model of the cloud is a spherical, homogeneous cloud with A_V=1.2 mag of visual extinction through the cloud center. Properties of dust particles are based on Draine's (2003) ``Milky Way'' dust model, with albedo a=0.67 and asymmetry parameter g=0.5 at the wavelength of the H $\alpha$ line. For more details of applying Monte Carlo method to the scattering of H $\alpha$ radiation, we refer to Mattila et al. (2007).

A general formula for the differential surface brightness of H $\alpha$ light towards a dust cloud, measured over the brightness of the adjacent sky, is

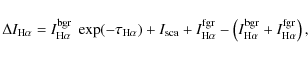
$\begin{displaymath}\Delta I_{\rm H\alpha} = I_{\rm H\alpha}^{\rm bgr}~\exp(-\tau... ...(I_{\rm H\alpha}^{\rm bgr} + I_{\rm H\alpha}^{\rm fgr}\right), \end{displaymath}$

(5)

where the first term on the right-hand side is the intensity of emission coming from behind the cloud attenuated by the optical depth through the cloud, the second term is the intensity of radiation scattered off the cloud, the third term is the intensity of emission between the cloud and the observer, and the term in parenthesis is the intensity of sky adjacent to the cloud. The radiative transfer calculations provide us with the value of $I_{\rm sca}$ as a function of optical depth through the cloud.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg6.eps} \end{figure}$	Figure 9: Intensity of H $\alpha$ surface brightness as a function of visual extinction. Dots are the observed values of intensity difference $\Delta I_{\rm H\alpha }$ . Dotted line: $I_{\rm sca}$ . Dashed line: $I_{\rm H\alpha}^{\rm bgr}(\exp(-\tau_{\rm H\alpha})-1)$ . Solid line: sum of the previous two lines, i.e., $\Delta I_{\rm H\alpha }$ .
Open with DEXTER

We have no a priori information about the relative values of $I_{\rm H\alpha}^{\rm bgr}$ and $I_{\rm H\alpha}^{\rm fgr}$ . Thus, in the model we use a free parameter, $k_{\rm bgr}$ , which is defined as

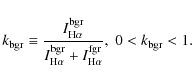
$\begin{displaymath}k_{\rm bgr} \equiv \frac{ I_{\rm H\alpha}^{\rm bgr} } { I_{... ...}^{\rm bgr} + I_{\rm H\alpha}^{\rm fgr} }, \; 0<k_{\rm bgr}<1. \end{displaymath}$

(6)

Figure 9 shows the observed intensity difference, $\Delta I_{\rm H\alpha }$ , and the results of radiative transfer calculations for two values of $k_{\rm bgr}$ . The dotted lines show the scattered intensity $I_{\rm sca}$ , the dashed lines show the calculated $I_{\rm H\alpha}^{\rm bgr}(\exp(-\tau_{\rm H\alpha})-1)$ , and the thick solid line is the sum of them both, i.e., $\Delta I_{\rm H\alpha }$ . The dashed lines indicate the surface brightness of the cloud, relative to the background sky, in the absence of scattering (a=0); the cloud would be seen in absorption. The case $k_{\rm bgr}=1.0$ provides a good fit to the data. Because of the high noise level of the data, we cannot determine an accurate value for the parameter $k_{\rm bgr}$ , although a value of about 0.5 must be a lower limit. Thus, we verify that the observed H $\alpha$ surface brightness can be explained solely by scattered radiation. The agreement also shows that the adopted dust scattering parameters of the Draine (2003) model are realistic.

In addition, we used the above-mentioned model cloud in radiative transfer calculations of continuum radiation (Juvela & Padoan 2003), giving us the surface brightness of the cloud at far-infrared wavelengths. The interstellar radiation field surrounding the cloud is taken from Mathis et al. (1983). Properties of dust particles are based on Draine's (2003) ``Milky Way'' dust model, not including stochastically heated dust grains. The derived 100 $\mu$ m, 170 $\mu$ m, and 240 $\mu$ m maximum surface brightnesses are about 12 MJy sr^-1, 24 MJy sr^-1, and 19 MJy sr^-1, respectively. The observed maximum surface brightnesses above the background are about 13 MJy sr^-1, 25 MJy sr^-1, and 21 MJy sr^-1, respectively. We then derived the dust temperature using the 100 $\mu$ m and 170 $\mu$ m maps. The minimum temperature is about 17.6 K, in good agreement with the temperature derived from IRIS and ISOSS data, of about 17.5 K (see Sect. 3.2).

4 Conclusions

We have studied the general properties of an undocumented large, nearby (distance $\sim$ 100 pc) translucent cloud. The cloud is without star formation, and thus illuminated only by the general interstellar radiation field. We have measured a drop in the temperature of the dust particles of about 1.2 K between the edge and the center of the cloud, the minimum dust temperature being $\sim$ 17.5 K. The total mass of the cloud is about 550-1000 $M_{\odot}$ . The cloud is detected in the 21 cm HI spin-flip line, and the atomic hydrogen mass of the cloud is about 40 $M_{\odot}$ . The excess of diffuse H $\alpha$ surface brightness of the cloud over the background sky can be naturally explained as the general interstellar radiation field being scattered off the dust grains.

Note added in proof

After acceptance of our article Knude derived a distance of 217 $\pm$ 26 pc for the cloud G294-24. Consequently, the mass of the cloud would be about 4.7 times higher than the value derived by us. No other conclusion of our article is affected by this new distance estimate. The method used by Knude is described in [arXiv:1006.3676] (Knude, J. 2010, A&A, submitted).

Acknowledgements

The work of K.L., M.J. and K.M. has been supported by the Finnish Academy through grants Nos. 1204415, 1210518, 1201269 and 117206, which is gratefully acknowledged. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This publication uses data from the Southern H-Alpha Sky Survey Atlas (SHASSA), which is supported by the National Science Foundation. The Wisconsin H-Alpha Mapper is funded by the National Science Foundation. This research has made use of SAOImage DS9, developed by Smithsonian Astrophysical Observatory

References

Bajaja, E., Arnal, E. M., Larrarte, J. J., et al. 2005, A&A, 440, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
del Burgo, C., & Cambrésy, L. 2006, MNRAS, 368, 1463 [NASA ADS] [CrossRef] [Google Scholar]
Buta, R. 1995, ApJS, 98, 739 [NASA ADS] [CrossRef] [Google Scholar]
Cambrésy, L., Boulanger, F., Lagache, G., & Stepnik, B. 2001, A&A, 375, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
Draine, B. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
Dwek, E., Arendt, R. G., Fixsen, D. J., et al. 1997, ApJ, 475, 565 [NASA ADS] [CrossRef] [Google Scholar]
ESA, The Hipparcos Cataloque 1997, ESA SP-1200 [Google Scholar]
Finkbeiner, D. P. A. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
Gaustad, J. E., McCullough, P. R., Rosing, W., & Van Buren, D. 2001, PASP, 113, 1326 [NASA ADS] [CrossRef] [Google Scholar]
Goerigk, W., Mebold, U., Reif, K., Kalberla, P. M. W., & Velden, L. 1983, A&A, 120, 63 [NASA ADS] [Google Scholar]
Haffner, L. M., Reynolds, R. J., Tufte, S. L., et al. 2003, ApJS, 149, 405 [NASA ADS] [CrossRef] [Google Scholar]
Juvela, M., & Padoan, P. 2003, A&A, 397, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Juvela, M. 2005, A&A, 440, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kilkenny, D., Luvhimbi, E., O'Donoghue, D., et al. 1995, MNRAS, 276, 906 [NASA ADS] [CrossRef] [Google Scholar]
Knude, J., & Høg, E. 1998, A&A, 338, 897 [NASA ADS] [Google Scholar]
Lehtinen, K., Juvela, M., Mattila, K., Lemke, D., & Russeil, D. 2007, A&A, 466, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [NASA ADS] [CrossRef] [Google Scholar]
Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
Mattila, K. 1970, A&A, 9, 53 [NASA ADS] [Google Scholar]
Mattila, K., Juvela, M., & Lehtinen, K. 2007 ApJ, 654, L131 [Google Scholar]
Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJSS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
Mizuno, A., Yamaguchi, R., Tachihara, K., et al. 2001, PASJ, 53, 1071 [NASA ADS] [CrossRef] [Google Scholar]
Reynolds, R. J., Chaudhary, V., Madsen, G. J., & Haffner, L. M. 2005, AJ, 129, 927 [NASA ADS] [CrossRef] [Google Scholar]
Stickel, M., Krause, O., Klaas, U., & Lemke, D. 2007, A&A, 466, 1205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Verschuur, G. L. 1974, Interstellar Neutral Hydrogen and its Small-Scale Structure, In Galactic and Extragalactic Radio Astronomy, ed. G. L. Verschuur, & K. I. Kellermann (Springer-Verlag), 27 [Google Scholar]

Footnotes

... G294-24: Present address: Department of Physics, Division of Geophysics and Astronomy, PO Box 64, 00014 University of Helsinki, Finland.
...2003): http://skymaps.info

All Figures

$\begin{figure} \par\includegraphics[width=15cm,clip]{13982fg1.eps} \end{figure}$	Figure 1: Map of visual extinction a) map of 644/677 nm continuum intensity, b) map of IRAS 100 $\mu$ m intensity and c) and map of H $\alpha$ intensity d). The value of background at each wavelength was determined within the circle, and then subtracted from the maps. The line in panel c) shows the location of the slew of the ISO Serendipitous Survey (ISOSS). In panel a), dots indicate the Hipparcos stars, while the ellipse delineates the extent of the cloud.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg2.eps} \end{figure}$	Figure 2: The observed H $\alpha$ surface brightness as a function of IRAS 100 $\mu$ m intensity a), visual extinction b) and 644/677 nm intensity c). The background values have been subtracted from each dataset. Note that the H $\alpha$ data in panels a) and b) are from Finkbeiner (2003), while in panel c) the data are from Gaustad et al. (2001).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{13982fg3.eps} \end{figure}$	Figure 3: Solid line: temperature of dust, $T_{\rm d}$ , along the ISOSS slew shown in Fig. 1c, derived from 100 $\mu$ m IRAS and 170 $\mu$ m ISOSS data. Dotted line: 100 $\mu$ m optical depth, $\tau(100~\mu$ m), along the same slew. Dashed line: 100 $\mu$ m surface brightness, $I(100~\mu$ m), along the same slew, divided by $1.4\times 10^4$ . Dash-dotted: visual extinction, A_V, along the same slew, divided by $7\times 10^2$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{13982fg4.eps} \end{figure}$	Figure 4: 100 $\mu$ m optical depth, derived from 100 $\mu$ m, 140 $\mu$ m, and 240 $\mu$ m DIRBE data. The ellipse, which is the same as in Fig. 1, delineates the area that was used to determine the total mass of the cloud.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg7.eps} \end{figure}$	Figure 5: Relation between 100 $\mu$ m optical depth and visual extinction. Typical 1- $\sigma$ errors are shown.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg5.eps} \end{figure}$	Figure 6: The reddening E(B-V) of Hipparcos stars as a function of their distances for the stars marked in Fig. 1a. The stars that are shown as filled circles are within the ellipse in Fig. 1a. The vertical line is at a distance of 100 pc.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg8.eps} \end{figure}$	Figure 7: Spectrum of 21 cm hydrogen line at the position $l=294.0\hbox {$^\circ $ }$ , $b=-24.5\hbox {$^\circ $ }$ . Histogram shows the observed spectrum, the three Gaussian functions fitted to the observed spectrum are shown as dotted lines, while the solid line shows the combination of the three Gaussians. The brightest component is related to the cloud G294-24.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg9.eps} \end{figure}$	Figure 8: Map of line area ([K km s^-1]) of 21 cm HI emission from the cloud G294-24. The ellipse, which is the same as in Fig. 1, delineates the area used to determine the atomic hydrogen mass of the cloud.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{13982fg6.eps} \end{figure}$	Figure 9: Intensity of H $\alpha$ surface brightness as a function of visual extinction. Dots are the observed values of intensity difference $\Delta I_{\rm H\alpha }$ . Dotted line: $I_{\rm sca}$ . Dashed line: $I_{\rm H\alpha}^{\rm bgr}(\exp(-\tau_{\rm H\alpha})-1)$ . Solid line: sum of the previous two lines, i.e., $\Delta I_{\rm H\alpha }$ .
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Scattered H emission from a large translucent cloud G294-24